ВВЕДЕНИЕ
Волны, локализованные вблизи и бегущие вдоль ребра упругого твердого клина, принято называть клиновыми. Они относятся к фундаментальным типам акустических волн, существующим в твердых телах. Большинство из таких типов обнаружено более века тому назад. Тем не менее, клиновые волны были найдены на удивление поздно – лишь в 1972 г. [1–3]. С тех пор опубликовано уже более 200 статей, посвященных их теоретическому и экспериментальному изучению. Такие исследования продолжаются и в настоящее время – см., например, [4–9]. В клиньях со свободными гранями и углом при вершине ${{\theta }_{w}}$ обсуждаемые моды существуют лишь в ограниченном угловом диапазоне ${{\theta }_{w}} < \pi .$ Как локализованные они отсутствуют, в частности, вблизи вершины трещины с плоскопараллельными берегами [10]. Такая геометрия соответствует предельному случаю клина с углом, равным $2\pi .$
Целью настоящей работы является демонстрация новой возможности существования локализованных волн в твердом клине с углом, близким к $2\pi .$ Правомерность этого утверждения о новизне следует из представленного ниже сравнения полученных результатов с литературными данными. Для реализации указанной возможности необходимо, чтобы вне твердого клина находился газ или жидкость. Такая геометрия соответствует клиновидной трещине, заполненной текучей средой. Для решения задачи применим простую и наглядную лучевую теорию, подобную той, что была раньше развита для остроугольного клина со свободной поверхностью [11, 12]. Используемый подход позволяет, с одной стороны, получить компактные приближенные аналитические выражения для фазовой скорости клиновых мод. С другой стороны, картина волновых лучей, рассчитанная для изучаемой задачи, демонстрирует степень локализации клиновых мод разных номеров у вершины клина, а также объясняет причины их появления.
СКОРОСТИ КЛИНОВЫХ МОД
Геометрия рассматриваемой задачи показана на рис. 1. Считаем, что в неограниченном изотропном твердом теле имеется узкий клиновидный вырез (который будем называть также выемкой) полуограниченной протяженности $r \geqslant 0$ с малым углом при вершине ${{\theta }_{c}},$ заполненный идеальной (невязкой) текучей средой. Границы выемки полагаются плоскими. В такой задаче нет геометрических параметров, с которыми можно было бы сравнивать длину волн. Поэтому геометрическая дисперсия для изучаемых мод отсутствует. Линию пересечения граней выемки будем считать совпадающей с осью $z$ цилиндрической системы координат.
Рис. 1.
Геометрия задачи. Лучевые траектории волноводных мод в заполненной текучей средой клиновидной щели в твердом теле.
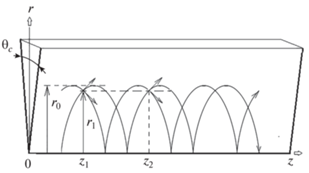
Если угол выемки достаточно мал, то бегущие в ней волны можно локально аппроксимировать решениями для нормальных мод в плоскопараллельном слое текучей среды толщиной $h,$ разделяющем два одинаковых изотропных полупространства. Нулевая симметричная мода в такой слоистой структуре, как показал Крауклис в 1962 г. [13], является аномально медленной. Ее фазовая скорость $\upsilon $ согласно результатам статей [13, 14] в пределе малых $h$ стремится к нулю по закону $\upsilon \approx {{(\gamma \omega h)}^{{1{\text{/}}3}}},$ где $\gamma = {{\left( {1 - {{\upsilon _{t}^{2}} \mathord{\left/ {\vphantom {{\upsilon _{t}^{2}} {\upsilon _{l}^{2}}}} \right. \kern-0em} {\upsilon _{l}^{2}}}} \right)\mu } \mathord{\left/ {\vphantom {{\left( {1 - {{\upsilon _{t}^{2}} \mathord{\left/ {\vphantom {{\upsilon _{t}^{2}} {\upsilon _{l}^{2}}}} \right. \kern-0em} {\upsilon _{l}^{2}}}} \right)\mu } {{{\rho }_{f}}}}} \right. \kern-0em} {{{\rho }_{f}}}},$ ${{\upsilon }_{t}}$ и ${{\upsilon }_{l}}$ – скорости поперечной и продольной объемных волн в твердом теле, $\mu $ – модуль сдвига, ${{\rho }_{f}}$ – плотность текучей среды. В противоположном пределе $h \to \infty $ обсуждаемая мода разделяется на две несвязанные синфазные волны Шолте–Гоголадзе равной амплитуды, локализованные у противоположных границ текучего слоя с твердым телом. Комбинация этих асимптотик дает простое аналитическое выражение для квадрата волнового числа ${{k}^{2}}$ симметричной моды, достаточно точное во всем диапазоне возможных значений $h$
(1)
${{k}^{2}} = \frac{{{{\omega }^{{4{\text{/}}3}}}}}{{{{{(\gamma h)}}^{{2{\text{/}}3}}}}} + k_{{{\text{SG}}}}^{2}.$(2)
$h = r2tg({{{{\theta }_{c}}} \mathord{\left/ {\vphantom {{{{\theta }_{c}}} 2}} \right. \kern-0em} 2}).$Волновое поле определяется интерференцией двух лучей, распространяющихся под углом $\alpha $ к оси $z.$ Их волновые множители зависят от обеих координат и в однородной среде выглядели бы так: $\exp (i{{k}_{z}}z \pm i{{k}_{r}}r),$ где ${{k}_{z}} = k\cos \alpha $ и ${{k}_{r}} = k\sin \alpha $ – проекции волнового вектора на соответствующие оси системы координат. Но в клиновидном слое из-за зависимости волнового числа $k$ от $r$ радиальный набег фазы определяется не произведением ${{k}_{r}}r,$ а интегралом $\int {{{k}_{r}}dr} .$ При этом под $\alpha $ следует понимать локальное значение угла, обеспечивающее сохранение проекции ${{k}_{z}}$ при изменении $r.$
С другой стороны, строгое решение волновой задачи описывает изменение фазы лишь при движении по координате $z.$ Для согласования лучевого и точного волнового подходов необходимо нивелировать набег фазы, связанный с изменением радиальной координаты для равноудаленных от вершины клина точек (расположенных, например, на расстояние r1 на рис. 1). Для этого достаточно потребовать, чтобы данный набег был кратен 2π. Следует, однако, учитывать, что его полное значение включает в себя два дополнительных слагаемых. Одно из них – это сдвиг фазы на каустике в точке поворота лучей, равный, как известно, $({{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}).$ Второе – сдвиг фазы волны при отражении от вершины выреза. Для оценки последнего воспользуемся следующими соображениями. При приближении волны к вершине выреза расстояние между противоположными границами стремится к нулю. Соответственно, стремится к нулю и скорость симметричной моды в слое текучей среды. В результате на краю выреза возникает скачок локальной скорости от нулевого значения для волноводной моды до конечной величины, относящейся к объемным волнам. Отношение эффективных импедансов для таких смежных сред равно бесконечности. Данная ситуация эквивалентна случаю отражения объемных волн от абсолютно жесткой границы со сдвигом фазы $( - \pi ).$ Это значение и будем использовать далее для изучаемых мод.
Из изложенных соображений и симметрии движения лучей от ребра клина до точки поворота и обратно вытекает следующее условие квантования радиального набега фазы
$n$ – ноль или целое число, ${{r}_{0}}$ – значение радиальной координаты в точках поворота лучей. В этих точках проекция ${{k}_{r}}$ обращается в ноль. При выполнении (3) проекция ${{k}_{z}}$ играет роль волнового числа клиновых волн, а $n$ определяет номер разных мод. Интеграл в формуле (3) после замены ${{k}_{r}} = \sqrt {{{k}^{2}} - k_{z}^{2}} $ и подстановки выражений (1) и (2) приобретает простой вид и вычисляется точно(4)
$b\int {\sqrt {{{r}^{{ - 2{\text{/}}3}}} - {{a}^{2}}} dr} = - \frac{b}{{{{a}^{2}}}}{{\left( {1 - {{a}^{2}}{{r}^{{2{\text{/}}3}}}} \right)}^{{3{\text{/}}2}}},$(5)
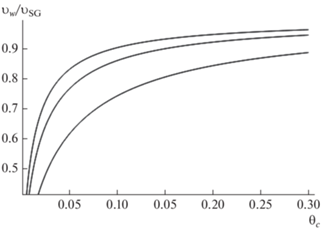
$\begin{gathered} {{\upsilon }_{w}} = {{{{\upsilon }_{0}}} \mathord{\left/ {\vphantom {{{{\upsilon }_{0}}} {\sqrt {1 + {{\upsilon _{0}^{2}} \mathord{\left/ {\vphantom {{\upsilon _{0}^{2}} {\upsilon _{{{\text{SG}}}}^{2}}}} \right. \kern-0em} {\upsilon _{{{\text{SG}}}}^{2}}}} }}} \right. \kern-0em} {\sqrt {1 + {{\upsilon _{0}^{2}} \mathord{\left/ {\vphantom {{\upsilon _{0}^{2}} {\upsilon _{{{\text{SG}}}}^{2}}}} \right. \kern-0em} {\upsilon _{{{\text{SG}}}}^{2}}}} }}, \\ \upsilon _{0}^{2} = \pi \left( {\tfrac{3}{4} + n} \right)\gamma 2tg({{{{\theta }_{c}}} \mathord{\left/ {\vphantom {{{{\theta }_{c}}} 2}} \right. \kern-0em} 2}), \\ {{\upsilon }_{{{\text{SG}}}}} = {\omega \mathord{\left/ {\vphantom {\omega {{{k}_{{{\text{SG}}}}}}}} \right. \kern-0em} {{{k}_{{{\text{SG}}}}}}}. \\ \end{gathered} $Рис. 2.
Зависимости относительных фазовых скоростей ${{{{\upsilon }_{w}}} \mathord{\left/ {\vphantom {{{{\upsilon }_{w}}} {{{\upsilon }_{{{\text{SG}}}}}}}} \right. \kern-0em} {{{\upsilon }_{{{\text{SG}}}}}}}$ для трех низших клиновых мод жидкостного типа ($n = 0,\,\,1,\,\,2$) от угла ${{\theta }_{c}}$ (в радианах) выреза в твердом теле для случая ${{\upsilon _{t}^{2}} \mathord{\left/ {\vphantom {{\upsilon _{t}^{2}} {\upsilon _{{{\text{SG}}}}^{2}}}} \right. \kern-0em} {\upsilon _{{{\text{SG}}}}^{2}}} = 2,$ ${{\upsilon _{l}^{2}} \mathord{\left/ {\vphantom {{\upsilon _{l}^{2}} {\upsilon _{t}^{2}}}} \right. \kern-0em} {\upsilon _{t}^{2}}} = 3,$ ${{{{\rho }_{s}}} \mathord{\left/ {\vphantom {{{{\rho }_{s}}} {{{\rho }_{f}}}}} \right. \kern-0em} {{{\rho }_{f}}}} = 4.$
ЛУЧЕВЫЕ ТРАЕКТОРИИ
Перейдем к расчету траектории волновых лучей. Тангенс касательной к ней равен производной ${{dz} \mathord{\left/ {\vphantom {{dz} {dr}}} \right. \kern-0em} {dr}}.$ С другой стороны, тот же тангенс можно выразить через отношение проекций ${{{{k}_{z}}} \mathord{\left/ {\vphantom {{{{k}_{z}}} {{{k}_{r}}}}} \right. \kern-0em} {{{k}_{r}}}}.$ Приравнивая друг другу эти выражения и заменяя ${{k}_{r}}$ через ${{k}_{z}}$ (${{k}_{r}} = \pm \sqrt {{{k}^{2}} - k_{z}^{2}} $), получаем уравнение для нахождения лучевых траекторий
(7)
${{dz} \mathord{\left/ {\vphantom {{dz} {dr}}} \right. \kern-0em} {dr}} = {{ \pm {{k}_{z}}} \mathord{\left/ {\vphantom {{ \pm {{k}_{z}}} {\sqrt {{{k}^{2}}(h) - k_{z}^{2}} }}} \right. \kern-0em} {\sqrt {{{k}^{2}}(h) - k_{z}^{2}} }}.$Интегрирование (7) дает связь координат на пути движения волновых лучей
(8)
$z = \mp {{{{k}_{z}}\sqrt {1 - {{a}^{2}}{{r}^{{2{\text{/}}3}}}} \left( {2 + {{a}^{2}}{{r}^{{2{\text{/}}3}}}} \right)} \mathord{\left/ {\vphantom {{{{k}_{z}}\sqrt {1 - {{a}^{2}}{{r}^{{2{\text{/}}3}}}} \left( {2 + {{a}^{2}}{{r}^{{2{\text{/}}3}}}} \right)} {\left( {b{{a}^{4}}} \right)}}} \right. \kern-0em} {\left( {b{{a}^{4}}} \right)}} + C.$Обратим внимание на следующее отличие лучевых траекторий для рассматриваемой задачи в сравнении с изгибными волнами в клиновидных пластинах [11, 12]. В последнем случае периодичность траекторий возникает естественным образом из-за входящей в решение функции синус. Изменение значения константы интегрирования $C$ для описания периодичности при этом не требовалось. Иное дело клиновые волны жидкостного типа. В решении (8) для них периодические тригонометрические функции отсутствуют, а фиксированное значение $C$ определяет только один цикл лучевой траектории. Для нахождения следующих циклов необходимо поэтому многократно изменять константу интегрирования. В итоге эта константа принимает ряд дискретных значений, образующих эквидистантную последовательность.
Результат численного расчета универсальных лучевых траекторий показан на рис. 1. В качестве координат $r$ и $z$ здесь использованы эффективные безразмерные значения $\tilde {r} = {{a}^{3}}r$ и $\tilde {z} = {{(z - C)b{{a}^{4}}} \mathord{\left/ {\vphantom {{(z - C)b{{a}^{4}}} {{{k}_{z}}}}} \right. \kern-0em} {{{k}_{z}}}},$ связанные между собой соотношением
(9)
$\tilde {z} = \mp \sqrt {1 - {{{\tilde {r}}}^{{2{\text{/}}3}}}} \left( {2 + {{{\tilde {r}}}^{{2{\text{/}}3}}}} \right).$Обращение в ноль квадратного корня в (8) и (9) соответствует точке поворота лучей ${{r}_{0}}.$ Отсюда находим эту точку ${{r}_{0}} = {{\pi (3{\text{/}}4 + n){{\upsilon }_{0}}} \mathord{\left/ {\vphantom {{\pi (3{\text{/}}4 + n){{\upsilon }_{0}}} \omega }} \right. \kern-0em} \omega }.$ В итоге ${{r}_{0}},$ а, значит, и область локализации волн с увеличением номера моды $n$ возрастает пропорционально ${{(3{\text{/}}4 + n)}^{{3{\text{/}}2}}}.$ Однако ни к каким последствиям типа появления отсечек это возрастание не приводит, поскольку здесь рассматривается модель полубесконечного клина.
СРАВНЕНИЕ С ИМЕЮЩИМИСЯ ДАННЫМИ
В отношении предшествующих публикаций по изучаемой теме следует упомянуть статью [15]. В ней экспериментально и численно методом конечных элементов исследовано распространение поверхностных акустических волн в пластине с заполненной жидкостью клиновидной выемкой конечной глубины. Были обнаружены локализация энергии в выемке, существование в изучаемой геометрии двух мод с отсечкой по углу жидкого клина и падение скорости волн с уменьшением угла. Однако причины этих особенностей так и не были объяснены. Кроме того, авторы статьи [15] не идентифицировали изучаемые ими акустические волны как самостоятельный тип, называя их поверхностными. Такое название подразумевает, что доминирующим на свойства этих волн считается влияние основной граничной плоскости пластины, а не граней клина. Для выемки конечной глубины имеются дополнительные причины локализации поверхностных акустических волн, существующих на основной плоской поверхности пластины. Во-первых, это два твердотельных клина, образованных пересечением поверхностей выемки и пластины. В каждом из них существуют свои локализованные клиновые моды. Причем эти моды взаимодействуют друг с другом через слой текучей среды. Во-вторых, грани ограниченной по глубине выемки имеют конечную ширину, образуя волновод для бегущих вдоль них граничных возмущений. В спектре таких волноводных поверхностных мод можно ожидать наличие не только однородных, но и неоднородных волн с меньшими скоростями, соответствующими локализации поля вблизи выемки. Отмеченные усложнения затрудняют анализ задачи и интерпретацию полученных в [15] результатов численного и натурного экспериментов. В настоящей работе в отличие от [15] изучаются волны в заполненной текучей средой клиновидной выемке бесконечной глубины. Выявление локализации поля именно в такой геометрии и позволяет утверждать, что это отдельный самостоятельный тип волн, принципиально отличающийся от поверхностных мод плоских границ твердых тел.
ВОЗМОЖНЫЕ ПРИМЕНЕНИЯ
Обсудим научные области, для которых результаты проведенного исследования могут представлять интерес. В начале текущего века зародилось перспективное научное направление, которое можно кратко назвать микрожидкостной акустоэлектроникой. См. об этом, в частности, обзор [16]. Практической целью исследований в данном направлении является создание нового класса микроэлектронных устройств типа “лабораторий на чипах”, альтернативно называемых также “биочипами”. В качестве вынуждающей силы для перемещения малых капель растворов и манипулирования ими в таких устройствах в основном используются поверхностные акустические волны. Альтернативой или дополнением могут служить клиновые моды, изучаемые в настоящей работе. К их плюсам относится отсутствие дифракционных потерь, так же, как и ложных сигналов, вызываемых дифракцией. Клиновидная выемка могла бы тогда одновременно использоваться в качестве и волновода акустических волн, и канала для акустического перемещения жидкости.
Низкая скорость клиновых мод может представлять интерес для их применений в акустооптике. Эффективность взаимодействия света и звука определяется коэффициентом акустооптического качества, обратно пропорциональным кубу фазовой скорости акустических волн. Для изучаемых мод данный коэффициент должен сильно возрастать в области малых углов клина ${{\theta }_{c}} \ll 1,$ где резко падает скорость. Значительное замедление изучаемых волн по сравнению со скоростью звука в воздухе наталкивает на мысль о возможности их применения для создания новых музыкальных инструментов. Та же низкая скорость делает эти волны более чувствительными к внешним воздействиям и перспективными для создания акустических датчиков различного рода, в частности датчиков расхода воды в клиновидных сливах и каналах и измерителей уровня жидкостей.
Сильную концентрацию энергии у вершины клина и связь с вязкими волнами можно было бы использовать для разработки и создания звукопоглотителей нового типа, основанных на клиновых волнах. Такая концентрация облегчает реализации высокоэффективных нелинейных взаимодействий акустических сигналов при небольших амплитудах внешних электрических возбуждений, что можно использовать в акустоэлектронных устройствах обработки сигнальной информации.
Другим предполагаемым применением представленных результатов является изучение медленной динамики твердых тел ограниченных размеров. Если тело покрыто сеткой мелких клиновидных трещин, заполненных воздухом или влагой, то они могут служить волноводными каналами для передачи акустических сигналов. Причем скорости сигналов будут значительно меньше, чем у объемных волн и в твердом теле, и в заполняющей трещины текучей среде.
Возможны также применения представленной теории для изучения динамики геологических объектов значительно бо́льших масштабов, таких как клиновидные узкие горные каньоны, магматические камеры, подледные озера, ледовый покров, разломы земной коры на суше и морском дне, океанические впадины. Например, у Марианского желоба глубоководная часть имеет форму поперечного сечения, близкую к острому клину, что предполагает существование в нем рассмотренных выше клиновых волн жидкостного типа.
ЗАКЛЮЧЕНИЕ
Итак, развитая теория предсказывает существование множества локализованных клиновых мод. Их скорость ${{\upsilon }_{w}}$ стремится к нулю при уменьшении угла жидкого клина ${{\theta }_{c}}$ по корневому закону ${{\upsilon }_{w}} \propto \sqrt {{{\theta }_{c}}} ,$ а не линейному, как для изгибных клиновых волн в остроугольных клиновидных пластинах.
Причиной появления таких мод является рефракция волновых лучей из-за зависимости скорости волноводных мод от локальной толщины клина. В рамках используемой модели этот механизм формирования локализованного поля описывается с помощью неоднородного профиля скорости волноводных мод как функции расстояния до ребра клина. Интересной особенностью данного профиля является частотная зависимость, принципиально отличающая его от статических профилей в традиционных задачах распространения волн в неоднородных средах. Именно эта зависимость приводит к полной компенсации возможных изменений с частотой скоростей клиновых волн, т.е. к отсутствию дисперсии. Данное свойство согласуется с отсутствием в рассматриваемой задаче каких-либо геометрических параметров, кроме длины волны.