ВВЕДЕНИЕ

Процесс исследования распространения волн вдоль поверхности жидкости имеет давнюю историю и берет свое начало еще с работ Эйлера, Лагранжа, Даламбера, Стокса и других. Обобщение этих исследований можно найти в большом количестве обзорных работ и монографий [1–3]. Волны могут оказывать влияние на перераспределение поверхностно-активных веществ вдоль поверхности жидкости [4, 5], меняют морфологию дна в море, реках и каналах [6]. Короткие капиллярные волны на склонах гравитационных волн [7], меняют шероховатость контактной поверхности, определяющую взаимодействие океана и атмосферы, (расчеты распространения капиллярных волн по сферической поверхности проведены в [8]) а также могут служить причиной усиления гравитационных волн в присутствии поверхностно-активных веществ [9]. В экспериментальных исследованиях капельных течений можно заметить сложность картины волнового переноса вещества, включающего образование вихрей, и тонких волокон [10].

Настоящая работа посвящена анализу и исследованию волновой компоненты решения дисперсионного уравнения, возникающего при распространении волн по свободной поверхности вязкой однородной жидкости.

МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА ЗАДАЧИ

Рассмотрим задачу о распространении поверхностных волн в вязкой однородной жидкости с кинематической вязкостью $\nu ,$ плотностью ${{\rho }_{0}},$ коэффициентом поверхностного натяжения $\sigma $, находящуюся в поле сил тяжести $\vec {g}.$ В декартовой системе координат $Oxyz{\text{,}}$ в которой ось $Oz$ направлена вертикально вверх, а плоскость $Oxy$ совпадает с равновесным положением свободной поверхности жидкости. Будем считать, что жидкость неограничена и занимает нижнее полупространство $z < 0,$ а вдоль свободной поверхности распространяется бегущая волна, задающая отклонение свободной поверхности от равновесного значения, которое описывается функцией $z = \zeta \left( {x,y,t} \right).$ Также будем рассматривать задачу в плоской постановке, т.е. будем полагать, что движение жидкости не зависит от горизонтальной координаты $y.$ Математическая формулировка задачи базируется на упрощенной системе фундаментальных уравнений [11], в которой пренебрегается эффектами, связанными с переносом вещества, тепла и стратификацией:

(1)
$z < \zeta {\text{:}}\,\,\left\{ \begin{gathered} \frac{{\partial{ \vec {u}}}}{{\partial t}} = - \left( {\vec {u} \cdot \nabla } \right)\vec {u} + \nu \Delta \vec {u} - \frac{1}{{{{\rho }_{0}}}}\nabla P + \vec {g} \hfill \\ \nabla \cdot \vec {u} = 0 \hfill \\ \end{gathered} \right..$

Здесь символом P обозначено гидродинамическое давление, а поле скоростей в двумерном случае представляется в виде $\vec {u} = u\overrightarrow {{{e}_{x}}} + \nu \overrightarrow {{{e}_{z}}} .$ Задача (1) должна быть дополнена граничными условиями на свободной поверхности жидкости $z = \zeta {\text{:}}$

(2)
$z = \zeta {\text{:}}\,\,\frac{{\partial \left( {z - \zeta } \right)}}{{\partial t}} + \vec {u} \cdot \nabla \left( {z - \zeta } \right) = 0,$
(3)
$P - {{P}_{0}} - \sigma \nabla \cdot \vec {n} - 2{{\rho }_{0}}\nu \vec {n} \cdot \left( {\vec {n} \cdot \nabla \vec {u}} \right) = 0,$
(4)
$\vec {\tau } \cdot \left( {\vec {n} \cdot \nabla \vec {u}} \right) + \vec {n}\left( {\vec {\tau } \cdot \nabla \vec {u}} \right) = 0,$
$\vec {n} = \frac{{\nabla \left( {z - \zeta } \right)}}{{\left| {\nabla \left( {z - \zeta } \right)} \right|}} = \frac{{ - {{\partial }_{x}}\zeta \overrightarrow {{{e}_{x}}} + \overrightarrow {{{e}_{z}}} }}{{\sqrt {1 + {{{\left( {{{\partial }_{x}}\zeta } \right)}}^{2}}} }},\,\,\,\,\vec {\tau } = \frac{{\overrightarrow {{{e}_{x}}} + {{\partial }_{x}}\zeta \overrightarrow {{{e}_{z}}} }}{{\sqrt {1 + {{{\left( {{{\partial }_{x}}\zeta } \right)}}^{2}}} }}.$
Здесь ${{P}_{0}}$ – атмосферное давление, а символами $\vec {n}$ и $\vec {\tau }$ обозначены вектор нормали и касательной к свободной поверхности соответственно. В случае двумерного движения можно ввести функцию тока $\psi $ такую, что $u = {{\partial }_{z}}\psi ,$ а $\nu = - {{\partial }_{x}}\psi .$ В линейном приближении по малому параметру, имеющему смысл отношения амплитуды к длине волны после проведения процедуры снесения граничных условий на равновесную поверхность $z = 0$ задача запишется в виде:
(5)
$z < 0{\text{:}}\,\,{{\partial }_{t}}\Delta \psi - \nu \Delta \Delta \psi = 0,$
(6)
$z = 0{\text{:}}\,\,{{\partial }_{t}}\zeta + {{\partial }_{x}}\psi = 0,$
(7)
$\nu {{\partial }_{{tz}}}\Delta \psi - {{\partial }_{{ttz}}}\psi + g{{\partial }_{{xx}}}\psi + 2\nu {{\partial }_{{txxz}}}\psi - \gamma {{\partial }_{{xxxx}}}\psi = 0,$
(8)
${{\partial }_{{zz}}}\psi - {{\partial }_{{xx}}}\psi = 0.$
Здесь символом $\gamma = {\sigma \mathord{\left/ {\vphantom {\sigma {{{\rho }_{0}}}}} \right. \kern-0em} {{{\rho }_{0}}}}$ обозначен нормированный на плотность коэффициент поверхностного натяжения жидкости.

РЕШЕНИЕ ЗАДАЧИ

Будем искать решение задачи первого порядка малости по амплитуде волны (5)–(8) в виде бегущей волны:

(9)
$\psi = {{A}_{ + }}{{e}^{{{{k}_{z}}z + i{{k}_{x}}x - i\omega t}}} + {{A}_{ - }}{{e}^{{{{k}_{z}}z - i{{k}_{x}}x - i\omega t}}}.$

Подстановка (9) в (5) приводит к дисперсионным соотношениям между компонентами волнового числа ${{k}_{x}}$ и ${{k}_{z}}{\text{:}}$

(10)
$\left( {k_{x}^{2} - k_{z}^{2}} \right)\left( {\nu \left( {k_{x}^{2} - k_{z}^{2}} \right) - i\omega } \right) = 0,$

Которое естественным образом распадается на два решения:

(11)
$k_{z}^{2} = k_{x}^{2},\,\,\,\,k_{l}^{2} = k_{x}^{2} + {{i\omega } \mathord{\left/ {\vphantom {{i\omega } \nu }} \right. \kern-0em} \nu }.$

В выражении (11) введено переобозначение компоненты волнового вектора ${{k}_{z}}$ на ${{k}_{l}}$ для одного из решений для отличия корней друг от друга. С учетом выражений (11) решение задачи необходимо искать в виде:

(12)
$\psi = \left( {{{A}_{ + }}{{e}^{{i{{k}_{x}}x - i\omega t}}} + {{A}_{ - }}{{e}^{{ - i{{k}_{x}}x - i\omega t}}}} \right)\left( {{{e}^{{{{k}_{z}}z}}} + B{{e}^{{{{k}_{l}}z}}}} \right).$

Подстановка (12) в граничные условия (6), (8) приводит к соотношениям:

(13)
$\zeta = \left( {{{A}_{ - }}{{e}^{{ - i{{k}_{x}}x - i\omega t}}} - {{A}_{ + }}{{e}^{{i{{k}_{x}}x - i\omega t}}}} \right)\left( {1 + B} \right){{{{k}_{x}}} \mathord{\left/ {\vphantom {{{{k}_{x}}} \omega }} \right. \kern-0em} \omega },$
(14)
$B = - \frac{{k_{x}^{2} + k_{z}^{2}}}{{k_{x}^{2} + k_{l}^{2}}} = - \frac{{2k_{x}^{2}}}{{2k_{x}^{2} + i{\omega \mathord{\left/ {\vphantom {\omega \nu }} \right. \kern-0em} \nu }}}.$

Подстановка (12) в динамическое граничное условие (7) приводит к дисперсионному уравнению, связывающему компоненты волнового вектора с частотой волнового движения и другими параметрами задачи:

(15)
$\gamma k_{x}^{4} - 3i\nu \omega k_{x}^{2}{{k}_{{z,l}}} + gk_{x}^{2} + {{k}_{{z,l}}}\left( {i\nu k_{{z,l}}^{2} - \omega } \right)\omega = 0.$

С учетом (11) дисперсионные уравнения (15) принимают вид:

(16)
$\begin{gathered} \gamma k_{z}^{3} - 2i\nu \omega k_{z}^{2} + g{{k}_{z}} - {{\omega }^{2}} = 0,\,\,\, \\ \gamma {{\left( {k_{l}^{2} - i{\omega \mathord{\left/ {\vphantom {\omega \nu }} \right. \kern-0em} \nu }} \right)}^{2}} - 2i\nu \omega \left( {k_{l}^{2} - i{\omega \mathord{\left/ {\vphantom {\omega \nu }} \right. \kern-0em} \nu }} \right){{k}_{l}} + \\ + \,\,g\left( {k_{l}^{2} - i{\omega \mathord{\left/ {\vphantom {\omega \nu }} \right. \kern-0em} \nu }} \right) + \omega {{k}_{l}}\left( {i\nu k_{l}^{2} - \omega } \right) = 0. \\ \end{gathered} $

Традиционно дисперсионное уравнение представляют в виде зависимости частоты от волнового числа и верхнее дисперсионное уравнение выглядит следующим образом:

(17)
${{\omega }^{2}} = \gamma k_{z}^{3} - 2i\nu \omega k_{z}^{2} + g{{k}_{z}}.$

В предельном переходе к идеальной жидкости $\nu \to 0$ верхнее дисперсионное уравнение в (16) перейдет в дисперсионное уравнение для идеальной жидкости, а нижнее – исчезнет:

(18)
$\gamma k_{z}^{3} + g{{k}_{z}} - {{\omega }^{2}} = 0$
или в более привычном виде:

(19)
$\omega = \sqrt {g{{k}_{z}}\left( {1 + {{\gamma k_{z}^{2}} \mathord{\left/ {\vphantom {{\gamma k_{z}^{2}} g}} \right. \kern-0em} g}} \right)} .$

Это позволяет говорить о том, что корень ${{k}_{z}}$ дисперсионного уравнения (16) отвечает за обобщение волнового движения идеальной жидкости на случай конечной вязкости, а корень ${{k}_{l}}$ – принципиально новая структура, возникающая из-за учета конечной вязкости. В настоящем исследовании подробно будет рассмотрен только корень, отвечающий за волновое движение вдоль поверхности жидкости.

Для простоты анализа корней обезразмерим дисперсионное уравнение. В качестве масштаба длины выберем $\sqrt[3]{{{{{{\nu }^{2}}} \mathord{\left/ {\vphantom {{{{\nu }^{2}}} g}} \right. \kern-0em} g}}},$ а в качестве масштаба времени – ${\gamma \mathord{\left/ {\vphantom {\gamma {\nu g}}} \right. \kern-0em} {\nu g}}.$ Тогда размерные компоненты волнового вектора и частоты запишутся через безразмерные в виде:

(20)
$\omega = {{\omega }_{*}}{{\nu g} \mathord{\left/ {\vphantom {{\nu g} \gamma }} \right. \kern-0em} \gamma },\,\,\,\,{{k}_{z}} = {{k}_{{z*}}}\sqrt[3]{{{g \mathord{\left/ {\vphantom {g {{{\nu }^{2}}}}} \right. \kern-0em} {{{\nu }^{2}}}}}},$
а дисперсионное уравнение (16) перепишется:

(21)
$\begin{gathered} k_{{z*}}^{3} - 2i{{\varepsilon }^{2}}{{\omega }_{*}}k_{{z*}}^{2} + \varepsilon {{k}_{{z*}}} - {{\varepsilon }^{3}}\omega _{*}^{2} = 0, \\ \varepsilon = \sqrt[3]{{{{{{\nu }^{4}}g} \mathord{\left/ {\vphantom {{{{\nu }^{4}}g} {{{\gamma }^{3}}}}} \right. \kern-0em} {{{\gamma }^{3}}}}}}, \\ k_{l}^{{*4}} - {{\varepsilon }^{2}}{{\omega }_{*}}\left( {2ik_{{l*}}^{3} + i + \omega } \right) - \\ - \,\,{{\varepsilon }^{3}}{{\omega }_{*}}{{k}_{{l*}}}\left( {1 + 3{{\omega }_{*}}} \right) + \varepsilon k_{{l*}}^{2}\left( {1 - 2i\omega } \right) = 0. \\ \end{gathered} $

Для физически реализуемых корней должно выполняться условие затухания движения с глубиной. Следовательно, решения дисперсионных уравнений (21) должны удовлетворять критериям отбора корней:

(22)
$\operatorname{Re} \left( {{{k}_{{z,l}}}} \right) \geqslant 0.$

В явном виде решения (21) здесь не приводятся из-за громоздкости выражений. Решение ${{k}_{l}}$ отвечает за сопутствующее высокоградиентное течение. Решение ${{k}_{z}}$ отвечает за волновую компоненту движения. Далее подробно будет рассмотрено только волновое решение ${{k}_{z}}.$

ДИСПЕРСИОННЫЕ ОТНОШЕНИЯ

Традиционно дисперсионные соотношения представляют в виде зависимости частоты от волнового числа. Но частота волнового движения несет в себе энергетический смысл, следовательно, должна определяться действительной положительной величиной. Волновое число, учитывающее пространственное затухание можно определять как комплексную величину. Действительная часть ${{k}_{x}}$ и мнимая часть ${{k}_{z}}$ отвечают за волновое движение, а мнимая часть kx и действительная часть ${{k}_{z}}$ характеризуют затухание движения с удалением волн от источника. Выбор описания и набора базовых параметров бегущих волн наиболее адекватно описывающего физически реализуемую ситуацию нуждается в экспериментальном обосновании.

Поскольку волновой вектор – это градиент фазы волны, то кажется логичным при построении выражения использовать только те компоненты, которые отвечают за волновое движение и не учитывают затухание:

(23)
$\left| k \right| = \sqrt {\operatorname{Re} {{{\left( {{{k}_{x}}} \right)}}^{2}} + \operatorname{Im} {{{\left( {{{k}_{z}}} \right)}}^{2}}} .$

Длина волны в таком случае задается соотношением:

(24)
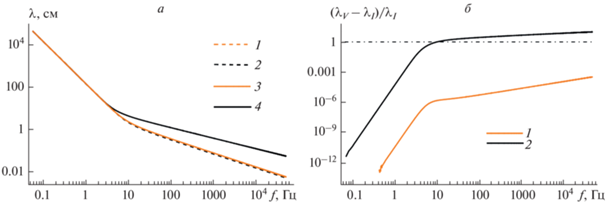
$\lambda = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {\sqrt {\operatorname{Re} {{{\left( {{{k}_{x}}} \right)}}^{2}} + \operatorname{Im} {{{\left( {{{k}_{z}}} \right)}}^{2}}} }}} \right. \kern-0em} {\sqrt {\operatorname{Re} {{{\left( {{{k}_{x}}} \right)}}^{2}} + \operatorname{Im} {{{\left( {{{k}_{z}}} \right)}}^{2}}} }}.$

Подставляя решение дисперсионного уравнения (16) в (24) с учетом (11) можно получить зависимость длины волны от частоты волнового движения. На рис. 1а представлены соответствующие зависимости для жидкостей с параметрами воды (кривые 1 и 3) ${{\rho }_{0}} = 1\,\,{{\text{г}} \mathord{\left/ {\vphantom {{\text{г}} {{\text{с}}{{{\text{м}}}^{{\text{3}}}}}}} \right. \kern-0em} {{\text{с}}{{{\text{м}}}^{{\text{3}}}}}},$ $g = 981\,\,{{{\text{см}}} \mathord{\left/ {\vphantom {{{\text{см}}} {{{{\text{с}}}^{{\text{2}}}}}}} \right. \kern-0em} {{{{\text{с}}}^{{\text{2}}}}}},$ $\sigma = 72\,\,{{{\text{дин}}} \mathord{\left/ {\vphantom {{{\text{дин}}} {{\text{см}}}}} \right. \kern-0em} {{\text{см}}}},$ $\nu = 0.01\,\,{{{\text{с}}{{{\text{м}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{\text{с}}{{{\text{м}}}^{{\text{2}}}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$ и жидкости с параметрами глицерина (кривые 2 и 4) ${{\rho }_{0}} = 1.26\,\,{{\text{г}} \mathord{\left/ {\vphantom {{\text{г}} {{\text{с}}{{{\text{м}}}^{{\text{3}}}}}}} \right. \kern-0em} {{\text{с}}{{{\text{м}}}^{{\text{3}}}}}},$ $g = 981\,\,{{{\text{см}}} \mathord{\left/ {\vphantom {{{\text{см}}} {{{{\text{с}}}^{{\text{2}}}}}}} \right. \kern-0em} {{{{\text{с}}}^{{\text{2}}}}}},$ $\sigma = 64.7\,\,{{{\text{дин}}} \mathord{\left/ {\vphantom {{{\text{дин}}} {{\text{см}}}}} \right. \kern-0em} {{\text{см}}}},$ $\nu = 11.746\,\,{{{\text{с}}{{{\text{м}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{\text{с}}{{{\text{м}}}^{{\text{2}}}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}.$ Пунктирными линиями (кривые 1 и 2) на рисунке изображены зависимости, полученные в модели с пренебрежением вязкостью. Сплошными линиями изображены линии в модели, учитывающей конечную вязкость. Из рисунка видно, что для жидкости с параметрами воды зависимости совпадают друг с другом с точностью до толщины линии. Для глицерина отличия заметны в области капиллярных волн. На рис. 1б показана невязка между длиной волны, рассчитанной в модели вязкой жидкости ${{\lambda }_{V}}$ и невязкой жидкости ${{\lambda }_{I}}$ в отношении к длине волны в идеальной жидкости ${{\left( {{{\lambda }_{V}} - {{\lambda }_{I}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\lambda }_{V}} - {{\lambda }_{I}}} \right)} {{{\lambda }_{I}}}}} \right. \kern-0em} {{{\lambda }_{I}}}}$ в зависимости от частоты. Литерой (1) обозначена зависимость для жидкости с параметрами воды, а литерой (2) – для жидкости с параметрами глицерина. Для гравитационных волн отличие в моделях несущественно как для слабовязких, так и для сильновязких жидкостей (порядка долей процентов), однако, с увеличением частоты отличие растет и для жидкости с большой вязкостью достигает 100% при частоте около 10 Гц и при дальнейшем увеличении частоты растет и становится заметной даже для слабовязких жидкостей.

Рис. 1.

Зависимость длины волны от частоты волнового движения (а). 1 – Кривая в модели идеальной жидкости с параметрами воды, 2 – в модели идеальной жидкости с параметрами глицерина, 3 – в модели вязкой жидкости с параметрами воды, 4 – в модели вязкой жидкости с параметрами глицерина. Разность между моделями вязкой и невязкой жидкости от частоты (б). 1 – Кривая для жидкости с параметрами воды, 2 – для жидкости с параметрами глицерина.

Скорость распространения фазового фронта и скорость распространения энергии также являются интересным предметом исследования и анализа. Для сравнения с экспериментом может быть удобно представление в виде зависимости от частоты или от длины волны. На рис. 2 и 3 изображены зависимости фазовой и групповой скорости волнового движения от частоты и длины волны соответственно. Зависимости, обозначенные литерой (1) и (2) построены в модели, учитывающей конечность вязкости, а зависимости с литерой (3) и (4) – в модели невязкой жидкости. Сплошными линиями обозначены зависимости групповой скорости (отвечающей за перенос энергии группой волн), а пунктирными – фазовой скорости. Из рисунков видно, что у гравитационных волн $\left( {\lambda \gg \delta _{g}^{\gamma } = \sqrt {\frac{\gamma }{g}} } \right)$ фазовая скорость опережает групповую, тогда как у капиллярных волн $\left( {\lambda \ll \delta _{g}^{\gamma }} \right)$ – наоборот. Расчеты показывают, что групповая и фазовая скорости сравниваются тогда, когда фазовая скорость принимает свое минимальное значение $C_{{ph}}^{{min}}.$ Для жидкости с параметрами воды это значение $C_{{ph}}^{{min}} = 23.05\,\,{{{\text{см}}} \mathord{\left/ {\vphantom {{{\text{см}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$ достигается при частоте $f_{{ph}}^{{min}} = 13.5\,\,{\text{Гц}}$ и длине волны $\lambda _{{ph}}^{{min}} = 1.71\,\,{\text{см}}.$ Для жидкости с параметрами глицерина это значение $C_{{ph}}^{{min}} = 40.85\,\,{{{\text{см}}} \mathord{\left/ {\vphantom {{{\text{см}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$ достигается при частоте $f_{{ph}}^{{min}} = 6.2\,\,{\text{Гц}}$ и длине волны $\lambda _{{ph}}^{{min}} = 6.59\,\,{\text{см}}.$

Рис. 2.

Зависимость групповой (1 и 3) и фазовой (2 и 4) скорости от частоты волнового движения в моделях вязкой (1 и 2) и невязкой (2 и 4) жидкости.

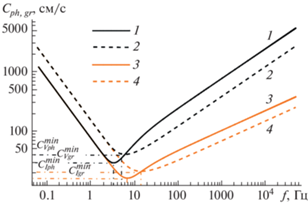
Рис. 3.

Зависимость групповой (1 и 3) и фазовой (2 и 4) скорости от длины волны в моделях вязкой (1 и 2) и невязкой (2 и 4) жидкости.

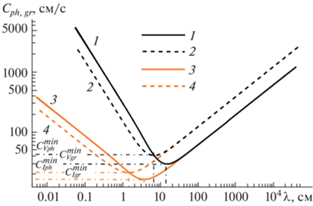
Также стоит отметить, что учет в модели конечной вязкости, во-первых, приводит к смещению характерных скоростей (минимальной групповой и минимальной фазовой скорости) в область больших длин волн (и меньших частот), а во-вторых, увеличиваются значения характерных скоростей.

ЗАКЛЮЧЕНИЕ

Проведен анализ распространения поверхностных капиллярно-гравитационных волн в вязкой однородной жидкости в плоской постановке в физически наблюдаемых переменных.

Показано, что учет вязкости приводит к увеличению минимальных скоростей распространения фазового фронта волны и скорости распространения энергии.

Установлено, что с учетом вязкости характерные значения скорости смещаются в область больших по сравнению с моделью идеальной жидкости длин волн и меньших частот.

Показано, что в вязкой жидкости помимо поверхностных волн существует еще один режим течения, не наблюдающийся в модели идеальной жидкости.

Работа выполнена при финансовой поддержке Российского научного фонда (проект № 19-19-00598).