Управление намагниченностью наноустройств без использования внешних магнитных полей, представляет большой интерес, поскольку такой подход открывает широкие возможности для разработки новых спинтронных и логических устройств, которые можно просто и эффективно интегрировать в классические электронные схемы. Управление намагниченностью в таких структурах возможно за счет протекания спин-поляризованного тока перпендикулярно поверхности границы раздела слоев структуры [1].

Также возможно переключение намагниченности за счет эффектов, которые связаны со спин-орбитальным взаимодействием. Сюда относят такие эффекты как спиновый эффект Холла [2] и эффект Рашбы–Эдельштейна [3, 4]. Спиновый эффект Холла заключается в том, что при пропускании тока через систему с большим спин-орбитальной взаимодействием, на границе между магнитным материалом и немагнитным материалом с большим спин-орбитальным моментом аккумулируются спин-поляризованные электроны. Далее эти электроны диффундируют в магнитный слой, что приводит к переключению намагниченности. Эффект Рашбы–Эдельштейна связан с нарушением симметрии поверхностных состояний на границе раздела двух слоев и с возникновением нескомпенсированного электрического поля, что приводит к появлению эффективного магнитного поля, непосредственно действующего на намагниченность магнитного слоя.

В обоих случаях создается эффект, схожий с возникновением дополнительного “эффективного магнитного поля”, которое влияет на намагниченность. Для оценки этого “эффективного магнитного поля” нами был использован метод адиабатического (низкочастотного) гармонического напряжения Холла. Такой подход впервые был предложен в работе [5], а подобная теория была разработана в первую очередь в статье [6].

Нами была исследована структура с намагниченностью, ориентированной в плоскости образца. Для описания динамики намагниченности используется уравнение Ландау–Лифшица–Гильберта:

где $\vec {M}$ – намагниченность образца, ${{\gamma }}$ – гиромагнитное отношение, ${{\alpha }}$ – константа затухания Гильберта, ${{\vec {H}}_{{eff}}}$ – эффективное магнитное поле. В эффективное поле входят внешнее постоянное поле, поле размагничивания, анизотропии, а также дополнительное поле, которое связано с протекающим в образце спин-поляризованным током. Данная составляющая имеет вид: где ${{a}_{J}}~$ – коэффициент затухания, ${{b}_{J}}$ – полевой член, $\vec {m}$ – единичный вектор намагниченности, $\vec {p}$ – единичный вектор направления поляризации немагнитного слоя структуры. При больших значениях тока как раз член $\Delta {{H}_{{sc}}}$ играет ключевую роль в переключении намагниченности. Гармонический метод позволяет эффективно измерять компоненты поля $\Delta {{H}_{{sc}}}.$ Для вектора $\vec {p},$ направленного по оси y, где за ось x принимается направление протекания тока. $\Delta {{H}_{{sc}}}$ имеет вид: где ${{{{\theta }}}_{0}}$ – это полярный угол равновесного положения намагниченности образца, а ${{{{\varphi }}}_{H}}$ азимутальный угол направления внешнего поля. Для образца, с намагниченностью в плоскости, верно, что ${{{{\theta }}}_{0}} \approx \frac{\pi }{2}.$ Дальнейшее теоретическое рассмотрение полагается на варьирование магнитной энергии образца по углам отклонения намагниченности от состояния равновесия, в предположении малости этого угла [6]. Это обстоятельство накладывает естественные ограничения на направление и величину внешнего поля, которое должно быть направлено приблизительно по нормали к образцу и, в конкретно данном методе, не выводить намагниченность из плоскости.

Формула для поля, порожденного коэффициентом затухания, имеет вид:

а для поля, порожденного полевым членом: где ${{\xi }} = \,\,~\frac{{\Delta {{R}_{P}}}}{{\Delta {{R}_{A}}}}$ – отношение изменения сопротивления, вызванного планарным эффектом Холла и вызванного аномальным эффектом Холла. ${{H}_{K}} = \frac{{{{K}_{{eff}}}}}{{{{M}_{s}}}},$ где ${{K}_{{eff}}}$ – эффективная энергия внеплоскостной анизатропии, ${{M}_{s}}$ – намагниченность насыщения.

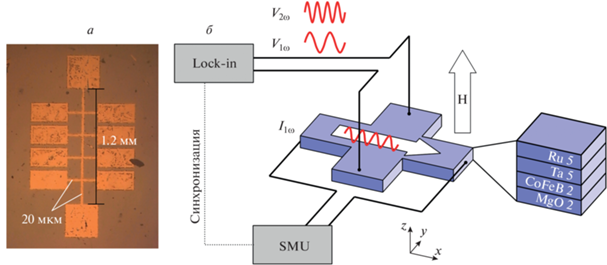
Нами был изучен образец, представляющий собой наноразмерную магнитную гетероструктуру, Структура слоев: MgO (2)|CoFeB (2)|Ta (5)|Ru (5) (в скобках указаны толщины слоев в нм). В качестве подложки использовался оксида магния(II). Намагниченность ориентирована в плоскости образца. Образец имеет крестообразную форму длиной 1.2 мм и шириной 20 мкм (см. рис. 1а).

Схема эксперимента показана на рис. 1б. Для генерации тока был использовался источник-измеритель SMU NI-PXIe-4137. Данная модель имеет встроенную функцию генератора сигналов произвольной формы, что позволяет формировать в том числе синусоидальный сигнал тока с частотами вплоть до ~5 кГц. Такая возможность позволяет использовать данный прибор совместно с синхронным детектором, чтобы делать измерения продольного и холловского напряжения на первой и на второй гармониках. Сразу после SMU дополнительно был установлен фильтр высоких частот, убирающий лишний высокочастотный шум, что важно для эффективного детектирования сигнала на второй гармонике. Сигнал с SMU подавался на образец, а также синхронизировался с синхронным усилителем Stanford Research 830. Через образец пропускался ток с максимальной плотностью 0.5 · 10⁷ A · см^–2. Подключение приборов к образцу производилось при помощи контактных зондов. Сам образец был помещен в постоянное магнитное поле, направленное перпендикулярно плоскости его поверхности. Поле варьировалось в пределах от –1500 до 1500 Э. В эксперименте измерялось как продольное напряжение, так и поперечное, холловское напряжение. Результаты исследования сравнивались с результатами, полученными в работе [7], а также с данными работ [6, 8–10], где порядок слоев был инвертирован (Ta|CoFeB|MgO).

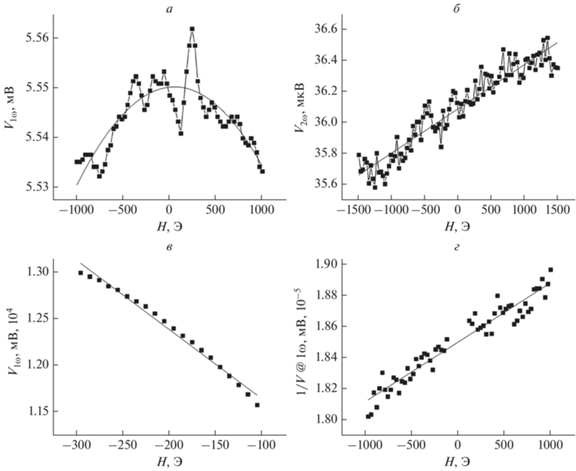
Результаты эксперимента представлены на рис. 2: рис. 2а и 2б – продольное напряжение, измеренное на первой и на второй гармонике, рис. 2в и 2г – поперечное (холловское) напряжение и величина, обратная амплитуде второй гармоники. Последнее представлено в таком виде для удобства аппроксимации и подстановки в формулу (5). Значение сигнала на первой гармонике при продольном подключении аппроксимируется параболой. Остальные величины аппроксимируется линейными зависимостями. В результате измерений для нашей структуры было получено значение ослабляющей компоненты поля ${{H}_{{DL}}} = 17\,\,{\text{Э}},$ что согласуется со значением, полученным в работе [8], где для схожих параметров было получено ${{H}_{{DL}}} = 15\,\,{\text{Э}}.$

Для получения значения полевого члена магнитное поле необходимо дополнительно немного отклонять от вертикали. Для этих целей был использован постоянный магнит, который создавал продольное поле величиной ~5 Э. В связи с этим, при малых величинах перпендикулярной компоненты поля (менее 100 Э) нарушалось условие ${{\theta }_{H}} \ll 1,$ используемое в выводе формул, что приводило к повышенной погрешности результатов измерений. Эти области были исключены из итоговых графиков. Помимо этого, в силу приближения ${{H}_{K}} \gg H,$ где ${{H}_{K}}$ оценивается примерно в 2000 Э [3], развертка по полю для первой гармоники ограничена по модулю 300 Э. Положительная область графика не рассматривается в силу наличия в этой области пиков, схожих по форме с пиками, которые получаются при измерении первой гармоники при продольном подключении. Оба этих графика аппроксимированы линейными зависимостями. Отношение планарного эффекта Холла к аномальному составляет 0.1. В результате исследований получено значение в ${{H}_{{FL}}} = 440\,\,{\text{Э}},$ что несколько меньше чем в работе [8], где ${{H}_{{FL}}}$ составляло 500 Э. Полученные в эксперименте значения несколько отличаются от значений, которые были получены в работе [7] и больше схожи со значениями из работы [4], где слои структуры были выращены в обратном порядке. Численные результаты в этих работах сопоставимы. Отклонение результатов в меньшую сторону мы связываем с особенностями технологии производства и точностью определения ${{H}_{K}},$ которое следует измерять отдельно, например, с помощью вибрационного магнитометра.

Получаемые в результате эксперимента величины напрямую связаны с фундаментальными физическими параметрами материалов, поэтому сразу возникает желание вычислить угол спин-холла. Однако, как показывает работа [8], стоит рассматривать полученные значения полей, создаваемых спиновым током, лишь как эффективные для данной конкретной структуры в целом, а не для входящих в нее отдельных немагнитных материалов. Так же стоит отметить, что имеет место зависимость параметров ${{H}_{{FL}}}$ и ${{H}_{{DL}}}$ от толщин слоев MgO и Ta, входящих в структуру, а также от температуры и подаваемой плотности тока. Первое обстоятельство связано с тем, что переходный слой между слоями структуры не идеально ровный и поэтому сильно влияет на создаваемое эффективное поле. Для извлечения корректных значений, относящихся не ко всей структуре в целом, а к отдельным ее слоям, необходимо проводить дополнительные исследования.

Таким образом, нами было продемонстрировано использование гармонического метода Холла для измерения и оценки эффективных магнитных полей, которые создаются спиновым током. Полученные результаты хорошо согласуются с описанными в литературе. Исследование структуры показало, что в начальном приближении прямой и обратный порядок следования слоев в структуре незначительно влияет на значение ${{H}_{{FL}}}$ и ${{H}_{{DL}}}.$ Метод показал свою эффективность и удобство использования.

Работа выполнена при поддержке Российского научного фонда (проект № 19-12-00432).