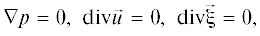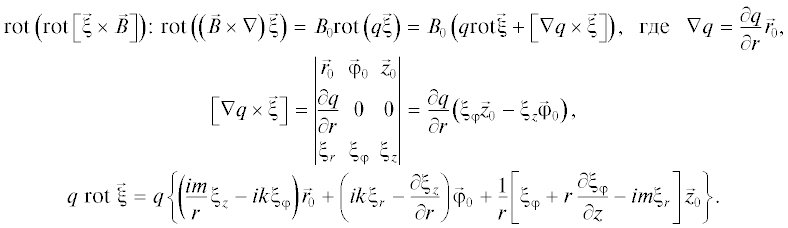ВВЕДЕНИЕ

Известно, что магнитное облако является наиболее геомагнитоэффективным корональным плазменным потоком, вызывающим глобальные геомагнитные бури. Впервые такие потоки были обнаружены достаточно давно [1] и введение термина было позднее [2]. Магнитные облака представляют собой магнитные трубки, имеющие в эклиптическом сечении размеры, превышающие несколько тысяч радиусов Земли (рис. 1а). В 1974 г. по прямым измерениям межпланетного магнитного поля (ММП) на космических аппаратах (КА) были обнаружены специфические структурные области межпланетных возмущений, характеризующиеся сильными регулярными ММП и резким фронтом (сильным разрывом) [3, 4]. Эти области были условно названы “магнитными областями”. В дальнейшем, начиная с 1981 г., их стали называть “магнитными облаками” по терминологии, предложенной в 50-х гг. [5]. Эти выбросы солнечного коронального вещества характеризуются значительным вращением вектора магнитного поля, сильным магнитным полем, низкой температурой ионов и низким динамическим давлением [6, 7]. Они могут содержать в своем объеме значительную отрицательную вертикальную Bz компоненту ММП [8] и поэтому вызывают наиболее интенсивные магнитные бури [9, 10]. В наших работах [11–13] также обращено внимание на физическую связь суббуревого процесса с магнитными облаками.

Рис. 1.

Схематическое изображение облака в виде магнитной трубки (а); фрагмент модельного цилиндрического магнитного облака (б).

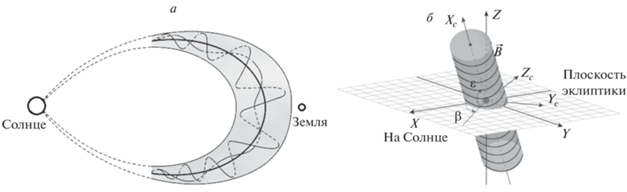
В настоящее время существует несколько моделей для описания структуры магнитных облаков. Наиболее распространенным является бессиловой подход [14]. Он предполагает, что токи в облаке параллельны (антипараллельны) линиям магнитного поля, а перпендикулярная компонента тока отсутствует. Этот подход используют для тороидальной [15, 16] или цилиндрической [17, 18] конфигураций поля в облаке. Для более точного приближения рассматриваемых моделей к реальному магнитному облаку для учета особенностей его переноса в межпланетном пространстве в модель облака добавляют его взаимодействие с солнечным ветром. В результате этого форма модельного облака меняется, отклоняясь от цилиндрической [19, 20]. Описание магнитных облаков выполняется также на не бессиловых моделях, в которых учитывается наличие в облаке не нулевой перпендикулярной компоненты тока [21]. Все эти модели и приближения согласуются друг с другом и, как показано в [19], усложнение модели в действительности не ведет к существенным уточнениям основных параметров облаков – величины магнитного поля на оси облака, его радиуса, прицельного параметра по отношению к Земле, углов наклона к плоскости эклиптики (углы β, ε на рис. 1б). Поскольку именно эти характеристики облаков являются ключевыми с точки зрения их геоэффективности [22–25], то в своих исследованиях мы используем простейшую бессиловую цилиндрическую модель [26–28].

Уравнения, описывающие распределение магнитного поля в бессиловой модели облака, получают исходя из уравнений Максвелла. Модельное представление цилиндрического магнитного облака показано на рис. 1б.

Работа посвящена аналитическому определению радиального распределения азимутальных и продольных возмущений компонент магнитного поля в теле коронального потока типа магнитного облака солнечного ветра. Найденные распределения далее сопоставляются с зарегистрированными параметрами возмущений магнитного поля на патрульном космическом аппарате (КА), пересекаемом телом магнитного облака. Инструментом для оценки качества выполненных аналитических расчетов выступает корреляционный анализ.

АНАЛИТИЧЕСКИЕ РАСЧЕТЫ В РАМКАХ МАГНИТОГИДРОДИНАМИЧЕСКОГО ПОДХОДА

Получим аналитические особенности радиального распределения магнитогидродинамических (МГД) возмущений компонент магнитного поля в модельном теле облака солнечного ветра в виде бессиловой бесконечной цилиндрической трубки со спиральным магнитным полем. Исследование возмущений выполняем в цилиндрической системе координат. Магнитогидродинамический подход дает возможность искать решение системы уравнения в виде радиальной зависимости малых гармонических азимутальных и продольных возмущений. В заключение аналитических расчетов получена система уравнений для радиальных зависимостей компонент возмущения магнитного поля в модельном облаке, которая позволяет перейти к уравнению второго порядка для смещения среды. Далее полученное уравнение решается численным методом.

Запишем исходную систему магнитогидродинамических уравнений в виде:

$\begin{gathered} \rho \frac{{d\vec {u}}}{{dt}} = - \nabla p + \frac{1}{c}\left[ {\vec {j} \times \vec {B}} \right],\,\,\,\,\frac{{d\rho }}{{dt}} + \rho {\text{div}}\vec {u} = 0, \\ {\text{rot}}\vec {B} = \frac{{4\pi }}{c}\vec {j},\,\,\,\,{\text{div}}\vec {B} = 0,\,\,\,\,{\text{rot}}\vec {E} = - \frac{1}{c}\frac{{\partial{ \vec {B}}}}{{\partial t}}. \\ \end{gathered} $

Модель спирального магнитного поля облака представляется следующими выражениями для компонент магнитного поля в цилиндрической системе координат [29]: $rot\vec {B} = \alpha \vec {B}$ ${{B}_{r}} = 0$ ${{B}_{Z}} = {{B}_{0}}{{J}_{0}}(\alpha r)$ ${{B}_{\varphi }} = {{B}_{0}}{{J}_{1}}(\alpha r),$ где $\alpha = \frac{{2.4}}{a},$ а – радиус цилиндрического облака, коэффициент 2.4 является первым корнем функции Бесселя. J0, J1 – функции Бесселя нулевого и первого порядка, являющихся каноническими решениями дифференциального уравнения Бесселя.

Обозначим смещение среды через ${{\vec {\xi },}}$ тогда скорость $\vec {u} = \frac{{\partial {{\vec {\xi }}}}}{{\partial t}}.$ При этом примем, что среда магнитного облака удовлетворяет следующим условиям:

где р – давление.

Считаем возмущения параметров среды (смещения ${{\vec {\xi }}}$) и магнитного поля ($\vec {b} \ll \vec {B}$) малыми, а поток среды отсутствующим. Последнее допущение возможно, поскольку за время пересечения облака космическим аппаратом оно практически не меняет свою геометрию. Тогда, исходя из уравнения магнитной гидродинамики ${\text{rot}}\vec {E} = - \frac{1}{c}\frac{{\partial{ \vec {B}}}}{{\partial t}},$ обобщенного уравнения Ома $\vec {E} = \frac{1}{с}\left[ {\vec {u} \times \vec {B}} \right] + \frac{{\vec {j}}}{\sigma }$ в условиях бесконечной проводимости $\sigma \to \infty $ для малых возмущений магнитного поля и смещения среды и, учитывая, что $\vec {u} = \frac{{\partial {{\vec {\xi }}}}}{{\partial t}},$ получим соотношение $\frac{{\partial{ \vec {b}}}}{{\partial t}} = {\text{rot}}\left[ {\frac{{\partial{ \vec {\xi }}}}{{\partial t}} \times \vec {B}} \right],$ дающее соотношение рассматриваемых возмущений: $\vec {b} = {\text{rot}}\left[ {\vec {\xi } \times \vec {B}} \right].$

В этом случае, согласно оставшимся МГД уравнениям, уравнение для возмущения смещения будет иметь вид:

(1)
$\begin{gathered} \frac{{{{\partial }^{2}}\vec {\xi }}}{{\partial {{t}^{2}}}} = \frac{1}{{4\pi \rho }}\left[ {\left( {{\text{rot\;}}\left( {{\text{rot}}\left[ {\vec {\xi } \times \vec {B}} \right]} \right)} \right) \times \vec {B}} \right] + \\ + \,\,\frac{1}{{4\pi \rho }}\left[ {{\text{rot}}\vec {B} \times {\text{rot}}\left[ {\vec {\xi } \times \vec {B}} \right]} \right]. \\ \end{gathered} $

Поскольку вычисления проводятся в цилиндрической системе координат, то для малых гармонических возмущений следует принять [29, 30]: $\vec {b},\vec {\xi } \sim \exp \left( { - i\omega t + im\varphi + ikz} \right).$ Далее вычисляем члены, входящие в уравнение (1) для смещения:

${\text{1) rot}}\left[ {\vec {\xi } \times \vec {B}} \right] = \left( {\vec {B}\nabla } \right)\vec {\xi } - \left( {\vec {\xi }\nabla } \right)\vec {B}.$

Учитывая $\nabla \Psi = \frac{{\partial \Psi }}{{\partial r}}{{\vec {r}}_{0}} + \frac{1}{r}\frac{{\partial \Psi }}{{\partial \varphi }}{{\vec {\varphi }}_{0}} + \frac{{\partial \Psi }}{{\partial z}}{{\vec {z}}_{0}}$ для произвольной скалярной функции Ψ получаем

$\begin{gathered} \left( {\vec {B}\nabla } \right)\vec {\xi } = \left( {{{B}_{\varphi }}\frac{1}{r}\frac{\partial }{{\partial \varphi }} + {{B}_{z}}\frac{\partial }{{\partial z}}} \right)\vec {\xi } = \\ = \,\,\left( {{{B}_{\varphi }}\frac{{im}}{r} + ik{{B}_{z}}} \right)\vec {\xi } = {{B}_{0}}q\left( r \right)\vec {\xi }, \\ \end{gathered} $
где $q = \frac{{im}}{r}{{J}_{1}} + ik{{J}_{0}}$

$\left( {\vec {\xi }\nabla } \right)\vec {B} = \left( {{{\xi }_{r}}\frac{\partial }{{\partial r}} + {{\xi }_{\varphi }}\frac{1}{r}\frac{\partial }{{\partial \varphi }}} \right)\left( {{{B}_{\varphi }}{{{\vec {\varphi }}}_{0}} + {{B}_{z}}{{{\vec {z}}}_{0}}} \right).$

Принимая во внимание модель магнитного поля, учтем следующие выражения:

$\begin{gathered} \frac{{d{{J}_{0}}\left( {\alpha r} \right)}}{{dr}} = - \alpha {{J}_{1}}\left( {\alpha r} \right),\,\,\,\,\frac{\partial }{{\partial r}}{{B}_{r}} = - \alpha {{B}_{0}}{{J}_{1}}\left( {\alpha r} \right), \\ \frac{{d{{J}_{1}}\left( {\alpha r} \right)}}{{dr}} = \frac{\alpha }{2}\left[ {{{J}_{0}}\left( {\alpha r} \right) - {{J}_{2}}\left( {\alpha r} \right)} \right],\,\,\,\, \\ \frac{{\partial {{B}_{\varphi }}}}{{\partial r}} = \frac{{\alpha {{B}_{0}}}}{2}\left( {{{J}_{0}} - {{J}_{2}}} \right) = \alpha {{B}_{0}}f\left( r \right), \\ {\text{где}}\,\,f = \frac{1}{2}\left( {{{J}_{0}} - {{J}_{2}}} \right). \\ \end{gathered} $

Учитывая, что, согласно [29, 30], $\frac{{\partial {{{\vec {\varphi }}}_{0}}}}{{\partial \varphi }} = - {{\vec {r}}_{0}},$ получаем

$\left( {\vec {\xi }\nabla } \right)\vec {B} = \alpha {{B}_{0}}{{\xi }_{r}}\left( {f{{{{{\vec {\varphi }}}}}_{0}} - {{J}_{1}}{{{\vec {z}}}_{0}}} \right) - \frac{{{{\xi }_{\varphi }}}}{r}{{B}_{0}}{{J}_{1}}{{r}_{0}}$
и далее запишем выражение для ротора в уравнении (1)

${\text{rot}}\left[ {\vec {\xi } \times \vec {B}} \right] = {{B}_{0}}\left[ {q\vec {\xi } + \alpha {{\xi }_{r}}\left( { - f{{{\vec {\varphi }}}_{0}} + {{J}_{1}}{{{\vec {z}}}_{0}}} \right) + \frac{{{{\xi }_{\varphi }}}}{r}{{J}_{1}}{{{\vec {r}}}_{0}}} \right].$

2) Принимая во внимание, что ${\text{rot}}{{\vec {\varphi }}_{0}} = \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r \times {{1}_{\varphi }}} \right){{\vec {z}}_{0}} = \frac{{{{z}_{0}}}}{r}.$

Вычисляем члены, возникающие вследствие действия второго ротора в (1)

Применим сокращение записи для ${\text{rot}}\left( {q\vec {\xi }} \right) = A{{\vec {r}}_{0}} + B{{\vec {\varphi }}_{0}} + C{{\vec {z}}_{0}},$

${\text{где}}\,\,\left\{ \begin{gathered} A = q\left( {\frac{{im}}{r}{{\xi }_{z}} - ik{{\xi }_{\varphi }}} \right) \hfill \\ B = q\left( {ik{{\xi }_{r}} - \frac{{\partial {{\xi }_{z}}}}{{\partial r}}} \right) - \frac{{\partial q}}{{\partial r}}{{\xi }_{z}} \hfill \\ C = \frac{q}{r}\left( {{{\xi }_{\varphi }} + r\frac{{\partial {{\xi }_{\varphi }}}}{{\partial r}} - im{{\xi }_{r}}} \right) + \frac{{\partial q}}{{\partial r}}{{\xi }_{r}} \hfill \\ \end{gathered} \right..$

Далее вычисляем члены, входящие в выражение:

$\begin{gathered} {\text{rot}}\left( {\left( {\vec {\xi }\nabla } \right)\vec {B}} \right) = {\text{rot}}\left( {\alpha {{B}_{0}}{{\xi }_{r}}\left( {f{{{\vec {\varphi }}}_{0}} - {{J}_{1}}{{{\vec {z}}}_{0}}} \right) - \frac{{{{\xi }_{\varphi }}}}{r}{{B}_{0}}{{J}_{1}}{{r}_{0}}} \right), \\ {\text{rot}}\left( {{{\xi }_{r}}f{{{\vec {\varphi }}}_{0}}} \right) = {{\xi }_{r}}f{\text{rot}}{{{{{\vec {\varphi }}}}}_{0}} + \left[ {\nabla \left( {{{\xi }_{r}}f} \right) \times {{{\vec {\varphi }}}_{0}}} \right],\,\,\,\,{\text{где}}\,\,\,\,{\text{rot}}{{{\vec {\varphi }}}_{0}} = \frac{{{{z}_{0}}}}{r}, \\ \nabla \left( {{{\xi }_{r}}f} \right) = f\nabla {{\xi }_{r}} + {{\xi }_{r}}\nabla f = f\left( {\frac{{\partial {{\xi }_{r}}}}{{\partial r}}{{{\vec {r}}}_{0}} + \frac{1}{r}\frac{{\partial {{\xi }_{r}}}}{{\partial \varphi }}\vec {\varphi }{{~}_{0}}\, + \frac{{\partial {{\xi }_{r}}}}{{\partial z}}{{{\vec {z}}}_{0}}} \right) = \\ = 1\left( {\frac{{\partial {{\xi }_{r}}}}{{\partial r}}{{{\vec {r}}}_{0}} + \frac{{im}}{r}\frac{{\partial {{\xi }_{r}}}}{{\partial \varphi }}{{{\vec {\varphi }}}_{0}} + ik{{\xi }_{z}}{{{\vec {z}}}_{0}}} \right) + {{\xi }_{r}}\frac{{\partial f}}{{\partial r}}{{{\vec {r}}}_{0}}, \\ \nabla \left( {{{\xi }_{r}}f} \right) = \left( {f\frac{{\partial {{\xi }_{r}}}}{{\partial r}} + {{\xi }_{r}}\frac{{\partial f}}{{\partial r}}} \right){{{\vec {r}}}_{0}} + f\frac{{im}}{r}{{\xi }_{r}}{{{\vec {\varphi }}}_{0}} + \left( {ikf{{\xi }_{r}} + \frac{{{{\xi }_{r}}f}}{r}} \right){{{\vec {z}}}_{0}}, \\ \left[ {\nabla \left( {{{\xi }_{r}}f} \right) \times {{{\vec {\varphi }}}_{0}}} \right] = \left( {\begin{array}{*{20}{c}} {{{{\vec {r}}}_{0}}}&{{{{\vec {\varphi }}}_{0}}}&{{{{\vec {z}}}_{0}}} \\ {f\frac{{\partial {{\xi }_{r}}}}{{\partial r}} + {{\xi }_{r}}\frac{{\partial f}}{{\partial r}}}&{\frac{{im}}{r}f{{\xi }_{r}}}&{\frac{{{{\xi }_{r}}f}}{r} + ikf{{\xi }_{r}}} \\ 0&1&0 \end{array}} \right) = - f{{\xi }_{r}}\left( {\frac{1}{r} + ik} \right){{{\vec {r}}}_{0}} + \left( {f\frac{{\partial {{\xi }_{r}}}}{{\partial r}} + {{\xi }_{r}}\frac{{\partial f}}{{\partial r}}} \right){{{\vec {z}}}_{0}}. \\ \end{gathered} $
Тогда ${\text{rot}}\left( {{{\xi }_{r}}f{{{\vec {\varphi }}}_{0}}} \right)$ = $ - f{{\xi }_{r}}\left( {\frac{1}{r} + ik} \right){{\vec {r}}_{0}}$ +  $ - f{{\xi }_{r}}\left( {\frac{1}{r} + ik} \right){{\vec {r}}_{0}} + \,\,\left( {f\frac{{\partial {{\xi }_{r}}}}{{\partial r}} + {{\xi }_{r}}\frac{{\partial f}}{{\partial r}} + {{\xi }_{r}}\frac{f}{r}} \right){{\vec {z}}_{0}}$
${\text{rot}}\left( {{{\xi }_{r}}{{J}_{1}}{{{\vec {z}}}_{0}}} \right) = {{\xi }_{r}}{{J}_{1}}{\text{rot}}{{\vec {z}}_{0}} + \left[ {\nabla \left( {{{\xi }_{r}}{{J}_{1}}} \right) \times {{{\vec {z}}}_{0}}} \right].$
Здесь ${\text{rot\;}}{{\vec {z}}_{0}} = 0$
$\begin{gathered} \nabla \left( {{{\xi }_{r}}{{J}_{1}}} \right) = {{\xi }_{r}}\nabla {{J}_{1}} + {{J}_{1}}\nabla {{\xi }_{r}} = {{\xi }_{r}}\frac{{\partial {{J}_{1}}}}{{\partial r}}{{{\vec {r}}}_{0}} + \,{{J}_{1}}\left( {\frac{{\partial {{\xi }_{r}}}}{{\partial r}}{{{\vec {r}}}_{0}} + \frac{{im}}{r}{{\xi }_{r}}{{{\vec {\varphi }}}_{0}} + ik{{\xi }_{r}}{{{\vec {z}}}_{0}}} \right) = \left( {{{\xi }_{r}}\frac{{\partial {{J}_{1}}}}{{\partial r}} + {{J}_{1}}\frac{{\partial {{\xi }_{r}}}}{{\partial r}}} \right){{{\vec {r}}}_{0}}\, + \\ + \,\,{{J}_{1}}\frac{{im}}{r}{{\xi }_{r}}{{{\vec {\varphi }}}_{0}} + {{J}_{1}}ik{{\xi }_{r}}{{{\vec {z}}}_{0}},\,\,\,\,\left[ {\nabla \left( {{{\xi }_{r}}{{J}_{1}}} \right) \times {{{\vec {z}}}_{0}}} \right] = \left( {\begin{array}{*{20}{c}} {{{{\vec {r}}}_{0}}}&{{{{\vec {\varphi }}}_{0}}}&{{{{\vec {z}}}_{0}}} \\ {\frac{\partial }{{\partial r}}\left( {{{\xi }_{r}}{{J}_{1}}} \right)}&{\frac{{im}}{r}{{J}_{1}}{{\xi }_{r}}}&{ik{{J}_{1}}{{\xi }_{r}}} \\ 0&0&1 \end{array}} \right) = \\ = \,\,\frac{{im}}{r}{{J}_{1}}{{\xi }_{r}}{{{\vec {r}}}_{0}} - \left( {\frac{\partial }{{\partial r}}\left( {{{\xi }_{r}}{{J}_{1}}} \right)} \right){{{\vec {\varphi }}}_{0}},\,\,\,\,{\text{rot}}\left( {{{\xi }_{\varphi }}\frac{{{{J}_{1}}}}{r}{{{\vec {r}}}_{0}}} \right) = {{\xi }_{\varphi }}\frac{{{{J}_{1}}}}{r}{\text{rot\;}}{{{\vec {r}}}_{0}} + \left[ {\nabla \left( {{{\xi }_{\varphi }}\frac{{{{J}_{1}}}}{r}} \right) \times {{{\vec {r}}}_{0}}} \right]. \\ \end{gathered} $
Здесь ${\text{rot\;}}{{\vec {r}}_{0}} = 0$

$\begin{gathered} \nabla \left( {{{\xi }_{\varphi }}\frac{{{{J}_{1}}}}{r}} \right) = {{\xi }_{\varphi }}\nabla \left( {\frac{{{{J}_{1}}}}{r}} \right) + \frac{{{{J}_{1}}}}{r}\nabla {{\xi }_{\varphi }} = {{\xi }_{\varphi }}\frac{\partial }{{\partial r}}\left( {\frac{{{{J}_{1}}}}{r}} \right){{{\vec {r}}}_{0}} + \,\,\frac{{{{J}_{1}}}}{r}\left( {\frac{{\partial {{\xi }_{\varphi }}}}{{\partial r}}{{{\vec {r}}}_{0}} + \frac{{im}}{r}{{\xi }_{\varphi }}{{{\vec {\varphi }}}_{0}} + ik{{\xi }_{\varphi }}{{{\vec {z}}}_{0}}} \right) = \\ = \,\,\left[ {{{\xi }_{\varphi }}\frac{\partial }{{\partial r}}\left( {\frac{{{{J}_{1}}}}{r}} \right) + \frac{{{{J}_{1}}}}{r}\frac{{\partial {{\xi }_{\varphi }}}}{{\partial r}}} \right]{{{\vec {r}}}_{0}} + \,\,\,\frac{{{{J}_{1}}{{\xi }_{\varphi }}}}{r}\left( {\frac{{im}}{r}{{{\vec {\varphi }}}_{0}} + ik{{{\vec {z}}}_{0}}} \right)\left[ {\nabla \left( {{{\xi }_{\varphi }}\frac{{{{J}_{1}}}}{r}} \right) \times {{{\vec {r}}}_{0}}} \right] = \\ = \left( {\begin{array}{*{20}{c}} {{{{\vec {r}}}_{0}}}&{{{{\vec {\varphi }}}_{0}}}&{{{{\vec {z}}}_{0}}} \\ {\left[ {{{\xi }_{\varphi }}\frac{\partial }{{\partial r}}\left( {\frac{{{{J}_{1}}}}{r}} \right) + \frac{{{{J}_{1}}}}{r}\frac{{\partial {{\xi }_{\varphi }}}}{{\partial r}}} \right]}&{\frac{{{{J}_{1}}{{\xi }_{\varphi }}im}}{{{{r}^{2}}}}}&{\frac{{{{J}_{1}}{{\xi }_{\varphi }}ik}}{r}} \\ 1&0&0 \end{array}} \right) = \, - \frac{{{{J}_{1}}{{\xi }_{\varphi }}ik}}{r}{{{\vec {\varphi }}}_{0}} - \,\,\frac{{{{J}_{1}}{{\xi }_{\varphi }}im}}{{{{r}^{2}}}}{{{\vec {z}}}_{0}} = \\ = \,\, - \frac{{{{J}_{1}}{{\xi }_{\varphi }}}}{r}\left( {ik{{{\vec {\varphi }}}_{0}} + \frac{{im}}{r}{{{\vec {z}}}_{0}}} \right) = {\text{rot}}\left( {{{\xi }_{\varphi }}\frac{{{{J}_{1}}}}{r}{{{\vec {r}}}_{0}}} \right). \\ \end{gathered} $

Таким образом найдены все члены уравнения для смещения:

$\frac{{{{\partial }^{2}}{{\vec {\xi }}}}}{{\partial {{t}^{2}}}} = \frac{1}{{4\pi \rho }}\left[ {\left( {{\text{rot\;}}\left( {{\text{rot}}\left[ {\vec {\xi } \times \vec {B}} \right]} \right)} \right) \times \vec {B}} \right] + \,\,\frac{1}{{4\pi \rho }}\left[ {{\text{rot}}\vec {B} \times {\text{rot}}\left[ {\vec {\xi } \times \vec {B}} \right]} \right] = \frac{1}{{4\pi \rho }}\vec {h} + \frac{1}{{4\pi \rho }}\vec {g}{\text{.}}$

В скалярной форме, после введения в обозначения составляющих hi и gi компонент векторов $\vec {h}$ и $\vec {g}{\text{,}}$ уравнение примет вид:

$\begin{gathered} - \frac{{{{\omega }^{2}}}}{{V_{A}^{2}}}{{\xi }_{r}} = {{h}_{{1r}}} + \alpha {{h}_{{2r}}} + \alpha {{h}_{{3r}}} + {{h}_{{4r}}} + \alpha {{g}_{{1r}}} + \alpha {{g}_{{2r}}} + \alpha {{g}_{{3r}}}; \\ - \frac{{{{\omega }^{2}}}}{{V_{A}^{2}}}{{\xi }_{\varphi }} = {{h}_{{1\varphi }}} + \alpha {{h}_{{2\varphi }}} + \alpha {{h}_{{3\varphi }}} + \alpha {{g}_{{1\varphi }}} + \alpha {{g}_{{4\varphi }}};\,\, - \frac{{{{\omega }^{2}}}}{{V_{A}^{2}}}{{\xi }_{z}} = {{h}_{{1z}}} + \alpha {{h}_{{2z}}} + \alpha {{h}_{{3z}}} + \alpha {{g}_{{1z}}}{{J}_{1}}{{\xi }_{r}}q + \alpha {{g}_{{4z}}}. \\ \end{gathered} $

Выполним вычисление составляющих вектора $\vec {h} = \left[ {{\text{rot}}\left( {{\text{rot}}\left[ {\vec {\xi } \times \vec {B}} \right]} \right) \times \vec {B})} \right],$ следуя модели ${\text{rot}}\vec {B} = \alpha \vec {B} = \beta {{B}_{0}}\left( {{{J}_{1}}{{{\vec {\varphi }}}_{0}} + {{J}_{0}}{{{\vec {z}}}_{0}}} \right)$ магнитного поля в облаке:

$\begin{gathered} {{{\vec {h}}}_{1}} = \left( {\begin{array}{*{20}{c}} {{{{\vec {r}}}_{0}}}&{{{{{{\vec {\varphi }}}}}_{0}}}&{{{{\vec {z}}}_{0}}} \\ A&B&C \\ 0&{{{J}_{1}}}&{{{J}_{0}}} \end{array}} \right) = {{{\vec {r}}}_{0}}\left( {B{{J}_{0}} - C{{J}_{1}}} \right) - {{{{{\vec {\varphi }}}}}_{0}}A{{J}_{0}} + {{{\vec {z}}}_{0}}A{{J}_{1}}, \\ {{{\vec {h}}}_{3}} = \left( {\begin{array}{*{20}{c}} {{{{\vec {r}}}_{0}}}&{{{{\vec {\varphi }}}_{0}}}&{{{{\vec {z}}}_{0}}} \\ {\frac{{im}}{r}{{J}_{1}}{{\xi }_{r}}}&{ - \frac{\partial }{{\partial r}}\left( {{{\xi }_{r}}{{J}_{1}}} \right)}&0 \\ 0&{{{J}_{1}}}&{{{J}_{0}}} \end{array}} \right) = - {{J}_{0}}\frac{\partial }{{\partial r}}\left( {{{\xi }_{r}}{{J}_{1}}} \right){{{\vec {r}}}_{0}} - \,\,{{J}_{0}}\frac{{im}}{r}{{J}_{1}}{{\xi }_{r}}{{{{{\vec {\varphi }}}}}_{0}} + \frac{{im}}{r}J_{1}^{2}{{\xi }_{r}}{{{\vec {z}}}_{0}},\,\,\,\, \\ {{{\vec {h}}}_{4}} = \left( {\begin{array}{*{20}{c}} {{{{\vec {r}}}_{{\text{0}}}}}&{{{{\vec {\varphi }}}_{0}}}&{{{{\vec {z}}}_{0}}} \\ 0&{ - \frac{{{{J}_{1}}{{\xi }_{\varphi }}}}{r}ik}&{ - \frac{{{{J}_{1}}{{\xi }_{\varphi }}im}}{{{{r}^{2}}}}} \\ 0&{{{J}_{1}}}&{{{J}_{0}}} \end{array}} \right) = {{{\vec {r}}}_{0}}\left( {\frac{{J_{1}^{2}{{\xi }_{\varphi }}im}}{{{{r}^{2}}}} - \frac{{{{J}_{1}}{{J}_{0}}{{\xi }_{\varphi }}ik}}{r}} \right) = \frac{{{{J}_{1}}{{\xi }_{\varphi }}}}{r}\left( {\frac{{{{J}_{1}}im}}{r} - {{J}_{0}}ik} \right){{{\vec {r}}}_{0}}. \\ \end{gathered} $

Вычисление составляющих вектора $\vec {g} = \left[ {{\text{rot}}\vec {B} \times {\text{rot}}\left[ {\vec {\xi } \times \vec {B}} \right]} \right],$ следуя модели ${\text{rot}}\vec {B} = \alpha \vec {B} = \beta {{B}_{0}}\left( {{{J}_{1}}{{{\vec {\varphi }}}_{0}} + {{J}_{0}}{{{\vec {z}}}_{0}}} \right)$ магнитного поля в облаке:

$\begin{gathered} {{{\vec {g}}}_{1}} = \left( {\begin{array}{*{20}{c}} {{{{\vec {r}}}_{0}}}&{{{{\vec {\varphi }}}_{0}}}&{{{{\vec {z}}}_{0}}} \\ 0&{{{J}_{1}}}&{{{J}_{0}}} \\ {{{\xi }_{r}}}&{{{\xi }_{\varphi }}}&{{{\xi }_{z}}} \end{array}} \right) = {{{\vec {r}}}_{0}}\left( {{{J}_{1}}{{\xi }_{z}} + {{J}_{0}}{{\xi }_{\varphi }}} \right) + {{{\vec {\varphi }}}_{0}}{{J}_{0}}{{\xi }_{r}} - {{{\vec {z}}}_{0}}{{\xi }_{r}}{{J}_{1}}, \\ {{{\vec {g}}}_{2}} = \left( {\begin{array}{*{20}{c}} {{{{\vec {r}}}_{0}}}&{{{{\vec {\varphi }}}_{0}}}&{{{{\vec {z}}}_{0}}} \\ 0&{{{J}_{1}}}&{{{J}_{0}}} \\ 0&{ - f}&0 \end{array}} \right) = {{{\vec {r}}}_{0}}{{J}_{0}}f,\,\,\,\,{{{\vec {g}}}_{3}} = \left( {\begin{array}{*{20}{c}} {{{{\vec {r}}}_{0}}}&{{{{\vec {\varphi }}}_{0}}}&{{{{\vec {z}}}_{0}}} \\ 0&{{{J}_{1}}}&{{{J}_{0}}} \\ 0&0&{{{J}_{1}}} \end{array}} \right) = {{{\vec {r}}}_{0}}J_{1}^{2}, \\ {{{\vec {g}}}_{4}} = \left( {\begin{array}{*{20}{c}} {{{{\vec {r}}}_{0}}}&{{{{\vec {\varphi }}}_{0}}}&{{{{\vec {z}}}_{0}}} \\ 0&{{{J}_{1}}}&{{{J}_{0}}} \\ {\frac{{{{\xi }_{\varphi }}{{J}_{1}}}}{r}}&0&0 \end{array}} \right) = {{{\vec {\varphi }}}_{0}}\frac{{{{\xi }_{\varphi }}{{J}_{0}}{{J}_{1}}}}{r} - {{{\vec {z}}}_{0}}\frac{{{{\xi }_{\varphi }}J_{1}^{2}}}{r}. \\ \end{gathered} $

Окончательно система уравнений для расчета смещений имеет следующий вид:

$\begin{gathered} - \frac{{{{\omega }^{2}}}}{{V_{A}^{2}}}{{\xi }_{r}} = \left( {{{J}_{0}}B - {{J}_{1}}C} \right) + \alpha {{J}_{1}}\left( {\frac{\partial }{{\partial r}}\left( {f{{\xi }_{r}}} \right) + \frac{{{{\xi }_{r}}f}}{r}} \right) - \alpha {{J}_{0}}\frac{\partial }{{\partial r}}\left( {{{\xi }_{r}}{{J}_{1}}} \right) + \\ + \,\,\left( {{{J}_{1}}\frac{{im}}{r} - {{J}_{0}}ik} \right)\frac{{{{J}_{1}}{{\xi }_{\varphi }}}}{r} + \alpha \left( {q\left( {{{J}_{1}}{{\xi }_{z}} - {{J}_{0}}{{\xi }_{\varphi }}} \right) + \alpha {{J}_{0}}f{{\xi }_{r}} + \alpha J_{1}^{2}{{\xi }_{r}}} \right); \\ - \frac{{{{\omega }^{2}}}}{{V_{A}^{2}}}{{\xi }_{\varphi }} = - A{{J}_{0}} - \alpha {{J}_{0}}f{{\xi }_{r}}\left( {1 + ik} \right) - \alpha {{J}_{0}}{{J}_{1}}\frac{{im}}{r}{{\xi }_{r}} + \alpha {{J}_{0}}{{\xi }_{r}}q + \alpha {{\xi }_{\varphi }}\frac{{{{J}_{0}}{{J}_{1}}}}{r}; \\ - \frac{{{{\omega }^{2}}}}{{V_{A}^{2}}}{{\xi }_{z}} = A{{J}_{1}} + \alpha {{J}_{1}}f{{\xi }_{r}}\left( {1 + ik} \right) + \alpha J_{1}^{2}\frac{{im}}{r}{{\xi }_{r}} - \alpha {{J}_{1}}{{\xi }_{r}}q - \alpha {{\xi }_{\varphi }}\frac{{J_{1}^{2}}}{r}; \\ A = q\left( {\frac{{im}}{r}{{\xi }_{z}} - ik{{\xi }_{\varphi }}} \right);\,\,\,\,B = q\left( {ik{{\xi }_{r}} - \frac{{\partial {{\xi }_{z}}}}{{\partial r}}} \right) - q{{\xi }_{z}}; \\ C = \frac{q}{r}\left( {{{\xi }_{\varphi }} + r\frac{{\partial {{\xi }_{\varphi }}}}{{\partial r}} - im{{\xi }_{r}}} \right) + \frac{{\partial q}}{{\partial r}}{{\xi }_{\varphi }};\,\,\,\,q = \frac{{im}}{r}{{J}_{1}} + ik{{J}_{0}};\,\,\,\,f = \frac{1}{2}\left( {{{J}_{0}} - {{J}_{2}}} \right). \\ \end{gathered} $

Интересующее нас распределение возмущения магнитного поля определяется согласно уравнению

$\frac{{\partial{ \vec {B}}}}{{\partial t}} = {\text{rot}}\left[ {\vec {u} \times \vec {B}} \right]$
и записывается в виде
$\begin{gathered} \vec {b} = {\text{rot}}\left[ {\vec {\xi } \times \vec {B}} \right] = \\ = \,\,{{B}_{0}}\left[ {q\vec {\xi } + \alpha {{\xi }_{r}}\left( { - f{{{\vec {\varphi }}}_{0}} + {{J}_{1}}{{{\vec {z}}}_{0}}} \right) + \frac{{{{\xi }_{\varphi }}}}{r}{{J}_{1}}{{{\vec {r}}}_{0}}} \right], \\ \end{gathered} $
где $\vec {B}$ – значение фонового магнитного поля в конкретных точках внутри магнитного облака.

СОПОСТАВЛЕНИЕ РАСЧЕТНЫХ НИЗКОЧАСТОТНЫХ ХАРАКТЕРИСТИК МОДЕЛЬНОГО СПИРАЛЬНОГО МАГНИТНОГО ОБЛАКА СОЛНЕЧНОГО ВЕТРА С ЗАРЕГИСТРИРОВАННЫМИ ВОЗМУЩЕНИЯМИ

Решение системы уравнений с целью получения радиального распределения компонент смещения для возмущений на разных частотах как параметров продолжено итерационным алгоритмом Эйлера [31]. В качестве граничного условия было выбрано отсутствие смещения на поверхности магнитной трубки ${{\xi }_{r}}(r = a) = 0.$

Известно, что метод Эйлера применяется для решения систем дифференциальных уравнений или дифференциальных уравнений высших порядков с предварительным приведением к системам уравнений первого порядка. Используя формулы Эйлера вычисляются параметры для следующей итерации и на каждой последующей итерации записываются значения найденных функций и их производных. Расчет прекращался при выполнении одного из условий: достигнуты предельное число итераций или граница расчетной области. Как показал численный счет, метод Эйлера продемонстрировал устойчивое решение системы уравнений для расчетной области согласующейся с областями реально наблюдаемых тел облаков. Результаты численного счета приведены ниже на рис. 2 и 3.

Рис. 2.

Сопоставление результатов счета (красные кривые – Bφ выч, Bz выч) с реальными данными (синие кривые – Bφ реал, Bz реал) для тела 22.01.2000. Сопоставление Bφ реал, Bφ выч, R = 0.43 (а); сопоставление Bz реал, Bz выч, R = = 0.47 (б).

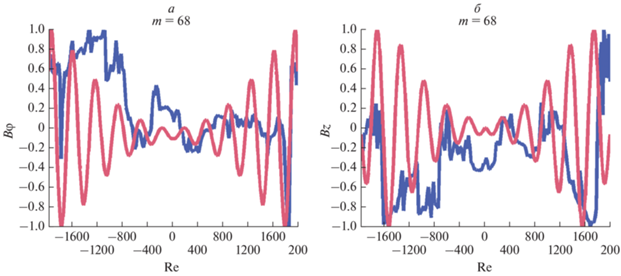
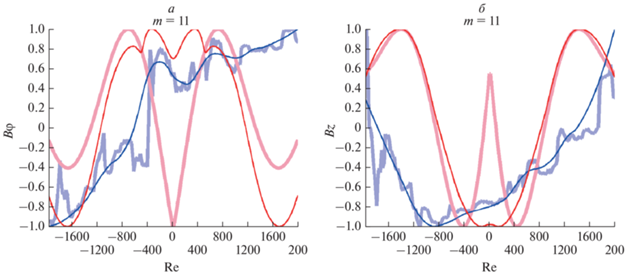
Рис. 3.

Сопоставление результатов счета с реальными данными для тела МО 10.11.2004 показано толстыми линиями. Постобработка цифровым сглаживающим фильтром расчетных и реальных данных представлена тонкими линиями. Красные кривые – Bφ выч, Bz выч, синие кривые – Bφ реал, Bz реал. Сопоставление Bφ реал и Bφ выч дает R = 0.31, после обработки сопоставление Bφ реал и Bφ выч дает R = 0.51 (а); сопоставление Bz реал, Bz выч дает R = 0.44, после обработки сопоставление Bz реал и Bz выч дает R = 0.58 (б).

Сопоставление рассчитанного радиального распределения компонент смещения магнитного поля в теле модельного облака с распределением компонент магнитного поля в теле зарегистрированного МО выполнялась для двух среднестатистических МО, зарегистрированных 22.01.2000 и 10.11.2004. Указаны начальные даты зарегистрированных событий.

Из всего объема имеющихся данных в общедоступных каталогах по МО далеко не все удовлетворяют модельному представлению. Критериями отбора были спиральность магнитного поля и минимальный наклон оси цилиндрического облака к плоскости эклиптики. Это означает, что тела магнитных облаков не всегда вписываются в выбранную идеализированную математическую модель. Найденные нами два МО близкие к идеальной модели мы считаем своей большой удачей. Указанные среднестатистические МО наиболее близки к идеальной математической модели. Данные возмущений взяты с минутным разрешением с КА АСЕ с узла http://cdaweb.gsfc.nasa.gov. Особенностью рассматриваемых облаков является ориентация их потоковой магнитной трубки близкая к вертикальной в солнечно-эклиптической системе координат. Особенностью сопоставления является необходимость замены регистрируемой динамики, т.е. временной зависимости возмущений, регистрируемых при пересечении облаком космического аппарата, на пространственное распределение возмущений. Это можно делать для низкочастотных возмущений с периодами сопоставимыми со временем пересечения. Для анализируемых в исследовании событий МО, время пересечения тела облака космическим аппаратом, составляло приблизительно 10 часов, что и определяло характерные периоды исследуемых возмущений.

Предварительные оценки величин волнового числа k и номера моды m, которые являются независимыми переменными в решаемой системе МГД уравнений, а также сам процесс сопоставления вычисленных и наблюдаемых радиальных распределений установили физические ограничения на диапазон их значений. В численных экспериментах волновое число k для НЧ флуктуаций выбиралось исходя из диапазона периодов, сопоставимых со временем пересечения МО космическим аппаратом. При заданном k номера подходящих мод m подбирались экспериментально таким образом, чтобы при сопоставлении пар азимутальных Bφ и продольных Bz компонент реальных (реал) и вычисленных (выч) возмущений магнитного поля отмечалась согласованность. Так, для МО 10.11.2004 оказалось, что m = 11, для МО 22.01.2000 – m = 68.

Необходимость исключения из рассмотрения незначащих высокочастотных колебаний для концентрации внимания на анализе НЧ флуктуаций компонент межпланетного магнитного поля, потребовала дополнительной обработки получаемых решений. Постобработка результатов счета и сопоставляемых с ними реальных данных выполнялась цифровым сглаживающим фильтром. Из них количественно по результатам корреляционного анализа выбирался наиболее удачный вариант описания связи соответствующих Bφ и Bz компонент. На рисунках 2 и 3 по оси ординат представлена условная амплитуда значений компонент поля, по оси абсцисс – радиальная развертка в масштабах радиуса Земли (Re) по срезу цилиндрической потоковой трубки с осью симметрии в центре. На рис. 2 демонстрируются результаты счета и сопоставляемых с ними реальных данных для тела МО 22.01.2000 без дополнительной обработки. Получены следующие коэффициенты корреляции: R = 0.43 между зарегистрированным Bφ реал и вычисленным Bφ выч; R = 0.47 между зарегистрированным Bz реал и вычисленным Bz выч. На рис. 3 демонстрируется постобработка результатов счета и сопоставляемых с ними реальных данных для тела МО 10.11.2004 цифровым сглаживающим фильтром при анализе периода НЧ флуктуаций 600 мин. Получены следующие коэффициенты корреляции: R = 0.44 между Bφ реал и Bφ выч; R = 0.31 между Bz реал и Bz выч. Постобработка цифровым сглаживающим фильтром расчетных и реальных данных повысила корреляцию: R = 0.51 между Bφ реал и Bφ выч; R = 0.58 между Bz реал и Bz выч.

Сопоставление показало, что аналитико-численное решение дает общее представление о радиальном распределении возмущенных компонент магнитного поля в теле МО, согласующееся с реально зарегистрированной динамикой параметров МО на патрульном КА.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Как видно из представленных графиков, аналитико-численное решение дает общее представление о радиальном распределении компонент смещения магнитного поля в теле магнитного облака для НЧ возмущений, согласующееся с реально зарегистрированной динамикой параметров на патрульном КА. Это подтверждается корреляционным анализом результатов. Совместная постобработка результатов счета и сопоставляемых с ними реальных данных усиливает их согласованность. В ходе исследования обнаружилось, что из всего объема имеющихся данных в общедоступных каталогах по МО далеко не все удовлетворяют модельному представлению в виде цилиндра со спиральным распределением магнитного поля. Это означает, что тела магнитных облаков не всегда вписываются в выбранную идеализированную математическую модель. Разумеется, существует достаточное количество магнитных облаков, которые достаточно близки к этим моделям. Их качественные особенности изучаемых возмущений совпадают с экспериментальными данными, но они формально не дают высокой степени корреляции с экспериментом. В связи с этим мы эти результаты не приводим. Выполненные исследования подтверждают обоснованность выбранной модели для тела магнитного облака и примененного МГД подхода к анализу колебаний в нем. Предлагаемый в исследовании метод может считаться дополнительным к анализу низкочастотных характеристик параметров магнитных облаков методами Фурье- и вейвлет-спектрального анализа.