ВВЕДЕНИЕ

Жидкокристаллические (ЖК) композитные материалы – это многокомпонентные вещества, уникально сочетающие в себе свойства жидких кристаллов (текучесть и анизотропию) с различными особенностями внедренных в них частиц дисперсной фазы [1–6]. ЖК матрицы в таких системах демонстрируют большое разнообразие возможных структур, причем многие из них могут проявляться в одном и том же материале [7]. При континуальном описании ЖК систем для характеристики расположения молекул используют единичный вектор (директор) $\vec {n},$ определяющий преимущественное направление длинных осей молекул. Так, например, в нематическом жидком кристалле (НЖК) – мезофазе, образованной ахиральными молекулами, – минимуму энергии в отсутствие внешних полей и ограничивающих поверхностей соответствует однородная параллельная ориентация молекул, т.е. пространственно однородное поле директора $\vec {n}.$ В средах же, образованных хиральными (несовместимыми со своим зеркальным отражением) молекулами – холестерических жидких кристаллах (ХЖК) – директор спирально закручен в пространстве вокруг некоторой оси, называемой осью холестерической спирали [8, 9]. В зависимости от типа ЖК-матрицы соответствующие свойства проявляются и в композитной жидкокристаллической системе. Однако хиральный ЖК композит, обладающий геликоидальной структурой, можно приготовить не только добавлением в холестерический ЖК примесных частиц, но и при помощи внедрения в нематический ЖК хиральных частиц различной физической природы [10–12].

В данной работе в рамках континуального подхода анализируется равновесная макроскопическая ориентационная структура суспензии хиральных феррочастиц на основе нематического жидкого кристалла в отсутствие внешних полей и границ. Из симметрийных соображений предложен дополнительный вклад в свободную энергию суспензии, описывающий самопроизвольную макроскопическую спиральность (геликоидальность) ориентационной структуры ахирального жидкого кристалла.

ПОСТАНОВКА ЗАДАЧИ

Рассмотрим неограниченный образец ЖК-суспензии хиральных феррочастиц на основе нематического жидкого кристалла, которую для краткости будем называть хиральным ферронематиком (ХФН). Под хиральными феррочастицами в предлагаемой модели ферросуспензии подразумеваются частицы ферромагнетика, обладающие постоянным магнитным моментом и такой формой, которая не совмещается со своим зеркальным отображением при любой комбинации вращений и перемещений. Характерным примером таких частиц являются магнитные наноспирали [13]. В континуальном подходе равновесная структура и равновесные ориентационные переходы в ХФН могут быть изучены из условия минимума функционала полной свободной энергии $F = \int_V {{{F}_{V}}dV} ,$ где объемную плотность свободной энергии рассматриваемой суспензии, учитывая конечное сцепление между примесной и ЖК подсистемами, представим в следующем виде [1, 14, 15]:

(1)
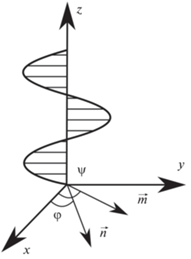
$\begin{gathered} {{F}_{V}} = {{F}_{1}} + {{F}_{2}} + {{F}_{3}} + {{F}_{4}} + {{F}_{5}} + {{F}_{6}}, \\ {{F}_{1}} = \frac{1}{2}\left[ {{{K}_{{11}}}{{{\left( {{\text{div}}\,\vec {n}} \right)}}^{2}}\, + \,{{K}_{{22}}}{{{\left( {\vec {n} \cdot {\text{rot}}\,\vec {n}} \right)}}^{2}}\, + \,{{K}_{{33}}}{{{\left( {\vec {n} \cdot {\text{rot}}\,\vec {n}} \right)}}^{2}}} \right], \\ {{F}_{2}} = - \frac{{Wf}}{d}{{\left( {\vec {n} \cdot \vec {m}} \right)}^{2}},\,\,\,\,{{F}_{3}} = \alpha f\left( {\vec {n} \cdot \vec {m}} \right)\left( {\vec {m} \cdot {\text{rot}}\vec {n}} \right), \\ {{F}_{4}} = \frac{{{{k}_{B}}T}}{\nu }f{\text{ln}}f,\,\,\,\,{{F}_{5}} = - \frac{{{{\chi }_{a}}}}{2}{{\left( {\vec {n} \cdot \vec {H}} \right)}^{2}}, \\ {{F}_{6}} = - {{M}_{S}}f\left( {\vec {m} \cdot \vec {H}} \right). \\ \end{gathered} $
Здесь $\vec {n}$ – директор НЖК, ${{K}_{{11}}},$ ${{K}_{{22}}},$ ${{K}_{{33}}}$ – модули ориентационной упругости НЖК (константы Франка), $\vec {m}$ – директор хиральных частиц (единичный вектор, характеризующий направление преимущественной ориентации длинных осей частиц), совпадающий с вектором намагниченности среды, $f$ – объемная доля примесных частиц в суспензии, $W > 0$ – поверхностная плотность энергии сцепления молекул НЖК с частицами, $\alpha $ – псевдоскалярная феноменологическая константа, $d$ и $\nu $ – поперечный диаметр и объем частицы. Слагаемое ${{F}_{1}}$ в (1) представляет собой плотность свободной энергии ориентационно-упругих деформаций поля директора $\vec {n}$ НЖК (потенциал Озеена–Франка). В ХФН ориентационное взаимодействие между подсистемами учтено с помощью вкладов ${{F}_{2}}$ и ${{F}_{3}}.$ Хорошо известный в физике ЖК суспензий вклад ${{F}_{2}}$ [14] связан с энергией поверхностного сцепления ЖК-матрицы и примесных частиц. В рассматриваемом случае константа $W$ считается положительной, обеспечивая тенденцию к параллельной ориентации директоров $\vec {n}$ и $\vec {m}$ (планарное сцепление). Кроме того, из симметрийных соображений в плотность свободной энергии (1) добавлен вклад ${{F}_{3}},$ обусловленный хиральностью примесных частиц, зависящий от билинейной комбинации директоров $\vec {n},$ $\vec {m}$ и пропорциональный объемной доле частиц $f.$ Наличие хиральной примеси приводит к нарушению исходной зеркальной симметрии среды, допуская наличие слагаемого в свободной энергии, содержащего произведение псевдоскалярной феноменологической константы $\alpha $ и первой степени псевдоскаляра $\vec {m} \cdot {\text{rot\;}}\vec {n}.$ Вклад энтропии смешения “идеального газа” примесных феррочастиц ХФН в (1) задается выражением ${{F}_{4}}$ [1]. Вклады ${{F}_{5}}$ и ${{F}_{6}}$ [14, 15] описывают взаимодействие диамагнитной ЖК-матрицы и феррочастиц с магнитным полем.

Прежде чем исследовать поведение рассматриваемой системы в магнитном поле, необходимо определить равновесную ориентационную структуру ХФН в основном состоянии. В этом случае нужно считать вклады ${{F}_{5}}$ и ${{F}_{6}}$ в свободную энергию (1) равными нулю. Равновесные решения для полей $\vec {n}$ и $\vec {m}$ (рис. 1) будем искать в виде:

(2)
$\vec {n} = \left( {{\text{cos}}\,\varphi ,{\text{sin}}\,\varphi ,0} \right),\,\,\,\,\vec {m} = \left( {{\text{cos}}\,\psi ,{\text{sin}}\,\psi ,0} \right).$
Рис. 1.

Хиральный ферронематик: геометрия задачи.

С учетом компонент директоров (2) безразмерная объемная плотность свободной энергии ХФН (1) примет вид:

(3)
$\begin{gathered} \frac{{{{F}_{V}}}}{{{{K}_{{22}}}q_{0}^{2}}} = \frac{1}{2}{{\left( {\frac{{d\varphi }}{{d\zeta }}} \right)}^{2}} - \\ - \,\,\frac{f}{{{{f}_{0}}}}{\text{co}}{{{\text{s}}}^{2}}\left( {\varphi - \psi } \right)\left( {\sigma + \frac{{d\varphi }}{{d\zeta }}} \right) + \kappa \frac{f}{{{{f}_{0}}}}{\text{ln}}{\kern 1pt} f, \\ \end{gathered} $
где $\zeta = {{\alpha {{f}_{0}}z} \mathord{\left/ {\vphantom {{\alpha {{f}_{0}}z} {{{K}_{{22}}}}}} \right. \kern-0em} {{{K}_{{22}}}}} \equiv {{q}_{0}}z$ – безразмерная координата, $\sigma = {{W{{f}_{0}}} \mathord{\left/ {\vphantom {{W{{f}_{0}}} {\left( {d{{K}_{{22}}}q_{0}^{2}} \right)}}} \right. \kern-0em} {\left( {d{{K}_{{22}}}q_{0}^{2}} \right)}}$ – безразмерная энергия сцепления между ЖК-матрицей и примесными хиральными частицами, $\kappa = {{{{k}_{B}}T{{f}_{0}}} \mathord{\left/ {\vphantom {{{{k}_{B}}T{{f}_{0}}} {\left( {\nu {{K}_{{22}}}q_{0}^{2}} \right)}}} \right. \kern-0em} {\left( {\nu {{K}_{{22}}}q_{0}^{2}} \right)}}$ – сегрегационный параметр, ${\text{\;}}{{f}_{0}} = {{N\nu } \mathord{\left/ {\vphantom {{N\nu } V}} \right. \kern-0em} V}$ – средняя концентрация примесных частиц.

Минимизация по углам $\varphi $ и $\psi $ полной свободной энергии $F$ суспензии с учетом (3) приводит к уравнениям:

(4)
$\begin{gathered} \frac{{{{d}^{2}}\varphi }}{{d{{\zeta }^{2}}}} - \frac{d}{{d\zeta }}\left( {\frac{f}{{{{f}_{0}}}}} \right){\text{co}}{{{\text{s}}}^{2}}\left( {\varphi - \psi } \right) - \\ - \,\,\frac{f}{{{{f}_{0}}}}{\text{sin}}{\kern 1pt} 2\left( {\varphi - \psi } \right)\left( {\sigma + \frac{{d\psi }}{{d\zeta }}} \right) = 0, \\ \end{gathered} $
(5)
$\frac{f}{{{{f}_{0}}}}{\text{sin}}2\left( {\varphi - \psi } \right)\left( {\sigma + \frac{{d\varphi }}{{d\zeta }}} \right) = 0,$
определяющим равновесное ориентационное состояние ХФН. Минимизация $F$ по объемной доле примесных частиц $f,$ дает следующее выражение, характеризующие равновесное распределение частиц в ЖК-матрице:
(6)
$\begin{gathered} f = {{f}_{0}}Q\,{\text{exp}}\left\{ {\frac{{\sigma + \varphi {\kern 1pt} '}}{\kappa }{\text{co}}{{{\text{s}}}^{2}}\left( {\varphi - \psi } \right)} \right\}, \\ {{Q}^{{ - 1}}} = {{p}^{{ - 1}}}\int\limits_0^p {{\text{exp}}\left\{ {\frac{{\sigma + \varphi {\kern 1pt} '}}{\kappa }{\text{co}}{{{\text{s}}}^{2}}\left( {\varphi - \psi } \right)} \right\}d\zeta } , \\ \end{gathered} $
где $Q$ – константа, определяемая условием постоянства числа примесных частиц в образце $\int_V {fdV} $ = = $N\nu ,$ а $p$ – период ориентационной структуры среды.

АНАЛИЗ РЕШЕНИЙ УРАВНЕНИЙ РАВНОВЕСИЯ

Проанализируем решения системы уравнений равновесия (4)–(6). Заметим, что первый интеграл уравнения равновесия (4) может быть записан следующим образом:

(7)
$\frac{{d\varphi }}{{d\zeta }} - \frac{f}{{{{f}_{0}}}}{\text{co}}{{{\text{s}}}^{2}}\left( {\varphi - \psi } \right) = C - 1,$
где $C$ – константа интегрирования.

Уравнение связи (5) дает три соотношения для углов ориентации директоров ЖК и примесной подсистем, а именно:

(8)
${\text{I:}}\,\,\varphi = \psi ,$
это решение соответствует параллельной ориентации $\vec {n}$ и $\vec {m}.$ Из уравнений (4) и (6) с учетом выражения (7) следует однородное распределение примесных частицы в НЖК-матрице: $~f = {{f}_{0}}.$ Это, в свою очередь, приводит к выражению ${{d\varphi } \mathord{\left/ {\vphantom {{d\varphi } {d\zeta }}} \right. \kern-0em} {d\zeta }} = C,$ т.е. линейной зависимости углов поворота директоров ХФН от пространственной координаты. В данном случае выражение для плотности свободной энергии ХФН (3) примет следующий вид:

$F_{V}^{{\left( {\text{I}} \right)}} = \frac{{{{C}^{2}}}}{2} - C - \sigma + \kappa {\kern 1pt} {\text{ln}}{\kern 1pt} {{f}_{0}}.$

Минимизируя $F_{V}^{{\left( {\text{I}} \right)}}$ по константе интегрирования $C,$ имеем

(9)
$F_{V}^{{\left( {\text{I}} \right)}} = - \frac{1}{2} - \sigma + \kappa {\kern 1pt} {\text{ln}}{\kern 1pt} {{f}_{0}}.$
(10)
${\text{II:}}\,\,\varphi = \psi + {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2},$
данное решение отвечает ортогональной ориентации директоров $\vec {n}$ и $\vec {m}$ в среде и так же приводит к однородному распределению частиц в ЖК матрице: $~f = {{f}_{0}}.$ Подстановка решения (10) в уравнение (4) дает выражение ${{d\varphi } \mathord{\left/ {\vphantom {{d\varphi } {d\zeta }}} \right. \kern-0em} {d\zeta }} = C - 1,$ соответственно, плотность свободной энергии ХФН (3) в этом случае примет вид

$F_{V}^{{\left( {{\text{II}}} \right)}} = \frac{{{{C}^{2}}}}{2} - C + \frac{1}{2} + \kappa {\kern 1pt} {\text{ln}}{\kern 1pt} {{f}_{0}}.$

Минимизация $F_{V}^{{\left( {{\text{II}}} \right)}}$ по константе интегрирования дает $C = 1,$ откуда следует

(11)
$F_{V}^{{\left( {{\text{II}}} \right)}} = \kappa {\kern 1pt} {\text{ln}}{\kern 1pt} {{f}_{0}}~$
и выражение ${{d\varphi } \mathord{\left/ {\vphantom {{d\varphi } {d\zeta }}} \right. \kern-0em} {d\zeta }} = 0,$ описывающее незакрученное ориентационное состояние среды с однородными полями директоров $\vec {n}$ и $\vec {m}.$
(12)
${\text{III:}}\,\,\frac{{d\varphi }}{{d\zeta }} = - \sigma ,$
это частное решение описывает закрученную ориентационную структуру суспензии, характеристики которой определяются параметром сцепления $\sigma $ и не зависят от концентрации хиральных частиц. В этом случае плотность свободной энергии примет вид

(13)
$F_{V}^{{\left( {{\text{III}}} \right)}} = \frac{{{{\sigma }^{2}}}}{2} + \kappa {\kern 1pt} {\text{ln}}{\kern 1pt} {{f}_{0}}.$

Сравнение выражений (9), (11) и (13) для энергий ХФН показывает, что минимальному значению плотности энергии соответствует выражение $F_{V}^{{\left( {\text{I}} \right)}}$ (9). Заметим, что оно меньше и плотности свободной энергии однородной фазы суспензии (${{d\varphi } \mathord{\left/ {\vphantom {{d\varphi } {d\zeta }}} \right. \kern-0em} {d\zeta }} = 0,$ $\varphi = \psi ,$ $f = {{f}_{0}}$):

$F_{V}^{{\left( 0 \right)}} = - \sigma + \kappa {\kern 1pt} {\text{ln}}{\kern 1pt} {{f}_{0}}.$

Таким образом, минимуму энергии ХФН в отсутствие внешних полей и ограничивающих поверхностей отвечает следующее решение (в размерном виде) уравнений равновесия (4)–(6):

$\varphi = \psi = \frac{{\alpha {{f}_{0}}}}{{{{K}_{{22}}}}}z,$
описывающее ориентационную структуру ХФН, задаваемую векторными полями (2)

(14)
$\vec {n} = \vec {m} = \left( {{\text{cos}}~{{q}_{0}}z,{\text{sin}}~{{q}_{0}}z,0} \right).$

Из формулы (14) видно, что оба директора (для нематика и частиц) вращаются вдоль оси $z~$ (см. рис. 1) с периодом ориентации

${{p}_{0}} = \frac{{2\pi }}{{{{q}_{0}}}},$
являющимся шагом спиральной (геликоидальной) структуры ХФН. Здесь параметр ${{q}_{0}} \equiv {{\alpha {{f}_{0}}} \mathord{\left/ {\vphantom {{\alpha {{f}_{0}}} {{{K}_{{22}}}}}} \right. \kern-0em} {{{K}_{{22}}}}}$ играет роль волнового числа (параметра хиральности) спирали. Он зависит от средней объемной доли хиральных частиц ${{f}_{0}},$ модуля кручения Франка ${{K}_{{22}}}$ и псевдоскалярной феноменологической константы $\alpha .$ Знак $\alpha $ определяет направление закручивания спирали ХФН. Для ${{f}_{0}}\sim {{10}^{{ - 5}}}$ [1, 14], ${{K}_{{22}}} \sim {{10}^{{ - 7}}}\,\,{\text{дин}}$ [8] и шага спиральной структуры ${{p}_{0}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{q}_{0}}}}} \right. \kern-0em} {{{q}_{0}}}} \sim {{10}^{{ - 3}}}\,\,{\text{см,}}$ доступного для регистрации в диапазоне видимого света, оценка неизвестной константы $\alpha ~\sim 10\,\,{{{\text{дин}}} \mathord{\left/ {\vphantom {{{\text{дин}}} {{\text{см}}}}} \right. \kern-0em} {{\text{см}}}}{\text{.}}$ Если предположить бóльшую величину шага у спиральной структуры ХФН, что свойственно, например, нематохолестерическим смесям, то значение константы $\alpha $ может быть уменьшено вплоть до типичных энергий сцепления ЖК с поверхностью W ~10–3–10–1 дин/см [16].

ЗАКЛЮЧЕНИЕ

Рассмотрен дополнительный вклад в функционал свободной энергии НЖК, обусловленный хиральной формой примесных частиц. Показано, что он приводит к формированию самопроизвольной макроскопической спиральности ориентационной структуры нематика, зависящей от концентрации примесной фазы и материальных параметров ЖК матрицы.

Работа выполнена при финансовой поддержке Минобрнауки России (проект № FSNF-2023-0004).