ЖЭТФ, 2019, том 155, вып. 1, стр. 69-95

СТАЦИОНАРНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ВТОРОГО

ПОРЯДКА ДЛЯ ФЕРМИОНОВ В ПРОСТРАНСТВЕ-ВРЕМЕНИ

КЕРРА - НЬЮМЕНА

В. П. Незнамов^*, И. И. Сафронов, В. Е. Шемарулин

ФГУП «РФЯЦ-ВНИИЭФ»

607188, Саров, Нижегородская обл., Россия

Поступила в редакцию 20 июня 2018 г.,

после переработки 20 июня 2018 г.

Принята к публикации 12 июля 2018 г.

При использовании для фермионов квантовомеханического уравнения второго порядка с эффективным

потенциалом поля Керра - Ньюмена (KN) получены результаты, качественно отличающиеся от резуль-

татов, получаемых при использовании уравнения Дирака. При наличии двух горизонтов событий до-

казано существование вырожденных стационарных связанных состояний заряженных и незаряженных

фермионов с квадратично-интегрируемыми волновыми функциями, обращающимися в нуль на горизон-

тах событий. Фермионы в таких состояниях локализованы вблизи горизонтов событий с максимумами

плотностей вероятности, отстоящими от горизонтов событий на доли комптоновской длины волны фер-

мионов в зависимости от величин констант связи, от величин углового и орбитального моментов j, l и от

величины азимутального квантового числа mϕ. В случае экстремальных полей KN показано отсутствие

стационарных связанных состояний фермионов для любых значений констант связи. Для заряженных

и незаряженных фермионов в поле голой сингулярности KN при определенных значениях физических

параметров показано существование дискретных энергетических спектров. В квантовой механике с урав-

нением второго порядка из-за регулярного поведения эффективных потенциалов поля KN в окрестности

начала координат голая сингулярность KN не несет угрозы космической цензуре.

DOI: 10.1134/S0044451019010061

чески расширенное множество Керра - Ньюмена по-

перечно связано через кольцо. Такая топология со-

храняется для метрики Керра и для «нулевой» гра-

1. ВВЕДЕНИЕ

витации G → 0.

В 1976 г. Чандрасекар [1,2], Пейдж [3], Тооп [4]

При наличии горизонтов событий в работах

показали, что в уравнении Дирака для точечного

[8-10, 15] показано отсутствие стационарных свя-

фермиона в пространстве-времени Керра [5] и Кер-

занных состояний уравнения Дирака для областей

ра - Ньюмена [6] можно провести разделение угло-

определения волновых функций фермиона вне и под

вых и радиальных переменных. С тех пор поведение

горизонтами событий. В данной работе в разд. 2 эти

фермиона во внешних полях Керра и Керра - Нью-

выводы также подтверждаются.

мена изучалось в многочисленных работах (см., на-

Ситуация качественно изменяется, если движе-

пример, [7-18]). В работах [19-22] уравнение Дирака

ние фермионов описывать самосопряженным урав-

изучалось в пространстве-времени Керра - Ньюмена

нением второго порядка со спинорной волновой

в пределе G → 0, где G — ньютонова постоянная

функцией. Впервые уравнение второго порядка во

всемирного тяготения.

внешнем электромагнитном поле было предложено

В работах [23, 24] и позднее в [21, 22] изучалась

Дираком [25]. Используя соотношение между верх-

нетривиальная топология метрик Керра и Керра -

ним и нижним спинорами дираковского биспинора,

Ньюмена, связанная с кольцевой сингулярностью. В

уравнение второго порядка можно записать в виде

работах [23,24] показано, что максимально аналити-

двух отдельных уравнений со спинорными волновы-

ми функциями. При этом для самосопряженности

^* E-mail: vpneznamov@vniief.ru, vpneznamov@mail.ru

уравнений второго порядка необходимо для каждо-

В. П. Незнамов, И. И. Сафронов, В. Е. Шемарулин

ЖЭТФ, том 155, вып. 1, 2019

го из них проводить неунитарные преобразования

нение Дирака, проведено разделение переменных,

подобия (см., например, [26]). В результате при ис-

представлена система уравнений для радиальных

пользовании самосопряженных уравнений второго

волновых функций, рассматриваются асимптоти-

порядка со спинорными волновыми функциями в

ки радиальных волновых функций, определяют-

квантовой механике частиц со спином 1/2 во внеш-

ся нерегулярные стационарные решения уравнения

них электромагнитных и гравитационных полях мо-

Дирака в поле KN. Рассмотрение проводится для

гут возникать и возникают новые физические след-

случая наличия двух горизонтов событий, для экс-

ствия.

тремального поля KN с единственным горизонтом

В данной работе уравнение второго порядка с

событий и для случая голой сингулярности KN.

эффективным потенциалом используется для описа-

В разд. 3 в геометрии KN получено самосопря-

ния движения фермионов в геометрии Керра - Нью-

женное уравнение второго порядка со спинорными

мена (KN). При соответствующих значениях на-

волновыми функциями фермионов. Обсуждаются

чальных параметров это уравнение описывает дви-

особенности эффективных потенциалов и асимпто-

жение фермионов в полях Шварцшильда [27] и

тики радиальной волновой функции уравнения вто-

Райсснера - Нордстрёма [28]. При отсутствии грави-

рого порядка.

тации уравнение второго порядка описывает дви-

жение фермионов в эффективном кулоновском по-

Особенности эффективных потенциалов и пове-

ле [26].

дение радиальных волновых функций свидетель-

При наличии двух горизонтов событий метри-

ствуют о возможности существования стационар-

ки KN для заряженных и незаряженных фермио-

ных связанных состояний фермионов как при на-

нов мы обосновали и доказали существование стаци-

личии двух горизонтов, так и для случая голой син-

онарных связанных состояний фермионов с квадра-

гулярности KN. Отсутствие потенциальной ямы для

тично-интегрируемыми волновыми функциями, об-

экстремального поля KN свидетельствует об отсут-

ращающимися в нуль на горизонтах событий. Фер-

ствии в этом случае связанных состояний фермио-

мионы в таких состояниях локализованы вблизи го-

нов.

ризонтов событий. Максимумы плотностей вероят-

ности обнаружения частиц отстоят от горизонта со-

В разд. 4 уравнение второго порядка с эффектив-

бытий на доли комптоновской длины волны ферми-

ным потенциалом после преобразования Прюфера

онов в зависимости от гравитационной и электро-

[30-33] и введения фазовой функции представляет-

магнитных констант связи, углового момента источ-

ся в виде системы нелинейных дифференциальных

ника поля KN, квантовых чисел углового и орби-

уравнений первого порядка.

тального моментов j, l и азимутального квантового

В разд. 5 приводятся результаты численных рас-

числа m_ϕ.

четов по определению стационарных связанных со-

Для экстремального поля KN с единственным

стояний фермионов в поле KN. Обсуждается так-

горизонтом событий доказана невозможность суще-

тика проведения расчетов в окрестностях особых

ствования стационарных связанных состояний фер-

точек (r = ±∞ — регулярные особые точки, r =

мионов.

= (r_±)_KN , r = r_cl — иррегулярные особые точки).

Для голой сингулярности KN при определен-

Здесь (r_±)_KN — радиусы внешнего и внутреннего

ных значениях физических параметров обоснова-

горизонтов событий, r_cl — радиус непроницаемого

но и численно показано существование дискретных

барьера, который может возникать при определен-

энергетических спектров частиц со спином 1/2.

ных значениях физических параметров вблизи на-

В геометрии Керра - Ньюмена эффективный по-

чала координат.

тенциал уравнения второго порядка конечен в нача-

ле координат. Следовательно, поле голой сингуляр-

В разд. 6 устанавливается отсутствие угрозы кос-

ности KN в квантовой механике движения ферми-

мической цензуре в квантовой механике движения

онов не несет угрозы космической цензуре. Анало-

фермионов в поле голой сингулярности KN.

гичные выводы ранее были сделаны для голой син-

гулярности Райсснера - Нордстрёма [28] и для ряда

В Заключении излагаются и обсуждаются основ-

времениподобных голых сингулярностей в кванто-

ные результаты работы.

вой механике бесспиновых частиц [29].

В Приложении приводится явный вид эффектив-

Работа построена следующим образом. В разд. 2

ных потенциалов уравнения второго порядка в поле

для геометрии KN получено самосопряженное урав-

KN.

ЖЭТФ, том 155, вып. 1, 2019

Стационарные решения уравнения второго порядка.. .

√

2. УРАВНЕНИЯ ДИРАКА В ПОЛЯХ КЕРРА

2. Случай r₀ = 2 a² + r2Q, (r₊)_KN = (r_-)_KN =

И КЕРРА - НЬЮМЕНА

= r₀/2 соответствует экстремальному полю Кер-

ра - Ньюмена.

В работе, как правило, используется система

√

3. Случай r₀ < 2 a² + r2Q соответствует голой

единиц ℏ = c = 1; сигнатура метрики плоского про-

странства Минковского выбрана равной

сингулярности поля Керра - Ньюмена. В этом слу-

чае f_KN > 0.

4. При Q = 0 метрика Керра - Ньюмена перехо-

η_αβ = diag[1, -1, -1, -1].

(1)

дит в метрику Керра с

(

)

r₀

Здесь и ниже подчеркнутые индексы являются ло-

Δ_K = r²f_K

=r²

(5)

r²

кальными. Индексы с греческими буквами прини-

√

r₀

r²⁰

мают значения 0, 1, 2, 3; индексы с латинскими бук-

(r_±)_KN =

-a².

(6)

вами — значения 1, 2, 3. Используется стандартное

правило суммирования по повторяющимся индек-

2.2. Самосопряженное уравнение Дирака

сам.

Если записать уравнения Дирака в гамильтоно-

вой форме, то гамильтонианы Чандрасекара [1, 2]

2.1. Метрики Керра и Керра - Ньюмена

и Пейджа [3] будут псевдоэрмитовыми с весовыми

Стационарная метрика Керра - Ньюмена харак-

множителями Паркера [35] в скалярных произве-

теризуется точечным источником с массой M, за-

дениях волновых функций. Самосопряженные га-

рядом Q, вращающимся с угловым моментом J =

мильтонианы с плоскими скалярными произведени-

= Mca. Метрику Керра-Ньюмена в координатах

ями волновых функций можно получить с исполь-

Бойера - Линдквиста (t, r, θ, ϕ) [34] можно предста-

зованием методов псевдоэрмитовой квантовой ме-

вить в виде

ханики [36-38]. В работах [38, 39] такие гамильто-

нианы были получены для метрик Керра и Кер-

(

)

r₀r - r2Q

ра - Ньюмена. В работе [40] для метрики Керра до-

ds² =

dt² +

казана эквивалентность самосопряженного гамиль-

r²

тониана в [38] и гамильтониана Чандрасекара в [1,2].

2a(r₀r-r2Q)

r2K

Недостатком гамильтониана в [38] является невоз-

sin² θ dt dϕ-

dr²-r2K dθ² -

r2K

Δ_KN

можность проведения разделения переменных. Ни-

(

)

a²(r₀r - r²

)

же для метрик Керра и Керра - Ньюмена получены

- r² +a² +

sin² θ sin² θ dϕ².

(2)

самосопряженные уравнения Дирака, допускающие

r²

разделение переменных.

Начнем с уравнений Дирака для метрик Керра и

В (2)

Керра - Ньюмена, полученных в работах Чандрасе-

r2K = r² + a² cos² θ,

кара, Пейджа и записанных в форме [9]:

(

)

r₀

r2Q

+a²

(G - 1)Ψ =

Δ_KN = r²f_KN = r²

⎛

⎞

r²

α₊

β₊

⎜

⎟

⎜

-1

β_-

ε(Δ_KN )α_-

⎟

r₀

= 2GM/c² — гравитационный радиус поля

√

⎜

⎟_×

⎜

⎟

Шварцшильда, r_Q =

GQ/c², G — гравитационная

-β₊

-1

⎝ ε(ΔKN )α-

⎠

постоянная, c — скорость света.√

−β_-

a₊

1. Если r₀ > 2 a² + r2Q, то

× Ψ = 0.

(7)

(

)(

)

(r₊)_KN

(r_-)_KN

В (7) Ψ — биспинорная волновая функция,

f_KN =

(3)

β_± =

√

ρ²

(

)

где (r_±)_KN — радиусы внешнего и внутреннего го-

∂

ctg θ

α_a sinθ

ризонтов событий поля Керра - Ньюмена,

× i

(ρ - iα_a cos θ)

∂θ

2ρ

√

(

)

∂

r₀

r²

√

α_a sinθ

(8)

(r_±)_KN =

-a² -r2Q.

(4)

ρ2K

∂t

sinθ ∂ϕ

В. П. Незнамов, И. И. Сафронов, В. Е. Шемарулин

ЖЭТФ, том 155, вып. 1, 2019

(

)

2α

α2a + α2Q

β_± =

√

Δ_KN = ρ²f_KN = ρ²

(14)

ρ²

(

)

∂

ctg θ

α_a sinθ

× i

(ρ + iα_a cos θ)

∂θ

2ρ²

В присутствии внешнего и внутреннего горизонтов

(

)

событий α² > α2a + α2Q

∂

√

α_a sinθ

(9)

ρ2K

∂t

sinθ ∂ϕ

(ρ - (ρ₊)_KN ) (ρ - (ρ_-)_KN )

f_KN =

(15)

ρ²

ε(Δ_KN )

α_± = -√

где

ρ2K|Δ_KN |

√

(

)

∂

|Δ_KN |

(ρ_±)_KN = α ± α² - α2a - α2Q.

(16)

× i(ρ²+α2a)

+iα_a

-α_emρ

∂t

∂ϕ

ρ²

(

)

Для экстремального поля KN α²

= α2a + α2Q,

∂

ρ-α

× i

(ρ - iα_a cos θ)

(10)

(ρ₊)_KN = (ρ_-)_KN = α и

∂ρ

2Δ_KN

2ρ²

(ρ - α)²

f_KN =

(17)

ε(Δ_KN )

ρ²

α_± = -√

ρ2K|Δ_KN |

√

При α² < α2a + α2Q реализуется случай голой сингу-

(

)

∂

|Δ_KN |

лярности поля KN. В формулах (10), (11)

× i(ρ²+α2a)

+iα_a

-α_emρ

∂t

∂ϕ

ρ²

{

(

)

∂

ρ-α

1, x ≥ 0,

× i

(ρ + iα_a cos θ)

(11)

ε(x) =

(18)

∂ρ

2Δ_KN

2ρ²

-1, x < 0.

Выражения (7)-(11) записаны в безразмерных пере-

Для получения более симметричного вида уравне-

менных

ния (7), в соответствии с [9], проведем некоторые

r₀

GMm

преобразования. Пусть S(ρ, θ) и Γ(ρ, θ) — диагональ-

ρ=

ε=

α=

l_c

2l_c

ℏc

M²

ные матрицы вида

√

r_Q

GQm

√α_fs

α_Q =

(12)

S = |Δ1/4KN|×

l_c

ℏc

M_P

[

× diag (ρ - iα_a cos θ)1/2, (ρ - iα_a cos θ)1/2,

α_a =

α_em =

=α_fs

l_c

ℏc

e²

]

(19)

(ρ + iα_a cos θ)1/2, (ρ + iα_a

cosθ)1/2 ,

Здесь l_c = ℏ/mc — комптоновская длина волны час-

√

тицы со спином 1/2; M_P =

ℏc/G = 2.2 · 10-5 г

Γ = -idiag[(ρ + iαa cosθ),-(ρ + iαa cosθ),

(1.2 · 10¹⁹ ГэВ) — планковская масса; α_fs = e²/ℏc ≈

- (ρ - iα_a cos θ), (ρ - iα_a cos θ)] .

≈ 1/137 — электромагнитная постоянная тонкой

структуры; α, α_em — гравитационная и электромаг-

Тогда преобразованная волновая функция

нитная константы связи; α_Q, α_a — безразмерные

константы, характеризующие источник электромаг-

Ψ= SΨ

(20)

нитного поля и отношение углового момента J к

удовлетворяет уравнению

массе M в метрике Керра - Ньюмена.

Величины ρ2K , Δ_KN в безразмерных переменных

ΓS(G - 1)S-1 Ψ = (R + A)Ψ = 0,

(21)

имеют вид

ρ2K = ρ² + α2a cos² θ,

(13)

где

⎛

√

⎞

iρ

|Δ_KN | D₊

⎜

√

⎟

⎜

-iρ

ε(Δ_KN )

|Δ_KN | D_-

⎟

R=^⎜

√

⎟,

(22)

⎜

⎟

⎝ ε(ΔKN )

|Δ_KN | D_-

-iρ

⎠

√

|Δ_KN | D₊

iρ

ЖЭТФ, том 155, вып. 1, 2019

Стационарные решения уравнения второго порядка.. .

⎛

⎞

-α_a cosθ

L₊

⎜

⎟

⎜

α_a cosθ

-L_-

⎟

A=^⎜

⎟.

(23)

⎜

⎟

⎝

L₊

-α_a cosθ

⎠

−L_-

α_a cosθ

В формулах (22), (23)

Матрицы в представлении Дирака - Паули связа-

ны с матрицами в представлении Вейля унитарным

∂

D_± =

∓

преобразованием:

∂ρ

Δ_KN

(

)

∂

=Mγ

M⁺, M⁺ = M-1,

(30)

× (ρ² + α2a)

+α_a

+ iα_emρ

(24)

∂t

∂ϕ

(

)

-I

(

)

M =

√

(31)

∂

L_± =

ctg θ ∓ i α_a sin θ

(25)

∂θ

∂t

sinθ ∂ϕ

В (31) I — двумерная единичная матрица.

Оператор R зависит только от радиальной перемен-

Проведем унитарное преобразование (31) волно-

ной ρ, а оператор A — только от угловых перемен-

вой функции (26), (27) и уравнения Дирака (21).

ных θ, ϕ.

Преобразованная функция

Φ_DP имеет вид

Если представить функцию

Ψ в виде

⎛

⎞

(R_- - R₊)S_-

Ψ(t, ρ, θ, ϕ) = e^-iεteimϕϕΦ(ρ, θ),

(26)

⎜

⎟

⎜

(R₊ - R_-)S₊

⎟

где

Φ_DP = MΦ(ρ, θ) =

√

⎜

⎟.

(32)

⎛

⎞

⎜

⎟

⎝ (R- + R+)S-

⎠

R_-(ρ)S_-(θ)

⎜

⎟

(R_- + R₊)S₊

⎜

⎟

+(ρ)S+(θ)

⎜ R

Φ(ρ, θ) =

^⎟,

(27)

⎜

⎟

⎝ R+(ρ)S-(θ)

⎠

Далее учтем свойство анзаца радиальных волновых

R_-(ρ)S₊(θ)

функций Чандрасекара - Пейджа [21,41],

то можно получить системы уравнений Чандрас-

R_-(ρ) = R∗+(ρ),

екара - Пейджа отдельно для радиальных функ-

(33)

R₊(ρ) = R^∗-(ρ),

ций R_∓(ρ) и для угловых сфероидальных гармо-

ник S_∓(θ).

и введем вещественные радиальные функции

Уравнения Дирака (7), (21) получены при ис-

g(ρ) = R_-(ρ) + R₊(ρ),

пользовании матриц Дирака с локальными индекса-

(34)

f (ρ) = i (R₊(ρ) - R_-(ρ)) .

ми в спинорном представлении (представление Вей-

ля):

(

)

(

)

С учетом (34) функцию

Φ_DP можно записать в виде

(

)

γ0W = -

γ^kW =

f (ρ)iσ³ξ_KN (θ)

-σ^k

Φ_DP =

√

(35)

(

)

(28)

g(ρ)ξ_KN (θ)

σ^k

α^kW = γ0W γ^kW =

Спинор ξ_KN (θ) равен

-σ

(

)

Ранее для записи гамильтонианов в полях

S_-(θ)

ξ_KN (θ) =

(36)

Шварцшильда, Райсснера - Нордстрёма [27, 28] на-

S₊(θ)

ми использованы матрицы в представлении Дира-

ка - Паули:

S_∓(θ) — сфероидальные гармоники для спина 1/2,

(

)

подчиняющиеся угловым уравнениям Чандрасека-

γ0DP =

ра - Пейджа. В отсутствие вращения α_a = 0 и

-1

(

)

(

)

-1/2Y (θ)

ξ_KN (θ) = ξ(θ) =

γ^kDP =

(29)

+1/2Y (θ)

-σ^k

(

)

где-1/2Y (θ), +1/2Y (θ) — сферические гармоники

α^kDP = γ0DP γ^kDP =

для спина 1/2 (см., например, [27, 28, 42]).

σ^k

В. П. Незнамов, И. И. Сафронов, В. Е. Шемарулин

ЖЭТФ, том 155, вып. 1, 2019

Спинор ξ_KN (θ) удовлетворяет уравнению

В (41)

(

)

(

)

(

)

∂

m_ϕ

γ⁵ =

iσ²

ctg θ

+σ¹

-α_aε sinθ +

∂θ

sinθ

)

(

)

- σ³αa cosθ ξ_KN(θ) = -λξ_KN(θ).

(37)

α2a

α_am_ϕ

α_em

ω=ε

(42)

ρ²

Из (37) следуют угловые уравнения Чандрасека-

ра - Пейджа для сфероидальных гармоник S_∓(θ)

Уравнение (41) является самосопряженным и в от-

(

)

сутствие вращения (α_a = 0) совпадает с уравнением

(

)

∂

m_ϕ

ctg θ S₊ - α_aε sin θ -

S₊ =

Дирака в поле Райсснера - Нордстрёма [28].

∂θ

sinθ

= -(λ - α_a cosθ)S_-,

2.3. Разделение переменных

(

)

(38)

(

)

∂

m_ϕ

ctg θ S_- + α_aε sin θ -

S_- =

Для уравнения (41) допустима стандартная про-

∂θ

sinθ

цедура разделения переменных. Сначала (41) запи-

= (λ + α_a cos θ)S₊.

сывается в виде системы уравнений для верхнего и

В отличие от полей Шварцшильда и Райсснера -

нижнего спиноров функции Ψ_KN . Затем использу-

ется уравнение (37) для ξ_KN (θ). В итоге получаются

Нордстрёма, константа разделения λ в (38) зависит

от ε, α_a, j, l, m_ϕ.

уравнения для вещественных радиальных функций

F_KN (ρ) = f(ρ)/ρ√fKN , GKN (ρ) = g(ρ)/ρ√fKN :

Преобразованное уравнение Дирака

(21) для

функции

Ψ_DP будет иметь вид

(

)

λ√f

f_KN

F_KN (ρ)-

(iγ³)M(R + A)M-1 Ψ_DP = 0.

(39)

dρ

ρ²

( (

)

α2a

α_am_ϕ

α_em

√

В (39) для удобства преобразованное уравнение сле-

- ε

f_KN

ρ²

ва умножено на матрицу iγ³. Кроме того, для срав-

нения с уравнением Дирака в полях Шварцшиль-

× G_KN(ρ) = 0,

(

(43)

да и Райсснера - Нордстрёма в уравнении (39) будем

λ√fKN )

f_KN

G_KN (ρ)+

использовать волновую функцию

dρ

ρ²

(

)

Ψ_DP

α2a

α_am

α_em

√

+ ε

f_KN

Ψ_KN =

√

(40)

ρ²

f_KN

× F_KN(ρ) = 0.

Перед тем, как написать уравнение (39) с уче-

том (40) в явном виде, следует отметить, что при

Уравнения (43) по своей структуре схожи с

использовании вещественных радиальных волновых

уравнениями для поля Райсснера - Нордстрёма. При

функций f(ρ), g(ρ) будут использоваться положи-

α_a = 0 (отсутствие вращения) уравнения (43) сов-

тельные значения Δ_KN ≥ 0, f_KN ≥ 0. В этом случае

падают с системой уравнений для поля Райсснера -

ε(Δ_KN ) = 1. При наличии горизонтов событий усло-

Нордстрёма.

вие Δ_KN ≥ 0 исключает из области определения

волновых функций сферический слой между внеш-

2.4. Асимптотика радиальных волновых

ним и внутренним горизонтами событий.

функций

В результате уравнение Дирака для Ψ_KN (40)

имеет вид

2.4.1. Наличие горизонтов событий (ρ+)KN ,

(

)

(ρ-)KN , α² > α^a + α^Q

√

ω-γ⁰

f_KN Ψ_KN =

Из уравнений (43) следует, что при ρ → ∞ веду-

{

(

)

∂

√f_KN

щие члены асимптотик имеют вид

-iγ⁰γ³

f_KN

∂ρ

ρ²

√

[

(

)

F_KN = C₁ϕ₁(ρ)e^-

1-ε² ρ + C₂ϕ₂(ρ)e

1-ε² ρ,

∂

× -iγ⁰γ⁵α_a cosθ - iγ⁰γ¹

ctg θ

^√1 - ε

∂θ

G_KN =

√

(44)

(

)]}

1+ε

m_ϕ

(

√

)

- γ⁰γ²

εα_a sinθ -

Ψ_KN.

(41)

1-ε² ρ

sinθ

× -C₁ϕ₁(ρ)e^-

1-ε² ρ+C₂ϕ₂(ρ)e

ЖЭТФ, том 155, вып. 1, 2019

Стационарные решения уравнения второго порядка.. .

В (44) ϕ₁(ρ), ϕ₂(ρ) — степенные функции от ρ; C₁,

Выражения (47), (48) показывают, что функции

C₂ — постоянные интегрирования.

F_KN (ρ), G_KN (ρ) являются квадратично-неинтегри-

При определении связанных состояний дираков-

руемыми на внутреннем горизонте событий ρ

ских частиц необходимо использовать лишь экспо-

= (ρ_-)_KN . Вид осциллирующих частей функций

ненциально убывающие решения (44), т. е. в этом

(47) для

случае C₂ = 0.

α_am_ϕ + α_em(ρ_-)_KN

ε=

При ρ

→ ρ₊ представим функции F_KN(ρ),

α2a + (ρ_-)2KN

G_KN (ρ) в виде

свидетельствует о реализации режима «падения»

частиц на внутренний горизонт событий [43, 44].

F_KN |ρ→(ρ

|ρ - (ρ₊)_KN |s+ ×

+ )KN =

Известно

[19], что при ρ

→ 0 существуют

∑

два квадратично-интегрируемых решения уравне-

× f(+)k|ρ - (ρ₊)_KN |^k,

ния Дирака в поле Керра - Ньюмена. Если предста-

k=0

(45)

вить

G_KN |ρ→(ρ

|ρ - (ρ₊)_KN |s+ ×

+ )KN =

∑

F_KN |ρ→0

=ρ^s

f(0)kρk,

× g(+)k|ρ - (ρ₊)_KN |^k.

k=0

(49)

k=0

∑

G_KN |ρ→0

=ρ

g(0)kρ^k,

Определяющее уравнение для системы (43) приво-

k=0

дит к решению

то решения определяющего уравнения для системы

(43) равны s₁ = 0, s₂ = 1 [20]. Для обоих реше-

(ρ₊)2KN

s₊ = -

±i

ний s₁, s₂ функции F_KN , G_KN при ρ → 0 явля-

(ρ₊)_KN - (ρ_-)_KN

( (

)

ются квадратично-интегрируемыми. Решение этой

α2a

α_am_ϕ

α_em

× ε

(46)

проблемы предложено в работе [21] с использова-

(ρ₊)2KN

(ρ₊)_KN

нием двухлистной топологии метрики Керра - Нью-

мена, позволяющей осуществлять начало интегри-

Формулы (45), (46) показывают, что функции

рования уравнений (43) с r → -∞.

F_KN (ρ), G_KN (ρ) являются квадратично-неинтег-

рируемыми на внешнем горизонте событий ρ

Граничные условия для экспоненциально убыва-

ющих решений при r → -∞ следуют из (44):

= (ρ₊)_KN . Вид осциллирующей части функций (45)

√

для

FKN = C2ϕ2(ρ)e

1-ε² ρ,

α_am_ϕ + α_em(ρ₊)_KN

ε=

√

(50)

α2a + (ρ₊)2KN

^√1 - ε

G_KN =

C₂ϕ₂(ρ)e

1-ε² ρ.

свидетельствует о реализации режима «падения»

^√1 + ε

частиц на внешний горизонт событий [43, 44].

2.4.2. Экстремальное поле Керра - Ньюмена

При ρ → (ρ_-)_KN представим функции F_KN (ρ),

((ρ+)KN = (ρ-)KN = α, α² = α^a + α^Q)

G_KN (ρ) в виде

При ρ → ∞ верна асимптотика (44). Как и в

F_KN |ρ→(ρ

|(ρ_-)_KN - ρ|s- ×

- )KN =

предыдущем разделе, мы заменяем неоднозначную

∑

асимптотику при ρ → 0 на асимптотику при ρ →

× f(-)k|(ρ_-)_KN - ρ|^k,

→ -∞ (50). При ρ → α слева и справа от горизонта

k=0

(47)

и при

G_KN |ρ→(ρ

|(ρ_-)_KN - ρ|s- ×

α_am_ϕ + α_emα

- )KN =

ε=

∑

α²

+α²

× g(-)k|(ρ_-)_KN - ρ|^k.

ведущая особенность эффективного потенциала

k=0

имеет вид (см. (85) и Приложение)

В этом случае решение определяющего уравнения

(

)

α_am_ϕ + α_emα

α⁴

для системы (43) имеет вид

U^F

ε=

eff

α2a

+α²

2(ρ - α)⁴

[

(

)]₂

(ρ_-)2KN

α2a

m_ϕα

α_em

s_- = -

±i

× ε

(51)

(ρ₊)_KN - (ρ_-)_KN

α²

( (

)

α2a

α_am_ϕ

α_em

что свидетельствует о реализации режима «паде-

× ε

(48)

(ρ_-)2KN

(ρ_-)_KN

ния» частиц на горизонт событий.

В. П. Незнамов, И. И. Сафронов, В. Е. Шемарулин

ЖЭТФ, том 155, вып. 1, 2019

2.4.3. Голая сингулярность Керра - Ньюмена

В отличие от (52), (53) решения (56), (57) могут быть

(α² < α2a + α2Q); ρ ∈ (0, ∞)

регулярными при определенных соотношениях на-

чальных параметров.

При ρ → ∞ справедлива асимптотика (44). Как и

В уравнениях для вещественных радиальных

в разд. 2.4.1, 2.4.2, мы будем использовать асимпто-

функций (43) обозначим

тику при ρ → -∞ (50) вместо неоднозначной асимп-

(

)

тотики при ρ → 0.

α2a

α_am_ϕ

α_em

ω(ρ) = ε

(58)

ρ²

2.5. Стационарные решения уравнения

Для решений (56), (57)

Дирака

ω(ρ = α, ε = ε_ext) = 0.

(59)

2.5.1. Нерегулярные стационарные решения

Первый неисчезающий член в разложении

уравнения Дирака

ω(ρ, ε = ε_ext) по степеням |ρ - α| равен

При наличии горизонтов событий (ρ₊)_KN ,

ω(ε = ε_ext)|_ρ→α = Ω|ρ - α|,

(60)

(ρ_-)_KN из выражений

(45)-(48) следует, что

существуют решения, для которых отсутствует ос-

где

циллирующая часть рассматриваемых асимптотик:

m_ϕα_a + α_emα

2α

2m_ϕα_a

α_em

Ω=-

(61)

α_am_ϕ + α_em(ρ_±)_KN

α² + α²

α³

α²

ε=

— метрика KN,

(52)

α2a + (ρ_±)²

Учитывая, что для экстремального поля KN

α_am_ϕ

(ρ - α)²

ε=

f^extKN =

(62)

α2a + (ρ_±)2K

2α(ρ_±)_K

ρ²

(53)

— метрика Керра (K), α_em = 0, α_Q = 0.

уравнения (43) при ρ → α можно записать в виде

(

)

(

)

В отсутствие вращения (α_a = 0 выражения (52),

|ρ-α| d

1+λ

F_KN - Ω+

G_KN = 0,

(53) совпадают с решениями для метрики Райссне-

α²

dρ

α²

)

(

)

(63)

ра - Нордстрёма (RN) и метрики Шварцшильда (S),

⁽ |ρ-α| d

1-λ

G_KN + Ω-

F_KN = 0.

подробно исследованными в работах [27, 28]:

α²

dρ

α²

α_em

Если представить

ε=

— метрика RN,

(54)

(ρ_±)_KN

∑

ε = 0 — метрика S.

(55)

F_KN |_ρ→α

= |ρ - α|^s f^extk|ρ - α|^k,

k=0

(64)

Для этих решений уравнения Дирака отсутству-

∑

G_KN |_ρ→α

= |ρ - α|^s g^extk|ρ - α|^k,

ет режим «падения» частиц на горизонты событий,

k=0

однако решения (52), (53) являются нерегулярны-

то решение определяющего уравнения для системы

ми из-за расходимости нормировочных интегралов

(63) равно

асимптотик волновых функций (45), (47) вблизи го-

√

ризонтов событий.

s1,2 = -1 ±

λ² + α² - α⁴Ω².

(65)

Для квадратичной интегрируемости функций F_KN ,

2.5.2. Регулярные стационарные решения

G_KN в (63) необходимо оставить решение (65) с по-

уравнения Дирака для экстремального поля

ложительным знаком перед квадратным корнем и,

Керра - Ньюмена ((ρ+)KN = (ρ-)KN = α,

кроме того, необходимо выполнение неравенства

α² = α2a + α2Q)

√

-2 + 2

λ² + α² - α⁴Ω² > -1,

(66)

В этом случае решения (52), (53) имеют вид

т. е.

α_am_ϕ + α_emα

ε_ext =

— метрика KN,

(56)

α2a + α²

λ² + α² - α⁴Ω²

> 1/4.

(67)

m_ϕ

Для метрики RN α⁴Ω² = α2em, λ² = κ². В этом слу-

ε_ext =

— метрика Керра,

2α

чае условие (67) совпадает с аналогичным условием,

(57)

α_em = 0, α_Q = 0.

определенным в работе [45].

ЖЭТФ, том 155, вып. 1, 2019

Стационарные решения уравнения второго порядка.. .

2.5.3. Регулярные стационарные решения

Обозначим

)

уравнения Дирака для голой сингулярности

⁽1 + λ√f_KN

Керра - Ньюмена (α² < α2Q + α2a)

A_KN = -

(68)

f_KN

ρ²

При учете двулистной структуры решения KN и

(

)

√

интегрировании системы уравнений (43) от ρ = -∞

B_KN =

ω+

f_KN

(69)

f_KN

до ρ = +∞ неопределенность в выборе решения при

ρ = 0 исчезает и при определенных значениях фи-

(

√

)

C_KN = -

ω-

f_KN

(70)

зических параметров будет существовать дискрет-

f_KN

ный энергетический спектр фермионов с квадратич-

)

но-интегрируемыми волновыми функциями.

⁽1 - λ√f_KN

D_KN = -

(71)

Итак, мы подтвердили выводы [8-10, 15] об от-

f_KN

ρ²

сутствии стационарных связанных состояний дира-

В формулах (69), (70) через ω обозначено выраже-

ковских частиц в поле KN при наличии горизон-

ние (42).

тов событий. Эти выводы относятся также к полям

Далее, если провести преобразования

Райсснера - Нордстрёма и Шварцшильда. Для экс-

тремальных полей Керра - Ньюмена и Керра стаци-

ψ^FKN = g_F F_KN (ρ),

(72)

онарные связанные состояния дираковских частиц

со спином 1/2 существуют для энергий (56), (57)

ψ^GKN = g_GG_KN (ρ),

(73)

при выполнении условия (67). Стационарные реше-

⎛

⎞

∫

ния уравнения Дирака существуют также для слу-

g_F (ρ) = exp⎝1

A_F(ρ′) dρ′⎠ ,

чая голой сингулярности KN.

(74)

Обратимся теперь к релятивистскому уравнению

1 dB_KN

второго порядка с эффективным потенциалом для

A_F (ρ) = -

-A_KN -D_KN,

dρ

метрики KN. С использованием этого уравнения мы

⎛

⎞

∫

получим качественно иные результаты по сравне-

g_G(ρ) = exp⎝1

A_G(ρ′) dρ′⎠ ,

нию с представленными в разд. 2.

(75)

dC_KN

A_G(ρ) = -

-A_KN -D_KN,

dρ

3. САМОСОПРЯЖЕННЫЕ УРАВНЕНИЯ

то для ψ^FKN и ψ^GKN получим самосопряженные урав-

ВТОРОГО ПОРЯДКА ДЛЯ СПИНОРНЫХ

нения типа Шредингера с эффективными потенци-

ВОЛНОВЫХ ФУНКЦИЙ ФЕРМИОНОВ В

алами U^Feff (ρ), U^Geff (ρ):

ГРАВИТАЦИОННЫХ И

ЭЛЕКТРОМАГНИТНЫХ ПОЛЯХ

d²ψ^FKN

(

)

КЕРРА - НЬЮМЕНА

E_Schr - U^Feff (ρ)

ψ^FKN = 0,

(76)

dρ²

d²ψ^GKN

(

)

Для получения уравнения второго порядка необ-

E_Schr - U^Geff (ρ)

ψ^GKN = 0.

(77)

dρ²

ходимо осуществить [46]

1) квадрирование уравнения Дирака;

В формулах (76), (77)

2) переход в уравнении второго порядка от бис-

E_Schr =

(ε² - 1).

(78)

пинорных к спинорным волновым функциям;

3) проведение неунитарного преобразования по-

В (76)

добия для обеспечения самосопряженности урав-

(

)₂

нения второго порядка со спинорными волновыми

dB_KN

U^Feff (ρ) = E_Schr +

функциями.

B_KN dρ

В результате, после разделения угловых и ради-

d²B_KN

(A_KN - D_KN ) -

альных переменных можно получить для преобразо-

4 B_KN dρ²

4 dρ

ванной радиальной функции ψ_KN (ρ) уравнение ти-

1 A_KN - D_KN dB_KN

−

(A_KN -D_KN )² +

па Шредингера с эффективным потенциалом.

B_KN

dρ

Такие уравнения можно получить из систе-

(79)

мы (43).

+ 2BKNC^KN.

В. П. Незнамов, И. И. Сафронов, В. Е. Шемарулин

ЖЭТФ, том 155, вып. 1, 2019

Явный вид потенциала (79) приведен в Приложе-

3.1.1. При ρ → ±∞

нии. В (77)

U^Feff (ε_KN )|_ρ→±∞

(

)₂

dC_KN

α_em

⁽ 1⁾

U^Geff (ρ) = E_Schr +

=ε_KN

+ (1 - 2ε2KN )

(83)

C_KN dρ

ρ²

d²C_KN

(A_KN - D_KN ) +

3.1.2. При наличии двух горизонтов событий

4 C_KN dρ²

4 dρ

(ρ₊)_KN , (ρ_-)_KN

1 A_KN - D_KN dC_KN

(A_KN -D_KN )² +

C_KN

dρ

eff

(ε_KN )|ρ→(ρ

± )KN =^-

32 (ρ - (ρ_±)_KN )²

B_KN C_KN .

(80)

(

)

(84)

В уравнениях (76), (77) выделено и одновремен-

|ρ - (ρ_±)_KN |3/2

но добавлено в (79), (80) слагаемое E_Schr (78). Это

Асимптотики (84) представляют собой потенциаль-

сделано, с одной стороны, для придания уравне-

ные ямы -K/(ρ - (ρ_±)_KN )² с коэффициентом K <

ниям (76), (77) вида уравнений типа Шредингера,

< 1/8, что свидетельствует о возможности суще-

а, с другой стороны, для обеспечения классической

ствования вблизи горизонтов событий стационар-

асимптотики эффективных потенциалов U^Feff , U^Geff

ных связанных состояний квантовомеханических

при ρ → ∞.

частиц (см., например, [43]).

Нормировочные интегралы для волновых функ-

3.1.3. Для экстремального поля KN ((ρ₊)_KN =

ций ψ^FKN и ψ^GKN в (76), (77) имеют вид

= (ρ_-)_KN = α, α² = α2a + α2Q) при ρ → α слева и

справа от горизонта событий

∫

(

)₂

N_F = ψ^FKN (ρ^′)

dρ^′,

(81)

(α2a + α²)(ε - ε_KN )²

U^Feff (ε = ε_KN)|_ρ→α = -

∫

2(ρ - α)⁴

(

)₂

(

)

N_G = ψ^GKN (ρ^′)

dρ^′.

(82)

(85)

|ρ - α|³

Уравнения (76), (77) и эффективные потенциа-

лы (79), (80) переходят друг в друга при ε → -ε,

λ → -λ, m_ϕ → -m_ϕ, α_em → -α_em. Отсюда сле-

U^Feff (ε = ε_KN)|_ρ→α = -

2(ρ - α)²

дует, что уравнения (76), (77) описывают движение

[

]

(

)

частиц и античастиц. В данной работе для частиц

- (λ² + α² - α⁴Ω²) +O

(86)

|ρ - α|

используется уравнение (76) для функции ψ^FKN (ρ) с

эффективным потенциалом U^Feff (79).

Из асимптотики (86) условие существования потен-

Основанием для этого может служить нереляти-

циальной ямы и условие существования в ней стаци-

вистский предел уравнения Дирака с исчезающим

онарных связанных состояний для регулярных ре-

при нулевом импульсе частицы (p = 0) нижним спи-

шений (56) (K < 1/8) можно записать в виде

нором, пропорциональным G(ρ). Аналогично ниж-

ний спинор с функцией G(ρ) исчезает для частицы

0 < λ² + α² - α⁴Ω² < 1/4.

(87)

при преобразовании Фолди - Ваутхайзена с любым

значением импульса p [47-49]. Наоборот, для анти-

3.1.4. При ρ → 0

частицы в нерелятивистском пределе p = 0 и при

U^Feff (ε_KN )|ρ→0 = const + O(ρ).

(88)

преобразовании Фолди - Ваутхайзена исчезает верх-

ний спинор биспинорной волновой функции, про-

В отличие от поля Райсснера - Нордстрёма

порциональный F (ρ).

(U^Feff (ε_RN )|ρ→0

3/8ρ²), эффективный потен-

циал KN (79) является регулярным при ρ = 0.

3.1. Особенности эффективных потенциалов

для стационарных решений ε = ε_KN

3.2. Непроницаемые потенциальные барьеры

Здесь и ниже для краткости обозначение ε_KN со-

Эффективный потенциал (79) может при неко-

ответствует стационарным решениям (52), (56).

торых значениях ρ = ρ^icl иметь особенности вида

ЖЭТФ, том 155, вып. 1, 2019

Стационарные решения уравнения второго порядка.. .

U^Feff |_ρ→ρi

∼

Левая и правая части (92) положительны и обра-

щаются в нуль при ρ = (ρ_±)_KN . Для двух областей

∼

⎛

√

⎞₂ ,

(89)

определения волновых функций мы можем предста-

2α

α2a + α2Q

вить уравнение (92) в виде

⎠

⎝ω +

ρ²

√

(ρ - (ρ₊)_KN ) (ρ - (ρ_-)_KN ) =

(

)

когда знаменатель в (89) обращается в нуль при од-

α_am_ϕ

α2aε+KN

-ε+KN ρ -

(93)

ном или нескольких значениях ρ = ρ^icl.

(ρ₊)_KN

Уравнение для определения ρ^icl имеет вид

× (ρ - (ρ₊)_KN ) , ρ ∈ [(ρ₊)_KN , ∞),

(

)

√

α2a

m_ϕα

α_em

((ρ₊)_KN - ρ) ((ρ_-)_KN - ρ) =

ρ²

(

)

√

α_am_ϕ

α2aε^-KN

= ε^-KNρ+

(94)

2α

α2a + α2Q

(ρ_-)_KN

= 0.

(90)

ρ²

× ((ρ_-)_KN - ρ) , ρ ∈ (-∞, (ρ_-)_KN ].

Особенности (89) могут содержаться во втором сла-

Решения ρ = (ρ₊)_KN в (93) и ρ = (ρ_-)_KN в (94) соот-

гаемом эффективного потенциала (79), равном

ветствуют особенностям эффективного потенциала

(

)₂

(

)₂

dB_KN



B_KN dρ



ρ→(ρ± )KN

(см. Приложение).

на горизонтах событий. Эти особенности уже учте-

При наличии решения уравнения (90) потенциал

ны при анализе в разд. 3.1.2.

(89) можно представить в виде

√

Разделив обе части (93) на

ρ - (ρ₊)_KN и обе

√

(

)

части (94) на

(ρ_-)_KN - ρ, получим уравнения для

U^Feff |_ρ→ρi

(91)

определения других особенностей для ρ = (ρ₊)_KN и

8(ρ - ρ^icl)²

|ρ - ρ^icl|

ρ = (ρ_-)_KN соответственно

Известно, что такие потенциальные барьеры

√

являются квантовомеханически непроницаемы-

(ρ - (ρ_-)_KN ) =

(

)

ми [50]¹⁾.

α_am_ϕ

α2aε+KN

-ε+KN ρ -

(95)

Далее рассмотрим условия возникновения осо-

(ρ₊)_KN

бенностей (91) при наличии двух горизонтов собы-

√

ρ - (ρ₊)_KN, ρ ∈ ((ρ₊)_KN,∞),

тий, для экстремальных полей KN и в случае голой

сингулярности KN.

α_am_ϕ + α_em(ρ₊)_KN

;

(96)

3.2.1. Наличие двух горизонтов событий

α2a + (ρ₊)²

(ρ+)KN , (ρ-)KN , α² > α^a + α^Q; области

√

определения волновых функций:

(ρ₊)_KN - ρ =

ρ ∈ [(ρ+)KN, ∞), ρ ∈ (-∞, (ρ-)KN]

(

)

α_am_ϕ

α2aε^-KN

= ε

ρ+

(97)

В этом разделе мы анализируем возможность су-

(ρ_-)_KN

ществования непроницаемых барьеров типа (91) для

√

(ρ_-)_KN - ρ, ρ ∈ (0, (ρ_-)_KN ),

стационарных решений ε_KN (52).

Уравнение (90) можно записать в виде

α_am_ϕ + α_em(ρ_-)_KN

√

ε^-KN =

(98)

(ρ - (ρ₊)_KN ) (ε - (ρ_-)_KN )

α2a + (ρ_-)²

(

)

Далее для анализа рассмотрим три варианта.

α2a

m_ϕα_a

α_em

1. Поле Керра: αQ = 0, αem = 0,

= -ε_KN

(92)

ρ²

√

(ρ_±)_K = α ±

α² - α²

¹⁾ Следует иметь в виду, что авторы [50] использовали

уравнение типа Шредингера (76) без множителя 2. В наших

α_am_ϕ

ε_K =

m_ϕ > 0,

0 < ε_K < 1.

обозначениях барьер K/(ρ-ρ^icl)² непроницаем, если K ≥ 3/8.

2α(ρ_±)_K

В. П. Незнамов, И. И. Сафронов, В. Е. Шемарулин

ЖЭТФ, том 155, вып. 1, 2019

2. Незаряженная частица со спином 1/2 в поле

на горизонте событий. Эта особенность учтена при

Керра - Ньюмена: α_em = 0, α_Q = 0,

анализе в разд. 3.1.3.

√

Далее будем исследовать уравнение (99) для ρ =

(ρ_±)_KN = α ± α² - α2Q - α2a,

= α. Как и в разд. 3.2.1, для анализа рассмотрим

три варианта.

α_am_ϕ

ε_KN =

m_ϕ > 0,

0 < ε_KN < 1.

1. Поле Керра: α_Q = 0, α_em = 0, α = α_a, ε_K =

α2a + (ρ_±)²

= m_ϕ/2α, m_ϕ > 0; 0 < ε^extK < 1.

Неравенства в вариантах 1, 2 для m_ϕ, ε_K, ε_KN будут

2. Незаряженная частица со спином 1/2 в поле

обсуждаться в разд. 5.

Керра - Ньюмена: α_em = 0, α_Q = 0, α² = α2a + α2Q,

3. Заряженная частица со спином 1/2 в поле Кер-

α_am_ϕ

ра - Ньюмена: α_em = 0, α_Q = 0,

ε^extKN =

m_ϕ > 0;

0 < ε^extKN < 1.

α2a + α²

√

(ρ_±)_KN = α ± α² - α2a - α2Q,

Неравенства в разд. 1.2 для m_ϕ, ε_K, ε_KN будут об-

суждаться в разд. 5.

α_am_ϕ + α_em(ρ_±)_KN

3. Заряженная частица со спином 1/2 в поле Кер-

ε_KN =

α2a + (ρ_±)²

ра - Ньюмена: α_em = 0, α_Q = 0, α² = α2a + α2Q,

Для области определения ρ > (ρ₊)_KN и для первых

α_am_ϕ + α_emα

ε^extKN =

двух вариантов решение уравнения (95) отсутствует.

α2a + α²

Наоборот, для первых двух вариантов и для области

определения ρ < (ρ_-)_KN существует единственное

Для области определения ρ > α и для первых

двух вариантов решения уравнения (99) отсутству-

решение (97) ρ = ρ_cl, при котором возникает непро-

ницаемый потенциальный барьер вида (91).

ют. Наоборот, для первых двух вариантов и для об-

ласти определения ρ < α существует единственное

Для третьего варианта и для обеих областей

определения ρ > (ρ₊)_KN , ρ < (ρ_-)_KN , алгебраиче-

решение ρ = ρ_cl, при котором возникает непроница-

емый потенциальный барьер вида (91).

ский анализ допустимых значений параметров, удо-

влетворяющих уравнениям (95), (97), затруднителен

Для третьего варианта и для обеих областей

определения ρ > α, ρ < α алгебраический анализ за-

из-за возможности реализации разных знаков ε, m_ϕ,

α_em. В данном случае возможность существования

труднителен. Возможность существования непрони-

цаемого потенциального барьера при заданных на-

непроницаемого потенциального барьера при задан-

ных начальных параметрах должна определяться

чальных параметрах должна определяться решени-

либо анализом эффективного потенциала, либо ре-

ем уравнения (99).

шением уравнений (95), (97).

3.2.3. Голая сингулярность Керра - Ньюмена

(α2a + α2Q > α²); области определения волновых

3.2.2. Экстремальное поле Керра - Ньюмена

функций: ρ ∈ (-∞, ∞)

(α² = α2a + α2Q, (ρ+)KN = (ρ-)KN = α); области

определения волновых функций:

В случае голой сингулярности KN для определе-

ρ ∈ [α,∞), ρ ∈ (-∞, α]

ния наличия или отсутствия непроницаемых потен-

В случае экстремального поля KN для обеих об-

циальных барьеров необходимо решать уравнение

ластей определения волновых функций уравнение

четвертой степени (90). Из-за громоздкости анали-

(90) можно записать в виде

тических решений целесообразно решать уравнение

(

)

(90) при заданных значениях начальных парамет-

α_am_ϕ

α2a

ров: α, α_Q, α_a, α_em, m_ϕ, ε. Второй способ — это ком-

ρ(ρ-α) =

-ε^extKNρ-

ε^ext

(ρ-α),

(99)

пьютерное исследование особенностей эффективно-

го потенциала (79) для некоторой выделенной обла-

α_am_ϕ + α_emα

сти значений начальных параметров.

ε^extKN =

(100)

α2a + α²

3.3. Асимптотика функций ψ^FKN (ρ, ε)

Решение ρ = α в уравнении (99) соответствует осо-

бенности эффективного потенциала

3.3.1. При ρ → ±∞ функция g_F (ρ) → ρ (см.

(

)₂

(74)) и

dB_KN



B_KN dρ



ψ^FKN |_ρ→±∞ = ρF_KN |_ρ→±∞.

(101)

ρ→α

ЖЭТФ, том 155, вып. 1, 2019

Стационарные решения уравнения второго порядка.. .

Для финитного движения частиц со спином 1/2 с

3.3.3. В случае экстремального поля KN пред-

учетом (44) имеем

ставим асимптотику функции ψ^FKN (ρ, ε^extKN ) в виде

√

∑

ψ^FKN |_ρ→∞ = C₁ϕ₁(ρ)ρe^-

1-ε² ρ,

(102)

ψ^FKN (ρ, ε^extKN)|_ρ→α

= |ρ - α|^s χ^extk|ρ - α|^k.

(108)

√

ψ^FKN |_ρ→-∞ = C₂ϕ₂(ρ)ρe

1-ε² ρ.

(103)

k=0

Из уравнения (76) с учетом (108), (86) можно запи-

3.3.2. При наличии двух горизонтов событий

сать определяющее уравнение

представим функцию ψ^FKN (ρ, ε_KN ) в виде

s(s - 1) +

-λ² -α² +α⁴Ω² =0

(109)

ψ^FKN (ε_KN )|ρ→(ρ

|ρ - (ρ₊)_KN |^s ×

+ )KN =

∑

с решениями

× χ(+)k|ρ - (ρ₊)_KN|^k

(104)

k=0

√

s1,2 =

λ² + α² - α⁴Ω².

(110)

при ρ → (ρ₊)_KN ,

Оба решения приводят к квадратично-интегрируе-

ψ^FKN (ε_KN )|ρ→(ρ

- )KN =

|(ρ_-)_KN - ρ|^s ×

мым функциям ψ^FKN (ε^extKN ) при выполнении усло-

∑

вий:

√

× χ(-)k|(ρ_-)_KN - ρ|^k

(105)

— для s₁ = 1/2 +

λ² + α² - α⁴Ω² должно вы-

k=0

полняться неравенство

при ρ → (ρ_-)_KN .

λ² + α² - α⁴Ω² > 0,

(111)

Из уравнения (76) с учетом (104), (105), (84) сле-

√

дует определяющее уравнение

— для s₂ = 1/2 -

λ² + α² - α⁴Ω² должно вы-

полняться неравенство

s(s - 1) + 3/16 = 0

(106)

1 > λ² + α² - α⁴Ω² > 0.

(112)

с решениями s₁ = 3/4, s₂ = 1/4.

Оба решения приводят к регулярным квадратич-

Условие существования потенциальной ямы (87) су-

но-интегрируемым решениям для волновой функ-

щественно ограничивает неравенства (111), (112), и

ции ψ^FKN (ρ, ε_KN ). Для однозначного выбора реше-

оба решения s1,2 должны удовлетворять неравен-

ния обратимся к асимптотикам (45)-(48) для ради-

ству

альных функций Дирака F_KN (ρ) при ε = ε_KN и к

преобразованию (72), (74).

1/4 > λ² + α² - α⁴Ω² > 0.

(113)

При ρ

→ (ρ_±)_KN преобразование g_F (ρ)

→

→ |ρ - (ρ_±)_KN |3/4 и в результате

При ρ → α преобразование (74) g_F (ρ) → |ρ - α|3/2.

Оба решения (65) для асимптотики F^extKN |_ρ→α

ψ^FKN (ε_KN )|ρ→(ρ

(64) преобразуются в соответствующие решения

± )KN =

[g_F (ρ)F_KN (ρ)] |ρ→(ρ± )KN⁼

(110) для асимптотики ψ^FKN (ε^extKN ) (108).

= C₃|ρ - (ρ_±)_KN|1/4.

(107)

Таким образом, для уравнения второго порядка

(76) из-за существования двух регулярных асимпто-

Асимптотики (107) соответствуют решению опреде-

тик в окрестности горизонта ρ = α невозможно по-

ляющего уравнения (106) s₂ = 1/4. Для решения

ставить краевую задачу о существовании собствен-

s1 = 3/4 отсутствует решение уравнения Дирака

ных функций и собственных значений.

F (ρ)|ρ→(ρ± )KN^{=const,ивэтомслучаепреобразо-}

Кроме того, авторы аналитически и численно не

вания (72) не существует. Ниже решения уравнения

второго порядка (76) с асимптотиками (107) будем

обнаружили область значений физических парамет-

ров, в которой справедливо неравенство (113).

использовать в качестве собственных функций ста-

Для уравнения Дирака эта проблема однозначно

ционарных связанных состояний фермионов с соб-

разрешается. Единственное физически приемлемое

ственными значениями ε_KN . Эти решения являют-

решение для волновой функции соответствует одно-

ся квадратично-интегрируемыми в окрестности го-

му из решений (65)

ризонтов событий. Отметим, что волновые функции

(107) на горизонтах событий (ρ₊)_KN , (ρ_-)_KN равны

√

s₁ = -1 +

λ² + α² - α⁴Ω².

(114)

нулю.

ЖЭТФ, вып. 1

В. П. Незнамов, И. И. Сафронов, В. Е. Шемарулин

ЖЭТФ, том 155, вып. 1, 2019

Условие квадратичной интегрируемости дираков-

Тогда

ских радиальных функций (66) записывается в виде

(ρ)

= tg Φ(ρ)

(122)

λ² + α² - α⁴Ω² > 1/4.

(115)

dψ^FKN (ρ)/dρ

и уравнение (76) можно записать в виде системы

При этом энергия стационарного связанного состо-

яния ε^extKN равна

нелинейных дифференциальных уравнений первого

порядка:

α_am_ϕ + α_emα

ε^extKN =

(116)

dΦ

α2a + α²

= cos² Φ + 2(E_Schr - U^Feff )sin² Φ,

(123)

dρ

Для метрики Керра (α_em = 0, α_Q = 0) выражения

d ln P

= (1 - 2(E_Schr - U^Feff )) sin Φ cos Φ.

(124)

(115), (116) имеют вид

dρ

m_ϕ

Отметим, что уравнение (124) должно решаться по-

λ² + α² - m2ϕ >

ε^extK =

(117)

2α

сле определения собственных значений ε_n и соб-

ственных функций Φ_n(ρ) из уравнения (123).

Решение ε^extK ранее получено в работе [51].

В уравнениях (123), (124) эффективный потен-

3.3.4. Рассмотрим асимптотику волновой функ-

циал U^Feff зависит от константы разделения λ. В от-

ции ψ^FKN |_ρ→ρi вблизи непроницаемых барьеров

личие от полей Шварцшильда и Райсснера - Норд-

(91). Определяющее уравнение для (76) с учетом

стрёма, для полей Керра и Керра - Ньюмена λ зави-

асимптотики (91) имеет вид

сит от ε, α_a, j, l, m_ϕ (см. угловые уравнения Чандра-

s(s - 1) - 3/4 = 0.

(118)

секара - Пейджа (38) для сфероидальных гармоник

S_±(θ)). При решении уравнений (123), (124) необхо-

Решения (118) равны s₁ = 3/2, s₂ = -1/2. Вто-

димо первоначально определять значения λ в зави-

рое решение соответствует ненормируемой волновой

симости от начальных параметров.

функции ψ^FKN и поэтому физически неприемлемо. В

Применим преобразование Прюфера к уравнени-

результате

ям (38). Пусть

ψ^FKN |_ρ→ρi

= C₄(|ρ - ρ^icl|)3/2.

(119)

S_-(θ) = S(θ)sinΦ(θ),

(125)

(θ) = S(θ) cos Φ(θ),

S₊

Преобразование (72), (74) в окрестностях ρ^icl яв-

ляется сингулярным, g_F (ρ) → |ρ - ρ^icl|-1/2. Из (72)

где

следует, что

S_-(θ)/S₊(θ) = tg Φ(θ),

(126)

(

)1/2

F_KN (ρ)|_ρ→ρi

≈ |ρ - ρ^icl|².

(120)

S(θ) =

S2-(θ) + S²⁺(θ)

(127)

Из численных расчетов следует, что зависимость

Тогда угловые уравнения Чандрасекара - Пейджа

(120) действительно реализуется в первом уравне-

(38) можно записать в виде

нии (43) для случая, когда выражение в скобках пе-

ред функцией G_KN (ρ) обращается в нуль (это соот-

dΦ(θ)

= λ + αa cosθcos(2Φ(θ))+

ветствует уравнению (90) для определения ρ^icl).

dθ

(

)

m_ϕ

- α_aε sinθ sin(2Φ(θ)) ,

(128)

sinθ

4. МЕТОД ФАЗОВЫХ ФУНКЦИЙ

(

)

Численные решения уравнения второго порядка

d ln S

m_ϕ

ctg θ+ α_aε sin θ-

cos(2Φ(θ)) +

типа Шредингера (76) удобно осуществлять с помо-

dθ

sinθ

щью фазовых функций Φ(ρ), Φ(θ).

+ αa cosθsin(2Φ(θ)).

(129)

Применим преобразование Прюфера [30-33] к

Граничные условия имеют вид

уравнению (76) с эффективным потенциалом (79):

ψ^FKN (ρ) = P(ρ)sinΦ(ρ),

для m_ϕ < 0 Φ(0) = kπ, Φ(π) =

+ kπ,

(130)

(121)

dψ^FKN (ρ)

для m_ϕ > 0 Φ(0) =

+ kπ, Φ(π) = kπ.

(131)

= P(ρ)cosΦ(ρ).

dρ

ЖЭТФ, том 155, вып. 1, 2019

Стационарные решения уравнения второго порядка.. .

В (130), (131) k = 0, ±1, ±2, . . .,

4.1.2. При наличии двух горизонтов событий,

)

пусть при ρ → (ρ₊)_KN ,

⁽π

tg Φ

= P_par(-1)j+mϕ = ±1,

(132)

Φ|ρ→(ρ

kπ + A|ρ - (ρ₊)_KN |.

(138)

+ )KN =

где P_par = 2(l - j) — четность.

Тогда

Ранее Незнамовым, Сафроновым [52] было реа-

лизовано численное решение уравнений (128), (129).

sinΦ|ρ→(ρ

+ )KN ≃±A|ρ-(ρ+⁾KN^|,

Результаты решения полностью согласуются с ре-

зультатами [42], полученными другим численным

cosΦ|ρ→(ρ

+ )KN ≃±1.

способом.

Из совместности (138) с уравнением (123) с учетом

В данной работе мы будем из уравнения (128)

ведущей особенности (см. (84))

первоначально определять λ(ε, α_a, l, j, m_ϕ) и Φ(θ).

Далее, из (123) определяем спектр ε_n и Φ_n(ρ). Из

U^Feff (ε_KN ) = -

уравнения (124) определяем P_n(ρ) и при необходи-

32 (ρ - (ρ₊)_KN )²

мости из уравнения (129) определяем S_n(θ). После

получаем

этого, в соответствии с (121), определяем собствен-

ную радиальную функцию_nψ^FKN (ρ) и при необхо-

A² = A

(139)

димости, в соответствии с (35), (36), (40) и (125), —

полную волновую функцию:

с решениями A₁ = 4, A₂ = 4/3.

Далее интегрируем уравнение (124) при ρ

→

nψKN(ρ, θ, ϕ) = nψKN(ρ)iσ³ξKN(θ).

(133)

→ (ρ₊)_KN с учетом ведущей особенности эффек-

тивного потенциала (84). В результате

4.1. Асимптотика функций Φ(ρ), P (ρ)

4.1.1. Для связанных состояний при ρ → ∞ с

P|ρ→(ρ+)KN⁼

{

учетом (102), (122) получаем

|ρ - (ρ₊)_KN |3/4, A₁ = 4,

=C₅

(140)

|ρ - (ρ+)KN |-1/4, A2 = 4/3,

tg Φ|_ρ→∞ = -√

1-ε²

(134)

Φ|_ρ→∞ = - arctg

√

+ kπ.

ψ^FKN (ε+KN )|ρ→(ρ

+ )KN =

1-ε²

{

4|ρ - (ρ₊)_KN |1/4,

A₁ = 4,

Для экспоненциально растущих решений в асим-

(141)

4/3|ρ - (ρ₊)_KN |3/4, A₂ = 4/3.

птотике (44) C₁ = 0, C₂ = 0 и с учетом (103), (122)

Сравнение с выражением (107) показывает, что

tg Φ|_ρ→∞ =

√

для нашего рассмотрения приемлемыми являются

1-ε²

(135)

решения (138), (140), (141) со значениями A₁ = 4 и

Φ|_ρ→∞ = arctg

√

+ kπ.

C₃ = 4C₅.

1-ε²

Аналогично при ρ → (ρ_-)_KN

Для связанных состояний при ρ → -∞ с учетом

(103), (122)

(142)

Φ|ρ→(ρ- )KN=-4|(ρ-⁾KN-ρ|+kπ,

C₃

(143)

tg Φ|_ρ→-∞ =

√

P|ρ→(ρ-)KN=-4|(ρ-⁾KN-ρ|-3/4,

1-ε²

(136)

ψ^FKN(ε_KN )|ρ→(ρ

(144)

- )KN =^C3|(ρ-⁾KN-ρ|1/4.

Φ|_ρ→-∞ = arctg

√

+ kπ.

1-ε²

4.1.3. По аналогии с разд. 4.1.2 асимптотики

Φ(ρ), P (ρ) в окрестности непроницаемых барьеров

Для экспоненциально растущих решений

(91) с учетом (119) равны

tg Φ|_ρ→-∞ = -√

1-ε²

Φ|_ρ→ρi

|ρ - ρ^icl| + kπ,

(145)

(137)

Φ|_ρ→-∞ = - arctg

√

+ kπ.

P|_ρ→ρi

= C₆(|ρ - ρ^icl|)1/2,

(146)

1-ε²

ψ^FKN |_ρ→ρi

= C₄(|ρ - ρ^icl|)3/2.

(147)

В (134)-(137) k = 0, ±1, ±2, . . .

В. П. Незнамов, И. И. Сафронов, В. Е. Шемарулин

ЖЭТФ, том 155, вып. 1, 2019

5. СТАЦИОНАРНЫЕ СВЯЗАННЫЕ

Ниже для случая голой сингулярности KN при

СОСТОЯНИЯ ФЕРМИОНОВ В ПОЛЕ

определении спектра ε_n будем использовать функ-

КЕРРА - НЬЮМЕНА

цию Φ(ε, ρ_max) = Φ(ε)|ρ=ρmax . Здесь ρ_max — макси-

мальное расстояние в численных расчетах. Как пра-

5.1. Численные решения уравнений для

вило, хорошую сходимость результатов обеспечива-

фазовых функций. Общие свойства фазовых

ет значение ρ_max = 10⁷.

функций

Численные расчеты выявили наличие следую-

Ниже мы сосредоточимся на численном методе

щих важных свойств функции Φ(ε, ρ_max) (подобные

решения уравнений (123), (124) для радиальных фа-

свойства функции Φ для более простых потенци-

зовых функций Φ(ρ), P(ρ). Аналогичный метод ре-

алов, не зависящих от ε, строго доказаны в рабо-

шения уравнений (128), (129) для угловых фазовых

тах [31-33]).

функций Φ(θ), P(θ) подробно изложен в работе [52].

1. Функция Φ(ε, ρ_max) монотонна при измене-

Для разрешенного набора значений -1 < ε < 1

нии ε.

численно решается задача Коши с заданным на-

2. В случае существования связанных состояний

чальным условием. Для решения задачи Коши ис-

с -1 < ε < 1 поведение Φ(ε, ρ_max) носит скачко-

пользуется неявный метод Рунге - Кутты пятого по-

образный характер. При достижении собственного

рядка с контролем размера шага (схема Ила трех-

значения ε_n функция Φ(ε, ρ_max) изменяется скачком

стадийного метода Радо II A [53]).

на π:

Определив решением (123) спектр ε_n, собствен-

[Φ(ε₀ - Δε, ρ_max)-Φ(ε_n + Δε, ρ_max)]|Δε→0 =

ные функции Φ_n(ρ) и интегрируя уравнение (124),

можно определить функции P_n(ρ) и с учетом (121)

= -nπ.

(150)

волновые функции_nψ^FKN (ρ). Далее можно опреде-

3. В случае отсутствия связанных состояний из-

лить плотность вероятности обнаружения фермио-

менение функции Φ(ε, ρ_max) во всем интервале -1 <

нов в состоянии с ε_n на расстоянии ρ в сферическом

< ε < 1 меньше величины π.

слое dρ:

w(ρ) = P2n(ρ) sin² Φ_n(ρ),

(148)

5.2. Наличие двух горизонтов событий

(ρ₊)_KN , (ρ_-)_KN ; α² > α2a + α2Q

. Область

и вероятность обнаружения связанных фермионов в

определения волновых функций

интервале [ρ₀, ρ]:

ρ ∈ [(ρ₊)_KN, ∞)

∫ρ

В этом случае существует решение (52):

W (ρ) = P2n(ρ^′) sin² Φ_n(ρ^′) dρ^′.

(149)

α_am_ϕ + α_em(ρ₊)

ε_KN =

(151)

ρ0

α2a + (ρ₊)²

При наличии двух горизонтов событий энер-

Для связанных состояний -1 < ε_KN < 1, поэтому

гия связанных состояний определяется равенства-

|α_am_ϕ + α_em(ρ₊)_KN | < α2a + (ρ₊)2KN .

(152)

ми (52), (53). В этом случае численно определяются

только собственные функции_nψ^FKN (ρ) (121), плот-

Решение (151) включает состояния с одноименными

ности вероятности (148) и интегральные вероятнос-

(α_em > 0) и разноименными (α_em < 0) зарядами ис-

ти (149).

точника поля RN и фермиона, а также состояния с

Волновые функции_nψ^FKN (ρ) в зависимости от

незаряженными фермионами.

области определения должны удовлетворять асимп-

При определении волновых функций с извест-

тотикам (102), (103), (107).

ным собственным значением (151) интегрирование

При решении уравнения (123) необходимо иметь

уравнения (123) осуществлялось «справа налево» от

в виду существование особых точек: ρ = ±∞, ρ =

ρ = ρ_max с граничным условием (134) до ρ = (ρ₊)_KN

= ρ^icl, ρ = (ρ±)KN . Численные расчеты с хоро-

с асимптотикой (138) и с решением уравнения (139)

шей сходимостью результатов начинались или за-

A₁ = 4. Поведение интегральных кривых уравнения

канчивались в окрестностях иррегулярных особых

(123) вблизи иррегулярной особой точки ρ = (ρ₊)_KN

точек ρ = (ρ_±)_KN , ρ = ρ^icl с Δρ_irr = 10-8. Выбор

аналогично ранее рассмотренному для поля RN [28].

максимального значения ρ_max в расчетах с имита-

Это связано с одинаковым поведением эффектив-

цией ρ → ±∞ определялся выполнением условий

ных потенциалов при ρ → (ρ₊)_KN и при ρ → (ρ₊)_RN

(134)-(137) с заданной точностью 10-7.

(см. (84) и формулу (55) в [28]).

ЖЭТФ, том 155, вып. 1, 2019

Стационарные решения уравнения второго порядка.. .

5.2.1. Анализ границ физической приемлемости

При наличии вращения (α_a = 0) из (157), (158) сле-

решения εKN при ρ ≥ (ρ+)KN . Результаты

дует, что энергия связанного фермиона никогда не

расчетов

достигает нуля при сколь угодно большом значе-

нии α:

Как и в разд. 3.2.1, будем рассматривать три ва-

рианта.

εKN = 0

при α → ∞.

(159)

1. Поле Керра: α_Q = 0, α_em = 0, (ρ₊)_K = α +

√

α² - α2a,

В данном случае отрицательные и нулевые энергии

α_am_ϕ

-1 < ε_KN ≤ 0 не реализуются и, следовательно,

ε_K =

(153)

2α(ρ₊)_K

m_ϕ > 0. Как и в варианте 1, связанные состояния

незаряженных фермионов с 0 < ε_KN < 1 характе-

Для экстремального поля Керра

((ρ₊)_K

ризуются параллельным направлением спина фер-

= (ρ_-)_K = α; α² = α2a) решение (153) равно

миона и углового момента источника поля KN.

m_ϕ

Из (157) следует, что неравенство ε_KN < 1 реа-

ε^extK =

(154)

2α

лизуется, если

Из (153), (154) следует, что при наличии вращения

α_am_ϕ < α2a + (ρ₊)2KN .

(160)

источника поля Керра (α_a = 0) энергия связанно-

го фермиона никогда не достигает нуля при сколь

3. Заряженная частица со спином 1/2 в поле Кер-

угодно большом значении гравитационной констан-

ра - Ньюмена: α_Q = 0, α_em = 0, (ρ₊)_KN

= α +

ты связи α:

√

+ α² -α2a -α2Q

ε_K = 0

при α → ∞.

(155)

α_am_ϕ + α_em(ρ₊)_KN

В этом случае отрицательные и нулевые энергии

ε_KN =

(161)

α2a + (ρ₊)²

-1 < ε_K ≤ 0 не реализуются. Это возможно лишь

для (153), (154) при m_ϕ > 0. Таким образом, свя-

Для экстремального поля KN ((ρ₊)_KN = α, α² =

занные состояния фермионов с 0 < ε_K < 1 в (153),

= α2a + α2Q) решение (161) равно

(154) характеризуются параллельным направлени-

ем спина фермиона и углового момента источника

α_am_ϕ + α_emα

ε^extKN =

(162)

поля Керра.

α2a + α²

Для реализации слабой связи фермиона ε_K ∼ 1

необходимо существование некоторого минимально-

Решение (161) зависит от пяти параметров: α_a, m_ϕ,

го значения α_min. При наличии горизонтов (гори-

α_em, α, α_Q, что затрудняет его алгебраический ана-

зонта) событий максимальное значение α^maxa дости-

лиз. Параметры m_ϕ, α_em могут иметь разные знаки,

гается для экстремального поля Керра (α_a = α). Из

и поэтому, в отличие от вариантов 1, 2, для ε_KN до-

(154) следует, что связь ε_K ∼ 1 достигается при

пустим весь разрешенный для связанных состояний

диапазон: -1 < ε_KN < 1. Отсюда следует очевидное

(m_ϕ)_min

α_min ∼

= 0.25.

(156)

неравенство:

Отсутствие вращения (α_a = 0) соответствует реше-

|α_am_ϕ + α_em(ρ₊)_KN | < α2a + (ρ₊)2KN .

(163)

нию для поля Шварцшильда ε_S = 0. В этом случае

α_min также равно 0.25 [27].

В результате мы получили следующие ограниче-

2. Незаряженная частица со спином 1/2 в поле

ния на физические параметры и энергии связанных

фермионов.

Керра - Ньюмена: α_Q = 0, α_em = 0, (ρ₊)_KN = α +√

1. Поле Керра: α_em = 0, α_Q = 0,

+ α² -α2a -α2Q,

α_am_ϕ

0 < ε_K < 1, m_ϕ > 0, α_am_ϕ < 2α(ρ₊)_K.

(164)

εKN =

(157)

α2a + (ρ₊)²

2. Незаряженная частица в поле Керра - Ньюме-

Для экстремального поля KN ((ρ₊)_KN = (ρ_-)_KN = α,

на: α_em = 0, α_Q = 0,

α² = α2a + α2Q) решение (157) равно

0 < ε_KN < 1, m_ϕ > 0,

α_am_ϕ

εextKN =

(158)

(165)

α2a

+α²

α_am_ϕ < α2a + (ρ₊)2KN .

В. П. Незнамов, И. И. Сафронов, В. Е. Шемарулин

ЖЭТФ, том 155, вып. 1, 2019

5.3. Наличие двух горизонтов событий

. Область

(ρ₊)_KN , (ρ_-)_KN ; α² > α2Q + α2a

2.5

-0.5

определения волновых функций

]

ρ ∈ (-∞,ρ_-

2.0

В этом случае существует решение (52)

1.5

α_am_ϕ + α_em(ρ_-)

ε_KN =

(167)

α2a + (ρ_-)²

1.0

0.3

Для связанных состояний фермиона -1 < ε_KN < 1,

0.5

поэтому

|α_am_ϕ + α_em(ρ_-)_KN | < α2a + (ρ_-)2KN

(168)

0.2

0.4

0.6

0.8

1.0

1.2

1.4

1.6

1.8

2.0

–(

)

+ KN

Решение (167) включает состояния с незаряженны-

ми фермионами (α_em = 0) и состояния с одноимен-

1.0

ными (α_em > 0) и разноименными (α_em < 0) заря-

0.9

дами источника поля KN и фермиона.

0.8

При определении волновых функций с извест-

0.7

0.3

ным собственным значением (167) интегрирование

0.6

-0.5

уравнения (123) осуществлялось «слева направо»

0.5

либо от ρ = -∞ с граничным условием (136), ли-

0.4

бо при наличии непроницаемого барьера от ρ = ρ_cl

0.3

с граничным условием (145). Интегрирование закан-

0.2

чивалось при ρ = (ρ_-)_KN аналогично ранее рас-

0.1

смотренному для поля RN [28]. Это связано с одина-

0.5

1.0

1.5

2.0

2.5

3.0

ковым поведением эффективных потенциалов при

–(

)

+ KN

ρ → (ρ_-)_KN и при ρ → (ρ_-)_RN (см. (84) и (56) в [28]).

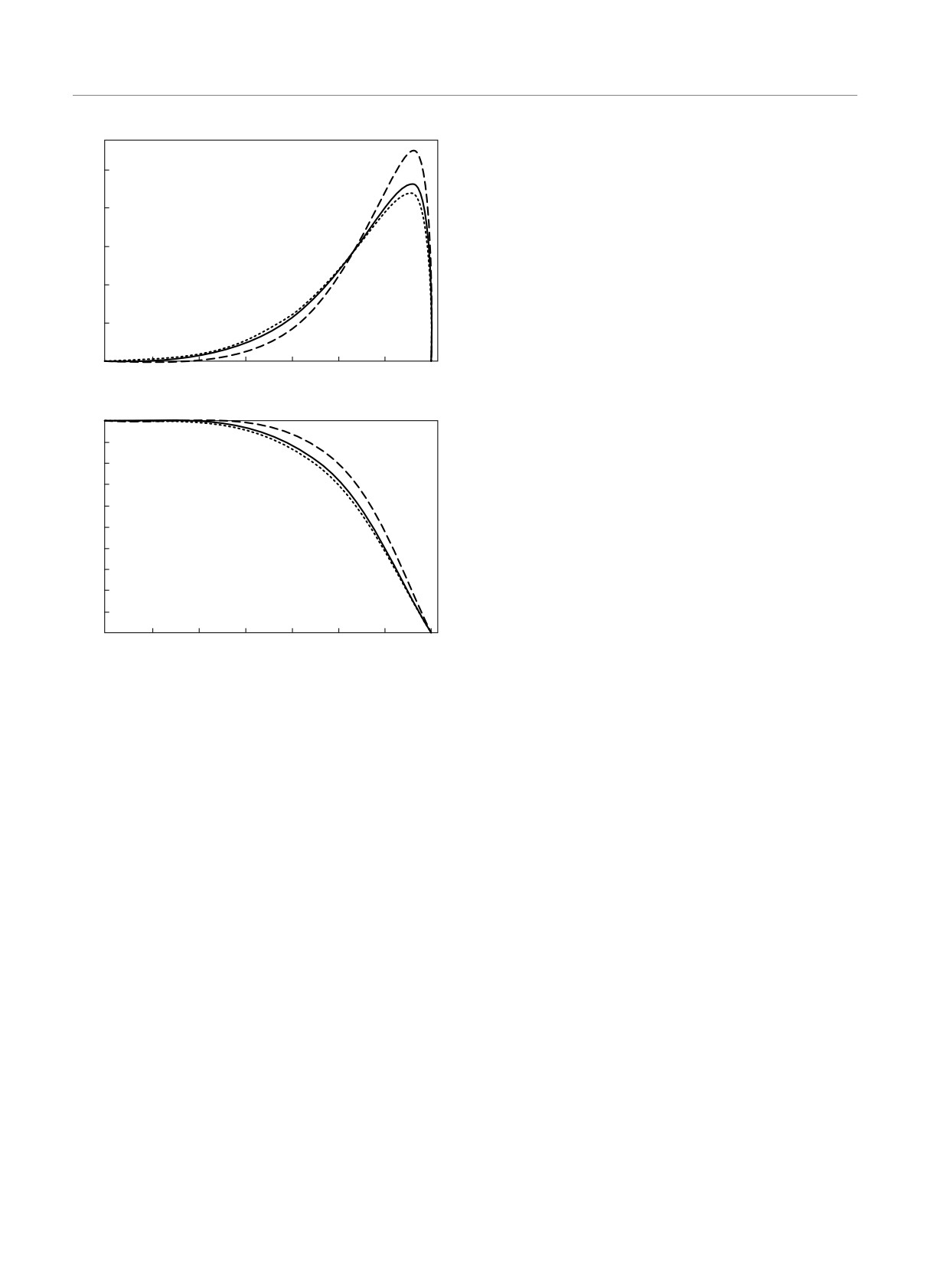
Рис. 1. Зависимости w(ρ - (ρ+)KN ) (а), W (ρ - (ρ+)KN )

5.3.1. Анализ границ физической приемлемости

(б) для связанных состояний с ε((ρ+)KN ) и α = 0.251,

αQ = 0.0251, αa = 0.125, mϕ = 1/2, αem = 0.3, 0, -0.5

решения εKN при ρ ≤ (ρ-)KN . Результаты

расчетов

Ниже мы ограничим себя рассмотрением менее

экзотичных систем с внутренними горизонтами со-

3. Заряженная частица в поле Керра - Ньюмена:

бытий (ρ_-)_KN ≥ 1, т. е. с радиусами, большими или

α_em = 0, α_Q = 0,

сравнимыми с комптоновской длиной волны ферми-

она l_c. Из неравенства

⎛

√

⎞

α2Q

α2a

- 1 < ε_KN < 1,

|α_am_ϕ + α_em(ρ₊)_KN | <

(ρ_-)_KN = α^⎝1 -

⎠_≥ 1

α²

< α2a + (ρ₊)2KN.

(166)

возникает автоматическое ограничение на величину

α при заданных значениях α2Q/α², α2a/α².

Как и выше в разд. 3.2.1, 5.2.1, будем рассматри-

В табл. 1 для некоторых значений параметров,

вать три варианта.

удовлетворяющих неравенствам (164)-(166) с α ≈

1. Поле Керра: α_Q = 0, α_em = 0, (ρ_-)_K = α -

√

≈ α_min = 0.251, приведены определенные из рас-

α² - α2a,

четов расстояния ρ_m от максимумов плотностей ве-

α_am_ϕ

роятности до горизонтов событий (ρ₊)_KN . На рис. 1

ε_K =

(169)

2α(ρ_-)_K

для параметров табл. 1 α = 0.251, α_Q = 0.0251, α_a =

= 0.125, m_ϕ = 1/2, α_em = 0.3, 0, -0.5 приведены

Из (169) следует, что ε_K = 0 при α → ∞, т. е. от-

нормированные плотности вероятности (148) и ин-

рицательные энергии -1 < ε_K < 0 не реализуются.

тегральные вероятности (149).

Это возможно лишь при m_ϕ > 0.

ЖЭТФ, том 155, вып. 1, 2019

Стационарные решения уравнения второго порядка.. .

Таблица 1. Характеристики связанных состояний фермионов с гравитационной константой связи α = 0.251

α_a

α_Q

α_em

l, j, m_ϕ

(ρ₊)_KN

ε_KN

ρ_m

0.125

0, 1/2, 1/2

0.469

-0.94

0.266

4.66

· 10-2

0.125

1, 3/2, 3/2

0.469

-1.9

0.797

1.12

· 10-2

0.125

0.0251

0, 1/2, 1/2

0.467

-0.94

0.267

4.65

· 10-2

0.125

0.0251

1, 3/2, 3/2

0.467

-1.99

0.802

1.12

· 10-2

0.0251

0.125

0, 1/2, 1/2

0.467

-0.99

0.057

4.04

· 10-2

0.0251

0.125

1, 3/2, 3/2

0.467

-1.99

0.172

8.54

· 10-3

0.125

0.0251

-0.5

0, 1/2, 1/2

0.467

-1.02

-0.732

2.78

· 10-2

0.125

0.0251

-0.5

1, 3/2, 3/2

0.467

-1.995

-0.197

8.55

· 10-3

0.125

0.0251

0.3

0, 1/2, 1/2

0.467

-0.89

0.866

6.91

· 10-2

0.125

0.0251

0.09

1, 3/2, 3/2

0.467

-1.88

0.982

1.18

· 10-2

0.0251

0.125

-0.4

0, 1/2, 1/2

0.467

-1.01

-0.796

2.58

· 10-2

0.0251

0.125

-0.4

1, 3/2, 3/2

0.467

-2.01

-0.682

6.68

· 10-3

0.0251

0.125

0.4

0, 1/2, 1/2

0.467

-0.98

0.911

5.76

· 10-2

0.0251

0.125

0.3

1, 3/2, 3/2

0.467

-1.98

0.812

9.71

· 10-3

0.125

0.0251

-0.3

0, 1/2, -1/2

0.467

-0.97

-0.866

2.24

· 10-2

0.125

0.0251

-0.09

1, 3/2, -3/2

0.467

-1.93

-0.981

4.26

· 10-3

0.125

0.0251

0.5

0, 1/2, -1/2

0.467

-1.1

0.732

4.02

· 10-2

0.125

0.0251

0.5

1, 3/2, -3/2

0.467

-2.05

1.197

6.73

· 10-3

0.0251

0.125

-0.4

0, 1/2, -1/2

0.467

-0.99

-0.911

2.23

· 10-2

0.0251

0.125

-0.3

1, 3/2, -3/2

0.467

-1.99

-0.812

5.85

· 10-3

0.0251

0.125

0.4

0, 1/2, -1/2

0.467

-1.02

0.796

4.85

· 10-2

0.0251

0.125

0.4

1, 3/2, -3/2

0.467

-2.02

0.682

8.79

· 10-3

α_am_ϕ + α_em(ρ_-)_KN

2. Незаряженная частица со спином 1/2 в поле

ε_KN =

(171)

α2a + (ρ_-)²

Керра - Ньюмена: α_Q = 0, α_em = 0, (ρ_-)_KN = α -√

- α² -α2a -α2Q,

В (171) параметры m_ϕ, α_em могут иметь разные зна-

α_am_ϕ

ки, и поэтому, в отличие от (169), (170), для ε_KN до-

εKN =

(170)

α2a + (ρ_-)²

пустим весь разрешенный диапазон для связанных

состояний: -1 < ε_KN < 1. Отсюда следует очевид-

Из (170) следует, что ε_KN = 0 при α → ∞, т. е. для

ное неравенство

связанных фермионов реализуется лишь положи-

тельный интервал разрешенных энергий 0 < ε_K < 1.

|α_am_ϕ + α_em(ρ_-)_KN | < α2a + (ρ_-)2KN .

(172)

Отсюда следует, что в (170) m_ϕ > 0.

В табл. 2 для трех рассмотренных вариантов при-

3. Заряженная частица со спином 1/2 в поле Кер-

ведены результаты некоторых демонстрационных

ра - Ньюмена: α_Q = 0, α_em = 0, (ρ_-)_KN

= α -

√

расчетов с характеристиками связанных состояний

− α² -α2a -α2Q,

фермионов с энергиями (169)-(171).

В. П. Незнамов, И. И. Сафронов, В. Е. Шемарулин

ЖЭТФ, том 155, вып. 1, 2019

Таблица 2. Характеристики связанных состояний фермионов под внутренним горизонтом событий поля KN с

гравитационной константой связи α = 10

α_a

α_Q α_em

l, j, m_ϕ

(ρ_-)_KN

ε_KN

ρ_m

ρ_cl

Частица в

0, 1/2, 1/2

1.34

-0.09

0.093

8 · 10-2

3.4 · 10-2

поле Керра

1, 3/2, 3/2

1.34

-0.26

0.28

7.6 · 10-2

0.104

-2

0, 1/2, 1/2

1.4

-0.091

0.093

8.3 · 10-2

3.6 · 10

Незаряженная

1, 3/2, 3/2

1.4

-0.27

0.278

7.9 · 10-2

0.111

частица в поле

0, 1/2, 1/2

1.4

-0.61

0.169

8.3 · 10-2

0.067

Керра - Ньюмена

1, 3/2, 3/2

1.4

-1.4

0.508

7.6 · 10-2

0.207

-1

0, 1/2, 1/2

1.4

-0.335

0.041

7.1 · 10-2

0.265

-1

1, 3/2, 3/2

1.4

-0.515

0.226

6.7 · 10-2

0.336

0.3

0, 1/2, 1/2

1.4

-0.018

0.108

8.7 · 10-2

-0.043

1, 3/2, 3/2

1.4

-0.03

0.33

9.3 · 10-2

-0.172

-1

0, 1/2, 1/2

1.4

-0.99

-0.304

8 · 10-2

0.139

-1

1, 3/2, 3/2

1.4

-1.8

0.035

7.2 · 10-2

0.263

Заряженная

0, 1/2, 1/2

1.4

-0.25

0.643

8.7 · 10-2

3.4 · 10-2

частица в поле

1, 3/2, 3/2

1.4

-1.02

0.981

8 · 10-2

0.13

Керра - Ньюмена

-1

0, 1/2, -1/2

1.4

-3

-0.145

6.5 · 10-2

0.2

-1

1, 3/2, -3/2

1.4

-2.9

-0.33

6.8 · 10-2

0.13

0, 1/2, -1/2

1.4

-3.05

-0.04

7.5 · 10-2

-7 · 10-2

1, 3/2, -3/2

1.4

-3

-0.23

7.6 · 10-2

-0.376

-1

0, 1/2, -1/2

1.4

-1.12

-0.643

8.6 · 10-2

0.024

-1

1, 3/2, -3/2

1.4

-1.57

-0.98

8.8 · 10-2

8.2 · 10-2

0, 1/2, -1/2

1.4

-1.56

0.304

9.4 · 10-2

-0.183

1, 3/2, -3/2

1.4

-2.2

-0.035

9.1 · 10-2

-0.312

В табл. 2 ρ_m — расстояние от внутреннего гори-

смотренных случаях существует непроницаемый по-

зонта событий до максимального значения плотно-

тенциальный барьер типа (91) с положительным

сти вероятности (148).

или отрицательным значением ρ_cl.

На рис. 2 для параметров табл. 2 α = 10, α_a = 5,

α_Q = 1, j = 1/2, l = 0, m_ϕ = 1/2, α_em = -1, 0, 0.3,

5.4. Голая сингулярность Керра - Ньюмена

приведены нормированные плотности вероятности

(α² < α2a + α2Q). Область определения

(148) и интегральные вероятности (149).

волновых функций ρ ∈ (0, ∞)

Результаты расчетов демонстрируют возмож-

ность существования стационарных связанных со-

В отличие от рассмотренных в разд. 5.2, 5.3,

стояний фермионов под внутренним горизонтом со-

для фермионов в поле голой сингулярности KN

бытий ρ_-. Эти состояния с энергиями ε_KN (171) ло-

при определенных значениях физических парамет-

кализованы вблизи горизонта событий ρ_-. Для лю-

ров существует невырожденный по n, j, l дискрет-

бых фермионов в поле Керра и для незаряженных

ный энергетический спектр.

фермионов в поле Керра - Ньюмена связанные со-

В численных расчетах интегрирование уравне-

стояния возможны лишь для значений m_ϕ > 0 в

ния (123) проводилось «слева направо» (от ρ_min до

энергетическом интервале 0 < ε_KN < 1.

ρ_max). При отсутствии непроницаемого барьера (91)

Для заряженных фермионов такие ограничения

интегрирование начинается от точки ρ_min = -10⁸

отсутствуют. Из расчетов видно, что во всех рас-

с граничным условием (136). При наличии непро-

ЖЭТФ, том 155, вып. 1, 2019

Стационарные решения уравнения второго порядка.. .

5.4.1. Поле Керра (α2a > α², αQ = 0, αem = 0)

-1

2.5

Рассмотрим состояния связанных фермионов

S1/2(l = 0, j = 1/2), P1/2(l = 1, j = 1/2) с парамет-

2.0

0.3

рами α = 0.1, α_a = 0.5, α_a = 0.9, α_Q = 0, α_em = 0,

m_ϕ = ±0.5. Полученные с помощью численных

1.5

расчетов значения λ, ρ_cl, 1 - ε_n приведены в табл. 3.

1.0

5.4.2. Поле Керра - Ньюмена (α2a + α2Q > α²)

0.5

Рассмотрим связанные состояния заряженных

0.2

0.4

0.6

0.8

1.0

1.2

1.4

(α_em = 0) и незаряженных (α_em = 0) фермионов

(

)

– KN

с квантовыми числами (l = 0, j = 1/2) и (l = 1, j =

= 1/2) с параметрами α = 0.25, α_Q = 0.5, α_a = 0.3,

1.0

= -1, 0, 0.1. В табл. 4-6 приве-

0.7, m_ϕ = ±0.5, α_em

-1

0.9

дены результаты расчетов дискретных энергетиче-

0.8

0.3

ских спектров 1 - ε_n.

0.7

Результаты расчетов демонстрируют существо-

0.6

вание в поле голой сингулярности KN стационар-

0.5

ных связанных состояний фермионов с дискретным

0.4

энергетическим спектром. В целом поведение плот-

0.3

ностей вероятности носит такой же характер, как и

0.2

при рассмотрении атомных систем в пространстве

0.1

Минковского.

0.2

0.4

0.6

0.8

1.0

1.2

1.4

(

)

– KN

6. КОСМИЧЕСКАЯ ЦЕНЗУРА

Рис. 2. Зависимости w((ρ-)KN -ρ) (а), W ((ρ-)KN -ρ) (б)

для связанных состояний с ε((ρ-)KN ) и α = 10, αQ = 1,

αa = 5, j = 1/2, l = 0, mϕ = +1/2, αem = -1, 0, 0.3

Гипотеза космической цензуры, предложенная в

работе [54], запрещает существование в природе син-

гулярностей, не прикрытых горизонтами событий.

Однако полное доказательство этой гипотезы отсут-

ствует до сих пор. Многие исследователи наряду

ницаемого барьера (91) интегрирование уравнения

с черными дырами рассматривают образование го-

(123) проводится от точки ρ_min = ρ_cl + Δρ_cl с гра-

лых сингулярностей, их стабильность и отличитель-

ничным условием (145). Хорошая математическая

ные особенности при экспериментальном наблюде-

сходимость результатов обеспечивается при выборе

нии [55-60].

Δρ_cl = 10-8, ρ_min = -10⁸, ρ_max = 10⁸.

В работе [29] показано, что существуют статичес-

кие метрики с времениподобными сингулярностями,

Уровни энергии в расчетах определялись в точ-

проявляющие себя полностью несингулярными при

ках, где функция Φ(ε, ρ_max) изменяется скачками на

рассмотрении квантовой механики бесспиновых час-

π в соответствии с (150).

тиц.

В работах [27, 28] мы получили подтверждение

Поскольку эффективный потенциал (79) зави-

результатов [29] применительно к движению фер-

сит от константы разделения λ, для каждого зна-

мионов под горизонтом метрики Шварцшильда и в

чения ε эта константа определяется решением урав-

поле голой сингулярности RN. Действительно, ве-

нения (128).

дущие особенности эффективных потенциалов для

Приведем результаты некоторых демонстраци-

этих метрик в окрестности сингулярности представ-

онных расчетов определения дискретного спектра

ляют собой бесконечно большие потенциальные ба-

1-ε_n.

рьеры:

В. П. Незнамов, И. И. Сафронов, В. Е. Шемарулин

ЖЭТФ, том 155, вып. 1, 2019

Таблица 3. Численные значения λ, ρ_cl, 1 - εn

n = 1, j = 1/2, n = 2, j = 1/2, n = 3, j = 1/2, n = 2, j = 1/2, n = 3, j = 1/2,

l=0

l=1

-0.502

-0.5

0.915

0.914

α_a = 0.5

ρ_cl

0.0023

0.0006

0.0003

0.0006

0.0003

m_ϕ = 0.5

1-ε_n

4.57 · 10-3

1.2 · 10-3

5.43 · 10-4

1.27 · 10-3

5.63 · 10-4

-1.5

1.23

α_a = 0.5

ρ_cl

-3.28

-3.66

-3.75

-3.66

-3.75

m_ϕ = -0.5

1-ε_n

5.14 · 10-3

1.28 · 10-3

5.66 · 10-4

1.28 · 10-3

5.64 · 10-4

-0.1

0.97

α_a = 0.9

ρ_cl

-0.716

-0.732

-0.736

-0.73

-0.735

m_ϕ = 0.5

1-ε_n

4.36 · 10-3

1.17 · 10-3

5.34 · 10-4

1.263 · 10-3

5.61 · 10-4

-1.9

1.49

α_a = 0.9

ρ_cl

-6.54

-7.88

-8.27

-7.86

-8.27

m_ϕ = -0.5

1-ε_n

4.9 · 10-3

1.25 · 10-3

5.56 · 10-4

1.28 · 10-3

5.65 · 10-4

Таблица 4. Численные значения λ, ρ_cl, 1 - εn при αem = -1

n = 1, j = 1/2, n = 2, j = 1/2, n = 3, j = 1/2, n = 2, j = 1/2, n = 3, j = 1/2,

l=0

l=1

-0.785

-0.733

-0.717

0.948

0.939

α_a = 0.3

ρ_cl

0.0611

0.047

0.042

0.044

m_ϕ = 0.5

1-ε_n

0.417

0.168

0.084

0.114

0.063

-1.2

-1.26

-1.28

1.09

1.11

α_a = 0.3

ρ_cl

-0.122

-0.144

-0.152

-0.148

-0.154

m_ϕ = -0.5

1-ε_n

0.515

0.195

0.095

0.14

0.073

-0.45

-0.364

-0.334

0.955

0.944

α_a = 0.7

ρ_cl

0.0082

-0.04

-0.058

-0.051

-0.062

m_ϕ = 0.5

1-ε_n

0.317

0.135

0.071

0.095

0.055

-1.51

-1.63

-1.66

1.29

1.32

α_a = 0.7

ρ_cl

-0.353

-0.446

-0.482

-0.463

-0.49

m_ϕ = -0.5

1-ε_n

0.41

0.164

0.083

0.124

0.066

)

⁽1

U^Seff |ρ→0 =

8ρ²

)

⁽1

Для голой сингулярности KN ситуация еще про-

U^RNeff |ρ→0 =

8ρ²

ще. Эффективный потенциал поля голой сингуляр-

ности KN регулярен в окрестности ρ = 0. Точка

В этих случаях сингулярности в начале коор-

ρ = 0 не является особой точкой в уравнении вто-

динат в квантовой механике прикрыты отталкива-

рого порядка для фермионов. Голая сингулярность

ющими барьерами, и наличие сингулярностей не

KN в квантовомеханическом взаимодействии с фер-

несет угрозы космической цензуре.

мионами не несет угрозы космической цензуре.

ЖЭТФ, том 155, вып. 1, 2019

Стационарные решения уравнения второго порядка.. .

Таблица 5. Численные значения λ, ρ_cl, 1 - εn при αem = 0

n = 1, j = 1/2, n = 2, j = 1/2, n = 3, j = 1/2, n = 2, j = 1/2, n = 3, j = 1/2,

l=0

l=1

-0.704

-0.701

-0.7

0.93

0.929

α_a = 0.3

ρ_cl

0.096

0.0943

0.094

m_ϕ = 0.5

1-ε_n

2.18 · 10-2

6.7 · 10-3

3.16 · 10-3

7.75 · 10-3

3.5 · 10-3

-1.295

-1.3

1.123

1.124

α_a = 0.3

ρ_cl

-0.569

-0.59

-0.595

-0.589

-0.595

m_ϕ = -0.5

1-ε_n

2.38 · 10-2

7.07 · 10-3

3.28 · 10-3

7.94 · 10-3

3.55 · 10-3

-0.309

-0.303

-0.301

0.93

0.929

α_a = 0.7

ρ_cl

-0.172

-0.183

-0.186

-0.182

-0.185

m_ϕ = 0.5

1-ε_n

2.02 · 10-2

6.4 · 10-3

3.07 · 10-3

7.64 · 10-3

3.46 · 10-3

-1.69

-1.7

1.35

1.353

α_a = 0.7

ρ_cl

-0.185

-0.206

-0.212

-0.204

-0.211

m_ϕ = -0.5

1-ε_n

2.31 · 10-2

6.94 · 10-3

3.24 · 10-3

8.06 · 10-3

3.59 · 10-3

Таблица 6. Численные значения λ, ρ_cl, 1 - εn при αem = 0.1

n = 1, j = 1/2, n = 2, j = 1/2, n = 3, j = 1/2, n = 2, j = 1/2, n = 3, j = 1/2,

l=0

l=1

-0.702

-0.7

0.929

0.928

α_a = 0.3

ρ_cl

0.11

0.109

m_ϕ = 0.5

1-ε_n

8.07 · 10-3

2.42 · 10-3

1.13 · 10-3

2.73 · 10-3

1.23 · 10-3

-1.3

1.124

1.125

α_a = 0.3

ρ_cl

-0.869

-0.896

-0.903

-0.895

-0.903

m_ϕ = -0.5

1-ε_n

8.53 · 10-3

2.5 · 10-3

1.16 · 10-3

2.75 · 10-3

1.24 · 10-3

-0.304

-0.301

-0.3

0.929

α_a = 0.7

ρ_cl

-0.216

-0.221

-0.223

-0.221

-0.222

m_ϕ = 0.5

1-ε_n

7.73 · 10-3

2.36 · 10-3

1.11 · 10-3

2.71 · 10-3

1.23 · 10-3

-1.7

1.353

1.354

α_a = 0.7

ρ_cl

-3.012

-3.335

-3.427

-3.315

-3.42

m_ϕ = -0.5

1-ε_n

8.4 · 10-3

2.47 · 10-3

1.15 · 10-3

2.77 · 10-3

1.25 · 10-3

7. ЗАКЛЮЧЕНИЕ

стей, связанных с наличием эргосферы, где g₀₀ ≤ 0

(в (2) равенство

В работе для квантовомеханического описания

движения фермионов в классическом поле Кер-

r₀r - r2Q

g₀₀ = 1 -

ра - Ньюмена представлено самосопряженное урав-

r²

нение второго порядка с эффективным потенциа-

лом. Вслед за предыдущей работой [39] мы отмеча-

определяет внешнюю и внутреннюю поверхности эр-

ем, что в эффективном потенциале (79) и в уравне-

госферы поля KN). Таким образом, квантовая ме-

нии второго порядка (76) нет каких-либо особенно-

ханика уравнения Дирака и уравнения второго по-

В. П. Незнамов, И. И. Сафронов, В. Е. Шемарулин

ЖЭТФ, том 155, вып. 1, 2019

рядка не выделяет каким-либо образом присутствие

ных связанных состояний, в отличие от радиаль-

эргосферы с g₀₀ ≤ 0.

ных функций уравнения Дирака, становятся квад-

В результате рассмотрения решений уравнения

ратично-интегрируемыми в окрестности горизонтов

второго порядка с эффективными потенциалами в

событий (ρ_±)_KN .

квантовой механике движения фермионов в класси-

Самосопряженное уравнение второго порядка

ческом поле Керра - Ньюмена получены результаты,

(76) может быть получено квадрированием кова-

качественно отличающиеся от результатов, получа-

риантного уравнения Дирака с переходом от бис-

емых при использовании уравнения Дирака.

пинорной к спинорной волновой функции и с про-

1. При наличии двух горизонтов событий (ρ_±)_KN

ведением соответствующего неунитарного преобра-

существуют регулярные решения с энергиями

зования подобия [46]. Для плоского пространства-

времени Минковского ковариантное уравнение вто-

α_am_ϕ + α_em(ρ_±)_KN

ε=

(173)

рого порядка для фермионов, движущихся во внеш-

α2a + (ρ_±)²

них электромагнитных полях, предложено П. Дира-

Эти решения представляют собой вырожденные ста-

ком еще в 1920-е гг. [25].

ционарные связанные состояния заряженных и неза-

Наше рассмотрение показывает (см. также

ряженных фермионов с квадратично-интегрируе-

[27, 28]), что использование уравнения второго

мыми волновыми функциями и с областями опре-

порядка расширяет возможности получения регу-

деления ρ ∈ [(ρ₊)_KN , ∞), ρ ∈ (-∞, (ρ_-)_KN ]. Волно-

лярных решений квантовой механики движения

вые функции слабо зависят от j, l и обращаются в

частиц со спином 1/2 во внешних гравитационных

нуль на горизонтах событий. Фермионы в связанных

и электромагнитных полях.

состояниях с подавляющей вероятностью локализо-

ваны вблизи горизонтов событий. Максимумы плот-

Авторы благодарят А. Л. Новоселову за суще-

ностей вероятности отстоят от горизонтов событий

ственную техническую помощь в подготовке статьи.

на расстоянии долей комптоновской длины волны

фермионов.

ПРИЛОЖЕНИЕ

2. В случае экстремальных полей KN выполне-

ние неравенства (87) фактически приводит к отсут-

Эффективные потенциалы гравитационных

ствию стационарных связанных состояний фермио-

и электромагнитных полей в

нов для любых значений констант связи.

самосопряженных уравнениях второго

3. Для поля голой сингулярности KN (α² < α2Q +

порядка

+ α2a) при определенных значениях физических па-

1. Поле Керра - Ньюмена.

раметров анализ эффективных потенциалов и пря-

В соответствии с (68)-(71) можно получить

мые численные решения уравнения типа Шредин-

гера показали существование стационарных связан-

{

⁽ dB_KN )²

f_KN

ных состояний как заряженных, так и незаряжен-

√

8 B²

dρ

ω_KN +

f_KN

ных фермионов.

[

(

√

)

4. Эффективный потенциал поля голой сингу-

× -

f^′

ω_KN +

f_KN

лярности KN регулярен в окрестности ρ = 0. Точка

f²

(

)]}₂

ρ = 0 не является особой точкой в уравнении второ-

f^′KN

ω^′KN +

√

(A.1)

го порядка для фермионов в поле голой сингуляр-

f_KN

ности KN. В результате голая сингулярность KN в

квантовомеханическом взаимодействии с фермиона-

ми не несет угрозы космической цензуре.

d²B_KN

f_KN

−

√

Регулярные решения для вырожденных стаци-

4 B_KN dρ²

4 ω_KN +

f_KN

[

(

√

)

онарных связанных состояний фермионов с энер-

(f^′KN)2

ω_KN+

f_KN

f^′′KN ×

гиями ε (173) получены с использованием уравне-

f3KN

f²

(

)

ния второго порядка (76) с эффективным потенци-

(

√

)

f^′KN

× ω_KN+

f_KN

f^′

ω^′KN+

√

алом (79). Волновая функция уравнения (76) связа-

f2KN

f_KN

на с одной из радиальных волновых функций урав-

(

)]

нения Дирака неунитарным преобразованием подо-

f^′′KN

(f^′KN )²

ω^′′KN +

(A.2)

f_KN

2√fKN -

бия (72). В результате волновые функции уравне-

4f3/2

ния второго порядка для вырожденных стационар-

ЖЭТФ, том 155, вып. 1, 2019

Стационарные решения уравнения второго порядка.. .

[

]

f^′KN

4α

6α2Q

α_em

(A - D) =

(A.3)

f^′′RN = -

ω_RN = ε -

4 dρ

ρ³

ρ⁴

2 ρf3/2KN

ρ²f1/2

α_em

2α_em

ω^′RN =

ω^′′RN = -

λ = κ.

(

ρ²

ρ³

1 A - D dB

f^′KN

4. Поле Шварцшильда (α_Q = 0, α_em = 0, α_a

= 0):

B dρ

f_KN

2ρf1/2KN

(

))

f^′KN

2α

4α

f_S = 1 -

f^′S =

f^′′S = -

√

(A.4)

ρ²

ρ³

ω_KN +

√f_KN ω^KN +

f_KN

ω_S = ε, ω^′S = ω^′′S = 0, λ = κ.

λ²

(A - D)² =

(A.5)

5. Кулоновское поле (плоское пространство-вре-

2f_KNρ²

мя, α = 0, α_Q = 0, α_a = 0):

α_em

f_C = 1, f^′C = f^′′C = 0, ω_C = ε -

BC = -

(ω2KN - f_KN ).

(A.6)

2f²

α_em

2α_em

В формулах (A.1)-(A.6)

ω^′C =

ω^′′C = -

λ = κ.

ρ²

ρ³

2α

α2a + α2Q

f_KN = 1 -

ρ²

ЛИТЕРАТУРА

df_KN

2α

2(α2a + α2Q)

f^′KN ≡

S. Chandrasekhar, Proc. Roy. Soc. A 349, 571 (1976).

dρ

ρ²

ρ³

S. Chandrasekhar, Proc. Roy. Soc. A 350, 565 (1976).

d²f_KN

4α

6(α2a + α2Q)

f^′′KN ≡

dρ²

ρ³

ρ⁴

D. Page, Phys. Rev. D 14, 1509 (1976).

(

)

α2a

α_am_ϕ

α_em

N. Toop, Preprint DAMTP, Cambridge Univ., Cam-

ω_KN = ε

ρ²

bridge (1976).

dω_KN

2εα_a

2α_am_ϕ

α_em

R. P. Kerr, Phys. Rev. Lett. 11, 237 (1963).

ω^′KN ≡

dρ

ρ³

ρ²

E. T. Newman, E. Couch, K. Chinnapared, A. Exton,

d²ω_KN

6εα2a

6α_am_ϕ

2α_em

A. Prakash, and R. Torrence, J. Math. Phys. 6, 918

ω^′′KN ≡

dρ²

ρ⁴

ρ³

(1965).

Сумма выражений E_Schr

(1/2)(ε²-1) и

E. G. Kalnins and W. Miller, J. Math. Phys. 33, 286

(A.1)-(A.6) приводит к выражению для эффектив-

(1992).

ного потенциала U^Feff (79). Для остальных рассмат-

F. Belgiorno and M. Martellini, Phys. Lett. B 453,

риваемых в работе электромагнитных и гравитаци-

17 (1999).

онных полей структура выражений для эффектив-

ных потенциалов не изменяется. Изменяются лишь

F. Finster, N. Kamran, J. Smoller, and S.-T. Yau,

выражения для f, f^′, f^′′, ω, ω^′, ω^′′.

Comm. Pure Appl. Math. 53, 902 (2000).

2. Поле Керра (α_Q = 0, α_em = 0):

10.

F. Finster, N. Kamran, J. Smoller, and S.-T. Yau,

2α

α2a

2α

2α2a

Comm. Pure Appl. Math. 53, 1201 (2000).

f_K = 1 -

f^′K =

ρ²

ρ³

11.

F. Finster, N. Kamran, J. Smoller, and S.-T. Yau,

(

)

Comm. Math. Phys. 230, 201 (2002).

4α

6α2a

α2a

α_am_ϕ

f^′′K = -

ω_K = ε

ρ³

ρ⁴

ρ²

12.

F. Finster, N. Kamran, J. Smoller, and S.-T. Yau,

Adv. Theor. Math. Phys. 7, 25 (2003).

2εα_a

2α_am_ϕ

6εα2a

6α_am_ϕ

ω^′K = -

ω^′′K =

ρ³

ρ⁴

13.

D. Batic, H. Schmid, and M. Winklmeier, J. Math.

3. Поле Райсснера - Нордстрёма (α_a = 0):

Phys. 46, 012504 (2005).

14.

D. Batic and H. Schmid, Progr. Theor. Phys. 116,

2α

α2Q

2α

2α²

f_RN = 1 -

f^′RN =

517 (2006).

ρ²

ρ³

В. П. Незнамов, И. И. Сафронов, В. Е. Шемарулин

ЖЭТФ, том 155, вып. 1, 2019

15.

M. Winklmeier and O. Yamada, J. Math. Phys. 47,

38.

M. V. Gorbatenko and V. P. Neznamov, J. Mod.

102503 (2006).

Phys. 6, 303 (2015); arXiv:1107.0844 [gr-qc].

16.

D. Batic and H. Schmid, Revista Colomb. Mat. 42,

39.

V. P. Neznamov and V. E. Shemarulin, Grav. Cosmol.

183 (2008).

24, 129 (2018), DOI:10.1134/S0202289318020111.

17.

M. Winklmeier and O. Yamada, J. Phys. A 42,

40.

M. V. Gorbatenko and V. P. Neznamov, Ann.

295204 (2009).

Phys. (Berlin) 526, 491 (2014), DOI:10.1002/andp.

18.

F. Belgiorno and S. L. Cacciatori, J. Math. Phys. 51,

201400035.

033517 (2010).

41.

I. M. Ternov, A. B. Gaina, and G. A. Chizhov, Sov.

19.

C. L. Pekeris, Phys. Rev. A 35, 14 (1987).

Phys. J. 23, 695 (1980).

20.

C. L. Pekeris and K. Frankowski, Phys. Rev. A 39,

42.

S. Dolan and J. Gair, Class. Quant. Grav. 26, 175020

518 (1989).

(2009).

21.

M. K.-H. Klissling and A. S. Tahvildar-Zadeh, J.

43.

Л. Д. Ландау, Е. М. Лифшиц, Квантовая ме-

Math. Phys. 56, 042303 (2015).

ханика. Нерелятивистская теория, Физматлит,

22.

A. S. Tahvildar-Zadeh, J. Math. Phys. 56, 042501

Москва (1963) [L. D. Landau and E. M. Lifshitz,

(2015).

Quantum Mechanics. Nonrelativistic Theory, Perga-

mon Press, Oxford (1965)].

23.

D. M. Zipoy, J. Math. Phys. 7, 1137 (1966).

44.

M. V. Gorbatenko, V. P. Neznamov, and E. Yu. Po-

24.

B. Carter, Phys. Rev. 174, 1559 (1968).

pov, Grav. Cosmol. 23, 245 (2017), DOI:10.1134/

25.

P. A. M. Dirac, The Principles of Quantum Mecha-

S0202289317030057; arXiv:1511.05058 [gr-qc].

nics, Clarendon Press, Oxford (1958).

45.

В. И. Докучаев, Ю. Н. Ерошенко, ЖЭТФ 144, 85

26.

Я. Б. Зельдович, В. С. Попов, УФН 105, 403 (1971)

(2013).

[Ya. B. Zeldovich and V. S. Popov, Sov. Phys. Usp.

14, 673 (1972)].

46.

В. П. Незнамов, ВАНТ, сер. Теор. и прикладн. фи-

зика, вып. 3, 43 (2017).

27.

В. П. Незнамов, И. И. Сафронов, ЖЭТФ 154,

(2018).

47.

L. L. Foldy and S. A. Wouthuysen, Phys. Rev. 78, 29

28.

В. П. Незнамов, И. И. Сафронов, В. Е. Шемару-

(1950).

лин, ЖЭТФ 154, (2018).

48.

В. П. Незнамов, ЭЧАЯ 37(1), 152 (2006) [Part.

29.

G. T. Horowitz and D. Marolf, Phys. Rev. D 52, 5670

Nucl. 37(1), 86 (2006)].

(1995).

49.

V. P. Neznamov and A. J. Silenko, J. Math. Phys.

30.

H. Pruefer, Math. Ann. 95, 499 (1926).

50, 122302 (2009).

31.

I. Ulehla and M. Havl´ıček, Appl. Math.25,

358

50.

J. Dittrich and P. Exner, J. Math. Phys. 26, 2000

(1980).

(1985).

32.

I. Ulehla, M. Havlıček, and J. Hořejš´ı, Phys. Lett.

51.

H. Schmid, Mathematische Nachrichten 274-275(1),

A 82, 64 (1981).

117 (2004); arXiv:math-ph/0207039v2.

33.

I. Ulehla, Rutherford Laboratory preprint RL-82-095

52.

V. P. Neznamov and I. I. Safronov, Int. J.

(1982).

Mod. Phys. D 25, 1650091 (2016); DOI:10.1142/

S0218271816500917.

34.

R. H. Boyer and R. W. Lindquist, J. Math. Phys. 8,

265 (1967).

53.

E. Hairer and G. Wanner, Solving Ordinary Diffe-

rential Equations II. Stiff and Differential-Algebraic

35.

L. Parker, Phys. Rev. D 22, 1922 (1980).

Problems, Springer-Verlag (1991), (1996); Э. Хай-

36.

M. V. Gorbatenko and V. P. Neznamov, Phys. Rev.

рер, Г. Ваннер, Решение обыкновенных дифферен-

D 82, 104056 (2010); arXiv:1007.4631 [gr-qc].

циальных уравнений, Мир, Москва (1999).

37.

M. V. Gorbatenko and V. P. Neznamov, Phys. Rev.

54.

R. Penrose, Rivista del Nuovo Cimento, Serie I, 1,

D 83, 105002 (2011); arXiv:1102.4067 [gr-qc].

Numero Speciale: 252 (1969).