ЖЭТФ, 2019, том 155, вып. 1, стр. 138-146

ВЛИЯНИЕ РАЗМЕРОВ НА УСЛОВИЯ ВОЗНИКНОВЕНИЯ

КРАЕВЫХ СОСТОЯНИЙ В ОДНОМЕРНЫХ СИСТЕМАХ

А. Д. Федосеев^*

Институт физики им. Л. В. Киренского Сибирского отделения Российской академии наук

660036, Красноярск, Россия

Поступила в редакцию 21 мая 2018 г.,

после переработки 21 июня 2018 г.

Принята к публикации 27 июня 2018 г.

Предложен критерий, позволяющий выявлять краевые состояния в случае, когда размеры системы срав-

нимы с длиной локализации этих состояний. Продемонстрировано применение алгоритма определения

краевых состояний в коротких системах на примерах модели Берневига - Хьюза - Жанга в геометрии

цилиндра, модели Китаева и цепочки со спин-орбитальным взаимодействием и наведенной сверхпрово-

димостью. Показано, что в одномерных системах конечной длины существуют области параметров, для

которых краевые состояния не возникают, хотя топологический индекс нетривиален, и, наоборот, проде-

монстрировано возникновение майорановских мод в областях с тривиальным топологическим индексом.

DOI: 10.1134/S0044451019010127

этом системы считались достаточно большими, что-

1. ВВЕДЕНИЕ

бы эффектами размеров системы можно было пре-

небречь. Выходом за пределы подобного подхода яв-

Свойства топологически нетривиальных систем

ляются работы [11, 12], в которых для случая од-

привлекают особое внимание исследователей в по-

номерных моделей конечных размеров было пока-

следние десятилетия [1-7]. Такие системы характе-

зано возникновение линий параметров, отвечающих

ризуются наличием топологически защищенных со-

возникновению майорановских мод, которые также

стояний в диэлектрической щели, что приводит, в

разделяли области с разной четностью основного со-

частности, к возможности движения фермиона без

стояния.

рассеяния на немагнитных примесях. Свойства та-

Несмотря на огромное количество работ, направ-

ких краевых состояний изучаются, как правило, на

ленных на изучение свойства краевых состояний в

полубесконечных моделях с одной границей, а вве-

системах с одной границей, особенности реализации

дение ограниченных систем в подавляющем боль-

краевых состояний в коротких цепочках изучаются

шинстве случаев связано с вычислительными труд-

крайне ограниченно [13-17]. Все эти работы сосре-

ностями. При этом полученные выводы для полубес-

доточены на выявлении особенностей свойств кра-

конечных систем переносятся на системы конечных

евых состояний, вызванных конечными размерами

размеров и наоборот.

систем, вопрос же о влиянии размеров на условия

Дополнительный интерес к системам, в которых

возникновения краевых состояний остается без рас-

реализуются краевые состояния, вызвало предска-

смотрения. Этот вопрос и является предметом об-

зание Китаевым нулевых краевых (майорановских)

суждения в данной работе.

мод в одномерных системах со сверхпроводящим

спариванием [8]. Обнаружение областей парамет-

2. ПРОБЛЕМА ИНТЕРПРЕТАЦИИ

ров, обеспечивающих возникновение майорановских

ХАРАКТЕРА СОСТОЯНИЯ В СИСТЕМАХ

мод в открытых системах, чаще всего осуществ-

КОНЕЧНЫХ РАЗМЕРОВ

ляется путем поиска топологически нетривиальных

Широко распространено представление о крае-

фаз при учете периодических граничных условий.

Для невзаимодействующих электронов классифика-

вых состояниях как о состояниях, волновая функ-

ция которых сосредоточена преимущественно в пер-

ция таких фаз проводилась в работах [9, 10]. При

вых атомных слоях [18]. Однако скорость убывания

^* E-mail: fad@iph.krasn.ru

амплитуды волновой функции может быть сколь

138

ЖЭТФ, том 155, вып. 1, 2019

Влияние размеров на условия возникновения краевых состояний. . .

|u |_n

0.8

0.4

|v |_n

0.6

0.3

0.4

0.2

0.1

|/t

0.25

1.0

|v |_n

0.20

0.8

0.15

0.6

0.10

0.4

0.05

0.2

-2

-1

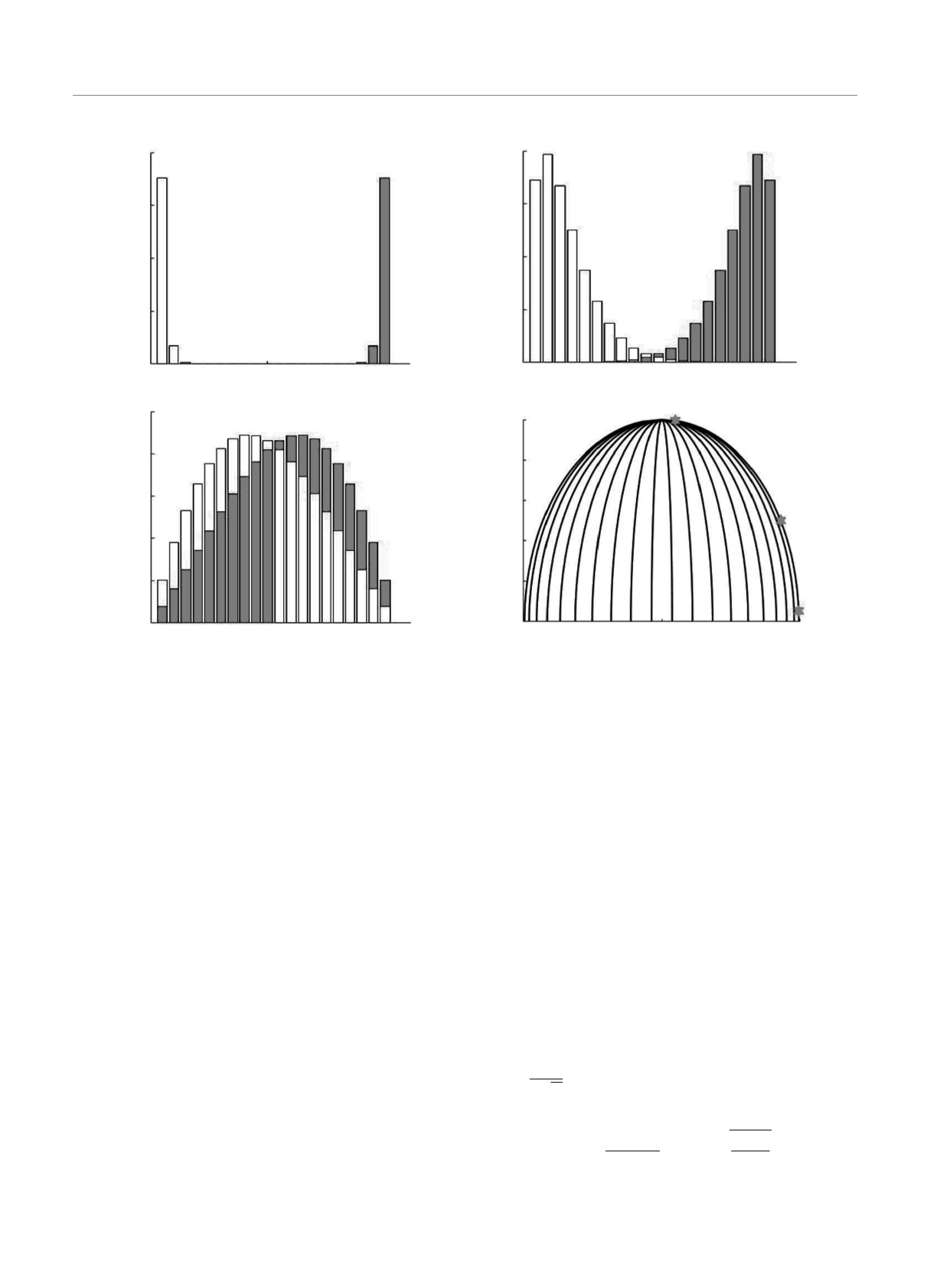
Рис. 1. Зависимость коэффициентов разложения (1) от номера узла (а,б,в) для особых линий параметров (г) в модели

Китаева для цепочки конечной длины. Несмотря на то что на рисунке в коэффициенты разложения имеют максимум

практически посередине цепочки, этот случай соответствует краевой моде

угодно малой, а характерная длина локализации

графику амплитуды на рис. 1в такое возбуждение

может составлять сотни атомных слоев. При этом

не является краевым с точки зрения локализации в

энергия такого одноэлектронного состояния будет

первых атомных слоях, оно все же обладает свой-

находиться в щели объемного спектра, а его свой-

ствами краевого. Во-первых, это возбуждение обла-

ства будут зависеть от граничных условий. В своих

дает энергией E = 0, которая заведомо находится в

работах и Тамм [19,20], и Шокли [21] подчеркивали

щели объемного спектра возбуждений. Во-вторых,

присутствие энергии краевых состояний в «запре-

это возбуждение возникает только при наличии в

щенных» полосах как важную характеристику кра-

цепочке открытых границ. В-третьих, следует обра-

евого состояния.

тить внимание на аналитическое выражение для ко-

эффициентов разложения оператора уничтожения

Проблемы, связанные с указанным выше опре-

такого возбуждения по одноузельным операторам.

делением по длине локализации, можно показать

Выражение для фермиевского оператора, соответ-

на двух примерах. Первым примером является со-

ствующего энергии возбуждения E = 0, имеет вид

стояние с нулевой энергией возбуждения на осо-

бых линиях [11] параметров в модели Китаева ко-

∑

нечной длины (рис. 1). При непрерывном измене-

d₀ =

√

[rⁿ sin φ_mn (c2n-1 + ic2N+2-2n)] ,

(1)

нии параметров вдоль особых линий в параметриче-

A n=1

ском пространстве, максимум амплитуды коэффи-

√

циентов разложения непрерывно смещается от края

πm

t-Δ

φ_m =

(рис. 1a) к центру цепочки (рис. 1в). И хотя согласно

(N + 1)

t+Δ

139

А. Д. Федосеев

ЖЭТФ, том 155, вып. 1, 2019

√

μ=2

t² - Δ² cosφ_m, m = 1, . . ., N,

энергия, близкая к объемной зоне, приводит к суще-

ственному увеличению области локализации краево-

где операторы c_j — майорановские. Видно, что ко-

го состояния.

эффициенты разложения имеют тенденцию к экспо-

Критерии краевого состояния также обсужда-

ненциальному убыванию от краев при любом значе-

лись в работе [23], в которой исследовалась модель

нии параметров, пока они находятся на особой ли-

Берневига - Хьюза - Жанга (BHZ) с периодически-

нии, но в случае, представленном на рис. 1в, длина

ми граничными условиями вдоль одного направле-

цепочки не позволяет увидеть это убывание из-за

ния и одной открытой границей вдоль другого. Ав-

того, что цепочка слишком короткая.

торы отметили, что локальная плотность состояния

Другим примером, иллюстрирующим возникаю-

со значением энергии, находящимся в щели объ-

щую в системах конечных размеров проблему, яв-

емного спектра, испытывает пространственные ос-

ляется модель BHZ с периодическими граничными

цилляции, вследствие которых максимум локальной

условиями вдоль одного направления и открытыми

плотности состояний смещается с первого от гра-

граничными условиями вдоль другого. Поскольку в

ницы слоя атомов в глубь системы. В работе было

такой геометрии можно ввести классификацию воз-

предложено для определения областей параметров,

буждений по величине квазиимпульса вдоль направ-

при которых существует краевое состояние, изучать

ления, в котором реализуются периодические гра-

действительные части показателей экспонент, вхо-

ничные условия, задача сводится к одномерной с

дящих в волновую функцию одноэлектронного со-

параметрами, зависящими от величины этого квази-

стояния.

импульса k. Характерный вид амплитуды волновой

В данной работе ограничимся обсуждением по-

функции на узлах вдоль направления, которое разо-

нятия краевых состояний в приближении сильной

мкнуто, для одноэлектронного состояния, испыты-

связи. В строгом смысле, краевое состояние мож-

вающего переход из краевого в некраевое при изме-

но определить только для полубесконечной систе-

нении квазиимпульса k, представлен на рис. 2. Ви-

мы с одной границей¹⁾: краевое состояние — это со-

ден непрерывный переход от явного вида краевого

стояние, локальная плотность вероятности которого

состояния к некраевому, который происходит осо-

стремится к нулю внутри полубесконечной решетки

бенно быстро в окрестности k = 1.76π, но по степени

локализации волновой функции невозможно устано-

lim

|Ψ_n|² → 0.

(2)

n→∞

вить значение квазиимпульса, при котором состоя-

ние перестает быть краевым.

Коэффициенты разложения волновой функции

одноэлектронного состояния по одноузельным со-

стояниям можно представить в виде суммы реше-

3. ОБОБЩЕНИЕ ПОНЯТИЯ КРАЕВЫХ

ний уравнений для коэффициентов без учета границ

СОСТОЯНИЙ НА СЛУЧАЙ ОДНОМЕРНЫХ

(общего уравнения). Такие решения общего урав-

СИСТЕМ КОНЕЧНЫХ РАЗМЕРОВ

нения представляют собой экспоненты и в случае,

когда гамильтониан безграничной системы обладает

Вопрос определения краевых состояний для од-

симметрией инверсии, входят в разложение попар-

номерных систем конечных размеров поднимался в

но: как eλj n и как e-λj n, причем число таких пар

работе [22], где был предложен расширенный ва-

равно числу уравнений на границе системы:

риант трактовки краевых состояний и исследова-

лись их свойства. Автор [22] предложил трактовку

∑

∑(

)

краевого состояния в одномерной системе конечного

Ψ = u_na+n|0〉, u_n =

A_je-λjn + B_jeλjn

(3)

размера как состояния, которое существует только

n=1

при наличии границы, и свойства которого опреде-

где сумма по j подразумевает суммирование по

ляются положением этой границы. На примере од-

указанным парам решений, а u_n и a+n могут быть

номерной системы с непрерывным периодическим

вектором-строкой и столбцом при учете спина и

потенциалом было продемонстрировано, что значе-

многозонной структуры системы.

ния энергий краевых состояний находятся в щели

Пусть все решения λ_j имеют отличную от нуля

объемного спектра, а скорость убывания волновой

действительную часть Re λ_j > 0. Тогда для полу-

функции краевого состояния находится в зависимо-

бесконечной системы из требования ограниченности

сти от положения значения энергии краевого состо-

яния в щели объемного спектра: энергия в середине

¹⁾ Автор выражает благодарность рецензенту, указавшему

щели отвечает быстрому убыванию, в то время как

на этот факт.

140

ЖЭТФ, том 155, вып. 1, 2019

Влияние размеров на условия возникновения краевых состояний. . .

волновой функции следует, что все коэффициенты

Краевое состояние в одномерной системе помимо

B_j = 0, а волновая функция (3) будет удовлетворять

предложенного критерия (4) можно определять ис-

определению краевого состояния (2).

ходя из энергии этого состояния. Так, если значение

Перейдем к рассмотрению случая, когда показа-

энергии состояния находится в объемном спектре, то

тель экспоненты одного из общих решений λ_j мни-

для такого состояния хотя бы один показатель экс-

мый. Поскольку число пар общих решений равня-

поненты λ_j должен быть чисто мнимым, посколь-

ется числу уравнений на границе, приравнять ну-

ку энергии объемных состояний являются решени-

лю одновременно соответствующие этой паре реше-

ем задачи на собственные значения того же общего

ний коэффициенты A_j и B_j невозможно. В таком

уравнения, и такое состояние является проникаю-

случае, волновая функция будет иметь незатухаю-

щим. В случае, когда значение энергии попадает в

щую компоненту, и такое состояние не будет крае-

щель объемного спектра, ни один показатель экспо-

вым. Очевидно, что в случае большего числа чисто

ненты мнимым быть не может, и состояние является

мнимых показателей экспонент общих решений со-

краевым.

стояние также будет иметь проникающий характер.

Таким образом, можно сформулировать математи-

ческий критерий для краевого состояния в одномер-

4. КРАЕВЫЕ СОСТОЯНИЯ В МОДЕЛИ BHZ

ной системе.

В ГЕОМЕТРИИ УЗКОЙ ПОЛОСЫ

Критерий

Детально проиллюстрируем применение предло-

Если все действительные части показателей экс-

женного критерия краевых состояний на примере

понент, являющихся решением общего уравнения

модели BHZ [2] с периодическими граничными усло-

для коэффициентов разложения волновой функции

виями вдоль оси x и открытыми граничными усло-

по узлам системы при заданной энергии состояния,

виями вдоль направления y. Гамильтониан модели

отличны от нуля, то состояние является краевым, в

BHZ в приближении сильной связи, следуя работе

противном случае оно является некраевым (прони-

[24], запишем в виде

кающим):

∑

[

]

∀λ_j : Re λ_j = 0.

(4)

H_BHZ =

-Δεa+nmσa_nmσ+Δεd+nmσd_nmσ

nmσ

Этот математический критерий является взаимно-

∑

[

]

однозначным строгому определению (2) краевого со-

(t-Δt)a+n′_m′_σanmσ+(t+Δt)dⁿ′_m′_σdnmσ

стояния в полубесконечной системе. Но в отличие от

NNσ

∑

[

последнего, он не требует неограниченности систе-

- iα σ

d+n+1mσa_nmσ - a+nmσdn+1mσ -

мы и может быть применен к одномерным системам

nmσ

]

конечного размера. Предложенный критерий неза-

- d+n-1mσa_nmσ +a+nmσdn-1mσ

висимо от размеров системы делит все состояния на

∑

[

+α

d+nm+1σa_nmσ + a+nmσdnm+1σ -

два класса.

nmσ

1. Одноэлектронные состояния, волновые функ-

]

- d+nm-1σa_nmσ -a+nmσdnm-1σ

(5)

ции которых экспоненциально убывают с краев си-

стемы. В полубесконечной системе такие состояния

Здесь индекс n отвечает нумерации узлов по оси x,

являются краевыми в строгом смысле этого слова. В

а m — по оси y, обозначение NN подразумевает сум-

системе конечных размеров этот же класс решений

мирование по ближайшим соседям.

отвечает основным свойствам краевых состояний:

Наличие периодических граничных условий поз-

локализация у границы и значение энергии, нахо-

воляет перейти к эффективно одномерному случаю,

дящееся в щели объемного спектра. Кроме того, эти

при этом к набору энергетических параметров до-

состояния возникают только при наличии границ и

бавляется величина квазиимпульса k вдоль оси x,

исчезнут в случае введения периодических гранич-

которая также будет влиять на реализацию краево-

ных условий. Исходя из сказанного выше подобные

го состояния. Волновая функция для одноэлектрон-

состояния в одномерных системах конечных разме-

ного состояния с проекцией спина σ и значением

ров следует называть краевыми.

квазиимпульса k имеет вид

2. Одноэлектронные состояния, в разложении ко-

торых (3) присутствует незатухающая компонента и

∑

∑[

]

которые следует называть некраевыми или проника-

Ψ_kσ

=A e^ikm

u_nσa+nmσ + v_nσd+nmσ

|0〉,

(6)

ющими.

n=1

141

А. Д. Федосеев

ЖЭТФ, том 155, вып. 1, 2019

0.5

0.8

0.15

0.04

0.4

0.6

0.03

k = 1.1

k = 1.3

0.10

k = 1.75

k = 1.767

0.3

0.4

0.02

0.2

0.05

0.2

0.01

0.1

100

0.03

0.020

k = 1.8

k = 1.77

k = 1.775

0.015

0.02

k = 1.768

0.010

0.01

0.005

100

Рис. 2. Зависимость амплитуды вероятности от номера узла для состояния с проекцией спина σ =↑ при переходе от

краевого к некраевому характеру в модели BHZ с геометрией типа цилиндра t = 0, Δt = 1, α = 0.5, Δε = 0.5, N = 100

для различных значений квазиимпульса k. Состояние k = 1.767π (правый верхний график) является краевым, в то время

как состояние k = 1.768π (левый нижний) — некраевым

где коэффициенты разложения являются решения-

энергии находятся в щели объемного спектра. Как

ми общего уравнения:

показывают численные расчеты, часто встречаются

объемные решения II типа, т.е. имеющие дополни-

Eu_nσ = (-Δε + t^-k)u_nσ - s_kσv_nσ +

тельно убывающую компоненту, и краевые решения

+ t^-(un+1mσ + un-1mσ) + α(vn+1σ - vn-1σ),

III типа, вызывающие пространственные осцилля-

Ev_nσ = (Δε + t+k)v_nσ - s_kσu_nσ +

ции плотности вероятности, что мешает отличать

(7)

объемные состояния от краевых по степени их ло-

+ t⁺(vn+1mσ + un+1mσ) - α(un+1σ - un-1σ),

кализации на границе (рис. 2).

t^±k = 2t^± cosk, t^± = t ± Δt,

s_kσ = 2ασ sink, σ = ±1.

Характерный вид зависимости λ от k для состоя-

Общее решение для коэффициентов разложения за-

ния, меняющего характер с краевого на некраевой в

писывается в следующем виде:

зависимости от величины k, и состояния, являюще-

гося некраевым при любых значениях k, представ-

u_nσ = ue^λn, v_nσ = ve^λn.

(8)

лен на рис. 3. Видно, что существует четко выра-

женная точка k_cr, для которой состояние перестает

При этом если λ является решением, то -λ и λ^∗ так-

быть краевым и становится объемным. Для случая,

же будут решениями. В таком случае существуют

представленного на рис. 2, квазиимпульс, при ко-

четыре типа наборов для λ = a + ib:

тором исчезает краевое состояние, имеет значение

I. λ = ±ib₁,

±ib₂;

kcr = 1.7675π. Эта же точка соответствует отщеп-

II. λ = ±a₁ + iπl,

±ib₁;

лению энергии состояния от зоны объемных состоя-

III. λ = ±a₁ ± ib₁;

ний. При этом поведение мнимой части показателя

IV. λ = ±a₁ + iπl₁,

±a₂ + iπl₂.

экспоненты b = Im λ роли не играет.

Здесь a и b — действительные и отличные от ну-

ля, а добавка +iπl, где l — целое, введена для уче-

та решений с знакопеременными действительными

Важным результатом является тот факт, что

решениями. Решения типа I и II имеют неубываю-

значение квазиимпульса k_cr, при котором появляют-

щую компоненту, а их энергии находятся в обла-

ся краевые состояния, зависит от длины цепочки N.

сти зонных решений, поэтому краевыми являться

Такая зависимость приведена на рис. 4. Это нагляд-

не могут. Решения типа III и IV представляют со-

но демонстрирует, что размеры одномерной системы

бой краевые решения, поскольку все их компоненты

влияют на условия возникновения краевых состоя-

убывают либо с правого, либо с левого края, и их

ний.

142

ЖЭТФ, том

155, вып. 1,

2019

Влияние размеров на условия возникновения краевых состояний. . .

II IV

III

IV II

1.5

1.0

0.5

–0.5

-1.0

-1

0.5

1.0

1.5

2.0

0.5

1.0

1.5

2.0

1.0

0.8

0.6

0.4

0.2

0.5

1.0

1.5

2.0

0.5

1.0

1.5

2.0

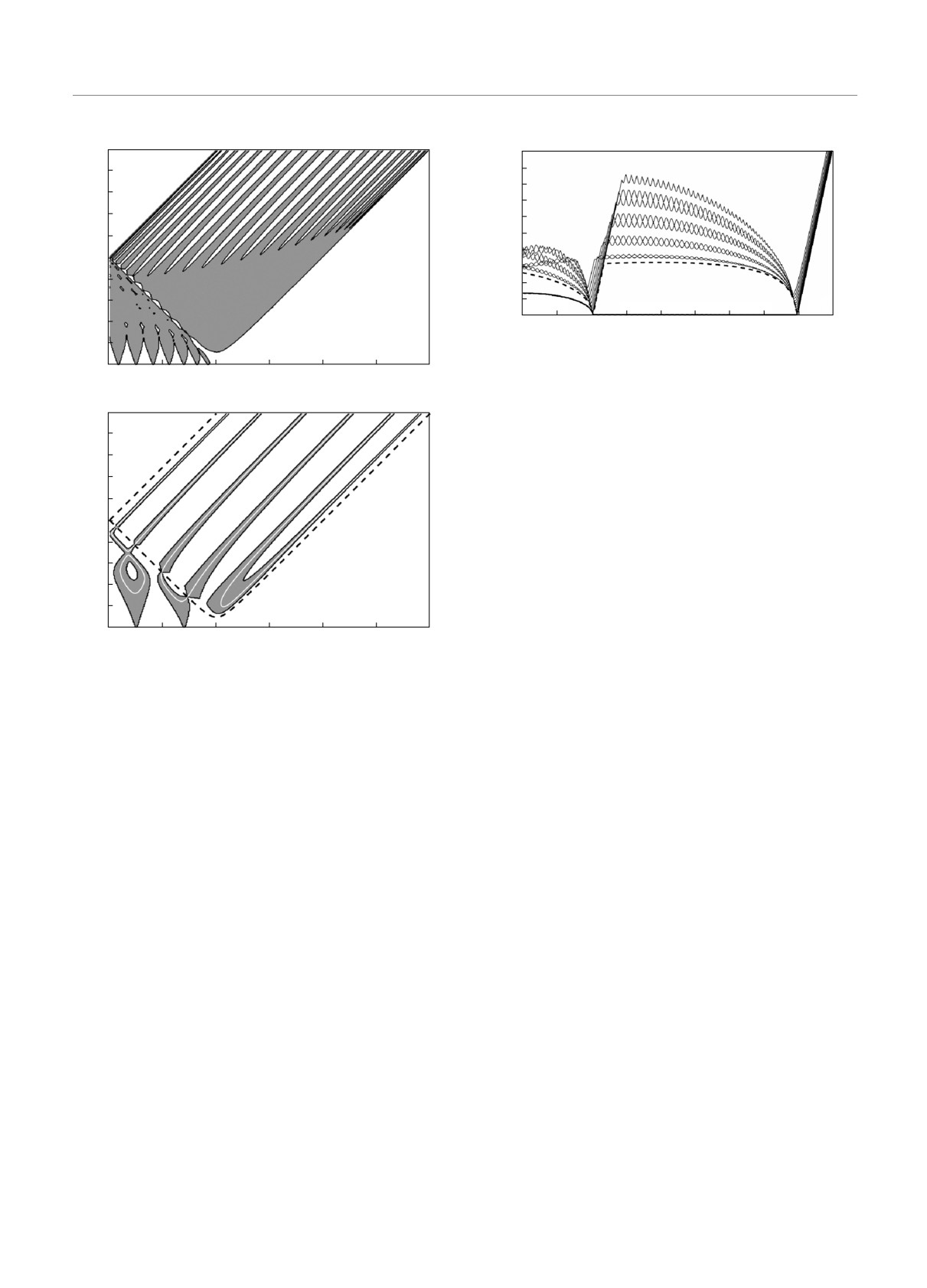
Рис. 3. Действительная a = Re λ сверху и мнимая b = Im λ снизу части показателей экспонент для решения, меняющего

свой характер с краевого на некраевое при изменении величины квазиимпульса k (слева) и являющегося некраевым во

всем диапазоне значений k (справа), в модели BHZ с геометрией цилиндра t = 0, Δt = 1, α = 0.5, Δε = 0.5, N = 100.

Римскими цифрами указан тип общих решений

5. КРАЕВЫЕ СОСТОЯНИЯ В МОДЕЛИ

рис. 5. Конечные размеры системы, помимо отме-

КИТАЕВА КОНЕЧНОЙ ДЛИНЫ

ченной ранее реализации нулевой моды только на

особых линиях [11], приводят к двум эффектам. Во-

Проиллюстрируем влияние размеров на условия

первых, линии, ограничивающие область реализа-

возникновения краевых возбуждений на примере

ции краевых состояний и определяемые в бесконеч-

модели Китаева [8]. Гамильтониан запишем в виде

но длинной цепочке выражением |μ| = ±2|t|, стано-

вятся зависящими от параметра сверхпроводящего

∑

(

)

спаривания |Δ| и область становится тем меньше,

H_K = - μa^†la_l - t

a^†lal+1 + a^†

a_l

l+1

чем короче цепочка. Во-вторых, при малых значе-

n=1

l=1

ниях |Δ| внутри области возникают карманы, рас-

∑

(

)

положенные между линиями реализации нулевых

Δa_lal+1 + Δ^∗a†l+1a^†

(9)

энергий возбуждения, где краевое состояние не воз-

l=1

никает. Это вызвано тем, что достаточно сильное

Области параметров, при которых возникают

перекрытие краевых возбуждений, стремящихся к

краевые состояния в такой модели, представлены на локализации на противоположных краях цепочки,

143

А. Д. Федосеев

ЖЭТФ, том 155, вып. 1, 2019

максимум достигается на линиях нулевых мод.

k_cr/

1.77

1.76

6. КРАЕВЫЕ СОСТОЯНИЯ В

1.75

ОГРАНИЧЕННОЙ ЦЕПОЧКЕ СО

СПИН-ОРБИТАЛЬНЫМ

1.74

ВЗАИМОДЕЙСТВИЕМ И НАВЕДЕННОЙ

1.73

СВЕРХПРОВОДИМОСТЬЮ

1.72

В качестве другого примера рассмотрим одно-

мерную цепочку со спин-орбитальным взаимодей-

100

ствием и наведенной сверхпроводимостью, поме-

щенную в магнитное поле [25, 26]:

Рис. 4. Зависимость значения kcr, соответствующего точ-

ке перехода состояния из краевого в некраевое в модели

∑

BHZ в геометрии цилиндра, от длины цилиндра N, t = 0,

H_wire =

(-μ + hσ) a+nσa_nσ -

Δt = 1, α = 0.5, Δε = 0.5. Штриховая линия соответству-

n=1,σ

ет значению kcr для случая N → ∞

(

)

∑

a+nσan+1σ +

σa⁺

an+1σ

/t|

nσ

n=1,σ

1.0

0.9

∑

0.8

Δa_n↑a_n↓ + H.c.

(10)

0.7

n=1

0.6

0.5

На диаграмме области химического потенциа-

0.4

ла μ и магнитного поля h, в которых возникают

0.3

краевые возбуждения, показаны на рис. 6. Как и

0.2

0.1

в случае модели Китаева, внутри области реализа-

ции краевых состояний, полученной из анализа то-

0.2

0.4

0.6

0.8

1.0

1.2

1.4

1.6

1.8

2.0

| /t|

пологического инварианта для периодических гра-

ничных условий, возникают карманы, где краевые

0.02

состояния отсутствуют ввиду конечной длины це-

почки. И напротив, для случая короткой цепочки в

0.15

области параметров, соответствующей тривиально-

E/|t|

0.10

му числу Майорана, существуют линии параметров,

при которых возникают майорановские моды.

0.05

Кроме того, в области параметров при μ < t

0.2

0.4

0.6

0.8

1.0

1.2

1.4

1.6

1.8

2.0

существует область реализации краевых состояний,

| /t|

которая не определяется из топологического инва-

рианта, поскольку эти состояния обладают хоть и

Рис. 5. Сверху: область существования краевых состояний

отщепленной от объемной зоны, но не экспоненци-

в модели Китаева при длине цепочки N = 20 обозна-

ально малой энергией (рис. 7). Эта область тем боль-

чена темным, белые линии — линии майорановских мод.

ше, а энергия возбуждения тем лучше отщеплена от

Снизу: зависимость a = Re λ и минимальной энергии воз-

объемной зоны, чем длиннее цепочка. Следует от-

буждения при |Δ/t| = 0.02, штриховая линия — граница

метить, что наличие топологического перехода, не

зоны объемных возбуждений, крестами обозначены зна-

чения химического потенциала, при которых реализуется

связанного с майорановскими модами, в этой обла-

майорановская мода

сти энергетических параметров было недавно обна-

ружено в работе [27] на основе анализа спиновых

и зарядовых характеристик достаточно длинной це-

приводит к попаданию энергии возбуждения в объ-

почки. Возможность возникновения краевых состо-

емную зону и изменению характера возбуждения на

яний в топологически тривиальной области также

некраевое. На рис. 5 также наглядно показана связь

ранее была показана на примере треугольной решет-

между величиной a = Re λ и тем, насколько глубо-

ки с неколлинеарным магнитным порядком и ки-

ко в щели находится краевое возбуждение, при этом

ральной сверхпроводимостью d-типа [28] в геомет-

144

ЖЭТФ, том 155, вып. 1, 2019

Влияние размеров на условия возникновения краевых состояний. . .

h/t

E/t

2.0

0.20

1.8

0.18

0.16

1.6

0.14

1.4

0.12

1.2

0.10

0.08

1.0

0.06

0.8

0.04

0.6

N = 20

0.02

0.4

0.2

0.4

0.6

0.8

1.0

1.2

1.4

1.6

1.8

0.2

0.5

1.0

1.5

2.0

2.5

3.0

Рис. 7. Зависимость первых 10 энергий собственных воз-

h/t

буждений в цепочке со спин-орбитальным взаимодействи-

2.0

ем и сверхпроводящим спариванием от величины химиче-

ского потенциала μ. Нижняя энергия возбуждения обозна-

1.8

чена черной сплошной линией, граница зоны объемных од-

1.6

ночастичных возбуждений — черной штриховой, α = 0.5t,

1.4

Δ = 0.1t, h = 0.6t, N = 100

1.2

1.0

показателем экспоненты для заданной энергии

0.8

состояния, что однозначно связано с нахождением

0.6

N = 6

энергии такого состояния за пределами области

0.4

разрешенных энергий объемных состояний. На при-

0.2

мерах модели BHZ, модели Китаева и цепочки со

спин-орбитальным взаимодействием и наведенной

0.5

1.0

1.5

2.0

2.5

3.0

сверхпроводимостью показано влияние конечной

длины цепочки на условия возникновения краевых

Рис. 6. Область реализации краевых состояний в цепоч-

решений в одномерных (и сводящихся к ним)

ке со спин-орбитальным взаимодействием и наведенной

системах. В частности, показано возникновение

сверхпроводимостью при N = 20 (а) и N = 6 (б). Тем-

внутри областей параметров с нетривиальным

ные области соответствуют параметрам, при которых су-

топологическим индексом карманов, где краевые

ществует краевое состояние. На нижнем рисунке белыми

состояния отсутствуют, а размер и число таких

линиями отмечены линии параметров, при которых реали-

карманов определяются длиной цепочки. Возник-

зуются майорановские моды в цепочке. Штриховой линией

новения подобных карманов следует ожидать и в

обозначены параметры, при которых закрывается объем-

других эффективно одномерных системах с конеч-

ная щель и меняется топологический инвариант, α = 0.5t,

Δ = 0.1t

ными размерами, где возникают линии параметров,

соответствующие реализации майорановских мод.

В случае цепочки со спин-орбитальным взаи-

рии цилиндра. Эти результаты показывают, что для

модействием и сверхпроводящим спариванием

поиска краевых решений с не экспоненциально ма-

предложенный алгоритм определения краевых

лой энергией и майорановских мод в коротких си-

состояний выявил область параметров, отвечающих

стемах метод анализа топологического инварианта

возникновению в цепочке краевых возбуждений с

не применим, и следует использовать иные способы,

конечной энергией, причем эту область невозможно

в частности, предложенный в данной работе.

обнаружить методом анализа топологического

инварианта.

7. ВЫВОДЫ

Автор выражает благодарность сотрудникам ла-

В работе предложен подход к определению кра-

боратории теоретической физики ИФ СО РАН за

евых состояний в одномерных системах конечных

многочисленные дискуссии и внимание к работе.

размеров. В качестве главного критерия выбра-

Исследование выполнено при финансовой под-

но отсутствие общего решения с чисто мнимым

держке РФФИ, Правительства Красноярского края,

145

ЖЭТФ, вып. 1

А. Д. Федосеев

ЖЭТФ, том 155, вып. 1, 2019

Красноярского краевого фонда поддержки науч-

10.

A. Yu. Kitaev, AIP Conf. Proc. 22 (2009).

ной и научно-технической деятельности в рамках

11.

S. Hegde, V. Shivamoggi, S. Vishveshwara et al., New

научного проекта № 17-42-240441 «Связанные май-

J. Phys. 17, 053036 (2015).

орановские фермионы в наноматериалах с силь-

ными электронными корреляциями и квантовый

12.

В. В. Вальков, В. А. Мицкан, М. С. Шустин, Пись-

транспорт электронов в устройствах на их ос-

ма в ЖЭТФ 106, 762 (2017).

нове», №18-32-00443 «Эффекты конечных разме-

13.

R. Chen and B. Zhou, Chin. Phys. B 25, 067204

ров и роль электронных корреляций при фор-

(2016).

мировании майорановских мод в низкоразмерных

системах со спин-орбитальным взаимодействием»,

14.

M.-C. Hsu, Y.-C. Lin, and C.-R. Chang, J. Appl.

№18-42-243017 «Проявление кулоновских взаимо-

Phys. 118, 043909 (2015).

действий и эффектов ограниченной геометрии в

15.

K. Hattori, J. Phys. Soc. Jpn. 84, 044701 (2015).

свойствах топологических краевых состояний нано-

структур со спин-орбитальным взаимодействием»,

16.

L. Ortiz, R. A. Molina, G. Platero et al., Phys. Rev.

№18-42-243018 «Контактные явления и магнитный

B 93, 205431 (2016).

беспорядок в проблеме формирования и детектиро-

17.

V. V. Valkov, A. O. Zlotnikov, A. D. Fedoseev et al.,

вания топологически защищенных краевых состоя-

J. Magn. Magn. Mat. 440, 37 (2017).

ний в полупроводниковых наноструктурах», а также

гранта Президента РФ (МК-3722.2018.2).

18.

А. Я. Беленький, УФН 134, 125 (1981).

19.

I. Tamm, Physik. Zeits. Sowjetunion 1, 733 (1932).

ЛИТЕРАТУРА

20.

И. Е. Тамм, Собрание научных трудов, Наука,

Москва (1975).

1. Б. А. Волков, О. А. Панкратов, Письма в ЖЭТФ

42, 145 (1985).

21.

W. Shockley, Phys. Rev. 56, 317 (1939).

2. B. A. Bernevig, T. L. Hughes, and S.-C. Zhang,

22.

S. Y. Ren, Electronic states in crystal of finite size,

Science 314, 1757 (2006).

Springer Tracts in Modern Physics 212.

3. L. Fu, C. L. Kane, and E. J. Mele, Phys. Rev. Lett.

23.

X. Dang, J. D. Burton, A. Kalitsov et al., Phys. Rev.

98, 106803 (2007).

B 90, 155307 (2014).

4. M. Z. Hasan and C. L. Kane, Rev. Mod. Phys. 82,

24.

Ф. Бег, П. Пужоль, Р. Рамазашвили, ЖЭТФ 153,

3045 (2010).

108 (2018).

5. D. V. Khomitsky and A. A. Chubanov, ЖЭТФ 145,

525 (2014).

25.

D. Sticklet, C. Bena, and P. Simon, Phys. Rev. Lett.

108, 096802 (2012).

6. В. А. Волков, В. В. Еналдиев, ЖЭТФ 149, 702

(2016).

26.

V. V. Val’kov and S. V. Aksenov, J. Magn. Magn.

Mat. 440, 112 (2017).

7. V. D. Kurilovich, P. D. Kurilovich, and I. S. Burmist-

rov, Phys. Rev. B 95, 115430 (2017).

27.

M. Serina, D. Loss, and J. Klinovaja, arXiv:1803.

00544v (2018).

8. A. Yu. Kitaev, Usp. Fiz. Nauk 44, 131 (2001).

9. A. P. Schnyder, S. Ryu, A. Furusaki et al., Phys. Rev.

28.

V. V. Val’kov, A. O. Zlotnikov, and M. S. Shustin,

B 78, 195125 (2008).

submitted to J. Magn. Magn. Mat. (2018).

146