ЖЭТФ, 2019, том 155, вып. 1, стр. 175-183

СОЛИТОНЫ ПОЛЯРИЗАЦИИ ЭЛЕКТРОНА

В СПИРАЛЬНОЙ МОЛЕКУЛЕ

А. А. Заболотский^*

Институт автоматики и электрометрии Сибирского отделения Российской академии наук

630090, Новосибирск, Россия

Поступила в редакцию 13 июня 2018 г.,

после переработки 23 июля 2018 г.

Принята к публикации 27 июля 2018 г.

Изучается эволюция спина электрона, движущегося по оси длинной спиральной молекулы, под действи-

ем внешнего поля. Поле создается диполями отдельных молекул, образующих сложную молекулярную

структуру, например, молекулу ДНК. Динамика поляризации электрона, вызванная спин-орбитальным

взаимодействием, описывается в рамках интегрируемого обобщения уравнений Манакова. В гамильтони-

ане модели учитывается фазовая кросс-модуляция, самомодуляция и аналоги гамильтонианов Рашбы и

Дрессельхауса. Соответствующий аппарат, основанный на решении задачи Римана - Гильберта, применен

для нахождения солитонных решений. Полученные одно- и двухсолитонные решения демонстрируют ряд

новых свойств. Показано, что локальное возмущение вызывает селективное влияние на поляризацию со-

литона и может быть использовано для управления положением спина электрона с помощью примесных

молекул или квантовых точек с постоянным дипольным моментом. Обнаружено, что спин-орбитальное

взаимодействие приводит к сильной пространственной модуляции формы солитонов. При столкновении

солитонов наблюдается перенос модуляции между солитонами и изменение ее амплитуды.

DOI: 10.1134/S0044451019010140

[6-14]. Этот эффект обусловлен спин-орбитальной

связью (СОС) между электронным импульсом и

1. ВВЕДЕНИЕ

молекулярным электрическим полем, создаваемым

спиральным расположением молекулярных дипо-

Изучение солитонов в органических спиральных

лей. COC хорошо известна из работ по физике по-

молекулах играет фундаментальную роль для опи-

лупроводников. Два фундаментальных типа СОС

сания денатурализации ДНК с помощью так назы-

описываются гамильтонианами Дрессельхауза [15] и

ваемой модели Пейарда - Бишопа [1,2]. Солитонный

Бычкова - Рашбы [16]. Пример реализации СОС по-

механизм переноса энергии, выделяемой из адено-

казан в работе [17]. Предложено много теоретиче-

зинтрифосфатного белка через α-спиральные бел-

ских моделей для объяснения экспериментальных

ки, представляется приоритетным [1]. Солитонные

данных, в том числе и для органических молекул

возбуждения учитываются при анализе зарядовых

[18-27]. Однако эти модели не приводят к доста-

и энергетических транспортных свойств молекул

точно хорошему количественному согласию с экспе-

ДНК [3-5]. Во всех этих сценариях предполагается,

риментальными данными. Недавно была отмечена

что органические молекулы достаточно деформиру-

важная роль влияния электрон-решеточного взаи-

емы и, следовательно, взаимодействие квазичастиц

модействия на перенос спина в органических спи-

(электронов или экситонов) и колебаний решетки

ральных молекулах [26]. Это указывает на необходи-

существенны. Более того, взаимодействие определя-

мость дополнения линейной квантовой теории нели-

ет существование устойчивых солитонов, когерент-

нейными процессами [24].

но распространяющихся вдоль молекулы.

В последнее десятилетие во многих эксперимен-

Нелинейное уравнение Шредингера (НУШ) ши-

тах показано существование хиральной спин-селек-

роко используется как универсальная математиче-

тивности в органических спиральных молекулах

ская модель для описания эволюции медленно ме-

няющегося волнового пакета в нелинейной среде и

^* E-mail: zabolotskii@iae.nsk.su

имеет множество применений. Метод обратной за-

175

А. А. Заболотский

ЖЭТФ, том 155, вып. 1, 2019

дачи рассеяния (МОЗР) был впервые разработан и

применен к НУШ Захаровым и Шабатом [28, 29]. В

определенных физических ситуациях одновременно

появляются два или более волновых пакета с раз-

личными несущими частотами. Их взаимодействие

описывается связанными НУШ. Если связь проис-

ходит только через межфазную модуляцию, чей ко-

эффициент равен коэффициенту фазовой самомо-

дуляции, то эта система, получившая название си-

стемы Манакова, является интегрируемой. Соответ-

ствующий аппарат МОЗР развит Манаковым [30].

Интерес к этой системе обусловлен широким спек-

Рис. 1. Спиральная молекула. Электрон движется по оси

тром ее приложений в разных областях физики.

z. Показаны дипольные моменты, направленные по тан-

Многосолитонные решения системы Манакова, де-

генциальным векторам

монстрирующие вращение поляризации вследствие

столкновений, получены разными методами (см.,

например, работы [30-32]). Найдены также неко-

туру с геометрическими параметрами, не завися-

торые интегрируемые обобщения этих уравнений

щими от переменных. В работах [24, 40, 42] исполь-

[33-35]. Уравнения Манакова заслуживают даль-

зовалась упрощенная схема расположения диполей

нейших подробных исследований, поскольку важны

вдоль оси молекулы, т. е. вдоль оси z. По-видимому,

для решения различных физических задач, в том

направление дипольных моментов от атомов угле-

числе с учетом СОС. Задача Римана - Гильберта

рода к атому азота в молекуле ДНК, т. е. по спи-

(РГ) широко используется для решения различных

ральной кривой, является более реалистичным [41],

интегрируемых уравнений [29], которые имеют при-

чем использованное в работах [24,40]. Поэтому в на-

ложения в различных частях физики: теории кон-

стоящей работе рассматриваем движение электрона

денсата Бозе - Энштейна, нелинейной оптики и мно-

сквозь винтовое расположение пептидных диполей,

гих других (см., например, [33-39]).

направленных вдоль тангенциальной составляющей

В настоящей работе изучаются новые специ-

пептидной спирали. Пусть диполи d_j расположены

фические нелинейные поляризационные эффекты,

в точках γ_j = {a cos(ks_j), a sin(ks_j), τs_j}, где a — ра-

определяемые спин-орбитальным взаимодействием

диус спирали, τ — ее шаг, s_j = jδ, δ — расстояние

электрона с полем диполей длинной спиральной мо-

между диполями на спирали, а их векторы направ-

лекулы или с локальным, зависящим от координаты

лены вдоль производной limδ→0(γj+1 - γ_j )/δ, т. е.

дипольным полем. Для этого получено интегриру-

емое обобщение системы уравнений, приведенной в

работах [24,40], которая выведена для описания эво-

d_j =

√

{-ak sin(ks_j), ak cos(ks_j), τ} ,

люции поляризации спина электрона при прохожде-

a²k² + τ²

нии сквозь спиральную молекулу.

см. рис. 1. Типичное число диполей за один оборот

вокруг оси в ДНК N_d = 10, a = 0.7 нм и b = 2π/k =

δ = 3.2 нм. Таким образом, общее электриче-

= N_d

2. ВЫВОД СИСТЕМЫ УРАВНЕНИЙ

ское поле на оси r = (0, 0, z) спиральной молеку-

МОДЕЛИ

лы, создаваемое диполями составляющих ее моле-

кул, имеет вид

2.1. Динамика спина электрона в

спиральной молекуле

∑

3 ((r - γ_n) · d_n) (r - γ_n) - d_n

E(z) =

[

]3/2

(1)

Суммарный дипольный момент пептидов, со-

4πϵ₀

a² + (z - nδ)²

ставляющих α-спиральные белки и другие макро-

молекулы, ориентирован вдоль оси молекулы [41].

Для большого числа молекул во всей спирали (N_m >

> 100) поле внутри нее на оси z можно считать

Как и в работах [24,40,42], рассматриваем схему, в

которой «внешний» электрон инжектируется в то-

постоянным. Сделаем предельный переход к непре-

∑

∫

рывной переменной_n → b/δ

du, (nδ - z)/b → u.

рец молекулы и движется вдоль ее центральной оси

(ось z на рис. 1). Молекула имеет спиральную струк-

Отсюда и из (1) получаем

176

ЖЭТФ, том 155, вып. 1, 2019

Солитоны поляризации электрона.. .

[

(

)

ikz

q₀

E_⊥(z)

E_x + iE_y =

HSOС =

4πϵ₀δb³

^z E^∗⊥(z)

⎡

⎤

(

)

]

∫∞

⎢

⎥

E_⊥(z)

⎢

3ue^ikbu

iakbe^ikbu

⎥

(4)

⎢

⎥

du =

(2)

)5/2

)3/2

E^∗⊥(z)

⎣

⎦

⁽a²

+u²

^−∞ b2+u2

b²

где q₀ = eℏ/(2mc)².

ikz

ik²e

⁽b²k⁾

Перенормируем линейную часть гамильтониана

K₁

(a - b) .

(3)

πϵ₀δb2

электрона

Здесь K₁ — модифицированная функция Бесселя

p2z

второго рода.

H₌

+ H_SOC =E_b H,

В то же время для короткой спирали (N_m ≈ 10)

поле сильно неоднородно. Поэтому дополнительно

где

считаем, что амплитуда поля E_⊥ = -i(E_x + iE_y)

H₌ -∂2s - γ_SOC H_SOC.

(5)

может локально зависеть от z. Эрмитовость га-

мильтониана СОС обусловлена его симметризован-

Здесь E_b

= ℏ²/2mb², s = z/b, ∂s

= ∂/∂s, без-

ной классической формой σ · (p × E), где вектор

размерный спин-орбитальный параметр γ_SOC

σ = (σ_x,σ_y,σ_z) c компонентами-матрицами Паули.

= ℏλE₀/(bE_b), E₀

= max |E_⊥|. Представим ста-

Для p = p_z e_z = ∂_ze_z гамильтониан СОС упрощает-

ционарное поле диполей в виде E

= E_⊥/E₀

ся до вида

= F(Z)eiφ(Z). Матричный оператор

H_SOC имеет вид

(

)

e^-iφ (∂_sF - i∂_sφF + 2F∂_s)

H_SOC =

(6)

e^iφ (∂_sF + i∂_sφF + 2F∂_s)

Следуя теории Давыдова [1], для описания элект-

2.2. Обобщенные уравнения Манакова и их

рон-решеточного взаимодействия добавим нелиней-

представление Лакса

ную часть к гамильтониану (5). В итоге получа-

ем двухкомпонентное НУШ, описывающее динами-

Полученные в итоге из (7) и (8) уравнения в ин-

ку спинорного состояния χ(s, t) = [χ_↑(s, t), χ_↓(s, t)]^T

тегрируемом случае являются частным случаем сле-

с нелинейной частью, связанной с самодействием из-

дующего обобщения уравнений Манакова:

за деформации решетки:

[

]

[

(

)

i∂_tχ(s, t) =

Hχ(s, t) -

∂_tp

h g

∂

N- 2

[

]

∂_tq

-h

∂s

- 2ε

χ^†(s, t) · χ(s, t) + κ²F(s)²

χ(s, t) .

(7)

(

)][

]

∂_sh

∂_sg

−

(10)

Здесь t = E_bt/ℏ — безразмерное время, t — физиче-

∂_sg

-∂_sh

ское время, знаки ε = +, - перед нелинейной частью

отвечают соответственно фокусирующей и дефоку-

[

]

сирующей средам. В уравнение (7) добавлен потен-

Здесь

N₌ i

∂2s - 2(pp₁ + qq₁ + W(s))

, h, g(s) ∈ R и

циал κ²F², κ ∈ R, создаваемый внешним полем с

нормированной амплитудой F .

p₁(s, t) = εp^∗(s, t), q₁(s, t) = εq^∗(s, t).

(11)

Перейдем к новым функциям

(χ_↑, χ_↓)^T =

Система уравнений (10), (11) является условием

(

совместности следующих линейных систем:

= κ p(s, t)e-iψ1(s)-iψ2(t), q(s, t)eiψ1(s)-iψ2(t)

)^T,

(8)

где

Θ_z = LΘ ≡ (iλΛ + U)Θ,

(12)

(

)

2ψ₁(s) = φ(s),

∂_tψ₂(t) = ∂_s(ψ₁(s))².

(9)

Θ_t =

-2iλ²Λ + V

Θ.

(13)

177

ЖЭТФ, вып. 1

А. А. Заболотский

ЖЭТФ, том 155, вып. 1, 2019

⎛

⎞

∂p

Здесь Θ — 3 × 3-матричная функция, λ — спект-

-pp₁

-pq₁

⎜

∂s

⎟

ральный параметр, Λ = diag(1, 1, -1), U = U₀ + U₁,

⎜

⎟

⎜

∂q

⎟

V = V₀ + V₁ - 2λU₀,

V₀ = i⎜

-p₁q

-qq₁

⎟,

(15)

⎜

⎟

⎛

⎞

∂s

⎝

⎠

∂p₁

∂q₁

⎜

⎟

pp₁ + qq₁

U₀ =

⎝ 0

⎠,

∂s

p₁

q₁

⎛

⎞

(14)

-h

-g

⎜

⎟

U₁ = i⎝ -g h

⎠,

⎛

⎞

gq + hp

⎜

⎟

V₁ = -⎝

gp - hq

⎠.

(16)

(

)

gq₁+hp₁

gp₁-hq₁

g²+h²-2W(s)

Условие совместности систем (10), (11) имеет вид

случаями (18) и (19). Для этих случаев в уравне-

ниях (7) κ = 1, ∂_sF (s) = 0 и κ = 0, ∂_sF (s) = 0

∂_sW(s) = g(s)∂_sg(s) + h(s)∂_sh(s).

(17)

соответственно.

√

Связь h и g с физическими параметрами системы

Обозначим w =

h² + g², w_± =

h² + g² ± h.

уравнений (7), (8) с учетом условий (9) можно пред-

Введем новую функцию Ψ = MΘ, где

ставить следующими вариантами:

⎛

⎞

e-iG(s)

-γ₀eiG(s)

g = -F = const, h = -∂_sψ₁ = const,

(18)

⎜

⎟

M =

⎝ γ₀e-iG(s)

eiG(s)

⎠.

(20)

g(s) = -F (s), h = 0.

(19)

√

Применение МОЗР к системе (10), (11) для произ-

вольных h(s), g(s) и даже для g(s), h = const ока-

В результате этого преобразования спектральная

залось слишком громоздким, поэтому ограничимся

проблема (12) принимает вид

(

)

∂M

∂_sΨ = LΨ = M-1LM - M-1

Ψ=

∂s

⎛

⎞

eiG(s)(gq + w₊p)

iλ

√

⎜

⎟

⎜

⎟

⎜

⎟

⎜

e-iG(s)(w₊q - gp)

⎟

⎜

iλ

√

⎟Ψ.

(21)

⎜

⎟

⎜

⎟

⎠

⎝ e-iG(s)(gp₁ + w_-q₁)

eiG(s)(gq1 - w-p1)

√

-iλ

Здесь для случая (18) γ₀ = w_-/g, G(s) = ws, а в

ходим, что для s → ±∞ фундаментальная матрица

∫s

случае (19) w_± = w = g(s), γ₀ = 1, G(s) =

g(s).

Ψ → e(iλΛs). Поэтому для функции

Ψ = ΦeiλΛs

(22)

3. ПРОБЛЕМА РИМАНА - ГИЛЬБЕРТА

находим Φ → I, s → ±∞, где I — единичная мат-

рица. Из (13), (21) и (22) с учетом калибровочного

3.1. Аналитические свойства

преобразования получаем

Сформулируем проблему РГ для систем (13),

∂_sΦ = iλ[Λ, Φ] + UΦ,

(23)

(21) в случае достаточно быстро убывающих при

s, t → ±∞ потенциалов p, q, p₁, q₁ → 0. Из (21) на-

∂_tΦ = -2iλ² [Λ, Φ] + VΦ,

(24)

178

ЖЭТФ, том 155, вып. 1, 2019

Солитоны поляризации электрона.. .

где [Λ, Φ] = ΛΦ - ΦΛ и

где

⎛

⎞

V =M-1V M, U =M-1UM.

(25)

s₁₃

⎜

⎟

G(λ) = E

⎝ 0

s₂₃

⎠E-1,

(33)

Из (12) и (25) следует tr U = 0. В итоге для функ-

ций Йоста Φ_± — решений системы (23) с асимпто-

s₃₁

s₃₂

тикой Φ_± → I, s → ±∞ — находим det(Φ_±) = 1, ∀s.

Решения Ψ = Φ₊E и Φ = Φ_-E линейной системы

и s₃₁ =s₂₁s₃₂ -s₃₁s₂₂, s₃₂ =s₃₁s₁₂ -s₁₁s₃₂.

(23) связаны матрицей рассеяния S с компонентами

s_ij(λ), i, j = 1, 2, 3,

3.2. Связь решений с потенциалом

Φ_-E = Φ₊ES(λ), λ ∈ R,

(26)

Разложение решения J₊ спектральной проблемы

(21) по степеням λ имеет вид

где E(s) = eiλΛs и det(S(λ)) = 1, ∀λ.

Интегрируя уравнения (23) с учетом асимптоти-

(

)

J₊(λ, s) = I +

Γ(s) + O

λ²

λ → ∞.

(34)

ки Φ, находим уравнения Вольтерра

Подставив (34) в (21), получаем для первой степе-

Φ_∓(λ, z) =

ни 1/λ

∫z

= I + E(y - z)U(y)Φ_∓(λ,y)E(z - y)dy.

(27)

L - iλΛ = i[Λ,Γ] =

∓∞

⎛

⎞

-2iΓ₁₃

Функция Φ_± состоит из следующих столбцов: Φ_± = ][

⎜

⎟

⎝

-2iΓ₂₃

⎠.

(35)

= φ[1]±, φ[2]±, φ^[3]

. Из (27) следует, что φ[3]- и φ[1]+ , φ^[2]+

2iΓ₃₁

2iΓ₃₂

допускают аналитическое продолжение в верхнюю

полуплоскость λ ∈ C₊, (Im λ > 0), а φ[1]-, φ[2]- и φ^[3]+ —

Сравнивая недиагональные компоненты матриц, по-

в нижнюю полуплоскость C_-, (Im λ < 0). Построим

лучаем

функцию Йоста следующим образом:

[

]

eiG(s)(g q + w₊ p)

√

= -2iΓ₁₃,

(36)

J₊(λ) = φ[1]-, φ[2]-, φ^[3]

eiλΛz =

= Φ₊(I - P) + Φ_-P.

(28)

e-iG(s)(q w₊ - g p)

√

= -2iΓ₂₃.

(37)

Здесь P = diag(1, 1, 0). Из формы J₊ следует ее ана-

литичность при λ ∈ C₊, а из выражения (27) —

3.3. Свойства симметрии

асимптотика

Матрица L в правой части (21) удовлетворяет

J₊(λ) → I, λ ∈ C₊ ∨ λ → ∞.

(29)

условию симметрии

Сопряженная к (23) система уравнений

[

]

L^†(λ^∗) = εC-1LC,

⎛

⎞

Φ_s = -iλ Λ,

- ΦU

(30)

w₊

⎜

⎟

(38)

C =

⎝ 0

w₊

⎠,

имеет матричное решение

Φ_± = Φ-1±. Обозначим

[

]_T

его строки

Φ=

φ^[1],φ[2],φ[3]

, из которых строим

функцию Йоста

где для (18) w_±, w — константы и для (19) w_± = w =

= g(s).

[

]_T

Для эрмитово-сопряженной спектральной про-

J_- = e-iλΛz

φ^[1]+,

φ[2]+,

φ[3]-

блемы (21) с учетом свойства (38) находим

= (1 - P )Φ-1+ + P Φ-1- ,

(31)

[

]

†

(Φ

C)_s = iλ Λ,Φ^†±C

+ εΦ^†±CU^†.

(39)

которая аналитична для λ ∈ C_- и J_-(λ) → I при

λ ∈ C_- ∨ λ → ∞. Для построенных функций Йоста

Таким образом, Φ^†±C — фундаментальное решение

проблема РГ формулируется как

†

как системы уравнений (39), так и (30), т. е. Φ

C =

J₊(λ)J_-(λ) = G(λ), λ ∈ R,

(32)

= C₀Φ-1± , где C₀ — постоянная матрица. В пределе

179

12*

А. А. Заболотский

ЖЭТФ, том 155, вып. 1, 2019

s → ∞ находим C₀ = C. Это означает, что Φ_± обла-

уравнения (44) по s и t, используя соответствующие

дает свойством инволюции

системы уравнений (23) или (24). В итоге находим

Φ^†± = -εCΦ-1±C-1.

(40)

v_k(s, t) = exp(iλ_kΛz - 2iλ2kΛt + iw²t)v(0)k,

(49)

С учетом (38) находим для функций Йоста J_± соот-

vk(s, t) = v(0)k exp(-iλ^kΛz + 2iλk2Λt - iw²t) C,

(50)

ношение

(0)

где v_k

v(0)k — постоянные векторы, связанные ин-

J†+(λ^∗) = -εCJ_-(λ)C-1.

(41)

волюцией (46).

Аналогично для матрицы рассеяния (26) получаем

Из сравнения уравнений (34) и (47) находим

⎡

⎤

S^†(λ^∗) = -εCS-1(λ)C-1,

(42)

∑

Γ₁₃

=i^⎣

v_jW-1vk⎦

(51)

что, в свою очередь, дает связь

λk = λ^∗k между со-

j,k=1

ответствующими нулями s₃₃(λ) и s₃₃(λ).

⎡

⎤

Используя определения J_± и матрицы рассея-

∑

Γ₂₃ = i^⎣

v_jW-1vk⎦

(52)

ния, находим

j,k=1

det J₊(λ) = s₃₃, det J_-(λ) = s₃₃,

(43)

Обозначим θ_j = iλ_jz - 2iλ2jt + iw²t, λ_j = ξ_j + iη_j

где s₃₃ = s₁₁s₂₂ -s₂₁s₁₂. Пусть {λ_k ∈ C₊, 1 ≤ k ≤ N}

{

}

ξ_j, η_j

∈ R, v(0)k = [α_k, β_k, 1]^T , и с учетом свойства

λk ∈ C-, 1 ≤ k ≤ N

— простые нули соответ-

симметрии (46) находим

ственно s₃₃ и s₃₃. Определим ядра v_k и v_k опера-

торов соответственно kerJ₊(λ_k) и kerJ_-(λk) следу-

w₊α^∗jα_k + w₊β^∗jβ_k

R_jk = -ε

(53)

ющим образом:

J₊(λ_k)v_k = 0, J_-(λk)vk = 0,

1≤k≤N.

(44)

Используя (36) и (37), получаем N-солитонное ре-

шение системы (10):

Остается найти свойства симметрии собственных

√

[

]

векторов v_k и

vk. Эрмитово сопряжение первого

-Γ₁₃w₊e-iG(s) + Γ₂₃geiG(s)

уравнения в (44) и инволюция (40) дают

(54)

g² + w

√

[

]

-εv^†kCJ_-(λk) = 0.

(45)

Γ₁₃ge-iG(s) + Γ₂₃w₊eiG(s)

q=-

(55)

g² + w²⁺

Отсюда и из второго из уравнений (44) получаем

следующую инволюцию:

где

vk = -εv^†kC.

(46)

[

]

[

]

Γ₁₃

∑

α_j

= -i

eθj-θk W-1jk

(56)

Γ₂₃

β_j

j,k=1

4. СОЛИТОННЫЕ РЕШЕНИЯ

Для нахождения солитонных решений следуем

[29] (глава III, § 2). Положим в (32) G = I. Решение

[

]

W_jk =

R_jkeθj+θk + e-θj

-θ_k .

(57)

проблемы РГ имеет вид

λ^∗j - λ_k

∑

v_jW-1jkv_k

J₊(λ) = I +

(47)

Пусть ε = -1. Обозначим R₁₁ = exp(-2ρ₁₁). Од-

λ-

λk

j,k=1

нополюсное решение N = 1 (54), (55) имеет вид

где

[

]

√

2iw

2η₁eθ1-θ1

vj vk

(

)

W_jk =

(48)

g² + w²⁺

ch(θ∗1 + θ₁ + ρ₁₁)

λ^∗j - λ_k

[ (

)

]

α₁w₊e-iG(s) - β₁geiG(s)

Нули λ_k и

λk от переменных не зависят. Зави-

(

)

(58)

iG(s)

α₁ge-iG(s) + β₁w₊e

симость векторов v_k(s, t) находим, дифференцируя

180

ЖЭТФ, том 155, вып. 1, 2019

Солитоны поляризации электрона.. .

1.0

0.8

|p|

1.0

0.6

0.5

0.4

-10

0.2

–10

-5

-10

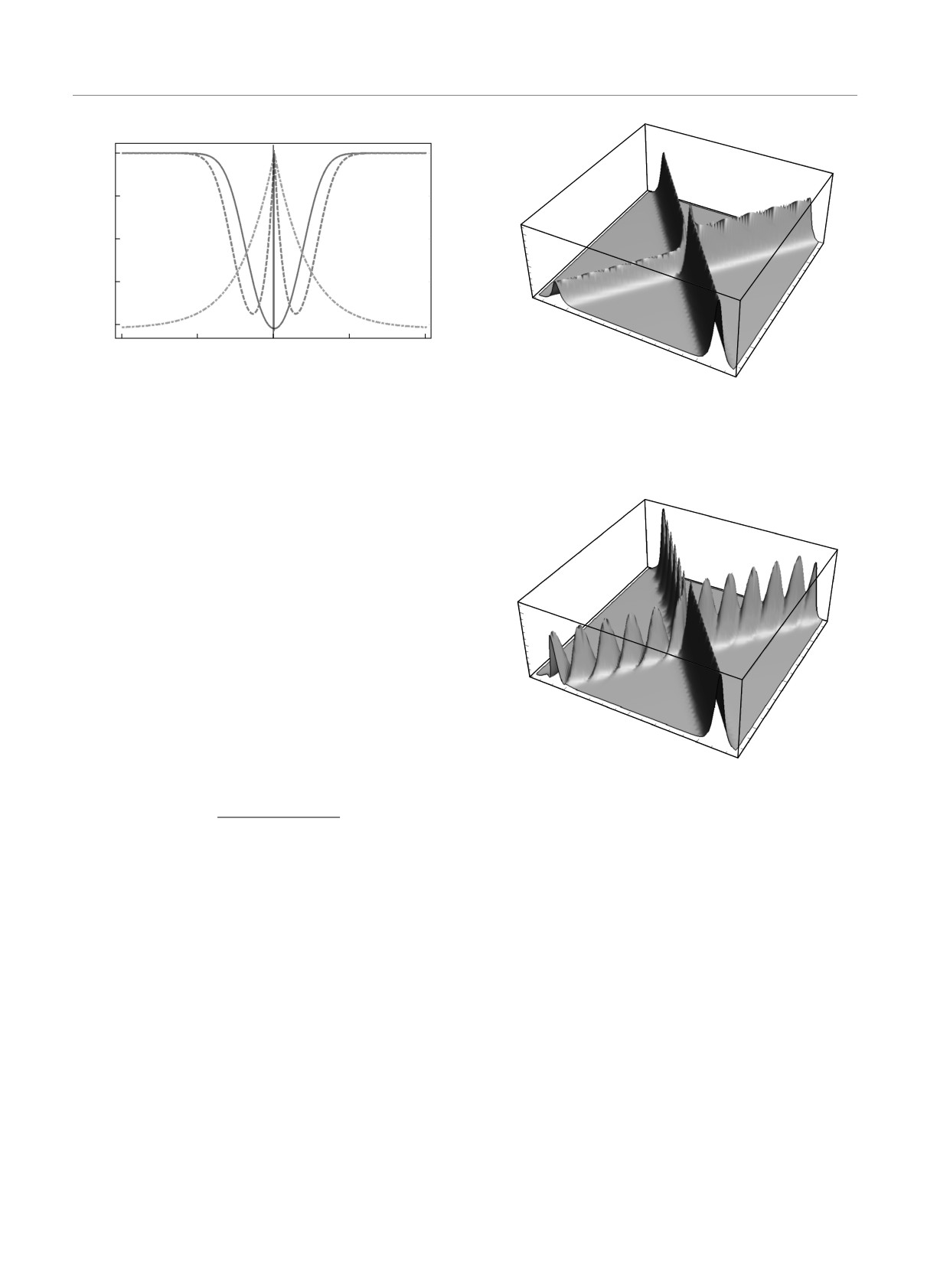
Рис. 2. Изменение поляризации Υ однополюсного реше-

Рис. 3. Форма импульса |p(s, t)|. Столкновение двух соли-

ния под действием локального спин-орбитального взаимо-

тонов с параметрами η1 = 1, η2 = 1, ξ1 = -0.4, ξ2 = 0.4,

действия. Сплошная линия отвечает потенциалу g(s) =

α1 = 1, α2 = -1, β1 = 0,β2 = 1, для коэффициентов СОС

(

)

(

)

= exp

-0.25s²

, штриховая — g(s) = sexp

-0.25s²

h = 1, g = 0

штрихпунктирная — g(s) = th (0.25s). Параметры соли-

тона следующие: η1 = 1, ξ1 = 0, α1 = -1, β1 = 1

5. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ И

ЗАКЛЮЧЕНИЕ

|p|

В случае (19) пространственная модуляция ам-

1.0

плитуды солитонов определяется фазой G(s). Из ре-

шения (58) следует, что СОС вызывает локальное

0.5

изменение поляризации электрона и ее динамика

определяется как начальными условиями, так и па-

раметрами СОС. Для однополюсного решения (см.

-10

формулу (58)) локальное дипольное поле приводит к

отклонению вектора поляризации. Затем поляриза-

-10

ция возвращается к исходному значению. На рис. 2

показано изменение поляризации электрона

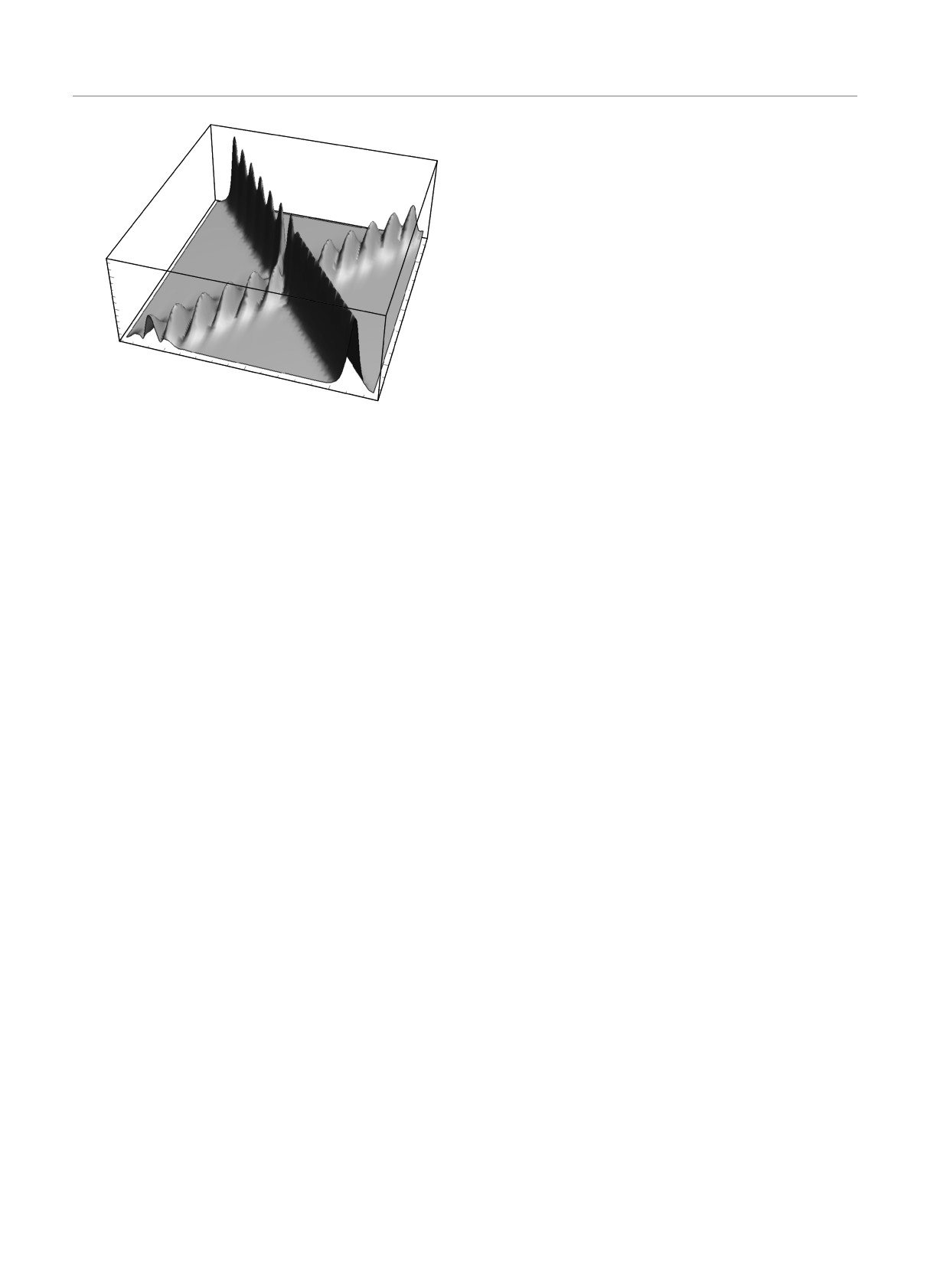
Рис. 4. Столкновение солитонов с параметрами η1 = 1,

|p(s, 0)| - |q(s, 0)|

η2 = 1, ξ1 = -0.4, ξ2 = 0.4, α1 = 1, α2 = -1, β1 = 0,

Υ=

β2 = 1, для коэффициентов СОС h = 1, g = 1

|p(s, 0)| + |q(s, 0)|

для солитонного решения (58) в случае (19) и раз-

ных внешних потенциалов g(s). Для локализован-

на рис. 3. Решение проявляет характерную для со-

ного воздействия G(s) → 0, s → ±∞, угол поворота

литонов уравнений Манакова динамику [30, 31, 36].

поляризации спина может быть детектором возму-

Влияние изменения фазы поля с координатой ∝ h

щения, вызванного внешним полем E. С другой сто-

не приводит к существенным отличиям поведения

роны, локальное поле, вызванное, например, посто-

солитонов от поведения в случае классических урав-

янными дипольными моментами квантовых точек,

нений Манакова [30].

расположенных по периметру кольца, может быть

Для сильного СОС g ∼ 1 возникает простран-

использовано для управления поляризацией элект-

ственная модуляция амплитуд импульсов |p| и |q|,

рона.

см. рис. 4, 5. На рис. 4 видно, что включение COC

Двухсолитонное решение (N = 2) демонстриру-

(g = 0) приводит к изменению амплитуд импуль-

ет новые для уравнений Манакова свойства, обу-

сов, наряду с появлением модуляции, для тех же

словленные СОС. На рис. 3-5 показана амплитуда

начальных условий, ср. рис. 3. Решения обобщен-

|p(s, t)| в процессе столкновения двух солитонов для

ной системы уравнений Манакова для g ∼ 1 демон-

разных параметров и коэффициентов СОС в случае

стрируют новый эффект — изменение и перенос про-

(18). Динамика солитонов для h = 1, g = 0 показана

странственной модуляции между солитонами при их

181

А. А. Заболотский

ЖЭТФ, том 155, вып. 1, 2019

E. Dıaz, R. P. A. Lima, and F. Dom´ınguez-Adame,

Phys. Rev. B 78, 134303 (2008).

B. Göhler, V. Hamelbeck, T. Z. Markus, M. Kettner,

G. F. Hanne, Z. Vager, R. Naaman, and H. Zacharias,

Science 331, 894 (2011).

|p|

Z. Xie, T. Z. Markus, S. R. Cohen, Z. Vager, R. Gu-

tiérrez, and R. Naaman, Nano Lett. 11, 4652 (2011).

1.0

D. Mishra, T. Z. Markus, M. Naaman, R. Kettner,

0.5

B. Gohler, H. Zacharias, N. Friedman, M. Sheves, and

C. Fontanesi, Proc. Nat. Acad. Sci. USA 110, 14872

-10

(2013).

-10

O. B. Dor, S. Yochelis, S. P. Mathew, R. Naaman,

and Y. Paltiel, Nat. Commun. 4, 2256 (2013).

Рис. 5. Столкновение солитонов с такими же параметрами,

10.

M. Kettner, B. Göhler, H. Zacharias, D. Mishra,

как на рис. 4, кроме η2 = 0.5

V. Kiran, R. Naaman, C. Fontanesi, D. H. Waldeck,

S. Sek, J. Pawlowski et al., J. Phys. Chem. C 119,

14542 (2015).

столкновении. На рис. 4 и 5 показана форма соли-

тонов в процессе столкновения для разных началь-

11.

P. C. Mondal, C. Fontanesi, D. H. Waldeck, and

ных условий. Для некоторых параметров модуляция

R. Naaman, ACS Nano 9, 3377 (2015).

амплитуды исчезает после столкновения полностью.

Этот эффект может быть использован для передачи

12.

H. Einati, D. Mishra, N. Friedman, M. Sheves, and

R. Naaman, Nano Lett. 15, 1052 (2015).

информации между импульсами.

В настоящей работе дано интегрируемое обобще-

13.

V. Kiran, S. P. Mathew, S. R. Cohen, I. Hernandez

ние модели Манакова с учетом спин-орбитального

Delgado, J. Lacour, and R. Naaman, Adv. Mater. 28,

взаимодействия. Точные солитонные решения пока-

1957 (2016).

зывают, что сильная СОС вызывает пространствен-

ную модуляцию и необычное поведение солитонов

14.

A. C. Aragonés, E. Medina, M. Ferrer-Huerta, N. Gi-

meno, M. Teixidó, J. L. Palma, N. Tao, J. M. Ugalde,

во время столкновения. Это поведение критически

E. Giralt, I. D´iez-Pérez et al., Small13, 1602519

зависит от начальных условий и коэффициента

(2017).

СОС. Полученные решения демонстрируют новые

возможности управления поляризацией электронов

15.

G. Dresselhaus, Phys. Rev. 100, 580 (1955).

полями диполей длинных спиральных молекул,

16.

Ю. А. Бычков, Э. И. Рашба, Письма в ЖЭТФ 39,

таких как ДНК, или локальным внешним потен-

66 (1984).

циалом, создаваемым дипольными органическими

молекулами или квантовыми точками.

17.

D. L. Campbell, G. Juzeliunas, and I. B. Spielman,

Phys. Rev. A 84, 025602 (2011).

Работа выполнена при финансовой поддержке

РФФИ (грант № 18-02-00379).

18.

S. Yeganeh, M. A. Ratner, E. Medina, and V. Mujica,

J. Chem. Phys. 131, 014707 (2009).

19.

E. Medina, F. López, M. A. Ratner, and V. Mujica,

ЛИТЕРАТУРА

Europhys. Lett. 99, 17006 (2012).

1. A. S. Davydov, Phys. Scripta 20, 387 (1979).

20.

R. Gutiérrez, E. D´iaz, R. Naaman, and G. Cuniberti,

2. M. Peyrard and A. R. Bishop, Phys. Rev. Lett. 62,

Phys. Rev. B 85, 081404 (2012).

2755 (1989).

21.

A.-M. Guo and Q.-F. Sun, Phys. Rev. Lett. 108,

3. S. Komineas, G. Kalosakas, and A. R. Bishop, Phys.

218102 (2012).

Rev. E 65, 061905 (2002).

22.

A.-M. Guo, E. D´ıaz, C. Gaul, R. Gutierrez, F. Do-

4. P. Maniadis, G. Kalosakas, K. O. Rasmussen, and

m´ınguez-Adame, G. Cuniberti, and Q.-F. Sun, Phys.

A. R. Bishop, Phys. Rev. E 72, 021912 (2005).

Rev. B 89, 205434 (2014).

182

ЖЭТФ, том 155, вып. 1, 2019

Солитоны поляризации электрона.. .

23. D. Rai and M. Galperin, J. Phys. Chem. C 117, 13730

32. T. Tsuchida, Prog. Theor. Phys. 111, 151 (2004).

(2013).

33. A. V. Mikhailov, Physica D 3, 73 (1981).

24. R. Gutiérrez, E. D´ıaz, C. Gaul, T. Brumme, F. Do-

34. V. E. Zakharov and E. I. Schulman, Physica D 4, 270

m´ınguez-Adame, and G. Cuniberti, J. Phys. Chem.

(1982).

C 117, 22276 (2013).

35. J. Ieda, T. Miyakawa, and M. Wadati, J. Phys. Soc.

25. E. Medina, L. A. Gonzalez-Arraga, D. Finkel-

Jpn. 73, 2996 (2004).

stein-Shapiro, B. Berche, and V. Mujica, J. Chem.

Phys. 142, 194308 (2015).

36. Deng-Shan Wang, Da-Jun Zhang, and Jianke Yang,

J. Math. Phys. 51, 023510 (2010).

26. S. Behnia, S. Fathizadeh, and A. Akhshani, J. Phys.

Chem. C 120, 2973 (2016).

37. A. A. Zabolotskii, Phys. Rev. E 75, 036612 (2007).

27. R. A. Caetano, Sci. Rep. 6, 23452 (2016).

38. A. A. Zabolotskii, Phys. Rev. E 77, 036603 (2008).

28. В. Е. Захаров, А. Б. Шабат, ЖЭТФ 61, 118 (1971)

39. A. A. Zabolotskii, Phys. Rev. A 80, 063616 (2009).

[Sov. Phys. JETP 34, 62 (1972)].

40. E. D´ıaz, R. Gutiérrez, C. Gaul, G. Cuniberti, and

29. S. P. Novikov, S. V. Manakov, L. P. Pitaevskii, and

F. Dom´ınguez-Adame, AIMS Mater. Sci. 4, 1052

V. E. Zakharov, Theory of Solitons: The Inverse Scat-

(2017).

tering Method, Springer-Verlag (1984).

30. С. В. Манаков, ЖЭТФ 65, 1392 (1973) [Sov. Phys.

41. D. Sengupta, R. N. Behera, J. C. Smith, and

JETP 38, 248 (1974)].

G. M. Ullmann, Structure 13, 849 (2005).

31. R. Radhakrishnan, M. Lakshmanan, and J. Hietarin-

42. R. Gutiérrez, E. D´ıaz, R. Naaman, and G. Cuniberti,

ta, Phys. Rev. E 56, 2213 (1997).

Phys. Rev. B 85, 081404 (2012).

183