ЖЭТФ, 2019, том 155, вып. 2, стр. 258-276

ДИНАМИКА КУБИТОВ В ПОЛЕ УНИПОЛЯРНЫХ ИМПУЛЬСОВ:

ПРОПАГАТОР МАГНУСА, «ОБОБЩЕННОЕ ПРАВИЛО

ПЛОЩАДЕЙ» И ДВИЖЕНИЕ НА ГРУППАХ

М. В. Денисенко^a, Н. В. Кленов^b,c, А. М. Сатанинc*

^a Нижегородский исследовательский университет им. Н. И. Лобачевского

603950, Нижний Новгород, Россия

^b Физический факультет, Московский государственный университет им. М. В. Ломоносова

119991, Москва, Россия

^c Всероссийский научно-исследовательский институт автоматики им. Н. Л. Духова

101000, Москва, Россия

Поступила в редакцию 25 августа 2018 г.,

после переработки 10 сентября 2018 г.

Принята к публикации 11 сентября 2018 г.

Обсуждается задача об ускорении квантовых вычислений путем управления состояниями кубитов корот-

кими униполярными импульсами с большой амплитудой. Предложен новый метод описания динамики

кубитов, основанный на представлении Магнуса для оператора эволюции (пропагатора) кубитов, кото-

рое позволяет найти решение задачи квантового контроля вне рамок теории возмущений. Эволюция

состояний многокубитной системы представлена как движение на специальной унитарной группе SU(N),

подобное вращению вектора Блоха на группе SU(2) в случае одного кубита. В качестве примера рас-

смотрено переключение одиночных кубитов при различных способах возбуждения. Обнаружено общее

соотношение, устанавливающее связь профиля импульса с результатом воздействия, подобное извест-

ному «закону площадей» для раби-импульсов. Детально изучено воздействие униполярных импульсов

на двухкубитную систему. Рассмотрена как симметричная конфигурация, когда параметры кубитов не

различаются и на них действует одинаковое магнитное поле со стороны флаксона, так и конфигурация

уровней, которая возникает в том случае, когда для одного кубита может стать возможным переход

на ближайший уровень под влиянием возмущения. Аналитическое рассмотрение проведено для общего

случая двух взаимодействующих кубитов — четырехуровневой системы. Для оценки точности аппрокси-

мации использовано прямое численное моделирование динамики многокубитной системы, а в качестве

критерия близости выполнения операций использована «степень соответствия» (fidelity). Показано, что

полученные выражения для пропагатора позволяют сформулировать условия для параметров импульса,

которые необходимы для выполнения логических операций.

DOI: 10.1134/S004445101902007X

традиционной раби-техники, где используются за-

полненные (радио-) импульсы, и переходе на управ-

1. ВВЕДЕНИЕ

ление униполярными импульсами магнитного по-

Количество последовательных операций над ре-

ля (см. работы [6-13] и цитированные в них ра-

гистром сверхпроводниковых кубитов [1-5] суще-

боты). Такие короткие импульсы могут быть со-

ственно ограничено временем декогерентности в та-

зданы в цифровых устройствах сверхпроводниковой

кой системе (∼ 100 мкс). Одним из путей преодо-

электроники с использованием возбуждений (флак-

ления указанного ограничения может стать реали-

сонов), несущих квант магнитного потока. Теория

зация «быстрой квантовой логики» для управле-

воздействия флаксонов на многокубитные системы

ния кубитами, которая позволит манипулировать

позволит получить не только количественные зна-

квантовыми состояниями с характерными времена-

чения для вероятностей перехода между уровнями,

ми ∼ 10 пс, что станет возможным при отказе от

но и установить качественные представления о за-

^* E-mail: sarkady@mail.ru

висимостях этих величин от параметров флаксона.

258

ЖЭТФ, том 155, вып. 2, 2019

Динамика кубитов в поле униполярных импульсов. . .

Это необходимо для «проектирования» импульсов и

Коэффициенты разложения u_j (j = 0, 1, . . ., N - 1)

разработки стратегии управления кубитами.

представлены в явном виде через собственные зна-

Теоретическое описание воздействия раби-им-

чения матрицы M(t). Отметим, что с точки зре-

пульсов на кубиты основано на резонансной теории

ния теории групп речь идет о разложении группо-

возмущений (приближении Раби) [14, 15] или ква-

вой экспоненты по матрицам группы SU(N) [30-32].

зиэнергетическом подходе в базисе Флоке

[16-19].

Эволюция состояния системы может быть представ-

Понятно, что основная парадигма раби-техники

лена как движение на такой группе, подобно пово-

[14, 15] — «закон площадей», основанный на резо-

роту вектора Блоха на группе SU(2) в случае одного

нансной теории возмущений — не выполняется для

кубита. Мы покажем, что коэффициенты разложе-

униполярных импульсов.

ния u_j благодаря существованию инвариантов Ка-

В данной работе предложен новый метод описа-

зимира [32] для матриц M(t) в группе SU(N) будут

ния динамики кубитов при управлении униполяр-

зависеть от меньшего числа параметров, чем сама

ными импульсами. Для определенности рассматри-

матрица M(t), поэтому будут медленными функци-

ваются потоковые кубиты на основе сверхпроводя-

ями времени.

щих контуров с тремя джозефсоновскими контакта-

В качестве примера продемонстрируем эффек-

ми (3JJ qubit) [1-3]. Предполагается, что управле-

тивность полученного выражения для описания ди-

ние осуществляется одиночными флаксонами, рас-

намики одного кубита при различных способах

пространяющимися по связанной магнитным обра-

возбуждения униполярными импульсами. Найден

зом с кубитами нелинейной волноводной линии, ре-

аналог обобщенного «закона площадей» в случае

ализованной на основе джозефсоновских систем с

униполярных импульсов, который в определенном

соответствующим образом подобранными парамет-

смысле действует подобно закону площадей в слу-

рами [20-22].

чае раби-возбуждения [15]. Полученное выражение

При исследовании переходов между стационар-

для пропагатора далее используется для описания

ными состояниями на временах, меньших времени

воздействия импульсов на двухкубитную систему.

декогерентности, будем решать временное уравне-

Сначала рассматривается симметричная конфигу-

ние Шредингера для вычисления оператора эволю-

рация, когда параметры кубитов не различаются и

ции U(t) — пропагатора системы, который определя-

на них действует одинаковое поле со стороны флак-

ет ее волновую функцию в любой момент времени:

сона. В этом случае матрица M(t) имеет размер-

ψ(t) = U(t)ψ(0), ψ(0) — начальное состояние. Обыч-

ность 3 × 3, т. е. принадлежит группе SU(3). Здесь

ной теории возмущений недостаточно для наших це-

же обсуждается трехуровневая система более обще-

лей, поскольку необходимо рассматривать сигналы

го вида, которая возникает, например, в том слу-

большой амплитуды для получения заметных изме-

чае, когда для одного кубита может стать возмож-

нений в населенности уровней. Для вычисления про-

ным переход на более высокий уровень под влияни-

пагатора U(t) n-кубитной системы используем две

ем флаксона. Показано, что и в этом случае зада-

идеи:

ча сводится к вычислению оператора эволюции для

— разложение Магнуса [23,24] для пропагатора в

матрицы M(t) в группе SU(3). Затем речь пойдет о

виде экспоненты U(t) = e-iM(t) от некоторого опера-

задаче управления кубитами в более общем случае

тора M(t) (оператора Магнуса), для которого име-

различными униполярными импульсами. Аналити-

ется простой алгоритм вычисления в виде ряда по

ческое рассмотрение проведено для двух кубитов —

степеням гамильтониана с любой требуемой точнос-

четырехуровневой системы, — хотя развитый алго-

тью [25-28];

ритм применим к любому числу кубитов (с учетом

— возможность за пределами рассмотрения в ба-

вычислительных ограничений). Для контроля ап-

зисе Флоке представить оператор Гамильтона для

проксимации мы используем прямое численное мо-

n кубитов матрицей N × N, где N = 2n, а зна-

делирование динамики многокубитной системы, а в

чит, и матрица M(t) также будет иметь размерность

качестве критерия близости выполнения операций

N ×N. Следовательно, по известной теореме Кэли-

использована «степень соответствия» (fidelity).

Гамильтона [29] пропагатор в данном случае может

2. УНИПОЛЯРНЫЕ ИМПУЛЬСЫ И СХЕМА

быть записан в виде разложения по степеням мат-

УПРАВЛЕНИЯ КУБИТАМИ

рицы M(t), причем максимальная степень получа-

ющегося полинома не выше N - 1:

В данном разделе представлено общее рассмот-

рение схемы управления регистром из небольшого

U (t) = u₀I+u₁M(t)+u₂M²(t) + . . . + uN-1MN-1(t).

числа кубитов униполярными импульсами с заве-

259

М. В. Денисенко, Н. В. Кленов, А. М. Сатанин

ЖЭТФ, том 155, вып. 2, 2019

Рис. 1. Схема уединенного кубита (типа 3JJ-кубита) и

управляющих импульсов (флаксонов), распространяющих-

ся по джозефсоновской передающей линии

домо широким спектром. Пусть в момент времени

Рис. 2. Схема связанных джозефсоновских кубитов, управ-

t = 0 система приготовлена в начальном состоя-

ляемых униполярными импульсами: последовательное (a)

нии ψ(0). Как хорошо известно, временная эволю-

и параллельное («симметричное») (б) расположение ку-

ция системы, гамильтониан которой H(t) зависит от

битов

времени, описывается уравнением

(

)

∂U(t)

iℏ

= H(t)U(t).

(1)

ψ_± =

√

∂t

∓1

В общем случае решение уравнения Шредингера (1)

с энергиями E_± = ±Δ/2 соответственно. Отметим,

представляется в виде ψ(t) = U(t)ψ(0), где введен

что ниже мы используем различные базисные функ-

оператор эволюции

ции для классификации состояний кубита, которые

⎛

⎞

будут связаны определяемыми унитарными пово-

∫

ротами. Эти функции будут различаться нижними

U (t) =

T exp^⎝-

dt₁H(t₁)^⎠ ,

(2)

ℏ

значками.

Пусть ψ(0) = ψ_-, тогда вероятность перехода

в состояние ψ₊ под влиянием изменения внешнего

T — оператор хронологического упорядочения. В

магнитного потока Φ_∼(t), пронизывающего сверх-

рассматриваемой задаче управления нас будет ин-

проводящий контур кубита (т. е. переход под дей-

тересовать случай, когда воздействие управляющей

ствием управляющей функции: ε(t) = I_pΦ_∼(t)/Φ₀,

функции нельзя учитывать по теории возмущений.

где Ip — ток джозефсоновского перехода, Φ0 —

квант потока [1]), определяется выражением

2.1. Однокубитные операции: схема

реализации и основные определения

P(-)→(+)(t) = |〈ψ₊|U(t)|ψ_-〉|² .

(4)

Сформулируем задачу о быстром управлении

Пусть также управляющий импульс имеет ха-

уединенным потоковым кубитом [1], схематично

рактерную амплитуду ε_m и характерную длитель-

изображенном на рис. 1. Гамильтониан кубита име-

ность τ. Ниже мы проанализируем два случая воз-

ет вид

буждения кубита, когда амплитуда ε_m может быть

как меньше, так и больше туннельного расщепления

Δ. Для конкретных расчетов будут использоваться

H(t) = -

(ε(t)σ_z + Δσ_x) ,

(3)

импульсы двух типов: прямоугольные импульсы ви-

да

где Δ — расстояние между уровнями кубита (тун-

нельное расщепление); ε(t) — управляющая функ-

ε(t) = ε_mθ(t)θ(τ - t)

(5)

ция (пропорциональная магнитному потоку, создан-

и импульсы с гауссовым профилем:

ному флаксоном в контуре кубита, см. рис. 1); σ_x,

(

)

σ_z — матрицы Паули.

(t - t₀)²

ε(t) = ε_m exp

(6)

Если управляющая функция равна нулю, то ку-

2τ²

бит может находиться в состояниях

260

ЖЭТФ, том 155, вып. 2, 2019

Динамика кубитов в поле униполярных импульсов. . .

где θ(t) — функция Хевисайда, t₀ — момент дости-

магнитного взаимодействия соответственно. Соглас-

жения максимума (в случае гауссова импульса (6)).

но [1,20] гамильтониан взаимодействующих кубитов

можно записать в виде

(

)

H =-

ε₁σ(1)z + Δ₁σ⁽¹⁾

⊗I⁽²⁾-

2.2. Двухкубитные операции: схема

(

)

реализации и основные определения

I⁽¹⁾ ⊗ ε₂σ(2)z+Δ₂σ⁽²⁾

Jσ(1)z ⊗σ(2)z

(7)

В случае управления парой связанных кубитов

предполагается, что каждый кубит описывается га-

где ε1,2 — управляющие функции вида (5) или (6)

мильтонианом типа (3) с соответствующими пара-

с соответствующими параметрами, Δ1,2 — туннель-

метрами и управляющей функцией. Взаимодействие

ное расщепление уровней кубитов, знак ⊗ означает

кубитов характеризуется единственным параметром

прямое произведение в пространстве состояний ку-

J. Константа связи может быть как положительной,

битов. Выражение (7) можно переписать в матрич-

так и отрицательной для ферро- или антиферро-

ной форме:

⎛

⎞

ε₁(t) + ε₂(t) + J

Δ₂

Δ₁

⎜

⎟

⎜

Δ₂

ε₁(t) - ε₂(t) - J

Δ₁

⎟

⎜

H (t) = -

^⎟.

(8)

⎜

⎟

⎝

Δ₁

-ε₁(t) + ε₂(t) - J

Δ₂

⎠

Δ₁

Δ₂

-ε₁(t) - ε₂(t) + J

В эксперименте с «последовательной» конфигу-

H^T (t) =

⎛

⎞

рацией (рис. 2а) импульсы могут приходить на пару

√

2ε(t)+

2Δ

кубитов в разные моменты времени и иметь разные

⎜

⎟

⎜

√

⎟

параметры (амплитуды и длительности) из-за раз-

⎜

2Δ

^⎟.

(10)

⎜

⎟

ной магнитной связи флаксона с кубитом, а также

⎝

⎠

√

иметь разные форму и скорости в различных обла-

2Δ

-2ε(t)+

стях активной джозефсоновской среды. В симмет-

Вывод выражения для гамильтониана (10) для три-

ричной («параллельной») конфигурации (рис. 2б)

можно организовать воздействие одинаковыми им-

плетного состояния кубитов, а также получение

уровней E^Tk и собственных векторов |T_k〉 (k = 1, 2, 3)

пульсами на кубиты в один и тот же момент вре-

мени, если использовать возможности трехмерного

при ε(t) → 0 приведены в Приложении А. Мы будем

интересоваться вероятностями перехода P_k→j (t) =

проектирования сверхпроводниковых схем для реа-

= |〈T_j |U(t)|T_k〉|² (k = 1, 2, 3), где пропагатор подчи-

лизации кубитной связи.

няется уравнению (1) с гамильтонианом (10).

В статическом случае параметры Δ_i определяют

Наряду с

«симметричным» гамильтонианом

спектр несвязанных кубитов: E_i = ±(1/2)Δ_i (при

(10), полезно рассмотреть трехуровневую модель бо-

= 0). Энергетические уровни E(2)j и волновые

лее общего вида, которая позволит исследовать вли-

функции |e_j〉 двух связанных кубитов (j = 1, 2, 3, 4)

яние соседних уровней на возможность управления

при ε1,2 → 0 приведены в Приложении А.

кубитами униполярными импульсами. Пусть уровни

В качестве начального состояния могут быть вы-

кубита связаны с третьим уровнем некоторым мат-

браны как состояния |e_j 〉, так и любая линейная

ричным элементом. Для простоты считается, что

комбинация этих состояний. Если начальные состо-

управляющий импульс влияет на все три состояния.

яния пары кубитов заданы вектором |e_k〉, то веро-

Модельный гамильтониан возьмем в виде

ятность перехода в состояние |e_j 〉 определяется вы-

⎛

⎞

2A αε(t)

ражением

⎜

⎟

H_m =

⎝ αε(t) Δ - A ε(t)

⎠.

(11)

P_k→j(t) = |〈e_j|U(t)|e_k〉|² .

(9)

ε(t)

-Δ - A

Представляет интерес также изучить возбужде-

Из (11) следует, что при ε(t) → 0 будет иметь место

ние одинаковых кубитов с параметрами Δ = Δ₁ =

трехуровневая система, для которой энергии состо-

= Δ₂ (симметричных) одинаковыми импульсами

яний определяются из условий: E₊ = (Δ - A)/2,

ε = ε₁ = ε₂ (см. рис. 2б). При этом гамильтони-

E_- = -(Δ + A)/2 и E_d = A (Δ ≤ A). Параметр α

ан системы кубитов в симметричной конфигурации

определяет степень влияния управления на населен-

имеет вид

ность верхнего уровня.

261

М. В. Денисенко, Н. В. Кленов, А. М. Сатанин

ЖЭТФ, том 155, вып. 2, 2019

3. РАЗЛОЖЕНИЕ МАГНУСА ДЛЯ

разложимая в ряд функция от матрицы представля-

ОПЕРАТОРА ЭВОЛЮЦИИ

ет собой полином степени не выше ее ранга. В рас-

сматриваемом случае из теоремы Кэли - Гамильтона

Построим аппроксимационное представление

следует разложение для экспоненты в виде

для оператора эволюции — разложение Магнуса:

e-iM(t) = u₀I + u₁M(t)+

U (t) = e-iM(t),

(12)

+ u₂M²(t) + . . . + uN-1MN-1(t),

(17)

где введен эрмитов оператор M, M⁺ = M. Соглас-

но [23], оператор M в общем случае определяется

где в правой части стоит матричный полином степе-

бесконечным рядом, слагаемые которого пропорци-

ни N - 1 (а также единичная матрица I_N×N ). Отме-

ональны соответствующим степеням исходного опе-

тим также, что конечность ряда (17) в разложении

ратора Гамильтона:

экспоненты следует из теории групп (см. [30-32]).

Пусть матрица M(t) приведена к диагонально-

M =M⁽¹⁾ +M⁽²⁾ +M⁽³⁾ +...

(13)

му виду M(t) = S^†(t)μ(t)S(t), где матрица уни-

тарного поворота S^†(t)S(t) = I, а элементы μ_j (t)

Далее, оператор U(t) в виде (12) подставляется в

(j = 1, 2, . . ., N) — собственные значения матрицы

(1) и в полученном выражении приравниваются со-

M (t), определяемые из соотношения

ответствующие слагаемые одинакового порядка ма-

лости слева и справа от знака равенства. Интегри-

det (M(t) - μ(t)I) = 0.

(18)

руя полученные соотношения, приходим к цепочке

Отметим, что матрица M(t) обладает свойством

выражений:

Tr(M(t)) = 0, поэтому

∫

μ₁(t) + μ₂(t) + . . . + μ_N (t) = 0.

M⁽¹⁾(t) =

dt₁H(t₁),

(14)

ℏ

Применяя указанный унитарный поворот к обеим

частям (17), получаем

∫

⎛

⎞

M⁽²⁾(t) =

dt₂

dt₁ [H(t₁), H(t₂)] ,

(15)

μ₁

μ²¹

μN1

2ℏ²

⎜

⎟

⎜

μ₂

μ²²

μN2

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

∫

⎜

⎟

⎜

⎟

M⁽³⁾(t) = -

dt₃

dt₂

dt₁ ×

⎜

⎟

⎜

⎟

4ℏ³

⎜

⎟

⎝ 1

μN-1

μ2N-1

μNN-1

⎠

{

[[H(t₁), H(t₂)] , H(t₃)] +

μ_N μ2N . . . μ^N

⎛

⎞

⎛

⎞

}

u₀

e-iμ1

[H(t₁), [H(t₂), H(t₃)]]

(16)

⎜

⎟

⎜

⎟

⎜

u₁

⎟

⎜

e-iμ2

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

и т. д. Если в теории имеется малый параметр, то

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟,

(19)

достаточно будет ограничиться в экспоненте уче-

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

том нескольких слагаемых по степеням этого пара-

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

метра. Эффективная численная методика опериро-

⎝ uN-2

⎠

⎝ e-iμN-1

⎠

вания с рядами, определяющими разложение Маг-

uN-1

e-iμN

нуса, а также численная процедура действия про-

пагатора на состояния системы описаны в работах

где слева возникла матрица Вандермонда, элемента-

по вычислительной физике (см., например, [25-28]

ми которой являются степени собственных значений

и цитированную там литературу).

матрицы M(t). Выполняя обращение матрицы Ван-

Зависимость волновой функции от времени нахо-

дермонда, можно выразить все коэффициенты раз-

дится согласно соотношению ψ(t) = U(t)ψ(0). Что-

ложения оператора U(t) (17) через собственные зна-

бы подействовать оператором эволюции в форме

чения матрицы M(t). Понятно, что при N = 2, 3, 4

(12) на начальное состояние, воспользуемся теоре-

это можно сделать аналитически, а при N > 4 —

мой Кэли - Гамильтона [29], согласно которой любая

при помощи численных методов.

262

ЖЭТФ, том 155, вып. 2, 2019

Динамика кубитов в поле униполярных импульсов. . .

Таким образом, практическое значение развитой

Решая (20) относительно u₀ и u₁, из (17) находим

методики состоит в том, что вектор состояний ку-

(

)

битов в текущий момент времени определяется со-

i sinμ(t)

U (t) = cos μ(t)

гласно (17) «мгновенным» значением пропагатора.

μ(t)

Как видно, полное вращение вектора определяется

(

)

действием на начальное состояние матричного поли-

M_z(t)

M_x(t) - iM_y(t)

(21)

нома, которое содержит различные степени матри-

M_x(t) + iM_y(t)

-M_z(t)

цы u_j M^j(t) с соответствующими весами u_j(t). Как

будет видно из дальнейшего, коэффициенты разло-

где компоненты вектора Блоха определяются соот-

жения u_j(t) могут слабо зависеть от времени.

ношением M(t) = (1/2) Tr(σM(t)).

3.2. Двухкубитные операции: общее

3.1. Однокубитные операции: общее

рассмотрение

Разработанный метод позволяет относительно

просто выйти за рамки рассмотрения двухуровне-

В качестве примера рассмотрим эволюцию состо-

вых систем, что для интересующих нас применений

яний одного кубита. В этом случае матрица M мо-

имеет критически важное значение: униполярное

жет быть разложена по матрицам Паули:

пикосекундное «флаксонное» воздействие на кван-

товую систему заведомо имеет широкий спектр и

M =M_xσ_x +M_yσ_y +M_zσ_z.

вполне может вести к возбуждению состояний, до-

статочно высоко расположенных по энергиям.

Собственные значения M равны μ

√

Рассмотрим далее два связанных кубита в сим-

= ± M2x + M2y + M2z, а выражение (19) сводится

метричной конфигурации (10). Последовательное

к уравнению

суммирование ряда (13) приводит к заполнению

(

)(

)

(

)

элементов матрицы, которая в данном случае рас-

u₀

e^-iμ

кладывается по матрицам Гелл-Манна λ_j (j = 1,

(20)

iμ

-μ

u₁

2, . . . , 8) группы SU(3) [30]:

⎛

⎞

M₃ +

√

M₈

M₁ - iM₂

M₄ - iM₅

⎜

⎟

⎜

⎟

∑

⎜

⎟

M =

M_jλ_j =

⎜

M₁ + iM₂

-M₃ +

√

M₈

M₆ - iM₇

⎟,

(22)

⎜

⎟

j=1

⎝

⎠

M₄ + iM₅

M₆ + iM₇

-√

M₈

где M_j = (1/2) Tr(λ_j M). Отметим, что мы рассмат-

(23) определяются формулой Кардано - Виета:

риваем значение матрицы M ≡ M(t) в момент вре-

√

(

)

мени t.

2πk

μ_k =

r cos θ +

k = 1,2,3.

(24)

Собственные значения M, определяемой (22), на-

ходятся из выражения

Отметим, что корни кубического уравнения зависят

всего от двух параметров (r и θ). Поскольку корни

μ³ -

C₂μ -

C₃ = 0,

(23)

найдены, можно определить коэффициенты разло-

жения u_j (t) в выражении

где введены так называемые инварианты Казимира

[30-32]:

U (t) = u₀I + u₁M(t) + u₂M²(t)

(25)

C₂ = Tr(M²) = r², C₃ = Tr(M³) =

√ cosθ,

путем обращения матрицы Вандермонда:

⎛

⎞⎛

⎞

⎛

⎞

которые, в свою очередь, определяют два парамет-

μ₁

μ²¹

u₀

e-iμ1

⎜

⎟⎜

⎟

⎜

⎟

ра: r и θ. Как известно [33], три корня уравнения

⎝ 1

μ₂

μ²²

⎠⎝ u1

⎠=

⎝ e-iμ2

⎠,

(26)

μ₃

μ²

u₂

e-iμ3

263

М. В. Денисенко, Н. В. Кленов, А. М. Сатанин

ЖЭТФ, том 155, вып. 2, 2019

где μ₁ + μ₂ + μ₃ = 0. Решение для (26) приведено в

когда параметры кубитов и параметры управляю-

Приложении B.

щих импульсов могут заметно различаться (группа

Рассмотрим теперь воздействие униполярного

SU(4) [30, 34]). В этом случае M ≡ M(t) расклады-

импульса на два связанных кубита в общем случае, вается по матрицам Гелл-Манна λ_j группы SU(4):

∑

M = M_jλ_j=

j=1

⎛

⎞

M₃ +

√

M₈ +

√

M₁₅

M₁ - iM₂

M₄ - iM₅

M₉ - iM₁₀

⎜

⎟

⎜

⎟

⎜

⎟

⎜

M₁ - iM₂

-M₃ +

√

M₈ +

√

M₁₅

M₆ - iM₇

M₁₁ - iM₁₂

⎟

⎜

⎟

⎜

⎟

(27)

⎜

⎟

⎜

M₄ + iM₅

M₆ + iM₇

√

M₁₅

M₁₃ - iM₁₄

⎟

⎜

⎟

⎝

⎠

M₉ + iM₁₀

M₁₀ + iM₁₂

M₁₃ + iM₁₄

-√

M₁₅

(

)

В общем случае собственные значения матрицы M,

μ₁ = r

-√

sinφsinθ -

cosθ

определяемой (27), находятся из выражения

(

)

μ₂ = r

+√

sinφsinθ -

cosθ

μ⁴ -

C₂μ² -

C₃μ +

(C²² - 2C₄) = 0,

(28)

(

)

(30)

μ₃ = r

-√

sinφsinθ +

cosθ

где также введены инварианты Казимира, опреде-

ляемые соотношениями C_n = Tr(Mⁿ). Входящие в

(

)

(28) коэффициенты удобно связать с тремя действи-

μ₄ = r

+√

sinφsinθ +

cosθ

тельными параметрами: r, θ и φ (см. [33,34]):

Отметим, что корни уравнения четвертой степени

r² = C₂, sinθ sin2θ cos2φ =

C₃,

зависят всего от трех параметров: r, θ и φ.

3r³

(

)

(29)

Таким образом, пропагатор кубитов в случае

2 sin² φ - 3

sin² θ

(

))

группы SU(4) определяется выражением

2 cos² φ - 3

sin² θ = 2(C²² - 2C₄).

Пусть решения (29) относительно r, θ и φ найдены,

U (t) = u₀I + u₁M(t) + u₂M²(t) + u₃M³(t),

(31)

тогда корни уравнения (28) выражаются формулой

Феррари (см. [34]):

где коэффициенты разложения u_j (j = 0, 1, 2, 3) на-

ходятся решением линейной системы уравнений:

⎛

⎞⎛

⎞

⎛

⎞

μ₁

μ²¹

μ³¹

u₀

e-iμ1

⎜

⎟⎜

⎟

⎜

⎟

⎜

μ₂

μ²²

μ³²

⎟⎜

u₁

⎟

⎜

−iμ2

⎟

⎜

⎟⎜

⎟

⎜ e

⎟.

(32)

⎜

⎟⎜

⎟

⎜

⎟

⎝ 1

μ₃

μ²³

μ³³

⎠⎝ u2

⎠

⎝ e-iμ3

⎠

-μ₁ - μ₂ - μ₃ μ₁ + μ₂ + μ₃

-(μ₁

+μ₂ +μ₃)³

u₃

ei(μ1+μ2+μ3)

4. ДЕЙСТВИЕ УНИПОЛЯРНЫХ

ИМПУЛЬСОВ НА КУБИТ: ПРИМЕРЫ И

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Проиллюстрируем применение развитой выше

Коэффициенты u_j (j = 0, 1, 2, 3), выраженные че-

теории на примере управления состояниями куби-

рез собственные значения матрицы M, выписаны в

та униполярными импульсами различной длитель-

явном виде в Приложении B.

ности и амплитуды.

264

ЖЭТФ, том 155, вып. 2, 2019

Динамика кубитов в поле униполярных импульсов. . .

4.1. Управление населенностями состояний

Пусть кубит в начальный момент времени приготов-

кубита при малой амплитуде униполярного

лен в состоянии ψ_-, т. е. «поляризован» вдоль оси x.

импульса

Волновая функция в новом базисе связана с исход-

ной соотношением ψ(t) = S-11ψ(t), поэтому переходу

Начнем с ситуации, когда параметры импульсов

ψ_- → ψ₊ в новом базисе будет соответствовать пе-

(5) и (6) таковы, что характерная амплитуда ε(t)

реход между состояниями ψ₀ → ψ₁, где ψ₀ = (1, 0)^T ,

управляющего импульса меньше туннельного рас-

ψ₁ = (0, 1)^T . С учетом проделанных выше унитар-

щепления Δ. Предварительно совершим унитарное

ных поворотов волновую функцию можно записать

преобразование гамильтониана (3): H(t) = S†1HS₁,

в виде

выбрав матрицу преобразования в виде

(

)

⎛

(

) (

)

⎞

sinμ

Δt

cosμ-i

M_z exp

-i

S₁ =

√

⎜

⎟

-1

⎜

⎟

ψ(t) =

(

)

(38)

⎝

⎠

sinμ

Δt

Результатом преобразования будет выражение для

-i

(M_x+iM_y) exp i

гамильтониана:

что приводит к выражениям для населенностей ви-

H (t) = -

(Δσ_z + ε(t)σ_x) .

(33)

да

(

)

M2z

Второе слагаемое в (33) при определенных парамет-

p₁(t) =

sin² μ(t),

рах для амплитуды и длительности сигнала может

μ(t)²

(39)

давать малый вклад, поэтому мы совершим второе

M²

p₀(t) = cos² μ(t) +

sin² μ(t),

каноническое преобразование, позволяющее выде-

μ(t)²

лить точно диагональный вклад в динамику систе-

где временная зависимость M_x, M_y, M_z определяет-

мы:

ся согласно (37). Пусть при t = 0 величины p₀ = 1,

H(t) = S†2H(t)S₂ - iS^† ∂S22,

(34)

p₁ = 0. Как видно из выражения (39), полный пе-

∂t

реворот «псевдоспина» p₀ = 0, p₁ = 1 после прило-

где S₂ = exp(-iΔtσ_z/2). Преобразованный гамиль-

жения униполярного импульса длительности τ бу-

тониан принимает вид

дет возможен, если одновременно выполняются два

(

)

-iΔt

условия: μ = π/2 и M_z = 0.

ε(t)

H(t) = -

(35)

В работе [11] предполагалось, что вклад сла-

eiΔt

гаемого M_z мал, поэтому для полного переворота

«псевдоспина» после действия импульса достаточно

а оператор эволюции U(t) подчиняется уравнению

было выполнения одного условия μ = π/2 или, что

∂U(t)

эквивалентно, равенства

iℏ

= H(t)U(t).

(36)

∂t

⎛

⎞₂

Фактически, мы переходим к представлению взаи-

∫

модействия, но в дальнейшем не используем теорию

⎝ dt ε(t) sin Δt⎠

возмущений для расчетов, а строим интерполяцион-

ный оператор эволюции. Согласно изложенной вы-

⎛

⎞₂

∫

ше методике оператор эволюции U(t) представляет-

+^⎝ dt ε(t)cosΔt⎠ = π²,

(40)

ся в форме Магнуса, U(t) = e-iM(t), а затем запи-

сывается в виде (21).

Далее для аналитических расчетов мы ограни-

что можно выполнить для импульсов прямоуголь-

чимся двумя членами в разложении (13), что соглас-

ной и гауссовой формы. Итак, в этом случае ве-

но (14) и (15) дает для коэффициентов разложения

роятность переворота определяется фурье-образом

по матрицам Паули выражения

управляющей функции импульса:

∫t

M_x + iM_y = -

dt₁ε(t₁)eiΔt1 ,

(37)

∫

M_z =

dt₂ε(t₂)

dt₁ε(t₁) sin Δ(t₁ - t₂).

что в определенном смысле обобщает «закон площа-

дей» для раби-импульсов.

265

М. В. Денисенко, Н. В. Кленов, А. М. Сатанин

ЖЭТФ, том 155, вып. 2, 2019

M ,M ,M_xyz

P, P_M

Для прямоугольного импульса (5) «обобщенное

1.0

правило площадей» сводится к условию для пара-

метров импульса для реализации инверсии состоя-

ния:

Δτ

π Δ

-0.5

sin

(41)

2 ε_m

0.5

которое выполняется при

-1.0

π Δ

< 1.

2 ε_m

При этом

-1.5

ε2m

M_z = -

(Δτ - sin Δτ).

(42)

4Δ²

t, пс

Если Δτ ≪ 1, то

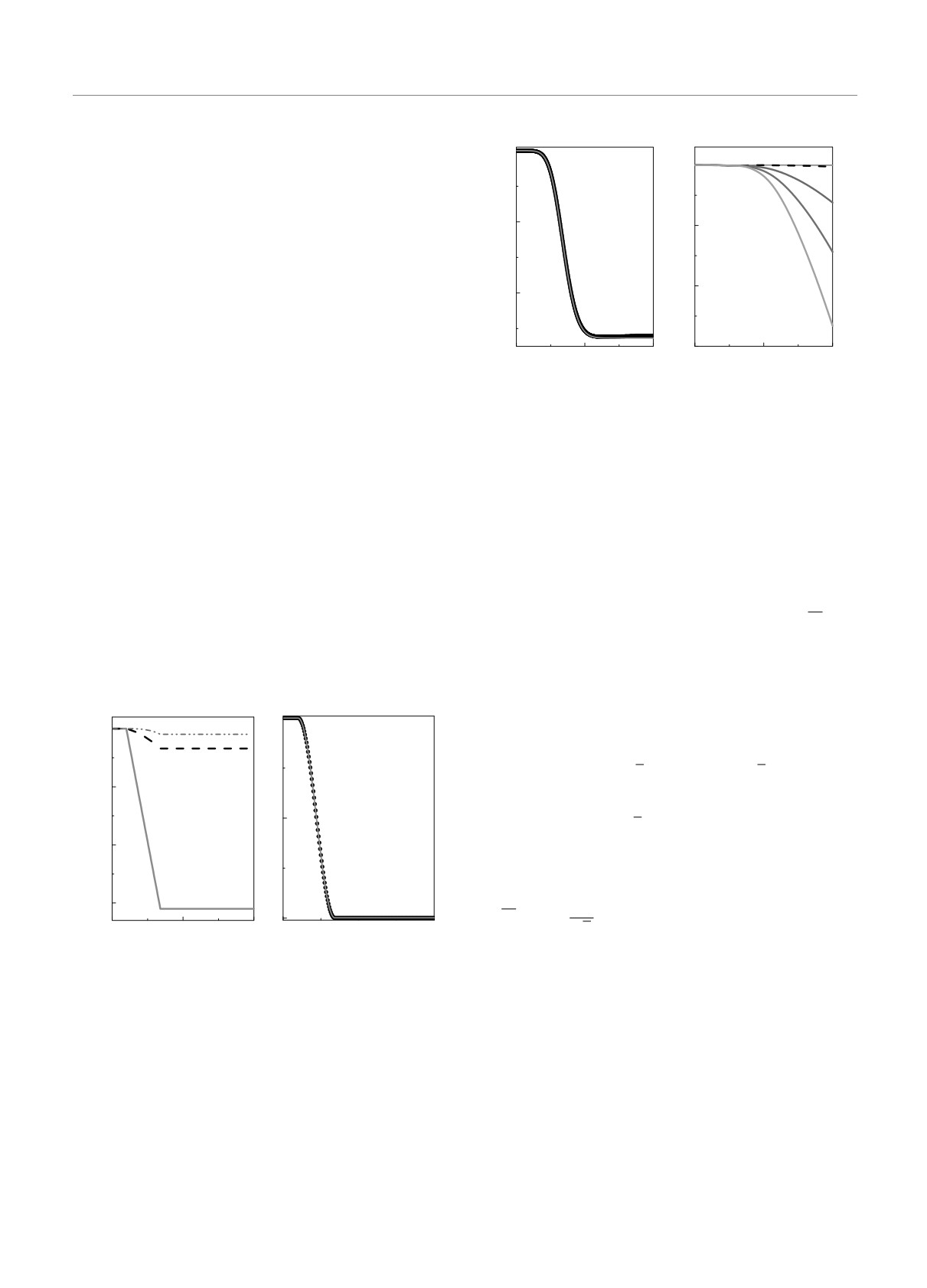
Рис. 3. (В цвете онлайн) а) Динамика элементов мат-

ε2m

рицы вращения, где Mx представляет красная кривая 1,

M_z ≈

(Δτ)³.

(43)

My — черная штриховая кривая 2, Mz — синяя штрих-

24Δ

пунктирная кривая 3. б) Временная эволюция населен-

Видно, что при Δτ ≪ 1 вклад параметра M_z в веро-

ности основного состояния кубита с туннельной энергией

ятность переворота «псевдоспина» мала и им можно

Δ = 0.005 ГГц, где красная кривая — результат решения

пренебречь. Это и дает нам крайне важное для реа-

уравнения Шредингера P (t), черные точки — аналитиче-

лизации на практике управляемых переходов между

ское решение PM (t) по Магнусу (39). Параметры управля-

базисными состояниями требование на малую дли-

ющего прямоугольного импульса: τ = t_off - tin = 10.5 пс

тельность внешнего воздействия.

(tin = 1 пс и toff = 11.5 пс), εm = 0.3 ГГц

В случае импульса гауссовой формы (6) предпо-

ложим, что для времени достижения максимума t₀

и длительности импульса τ выполнено неравенство

4.2. Управление населенностями состояний

τ ≪ t₀. В этом случае в интеграле (37) пределы ин-

кубита при большой амплитуде

униполярного импульса

тегрирования можно распространить до ±∞, тогда

^√π

Пусть теперь амплитуда поля флаксона тако-

M_x + iM_y = -

ε_mτeiΔt0 e-(Δτ)2/².

(44)

ва, что это воздействие сильно изменяет расстояние

между уровнями. Отличие от рассмотренной выше

Отсюда следует, что, если при соответствующем вы-

ситуации здесь будет состоять в том, что разложе-

боре параметров вклад от M_z мал, то возможно пол-

ние Магнуса следует вести по другому параметру.

ное переключение кубита при

Считая первое слагаемое в (3) основным приближе-

^√π

нием, предварительно совершим каноническое пре-

ε_mτe-(Δτ)2/² =

(45)

образование, выделяющее основной вклад:

Проиллюстрируем сказанное путем расчета времен-

ных зависимостей M_x, M_y, M_z согласно (37), а

H(t) = S†3H(t)S₃ - iS^† ∂S33,

(46)

∂t

также сравним полученные данные с результатами

где

решения уравнения Шредингера. Если параметры

управляющего импульса таковы, что Δτ ≪ 1, то

∫

компонента M_z (определенная формулой (37)) вно-

S₃ = exp(-iβ(t)σ_z/2), β(t) = dt₁ε(t₁).

сит малый вклад в вероятность переворота «псев-

доспина», что наглядно продемонстрировано на

рис. 3а. Временная динамика кубита, установленная

Выражение (46) представимо в виде

решением уравнения Шредингера (красная кривая

(

)

на рис. 3б), и приближенное аналитическое реше-

e-iβ(t)

H(t) = -

(47)

ние по Магнусу (черные точки на рис. 3б) хорошо

eiβ(t)

согласуются. Как видно из рис. 3б, при выбранных

параметрах прямоугольного униполярного импуль-

Оператор эволюции берется в форме Магнуса:

са населенности уровней кубита полностью инвер-

U (t) = exp(-iM(t)), где элементы матрицы M(t)

тировались (произошел переворот «псевдоспина»).

определяются следующими выражениями:

266

ЖЭТФ, том 155, вып. 2, 2019

Динамика кубитов в поле униполярных импульсов. . .

∫

Δ²

M_x + iM_y = -

dt₁eiβ(t1),

(48)

M_z =

dt₂

dt₁ sin(β(t₁) - β(t₂)).

(49)

В свою очередь, волновая функция при начальном

условии ψ(0) = ψ_- будет определена как

⎛

(

) (

)

⎞

sinμ

β(t)

cosμ - i

(M_z + M_x - iM_y exp

-i

⎜

⎟

⎜

⎟

ψ(t) =

√

(

) (

)

(50)

⎝

⎠

sinμ

β(t)

cosμ + i

(M_z - M_x - iM_y exp i

Вероятность переворота «псевдоспина» находится

интегрированием уравнения Шредингера. Мы рас-

из выражения

смотрим инвертирование населенностей уровней ку-

бита в поле большой амплитуды, без дополнительно-

(

)₂

sinμ

го условия на соотношение расстояния между уров-

p₊(t) = cosμ sin

+M_z

cos

нями кубита и длительности управляемого импуль-

)₂ (

)₂

са. В этом случае наблюдается хорошее согласие

⁽sinμ

M_x sin

+ My cos

(51)

численного и аналитического решений для матрич-

ных элементов и населенностей, что продемонстри-

В качестве примера приведем выражения для эле-

ровано на рис. 4. Как видно из рис. 4а, уход вектора

ментов матрицы поворота в случае действия им-

«псевдоспина» при вращении по сфере Блоха обу-

пульса с «прямоугольной» огибающей:

словлен функцией M_z (см. оценку согласно (54)).

Обсудим кратко вопрос о точности аппроксима-

ции при разложении по Магнусу. Приближенное вы-

M_x(t) = -

2ε_m

ражение для оператора эволюции обозначим как

{

sin(ε_mt),

t<τ,

U_M : ψ_M(t) = U_M (t)ψ(0). В качестве критерия бли-

(52)

зости в квантовой теории информации принято вы-

sin(ε_mτ) + (t - τ)ε_m cos(ε_mτ), t > τ,

брать меру близости (fidelity) F (t), определяемую

как



M_y(t) = -



2ε_m

F (t) =

〈ψ(0)|U^†

(t)U(t)|ψ(0)〉

².

(55)

{

1 - cos(ε_mt),

t<τ,

При F (t) = 1 мы имеем точную аппроксимацию для

(53)

1- cos(ε_mτ)+(t-τ)ε_m sin(ε_mτ), t > τ,

оператора эволюции.

Будем вычислять величины согласно изложен-

ной выше схеме по формулам

M_z ≈

(54)

4ε²

P (t) = |〈ψ₁|ψ(t)〉|² , P_M (t) = |〈ψ₁|ψ_M (t)〉|² .

Как видно, в данной ситуации разложение Магну-

Рисунок 5а демонстрирует поведение населенности

са проводится по параметру Δ/ε_m. Однако вероят-

основного состояния кубита при различных значе-

ность перехода зависит от двух интегралов:

ниях туннельных констант Δ. Как видно, прибли-

женное представление оператора эволюции согласно

∫t

∫

Магнусу (пунктирные линии) и прямое численное

M_x+iM_y =

dt₁e-iβ(t1), β(t) =

dt₁ε(t₁).

решение уравнения Шредингера (сплошные линии)

хорошо согласуются друг с другом при выбран-

ных параметрах. Из результатов, представленных

Это означает, что при рассматриваемом способе воз-

на рис. 5, видно, что наибольшая сходимость до-

буждения вероятность перехода не сводится лишь к

стигается при выполнении условия Δτ

≪ 1, что

фурье-преобразованию управляющей функции им-

пульса.

обеспечивает сходимость ряда в разложении Маг-

нуса [23]. При этом расхождение аналитических и

Проиллюстрируем полученные выводы путем

расчета по развитой методике и прямым численным

численных результатов расчетов составляет прибли-

267

М. В. Денисенко, Н. В. Кленов, А. М. Сатанин

ЖЭТФ, том 155, вып. 2, 2019

зительно 1.2 % для Δτ ≈ 0.1 (см. оранжевую кри-

P, P_M

1.0

вую на рис. 5б). Заметим, что увеличение туннель-

1.000

ной константы кубита Δ ведет к увеличению сте-

пени несовпадения населенностей (см. рис. 5б). Как

следует из описанной выше теории, для улучшения

0.8

0.999

сходимости необходимо рассматривать большее чис-

ло слагаемых в разложении матрицы Магнуса (13),

что всегда можно сделать при проведении числен-

0.998

ных расчетов.

0.6

0.997

5. ПЕРЕХОДЫ В СИСТЕМЕ СВЯЗАННЫХ

КУБИТОВ ПОД ДЕЙСТВИЕМ

t, пс

УНИПОЛЯРНЫХ ИМПУЛЬСОВ

Рис.

5. (В цвете онлайн) a) Динамика населеннос-

тей основного состояния кубита, полученных в резуль-

В данном разделе развитая выше техника расче-

тате численного моделирования (непрерывная кривая

та применяется для анализа вероятностей переклю-

P(t)) и аналитического решения (точки PM (t)) при

чения как двух симметричных кубитов, так и двух

Δ = 0.05 ГГц. б) Поведение «точности» F(t) для различ-

кубитов с произвольным соотношением параметров.

ных значений туннельных констант (красная кривая 1) —

Δ = 0.0025 ГГц, черная 2 — Δ = 0.01 ГГц, синяя 3 —

Δ = 0.05 ГГц, зеленая 4 — Δ = 0.075 ГГц, оранжевая

5.1. Возбуждение населенностей связанных

5 — Δ = 0.1 ГГц). Использованы следующие параметры

кубитов в симметричной (параллельной)

гауссова импульса: τ = 1 пс, t0 = 3 пс, εm = 0.65 ГГц

конфигурации

Начнем рассмотрение с анализа вероятностей

на (10), который после унитарного поворота H(t) =

возбуждения уровней двух симметричных кубитов.

= S^†H^ST(t)S - iS^†∂S/∂t с матрицей

Мы стартуем с зависящего от времени гамильтониа-

⎛

⎞

eiφ1(t)/2

⎜

⎟

S(t) =

⎝

eiφ2(t)/2

⎠,

(56)

M ,M ,M_xyz

P, P_M

1.0

e-iφ3(t)/2

φ₁(t) = χ(t) +

J t, φ₂(t) = -

J t,

–0.5

∫

0.5

φ₃(t) = χ(t) +

J t, χ(t) = ε(t^′) dt^′,

-1.0

приобретает вид

⎛

⎞

e-iα(t)

-1.5

⎜

⎟

H(t) = -√

⎝ eiα(t)

e-iβ(t)

⎠,

(57)

t, пс

eiβ(t)

Рис. 4. (В цвете онлайн) а) Динамика элементов матрицы

где α(t) = χ(t) + Jt, β(t) = χ(t) - Jt.

вращения, где Mx представляет красная кривая 1, My —

В этом приближении

черная штриховая кривая 2, Mz — синяя штрихпунктирная

⎛

⎞

кривая 3. б) Временная эволюция населенности основного

M₁ - iM₂

⎜

⎟

состояния кубита с туннельной энергией Δ = 0.05 ГГц, где

M =

⎝ M1 + iM₂

M₆ - iM₇

⎠, (58)

красная кривая — результат решения уравнения Шредин-

M₆ + iM₇

гера P (t), черные точки — аналитическое решение PM (t)

по Магнусу (39). Параметры управляющего прямоуголь-

где

ного импульса: τ = toff - tin = 2.4 пс (tin = 1 пс и

∫^t

t_off = 3.4 пс), εm = 0.3 ГГц

M₁ + iM₂ = -Δ eiα(t′)dt^′,

268

ЖЭТФ, том 155, вып. 2, 2019

Динамика кубитов в поле униполярных импульсов. . .

∫t

P, P_M

M₆ + iM₇ = -Δ eiβ(t′)dt^′.

1.0

1.000

0.8

0.998

Матрица M имеет следующие собственные зна-

чения: 0, -μ, μ, где

0.996

0.6

√

0.994

μ= M²¹ +M²² +M²⁶ +M²⁷.

0.4

0.992

Коэффициенты разложения в выражении (25) име-

ют вид

0.2

0.990

sinμ

cosμ - 1

0.988

u₀ = 1, u₁ = -i

u₂ =

μ²

t, пс

Таким образом, с учетом полученных собствен-

ных значений пропагатор для симметричной конфи-

Рис. 6. (В цвете онлайн) a) Временная динамика на-

гурации кубитов согласно (25) определяется выра-

селенностей двух связанных идентичных кубитов (Δ =

жением

= Δ1 = Δ2, J = 0.01 ГГц), где непрерывные кривые P (t)

представляют результаты численного моделирования, а

sinμ

cosμ - 1

U (t) = I - i

M (t) +

M²(t).

(59)

точками показаны аналитические решения PM (t). Здесь

μ²

основному состоянию соответствуют красные кривые 1,

промежуточному состоянию — черные кривые 2, возбуж-

Вероятность перехода между состояниями в этом

денному состоянию — синие кривые 3. б) Поведение «точ-

случае |T_j〉, индуцируемого униполярным воздей-

ности» F (t) для различных значений туннельных констант

ствием, вычисляется согласно выражению

(красная кривая 1) соответствует Δ = 0.0025 ГГц, черная



2 — Δ = 0.01 ГГц, синяя 3 — Δ = 0.05 ГГц, зеленая 4 —



sinμ(t)



P_k→j(t) =

k,j - i

〈T_j |M(t)|T_k〉 +

Δ = 0.075 ГГц, оранжевая 5 — Δ = 0.1 ГГц). Использова-

δ

μ(t)

ны следующие параметры импульса: τ = 3 пс, t0 = 1 пс,



cosμ(t) - 1



εm = 0.65 ГГц

〈T_j|M²(t)|T_k〉^

(60)

μ²(t)

На рис. 6 представлены результаты численно-

го решения уравнения Шредингера и аналитичес-

ухода состояний кубита на удаленный уровень под

ких расчетов (выполненных согласно (60)) времен-

влиянием униполярных импульсов, т. е. «распад»

ной динамики населенностей уровней двух иден-

состояния из-за ухода из подпространства состоя-

тичных кубитов. Из рис. 6а следует, что поведение

ний кубита. Рассмотрим наиболее интересную ситу-

рассчитанных различными методами населенностей

ацию, когда характерная амплитуда сигнала больше

хорошо согласуется. Кроме того, проведена оценка

или сравнима с расстоянием между уровнями куби-

«точности» сходимости численного моделирования

та (ε ∼ Δ), которая в то же время слабо связыва-

и теоретических расчетов по Магнусу. По анало-

ет состояния кубита с удаленным уровнем α ≪ 1.

гии со случаем одного кубита была рассчитана мера

Чтобы выделить главный вклад при указанных па-

близости (fidelity) F (t), определяемая по формуле

раметрах, совершим унитарный поворот гамильто-

(55). Показано, что чем лучше выполнено неравен-

ниана (11) с матрицей

ство Δτ ≪ 1, тем выше точность, что определяет-

ся сделанным предположением в теории по аппрок-

⎛

⎞

симации оператора эволюции (число удерживаемых

слагаемых в разложении (17)). Отметим, что для

⎜

⎟

⎜

⎟

представленных расчетов при Δτ ≈ 0.3 (оранжевая

⎜

⎟

⎜

⎟

√

кривая на рис. 6) ошибка расчетов составляет 1.2 %.

U_m =

⎜

⎟

(61)

⎜

⎟

⎜

⎟

⎜

⎟

⎝

⎠

5.2. Вероятность ухода на удаленный

√

-√

уровень

Обратимся теперь к анализу гамильтониана (11),

В результате гамильтониан (11) преобразуется к ви-

который призван продемонстрировать вероятность

ду

269

М. В. Денисенко, Н. В. Кленов, А. М. Сатанин

ЖЭТФ, том 155, вып. 2, 2019

⎛

⎞

αε(t)

S_m(t) =

√

⎜

⎟

⎛

⎞

⎜

⎟

e^-iAt

⎜

αε(t)

⎟

H_m =

⎜

√

ε(t)

⎟

(62)

⎜

⎟

⎜

⎟

⎝

ei(At+χ(t))/2

⎠,

(63)

⎜

⎟

⎝

⎠

αε(t)

ei(At-χ(t))/2

√

-ε(t)

где

∫

χ(t) = ε(t^′) dt^′,

Следующий шаг — выделить диагональный вклад,

что достигается последующим поворотом с матри-

цей

а гамильтониан приобретает вид

⎛

⎞

i(3At-χ(t))/2

√

ε(t)ei(3At+χ(t))/2

√ ε(t)e

⎜

⎟

⎜

⎟

⎜

√ ε(t)e-i(3At+χ(t))/2

Δe-iχ(t)

H(t) =

^⎟.

(64)

⎜

⎟

⎝

⎠

√ ε(t)e-i(3At-χ(t))/2

Δeiχ(t)

∫

Следовательно, матрица Магнуса в этом приближе-

нии равна

M₆ + iM₇ =

eiχ(t′)dt^′.

⎛

⎞

M₁ - iM₂

M₄ - iM₅

⎜

⎟

При произвольных параметрах системы дальней-

M =

⎝ M1 + iM₂

M₆ - iM₇

⎠, (65)

ший анализ (65) возможен только с использовани-

M₄ + iM₅

M₆ + iM₇

ем численных методов. Упрощение можно получить,

где

если параметр связи кубита с верхним уровнем α

мал (α ≪ 1). Это означает, что элементы матрицы

∫

Магнуса M₁, M₂, M₄ и M₅ малы по сравнению с M₆

M₁ + iM₂ =

√

ε(t^′)e-i(3At′-χ(t′))/2,

и M₇.

Разложим пропагатор по малому параметру.

∫

Действуя в рамках теории возмущений, гамильто-

M₄ + iM₅ =

√

ε(t^′)e-i(3At′-χ(t′))/2dt^′,

ниан (14) представим в виде H(t) = H₀(t) + V (t),

где

⎛

⎞

⎜

⎟

H₀(t) =

⎝ 0

Δe-iχ(t)

⎠,

Δeiχ(t)

(66)

⎛

⎞

ei(3At+χ(t))/2 ei(3At-χ(t))/2

αε(t)

⎜

⎟

V (t) =

√

⎝ e-i(3At+χ(t))/2

⎠.

e-i(3At-χ(t))/2

(

)

∫

Пропагатор ищем в виде U(t) = U₀(t)

I + S⁽¹⁾(t)

где U₀(t) определяется зависящим от времени га-

S⁽¹⁾(t) = -i dt^′U-10(t^′)V (t^′)U₀(t^′).

(67)

мильтонианом

∂U₀(t)

iℏ

= H₀(t)U₀(t).

Таким образом, пропагатор U₀(t) можно найти со-

∂t

гласно (21), а поправку рассчитать по формуле (67).

Пусть кубит первоначально находился в основном

Из уравнения (1) получаем

состоянии с волновой функцией 〈ψ_-| = (1 0 0); нас

270

ЖЭТФ, том 155, вып. 2, 2019

Динамика кубитов в поле униполярных импульсов. . .

интересует вероятность ухода на удаленный уровень

счет осциллирующего множителя, пропорциональ-

〈ψ_u| = (0 0 1). Расчет по указанной схеме приводит

ного ei3At′/². Эти соображения дают основания рас-

к выражению

считывать на практическую реализацию быстрых

переходов между базисными состояниями кубитов



под действием коротких импульсов с заведомо ши-

∫



роким спектром.

p_u(t) =



dt^′ε(t^′)ei3At′/² ×



(

5.3. Динамика населенности состояний

× -ieiχ(t′)/2 sinμ(t′)

m^-(t^′) +

связанных кубитов под действием

μ(t^′)

2

униполярных импульсов в общем случае

(

))



Как известно, параметры туннельного расщепле-

+ e-iχ(t′)/2 cosμ(t^′)-isinμ(t′)

m^-(t^′)

(68)



μ(t^′)



ния связанных кубитов численно малы [1], поэтому

при проведении аналитических расчетов мы остано-

где

вимся на анализе ситуации, когда выполнены соот-

ношения Δ₁ ∼ Δ₂ ≪ ε₁ ∼ ε₂. В этом случае вклад

∫

от амплитуды сигнала будет учтен точно путем со-

m^-(t) =

dt₁eiχ(t1).

(69)

ответствующего унитарного поворота, а слагаемые,

зависящие от туннельных констант, можно учесть

Как и следовало ожидать, вероятность перехода на

по теории возмущений.

удаленный уровень квадратично зависит от малого

Начнем рассмотрение с выражения (8). Основ-

параметра α. Анализ (68) показывает, что если энер-

ной вклад обусловлен слагаемыми на главной диа-

гия удаленного уровня велика (A ≫ Δ), то инте-

гонали. Совершая унитарное преобразование, выде-

грал в (68) будет дополнительно сильно подавлен за

ляющее главный вклад, приходим к выражению

⎛

⎞

Δ₂e-i(Jt+χ2(t)) Δ₁e-i(Jt+χ1(t))

⎜

⎟

⎜

Δ₂ei(Jt+χ2(t))

Δ₁ei(Jt-χ1(t))

⎟

H =-

⎜

^⎟,

(70)

⎜

⎟

Δ₂ei(Jt-χ2(t))

⎝ Δ1ei(Jt+χ1(t))

⎠

Δ₁e-i(Jt-χ1(t)) Δ₂e-i(Jt-χ2(t))

где

∫^t

χ_j(t) = ε_j(t^′)dt^′ (j = 1, 2).

Ограничимся первым приближением по туннельным константам при составлении матрицы M(t). Тогда

согласно (27), получаем

⎛

⎞

M₁ - iM₂

M₄ - iM₅

⎜

⎟

⎜

M₁ + iM₂

M₁₁ - iM₁₂

⎟

M =^⎜

^⎟,

(71)

⎜

⎟

⎝ M4 + iM5

M₁₃ - iM₁₄

⎠

M₁₁ + iM₁₂ M₁₃ + iM₁₄

∫

где

M₁₁ + iM₁₂ = -

e^-i(Jt′-χ1(t′)⁾dt^′,

∫

Δ₂

∫

M₁ + iM₂ = -

eⁱ(Jt′+χ2(t′)⁾dt^′,

Δ₂

M₁₃ + iM₁₄ = -

e^-i(Jt′-χ2(t′)⁾dt^′.

∫

Пропагатор кубитов будет определяться выражени-

Δ₁

M₄ + iM₅ = -

eⁱ(Jt′+χ1(t′)⁾dt^′,

ем (21), а коэффициенты u_j (j = 0, 1, 2, 3) — вычис-

ляться согласно формулам Приложения В.

271

М. В. Денисенко, Н. В. Кленов, А. М. Сатанин

ЖЭТФ, том 155, вып. 2, 2019

Чтобы получить наглядное выражение для

P, P_M

1.0

пропагатора, рассмотрим специальный случай,

когда параметры управляющих импульсов и ку-

1.000

битов удовлетворяют дополнительным условиям:

0.8

ε(t) = ε₁(t) = ε₂(t), а Δ₁ = Δ, Δ₂ = Δ + δ, δ ≪ 1.

0.6

0.999

Введем обозначение K² = M²¹ + M²² + M²¹¹ + M²¹².

В этом приближении имеем соотношения M₄ = M₁,

0.4

M₅ = M₂, M₁₃ = M₁₁, M₁₄

= M₁₂. Тогда из

0.998

(70) найдем приближенные собственные значения

0.2

матрицы M (с точностью порядка δ):

0.997

√

(M²¹ + M²²)(M²¹¹ + M²¹²)

μ₁ = -

μ₂ = -μ₁,

t, пс

(

)

√

μ₃ = -

μ₄ = -μ₃.

Рис. 7. a) Временная динамика населенностей двух связан-

ных кубитов, где непрерывные кривые P (t) получены пу-

Выражения из Приложения В позволяют записать

тем численного моделирования, а точки — аналитические



√

решения PM (t). Здесь населенность основного состояния



eⁱ

(i = 1) — красные кривые 1, населенность второго уровня

P_k→j(t) =

δk,j-i〈ej|M(t)|ek〉+

〈e_j |M²(t) +



2K²

(i = 2) — черные кривые 2, третьего уровня (i = 3) —

синие кривые 3 и наивысшего уровня (i = 4) — зеле-

2



ные кривые 4. б) Поведение «точности» F (t) для различ-

〈e_j |M³(t)|e_k〉^

(72)

2K²

ных значений туннельных констант (красная кривая 1 —

= 0.01 ГГц, синяя 3 —

Δ1 = 0.0025 ГГц, черная 2 — Δ1

Таким образом, полученное выражение для пропа-

Δ1 = 0.05 ГГц, зеленая 4 — Δ1 = 0.075 ГГц, оранжевая

гатора позволяет вычислить любые вероятности пе-

5 — Δ1 = 0.1 ГГц). Параметры импульсов ε1(t) = ε2(t) и

реходов между состояниями двух произвольных ку-

кубитов Δ2 = Δ1 + δ: τ = 1 пс, t0 = 5 пс, εm = 0.5 ГГц,

битов.

δ = 0.01 ГГц, J = 0.01 ГГц

В случае двух заметно различающихся по па-

раметрам кубитов проведем анализ временной ди-

намики под действием управляющих униполярных

одиночных униполярных импульсов магнитного по-

импульсов. На рис. 7 приведено сравнение расчетов

ля с заведомо широким спектром. Результаты по-

численного моделирования и аналитических выра-

казали эффективность использования развитой ме-

жений, полученных на основе разложения Магнуса.

тодики на основе разложения Магнуса для анали-

Для иллюстрации предполагалось, что на каждый

за процедур управления кубитными системами ко-

из кубитов одновременно воздействует гауссов сиг-

роткими униполярными импульсами. В частности,

нал одинаковой амплитуды (см. рис. 2б). Из рис. 7

техника расчета хорошо описывает динамику ку-

видно, что после воздействия импульса населенно-

битов при управлении флаксонами в цепях быст-

сти кубитов быстро стабилизируются, а максималь-

рой одноквантовой логики. Важно подчеркнуть, что

ное расхождение результатов теории и численного

при определенных условиях на амплитуду и дли-

расчета (fidelity) F (t) при Δ₁τ ≈ 0.1 (см. оранже-

тельность сильного и ультракороткого воздействия

вую кривую на рис. 7) составляет приблизительно

(разд. 5.2) возможны селективные переходы в мно-

3 %, что говорит о хорошей аппроксимации в рам-

гоуровневой системе. Дальнейшее развитие предло-

ках построенной выше теории и о возможности ее

женной концепции возможно при переходе к управ-

расширения на регистр из N связанных кубитов.

лению посредством цепей сверхпроводниковой адиа-

Отметим, что точность может быть дополнительно

батической логики с ультрамалой диссипацией энер-

повышена путем учета следующих слагаемых в раз-

гии [35-38].

ложении Магнуса.

В перспективе такая методика позволит до-

биться эффективного управления состояниями как

отдельных кубитов, так и квантовых регистров на

6. ЗАКЛЮЧЕНИЕ

пикосекундных временах. Предложенный подход

В работе представлен новый подход для опи-

существенно ускоряет численные расчеты управля-

сания эволюции состояний кубитов под действием

ющих цепей для многокубитных систем, поскольку

272

ЖЭТФ, том 155, вып. 2, 2019

Динамика кубитов в поле униполярных импульсов. . .

1√

метод Магнуса основан на использовании интерпо-

E⁽²⁾⁴ =

J² + (Δ₁ + Δ₂)²,

ляционных процедур и не привязан к выбору шага

〈e₄| = N₄(-k₄, -(Δ₁ + Δ)₂, -(Δ₁ + Δ₂), k₄),

в дискретных схемах. Заметим, что данная техника

√

(A.1)

работает за рамками теории возмущений, когда на

k₄ = -J +

J² + (Δ₁ + Δ₂)²,

(√

)-1

систему действуют сигналы большой амплитуды

для получения заметных населенностей уровней.

N₄ =

2 (k²⁴ + (Δ₁ + Δ₂)²)

Важным преимуществом предлагаемого метода

Для двух одинаковых кубитов Δ = Δ₁ = Δ₂

является также то, что после действия импульса

(симметричных), возбуждаемых одинаковыми им-

пропагатор практически не меняется. Поэтому в

пульсами ε = ε₁ = ε₂, можно совершить унитарный

рамках данного подхода возможна дальнейшая

поворот c матрицей

оптимизация параметров управляющих импульсов

⎛

⎞

для инициализации заданных состояний и реализа-

ции различных алгоритмов.

⎜

⎟

⎜

⎟

√

-√

⎜

⎟

⎜

⎟

U^ST =

⎜

⎟,

(A.2)

Работа выполнена при финансовой поддерж-

⎜

⎟

⎜

√

⎟

ке РНФ (грант

№18-72-00158), РФФИ (гран-

⎝

⎠

ты

№№ 17-12-01079,

16-57-51045,

16-29-09515,

18-07-01206) и в рамках выполнения проектной

разложив тем самым гамильтониан на неприводи-

части госзадания Министерства образования и

мые представления:

науки РФ № 3.3026.2017/ПЧ (разд. 2.1).

(U^ST )-1HU^ST = -

⎛

√

⎞

ПРИЛОЖЕНИЕ А

2ε(t) + J

2Δ

⎜

√

⎟

⎜

2Δ

-J

2Δ

⎟

Собственные значения и собственные функции

⎜

√

^⎟. (A.3)

⎜

⎟

оператора Гамильтона для двух связанных кубитов

⎝

2Δ

-2ε(t) + J

⎠

без учета внешнего воздействия (ε1,2 → 0) находятся

-J

из стационарного уравнения Шредингера с гамиль-

тонианом (8):

В этом случае волновая функция синглетного со-

стояния может рассматриваться независимо, а для

√

изучения динамики можно ограничиться матрицей

E⁽²⁾¹ = -¹

J² + (Δ₁ + Δ₂)²,

меньшей размерности

〈e₁| = N₁(k₁, Δ₁ + Δ₂, Δ₁ + Δ₂, k₁),

√

H^ST (t) = -

k₁ = J +

J² + (Δ₁ + Δ₂)²,

⎛

√

⎞

(√

)-1

2ε(t) + J

2Δ

√

⎜

⎟

N₁ =

2 (k²¹ + (Δ₁ + Δ₂)²)

⎝

2Δ

-J

2Δ

⎠. (A.4)

√

2Δ

-2ε(t) + J

√

E⁽²⁾² = -¹

J² + (Δ₁ - Δ₂)²,

Удобно выделить из H^ST

диагональную матрицу,

〈e₂| = N₂(-k₂, Δ₁ - Δ₂, -Δ₁ + Δ₂, k₂),

которая изменяет только общую фазу компонентов

√

волновой функции и бесследную матрицу H^T (t),

k₂ = J +

J² + (Δ₁ - Δ₂)²,

определяющую нетривиальную динамику триплет-

(

)-1

√

ного состояния:

N₂ =

Jk₂ + (Δ₁ - Δ₂)²

√

HT (t) = -

E⁽²⁾³ =

J² + (Δ₁ - Δ₂)²,

⎛

⎞

√

2ε(t) +

2Δ

⎜

⎟

〈e₃| = N₃(-k₃, -Δ₁ + Δ₂, Δ₁ - Δ₂, k₃),

⎜

√

⎟

⎜

√

2Δ

^⎟. (A.5)

⎜

⎟

k₃ = -J +

J² + (Δ₁ - Δ₂)²,

⎝

⎠

√

(√

)-1

2Δ

-2ε(t) +

N₃ =

2 (-Jk₃ + (Δ₁ - Δ₂)²)

273

ЖЭТФ, вып. 2

М. В. Денисенко, Н. В. Кленов, А. М. Сатанин

ЖЭТФ, том 155, вып. 2, 2019

Нетрудно видеть, что при ε(t) = 0 трем собственным

Как видно, состояние |T₂〉, соответствующее уров-

значениям гамильтониана (10)

ню ET2 , является симметричным белловским (пере-

путанным) состоянием.

√(

)₂

ET1 = -

ET2 =

+Δ²,

ПРИЛОЖЕНИЕ B

√(

)₂

Для дальнейших приложений полезно получить

ET3 =

+Δ²

в явном виде выражения для коэффициентов раз-

ложения пропагатора по степеням матрицы M(t)

соответствуют три функции, которые можно обо-

трехуровневой (группа SU(3)) и четырехуровневой

значить как

(группа SU(4)) систем.

(√

В случае группы SU(3) коэффициенты разложе-

〈T₁| = NT1 (-1, 0, 1), NT1 =

)-1 ,

ния пропагатора U(t) связанных кубитов по степе-

(_√

√

)

〈T₂| = NT2

2 Δ, -J +

J² + 4Δ²,

2Δ ,

ням матрицы M(t) определяются системой линей-

(

ных уравнений:

(

√

)₂)-1

NT2 =

4Δ² +

-J +

J² + 4Δ²

⎛

⎞⎛

⎞

⎛

⎞

μ₁

μ²¹

u₀

e^-iμ

(A.6)

⎜

⎟⎜

⎟

⎜

⎟

〈T₃| = NT3 ×

⎝ 1

μ₂

μ²²

⎠⎝ u1

⎠=

⎝ e-iμ2

⎠, (B.1)

(_√

(

√

)

√

)

μ₃

μ²

u₂

e-iμ3

2 Δ, - J +

J² + 4Δ²

2Δ ,

(

√

)₂)-1

где μ₁ +μ₂ +μ₃ = 0. Обращая матрицу Вандермонда,

NT3 =

4Δ² + J +

J² + 4Δ²

приходим к выражению:

(

)

u₀ =

μ₂(μ₁ + μ₂)(μ₁ + 2μ₂)e-iμ1 - μ₁(μ₁ + μ₂)(2μ₁ + μ₂)e-iμ2 - μ₁μ₂(μ₁ - μ₂

)ei(μ1+μ2)

V₃

)

1 (

u₁ =

-μ₁(μ₁ + 2μ₂)e-iμ1 + μ₂(2μ₁ + μ₂)e-iμ2 + (μ²¹ - μ²²

)ei(μ1 +μ2)

V₃

(B.2)

)

1 (

u₂ =

-(μ₁ + 2μ₂)e-iμ1 + (2μ₁ + μ₂)e-iμ2 - (μ₁ - μ₂

)ei(μ1+μ2)

V₃

V₃ = (μ₂ - μ₁)(2μ₁ + μ₂)(2μ₂ + μ₁).

В случае группы SU(4) коэффициенты разложения пропагатора U(t) кубитов по степеням матрицы M(t)

определяются системой линейных уравнений:

⎛

⎞⎛

⎞

⎛

⎞

μ₁

μ²¹

μ³¹

u₀

e-iμ1

⎜

⎟⎜

⎟

⎜

⎟

⎜

⎟⎜

⎟

⎜

−iμ2

⎟

μ₂

μ²²

μ³²

u₁

⎜

⎟⎜

⎟

⎜ e

^⎟.

(B.3)

⎜

⎟⎜

⎟

⎜

⎟

⎝ 1

μ₃

μ²³

μ³³

⎠⎝ u2

⎠

⎝ e-iμ3

⎠

-μ₁ - μ₂ - μ₃ μ₁ + μ₂ + μ₃

-(μ₁ + μ₂ + μ₃)³

u₃

ei(μ1+μ2+μ3)

В данном случае детерминант матрицы Вандермонда равен

V₄ = (μ₁ - μ₂)(μ₁ - μ₃)(μ₂ - μ₃)(2μ₁ + μ₂ + μ₃)(μ₁ + μ₂ + μ₃)(μ₁ + μ₂ + 2μ₃).

(B.4)

Вычисляя обратную матрицу, решение (B.3) запишем в виде

(

)

u₀ =

ν₀₁ei(μ1+μ2+μ3) + ν₀₂eiμ3 + ν₀₃e-iμ2 + ν₀₄e-iμ1

(B.5)

V₄

)

1 (

u₁ =

ν₁₁e-iμ1 + ν₁₂ei(μ1+μ2+μ3) + ν₁₃ei(μ1+μ2+μ3) + ν₁₄eiμ1

(B.6)

V₄

)

1 (

u₂ =

ν₂₁e-iμ2 + ν₂₂e-iμ1 + ν₂₃ei(μ1+μ2+μ3) + ν₂₄

e-i(μ1+μ2-μ3)

(B.7)

V₄

)

1 (

u₃ =

ν₃₁ei(μ1+μ2-μ3) + ν₃₂eiμ3 + ν₃₃e-iμ2 + ν₃₄e-iμ1

(B.8)

V₄

274

ЖЭТФ, том 155, вып. 2, 2019

Динамика кубитов в поле униполярных импульсов. . .

где коэффициенты определены соотношениями

ν₀₁ = μ₁μ₂μ₃(μ₁ - μ₂)(μ₁ - μ₃)(μ₂ - μ₃),

ν₀₂ = μ₁μ₂(-μ₁ + μ₂)(μ₁ + μ₂ + μ₃)(2μ₁ + μ₂ + μ₃)(μ₁ + 2μ₂ + μ₃),

(B.9)

ν₀₃ = μ₁μ₂(-μ₁ + μ₂)(μ₁ + μ₂ + μ₃)(2μ₁ + μ₂ + μ₃)(μ₁ + μ₂ + 2μ₃),

ν₀₄ = μ₂μ₃(μ₁ - μ₃)(μ₁ + μ₂ + μ₃)(μ₁ + 2μ₂ + μ₃)(μ₁ + μ₂ + 2μ₃),

(

)

ν₁₁ = (-μ₂ - μ₃)(μ₁ + 2μ₂ + μ₃)(μ₁ + μ₂ + 2μ₃)

(μ₁ + μ₂)(μ₂ + μ₃) + μ²³

ν₁₂ = (μ₂ - μ₃)(μ₁ - μ₃)(μ₂ - μ₃)(μ₂μ₃ + μ₁(μ₂ - μ₃)),

(

)

(B.10)

ν₁₃ = (-μ₂ + μ₃)(2μ₁ + μ₂ + μ₃)(μ₁ + 2μ₂ + μ₃)

μ²¹ + (μ₁ + μ₂)(μ₂ + μ₃)

(

)

ν₁₄ = (μ₁ - μ₃)(2μ₁ + μ₂ + μ₃)(μ₁ + μ₂ + 2μ₃)

μ²¹ + (μ₁ + μ₃)(μ₂ + μ₃)

ν₂₁ = μ₂(-μ₂ + μ₃)(μ₁ + μ₂ + 2μ₃)(2μ₁ + μ₂ + μ₃),

ν₂₂ = μ₁(μ₂ - μ₃)(μ₁ + 2μ₂ + μ₃),

(B.11)

ν₂₃ = (μ₂ - μ₃)(μ₁ - μ₃)(μ₁ - μ₃)(μ₁ + μ₂ + μ₃),

ν₂₄ = μ₃(2μ₁ + μ₂ + μ₃)(μ₁ + 2μ₂ + μ₃),

ν₃₁ = (μ₁ - μ₂)(μ₁ - μ₃)(μ₂ - μ₃),

ν₃₂ = (μ₁ - μ₃)(μ₂ - μ₃)(μ₂μ₃ + μ₁(μ₂ - μ₃)) ,

(B.12)

ν₃₃ = (-μ₂ + μ₃)(2μ₁ + μ₂ + μ₃)(μ₁ + 2μ₂ + μ₃),

ν₃₄ = (μ₂ - μ₃)(2μ₁ + μ₂ + μ₃)(μ₁ + μ₂ + 2μ₃).

ЛИТЕРАТУРА

12.

P. J. Liebermann and F. K. Wilhelm, Phys. Rev.

Appl. 6, 024022 (2016).

Y. Makhlin, G. Schön, and A. Schnirman, Rev. Mod.

13.

N. V. Klenov, A. V. Kuznetsov, I. I. Soloviev et al.,

Phys. 73, 357 (2001).

Low Temp. Phys. 43, 789 (2017).

J. Q. You and F. Nori, Phys. Today 58(11), 42 (2005).

14.

I. I. Rabi, Phys. Rev. 29, 174 (1927).

J. Clarke and F. K. Wilhelm, Nature 453, 1031

15.

Л. Аллен, Дж. Эберли, Оптические резонансы и

(2008).

двухуровневые атомы, Мир, Москва (1978).

M. H. Devoret and R. J. Schoelkopf, Science 339,

16.

Ya. B. Zeldovich, Zh. Eksp. Teor. Fiz. 51, 1492 (1966)

1169 (2013).

[Sov. Phys. JETP 24, 1006 (1967)].

F. Yan, S. Gustavsson, A. Kamal et al., Nature Com-

17.

V. I. Ritus, Zh. Eksp. Teor. Fiz. 51, 1544 (1966) [Sov.

mun. 7, 12964 (2016).

Phys. JETP 24, 1041 (1967)].

18.

M. Grifoni and P. H. Hanngi, Phys. Rep. 304, 219

D. V. Averin, K. Rabenstein, and V. K. Semenov,

(1998).

Phys. Rev. B 73, 094504 (2006).

19.

A. M. Satanin, M. V. Denisenko, S. Ashhab, and

A. Fedorov, A. Shnirman, G. Schoen, and A. Kidiya-

F. Nori, Phys. Rev. B 85, 184524 (2012).

rova-Shevchenko, Phys. Rev. B 75, 224504 (2007).

20.

A. V. Ustinov, M. Cirillo, and B. A. Malomed, Phys.

I. I. Soloviev, N. V. Klenov, A. L. Pankratov et al.,

Rev. B 47, 8357(R) (1993).

Phys. Rev. E 87, 060901(R) (2013).

21.

O. A. Mukhanov, V. K. Semenov, and K. K. Likha-

I. I. Soloviev, N. V. Klenov, S. V. Bakurskiy et al.,

rev, IEEE Trans. Magn. MAG 23, 759 (1987).

Appl. Phys. Lett. 105, 202602 (2014).

22.

I. I. Soloviev, N. V. Klenov, S. V. Bakurskiy et al.,

Beilstein J. Nanotechnol. 8, 2689 (2017).

10.

I. I. Soloviev, N. V. Klenov, A. L. Pankratov et al.,

Phys. Rev. B 92, 014516 (2015).

23.

W. Magnus, Comm. Pure Appl. Math. 7, 649 (1954).

11.

N. V. Klenov, A. V. Kuznetsov, I. I. Soloviev et al.,

24.

P. Pechukas and J. L. Light, J. Chem. Phys. 44, 3897

Beilstein J. Nanotechnol. 6, 1946 (2015).

(1966).

275

М. В. Денисенко, Н. В. Кленов, А. М. Сатанин

ЖЭТФ, том 155, вып. 2, 2019

25. P. A. Rodgers and S. Swain, Phys. B: Atom. Mol.

32. А. Барут, Р. Рончка, Теория представления групп

Phys. 20, 617 (1987).

и ее приложения, т. 1, Мир, Москва (1980).

26. A. Alvermann and H. Fehske, J. Comput. Phys. 230,

33. М. Абрамовиц, И. Стиган, Справочник по спе-

5930 (2011).

циальным функциям, с формулами, графиками

и математическими таблицами, Наука, Москва

27. T. V. Laptyeva, E. A. Kozinov, I. B. Meyerov,

(1979).

M. V. Ivanchenko, S. Denisov, and P. Hänggi,

34. T. Tilma, M. Byrd, and E. C. G. Sudarshan, J. Phys.

Comput. Phys. Commun. 201, 85 (2016).

A: Math. Gen. 35, 10445 (2002).

28. M. V. Denisenko, N. V. Klenov, and A. M. Satanin,

35. N. Takeuchi, D. Ozawa, Y. Yamanashi, and N. Yoshi-

J. Phys.: Conf. Ser. 955, 012004 (2018).

kawa, Supercond. Sci. Technol. 26, 035010 (2013).

29. Ф. Р. Гантмахер, Теория матриц, Наука, Москва

36. A. E. Schegolev, N. V. Klenov, I. I. Soloviev, and

(1966).

M. V. Tereshonok, Beilstein J. Nanotechnol. 7, 1397

(2016).

30. Нгуен Ван Хьеу, Лекции по теории унитарной

симметрии элементарных частиц, Атомиздат,

37. N. Takeuchi and N. Yoshikawa, Phys. Rev. E 97,

Москва (1967).

012124 (2018).

31. С. Адлер, Р. Дашен, Алгебры токов и их приме-

38. R. McDermott, M. G. Vavilov, B. L. T. Plourde et

нение в физике частиц, Мир, Москва (1970).

al., Quant. Sci. Technol. 3, 024004 (2018).

276