ЖЭТФ, 2019, том 155, вып. 3, стр. 387-395

РЕЛЯТИВИСТСКОЕ МОДЕЛИРОВАНИЕ РАСПРОСТРАНЕНИЯ

УЛЬТРАКОРОТКИХ ЭЛЕКТРОННЫХ ИМПУЛЬСОВ

И. В. Кочиков^a, Р. Дж. Дуэйн Миллерb,c*, А. А. Ищенкоd**

^a Московский государственный университет им. М. В. Ломоносова,

Научно-исследовательский вычислительный центр

119991, Москва, Россия

^b The Max Planck Institute for the Structure and Dynamics of Matter,

Hamburg Centre for Ultrafast Imaging

22761, Hamburg, Germany

^c Факультеты химии и физики Университета Торонто

M5S 3H6, Торонто, Канада

^d МИРЭА — Российский технологический университет

119571, Москва, Россия

Поступила в редакцию 29 июня 2018 г.,

после переработки 14 сентября 2018 г.

Принята к публикации 17 сентября 2018 г.

Рассматривается динамика электронного импульса в области дрейфа, где отсутствуют ускоряющие поля,

причем особое внимание уделяется оценке параметров, существенных для атомной визуализации, т. е.

для непосредственного наблюдения динамики атомов. Электронный пучок моделируется как система N

частиц с N = 1000 и N = 10000 электронов. Пучок распространяется в течение определенного периода

времени (от 1 до 4 нс). Вычисляются параметры распределения электронов по координатам и скоростям,

характеризующие временной профиль и неопределенность длины волны электронов в образце. Нереляти-

вистское приближение дает удовлетворительные результаты (с погрешностью ниже 15 %) при моделиро-

вании удлинения и уширения коротких электронных импульсов с энергиями до 30 кэВ. Результаты такого

моделирования могут быть весьма неточными для промежуточных энергий (300 кэВ), а для быстрых

релятивистских пучков (3 МэВ) они становятся совершенно неверными. Предлагается решение задачи,

позволяющее получить количественные оценки. Использование импульсов высоких энергий приводит к

почти полному исчезновению эффекта кулоновского отталкивания. Дисперсия скоростей электронов при

более высоких энергиях также значительно уменьшается. Для электронов с энергией 3 МэВ длительность

электронного импульса, а также его радиус заметно не меняются даже после распространения пучка в

течение 4 нс (что соответствует расстоянию 1.2 м). Даже при энергии 300 кэВ увеличение длительности

импульса пренебрежимо мало при времени пролета электронов до 1 нс (расстояние 0.2 м). Обобщена

упрощенная модель среднего поля [13] на релятивистские электронные импульсы. Ее результаты нахо-

дятся в хорошем соответствии с прямым динамическим моделированием.

DOI: 10.1134/S0044451019030015

ловедении (см. обзоры [1-4]). Методы сверхбыст-

рой электронной микроскопии, электронной ди-

1. ВВЕДЕНИЕ

фракции, электронной кристаллографии и нанокри-

Определение характеристик структурной дина-

сталлографии открыли возможность изучения ко-

мики вещества с высоким пространственно-времен-

герентной структурной динамики вещества. Клю-

ным разрешением открывает новое понимание вза-

чевым параметром экспериментальных установок

имосвязи элементов триады «структура-динамика-

сверхбыстрой электронной микроскопии и электро-

функция» в физике, химии, биологии и материа-

нографии является временное разрешение, введен-

ное в работах [5,6], которое определяется длитель-

^* R. J. Dwayne Miller

ностью электронных импульсов. Известно, что дли-

^** E-mail: aischenko@yasenevo.ru

387

И. В. Кочиков, Р. Дж. Дуэйн Миллер, А. А. Ищенко

ЖЭТФ, том 155, вып. 3, 2019

тельность фотоэлектронного импульса в непосред-

исследовать электронные пучки с энергиями 30, 300

ственной близости от фотокатода равна длительнос-

и 3000 кэВ, для которых релятивистские эффекты

ти импульса лазера накачки [7]. Однако из-за ку-

проявляются соответственно пренебрежимо слабо,

лоновского отталкивания и разброса скоростей фо-

значительно и сильно. Эти энергии соответствуют

тоэлектронов сверхкороткие электронные сгустки,

скоростям электронов 0.328c, 0.777c, 0.989c и зна-

движущиеся от фотокатода к образцу, размываются

чениям релятивистского фактора γ, равным 1.0587,

при приближении к исследуемому образцу. Понима-

1.587 и 6.87. Начальная дисперсия энергий электро-

ние динамики кулоновского отталкивания электро-

нов задавалась на уровне 0.6 эВ.

нов имеет решающее значение для проектирования

Электронный пучок моделировался известны-

технологий следующего поколения [7-11].

ми методами классической молекулярной динамики

Проблема уширения и удлинения ультракорот-

как система взаимодействующих частиц. Моделиру-

ких электронных импульсов вследствие кулоновско-

емая система состояла из N = 1000 и N = 10000

го отталкивания неоднократно рассматривалась в

электронов. Пучок распространялся в течение опре-

научной литературе (см. недавнюю обзорную работу

деленного периода времени (от 1 до 4 нс). Во время

[12]). До недавнего времени эффекты отталкивания

моделирования его распространения записывались

оценивались с помощью простых аналитических мо-

параметры распределения электронов по координа-

делей. Однако современные вычислительные сред-

там и скоростям. На заданном расстоянии, установ-

ства позволяют проводить прямое численное моде-

ленном в соответствии с выбранным временем рас-

лирование ансамбля электронов (во всяком случае

пространения, регистрировались времена прилета

до N = 10⁵ электронов), распространяющихся в об-

электронов, что позволило определять временную

ласти между ускоряющим блоком и образцом.

протяженность электронного сгустка. В то же время

определялось распределение электронов по энерги-

Влияние кулоновского отталкивания на распро-

ям в плоскости регистрирующей системы (детекто-

странение электронов было подробно рассмотрено в

ра), позволяющее вычислять неопределенность дли-

работе [13], в которой было получено эффективное

ны волны электрона в образце.

и точное решение задачи. Дальнейшие улучшения

Число электронов в этом исследовании было

для случаев более высоких плотностей заряда были

ограничено как общими соображениями, так и

предложены в работах [14-28]¹⁾.

вычислительными возможностями. Моделирование

Настоящая статья посвящена динамике распро-

движения системы из 10⁴ электронов потребовало

странения электронных импульсов в так называе-

1.3 с на один временной шаг на ПК с распараллели-

мой дрейфовой области, где на них не влияют внеш-

ванием вычислений. С некоторой корректировкой

ние поля. Эта задача подробно обсуждалась в рабо-

вычислительного алгоритма возможно и моде-

те [13], в которой, однако, не учитывались реляти-

лирование N

= 10⁵ электронов (при увеличении

вистские эффекты. Нерелятивистское приближение

числа электронов время моделирования возрастает

вполне оправдано для электронных пучков с энер-

как N²).

гией 30 кэВ, рассматриваемых в этой работе, од-

В настоящей работе при рассмотрении влия-

нако последующие исследования показали, что уже

ния пространственного заряда (кулоновских эффек-

при энергиях 200-300 кэВ релятивистские эффек-

тов) особое внимание уделяется параметрам, кото-

ты становятся сильнее, чем можно было бы ожи-

рые влияют на возможность непосредственного на-

дать, а для импульсов 1 МэВ и выше картина удли-

блюдения динамики атомов. Эта работа определя-

нения импульса совершенно изменяется [16, 27, 28].

ет фундаментальные пространственные и времен-

Для упрощения сравнения результатов с упомяну-

ные пределы, в которых возможна атомная визуа-

той работой [13] в дальнейшем будем рассматри-

лизация с использованием электронных пучков, а

вать короткий электронный импульс длительностью

также предлагает простые методы определения па-

90 фс и диаметром 0.5 мм. В этих условиях элек-

раметров, необходимых для достижения желаемо-

тронный импульс напоминает плоский диск толщи-

го пространственно-временного разрешения с мак-

ной (вдоль оси распространения) не более 27 мкм.

симально возможными отношением сигнала к шуму

Первоначальное распределение заряда предполага-

и/или контрастностью изображения.

ется гауссовым по всем трем координатам. Будем

2. МЕТОД МОДЕЛИРОВАНИЯ

¹⁾ Код GPT [15] использован для расчетов, включающих

10⁵ частиц, с тем же начальным изотропным распределени-

Для интегрирования динамических уравнений

ем импульсов электронов, что и в [14].

использовался алгоритм Верле [29]. Эта схема ши-

388

ЖЭТФ, том 155, вып. 3, 2019

Релятивистское моделирование распространения. . .

роко используется в молекулярной динамике и хо-

Здесь снова все значения в правой части вычисля-

рошо изучена в отношении выбора шага по време-

ются при t = t_r. Эти уравнения могут быть перепи-

ни, устойчивости, сохранения энергии и других ин-

саны так, чтобы включать только текущее время, но

тегралов движения и т.д. Уравнения этой схемы за-

подобная модификация возможна только для равно-

писываются в виде

мерно движущихся зарядов.

В электронном пучке электроны не движут-

r(t + Δt) = 2r(t) - r(t - Δt) + a(t)(Δt)²,

ся равномерно, однако их относительные движе-

или (в схеме со скоростями):

ния происходят при нерелятивистских скоростях (до

10⁵ м/с, как показывают расчеты), и, следователь-

но, эффекты неравномерности движения пренебре-

r(t + Δt) = r(t) + v(t)Δt +

a(t)(Δt)²,

жимо малы, в то время как схема моделирования

значительно усложняется.

v(t + Δt) = v(t) +

[a(t) + a(t + Δt)] Δt.

Величина шага моделирования выбиралась та-

Ускорение a(t), входящее в эти уравнения, можно

ким образом, чтобы изменение расстояний за один

найти из соотношения

временной шаг было намного меньше, чем сред-

нее расстояние между электронами с наибольшими

= F = e(E + [v × B]),

относительными скоростями до 50000 м/с. Другим

критерием выбора шага по времени была независи-

где F — сила Лоренца, E и B — соответственно на-

мость результатов моделирования от величины ша-

пряженность электрического поля и магнитная ин-

га. С учетом того, что в этом исследовании средние

дукция. Последнее уравнение можно разрешить от-

расстояния между электронами в импульсе состав-

носительно ускорения:

ляли от 9 до 19 мкм, было найдено, что удовлетво-

{

}

рительная точность моделирования достигается при

(v · F)v

F-

временном шаге в 2-5 пс.

γm

c²

В многочастичной задаче, рассматриваемой в

√

где γ = 1/

1 - v²/c². Электрическое и магнитное

этой работе, определяющее значение имеет адекват-

поля, создаваемые одним движущимся электроном,

ное моделирование интегральных свойств электрон-

определяются путем дифференцирования запазды-

ного сгустка (например, распределение электронов

вающих потенциалов Лиенара - Вихерта [30]:

в фазовом пространстве - по положению и по скоро-

стям), а не точное воспроизведение траекторий от-

ϕ(r, t) =

дельных электронов. Устойчивость полученных рас-

4πε₀ R(1 - β · n)

пределений контролировалась в ходе моделирова-

ния путем проверки сохранения интегралов движе-

μ₀c

eβ

β(t_r)

A(r, t) =

ϕ(r, t),

ния и проведения множества вычислительных экс-

4π R(1 - β · n)

периментов с псевдослучайными начальными дан-

где r — точка пространства, в которой вычисляется

ными.

поле, r₀ — положение источника (электрона), R =

Другим возможным подходом к численному мо-

= |r - r₀|, β = v/c, n = (r - r₀)/R, а все значения

делированию может быть решение нерелятивистс-

R, β и n вычисляются с учетом запаздывания, т.е.

кой динамической задачи в системе координат, дви-

для положения источника в более ранний момент

жущейся со средней скоростью импульса, с после-

времени:

дующим преобразованием результатов в лаборатор-

|r - r₀(t_r)|

t_r = t -

ную систему отсчета. Этот подход, однако, приводит

к получению положений электронов пучка в лабо-

Если заряд Q движется без ускорения, то его поля

раторной системе в разные моменты времени и, во

можно записать как

всяком случае, требует отдельного преобразования

n-β

координат и скоростей для каждой частицы. Хотя

E(r, t) =

4πε₀ γ²(1 - n · β)³R²

мы и не используем этот подход в динамическом мо-

делировании, он применяется при построении реля-

тивистской формы аналитической модели среднего

B(r, t) =

[v × E].

поля в разд. 4 настоящей статьи.

c²

389

И. В. Кочиков, Р. Дж. Дуэйн Миллер, А. А. Ищенко

ЖЭТФ, том 155, вып. 3, 2019

1.8

640

1.6

620

1.4

600

1.2

580

1.0

560

0.8

540

0.6

520

0.4

500

0.2

480

1.0

2.0

3.0

4.0

1.0

2.0

3.0

4.0

Время распространения, нс

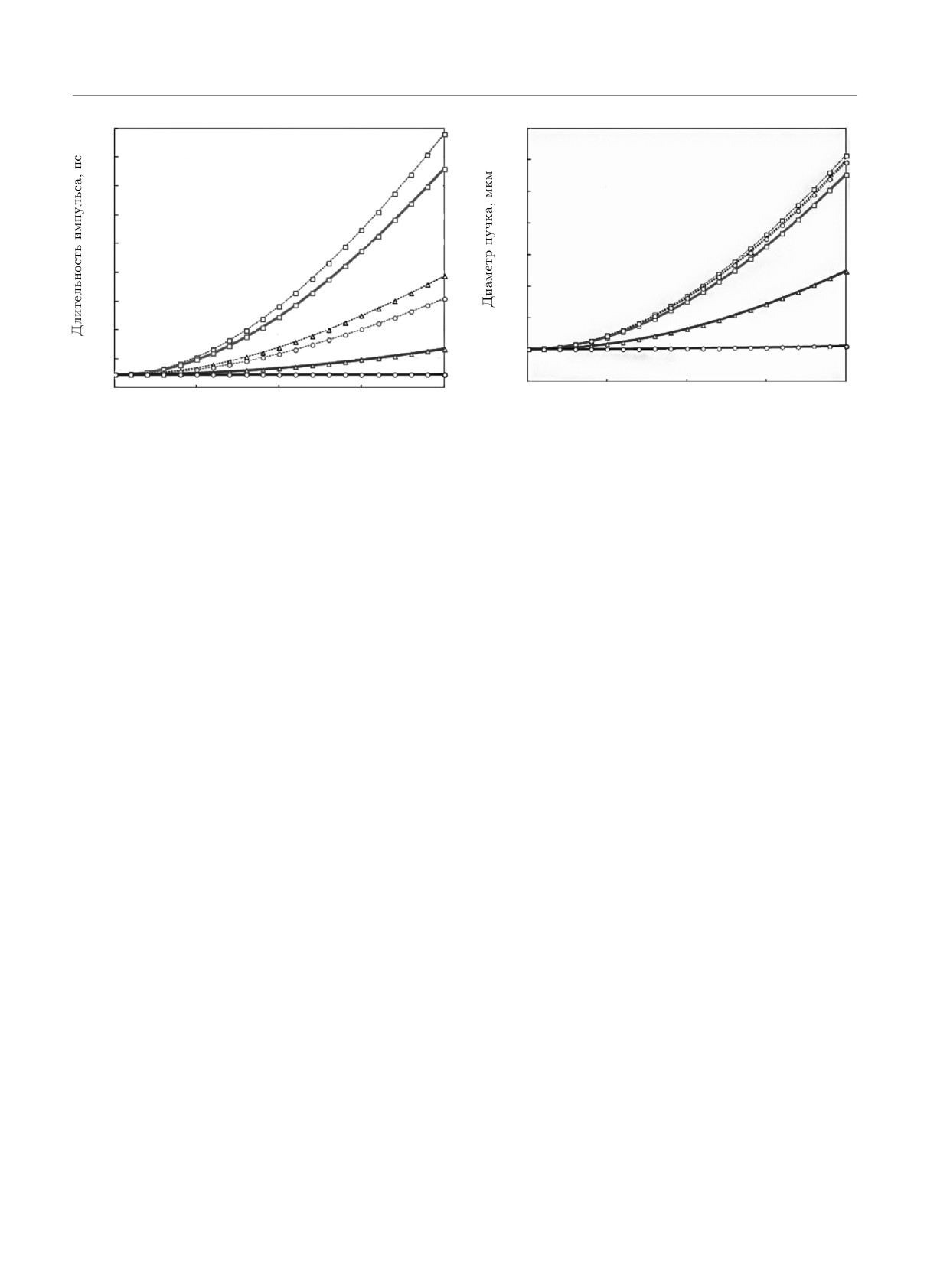
Рис. 2. (В цвете онлайн) Диаметры электронного сгустка

Рис. 1. (В цвете онлайн) Длительности импульса для

для разных моделей распространения и энергий электро-

разных моделей распространения и энергий электронов.

нов. Результаты релятивистской модели показаны сплош-

Результаты релятивистской модели показаны сплошными

ными линиями, результаты статической кулоновской мо-

линиями, результаты статической кулоновской модели —

дели — пунктирными линиями. Энергии соответствуют

пунктирными линиями. Энергии соответствуют

кэВ

30 кэВ (квадраты), 300 кэВ (треугольники) и 3 МэВ (круж-

(квадраты), 300 кэВ (треугольники) и 3 МэВ (кружки)

ки)

3. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

ных моделей распространения и энергий электронов

При моделировании динамики электронов мы

приведены на рис. 1.

ожидаем, что вследствие сил кулоновского отталки-

Отметим, что даже в нерелятивистском прибли-

вания электронный сгусток будет расширяться по

жении результаты моделирования оказываются раз-

всем направлениям. Кроме того, мы ожидаем уве-

личными для разных энергий электронов. Это объ-

личения разброса электронов по энергиям (скоро-

ясняется тем, что при фиксированной длительно-

стям), поскольку более медленные электроны в кон-

сти начального импульса его геометрическая дли-

це сгустка будут дополнительно замедляться опере-

на больше для более высоких энергий (и, соответ-

жающими электронами, а электроны в начале сгуст-

ственно, средней скорости электронов) и кулонов-

ка будут ускоряться отставшими электронами.

ское взаимодействие уменьшается из-за увеличения

В релятивистском случае следует ожидать мень-

среднего расстояния между электронами. Уменьше-

шего уширения распределения электронов по ско-

ние длительности импульса для случаев с высокой

ростям. Одна из причин заключается в том, что си-

энергией оказывается значительным. Это уменьше-

ла отталкивания электронов, движущихся в одном

ние становится еще более существенным, если срав-

направлении, уменьшается за счет появления маг-

нивать результаты не для одинакового времени рас-

нитного поля. Другая причина состоит в увеличении

пространения, а для одинакового расстояния до об-

массы высокоэнергетических электронов и, следова-

разца. Тот же эффект, хотя и в меньшей степе-

тельно, в уменьшении их ускорения. Эти факторы

ни, наблюдается для диаметра электронного сгустка

уменьшают ускорение отталкивания в γ² раз для па-

(рис. 2). В этом случае нерелятивистское приближе-

раллельно движущихся электронов и с еще большим

ние дает одинаковые результаты для разных энер-

коэффициентом γ⁵ для электронов, следующих друг

гий (рис. 2).

за другом по одной траектории. Величина эффекта

Для объяснения показанного выше поведения

зависит и от формы электронного импульса.

размеров электронного импульса в продольном и по-

Результаты нерелятивистского моделирования в

перечном направлениях полезно рассмотреть эволю-

сравнении с релятивистским показаны ниже на ри-

цию распределения электронов по скоростям во вре-

сунках, где приведены данные для сгустка, содер-

мя распространения импульса. На рис. 3 видно, что

жащего N = 10000 электронов, для энергий 30 кэВ,

для низкоэнергетических электронов дисперсия их

300 кэВ и 3 МэВ. Длительности импульса для раз-

скоростей близка к изотропной, в то время как в слу-

390

ЖЭТФ, том 155, вып. 3, 2019

Релятивистское моделирование распространения. . .

1.0

2.0

3.0

4.0

1.0

2.0

3.0

4.0

Время распространения, нс

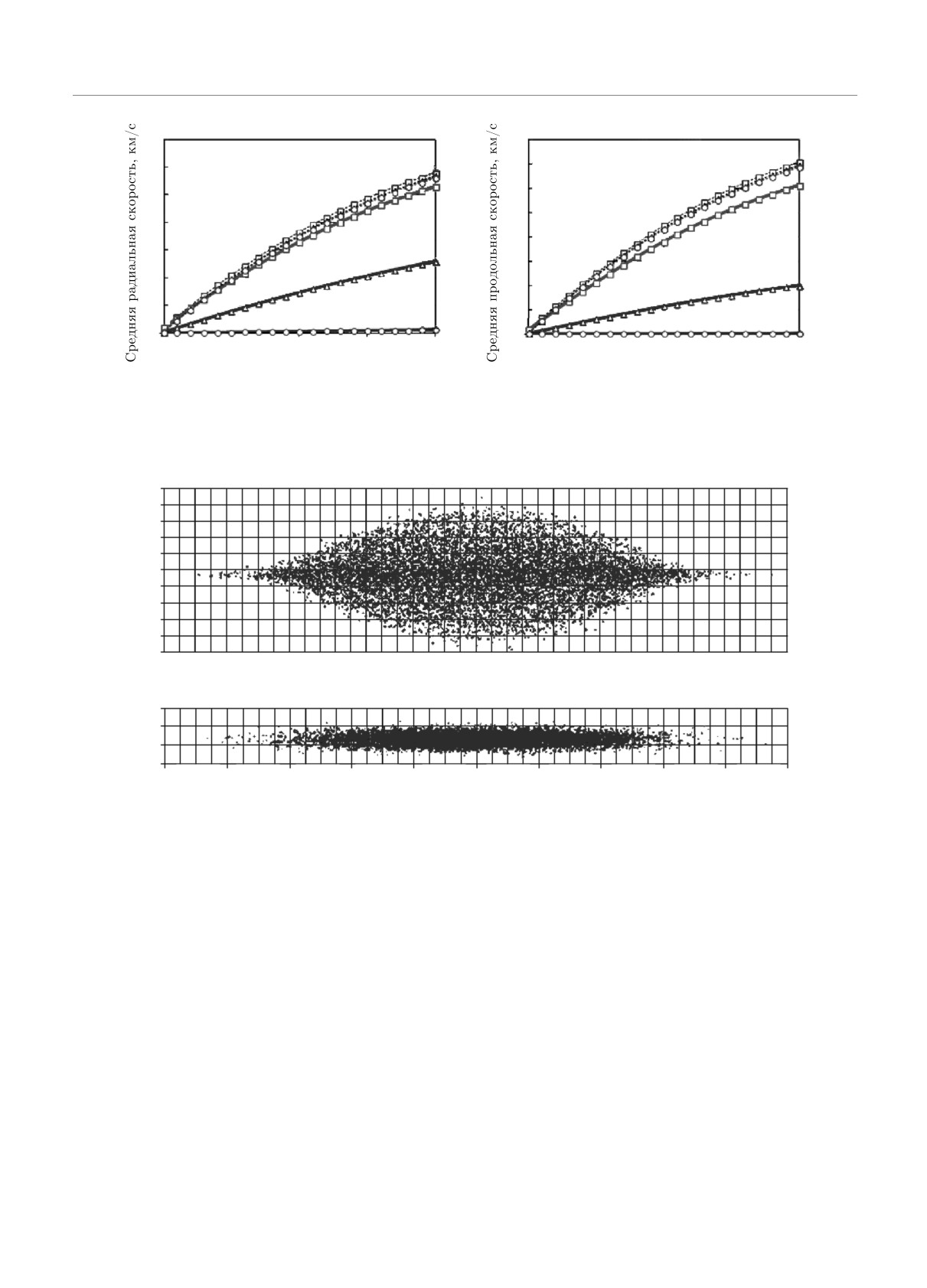
Рис. 3. (В цвете онлайн) Средние радиальная (а) и продольная (б) составляющие скорости электронов в импульсе в

течение времени распространения. Обозначения совпадают с обозначениями рис. 1, 2. График продольной скорости

соответствует ее отклонению от средней скорости пучка

1200

1100

1000

900

800

-1000

-800

-600

-400

-200

200

400

600

800

1000

3050

3000

2950

2900

–1000

–800

–600

–400

–200

200

400

600

800

1000

Рис. 4. (В цвете онлайн) Форма импульса с 10000 электронами после распространения в течение 4 нс для импульсов с

энергиями 30 кэВ (а) и 3 МэВ (б). Все размеры указаны в мкм

чае высоких энергий разброс продольных скоростей

Численное моделирование позволяет проследить

подавляется в гораздо большей степени, чем разброс

эволюцию электронной плотности в процессе рас-

радиальных скоростей. Моделирование в нереляти-

пространения электронного сгустка. Для сгустков,

вистском приближении не учитывает этих эффек-

представляющих собой равномерно заряженные

тов.

сфероиды, было обнаружено, что форма сгуст-

Как уже было отмечено выше, в течение времени

ка и равномерное распределение заряда в нем

распространения исходный импульс расширяется во

сохраняются в процессе распространения. Этот

всех направлениях. Как правило, прямое моделиро-

вывод был подтвержден как приближенными

вание позволяет получить гораздо более подробную

теоретическими моделями, так и прямым молеку-

информацию о динамике пучка, чем обычные при-

лярно-динамическим моделированием [31]. Однако

близительные оценки, хотя это и достигается за счет

недавнее исследование электронного облака с

больших вычислительных затрат. В качестве приме-

гауссовым начальным распределением плотности

ра приведем два изображения электронных сгустков

показало, что профиль электронной плотности со

с энергиями электронов 30 кэВ и 3 МэВ (рис. 4).

временем изменяет свою форму, причем в пери-

391

И. В. Кочиков, Р. Дж. Дуэйн Миллер, А. А. Ищенко

ЖЭТФ, том 155, вып. 3, 2019

80000

70000

60000

50000

40000

30000

20000

10000

0.1

0.2

0.3

Расстояние от оси пучка, мм

Рис. 5. (В цвете онлайн) Эволюция распределения плотно-

сти электронов в электронном сгустке в процессе его рас-

пространения: кривая 1 — через 0 нс; 2 — 0.5 нс; 3 — 1 нс;

4 — 1.5 нс; 5 — 2 нс. Начальное распределение электронов

гауссово, сгусток содержит 50000 электронов

ферийных областях облака возникают максимумы

Рис. 6. (В цвете онлайн) Распределение 5000 электронов в

плотности заряда [17]. Мы подтвердили эти резуль-

тонком слое, вырезанном из середины электронного сгуст-

ка, через 0.25 нс (а), 0.5 нс (б), 0.75 нс (в) и 1 нс (г) по-

таты путем моделирования дрейфа электронных

сле его распространения. Сторона каждого квадрата равна

пучков с энергиями

100

300

кэВ. Численные

0.1 мм

эксперименты охватывали случаи с различными

начальными условиями, в том числе электронные

облака сфероидальной и цилиндрической формы

него кулоновского поля электронов, действующего

как с однородной электронной плотностью, так и с

на один выбранный электрон на переднем (или

плотностью, описываемой гауссовым распределени-

заднем) фронте импульса. Сначала вычисляется

ем. На рис. 5 и 6 показаны радиальный профиль

электрический потенциал заряженного диска на его

плотности и распределение электронов в тонком

оси симметрии:

слое, вырезанном из середины электронного сгустка

(√

)

Ne²

с начальным диаметром 0.1 мм и энергией 100 кэВ.

V (z) =

z² + a² - z

(1)

Моделирование с начальным равномерным рас-

2πε₀a²

пределением заряда и сфероидальной формой обла-

где a — радиус диска, координата z измеряется от

ка приводит к соответствующим образом масшта-

центра диска. Обозначим толщину диска как l. Для

бированным однородным профилям плотности. На-

электрона на переднем крае диска (z = l/2) ускоря-

ше моделирование подтверждает результаты работ

ющая электрическая сила равна

[28, 31]. Эксперименты с меньшим числом электро-



[

]

dv_z



Ne²

нов (N = 10000 и N = 2000) показывают, что уши-



√

(2)



2πε₀a²

рение пучка и появление ударной волны плотности

z=l/2

l² + 4a²

требуют большего времени распространения, но в

В то же время длина импульса (взятого как расстоя-

остальном существенные особенности процесса оста-

ние между электронами на переднем и заднем краях

ются неизменными.

диска) удовлетворяет условию

4. АНАЛИТИЧЕСКАЯ МОДЕЛЬ ДЛЯ

= 2v_z.

РЕЛЯТИВИСТСКОГО СЛУЧАЯ

В нашем исследовании эта модель была примене-

Существует простая теоретическая модель,

на в нерелятивистском приближении с небольшими

предсказывающая удлинение электронного им-

изменениями для учета различных форм электрон-

пульса вследствие отталкивания электронов (см.

ного сгустка. Уравнение (1) было выведено для рав-

цитированную работу Сивика и др. [13], а также

номерно заряженного диска радиуса a. Если предпо-

[18, 22, 32-34]). Она основана на вычислении сред-

ложить гауссово распределение плотности заряда,

392

ЖЭТФ, том 155, вып. 3, 2019

Релятивистское моделирование распространения. . .

(

)

r²

сгустка t₀ = γβz₀c ∼ 0.01γ пс (для длины сгустка

ρ(r) =

exp

2πa²

2a²

30 мкм), а интересующий нас временной масштаб

намного превышает это значение. В результате по-

результат для потенциала на оси z становится рав-

лучаем

ным

(

)∫∞

(

)

z′1(t^′) = -z′2(t^′) =

L₀(γl₀, t^′).

u²

V (z) =

exp

du =

4πε₀a²

2a²

Возвращаясь в лабораторную систему отсчета в мо-

(

)

(

)

мент времени t^′, получим

^√π

exp

erfc

√

z₁(t₁) = γ [z′1(t^′) + V t^′] , z₁(t₂) = γ [z′2(t^′) + V t^′] ,

4πε₀a

2a²

(

)

(

)

что для напряженности электрического поля дает

Vz′1

Vz′2

t₁ = γ t^′ +

t₂ = γ t^′ -

c²

[

(

)

(

)]

^√π

z²

E(z) =

exp

erfc

√

Координаты электронов вновь соответствуют раз-

4πε₀a²

2a²

личным моментам времени. Выберем средний из

них,

Здесь erfc(x) = (2/√π)∫∞

exp(-t²)dt. Значение от-

талкивающей силы eE(z) использовалось вместо

t₁ + t₂

=γt^′ +γ

(z′1 + z′2) ≈ γt^′,

правой части в уравнении (2).

c²

Мы нашли удовлетворительное согласие анали-

и вычислим положения электронов для этого момен-

тической схемы с результатами моделирования в

та, полагая, что скорости электронов лишь незначи-

нерелятивистском приближении, хотя эффективное

тельно отличаются от средней скорости сгустка:

число электронов, принятое равным N/2 в работе

v₁(t₁)γV z′1

[13], для лучшего соответствия результатов оказа-

z₁(t) = z₁(t₁) -

≈

c²

лось необходимым заменить на N/3.5. Это разли-

z′1

чие обусловлено более существенным экранирова-

≈ γ [z′1(t^′) + V t^′] - β²γz′1 =

+γVt^′,

нием зарядов для гауссова распределения, а так-

же несколько иным определением длительности им-

v₂(t₁)γV z′2

пульса.

z₂(t) = z₂(t₁) +

≈

c²

Простейшим способом распространения этой

z′2

аналитической модели на релятивистский случай

≈ γ [z′2(t^′) + V t^′] - β²γz′2 =

+γVt^′.

является переход в систему координат, движущуюся

вместе с импульсом (где применимо нерелятивист-

Длина импульса выражается как

ское приближение) с последующим обратным

переходом в лабораторную систему отсчета. Рас-

l(t) = z₁(t) - z₂(t) =

[z′1(t^′) - z′2(t^′)] =

смотрим два электрона в передней и задней частях

(

)

электронного импульса. Введем функцию L₀(l₀, t),

L₀(γl₀, t^′) =

L₀

γl₀,

которая является решением нерелятивистского

уравнения (2) с начальными условиями l(0) = l₀,

где сделан переход ко времени в лабораторной си-

v(0) = 0.

стеме t вместо связанного со сгустком времени t^′.

В начальный момент времени координаты элект-

Окончательное релятивистское соотношение имеет

ронов в лабораторной системе отсчета равны z₁ =

вид

= z₀, z₂ = -z₀, где z₀ = L₀(l₀, t)/2, а их скорости

(

)

равны скорости облака. В системе отсчета, связан-

L(l₀, t) =

L₀

γl₀,

(3)

ной с электронным сгустком, координаты электро-

нов есть γz₀ и -γz₀ в моменты времени t′1 = -t₀,

Заметим, что релятивистский фактор γ входит в

t′2 = t0, t0 = γV z0/c2. Решение уравнений в этой

это уравнение тремя различными способами, и каж-

движущейся системе дает

дый из них приводит к уменьшению длительности

импульса при увеличении γ.

z′1(t^′) =

L₀(γl₀, t^′-t′0), z′2(t^′) = -

L₀(γl₀, t^′+t′0).

На рис. 7 показано очень хорошее соответствие

результатов, полученных при численном моделиро-

Поправка t₀ для моментов времени фактически

вании, результатам, полученным при использовании

несущественна, поскольку в системе электронного

уравнения (3).

393

И. В. Кочиков, Р. Дж. Дуэйн Миллер, А. А. Ищенко

ЖЭТФ, том 155, вып. 3, 2019

1.8

Работа выполнена при поддержке РФФИ

1.6

(проект № 16-29-1167 ОФИ_м). Один из авторов

1.4

(Р. Дж. Дуэйн Миллер) выражает благодарность

за поддержку Обществу Макса Планка.

1.2

1.0

0.8

ЛИТЕРАТУРА

0.6

A. H. Zewail and J. M. Thomas, 4D Electron Micro-

0.4

scopy: Imaging in Space and Time, Imperial College

0.2

Press, London (2010).

0.5

1.0

1.5

2.0

2.5

3.0

3.5

4.0

A. A. Ischenko and S. A. Aseyev, Time Resolved

Время распространения, нс

Electron Diffraction: For Chemistry, Biology and Ma-

terial Science, Elsevier, New York (2014).

Рис.

7. (В цвете онлайн) Длительности электронного

импульса, полученные при моделировании (квадраты —

J. S. Baskin and A. H. Zewail, C. R. Phys. 15, 176

30 кэВ, кресты — 100 кэВ, треугольники — 300 кэВ, круж-

(2014).

ки — 3 МэВ). Сплошными линиями показаны оценки со-

гласно (3)

А. А. Ищенко, С. А. Асеев, В. Н. Баграташвили,

В. Я. Панченко, Е. А. Рябов, УФН 184, 681 (2014).

A. A. Ischenko, V. N. Bagratashvili, V. V. Golubkov,

5. ВЫВОДЫ

V. P. Spiridonov, A. V. Zgurskiy, and A. S. Akhma-

nov, Appl. Phys. B 32, 161 (1983).

Результаты применения релятивистских дина-

С. А. Ахманов, В. Н. Баграташвили, В. В. Голуб-

мических уравнений показывают, что нерелятивист-

ков, А. В. Згурский, А. А. Ищенко, С. А. Крику-

ское приближение дает удовлетворительные резуль-

нов, В. П. Спиридонов, В. Г. Тункин, Письма в

ЖТФ 11, 157 (1985).

таты (с погрешностью 15 % и менее) для модели-

рования удлинения и уширения коротких элект-

A. Gliserin, M. Walbran, F. Krausz, and P. Baum,

ронных импульсов при энергиях до 30 кэВ. В то

Nature Comm. 6, 8723 (2015).

же время результаты такого моделирования могут

Б. Н. Миронов, С. А. Асеев, В. Г. Миногин,

быть весьма неточными для промежуточных энер-

С. В. Чекалин, ЖЭТФ 133, 1155 (2008).

гий (300 кэВ), а для быстрых релятивистских пуч-

ков (3 МэВ) они становятся совершенно неверными.

Б. Н. Миронов, В. О. Компанец, С. А. Асеев,

Использование импульсов высоких энергий

А. А. Ищенко, О. В. Мисочко, С. В. Чекалин,

(300 кэВ и более) приводит к почти полному ис-

Письма в ЖЭТФ 103, 597 (2016).

чезновению эффекта кулоновского отталкивания,

10.

Б. Н. Миронов, В. О. Компанец, С. А. Асеев,

причем его значительное уменьшение отмечается

А. А. Ищенко, И. В. Кочиков, О. В. Мисочко,

уже при энергиях выше 100 кэВ. Дисперсия скорос-

С. В. Чекалин, Е. А. Рябов, ЖЭТФ 151, 494

тей электронов при высоких энергиях существенно

(2017).

уменьшается. Для электронов с энергией 3 МэВ

11.

A. A. Ischenko, Yu. I. Tarasov, E. A. Ryabov,

длительность электронного импульса и его радиус

S. A. Aseyev, L. Schafer, Fine Chem. Technol. 12,

заметно не изменяются даже после его распростра-

5 (2017).

нения в течение 4 нс, что соответствует расстоянию

1.2 м. Даже при энергии электронов 300 кэВ увели-

12.

A. A. Ischenko, P. M. Weber, and R. J. Dwayne Mil-

чение длительности импульса пренебрежимо мало

ler, Chem. Rev. 117, 11066 (2017).

для времени распространения

нс (расстояние

13.

B. J. Siwick, J. R. Dwyer, R. E. Jordan, and

0.2 м).

R. J. Dwayne Miller, J. Appl. Phys. 92, 1643 (2002).

Простая аналитическая модель среднего поля,

14.

O. J. Luiten, S. B. van der Geer, M. J. de Loos,

предложенная в работе

[13], распространена на

F. B. Kiewiet, and M. J. van der Wiel, Phys. Rev.

быстрые релятивистские электронные импульсы с

Lett. 93, 094802 (2004).

хорошим соответствием результатам прямого дина-

мического моделирования.

15.

Y. Li, http://www.pulsar.nl/gpt.

394

ЖЭТФ, том 155, вып. 3, 2019

Релятивистское моделирование распространения. . .

16. K. Flottmann, S. M. Lidia, and P. Piot, in Proc. of the

26. M. Hada, K. Pichugin, and G. Sciaini, Eur. Phys. J.

2003 Particle Accelerator Conference (2003), p. 3500.

Special Topics 222, 1093 (2013).

17. B. W. Reed, J. Appl. Phys. 100, 034916 (2006).

27. B. L. Beaudoin, J. C. T. Thangaraj, D. Edstrom

Jr., J. Ruan, A. H. Lumpkin, D. Broemmelsiek,

18. M. Michalik and J. E. Sipe, J. Appl. Phys. 99, 054908

K. A. Carlson, D. J. Crawford, A. Romanov,

(2006).

J. K. Santucci, G. Stancari, R. Thurman-Keup, and

A. Warner, Phys. Plasmas 23, 103107 (2016).

19. T. van Oudheusden, E. F. de Jong, S. B. van der Geer,

W. P. E. M. O. Root, O. J. Luiten, and B. J. Siwick,

28. B. S. Zerbe, X. Xiang, C.-Y. Ruan, S. M. Lund, and

J. Appl. Phys. 102, 093501 (2007).

P. M. Duxbury, Phys. Rev. Accel. Beams 21, 06421

(2018).

20. P. Musumeci, M. S. Gutierrez, J. T. Moody,

C. M. Scoby, J. B. Rosenzweig, and T. Tran, Phys.

29. H. Grubmüller, H. Heller, A. Windemuth, and

Rev. Lett. 100, 244801 (2008).

K. Schulten, Mol. Simulations 6, 121 (1991).

21. Y.-E. Sun, P. Piot, A. Johnson, A. H. Lumpkin,

30. W. K. H. Panofsky and M. Philips, Classical Elect-

T. J. Maxwell, J. Ruan, and R. Thurman-Keup, Phys.

ricity and Magnetism, Addison-Wesley Publ. Co.,

Rev. Lett. 105, 234801 (2010).

Massachusetts (1969).

22. J. A. Berger and W. A. Schroeder, J. Appl. Phys.

31. M. Grech, R. Nuter, A. Mikaberidze, P. Di Cintio,

108, 124905 (2010).

L. Gremillet, E. Lefebvre, U. Saalmann, J. M. Rost,

and S. Skupin, Phys. Rev. E 84, 056404 (2011).

23. T. van Oudheusden, P. L. E. M. Pasmans,

S. B. van der Geer, M. J. de Loos, M. J. van der Wiel,

32. B.-L. Qian and H. E. Elsayed-Ali, J. Appl. Phys. 94,

and O. J. Luiten, Phys. Rev. Lett. 105, 264801

803 (2003).

(2010).

24. F. Carbone, P. Musumeci, O. J. Luiten, and C. He-

33. B. J. Siwick, J. R. Dwyer, R. E. Jordan, and

R. J. Dwayne Miller, J. Appl. Phys. 94, 807 (2003).

bert, Chem. Phys. 392, 1 (2012).

25. Z. Tao, H. Zhang, P. M. Duxbury, M. Berz, and

34. B.-L. Qian and H. E. Elsayed-Ali, J. Appl. Phys. 91,

C.-Y. Ruan, J. Appl. Phys. 111, 044316 (2012).

462 (2002).

395