ЖЭТФ, 2019, том 155, вып. 3, стр. 460-471

ДИФФУЗИЯ ФОТОНОВ В СЛУЧАЙНЫХ СРЕДАХ

И АНИЗОТРОПИЯ РАССЕЯНИЯ В МОДЕЛЯХ

ХЕНЬИ - ГРИНШТЕЙНА И РЭЛЕЯ - ГАНСА

В. Л. Кузьминa*, А. Ю. Вальковa,b**, Л. А. Зубков^c

^a Санкт-Петербургский политехнический университет Петра Великого

195251, Санкт-Петербург, Россия

^b Санкт-Петербургский государственный университет

199034, Санкт-Петербург, Россия

^c Drexel University, School of Biomedical Engineering

19104, Philadelphia, Pennsylvania, United States

Поступила в редакцию 31 августа 2018 г.,

после переработки 31 августа 2018 г.

Принята к публикации 27 сентября 2018 г.

Проведено численное моделирование методом Монте-Карло интенсивности многократного обратно-

рассеянного излучения как функции расстояния источник-приемник для моделей анизотропного рас-

сеяния Хеньи - Гринштейна и Рэлея - Ганса. Найдено, что вопреки обычному предположению диффузи-

онного режима об универсальности описания рассеяния в терминах коэффициента экстинкции и транс-

портной длины, интенсивность многократного рассеяния зависит от вида фазовой функции и от степени

анизотропии даже для систем с одинаковыми значениями коэффициентов экстинкции и транспортных

длин. При этом фазовая функция Рэлея - Ганса дает более чувствительные к анизотропии рассеяния

результаты, чем функция Хеньи - Гринштейна.

DOI: 10.1134/S0044451019030088

ется эмпирическая фазовая функция Хеньи- Грин-

штейна (ХГ), что связано, в основном, с ее матема-

1. ВВЕДЕНИЕ

тическим удобством. Эта функция непосредственно

Интерес к переносу лазерного излучения в слу-

включает в себя параметр g.

чайной среде в большой степени связан в послед-

Однако анизотропия рассеяния и сам параметр

нее время с биомедицинскими приложениями (см.

g зависят от физических свойств рассеивателей и,

[1-4]). Одной из основных задач здесь является

прежде всего, их размеров. Простейшей моделью,

определение оптических параметров среды, коэф-

исходящей из размеров рассеивателей, является мо-

фициента рассеяния, μ_s, и коэффициента абсорб-

дель суспензии твердых сфер, что соответствует фа-

ции, μ_a, которые, в свою очередь, используются для

зовой функции Рэлея - Ганса (РГ). Формально, опи-

определения физиологического состояния тканей.

сание однократного рассеяния на основе формул Ми

Важной проблемой при их определении является

является более точным в сравнении с моделью РГ.

учет анизотропии индикатрисы однократного рас-

Однако использование формул Ми с одновременным

сеяния, или фазовой функции. Из эксперимента из-

использованием уравнения переноса, соответствую-

влекается приведенный коэффициент рассеяния μ^′s,

щего уравнению Бете - Солпитера, с ограничением

связанный с коэффициентом рассеяния μ_s опреде-

парными корреляторами диэлектрической проница-

лением μ^′s = (1 - g)μ_s [5], где параметр g = 〈cos θ〉 —

емости и лестничным приближением, представляет

средний косинус угла рассеяния, характеризующий

собой превышение точности [6].

степень анизотропии рассеяния. Наиболее часто ис-

Метод Монте-Карло (МК) в применении к за-

пользуемой моделью анизотропного рассеяния явля-

даче переноса излучения представляет собой стоха-

^* E-mail: kuzmin_vl@mail.ru

стическое вычисление многократных интегралов пу-

^** E-mail: e-mail: alexvalk@mail.ru

тем статистической выборки мощностью N_in мно-

460

ЖЭТФ, том 155, вып. 3, 2019

Диффузия фотонов в случайных средах. . .

гомерных массивов размерностью до 3n_sc, пред-

позволяет найти обратное преобразование кумуля-

ставляющих собою координаты n_sc актов рассея-

тивной функции в элементарном виде, что может

ния. Решающим шагом, определяющим эффектив-

быть использовано при моделировании переноса из-

ность МК-алгоритма, со времен Метрополиса яв-

лучения в жидко-кристаллических средах [15-17].

ляется правильное семплирование, отражающее ха-

В настоящей работе найденная в явной форме

рактер функции распределения. Наиболее эффек-

кумулятивная функция модели Рэлея - Ганса позво-

тивное семплирование основано на методе обратного

лила эффективно реализовать для этой модели ме-

преобразования, сводящем пространственные инте-

тод обратного преобразования и выполнить модели-

гралы, понимаемые как свертки физических пере-

рование многократного рассеяния для обоих видов

менных со сложными распределениями, к интегра-

фазовых функций одновременно.

лам по равномерно распределенным величинам. Од-

На основе развитого алгоритма стохастиче-

нако на практике такой метод обычно используется

ского моделирования многократного рассеяния

лишь в простейших случаях, когда возможно анали-

выполнен численный расчет сигналов, измеряемых

тическое обращение кумулятивной (интегральной)

современной методикой диффузионной ближне-

функции распределения. В более сложных ситуа-

инфракрасной спектроскопии (DNIRS — diffuse near

циях обычно используются другие подходы. Так, в

infrared spectroscopy); расчет дополнен сравнением

работе [7] для решения задачи МК-моделирования

с экспериментальными данными. Показано, что в

многократного рассеяния предлагается метод сем-

целом для зависимости от расстояния источник-

плирования, пригодный для трехмерных анизотроп-

приемник интенсивности обратно рассеянного

ных фазовых функций, основанный на кусочной ап-

излучения в рамках моделей ХГ и РГ расчеты

проксимации плотности распределения.

дают сходную картину. Однако на расстояниях

Ранее мы кратко описали применение метода

порядка десяти транспортных длин, типичных для

семплирования, основанного на кусочном модели-

биомедицинских приложений, обнаружена различ-

ровании кумулятивной функции распределения, что

ная скорость приближения к стандартному случаю

дало возможность применять метод обратного пре-

изотропного рассеяния при уменьшении степени

образования к фазовой функции РГ [8], рассчитав, в

анизотропии для РГ- и ХГ-моделей; количественно

частности, угловую зависимость интенсивности об-

на малых расстояниях модель РГ приводит к боль-

ратного рассеяния в диффузионном режиме. Здесь

шим значениям интенсивности обратного рассеяния

мы приводим результаты моделирования в усло-

нежели модель ХГ.

виях, типичных для современного эксперимента и

Мы выполнили моделирование интенсивности

практических применений [9-11], с разделенными

обратного рассеяния в современной постановке экс-

пространственно источником и приемником излуче-

перимента как функцию расстояния между источ-

ния. В рамках обычных представлений диффузион-

ником и приемником, расположенными на поверх-

ной теории переноса излучения считается [5], что

ности модели биоткани (биофантома). Мы нашли

при одинаковых значениях коэффициента абсорб-

заметную зависимость от вида фазовой функции и

ции и транспортной длины поведение систем уни-

степени анизотропии рассеяния; эта зависимость на-

версально и не зависит от анизотропии рассеяния.

блюдается в том числе для систем с равными зна-

Мы обнаружили, что масштабного перехода μ_s → μ^′s

чениями приведенных коэффициентов рассеяния и

недостаточно для учета анизотропии; в частности,

абсорбции, для которых диффузионное приближе-

мы нашли, что интенсивность обратного рассеяния

ние предполагает универсальность поведения. Ин-

продолжает зависеть от степени анизотропии и вида

тенсивность многократного рассеяния строго назад

фазовой функции даже для систем с одинаковыми

изменяется с ростом анизотропии рассеяния, замет-

значениями коэффициента μ^′s.

но различаясь для рассматриваемых моделей, во-

Для распределения по углам рассеяния в виде

преки распространенному положению об универ-

модели ХГ легко находится в элементарном виде об-

сальности описания рассеяния в диффузионном ре-

ратное преобразование для кумулятивной, или ин-

жиме, при котором конкретный вид фазовой функ-

тегральной, функции распределения. Использова-

ции становится не важен в пределе высоких кратно-

ние фазовой функции Ми [12] и ряда других функ-

стей рассеяния.

ций [13,14] затруднено именно из-за невозможности

В разд. 2 изложено описание переноса излуче-

получить кумулятивную функцию, приемлемую для

ния в терминах уравнения Бете - Солпитера; разд. 3

создания обозримого численного алгоритма. Отме-

содержит точные результаты для изотропного рас-

тим, что функция вида Орнштейна - Цернике также

сеяния; разд. 4 описывает алгоритм моделирования

461

В. Л. Кузьмин, А. Ю. Вальков, Л. А. Зубков

ЖЭТФ, том 155, вып. 3, 2019

Монте-Карло; в разд. 5 на основе полученной куму-

〈δε(r₁) . . . δε(r_n)δε^∗(r′1) . . . δε^∗(r^′m)〉. В результате ха-

лятивной функции развит метод обратного преобра-

отизации по разности фаз, возникающей при много-

зования для фазовой функции РГ; в разд. 6 приво-

кратном рассеянии, при условии слабого рассеяния

дятся результаты моделирования; разд. 7 содержит

λ ≪ l, где λ — длина волны, а l — средняя длина

Заключение.

свободного пробега фотона, отлична от нуля толь-

ко некогерентная составляющая (главный вклад в

2. ПЕРЕНОС ИЗЛУЧЕНИЯ В РАМКАХ

которую вносит лестничная, в диаграммных терми-

УРАВНЕНИЯ БЕТЕ - СОЛПИТЕРА

нах) последовательности актов рассеяния полей δE

Распространение и рассеяние монохроматиче-

и δE^∗ на одной и той же последовательности флук-

ской световой волны в случайной среде будем опи-

туаций. Предполагая радиус корреляции r_c флук-

сывать, используя волновое уравнение в интеграль-

туаций δε не слишком большим, r_c ≪ l, получим с

ной форме:

учетом теоремы Вика

∫

E(r) = E₀(r)+

dr₁T₀(r - r₁)δε(r₁)E(r₁),

(1)

〈δε(r₁) . . . δε(r_n)δε^∗(r′1) . . . δε^∗(r^′m)〉_L =

4π

∏

где E₀(r) и E(r) — спектральные компоненты по-

=δ_nm

〈δε(r_i)δε^∗(r^′i)〉.

(4)

ля в однородной среде и случайного поля в среде с

i=1

флуктуациями диэлектрической проницаемости δε,

Оставляя только такие лестничные составляющие

а T₀(r-r₁) = k²⁰|r-r₁|-1 exp(ik₀|r-r₁|) — функция

многочастичных корреляторов, некогерентную

Грина (c точностью до множителя 1/4π) в вакууме в

часть интенсивности рассеянного излучения пред-

частотном представлении. Такое же уравнение опре-

ставим в виде ряда по кратностям рассеяния:

деляет функцию Грина в случайной среде:

T_fl(r, r^′) = T₀(r - r^′)+

〈δE^∗(r)δE(r)〉_L =

∫

∑

dr₁T₀(r - r₁)δε(r₁)T_fl(r₁, r^′).

(2)

dr₁ . . . dr_ndr′1 . . . dr^′n ×

4π

(4π)2n

n=1

Усредненная по флуктуациям диэлектрической про-

× T^∗oi(r - r^′n)T_oi(r - r_n)〈δε(r_n)δε^∗(r^′n)〉×

ницаемости функция Грина T_fl имеет в главном по-

∏

рядке вид

× T^∗(r′i+1 - r^′i)T(ri+1 - r_i)〈δε(r_i)δε^∗(r^′i)〉×

T (r - r₁) = 〈T_fl(r - r₁)〉 = k²|r - r₁|-1 exp(ik|r - r₁|),

i=1

× E^∗(r′1)E(r₁),

(5)

где k = nk₀, n — показатель преломления.

Итерируя волновое уравнение (1), представим

где T_oi(r-r_n) — усредненная по флуктуациям функ-

E(r) в виде ряда по степеням флуктуаций диэлек-

ция Грина с аргументами, r и r_n, расположенными,

трической проницаемости δε(r):

соответственно, вне и внутри случайной среды; на

∑

∏

большом расстоянии до среды она представляется

E(r) = E₀(r) +

dr_iδε(r_i) ×

во фраунгоферовом приближении как

(4π)ⁿ

n=1

i=1

T_oi(r₀ - r₁) = T(r₀)exp(-ik_f r₁).

× T₀(r - r_n). . . T₀(r₂ - r₁)E₀(r₁).

(3)

Среднее 〈δE^∗(r)δE(r)〉 по конфигурациям рассе-

Оптическая теорема связывает коэффици-

ивателей произведения флуктуации поля δE(r) =

ент рассеяния μ_s и интеграл по телесному углу

= E(r) - 〈E(r)〉 на комплексно-сопряженное дает

от фурье-образа коррелятора диэлектрической

с точностью до стандартных множителей интенсив-

проницаемости

ность рассеянного излучения для точки наблюдения

∫

r, расположенной вне рассеивающей среды.

G(q) =

d(r - r^′)eiq(r-r′)〈δε(r)δε^∗(r^′)〉.

(6)

(4π)²

Это выражение, 〈δE^∗(r)δE(r)〉, представляется в

виде произведения двух итерационных рядов для

В случае скалярного поля

поля и его комплексно-сопряженного. При стати-

∫

стическом усреднении по конфигурациям рассеи-

μ_s = k⁴

dΩ_f G(k_f - k_i).

(7)

вателей отдельные слагаемые произведения итера-

ционных рядов содержат многочастичные корреля-

Для электромагнитного поля в (7) добавляется рэ-

ционные функции диэлектрической проницаемости

леевский множитель: G → G(1 + cos² θ_f )/2.

462

ЖЭТФ, том 155, вып. 3, 2019

Диффузия фотонов в случайных средах. . .

k_f

r₂

r₁

k_i

k_f

r₁

k_i

k_f

r₂

r₃

r₁

k_i

k*f

k*i

k*f

k*i

k*f

k*i

r₂

r₁

r₂

r₃

r₁

Рис. 1. Схематическое представление уравнения Бете - Солпитера в виде фейнмановских диаграмм. Заштрихованный

прямоугольник — пропагатор Бете - Солпитера, волнистая линия — коррелятор флуктуаций диэлектрической проницае-

мости; внутренние линии — полевые функции Грина; стрелки — входящие или выходящие плоские волны; по зачерненным

вершинам проводится интегрирование

Пусть z — декартова координата точки r

Уравнение Бете - Солпитера, описывающее пере-

= (r_⊥, z), нормальная к границам плоскопараллель-

нос стационарного излучения, запишем в виде

ного слоя толщиной T , z

∈ [0; T ]; T

= ∞ со-

ответствует полупространству. Определим некоге-

Γ(r₂, r₁ | k_f , k_i) = k⁴⁰G(k_f - k_i)δ(r₂ - r₁) +

∫

рентную часть интенсивности рассеянного назад из-

лучения, отнесенную к плотности энергии падающе-

+k⁴

dr₃G(k_f - k₂₃)Λ(r₂ - r₃)Γ(r₃, r₁ | k₂₃, k_i),

го поля, как

где пропагатор Γ(r₂, r₁ | k_f , k_i) описывает распро-

странение излучения, падающего в точке r₁ и выхо-

∫∞

∫

дящего из точки r₂, с начальным k_i и финальным k_f

J (s_i, s_f ) = 4π dz₁

dr₂Γ(r₂, r₁ | k_f , k_i) ×

волновыми векторами; k_ij — волновой вектор вдоль

z2>0

направления из r_i в r_j , k₀ = 2π/λ — волновое число,

× exp(-μ(s_f z₂ + s_iz₁)) ,

(8)

λ — длина волны в вакууме; пропагатор однократ-

ного рассеяния Λ(r) = r-2 exp(-μr) представляет

где s_i = 1/ cos θ_i s_f = 1/ cos θ_f , θ_i — угол падения,

собой произведение комплексно-сопряженной пары

θ_f — угол обратного рассеяния, отсчитываемый от

функций Грина скалярного поля с учетом множите-

обратного направления. Пропагатор Γ(r₂, r₁ | k_f , k_i)

ля k⁴⁰, μ = μ_s +μ_a — коэффициент экстинкции, μ_a —

возникает как результат суммирования лестнично-

коэффициент поглощения.

го ряда по кратностям рассеяния. Формально этот

Вводя нормированную фазовую функцию

ряд имеет вид операторной геометрической прогрес-

∕∫

сии; его суммирование приводит к замкнутому урав-

p(kf k_i) = G(k_f - k_i)

dΩ_f G(k_f - k_i),

(9)

нению, известному как уравнение Бете - Солпитера

(см. рис. 1).

где

k обозначает единичный вектор вдоль k, урав-

Лестничное приближение требует, чтобы длина

нение Бете - Солпитера представим в виде

волны, а также размер неоднородностей и радиус их

корреляций были меньше длины рассеяния, λ ≪ l_ext

Γ(r₂, r₁ | k_f , k_i) = μ_sp(kf k_i)δ(r₂ - r₁) +

и d, r_c ≪ l_ext. Это требование в рассматриваемых

∫

приложениях выполняется: длина волны и размеры

+ μ_s dr₃p(kf k₂₃)Λ(r₂ - r₃)Γ(r₃,r1 |k₂₃,k_i).

(10)

рассеивателей порядка микрона, а длина экстинк-

ции в биосистемах порядка десятков микрон и более.

Когерентная часть интенсивности обратного рас-

Необходимо также выполнение условия слабой ин-

сеяния дается формулой (8) при замене экспоненты

тенсивности флуктуаций диэлектрической проница-

на произведение

емости, δε ≪ 1; это требование позволяет учитывать

только такие конфигурации, где расстояния между

exp(-μ(s_f + s_i)(z₁+z₂)/2)cos((k_i+k_f )(r₁-r₂)).

каждыми последовательными актами рассеяния со-

измеримы с длиной экстинкции, и можно не учиты-

Для рассеяния строго назад этот вклад за вычетом

вать конфигурации, в которых расстояния между

вклада однократного рассеяния дает удвоение ин-

отдельными актами рассеяния определяются ради-

тенсивности; здесь мы его не рассматриваем в силу

усом корреляции.

угловой узости пика.

463

В. Л. Кузьмин, А. Ю. Вальков, Л. А. Зубков

ЖЭТФ, том 155, вып. 3, 2019

3. ТОЧНЫЕ РЕЗУЛЬТАТЫ ДЛЯ

J⁽³⁾(1, 1) =

ln² 2 +

ln 2 -

π²,

ИЗОТРОПНОГО РАССЕЯНИЯ

J⁽⁴⁾(1, 1) ≈ 0.206753.

Итерируя уравнение Бете - Солпитера, запишем

интенсивность в виде ряда по кратностям рассея-

Мы используем эти значения для контроля точ-

ния:

ности численных симуляций многократного рассея-

ния. Точное решение задачи об угловом распределе-

∑

нии интенсивности рассеяния от полупространства,

J (s_i, s_f ) = J⁽¹⁾(s_i, s_f ) +

J(n)(s_i, s_f ),

(11)

n=2

известной как задача Милна, для изотропного рас-

сеяния можно представить в виде (см. [18, 19])

где

J⁽¹⁾(s_i, s_f ) = 4π(μ_s/μ)(s_f + s_i)-1p(kf k_i)

J (s_i, s_f ) =

exp(-H(s_i) - H(s_f )) ,

(14)

s_i + s

— вклад однократного рассеяния, а J(n)(s_i, s_f ) —

рассеяния n-го порядка, n > 1.

∫

∞

(

)

ds^′

arctg s^′

Аналитически вычисляются для полупростран-

H(s) =

(15)

s² + s′2

s^′

ства также вклады двух и трех кратных рассеяний.

Интенсивность двукратного рассеяния имеет вид

В направлении строго назад J(1, 1) ≈ 4.22768 [20].

∫

∞

∫

J⁽²⁾(s_i, s_f ) = (μ_s/4π)²

dz₁

dr₂

dr₃ ×

4. МОДЕЛИРОВАНИЕ МОНТЕ-КАРЛО

z2>0

× Λ(r₃ - r₁)δ(r₁ - r₃)exp(-μ(s_f z₂ + s_iz₁)).

(12)

В стохастическом методе интенсивность рассея-

ния представляет собой среднее по выборке N_in па-

В силу цилиндрической симметрии интеграл по

дающих фотонов

поперечным переменным легко преобразуется:

∫

∑

J_ω(ρ) =

J(i)ω(ρ),

(16)

dr₃Λ(r₃ - r₁) = 2π

dz₃

ρ dρ r-2e^-μr,

i=1

z1, z3>0

√

где вклад отдельного фотона Jωi)(ρ) является сум-

где r =

ρ² + |z₃ - z₁|²; заменяя переменные инте-

мой вкладов отдельных кратностей рассеяния

грирования ρ на r и r на t, r = |z₃ - z₁|t, приводим

∑

(

)

внутренний интеграл к виду

J(i)ω(ρ) =

W(i)ne-μzni) cos c-1ωR(i)

+θ₀

(17)

n<nsc

∫

∞

dr₃Λ(r₃ - r₁) = 2π

dz₃

t-1dt ×

Здесь

— ненормированный вес i-го фотона, а

z3>0

zni) — его расстояние до границы от точки n-го ак-

та рассеяния rni), в соответствии с формулой (8), а

× exp(-μ(s_f z₂ + s_iz₁ + t|z₃ - z₁|)),

(i)

∑

величина R

=z(i)

+zni) представля-

+ j≥2rj

j-1

после чего элементарно вычисляются интегралы от

ет собой оптический путь, пройденный i-м фотоном,

экспонент по z₁, z₂, с учетом дельта-функции,

испытавшим n актов рассеяния, ω — частота моду-

ляции. В случае ω = 0 моделируется сигнал DNIRS

μ_s

стационарного CW-излучения. При выборе θ₀ = 0

J⁽²⁾(s_f , s_i) =

μ²

и θ₀ = π/2 измеряются два независимых сигнала,

)

⁽ ln(1 + s_f )

ln(1 + s_i)

позволяющие определить два параметра — ампли-

(13)

2(s_f + s_i)

s_f

s_i

туду и фазовый сдвиг рассеянного модулированно-

го излучения в методике диффузных волн фотонной

В случае изотропного рассеяния, p(kf ·

k_i) =

плотности (DPDW — diffuse photon density wave) в

= 1/4π, нормального падения и рассеяния строго

частотном представлении.

назад в отсутствие поглощения мы получаем для по-

Вес

n с учетом геометрии задачи представ-

лупространства и низших порядков рассеяния:

ляет собой случайное значение подынтегрального

выражения многократного пространственного ин-

J⁽¹⁾(1, 1) = 0.5, J⁽²⁾(1, 1) =

ln 2,

теграла, возникающего как итерация n-го порядка

464

ЖЭТФ, том 155, вып. 3, 2019

Диффузия фотонов в случайных средах. . .

уравнения Бете - Солпитера (10). При реализации

нее число фотонов, покидающих среду после n актов

процедуры итераций возникает стохастическая по-

рассеяния.

следовательность, или траектория точек рассеяния

Мы использовали указанное выше точное зна-

r₁, . . ., r_n.

чение интенсивности рассеяния назад от полупро-

В случае попадания фотона за пределы ограни-

странства для изотропной индикатрисы, J(1, 1) ≈

≈ 4.22768, полученное при решении задачи Мил-

ченной среды направление его движения следует по-

на, для проверки корректности используемых про-

вернуть согласно законам отражения, умножая вес

на коэффициент отражения Френеля (см. [21,22]). В

граммных кодов. Мы нашли, что в рамках развитой

нами модели (17) с точностью до одного процента

часто рассматриваемом случае пренебрежения от-

ражением на границе (формально — при равен-

значение J(1, 1) = 4.23 ± 0.05 воспроизводится уже

при объеме выборки N_in = 10⁴ со временем счета

стве вещественных частей показателей преломле-

ния) вклад траектории с вершиной вне среды от-

несколько минут на обычном персональном компью-

тере при использовании одного ядра ЦП, в то вре-

брасывается в нашем алгоритме; таким образом вес

мя как в рамках общепринятого метода регистрации

n представляет собой произведение коэффициен-

рассеяния MCML, та же точность достигается при

тов Френеля; в частном случае рассеяния без отра-

выборке не менее миллиона, N_in ≥ 10⁶; число актов

жения равенство этого коэффициента нулю эквива-

рассеяния в обоих случаях не менее n = 10⁵.

лентно учету ограниченности среды.

Время счета почти линейно зависит от объема

выборки N_in, а также растет с ростом максималь-

5. МЕТОД ОБРАТНОГО ПРЕОБРАЗОВАНИЯ

но возможного числа актов рассеяния n_sc, учиты-

ДЛЯ ФАЗОВОЙ ФУНКЦИИ РГ

ваемого в сумме (17); в работе [23] было показано,

что результаты численного моделирования стабиль-

При МК-моделировании переноса излучения

ны в полубесконечной среде с точностью до процен-

стандартно используются две подстановки метода

та при n_sc ≤ 10⁵. При фиксированной транспортной

обратного преобразования: подстановка, основанная

длине l_tr = 1/μ^′s число учитываемых актов рассе-

на экспоненциальном распределении расстояний

яния должно увеличиваться с уменьшением длины

между рассеивателями, и подстановка, основанная

рассеяния l_s = l_tr(1 - g), т. е. с увеличением пара-

на фазовой функции угла рассеяния.

метра анизотропии g.

Для вычисления случайного значения подынте-

Описываемая процедура построения алгорит-

грального выражения, соответствующего n-му чле-

ну в (11), мы рекуррентно порождаем случайную

ма вычисления интенсивности рассеяния полностью

траекторию событий рассеяния в точках r_j , j =

повторяет известную процедуру MCML [21] вплоть

= 1, . . ., n, используя на каждом шаге две указан-

до момента, когда фотон покидает среду.

ные процедуры обратного преобразования. Расстоя-

В нашем подходе вклад диаграммы с фотоном,

ние r^′j = |r_j - rj-1| разыгрывается с помощью пере-

покинувшим среду, отбрасывается по условию огра-

менной ξ_j = exp(-μr^′j ), а полярный угол θ_j , отсчи-

ниченности области интегрирования. Вклад в сиг-

тывающийся от предыдущего направления рассея-

нал дает каждая диаграмма, как среднее экспонент

ния r′j-1, с помощью переменной

затухания exp(-μzni)); их величина определяется

координатами каждого акта рассеяния.

∫

Для сравнения рассматриваемого алгоритма с

(18)

χ_j = 2π p(t^′)dt^′, t_j = cosθ_j.

алгоритмом MCML мы рассчитали сигнал как чис-

-1

ло фотонов, покинувших среду, в соответствии с

методом MCML, и альтернативно согласно выра-

Переходя последовательно для каждого j = 2, 3, . . .

жению (17), которое можно интерпретировать как

от 3D-интегрирования по r_j к интегрированию по

среднее указанных экспонент, т. е. как среднее функ-

разностной переменной r^′j = r_j - rj-1, имеем

ций, описывающих затухание излучения, возвраща-

ющегося назад, к границе среды, испытав n актов

∫

рассеяния; напомним, что этот экспоненциальный

dr^′j Λ(r^′j )p(t_j )f(r^′j , t_j ) =

2πμ

множитель возникает при постановке задачи о рас-

∫1

∫

∫2π

сеянии во фраунгоферовом приближении для функ-

(

)

× dξ_j dχ_j

dφ_j f

-μ-1 ln ξ_j, t(χ_j)

(19)

ции Грина с точкой наблюдения вдали от среды.

На основе процедуры MCML рассчитывается сред-

465

ЖЭТФ, вып. 3

В. Л. Кузьмин, А. Ю. Вальков, Л. А. Зубков

ЖЭТФ, том 155, вып. 3, 2019

где f(r^′j , t_j ) — произвольная функция, t_j = t(χ_j ) —

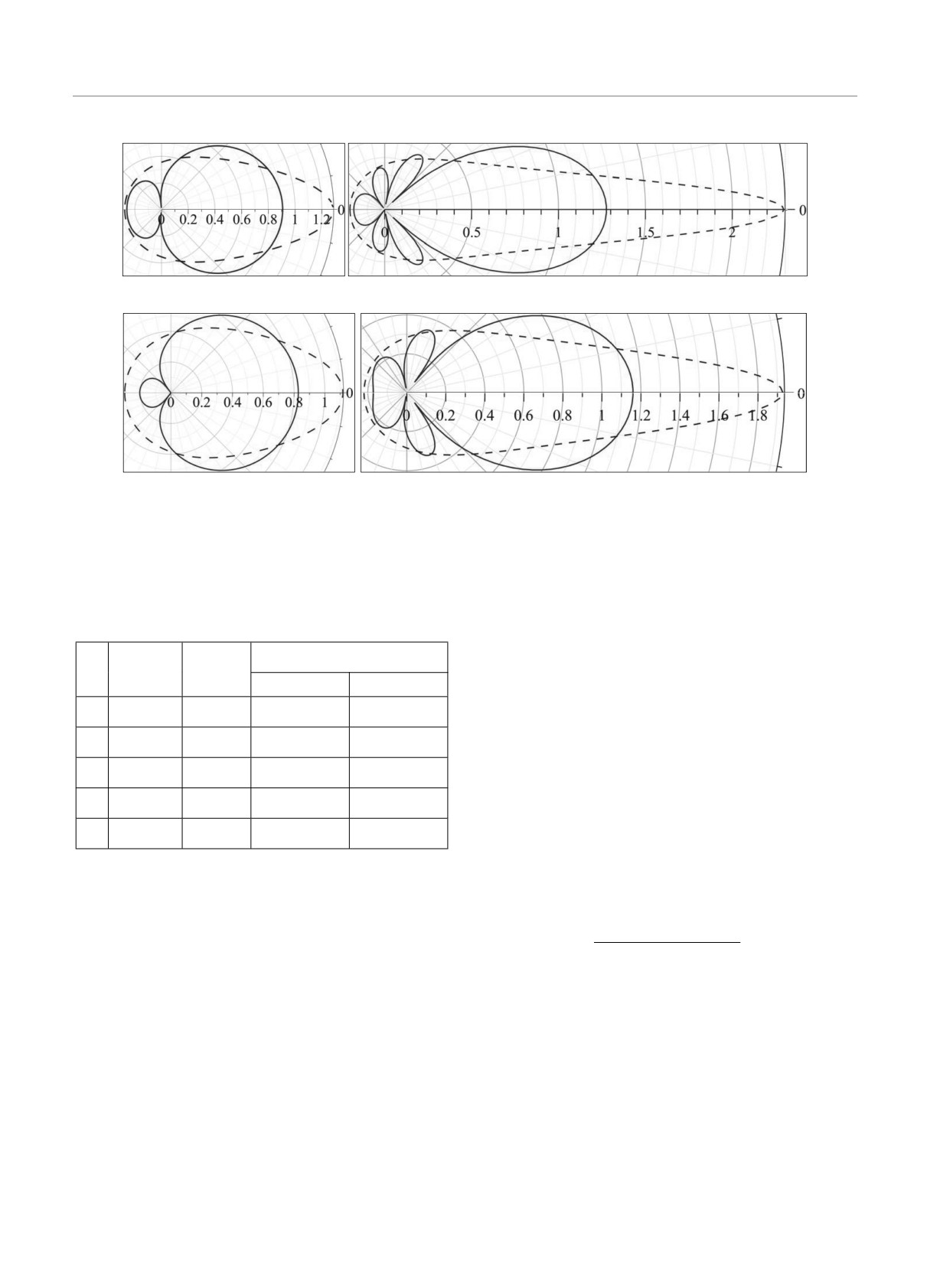
На рис. 2 мы представили фазовые функции ХГ и

обратная функция к χ_j = χ(t_j) в (18), φ_j — ази-

РГ для четырех значений параметров анизотропии

мутальный угол. Интегрирование в (19) выполня-

g, сжав для иллюстративности при больших значе-

ется усреднением по выборке равномерно распреде-

ниях интенсивности масштаб нелинейным образом.

ленных случайных переменных ξ_j , χ_j ∈ [0; 1] и φ_j ∈

Из (20) получаем χ^′ = F(q)/F(2kR). Обратное

∈ [0; 2π].

преобразование дает величину

√

Вводя переменную q = kR

2(1 - t) для (18), по-

q = F-1(x),

(27)

лучаем

∫q

где x = F (2kR)χ^′, 0 ≤ x ≤ F (2kR) < 1.

1 - χ = 2π(kR)-2 p(q^′)q^′dq^′.

(20)

Используя теорему Лагранжа об обращении ря-

дов, получим из (24) разложение

Здесь учтено условие нормировки

729

21627

q² =

x² +

x³ + . . . ,

(28)

560

22400

∫

2π(kR)-2

p(q^′)q^′dq^′ = 1.

(21)

по которому можно вычислять значения обратной

функции q

= F-1(x). Однако этот ряд сходит-

) ≈ 0.9528, где

ся только при |x|

< x₁ = F(q₁

Если рассматривать функцию 2π(kR)-2p(q^′) как

q₁ ≈ 4.4934 — наименьший положительный корень

плотность распределения величины q′ ∈ [0; 2kR],

уравнения tg(q) = q. В точке |x| = x₁ ряд расходит-

то согласно (20) функция χ^′(q) = 1 - χ(q) имеет

ся, так как (F-1)^′(x₁) = ∞ в силу F^′(q₁) = 0. По-

смысл кумулятивной функции распределения, кото-

этому разложение (28) практически полезно только

рая равна вероятности того, что величина q^′ нахо-

при x меньших x₁ и не слишком близких к нему.

дится в интервале (-∞; q).

Индикатриса рассеяния F^′(q) ∝ p(q) обращает-

Фазовую функцию РГ можно записать как

ся в нуль во всех точках q_m > 0, удовлетворяющих

уравнению

p(q) = 2(πA)-1q-6(sin q - q cos q)².

(22)

q_m = tg q_m.

(29)

По условию (21) постоянная A = (kR)-2F(q_max), где

, для которых интен-

Его корни определяют углы θ_m

∫q

сивность однократного рассеяния равна нулю,

F (q) = 4 q′-5(sin q^′ - q^′ cos q^′)²dq^′,

(23)

θ_m = 2 arcsin

(30)

max

q_max = 2kR — наибольшее физически возможное

Для вычисления q_m удобен асимптотический ряд

значение безразмерного параметра q. Существенно,

что F (q) является элементарной функцией,

146

q_m = r_m -

3r3m

15r5m

105r7m

F (q) = q-4(q⁴ - q² + q sin 2q - sin² q),

(24)

781

16328

+···,

(31)

0 ≤ F(q) < 1.

⁻ 315r9_m -

3465r¹¹

Фазовая функция ХГ

где r_m = π(m + 1/2), m ≥ 1. В точках

1-g

p_HG(t) =

(25)

4π (1 + g² - 2gt)3/2

x_m = F(q_m) = q2m/(1 + q2m)

была впервые предложена для рассеяния в астро-

обратная функция F-1(x) имеет сингулярности про-

(

)_′

физике [24]. Подставляя (25) в (18) легко получить

изводной

F-1(x)

∝ (x - x_m)-2/3.

для этой модели кумулятивную функцию распреде-

Эти сингулярности мы учитываем в числен-

ления по углу θ в виде элементарной функции. Ши-

ном алгоритме кусочной аппроксимации F-1(x) так,

рокое распространение ХГ-модели для МК-модели-

чтобы ее первая производная имела правильные осо-

рования рассеяния в различных физических систе-

бенности в точках x_m. При x < x₁ ≈ 0.9528, не очень

мах связано с тем, что здесь несложной элементар-

близких к x₁, используется аппроксимация (28) вы-

ной функцией оказывается также и функция, обрат-

сокого порядка.

ная к кумулятивной:

Мы выбрали параметры среды, характерные для

2(1 + g²)χ(gχ + 1 - g) - (1 - g)

водной суспензии интралипида, используемой в ка-

(26)

честве биомодели (биофантома) при моделировании

(2gχ + 1 - g)²

466

ЖЭТФ, том 155, вып. 3, 2019

Диффузия фотонов в случайных средах. . .

= 685 нм

g = 0.773

g = 0.926

R = 250 нм

R = 500 нм

= 830 нм

g = 0.705

g = 0.895

R = 250 нм

R = 500 нм

Рис. 2. Фазовые функции ХГ (штриховые линии) и РГ (сплошные линии) для двух длин волн и сред с четырьмя пара-

метрами анизотропии g и соответствующими им радиусами рассеивателей R; показатель преломления n = 1.33

Таблица 1. Некоторые особые точки qm, xm и со-

денных значений длины волны и показателя пре-

ответствующие им углы θm для λ = 685 нм и

ломления имеем q_max ≈ 6.100, x_max ≈ 0.9738 при

n = 1.33

R = 250 нм, и q_max ≈ 12.20, x_max ≈ 0.9933... при

R = 500 нм. В клетках, содержащих прочерки, нару-

θ_m

шается условие q_m < q_max и θ_m не существуют. Ряд

m q_m

x_m R = 250 нм R = 500 нм

(28) можно использовать в области, реализуемой с

вероятностью ξ^′ = x₁/x_max ≈ 0.978 при R = 250 нм

4.4934

0.95281

94.9^◦

43.2^◦

и ξ^′ ≈ 0.959 при R = 500 нм; отметим, что в уг-

7.7253

0.98352

78.6^◦

ловых переменных для применимости (28) это дает

соответственно интервалы θ < 94.9^◦ и θ < 43.2^◦,

10.904

0.99166

126.7^◦

сужающиеся с ростом размера частиц с ростом вы-

14.066

0.99550

тянутости индикатрисы.

32.956

0.99908

В модели ХГ анизотропия рассеяния определя-

ется параметром g = 〈cosθ_s〉, а в модели РГ — пара-

метром kR, связанным с g соотношением [8]

биоткани. В работе [25] были выполнены измерения

фазового сдвига и амплитуды DPDW в частотно-

4 - (kR)-2 Cin(4kR)

- 3,

(32)

доменном инcтрументарии с длиной волны λ

F (2kR)

= 685 нм и показателем преломления воды n = 1.33.

Для системы твердых сфер с R = 250 нм величина

где Cin(x) — интегральный косинус.

kR ≈ 3.05 и из (32) имеем g = 0.7727. Эта пара

параметров применяется далее при сравнительном

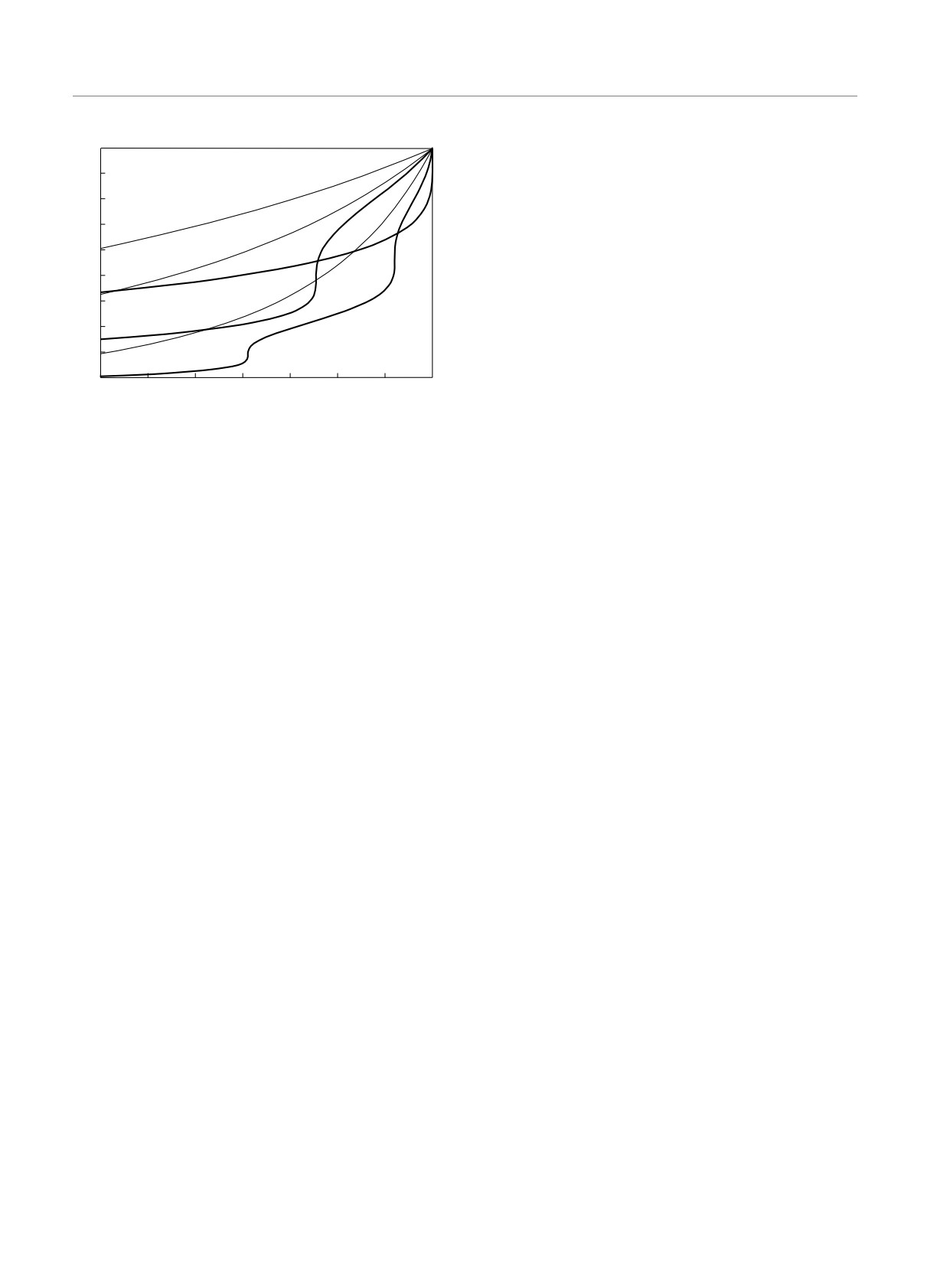
Рисунок 3 [8] показывает существенное отличие

анализе моделей ХГ и РГ.

кумулятивных функций распределения, используе-

В табл. 1 приведены некоторые значения q_m и

мых при МК-симуляциях многократного рассеяния,

x_m; для типичных размеров частиц R = 250 нм

для моделей ХГ и РГ с равными параметрами анизо-

и R = 500 нм, приведены также углы рассеяния

тропии g. В частности, для кривых РГ видны точки

(30), где фазовая функция РГ обращается в нуль;

сингулярностей производных, отвечающие обраще-

мы положили λ = 685 нм, n = 1.33. Для приве-

нию в нуль интенсивности рассеяния.

467

В. Л. Кузьмин, А. Ю. Вальков, Л. А. Зубков

ЖЭТФ, том 155, вып. 3, 2019

1- t

ственно более вытянутым характером индикатрисы

2.0

рассеяния ХГ по сравнению с индикатрисой РГ на

1.8

узком участке вперед, что хорошо видно на рис. 2.

Этот пик интегрально вносит весьма малый вклад в

1.6

рассеяние, но заметно увеличивает необходимые для

1.4

достижения нужной точности эффективные кратно-

1.2

сти n_sc в алгоритме МК.

1.0

Отметим, что с ростом анизотропии значения ин-

тенсивности рассеяния от полупространства J(1, 1)

0.8

для моделей РГ и ХГ все более различаются, что

0.6

указывает на нарушение стандартного представле-

0.4

ния об универсальности описания многократного

рассеяния в терминах l_tr

и и g.

0.93

0.94

0.95

0.96

0.97

0.98

0.99

1.00

Для сравнения результатов расчета в рамках мо-

делей РГ и ХГ мы взяли данные, полученные пу-

Рис. 3. Угловая переменная 1 - t = 1 - cos θ как функ-

тем измерения для суспензии интралипида в мето-

ция кумулятивной вероятности χ^′ для моделей ХГ (тонкие

дологии DPDW в частотном домене [25] с концен-

линии) и РГ (толстые линии) в области χ^′ близких к еди-

трацией от 0.5 до 2 объемных процентов для часто-

нице: 1 — g = 0.654; 2 — g = 0.786; 3 — g = 0.931. В

ты модуляции (2π)-1ω = 100-200 МГц и ближне-

модели РГ этим значениям g, согласно (32), соответству-

инфракрасного излучения с длинами волны λ =

ют kR = 2.31, 3.21, 6.42

= 685 нм или 830 нм.

На рис. 4 мы представили функцию ослабления

Φ(ρ) = ln(ρ2j(ρ)), обычно используемую при ин-

6. МОДЕЛИРОВАНИЕ DPDW

терпретации измерений, в зависимости от рассто-

яния источник-приемник, в сравнении с результа-

Мы выполнили расчеты интенсивности обратно-

тами численного моделирования на основе фазо-

го рассеяния в зависимости от расстояния между

вых функций РГ и ХГ. Экспериментальные дан-

источником и приемником, расположенными на по-

ные представлены для однопроцентной концентра-

верхности образца. Пусть сигнал образован вкла-

ции водного раствора интралипида. При моделиро-

дом излучения, попадающего на поверхности в коль-

вании обратного рассеяния излучения с длиной вол-

цо радиуса ρ и шириной Δρ ≪ ρ; определим ло-

ны λ = 685 нм мы положили [25] коэффициент рас-

кальную интенсивность обратного рассеяния j(ρ) =

сеяния μ^′s = 10.5 см-1 и коэффициент поглощения

= S-1J(1, 1) как отношение полной интенсивности

μ_a = 0.004 см-1, что практически совпадает с дан-

J (1, 1) в кольце, к площади кольца, S = 2πρΔρ.

ными для чистой воды при этой длине волны; по-

В табл. 2 приведены результаты для рассеяния

казатель преломления n = 1.33. В соответствии с

точно назад, J(1, 1), для фазовых функций ХГ и РГ

оценками производителя, мы положили радиус час-

от полубесконечной среды для различной степени

тиц интралипида R = 250 нм. Формула (32) при

анизотропии. Видно прекрасное согласие с точным

этом размере рассеивателей дает значение парамет-

решением задачи Милна при g = 0, что можно рас-

ра анизотропии g = 0.773, которое далее мы ис-

сматривать как верификацию численных расчетов.

пользуем при моделировании с функцией ХГ. Пе-

Приведены значения J(1, 1), полученные при учете,

реходя к моделированию рассеяния с длиной волны

в порядке возрастания, n_sc/100, n_sc/10, и n_sc = 2·10⁶

λ = 830 нм, при том же значении размера частиц

актов рассеяния, и время счета на обычном персо-

из формулы (32) получаем g = 0.705; приведенный

нальном компьютере при использования одного яд-

коэффициент рассеяния с изменением длины волны

ра ЦП. Отметим здесь, что, как оказалось, расчеты

при этом уменьшается [6] (μ^′s = 8.74 см-1); адсорб-

по модели ХГ требуют для достижения той же чис-

ция воды для указанной длины волны увеличивает-

ленной точности больших значений N_in и n_sc и, со-

ся, μ_a = 0.04 см-1.

ответственно, большего машинного времени, чем по

Как видно на графиках, интенсивность, рассчи-

модели РГ. Данный факт может, на первый взгляд,

танная с фазовой функцией РГ, превышает значе-

показаться удивительным, поскольку аналитически

ния, полученные в модели ХГ, в особенности в облас-

кумулятивная функция ХГ выглядит проще, чем

ти малых расстояний источник-приемник, где доля

аналогичная функция РГ. Мы объясняем это суще-

вклада низших кратностей рассеяния, сохраняющих

468

ЖЭТФ, том 155, вып. 3, 2019

Диффузия фотонов в случайных средах. . .

Таблица 2. Интенсивность J(1, 1) многократного рассеяния строго назад от полупространства для моделей ХГ и

РГ для пяти различных значений анизотропии, заданных параметрами g и R. При g = 0 (R = 0) результаты обеих

моделей идентичны; указано также теоретическое значение для асимптотически предельно большой анизотропии

g = 1. Приведены данные при учете nsc/100, nsc/10 и nsc актов рассеяния. Погрешности интенсивности при nsc

актах рассеяния порядка 0.2-0.3 %, соответствующее время счета τ

Параметры

Интенсивность, J(1, 1)

τ,

N_in

ХГ

РГ

Теория

нм

мин

n_sc/100

n_sc/10

n_sc n_sc/100 n_sc/10 n_sc

10⁵

2 · 10⁶

4.16

4.21

4.22

4.16

4.21

4.22

4.22768 [20]

0.211

100

10⁵

2 · 10⁶

4.20

4.24

4.25

4.19

4.24

4.25

0.467

150

10⁵

2 · 10⁶

4.28

4.34

4.36

4.34

4.39

4.40

0.773

250

5 · 10⁵

2 · 10⁶

150

4.39

4.47

4.50

4.53

4.63

4.65

0.925

500

10⁵

4 · 10⁶

4.46

4.60

4.64

4.58

4.69

4.72

∞

4.8897 [26]

специфику угловой зависимости фазовой функции,

мые суспензии с радиусами рассеивателей R = 250,

возрастает.

R = 150, R = 100 нм и соответствующими парамет-

Численные значения интенсивности, полученные

рами g = 0.773, g = 0.467, g = 0.211, в зависимости

для анизотропного рассеяния, превышают результа-

от расстояния источник-детектор для среды, зани-

ты для изотропного рассеяния для обеих моделей

мающей полупространство.

(опять за исключением малых расстояний).

Графики демонстрируют существенное различие

Отметим, что наклоны кривых практически сов-

при описании рассеяния в рамках моделей ХГ и РГ

падают для расстояний, превышающих несколько

с равными коэффициентами рассеяния и равными

транспортных длин, ρ ≥ 0.6 см, для обеих моделей

параметрами анизотропии g.

анизотропии. При малых расстояниях измеренные

Представленные на рисунках данные указывают

и рассчитанные значения несопоставимы, посколь-

на явно выраженную зависимость от степени анизо-

ку на таких расстояниях существенным становит-

тропии: на малых расстояниях до двух транспорт-

ся учет конечности диаметра падающего пучка ла-

ных длин интенсивность обратного рассеяния сре-

зерного излучения, в то время как в моделирова-

дами с анизотропией g = 0.77 превышает интен-

нии он представляется как предельно узкий пучок

сивность обратного рассеяния средой с изотропным

(см. [21]).

рассеянием в 1.3 раза в случае ХГ-анизотропии и

Численные результаты на рис. 4 получены с уче-

более чем в 1.5 раза в случае РГ-анизотропии, при

том эффектов внутреннего отражения, обусловлен-

одном и том же значении коэффициентов μ^′s и μ_a.

ного скачком показателя преломления на грани-

В случае сравнения расчетов рассеяния средами с

це; эти эффекты сглаживают различие в поведе-

меньшей анизотропией, g = 0.47, это превышение

нии сигналов DNIRS, обусловленное видом фазовых

составляет приблизительно 1.3 и 1.2 соответствен-

функций. Для иллюстрации различия между дву-

но для фазовых функций РГ и ХГ. Эти данные мо-

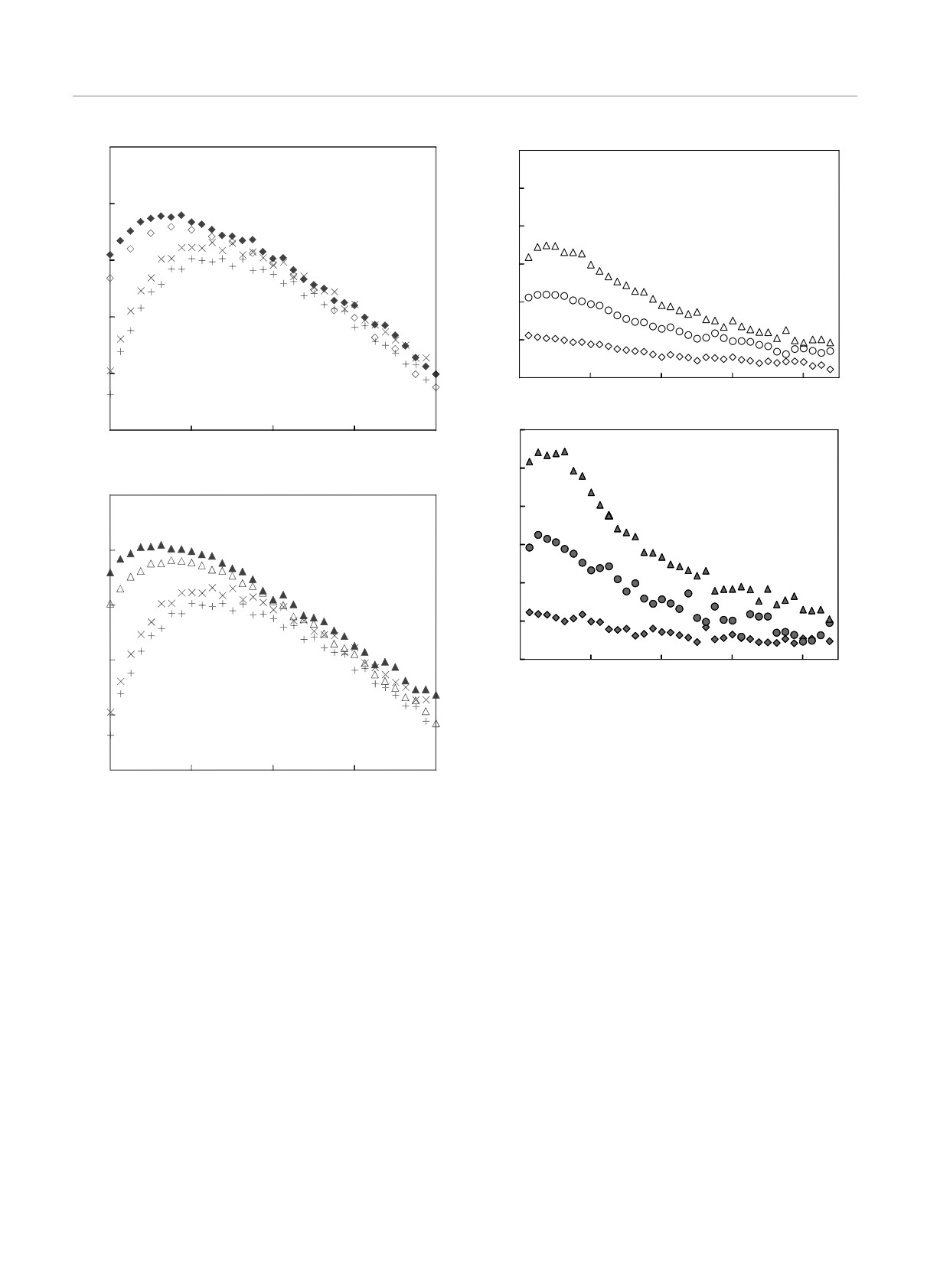
мя моделями анизотропии мы представили отноше-

гут позволить определить экспериментально, какой

ния интенсивностей j_HG и j_RG, вычисленных для

механизм рассеяния, РГ или ХГ, ближе к реально-

двух моделей анизотропии, к интенсивности j_iso,

му, путем измерений в средах с различными значе-

наблюдаемой в системе с изотропным рассеянием,

ниями параметра g. Отметим, что на расстояниях

с теми же оптическими параметрами; мы выпол-

порядка десяти транспортных длин и более исчеза-

нили моделирование для случая равных показате-

ет различие между данными для рассматриваемых

лей преломления на границе. На рис. 5 для излу-

моделей ХГ и РГ, в обоих случаях интенсивность

чения с λ = 685 нм приведены отношения j_RG/j_iso

обратного рассеяния приближается к интенсивности

и j_HG/j_iso для трех различных значений парамет-

j_iso изотропной модели, подтверждая общее утверж-

ров анизотропии, описывающих три предполагае-

дение диффузионной теории об универсальности пе-

469

В. Л. Кузьмин, А. Ю. Вальков, Л. А. Зубков

ЖЭТФ, том 155, вып. 3, 2019

HG iso

–5.5

1.6

1.5

-5.7

1.4

-5.9

1.3

1.2

-6.1

1.1

-6.3

1.0

0.1

0.3

0.5

0.7

0.9

, см

RG iso

-6.5

1.6

0.2

0.4

0.6

0.8

1.0

см

1.5

-5.5

1.4

-5.7

1.3

1.2

-5.9

1.1

1.0

-6.1

0.1

0.3

0.5

0.7

0.9

, см

-6.3

Рис. 5. Интенсивности рассеяния, рассчитанные для моде-

лей среды с анизотропным рассеянием (jHG или jRG), от-

несенные к соответствующей интенсивности для изотроп-

-6.5

ной модели jiso: a) △ — g = 0.77, ◦ — g = 0.47, ♦ —

0.2

0.4

0.6

0.8

1.0

g = 0.21; б) ▴ — R = 250 нм (g = 0.77), • — R = 150 нм

см

(g = 0.47), ♦ — R = 100 нм (g = 0.21); ltr = 950 мкм,

λ = 685 нм

Рис. 4. Функция затухания Φ(ρ) = ln(ρ²j(ρ)) в зависимо-

сти от расстояния источник-приемник, измеренная в од-

но в рамках одной из двух моделей: широко исполь-

нопроцентном по объему водном растворе интралипида с

зуемой для моделирования функции Хеньи - Грин-

показателем преломления n = 1.33, для двух длин волн:

штейна, удобной в силу простоты обратной куму-

λ = 685 нм (×), и λ = 830 нм (+), и рассчитанная на

лятивной функции распределения, и функции Рэ-

основе двух моделей: ХГ (♦), РГ (▴) при λ = 685 нм, и

лея - Ганса, позволяющей моделировать оптические

моделей ХГ (♦), РГ (△) при λ = 830 нм; частота модуля-

свойства ткани или биофантома на основе физиче-

ции ω = 100 · 2π

ской модели суспензии.

реноса излучения в указанном диапазоне расстоя-

Развитый алгоритм моделирования, являющий-

ний для систем с одинаковым значением транспорт-

ся модификацией стандартного метода MCML, ве-

ной длины.

рифицирован путем сопоставления численных ре-

зультатов с известными точными результатами для

7. ЗАКЛЮЧЕНИЕ

изотропного рассеяния.

Мы выполнили численное моделирование интен-

При описании угловой зависимости сечения рас-

сивности обратного рассеяния в полубесконечной

сеяния, или фазовой функции, современный алго-

случайной среде, имитирующей биоткань, с учетом

ритм моделирования Монте-Карло существенно ис-

анизотропии рассеяния, описываемой альтернатив-

пользует метод обратного преобразования кумуля-

470

ЖЭТФ, том 155, вып. 3, 2019

Диффузия фотонов в случайных средах. . .

тивной угловой функции распределения. Его реа-

E. V. Aksenova, D. I. Kokorin, and V. P. Romanov,

лизация в модели ХГ общеизвестна; в настоящей

Comp. Phys. Comm. 196, 384 (2015).

работе этот метод реализован для модели РГ на

В. Л. Кузьмин, А. Ю. Вальков, Письма в ЖЭТФ

основе найденной в замкнутом виде кумулятивной

105, 261 (2017).

функции. В области углов рассеяния, реализуемых

с большей вероятностью, порядка 0.8, функция об-

T. Binzoni, and F. Martinelli, Appl. Opt. 54, 5320

ратного преобразования аппроксимируется в виде

(2015).

конечного полинома высокого порядка. А в области

10.

D. A. Boas, S. Sakadžić, J. Selb, P. Farzam,

больших углов, реализуемых с вероятностью поряд-

M. A. Franceschini, and S. A. Carp, Neurophotonics

ка 0.2, мы моделировали ее путем кусочного сшива-

3, 031412 (2016).

ния обратных кубических парабол на участках меж-

ду точно известными точками сингулярности обрат-

11.

D. Diaz, A. Lafontant, M. Neidrauer, M. S. Wein-

garten, R. DiMaria-Ghalili, E. Scruggs, J. Rece,

ной функции, так чтобы правильно передать эти

G. W. Fried, V. L. Kuzmin, and L. Zubkov, J.

сингулярности. Данная процедура позволяет выпол-

Biomed. Opt. 22, 25003 (2017).

нять моделирование рассеяния в рамках развитого

алгоритма одинаково эффективно для обеих фазо-

12.

D. Toublanc, Appl. Opt. 35, 3270 (1996).

вых функций.

13.

Q. Liu and F. Weng, Appl. Opt. 45, 7475 (2006).

Исследуя интенсивность обратного рассеяния

как функцию расстояния источник-приемник,

14.

H. R. Gordon, Opt. Express 15, 5572 (2007).

мы обнаружили ее зависимость от вида функции

15.

Е. В. Аксенова, В. Л. Кузьмин, В. П. Романов,

распределения и степени анизотропии рассеяния.

ЖЭТФ 135, 587 (2009).

Различие описаний в рамках двух моделей уве-

личивается с ростом анизотропии, что позволяет

16.

В. Л. Кузьмин, А. Ю. Вальков, Опт. и спектр. 111,

определить предпочтительность той или другой

497 (2011).

фазовой функции при интерпретации сигналов

17.

E. V. Aksenova, D. I. Kokorin, and V. P. Romanov,

DNIRS путем анализа данных, выполненных в

Phys. Rev. E 89, 052506 (2014).

системах с одинаковыми значениями приведенного

коэффициента рассеяния, но с различными значе-

18.

Е. Е. Городничев, С. Л. Дударев, Д. Б. Рогозкин,

ниями параметра анизотропии.

ЖЭТФ 96, 847 (1989).

19.

V. L. Kuzmin, V. P. Romanov, and E. V. Aksenova,

Работа выполнена при финансовой поддержке

Phys. Rev. E 65, 016601 (2001).

РФФИ (грант № 16-02-00465A). Авторы благодарны

Д. И. Кокорину за помощь в вычислениях.

20.

T. M. Nieuwenhuizen and J. M. Luck, Phys. Rev.

E 48, 569 (1993).

ЛИТЕРАТУРА

21.

L. H. Wang, S. L. Jacques, and L. Q. Zheng, Comput.

Meth. Prog. Bio. 47, 131 (1995).

1. V. V. Tuchin, Handbook of Optical Biomedical Diag-

nostics, 2nd ed. SPIE Publ., Bellingham, WA (2016).

22.

T. H. Pham, O. Coquoz, J. B. Fishkin, E. Anderson,

and B. J. Tromberg, Rev. Sci. Instrum. 71, 2500

2. T. Durduran, R. Choe, W. B. Baker, and A. G. Yodh,

(2000).

Rep. Prog. Phys. 73, 076701 (2010).

23.

M. H. Eddowes, T. N. Mills, and D. T. Delpy, Appl.

3. В. В. Тучин, Оптика биологических тканей. Ме-

Opt. 34, 2261 (1995).

тоды рассеяния света в медицинской диагности-

ке, Физматлит, Москва (2012).

24.

L. G. Henyey, and J. L. Greenstein, Astrophys. J. 93,

4. T. Vo-Dinh, Biomedical Photonics Handbook, V. II,

70 (1941).

2nd ed. CRC Press, New York (2015).

25.

V. L. Kuzmin, M. T. Neidrauer, D. Diaz, and

5. А. Исимару, Распространение и рассеяние волн в

L. A. Zubkov, J. Biomed. Opt. 20, 5006 (2015).

случайно-неоднородных средах, Том 1, Мир, Моск-

ва (1981).

26.

E. Amic, J. M. Luck, and T. M. Nieuwenhuizen, J.

6. В. Л. Кузьмин, ЖЭТФ 127, 1173 (2005).

Phys. A: Mathematical and General 29, 4915 (1996).

471