ЖЭТФ, 2019, том 155, вып. 3, стр. 472-480

ФУНКЦИЯ ГРИНА УРАВНЕНИЯ ШРЕДИНГЕРА

В МЕТОДЕ КВАНТОВАНИЯ ПОТЕНЦИАЛА

Б. Я. Балагуров^*

Институт биохимической физики им. Н. М. Эмануэля Российской академии наук

119334, Москва, Россия

Поступила в редакцию 25 сентября 2018 г.,

после переработки 25 сентября 2018 г.

Принята к публикации 29 сентября 2018 г.

Задача определения функции Грина G(r, r^′) для стационарного уравнения Шредингера рассмотрена в

рамках метода квантования потенциала. Найдено выражение для G(r, r^′) через собственные функции и

собственные значения этого метода. Доказана эквивалентность использованного и традиционного спо-

собов решения рассмотренной задачи.

DOI: 10.1134/S004445101903009X

При этом предложенный в книге [2] подход дает по-

следовательную схему вычисления функции Грина.

1. ВВЕДЕНИЕ

Заметим, что задачу об упругом рассеянии так-

же можно трактовать как проблему отклика на

При решении большинства задач квантовой ме-

внешнее воздействие — падающую плоскую волну.

ханики используются различные варианты теории

Однако при решении этой задачи для определе-

возмущений [1]. В этих задачах ищется, как прави-

ния функции Грина необходим другой, отличный от

ло, отклик квантовомеханической системы на неко-

приведенного в книге [2], способ ее вычисления, не

{

}

торое внешнее воздействие, например, слабое элек-

требующий привлечения системы

ψ^(+)k(r)

трическое поле. Для нахождения такого отклика

В настоящей работе для вычисления функции

нужно решить некоторое неоднородное уравнение,

Грина G(r, r^′) применен альтернативный использо-

следующее из исходного уравнения Шредингера при

ванному в книге [2] подход, основанный на мето-

введении малой добавки в гамильтониан, обуслов-

де квантования потенциала [3]. Впервые подобный

ленной внешним воздействием. Обычным способом

метод был предложен в работе [4], в которой в

решения таких уравнений является разложение ис-

качестве объекта квантования выбиралась некото-

комой поправки к волновой функции по полной си-

рая константа, введенная в уравнение Шредингера

стеме волновых функций невозмущенного гамильто-

как множитель к потенциальной энергии. Сходный

ниана. При традиционном подходе [1] используется

подход, при котором квантуется глубина потенци-

образующая полный набор совокупность волновых

альной ямы, развивался в работе [5] и применялся

функций ψ_ν(r) связанных состояний (если они есть в

при решении различных физических задач (см. так-

данном потенциале) с системой волновых функций

же [3]).

ψ^(+)k(r) непрерывного спектра энергии — решений

Использование метода из книги [3] позволило вы-

задачи об упругом рассеянии плоской волны.

Проблему отыскания откликов квантовомехани-

разить величину G(r, r^′) через собственные функ-

ции ϕ_ν (r) и собственные значения α_ν этого мето-

ческой системы на разнообразные внешние воздей-

да. Полученная общая формула для функции Гри-

ствия можно унифицировать, введя функцию Гри-

на G(r, r^′) для невозмущенного уравнения Шредин-

на не содержит посторонних элементов вроде плос-

кой волны и воспроизводит известные результаты

гера. Использование метода разложения по системе

{

}

функций

ψ_ν(r), ψ^(+)k(r)

позволяет найти для ве-

в различных предельных случаях. Применение най-

денного для G(r, r^′) выражения в задаче об упругом

личины G(r, r^′) точное формальное выражение [2].

рассеянии дает решение этой проблемы, совпадаю-

^* E-mail: balagurov@deom.chph.ras.ru, byabalagurov@mail.ru

щее с полученным в статье [6]. Отметим, что методы

472

ЖЭТФ, том 155, вып. 3, 2019

Функция Грина уравнения Шредингера. ..

книг [2, 3] приводят к кардинально различающимся

Выражения для собственных значений и соб-

по форме выражениям для функции Грина. Тем не

ственных функций при отрицательных (ε = -κ² <

менее, как показано в настоящей работе, оба подхо-

< 0) и положительных (ε = k² > 0) энергиях сле-

да к вычислению величины G(r, r^′) эквивалентны.

дуют из формул для комплексных ε = q² в соответ-

ствующих пределах; q → iκ и q → k + i0, так что

2. НУЛЕВАЯ ФУНКЦИЯ ГРИНА

α_ν(κ) = α_ν(iκ), ϕ_ν(κ; r) =

ϕ_ν(iκ; r),

(7)

Представим потенциальную энергию U(r) в ви-

де U(r) = U⁰ v(r), где U⁰ — величина потенциала, а

α(+)ν(k) = α_ν(k+i0), ϕ(+)ν(k; r) =

ϕ_ν(k+i0; r).

(8)

функция v(r) задает его форму. Далее ограничим-

ся, как и в работе [6], рассмотрением случая, когда

Как функции энергии величины αν+)(k) и ϕν+)(k; r)

0 ≤ v(r) ≤ 1 и v(r) при r → ∞ достаточно быст-

определены на верхнем берегу разреза на физиче-

ро (например, экспоненциально) обращается в нуль.

ском листе, а α_ν (κ) и ϕ_ν (κ; r) — на отрицательной

Стационарное уравнение Шредингера запишем в ви-

вещественной полуоси этого листа.

{

}

де

Система функций

ϕ_ν(r)

ортонормирована с

весом v(r):

∇² ψ(r) + ε ψ(r) = α v(r)ψ(r),

(1)

∫

ϕ_μ(r)ϕν(r)v(r)dr = δμν

(9)

где ε = 2mE/ℏ², α = 2mU⁰/ℏ².

Задачу определения функции Грина для уравне-

и, по предположению, полна, так что выполняется

ния (1) будем решать в общем случае комплексной

соотношение

энергии

∑

v(r)

ϕ_ν(r)ϕν(r′) = δ(r - r′).

(10)

ε(q) = q², q = k + iκ,

(2)

используя метод квантования потенциала.

Для потенциалов с конечным радиусом действия это

1. Собственные функции

ϕ_ν(r) этого метода яв-

равенство справедливо для тех r и r^′, для которых

ляются решениями уравнения

v(r) = 0 и v(r^′) = 0. В соотношениях (9) и (10) обе

собственные функции относятся к одной и той же

∇²

ϕ_ν(r) + q²

ϕ_ν(r) = α_ν(q)v(r)ϕν(r)

(3)

энергии.

Нулевая функция Грина

G⁰(r - r^′) является ре-

с асимптотическим поведением

шением уравнения

iqr

r→∞:

ϕ_ν(r) ∼

(4)

∇^2r G⁰(r - r^′) + q² G⁰(r - r^′) = δ(r - r^′)

(11)

(Величины, относящиеся к комплексной энергии,

c условием

G⁰(r - r^′) → 0 при r → ∞ и имеет вид

снабжаем черточкой сверху.) При выборе для соб-

ственной функции асимптотики вида (4) должно

G⁰(r - r^′) = -

eiq|r-r′|.

(12)

4π |r - r^′|

выполняться условие

С помощью (11) дифференциальное уравнение (3)

Im q = κ > 0,

(5)

преобразуем в интегральное

∫

которое обеспечивает обращение

ϕ_ν(r) в нуль в пре-

ϕ_ν(r) = α_ν(q)

G⁰(r - r^′)

ϕ_ν(r^′)v(r^′)dr^′.

(13)

деле r → ∞. Следовательно, собственные функции

ϕ_ν(r) и собственные значения α_ν(q) определены на

Отсюда находим асимптотическое выражение для

верхней полуплоскости комплексной переменной q,

собственной функции при r → ∞:

чему отвечает физический лист [1] соответствующей

римановой поверхности комплексной энергии. Для

α_ν(q) u_ν(n, q) e^iqr

ϕ_ν(r) ∼ -

(14)

собственных значений α_ν = α_ν (q) и функций

ϕ_ν =

4π

ϕ_ν(q; r) имеют место соотношения симметрии [3,6]

где n = r/r и

α_ν(- q^∗) = α^∗ν(q),

ϕ_ν(- q^∗; r) =

ϕ^∗ν(q; r),

(6)

∫

u_ν(n, q) = e-iqn·r

ϕ_ν(r) v(r) dr.

(15)

справедливые при Im q > 0.

473

Б. Я. Балагуров

ЖЭТФ, том 155, вып. 3, 2019

Величины

u_ν(- n, q) являются коэффициента-

Здесь P^ml(x) — присоединенные полиномы Лежанд-

ми разложения функции exp(iqn · r) по системе

ра [7] и

{

}

ϕ_ν(r)

∑

= {sinθ cosφ, sinθ sinφ, cosθ}.

(25)

eiqn·r =

u_ν(- n, q)

ϕ_ν(r).

(16)

{

}

Система сферических функций

Y (λ)lm (n)

(λ = 1,

Здесь n — произвольный единичный вектор.

2) является ортонормированной:

Заменим в уравнении (13) r^′ на r^′′, затем умно-

∫

жим его на

ϕ_ν(r^′)/α_ν(q) и просуммируем по ν:

′

(n) dn = δ_λλ′ δ_ll′ δ_mm′ ,

(26)

∫

ϕ_ν(r)

ϕ_ν(r^′)

G⁰(r - r^′′) ×

где dn = do = sin θ dθ dφ, и полной:

α_ν

(q)

[

]

∑ l∑

∑

(λ)

Y_l

(n) Y(λ)lm(n^′) = δ(n - n^′),

(27)

× v(r^′′)

ϕ_ν(r^′′)

ϕ_ν(r^′) dr^′′.

(17)

λ=1 l=0 m=0

Согласно соотношению (10) выражение в квадрат-

ных скобках равно δ(r^′′ - r^′). Поэтому из равенства

δ(n - n^′) =

δ(θ - θ^′) δ(φ - φ^′).

(28)

sinθ

(17) получаем следующее представление для нуле-

вой функции Грина:

Отметим также, что

∑

ϕ_ν(r)

ϕ_ν(r^′)

G⁰(r - r^′) =

(18)

(λ)

2l + 1

α_ν(q)

∑∑^l Y_l

(n) Y(λ)lm(n^′) =

P_l(n · n^′),

(29)

4π

λ=1 m=0

В случае потенциала с конечным радиусом действия

где P_l(x) — обычные полиномы Лежандра.

представление (18) имеет место, если хотя бы для

Собственную функцию

ϕ_ν(r)

ϕ_λlmn(r, θ, φ)

одного из радиус-векторов r или r^′ функция v(r) от-

представим в виде

лична от нуля.

Согласно [5] для энергии связанного состояния ν,

ϕ_λlmn(r) =

ϕ_ln(r)Y(λ)lm(n).

(30)

если оно есть в потенциале α v(r), имеем выражение

ε_ν = -κ2ν, где κ_ν — решение уравнения

Радиальная собственная функция

ϕ_ln(r) подчиня-

ется уравнению

α_ν(κ) = α.

(19)

d²

ϕ_ln(r)

l(l + 1)

Волновая функция ψ_ν(r) этого состояния имеет вид

ϕ_ln(r)+

dr²

r dr

r²

ψ_ν(r) = C_ν ϕ_ν(κ_ν; r),

(20)

+ q²

ϕ_ln(r) = α_ln(q)v(r)ϕln(r).

(31)

)-1/2

Индексом n отмечены различные решения уравне-

([

]

dα_ν

^[ dε_ν (α)]1/2

ния (31) при фиксированном l. Система радиальных

C_ν =

(21)

dεε=-κ2

dα

собственных функций {ϕln(r)} при фиксированном

l ортонормирована,

2. Для потенциалов с центральной симметрией

∞

∫

рассматриваемая задача может быть упрощена пу-

тем отделения от

ϕ_ν(r) и других функций соответ-

ϕ_ln(r)ϕln′ (r)v(r)r2 dr = δnn′

(32)

ствующих угловых частей. Для этого введем веще-

ственные сферические функции Y(λ)lm(n):

и полна,

Y (1)lm (n) = alm P^ml(cos θ)cosmφ,

0≤m≤l,

(22)

∑

v(r)

ϕ_ln(r)ϕln(r′) =

δ(r - r^′).

(33)

r²

Y (2)lm (n) = alm P^ml(cosθ)sinmφ,

1≤m≤l;

(23)

¯0(r - r′) из (12) справедливо разложение

Для

[

]1/2

∑

2l + 1

(l-m)!

G⁰(r - r^′) =

(r, r^′) Y(λ)lm(n) Y(λ)lm(n^′)

(34)

a_lm =

l = 0,1,2,...

(24)

2π(1+δm0) (l+m)!

λlm

474

ЖЭТФ, том 155, вып. 3, 2019

Функция Грина уравнения Шредингера. ..

с парциальной нулевой функцией Грина

приведем выражение (16) к следующему виду:

{

}

∑

{∑

(r, r^′) = -iq h(1)l(qr) j_l(qr^′) θ(r - r^′) +

eiqn·r =

(- 1)^l

u_ln(q)

ϕ_ln(r)

}

λlm

+ j_l(qr)h(1)l(qr^′)θ(r^′ - r)

(35)

× Y (λ)lm (n)Y (λ)lm (m).

(44)

Здесь j_l(x) и h(1)l(x) — сферические функции соот-

ветственно Бесселя и Ханкеля (первого рода) [8];

Здесь m

= r/r и учтено, что Y(λ)lm(-n)

θ(x) = 1 при x > 0 и θ(x) = 0 при x < 0. Выра-

= (-1)^l Y(λ)lm(n). Согласно (42) сумма в фигур-

жение (35) удовлетворяет уравнению

ных скобках равна 4π (- i)^l j_l(qr), так что из (44)

получаем

}

^{ ∂²

∂

l(l + 1)

∑

+q²

(r, r^′) =

eiqn·mr = 4π

i^l j_l(qr)Y(λ)lm(n)Y(λ)lm(m).

(45)

∂r²

r ∂r

r²

λlm

δ(r - r^′)

(36)

r²

После суммирования по λ и m отсюда следует

Из формулы (18) следует еще одно представле-

∑

ние для парциальной нулевой функции Грина:

eiqn·mr =

i^l j_l(qr)(2l + 1)P_l(n · m).

(46)

l=0

∑

ϕ_ln(r)ϕln(r′)

(r, r^′) =

(37)

Равенства (45) и (46) представляют собой обобще-

α_ln(q)

ние разложения плоской волны eik·r [1] на случай

также удовлетворяющее, в силу

(31), уравне-

комплексной энергии.

нию (36).

Из выражения (35) с учетом асимптотик (39) при

Уравнение (31) с помощью

(r, r^′) преобразуем

q → ∞ следует

к интегральному виду

{

}

(r, r^′) ≈

eiq|r-r′| - (- 1)^l eiq(r+r′)

(47)

∫∞

2iqrr^′

ϕ_ln(r) = α_ln(q)

(r, r^′)ϕln(r′)v(r′)(r′)2 dr′.

(38)

Подстановка (47) в формулу (34) при q → ∞ дает

{

Поскольку при x → ∞

G⁰(r - r^′) ≈

eiq|r-r′| δ(m - m^′)-

(

2iqrr^′

π⁾

}

h(1)l(x) ≈ (-i)l+1 e

j_l(x) ≈

sin x-l

(39)

- eiq(r+r′) δ(m + m^′)

(48)

из уравнения (38) при r → ∞ следует

Отсюда следует, что

G⁰(r-r^′) = 0 в пределе q → ∞.

iqr

Если в потенциале α v(r) имеются связанные со-

α_ln(q) u_ln(q) e

ϕ_ln(r) ≈ -

(40)

стояния, то для соответствующих уровней энергии

4π

имеем ε_ln = -κ2ln, где κ_ln — корни уравнения

∫

∞

α_ln(κ) = α.

(49)

u_ln(q) = 4π (-i)^l j_l(qr)

ϕ_ln(r)v(r)r² dr.

(41)

Для радиальной волновой функции связанного со-

стояния ψ_ln(r) в этом случае получаем выражение

Величина i^l u_ln(q)/(4π) является коэффициен-

том разложения функции j_l(qr) по системе

ϕ_ln(r)},

ψ_ln(r) = C_ln ϕ_ln(κ_ln, r),

(50)

так что

∑

)-1/2

j_l(qr) =

u_ln(q)

ϕ_ln(r)

(42)

([dα_ln ]

^[ dε_ln(α)]1/2

4π

C_ln =

(51)

dεε=-κ2

dα

ϕ_ln(r), взятой при ε = q².

Здесь функция ψ_ln(r) определена следующим обра-

Положив

зом:

u_ν(n, q) = u_λlmn(n, q) = u_ln(q)Y(λ)lm(n),

(43)

ψ_ν(r) = ψ_λlmn(r) = ψ_ln(r)Y(λ)lm(n).

475

Б. Я. Балагуров

ЖЭТФ, том 155, вып. 3, 2019

∫

3. ПОЛНАЯ ФУНКЦИЯ ГРИНА

ψ_ν(r)ψ^(+)k(r)dr = 0.

(58)

Полная функция Грина

^G(r, r^′) для стационар-

Применив к

^G(r, r^′) из (55) оператор ∇^2r + q² -

ного уравнения Шредингера (1) является решением

−αv(r), убедимся, что это выражение удовлетворя-

уравнения

ет уравнению (52) в силу выполнения соотношения

{

}

полноты (54).

∇^2r + q² - α v(r)

^G(r, r^′) = δ(r - r^′)

(52)

Согласно (55) величина

^G(r, r^′) является анали-

тической функцией комплексной переменной ε на

с условием

^G(r, r^′) → 0 при r → ∞.

всем физическом листе за исключением, возможно,

1. При традиционном подходе

[2] величина

некоторых точек на отрицательной действительной

^G(r, r^′) ищется с помощью разложения по полной

полуоси. Так, если в данном потенциале есть свя-

системе волновых функций — решений уравнения

занное состояние с энергией ε_ν , то в выражении (55)

(1). Это, прежде всего, волновые функции ψ_ν (r)

присутствует полюс, при приближении к которому

связанных состояний (если они есть в данном

имеем при ε → ε_ν :

потенциале) с уровнями энергии ε_ν

< 0. К ним

необходимо добавить волновые функции ψ^(+)k(r)

ψ_ν(r)ψ_ν(r^′)

^G(r, r^′) ≈

(59)

непрерывного спектра энергий (ε

= k² > 0) —

ε-ε_ν

решения задачи об упругом рассеянии плоской

При α → 0 из формулы (55) следует выражение

волны с асимптотикой r → ∞:

для нулевой функции Грина

G⁰(r-r^′). Действитель-

ikr

но, при α = 0 отсутствуют связанные состояния, а

ψ^(+)k(r) ≈ eik·r + f(n, m)

(53)

функция ψ^(+)k(r) сводится к плоской волне eikr, так

что при α → 0

Здесь f(n, m) — амплитуда рассеяния, n = k/k и

∫

eik·(r-r′) dk

m = r/r.

^G(r, r^′) →

G⁰(r - r^′) =

(60)

{

}

ε-k²

(2π)³

Совокупность

ψ_ν(r), ψ^(+)k(r)

образует полную

систему, так что [2]

Отсюда при ε = q² для нулевой функции Грина сле-

∫

дует выражение (12).

∑

Для вычисления следующих членов ряда по сте-

ψ_ν(r)ψ_ν(r^′) + ψ^(+)k(r)ψ(+)∗k(r^′)

(2π)

пеням α нужно найти соответствующее разложе-

(+)

ние для функции ψ_k

(r). Удобнее, однако, получать

= δ(r - r^′).

(54)

разложение функции Грина по степеням α непосред-

Звездочкой в соотношении (54) обозначена операция

ственно. С этой целью перейдем от дифференциаль-

комплексного сопряжения; волновые функции свя-

ного уравнения (52) к интегральному:

занных состояний считаются вещественными.

^G(r, r^′) =

G⁰(r - r^′) +

Решение уравнения (52) с помощью разложения

{

}

∫

по системе

ψ_ν(r), ψ^(+)k(r)

дает следующее выра-

+α

G⁰(r - r₁) v(r₁)

^G(r₁, r^′) dr₁.

(61)

жение для функции Грина [2]:

Для слабого потенциала уравнение (61) может ре-

∑

ψ_ν(r)ψ_ν(r^′)

шаться итерациями — разложением по степеням α.

^G(r, r^′) =

ε-ε_ν

В результате получим следующий ряд:

∫

(+)

ψ_k

(r) ψ(+)∗k(r^′) dk

^G(r, r^′) =

G⁰(r - r^′) +

(55)

ε-k²

(2π)³

∫

+α

G⁰(r - r₁) v(r₁)

G⁰(r₁ - r^′) dr₁

При выводе формулы (55) использовались следую-

∫∫

щие соотношения ортонормированности для волно-

+ α²

G⁰(r - r₁) v(r₁)

G⁰(r₁ - r₂) v(r₂) ×

вых функций [2]:

∫

× G⁰(r₂ - r^′)dr1 dr₂ + . . .

(62)

ψ_μ(r)ψ_ν(r)dr = δ_μν,

(56)

Для центрально-симметричных потенциалов по-

ложим

∫

∑

^G(r, r^′) =

(r, r^′)

Y (λ)lm (m)Y (λ)lm (m^′),

(63)

ψ^(+)k(r) ψ(+)∗k′

(r) dr = (2π)³ δ(k - k^′),

(57)

λm

476

ЖЭТФ, том 155, вып. 3, 2019

Функция Грина уравнения Шредингера. ..

где парциальная функция Грина

(r, r^′) подчиня-

и т. д. В результате из разложения (62) получаем

ется уравнению

∑

ϕ_ν(r)ϕν(r′)

^G(r, r^′) =

G⁰(r - r^′) +

}

α_ν(q)

^{ ∂²

∂

l(l + 1)

+q²-

- αv(r)

(r, r^′) =

{

}

[

]₂

[

]₃

∂r²

r ∂r

r²

+...

(70)

δ(r - r^′)

α_ν(q)

(64)

r²

откуда следует

В этом случае ψ_ν(r) = ψ_λlmn(r) = ψ_ln(r)Y(λ)lm(m) и

∑

ϕ_ν(r)ϕν(r′)

^G(r, r^′) =

G⁰(r-r^′)+α

[

(71)

∑

α_ν(q)

α_ν(q)-α

ψ^(+)k(r) = 4π

ψ(+)kl(r)

Y (λ)lm (n)Y (λ)lm (m),

(65)

λm

Выражение (71) применимо при всех r и r^′ для

любых потенциалов, в том числе и с конечным ради-

где n = k/k и m = r/r.

усом действия. Если при этом имеет место разложе-

Подстановка этих функций в формулу (55) дает

ние (18) для нулевой функции Грина, то выражение

для

^G(r, r^′) приобретает компактный вид:

∑

ψ_ln(r)ψ_ln(r^′)

G_l(r, r^′) =

∑

ϕ_ν(r)ϕν(r′)

ε-ε_ln

^G(r, r^′) =

(72)

α_ν(q) - α

∞

∫

ψ(+)kl(r)ψ(+)∗kl(r^′)

Здесь по крайней мере один из радиус-векторов дол-

k² dk.

(66)

ε-k²

жен принадлежать области пространства, где v(r) =

= 0. Нетрудно видеть, что выражения (71) и (72)

Аналогичным образом из соотношения (54) получа-

удовлетворяют уравнениям (52) и (61).

ем

Выражения (71) и

(72) для функции Грина

^G(r, r^′) обладают теми же, что и (55), аналитически-

∫

∞

∑

ми свойствами. Действительно, собственные функ-

(+)∗

ψ_ln(r)ψ_ln(r^′) +

ψ(+)kl(r)ψ

(r^′) k² dk =

ции

ϕ_ν(r) и собственные значения α_ν(q) определены

как регулярные величины при Im q > 0, т. е. на всем

δ(r - r^′)

физическом листе. Кроме того, выражения (71), (72)

(67)

r²

при ε = ε_ν = - κ2ν, где κ_ν — корень уравнения (19),

также имеют полюс и вблизи него принимают при

При наличии связанного состояния имеем при

ε → ε_ν вид

ε→ε_ln

ϕ_ν(κ_ν; r)ϕ_ν(κ_ν; r^′)

^G(r, r′) ≈

ψ_ln(r)ψ_ln(r^′)

ε-ε_ν

G_l(r, r^′) ≈

(68)

ε-ε_ln

)-1

([dα_ν(ε)^]

(73)

где ε_ln — энергия этого состояния.

dε

ε=εν

2. Заметим, что в случае потенциала с конеч-

ным радиусом действия ряд (62) содержит, начи-

Волновая функция ψ_ν(r) соответствующего связан-

ная с линейного по α члена, нулевые функции Гри-

ного состояния выражается через ϕ_ν (κ_ν ; r) согласно

на, в которых по крайней мере один из координат-

(20), (21), так что выражения (73) и (59) совпадают.

ных векторов принадлежит области пространства,

Для слабого потенциала (α → 0) из (71), (72) оче-

где v(r) = 0. Это обстоятельство позволяет исполь-

видным образом следует разложение (62) для функ-

зовать для них разложение (18). Так,

ции Грина.

При q → ∞ имеем |α|/|α_ν (q)| → 0, поэтому из

∫

выражения (70) при q → ∞ получаем

G⁰(r - r₁) v(r₁)

G⁰(r₁ - r^′) dr₁ =

^G(r, r^′) ≈

G⁰(r - r^′)

(74)

∑

ϕ_μ(r)

ϕ_ν(r^′)

α_μ(q) α_ν(q)

c соответствующей асимптотикой (48) для нулевой

μ ν

∫

функции Грина, так что

∑

ϕ_ν(r)ϕν(r′)

ϕ_μ(r₁)ϕν(r1) v(r1)dr1 =

[

]₂

(69)

lim

^G(r, r^′) = 0.

(75)

α_ν(q)

q→∞

477

Б. Я. Балагуров

ЖЭТФ, том 155, вып. 3, 2019

Для парциальной функции Грина согласно (71),

где n = k/k и m = r/r. При выводе выражения

(72) имеем

(82) использована асимптотическая формула (14)

для собственной функции

ϕ_ν(r) при q = k + i0.

∑

ϕ_ln(r

ϕ_ln(r^′)

G_l(r, r^′) =

(r, r^′)+α

(76)

В случае потенциала с центральной симметрией

α_ln(q)(α_ln(q) - α)

для парциальной амплитуды рассеяния f_l(k), опре-

деленной согласно

∑

ϕ_ln(r)ϕln(r′)

∑

G_l(r, r^′) =

(77)

α_ln(q) - α

f (n, m) = 4π

f_l(k)Y(λ)lm(n)Y(λ)lm(m),

(83)

λlm

Вблизи полюса (ε → ε_ln) для функции G_l(r, r^′) с

учетом связи (50), (51) волновой функции ψ_ln(r)

из (82) получаем следующее выражение [6]:

с собственной функцией ϕ_ln(r) получаем выраже-

ние (68).

f_l(k) = (-1)l+1

3. В задаче об упругом рассеянии плоской волны

(4π)²

eik·r на потенциале αv(r) требуется найти волновую

∑

α(+)ln(k)

[

]₂

u(+)ln(k)

(84)

функцию ψ^(+)k(r) — решение уравнения (1) (при ε =

α(+)ln(k) - α

= k²) с асимптотическим поведением вида (53).

Положим

Здесь, как и выше, учтено, что Y(λ)lm(-n)

ψ^(+)k(r) = eik·r + ϕ(r),

(78)

= (-1)^l Y (λ)lm (n).

где функция ϕ(r) описывает рассеянную волну. Под-

становка (78) в (1) приводит к неоднородному урав-

4. ЭКВИВАЛЕНТНОСТЬ ПРЕДСТАВЛЕНИЙ

нению для ϕ(r):

ФУНКЦИИ ГРИНА

∇² ϕ(r) + k² ϕ(r) - αv(r)ϕ(r) = α v(r)eik·r.

(79)

В предыдущем разделе с помощью разных мето-

Уравнение (79) решаем с помощью функции Грина.

дик для функции Грина

^G(r, r^′) были выведены раз-

В результате получаем

личающиеся по виду выражения (представления).

∫

Оба выражения обладают, тем не менее, одинако-

ψ^(+)k(r) = eik·r+α G⁽⁺⁾(r, r^′)eik·r′ v(r^′)dr^′,

(80)

выми общими свойствами и просто описывают одну

и ту же величину

^G(r, r^′) разными способами, по-

где G⁽⁺⁾(r, r^′) — функция

^G(r, r^′) при q = k + i0.

этому между этими представлениями должна суще-

В выражении (80) координата r^′ принадлежит

ствовать непосредственная связь.

области, в которой v(r^′) = 0. Это позволяет исполь-

Для выяснения соответствия между выражени-

зовать для функции Грина G⁽⁺⁾(r, r^′) представление

ями (55) и (72) рассмотрим интеграл

(72) при q = k + i0, так что для волновой функции

∫

непрерывного спектра энергии ψ^(+)k(r) отсюда сле-

^G(ϵ; r, r^′) dϵ

(85)

дует выражение

ϵ-ε

2πi

∑

u⁽⁺⁾(- n, k)

ψ^(+)k(r) = eik·r + α

ϕ(+)ν(r),

(81)

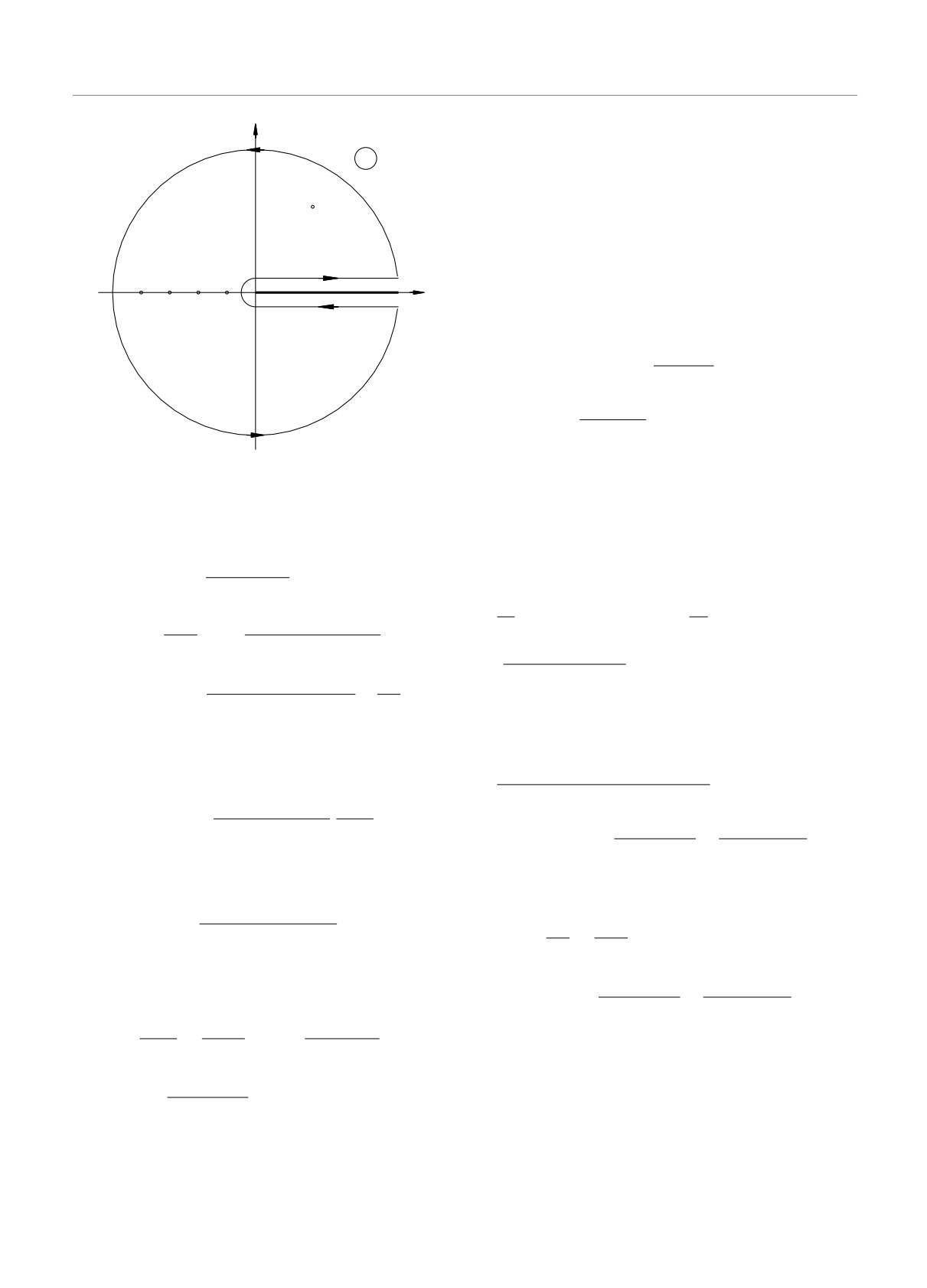
взятый по изображенному на рисунке замкнуто-

αν+)(k) - α

му контуру, состоящему из бесконечно удаленной

совпадающее с найденным в работе [6]. При выводе

окружности и обхода вокруг разреза. Здесь у функ-

формулы (81) учтено определение (15) для величи-

ции Грина в явном виде указана опускавшаяся

ны u(n, q) при q = k + i0.

прежде зависимость от энергии.

При r

→ ∞ из формулы (81) для функции

Величина (85) равна, с одной стороны, сумме

ψ^(+)k(r) следует асимптотическое выражение вида

вычетов подынтегрального выражения в полюсах

(53) с амплитудой рассеяния [6]

функции Грина при ϵ = ε_ν (если в данном потенциа-

ле имеются соответствующие связанные состояния),

∑

αν+)(k)

а также при ϵ = ε. С другой стороны, интеграл по

f (n, m) = -

бесконечно удаленной окружности, с учетом преде-

4π

αν+)(k) - α

ла (75) для функции Грина при q → ∞ равен ну-

× u(+)ν(-n, k)u(+)ν(m, k),

(82)

лю, так что остается только интегрирование вдоль

478

ЖЭТФ, том 155, вып. 3, 2019

Функция Грина уравнения Шредингера. ..

Далее нам понадобится некоторое соотношение,

которое выводится следующим образом. Умножим

уравнение для функции ϕν+)(k; r) =

ϕ_ν(k + i0; r)

∇² ϕ(+)ν(r)+k² ϕ(+)ν(r) = α(+)ν(k)v(r)ϕ(+)ν(r)

(90)

на ϕμ+)∗(k; r)|, dr|, соответствующее уравнение для

ϕμ+)∗(k; r) — на ϕν+)(k; r)dr, затем вычтем их друг

из друга и проинтегрируем по всему пространству.

В результате получим равенство

{

∫ [

∂ϕν+)(r)

lim

r²

ϕ(+)∗μ(r)

r→∞

∂r

]

}

∂ϕμ+)∗(r)

(

)

- ϕ(+)ν(r)

α(+)ν - α(+)∗μ

∂r

∫

× ϕ(+)ν(r)ϕ(+)∗μ(r)v(r)dr,

(91)

в левой стороне которого интеграл преобразован в

берегов разреза. В результате с использованием вы-

поверхностный по сфере радиуса r → ∞. Используя

ражения (72) получаем

для вычисления этого интеграла асимптотику (14)

∑

ψ_ν(r)ψ_ν(r^′)

при q = k + i0, найдем соотношение

^G(ε; r, r^′) =

ε-ε_ν

∫

∫∞

u(+)ν(n, k)u(+)∗μ(n, k)

{∑ ϕ(+)ν(ϵ; r)ϕ(+)ν(ϵ; r′)

2π

4π

ϵ-ε

∫

αν+)(ϵ) - α

αν+)(k)-αμ+)∗(k)

}

ϕ(+)ν(r)ϕ(+)∗μ(r)v(r)dr.

(92)

∑

αν+)(k)αμ+)∗(k)

ϕν+)∗(ϵ; r)ϕν+)∗(ϵ; r^′)

dϵ

(86)

2πi

αν+)∗(ϵ) - α

Из равенства (87), с учетом соотношения (92) и

При выводе равенства (86) учтены соотношения (6),

тождества

а также (20), (21).

Рассмотрим теперь интеграл

αμ+)∗(k) - αν+)(k)

(

) (

) =

∫

(+)

αμ+)∗(k) - α αν+)(k) - α

ψ_k

(r) ψ(+)∗k(r^′) dk

I(ε) =

(87)

ε-k²

(2π)³

(93)

αν+)(k) - α

αμ+)∗(k) - α

Заметим, что выражение (81) для ψ^(+)k(r) с учетом

разложения (16) при q = k + i0 принимает вид

находим

∑

αν+)(k)uν+)(- n, k)

∫

∞

ψ^(+)k(r) =

ϕ(+)ν(r).

(88)

dϵ

αν+)(k) - α

I(ε) =

2πi

ϵ-ε

Полагая в равенстве (87) dk = k² dk dn и используя

{

}

∑∑

выражение (88), получим

∞

αν+)(k) - α

αμ+)∗(k) - α

∫

ν μ

k² dk∑∑ αν+)(k)

I(ε) =

× ϕ(+)ν(ϵ; r)ϕ(+)∗μ(ϵ; r^′)×

(2π)³

ε-k²

ν μ

αν+)(k)-α

∫

× ϕ(+)ν(ϵ; r^′′)ϕ(+)∗μ(ϵ; r^′′)v(r^′′)dr^′′,

(94)

αμ+)∗(k)

ϕ(+)ν(r)ϕ(+)∗μ(r^′)×

αμ+)∗(k)-α

∫

где ϵ = k². Наконец, используя соотношение полно-

ты (10) при q = k + i0, получим

× u(+)ν(-n, k)u(+)∗μ(-n, k)dn.

(89)

479

Б. Я. Балагуров

ЖЭТФ, том 155, вып. 3, 2019

∫∞

2. А. И. Базь, Я. Б. Зельдович, А. М. Переломов, Рас-

{∑ ϕ(+)ν(ϵ; r)ϕ(+)ν(ϵ; r′)

I(ε) =

сеяние, реакции и распады в нерелятивистской

ϵ-ε

αν+)(ϵ) - α

квантовой механике, Наука, Москва (1971).

}

∑

ϕμ+)∗(ϵ; r)ϕμ+)∗(ϵ; r^′)

dϵ

3. Б. Я. Балагуров, Квантование потенциала в урав-

(95)

αμ+)∗(ϵ) - α

2πi

нении Шредингера, URSS, Москва (2018).

Отсюда следует, что выражение (86), с учетом опре-

4. S. Weinberg, Phys. Rev. 131, 440 (1963).

деления I(ε) из (87), принимает вид (55), так что

5. B. Ya. Balagurov, J. Comp. Methods in Sciences and

представления функции Грина (55) и (72) эквива-

Engineering, Vol. 10, №№4-6, 105 (2010).

лентны.

6. Б. Я. Балагуров, ЖЭТФ 154, 543 (2018).

ЛИТЕРАТУРА

7. Г. Бейтмен, А. Эрдейи, Высшие трансцендентные

функции, т. I. Наука, Москва (1973).

1. Л. Д. Ландау, Е. М. Лифшиц, Квантовая меха-

ника. Нерелятивистская теория, Наука, Москва

8. Г. Бейтмен, А. Эрдейи, Высшие трансцендентные

(1989).

функции, т. II. Наука, Москва (1974).

480