ЖЭТФ, 2019, том 155, вып. 3, стр. 490-500

ИССЛЕДОВАНИЕ ЦИЛИНДРИЧЕСКИХ ПОЛИТРОП В СЛУЧАЕ

НЕНУЛЕВОЙ КОСМОЛОГИЧЕСКОЙ ПОСТОЯННОЙ

М. Шариф^*, С. Садик^**

Математический факультет, Университет Пенджаба

54590, Лахор, Пакистан

Поступила в редакцию 13 марта 2018 г.,

после переработки 20 июля 2018 г.

Принята к публикации 24 сентября 2018 г.

(Перевод с английского)

STUDY OF CYLINDRICAL POLYTROPES

WITH COSMOLOGICAL CONSTANT

M. Sharif, S. Sadiq

Исследуется цилиндрически-симметричное распределение идеальной жидкости с ненулевой космологи-

ческой постоянной для двух случаев политропного уравнения состояния. Сформулированы и численно

решены соответствующие структурные уравнения. Оказалось, что полученные политропные модели явля-

ются перспективными с точки зрения физики, поскольку удовлетворяют всем энергетическим условиям.

Проанализирована устойчивость политроп путем возмущения материальных переменных, а именно, по-

литропной постоянной и политропного индекса, и построена функция распределения силы. Найдено, что

при возмущении политропной постоянной компактный объект является устойчивым во всех случаях, в

то время как возмущение политропного индекса приводит к устойчивым результатам только в первом

случае политропного уравнения состояния.

DOI: 10.1134/S0044451019030118

выполнения политропного соотношения между дав-

лением и плотностью. Такие звездные модели были

названы политропными звездами, они представля-

1. ВВЕДЕНИЕ

ют собой грубую аппроксимацию более реалистич-

ных звездных моделей. Все это способствовало при-

Исследование физических аспектов поведения

влечению внимания исследователей к моделирова-

звездных объектов, а также различных этапов их

нию компактных объектов с помощью политропно-

эволюции является одной из наиболее интригующих

го УС.

проблем релятивистской астрофизики. Такие фак-

Структура политроп определяется уравнением

торы как конденсация газообразных составляющих

и собственная гравитация играют важную роль в

Лейна - Эмдена, которое представляет собой сис-

тему нелинейных дифференциальных уравнений

формировании структуры небесных тел и в их эво-

люции. Внутренние законы этих объектов хорошо

(уравнение гидростатического равновесия и уравне-

описывает уравнение состояния (УС). В работе [1]

ние сохранения массы). В работе [2], являющейся

пионерской в области исследования изотропных ре-

показано, что при специальном выборе температу-

ры распределенного в звезде газа можно добиться

лятивистских сферических систем с политропным

УС, было получено численное решение структурных

^* E-mail: msharif.math@pu.edu.pk

уравнений. В работе также обсуждалось, что гра-

^** E-mail: sobiasadiq.01@gmail.com

витационный коллапс массивных звезд может слу-

490

ЖЭТФ, том 155, вып. 3, 2019

Исследование цилиндрических политроп.. .

жить механизмом выделения большого количества

янная существенно влияет на политропы на мас-

энергии. В работе [3] был найден класс точных реше-

штабах длин, сравнимых с космологической посто-

ний для статической политропной сферы, а также

янной.

оценивались различные физические свойства, кото-

рые можно получить с использованием реалистич-

Хорошо известно, что сферически-симметрич-

ной модели звезды. В работе [4] исследовались как

ные статические решения полевых уравнений Эйн-

изотропные, так и анизотропные сферически-сим-

штейна являются основой общей теории относитель-

метричные релятивистские политропы и были полу-

ности, однако цилиндрически-симметричные стати-

чены численные решения структурных уравнений,

ческие решения не так хорошо известны. Иссле-

описывающих политропы. В работе [5] были постро-

дование несферических самогравитирующих систем

ены анизотропные конформно-плоские политропы

по своей значимости идет вслед за исследованием

со сферической симметрией, а с помощью энергети-

цилиндрических решений полевых уравнений Эйн-

ческих условий была проверена их эффективность.

штейна в виде гравитационных волн. В связи с

В работе [6] рассматривалась политропная заряжен-

этим многие авторы стремились найти цилиндри-

ная сфера с обобщенным политропным УС и было

ческие решения, а также исследовать физические

показано, что устойчивость моделей увеличивается

свойства звездных моделей в контексте цилиндри-

с уменьшением параметра компактности.

ческой симметрии. В работе [11] рассматривалась

устойчивость цилиндрических политроп и было по-

В соответствии с последними наблюдательны-

лучено, что, в отличие от сферических политроп,

ми данными современной космологии, наша Вселен-

они являются устойчивыми. В работе [12] изучались

ная ускоренно расширяется, что подтверждается су-

цилиндрически-симметричные самогравитирующие

ществованием необычного вида энергии, известной

жидкости и было получено, что материальные ве-

как темная энергия. Согласно некоторым теорети-

личины оказывают значительное влияние на дина-

ческим результатам, темная энергия может описы-

мику распределения цилиндрически-симметричной

ваться космологической постоянной (также интер-

материи. В работе [13] исследовалось формиро-

претируемой как плотность энергии вакуума), ко-

вание анизотропных цилиндрических компактных

торая характеризуется отрицательным давлением.

объектов с ненулевой космологической постоянной,

Эти наблюдения привлекли внимание к исследова-

для этих объектов проверялись условия регулярнос-

ниям астрофизических объектов с ненулевой космо-

ти и устойчивости. В работе авторов [14] в кон-

логической постоянной. В работе [7] были получены

формно-плоском контексте были сформулированы

решения полевых уравнений Эйнштейна для сфери-

цилиндрические модели для анизотропных полит-

чески-симметричного распределения масс в случае

роп и было получено, что компактность моделей

ненулевой космологической постоянной. В этой ра-

возрастает. В работе [15] представлен общий фор-

боте также исследовалась структура несферических

мализм для заряженной анизотропной цилиндриче-

компактных объектов и были получены их звездные

ской политропы, причем оказалось, что одна из рас-

свойства, такие как масса, радиус, давление и плот-

сматриваемых моделей является приемлемой с точ-

ность.

ки зрения физики.

В работе [8] рассматривалась неустойчивость

В настоящей работе рассматриваются изотроп-

сферически-симметричного распределения материи

ные цилиндрические политропы в случае ненулевой

в случае ненулевой космологической постоянной.

космологической постоянной. Работа построена сле-

Было получено, что при большой космологической

дующим образом. В следующем разделе обсужда-

постоянной увеличивается значение критического

ется распределение материи для двух случаев по-

адиабатического индекса. В работе [9] обсуждалось

литропного УС для цилиндрически-симметричного

формирование анизотропных компактных звезд в

пространства-времени. Это необходимо для постро-

случае ненулевой космологической постоянной и бы-

ения структурных уравнений, с помощью которых

ло получено, что предложенная модель справедлива

можно исследовать физические характеристики по-

для любой компактной звезды. В работе [10] иссле-

литроп. Затем полученные модели анализируются

довалось влияние ненулевой космологической по-

численно. Также исследуются энергетические усло-

стоянной на сферически-симметричные политропы

вия для рассматриваемых моделей. В разд. 3 про-

для случая идеальной жидкости и анализировались

веден анализ устойчивости политропных моделей с

физические свойства политропной сферы. Было по-

использованием расщепления. В последнем разделе

лучено, что отталкивающая космологическая посто-

сформулированы основные результаты.

491

М. Шариф, С. Садик

ЖЭТФ, том 155, вып. 3, 2019

2. РАСПРЕДЕЛЕНИЕ ЖИДКОСТИ И

В работе [17] C-энергия для цилиндрического

СТРУКТУРНЫЕ УРАВНЕНИЯ

пространства-времени определяется как

Сформулируем уравнения общей теории относи-

(1 - l-2∇^α r∇_α r),

тельности, которые описывают равновесное состо-

яние цилиндрически-симметричного распределения

где

материи, удовлетворяющие политропному УС. Ли-

нейный элемент, соответствующий статической ци-

ρ² = ζ(1)aζa(1), l² = ζ(2)aζa(2),

r = ρl.

линдрической симметрии, имеет вид [16]

Здесь ρ, l и r — радиус окружности, удельная длина

ds² = -A²(r) dt² + B²(r) dr² + C²(r) dφ² + dz². (1)

и радиус области, соответственно, а

Предполагается, что такой конфигурации соответ-

∂

ствует идеальная жидкость, ограниченная гиперпо-

ζ(1) =

ζ₍₂₎ =

∂φ

∂z

верхностью Σ, так что

— векторы Киллинга для цилиндрической системы.

rΣ = const.

C-энергия для нашего линейного элемента принима-

Тензор энергии-импульса для такого распределения

ет вид

(

)

материи имеет вид

m(r) =

(7)

B²

T_αβ = (ρ + P)V_αV_β + Pg_αβ,

(2)

Закон сохранения

где ρ, P и V_α — плотность энергии, изотропное дав-

Tαβ;α = 0

ление и 4-скорость, соответственно. В сопутствую-

щей стстеме координат 4-скорость имеет вид

дает

A^′

V_α = -Aδ0α ⇒ V_αV^α = -1.

P^′ +

(ρ + P ) = 0.

(8)

Соответствующие полевые уравнения

Используя уравнения (4) и (7), получаем

R_αβ -

Rg_αβ + Λg_αβ = 8πT_αβ

A^′

8πrP - rΛ

1 - 8m

принимают вид

)

где

′

⁽B^′C

C^′′

∫

8πρ + Λ =

B²

m = 2π

rρ dr

(9)

)

′

⁽A^′C

8πP - Λ =

B²

— полная масса внутри цилиндрического компакт-

)

⁽A

′′

A^′B^′

ного объекта. Тогда уравнение (8) принимает вид

8πP - Λ =

B²

8πrP - rΛ

)

′′

P^′ +

(ρ + P ) = 0.

(10)

⁽A

A^′B^′

B^′C^′

A^′C^′

C^′′

1 - 8m

8πP-Λ =

B²

Оказалось, что распределение материи отражает ре-

где штрих обозначает дифференцирование по r, а

альную картину, если оно удовлетворяет некото-

Λ — космологическая постоянная. Пусть C(r) = r —

рым условиям, известным как энергетические усло-

координата Шварцшильда. Тогда полевые уравне-

вия. Для конфигурации, соответствующей изотроп-

ния редуцируются к виду

ной жидкости, эти условия имеют вид

)

′

⁽B

8πρ + Λ =

(3)

(i) ρ ≥ 0,

rB²

)

(ii) ρ + P ≥ 0,

′

⁽A

(11)

8πP - Λ =

(4)

(iii) ρ - P ≥ 0,

rB²

)

′′

(iv) ρ + 3P ≥ 0.

⁽A

A^′B^′

8πP - Λ =

(5)

B²

))

Теперь рассмотрим звездный объект для двух

′′

⁽A

A^′B^′

⁽B^′

A^′

случаев политропного УС и сформулируем струк-

8πP-Λ =

(6)

B²

r B

турные уравнения.

492

ЖЭТФ, том 155, вып. 3, 2019

Исследование цилиндрических политроп.. .

2.1. Случай 1

(1-nα+(1+n)αΦ₀) (Φn0(1-nα+nαΦ₀)-λ)

8(1 + n)αv

Для этого случая рассмотрим

⎡

⎢

2Φn0

P = kργ0 = kρ1+(1/n)0, ρ - ρ₀ = nP,

(12)

⎢

+ 8(1 + n) ×

⎣

8(1 + n)αv

где γ и n — порядок политропы и ее показатель,

⎤

соответственно, k — константа, а ρ₀ — барионная

dΦ₀⎥

плотность. Введем новые переменные:

× αA2x2Φ2n0(1 - nα + nαΦ0) + 2nxΦn-1

⎥

⎦⁺

√

[

P_c

ρ₀(r)

4πρ_c

2xΦn0

α=

Φn0(ξ) =

nΦn-10 (1-nα+α(n+1)Φ₀)² +

ρ_c

ρ0c

α(n + 1)

8(1+n)αv

(13)

ρ_vac

m(r)A

] dΦ₀

λ=

v(ξ) =

+ α(n + 1) (Φn0(1 - nα + nαΦ₀) - λ)

8πρ_c

4πρ_c

d²Φ₀

A-2

= 0.

(16)

Здесь ρ0c и ρ_c — центральные значения плотности

dx²

барионной и полной энергии, P_c — давление, а ρ_vac —

Это уравнение называется уравнением Лейна - Эм-

плотность энергии вакуума. Члены ξ, λ, Φ₀(ξ) и

дена, оно описывает политропу в состоянии гидро-

v(ξ) — безразмерная радиальная координата, космо-

статического равновесия. Для энергетических усло-

логическая постоянная, параметр плотности и мас-

вий в этом случае получаем

совый параметр, соответственно;

A — константа,

имеющая размерность обратной длины. Значение

(i) 1 - nα + nαΦ₀ ≥ 0,

Λ оказалось равным 1.3 · 10-56 см-2, при этом со-

ответствующая плотность энергии вакуума равна

(ii) 1 - nα + α(n + 1)Φ₀ ≥ 0,

(17)

10-29 г/см³ [10]. Подставляя уравнение (13) в урав-

(iii) 1 - nα + α(n - 1)Φ₀ ≥ 0,

нения (10) и (9), получим

(iv) 1 - nα + α(n + 3)Φ₀ ≥ 0.

dΦ₀

Заметим, что уравнения (14) и (15) представля-

+2A2xΦn0(Φn0(1 - nα + nαΦ0) - λ)×

ют собой систему двух дифференциальных уравне-

(

)

ний для двух неизвестных (Φ₀ и v). Решим эти урав-

8α(n + 1)v

× (1-nα+α(n+1)Φ₀)

= 0,

(14)

нения численно с начальными условиями

v(0) = 0, Φ₀(0) = 1.

(18)

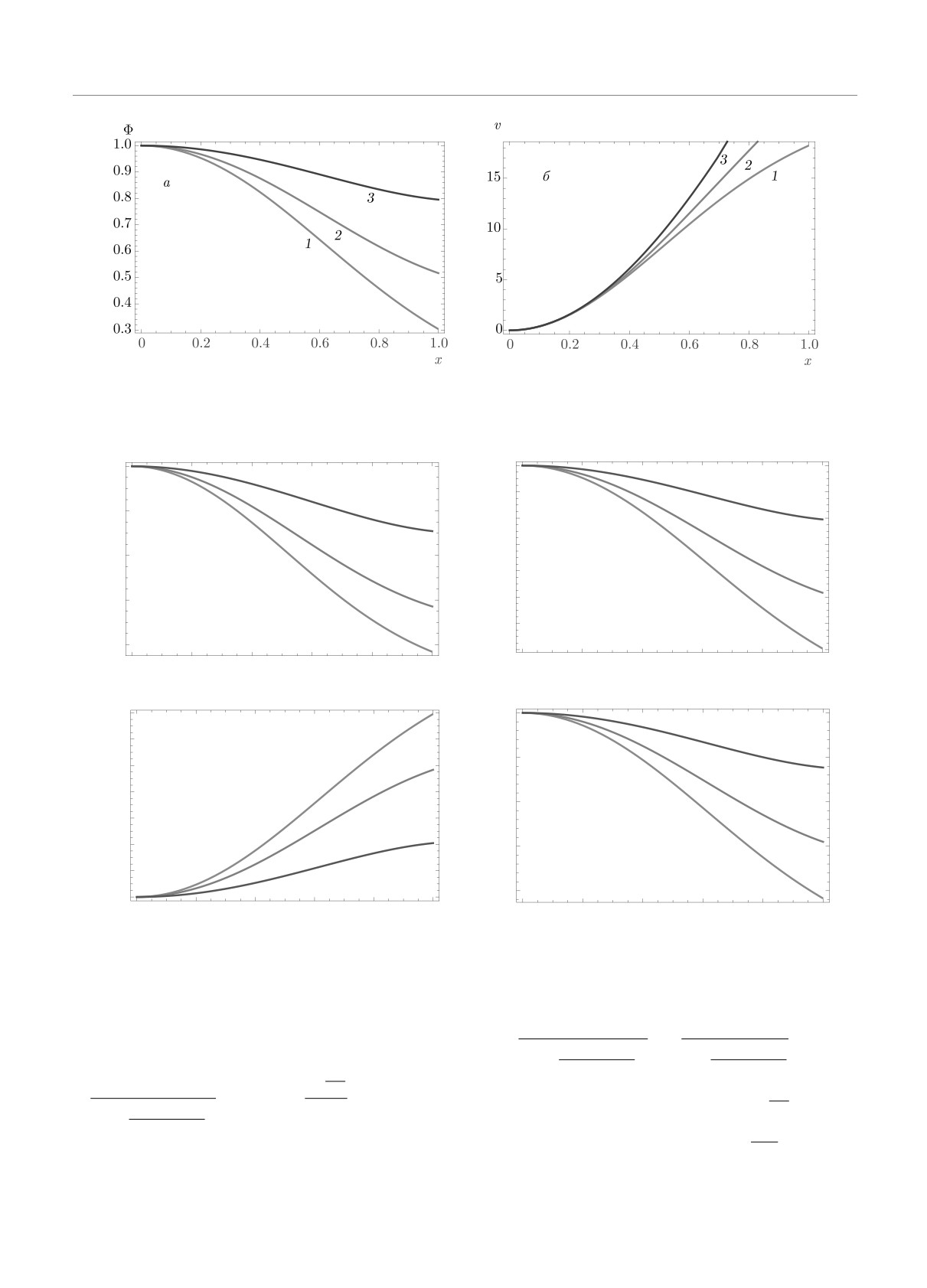
На рис. 1 приведены решения уравнений (14) и

A²xΦn0

(1 - nα + nαΦ₀) = 0,

(15)

(15) для случаев нулевой и ненулевой космологичес-

кой постоянной. На рис. 1а приведены зависимости

Φ₀. Видно, что эта величина может быть положи-

где

тельной внутри объекта и убывает при удалении от

центра звезды. Более того, при λ = 0 величина Φ₀

x=ξ/A,

уменьшается быстрее. На рис. 1б приведены зави-

симости безразмерной массовой функции v. Видно,

что v имеет большие значения при больших значе-

A=r_ΣA.

ниях λ. Это означает, что увеличение λ приводит к

более компактным моделям. На рис. 2 приведены за-

Приведенные выше уравнения описывают внут-

висимости энергетических условий для случаев ну-

реннюю структуру цилиндрического компактного

левой и ненулевой космологической постоянной. На

объекта. Дифференцируя уравнение (14) по x, а за-

рисунке видно, что при всех значениях λ выполнены

тем, используя уравнение (15), получаем

энергетические условия.

493

М. Шариф, С. Садик

ЖЭТФ, том 155, вып. 3, 2019

Энергетические условия в этом случае имеют вид

тогда плотность энергии и давление тоже будут

испытывать возмущение:

(i) Φⁿ ≥ 0,

(ii) 1 + αΦ ≥ 0,

P = hP,

ρ= ρ₀ + nhP,

(25)

(23)

(iii) 1 - αΦ ≥ 0,

где h =

k/k, а тильдой обозначены возмущенные

величины. Подставляя возмущенные параметры в

(iv) 1 + 3αΦ ≥ 0.

уравнение (24), получим

⎡

Решаем уравнения (20) и (21) и получаем зависимос-

ти Φ и v, показанные на рис. 3. На рисунке вид-

⎢

dΦ₀

8πξρ_c(αΦ₀ - λ)

R₌ ρ_cΦn0

⎢Ahα(n+1)

(

) ×

но, что полученные зависимости аналогичны зави-

⎣

dξ

8α(n + 1)v

симостям, полученным для Случая 1. Энергетичес-

A 1-

кие условия также выполнены (см. рис. 4).

⎤

⎥

× (1 - nα + α(n + 1)hΦ₀)

3. РАСЩЕПЛЕНИЕ ПОЛИТРОП

⎦

Релятивистские звездные модели не работают,

что соответствует нарушенному состоянию системы.

если они не устойчивы относительно флуктуаций по

Используя соотношение

материальным переменным, например, давлению и

плотности энергии. Их небольшое возмущение нару-

шает состояние равновесия небесных тел, что при-

4πρ²

водит к возникновению разнообразных интересных

можно переписать это уравнение в виде

явлений, таких как коллапс, расширение, расщеп-

dΦ₀

2ξΦn0(αΦ₀ - λ)

ление и опрокидывание. Расщепление и опрокиды-

R = hΦⁿ

α(n + 1)

dξ

8α(n + 1)v

вание самогравитирующих объектов соответствуют

появлению в распределении материи радиальных

сил с разными знаками [18]. Если радиальная си-

× (1 - nα + α(n + 1)hΦ₀).

(26)

ла направлена внутрь компактного объекта и ме-

няет свой знак в некоторой точке (точке расщепле-

Теперь разложим функцию

R в ряд Тейлора и

ния), то происходит расщепление, в противном слу-

получим

чае происходит опрокидывание. Это не имеет отно-

шения к коллапсу или расширению материи, а лишь

δR=

R(ξ, 1 + h, v + δv) =

R(ξ, 1, v) +

к тенденции к расщеплению в некоторой конкретной



точке внутри жидкости. Проанализируем устойчи-



∂R

вость моделей цилиндрических политроп с исполь-



δh +



δv.

(27)

∂h



∂v



зованием расщепления. Для этого функцию распре-

h=1,v=v

деления силы определим как

Поскольку в невозмущенном состоянии система на-

ходится в равновесии, имеем

8πrP - rΛ

(ρ + P ).

(24)

1 - 8m

R(ξ, 1, v) = 0.

Для каждого случая мы нарушаем состояние равно-

Из уравнения (26) получаем

весия системы, возмущая плотность энергии и дав-



∂R

2αξΦ1+n0

ление посредством возмущения политропных пара-



метров.

∂h



8(1 + n)αv

h=1,v=v

[

]

3.1. Случай 1

× (n + 1) (αΦ₀ - λ) + (1 - nα + (1 + n)αΦ₀)

Сначала введем возмущение политропной посто-

янной, а именно,

dΦ₀

+Φⁿ

(28)

⁰ dξ

k→

k₌ k + δk,

496

ЖЭТФ, том 155, вып. 3, 2019

Исследование цилиндрических политроп.. .



∂R

16(1 + n)αξΦn0 (-λ + αΦ₀)(1 - nα + (1 + n)αΦ₀)



(

)₂

(29)

∂v



8(1 + n)αv

h=1,v=v

A 1-

Более того, массовая функция в этом случае дает

∂v

nαA

δv =

δh =

f₁(ξ)δh,

(30)

∂h

где

∫ξ

f₁(ξ) =

ξΦn+10

ξ.

Подставляя уравнения (28)-(30) в уравнение (27), для функции силы получаем

(

A(1 + n)αξΦ₀ (-λ + αΦ₀)

AαξΦ₀ (1 - nα + (1 + n)αΦ₀)

δ R₁ = δhΦⁿ

A - 8(1 + n)αv

)

A²n(1 + n)α²ξf₁(ξ)(-λ + αΦ₀) (1 - nα + h(1 + n)αΦ₀)

dΦ₀

A - 8(1 + n)αv)²

dξ

Используя переменную ξ = xA, перепишем это уравнение в виде

⎛

⎜2(1+n)xAαΦ0 (αΦ0 - λ)

2xAαΦ0 (1 - nα + (1 + n)αΦ0)

⎜

δ R₁ = δhΦn0

⎝

8(1 + n)αv

⎞

dΦ₀

⎟

8n(1 + n)xAα2f1(x) (αΦ0 - λ) (1 - nα + h(1 + n)αΦ0)

⎟

(

)₂

+ dx

⎟

(31)

⎠

8(1 + n)αv

Для анализа расщепления приведем зависимости функции распределения силы для фиксированных показа-

теля политропы и параметра α и для различных значений космологической постоянной, см. рис. 5а. Видно,

что цилиндрические политропы остаются устойчивыми при любом выборе параметров n, α и λ.

Теперь введем возмущение политроп посредством возмущения политропного индекса,

n → ñ = n + δn,

тогда получим

(

)

(

Aρ_cΦn0

-λ + αΦ1+n0

A - 8(1 + n)αv)((1 - nα)lnΦ₀ + αΦ₀)

δR₂ =

(

)₂

8(1 + n)αv

)

+ 4(1 + n)xA2αf2(x)(1 - nα + nαΦ0) δh,

(32)

где

На рис. 5б показаны зависимости функции рас-

пределения силы для различных значений космоло-

∫x

гической постоянной. Видно, что при возмущении

f₂(x) =

xΦn0 lnΦ₀dx.

n компактный объект остается устойчивым при лю-

бом выборе параметров.

497

ЖЭТФ, вып. 3

М. Шариф, С. Садик

ЖЭТФ, том 155, вып. 3, 2019

3.2. Случай 2

Для анализа расщепления приведем зависимости

функции распределения силы при фиксированных

Сначала введем возмущение политропной посто-

политропном индексе и параметре α и при раз-

янной, а именно,

личных значениях космологической постоянной, см.

k→

k₌ k + δk,

рис.

6а. Видно, что цилиндрические политропы

остаются устойчивыми при любом выборе парамет-

тогда плотность энергии и давление также будут ис-

ров n, α и λ.

пытывать возмущение:

Теперь введем возмущение политроп посред-

ρ₀

ством возмущения политропного индекса,

P = hP,

ρ=

(33)

n → ñ = n + δn,

(1 + hkρ1/n0)n

тогда получим

где h =

k/k, а тильдой обозначены возмущенные

[(

величины. Используя приведенное выше уравнение,

Φⁿ lnΦ dΦ

δR₄ =

+2A(1 + αΦ) ×

для возмущенной плотности энергии получаем

A d

{

ρ= ρ + nP(1 - h),

(AxαΦn+1 -

Axλ)(1 + ln Φ)Φⁿ

A - 8α(n + 1)v

где мы использовали соотношение

})

8α(AxαΦn+1-λAx)

h = 1 + δh.

+32πρ_cΦⁿ(1+αΦ) ×

A-8α(n+1)v)²

Подставляя возмущенные параметры в уравнение

{

}

]

(AxαΦn+1 - λAx)

(24), получаем уравнение

f₄(x) δn,

(35)

A - 8α(n + 1)v)²

8πξαρ_cΦn+1 - 8πρ_cλ

R₌ hαρ_cA˘(n + 1)Φⁿ dΦ+

где

∫

dξ

A - 8α(n + 1)v

f₄(x) =

xΦⁿ ln Φ dx.

× {ρ_cΦⁿ[1 + α{n + h(1 - n)}Φ]},

На рис. 6б,в,г приведена функция распределения си-

описывающее возмущенное состояние системы. Ис-

лы для различных значений космологической посто-

пользуя безразмерную переменную

янной. Видно, что политропная модель испытывает

расщепление при увеличении значения λ, т. е. при

4πρ²

возмущении n наличие ненулевой космологической

постоянной приводит к неустойчивым моделям.

перепишем это уравнение в виде

{

}

4. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ

dΦ

8πξαρ_cΦn+1 - 8πρ_cλ

R = hΦⁿ

dξ

4πρ_c

A - 8α(n + 1)v

Самогравитирующие компактные объекты при-

надлежат важному классу астрономических тел,

× (ρ_cΦⁿ[1 + α{n + h(1 - n)}Φ]) .

изучение которых в последнее время стало осо-

Используя разложение в ряд Тейлора, получаем

бенно важным. В настоящей работе в рамках об-

щей теории относительности исследован политроп-

[

ный компактный объект с изотропным распреде-

dΦ

δR₃ =

лением материи для цилиндрически-симметричного

A d

{

(

)}

пространства-времени в случае ненулевой космоло-

1 + αΦ

гической постоянной. В выбранной геометрии была

Aα(n+1)Φ-4nαf₃(x)

A-8α(n+1)v

использована радиальная координата Шварцшиль-

(

)]

да и рассмотрены полевые уравнения. Два нелиней-

8παρ_cxAΦn - 8πρcλAx

ных обыкновенных дифференциальных уравнения,

δh,

(34)

A - 8α(n + 1)v

описывающих внутреннюю структуру компактного

объекта, сформулированы для двух случаев полит-

где

∫x

ропного УС. По аналогии с политропной сферой,

f₃(x) =

xΦn+1dx.

политропный цилиндр характеризуется тремя без-

размерными параметрами, а именно, политропным

498

ЖЭТФ, том 155, вып. 3, 2019

Исследование цилиндрических политроп.. .

R₁

R₂

400

-0.1

200

-0.2

-0.3

-0.4

-200

-0.5

-400

-0.6

0.2

0.4

0.6

0.8

1.0

0.2

0.4

0.6

0.8

1.0

Рис.

5. Зависимости δ

R₁ (а) и δ

R₂ (б) от x для λ = 0 (1), 0.3 (2) и 0.7 (3) при n = 1.5, α = 0.2

R₃

R₄

1.2 . 10^-7

0.008

1.0. 10^-7

0.006

0.8. 10^-7

0.6. 10^-7

0.004

0.4. 10^-7

0.002

0.2. 10^-7

0.2

0.4

0.6

0.8

1.0

0.2

0.4

0.6

0.8

1.0

R₄

0.0004

1.10^-6

0.0002

-0.0002

-1 . 10^-6

-0.0004

-2. 10^-6

-0.0006

-0.0008

-3. 10^-6

0.2

0.4

0.6

0.8

1.0

0.2

0.4

0.6

0.8

1.0

Рис. 6. Зависимости δR3 (а) и δR4 (б,в,г) от x для λ = 0 (1), 0.3 (2) и 0.7 (3) при n = 1.5, α = 0.2

индексом n, релятивистским параметром α, отража-

гической постоянной λ она растет быстрее, чем в

ющим роль релятивистских эффектов в его струк-

ее отсутствие. Перспективность полученных моде-

туре, и космологической постоянной, отражающей

лей с точки зрения физики исследовалась с помо-

роль плотности вакуумой энергии. В работе числен-

щью энергетических условий; было получено, что

но решены структурные уравнения и получено, что

рассматриваемые модели удовлетворяют всем энер-

массовая функция является монотонно возрастаю-

гетическим условиям как для нулевой, так и для

щей. Оказалось, что в случае ненулевой космоло-

ненулевой космологической постоянной.

499

М. Шариф, С. Садик

ЖЭТФ, том 155, вып. 3, 2019

Анализ устойчивости звездных моделей очень

S. Thirukkanesh and F. C. Ragel, Pramana J. Phys.

важен для проверки их перспективности с точки

78, 687 (2012).

зрения физики. В работе использовалось понятие

L. Herrera and W. Barreto, Phys. Rev. D 87, 087303

расщепления, а система выводилась из состояния

(2013).

равновесия при помощи возмущений. Возмущение

плотности энергии и давления системы вводилось

L. Herrera, A. Di Prisco, W. Barreto, and J. Ospino,

для двух случаев политропного уравнения состоя-

Gen. Relativ. Gravit. 46, 1827 (2014).

ния. Для Случая 1 вводилось возмущение полит-

M. Azam, S. A. Mardan, I. Noureen, and M. A. Reh-

ропной постоянной и политропного индекса и стро-

man, Eur. Phys. J. C 76, 315 (2016).

ились зависимости функций распределения силы

δR₁ иδ

R₂, описывающие полные радиальные силы.

O. Zubairi, A. Romero, and F. Weber, J. Phys.: Conf.

Было найдено, что полученные в Случае 1 моде-

Ser. 615, 012003 (2015).

ли устойчивы относительно возмущений при любом

C. G. Böhmer and T. Harko, Phys. Rev. D 71, 084026

выборе n, α и λ, а модели, полученные в Случае

(2005).

2, устойчивы только при возмущенной политропной

постоянной. Для анизотропных сферических по-

S. M. Hossein, F. Rahaman, J. Naskar, M. Kalam,

and S. Ray, Int. J. Mod. Phys. D 21, 1250088 (2012).

литроп расщепление и опрокидывание происходят,

когда плотность энергии и локальная анизотропия

10.

Z. Stuchlık, S. Hled´ık, and J. Novotný, Phys. Rev.

системы возмущаются посредством возмущения по-

D 94, 103513 (2016).

литропной постоянной и политропного индекса [19],

в то время как для изотропной цилиндрически-сим-

11.

M. A. Scheel, S. L. Shapiro, and S. A. Teukolsky,

Phys. Rev. D 48, 592 (1993).

метричной жидкости в обоих случаях для ненулевой

космологической постоянной устойчивые модели

12.

L. Herrera, A. Di Prisco, J. Ospino, and E. Fuen-

получаются при возмущении политропной посто-

mayor, J. Math. Phys. 42, 2129 (2001).

янной.

13.

G. Abbas, S. Nazeer, and M. A. Meraj, Astrophys.

Space Sci. 354, 449 (2014).

Авторы выражают благодарность Высшей ко-

миссии по образованию, Исламабад, Пакистан,

14.

M. Sharif and S. Sadiq, Can. J. Phys. 93, 1583 (2015).

за финансовую поддержку в рамках программы

15.

M. Azam, S. A. Mardan, I. Noureen, and M. A. Reh-

Indigenous Ph.D. 5000 Fellowship Phase-II, Batch-III.

man, Eur. Phys. J. C 76, 510 (2016).

16.

M. Sharif and M. Azam, Mon. Not. Roy. Astron. Soc.

430, 3048 (2013).

ЛИТЕРАТУРА

17.

K. S. Thorne, Phys. Rev. B 138, 251 (1965).

1. A. S. Eddington, The Internal Constitution of Stars,

18.

L. Herrera, Phys. Lett. A 165, 206 (1992).

Cambridge University Press (1926).

19.

L. Herrera, E. Fuenmayor, and P. León, Phys. Rev.

2. R. F. Tooper, Astrophys. J. 140, 434 (1964).

D 93, 024047 (2016).

500