ЖЭТФ, 2019, том 155, вып. 4, стр. 645-653

ОЦЕНКА СЛОЖНОСТИ РЕАЛИЗАЦИИ АЛГОРИТМА ГРОВЕРА

ДЛЯ ПЕРЕБОРА КЛЮЧЕЙ АЛГОРИТМОВ БЛОЧНОГО

ШИФРОВАНИЯ ГОСТ Р 34.12-2015

Д. В. Денисенкоa,b*, Г. Б. Маршалкоb**, М. В. Никитенковаb***,

В. И. Рудскойb****, В. А. Шишкин^b†

^a Московский государственный технический университет им. Н. Э. Баумана

105005, Москва, Россия

^b Технический комитет по стандартизации ТК 26

127287, Москва, Россия

Поступила в редакцию 23 октября 2018 г.,

после переработки 23 октября 2018 г.

Принята к публикации 29 октября 2018 г.

В рамках подхода, предложенного в работе [3], исследуется вопрос оценки необходимых ресурсов кван-

тового вычислителя для решения задачи поиска ключей алгоритмов блочного шифрования «Кузнечик»

и «Магма», определяемых национальным стандартом ГОСТ Р 34.12-2015, с использованием квантового

алгоритма Гровера.

DOI: 10.1134/S0044451019040072

эффективно решается с использованием алгорит-

ма Гровера [2] и может быть использована при

криптоанализе алгоритмов шифрования [3-5].

1. ВВЕДЕНИЕ

В настоящее время фундаментальные исследова-

ния направлены на создание квантовых вычислите-

Теория квантовых вычислений стремительно

лей, в связи с чем указанные квантовые алгоритмы

развивается с конца прошлого века. К настояще-

могут рассматриваться в качестве одной из возмож-

му моменту построен ряд формальных моделей

ных угроз безопасности современных криптографи-

квантовых вычислений, для которых показано,

ческих алгоритмов и протоколов.

что квантовая природа объектов, с использова-

нием которых проводятся вычисления, позволяет

В данной работе на основе подхода, предложен-

эффективно решать определенные задачи, име-

ного в [3], получены оценки ресурсов квантового вы-

числителя, необходимых для поиска ключа опреде-

ющие непосредственное отношение к стойкости

криптографических примитивов. К таким задачам

ляемых национальным стандартом ГОСТ Р 34.12-

относится задача о скрытой подгруппе, возникаю-

2015 [6] алгоритмов блочного шифрования «Кузне-

щая при анализе различных схем асимметричного

чик» и «Магма» с помощью алгоритма Гровера.

шифрования и цифровой подписи. Частным слу-

чаем этой задачи является факторизация целых

чисел, эффективное решение которой предлагает

2. КВАНТОВЫЙ КОМПЬЮТЕР

алгоритм Шора [1]. Другим важным приложением

квантовых вычислений является задача поис-

ка в неупорядоченном массиве данных, которая

Согласно [5], реализация алгоритма на кванто-

вом вычислителе может быть представлена в виде

^* E-mail: DenisenkoDV@bmstu.ru

четырехуровневой иерархической модели:

^** E-mail: marshalko_gb@tc26.ru

— уровень математической абстракции, ко-

^*** E-mail: marina-nic-msc@yandex.ru

^**** E-mail: rudskoy_vi@tc26.ru

торый формализует математическое описание реа-

^† E-mail: shishkin_va@tc26.ru

лизуемого квантового алгоритма;

645

Д. В. Денисенко, Г. Б. Маршалко, М. В. Никитенкова и др.

ЖЭТФ, том 155, вып. 4, 2019

— логический уровень, который подразумева-

H n

2|ⁿⁿ| - I_n

H n

ет конкретную реализацию алгоритма с расчетом

требуемого количества логических кубитов;

— уровень коррекции ошибок, который под-

разумевает реализацию квантовых корректирую-

Рис. 1. Алгоритм Гровера

щих кодов, предназначенных для исправления оши-

бок измерений и декогерентизации физических ку-

{

битов;

U_ω |x〉 |y〉 = |x〉|y ⊕ 1〉, если x = ω,

(2)

— физический уровень, подразумевающий ис-

U_ω |x〉 |y〉 = |x〉|y〉,

если x = ω,

пользование конкретной технологии реализации ку-

или кратко U_ω |x〉 |y〉 = |x〉 |y ⊕ f(x)〉. Легко убедить-

битов.

ся, что если вспомогательный кубит приведен в со-

Отметим, что последние два уровня непосредствен-

стояние

но определяются физическими параметрами ис-

|-〉 =

√ (|0〉 - |1〉) = H |1〉 ,

пользуемой технологии реализации кубитов и в

дальнейшем изложении рассматриваться не будут.

то действие оператора U_ω в форме (2) эквивалентно

Нас интересует оценка минимального количества

заданию в форме (1):

{

логических кубитов, достаточного для реализации

- |x〉 ⊗ |-〉 , если x = ω,

алгоритма Гровера в задаче поиска ключа алго-

U_ω(|x〉 ⊗ |-〉) =

|x〉 ⊗ |-〉 ,

если x = ω.

ритмов блочного шифрования, определяемых ГОСТ

Р 34.12-2015, по нескольким известным парам от-

Далее алгоритм действует следующим образом.

крытого и зашифрованного текстов.

Формируется состояние, являющееся равномерной

суперпозицией всех N = 2ⁿ значений аргумента x

(для чего потребуется n кубитов):

3. АЛГОРИТМ ГРОВЕРА

∑

|s〉 =

√

|x〉 .

Пусть имеется проиндексированное множество

N x=0

из N = 2ⁿ элементов. Требуется в этом множестве

найти индекс элемента, удовлетворяющего некото-

К этому состоянию (или к состоянию |s〉 ⊗ |-〉, в

рому критерию поиска, причем предполагается, что

зависимости от способа задания оператора оракула)

такой элемент существует и единственен. Иными

применяется оператор «итерации Гровера», состо-

словами, можно считать, что задана некоторая бу-

ящий из последовательного применения оператора

лева функция f : V_n → V₁, причем f(x) = 1 тогда

оракула U_ω и оператора «рассеивания Гровера» U_s,

и только тогда, когда элемент множества с индек-

который задается следующим образом:

сом x удовлетворяет критерию поиска (x = ω). При

U_s = 2 |s〉〈s| - I,

этом считается, что указанная функция f реализо-

вана как черный ящик или оракул. При решении за-

где I — единичный оператор (единичная матрица

дачи на классическом вычислителе в общем случае

размера 2ⁿ × 2ⁿ).

необходимо перебрать все возможные значения ин-

После определенного количества итераций Гро-

√

декса, что в итоге дает трудоемкость порядка O(N).

вера, порядка O(

N ), выполняется измерение всех

Реализуемый на квантовом вычислителе алго-

(или первых n) кубитов, а результат измерения с

√

ритм Гровера (см. [2]) имеет трудоемкость O(

N ).

большой вероятностью будет давать искомое значе-

Прежде всего, считается, что существует квантовый

ние ω. Алгоритм проиллюстрирован на рис. 1.

оракул, проверяющий выполнение критерия поис-

Алгоритм I. Алгоритм Гровера

ка, который представляет собой унитарный опера-

Вход. Множество {a₁, a₂, . . . , a_N } из N = 2ⁿ эле-

тор U_ω, действующий следующим образом:

ментов, f : V_n → V₁, f(x) = 1 тогда и только тогда,

{

когда a_x удовлетворяет некоторому критерию поис-

U_ω |x〉 = - |x〉, если x = ω, т. е. f(x) = 1,

ка, причем количество таких x, на которых f(x) = 1,

(1)

U_ω |x〉 = |x〉 ,

если x = ω, т. е. f(x) = 0.

в общем случае равно M (в нашем случае полагаем

M = 1), x — номер элемента a_x в двоичной системе

Чтобы связать квантовый оракул с классической бу-

счисления, т. е. x ∈ V_n.

левой функцией f, используют эквивалентное зада-

Выход. С вероятностью p > 1/2 произвольный

ние со вспомогательным кубитом |y〉:

a_x′ : f(x^′) = 1.

646

ЖЭТФ, том 155, вып. 4, 2019

Оценка сложности реализации алгоритма Гровера...

1. Инициализация n + 1 кубитов в состояние

∈ 1, t, что приводит к некорректной результирую-

|ψ₀〉

= |0〉^⊗n |1〉 (дополнительные рабочие кубиты

щей оценке требуемых для реализации алгоритма

инициализируются в зависимости от вида функ-

Гровера ресурсов.

ции f).

Таким образом, требуемые для реализации алго-

2. Применение вентилей Адамара H:

ритма Гровера ресурсы (количество кубитов и кван-

товых вентилей) могут быть оценены как произве-

∑

|0〉 - |1〉

дение соответствующих оценок для ресурсов одной

|ψ₁〉 =

√

|i〉 ⊗

√

итерации на среднее число итераций алгоритма Гро-

i=0

вера (этапом измерения мы в данном случае прене-

√

брегаем). При этом каждая итерация, как уже отме-

3. Применение «итерации Гровера» (π/4)

N/M

раз:

чалось, представляет собой последовательное при-

а) Изменение знака у амплитуды целевого состо-

менение оператора оракула U_ω и оператора «рассе-

ивания Гровера» U_s. Для оператора «рассеивания

яния для всех i ∈ 0, N - 1 (в терминах монографии

[7] — применение оракула О)

Гровера» количество квантовых операторов tUω бу-

дем оценивать в соответствии c работами [3, 4], а

−-→ (-1)f(i) |i〉 ;

оценке количества квантовых операторов tUs, тре-

буемых для реализации оракула U_ω, посвящены сле-

б) Инверсия относительно среднего (в терминах

дующие разделы настоящей статьи.

монографии [7] — применение оператора 2 |ψ〉〈ψ|-I,

Итоговая оценка требуемого количества кванто-

где I — единичная матрица размером 2ⁿ × 2ⁿ):

вых операторов для алгоритма Гровера составляет

— применить оператор H^⊗n;

√

— применить оператор 2 |0〉〈0| - I;

N (tUω + tUs).

(3)

— применить оператор H^⊗n.

4. Измерение кубитов, с вероятностью p > 1/2

получим произвольный a_x′ : f(x^′) = 1.

4. РЕАЛИЗАЦИЯ ОДНОЙ ИТЕРАЦИИ

Рассмотрим произвольный алгоритм блочного

АЛГОРИТМОВ ШИФРОВАНИЯ

шифрования с длиной ключа n битов и длиной бло-

«КУЗНЕЧИК» И «МАГМА»

ка m битов E : V_n × V_m → V_m. Пусть известно

Для того чтобы реализовать унитарный опера-

некоторое количество пар открытых и шифрован-

тор U_ω, соответствующий произвольному блочному

ных текстов, полученных при шифровании на од-

шифру E : V_n × V_m → V_m, необходимо представить

ном и том же ключе K ∈ V_n, C_i = E(P_i, K), i ∈ 1, t,

его функцию зашифровывания в виде квантовой

и решается стандартная задача по восстановлению

схемы. Отображение E : V_n × V_m → V_m состоит из

ключа. Для применения алгоритма Гровера перед

m булевых координатных функций f_i(x₁, . . ., xn+m),

нами стоит задача построения оператора U_ω. Преж-

i ∈ 1,m. Реализация булевой функции f(x₁,...,x_n)

де всего заметим, что мы требовали, чтобы решение

в виде квантовой схемы в общем случае приведена

задачи было единственным, т. е. ключ шифрования

на рис. 2.

по заданному набору входов и выходов определялся

Полином Жегалкина булевой функции

однозначным образом. С учетом расстояния един-

f_i(x₁, . . ., xm+n) можно реализовать с помощью

ственности шифра [8] количество пар текстов долж-

обобщенных вентилей CNOT(C|t) (см. [7, 9, 10]),

но быть не менее t = ⌈n/m⌉.

в которых управляемый кубит t контролиру-

В этом случае с большой вероятностью ключ бу-

ется некоторым множеством кубитов C. Для

дет единственным, а соответствующая булева функ-

реализации обобщенных вентилей CNOT(C|t) не

ция оракула f : V_n → V₁ определяется следующим

требуется использование дополнительных кубитов

образом:

⋀

|xⁿ

f (x) = z (E(P_i, x) ⊕ C_i)) ,

U_f

i=1

f x

где z : V_m → V₁, причем z(x) = 1, если x = 0^m, и

z(x) = 0 в противном случае.

Рис. 2. Общий вид квантовой схемы, реализующей булеву

Отметим, что в работе [3] используется завышен-

функцию f(x1, . . . , xn)

ная оценка для требуемого числа пар (P_i, C_i), i ∈

647

Д. В. Денисенко, Г. Б. Маршалко, М. В. Никитенкова и др.

ЖЭТФ, том 155, вып. 4, 2019

(см. [7], с. 184). Следовательно, для реализации

f_i(x₁, . . ., xn+m) требуется n + m + 1 кубитов, а

количество обобщенных вентилей CNOT(C|t) не

превосходит количества слагаемых в полиноме

Жегалкина рассматриваемой булевой функции.

Таким образом, если координатные функции

шифра E : V_n ×V_m → V_m легко представимы в виде

полинома Жегалкина, то для реализации соответ-

Рис. 3. Квантовая схема одной итерации алгоритма «Куз-

ствующей квантовой схемы алгоритма шифрования

нечик»

достаточно n + m + m кубитов.

Алгоритмы блочного шифрования строят таким

но оценить по количеству слагаемых в полиномах

образом, что получить аналитические выражения

Жегалкина координатных функций S-боксов. Суще-

для координатных функций E : V_n × V_m → V_m в

ствуют другие способы реализации подстановок в

виде полиномов Жегалкина с практической точки

виде квантовых схем. Например, в работе [3] уда-

зрения невозможно. В связи с этим, для того чтобы

лось найти квантовую схему, задающую байтовый

представить E : V_n ×V_m → V_m в виде квантовой схе-

S-бокс алгоритма AES с помощью 9 кубитов. Одна-

мы, необходимо представить блочный шифр в виде

ко в данной работе будем считать, что подстановки

композиции базовых преобразований, а затем каж-

s ∈ S(V_m) реализуются путем представления коор-

дое базовое преобразование блочного шифра пред-

динатных функций f_i(x₁, . . . , x_m), i ∈ 1, m, в виде

ставить в виде квантовой схемы.

полиномов Жегалкина.

Таблица 1. Количество дополнительных кубитов и кван-

товых вентилей при выполнении базовых преобразований

4.1. Реализация одной итерации алгоритма

алгоритмов блочного шифрования

«Кузнечик»

Для реализации одной итерации функции за-

Кол-во

шифровывания E : V₁₂₈ × V128 → V128 алгорит-

Операция

доп. ку-

ма ГОСТ Р 34.12-2015 «Кузнечик», которая со-

вентилей

битов

стоит из сложения внутреннего вектора внутрен-

P ⊕ Key

него состояния со 128-битным ключом K, парал-

лельного применения шестнадцати 8-битных под-

n³ +

n² -

становок и применения линейного преобразования

P ⊞ Key mod 2ⁿ

L : V₁₂₈ → V₁₂₈, в виде квантовой схемы требуется

n+8

128 + 128 + 128 + 128 = 512 кубитов (рис. 3).

При побитовом наложении итерационного ключа

Подстановка

N_s

в алгоритме «Кузнечик» потребуется 128 вентилей

Линейное

≤ m(m - 1)

CNOT.

преобр.

Количество слагаемых в полиномах Жегалкина

Цикл. сдвиг

координатных функций подстановки π : Z₂8 → Z₂8

алгоритма «Кузнечик» равно 133, 130, 103, 125,

108, 123, 132, 123 соответственно порядковым но-

Традиционно блочные шифры строятся на осно-

мерам координатных функций, т. е. для реализа-

ве композиции элементарных преобразований, к ко-

ции π : Z₂8 → Z₂8 требуется 977 обобщенных вен-

торым относятся сложение вектора внутреннего со-

тилей CNOT(C|t). Следовательно, для реализации

стояния P с ключом K (модульное или побитовый

S : V₁₂₈ → V₁₂₈ требуется 16 · 977 = 15632 вентиля

XOR), нелинейное преобразование — подстановка S,

CNOT(C|t).

линейные преобразования — умножения на матрицу

Для реализации линейного преобразования ал-

L, сдвиги. В табл. 1 представлены оценки достаточ-

горитма «Кузнечик» в виде умножения 128-битного

ного количества ресурсов (см. [7, 11, 12]) для реали-

вектора на матрицу размером 128 × 128 бит потре-

зации таких элементарных преобразований.

буется 7879 вентилей CNOT. Однако данное линей-

Отметим, что N_s — количество вентилей для ре-

ное преобразование может также быть реализовано

ализации S-боксов, как было показано выше, мож-

с помощью 16 итераций линейного регистра сдви-

648

ЖЭТФ, том 155, вып. 4, 2019

Оценка сложности реализации алгоритма Гровера...

га. В этом случае для реализации одной итерации

5,7,6,11 соответственно порядковым номерам коор-

потребуется 415 вентилей, а для всего преобразова-

динатных функций, т. е. для реализации S-боксов

ния — 6640. Оценка количества ресурсов для реали-

алгоритма «Магма» потребуется всего 226 обобщен-

зации одного раунда алгоритма «Кузнечик» в виде

ных вентилей CNOT(C|t).

квантовой схемы приведена в табл. 2.

Циклический сдвиг влево на 11 бит (линейного

преобразования алгоритма «Магма») может быть

реализован с помощью программной перенумерации

Таблица 2. Количество кубитов и вентилей при реализа-

кубитов (см. табл. 1).

ции одного раунда алгоритма «Кузнечик»

Побитовый XOR двух 32-битных полублоков

требует 32 вентиля CNOT. Столько же вентилей по-

Кол-во кубитов

Кол-во вентилей

надобится для перезаписи полублока, значение ко-

512

128 + 15632 + 6640 = 22400

торого было изменено при наложении раундового

ключа. Необходимое количество ресурсов для реа-

лизации одного раунда алгоритма «Магма» приве-

дено в табл. 3.

4.2. Реализация одной итерации алгоритма

«Магма»

Таблица 3. Количество кубитов и вентилей при реализа-

ции одного раунда алгоритма «Магма»

Каждая итерация функции зашифровывания

E : V₃₂ × V₆₄ → V₆₄ алгоритма ГОСТ Р 34.12-2015

Кол-во кубитов

Кол-во вентилей

«Магма», являющегося так называемой сетью Фей-

161

32 + 23256 + 226 + 32 = 23546

стеля, преобразует 32-битный подвектор 64-битно-

го вектора внутреннего состояния. Для реализации

этого преобразования, которое состоит из наложе-

ния ключа по модулю 2³², применения восьми 4-бит-

ных подстановок, циклического сдвига на 11 и по-

5. ОЦЕНКА КОЛИЧЕСТВА РЕСУРСОВ ДЛЯ

битового сложения со вторым подвектором, в виде

РЕАЛИЗАЦИИ АЛГОРИТМОВ

квантовой схемы потребуется 32 + 32 + 32 + 32 +

«КУЗНЕЧИК» И «МАГМА»

+ 32 + 1 = 161 кубит (см. рис. 4).

В предыдущем разделе получены оценки доста-

Оценим количество обобщенных вентилей

CNOT(C|t).

точного количества кубитов и обобщенных венти-

лей CNOT(C|t) для реализации одной итерации ал-

При наложении раундового ключа в алгоритме

горитма «Кузнечик» и одной итерации алгоритма

«Магма» потребуется (см. [11])

«Магма». В данном разделе рассмотрим два подхо-

да к реализации алгоритмов «Кузнечик» и «Маг-

32³ +

32² -

32 + 8 = 23256 вентилей CNOT.

ма». Основная проблема, возникающая при реализа-

ции схем рассматриваемого типа, - рост числа куби-

Количество слагаемых в полиномах Жегалкина

тов вследствие необходимости приведения использу-

координатных функций подстановок π_i : Z₂4 → Z₂4,

емых преобразований к унитарному виду. В связи с

i = 0, 1, . . ., 7, алгоритма «Магма» равно 7,5,7,4;

этим возникает два подхода к реализации.

4,10,6,8; 7,9,7,11; 6,9,8,10; 2,8,7,9; 7,7,5,5;

7,8,6,8;

Первый подход к реализации алгоритмов

—

без повторного использования кубитов. Общая схе-

E^†

ancilla

E^†

S(b

<11

|a LSX(k,b)

E^†

|E(E(...E(k,x)))

Рис. 4. Квантовая схема одной итерации алгоритма «Маг-

Рис. 5. Композиция раундовых преобразований без эконо-

ма»

мии кубитов

649

Д. В. Денисенко, Г. Б. Маршалко, М. В. Никитенкова и др.

ЖЭТФ, том 155, вып. 4, 2019

ма вычисления композиции нескольких итераций

после обращения первого раунда с помощью венти-

условного алгоритма E : V_n × V_m → V_m приведе-

лей Паули происходит обнуление 128 кубитов, в ко-

на на рис. 5.

торые записан блок открытого текста P (мы вос-

При такой реализации количество вентилей и ку-

станавливаем ключ по известным парам открытого

битов можно оценить путем перемножения количе-

и шифрованного текстов). Следовательно, для ре-

ства итераций на соответствующее количество ре-

ализации схемы без учета алгоритма развертыва-

сурсов, необходимое на один раунд блочного шиф-

ния ключа требуется не более 16 · 128 + 16 · 15632 +

ра. Отметим, что количество вентилей необходимо

+ 14 · 6640 + 128 = 345248 обобщенных вентилей.

еще умножить на 2, чтобы учесть применение об-

Алгоритм развертывания ключа представляет

ратных преобразований E^† , необходимых для того,

собой 32-раундовую сеть Фейстеля, функция услож-

чтобы после измерения получить не только какой-то

нения которой совпадает с итерационным преоб-

зашифрованный текст E(E(. . . E(k, x))), но и пару

разованием алгоритма «Кузнечик», где вместо до-

(k, x), на которой этот зашифрованный текст полу-

бавления ключа используется добавление фиксиро-

чен, а также для того, чтобы избавиться от «запу-

ванных констант. Квантовая схема одной итерации

танных» (см. [7]) состояний системы.

представлена на рис. 7, для ее реализации требу-

Второй подход — это использованная в работе [3]

ется 128 + 128 = 256 вспомогательных кубитов и

реализация с повторным использованием кубитов.

2 · (128 + 15632 + 6640) + 128 + (128 · 3) = 45312

Идея данного подхода заключается в том, что, вы-

обобщенных вентилей. Для 32 итераций требуется

полнив первоначально несколько преобразований,

32 · 45312 = 1449984 вентилей.

мы можем вернуть в начальное состояние часть за-

На рис. 6 в блоках Ki (i = 1, 2, 3, 4) формируют-

действованных кубитов, применив обратные преоб-

ся раундовые ключи алгоритма шифрования «Куз-

разования, с тем чтобы использовать данные куби-

нечик» (см. описание алгоритма [6]). Каждый такой

ты в последующих вычислениях (см. рис. 6). При

блок включает 8 итераций квантовой схемы, изоб-

этом должны быть выполнены следующие условия:

раженной на рис. 7.

— обратные преобразования должны применять-

Квантовая схема одной итерации без повторного

ся в обратном порядке по отношению к прямым пре-

использования кубитов представлена на рис. 8, для

образованиям с тем, чтобы иметь возможность про-

ее реализации требуется 128 · 3 = 384 вспомогатель-

вести преобразования над кубитами, находящимися

ных кубита и 128 + 128 + 15632 + 6640 + 128 = 22656

в соответствующем состоянии;

обобщенных вентилей. Для 32 итераций требуется

— обратное преобразование должно применяться

256 + 32 · 384 = 12544 кубита и 32 · 22656 = 724992

по крайней мере после одного прямого преобразова-

вентиля.

ния с тем, чтобы сохранить состояние, полученное

Оценки количества кубитов и вентилей, необхо-

применением соответствующего прямого преобразо-

димых для реализации в виде квантовой схемы про-

вания.

цедуры зашифровывания одного блока открытого

текста блочным шифром «Кузнечик», приведены в

табл. 4 и 5.

5.1. Алгоритм «Кузнечик»

В алгоритме ГОСТ Р 34.12-2015 «Кузнечик»

Таблица 4. Реализация алгоритма «Кузнечик» с повтор-

применяется 9 полных итераций, а в 10-й итера-

ным использованием кубитов

ции применяется только наложение ключа. Кван-

товая схема, реализующая 10 раундов алгоритма

Кол-во кубитов Кол-во CNOT(C|t)

«Кузнечик» (см. описание алгоритма [6]) с повтор-

1024

1795232

ным использованием кубитов, продемонстрирована

на рис.

Таблица 5. Реализация алгоритма «Кузнечик» без по-

Для реализации квантовой схемы, приведенной

вторного использования кубитов

на рис. 6, требуется 8 · 128 = 1024 кубита, причем

алгоритм развертывания раундовых ключей уже

Кол-во кубитов

Кол-во CNOT(C|t)

учтен. Для простоты будем считать, что для вычис-

ления S и S^†, а также для вычисления L и L^† тре-

128+ 256 · 9 + 12544 =

9·22400+128+724992 =

буется одинаковое количество вентилей. На рис. 6

= 14976

= 926720

побитовый XOR 128-битных блоков выполняется 16

раз, 16 раз применяется S и 14 раз вычисляется L,

650

ЖЭТФ, том 155, вып. 4, 2019

Оценка сложности реализации алгоритма Гровера...

128

|K₁

128

|K₂

128

S^†

128

S^†

L^†

128

L^†

S^†

128

S^†

128

S^†

L^†

128

L^†

128

S^†

128

Рис.

6. Квантовая схема 10 раундов алгоритма «Кузнечик» с повторным использованием кубитов (а — первые четыре

итерации алгоритма, б — оставшиеся пять полных итераций и одна неполная)

128

|K2i-1

X[C

]

X[C

]

|LSX[C

](K

)

8(i-1)+j

2i-1

128

|K2i

|K2i-1

128

S^†

128

L^†

Рис.

7. Квантовая схема для одной итерации алгоритма развертывания ключа алгоритма шифрования «Кузнечик» с

повторным использованием кубитов, i = 1, 2, 3, 4, j = 1, 2, . . . , 8

128

|K2i-1

X[C

]

|X[C

](K

)

8(i-1)+j

2i-1

128

|K2i

128

|SX[C

](K

)

8(i-1)+j

2i-1

128

|LSX[C

](K

)

8(i-1)+j

2i-1

128

|K2i-1

Рис. 8. Квантовая схема для одной итерации алгоритма развертывания ключа алгоритма шифрования «Кузнечик» без

повторного использования кубитов, i = 1, 2, 3, 4, j = 1, 2, . . . , 8

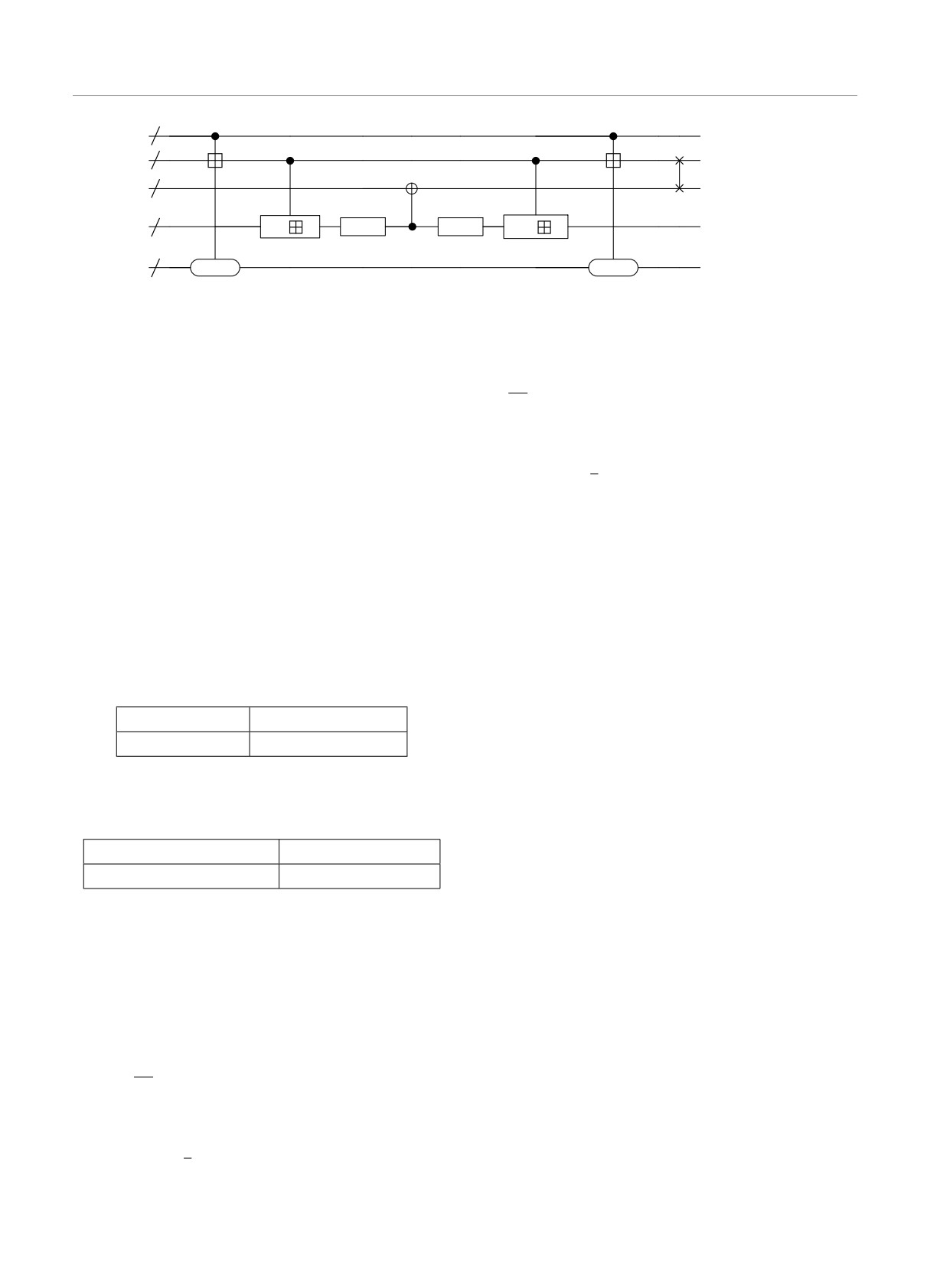
5.2. Алгоритм «Магма»

В силу простоты алгоритма формирования ите-

рационных ключей алгоритма «Магма», для записи

всех раундовых ключей требуется 256 кубитов. Для

Квантовая схема, реализующая процедуру за-

записи блока открытого текста требуется 64 куби-

шифровывания одного блока открытого текста с по-

та, а для хранения промежуточных значений — еще

мощью алгоритма «Магма» с повторным исполь-

33 дополнительных кубита, т.е. общее количество

зованием кубитов, состоит из 32 последовательных

кубитов равно 256 + 64 + 32 + 1 = 353. Для оценки

применений квантовой схемы на рис. 9.

651

Д. В. Денисенко, Г. Б. Маршалко, М. В. Никитенкова и др.

ЖЭТФ, том 155, вып. 4, 2019

|a LSX(k, b)

S(b

<11

> 11

S†(b

ancilla

Рис. 9. Квантовая схема одной итерации алгоритма «Магма» с повторным использованием кубитов

количества обобщенных вентилей воспользуемся ре-

Для поиска ключа алгоритма «Магма» требует-

зультатами, полученными в разд. 4.2. Для наложе-

ся ⌈²⁵⁶⁶⁴ ⌉ = 4 пары блоков открытого и шифрованно-

ния раундового ключа необходимо 23256 вентилей,

го текстов, поэтому для применения алгоритма Гро-

для реализации S-боксов потребуется 226 обобщен-

вера к алгоритму «Магма» требуется

ных вентилей, побитовый XOR двух 32-битных по-

— 256 + 64 · 4 + 32 + 1 + 1 = 546 кубитов;

лублоков требует 32 вентилей. С учетом процедуры

— не менее π4 · 2¹²⁸(tUω + tUs ) вентилей.

обращения кубитов, показанной на рис. 9, количе-

Значение tUω оцениваем количеством операторов

ство обобщенных вентилей равно 23256+ 226 + 32 +

CNOT(C|t) по табл. 4 и 6. При этом количество вен-

+ 226 + 23256 + 32 · 3 = 47092.

тилей в данных таблицах необходимо умножить на

Оценки количества кубитов и вентилей, необхо-

2 для обращения схем.

димых для реализации блочного шифра «Магма»

Для того чтобы понять, как точно посчитать

в виде квантовой схемы (применительно к одному

количество вентилей tUs , воспользуемся результа-

блоку открытого текста), приведены в табл. 6 и 7.

тами работы

[4]. Для обоих алгоритмов ГОСТ

Р 34.12-2015 в процедуре «рассеивания Гровера» к

ключу последовательно применяются 256 вентилей

Таблица 6. Реализация алгоритма «Магма» с повторным

Адамара H, 256 вентилей Паули X, один вентиль

использованием кубитов

Адамара H, один обобщенный CCNOT, один вен-

тиль Адамара H, 256 вентилей Паули X и еще 256

Кол-во кубитов Кол-во CNOT(C|t)

вентилей Адамара H, т. е. всего 1027 квантовых вен-

353

47092·32=1506944

тилей. Кроме того, при изменении флагового куби-

та происходит проверка на совпадение с известными

Таблица 7. Реализация алгоритма «Магма» без повтор-

блоками шифрованного текста, для которой допол-

ного использования кубитов

нительно требуется не более 256 вентилей Паули Х,

один обобщенный CCNOT и еще не более 256 венти-

Кол-во кубитов

Кол-во CNOT(C|t)

лей Паули Х для возврата соответствующих кубитов

256+64·32+1+64 = 2369

23546 · 32 = 753472

в исходное состояние перед проверкой, т. е.

1027 + 1 ≤ tUs ≤ 1027 + 512 + 1.

Перед процедурой измерения переводить флаго-

5.3. Общая оценка количества квантовых

вый кубит в первоначальное состояние |1〉 = H |-〉

ресурсов для применения алгоритма

не обязательно, поэтому осталось учесть еще один

Гровера в задаче поиска ключей алгоритмов

вентиль Адамара, применяемый при формировании

блочного шифрования ГОСТ Р 34.12-2015

состояния |-〉 = H |1〉 на флаговом кубите.

Для поиска ключа алгоритма «Кузнечик» тре-

буется ⌈²⁵⁶¹²⁸ ⌉ = 2 пары блоков открытого и шифро-

6. ЗАКЛЮЧЕНИЕ

ванного текстов, поэтому для применения алгорит-

ма Гровера к алгоритму «Кузнечик» требуется

Полученные результаты позволяют оценить чис-

— 1024 + (1024 - 256) + 1 = 1793 кубита;

ло логических кубитов, необходимых для реализа-

— не менее π4 · 2¹²⁸(tUω + tUs ) вентилей.

ции рассмотренных алгоритмов. Для реализации

652

ЖЭТФ, том 155, вып. 4, 2019

Оценка сложности реализации алгоритма Гровера...

логических кубитов вследствие процессов декоге-

L. K. Grover, in Proc. STOC1996, pp. 212-219, ACM

рентизации потребуется использование кодов кор-

(1996).

рекции квантовых ошибок, что, в свою очередь, под-

разумевает примерно на порядок большее число фи-

M. Grassl, B. Langenberg, M. Roetteler, and R. Stei-

зических кубитов. Например, код Шора позволяет

nwandt, arXiv:1512.04965v1.

кодировать один логический кубит девятью физи-

Д. В. Денисенко, М. В. Никитенкова, ЖЭТФ 155,

ческими кубитами. Коды Стина (CSS-коды) позво-

32 (2019).

ляют кодировать один логический кубит пятью фи-

зическими кубитами — это минимальное количество

M. Amy, O. Di Matteo, V. Gheorghiu, M. Mosca,

физических кубитов для исправления одной ошибки

A. Parent, and J. Schanck, ePrint Report 2016/992.

(см. [7]).

Работы [13, 14] посвящены теоретическим оцен-

ГОСТ Р 34.12-2015, Информационные техноло-

гии. Защита информации. Блочные шифры.

кам минимального времени выполнения одного

квантового вентиля на одном кубите. В случае

M. A. Nielsen and I. L. Chuang, Quantum Compu-

реализации кубита с помощью иона Ca⁺ в ловушке

tation and Quantum Information, Cambridge Univ.

это время составляет порядка 6.62 · 10-16 с, что

Press, Cambridge (2010).

значительно меньше, чем время выполнения одного

К. Шеннон, в кн. Работы по теории связи и ки-

вентиля на практике: 10-9 с.

бернетике, Изд-во иностр. лит., Москва (1963).

Грубые оценки времени потери когерентности

(декогерентизации), времени выполнения одной опе-

A. Younes and J. Miller, arXiv:quant-ph/0304099v1.

рации над кубитом и максимального числа опе-

раций, последовательно выполняемых над кубитом

10.

S. Ding and Z. Jin, ICCCAS 2007, Beijing, China,

(максимальной длины квантовой схемы), приведены

DOI:10.1109/ICCCAS.2007.4348267 (2007).

в работе [7], табл. 7.1, с. 278.

В марте 2018 г. компания Google представила 72-

11.

P. Kaye, arXiv:quant-ph/0408173.

кубитный квантовый процессор Bristlecone на базе

сверхпроводников (см. [15]). Согласно [16, 17], вре-

12.

D. Beckman, A. N. Chari, and J. Preskill, arXiv:org/

мя когерентности систем на базе сверхпроводников

abs/quant-ph/9602016.

составляет около 100 мкс, а минимальное время при-

менения однокубитового вентиля, согласно [18] (см.

13.

S. Ashhab, P. C. Groot, and F. Nori, arXiv:1202.

табл. 2 на с. 20), составляет 5 нс. Таким образом,

5872v2 [quant-ph].

к кубитам на базе сверхпроводников можно успеть

= 20000 однокубитовых

14.

L. B. Levitin, T. Toffoli, and Z. Walton, arXiv:

10-9

quant-ph/0211167v3.

вентилей, после чего система перейдет в некоторое

основное состояние, и состояние суперпозиции ку-

15.

research.googleblog.com/2018/03/a-preview-of-

битов будет разрушено. Тем не менее, согласно [18]

bristlecone-googles-new.html?m=1.

количество вентилей, которые на современном этапе

развития квантовых технологий могут быть приме-

16.

J. M. Martinis and A. Megrant, arXiv:1410.5793v1.

нены к кубитам на базе сверхпроводников, состав-

ляет порядка 10³.

17.

J. Portes, Decoherence, Superconducting Qubits, and

the Possibility of Quantum Computing, Columbia

Univ. (2015).

ЛИТЕРАТУРА

1. P. W. Shor, SIAM J. Comput. 26, 1484 (1997).

18.

G. Wendin, arXiv:1610.02208v2.

653