ЖЭТФ, 2019, том 155, вып. 4, стр. 750-758

ЭКСПОНЕНЦИАЛЬНАЯ ГРАНИЦА ДЛЯ СКОРОСТИ

НАГРЕВАНИЯ ПЕРИОДИЧЕСКИ УПРАВЛЯЕМЫХ

СПИНОВЫХ СИСТЕМ

В. Е. Зобовa*, М. М. Кучеров^b

^a Институт физики им. Л. В. Киренского Сибирского отделения Российской академии наук

660036, Красноярск, Россия

^b Институт космических и информационных технологий Сибирского федерального университета

660074, Красноярск, Россия

Поступила в редакцию 6 ноября 2018 г.,

после переработки 22 ноября 2018 г.

Принята к публикации 22 ноября 2018 г.

Для системы ядерных спинов твердого тела при наличии неоднородного магнитного поля найдена стро-

гая граница для скорости нагревания системы под воздействием высокочастотного магнитного поля,

которое применяют, например, для создания эффективных гамильтонианов. Рассмотрена автокорреля-

ционная функция (АКФ) спина, вращающегося в локальном поле, флуктуации которого заданы гауссов-

ским случайным процессом. Корреляционная функция случайного поля взята в виде суммы статического

неоднородного вклада и зависящего от времени вклада, выраженного самосогласованным образом через

АКФ спина. Исследованы особые точки АКФ на оси мнимого времени, координаты которых определяют

показатели экспоненциальных асимптотик в высокочастотной области. Получены зависимости координат

от неоднородности поля при различных приближениях. Показано, что крыло спектра АКФ в кумулянтном

приближении служит строгой верхней границей для крыла спектра АКФ и, следовательно, для скорости

нагревания системы при воздействии на нее переменных магнитных полей. Установлено, что случай-

но распределенные неоднородные магнитные поля увеличивают крылья спектров АКФ и, тем самым,

ускоряют нагревание системы.

DOI: 10.1134/S0044451019040187

систем применяют теорию Флоке или Магнуса

[8-11]. Нужная эволюция системы под действием

среднего гамильтониана сопровождается ее пара-

1. ВВЕДЕНИЕ

зитным нагреванием высшими гармониками. От

Перспективным способом изучения сложных

скорости нагревания зависит длительность этапа

квантовых систем является их моделирование на

моделирования и, тем самым, эффективность мето-

других квантовых системах

[1-3]. Бурное раз-

да. В работах [12-17] найдены качественные оценки

витие такого направления в настоящее время

для границы скорости нагревания, показавшие

связано с развитием экспериментальных методов

ее экспоненциальное замедление при увеличении

когерентного управления квантовыми системами

частоты осцилляций.

[2-7], такими, как ионы и атомы в ловушках,

электронные парамагнитные центры в твердых

Практическое применение преобразования га-

мильтонианов импульсами радиочастотных полей

телах и сверхпроводящие системы. Для получения

эффективного гамильтониана, необходимого для

было реализовано еще в 70-х гг. для получения спек-

моделирования, к системе прикладывают мощные

тров ЯМР высокого разрешения в твердых телах

периодические воздействия, например, лазерные

[18, 19] и получило название «спиновая алхимия».

импульсы, импульсы радиочастотных или сверх-

Термодинамическая теория образования квазирав-

высокочастотных полей. Для описания эволюции

новесного состояния системы при малых временах

и последующего нагревания была разработана в ра-

^* E-mail: rsa@iph.krasn.ru

ботах [20, 21] и объяснила результаты эксперимен-

750

ЖЭТФ, том 155, вып. 4, 2019

Экспоненциальная граница для скорости нагревания. . .

тов. Для скорости нагревания были выведены фор-

зируем соотношение между АКФ, полученными с

мулы, выражавшие ее через спиновые временные

помощью различных приближений. В разд. 3 мы

корреляционные функции, хотя расчет самих этих

изучаем влияние неоднородного магнитного поля

функций выполнен не был. Преимущество систем

на АКФ. Координаты их ближайших особых точек

ядерных спинов по сравнению с другими квантовы-

на оси мнимого времени рассчитаны через радиусы

ми системами состоит в известных взаимодействи-

сходимости рядов для АКФ по степеням времени.

ях, достаточной изолированности от других подси-

Выполнено сравнение зависимостей этих координат

стем, возможности управления и наблюдения мето-

от величины неоднородного уширения для реше-

дами ЯМР. Поэтому в таких системах удается пе-

ний разных уравнений. В разд.

обсуждаются

рейти от качественных оценок границ для скорости

полученные результаты. Наконец, в Приложении

нагревания к количественным оценкам. В настоя-

выведены аппроксимирующие функции для ука-

щей работе мы найдем строгую оценку, выражен-

занных зависимостей координат, рассчитанных

ную, как это принято, через второй момент спектра

численно.

ЯМР.

В основу данной работы положено хорошо заре-

2. ГАУССОВСКОЕ СЛУЧАЙНОЕ

комендовавшее себя в таких системах представле-

ЛОКАЛЬНОЕ ПОЛЕ

ние флуктуирующего во времени локального поля

на спинах гауссовским случайным процессом. Такое

Рассмотрим вращение магнитного момента μ(t)

приближение было предложено в работах Андерсо-

в гауссовском случайном магнитном поле h(t).

на [22], Кубо [23] и обусловлено большим числом

Уравнение движения можно записать в виде [30,31]

независимых вкладов со стороны спинов, окружа-

ющих каждый спин. Этот подход был эффективно

μ(t) =

^ĥ(t)μ(t),

(1)

применен к решению задач спиновой динамики, на-

где матрица оператора

^ĥ(t) имеет одинаковый вид:

пример, в работах [22-26]. В указанных работах кор-

⎛

⎞

реляционная функция гауссовского поля выбира-

-h^z(t) h^y(t)

лась из физических соображений. Мы, следуя рабо-

⎟

^ĥ(t) =^⎝ h^z(t)

-h^x(t)

⎠,

(2)

там [27,28], будем задавать эту функцию самосогла-

−h^y(t) h^x(t)

сованным образом через автокорреляционные функ-

ции (АКФ) спинов [29-31]. Ранее мы применили та-

как для обычных векторов μ, так и для векторных

кой подход к объяснению экспоненциальных кры-

операторов μ = γS в квантовомеханическом случае.

льев спектров различных корреляционных функций

Будем искать решение уравнения (1) в виде ря-

гомоядерных систем [32-34], гетероядерных систем

да по числу операторов (матриц) поля. Таким путем

[35], магниторазбавленных систем [36, 37] и спино-

для АКФ получаем

вых пакетов [38]. Сейчас с помощью этого метода мы

∫

найдем строгие границы для скорости поглощения

∑

Γ_α(t) =

dt₁ ×

энергии высокочастотного поля при наличии неод-

n=0 0

нородного магнитного поля. Такое поле существен-

∫

но изменяет динамику спиновых систем, например,

по мнению многих авторов (см. обзор [39]), может

× dt₂ . . .

dt2n

^ĥ(t₁)^ĥ(t₂) . . .ĥ(t2n)

(3)

αα

вызывать переход системы из термализованного со-

стояния в многочастичное локализованное состоя-

где скобки 〈. . .〉 обозначают усреднение по реализа-

ние, характеризуемое замедлением распространения

циям гауссовского случайного поля, а стоящий вни-

энергии внутри системы. С другой стороны, из ка-

зу индекс «αα» — матричный элемент произведения

чественных оценок, выполненных в работах [16, 38],

матриц. Например, для произведения двух матриц

следует, что неоднородное магнитное поле ведет к

получаем

росту высокочастотных асимптотик АКФ. Пробле-

^ĥ(t₁)^ĥ(t₂)

= -g_z(t₁ - t₂) - g_y(t₁ - t₂),

ма влияния неоднородного магнитного поля на ди-

намику спиновых систем нуждается в дальнейшем

где мы ввели обозначение для корреляционной

изучении.

функции проекции поля в разные моменты време-

Структура настоящей статьи следующая. В

ни

разд. 2 мы рассматриваем движение магнитного

〈h^α(t₁)h^α(t₂)〉 = g_α(t₁ - t₂).

(4)

момента в гауссовском случайном поле и анали-

751

В. Е. Зобов, М. М. Кучеров

ЖЭТФ, том 155, вып. 4, 2019

Среднее от произведения нечетного числа гауссовых

Коэффициенты M2nα являются моментами спектра

переменных обращается в нуль, а среднее от произ-

функции АКФ (3) [40]. В случае статических гаус-

ведения четного числа является суммой по всевоз-

совских полей

можным спариваниям одноименных проекций. В об-

g_α(t) = 〈h2α〉 ≡ Δ2α

(10)

щем случае результат усреднения зависит от набора

проекций и последовательности их расположения в

коэффициенты рядов (3) и (9) совпадают, тогда как

произведении. Это усложнение связано с непереста-

в общем случае это не так. Каждый член ряда (3)

новочностью поворотов вокруг разных осей.

является произведением рядов по степеням времени

Исключение составляет частный случай поля,

функций g_α(t).

направленного вдоль одной оси. Если, например,

Проиллюстрируем соотношение коэффициентов

h^z = 0, h^x = h^y = 0, то ряд (3) легко суммирует-

рядов для (6), (8) и для решения уравнения (7) на

ся в экспоненциальную функцию

примере изотропного постоянного гауссовского поля

⎧

⎫

g_x(t) = g_y(t) = g_z(t) = Δ². В этом случае находим

∫

t^′

⎨ ∫t

⎬

Γ0x(t) = exp

g_z(t′′) dt′dt′′

(5)

(2n)!

⎩

⎭

Mc2n =

Δ2n, M1,2n =

2ⁿΔ2n,

n!(n + 1)!

Такой результат обусловлен зависимостью величи-

тогда как точные значения для ряда (3) в этом слу-

ны слагаемого в (3) не от взаимного расположения

чае [23, 30, 31]

разных пар, а лишь от временного интервала меж-

2(2n + 1)!

ду моментами действия спаренных проекций. В так

M2n =

Δ2n.

2ⁿn!3

называемом кумулянтном приближении это условие

Имеет место соотношение (при n > 1)

распространяется на трехкомпонентное поле, что ве-

дет к результату

Mc2n > M2n > M1,2n,

(11)

⎧

⎫

∫

t^′

⎨ ∫t

⎬

которое отражает условия вывода соответствующих

Γ_cx(t) = exp

(g_z(t^′′) + g_y(t′′)) dt′dt′′

(6)

выражений. В уравнении (8) просуммирована часть

⎩

⎭

ряда (3), тогда как в кумулянтном выражении (6)

взяты все варианты спаривания, но с завышенными

В общем случае, сгруппировав члены получен-

коэффициентами.

ного после усреднения в (3) ряда по различным схе-

Вернемся к зависящему от времени гауссовскому

мам спаривания и выполнив частичное суммирова-

полю и зададим его в самосогласованном приближе-

ние, как это описано в работах [27, 30, 31], мы полу-

нии. В этом приближении [27, 31, 32] корреляцион-

чаем для АКФ систему интегральных уравнений

ные функции поля выразим через АКФ спинов

∫t

g_α(t) = Δ2αΓ_α(t).

(12)

Γ_α(t) = - G_α(t - t₁)Γ_α(t₁)dt₁,

(7)

Временные ряды (9) для разных функций удобно

где функция памяти представлена в виде ряда по

сравнивать после перехода к мнимому времени t =

числу пар с различной схемой спаривания. Выраже-

= iτ, когда эти ряды становятся рядами с поло-

ния для вкладов в G_α(t), содержащих от 2 до 4 пар,

жительными членами. Выберем для определенности

приведены в работе [31]. Например, в простейшем

направление осей координат так, чтобы выполня-

случае одной пары имеем уравнение

лось условие

Δ2z ≥ Δ2y ≥ Δ2x.

(13)

∫

Γ1x(t) = -

{g_z(t - t₁)Γ1y(t - t₁) +

Тогда для гарантированного получения для АКФ

приближения с максимальными коэффициентами,

+ g_y(t - t₁)Γ1z(t - t₁)}Γ1x(t₁)dt₁.

(8)

X (t), следует в кумулянтном приближении (6) взять

самосогласованным образом такую же функцию

Иначе, АКФ (3) может быть представлена в виде

X (t) для поля, т. е. записать уравнение

ряда по степеням времени

⎧

⎫

∫

t^′

⎨

⎬

∑

(-1)ⁿ

X (t) = exp

-(Δ2z + Δ2y )

X (t^′′) dt^′dt^′′

(14)

Γ_α(t) =

M2nαt2n.

(9)

⎩

⎭

(2n)!

n=0

752

ЖЭТФ, том 155, вып. 4, 2019

Экспоненциальная граница для скорости нагревания. . .

Полученное уравнение Блума - Хаббарда [28] имеет

случайного разброса ларморовых частот спинов на

решение

динамику. Предположим, что такой разброс произо-

шел из-за неоднородного локального магнитного по-

X (t) =

( √

) =

ля, направленного вдоль оси z и заданного гауссо-

ch2 t (Δ2z + Δ2y )/2

вым распределением с плотностью

(

)

( √

(15)

(ω_i - ω₀)²

P (ω_i) =

√

exp

(20)

cos²

it (Δ2z + Δ2y)/2

2πW²

2W²

С другой стороны, для получения функции Z(t) с

где ω₀ — средняя частота, W² — дисперсия.

гарантированно меньшими коэффициентами следу-

Причин разброса резонансных частот может

ет взять решение уравнения

быть много. В частности, это может произойти

∫t

вследствие взаимодействия с системой спинов дру-

Z(t) = -(Δ2x + Δ2y ) Z²(t - t₁)Z(t₁) dt₁.

(16)

гого сорта в гетероядерных кристаллах. Такой слу-

чай был рассмотрен нами в работе [35] на приме-

Решения уравнений (14) и (16) имеют особые

ре кристалла LiF. Полученные там общие форму-

точки на оси мнимого времени [29-32], в окрестнос-

лы позволяют вывести выражения для первых пя-

ти которых АКФ имеет вид

ти коэффициентов ряда (моментов) (9) в аксиально-

симметричном случае Δ2x = Δ2y = Δ2X . Положив в

A_α

Γ_α(t) ≈

(17)

формулах¹⁾ работы [35] Δ2FL = W², Δ2LL = Δ2XL =

(it ± τ₀)²

= 0, находим в нашем случае

Для уравнения (14) это следует из его решения (15),

тогда как для уравнений (16) и (7) в этом можно

M2X = W² + Δ2z + Δ2X,

(21)

убедиться после подстановки в них главной части

решений (17) (см. Приложение).

M4X = 3W⁴ + 3Δ4z + (4Δ2X + 6Δ2z)W² +

Координата ближайшей к началу координат осо-

бой точки определяет радиус сходимости рядов (9).

+ 5Δ4X + 6Δ2zΔ2X,

Поэтому эта координата может быть найдена через

M6X = 15W⁶ + 15Δ6z + (21Δ2X + 45Δ2z)W⁴ +

отношение моментов высокого порядка как предел

+ 51Δ6X + 73Δ2zΔ4X + 55Δ4zΔ2X +

при n → ∞ величины

+ (45Δ4X + 45Δ4z + 76Δ2zΔ2X )W²

2n(2n + 1)M2(n-1)

τ20n =

(18)

M8X = 105W⁸ + (144Δ2X + 420Δ2z)W⁶ +

M2n

+ (448Δ4X + 630Δ4z + 988Δ2zΔ2X )W⁴ +

Эта формула аналогична формуле Даламбера для

{

1678Δ2zΔ4X + 1544Δ4zΔ2X + 420Δ6z +

радиуса сходимости ряда, в которой мы заменили

}

коэффициент 2n(2n - 1) на 2n(2n + 1), поскольку

+ 914Δ6X

W² + 1470Δ2zΔ6X + 861Δ8X +

нам известен показатель сингулярности в (17) рав-

+ 105Δ8z + 1378Δ4zΔ4X + 700Δ6zΔ2X,

(22)

ный двум.

M10X = 945W¹⁰ + (1245Δ2X + 4725Δ2z)W⁸ +

Соотношение между коэффициентами рядов (9)

+ (5856Δ4X +9450Δ4z+15120Δ2zΔ2X )W⁶ +

для решений уравнений (7) и (14), положительных

{

36858Δ2zΔ4X + 37890Δ4zΔ2X +

на оси мнимого времени, приводит к соотношению

}

между самими этими функциями и, следовательно,

+ 9450Δ6z + 16676Δ6X

W⁴ +

{

между координатами ближайших особых точек

27643Δ8X + 57858Δ6XΔ2z +

√

+ 64744Δ4XΔ4z + 35400Δ2XΔ6z +

τ₀ > τ_c = π/

2(Δ2z + Δ2y) .

(19)

}

W² + 43989Δ2zΔ8X +

+ 4725Δ8z

+ 21847Δ10X + 945Δ10z + 48498Δ4zΔ6X

3. НЕОДНОРОДНОЕ МАГНИТНОЕ ПОЛЕ

+ 33742Δ6zΔ4X + 11385Δ8zΔ

Самосогласованное флуктуирующее во времени

поле, рассмотренное выше, создается спин-спино-

¹⁾ В формуле (A.1) [35] для M(F)8X есть опечатка: правиль-

вым взаимодействием между спинами с одинако-

ное четвертое слагаемое в фигурных скобках 420Δ6FF , а не

выми ларморовыми частотами. Исследуем влияние

420Δ6XL.

753

ЖЭТФ, вып. 4

В. Е. Зобов, М. М. Кучеров

ЖЭТФ, том 155, вып. 4, 2019

(

)

²M₂

Выразим моменты в единицах второго момента,

взяв для определенности, как для ДДВ, Δ2z = 4Δ2X.

Введем обозначения

M₂ = M2X = B² + W², B² = Δ2z + Δ2x,

w² =

b² =

B² ,

(23)

M₂

Δ2z

4b²

Δ2x

b²

M₂

Находим

M4X

2b⁴

2b²w²

=3+

M²²

5²

M6X

24b²

56b⁴w²

308b⁶

= 15 -

w⁴ -

M³²

5²

5³

M8X

= 160.7504b⁸+473.68b⁶w²+579.2b⁴w⁴ +

0.01

0.1

M⁴

(24)

B M /2

+ 364.8b²w⁶ + 105w⁸,

M10X

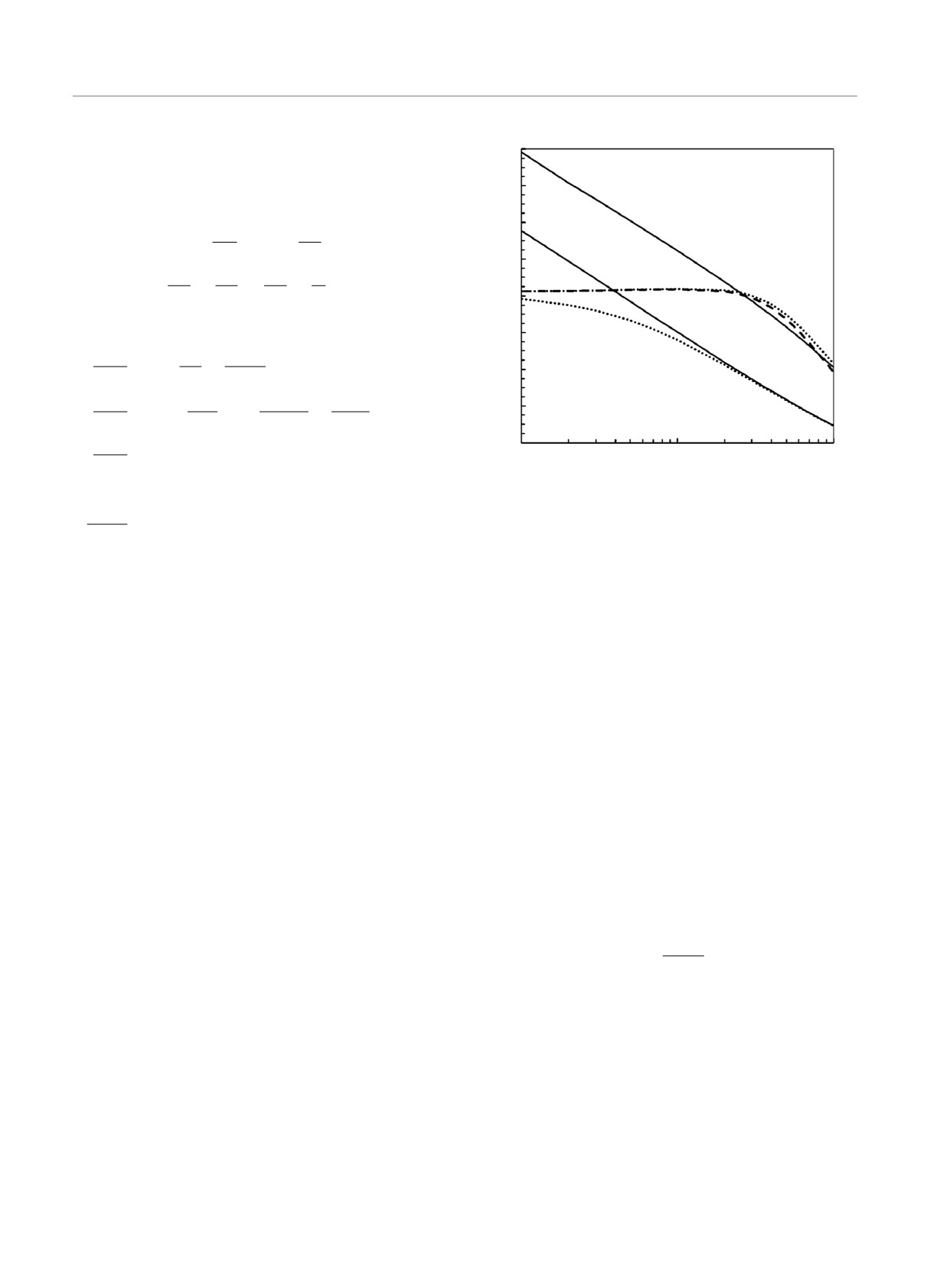
Рис. 1. Зависимости от отношения B²/M2 координат осо-

= 2244.96b¹⁰ + 7632.286b⁸w² +

бых точек, рассчитанных по формуле (18). Верхняя сплош-

M⁵

ная линия — результаты расчета для уравнения (31) при

+ 11001.18b⁶w⁴ + 8701.44b⁴w⁶ +

n = 70. Нижняя сплошная линия — результаты расчета

+ 4029b²w⁸ + 945w¹⁰.

для уравнения (25) при n = 70. Верхняя и нижняя пунк-

тирные линии рассчитаны для тех же уравнений, но при

По полученным формулам (23), (24) мы рассчи-

n = 5. Штриховая линия рассчитана по отношению пол-

тали M8X и M10X при разных значениях W² и по

ных моментов M8X /M10X (24)

их отношению оценили радиус сходимости ряда по

степеням времени по формуле (18). Результат пока-

зан на рис. 1. Величина τ²⁰ растет с ростом W² при

неоднородного магнитного поля и получим уравне-

малых W². При больших значениях W² рост пре-

ние

кращается, поскольку в этом пределе величина мо-

ментов малого порядка определяется неоднородным

D(t) =

⎧

⎫

полем. Для гауссовой функции M₁₀/M₈ = 9M₂, по-

∫t

∫

t^′

⎨

⎬

этому мы наблюдаем предельное значение 110/9 =

= exp

-B²

D(t^′′) dt^′dt^′′ - W²t²/2

(25)

⎩

⎭

= 12.22. Если увеличить порядки моментов в фор-

муле (18), то для гауссовой функции величина оцен-

ки радиуса сходимости росла бы пропорционально

При W² = 0 мы не знаем решения этого уравнения,

порядку, тогда как при учете ДДВ рост остановит-

однако можем рассчитать координату особой точки

ся. Таким образом, если в спиновых системах без

τc0 через радиус сходимости ряда по степеням вре-

неоднородного поля [29-35] радиус сходимости уда-

мени:

лось оценить по десятому моменту с точностью в

∑

(-1)ⁿ

несколько процентов, то при большом неоднород-

D(t) =

D_nt2n,

(26)

(2n)!

ном поле нужны моменты более высокого порядка.

n=0

К сожалению, нам они не известны, поскольку их

для коэффициентов которого из (25) получаем ре-

вычисление очень сложная задача, не решенная на

куррентное уравнение

сегодняшний день. А поскольку для полного уравне-

(

)

∑

ния (7) мы не можем рассчитать моменты высокого

2n+1

Dn+1

=B²

D_n-kD_k+(2n+1)W²D_n.

порядка, обратимся к приближенным уравнениям,

k=0

описанным в предыдущем разделе.

В кумулянтном приближении повороты в раз-

Результаты расчета τ2c0 по формуле (18) показаны

ных полях учитываются как независимые, поэтому

на рис. 1. Эта зависимость хорошо аппроксимирует-

в уравнении (14) просто добавим новое слагаемое от

ся (см. рис. 2) функцией

754

ЖЭТФ, том 155, вып. 4, 2019

Экспоненциальная граница для скорости нагревания. . .

∫

²M₂

Γ_z(t) = -aB2 Γ2x(t1)Γz(t - t1) dt1

(30)

через АКФ x-компоненты спина, для которой, сле-

дуя [32], записываем уравнение

∫t

Γ_x(t) = G₀(t) - ε

G₀(t - t₁)×

∫

Γ_z(t₁ - t₂)Γ_x(t₁ - t₂)Γ_x(t₂)dt₁dt₂.

(31)

Уравнения (30) и (31) получены в приближении, ко-

торое состоит в том, что взаимодействия с полями

x и y делят интервал эволюции на участки, меж-

ду которыми нет корреляции полей (спаривания).

0.001

0.01

0.1

Константы в уравнениях определяются величинами

поперечных полей:

B /M²²

B²

2B²

ε=

= Δ2y, aB² =

=Δ2y +Δ2x,

Рис. 2. Зависимости от отношения B²/M2 координат осо-

(32)

бых точек решений уравнения (31) с (32), упрощенного

4B²

варианта (35) и уравнения (25), соответственно сверху

Δ2z =

вниз. Сплошные линии — результаты расчетов по формуле

Для расчета коэффициентов временных рядов из

(A.11). Штриховые линии —результаты расчетов соответ-

ственно по формулам (34), (A.12) и (A.14). Пунктирная

(29)-(31) получаем систему рекуррентных уравне-

линия проведена по формуле (27)

ний

(

)

∑

2n + 1

Gn+1 =

B²

G_kZ_n-k +

}

^{2M₂

k=0

τ2c0M₂ = 2.35 ln

+ 3.05.

(27)

B²

+ (2n + 1)W²G_n,

∑

τ2c0 дает нижнюю границу для показателя τ²⁰:

Zn+1

= aB²

Z_n-k

X_k-mX_m,

k=0

m=0

(33)

τ²⁰ > τ2c0.

(28)

∑

Xn+1 = Gn+1 + ε

G_n-k

X_k-m ×

Граница (27) математически строгая, но доволь-

k=0

m=0

(

)

но грубая, поскольку она не учитывает анизотропию

∑

вращения в системах с ДДВ, связанную с выделен-

Z_m-pX_p,

ностью вращения вокруг одной из осей — оси z. Для

p=0

секулярной части ДДВ в сильном магнитном поле

где G_n, Z_n и X_n — коэффициенты рядов вида (26)

Δ2x = Δ2y и Δ2z = 4Δ2x. В этом случае для повыше-

соответственно для функций G₀(t), Γ_z(t) и Γ_x(t).

ния точности приближения на первом этапе предло-

Рассчитанные по этим коэффициентам координаты

жено учитывать только вращение вокруг оси z [32].

особых точек приведены на рис. 1. Зависимость τ²⁰

Поскольку повороты вокруг локальных z-полей от

от B²/M₂ хорошо описывается (см. Приложение)

ДДВ и от неоднородного магнитного z-поля скла-

функцией

дываются, мы получаем пропагатор

^{10M

⁽5M₂ )}

τ²⁰M₂ = 2 ln

+ 2.3.

(34)

⎧

⎫

B²

∫t

∫t′

⎨

⎬

W²t²

Помимо результата, полученного по коэффициен-

G₀(t) = exp

-Δ²

Γ_z(t^′)dt^′dt^′′-

(29)

⎩

⎭

там с n = 70, на рис. 1 для сравнения приведен ре-

зультат для n = 5. Видно, что результат для уравне-

Корреляционная функция z-поля в самосогласован-

ния (31) действительно близок к результату по мо-

ном приближении определяется уравнением

ментам M₁₀ полного уравнения (7). Ранее в работе

755

12*

В. Е. Зобов, М. М. Кучеров

ЖЭТФ, том 155, вып. 4, 2019

[38] мы исследовали упрощенный вариант уравне-

частоту в единицах

√M₂, то поглощение падает, по-

ния, получающийся из уравнения (31) при

скольку τ²⁰M₂ растет логарифмически. Сам же мас-

√

штаб

M₂ растет пропорционально W. Причина в

ε = 0, a = 1/2, B² = Δ2z.

(35)

том, что большие частоты на крыле спектра АКФ

образуются вследствие модуляции локального поля

Соответствующая зависимость (A.7) проходит

от окружающих спинов, осциллирующих в попереч-

несколько ниже (34) (см. рис. 2).

ном поле (флип-флоп-поворотов). С ростом W ам-

плитуда таких осцилляций падает, но частота рас-

отражает

тет. Логарифмический сомножитель в τ₀

4. ОБСУЖДЕНИЕ

это уменьшение амплитуды. Вместе с тем он выра-

жает очевидное свойство системы, что без ДДВ не

Вид АКФ в окрестности ближайших к началу

будет экспоненциального крыла. В этой связи заме-

координат особых точек (17) определяет вид высо-

тим, что в оценочной формуле для показателя экс-

кочастотных асимптотик АКФ при τ₀|ω| ≫ 1:

поненты, полученной в работе [16], отсутствует та-

g_x(ω) ≈ A_x|ω| exp(-τ₀|ω|).

(36)

кой логарифмический сомножитель. Это говорит о

том, что предложенная в [16] оценка границы хотя и

Из соотношения между координатами особых точек

верная, но грубая, полученная с большим запасом.

(28) следует соотношение между крыльями спект-

Примененное выше приближение гауссовского

ров

СФП не учитывает корреляции между вкладами в

поле от разных спинов окружения, приводящей к

g_x(ω) ≈ A_x|ω| exp(-τ₀|ω|) <

образованию петель из связей на решетке и мно-

гократных связей. В случае взаимодействия бли-

< A_cx|ω| exp(-τc0|ω|) = g_cx(ω).

(37)

жайших соседей показана малость корреляционно-

Тем самым крыло спектра функции кумулянтного

го вклада для решеток большой размерности про-

приближения g_cx(ω) служит верхней границей для

странства [33]. Оценки показывают их малость и в

крыла спектра АКФ (3).

трехмерных решетках с ДДВ [16, 34]. И в том, и

Другие временные корреляционные функции

в другом случаях корреляционные эффекты ослаб-

рассматриваемой спиновой системы будут иметь

ляют действие полей и приводят к увеличению τ₀.

особенности в тех же точках оси мнимого вре-

Следовательно, функция кумулянтного приближе-

мени. Поэтому крылья их спектров будут иметь

ния g_cx(ω) (37) останется строгой границей для ско-

одинаковый экспоненциальный сомножитель и

рости нагревания в реальных спиновых системах.

будут различаться только предэкспоненциальными

коэффициентами. Для всех таких функций крыло

ПРИЛОЖЕНИЕ

функции g_cx(ω) будет служить верхней границей,

в том числе, для спектра поглощения ЯМР и для

Исследуем поведение АКФ в окрестности бли-

скорости нагрева системы высокими гармониками

жайших особых точек на оси мнимого времени. Вид

при периодическом управлении. И в том, и в другом

(17) для АКФ в окрестности особенности следует из

случаях скорости процессов поглощения энергии

вида нелинейных уравнений для них. В этом мож-

выражаются через образ Фурье от корреляционной

но убедиться методом, аналогичным методу Пенле-

функции полного спина системы, умноженный на

ве для анализа подвижных особенностей нелиней-

квадрат амплитуды радиочастотного поля [40] или

ных обыкновенных дифференциальных уравнений

квадрат амплитуды соответствующей гармоники

[41]. Возьмем АКФ вблизи особенности в виде

периодического воздействия [16, 20, 21].

Формула (36) показывает, что поглощение энер-

Γ_α(t) ≈ -A_α(t - iτ₀)^-p

(A.1)

гии на крыле имеет экспоненциальную малость, т. е.

и подставим в уравнение (8) при условии (12). Вы-

затухает по экспоненциальному закону с ростом час-

числив наиболее расходящуюся часть интеграла в

тоты. Полученные в настоящей работе результаты

правой части уравнения (8) и выполнив дифферен-

позволяют исследовать зависимость скорости про-

цирование в его левой части, находим

цесса от величины неоднородного уширения W . Со-

гласно (27) и (34), коэффициент τ₀ перед частотой в

A_xp

A_zA_y(Δ2z + Δ2y)

показателе экспоненты в (36) уменьшается с ростом

√

≈

(A.2)

W, вследствие роста

M₂ (23). Если же измерять

(t - iτ₀)p+1

(2p - 1)(t - iτ₀)2p-1

756

ЖЭТФ, том 155, вып. 4, 2019

Экспоненциальная граница для скорости нагревания. . .

}

Для выполнения равенства в (A.2) показатели сте-

^{ (M₂ - ε)τ²

G₀(iτ) = exp

пеней и коэффициенты должны совпадать:

(

)

(A.8)

M₂τ²

Γ_x(iτ) = exp

p+1 = 2p-1, A_xp(2p-1) = A_z A_y(Δ2z+Δ2y). (A.3)

Из первого уравнения в (A.3) следует p = 2. Нели-

где M₂ = B²+W², а для интеграла от функции оши-

нейные уравнения того же приближения, что и (8),

бок мнимого аргумента взято асимптотическое зна-

для АКФ двух других спиновых компонент дают

чение. Функции (A.7) и (A.8) не имеют особых точек

еще два равенства:

на конечном расстоянии от начала координат. По-

явление таких особенностей обусловлено нелинейно-

6A_y = A_zA_xM2y,

6A_z = A_yA_xM2z,

(A.4)

стью уравнений (29)-(31). Нелинейность проявится

при тех значениях мнимого времени, при которых в

где M2x = (Δ2z + Δ2y), M2y = (Δ2z + Δ2x), M2z =

показателе экспоненты для G₀(iτ) (29) нелинейный

= (Δ2x + Δ2y). Из системы трех уравнений для амп-

вклад от Γ_z(t) превзойдет линейный (A.8). Отсюда

литуд (A.3), (A.4) находим

получаем условие

√

aB²Δ2z

(M₂ - ε)τ²

exp(M₂τ²) ≥

A_α = 6

M2α/(M2xM2yM2z).

(A.5)

16M³²τ²

Перейдем к нелинейному уравнению для АКФ

которое после подстановки значений параметров

общего вида (7). В ряду для функции памяти G_α(t)

(32) приводит к уравнению для оценки τ₀

)

(

)

при переходе от члена с m парами к члену с

⁽5M₂

B²

M₂τ²⁰ = 2 ln

M₂τ²

+ ln

. (A.9)

m + 1 парой добавляется сомножитель g_β(t_k - t_q) =

B²

5M₂

= Δ2βΓ_β(t_k - t_q) и одновременно интегрирование по

временным переменным t_k и t_q. Следовательно, вид

Из (A.9) находим искомую оценку

(17) особенности (A.1) с p = 2 сохранится и при

^{10M₂

⁽5M₂ )}

τ²⁰M₂ = 2 ln

+c₁.

(A.10)

включении остальных членов ряда для функции па-

B²

мяти, хотя при этом изменятся сами величины A_α

и τ₀.

Соответствующая зависимость при c₁

= 2.3 (34)

Исследуем теперь поведение АКФ в окрестно-

приведена на рис. 2 и хорошо описывает результа-

ты численного расчета τ₀, который проводился по

сти ближайших особых точек на оси мнимого време-

ни при наличии неоднородного магнитного поля на

формуле

примере решения нелинейных уравнений (29)-(31).

τ20n = n(2n + 1){Xn-1/X_n + Zn-1/Z_n} (A.11)

Подставим сингулярные части в виде (17) соответ-

ствующих функций в уравнения (29)-(31). Решив

при n = 85. Эта формула позволила сгладить осцил-

уравнения для коэффициентов при сингулярных ча-

ляции τ0n при B²/M₂ < 0.01, обусловленные анизот-

стях, находим

ропией ДДВ.

√

Для упрощенного варианта уравнения (31) с па-

2/Δ2z

12/aB²Δ2z

Γ_z(t) ≈

Γ_x(t) ≈

раметрами (35) мы в работе²⁾ [38] нашли зависи-

(it ± τ₀)²

(A.6)

мость координаты особой точки

(

) √12/aB2Δ2_z

G₀(t) ≈

^{8M₂

⁽4M₂ )}

3Δ²

(it ± τ₀)2

τ²⁰M₂ = 2 ln

+ 2.3,

(A.12)

B²

Найдем оценку для величины τ²⁰ при W²/B² ≫

которая, как видно на рис. 2, проходит несколько

≫ 1. Рассмотрим на оси мнимого времени t = iτ

ниже (A.10).

линеаризованный вариант системы уравнений

Подобным образом для уравнения (25) находим

(29)-(31):

2/B²

∫

τ1

D(t) ≈

(A.13)

(it ± τc0)²

Γ_z(iτ) = 1 + aB²

Γ2x(iτ₂)dτ₁dτ₂ ≈

а для τ2c0 при W²/B² ≫ 1 получаем оценку

≈

exp(M₂τ²), (A.7)

²⁾ В уравнении (20) [38] есть опечатка: правильно X_kZ_n-k,

4M²²τ2

а не X_n-k Z_k.

757

В. Е. Зобов, М. М. Кучеров

ЖЭТФ, том 155, вып. 4, 2019

)}

^{2M₂

⁽2M₂

19.

Р. Эрнст, Дж. Боденхаузен, А. Вокаун, ЯМР в од-

τ²⁰M₂ = 2 ln

+c₂,

(A.14)

B²

ном и двух измерениях, Мир, Москва (1990).

которая приведена на рис. 2 и хорошо согласуется

20.

Ю. Н. Иванов, Б. Н. Провоторов, Э. Б. Фельдман,

с результатами численного расчета при c₂ = 1.62 на

ЖЭТФ 75, 1847 (1978).

интервале B²/W² < 0.1. Там же показана аппрок-

21.

Б. Н. Провоторов, Э. Б. Фельдман, ЖЭТФ 79,

симирующая функция (27), которая лучше передает

2206 (1980).

поведение τc0 при малых неоднородных полях.

22.

P. W. Anderson and P. R. Weiss, Rev. Mod. Phys.

25, 269 (1953).

ЛИТЕРАТУРА

23.

R. Kubo and T. Toyabe, Magnetic Resonance and

R. P. Feynman, Int. J. Theor. Phys. 21, 467 (1982).

Relaxation, ed. by R. Blinc, North-Holland, Amster-

dam (1967), p. 810.

I. Georgescu, S. Ashhab, and F. Nori, Rev. Mod.

Phys. 86, 153 (2014).

24.

Г. Е. Карнаух, А. А. Лундин, Б. Н. Провоторов,

К. Т. Сумманен, ЖЭТФ 91, 2229 (1986).

J. Preskill, Quantum 2, 79 (2018); arXiv:1801.00862.

25.

М. И. Булгаков, А. Д. Гулько, Ф. С. Джепаров,

И. И. Рябцев, И. И. Бетеров, Д. Б. Третьяков,

С. В. Степанов, С. С. Тростин, Письма в ЖЭТФ

В. М. Энтин, Е. А. Якшина, УФН 186, 206 (2016).

58, 614 (1993).

S. Choi, J. Choi, R. Landig, G. Kucsko, H. Zhou,

26.

F. S. Dzheparov and D. V. Lvov, Appl. Magn. Res.

J. Isoya, F. Jelezko, S. Onoda, H. Sumiya, V. Khe-

mani, C. Keyserlingk, N. Y. Yao, E. Demler, and

48, 989 (2017).

M. D. Lukin, Nature 543, 221 (2017).

27.

P. Borckmans and D. Walgraef, Physica 35,

S. Choi, N. Y. Yao, and M. D. Lukin, Phys. Rev. Lett.

(1967); Phys. Rev. 167, 282 (1968).

119, 183603 (2017).

28.

M. Blume and J. Hubbard, Phys. Rev. B 1, 3815

P. I. Bunyk, E. M. Hoskinson, M. W. Johnson,

(1970).

E. Tolkacheva, F. Altomare, A. J. Berkley, R. Harris,

29.

V. E. Zobov, Phys. Lett. A 119, 315 (1986).

J. P. Hilton, T. Lanting, A. J. Przybysz, and J. Whit-

taker, IEEE Trans. App. Supercond. 24, 1700110

30.

В. Е. Зобов, ТМФ 77, 426 (1988).

(2014); arXiv:1401.5504.

31.

В. Е. Зобов, ТМФ 84, 111 (1990).

M. Bukov, L. D’Alessio, and A. Polkovnikov, Adv.

Phys. 64, 139 (2015).

32.

A. A. Lundin, A. V. Makarenko, and V. E. Zobov, J.

Phys.: Condens. Matter 2, 10131 (1990).

A. Eckardt and E. Anisimovas, New J. Phys. 17,

093039 (2015).

33.

В. Е. Зобов, М. А. Попов, ТМФ 136, 463 (2003).

10.

Е. И. Кузнецова, Э. Б. Фельдман, Д. Э. Фельдман,

34.

В. Е. Зобов, М. А. Попов, ЖЭТФ 124, 89 (2003).

УФН 186, 647 (2016).

35.

В. Е. Зобов, М. А. Попов, ЖЭТФ 127, 877 (2005).

11.

A. Eckardt, Rev. Mod. Phys. 89, 011004 (2017).

36.

В. Е. Зобов, М. М. Кучеров, Письма в ЖЭТФ 103,

12.

D. A. Abanin, W. De Roeck, and F. Huveneers, Phys.

780 (2016).

Rev. Lett. 115, 256803 (2015).

37.

В. Е. Зобов, М. М. Кучеров, ЖЭТФ 151, 174

13.

T. Mori, T. Kuwahara, and K. Saito, Phys. Rev. Lett.

(2017).

116, 120401 (2016).

38.

В. Е. Зобов, М. М. Кучеров, Письма в ЖЭТФ 107,

14.

T. Kuwahara, New J. Phys. 18, 053034 (2016).

578 (2018).

15.

D. A. Abanin, W. De Roeck, W. W. Ho, and F. Hu-

39.

D. A. Abanin and Z. Papić, Ann. Phys. (Berlin) 529,

veneers, Phys. Rev. B 95, 014112 (2017).

1700169 (2017).

16.

W. W. Ho, I. Protopopov, and D. A. Abanin, Phys.

Rev. Lett. 120, 200601 (2018).

40.

А. Абрагам, Ядерный магнетизм, Изд-во иностр.

лит., Москва (1963).

17.

F. Machado, G. D. Meyer, D. V. Else, C. Nayak, and

N. Y. Yao, arXiv:1708.01620.

41.

В. В. Голубев, Лекции по аналитической тео-

рии дифференциальных уравнений, Гостехиздат,

18.

U. Haeberlen and J. S. Waugh, Phys. Rev. 175, 453

Москва (1950).

(1968).

758