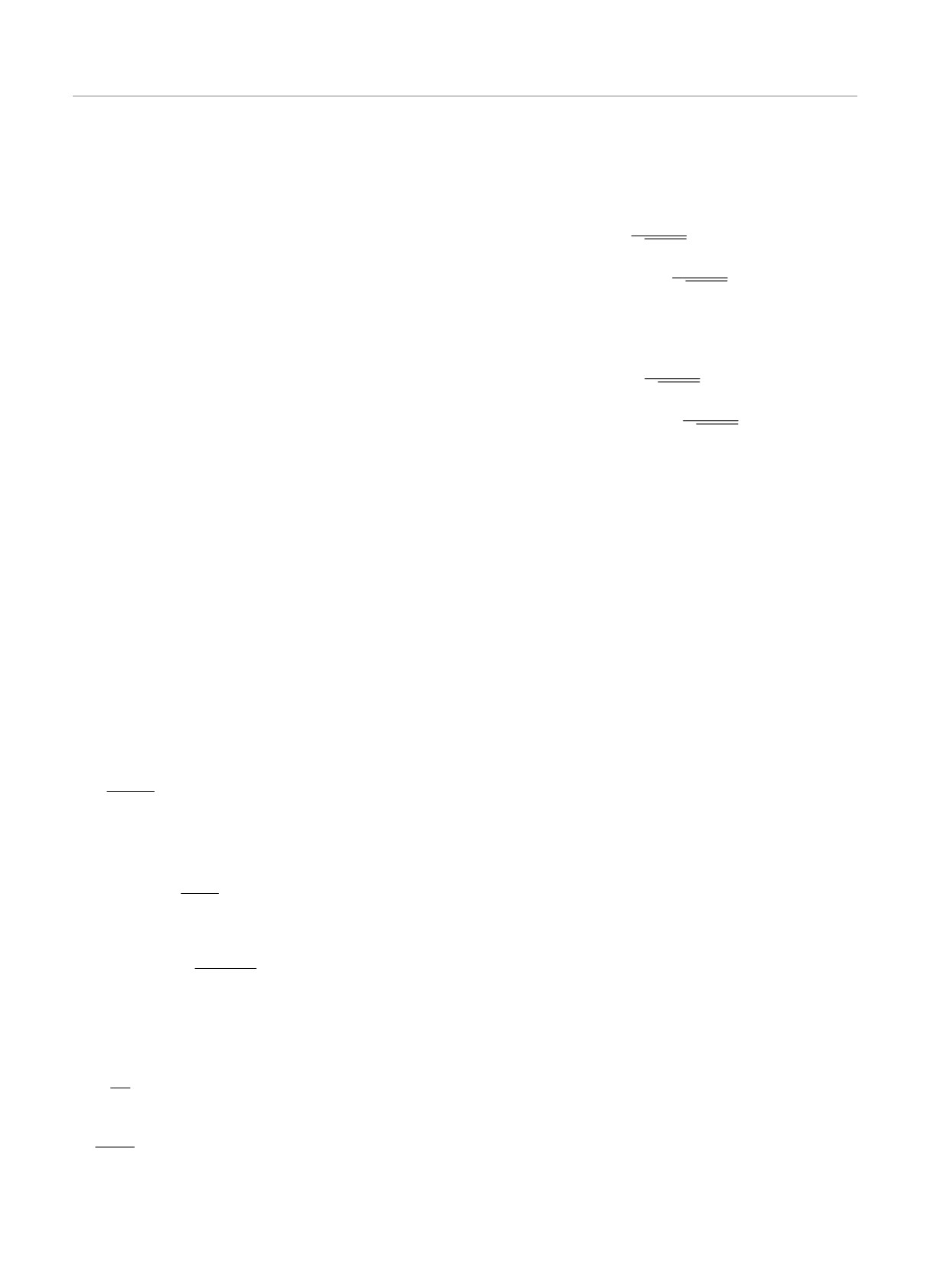ЖЭТФ, 2019, том 155, вып. 5, стр. 792-805

СТАЦИОНАРНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА

ДЛЯ ФЕРМИОНОВ ВО ВНЕШНЕМ КУЛОНОВСКОМ ПОЛЕ

В. П. Незнамовa,b*, И. И. Сафронов^a

^a ФГУП «РФЯЦ-ВНИИЭФ»

607188, Саров, Нижегородская обл., Россия

^b Национальный исследовательский ядерный университет «МИФИ»

115409, Москва, Россия

Поступила в редакцию 3 октября 2018 г.,

после переработки 25 января 2019 г.

Принята к публикации 25 января 2019 г.

Изучены самосопряженные уравнения второго порядка со спинорными волновыми функциями для фер-

мионов, движущихся во внешнем кулоновском поле. Для стационарных состояний уравнения характе-

ризуются разделенными состояниями с положительной и отрицательной энергиями, и это приводит к

возможности вероятностной интерпретации. Для кулоновского поля притяжения энергетический спектр

уравнения второго порядка совпадает со спектром уравнения Дирака, в то время как плотности вероят-

ности состояний несколько различаются. Для кулоновского поля отталкивания существует непроницае-

мый потенциальный барьер, радиус которого зависит от классического радиуса электрона и от энергии

электрона. Существование непроницаемого барьера не противоречит результатам экспериментов по изу-

чению внутренней структуры электрона и не влияет в низшем порядке теории возмущений на сечение

кулоновского рассеяния электронов. Наличие непроницаемого барьера может приводить к конфайнмен-

ту позитронов в сверхкритических ядрах с Z ≥ 170 при реализации спонтанного испускания вакуумных

электрон-позитронных пар.

DOI: 10.1134/S0044451019050031

мер, при наличии горизонтов событий нерегуляр-

ные стационарные решения уравнения Дирака во

внешних гравитационных и электромагнитных по-

1. ВВЕДЕНИЕ

лях Шварцшильда, Райсснера - Нордстрёма, Кер-

ра, Керра - Ньюмена становятся регулярными ста-

В квантовой механике движение частиц со спи-

ционарными решениями уравнений второго порядка

ном 1/2 описывается, как правило, уравнением Ди-

с квадратично-интегрируемыми спинорными волно-

рака с производными первого порядка по простран-

выми функциями [3-5].

ственно-временным переменным биспинорной вол-

Настоящая работа посвящена анализу стацио-

новой функции [1]. В [1] Дирак получил также урав-

нарных решений уравнений второго порядка для

нение второго порядка для фермионов, движущихся

фермионов, движущихся в плоском пространстве-

во внешнем электромагнитном поле.

времени во внешнем кулоновском поле.

Движение фермионов во внешних силовых по-

Работа построена следующим образом.

лях можно описывать также самосопряженными

уравнениями со спинорными волновыми функция-

В разд. 2 для связности изложения приводятся

ми [2]. В процессе преобразования от уравнения Ди-

уравнения Дирака для биспинорной волновой функ-

рака первого порядка к самосопряженному урав-

ции. Приводятся также несамосопряженные урав-

нению второго порядка энергия спиновой частицы

нения второго порядка для спинорных волновых

сохраняется, в то время как плотности вероятно-

функций.

сти обнаружения частиц различаются. Это приво-

В разд. 3 анализируются уравнения Дирака со

дит к новым физическим следствиям. Так, напри-

спинорными волновыми функциями и устанавлива-

ется их связь с уравнениями Дирака в представле-

^* E-mail: vpneznamov@vniief.ru, vpneznamov@mail.ru

нии Фолди - Ваутхайзена [6].

792

ЖЭТФ, том 155, вып. 5, 2019

Стационарные решения уравнения второго порядка.. .

[

]

В разд. 4 для фермионов и антифермионов во

p⁰ - eA⁰ (r, t) - α · (p - eA(r, t)) - βm

внешнем кулоновском поле получены самосопря-

× Ψ(r,t) = 0.

(1)

женные уравнения второго порядка со спинорны-

ми волновыми функциями. Примечательно, что эти

Здесь и ниже мы используем систему единиц ℏ =

уравнения выведены с использованием замкнутых

= c = 1 и сигнатуру пространства-времени Минков-

преобразований подобия. После разделения пере-

ского

менных получены уравнения для радиальных вол-

новых функций. Показана допустимость вероят-

g_μν = diag[1, -1, -1, -1].

(2)

ностной интерпретации спинорных волновых функ-

ций, одинаковой с интерпретацией для волновых

В формуле (2) μ, ν = 0, 1, 2, 3. В (1) Ψ (r, t) — бис-

функций уравнения Клейна - Гордона с разделенны-

ми состояниями с положительной и отрицательной

пинорная волновая функция; A⁰ (r, t) , A(r, t) — по-

тенциалы электромагнитного поля; α^k, β — четы-

энергиями [7].

∂

рехмерные матрицы Дирака, k = 1, 2, 3; p⁰ = i_∂

В разд. 5 анализируются решения уравнения

p = -i∇.

второго порядка в кулоновском поле притяжения.

Дирак также получил уравнение второго поряд-

Показано, что при одинаковом энергетическом

ка [1]

спектре водородоподобных атомов плотности

вероятности обнаружения фермионов в соответ-

]

[(

)

ствующих энергетических состояниях несколько

p⁰-eA⁰

2 -(p-eA)2 -m²+eΣ · H - iα · E ×

отличаются от плотностей вероятности, вычислен-

ных с помощью собственных функций уравнения

× Ψ(r,t) = 0,

(3)

Дирака. Это отличие возрастает с ростом порядко-

(

)

вого номера Z.

где Σ =

, σ^k — двумерные матрицы Пау-

В разд. 6 анализируются уравнения второго по-

рядка в кулоновском поле отталкивания. Показано

ли; H = rotA, E = -∂A/∂t - ∇A⁰ — магнитное и

существование непроницаемого потенциального ба-

электрическое поля.

рьера с радиусом, пропорциональным классическо-

Пусть

му радиусу фермиона и обратно пропорциональным

энергии фермиона (при E ≫ mc²), где E и m — энер-

(

)

гия и масса фермиона, c — скорость света. Показано,

ϕ (r, t)

Ψ (r, t) =

(4)

что существование непроницаемого барьера не про-

χ (r, t)

тиворечит результатам экспериментов по зондиро-

ванию внутренней структуры электрона и не влия-

где ϕ (r, t) , χ (r, t) — спинорные волновые функции.

ет в низшем порядке теории возмущений на сечение

Тогда плотность вероятности для уравнений (1),

кулоновского рассеяния электронов.

(3) определяется равенством

Наличие непроницаемого барьера может приво-

дить к удержанию (конфайнменту) позитронов в

wD = Ψ⁺ (r, t) Ψ (r, t) =

сверхкритических ядрах с Z ≳ 170 при реализа-

ции испускания вакуумных электрон-позитронных

= ϕ+ (r,t)ϕ(r,t) + χ+ (r,t)χ(r,t).

(5)

пар [8-10].

В Заключении проводится обсуждение получен-

Из уравнения (1) следуют выражения

ных результатов.

(

)

p⁰ - eA⁰ - m

ϕ = σ · (p - eA)χ,

(6)

(

)

p⁰ - eA⁰ + m

χ = σ · (p - eA)ϕ,

2. УРАВНЕНИЕ ДИРАКА ДЛЯ

БИСПИНОРНОЙ ВОЛНОВОЙ ФУНКЦИИ

χ=

σ · (p - eA)ϕ,

Для фермионов с массой m и зарядом e, движу-

p⁰ - eA⁰ + m

(7)

щихся во внешнем электромагнитном поле, уравне-

ϕ=

σ · (p - eA)χ.

ние Дирака можно записать в следующем виде:

p⁰ - eA⁰ - m

793

В. П. Незнамов, И. И. Сафронов

ЖЭТФ, том 155, вып. 5, 2019

3. УРАВНЕНИЯ ДИРАКА СО

Уравнения (8), (9) и (10), (11) являются точными

СПИНОРНЫМИ ВОЛНОВЫМИ

уравнениями со спинорными волновыми функция-

ФУНКЦИЯМИ

ми ϕ (r, t), χ (r, t). Однако эти уравнения являют-

ся несамосопряженными. Источником несамосопря-

Используя (7), из уравнения (3) получим два от-

женности является переход от уравнения Дирака с

дельных уравнения для спиноров ϕ (r, t) , χ (r, t):

биспинорной волновой функцией к уравнениям (8),

(9) и (10), (11) с разделенными состояниями по зна-

[(

)₂

p⁰ - eA⁰

- (p - eA)² - m² + eσ · H -

ку энергии фермиона и со спинорными волновыми

]

функциями.

- ieσ · E

σ · (p-eA) ϕ(r,t) = 0,

(8)

В квантовой механике гамильтонианы стацио-

p⁰-eA⁰+m

нарных состояний являются эрмитовыми и самосо-

пряженными операторами. При отсутствии гамиль-

[(

)₂

тонова подхода операторы в уравнениях для вол-

p⁰ - eA⁰

- (p - eA)² - m² + eσ · H -

новых функций стационарных состояний должны

]

быть также эрмитовыми и самосопряженными. Для

- ieσ · E

σ · (p-eA) χ(r,t) = 0.

(9)

этого с помощью неунитарных преобразований по-

p⁰-eA⁰-m

добия уравнения для волновых функций должны

Уравнения (8), (9) являются несамосопряженными,

быть приведены к самосопряженному виду.

так как множители в последних слагаемых в общем

Ранее при переходе от биспинорных волновых

случае не коммутируют друг с другом.

функций уравнения Дирака к спинорным волно-

Из равенств (6), (7) можно также получить неса-

вым функциям аналогичная проблема возникаю-

мосопряженные уравнения

щей несамосопряженности уравнений для них также

разрешалась применением неунитарных преобразо-

[

ваний подобия (эта проблема возникает при анали-

p⁰ - eA⁰ - m - σ · (p - eA) ×

зе релятивистских поправок к движению частиц со

]

спином 1/2 в электростатическом поле с точностью

σ · (p - eA) ϕ = 0,

(10)

до членов порядка v²/c², где v — скорость частицы

p⁰ - eA⁰ + m

(см., например, [11]).

Преобразования подобия сохраняют энергии сос-

[

тояний, но не сохраняют их вероятности. В отли-

p⁰ - eA⁰ + m - σ · (p - eA) ×

чие от уравнений (8), (9) преимуществом уравнений

]

(10), (11) является существование для них замкну-

σ · (p - eA) χ = 0.

(11)

p⁰ - eA⁰ - m

тых преобразований подобия (31).

При получении уравнений (8), (9) и (10), (11) мо-

Уравнения (8), (10) отличаются, соответственно, от

жет возникнуть вопрос об адекватности равенств (7)

уравнений (9), (11) заменой p⁰ → -p⁰, p → -p, e →

при стремлении их знаменателей к нулю. Однако

→ -e.

в этом случае (см. разд. 6) для физически прием-

Для стационарных состояний решениям уравне-

лемых стационарных решений уравнений (10), (11)

ний (8), (10) соответствуют состояния с положитель-

существуют следующие асимптотики:

ной энергией фермиона, решениям уравнений (9),

— для частиц (E > 0)

(11) соответствуют состояния с отрицательной энер-

гией:

E - eA⁰ + m|_r→r

∼r-r_cl,

p⁰ϕ = |E| ϕ,

ϕ|r→rcl ∼ (r - r_cl)² ,

(12)

p⁰χ = - |E| χ,

χ|

∼ const1,

r→r_cl

где E — энергия фермиона. В случае стационарных

состояний электромагнитные потенциалы A⁰ (r),

— для античастиц (E < 0)

A^k (r) не зависят от времени.

В (8), (9) и (10), (11) мы разделили состояния с

- |E| + eA⁰ - m|_r→r

∼r-r_cl,

положительной и отрицательной энергиями. В (12)

χ|r→rcl ∼ (r - r_cl)² ,

уравнение для ϕ соответствует частицам; уравнение

для χ соответствует античастицам.

ϕ|

∼ const2.

r→r_cl

794

ЖЭТФ, том 155, вып. 5, 2019

Стационарные решения уравнения второго порядка.. .

√

Эти асимптотики, с учетом обозначения p = -i∇,

H_FW = β m² + (p - eA)² - eΣ · H.

(17)

согласуются с равенствами (7). Отметим, что кажу-

щаяся сингулярность в (7) возникает лишь в куло-

Выражения (16), (17) справедливы для любой вели-

новских полях отталкивания.

чины магнитного поля.

Обратимся теперь к вопросу о вероятностной ин-

2. A^k (r) = 0, A⁰ (r) = 0. В этом случае, под-

терпретации волновых функций в уравнениях (10),

ставляя в знаменатель правой части уравнения (13)

(11) при наличии стационарных состояний

(12).

E⁰ = m, получим

Начнем с уравнения (10):

(

p²

ie∇A⁰p

(

)

E(1)ϕ = eA0 + m +

4m²

Eϕ =

m + eA⁰ + σ · (p - eA)

[

])

σ·

e∇A0 ×p

σ · (p - eA)ϕ.

(13)

ϕ.

(18)

E - eA⁰ + m

4m²

1. Если A⁰ (r) = 0, то методом последователь-

Уравнение (18) является несамосопряженным. Для

ных приближений, подставляя в знаменатель пра-

приведения его к самосопряженному виду необходи-

вой части (13)

мо провести неунитарное преобразование подобия

[σ · (p - eA)]

ϕ(1)sc = g(1)ϕϕ,

(19)

E⁰ = m, E⁽¹⁾ = m +

где с точностью до p² и eA⁰

[σ · (p - eA)]

[σ · (p - eA)]⁴

p²

eA⁰

E⁽²⁾ = m +

,...,

g(1)ϕ = 1 +

8m³

8m²

(20)

(

)-1

можно получить замкнутое выражение для гамиль-

p²

eA⁰

g(1)ϕ

=1-

тониана уравнения (13):

8m²

Тогда

Eϕ = H(+)FWϕ =

(

)

E⁽¹⁾ϕ(1)sc = H(1)FW ϕ(1)sc =

[σ · (p-eA)]

[σ · (p-eA)]⁴

= m+

+... ϕ=

(

8m³

p²

ie∇A⁰p

=g⁽¹⁾

eA⁰ + m +

√

4m²

= m² + (p - eA)² - eσ · Hϕ.

(14)

[

]

)(

)-1

σ·

e∇A⁰ × p

g(1)ϕ

ϕ(1)sc =

4m²

Для стационарных состояний уравнения (11) анало-

(

гичная процедура приводит к уравнению с отрица-

p²

ΔeA⁰

тельным знаком перед квадратным корнем:

= eA⁰ + m +

8m²

[

])

Eχ = H(-)FWχ =

σ·

e∇A⁰ × p

ϕ(1)sc,

(21)

√

4m²

= - m² + (p - eA)² - eσ · Hχ.

(15)

где Δ = ∇² — лапласиан.

В (14), (15) H = rot A — магнитное поле. Урав-

Уравнение (11) для состояний c E < 0 имеет вид

нения (14), (15) показывают, что волновые функ-

(

)

ции ϕ (r, t) , χ (r, t) являются волновыми функция-

Eχ = eA⁰ - m + σ · p

σ · p χ. (22)

ми уравнения Дирака в представлении Фолди - Ва-

E - eA⁰ - m

утхайзена [12]. В этом представлении биспинорная

Подставляя в знаменатель правой части (22) E⁽⁰⁾ =

волновая функция и гамильтониан могут быть пред-

= -m, получаем

ставлены в виде [12, 13]

(

)

p²

ie∇A⁰p

ϕ (r)

E⁽¹⁾χ = eA⁰ - m -

Ψ_FW (r, t) =

e^-iEt, E > 0,

4m²

[

])

(

)

(16)

σ·

e∇A⁰ × p

χ.

(23)

Ψ_FW (r, t) =

e^-iEt, E < 0,

4m²

χ (r)

795

В. П. Незнамов, И. И. Сафронов

ЖЭТФ, том 155, вып. 5, 2019

Для приведения (23) к самосопряженному виду ис-

3. В случае A⁰ (r) = 0 переход к представлению

пользуем равенство

Фолди - Ваутхайзена с эрмитовым гамильтонианом

осуществляется приведением уравнений (10),

H_FW

χ_sc = g(1)χχ,

(24)

(11) к самосопряженному виду. При этом уравне-

ния и волновые функции ϕ (r, t) , χ (r, t) подвергают-

где с точностью до p² и eA⁰

ся неунитарным преобразованиям подобия.

eA⁰

4. В представлении Фолди- Ваутхайзена плот-

g(1)χ = 1 +

8m²

ность вероятности в соответствии с (27) равна

(25)

(

)-1

p²

eA⁰



g(1)χ

=1-



w_ϕ = ϕ(n)+ϕ(n)



E > 0,

8m²

n→∞



(29)

Имеем



w_χ = χ(n)+χ(n)



E < 0.

(

n→∞

ΔeA⁰

Поскольку переход в представление Фолди- Ваут-

E⁽¹⁾χ(1)sc = eA⁰ - m -

8m²

хайзена можно осуществить унитарным преобразо-

[

])

ванием уравнения Дирака с биспинорной волновой

σ·

e∇A⁰ × p

χ_xc.

(26)

функцией [14, 15], плотности вероятности (29) сов-

4m²

падают с дираковской плотностью вероятности (5).

Уравнения (21), (26) представляют собой первые

члены разложения гамильтониана Фолди - Ваутхай-

4. САМОСОПРЯЖЕННЫЕ УРАВНЕНИЯ

зена во внешнем поле A⁰ (r) [6].

ВТОРОГО ПОРЯДКА СО СПИНОРНЫМИ

В результате после проведения процедуры после-

ВОЛНОВЫМИ ФУНКЦИЯМИ И

довательных приближений для стационарных реше-

ВЕРОЯТНОСТНАЯ ИНТЕРПРЕТАЦИЯ

ний уравнений (10), (11) можно получить гамиль-

Если умножить уравнение (10) слева на опера-

тониан Фолди- Ваутхайзена в виде ряда по степе-

(

)

ням p² и eA⁰. При этом на каждом этапе последо-

тор

p⁰ - eA⁰ + m

, а уравнение (11) — на оператор

(

)

p⁰ - eA⁰ - m

, то получим уравнения (8), (9). Для

вательных приближений волновые функции уравне-

ний (10), (11) будут подвергаться соответствующим

стационарных состояний (12) решениями уравнений

(8), (9), как и уравнений (10), (11), являются разде-

неунитарным преобразованиям подобия:

(

)

ленные состояния с положительной и отрицатель-



ϕ(n) (r)



ной энергиями фермиона.

Ψ_FW (r, t) =



e^-iEt, E > 0,



В случае A⁰ (r) = 0 при наличии стационарных

n→∞

(

)

(27)

состояний уравнения (8), (9) являются самосопря-



женными, их решения совпадают с решениями урав-

Ψ_FW (r, t) =



e^-iEt, E < 0,

χ(n) (r)



нения Дирака в представлении Фолди - Ваутхайзена

n→∞

(см. (14), (15)).

где



Пусть A⁰ (r) = 0, A^k (r) = 0. В этом случае урав-



ϕ(n) (r)

= g(n)ϕϕ(r),

нения (8), (9) с заменой p⁰ → E (наличие стаци-

n→∞



(28)

онарных состояний) необходимо приводить к само-



χ(n) (r)

= g(n)χχ(r).

сопряженному виду. Примечательно, что в отличие

n→∞

от уравнений (10), (11) для уравнений (8), (9) опе-

При наличии стационарных состояний анализ урав-

раторы преобразования записываются в замкнутом

нений (10), (11) со спинорными волновыми функци-

виде:

ями приводит к следующим выводам.

Φ = g_ϕϕ,

1. В случае A⁰ (r) = 0, A^k (r) = 0 уравнения (10),

(30)

(11) приводятся к уравнению Дирака в представ-

X = g_χχ,

лении Фолди - Ваутхайзена с разделенными состоя-

где

ниями с положительной и отрицательной энергия-

(

)-1/2

ми фермиона. Гамильтониан H_FW имеет замкнутый

g_ϕ =

E - eA⁰ + m

(

)

(31)

вид (см. (17)).

g_χ =

|E| + eA⁰ + m

-1/2 .

2. В случае A⁰ (r) = 0, A^k (r) = 0 гамильтониан

H_FW можно получить лишь в виде ряда по степеням

После преобразований уравнения (8), (9) имеют са-

p² и eA⁰ (первые члены ряда см. в (21), (26)).

мосопряженный вид:

796

ЖЭТФ, том 155, вып. 5, 2019

Стационарные решения уравнения второго порядка.. .

[(

)₂

g_ϕ E - eA⁰

-p² -m² -

(36) отличаются от плотностей вероятности (5), (29)

]

для уравнения Дирака. О масштабе отличий гово-

ieσEσp g-1ϕΦ =

рится в следующих разделах работы.

E - eA⁰ + m

[

Преобразования подобия сохраняют энергии со-

(

)₂

e²E²

стояний. Энергии частицы со спином 1/2 в уравне-

= E-eA⁰

-p²-m²-

4 (E-eA⁰+m)²

ниях второго порядка (32), (33) совпадают с соот-

]

ветствующими энергиями в уравнении Дирака (1) и

e div E

eσ · [E × p]

Φ = 0,

(32)

в уравнении Дирака в представлении Фолди- Ваут-

2 (E-eA⁰+m)

E-eA⁰+m

хайзена.

Для центрально-симметричного кулоновского

[(

)₂

потенциала уравнения (32), (33) допускают раз-

g_χ E - eA⁰

-p² -m² -

]

деление переменных в сферических координатах

(r, θ, ϕ).

ieσEσp g-1χX =

E - eA⁰ - m

Если представить спиноры Φ (r), X (r) в виде

[

(

)₂

e²E²

= E-eA⁰

-p²-m²-

Φ (r, θ, ϕ) = F (r) Ωjlmϕ (θ, ϕ) ,

(37)

4 (E-eA⁰-m)²

]

e div E

eσ · [E × p]

X = 0.

(33)

2 (E - eA⁰ - m)

E - eA⁰ - m

X(r, θ, ϕ) = G(r) (-1)(1+l-l′)/2 Ω_jl′mϕ (θ, ϕ),

(38)

Уравнение (32) описывает частицы со спином 1/2 с

где Ωjlmϕ , Ω_jl′mϕ — шаровые спиноры [16]; l = j ±

положительной энергией. Уравнение (33) описывает

±1/2, l^′ = 2j-1; j, l — полный и орбитальный момен-

античастицы с отрицательной энергией. Уравнения

ты частицы со спином 1/2; m_ϕ = -j, -j + 1, . . ., j —

(32), (33) отличаются друг от друга знаком перед

проекция полного момента j, то для радиальных

массовым членом. Оба уравнения можно записать

функций F (r) , G(r) можно получить уравнения

в виде, характерном для представления Фолди- Ва-

типа Шредингера с эффективными потенциалами

утхайзена:

U^Feff (r), U^Geff (r):

[

(

)₂

e²E²

(

)

E-eA⁰

-p²-m²-

4 (E-eA⁰+βm)²

r²

F (r) +

]

r² dr

e div E

eσ · [E × p]

(

)

E_Schr - U^Feff (r)

F (r) = 0,

(39)

2 (E - eA⁰ + βm)

E - eA⁰ + βm

× Ψ(r,t) = 0,

(34)

(

)

где Ψ (r, t) — биспинор,

r²

G (r) +

r² dr

(

)

(

)

Φ (r)

E_Schr - U^Geff (r)

G (r) = 0.

(40)

Ψ (r, t) =

e^-iEt, E > 0,

(

)

(35)

В формулах (39), (40)

Ψ (r, t) =

e^-iEt, E < 0.

E² - m²

X (r)

E_Schr =

(41)

Как известно, (см., например, [7]) при разделении

состояний с положительной и отрицательной энер-

(

)₂

κ (κ + 1)

гиями для уравнения Клейна - Гордона допустима

U^Feff (r) = EeA⁰ -

eA⁰

2r²

вероятностная интерпретация. Плотности вероятно-

(

)

сти для уравнения (34) и уравнений (32), (33) равны

d²

eA⁰

⁽ deA⁰ )²

dr²

w_Φ = Φ⁺Φ, E > 0,

(36)

+ 4 E + m - eA0 ⁺

8 (E + m - eA⁰)²

w_X = X⁺X, E < 0.

deA⁰

Поскольку преобразования (31) отличаются от пре-

(42)

образований (20), (25), (28), плотности вероятности

2 r(E + m - eA⁰)

797

В. П. Незнамов, И. И. Сафронов

ЖЭТФ, том 155, вып. 5, 2019

∕

(

)₂

κ (κ + 1)

eA⁰ (ρ) = -Zα²

r, используемого в уравнениях Ди-

U^Geff (r) = EeA⁰ -

eA⁰

2r²

рака. Видно существенное различие зависимостей

(

)

⁽ deA⁰ )²

U^Feff (ρ) и eA⁰ (ρ). Отметим, что три области, обсуж-

d²

eA⁰

давшиеся выше, можно получить также в результа-

dr²

4 E - m - eA⁰

те строгого математического анализа уравнения Ди-

8 (E - m - eA⁰)²

рака с сингулярным потенциалом eA⁰ (ρ) [18,19]. От-

deA⁰

метим также, что проблема «падения на центр» при

(43)

Z > 137 разрешается при учете конечных размеров

2 r(E - m - eA⁰)

атомных ядер [8-10]. Аналогичный анализ асимпто-

В (42), (43) κ — квантовое число уравнения Дирака,

тик U^Feff (ρ) (42) с другим разбиением на три области

{

можно провести для допустимых значений κ = ±1.

- (l + 1) , j = l + 1/2,

κ = ∓1,∓2,... =

(44)

Энергетический спектр и собственные функции

j = l - 1/2.

уравнения типа Шредингера (39) мы определяли

численно, используя преобразование Прюфера [20]

Далее уравнение (39) мы используем для анализа

и метод фазовых функций [21-23]. Некоторые по-

движения фермионов в кулоновских полях различ-

дробности приведены в Приложении. Ранее этот ме-

ной интенсивности.

тод численных решений уравнений типа Шредин-

гера применительно к движению фермионов в по-

5. УРАВНЕНИЯ ВТОРОГО ПОРЯДКА В

лях Шварцшильда, Райсснера - Нордстрёма, Кер-

КУЛОНОВСКОМ ПОЛЕ ПРИТЯЖЕНИЯ

ра - Ньюмена подробно излагался в работах [3-5].

В результате расчетов показано, что энергетиче-

Рассмотрим решения уравнения типа Шрединге-

ский спектр уравнения второго порядка (39), как

ра (39) для фермионов в кулоновском поле eA⁰ (r) =

∕

и должно быть, совпадает со спектром водородо-

= -Ze²

r, где Z — порядковый номер атомных

подобных атомов, получаемым решением уравнения

ядер. Ниже будем использовать безразмерные вели-

Дирака (1).

чины ε = E/m, ρ = r/l_c, где l_c = ℏ/mc — компто-

Несколько иная ситуация возникает при срав-

новская длина волны фермиона.

нении плотностей вероятности (5) (с собственными

Асимптотика эффективного потенциала (42) при

функциями уравнения Дирака (1)) с плотностями

ρ → 0 имеет вид

вероятности (36) (с собственными функциями урав-

(

)

нений (32), (33)). Ниже мы ограничимся сравнением



(Zα)² - 3/4 +

1-κ



U^Feff

(45)

плотностей вероятности с радиальными волновыми

ρ→0

2ρ²

функциями уравнения Дирака (1) и уравнения (32)

∕

где α = e²

ℏc — электромагнитная постоянная тон-

для состояний с E > 0. Соответствующий анализ

кой структуры.

с использованием уравнения (33) для состояний с

В асимптотике (45) в зависимости от Z мож-

E < 0 можно провести аналогичным образом.

но выделить три характерных области. Для приме-

Выделим в представлении биспинорной волно-

ра рассмотрим эти области для связанных состоя-

вой функции радиальные функции ϕ(ρ), χ (ρ):

ний 1S_1/2 (κ = -1), 2P1/2 (κ = +1). В первой области

√

1≤Z <

3/2α при ρ → 0 существует положитель-

ϕ(ρ, t) = ϕ(ρ)Ωjlmϕ (θ, ϕ)e^-iεt,

∕

(46)

ный барьер ∼ 1

ρ² с последующей потенциальной

√

∕

χ (ρ, t) = χ (ρ) (-1)(1+l-l′)/2 Ω_jl′mϕ (θ, ϕ) e^-iεt,

ямой. При Z = Z_cr =

2α ≈ 118.7 потенциаль-

ный барьер исчезает; для Z > Z_cr при ρ → 0 оста-

где Ωjlmϕ , Ω_jl′mϕ — шаровые спиноры [16] (см. так-

∕

ется потенциальная яма -K

ρ². Во второй области

же (37), (38)).

119 ≤ Z ≤ 137 коэффициент K ≤ 1/8, что допускает

Тогда для дираковских волновых функций в со-

существование фермионных стационарных связан-

ответствии с (5) вероятность обнаружения фермио-

ных состояний [17]. В третьей области Z > 137 при

на на расстоянии ρ в сферическом слое dρ равна

ρ → 0 существует потенциальная яма с K > 1/8, что

свидетельствует о реализации режима «падения на

w_D (ρ) = (ϕ^∗ (ρ)ϕ(ρ) + χ^∗ (ρ)χ (ρ))ρ²dρ.

(47)

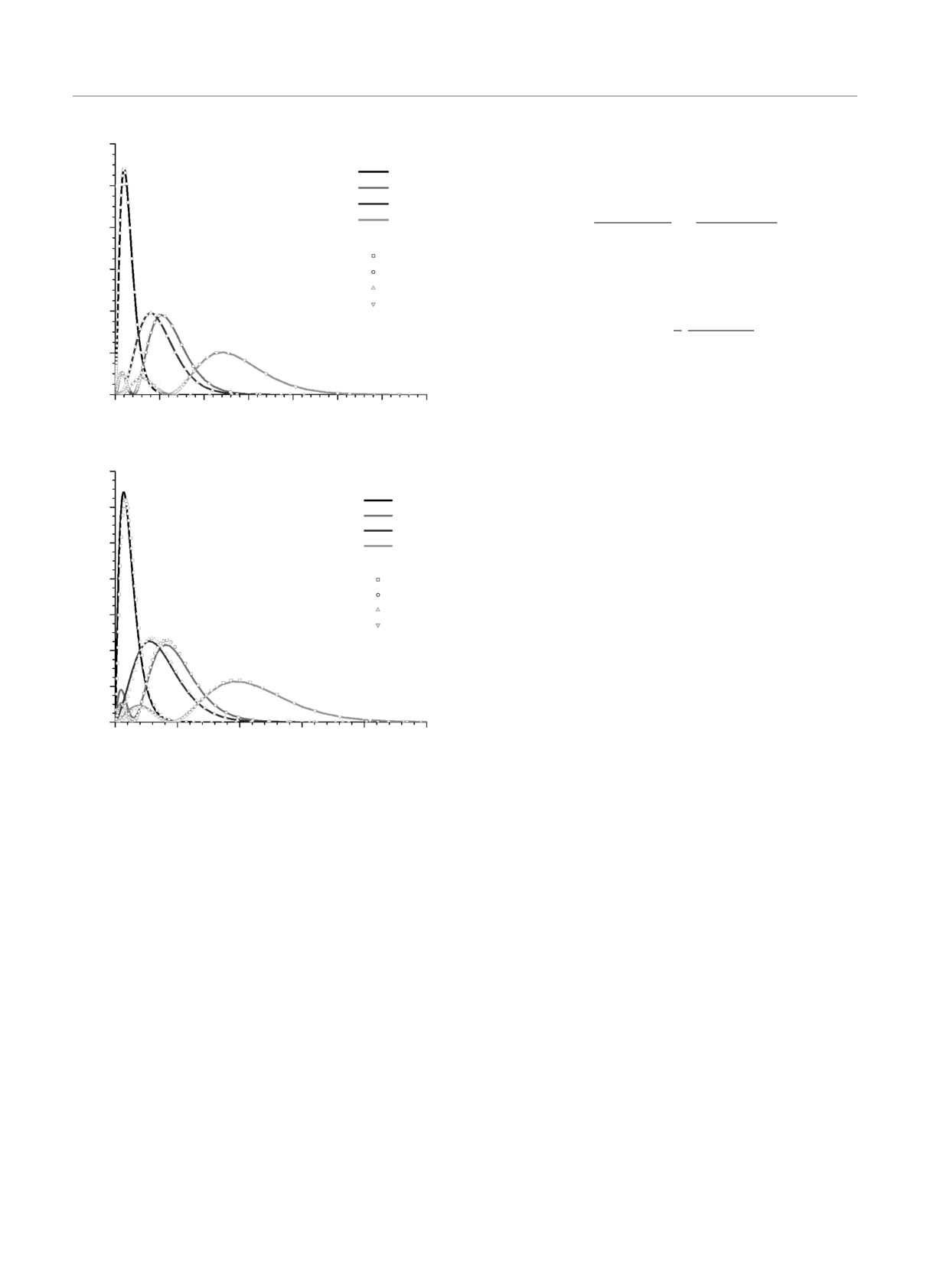
центр» [17]. На рис. 1 для Z = 1, 119, 140 приведены

(

)

зависимости U^Feff (ρ) при κ = -1

1S1/2

Аналогичная вероятность с собственными функци-

Для сравнения на рис. 1 для Z

= 1, 119, 140

ями уравнения второго порядка (39) равна (см. (36),

приведены зависимости кулоновского потенциала

(37), (30))

798

ЖЭТФ, том 155, вып. 5, 2019

Стационарные решения уравнения второго порядка.. .

U_eff

0.03

0.02

-20

Z = 1

0.01

–40

-0.01

(Z )

- 3/4 + (1 -

)

–60

-0.02

U_eff|

-0.03

2²

-80

Z = 1,

= -1(1S

), E/mc

-0.04

1/2

–0.05

-100

0.2

0.4

0.6

0.8

1.0

1.2

1.4

1.6

1.8

2.0

0.002

0.004

0.006

0.008

0.010

U_eff

Z =

119

-50

-20

Z =

140

Z = 119

-100

Z = 140

–40

Z_cr

3/2

118.7

-150

-60

U_eff|

-200

-80

-250

-100

–300

0.2

0.4

0.6

0.8

1.0

0.01

0.02

0.03

0.04

0.05

Рис. 1. Зависимости U_eff (ρ) и V (ρ) = -Zα/ρ для Z = 1 (а), 119, 140 (б)

w_Φ (ρ) = F^∗ (ρ)F (ρ)ρ²dρ =

На рис. 2 по оси абсцисс расстояния приведены

в атомных единицах ρ_a

= (r/ℏ²)me² = αρ.

∕

ϕ^∗ (ρ)ϕ(ρ)ρ²dρ.

(48)

ε+Zα²

ρ+1

Для атома водорода (Z = 1) относительный

вклад слагаемого χ^∗ (ρ) χ (ρ) в

(47) составляет

порядка 10-7. С этой степенью точности мы видим

Уже на данном этапе без вычислений видно,

совпадение плотностей вероятности (47) и (48).

что вероятности (47), (48) отличаются друг от дру-

Для водородоподобного атома с Z = 100 вес сла-

га. Кулоновские функции водородоподобных атомов

гаемого χ^∗ (ρ) χ (ρ) составляет приблизительно 16 %.

χ (ρ) не обращаются в нуль во всей области опре-

При качественном совпадении зависимостей w_D (ρ)

деления (0, ∞), в то время как функции ϕ (ρ) один

и wΦ (ρ) мы видим и некоторые небольшие разли-

или несколько раз обращаются в нуль для возбуж-

чия. Влияние этих различий на величину матрич-

денных энергетических состояний [24]. Вероятность

ных элементов реальных физических процессов тре-

(48) пропорциональна ϕ^∗ (ρ) ϕ (ρ), поэтому она отли-

бует дополнительного изучения. Однако очевидно,

чается от вероятности (47). Посмотрим на масштаб

что влияние будет малым и в целом можно заклю-

этих отличий. На рис. 2 для состояний 1S1/2, 2S1/2,

чить, что уравнение второго порядка со спинорными

2P1/2, 3P1/2 и Z = 1, 100 приведены вычисленные

волновыми функциями и уравнение Дирака описы-

плотности вероятности (47), (48).

вают движение фермионов в кулоновском поле при-

799

В. П. Незнамов, И. И. Сафронов

ЖЭТФ, том 155, вып. 5, 2019

В естественных единицах радиус r_cl пропорциона-

0.6

w_D:

лен классическому радиусу заряженного фермиона

∕

mc²:

1/2

rf = Ze²

0.5

1/2

(

∕

)

1/2

e²

mc²

1/2

rcl =

∕

(51)

0.4

1+E

mc²

1+E

mc²

w_Ф:

1S_1/2

0.3

Ведущая асимптотика потенциала (42) при ρ → ρ_cl

1/2

имеет вид

1/2

0.2



U^Feff

(52)

ρ→ρ

8 (ρ - ρ_cl)²

0.1

Если при ρ → ρ_cl представить радиальную функцию

F (ρ) как

∑

F (ρ)|ρ→ρcl = (ρ - ρ_cl)s

f_k (ρ - ρ_cl)k,

(53)

k=0

w_D:

то определяющее уравнение для (39) с учетом (52)

1S_1/2

2S_1/2

приводит к двум решениям s₁ = 3/2, s₂ = -1/2 и

2P_1/2

1/2

F₁|_ρ→ρ

= f⁽¹⁾⁰(ρ - ρ_cl)3/2 ,

(54)

w_Ф:

1S_1/2

F₂|_ρ→ρ

= f⁽²⁾⁰(ρ - ρ_cl)-1/2 .

(55)

1/2

Решение (55) квадратично-неинтегрируемо, и поэто-

1/2

му физически неприемлемо.

Решение (54) с учетом (30), (31), (37), (46) приво-

дит к зависимостям дираковских радиальных функ-

ций ϕ (ρ), χ (ρ):

0.05

0.10

0.15

0.20

0.25

ϕ|ρ→ρcl ∼ (ρ - ρ_cl)² ,

(56)

χ|ρ→ρcl ∼ const1.

Рис. 2. (В цвете онлайн) Сопоставление плотностей веро-

ятности wD (ρ) и wΦ (ρ) для Z = 1 (а), 100 (б)

Для решений уравнения Дирака в поле Кер-

ра - Ньюмена с ε

< 1 в случае существования

потенциального барьера (52) с последующей потен-

тяжения с идентичными энергетическими спектра-

циальной ямой ранее численно показано поведение

ми и близкими друг к другу плотностями вероятнос-

радиальных функций в точном соответствии с

ти.

асимптотикой (56) [5].

Однако кулоновские функции непрерывного

спектра водородоподобных атомов с ε

> 1 для

6. УРАВНЕНИЯ ВТОРОГО ПОРЯДКА В

потенциала (49) не обращаются в нуль при ρ = ρ_cl,

КУЛОНОВСКОМ ПОЛЕ ОТТАЛКИВАНИЯ.

а равны некоторым константам [16]. Такое пове-

НЕПРОНИЦАЕМЫЕ ПОТЕНЦИАЛЬНЫЕ

дение приводит к нефизической асимптотике (55)

БАРЬЕРЫ

волновой функции уравнения второго порядка

В этом случае кулоновский потенциал

(39). Очевидно, что для кулоновского потенциала

∕

отталкивания должно также существовать второе

eA⁰ (ρ) = Zα²

ρ.

(49)

решение уравнения Дирака с асимптотикой (56).

В отличие от (49) эффективный потенциал (42) син-

Численный анализ интегральных кривых реше-

гулярен при

ния уравнения Дирака (1) для радиальных функций

ϕ(ρ), χ (ρ) показывает, что решение с асимптотикой

ρ_cl = Zα/(ε + 1).

(50)

(56) действительно существует. Примечательно, что

800

ЖЭТФ, том 155, вып. 5, 2019

Стационарные решения уравнения второго порядка.. .

U_eff

6.10⁶

5.10⁶

Z = 1,

= -1,

= 0.00365

4.10⁶

Z = 1

3. 10⁶

2. 10⁶

1. 10⁶

0.002

0.004

0.006

0.008

0.010

0.005

0.010

0.015

0.020

0.025

0.030

U_eff

2500

2000

Z = 140,

= -1,

1500

= 0.51

Z = 140

1000

500

-500

-1000

-1500

0.2

0.4

0.6

0.8

1.0

Рис. 3. Зависимости U_eff (ρ) и V (ρ) = Zα/ρ для Z = 1 (а), 140 (б)

это решение на расстоянии нескольких комптонов-

на. Выражение для радиуса непроницаемого барье-

ских длин волн от ρ = ρ_cl начинает совпадать с

ра (51) приобретает вид

кулоновскими функциями непрерывного спектра с

2r_e

ε > 1.

r(e)

∕

(57)

1 + 2E

m_ec²

На рис. 3 приведены зависимости U^Feff (ρ) для

Z = 1, κ = -1, ε ≈ 1 и Z = 140, κ = -1, ε ≈

∕

В (57) r_e = e²

m_ec² — классический радиус электро-

≈ 1. Также для сравнения приведены зависимости

(

)

∕

на. Для покоящегося электрона

E=m_ec²

радиус

eA⁰ (ρ) = Ze²

ρ для Z = 1, Z = 140.

барьера равен двум третям классического радиуса

Для асимптотики (54) потенциальный барьер

электрона. При E ≫ m_ec² радиус барьера уменьша-

(52) является квантовомеханически непроницаемым

ется обратно пропорционально энергии электрона в

[25]. Возникает вопрос: соответствует ли существо-

системе центра масс.

вание непроницаемого барьера при ρ

= ρ_cl из-

При зондировании внутренней структуры элект-

вестным к настоящему времени экспериментальным

рона во всех возможных экспериментах с электрон-

данным?

электронным рассеянием должна фиксироваться

невозможность проникновения электронов в об-

6.1. Зондирование внутренней структуры

ласть r < r(e)cl.

электрона

В экспериментах с электрон-позитронным рас-

В случае рассеяния электрона на электроне при-

сеянием, проведенных в конце XX века на уско-

веденная масса m = m_e/2, где m_e — масса электро- рителе LEP (ЦЕРН), при энергии в системе цен-

801

ЖЭТФ, вып. 5

В. П. Незнамов, И. И. Сафронов

ЖЭТФ, том 155, вып. 5, 2019

тра масс E = 200 ГэВ внутренняя структура элек-

σ · [E × p_i] = -iσ · [q × p_i]A0 (q).

тронов и позитронов не проявляется при rmin ≈

В итоге вершинный оператор (59) равен

≈ 2·10-18 см (см., например, [26]). Очевидно, в ана-

(

)

логичных гипотетических экспериментах с элект-

σp_f σp_i

V⁰¹ = e E_i + m +

(61)

рон-электронным рассеянием величина r_min будет

E_i + m

несколько большей. Радиус непроницаемого барье-

ра (57) при E = 200 ГэВ равен r(e)cl = 0.7 · 10-18 см,

Свободные решения уравнения Клейна - Гордона и

т. е.

уравнений (32), (33) в виде плоских волн в непре-

рывном спектре записываются следующим образом:

r(e)cl < r_min.

(58)

Φ=

√ e^-ipxΦ_s,

На данном этапе существование непроницаемого ба-

(2π)3/2

2E_p

рьера (52) с радиусом (57) не противоречит экспери-

(62)

ментальным данным по зондированию внутренней

√ e^ipxX_s.

3/2

(2π)

2E_p

структуры электрона.

√

В (62) E_p =

m² + p²; Φ_s, X_s — нормированные

6.2. Сечение рассеяния электрона в

спиновые функции Паули.

кулоновском поле

В результате амплитуду перехода для рассеяния

электрона в кулоновском поле можно записать в ви-

Будем рассматривать кулоновское рассеяние

де

электрона в низшем порядке по e, используя са-

мосопряженное уравнение второго порядка (32) со

∫

спинорной волновой функцией Φ (r).

S_fi = -i d⁴xΦ⁺ (x, p_f , s_f) V⁰¹A⁰ (x)Φ (x, p_i, s_i) =

Диаграмма Фейнмана имеет вид

iδ (E_f - E_i)



Φ+s

〈p_f

^V⁰¹A⁰pi〉Φsi =

(2π)²

Ze²

δ (E_f - E_i)

= -i

Φ+s

q²

(2π)²

(

)

V₁

× E_i +m+

σp_f σp_i Φsi.

(63)

E_i

Амплитуда (63) совпадает с соответствующей амп-

литудой S_fi, ранее вычисленной в работе [14] для

представления Фолди - Ваутхайзена.

В первом порядке по e вершинный оператор V⁰¹

Далее обычными методами с помощью матрич-

равен (см. уравнение (32))

ного элемента S_fi можно получить дифференциаль-

[

]

div E

σ · [E × p]

ное сечение рассеяния Мотта, переходящее в нере-

V⁰¹ = e E_f + E_i -

(59)

E_i + m

лятивистском случае в сечение Резерфорда (см., на-

пример, [7]).

По сравнению с уравнением Клейна - Гордона для

Таким образом, мы показали, что в низшем по-

бесспиновых частиц наличие спина у электрона при-

(

)

рядке теории возмущений

∼e⁴

наличие непрони-

водит к появлению двух последних слагаемых в вер-

цаемого барьера (52) не влияет на величину сечения

шинном операторе (59). Для статического кулонов-

кулоновского рассеяния электронов. Для выводов о

ского потенциала

величине радиационных поправок к сечению рас-

∫

сеяния необходимы соответствующие расчеты диа-

A^μ (q) ≡ d⁴xe^iqxA^μ (x) =

грамм высших порядков теории возмущений.

2πδ (E_f - E_i)g^μo.

(60)

|q|²

6.3. Позитронный конфайнмент в

сверхкритических ядрах

В (60) q = p_f - p_i, p0f = p0i, q = p_f - p_i, p2f = p2i.

Для позитронов непроницаемый барьер (52) су-

С учетом (60)

ществует в случае кулоновского поля атомных ядер

∕

E = -∇A⁰ = iqA0 (q), divE = q²A0 (q),

-eA⁰ (r) = Ze2

r. Для полностью ионизованных

802

ЖЭТФ, том 155, вып. 5, 2019

Стационарные решения уравнения второго порядка.. .

U_eff

ны самосопряженные уравнения второго порядка со

2500

спинорными волновыми функциями. Для стацио-

нарных состояний уравнения характеризуются раз-

2000

деленными состояниями с положительной и отрица-

тельной энергиями, что приводит к возможности ве-

1500

роятностной интерпретации. Для кулоновского поля

= 0.62l

= 2.4 . 10^-11 см

1000

притяжения энергетический спектр уравнения вто-

рого порядка совпадает со спектром уравнения Ди-

500

рака. Плотности вероятности состояний уравнения

второго порядка несколько отличаются от плотнос-

тей вероятности состояний уравнения Дирака. Это

-500

отличие возрастает с увеличением порядкового но-

мера Z.

-1000

При использовании уравнения второго поряд-

ка для кулоновского поля отталкивания существует

–1500

0.2

0.4

0.6

0.8

1.0

непроницаемый потенциальный барьер, радиус ко-

торого зависит от классического радиуса электрона

и от энергии электрона:

Рис. 4. Зависимость U_eff (ρ) при движении позитрона в

кулоновском поле отталкивания с Zscr = 170

Ze²

rcl =

(

∕

mc² 1 +

mc²

стабильных атомов диапазон изменения Z в (51) со-

ставляет от Z = 1 (ядро атома водорода) до Z = 92

Существование непроницаемого барьера не проти-

(ядро U²³⁸). Для покоящегося в системе центра масс

воречит экспериментальным данным по зондирова-

позитрона согласно (51) радиус барьера (52) изменя-

нию внутренней структуры электрона и не влияет в

(

)

ется от 1.4·10-13 см (Z = 1) до 1.3·10-11 см (Z = 92).

низшем порядке теории возмущений

∼e⁴

на сече-

При дальнейшем гипотетическом увеличении Z до

ние кулоновского рассеяния электронов.

Z = Z_scr ≈ 170 энергетический уровень основного

Наличие непроницаемого барьера может приво-

состояния электрона в кулоновском поле ядра дос-

дить к конфайнменту позитронов в сверхкритичес-

тигает верхней границы нижнего континуума E =

ких ядрах с Z ≳ 170 при реализации спонтанного

= -m_ec². Тогда в случае незанятых электронами

испускания вакуумом электрон-позитронных пар.

S-состояний на K-оболочке происходит спонтанное

Существование непроницаемого барьера опосре-

рождение двух электрон-позитронных пар [8-10].

довано выявляет связь спина и заряда элементар-

Электроны занимают свободную K-оболочку, заряд

ных частиц. Действительно, для бесспиновых час-

атома уменьшается на две единицы, а позитроны

тиц и при разноименных знаках заряда спиновой

уходят из атомной системы, где, в принципе, могут

частицы и кулоновского потенциала непроницаемый

быть зарегистрированы.

барьер отсутствует; при одноименных знаках за-

Однако при наличии непроницаемого барьера

ряда спиновой частицы и кулоновского потенциа-

(52) возможен вариант позитронного конфайнмен-

ла непроницаемый барьер присутствует. Расположе-

та. Родившиеся позитроны будут находиться внут-

ние барьера изменяется с изменением энергии части-

ри непроницаемого барьера с r = r_cl (см. рис. 4). В

цы. Будущие модели внутренней структуры лепто-

дальнейшем позитроны аннигилируют с электрона-

нов должны количественно описывать установлен-

ми K-оболочки с испусканием γ-квантов, и система

ную выше качественную связь спина и заряда час-

возвратится в исходное состояние с Z = Z_scr с даль-

тиц.

нейшим повторением событий. Для внешнего мира

Использование

самосопряженных уравне-

источником информации о процессах в атомной си-

ний второго порядка со спинорными волновыми

стеме с Z = Z_scr будет источник γ-квантов анниги-

функциями уже привело к новым физическим

ляции электронов с позитронами.

результатам.

Во внешних гравитационных и электромагнит-

7. ЗАКЛЮЧЕНИЕ

ных полях Шварцшильда, Райсснера - Нордстрёма,

Для квантовомеханического описания движения

Керра, Керра - Ньюмена получены регулярные ста-

фермионов во внешнем кулоновском поле получе-

ционарные решения уравнений второго порядка с

803

В. П. Незнамов, И. И. Сафронов

ЖЭТФ, том 155, вып. 5, 2019

квадратично-интегрируемыми спинорными волно-

Отметим, что уравнение (A.5) должно решаться

выми функциями [3-5]. Для уравнения Дирака эти

после определения из уравнения (A.4) собственных

решения являются нерегулярными и квадратич-

значений ε_n и собственных функций Φ_n (r).

но-неинтегрируемыми.

Для связанных состояний при r → ∞ получаем

Наши исследования показали, что использова-

ние самосопряженных уравнений второго порядка

tg Φ|_r→∞ = -√

1-ε²

со спинорными волновыми функциями позволяет

(A.6)

расширить возможности получения регулярных

Φ|_r→∞ = - arctg

√

+ kπ.

1-ε²

решений квантовой механики во внешних грави-

тационных и электромагнитных полях. При этом

Для экспоненциально растущих решений при

решения уравнений второго порядка в плоском

r → ∞ имеем

пространстве-времени не противоречат на данном

этапе исследований существующим эксперимен-

tg Φ|_r→∞ =

√

тальным данным.

1-ε²

(A.7)

Φ|_r→∞ = arctg

√

+ kπ.

Благодарности. Авторы благодарят за плодо-

1-ε²

творные дискуссии Г. М. Тер-Акопьяна, К. О. Вла-

В выражениях (A.6), (A.7) k = 0, ±1, ±2, . . .

сова, М. В. Горбатенко, В. А. Жмайло, А. И. Миль-

Численный метод решения уравнений типа (A.4),

штейна, В. Е. Шемарулина. Авторы благодарят

(A.5) с асимптотиками (A.6), (A.7) подробно изло-

А. Л. Новоселову за существенную техническую по-

жен в работах [3-5, 27].

мощь в подготовке статьи.

ЛИТЕРАТУРА

ПРИЛОЖЕНИЕ

P. A. M. Dirac, The Principles of Quantum Mecha-

Преобразование Прюфера и граничные

nics, Clarendon Press (1958).

условия

В. П. Незнамов, Теор. матем. физика 197, 493

Для численного решения уравнений (39), (40) мы

(2018).

использовали преобразование Прюфера [20-23].

В качестве примера рассмотрим уравнение (39).

В. П. Незнамов, И. И. Сафронов, ЖЭТФ 154, 761

Для функции f (r) = rF (r) уравнение (39) имеет

(2018).

вид

В. П. Незнамов, И. И. Сафронов, В. Е. Шемару-

(

)

d²f (r)

лин, ЖЭТФ 154, 802 (2018).

E_Schr - U^Feff (r)

f (r) = 0.

(A.1)

dr²

В. П. Незнамов, И. И. Сафронов, В. Е. Шемару-

Пусть

лин, ЖЭТФ 155, 69 (2019).

f (r) = P (r) sin Φ (r) ,

L. L. Foldy and S. A. Wouthuysen, Phys. Rev. 78, 29

df (r)

(A.2)

(1950).

= P (r)cosΦ(r).

Д. Д. Бьеркен, С. Д. Дрелл, Релятивистская

Тогда

квантовая теория, т. 1, Наука, Москва (1978).

f (r)

I. Ya. Pomeranchuk and Ya. A. Smorodinsky, J. Phys.

= tg Φ (r)

(A.3)

df (r)/dr

USSR 9, 97 (1945).

и уравнение (A.1) можно записать в виде системы

W. Pieper and W. Griener, Zs. Phys. 218, 327 (1969).

нелинейных дифференциальных уравнений первого

10.

Я. Б. Зельдович, В. С. Попов, УФН 105, 403 (1971)

порядка:

[Ya. B. Zeldovich and V. S. Popov, Sov. Phys. Usp.

dΦ

(

)

14, 673 (1972)].

= cos² Φ + 2

E_Schr - U^Feff

sin² Φ,

(A.4)

11.

А. С. Давыдов, Квантовая механика, Физматлит,

Москва (1973).

d ln P

(

))

1-2

E_Schr - U^Feff

sinΦ cosΦ. (A.5)

12.

K. M. Case, Phys. Rev. 95, 1323 (1954).

804

ЖЭТФ, том 155, вып. 5, 2019

Стационарные решения уравнения второго порядка.. .

13. V. P. Neznamov and A. J. Silenko, J. Math. Phys.

20. H. Pruefer, Math. Ann. 95, 499 (1926).

50, 122302 (2009); arXiv:0906.2069 (math-ph).

21. I. Ulehla and M. Haviček, Appl. Math. 25, 358 (1980).

14. В. П. Незнамов, ЭЧАЯ 37(1), 152 (2006).

22. I. Ulehla, M. Haviček, and J. Hořejši, Phys. Lett.

A 82, 64 (1981).

15. В. П. Незнамов, ЭЧАЯ 43(1), 33 (2012).

23. I. Ulehla, Rutherford Laboratory preprint RL-82-095

16. В. Б. Берестецкий, Е. М. Лифшиц, Л. П. Пита-

(1982).

евский, Квантовая электродинамика, Физматлит,

Москва (2006).

24. Г. Бете, Э. Солпитер, Квантовая механика ато-

мов с одним и двумя электронами, Физматгиз,

17. Л. Д. Ландау, Е. М. Лифшиц, Квантовая ме-

Москва (1960).

ханика. Нерелятивистская теория, Физматгиз,

25. J. Dittrich and P. Exner, J. Math. Phys. 26, 2000

Москва (1963).

(1985).

18. B. L. Voronov, D. M. Gitman, and I. V. Tyutin,

26. G. Gabrielse, D. Hanneke, T. Kinoshita, M. Noi, and

Theor. Math. Phys. 150(1), 34 (2007).

B. Odom, Phys. Rev. Lett. 97, 030802 (2006).

19. D. M. Gitman, I. V. Tyutin, and B. L. Voronov,

27. В. П. Незнамов, И. И. Сафронов, В. Е. Шемару-

Self-adjoint Extensions in Quantum Mechanics,

лин, ВАНТ, сер. Теоретическая и прикладная фи-

Springer Science&Business Media, New York (2012).

зика, вып. 1, 63 (2018).

805