ЖЭТФ, 2019, том 155, вып. 5, стр. 914-946
© 2019
ФРУСТРАЦИОННЫЕ СВОЙСТВА
ОДНОМЕРНОЙ МОДЕЛИ ИЗИНГА
А. В. Зарубинa*, Ф. А. Кассан-Оглыa, А. И. Прошкинa, А. Е. Шестаковb
a Институт физики металлов им. М. Н. Михеева Уральского отделения Российской академии наук
620108, Екатеринбург, Россия
b Российский федеральный ядерный центр — ВНИИТФ им. академика Е. И. Забабахина
456770, Снежинск, Челябинская обл., Россия
Поступила в редакцию 9 ноября 2018 г.,
после переработки 9 ноября 2018 г.
Принята к публикации 28 ноября 2018 г.
Исследованы фрустрационные свойства модели Изинга на одномерной моноатомной эквидистантной ре-
шетке во внешнем однородном магнитном поле с учетом обменных взаимодействий атомных спинов на
узлах первых (ближайших) и вторых соседей. Методом трансфер-матрицы Крамерса - Ваннье получены
точные аналитические выражения для термодинамических и магнитных характеристик системы, а также
фурье-образа парной спин-спиновой корреляционной функции и волнового вектора магнитного диффуз-
ного рассеяния с учетом обменного взаимодействия между спинами на узлах ближайших соседей во
внешнем магнитном поле и с учетом также обменного взаимодействия между спинами на узлах вто-
рых соседей, но без магнитного поля. Сформулированы критерии возникновения магнитных фрустраций
при наличии конкуренции не только между энергиями обменных взаимодействий, но и между ними и
энергией внешнего магнитного поля. Найдены точки фрустраций и величины фрустрационных магнит-
ных полей, зависящие от величин и знаков обменных взаимодействий. Исследованы особенности данной
модели в режиме фрустрации и его окрестностях. Представлен и проанализирован набор характерных
признаков, присущих наблюдаемым величинам систем с магнитными фрустрациями. Показано, что учет
конкурирующих обменных взаимодействий спинов на узлах первых и вторых соседей позволяет опи-
сать поведение волнового вектора магнитного диффузного рассеяния для соразмерных, несоразмерных
и lock-in-структур.
DOI: 10.1134/S0044451019050158
магнетики Жераром Тулузом в 1977 г. были назва-
ны фрустрированными [7, 8].
1. ВВЕДЕНИЕ
Экспериментальный материал по фрустрирован-
ным магнитным системам в реальных кристаллах и
В последние годы системы с магнитными фруст-
некристаллических веществах весьма богат и изоби-
рациями — стремительно развивающая отрасль ис-
лует новыми явлениями и необычными свойства-
следований, которая охватывает все новые и новые
ми. Однако надлежащая интерпретация и теоре-
объекты, такие как спиновая жидкость, спиновый
тическое объяснение множества экспериментальных
лед и, конечно, реальные кристаллы с различными
фактов и новых эффектов в настоящее время отсут-
структурами, такими как ГЦК, ГПУ, NaCl, пиро-
ствуют, а ряд свойств фрустрированных систем еще
хлор, гранат, шпинель и другие [1-6]. Само явле-
недостаточно понятен.
ние магнитных фрустраций было обнаружено в се-
В представленной работе исследуются фрустра-
редине семидесятых годов двадцатого века в магне-
ционные свойства одномерной модели Изинга на
тиках, проявляющих необычные свойства, это явле-
моноатомной эквидистантной решетке во внешнем
ние объяснялось сильным вырождением основного
магнитном поле с учетом обменных взаимодействий
состояния системы и невозможностью магнитного
атомных спинов на узлах ближайших, а также и
упорядочения даже при нулевой температуре. Такие
вторых соседей. Такая модель позволяет получить
* E-mail: Alexander.Zarubin@imp.uran.ru
точное решение в термодинамическом пределе, что
914
ЖЭТФ, том 155, вып. 5, 2019
Фрустрационные свойства одномерной модели Изинга
∑
∑
∑
∑
дает возможность качественно рассмотреть искомые
...=
...,
характеристики, в том числе и объяснить свойства
{σ}
σ1=±1 σ2=±1 σN =±1
магнетиков, обусловленные фрустрациями, которые
функция Vn может быть представлена [9] в незави-
недоступны в рамках теории возмущений [9].
симом от индекса узла виде
Безусловно, модель Изинга давно и широко ис-
пользуется в теории магнетизма и имеет набор хоро-
V = exp(K1σσ′ + K2σσ′′ + Bσ)
(3)
шо известных решений [10-12], но системного опи-
сания ее фрустрационных свойств не проводилось.
и выражена через безразмерные коэффициенты
Таким образом, вычисление термодинамических
1
и магнитных характеристик, а также фурье-образа
K1,2 = βJ1,2, B = βμ0gH, β =
kBT
парной спин-спиновой корреляционной функции од-
номерных (или квазиодномерных) магнетиков в мо-
Отметим, что в дальнейших преобразованиях такие
дели Изинга позволяет найти необходимую инфор-
величины, как магнетон Бора (μ0), фактор Ланде
мацию о фрустрации системы [13-15] и связать ее
(g) и постоянная Больцмана (kB ), будут положены
с экспериментальными наблюдаемыми, в том числе
равными единице, а величины T , H, J2 будут из-
и спектральными характеристиками упругого маг-
меряться в единицах |J1|, как это принято в теории
нитного рассеяния неполяризованных нейтронов,
низкоразмерных систем.
что дает возможность адекватно провести интерпре-
При наложении циклических граничных условий
тацию магнитной структуры вещества.
Борна - Кармана
σN+1 = σ1
2. ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ
ИЗИНГОВСКОЙ ЦЕПОЧКИ
получаем для статистической суммы (2) выражение
Одномерная классическая модель Изинга с уче-
Z = TrVN,
(4)
том обменных взаимодействий между атомными
где V — трансфер-матрица Крамерса - Ваннье [16],
спинами на узлах первых (ближайших) и вторых
элементы которой задаются правилом (3)
(следующим за ближайшими) соседей с зееманов-
ским членом задается гамильтонианом вида
Vσσ′ = 〈σ|V |σ′〉.
(5)
∑
∑
Размерность такой квадратной трансфер-матрицы
H = -J1
σnσn+1 - J2
σnσn+2 -
одномерной спиновой модели определяется выраже-
n=1
n=1
нием
∑
d=cb,
(6)
-μ0gH σn,
(1)
n=1
где c — число состояний на узле (в классической
модели Изинга c = 2), а b — число обменных взаи-
где J1 — параметр обменного взаимодействия меж-
модействий спинов цепочки в задаче.
ду спинами на ближайших узлах линейной решет-
Трансфер-матрица V является эрмитовой, и с
ки, J2 — параметр обменного взаимодействия меж-
помощью унитарного преобразования P ее можно
ду спинами на следующих за ближайшими узлах
преобразовать к диагональной форме:
решетки, H — величина напряженности внешнего
однородного магнитного поля (направленного вдоль
V= P-1VP = diag(λ1, λ2, . . ., λd),
(7)
оси z), символом σn обозначается z-проекция опера-
тора спина атома величины σ = ±1, находящегося
где символом diag обозначена диагональная матри-
на узле n, а N — количество самих узлов спиновой
ца, на главной диагонали которой расположены ее
цепочки.
собственные значения. Размерность такой матрицы
Статистическая сумма рассматриваемой модели
(7) равна величине d (6).
равна
∑
∑∏
В этом случае статистическая сумма (4) перепи-
Z = e-βH =
Vn,
(2)
сывается следующим образом:
{σ}
{σ} n
∑
где суммирование ведется по всем возможным кон-
Z = Tr
VN = λNi .
(8)
фигурациям системы, т. е.
i=1
915
10*
А. В. Зарубин, Ф. А. Кассан-Оглы, А. И. Прошкин, А. Е. Шестаков
ЖЭТФ, том 155, вып. 5, 2019
При этом величина (4) не меняется, поскольку след
3. ФУРЬЕ-ОБРАЗ ПАРНОЙ
матрицы является ее инвариантом.
СПИН-СПИНОВОЙ КОРРЕЛЯЦИОННОЙ
Отметим, что выбор диагонализирующей мат-
ФУНКЦИИ
рицы возможен множеством способов, но мы под-
Важнейшей характеристикой системы является
бираем диагонализирующую матрицу таким обра-
фурье-образ парной спин-спиновой корреляционной
зом, что на первом месте в матрице (7) стоит глав-
функции (КФ), которая может служить прототи-
ное (единственное максимальное вещественное) соб-
пом для расчета интенсивности упругого магнитно-
ственное значение, которое всегда существует по
го рассеяния неполяризованных нейтронов,
теореме Фробениуса - Перрона [17].
Если на первое место в спектре трансфер-мат-
1∑∑
K(q) =
〈σnσm〉e-iqa(m-n),
(14)
рицы поставить ее главное собственное значение, то
N
n,m {σ}
статистическую сумму (8) можно переписать как
[
]
)
N
)N
где q — волновой вектор рассеяния, a — постоянная
(λ2
(λd
Z =λN1
1+
+...+
(9)
решетки, а угловые скобки означают усреднение:
λ1
λ1
〈. . .〉 = Tr e-βH . . . / Tr e-βH.
Тогда при переходе к термодинамическому преде-
лу (N → ∞) в выражении (9) все слагаемые, кроме
Тогда функция (14) в матричной форме (с заменой
первого, стремятся к нулю,
u = m - n) имеет вид
)N
(λi
∑
∑
1
lim
= 0, i = 2, 3, . . ., d,
K(q) =
κue-iqau,
(15)
N →∞ λ1
N
n=1 u=-N
поэтому получаем выражение для статистической
суммы:
Tr(σVu σVN-u)
κu = 〈σuσN-u〉 =
,
(16)
Z =λN1.
Tr
VN
где
В результате все термодинамические и магнит-
σ = P-1σP.
(17)
ные функции системы — свободная энергия систе-
мы, приходящаяся на один спин,
При этом для КФ должно выполняться условие со-
хранения числа рассеянных частиц —
T
F =-
ln Z = -T ln λ1,
N
∫
a
энтропия
K(q) dq = 〈σ2〉 = 1.
(18)
2π
0
∂F
T ∂λ1
S =-
= ln λ1 +
,
(10)
∂T
λ1 ∂T
теплоемкость
4. ФРУСТРАЦИИ НА ИЗИНГОВСКОЙ
ЦЕПОЧКЕ С УЧЕТОМ ОБМЕННОГО
2
∂2F
T ∂λ1
T
∂2λ1
ВЗАИМОДЕЙСТВИЯ СПИНОВ НА УЗЛАХ
C = -T
=2
+
-
∂T2
λ1 ∂T
λ1 ∂T2
БЛИЖАЙШИХ СОСЕДЕЙ
2
T
-
(∂λ1)2,
(11)
Для начала рассмотрим простейший случай,
λ2
∂T
1
для чего будем учитывать обменное взаимодействие
намагниченность
только между спинами на узлах ближайших соседей
и без учета внешнего магнитного поля. В этом слу-
∂F
T ∂λ1
M =-
=
(12)
чае гамильтониан (1) имеет вид
∂H
λ1 ∂H
∑
и магнитная восприимчивость
H = -J1
σnσn+1,
)2
n
∂2F
∂M
T
(∂λ1
T ∂2λ1
χ=-
=
=-
+
(13)
тогда элементы трансфер-матрицы (5) определяют-
∂H2
∂H
λ2
1
∂H
λ1 ∂H2
ся выражением
— определяются только через главное собственное
значение трансфер-матрицы [9, 18, 19].
Vσσ′ = 〈σ|eK1σσ′ |σ′〉 = eK1σσ′ ,
916
ЖЭТФ, том 155, вып. 5, 2019
Фрустрационные свойства одномерной модели Изинга
а размерность самой матрицы — d = 2, согласно
где приведенный корень —
правилу (6).
λ2
eK1 - e-K1
Далее, воспроизводя известный результат [9], за-
Λ=
=
= th K1.
(25)
λ1
eK1 + e-K1
пишем трансфер-матрицу
(
)
(
)
Поскольку в термодинамическом пределе
-K1
V++ V+-
eK1
e
V=
=
,
(19)
lim ΛN = 0,
V-+ V--
e-K1
eK1
N →∞
собственные значения которой равны
функция (24) переписывается в форме
λ1 = eK1 + e-K1 = 2 chK1,
(20)
κu = Λu.
Отсюда выражение для КФ (15) в термодинамичес-
λ2 = eK1 - e-K1 = 2 shK1,
ком пределе имеет окончательный вид
причем главное собственное значение определено
первым (20).
1-Λ2
K(q) =
(26)
Теперь можно записать и энтропию
1 - 2Λcos(qa) + Λ2
Полученную функцию
(26) следует назвать
S = ln(2chK1) - K1 thK1 =
функцией магнитного диффузного рассеяния, так
λ2
λ1 + λ2
= ln λ1 -
ln
(21)
как при конечной температуре она обладает нену-
λ1
2
левыми значениями для любого волнового вектора,
и теплоемкость системы
а не только в положениях брэгговских рефлексов.
(
)2
(
)2
Отметим, что функция (26) аналогична выраже-
K1
2
λ1 + λ2
C =
=
ln
(22)
нию для интенсивности диффузного рентгеновского
ch K1
λ1
2
рассеяния для эквиатомной линейной решетки, по-
как через переменные гамильтониана, так и через
лученному в 1948 г. Андре Гинье [20,21].
собственные значения трансфер-матрицы.
Следует обратить внимание на то, что для полу-
Таким образом, в диагонализированной форме
ченной КФ (26) выполняется условие (18).
трансфер-матрица (7) записывается как
Для описания интенсивности функции магнит-
(
)
ного диффузного рассеяния определим положения
λ1
0
максимумов и минимумов КФ (26), которые имеют
V= P-1VP =
,
0
λ2
значения
π + 2πk
2πk
где сама диагонализирующая матрица выбрана в
q0 =
,
q1 =
,
k∈Z
(27)
a
a
виде
(
)
(
)
в зависимости от знака приведенного корня (25).
√
√
2
1
-1
2
1
1
В свою очередь, амплитуда КФ (26) в положениях
P=
,
P-1 =
2
1
1
2
-1
1
экстремумов (27) задаются следующими функция-
ми:
1-Λ
Также для записи функции (16) в матричной
K(q0) =
=e-2K1,
(28)
форме введем следующую проекционную матрицу:
1+Λ
(
)
1
1+Λ
K(q1) =
=
=e2K1.
(29)
1
0
K(q0)
1-Λ
σ=
,
(23)
0
-1
4.1. Магнитная фазовая диаграмма
тогда, согласно преобразованию (17), запишем
основного состояния системы
(
)
0
-1
Дальнейшее исследование модели будет опирать-
σ=
ся на магнитную фазовую диаграмму, структура ко-
-1
0
торой определяется поведением минимальной энер-
В рассматриваемом случае функция (16) имеет
гии конфигураций спиновой системы в основном со-
вид
стоянии в зависимости от параметров модели
-u
Λu + ΛNΛ
κu =
,
(24)
E0 = min{E}.
(30)
1+ΛN
917
А. В. Зарубин, Ф. А. Кассан-Оглы, А. И. Прошкин, А. Е. Шестаков
ЖЭТФ, том 155, вып. 5, 2019
Сама энергия конфигурации задается оператором
полной энергии системы (1) и находится из функ-
S
ции
∑
0.7
1
E=-
εi,
m
i=1
∑ σi+b-pσi+b + σi+bσi+b+p
εi = Hσi+b + Jp
,
2
p=1
4
3
где m — количество узлов в конфигурации, b — чис-
2
0
T
ло обменных взаимодействий спинов цепочки в зада-
1
-1
-1/2
0
че, Jp — параметр обменного взаимодействия меж-
1/2
0
1
J1
ду спинами на соседних узлах линейной решетки
p-уровня, H — величина напряженности внешнего
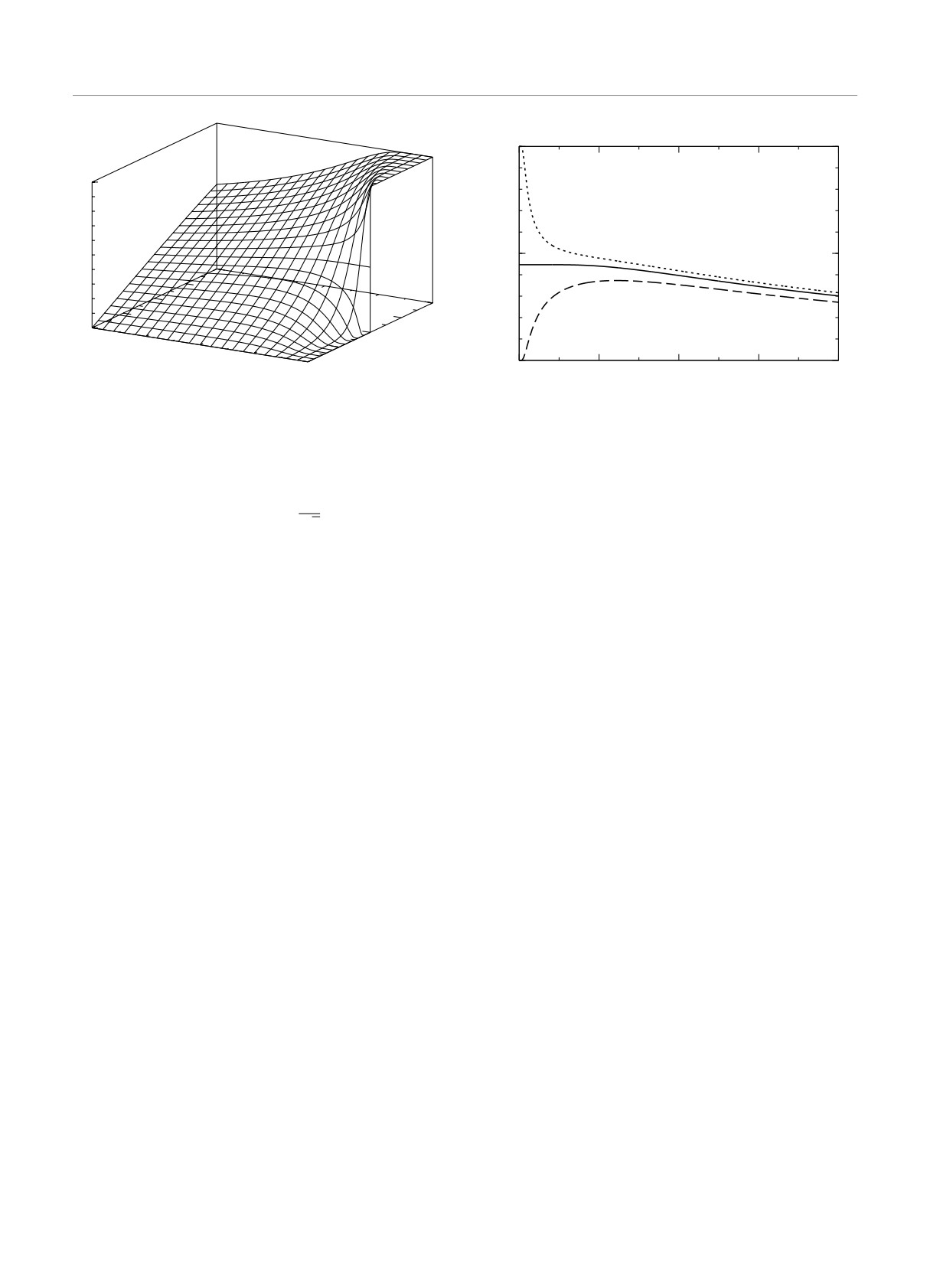
Рис. 1. Энтропия изинговской цепочки (21) с учетом об-
магнитного поля.
менного взаимодействия только между спинами на узлах
Таким образом, в зависимости от знака парамет-
ближайших соседей
ра обменного взаимодействия спинов цепочки в дан-
ной модели при нулевой температуре реализуются
два набора возможных спиновых конфигураций, об-
Отсюда видно, что равенство энергий двух конфигу-
ладающих минимальной энергией. Первый тип кон-
раций при нулевой температуре соответствует усло-
фигураций при J1 < 0 характеризуется антифер-
вию
ромагнитным упорядочением неелевского типа, что
EA2 = EF2,
соответствует набору
а в точке фазового пространства
{
}
+1
-1
+1
-1
+1
-1
CA2 =
,
(31)
J1 = 0
(33)
−1
+1
-1
+1
-1
+1
происходит качественное изменение магнитной
состоящему из двух последовательностей (с чередо-
структуры основного состояния, которое характери-
ванием проекций спина вдоль и против z-направле-
зуется тем, что помимо двух антиферромагнитных
ния) с равными энергиями
CA2 (31) и двух ферромагнитных CF2 (32) конфи-
гураций имеют минимальную энергию и другие
EA2 = J1.
спиновые конфигурации, в том числе и бесконечное
Для такой конфигурации введем индексное обозна-
множество конфигураций, не обладающих никакой
чение A2.
трансляционной инвариантностью.
Второй тип конфигураций при J1 > 0 соответ-
ствует ферромагнитному упорядочению
4.2. Термодинамика системы в режиме
{
}
фрустрации
+1
+1
+1
+1
+1
+1
CF2 =
(32)
-1
-1
-1
-1
-1
-1
В обнаруженной особой точке фазового про-
странства (33) при нулевой температуре энтропия
и состоит из двух последовательностей (вдоль и про-
системы (21) не равна нулю, а равна натуральному
тив z-направления) с равными энергиями
логарифму двух,
EF 2 = -J1.
lim
S(J1 = 0) = ln 2 ≈ 0.693,
T →0
Для обозначения такой конфигурации введем ин-
как показано на рис. 1.
декс F2.
Здесь следует обратить внимание на то, что дан-
Получаем, что энергию основного состояния сис-
ный результат не противоречит третьему началу
темы (30) в рассматриваемом случае можно запи-
термодинамики, поскольку энтропия определяется
сать в виде
через ее дифференциал
{
EA2, J1 ≤ 0,
E0 =
δQ
dS =
,
EF2, J1 ≥ 0.
T
918
ЖЭТФ, том 155, вып. 5, 2019
Фрустрационные свойства одномерной модели Изинга
с точностью до постоянной интегрирования S0 ≥ 0,
S
0.7
и лишь в формулировке теоремы Нернста - Планка
для равновесных систем с невырожденным основ-
ным состоянием данная постоянная выбирается ну-
левой, S0 = 0 [22].
С другой стороны, если энтропия Гиббса основ-
ного состояния системы больше нуля,
S(T = 0) = ln W > 0,
то это говорит о том, что статистический вес дан-
ного состояния больше единицы, W
> 1, а сама
система испытывает вырождение, поскольку ее ста-
0
1
2
3
4
тистический вес определяет кратность вырождения
T
состояния [23].
Рис. 2. Энтропия изинговской цепочки (21) с учетом об-
Именно такое состояние системы, в котором эн-
менного взаимодействия только между спинами на уз-
тропия основного состояния не равна нулю,
лах ближайших соседей, где значения параметра |J1| =
lim S > 0,
(34)
= {1/4; 1/2; 1} соответствуют штриховой, сплошной и
T →0
пунктирной линиям на графике
следует называть фрустрированным.
Таким образом, в данном случае статистический
C
вес системы в основном состоянии в режиме фруст-
1/2
рации равен двум,
W = 2,
а вне этой особой точки (33) равен единице,
1/4
W = 1,
(35)
при этом нуль-температурная энтропия системы
равна нулю,
lim S = 0,
(36)
T →0
что соответствует третьему началу термодинамики
0
1
2
3
4
в формулировке Планка [22], а сама система стано-
T
вится невырожденной.
Рис. 3. Теплоемкость изинговской цепочки (22) (с обозна-
При бесконечно большой температуре (при лю-
чениями линий в соответствии с рис. 2)
бом значении обменного параметра) энтропия равна
натуральному логарифму двух —
но в промежуточных значениях по температуре теп-
lim S = ln 2,
(37)
T →∞
лоемкость имеет пик, как показано на рис. 3. Пове-
дение максимума теплоемкости определяется реше-
где W = 2 — число состояний на узле в рассмат-
нием уравнения
риваемой модели. Поведение энтропии системы при
конечных значениях параметра обменного взаимо-
K1 th K1 = 1
действия спинов на узлах ближайших соседей це-
почки представлено на рис. 2.
и продемонстрировано на рис. 4.
При стремлении к нулевой или бесконечно боль-
шой температуре и при любом значении параметра
4.3. Поведение функции магнитного
обменного взаимодействия спинов цепочки теплоем-
диффузного рассеяния
кость системы (22) равна нулю,
В случае антиферромагнитного параметра обме-
lim
C = 0, lim
C = 0,
(38)
на спинов цепочки (J1 < 0) знак приведенного кор-
T →0
T →∞
919
А. В. Зарубин, Ф. А. Кассан-Оглы, А. И. Прошкин, А. Е. Шестаков
ЖЭТФ, том 155, вып. 5, 2019
T
K(q)
1
10
5
4
1/2
3
2 T
0
1
– /2
0
/2
0
3 /2
2
5 /2
aq
0
-1
-1/2
0
1/2
1
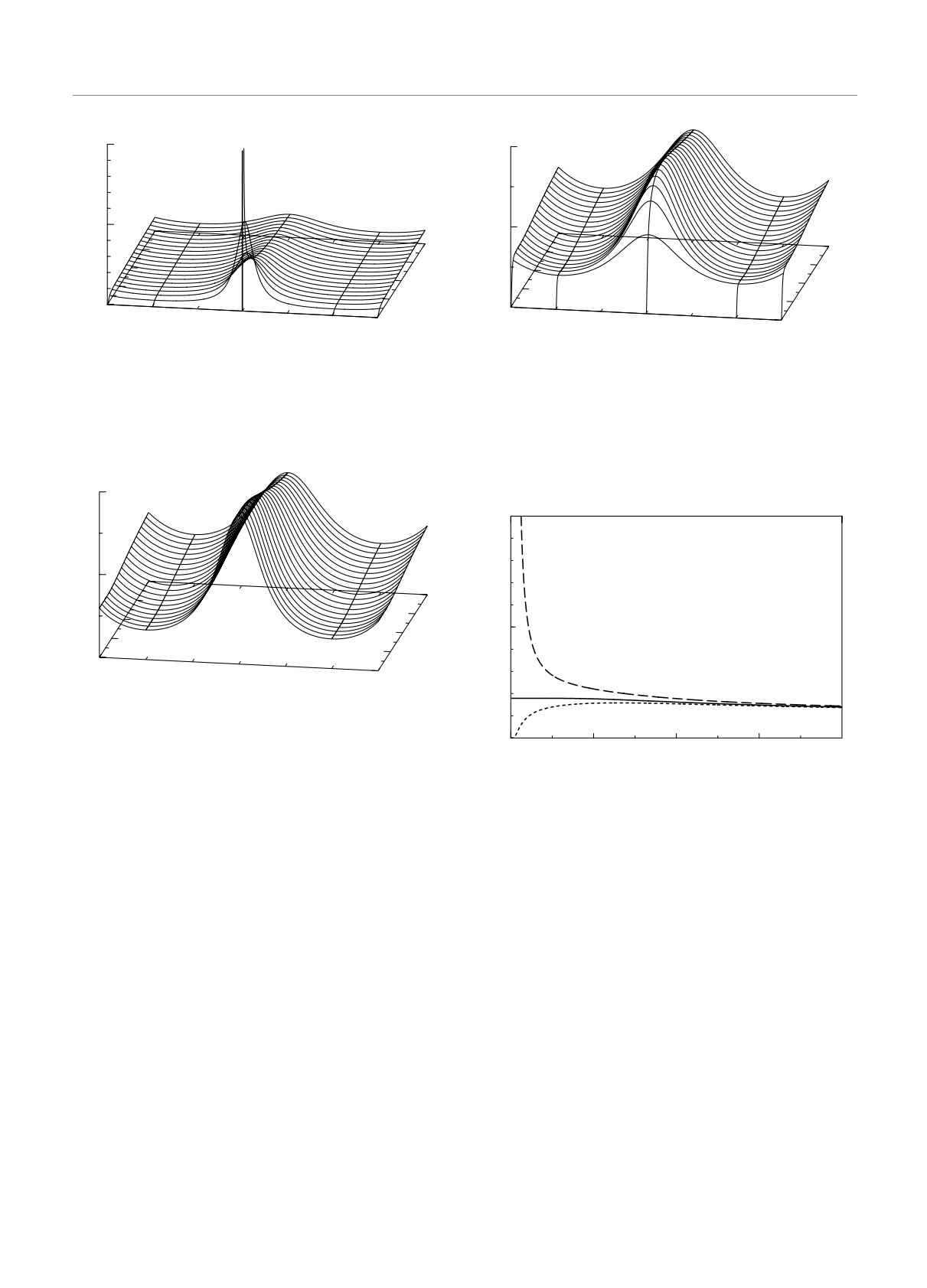
Рис. 5. КФ изинговской цепочки (26) с антиферромагнит-
J1
ным обменным взаимодействием только между спинами
на узлах ближайших соседей (J1 = -1) в зависимости от
Рис.
4. Температурное поведение пиков теплоемкости
вектора рассеяния и температуры
изинговской цепочки (22) с учетом обменного взаимодей-
ствия только между спинами на узлах ближайших соседей
от параметра спинового обмена
K(q )0
10
ня (25) всегда отрицателен, следовательно, получа-
ем решения (27) для положений максимумов
qA0 = q0
(39)
5
и минимумов
qA1 = q1
функции магнитного диффузного рассеяния КФ
(26).
В свою очередь, поведение амплитуды максиму-
мов КФ определяется выражением (28), т. е.
0
1
2
3
4
T
K(qA0) = K(q0),
(40)
Рис. 6. Температурное поведение амплитуды максимумов
а амплитуды минимумов задаются функцией (29)
КФ изинговской цепочки (40) (с обозначениями линий в
как
соответствии с рис. 2)
1
K(qA1) =
= K(q1).
(41)
K(qA0)
Температурная эволюция КФ представлена на
и минимумов,
рис. 5, а экстремумов функции — на рис. 6, 7.
1
С другой стороны, в случае ферромагнитного об-
K(qF1 ) =
= K(q0).
K(qF0 )
мена спинов цепочки (J1 > 0) знак приведенного
корня (25) всегда положителен, и отсюда получаем
Следует обратить внимание на то, что в слу-
обратное предыдущему случаю решение для поло-
чаях антиферромагнитного и ферромагнитного об-
жений максимумов
менных взаимодействий спинов на узлах ближай-
qF0 = q1
(42)
ших соседей соответствующие функции магнитного
диффузного рассеяния изинговской цепочки (26) по
и минимумов
форме одинаковы и различаются лишь сдвигом по
qF1 = q0
величине q на половину периода π/a. Таким обра-
функции (26).
зом, при ферромагнитном обменном параметре пи-
Соответственно ведут себя и амплитуды макси-
ки КФ находятся в точках пространства рассеяния
мумов,
qF0 (42), соответствующих положениям брэгговских
K(qF0 ) = K(q1),
рефлексов
920
ЖЭТФ, том 155, вып. 5, 2019
Фрустрационные свойства одномерной модели Изинга
K(q )1
при этом имея нулевую интенсивность в положени-
1
ях минимума,
lim
K(qA1) = lim
K(qF1 ) = 0.
T →0
T →0
В точке фрустрации (33) приведенный корень
1/2
(25) всегда равен нулю,
Λ = 0,
что меняет поведение КФ (26), и амплитуда данной
функции становится равной единице,
0
1
2
3
4
K(q, J1 = 0) = 1,
(44)
T
Рис. 7. Температурное поведение амплитуды минимумов
при любой температуре. Поэтому интенсивность КФ
КФ изинговской цепочки (41) (с обозначениями линий в
(26) фрустрированной системы не имеет экстрему-
соответствии с рис. 2)
мов и равномерно распределена в обратном про-
странстве при любой температуре, так же как и для
нефрустрированной системы при бесконечно боль-
2πk
шой температуре.
qB =
,
k ∈ Z,
(43)
a
Таким образом, при отсутствии обмена между
а при антиферромагнитном обмене рассеяние кон-
спинами цепочки (J1 = 0) реализуется парамагнит-
центрируется ровно посередине между брэгговски-
ное состояние системы, характеризуемое тем, что
ми положениями в позициях qA0 (39), т. е. со сдвигом
все 2N конфигураций системы имеют одинаковую
на половину периода относительно первых. Анало-
вероятность и обладают одинаковой энергией, т.е.
гично располагаются и минимумы функции (26).
дают одинаковый вклад в рассеяние при любом зна-
Выражения для амплитуды максимумов (28) и
чении волнового вектора. Поскольку энтропия в па-
минимумов (29) КФ при различных знаках парамет-
рамагнитном состоянии не равна нулю,
ра обменного взаимодействия спинов цепочки связа-
S(J1 = 0) = ln 2,
ны условиями
1
1
и одинакова (максимальна) при любой температу-
K(qA0) =
,
K(qA1) =
ре, изинговский парамагнетик является абсолютно
K(qF0 )
K(qF1 )
фрустрированной системой.
При бесконечно высоких температурах ампли-
туда КФ в положениях максимумов и минимумов
5. ФРУСТРАЦИИ НА ИЗИНГОВСКОЙ
одинакова, т. е. интенсивность КФ равномерно рас-
ЦЕПОЧКЕ С УЧЕТОМ ВНЕШНЕГО
пределяется по обратному пространству при любом
МАГНИТНОГО ПОЛЯ ПРИ ОБМЕННОМ
значении параметра обмена спинов цепочки
ВЗАИМОДЕЙСТВИИ СПИНОВ НА УЗЛАХ
БЛИЖАЙШИХ СОСЕДЕЙ
lim
K(qA0) = lim
K(qA1) = 1,
T →∞
T →∞
Аналогичным образом рассмотрим модель Изин-
га в случае, учитывающем зеемановский вклад в об-
lim
K(qF0 ) = lim
K(qF1 ) = 1,
T →∞
T →∞
щую энергию системы, тогда гамильтониан (1) будет
а при понижении температуры концентрируется, со-
иметь вид
ответственно, в отдельных точках обратного про-
∑
∑
странства qA0 или qF0 .
H = -J1
σnσn+1 - H σn,
n
n
При стремлении температуры к нулю пики КФ
приобретают форму дельта-функции в соответству-
а элементы трансфер-матрицы (5) будут опреде-
ющих точках пространства рассеяния,
ляться выражением
lim
K(qA0) = lim
K(qF0 ) = ∞,
Vσσ′ = 〈σ|eK1σσ′+Bσ|σ′〉 = eK1σσ′+Bσ,
T →0
T →0
921
А. В. Зарубин, Ф. А. Кассан-Оглы, А. И. Прошкин, А. Е. Шестаков
ЖЭТФ, том 155, вып. 5, 2019
а ее размерность, согласно правилу (6), равна d = 2.
Также намагниченность можно выразить и через
Явный вид трансфер-матрицы может быть полу-
собственные значения трансфер-матрицы,
чен аналогично предыдущему случаю (19) и пред-
√
√
ставлен как
λ21 + λ22 - 2
λ21λ22 + 4
M =
,
(50)
(
)
λ1 - λ2
-K1+B
eK1+B e
V=
,
(45)
как и магнитную восприимчивость (13),
e-K1-B eK1-B
(
)3
1
2
λ1 + λ2
а ее собственные значения записаны в виде
χ=
√
(51)
(
√
)
T λ1 -λ2 λ1λ2 +
λ21λ22 + 4
λ1 = eK1
ch B + sh2 B + e-4K1
,
(46)
Диагонализирующая матрица в данном случае
(
√
)
выбрана в виде
λ2 = eK1
ch B - sh2 B + e-4K1
P=
Здесь первым выбран корень (46), который является
⎛
⎞
(λ1-λ2)(1+M)
(λ1-λ2)(1-M)
главным собственным значением матрицы (45).
-
⎜
⎟
⎜
2
2
⎟
Отсюда энтропия
(10) и теплоемкость
(11)
=
,
⎝
2
2
⎠
системы представимы через собственные значения
λ1(1+M)+λ2(1-M) λ1(1+M)+λ2(1-M)
трансфер-матрицы следующим образом:
(
)
где M — намагниченность (50). Тогда матрица (17)
4
ln ψ1
имеет форму
S = lnλ1 - λ1 - λ2 - 2ψ2 -
-
λ1ψ2
1
λ1 - λ2
(
)
)
M M -1
ψ2
(λ1 +
λ2
- 2
ln
+ψ2
,
(47)
σ=
λ1 - λ2
2
-M - 1
-M
Отсюда получаем, что в рассматриваемом слу-
(
)2
чае функция (16) записывается как
λ1 + λ2
2
ln ψ1
C =2
+
λ1 - λ2
λ1 - λ2
ψ1
M2(1+ΛN)+(1-M2)(Λu+ΛNΛ-u)
(
)
2
κu =
,
(52)
λ1 + λ2
1
2
ln ψ1
1+ΛN
+2
(λ22 - 2ψ21) +
λ1 - λ2
λ1 λ1 - λ2 ψ1
где приведенный корень равен
[
2
λ1 + λ2
2
1
(λ1 + λ2 + 2ψ2)]
√
+
ln
+
λ1 - λ2
λ1 - λ2 ψ1
2ψ1
λ2
ch B - sh2 B + e-4K1
Λ=
=
√
(53)
(
)
λ1
2
ch B + sh2 B + e-4K1
ψ2 lnψ1
1
4
(λ1 + λ2 + 2ψ2)
+2
ln
+
λ1 - λ2
λ1 - λ2 ψ1
2ψ1
В термодинамическом пределе функция (52) приоб-
(
)
2
1
4
ψ2
ретает вид
+2
ln ψ1
,
(48)
λ1 λ1 - λ2 ψ1
κu = M2 + (1 - M2)Λu.
где
√
√
В результате проделанных преобразований вы-
λ1λ2 +
λ21λ22 + 4
ψ1 =
,
ражение для КФ (15) состоит теперь из двух слага-
2
емых:
√
√
K(q) = M2L(q) + D(q).
(54)
λ21 + λ22 - 2
λ21λ22
+4
ψ2 =
Первое слагаемое есть модулированная квадратом
2
намагниченности функция Лауэ,
Намагниченность на один спин (12) имеет вид
1
sin2 (qa(N + 1)/2)
L(q) =
,
(55)
shB
M =
√
(49)
N sin2 (qa/2)
sh2 B + e-4K1
описывающая брэгговское рассеяние, определяемая
Напомним, что выражение (49) есть один из резуль-
только исходной кристаллической решеткой и не за-
татов работы Изинга [10].
висящая от параметра обменного взаимодействия
922
ЖЭТФ, том 155, вып. 5, 2019
Фрустрационные свойства одномерной модели Изинга
спинов цепочки и величины напряженности внеш-
Индексное обозначение конфигурации соответству-
него магнитного поля. Второе слагаемое — функция
ет введенному ранее.
магнитного диффузного рассеяния во внешнем маг-
Второй тип конфигураций при H ≥ -2J1 харак-
нитном поле:
теризуется ферромагнитным упорядочением и соот-
2
ветствует набору
1-Λ
D(q) = (1 - M2)
(56)
1 - 2Λcos(qa) + Λ2
{
}
CF1 =
+1
+1
+1
+1
+1
+1
,
(60)
Следует обратить внимание, что выражение для
КФ (54) описывает особое явление, связанное с
состоящему из единственной последовательности
пропорциональным квадрату намагниченности пе-
(спины в которой ориентируются вдоль направле-
рераспределением интенсивности рассеяния между
ния внешнего магнитного поля) с энергией
магнитными диффузными (56) и ядерными брэггов-
скими (55) рефлексами. Отсюда получаем, что в об-
EF1 = -(J1 + H).
ласти нулевой или малой намагниченности спектр
рассеяния определяется лишь магнитными диффуз-
Для этой конфигурации введем индексное обозначе-
ными рефлексами. И наоборот, в пределе больших
ние F1.
значений напряженности внешнего магнитного поля
Отметим, что конфигурационная спиновая по-
и низких температур при намагниченности насыще-
следовательность
ния магнитное диффузное рассеяние полностью ис-
{
}
чезает, а остаются только немодулированные брэг-
-1
-1
-1
-1
-1
-1
,
говские рефлексы.
Отметим, что в данном случае условие (18) вы-
присутствующая в предыдущем случае (32), здесь
полняется для полной КФ (54).
уже отсутствует, поскольку ее энергия
Экстремумы функции магнитного диффузного
рассеяния КФ (56) определяются положениями вол-
E = -(J1 - H)
новых векторов
π + 2πk
2πk
не минимальна при нулевой температуре.
q0 =
,
q1 =
,
k ∈ Z,
(57)
a
a
Таким образом, энергия основного состояния си-
с соответствующими амплитудами
стемы (30) в данном случае имеет следующий вид:
1-Λ
{
D(q0) = (1 - M2)
,
(58)
1+Λ
EA2, H ≤ -2J1,
E0 =
(61)
1+Λ
EF1, H ≥ -2J1.
D(q1) = (1 - M2)
(59)
1-Λ
Магнитная фазовая диаграмма основного состояния
Функции интенсивности функции магнитного
показана на рис. 8.
диффузного рассеяния КФ (56) в точках экстрему-
Согласно функции (61), общая фазовая граница
ма связаны между собой следующим образом:
двух представленных спиновых конфигураций (слу-
D(q0)
1-M2
=
чай, когда EA2 = EF1) при антиферромагнитном
1-M2
D(q1)
параметре обмена спинов цепочки (J1 < 0) соответ-
ствует соотношению параметров модели
5.1. Магнитная фазовая диаграмма
основного состояния системы
H/|J1| = 2,
(62)
В данном случае при нулевой температуре в мо-
при котором происходит перестройка упорядочения
дели реализуются два набора возможных спиновых
основного состояния, и количество конфигураций
конфигураций, обладающих минимальной энергией.
системы с минимальной энергией больше, чем сум-
Первый тип конфигураций при H ≤ -2J1 характе-
ма количеств конфигураций CA2 и CF1. Это связано
ризуется антиферромагнитным упорядочением нее-
с тем, что в момент перемагничивания системы во
левского типа и соответствует набору CA2 (31), со-
внешнем магнитном поле (62) в основном состоянии
стоящему из двух чередующихся спиновых последо-
присутствует также бесконечное множество спино-
вательностей с равными энергиями
вых конфигураций, в том числе и с нарушением
EA2 = J1.
трансляционной инвариантности.
923
А. В. Зарубин, Ф. А. Кассан-Оглы, А. И. Прошкин, А. Е. Шестаков
ЖЭТФ, том 155, вып. 5, 2019
H
2
S
0.7
CF1
4
1
3
2
CA2
T
0
1
1
2
0
3
4
H
Рис. 9. Энтропия изинговской цепочки (47) с антифер-
ромагнитным обменным взаимодействием между спинами
0
на узлах ближайших соседей (J1 = -1) во внешнем маг-
-1
0
1
нитном поле
J1
Рис. 8. Магнитная фазовая диаграмма основного состоя-
S
ния изинговской цепочки во внешнем магнитном поле при
0.7
учете обменного взаимодействия между спинами на узлах
ближайших соседей цепочки
5.2. Термодинамика системы в режиме
фрустрации
При антиферромагнитном обмене спинов цепоч-
ки (J1 < 0) во внешнем магнитном поле (62) и при
нулевой температуре энтропия системы имеет нену-
левое значение,
(
)
√
0
1
2
3
4
H
1+
5
lim
S
=2
= ln
≈ 0.481,
(63)
T
T →0
|J1|
2
Рис. 10. Энтропия изинговской цепочки (47) с антифер-
равное натуральному логарифму золотого сечения.
ромагнитным обменным взаимодействием между спинами
Следовательно, согласно условию (34), система в
на узлах ближайших соседей (J1 = -1) вблизи фрустриру-
данном режиме фрустрирована, а внешнее магнит-
ющего внешнего магнитного поля, где значения параметра
ное поле (62) является фрустрирующим.
H/|J1| = {1.8; 2; 2.1} соответствуют штриховой, сплош-
Таким образом, в данном случае именно внеш-
ной и пунктирной линиям на графике
ний фактор, а именно, внешнее магнитное поле ста-
новится инструментом, формирующим фрустраци-
онный режим в системе.
рис. 10. При бесконечно большой температуре и при
Поведение энтропии в зависимости от парамет-
любых значениях обменного взаимодействия спинов
ров модели представлено на рис. 9.
на узлах ближайших соседей и величины напряжен-
Получаем, что статистический вес системы в ос-
ности внешнего магнитного поля энтропия есть на-
новном состоянии в режиме фрустрации (62) равен
туральный логарифм двойки (37).
золотому сечению,
√
Намагниченность системы (50) при антифер-
1+
5
W =
,
(64)
ромагнитном обменном параметре спинов цепочки
2
(J1 < 0) во фрустрирующем внешнем магнитном по-
а вне этого режима — единице (35), и нуль-темпера-
ле (62) и нулевой температуре имеет конечное зна-
турная энтропия равна нулю (36), как показано на
чение, меньшее намагниченности насыщения:
924
ЖЭТФ, том 155, вып. 5, 2019
Фрустрационные свойства одномерной модели Изинга
M
M
1
1
1/2
4
0
3
4
2
3
H
2
1
1
T
0
0
1
2
3
4
T
Рис. 11. Намагниченность изинговской цепочки (50) с ан-
тиферромагнитным обменным взаимодействием между
Рис. 12. Намагниченность изинговской цепочки (50) с ан-
спинами на узлах ближайших соседей (J1 = -1) во внеш-
тиферромагнитным обменным взаимодействием между
нем магнитном поле
спинами на узлах ближайших соседей (J1 = -1) вблизи
фрустрирующего внешнего магнитного поля (с обозначе-
ниями линий в соответствии с рис. 10)
1
lim
M (H/|J1| = 2) =
√ ≈ 0.447.
T →0
5
Во внешних магнитных полях, меньших фрустриру-
Магнитная восприимчивость (13) при антифер-
ющего (62), нуль-температурная намагниченность
ромагнитном обменном параметре спинов цепочки
отсутствует, а в больших магнитных полях демон-
(J1 < 0) и во фрустрирующем внешнем магнитном
стрирует насыщение,
поле (62) при нулевой температуре стремится к бес-
конечности:
lim
M (H/|J1| < 2) = 0, lim
M (H/|J1| > 2) = 1,
T →0
T →0
lim
χ(H/|J1| = 2) = ∞,
T →0
как показано на рис. 11. Отсюда следует, что темпе-
ратурная зависимость намагниченности проявляет
а вне этого поля при нулевой температуре, так же
разные типы поведения во внешних магнитных по-
как и в любом другом внешнем магнитном поле при
лях, меньших, равных и больших фрустрирующего
бесконечно большой температуре, восприимчивость
магнитного поля (62) (см. рис. 12).
равна нулю:
В случае ферромагнитного обмена спинов цепоч-
ки (J1 > 0) при конечном внешнем магнитном поле
lim
χ = 0, lim χ = 0,
T →0
T →∞
(H > 0) намагниченность основного состояния все-
гда максимальна и равна единице,
что можно увидеть на рис. 13.
При нулевой и бесконечно большой температу-
lim
M (J1 > 0) = 1.
рах, а также при любом значении параметра об-
T →0
менного взаимодействия спинов на узлах ближай-
При бесконечно большой температуре и при лю-
ших соседей и величины напряженности внешнего
бом значении обменного взаимодействия спинов на
магнитного поля теплоемкость системы равна ну-
узлах ближайших соседей и величины внешнего
лю (38). В промежуточных значениях температу-
магнитного поля намагниченность отсутствует:
ры функция теплоемкости имеет максимум, а вбли-
lim M = 0.
зи фрустрирующего внешнего магнитного поля дан-
T →∞
ный пик расщепляется на острый и куполообразный
Отметим, что выражения для энтропии и намаг-
максимумы, как показано на рис. 14. Отметим, что
ниченности системы в режиме фрустрации при ну-
формирующийся при малых температурах острый
левой температуре для произвольного спина в од-
пик теплоемкости при приближении к фрустраци-
номерной модели Изинга с учетом обменного взаи-
онному магнитному полю исчезает точно в точке
модействия только между спинами на узлах бли-
фрустраций, а при удалении от нее пропадает уже
жайших соседей во внешнем магнитном поле были
куполообразный максимум. Таким образом, в точке
получены в наших работах [24, 25].
фрустрации теплоемкость имеет один размытый ку-
925
А. В. Зарубин, Ф. А. Кассан-Оглы, А. И. Прошкин, А. Е. Шестаков
ЖЭТФ, том 155, вып. 5, 2019
T
4
3
3
2
2
1
1
0
1
2
3
4
0
1
2
3
4
T
H
Рис. 13. Магнитная восприимчивость изинговской цепоч-
Рис. 15. Положение пиков теплоемкости изинговской це-
ки (51) с антиферромагнитным обменным взаимодействи-
почки (48) с антиферромагнитным обменным взаимо-
ем между спинами на узлах ближайших соседей (J1 = -1)
действием между спинами на узлах ближайших соседей
вблизи фрустрирующего внешнего магнитного поля (с обо-
(J1 = -1) во внешнем магнитном поле
значениями линий в соответствии с рис. 10)
5.3. Поведение функции магнитного
C
диффузного рассеяния
2/5
В случае антиферромагнитного параметра обме-
на спинов цепочки (J1 < 0) знак приведенного кор-
ня (53) всегда отрицателен и поэтому, согласно ре-
шениям (57), получаем соответствующие значения
волнового вектора для положений максимумов,
1/5
qA0 = q0,
(65)
и минимумов
qA1 = q1
функции магнитного диффузного рассеяния
КФ (56).
0
1
2
3
4
Также легко видеть, что амплитуда максиму-
T
мов функции магнитного диффузного рассеяния
Рис. 14. Теплоемкость изинговской цепочки (48) с анти-
КФ определяется выражением (58), где
ферромагнитным обменным взаимодействием между спи-
нами на узлах ближайших соседей (J1 = -1) вблизи
D(qA0) = D(q0),
(66)
фрустрирующего внешнего магнитного поля (с обозначе-
ниями линий в соответствии с рис. 10)
а амплитуда минимумов задается функцией (59) как
D(qA1) = D(q1).
(67)
Так, при любом значении обменного параметра
полообразный пик. Ход максимумов теплоемкости
спинов цепочки, величины напряженности внешнего
приведен на рис. 15.
магнитного поля и при бесконечно большой темпе-
Описанные здесь поведения магнитного вкла-
ратуре магнитное диффузное рассеяние однородно,
да теплоемкости и магнитной восприимчивости во
т. е. амплитуды максимумов и минимумов функции
внешнем магнитном поле наблюдаются в реальных
магнитного диффузного рассеяния КФ (56) совпа-
кристаллах, например, в антиферромагнетиках на
дают и равны единице,
основе редкоземельных металлов [6, 26-31] или со-
единений актиноидов [32].
lim
D(qA0) = lim
D(qA1) = 1.
T →∞
T →∞
926
ЖЭТФ, том 155, вып. 5, 2019
Фрустрационные свойства одномерной модели Изинга
D(q)
D(q)
10
2
5
1
4
4
3
3
2 T
2 T
0
1
0
1
– /2
0
/2
0
– /2
0
/2
0
3 /2
2
3 /2
2
5 /2
5 /2
aq
aq
Рис. 16. Функция магнитного диффузного рассеяния КФ
Рис. 18. Функция магнитного диффузного рассеяния КФ
изинговской цепочки (56) с антиферромагнитным обмен-
изинговской цепочки (56) с антиферромагнитным обмен-
ным взаимодействием между спинами на узлах ближай-
ным взаимодействием между спинами на узлах ближай-
ших соседей (J1
= -1) во внешнем магнитном поле
ших соседей (J1
= -1) во внешнем магнитном поле
(H/|J1| = 1.8) вблизи режима фрустрации
(H/|J1| = 2.1) вблизи режима фрустрации
D(q)
2
D(q
)
0
10
1
4
3
5
2 T
0
1
– /2
0
/2
0
3 /2
2
5 /2
aq
Рис. 17. Функция магнитного диффузного рассеяния КФ
изинговской цепочки (56) с антиферромагнитным обмен-
0
1
2
3
4
ным взаимодействием между спинами на узлах ближай-
T
ших соседей (J1
= -1) во внешнем магнитном поле
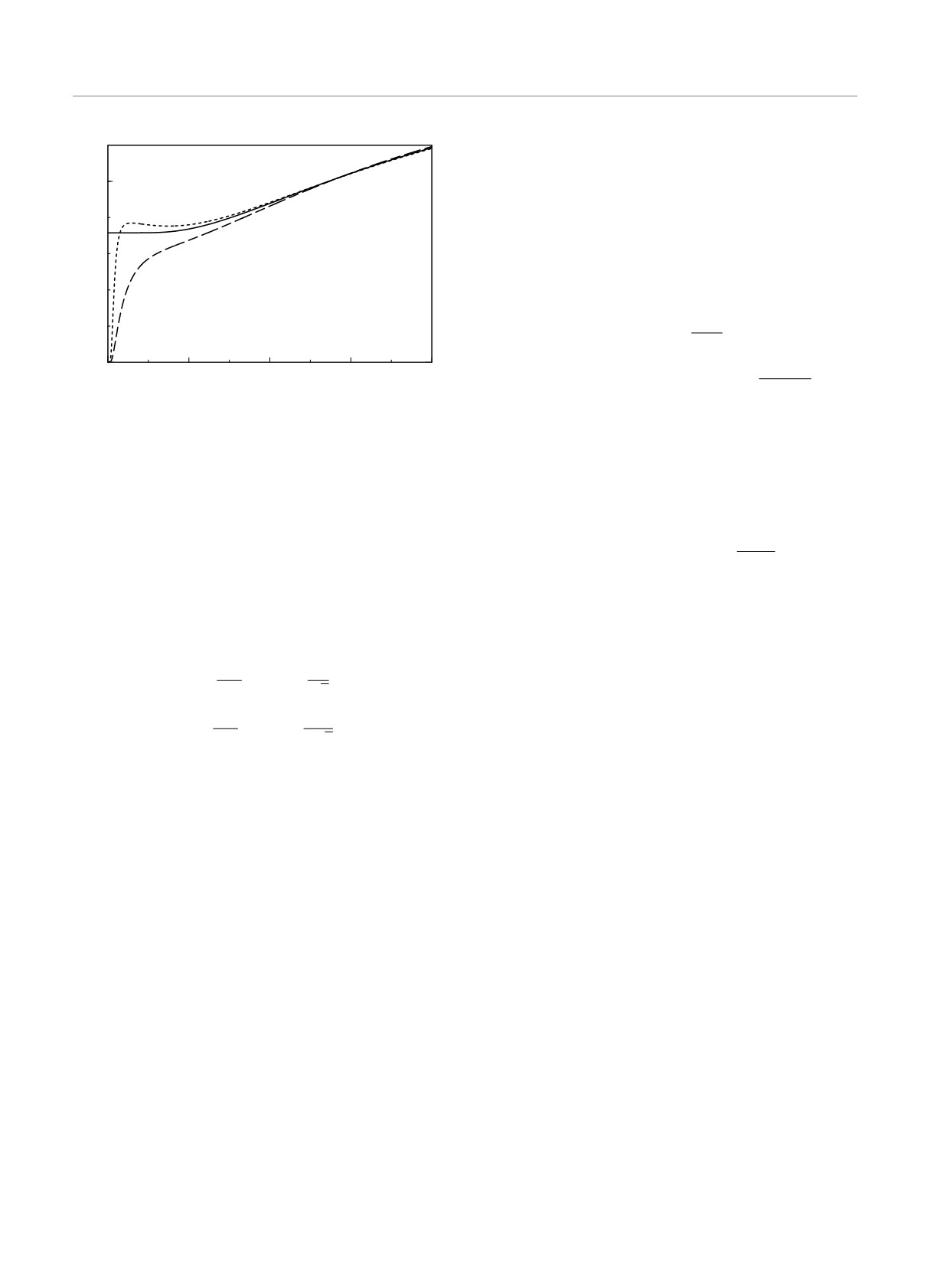
Рис. 19. Температурное поведение амплитуды максимумов
(H/|J1| = 2) в режиме фрустрации
функции магнитного диффузного рассеяния КФ изингов-
ской цепочки (66) с антиферромагнитным обменным взаи-
При понижении температуры рассеяние концентри-
модействием между спинами на узлах ближайших соседей
руется в положениях qA0 (65), т. е. точно посередине
(J1 = -1) вблизи фрустрирующего внешнего магнитного
между брэгговскими пиками (43).
поля (с обозначениями линий в соответствии с рис. 10)
Здесь следует отметить, что картина рассеяния
существенно зависит от величины внешнего магнит-
ного поля. Так, в магнитном поле, меньшем, равном
lim
D(qA0, H/|J1| < 2) = ∞,
и большем поля фрустрации системы (62), поведе-
T →0
ние функции рассеяния различно, как показано на
рис. 16, 17, 18, а поведение интенсивности функции
lim
D(qA1, H/|J1| < 2) = 0.
T →0
магнитного диффузного рассеяния КФ показано на
рис. 19, 20.
В магнитных полях, больших фрустрирующих, ко-
При нулевой температуре во внешних магнитных
гда основное состояние характеризуется единствен-
полях, меньших фрустрирующего, когда реализует-
ной ферромагнитной конфигурацией (60), интенсив-
ся конфигурация с антиферромагнитным упорядо-
ность магнитного диффузного рассеяния при нуле-
чением неелевского типа (31), функция магнитного
вой температуре отсутствует:
диффузного рассеяния КФ имеет вид дельта-функ-
ции, т. е.
lim
D(qA0, H/|J1| > 2) = lim
D(qA1, H/|J1| > 2) = 0,
T →0
T →0
927
А. В. Зарубин, Ф. А. Кассан-Оглы, А. И. Прошкин, А. Е. Шестаков
ЖЭТФ, том 155, вып. 5, 2019
D(q )1
В рассматриваемой области значений параметров
модели искомых фрустрированных состояний нет.
Сами термодинамические функции системы име-
1/2
ют чрезвычайно простой вид. Так, энтропия (47),
теплоемкость (48), намагниченность (50) и магнит-
ная восприимчивость (51) системы соответственно
переписываются к виду
S(J1 = 0) = ln(2 ch B) - B th B,
(
)2
B
C(J1 = 0) =
,
ch B
1
0
1
2
3
4
M (J1 = 0) = th B, χ(J1 = 0) =
T
T ch2 B
Отметим, что в рассматриваемом случае выражения
Рис. 20. Температурное поведение амплитуды минимумов
для энтропии и теплоемкости системы соответствен-
функции магнитного диффузного рассеяния КФ изингов-
но совпадают с функциями (21) и (22) при замене
ской цепочки (67) с антиферромагнитным обменным взаи-
K1 ⇒ B.
модействием между спинами на узлах ближайших соседей
Функция магнитного диффузного рассеяния КФ
(J1 = -1) вблизи фрустрирующего внешнего магнитного
поля (с обозначениями линий в соответствии с рис. 10)
(56) здесь может быть представлена как
1
а в промежуточных температурах функция имеет
D(q, J1 = 0) = 1 - M2 =
,
(68)
ch2 B
максимум, как показано на рис. 18, 19.
Во фрустрирующем внешнем магнитном поле
поскольку приведенный корень (53) равен нулю. Та-
(62) при нулевой температуре амплитуды максиму-
ким образом, функция (68) не имеет пиков (как в
мов (66) и минимумов (67) функции (56) имеют со-
случае функции (56)) и не константа во всем диапа-
ответствующие конечные значения:
зоне своих значений (как в случае функции (44)), а
(
)
H
4
описывает диффузный фон, пропорциональный ве-
lim
D qA0,
=2
=
√ ≈ 1.789,
T →0
|J1|
5
личине 1 - M2.
(
)
H
4
lim
D qA1,
=2
=
√ ≈ 0.358.
T →0
|J1|
5
5
6. ФРУСТРАЦИИ НА ИЗИНГОВСКОЙ
Таким образом, в рассматриваемом фрустрацион-
ЦЕПОЧКЕ С УЧЕТОМ ОБМЕННЫХ
ном режиме происходит перестройка основного со-
ВЗАИМОДЕЙСТВИЙ СПИНОВ НА УЗЛАХ
стояния, когда статистический вес конфигураций
ПЕРВЫХ И ВТОРЫХ СОСЕДЕЙ
больше единицы (W > 1), и помимо антиферромаг-
Теперь найдем характеристики модели Изинга
нитных (31) и ферромагнитных (60) конфигураций
при учете обменных взаимодействий между спина-
имеют минимальную энергию и другие конфигура-
ми на узлах первых и вторых соседей. В этом случае
ции, в том числе и не обладающие трансляционной
гамильтониан (1) записывается в виде
инвариантностью.
∑
∑
В конце следует сказать, что изинговский пара-
H = -J1
σnσn+1 - J2 σnσn+2.
магнетик при отсутствии обменного взаимодействия
n
n
спинов на узлах ближайших соседей (J1 = 0) во
Здесь следует отметить, что первое успешное
внешнем магнитном поле (H > 0) в основном состо-
точное решение одномерной модели Изинга с об-
янии (T = 0) характеризуется лишь одной конфигу-
менными взаимодействиями спинов на узлах первых
рацией CF1 (60), в которой спины цепочки сориен-
и вторых соседей принадлежит Джону Стефенсону
тированы вдоль направления внешнего магнитного
[33]. Его решение опиралось на формальный прием
поля, поэтому энтропия и намагниченность системы
Добсона [34], который не позволяет получить реше-
соответственно равны
ние модели во внешнем магнитном поле с учетом
lim
S(J1 = 0, H > 0) = 0,
обменных взаимодействий спинов на узлах первых
T →0
и вторых соседей. В своем решении мы не будем ис-
lim
M (J1 = 0, H > 0) = 1.
пользовать алгоритм Стефенсона.
T →0
928
ЖЭТФ, том 155, вып. 5, 2019
Фрустрационные свойства одномерной модели Изинга
В данном случае элементы трансфер-матрицы
V=
⎛
⎞
(5) задаются выражением
V++,++ V++,+- V++,-+ V
++,--
⎜
⎟
⎜
V+-,++ V+-,+- V+-,-+ V+-,--
⎟
Vσσ′,σ′′σ′′′ = 〈σσ′|eK1σσ′+K2σ′′σ′′′ |σ′′σ′′′〉 =
⎜
=
⎟,
(70)
⎜
⎟
⎝ V-+,++ V-+,+- V-+,-+ V-+,--
⎠
= eK1σσ′+K2σ′′σ′′′δσ′σ′′,
(69)
V--,++ V--,+- V--,-+ V--,--
где δσ′σ′′
— символ Кронекера. Размерность тран-
сфер-матрицы равна d = 4 (6), а сама матрица опре-
поэтому, подставив сюда значения функции (69),
деляется как
выпишем явный вид трансфер-матрицы:
⎛
⎞
eK1+K2
eK1-K2
0
0
⎜
⎟
⎜
0
0
e-K1+K2
e-K1-K2
⎟
V=⎜
⎟.
(71)
⎜
⎟
⎝ e-K1-K2 e-K1+K2
0
0
⎠
0
0
eK1-K2
eK1+K2
Отметим, что впервые данная матрица была полу-
где
λ1 + λ2 + λ3 + λ4
чена Такехико Огучи [35].
ψ0 =
,
Найденная трансфер-матрица (71) имеет следу-
2
√
ющий набор собственных значений:
√
λ1λ2 +
λ21λ22 + 4
(
√
)
ψ1 =
2
λ1,2 = eK2 chK1 ± sh2 K1 + e-4K2
,
(72)
При следующем выборе диагонализирующей
(
√
)
матрицы —
λ3,4 = eK2 shK1 ± ch2 K1 - e-4K2
⎛
⎞
p1
p2
-p6
-p6
√
⎜
⎟
Как отмечалось ранее, первый корень (72) — глав-
2
⎜
5
p5
p3
p4
⎟
⎜ p
P=
⎟,
ное собственное значение трансфер-матрицы (71).
⎜
⎟
2
p5
-p3
-p4
⎝ p5
⎠
Теперь можно записать термодинамические
p1
p2
p6
p6
функции системы, выраженные через собственные
значения трансфер-матрицы. Таким образом, энтро-
пия системы (10) имеет вид
λ1-λ2+λ3+λ4
λ1-λ2-λ3-λ4
p1 =
,
p2 = -
,
2
2
λ3 + λ4
λ1+λ2-λ3+λ4
λ1+λ2+λ3-λ4
S = lnλ1 -
ln ψ0 -
p3 =
,
p4 =
,
λ1 - λ2
2
2
(
)
2
ln ψ1
-2
λ1 - ψ0 -
,
(73)
2
2
λ1ψ2
λ1 - λ2
p5 =
,
p6 =
1
λ1+λ2+λ3+λ4
λ1+λ2-λ3-λ
4
а теплоемкость (11) —
— диагонализированная трансфер-матрица (7) име-
ет вид
(
)2
λ1 + λ2
2
ln ψ1
C =2
+
V= P-1VP = diag(λ1, λ2, λ3, λ4).
λ1 - λ2
λ1 - λ2
ψ1
(
)
2
λ1 + λ2
2
1
ln ψ1
Проекционная матрица в данном случае определя-
+2
(λ22 - 2ψ21) +
λ1 - λ2
λ1 - λ2 λ1 ψ1
ется через прямое произведение (произведение Кро-
(
)2
некера) единичной матрицы и матрицы (23) как
λ1 + λ2
2
1
ψ0
+
ln
+
(
)
(
)
λ1 - λ2
λ1 - λ2 ψ1
ψ1
(
)
1
0
1
0
2
λ3 + λ4
2
2
ψ0
σ=
⊗
= diag(1, 1, -1, -1).
+
ln ψ1 ln
+
0
1
0
-1
λ1 - λ2
λ1 - λ2 ψ1
ψ1
(
)
2
2
λ3 + λ4 ln ψ1
Отметим, что умножение на единичную матрицу
+2
,
(74)
λ1 - λ2
λ1
ψ1
справа дает для КФ тот же результат.
929
11
ЖЭТФ, вып. 5
А. В. Зарубин, Ф. А. Кассан-Оглы, А. И. Прошкин, А. Е. Шестаков
ЖЭТФ, том 155, вып. 5, 2019
В свою очередь, матрица (17) может быть запи-
Далее, приведя к общему знаменателю сумму в
сана в виде
формуле (77), выпишем окончательный вид КФ
⎛
⎞
0
0
s1
s2
K(q) =
⎜
⎟
⎜
0
0
s3
s4
⎟
1-Λ3Λ4
σ=⎜
⎟,
(1 - Λ23)(1 - Λ24)
⎜
⎟
1+Λ3Λ4
s6
0
0
⎝ s5
⎠
=
(78)
(1-2Λ3 cos(qa)+Λ23)(1-2Λ4 cos(qa)+Λ24)
s7
s8
0
0
Отметим, что в числителе функции (78) коэффици-
где
ент при cos(qa) равен нулю.
s1 = [(λ1 - λ3)2 - (λ2 + λ4)2]f1 + f2,
Полученное выражение для КФ (78) описывает
s2 = [(λ1 - λ4)2 - (λ2 + λ3)2]f1 + f2,
магнитное диффузное рассеяние на спиновой цепоч-
ке. Условие (18) для КФ (78) здесь также выполня-
s3 = [(λ1 + λ4)2 - (λ2 - λ3)2]f1 - f2,
ется.
s4 = [(λ1 + λ3)2 - (λ2 - λ4)2]f1 - f2,
Положения экстремумов КФ (78) задаются уже
λ1 + λ2 + λ3 + λ4
1
тремя значениями векторов в пространстве рассея-
f1 =
,
23
λ1 - λ2
ния. Первый волновой вектор равен
2
1
1
2πk
f2 = -
q0 =
Re(arccosX) ±
,
k ∈ Z,
(79)
λ1 + λ2 - λ3 - λ4 λ1 - λ2
a
a
Оставшиеся коэффициенты матрицы можно полу-
(
)
1
1
1
чить из соотношений
X =
Λ3 +
+Λ4 +
=
4
Λ3
Λ4
√
s1s5 = s4s8 = Υ3, s2s7 = s3s6 = Υ4,
1
shK1
=-
e2K2
sh2 K1 + e-4K2,
(80)
2 sh(2K2)
где
а второй и третий векторы определяются как
(λ1 + λ2)(λ3 + λ4)
Υ3 + Υ4 = 1, Υ3 - Υ4 =
π + 2πk
2πk
(λ1 - λ2)(λ3 - λ4)
q1 =
,
q2 =
,
k ∈ Z.
(81)
a
a
Теперь распишем функцию (16)
Амплитуда экстремумов КФ (78) в положениях
волновых векторов (79) задается функцией
Υ3Λu3 + Υ4Λu4
κu =
+
1+ΛN2 +ΛN3 +ΛN
Λ3(1 - Λ23)Λ4(1 - Λ24)
4
K(q0) = -4
,
(82)
(Λ3 - Λ4)2(1 - Λ23Λ24)
ΛN3 Λ-u3 + ΛN2 Λu4Λ-u2 + ΛN4 Λu2Λ-u4
+Υ3
+
1+ΛN2 +ΛN3 +ΛN
4
а в положениях (81) соответственно
ΛN4Λ-u4 + ΛN2Λu3Λ-u2 + ΛN3Λu2Λ-u3
2
2
2
+Υ4
,
(75)
K(q1) =
+
-
- 1,
(83)
1+ΛN2 +ΛN3 +ΛN
4
1+Λ3
1+Λ4
1+Λ3Λ4
где
2
2
2
K(q2) =
+
-
- 1.
(84)
1-Λ3
1-Λ4
1+Λ3Λ4
Λi =
λi , i = 2, 3, 4,
Λ2 = -Λ3Λ4.
Отметим, что свойства четности гиперболиче-
λ1
ских функций определяют нам симметрию собствен-
В термодинамическом пределе функция (75) приоб-
ных значений трансфер-матрицы относительно из-
ретает следующий вид:
менения знака параметра обмена между спинами на
узлах ближайших соседей:
κu = Υ3Λu3 + Υ4Λu4,
(76)
λ1(-J1) = λ1(J1), λ3(-J1) = -λ4(J1).
(1 - Λ3Λ4)(Λ3 + Λ4)
Υ3 - Υ4 =
Отсюда легко выписать свойства симметрии функ-
(1 + Λ3Λ4)(Λ3 - Λ4)
ций интенсивности КФ из выражений (82):
Теперь, подставив функцию (76) в выражение для
КФ (15), получим
K(q0, -J1) = K(q0, J1),
а также из (83) и (84):
∑
1-Λ2i
K(q) =
(77)
Υi 1 - 2Λi cos(qa) + Λ2i
K(q1, -J1) = K(q2, J1).
i=3
930
ЖЭТФ, том 155, вып. 5, 2019
Фрустрационные свойства одномерной модели Изинга
J2
6.1. Магнитная фазовая диаграмма
основного состояния системы
1
В данном случае при нулевой температуре реа-
лизуются три набора возможных спиновых конфи-
гурации, обладающих минимальной энергией. Пер-
вый тип конфигураций (при J1 < 0 и J2 ≥ J1/2) ха-
рактеризуется антиферромагнитным упорядочени-
CA2
CF2
ем неелевского типа CA2 (31) с энергией
0
EA2 = J1 - J2.
Индексное обозначение конфигурации соответству-
ет введенному ранее.
Второй тип (при J2 ≤ 0, J2 ≤ J1/2 и J2 ≤ -J1/2)
определяется также антиферромагнитным упорядо-
CA4
чением, но с учетверением периода,
⎧
⎫
⎪
+1
+1
-1
-1
+1
+1
⎪
-1
0
1
⎪
⎪
⎨
⎬
J1
+1
-1
-1
+1
+1
-1
CA4 =
,
(85)
⎪
−1
+1
+1
-1
-1
+1
⎪
⎪
⎪
Рис. 21. Магнитная фазовая диаграмма основного состо-
⎭
⎩ -1
-1
+1
+1
-1
-1
яния изинговской цепочки с учетом обменного взаимодей-
ствия между спинами на узлах первых и вторых соседей
и состоит из четырех вариантов спиновых после-
цепочки
довательностей с равными энергиями (обозначение
конфигурации — A4), с энергией
количество конфигураций системы с минимальной
EA4 = J2.
энергией больше, чем сумма количеств конфигура-
Третий тип (при J1 > 0 и J2 ≥ -J1/2) определяется
ций CA4 и CA2, а также CA4 и CF2. Как уже от-
ферромагнитным упорядочением CF2 (32) с энерги-
мечалось ранее, такое состояние системы при нуле-
ей
вой температуре связано с перестройкой магнитной
EF2 = -(J1 + J2).
структуры и возникновением бесконечного множе-
ства спиновых конфигураций, в том числе и с нару-
Таким образом, энергия основного состояния
шением трансляционной инвариантности.
системы (30) в данном случае записывается в виде
⎧
Видно, что магнитная фазовая диаграмма основ-
⎨EA2, J1 < 0 ∧ J2 ≥ J1/2,
ного состояния модели (см. рис. 21) содержит четы-
E0 =
EA4, J2 ≤ 0 ∧ J2 ≤ J1/2 ∧ J2 ≤ -J1/2,
ре варианта отношений параметров обменных взаи-
⎩
модействий между спинами на узлах первых и вто-
EF2, J1 > 0 ∧ J2 ≥ -J1/2.
рых соседей изинговской цепочки:
Отсюда следует, что при следующих соотношениях
обменных параметров спинов цепочки в модели —
(J1 > 0, J2 > 0), (J1 < 0, J2 > 0),
(87)
⎧
⎨2J2,
J1 < 0 ∧ J2 ≤ 0,
(J1 > 0, J2 < 0), (J1 < 0, J2 < 0).
(88)
J1 =
-2J2, J1 > 0 ∧ J2 ≤ 0,
⎩
0,
J2 ≥ 0
Только два последних случая (88) описывают сис-
тему с конкурирующими обменными взаимодейст-
— происходит перестройка спиновой конфигурации
виями. Именно в этих двух квадрантах магнит-
основного состояния, как показано на магнитной
ной фазовой диаграммы (рис. 21) с антиферро-
фазовой диаграмме модели на рис. 21.
антиферромагнитным (AA: J1 < 0 и J2 < 0) и фер-
При антиферромагнитном обменном параметре
ро-антиферромагнитным (FA: J1 > 0 и J2 < 0) вари-
между спинами на узлах вторых соседей (J2 < 0) в
антами параметров обменных взаимодействий меж-
точках фазовой диаграммы
ду спинами на узлах первых и вторых соседей су-
J1 = ±2J2
(86)
ществуют фрустрации.
931
11*
А. В. Зарубин, Ф. А. Кассан-Оглы, А. И. Прошкин, А. Е. Шестаков
ЖЭТФ, том 155, вып. 5, 2019
S
0.7
S
0.7
4
3
2
0
T
1
–1
-3/4
-1/2
0
-1/4
0
1
2
3
4
J2
T
Рис. 22. Энтропия изинговской цепочки (73) с конкуриру-
Рис. 23. Энтропия изинговской цепочки (73) в случае
ющими обменными взаимодействиями между спинами на
конкурирующих обменных взаимодействий между спи-
узлах первых и вторых соседей (|J1| = 1, J2/|J1| < 0)
нами на узлах первых и вторых соседей вблизи точки
фрустрации системы, где значения параметров |J1| = 1,
J2/|J1| = {-2/5; -1/2; -3/5} соответствуют штриховой,
6.2. Термодинамика системы в режиме
сплошной и пунктирной линиям на графике
фрустрации
В системе с конкурирующими обменными взаи-
модействиями спинов на узлах первых и вторых со-
C
седей (88) и при соотношении обменных параметров
2/5
спинов цепочки (86), когда
J2/|J1| = -1/2,
(89)
нуль-температурная энтропия (10) не равна нулю:
(
)
√
1/5
J2
1
1+
5
lim
S
=-
= ln
,
(90)
T →0
|J1|
2
2
а равна натуральному логарифму золотого сечения.
Следовательно, система в данном состоянии фруст-
рирована.
Поведение энтропии в зависимости от парамет-
0
1
2
3
4
ров модели показано на рис. 22.
T
Данная ситуация аналогична предыдущему слу-
Рис. 24. Теплоемкость изинговской цепочки (74) в случае
чаю (63), когда в режиме фрустрации при нулевой
конкурирующих обменных взаимодействий между спина-
температуре статистический вес системы равен зо-
ми на узлах первых и вторых соседей вблизи точки фруст-
лотому сечению (64). Вне режима фрустрации ста-
рации системы (с обозначениями линий в соответствии с
тистический вес равен единице, а нуль-температур-
рис. 23)
ная энтропия — нулю (36). Также при любых со-
отношениях обменных параметров спинов цепочки
и бесконечно большой температуре энтропия равна
формируют режим так называемых геометрических
натуральному логарифму двух (37). На рис. 23 по-
фрустраций.
казана эволюция энтропии системы в окрестности
существования режима фрустрации.
Отметим, что выражения для энтропии системы
Следует обратить внимание на то, что в дан-
в режиме фрустрации при нулевой температуре для
ном случае именно пространственное расположение
произвольного спина в одномерной модели Изинга
атомных спинов и знаки параметров обменов меж-
с учетом обменных взаимодействий спинов на узлах
ду спинами на узлах первых и вторых соседей, при-
первых и вторых соседей получены в наших рабо-
водящие к конкуренции обменных взаимодействий,
тах [25, 36].
932
ЖЭТФ, том 155, вып. 5, 2019
Фрустрационные свойства одномерной модели Изинга
T
нению с предыдущими случаями и имеет макси-
мумы интенсивности для антиферро-антиферромаг-
нитного и ферро-антиферромагнитного вариантов
параметров обмена в положениях вектора рассеяния
1
(79), т. е.
qAA0 = q0, qFA0 = q0,
(91)
а положения минимумов данной функции определя-
ются уже соответствующими условиями для волно-
вого вектора (81):
qAA1 = q1, qAA2 = q2
(92)
0
и
-1
-1/2
0
qFA1 = q2, qFA2 = q1.
(93)
J2
Следовательно, амплитуда максимумов КФ (78)
Рис. 25. Положение пиков теплоемкости изинговской це-
в положениях (91) задается выражением (82), т. е.
почки (74) в случае конкурирующих обменных взаимодей-
ствий между спинами на узлах первых и вторых соседей
K(qAA0) = K(q0), K(qFA0) = K(q0),
(94)
(|J1| = 1, J2/|J1| < 0) вблизи точки фрустрации системы
а амплитуды минимумов в положениях (92) уже
определяются выражениями (83) и (84):
При нулевой и бесконечно большой температу-
рах и при любых соотношениях параметров обме-
K(qAA1) = K(q1), K(qAA2) = K(q2),
(95)
на спинов цепочки теплоемкость системы равна ну-
лю (38). В промежуточных же значениях по темпе-
K(qFA1) = K(q2), K(qFA2) = K(q1).
(96)
ратуре теплоемкость имеет пик, а вблизи фрустри-
Следует отметить, что в случаях антиферро-ан-
рованного положения данный пик расщепляется на
тиферромагнитного и ферро-антиферромагнитного
острый и куполообразный максимумы, как показа-
вариантов параметров обменных взаимодействий
но на рис. 24. При приближении к точке фрустрации
спинов на узлах первых и вторых соседей функ-
(89) максимумы теплоемкости расходятся, и в самой
ции магнитного диффузного рассеяния изинговской
точке фрустрации острый пик исчезает, а при уда-
цепочки (78) по форме одинаковы, но различаются
лении от данной точки пропадает уже куполообраз-
лишь тем, что соответствующие положения макси-
ный максимум. Поведение пиков теплоемкости про-
мумов и минимумов сдвинуты на половину периода,
демонстрировано на рис. 25.
т. е. на величину (π/a).
Следует заметить, что в режиме конкуренции об-
Таким образом, при слабом обменном взаимодей-
менных взаимодействий спинов в системе (88) пове-
ствии спинов цепочки на узлах вторых соседей,
дение энтропии (73) и теплоемкости (74) симметрич-
но относительно замены J1 ⇒ -J1, как показано на
-1/4 ≤ J2/|J1| < 0,
рис. 23 и 24.
Описанное выше расщепление пика на темпера-
поведение магнитного диффузного рассеяния КФ
турной эволюции магнитного вклада в теплоемкость
(78) (см. рис. 26) качественно не отличается от ранее
наблюдается в реальных антиферромагнетиках на
рассмотренного антиферромагнитного случая (см.
основе редкоземельных металлов [6, 30, 37-39]), а
рис. 5).
также соединений актиноидов [32].
При соотношении обменных параметров спинов
цепочки
J2/|J1| < -1/4
6.3. Поведение функции магнитного
температурная эволюция функции магнитного диф-
диффузного рассеяния
фузного рассеяния КФ (78) демонстрирует суще-
При конкурирующих обменных взаимодействи-
ствование максимумов в несоразмерных положени-
ях спинов на узлах первых и вторых соседей (88)
ях (91), как показано на рис. 27. В данном случае
функция магнитного диффузного рассеяния КФ
возникновение несоразмерных структур обусловле-
(78) обладает более сложной структурой по срав-
но конкуренцией обменных взаимодействий между
933
А. В. Зарубин, Ф. А. Кассан-Оглы, А. И. Прошкин, А. Е. Шестаков
ЖЭТФ, том 155, вып. 5, 2019
K(q)
10
aq
0
2
3 /2
5
4
3
4
2 T
/2
3
0
1
2
– /2
T
0
/2
0
3 /2
2
1
5 /2
aq
-1
–3/4
-1/2
-1/4
0
J2
Рис. 26. КФ изинговской цепочки (78) с антиферро-анти-
ферромагнитным вариантом параметров обменных взаи-
Рис. 28. Температурное поведение максимумов КФ изин-
модействий спинов цепочки (J1 = -1, J2/|J1| = -1/5)
говской цепочки (91) в зависимости от обменных пара-
K
метров с антиферро-антиферромагнитным вариантом па-
4
раметров обменных взаимодействий спинов цепочки (J1 =
= -1, J2/|J1| < 0)
1
K(q)
3
10
2
2
3
5
1
4
5
3
4
2 T
0
0
1
0
2
aq
– /2
0
/2
0
3 /2
2
5 /2
aq
Рис. 27. КФ изинговской цепочки (78) с антиферро-анти-
ферромагнитным вариантом параметров обменных взаи-
Рис. 29. КФ изинговской цепочки (78) с антиферро-анти-
модействий спинов цепочки (J1 = -1, J2/|J1| = -2/5)
ферромагнитным вариантом параметров обменных взаи-
при различных температурах (T = 1/3, 1/2, 1, 2, 8), ука-
модействий спинов цепочки (J1 = -1, J2/|J1| = -2/5)
занных в соответствии с нумерацией линий на графике
спинами на узлах первых и вторых соседей в рас-
Волновой вектор на интервале значений соотно-
сматриваемой одномерной спиновой системе.
шений обменных параметров спинов
Поведение волнового вектора несоразмерных пи-
ков (91) определяется двумя ветвями, где первая
-1/2 < J2/|J1| < -1/4
(98)
ветвь задается выражением (91), а вторая —
при понижении температуры демонстрирует точку
qAA0 = 2π/a - q0, qFA0 = 2π/a - q0.
(97)
смыкания несоразмерных пиков в положении, ниже
которого волновой вектор не зависит от температу-
Эволюция ветвей рассматриваемого вектора рассе-
ры, как показано на рис. 28 или 29. Такой эффект
яния показана на рис. 28.
носит название запирания волнового вектора, или
Здесь следует обратить внимание на то, что
lock-in-перехода.
функция (79), определяющая температурную эво-
Температурная эволюция точки lock-in-перехода
люцию волнового вектора для любых величин и зна-
(см. рис. 28) при конкурирующих обменных взаи-
ков параметров обменных взаимодействий спинов
модействиях спинов цепочки (88) имеет выражение
цепочки, имеет важное значение и позволяет ана-
лизировать как соразмерные, так и несоразмерные
T
Φ
структуры.
J2 = -
ln
,
(99)
4
4
934
ЖЭТФ, том 155, вып. 5, 2019
Фрустрационные свойства одномерной модели Изинга
J2
K(q )0
10
-1/4
lock-in
5
-1/2
0
1
2
3
4
T
0
1
2
3
4
T
Рис. 30. Температурная эволюция хода lock-in-перехода
(99) в случае конкурирующих обменных взаимодействий
Рис. 31. Температурное поведение амплитуды максимумов
между спинами на узлах первых и вторых соседей (88).
КФ изинговской цепочки (94) с антиферро-антиферро-
Предельные значения эволюции (100) отмечены на гра-
магнитным вариантом параметров обменных взаимодей-
фике пустой (T = 0) и сплошной (T = ∞) квадратными
ствий спинов цепочки вблизи точки фрустрации систе-
метками
мы (с обозначениями линий в соответствии с рис. 23).
Треугольной меткой указано положение lock-in-перехода,
√
√
а штрихпунктирная линия демонстрирует ход амплитуды
Φ = 3+ch(2K1)+sign(K1)
2sh K1
3+5 ch(2K1)
максимума КФ ниже lock-in-перехода
и продемонстрирована на рис. 30.
K(q )1
Предельные положения такой температурной
10
эволюции lock-in-перехода (99) соответственно рав-
ны
1
1
lim
J2(T) = -
,
lim
J2(T) = -
(100)
T →0
4
T →∞
2
и на рис. 30 отмечены квадратами.
5
Таким образом, lock-in-переход происходит при
значении обменных параметров спинов цепочки,
определяемых правилом (99), и величине волново-
го вектора
(
)
2π
1
2π
qAA0 =
+k
,
qFA0 =
k, k ∈ Z.
0
1
2
3
4
a
2
a
T
Заметим, что при соотношении параметров об-
Рис. 32. Температурное поведение амплитуды минимумов
менных взаимодействий спинов (98) и температу-
КФ изинговской цепочки (95) с антиферро-антиферромаг-
рах, меньших температур lock-in-перехода, функция
нитным вариантом параметров обменных взаимодействий
спинов цепочки вблизи точки фрустрации системы (с обо-
(79) выходит из области определения, т. е. ее аргу-
значениями линий в соответствии с рис. 23). Треугольной
мент (80) становится больше единицы,
меткой указано положение lock-in-перехода, а штрихпунк-
|X| > 1,
(101)
тирная линия демонстрирует ход амплитуды максимума
КФ ниже lock-in-перехода
а сама функция (79) становится комплексной ве-
личиной. Именно поэтому в определении перемен-
Указанная особенность в описании максимума
ной (79) стоит функция взятия вещественной части.
КФ показана на рис. 31 и 32, где первая линия раз-
В рассматриваемом интервале переменных макси-
делена на два участка треугольной меткой, кото-
мум КФ находится в положении q1 (81), и ампли-
рая указывает на положение lock-in-перехода (см.
туда этого максимума описывается уже функцией
рис. 30), что соответствует условию равенства еди-
K(qAA1) (83).
нице параметра (80) —
935
А. В. Зарубин, Ф. А. Кассан-Оглы, А. И. Прошкин, А. Е. Шестаков
ЖЭТФ, том 155, вып. 5, 2019
K(q)
K(q)
10
2
5
1
4
4
3
3
2
2 T
T
0
1
0
1
– /2
0
/2
0
– /2
0
/2
0
3 /2
2
3 /2
2
5 /2
5 /2
aq
aq
Рис. 33. КФ изинговской цепочки (78) с антиферро-анти-
Рис. 34. КФ изинговской цепочки (78) с антиферро-анти-
ферромагнитным вариантом параметров обменных взаи-
ферромагнитным вариантом параметров обменных взаи-
модействий спинов цепочки (J1 = -1, J2/|J1| = -1/2) в
модействий спинов цепочки (J1 = -1, J2/|J1| = -3/5)
режиме фрустраций
T
2 /3
4 /3
|X| = 1.
2
Первый участок линии, находящийся в интервале
температур, больших температуры lock-in-перехода,
и отмеченный штриховой линией, соответствует па-
раметрам модели, при которых условие (101) не
соблюдается. Второй участок, показанный штрих-
1
пунктирной линией, соответствует соблюдению это-
го условия (101).
Также следует отметить, что на рис. 31 и 32
штрихпунктирные линии совпадают, поскольку они
демонстрируют одно и тоже поведение амплитуды
максимумов КФ при температурах, меньших темпе-
0
/2
3 /2
2
ратуры lock-in-перехода.
aq0
При соотношении обменных параметров спинов
цепочки, равном
Рис. 35. Температурное поведение положений максимумов
КФ изинговской цепочки (91) с антиферро-антиферромаг-
J2/|J1| = -1/2,
(102)
нитным вариантом параметров обменных взаимодействий
спинов цепочки вблизи точки фрустрации системы (с обо-
система находится в состоянии фрустрации, при
значениями линий в соответствии с рис. 23)
этом lock-in-переход не происходит. Интенсивность
КФ (78) в режиме фрустрации показана на рис. 33.
В случае соотношения параметров обменных вза-
имодействий спинов
Далее рассмотрим эволюцию интенсивности
функции магнитного диффузного рассеяния КФ в
J2/|J1| < -1/2
режиме фрустрации и его окрестностях.
КФ ведет себя уже четвертым образом (см. рис. 34).
В данном контексте интересно остановиться на
Таким образом, поведение функции магнитного
поведении ветвей вектора магнитного диффузного
диффузного рассеяния КФ (78) в режиме фрустра-
рассеяния в предельных положениях, т. е. при нуле-
ции (102) и вне его имеет принципиально различный
вой и бесконечно большой температурах. Так, при
характер (см. рис. 29, 33 и 34). Данное различие вид-
антиферро-антиферромагнитном варианте парамет-
но из температурной эволюции положений максиму-
ров обменных взаимодействий между спинами на
мов КФ (рис. 35), а также амплитуды максимумов
узлах первых и вторых соседей (J1 < 0, J2 < 0) пер-
и минимумов (рис. 31, 32, 36) в точке фрустрации и
вая ветвь вектора (91) имеет соответствующие для
ее окрестностях.
каждой температуры значения
936
ЖЭТФ, том 155, вып. 5, 2019
Фрустрационные свойства одномерной модели Изинга
K(q )2
J2
2 /3
4 /3
0
1/2
-1/4
-1/2
1/4
-3/4
-1
0
1
2
3
4
0
/2
3 /2
2
T
aq0
Рис. 36. Температурное поведение амплитуды минимумов
Рис. 37. Поведение положений максимумов КФ изин-
КФ изинговской цепочки (95) с антиферро-антиферромаг-
говской цепочки (91) с антиферро-антиферромагнитным
нитным вариантом параметров обменных взаимодействий
вариантом параметров обменных взаимодействий спинов
спинов цепочки вблизи точки фрустрации системы (с обо-
цепочки при нулевой (103) (сплошная линия) и беско-
значениями линий в соответствии с рис. 23)
нечно большой (104) (пунктирная линия) температурах.
Значения волнового вектора рассеяния в положении точ-
ки фрустрации системы указаны на графике светлыми
(T = 0) (109) и темными (T → ∞) (107) точками, а волно-
lim
qAA0 =
T →0
вые векторы, соответствующие начальной и конечной точ-
⎧
1
J2
1
кам lock-in-перехода (100), обозначены квадратами (ср. с
⎪
+ k,
<-
,
⎪4
|J1|
2
рис. 30)
⎨
√
2π
1
1
5
J
2
1
=
-
arccos
,
=-
,
(103)
a ⎪2
2π
4
|J1|
2
⎪
и
⎪1
1
J2
⎩
+ k,
-
<
<0
2
2
|J1|
lim
qAA0 =
T →∞
⎧
1
J1
J2
1
и
⎪
arccos
,
<-
,
⎪
2π
4J2
|J1|
4
⎪
⎨
2π
2
J2
1
=
+ k,
=-
,
(106)
lim
qAA0 =
a ⎪3
|J1|
2
T →∞
⎪
⎧
⎪1
1
J2
1
J1
J2
1
⎪1-
arccos
,
<-
,
⎩
+ k,
-
≤
< 0,
⎪
2π
4J2
|J1|
4
2
4
|J1|
⎨
2π
1
J2
1
как показано на рис. 37.
=
+ k,
=-
,
(104)
a ⎪3
|J1|
2
Из представленных выражений (104) и (106) сле-
⎪
⎪
1
J2
⎩1
дует, что в режиме фрустрации (102) поведение вол-
+ k,
-
≤
< 0,
2
4
|J1|
нового вектора магнитного диффузного рассеяния
определяется предельными значениями при беско-
а вторая (97) —
нечно большой температуре,
(
)
J
2
1
lim
qAA0
=-
=
lim
qAA0 =
T →∞
|J1|
2
T →0
⎧
2π
⎪3
J2
1
=
(QAA∞ + k), k ∈ Z,
(107)
+ k,
<-
,
a
⎪4
|J1|
2
⎪
√
где величина
2π⎨1
1
5
J
2
1
1
1
=
+
arccos
,
=-
,
(105)
QAA∞ =
∓
(108)
a ⎪2
2π
4
|J1|
2
⎪
2
6
⎪
1
J2
⎩1
задает положения пиков в позициях 1/3 и 2/3 пери-
+ k,
-
<
<0
2
2
|J1|
ода для соответствующих ветвей.
937
А. В. Зарубин, Ф. А. Кассан-Оглы, А. И. Прошкин, А. Е. Шестаков
ЖЭТФ, том 155, вып. 5, 2019
T
а при нулевой температуре —
4
(
)
J2
1
lim
qFA
=-
=
0
T →0
|J1|
2
3
2π
(
)
=
QFA∞ ±
Q+k
,
k ∈ Z,
a
где волновой вектор не достигает значения QFA∞ пе-
2
¯ (110).
риода на величину
Амплитуда максимумов КФ (94) при конкури-
1
рующих обменных взаимодействиях спинов цепочки
(88) в точке фрустрации (102) и при нулевой темпе-
ратуре имеет конечное значение
0
(
)
J2
1
2 /3
65 /96
aq0*
67 /96
aq0
lim
K qAA0,
=-
=
T →0
|J1|
2
(
)
Рис. 38. Температурное поведение положений максимумов
J2
1
16
= lim
K qFA0,
=-
=
√ ≈ 2.385,
КФ изинговской цепочки (91) с антиферро-антиферромаг-
T →0
|J1|
2
3
5
нитным вариантом параметров обменных взаимодействий
а амплитуды минимумов (95) и (96) — соответствен-
спинов цепочки в точке фрустрации системы (J1 = -1,
но
J2/|J1| = -1/2), где q0 определено в виде (109). Круж-
(
)
ками указаны предельные положения волнового вектора
J2
1
lim
K qAA1,
=-
=
рассеяния в режиме фрустрации при нулевой температу-
T →0
|J1|
2
(
)
ре (светлый символ) и бесконечно большой температуре
J2
1
(темный символ)
= lim
K qFA1,
=-
=
T →0
|J1|
2
√
√
3
5+5
3
5-5
=
=
+ 1 ≈ 1.171
При нулевой температуре волновой вектор не до-
10
10
стигает указанных выше значений (107) и равен
и
(
)
(
)
J2
1
J2
1
lim
K qAA2,
=-
=
q∗0 = lim
0
qAA
=-
=
T →0
|J1|
2
T →0
|J1|
2
(
)
(
)
J
2
1
2π
= lim
K qFA2,
=-
=
=
QAA∞ ±
Q+k
,
k ∈ Z,
(109)
T →0
|J1|
2
a
√
√
3
5-5
3
5+5
где отклонение от величины (108) равно
=
=
- 1 ≈ 0.171.
(
√
)
10
10
1
5
Q=
Следует сказать, что при бесконечно большой
π - 3arccos
≈ 0.011.
(110)
6π
4
температуре функция магнитного диффузного рас-
сеяния КФ (78) размыта, а интенсивность максиму-
Такое поведение положений максимумов функции
мов
магнитного диффузного рассеяния КФ продемон-
стрировано на рис. 37 и отмечено кружками, а более
lim
K(qAA0) = 1, lim
K(qFA0) = 1
T →∞
T →∞
подробно показано на рис. 38.
и минимумов функции
В случае ферро-антиферромагнитного варианта
обменных взаимодействий спинов на узлах первых
lim
K(qAA1) = lim
K(qAA2) = 1,
T →∞
T →∞
и вторых соседей (J1 > 0, J2 < 0) положение векто-
ра магнитного диффузного рассеяния отличается от
lim
K(qFA1) = lim
K(qFA2) = 1
T →∞
T →∞
рассмотренного выше случая на величину в полови-
неразличимы между собой и равны единице.
ну периода (π/a). Таким образом, в режиме фруст-
При уменьшении температуры у функции маг-
рации первая ветвь вектора рассеяния (91) при бес-
нитного диффузного рассеяния КФ (78) формиру-
конечно большой температуре имеет выражение
(
)
ются пики в положениях (91), интенсивность кото-
J2
1
2π
(
)
lim
qFA
=-
=
QFA∞+k
,
k ∈ Z,
рых вне режима фрустраций при нулевой темпера-
0
T →∞
|J1|
2
a
туре достигает бесконечности,
1
QFA∞ = ∓
,
lim
K(qAA0) = ∞, lim
K(qFA0) = ∞,
6
T →0
T →0
938
ЖЭТФ, том 155, вып. 5, 2019
Фрустрационные свойства одномерной модели Изинга
а амплитуды минимумов (92) и (93) уменьшаются
а в работах [49,50] — уже в интервале
(
)
(
)
до нуля:
2π
1
2π
1
+k
<q0 ≤
+k
,
k ∈ Z,
lim
K(qAA1) = lim
K(qAA2) = 0,
a
6
a
4
T →0
T →0
что соответствует случаям антиферро-антиферро-
lim
K(qFA1) = lim
K(qFA2) = 0.
магнитного и ферро-антиферромагнитного вариан-
T →0
T →0
тов параметров обменных взаимодействий между
Такое поведение хода интенсивности КФ показано
спинами на узлах первых и вторых соседей.
на рис. 31, 32, 36.
В конце этого раздела следует сказать, что из-
Далее следует обратить внимание на то, что
менение волнового вектора (79) в несоразмерных
описанное выше характерное поведение максимумов
положениях происходит непрерывно с изменением
КФ в несоразмерных положениях можно встретить
температуры, как продемонстрировано на рис. 28.
на нейтронограммах реальных антиферромагнети-
Это отличается от результатов теории среднего поля
ков на основе соединений редкоземельных металлов,
и расчетов методом Монте-Карло в модели Изинга
в которых обнаруживается lock-in-переход. Напри-
[49-52], а также в модели ANNNI или модели Френ-
мер, в магнетиках на основе лантана [40,41], празео-
кель - Конторовой [53-58], в которых эволюция вол-
дима [42], европия [43, 44] или тербия [45] нейтро-
нового вектора рассеяния связана с существовани-
нографические спектры демонстрируют существо-
ем бесконечного каскада фазовых переходов, описы-
вание двух ветвей волнового вектора рассеяния в
ваемых фрактальными структурами, и названных
несоразмерных положениях на интервале
«дьявольской лестницей». Экспериментально явле-
(
)
(
)
2π
1
2π
2
ние таких каскадных переходов не было обнаруже-
+k
<q0 <
+k
,
k∈Z
a
3
a
3
но. Подробное обсуждение этой темы
— предмет
отдельного рассмотрения.
с объединением пиков при lock-in-переходе в поло-
жении
(
)
2π
1
q0 =
+k
,
k ∈ Z.
7. ФРУСТРАЦИИ НА ИЗИНГОВСКОЙ
a
2
ЦЕПОЧКЕ С УЧЕТОМ ВНЕШНЕГО
Такая температурная эволюция нейтронографичес-
МАГНИТНОГО ПОЛЯ ПРИ ОБМЕННОМ
ких рефлексов аналогична характеру поведения
ВЗАИМОДЕЙСТВИИ СПИНОВ НА УЗЛАХ
волнового вектора (91) в случае антиферро-анти-
ПЕРВЫХ И ВТОРЫХ СОСЕДЕЙ
ферромагнитного варианта обменных параметров,
При воздействии на спиновую цепочку внешнего
как показано на рис. 35 и 27.
магнитного поля и учете обменных взаимодействий
Для монопниктида плутония PuSb [46] и анти-
спинов на узлах первых и вторых соседей гамиль-
ферромагнетиков типа LiNiPO4 [47] несоразмерные
тониан модели Изинга имеет вид (1), а элементы
пики формируются в интервале
трансфер-матрицы Крамерса - Ваннье (5) определя-
(
)
(
)
2π
1
2π
1
ются следующим образом —
-
+k
<q0 <
+k
,
k∈Z
a
6
a
6
Vσσ′,σ′′σ
′′′
= 〈σσ′|eK1σσ′ +K2σ′σ′′+Bσ|σ′′σ′′′〉 =
с их объединением при lock-in-переходе в положении
+Bσδσ′σ′′ ,
=eK1σσ′+K2σ′′σ′′′
2π
q0 =
k, k ∈ Z,
где размерность самой матрицы равна d = 4, соглас-
a
но правилу (6).
как в случае ферро-антиферромагнитного варианта
В общем виде трансфер-матрица задается в фор-
обменных взаимодействий, между спинами на узлах
ме (70), а в явном виде может быть получена умно-
первых и вторых соседей (91).
жением слева матрицы (71) на диагональную поле-
Также в реальных антиферромагнетиках на ос-
вую матрицу
нове редкоземельных элементов можно видеть на
нейтронограммах формирование несоразмерных пи-
B = diag(eB,eB,e-B,e-B).
ков вне режима lock-in-перехода. Например, в анти-
Характеристическое уравнение такой тран-
мониде церия (CeSb) обнаружены пики в интервале
сфер-матрицы является полиномом четвертой
значений [48]
степени, а собственные значения ее выражаются
(
)
(
)
2π
1
2π
1
в радикалах и имеют в этом случае довольно
+k
≤q0 <
+k
,
k ∈ Z,
сложный вид.
a
4
a
3
939
А. В. Зарубин, Ф. А. Кассан-Оглы, А. И. Прошкин, А. Е. Шестаков
ЖЭТФ, том 155, вып. 5, 2019
H
7.1. Магнитная фазовая диаграмма
4
основного состояния системы
При различных параметрах данной модели в ос-
CF1
новном состоянии реализуются четыре набора воз-
можных спиновых конфигураций, обладающих ми-
3
нимальной энергией. Первый тип характеризует-
ся антиферромагнитным упорядочением неелевско-
CA3
го типа, что в интервале полей H ≤ -2(J1 - 2J2) и
H ≤ -2J1 соответствует набору CA2 (31) с энергией
2
EA2 = J1 - J2,
второй также характеризуется антиферромагнит-
1
ным упорядочением, но с утроением периода (обо-
значение конфигурации — A3),
C
CA2
A4
⎧
⎫
⎨
+1
+1
-1
+1
+1
-1
⎬
0
-2
-1
0
CA3 =
+1
-1
+1
+1
-1
+1
,
⎩
⎭
J2
-1
+1
+1
-1
+1
+1
Рис. 39. Магнитная фазовая диаграмма основного состо-
в интервале полей H ≥ -2(J1 - 2J2), H ≥ J1 - 2J2
яния изинговской цепочки с учетом внешнего магнитного
поля в области конкурирующих обменных взаимодействий:
и H ≤ -2(J1 +J2) и состоит из трех вариантов спи-
при антиферро-антиферромагнитном варианте парамет-
новых последовательностей с равными энергиями:
ров обменных взаимодействий спинов цепочки (J1 = -1,
J1 + J2 - H
J2/|J1| ≤ 0)
EA3 =
,
3
H
третий опять характеризуется антиферромагнит-
4
ным упорядочением с учетверением периода CA4
(85) и в интервале полей H
≤ J1 - 2J2 и H ≤
≤ -(J1 + 2J2) обладает энергией
3
EA4 = J2,
CF1
и последний четвертый характеризуется ферромаг-
нитным упорядочением CF1 (60) и в интервале по-
2
лей H ≥ -2J1, H ≥ -2(J1 + J2) и H ≥ -(J1 + 2J2)
имеет энергию
EF1 = -(J1 + J2 + H).
1
В данном случае видно, что учет внешнего маг-
нитного поля усложняет магнитную фазовую диа-
CA4
грамму, а энергия основного состояния (30) имеет
следующий вид:
0
⎧
-2
-1
0
⎪EA2, H ≤ -2(J1 - 2J2) ∧ H ≤ -2J1,
J2
⎪
⎪
⎪EA3, H ≥ -2(J1 - 2J2) ∧ H ≥ J1 - 2J2
⎨
Рис. 40. Магнитная фазовая диаграмма основного состо-
∧H ≤ -2(J1 + J2),
яния изинговской цепочки с учетом внешнего магнитно-
E0 =
⎪EA4, H ≤ J1 - 2J2 ∧ H ≤ -(J1 + 2J2),
го поля в области конкурирующих обменных взаимодей-
⎪
⎪
ствий: при ферро-антиферромагнитном варианте парамет-
⎪EF1, H ≥ -2J1 ∧ H ≥ -2(J1 + J2)
⎩
ров обменных взаимодействий спинов цепочки (J1 = +1,
∧H ≥ -(J1 + 2J2).
J2/|J1| ≤ 0)
940
ЖЭТФ, том 155, вып. 5, 2019
Фрустрационные свойства одномерной модели Изинга
Видно, что на магнитной фазовой диаграмме ос-
Именно в этих внешних магнитных полях
новного состояния модели (как и в предыдущем слу-
⎧
⎪HAA0, J1 < 0 ∧ J2 ≤ 0,
чае) существует четыре варианта отношений пара-
⎪
⎨
метров обменных взаимодействий между спинами
HAA1, J1 < 0 ∧ J2 ≤ 0 ∧ J2/J1 ≤ 1/2,
H =
на узлах первых и вторых соседей — (87) и (88) — и
⎪HAA2, J1 < 0 ∧ J2 ≤ 0 ∧ J2/J1 ≥ 1/2,
⎪
лишь только два последних (88) описывают систему
⎩HFA, J1 > 0 ∧ J2 ≤ 0 ∧ J2/J1 ≤ -1/2
с конкурирующими обменными взаимодействиями
спинов цепочки. Это случаи антиферро-антиферро-
происходит перестройка основного состояния и си-
магнитного (AA: J1 < 0 и J2 < 0) и ферро-антифер-
стема испытывает фрустрации.
ромагнитного (FA: J1 > 0 и J2 < 0) вариантов па-
раметров обмена спинов цепочки. Именно в этих об-
7.2. Нуль-температурные энтропия
ластях магнитной фазовой диаграммы системы (см.
и намагниченность системы во
рис. 39, 40) имеются фрустрации.
фрустрирующих внешних магнитных полях
В случае антиферро-антиферромагнитного ва-
рианта параметров обменных взаимодействий меж-
При антиферро-антиферромагнитном варианте
ду спинами на узлах первых и вторых соседей (J1 <
параметров обменных взаимодействий спинов на уз-
< 0 и J2 ≤ 0) существуют два фрустрирующих маг-
лах первых и вторых соседей (J1 < 0 и J2 ≤ 0) в мо-
нитных поля. Оба эти поля появляются в точке
дели Изинга во внешнем магнитном поле в основном
состоянии в полях, меньших нижнего фрустрирую-
J2/|J1| = 0, H/|J1| = 2,
(111)
щего магнитного поля,
что соответствует описанному выше случаю — (62).
0≤H <HAA1,
0≤H <HAA2,
После этого верхнее и нижнее магнитные поля рас-
ходятся, причем с уменьшением параметра J2/|J1|
нуль-температурные энтропия и намагниченность
верхнее магнитное поле растет по линейному зако-
равны нулю:
ну,
HAA0 = -2(J1 + J2),
(112)
lim
S = 0, lim M = 0.
T →0
T →0
а нижнее магнитное поле —
Во внешнем магнитном поле, равном первому ниж-
нему фрустрирующему полю HAA1 (113), энтропия
HAA1 = -2(J1 - 2J2),
0 < J2/J1 ≤ 1/2
(113)
и намагниченность при нулевой температуре соот-
— сначала падает до нуля при
ветственно равны
J2/|J1| = -1/2, H/|J1| = 0,
(114)
lim
S(HAA1) ≈ 0.281, lim
M (HAA1) ≈ 0.177,
T →0
T →0
после чего растет —
а в магнитном поле, равном уже второму нижнему
фрустрирующему полю HAA2 (115), имеем
HAA2 = J1 - 2J2, J2/J1 ≥ 1/2,
(115)
lim
S(HAA2) ≈ 0.199, lim
M (HAA2) ≈ 0.159.
T →0
T →0
как показано на рис. 39.
В случае ферро-антиферромагнитного варианта
В Приложении представлены полные точные анали-
параметров обменных взаимодействий между спи-
тические выражения для указанных энтропии и на-
нами на узлах первых и вторых соседей (J1 > 0
магниченности системы: (120) и (121), а также (122)
и J2 ≤ 0) существует всего одно фрустрирующее
и (123).
внешнее магнитное поле, которое возникает при
В интервалах между нижним и верхним фруст-
рирующими магнитными полями,
J2/|J1| = -1/2, H/|J1| = 0
(116)
HAA1 < H < HAA0, HAA2 < H < HAA0,
и далее с уменьшением параметра J2/|J1| растет по
закону
нуль-температурные энтропия и намагниченность
соответственно равны
HFA = -(J1 + 2J2), J2/J1 ≤ -1/2,
(117)
1
как можно видеть на рис. 40.
lim
S = 0, lim
M =
T →0
T →0
3
941
А. В. Зарубин, Ф. А. Кассан-Оглы, А. И. Прошкин, А. Е. Шестаков
ЖЭТФ, том 155, вып. 5, 2019
S
0.7
M
1
0
4
1
3
2
0
2 H
H
1
0
3
-1
-1
0
J2
-2
4
J
-2
2
Рис. 41. Нуль-температурная энтропия изинговской цепоч-
Рис. 42. Нуль-температурная намагниченность изингов-
ки во внешнем магнитном поле с антиферро-антиферро-
ской цепочки во внешнем магнитном поле с антиферро-
магнитным вариантом параметров обменных взаимодей-
антиферромагнитным вариантом параметров обменных
ствий спинов цепочки (J1 = -1, J2/|J1| < 0). Штрихо-
взаимодействий спинов цепочки (J1 = -1, J2/|J1| < 0).
выми линиями и метками отмечены значения энтропии во
Штриховыми линиями и метками отмечены значения на-
фрустрирующих магнитных полях
магниченности во фрустрирующих магнитных полях
Во внешнем магнитном поле, равном верхнему
В случае ферро-антиферромагнитного варианта
фрустрирующему полю HAA0 (112), энтропия и на-
параметров обменного взаимодействия между спи-
магниченность соответственно равны
нами на узлах первых и вторых соседей (J1 > 0 и
J2 ≤ 0) в модели Изинга во внешнем магнитном по-
lim
S(HAA0) ≈ 0.382, lim
M (HAA0) ≈ 0.611.
ле в основном состоянии в интервале полей от нуля
T →0
T →0
до фрустрирующего поля (0 ≤ H < HFA) нуль-тем-
В Приложении указаны точные значения для них,
пературные энтропия и намагниченность равны ну-
см. выражения (118) и (119).
лю —
Также следует отметить, что в точке (J2/|J1| =
lim
S = 0, lim M = 0
T →0
T →0
= -1/2, H/|J1| = 0) (114) нуль-температурная энт-
— а во внешнем магнитном поле, равном фрустри-
ропия соответствует выражению (90), а нуль-темпе-
рующему HFA (117), при нулевой температуре эн-
ратурная намагниченность равна нулю, т. е.
тропия и намагниченность конечны и равны соот-
√
ветственно
1+
5
lim
S = ln
≈ 0.481, lim M = 0.
T →0
2
T →0
lim
S(HFA) ≈ 0.322, lim
M (HFA) ≈ 0.397.
T →0
T →0
В точке (J2/|J1| = 0, H/|J1| = 2) (111) нуль-темпе-
В Приложении указаны точные выражения для
ратурная энтропия соответствует значению (63), а
этих величин, см. выражения (124) и (125).
нуль-температурная намагниченность больше нуля:
В точке (J2/|J1|
= -1/2, H/|J1|
= 0) (116)
√
1+
5
1
нуль-температурная энтропия соответствует выра-
lim
S = ln
,
lim
M =
√ ≈ 0.447.
T →0
T →0
жению (90), а намагниченность равна нулю,
2
5
√
В свою очередь, во внешних магнитных полях,
1+
5
lim
S = ln
,
lim M = 0.
больших верхнего поля фрустрации (H > HAA0),
T →0
2
T →0
нуль-температурная энтропия равна нулю, а
Во внешних магнитных полях, больших фрустриру-
нуль-температурная намагниченность — единице:
ющего (H > HFA),
lim
S = 0, lim M = 1.
lim
S = 0, lim M = 1.
T →0
T →0
T →0
T →0
Поведение энтропии и намагниченности системы
Таким образом, полевая зависимость нуль-тем-
при нулевой температуре показано на рис. 41 и 42.
пературной энтропии имеет ненулевые значения
942
ЖЭТФ, том 155, вып. 5, 2019
Фрустрационные свойства одномерной модели Изинга
только в положениях фрустрирующих магнитных
Определено, что важнейшим признаком сущест-
полей, а полевая эволюция нуль-температурной на-
вования магнитных фрустраций в системе являет-
магниченности в диапазоне значений от нуля до еди-
ся отличное от нуля значение нуль-температурной
ницы ступенчата, где количество ступенек опреде-
энтропии в этом режиме, и данное свойство не про-
ляется числом фрустрирующих полей.
тиворечит третьему началу термодинамики. Также
Подробный анализ термодинамических и маг-
следует отметить тот факт, что нуль-температурная
нитных характеристик системы, в том числе слож-
энтропия может иметь одну и ту же величину
ного поведения теплоемкости и функции магнитно-
для целых интервалов значений параметров моде-
го диффузного рассеяния вблизи точки фрустрации
ли. В качестве особого примера продемонстрирова-
системы, а также формирования несоразмерных пи-
но, что изинговский парамагнетик является абсо-
ков требует отдельного исследования.
лютно фрустрированной системой, так как его энт-
ропия также отлична от нуля и не зависит от тем-
пературы.
8. ЗАКЛЮЧЕНИЕ
Одной из общих особенностей фрустрированных
В работе методом трансфер-матрицы Крамер-
систем является обнаруженный эффект расщепле-
са - Ваннье получены точные аналитические выра-
ния пика на температурной эволюции магнитно-
жения для энтропии, теплоемкости, намагниченно-
го вклада теплоемкости в непосредственной окрест-
сти и магнитной восприимчивости одномерной моде-
ности режима фрустрации. Температурное поведе-
ли Изинга с учетом обменных взаимодействий меж-
ние намагниченности во внешнем магнитном поле
ду спинами на узлах ближайших и вторых за бли-
фрустрации и сколь угодно малом отклонении от
жайшими соседей во внешнем магнитном поле. Так-
него демонстрирует кардинально различные типы
же определено точное решение для КФ в исследуе-
поведения при приближении к абсолютному нулю
мой модели с учетом обменного взаимодействия спи-
температуры. Таким образом, в случае единствен-
нов на узлах ближайших соседей во внешнем маг-
ного фрустрационного магнитного поля нуль-темпе-
нитном поле, а также и с учетом обменных взаимо-
ратурная намагниченность равна нулю во внешних
действий спинов на узлах первых и вторых соседей
магнитных полях, меньших фрустрационного, а в
без внешнего магнитного поля.
магнитных полях больших — равна единице, при
Построена магнитная фазовая диаграмма моде-
этом в магнитном поле, равном фрустрационному,
ли, а также проведен анализ конфигурационных
нуль-температурная намагниченность имеет проме-
особенностей основного состояния и фрустрацион-
жуточное значение. Магнитная восприимчивость во
ных свойств системы. Сформулированы критерии
внешнем магнитном поле фрустрации имеет острый
и определены соотношения параметров модели, при
пик, который при нулевой температуре стремится
которых возникают магнитные фрустрации в рас-
к бесконечности, а сама функция превращается в
сматриваемых одномерных спиновых системах. Вы-
дельта-функцию.
яснено, что фрустрации обусловлены конкуренци-
При исследовании фрустрационных свойств сис-
ей как между энергиями обменных взаимодействий
темы наиболее показательно характерное поведение
спинов (так называемые геометрические фрустра-
функции магнитного диффузного рассеяния КФ в
ции), так и между ними и энергией внешнего маг-
режиме фрустрации и его окрестности при стремле-
нитного поля. Таким образом, показано, что в ре-
нии температуры к абсолютному нулю. В этом слу-
жиме фрустрации система испытывает перестройку
чае в точке фрустрации функция магнитного диф-
магнитной структуры основного состояния, которое
фузного рассеяния плавно распределена по обрат-
начинает в себя включать сопоставимое с размером
ному пространству и имеет конечное значение, а
системы множество спиновых конфигураций, в том
при сколь угодно малом отклонении от положения
числе и с отсутствием трансляционной инвариант-
фрустрации она принимает форму дельта-функции
ности.
либо теряет интенсивность до нуля (во внешнем маг-
Проанализировано характерное поведение энт-
нитном поле, большем фрустрирующего). Важно от-
ропии, теплоемкости, намагниченности, магнитной
метить, что указанные особенности поведения маг-
восприимчивости и функции магнитного диффузно-
нитного диффузного рассеяния являются основным
го рассеяния КФ системы в режиме фрустрации и
экспериментально наблюдаемым показателем суще-
вблизи него, показано кардинальное отличие в по-
ствования фрустрированных состояний в магнетике.
ведении магнитной системы во фрустрационной об-
В качестве еще одного нетривиального резуль-
ласти и вне нее.
тата работы можно выделить то, что внешнее маг-
943
А. В. Зарубин, Ф. А. Кассан-Оглы, А. И. Прошкин, А. Е. Шестаков
ЖЭТФ, том 155, вып. 5, 2019
нитное поле порождает перекачку магнитного диф-
сти при нулевой температуре в случае конкурирую-
фузного рассеяния КФ (54), ширина пиков которого
щих обменных взаимодействий между спинами на
сильно зависит от температуры, строго в положения
узлах первых и вторых соседей (88) для изинговской
ядерных брэгговских рефлексов, определяемых ис-
спиновой цепочки во внешнем магнитном поле.
ходной кристаллической решеткой.
Таким образом, в случае антиферро-антиферро-
Также в случае конкуренции обменных взаимо-
магнитного варианта параметров обменных взаимо-
действий между спинами на узлах первых и вто-
действий спинов на узлах первых и вторых соседей
рых соседей в работе получено точное аналитиче-
(J1 < 0, J2 < 0) во фрустрирующем магнитном поле
ское выражение температурной зависимости вол-
HAA0 (112) нуль-температурные энтропия и намаг-
нового вектора магнитного диффузного рассеяния
ниченность соответственно равны
(79) для всего интервала значений параметров об-
)]
[1(
1
менных взаимодействий, что позволяет описывать
lim
S(HAA0) = ln
1+ϑ0+
≈ 0.382,
(118)
T →0
3
ϑ0
поведение как соразмерных, так и несоразмерных
структур, в том числе и lock-in-переход. Кроме то-
√√
(33 + 22)33 + 33 + 2
го, при интерпретации экспериментальных нейтро-
ϑ0 =3
,
2
нограмм эта функция дает возможность определять
величины и знаки обменных взаимодействий спинов
(
)
из поведения волнового вектора.
1
22
1
lim
M (HAA0) =
1+ν0 +
≈
Как показывает сравнение температурной эво-
T →0
3
33 + 22 ν0
люции волнового вектора в экспериментах по маг-
≈ 0.611,
(119)
нитному упругому рассеянию нейтронов на реаль-
(
)2/3
ных кристаллах с проведенными расчетами в од-
2
3
√√
ν0 =
(33 + 22)33 + (33 + 22).
номерной модели, полученные в работе результаты
33 + 22
позволяют целенаправленно проводить эксперимен-
Во фрустрирующем магнитном поле HAA1 (113) —
тальные исследования реальных магнитных объек-
)]
тов с фрустрациями при использовании КФ в каче-
[1(
3
lim
S(HAA1) = ln
ϑ1 +
≈ 0.281,
(120)
стве прототипной.
T →0
3
ϑ1
Таким образом, предложенная схема анализа
√√
позволяет рассмотреть широкий круг явлений в
(33 - 22)33 + 33
ϑ1 =3
,
одномерных (или квазиодномерных) магнитных
2
системах с фрустрациями и описать их связь
(
)
со спектральными особенностями упругого маг-
1
22
1
lim
M (HAA1) =
1+ν1 -
≈
нитного рассеяния неполяризованных нейтронов.
T →0
3
33 - 22 ν1
Развитый в работе математический аппарат дает
≈ 0.177,
(121)
возможность решать подобные задачи в более
(
)2/3
сложных моделях статистической физики, в част-
√√
2
3
ности, в многокомпонентных спиновых моделях с
ν1 =
(33 - 22)33 - (33 - 22),
33 - 22
дискретной симметрией и произвольным значением
а также во фрустрирующем магнитном поле HAA2
спина.
(115) —
[
√
]
Финансирование. Работа выполнена в рам-
1
1
ках государственного задания Федерального агент-
lim
S(HAA2) = ln ζ2 +
- (2ζ2)2
≈
T →0
2
ζ2
ства научных организаций России (тема «Квант»,
№01201463332) и при частичной финансовой под-
≈ 0.199,
(122)
держке Уральского отделения Российской академии
√
наук (проект № 18-2-2-11).
1
ϑ2
4
ζ2 =
-
,
2
3
ϑ2
ПРИЛОЖЕНИЕ
√√
(33 + 28)33 + 33
В качестве приложения приведем точные анали-
ϑ2 =3
,
2
тические выражения для энтропии и намагниченно-
944
ЖЭТФ, том 155, вып. 5, 2019
Фрустрационные свойства одномерной модели Изинга
lim
M (HAA2) =
6.
Frustrated Spin Systems, ed. by H. T. Diep, 2nd
T →0
√
edition, World Scientific, New Jersey (2013).
2
3
2
1
= -η2+
-η22 +
≈ 0.159,
(123)
7.
G. Toulouse, Commun. Phys. 2, 115 (1977).
33 + 28
33 + 28 η2
8.
J. Vannimenus and G. Toulouse, J. Phys. C: Sol. St.
√
8
Phys. 10, L537 (1977).
3
1 ν2
2
1
η2 =
+
-
,
33 + 28
22 3
(33 + 28)2 ν2
9.
Р. Бэкстер, Точно решаемые модели в статисти-
ческой механике, Мир, Москва (1985).
3
√√
2
3
ν2 = 22/3
(33 + 28)33 + 33.
33 + 28
10.
E. Ising, Z. Phys. 31, 253 (1925).
В случае ферро-антиферромагнитного варианта
11.
S. G. Brush, Rev. Mod. Phys. 39, 883 (1967).
параметров обменных взаимодействий спинов на уз-
12.
M. Niss, Arch. Hist. Exact Sci. 59, 267 (2005).
лах первых и вторых соседей (J1
> 0, J2
< 0)
во фрустрирующем магнитном поле HFA
(117)
13.
F. A. Kassan-Ogly, Phase Transitions 74, 353 (2001).
нуль-температурные энтропия и намагниченность
14.
Ф. А. Кассан-Оглы, Е. В. Кормильцев, В. Е. Найш,
системы равны
И. В. Сагарадзе, ФТТ 31, 43 (1989).
lim
S(HFA) =
15.
A. V. Zarubin, F. A. Kassan-Ogly, and A. I. Proshkin,
T →0
[
]
Mater. Sci. Forum 845, 122 (2016).
1
1
√ 1 1
3
= ln ζ3+
+
-(2ζ3)2+
≈ 0.322,
(124)
4
2
23 ζ3
4
16.
H. A. Kramers and G. H. Wannier, Phys. Rev. 60,
252 (1941).
√
1
ϑ3
4
1
ζ3 =
-
+
,
17.
R. A. Horn and C. R. Johnson, Matrix Analysis, 2nd
2
3
ϑ3
4
edition, Cambridge Univ. Press, Cambridge (2013).
√√
3
(33 + 28)33 - 3
18.
G. Mussardo, Statistical Field Theory: An Introduc-
ϑ3 =3
,
2
tion to Exactly Solved Models in Statistical Physics,
Oxford Univ. Press, Oxford, New York (2010).
lim
M (HFA) =
19.
W. Nolting and A. Ramakanth, Quantum Theory of
T →0
√
Magnetism, Springer, Berlin, Heidelberg (2009).
2
3
2
1
=η3+
-η23 +
≈ 0.397,
(125)
20.
A. Guinier and R. Griffoul, Acta Crystallogr. 1, 188
33 + 28
33 + 28 η3
(1948).
√
8
21.
А. Гинье, Рентгенография кристаллов. Теория и
3
1 ν3
2
1
η3 =
+
-
,
практика, Физматгиз, Москва (1961).
33 + 28
22 3
(33 + 28)2 ν3
22.
А. Зоммерфельд, Термодинамика и статистичес-
3
√√
2
3
кая физика, Изд-во иностр. лит., Москва (1955).
ν3 = 22/3
(33 + 28)33 + 33.
33 + 28
23.
W. Nolting, Theoretical Physics 8: Statistical Physics,
Springer, Cham (2018).
ЛИТЕРАТУРА
24.
A. V. Zarubin, F. A. Kassan-Ogly, M. V. Medvedev,
1. Ф. А. Кассан-Оглы, Б. Н. Филиппов, Изв. РАН,
and A. I. Proshkin, Sol. St. Phenom. 233-234, 212
сер. физ. 74, 1513 (2010).
(2015).
2. B. Normand, Contemp. Phys. 50, 533 (2009).
25.
A. Proshkin, F. Kassan-Ogly, A. Zarubin, T. Pono-
mareva, and I. Menshikh, EPJ Web Conf. 185, 03004
3. L. Balents, Nature 464, 199 (2010).
(2018).
4. Introduction to Frustrated Magnetism: Materials,
26.
J. G. Sereni, in Handbook on the Physics and Che-
Experiments, Theory, ed. by C. Lacroix, P. Mendels,
mistry of Rare Earths. 15, Elsevier (1991), Ch. 98,
and F. Mila, Springer, Berlin, Heidelberg (2011).
p. 1-59.
5. J.-F. Sadoc and R. Mosseri, Geometrical Frustration,
27.
T. Matsumura, H. Shida, and T. Suzuki, Physica B
Cambridge Univ. Press, New York (1999).
230-232, 738 (1997).
945
12
ЖЭТФ, вып. 5
А. В. Зарубин, Ф. А. Кассан-Оглы, А. И. Прошкин, А. Е. Шестаков
ЖЭТФ, том 155, вып. 5, 2019
28.
H. Tsujii, C. R. Rotundu, Y. Takano, B. Andraka,
44.
T. Chattopadhyay, P. J. Brown, and H. G. von Schne-
Y. Aoki, H. Sugawara, and H. Sato, J. Magn. Magn.
ring, EuroPhys. Lett. 6, 89 (1988).
Mater. 272-276, 173 (2004).
45.
F. Pfuner, S. N. Gvasaliya, O. Zaharko, L. Keller,
29.
Y. Sato, H. Morodomi, Y. Inagaki, T. Kawae, and
J. Mesot, V. Pomjakushin, J.-H. Chu, I. R. Fisher,
H. S. Suzuki, J. Phys.: Conf. Ser. 568, 042027 (2014).
and L. Degiorgi, J. Phys.: Condens. Matter 24,
036001 (2012).
30.
M. A. Avila, S. L. Bud’ko, and P. C. Canfield, J.
Magn. Magn. Mater. 270, 51 (2004).
46.
P. Burlet, S. Quezel, J. Rossat-Mignod, J. C. Spirlet,
J. Rebizant, W. Müller, and O. Vogt, Phys. Rev.
31.
Y. Kobayashi, T. Onimaru, M. A. Avila, K. Sasai,
B 30, 6660 (1984).
M. Soda, K. Hirota, and T. Takabatake, J. Phys. Soc.
Jpn. 77, 124701 (2008).
47.
D. Vaknin, J. L. Zarestky, J.-P. Rivera, and
32.
P. Santini, R. Lémanski, and P. Erdös, Adv. Phys.
H. Schmid, Phys. Rev. Lett. 92, 207201 (2004).
48, 537 (1999).
48.
J. von Boehm and P. Bak, Phys. Rev. Lett. 42, 122
33.
J. Stephenson, Can. J. Phys. 48, 1724 (1970).
(1979).
34.
J. F. Dobson, J. Math. Phys. 10, 40 (1969).
49.
P. Bak and J. von Boehm, Phys. Rev. B 21, 5297
(1980).
35.
T. Oguchi, J. Phys. Soc. Jpn. 20, 2236 (1965).
36.
A. I. Proshkin and F. A. Kassan-Ogly, Mater. Sci.
50.
P. Bak, Rep. Progr. Phys. 45, 587 (1982).
Forum 845, 93 (2016).
51.
W. Selke and M. E. Fisher, Phys. Rev. B 20, 257
37.
H. Wada, H. Imai, and M. Shiga, J. Alloys Comp.
(1979).
218, 73 (1995).
52.
E. B. Rasmussen and S. J. Knak Jensen, Phys. Rev.
38.
V. Goruganti, K. D. D. Rathnayaka, J. H. Ross,
B 24, 2744 (1981).
Y.
Öner, C. S. Lue, and Y. K. Kuo, J. Appl. Phys.
103, 073919 (2008).
53.
M. E. Fisher and W. Selke, Phys. Rev. Lett. 44, 1502
(1980).
39.
O. Pavlosiuk, D. Kaczorowski, X. Fabreges, A. Guka-
sov, and P. Wisniewski, Sci. Rep. 6, 18797 (2016).
54.
W. Selke and P. M. Duxbury, Z. Phys. B 57, 49
(1984).
40.
S. Wakimoto, S. Lee, P. M. Gehring, R. J. Birgeneau,
and G. Shirane, J. Phys. Soc. Jpn. 73, 3413 (2004).
55.
W. Selke, Phys. Rep. 170, 213 (1988).
41.
S. Wakimoto, H. Kimura, M. Fujita, K. Yamada,
56.
W. Selke, in Phase Transitions and Critical Pheno-
Y. Noda, G. Shirane, G. Gu, H. Kim, and R. J. Bir-
mena, ed. by C. Domb and J. L. Lebowitz, Acad.
geneau, J. Phys. Soc. Jpn. 75, 074714 (2006).
Press, London (1992), Ch. 1, p. 1.
42.
R. Kajimoto, H. Yoshizawa, Y. Tomioka, and Y. To-
kura, Phys. Rev. B 63, 212407 (2001).
57.
S. Aubry, J. Phys. C: Sol. St. Phys. 16, 2497 (1983).
43.
T. Chattopadhyay, P. J. Brown, P. Thalmeier, and
58.
S. Aubry, K. Fesser, and A. R. Bishop, Ferroelectrics
H. G. von Schnering, Phys. Rev. Lett. 57, 372 (1986).
66, 151 (1986).
946