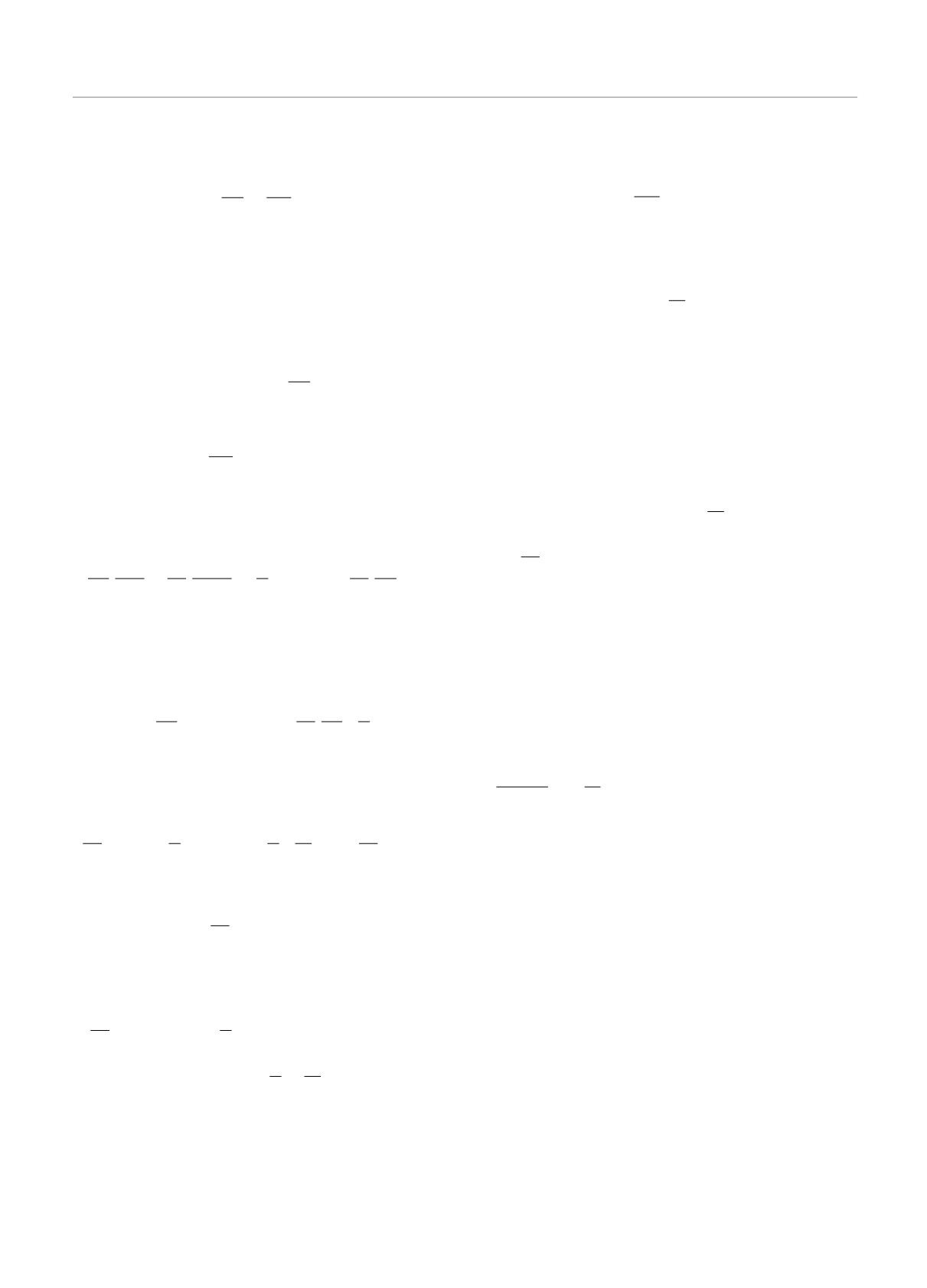ЖЭТФ, 2019, том 156, вып. 1 (7), стр. 105-117

О ВЛИЯНИИ НЕИЗОТЕРМИЧНОСТИ НА РАННИЕ СТАДИИ

СПИНОДАЛЬНОГО РАСПАДА

В. Г. Лебедевa,b*, П. К. Галенкоc,d**

^a Институт математики, информационных технологий и физики,

Удмуртский государственный университет

426034, Ижевск, Россия

^b Научный центр МФМ УдмФИЦ Уральского отделения Российской академии наук

426067, Ижевск, Россия

^c Friedrich-Schiller-Universität Jena, Physikalisch-Astronomische Fakultät

D-07743, Jena, Germany

^d Лаборатория многомасштабного математического моделирования,

Уральский федеральный университет

620002, Екатеринбург, Россия

Поступила в редакцию 27 сентября 2018 г.,

после переработки 7 января 2019 г.

Принята к публикации 10 января 2019 г.

Предложена неизотермическая модель спинодального распада для бинарной системы, описываемой энер-

гией Гинзбурга - Ландау. Для совместной системы уравнений, описывающих перераспределение примеси

и температуры, исследованы начальные стадии спинодального распада. Получено дисперсионное урав-

нение и показатель роста неустойчивости спинодальных структур. Найдены температурные зависимости

показателя роста и волнового числа, соответствующего максимуму неустойчивости. Обнаруженное раз-

личие в дисперсионном соотношении изотермической и неизотермической моделей показывает, что кри-

терием влияния температурных флуктуаций на спинодальный распад является значение безразмерного

параметра Γ, при больших значениях которого Γ ≥ 1000 учет флуктуаций температуры в виде шума

будет заведомо недостаточным из-за изменения дисперсионной структуры уравнений, указывающей на

необходимость учета неизотермического поведения системы.

DOI: 10.1134/S0044451019070113

тальные данные не всегда согласуются с линейным

поведением дисперсионного соотношения в модели

Кана - Хилльярда [5,6]. Было замечено [10], что ли-

1. ВВЕДЕНИЕ

нейное поведение дисперсионного соотношения на

ранних стадиях спинодального распада характерно

Процессы самопроизвольного разделения кон-

для систем с дальнодействием, в то время как для

денсированных сред на области с разными соста-

систем с короткодействием существенны нелиней-

вами примеси, называемые спинодальным распа-

ные эффекты [13, 14]. Понимание физической при-

дом, широко известны еще с 1950-х гг. Спинодаль-

роды ранних стадий спинодального распада явля-

ный распад наблюдался во многих экспериментах

ется основной проблемой в теории данного явления

на полимерных смесях [1], жидких растворах [2,3]

на сегодняшний день. На поздних стадиях спино-

и металлических системах [4]. Феноменологическое

дального распада, когда уже произошло разделение

описание явления в изотермических условиях было

растворов на области с различными концентрация-

предложено Каном и Хилльярдом [5, 6], теоретиче-

ми, начиная с работы [15], в основном исследуется

ски развито и экспериментально протестировано в

проблема описания сценариев коалесценции и воз-

работах [7-10]. Оказалось [11, 12], что эксперимен-

можного кроссовера между ними. Поскольку приро-

да явлений на начальных и конечных стадиях спи-

^* E-mail: lvg@udsu.ru

^** E-mail: Peter.Galenko@uni-jena.de

нодального распада существенно различается, далее

105

В. Г. Лебедев, П. К. Галенко

ЖЭТФ, том 156, вып. 1 (7), 2019

)

ограничимся исследованием только начальных ста-

∂x

⁽δF

=M_D∇²

+ ξ(r, t),

(1)

дий.

∂t

δx

К причинам нелинейности на ранних стадиях мо-

где ∇ — оператор градиента, x(r, t) — локальное от-

гут быть отнесены локальная неравновесность про-

клонение от среднего значения концентрации при-

цесса спинодального распада [16-21], броуновское

месного компонента в бинарном растворе, M_D — по-

движение [22], а также неизотермичность процес-

ложительный транспортный коэффициент (мобиль-

са в растворах. Большинство выполненных теоре-

ность), связанный с коэффициентом диффузии при-

тических работ по спинодальному распаду исполь-

месного компонента, ξ(r, t) — тепловой шум, F —

зует так называемое изотермическое приближение.

полная свободная энергия системы:

Это приближение в рамках сплошной среды обыч-

∫ (

)

но подразумевает, что температура системы может

F = f(x) +

ε²(∇x)²

dV₀,

(2)

меняться со временем, но в любой момент она оста-

ется однородной по пространству. В рамках данной

dV₀ — элемент пространственного объема, занято-

работы, говоря о «неизотермичности» спинодально-

го раствором. Коэффициент ε², пропорциональный

го распада, будем далее полагать, что распределе-

квадрату корреляционной длины для флуктуаций

ние температуры является неоднородным и меняет-

концентрации в растворе [5], и плотность свободной

ся как по пространству, так и во времени.

энергии f(x) определяются равновесными свойства-

Ранее температурные флуктуации были введе-

ми бинарной системы. Выражение ε²(∇x)² в теории

ны в процесс спинодального распада в работах [7,8].

Кана - Хилльярда описывает вклад энергии грани-

В работе [23] неизотермичность при фазовом разде-

цы между областями с различными концентрация-

лении была учтена в связи с тепловым расширени-

ми. Если f(x) имеет единственный минимум, то

ем и влиянием упругих напряжений на спинодаль-

уравнение (1) приводит к уравнению диффузии с

ный распад в твердых растворах. Более современ-

характерным дисперсионным соотношением [9]

ные подходы к построению неизотермической моде-

ω = -k²(D₀ + M_Dε²k²)

ли спинодального распада предлагались в работах

[24, 25]. Однако в этих работах полностью отсут-

между частотой ω и волновым числом k, где

ствует качественное исследование динамики пред-

вклад градиентного слагаемого предполагается

ложенных моделей. Поэтому на данный момент яв-

малым по сравнению с коэффициентом диффузии

ляется актуальным понимание характера и степе-

D₀ ≡ M_D(∂²f(x)/∂x²):

ни влияния неизотермичности на спинодальный рас-

M_Dε²k² ≪ D₀.

пад. Численное исследование спинодального распа-

да на основе модели Кана - Хилльярда при нали-

Разделение на области с разными концентрация-

чии как температурной зависимости термодинами-

ми по механизму спинодального распада происхо-

ческого потенциала, так и случайного теплового шу-

дит, если f(x) имеет два минимума. Тогда в области

ма, выполнено в работе [26], в которой показано

между минимумами коэффициент диффузии отри-

влияние неизотермичности на положение экстрему-

цателен (D₀ < 0) и в дисперсионном соотношении

мов корреляционной функции. В настоящей работе

ω = k²(|D₀| - M_Dε²k²) слагаемое с k⁴ ограничивает

предложено самосогласованное термодинамическое

рост коротковолновых возмущений, что указывает

описание неизотермического спинодального распа-

на стабилизирующую роль вклада ε²(∇x)² в выра-

да на основе подхода [27] и выполнено полуаналити-

жении (2).

ческое исследование начальных стадий распада для

Уравнение CHC (1) рассматривается в LBM-под-

модельной бинарной системы (раствора) с энергией

ходе [8] как набор уравнений Ланжевена с независи-

Гинзбурга - Ландау, зависящей от температуры.

мым случайным источником ξ(r, t) в каждой точке

пространства. Поскольку набор уравнений Ланже-

вена эквивалентен уравнению Фоккера - Планка для

распределения вероятности [28], в работе [8] были

2. МОДЕЛЬ ЛАНГЕРА - БАРОНА - МИЛЛЕРА

(LBM-МОДЕЛЬ)

сделаны определенные предположения относитель-

но структуры данного распределения вероятностей,

Модель Лангера - Барона - Миллера (LBM-мо-

что позволило получить уравнение движения для

дель) описывает спинодальный распад в началь-

структурного фактора S(k, t), являющегося фурье-

ный период времени и начинается с уравнения Ка-

преобразованием одновременной парной корреляци-

на - Хилльярда - Кука (CHC) [5-7]

онной функции 〈x(r₁, t)x(r₂, t)〉 по разности r₁ - r₂.

106

ЖЭТФ, том 156, вып. 1 (7), 2019

О влиянии неизотермичности на ранние стадии.. .

Эволюция структурного фактора сопоставлялась с

обработке эксперимента, но для прямого моделиро-

экспериментами по рассеянию света в бинарных

вания предлагает два варианта:

жидкостях [29]. Из-за того, что система переводи-

1) моделировать уравнение CHC (1) с шумом и

лась в нестабильное состояние с помощью снятия

усреднять результат по конкретным реализациям;

давления, LBM-модель хорошо описывает получен-

2) моделировать уравнение Фоккера - Планка и

ные структурные факторы, если учесть адиабатич-

далее находить корреляционные функции (в том

ность процесса [30]. Исключение составляют началь-

числе и структурный фактор) по найденной функ-

ные моменты времени, когда теоретическая кривая

ции распределения.

запаздывает по сравнению с экспериментальными

На практике оба подхода 1) и 2) обычно не ис-

данными. Несколько позже теория LBM была коли-

пользуются, поскольку уравнение СНС моделирует-

чественно подтверждена с помощью рассеяния рент-

ся либо совсем без теплового шума [35-38], либо с

геновских лучей на ранних стадиях спинодального

тепловым шумом [39-41], но без усреднений по воз-

распада твердого раствора Al0.62Zn0.38 в работе [31].

можным реализациям.

Однако до сих пор нет окончательного ответа на во-

прос, в чем причина расхождения теоретических и

Причин такой разницы в подходах много, но в

экспериментальных данных по структурному фак-

целом можно констатировать, что парадигмы ком-

тору в начальные моменты времени, найденные в

пьютерного моделирования и теоретического опи-

работе [30].

сания спинодального распада существенно отлича-

В качестве причин наблюдаемых различий меж-

ются друг от друга. Естественно возникает вопрос

ду теоретическими и экспериментальными данными

о том, как максимально сблизить их между собой.

В этом смысле исследование влияния неизотермич-

по структурному фактору рассматривалась локаль-

ная неравновесность процесса спинодального рас-

ности на спинодальный распад также очень акту-

ально: взаимодействие температуры и концентра-

пада [16-21] в начальные моменты времени, обу-

словленная релаксацией потоков. Феноменологиче-

ции должно менять дисперсионную структуру урав-

нений, приводя к единой модели вместо «двуликого

ски динамика потоков зависит от времени их ре-

лаксации, изменение величины которого приводит к

Януса». Поэтому кратко рассмотрим вывод неизо-

термической модели спинодального распада и про-

характерному поведению показателя роста неустой-

чивых мод [19, 20]. Полное количественное описа-

анализируем дисперсионное соотношение модели в

ние экспериментальных данных [10-12] может быть

сравнении с уравнением Кана - Хилльярда.

получено лишь в результате сравнительного анали-

за эффектов локальной неравновесности, неизотер-

мичности и броуновского движения. Вопрос о вли-

4. МОДИФИКАЦИЯ МОДЕЛИ

янии неизотермичности процесса на спинодальный

КАНА - ХИЛЛЬЯРДА

распад обсуждается в данной работе на примере

простой термодинамической модели. Влияние бро-

уновского движения требует отдельного рассмотре-

Для упрощенного вывода модели Кана - Хил-

ния.

льярда в условиях неизотермичности пренебрежем

локально неравновесными эффектами, учитываю-

щими релаксацию потоков [16-21]. Это означает,

что неоднородные изменения температуры рассмат-

3. КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ

риваются на интервалах времени, превышающих

характерные времена установления диффузионных

После формулировки LBM-модели [8], ее анализа

и сравнения ее решений с экспериментальными дан-

потоков.

ными [29,30] процесс спинодального распада интен-

Рассмотрим простейшую систему, описывающую

сивно изучался методами математического модели-

спинодальный распад и одновременно позволяю-

рования [21] с учетом расширения термодинамиче-

щую учесть неизотермичность процесса. Потенциал

ского описания [18,32] и с приложением полученных

Гиббса полной системы в силу аддитивности должен

результатов в материаловедении [33,34]. В этой свя-

складываться из объемного потенциала и энергии

зи нужно отметить, что формально LBM-модель иг-

границы между областями с разными значениями

норирует динамику параметра порядка и непосред-

концентрации x(r, t). Поле температур обозначим

ственно напрямую описывает динамику структур-

как T (r, t). Задачу будем считать изобарической, по-

ного фактора, что создает удобство ее анализа при

лагая давление равным нулю. В качестве управля-

107

В. Г. Лебедев, П. К. Галенко

ЖЭТФ, том 156, вып. 1 (7), 2019

ющего функционала неизотермической, изобариче-

выделяя полные квадраты в (10), находим выраже-

ской системы выберем энтропию системы

ния для потоков:

∫ (

)

∂G

M_T

S =-

(∇x)²

dV₀,

(3)

JT = -

∇T = -λ∇T,

(11)

∂T

2T₀

T²

где λ — коэффициент температуропроводности рас-

где G = G(T, x) — плотность потенциала Гиббса,

T₀ — температура начального состояния раствора.

твора, и

Пренебрегая изменением объема и внутренними

(

)

T₀

напряжениями в процессе спинодального распада и

J_D = -M_D∇

μ-ε²∇²x

(12)

выражая плотность энтальпии H(x, T ) через плот-

ность потенциала Гиббса G(x, T ),

Величины M_T > 0, M_D > 0 — положительные мо-

бильности потоков.

∂G

H =G-T

(4)

В итоге находим, что динамика спинодального

∂T

распада, учитывающая непрерывное изменение тем-

запишем закон сохранения энтальпии:

пературы, управляется связанной системой уравне-

∂H

ний, включающих в себя уравнение Кана - Хилльяр-

= -∇ · J_T ,

(5)

∂t

да, модифицированное эффективным химическим

потенциалом

где J_T — тепловой поток. Исходя из выражения (4) и

T₀

вычисляя частные производные сложной функции,

μ_eff (T, x) = μ

(13)

представим уравнение (5) как

∂x

[

(

)]

(

)

=∇·

M_D∇

μ_eff (T, x) - ε²∇²x

(14)

∂T ∂²G

∂x

∂²G

∂x ∂G

∂t

∇·J_T +

(6)

∂t ∂T2

∂t ∂T∂x

∂t ∂x

и уравнение теплопроводности (7) с потоком (11).

Поскольку теплоемкость при постоянном давлении

равна C_p = -T (∂²G/∂T²), определяя химический

5. ТЕРМОДИНАМИЧЕСКИЙ ПОТЕНЦИАЛ

потенциал как μ = (∂G/∂x), перейдем от соотноше-

ния (6) к уравнению теплопроводности:

Для качественного изучения влияния неизотер-

мичности на спинодальный распад выберем объем-

∂T

∂x

∂ (μ⁾

C_p

= -∇ · J_T + T²

(7)

ную плотность энергии Гиббса в виде модельного

∂t

∂t ∂T T

потенциала Гинзбурга - Ландау [43]

С другой стороны, дифференцирование энтропии

(

)

(3) по времени может быть приведено с помощью

G(T, x)

-1

(x - x_c)² + B₀(x - x_c)⁴.

(15)

соотношения (6) к выражению

g₀

T_c

∫ [

(

ε²

⁾∂x^]

В качестве параметров потенциала Гиббса исполь-

∇·J_T+

∇²x

dV₀. (8)

T₀

∂t

зуем g₀ = 1.88 · 10⁴ Дж/см³, B₀ = 0.45, x_c = 0.5,

= 1400 K, выбранные из соображений наглядно-

T_c

Используя закон сохранения примеси

сти. Соответствующая поверхность энергии Гиббса

представлена на рис. 1. В силу симметрии потенци-

∂x

= -∇ · J_D,

(9)

ала по концентрации бинодаль и спинодаль модель-

∂t

ной системы определяются условиями (∂G/∂x)_T

где J_D — диффузионный поток, выражение (8) мож-

и (∂²G/∂x²)_T = (∂μ/∂x)_T = 0. Графики бинодали и

но записать в виде

спинодали представлены на рис. 2.

∫ [

⁽1⁾

= J_T ·∇

6. НАЧАЛЬНЫЕ СТАДИИ

(

)]

НЕИЗОТЕРМИЧЕСКОГО

- J_D ·∇

∇²x dV₀.

(10)

T₀

СПИНОДАЛЬНОГО РАСПАДА

Из условия неотрицательности изменения энтропии

Рассмотрим идеализированную ситуацию, когда

в процессах релаксации (dS/dT ≥ 0), пользуясь име-

раствор со средней концентрацией x и температу-

ющимся произволом в определении потоков [42] и

рой T₀ очень быстро (мгновенно) охлаждается до

108

ЖЭТФ, том 156, вып. 1 (7), 2019

О влиянии неизотермичности на ранние стадии.. .

G/g₀

Вводя коэффициент температуропроводности a,

a = κ/C_p, и коэффициент диффузии D₀,

500

∂μ

D₀ = M_Dμ_x, где μ_x ≡

(16)

∂x

-500

перепишем уравнения (7) и (14) в виде

-1000

∂x

= -|D₀|

∇²x+

-1500

∂t



 (

)

D0

)

∂

⁽μ



-2000

∇²T - ε²∇⁴x

_μ

 T

⁰∂T T

(17)

-2500

∂T

T² ∂x

∂ (μ⁾

= a∇²T +

∂t

C_p ∂t ∂T T

Здесь предполагается, что начальная концентрация

0.25

1250

0.50

1000

x и (мгновенная) температура T(r,t) соответствуют

x, ат. доли

0.75

750

500

области спинодали для потенциала Гиббса G(T, x),

1.00

T, K

т. е. при заданном x температура T находится ниже

Рис. 1. Зависимость энергии Гинзбурга - Ландау (15) от

критической:

температуры T и концентрации примеси x

T < T_c[1 - 6B₀(x - x_c)²].

T, K

7. ФУРЬЕ-АНАЛИЗ

1400

Рассмотрим одномерную задачу эволюции на-

чальных стадий спинодального распада в неогра-

1200

ниченной области с пространственной координатой

z. Отклонения концентрации и температуры от их

1000

средних значений в любой момент времени могут

быть записаны через фурье-компоненты (x_k, T_k) как

800

(

)

(

)

∑

x-x

x_k

eωt+ikz,

(18)

T -

T_k

600

где величина ω является частотой фурье-гармоники

400

с волновым числом k.

0.2

0.4

0.6

0.8

1.0

Подстановка фурье-разложения (18) в уравнения

Концентрация x, мольные доли

(17) приводит к следующему дисперсионному соот-

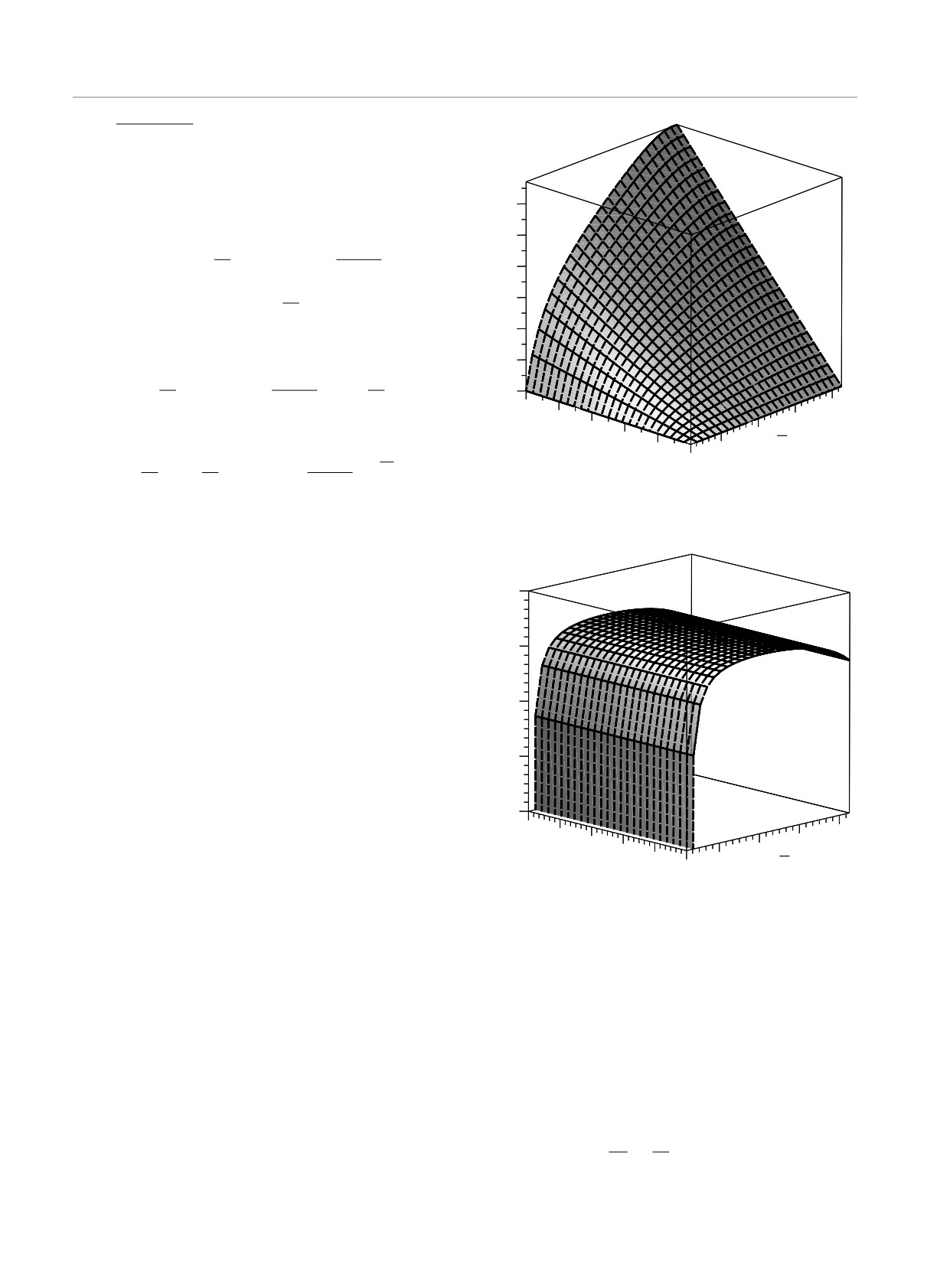
Рис.

2. Бинодаль (пунктирная кривая) и спинодаль

ношению:

(сплошная кривая) потенциала Гинзбурга - Ландау (15)

[

(

)]

T₀

T ε

(ω + ak2) ω -

|D₀|k2

k²

T₀ |μ_x|

|D₀|

T²T₀

+μ

ωk² = 0,

(19)

|μ_x| C_p

температуры

T, которая далее поддерживается по-

стоянной на границах образца. Будем также пола-

где

)

∂ (μ



гать, что в начальный момент флуктуации началь-

μ=



∂T T

ного состава и начального распределения темпера-

туры настолько малы, что можно пренебречь про-

После замены

странственными производными теплоемкости C_p,

|μ_x|

T₀

теплопроводности λ, коэффициента диффузии D₀,

k² = q²

ε²

(20)

а также производными от химического потенциала

|μ_x|

T₀

∂μ/∂x и ∂(μ/T )/∂T .

ω = Ω|D₀|

ε²

109

В. Г. Лебедев, П. К. Галенко

ЖЭТФ, том 156, вып. 1 (7), 2019

√

где

|μ_x|T₀/ε²T, |D0μx|T0/ε2T¯ — характерные мас-

штабы волнового числа и частоты, а также исполь-

/q²

зуя обозначение τ = |D₀|/a, нетрудно привести дис-

персионное соотношение (19) к квадратному урав-

1.2

нению

(

)

1.0

T₀

T²T₀

τΩ² + Ωq²

1-τ

(1 - q²) + τ μ²

C_p|μ_x|

0.8

T₀

0.6

(1 - q²) q⁴ = 0.

(21)

0.4

Теперь, вычисляя дискриминант уравнения (21)

0.2

[

]₂

T₀

T²T₀

T₀

D = 1-τ

(1 - q²)+τ μ²

+4τ

(1-q²),

C_p|μ_x|

400

0.2

600

находим корни квадратного уравнения:

0.4

800

0.6

T, K

[

]

0.8

1000

√

q²

T₀

T²T₀

1.0

Ω^±q = -

1-τ

(1-q²)+τ μ²

D . (22)

2τ

C_p|μ_x|

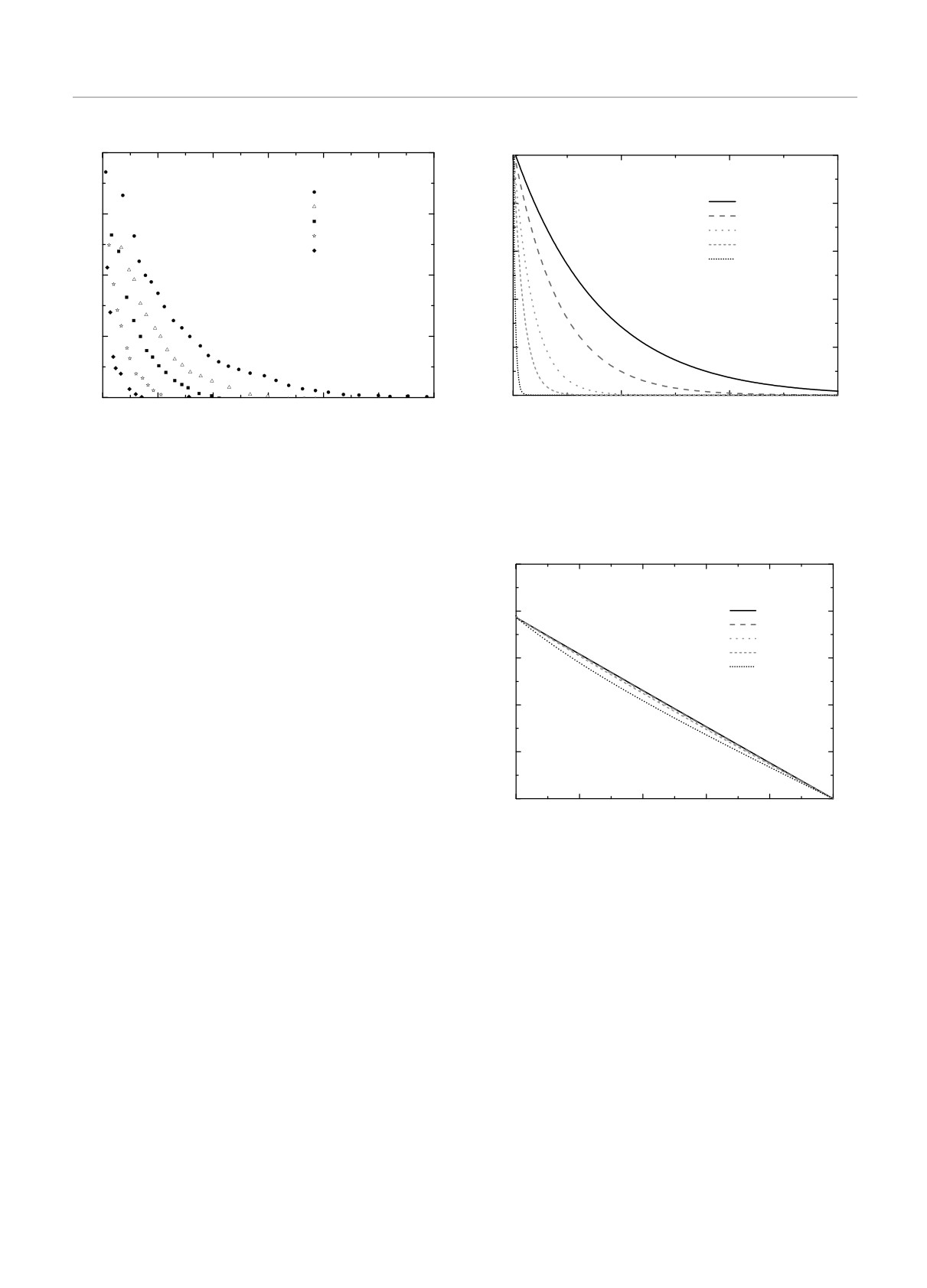
Рис. 3. Зависимость Ω⁺q /q² от квадрата волнового числа

q² и средней температуры

Соответствующие зависимости Ω^±q/q² от темпера-

туры и волнового числа представлены на рис. 3 и

4 при следующих значениях параметров: началь-

–

ная концентрация раствора x = 0.25, начальная

температура раствора T₀ = 1410 K, параметр ε =

= 6.2 · 10-8 (Дж/см)1/2, коэффициент диффузии

|D₀| = 5.5 · 10-5 см²/c, коэффициент температуро-

-100

проводности a = 2.2·10-3 см²/c и теплоемкость C_p =

= 0.5 Дж/(см³·K). На рис. 3 и 4 видно, что растущие

решения соответствуют только Ω+q, в то время как

-200

Ω^-q всегда отрицательна и определяет затухающие

гармоники.

На рис. 3 также видно, что Ω+q/q² изменяется ли-

-300

нейно от q² при каждой фиксированной температу-

ре, что воспроизводит зависимость Ω(q)/q² для мо-

-400

дели Кана - Хилльярда в изотермической ситуации.

400

Поэтому, казалось бы, такая ситуация тоже долж-

0.2

0.4

600

на противоречить экспериментальным данным [10].

0.6

800

0.8

1000

T, K

q²

1.0

Однако похожесть этих двух зависимостей не долж-

на вводить в заблуждение. Полное решение неизо-

Рис. 4. Зависимость Ω-q/q² от квадрата волнового числа

термической модели, в отличие от модели Кана -

q² и средней температуры

Хилльярда, определяется суперпозицией двух неза-

висимых решений, соответствующих как Ω+q, так и

Ω^-q (см. рис. 4). Поэтому динамика роста началь-

ти (a→∞), после деления уравнения (17) на коэф-

ных возмущений в неизотермической модели может

фициент a остается единственное физически разум-

принципиально отличаться от таковой в модели Ка-

ное решение на бесконечном интервале в виде

T =

на - Хилльярда.

= const. Соответственно, при a → ∞ получим τ → 0.

Нетрудно видеть, что модель Кана - Хилльяр-

В пределе τ → 0 дисперсионное уравнение (21) с

да появляется при представленной дисперсии (22)

точностью до температурного множителя сводится

только в двух предельных ситуациях. Действитель-

к линейному (по q²) закону дисперсии Кана - Хил-

но, при конечных значениях температуропроводнос-

льярда:

ти параметр τ будет малой, но конечной величи-

Ω_q

T₀

(1 - q²).

(23)

ной. В случае очень высокой температуропроводнос-

q²

110

ЖЭТФ, том 156, вып. 1 (7), 2019

О влиянии неизотермичности на ранние стадии.. .

Более интересная ситуация связана с тем, что

дисперсию Кана - Хилльярда можно получить, рас-

смотрев вклад в дисперсионное уравнение (22) от

слагаемого, пропорционального

T²/C_p. Появление

такого безразмерного множителя отнюдь не случай-

но, поскольку, следуя [44], нетрудно показать, что

в изобарическом случае

T²/C_p является дисперсией

флуктуаций температуры в каноническом ансамбле

(см. Приложение), откуда

τT₀

Γ≡

μ² ∝ 〈(ΔT)²〉.

C_p |μ_x|

Предел Γ → 0 соответствует пределу малости флук-

туаций температуры, так что в результате исходное

400

600

800

1000

T, K

дисперсионное соотношение (19) сводится к произ-

ведению множителей

Рис. 5. Зависимость безразмерного параметра Γ от сред-

[

(

)]

ней температуры

T для потенциала Гинзбурга - Ландау

T₀

T ε²

(ω + ak²) ω -

|D₀|k2

k²

= 0,

при x = 0.25

T₀ |μ_x|

которые определяют дисперсию двух независи-

терием необходимости учета температурных флук-

мых уравнений (теплопроводности и уравнения

туаций в системе. В частности, для бинарных си-

Кана - Хилльярда). Появляющееся в пределе Γ →

стем критерий Γ может быть рассчитан на основе

→ 0 уравнение Кана-Хилльярда содержит лишь

открытой термодинамической базы данных NIMS

среднюю температуру, переопределяющую коэф-

[45]. Для рассмотренного в данной работе потенци-

фициент диффузии, в то время как флуктуации

ала Гинзбурга - Ландау зависимость Γ от средней

температуры никак не влияют на спинодальный

температуры

T при заданной концентрации x = 0.25

распад.

представлена на рис. 5. При температурах, близких

Наоборот, при условии Γ ≫ 1 вкладом тепло-

к границе спинодали, Γ → ∞ из-за определения гра-

вых флуктуаций пренебречь нельзя, поскольку име-

ницы как

ем сильно связанную систему уравнений, где тепло-

вой шум должен играть важную роль. Появление

∂²G

∂μ

T² τT₀

тепловых флуктуаций 〈ΔT²〉 в дисперсионном соот-

≡

≡μ_x =0

⇒ Γ=

μ² → ∞.

∂x²

∂x

C_p |μ_x|

ношении (22) можно интерпретировать как резуль-

тат усреднения динамики спинодального распада по

При уменьшении температуры

T, после некоторо-

случайным внешним силам. Физически возникнове-

го плато на графике параметр Γ снова начинает

ние случайных сил происходит за счет локально-

монотонно увеличиваться. Из рис. 5 можно сде-

го изменения концентрации примеси, обусловлива-

лать вывод, что особенно сильно влияние флуктуа-

ющей флуктуирующий источник в уравнении теп-

ций температуры должно проявляться при пересе-

лопроводности (17), нормированный на дисперсию

чении границ спинодали и (значительно слабее) при

флуктуаций температуры. Обычно τ ≪ 1, поэтому

достаточно низких температурах. Поскольку в ре-

процессы распространения тепла происходят гораз-

альности процесс охлаждения не является мгновен-

до быстрее диффузионных, приводя к появлению

ным, флуктуации температуры должны проявлять-

быстро меняющихся тепловых потоков, играющих,

ся именно на начальных стадиях спинодального рас-

в соответствии с идей Кука [7], роль случайных сил

пада, оставаясь несущественными на больших вре-

в уравнении для концентрации.

менах.

Таким образом, учет случайных флуктуаций, ко-

Отличие в поведении изотермической и неизо-

торый сделан в модели LBM [8] для согласования с

термической моделей Кана - Хилльярда можно уви-

экспериментальными данными, в рамках неизотер-

деть уже из анализа максимально неустойчивой фу-

мической модели спинодального распада появляет-

рье-моды. Поверхность производной dΩ+q/dq² из ре-

ся естественным образом. Более того, проведенный

шения (22) представлена на рис. 6. Решая уравнение

фурье-анализ показывает, что значения безразмер-

dΩ+q/dq² = 0, находим, что волновое число, соот-

ного параметра Γ могут служить некоторым кри-

ветствующее максимуму неустойчивости, меняется

111

В. Г. Лебедев, П. К. Галенко

ЖЭТФ, том 156, вып. 1 (7), 2019

наковы для всех фурье-компонент: xq0)

= const.

d +/dq2

Ненормированные собственные векторы, соответ-

ствующие Ω_±, выберем в виде

1.0

⎛

⎞

⎜

⎟

0.5

⎜

T²

⎟

v^±q =

⎜

(

)

⎟,

(24)

⎝

q²

⎠

C_p

τΩ^q

а общее решение для фурье-гармоники q будет

-0.5

иметь вид

(

)

-1.0

=A_qv+qeωqt^′+iqz′ +B_qv^-qeωqt^′+iqz′,

(25)

0.2

400

0.4

600

где t^′, z^′ — безразмерные время и координата, свя-

0.6

800

0.8

1000

T, K

занные с t, z изменением масштаба (20). Поскольку

q²

1.0

exp(ω⁺t) входит в обе переменные (T, x), неустой-

Рис. 6. Зависимость производной dΩ+q/dq² от средней тем-

чивость, определяющая спинодальный распад, бу-

пературы

T и квадрата волнового числа q²

дет проявляться также в локальном увеличении

температурного поля, обусловленном источником

(∝ ∂x/∂t) в уравнении теплопроводности (17). Ис-

q2max

пользуя начальные условия, для коэффициентов A_q,

0.500

B_q имеем следующую систему уравнений:

A_q + B_q = x(0)q,

(26)

0.499

A_q

B_q

= 0.

1 + q²/τΩ+q

1 + q²/τΩ

Вычисляя фурье-амплитуды из системы (26) и опре-

0.498

деляя структурный фактор как S_q(t) = N-1q|x_q(t)|²,

нетрудно рассчитать эволюцию структурного фак-

тора со временем. Нормировочный коэффициент

выбран равным N_q

= |x_q(0)|². Соответствующие

0.497

400

600

800

1000

графики при различных температурах представле-

T, K

ны на рис. 8-10. Из приведенных графиков хорошо

видно, что скорость формирования периодической

Рис. 7. Зависимость квадрата волнового числа q2max от

спинодальной структуры существенно увеличивает-

средней температуры

ся при понижении температуры.

Отметим, что на рис. 8-10 структурный фактор

представлен для достаточно больших безразмерных

(хотя и довольно медленно при выбранных парамет-

времен, которые фактически соответствуют позд-

рах модели) при изменении средней температуры, в

ним стадиям развития спинодального распада. Хо-

отличие от постоянного максимума изотермической

тя средняя температура на таких временах прак-

модели Кана - Хилльярда. Соответствующая зави-

тически не меняется в силу выбранных граничных

симость представлена на рис. 7.

условий, однако распределение примеси становит-

ся крайне неоднородным, о чем говорит сам струк-

турный фактор. В силу линеаризации задачи для

8. СТРУКТУРНЫЙ ФАКТОР

фурье-анализа, его решения можно полагать спра-

НЕИЗОТЕРМИЧЕСКОЙ МОДЕЛИ

ведливыми до времен t₀ ≈ 1/Ω+q, на больших вре-

Для простоты будем считать, что в началь-

менах t > t₀ требуется уже численное исследова-

ный момент флуктуации температуры отсутствуют

ние полной нелинейной задачи (17). Поэтому графи-

= 0, а флуктуации состава по величине оди-

ки (рис. 8-10) здесь представлены для наглядности,

112

ЖЭТФ, том 156, вып. 1 (7), 2019

О влиянии неизотермичности на ранние стадии.. .

S_q

3.0

2.5

T = 1100 K

T = 700 K

t = 0

t = 1

t = 0

2.0

t = 3

t = 1

t = 6

t = 3

t = 6

1.5

1.0

0.5

1.0

1.5

2.0

0.5

1.0

1.5

2.0

q²

Рис. 10. Зависимости структурного фактора Sq от квад-

Рис. 8. Зависимости структурного фактора Sq от квадра-

рата волнового числа q² в разные моменты времени t при

та волнового числа q² в разные моменты времени t при

температуре

T = 700 K

температуре

T = 1100 K

9. ПОКАЗАТЕЛЬ РОСТА

S_q

Важной характеристикой спинодального распа-

да, измеряемой в экспериментах, является показа-

тель роста R(q², t), точнее R(q², t)/q², определяемый

как

T = 900 K

dS_q

t = 0

R(q², t) =

(27)

S_q dt

t = 1

t = 3

Показатель роста для уравнения Кана - Хилльярда

t = 6

легко определяется из закона дисперсии

R(q², t)q-2 = 2(1 - q²).

(28)

Он линеен по q² и не зависит от времени. Ре-

альный график R(q², t)/q² представлен на рис. 11.

Зависимость R(q)q-2 от q² для твердого раство-

0.5

1.0

1.5

2.0

ра Al-12.1 ат. % Zn при температуре

= 293 K

q²

[46, 47] демонстрирует сильную нелинейность и за-

висимость от времени. Поскольку различие между

Рис. 9. Зависимости структурного фактора Sq от квадра-

зависимостью (28) и зависимостями на рис. 11 соб-

та волнового числа q² в разные моменты времени t при

температуре

T = 900 K

ственно и составляет основное противоречие меж-

ду теорией и экспериментом, рассмотрим показа-

тель роста в рамках неизотермической модели. Для

сравнения приведем графики показателя роста на

рис. 12 и 13. Обоим рисункам соответствуют одни

чтобы показать зависимость процесса спинодально-

и те же параметры модели, за исключением пара-

го распада от средней температуры

T. Можно ожи-

метра Γ, принимающем значения Γ₁ = 66.44 · 10² на

дать, что нелинейность задачи внесет некоторые из-

рис. 12 и Γ₂ = 66.44 на рис. 13. Параметр Γ₁ выбран

менения в вид структурного фактора на поздних

из соображений «схожести» с рис. 11, в то время

стадиях, но их качественная зависимость от q² изме-

как на рис. 13 Γ₂ = 0.01Γ₁, чтобы продемонстри-

нится достаточно слабо, поскольку «червеобразная»

ровать влияние величины Γ на показатель роста. В

структура распределения примеси к моменту време-

частности, рис. 12 показывает, что модель неизотер-

ни t₀ будет близка к стационарному состоянию.

мического спинодального распада качественно спо-

113

ЖЭТФ, вып. 1 (7)

В. Г. Лебедев, П. К. Галенко

ЖЭТФ, том 156, вып. 1 (7), 2019

-2

.100,

-1

R(q )q

нм

R(q )q^2-2

2.0

t = 5 мин

t= 0.0001

t = 9 мин

1.5

t= 0.0002

t = 15 мин

t= 0.0005

t = 33 мин

t= 0.001

t = 65 мин

t= 0.005

1.0

0.5

1.0

1.5

2.0

2.5

3.0

0.2

0.4

0.6

-2

q², нм

q²

Рис. 11. Типичные экспериментальные зависимости пока-

Рис.

12. Теоретические зависимости показателя роста

зателя роста R(q)q-2 от q² для Al-12.1 ат. % Zn в разные

R(q)q-2 от q² в разные моменты времени при средней тем-

моменты времени при средней температуре

T = 293 K

пературе

T = 300 K и Γ = 66.44 · 10²

[46, 47]

R(q )q^2-2

1.0

собна описать экспериментальные данные для ре-

альных систем. Количественного сравнения неизо-

0.8

t= 0.0001

термической модели с результатами работы [46, 47]

t= 0.0002

не проводилось из-за отсутствия в открытой печати

t= 0.0005

детальной информации об эксперименте и теплофи-

t= 0.001

0.6

t= 0.005

зических данных материалов. Также отметим, что

графики на рис. 12 соответствуют малым временам

0.4

безразмерного времени, когда линейное приближе-

ние (и соответствующее разложение в ряд Фурье) в

неизотермической модели является вполне обосно-

0.2

ванным.

0.2

0.4

0.6

0.8

1.0

10. ЗАКЛЮЧЕНИЕ И ВЫВОДЫ

q²

В работе, исходя из принципа возрастания энтро-

Рис.

13. Теоретические зависимости показателя роста

пии, получено неизотермическое обобщение модели

R(q)q-2 от q² в разные моменты времени при средней тем-

Кана - Хилльярда спинодального распада, которое

пературе

T = 300 K и Γ = 66.44

основано на совместной динамике концентрационно-

го поля x(r, t) и поля температур T (r, t).

Анализ ранних стадий спинодального распада

ми Γ ∝ 〈ΔT²〉. Только в случае достаточно большой

показывает, что влияние неизотермичности на ди-

температуропроводности (по отношению к коэффи-

намику примеси не сводится только к учету слу-

циенту диффузии) или малого параметра Γ, как это

чайных сил, как это рассматривалось в более ран-

видно из сравнения рис. 12 и рис. 13, зависимость

них работах [7, 8]. Природа взаимодействия темпе-

R(q²)q-2 становится близкой к линейной. Более то-

ратурных изменений и спинодального распада ока-

го, параметр Γ можно рассматривать как некоторый

зывается гораздо сложнее, чем это представлялось

критерий, говорящий о необходимости учета неизо-

в указанных работах, и проявляется в нелинейном

термичности. Поскольку в реальном процессе любая

изменении дисперсионного соотношения, определя-

система при переохлаждении проходит через грани-

емом параметром τ = |D₀|/a и безразмерной вели-

цы лабильности, в такие моменты Γ всегда будет

чиной Γ, связанной с температурными флуктуация-

принимать большие значения, следовательно, клас-

114

ЖЭТФ, том 156, вып. 1 (7), 2019

О влиянии неизотермичности на ранние стадии.. .

сическое уравнение Кана - Хилльярда может быть

Удмуртской Республики в рамках научного проекта

использовано для описания и моделирования спино-

№18-42-180002, а также при частичной поддержке

дального распада без учета температурных флукту-

по проекту Российского фонда фундаментальных

аций лишь в каких-то идеальных ситуациях.

исследований № 18-02-00643 и German Space Center

Даже без учета различий в дисперсионном по-

Space Management (contract № 50WM1541).

ведении предложенной неизотермической модели

по сравнению с LBM- или CHC-подходами, с чи-

ПРИЛОЖЕНИЕ

сто вычислительной точки зрения данная неизотер-

Вероятность флуктуаций в каноническом

мическая модель обладает существенным преиму-

ансамбле

ществом при компьютерном моделировании спино-

Вероятность флуктуации в каноническом ан-

дального распада. Это определяется тем, что про-

самбле определяется соотношением (112,3) из [44]:

цесс совместного решения уравнений спинодально-

⁽ ΔP ΔV - ΔT ΔS⁾

го распада (14) с уравнением теплопроводности (7)

ω ∝ exp

и (11) позволяет решать задачу моделирования как

полностью детерминированную, не требуя усредне-

Из этой общей формулы можно найти флуктуации

ния результатов по случайному источнику, что необ-

различных термодинамических величин. В учебни-

ходимо в LBM- или CHC-моделях.

ке [44] в качестве переменных выбраны V и T, по-

В данной работе исследовано влияние неизотер-

скольку это независимые случайные переменные.

мичности на динамику спинодального распада толь-

Мы выберем в качестве переменных P и T . Тогда

ко с точки зрения температурных изменений в рас-

творе. Однако существуют и другие факторы, вли-

⁽∂S⁾

⁽∂S)ΔP=

ΔS =

ΔT +

яющие на спинодальный распад: броуновское дви-

∂T_P

∂P_T

жение капель с разной концентрацией [22], с их по-

C_p

⁽∂V)ΔP,

следующим слипанием; появление метастабильных

ΔT -

∂T_P

зародышей новой фазы при переохлаждении рас-

твора, конкурирующих с процессом спинодального

⁽∂V⁾

⁽∂V)ΔP.

ΔV =

ΔT +

распада; появление внутренних напряжений (в твер-

∂T_P

∂P_T

дых растворах) и прочие сопутствующие явления.

Вероятность флуктуации определяется выражением

Поскольку влияние таких факторов на сегодняш-

ний день изучено довольно слабо, остается актуаль-

ΔP ΔV - ΔT ΔS =

ным как развитие экспериментальных методов ис-

]

^[(∂V⁾

⁽∂V⁾

следования спинодального распада, так и расшире-

ΔT +

ΔP ΔP -

∂T_P

∂P_T

ние теоретических моделей за счет учета новых эф-

]

фектов.

^[C_p

⁽∂V⁾

−

ΔT -

ΔP ΔT =

Поскольку неизотермическая модель спино-

∂T_P

дального распада обладает большой общностью

C_p

⁽∂V⁾

⁽∂V)ΔTΔP.

по сравнению с классической моделью Кана -

ΔT² +

ΔP² + 2

∂P_T

∂T_P

Хилльярда, включая ее как частный случай, она

должна быть применима и к поздним стадиям

Таким образом, флуктуации ΔT и ΔP коррелиро-

спинодального распада. Однако вопрос о том, к

ваны, но для изобарической системы, рассмотрен-

каким эффектам может привести неизотермич-

ной в данной работе, принципиально отсутствуют

ность в описании задачи спинодального распада

флуктуации давления, ΔP

≡ 0, поэтому вероят-

на поздних стадиях, должен решаться в отдельном

ность флуктуации температуры оказывается равна

(

)

исследовании, выполненном на основе численного

C_p

моделирования. Такое численное исследование и

ω ∝ exp

ΔT²

T²

последующее сопоставление с экспериментом акту-

ально и для ранних стадий спинодального распада.

Отсюда следует утверждение, что дисперсия флук-

туаций температуры для канонического ансамбля в

переменных P, T определяется выражением

Финансирование. Исследование выполнено

〈(ΔT )²〉 =

T² .

при финансовой поддержке Российского фонда

C_p

фундаментальных исследований и Правительства

115

В. Г. Лебедев, П. К. Галенко

ЖЭТФ, том 156, вып. 1 (7), 2019

Отметим также то обстоятельство, что дан-

14.

M. Laradji, M. Grant, M. J. Zuckennann et al., Phys.

ная работа «инвариантна» относительно замены

Rev. B 41, 4646 (1990).

«изохоричность-изобаричность», поскольку эти ха-

15.

E. D. Siggia, Phys. Rev. A 20, 595 (1979).

рактеристики явно нигде не использовались. По-

этому, анонсируя в качестве управляющего потен-

16.

P. Galenko, Phys. Lett. A 287, 190 (2001).

циала свободную энергию, можно было бы полу-

17.

P. Galenko and D. Jou, Phys. Rev. E 71, 046125

чить формулу (112,6) из [44], отличающуюся заме-

(2005).

ной C_p → C_V в выражении для дисперсии темпера-

18.

P. Galenko and D. Jou, Physica A 388, 3113 (2009).

турных флуктуаций. Потенциал Гинзбурга - Ландау

можно считать и свободной энергией и потенциалом

19.

P. Galenko and V. Lebedev, Phil. Mag. Lett. 87, 821

Гиббса, поскольку он не зависит от объема или дав-

(2007).

ления. В данном исследовании выбор названия «по-

20.

P. K. Galenko and V. G. Lebedev, JETP Lett. 86,

тенциал Гиббса» для потенциала Гинзбурга - Лан-

458 (2007).

дау, а значит, и «изобаричность» системы связаны

исключительно с тем, что описание термодинамики

21.

N. Lecoq, H. Zapolsky, and P. Galenko, Eur. Phys. J.

реальных материалов [32,45] основано на потенциа-

Spec. Top. 177, 165 (2009).

лах Гиббса.

22.

A. Oprisan, S. A. Oprisan, J. J. Hegseth et al., Phys.

Rev. E 77, 051118 (2008).

ЛИТЕРАТУРА

23.

E. L. Huston, J. W. Cahn, and J. E. Hilliard, Acta

Metall. 14, 1053 (1966).

Н. Jinnai, Т. Hashimoto, D. Lee et al., Macromole-

24.

H. W. Alt and I. Pawlow, Physica D 59, 389 (1992).

cules 30, 130 (1997).

25.

A. Miranville and G. Schimperna, Discr. Cont. Dyn.

F. Mallamace, N. Micali, and S. Trusso, J. Phys.:

Syst. B 5, 753 (2005).

Cond. Matt. 8, A81 (1996).

26.

M. Krivilyov, D. Aflyatunova, V. Lebedev, and

N. F. Bunkin, A. V. Lobeev, and G. A. Lyakhov,

P. K. Galenko, Comp. Mat. Sci. 158, 289 (2019).

УФН 167, 1069 (1997).

27.

D. A. Danilov, V. G. Lebedev, and P. K. Galenko, J.

J. Mainville, Y. S. Yang, K. R. Elder et al., Phys.

Non-Eq. Therm. 39(2), 93 (2014).

Rev. Lett. 78, 258 (1997).

28.

H. Risken, The Fokker-Planck Equation: Methods of

J. W. Cahn and J. E. Hilliard, J. Chem. Phys. 28,

Solutions and Applications, Springer-Verlag, Berlin

258 (1958).

(1984), p. 452.

J. W. Cahn, Acta Metall. 9, 795 (1961).

29.

A. E. Bailey and D. S. Canell, Phys. Rev. Lett. 70,

2110 (1993).

Н. Е. Cook, Acta Metall. 18, 297 (1970).

30.

J. P. Donley and S. Langer, Phys. Rev. Lett. 71, 1573

J. S. Langer, M. Bar-on, В. П. Скрипов, А. В. Скри-

(1993).

пов, H. D. Miller, Phys. Rev. A 11, 1417 (1975).

31.

J. Mainville, Y. S. Yang, K. R. Elder et al., Phys.

В. П. Скрипов, А. В. Скрипов, УФН 128, 193

Rev. Lett. 78, 2787 (1997).

(1979) [V. P. Skripov and A. V. Skripov, Sov. Phys.

32.

M. Hillert, Phase Equilibria, Phase Diagrams and

Usp. 22, 389 (1979)].

Phase Transformations: Their Thermodynamic Ba-

10.

K. Binder and P. Fratzl, in Phase Transformations in

sis, Cambridge Univ. Press, New York (2008), p. 510.

Materials, ed. by G. Kostorz, Wiley-VCH, Weinheim

33.

H. Zapolsky, C. Pareige, L. Marteau, D. Blavette, and

(2001), p. 409.

L. Q. Chen, Calphad 25, 125 (2001).

11.

N. S. Andreev, G. G. Boiko, and N. A. Bokov, J.

34.

D. J. Seol, S. Y. Hu, Y. L. Li, J. Shen, K. H. Oh, and

Non-Cryst. Solids 5, 41 (1970).

L. Q. Chen, Met. Mater. Int. 9, 61 (2003).

12.

N. S. Andreev and E. A. Porai-Koshits, Discuss. Fa-

35.

S. Lezama-Alvareza, E. O. Avila-Davilab, V. M. Lo-

raday Soc. 50, 135 (1970).

pez-Hirataa et al., Mat. Research 16(5), 975 (2013).

13.

К. Binder, Phys. Rev. A 29, 341 (1984).

36.

S. Dai and Q. Du, J. Comp. Phys. 310, 85 (2016).

116