ЖЭТФ, 2019, том 156, вып. 1 (7), стр. 140-166
© 2019
КЛАССЫ СЛОЖНОСТИ УГЛОВЫХ ДИАГРАММ
ПРОВОДИМОСТИ МЕТАЛЛОВ В
СИЛЬНЫХ МАГНИТНЫХ ПОЛЯХ
А. Я. Мальцев*
Институт теоретической физики им. Л. Д. Ландау Российской академии наук
142432, Черноголовка, Московская обл., Россия
Поступила в редакцию 20 января 2019 г.,
после переработки 20 января 2019 г.
Принята к публикации 24 января 2019 г.
Рассмотрены угловые диаграммы, описывающие зависимость магнитопроводимости металлов от на-
правления магнитного поля в сильных магнитных полях. Как можно показать, все угловые диаграммы
проводимости можно разбить на конечное число классов, обладающих различной сложностью. Наиболь-
ший интерес среди таких диаграмм представляют диаграммы, обладающие максимальной сложностью,
которые могут возникать для металлов с достаточно сложными поверхностями Ферми. При описании
структуры сложных диаграмм помимо описания собственно проводимости важнейшую роль играет опи-
сание холловской проводимости для различных направлений магнитного поля. Для оценки сложности
угловых диаграмм проводимости металлов оказывается удобным также сравнение таких диаграмм с
полными математическими диаграммами, определенными (формально) для всего дисперсионного соот-
ношения.
DOI: 10.1134/S0044451019070150
если на ней присутствуют области, соответствую-
щие появлению открытых траекторий на поверхно-
сти Ферми, т. е. появлению устойчивых открытых
1. ВВЕДЕНИЕ
электронных траекторий. Основное внимание здесь
будет уделено именно таким угловым диаграммам
В настоящей работе рассматриваются угловые
диаграммы электропроводности металлов, обладаю-
проводимости. Как оказывается, диаграммы тако-
го класса естественно разделить на два типа — бо-
щих произвольными поверхностями Ферми, в силь-
ных магнитных полях. Хорошо известно, что осо-
лее простые (тип A) и диаграммы, которые можно
назвать ультрасложными (тип B) в соответствии с
бенности проводимости металлов в этом пределе
обусловлены, в первую очередь, особенностями ква-
их действительно сложной структурой. Мы прове-
дем описание и сопоставление сложности обоих ти-
зиклассических электронных траекторий, возника-
пов диаграмм с наиболее сложными диаграммами,
ющих на поверхности Ферми в присутствии внеш-
а именно, диаграммами, определенными для всего
него магнитного поля. При этом все нетривиальные
дисперсионного закона. Диаграммы последнего ти-
особенности в поведении проводимости в этом слу-
па являются до некоторой степени абстрактными
чае связаны, главным образом, с появлением неза-
с точки зрения теории нормальных металлов, тем
мкнутых электронных траекторий, возникающих на
поверхностях Ферми достаточно сложной формы.
не менее, рассмотрение таких диаграмм дает удоб-
ный инструмент для построения общего подхода к
Как следствие этого, сложность угловых диаграмм
описанию диаграмм, определяющих проводимость
проводимости определяется непосредственно нали-
нормальных металлов, и, в частности, позволяет
чием и типом возникающих на поверхности Ферми
описать «области возникновения» диаграмм типа A
открытых траекторий при различных направлениях
или B и оценить «вероятность» появления диаграмм
магнитного поля B. Угловая диаграмма может быть
обоих типов для металлов с дисперсионным зако-
при этом отнесена к «достаточно сложному» типу,
ном заданного типа. Рассмотрение диаграмм, опре-
* E-mail: maltsev@itp.ac.ru
деленных для всего дисперсионного закона, позво-
140
ЖЭТФ, том 156, вып. 1 (7), 2019
Классы сложности угловых диаграмм проводимости металлов. ..
ляет также включить в классификацию естествен-
ным образом и более простые диаграммы, отвечаю-
щие появлению лишь замкнутых или неустойчивых
B
открытых траекторий на поверхности Ферми.
Ниже мы приведем краткое описание связи по-
ведения магнитопроводимости с поведением квази-
классических электронных траекторий на поверх-
ности Ферми металла, что позволит нам, собствен-
но, трактовать угловые диаграммы, описывающие
поведение траекторий на поверхности Ферми, как
диаграммы проводимости в сильных магнитных по-
лях. В последующих разделах мы более подробно
Рис. 1. Траектории системы (1.2) на поверхности постоян-
рассмотрим структуру поверхности Ферми при воз-
ной энергии достаточно сложной формы
никновении на ней устойчивых открытых траекто-
рий, особенности угловых диаграмм проводимости
для всего дисперсионного закона и для фиксирован-
ной поверхности Ферми и проведем сопоставление
Система (1.2) является интегрируемой с анали-
тической точки зрения, в частности, ее траектории в
структуры диаграмм обоих типов. Как следствие,
мы приведем в итоге общую схему естественного
p-пространстве задаются пересечениями поверхнос-
разделения угловых диаграмм проводимости в ме-
тей постоянной энергии ϵ(p) = const с плоскостя-
таллах на различные классы.
ми, ортогональными B. Надо сказать, что описание
Как хорошо известно, электронные состояния в
геометрии таких траекторий для достаточно слож-
ной 3-периодической поверхности в p-пространстве
кристалле параметризуются значениями квазиим-
пульса p = (p1, p2, p3) , при этом любые два значе-
представляет собой крайне нетривиальную задачу
(см. рис. 1). Легко видеть также, что наиболее слож-
ния p , отличающиеся на вектор обратной решетки
ным при этом является описание геометрии откры-
a = n1a1 + n2a2 + n3a3, n1,n2,n3 ∈ Z,
(1.1)
тых (незамкнутых) траекторий (1.2) в p-простран-
стве.
задают одно и то же электронное состояние.
Хорошо известно также, что траекториям систе-
Как также хорошо известно, базисные векторы
мы (1.2) в p-пространстве соответствуют квазиклас-
(a1, a2, a3) обратной решетки могут быть выбраны
сические электронные траектории в координатном
в виде
пространстве, которые имеют несколько более слож-
l2 × l3
l3 × l1
a1 = 2πℏ
,
a2 = 2πℏ
,
ную форму (в частности, они не являются плос-
(l1, l2, l3)
(l1, l2, l3)
кими). Однако форма электронных траекторий в
l1 × l2
x-пространстве в действительности тесно связана с
a3 = 2πℏ
,
их формой в p-пространстве, так, проекции траекто-
(l1, l2, l3)
рий в x-пространстве на плоскость, ортогональную
где (l1, l2, l3) представляют базис прямой решетки
B, подобны траекториям в p-пространстве, поверну-
кристалла.
тыми на 90◦. Последнее свойство делает геометрию
Изменение значений квазиимпульса в присут-
траекторий системы (1.2) чрезвычайно важной при
ствии внешнего постоянного магнитного поля опи-
описании транспортных явлений в нормальных ме-
сывается системой (см., например, [1-3])
таллах в присутствии сильных магнитных полей.
e
e
p=
[vgr (p) × B] ≡
[∇ϵ(p) × B] ,
(1.2)
Важнейшая роль геометрии траекторий системы
c
c
(1.2) в описании гальваномагнитных явлений в нор-
где ϵ(p) определяет зависимость энергии электрон-
мальных металлах была указана в работах школы
ного состояния от квазиимпульса (дисперсионное
И. М. Лифшица в 1950-х гг. [4-6]. В этот период
соотношение) для фиксированной зоны проводимос-
было изучено в действительности множество вопро-
ти. В силу того, что любые два значения квази-
сов, связанных с особенностями электронных явле-
импульса, различающиеся на вектор обратной ре-
ний, обусловленных нетривиальной геометрией по-
шетки, задают одно и то же электронное состояние,
верхности Ферми, в частности, вопросов, связанных
функция ϵ(p) является 3-периодической функцией
с геометрией траекторий системы (1.2), и рассмот-
в p-пространстве с периодами a1, a2, a3.
рено множество важных примеров траекторий раз-
141
А. Я. Мальцев
ЖЭТФ, том 156, вып. 1 (7), 2019
2. среднее направление всех устойчивых откры-
тых траекторий в p-пространстве одинаково при
заданном направлении B и задается пересечением
плоскости, ортогональной B, и некоторой целочис-
ленной плоскости Γ, неизменной при малых враще-
ниях B и вариациях уровня ϵ.
Свойства (1) и (2) устойчивых открытых траек-
Рис. 2. Вид устойчивой открытой траектории системы
торий имеют непосредственное проявление в поведе-
(1.2) в плоскости, ортогональной B
нии гальваномагнитных явлений в металлах в при-
сутствии сильных магнитных полей. Именно, силь-
ная анизотропия электронных траекторий (в x- и
ных типов на различных поверхностях Ферми (см.,
p-пространствах) приводит к резкой анизотропии
например, [1-12]). Мы, конечно, не сможем здесь
проводимости в плоскости, ортогональной B, в пре-
дать даже краткого обзора этих вопросов или при-
деле ωBτ ≫ 1. Предельные значения тензора про-
вести сколько-нибудь полной библиографии по дан-
водимости в x-пространстве могут быть при этом
ной тематике. Нас будет, в действительности, инте-
представлены в виде
ресовать картина полного математического описа-
⎛
⎞
0
0
0
ния структуры системы (1.2), базирующегося на ре-
ne2τ
⎜
⎟
зультатах исследования этой системы в более позд-
σkl∞ =
⎝ 0
∗
∗
⎠
(1.3)
m∗
ний период. Отметим, что форма траекторий (1.2)
0
∗
∗
начинает играть действительно существенную роль
при условии, что ось x совпадает со средним направ-
в рассматриваемых нами явлениях при выполне-
лением устойчивых открытых траекторий в p-про-
нии условия ωBτ
≫ 1, где ωB = eB/m∗c имеет
странстве.
смысл некоторой эффективной циклотронной час-
Легко видеть, что вклад (1.3) существенно отли-
тоты в кристалле и τ представляет собой среднее
чается от вклада замкнутых траекторий в том же
время свободного пробега электронов [4].
пределе (см. [4])
Задача полной классификации различных типов
⎛
⎞
открытых траекторий системы (1.2) с произволь-
0
0
0
ными (периодическими) дисперсионными законами
ne2τ
⎜
⎟
σkl∞ =
⎝ 0
0
0
⎠
ϵ(p) была поставлена Новиковым [13] и активно ис-
m∗
0
0
∗
следовалась в его топологической школе в последу-
ющие десятилетия. Можно сказать, что в настоящее
(в обеих формулах обозначение «∗» представляет
время получено достаточно полное описание всех
некоторую безразмерную константу порядка 1).
типов траекторий (1.2), базирующееся на довольно
Свойства тензора (1.3) послужили основанием
глубоких математических теоремах. Надо отметить,
для введения в работе [17] (см. также [18]) новых то-
что наиболее серьезные прорывы в решении данной
пологических характеристик (топологических кван-
проблемы были сделаны в работах [14-16], где было
товых чисел), наблюдаемых в проводимости нор-
получено описание открытых траекторий (1.2), ко-
мальных металлов со сложными поверхностями
торые можно в определенном смысле назвать устой-
Ферми.
чивыми открытыми траекториями.
Действительно, как нетрудно видеть, среднее
Уточним здесь, что мы будем называть откры-
направление устойчивых открытых траекторий в
тые траектории системы (1.2) устойчивыми, если
p-пространстве совпадает с направлением наиболь-
они не исчезают и сохраняют свою глобальную гео-
шего подавления проводимости в плоскости, орто-
метрию при малых вращениях направления B, а
гональной B, и, таким образом, наблюдаемо экс-
также вариациях энергетического уровня ϵ. Как сле-
периментально. В силу устойчивости таких траек-
дует из результатов работ [14-16], устойчивые от-
торий экспериментально наблюдаема и целочислен-
крытые траектории системы (1.2) обладают следую-
ная плоскость Γ, заметаемая направлениями наи-
щими замечательными свойствами:
большего подавления проводимости при малых вра-
1. каждая устойчивая открытая траектория си-
щениях направления B. Целочисленные парамет-
стемы (1.2) лежит в прямой полосе конечной ши-
ры плоскости Γ представляют собой топологические
рины в плоскости, ортогональной B, проходя ее на-
квантовые числа, наблюдаемые в проводимости в
сквозь (рис. 2);
сильных магнитных полях.
142
ЖЭТФ, том 156, вып. 1 (7), 2019
Классы сложности угловых диаграмм проводимости металлов. ..
Рис. 4. Вид хаотических траекторий типа Дынникова в
плоскостях, ортогональных B, в p-пространстве
торий (см. [4]), имеющих рациональные направле-
ния в p-пространстве. Последние, однако, могут как
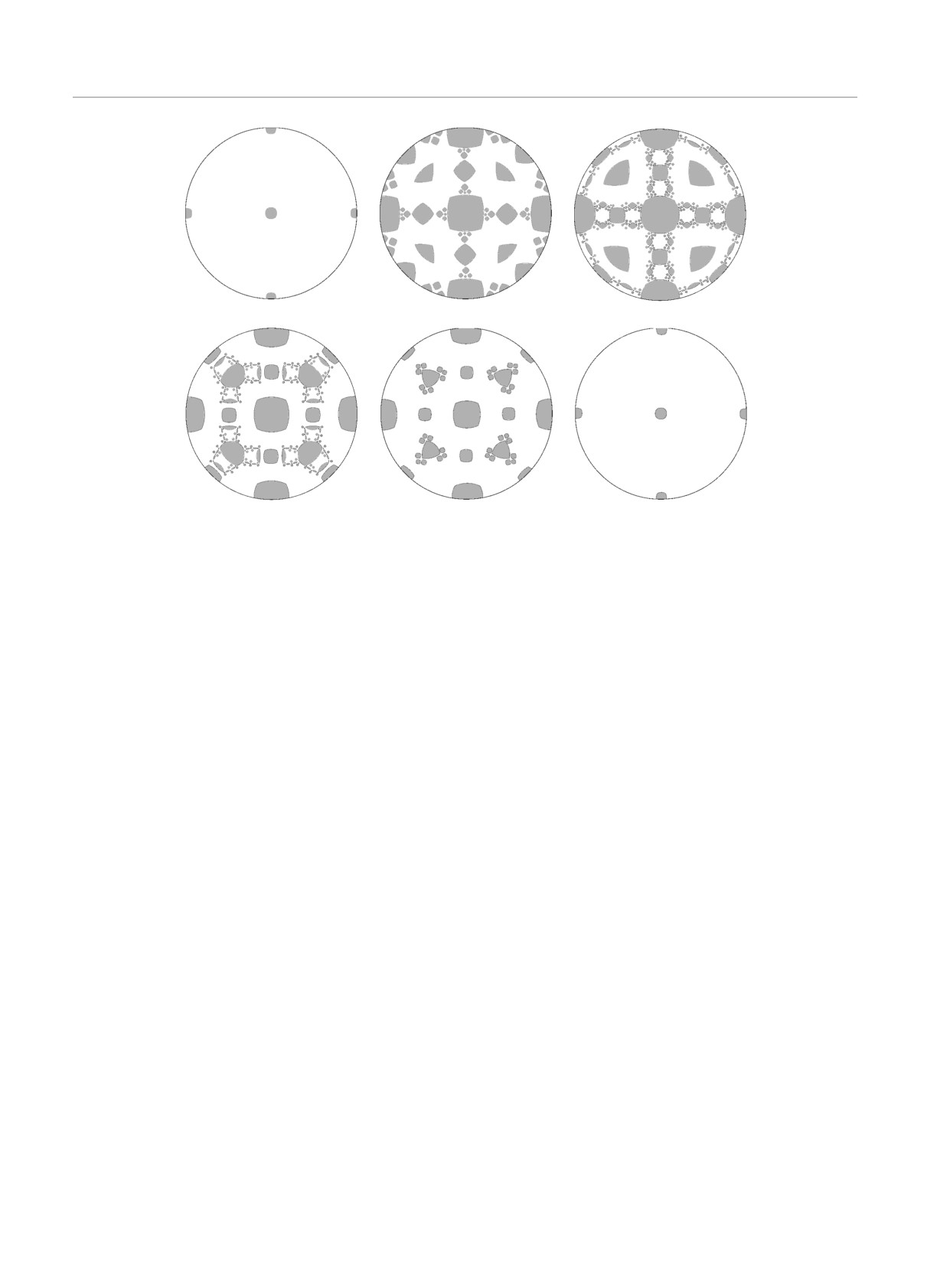
Рис. 3. Зоны устойчивости Ωα в пространстве направлений
B, соответствующие появлению семейств устойчивых от-
принадлежать устойчивому семейству (если B/B ∈
крытых траекторий системы (1.2) с различными числами
∈ Ωα), так и быть неустойчивыми (если B/B ∈ Ωα).
(M1α, M2α, M3α) на поверхности Ферми
Необходимо теперь сказать, что кроме устойчи-
вых открытых траекторий и периодических траек-
торий системы (1.2), имеющих сравнительно про-
Отметим здесь, что целочисленность плоскости
стую форму, на достаточно сложных поверхностях
Γ означает, что она порождена двумя векторами об-
Ферми могут возникать также траектории, поведе-
ратной решетки (1.1). В частности, она не обязана
ние которых имеет более сложный «хаотический»
совпадать в общем случае с какой-либо из кристал-
характер.
лографических плоскостей, вместо этого, она ор-
Первый пример траектории такого типа был по-
тогональна некоторому кристаллографическому на-
строен Царевым [19] для направления B ирраци-
правлению в x-пространстве. Таким образом, на-
ональности 2 (плоскость, ортогональная B, содер-
блюдаемая при измерениях магнитопроводимости
жит вектор обратной решетки). Траектории Царева
целочисленная плоскость Γ может быть представ-
могут возникать на поверхностях Ферми рода g ≥
лена некоторой тройкой целых чисел (M1, M2, M3),
≥ 3 и обладают явным хаотическим поведением на
задающих некоторое целочисленное направление в
этих поверхностях. Вместе с тем, в плоскостях, ор-
кристаллической решетке.
тогональных B, траектории типа Царева обладают
Каждая из топологических троек (M1α, M2α, M3α)
асимптотическим направлением и их вклад в прово-
относится к выделенному семейству устойчивых от-
димость в действительности также сильно анизот-
крытых траекторий системы (1.2), соответствующе-
ропен. В частности, мы также должны иметь здесь
му некоторой зоне устойчивости Ωα в пространстве
соотношение (1.3) в пределе ωBτ → ∞. При более
направлений B (рис. 3). Как мы уже сказали, в тео-
тщательном рассмотрении, однако, вклад траекто-
рии нормальных металлов естественным является
рий Царева в электропроводность имеет в действи-
рассмотрение траекторий системы (1.2) лишь на од-
тельности некоторые отличия от вкладов устойчи-
ном энергетическом уровне ϵ(p) = ϵF , соответству-
вых открытых или периодических траекторий, что
ющем энергии Ферми металла. Естественно опреде-
может быть выявлено в достаточно точных экспери-
лить границы зон устойчивости Ωα для нормального
ментах. Траектории типа Царева являются при этом
металла условием существования открытых траек-
неустойчивыми как по отношению к малым враще-
торий соответствующего семейства на поверхности
ниям направления B, так и по отношению к вариа-
Ферми SF
циям уровня Ферми.
ϵ(p) = ϵF .
Более сложные примеры хаотических траекто-
Отметим также, что соотношение (1.3) верно, в
рий на сложных поверхностях Ферми даются тра-
частности, и для периодических открытых траек-
екториями типа Дынникова [20]. Траектории Дын-
143
А. Я. Мальцев
ЖЭТФ, том 156, вып. 1 (7), 2019
всему дисперсионному соотношению ϵ(p) [23]. Зо-
ны Ω∗α образуют, как правило, более сложное мно-
жество в пространстве направлений B (рис. 5), в
частности, каждая из зон Ωα является подмноже-
ством более обширной зоны Ω∗α. В данной работе
мы остановимся на обсуждении сложности угловых
диаграмм на S2, представляющих зоны устойчиво-
сти для фиксированной поверхности Ферми, и, в
частности, проведем некоторое сравнение их с диа-
граммами, определенными для всего дисперсионно-
го закона.
Отметим здесь также, что довольно широкий
круг вопросов, касающихся описания устойчивых
траекторий системы (1.2), как с точки зрения их то-
пологического описания, так и с точки зрения тео-
рии транспортных явлений в металлах, был пред-
ставлен в работах [24-32].
Рис. 5. Зоны устойчивости Ω∗α, соответствующие появле-
2. ТОПОЛОГИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ
нию семейств устойчивых открытых траекторий системы
ПОВЕРХНОСТИ ФЕРМИ И ЗОНЫ
(1.2) с различными числами (M1α, M2α, M3α) хотя бы на од-
УСТОЙЧИВОСТИ В СЛУЧАЕ
ном из уровней энергии ϵ(p) = const (весьма схематично,
ВОЗНИКНОВЕНИЯ УСТОЙЧИВЫХ
показано лишь конечное число зон)
ОТКРЫТЫХ ТРАЕКТОРИЙ
Главное внимание будет уделяться поверхно-
никова могут возникать лишь при направлениях B
стям Ферми, имеющим достаточно сложную фор-
максимальной иррациональности и обладают явным
му. Определим сразу, что мы имеем под этим в
хаотическим поведением как на поверхности Ферми,
виду. Прежде всего отметим хорошо известное об-
так и в накрывающем p-пространстве (рис. 4). Глав-
стоятельство, что полное пространство физических
ной особенностью вклада таких траекторий в элек-
состояний для фиксированной зоны проводимости
тропроводность является при этом резкое подавле-
представляет собой трехмерный тор T3 с топологи-
ние проводимости вдоль направления B в пределе
ческой точки зрения. Действительно, в силу ука-
ωBτ → ∞ [21]. В целом, вкладу траекторий типа
занной выше эквивалентности состояний с квази-
Дынникова в тензор электропроводности свойствен-
импульсами, различающимися на векторы обратной
но убывание проводимости во всех направлениях в
решетки, полный набор состояний для заданной зо-
пределе ωBτ → ∞ и появление дробных степеней
ны проводимости (зона Бриллюэна) представляет
параметра ωBτ в асимптотиках компонент тензора
собой фактор-пространство
[21, 22]. Как и траектории типа Царева, траектории
типа Дынникова являются неустойчивыми как по
T3 = R3/L
отношению к малым вращениям направления B, так
и по отношению к вариациям уровня Ферми. Как
(отметим также, что мы не рассматриваем здесь
мы увидим ниже, появление хаотических траекто-
спиновые переменные, которые не будут играть су-
рий (обоих типов) будет связано, главным образом,
щественной роли в наших рассуждениях). Как след-
с наиболее сложными угловыми диаграммами (ти-
ствие этого, любая (несингулярная) энергетическая
па B), где соответствующие направления B будут
поверхность ϵ(p) = const может также рассматри-
играть (наряду с зонами Ωα) весьма важную роль в
ваться (после факторизации) как гладкая компакт-
структуре таких диаграмм.
ная поверхность, вложенная в T3. Как компактная
Как мы уже сказали выше, кроме зон устойчи-
гладкая двумерная поверхность каждая такая по-
вости, определяемых некоторой фиксированной по-
верхность (в частности, поверхность Ферми) пред-
верхностью Ферми, можно в действительности вве-
ставляет собой поверхность определенного рода g ≥
сти также зоны устойчивости Ω∗α, соответствующие
≥ 0 (рис. 6).
144
ЖЭТФ, том 156, вып. 1 (7), 2019
Классы сложности угловых диаграмм проводимости металлов. ..
а
б
в
B
Рис. 6. Топология замкнутых поверхностей рода 0 (а),
1 (б), 2 (в) и т. д.
а
б
Рис. 8. Цилиндр замкнутых траекторий (1.2), ограничен-
ный сингулярными замкнутыми траекториями
в
г
B
Рис. 7. Примеры поверхностей Ферми ранга 0 (а), 1 (б),
Рис. 9. Носитель открытых траекторий системы (1.2) в
2 (в), 3 (г)
расширенном p-пространстве
Кроме топологического рода поверхность Ферми
очередь, структура поверхности Ферми при направ-
SF характеризуется также рангом, определяемым
лении B, лежащем в одной из зон устойчивости Ωα,
как размерность образа отображения
при этом мы можем для простоты полагать, что B
имеет направление общего положения (в частности,
H1(SF ) → H1(T3)
плоскость, ортогональная B, не содержит векторов
при вложении SF → T3. Нетрудно видеть, что ранг
обратной решетки).
поверхности Ферми может принимать значения 0, 1,
Рассмотрим, следуя
[23], множество несингу-
2 и 3 (рис. 7). Скажем сразу, что мы будем считать
лярных замкнутых траекторий системы (1.2) при
здесь поверхность Ферми достаточно сложной, если
B/B ∈ Ωα. Нетрудно видеть, что это множество
ее ранг равен 3. Нетрудно показать, что для рода по-
представляет собой конечный набор (неэквивалент-
верхности Ферми мы должны в этом случае также
ных) цилиндров, ограниченных сингулярными за-
иметь соотношение g ≥ 3.
мкнутыми траекториями системы (1.2) (рис.
8).
Приведем теперь кратко описание структуры
Удалим теперь все такие цилиндры замкнутых тра-
сложной поверхности Ферми при наличии на ней
екторий из поверхности Ферми. Оставшаяся часть
устойчивых открытых траекторий системы (1.2).
поверхности Ферми представляет собой часть, за-
Отметим, что наличие такой структуры является
полненную открытыми траекториями системы (1.2).
при этом общим свойством системы (1.2) и выте-
Нетрудно видеть, что полученная таким образом но-
кает из строгих топологических результатов, пред-
вая поверхность должна состоять из конечного чис-
ставленных в работах [14, 16, 23]. Нам будет наибо-
ла (неэквивалентных) связных компонент, которые
лее удобно использовать описание, представленное в
могут быть названы «носителями» открытых тра-
работе [23], где рассматривались все открытые тра-
екторий. Отметим также, что образовавшиеся пос-
ектории системы (1.2), возникающие для заданно-
ле удаления цилиндров замкнутых траекторий от-
го дисперсионного соотношения ϵ(p). Для просто-
верстия могут быть «заклеены» плоскими диска-
ты мы будем предполагать, что поверхность Ферми
ми, ортогональными B, так что новая (редуциро-
представлена одной компонентой связности, имею-
ванная) поверхность может рассматриваться так-
щей ранг 3. Нас здесь будет интересовать, в первую
же и как замкнутая периодическая поверхность в
145
10
ЖЭТФ, вып. 1 (7)
А. Я. Мальцев
ЖЭТФ, том 156, вып. 1 (7), 2019
B
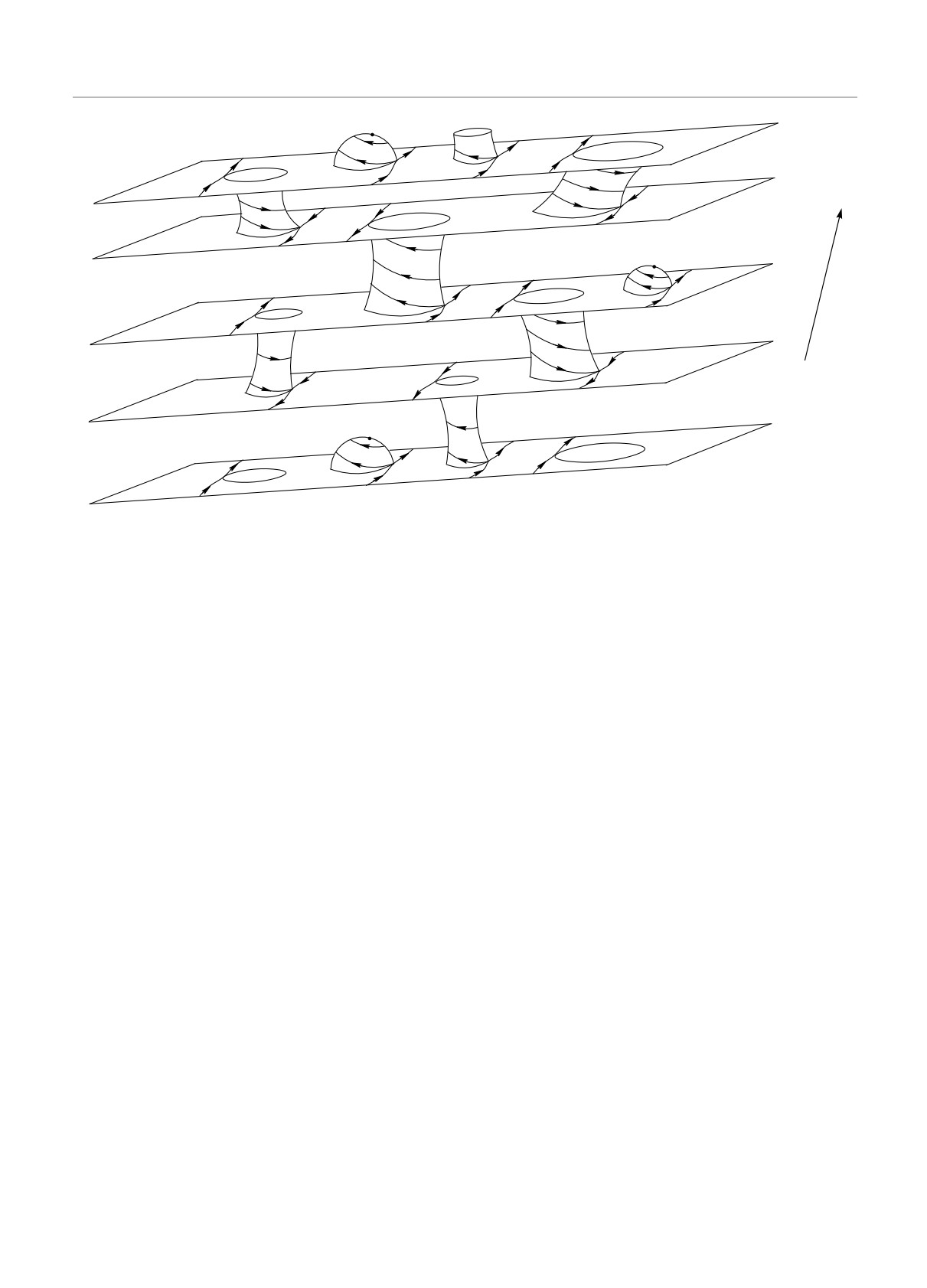
Рис. 10. Представление поверхности Ферми, несущей устойчивые открытые траектории системы (1.2)
p-пространстве. Полученная поверхность также мо-
редуцированной поверхности Ферми задается при
жет быть профакторизована по векторам обратной
этом конечным четным числом, равным количеству
решетки и рассматриваться как замкнутая двумер-
двумерных торов T2 в зоне Бриллюэна (T3).
ная поверхность, вложенная в T3.
Можно видеть таким образом, что для направ-
Важнейшее свойство редуцированной таким
лений B общего положения, лежащих в какой-либо
образом поверхности Ферми при наличии на
из зон устойчивости Ωα, полная поверхность Фер-
ней устойчивых открытых траекторий системы
ми всегда представима в виде набора параллельных
(1.2) может быть сформулировано следующим
целочисленных плоскостей (с отверстиями), несу-
образом [14,16]:
щих открытые траектории системы (1.2), соединен-
каждый из носителей открытых траекторий
ных компонентами, состоящими только из замкну-
представляет собой двумерный тор T2, вложенный
тых траекторий (1.2). В нашем случае мы будем все-
в T3 с фиксированным отображением в гомоло-
гда полагать, что такие компоненты представляют
гиях, однозначно определенным для всей зоны
собой отдельные цилиндры замкнутых траекторий,
устойчивости Ωα.
ограниченные сингулярными замкнутыми траекто-
Возвращаясь к расширенному p-пространству,
риями (рис. 10). В действительности, более сложная
можно также сформулировать приведенное выше
структура этих компонент (наличие нескольких ци-
утверждение в следующем виде:
линдров замкнутых траекторий с дополнительны-
ми особыми точками) может привнести некоторые
каждый из носителей открытых траекторий в
дополнительные особенности в общую картину (на-
p-пространстве представляет собой целочисленную
периодически деформированную плоскость задан-
пример, неодносвязность зон устойчивости). Однако
такая структура является крайне маловероятной в
ного направления, неизменного для всей зоны устой-
реальной ситуации, так что мы не рассматриваем ее
чивости Ωα (рис. 9).
здесь.
Полная редуцированная поверхность Ферми
представляет собой, таким образом, бесконечный
Представление поверхности Ферми в виде, пока-
набор целочисленных периодически деформиро-
занном на рис. 10, в общем случае не является един-
ванных параллельных плоскостей фиксированного
ственным и, в частности, мы имеем различные та-
направления в p-пространстве. Количество неэкви-
кие представления одной и той же поверхности для
валентных целочисленных плоскостей (т. е. пред-
различных зон устойчивости Ωα, Ωβ . Нужно отме-
ставляющих различные электронные состояния) в
тить также, что представление на рис. 10 отража-
146
ЖЭТФ, том 156, вып. 1 (7), 2019
Классы сложности угловых диаграмм проводимости металлов. ..
ет главные особенности топологической структуры
системы (1.2) на поверхности Ферми и может быть
существенно сложнее с визуальной точки зрения.
Нетрудно видеть, что представленная структура
поверхности Ферми является устойчивой по отноше-
нию к малым вращениям направления магнитного
поля и объясняет наличие замечательных свойств
устойчивых открытых траекторий системы (1.2),
B
приведенных выше. Можно видеть также, что все
носители открытых траекторий могут быть в дей-
ствительности разделены на два класса в соответ-
ствии с направлением движения вдоль траекторий
(вперед или назад) в расширенном p-пространстве.
Кроме того, можно разделить на два класса также
цилиндры замкнутых траекторий, представленные
на рис. 10, в соответствии с тем, траектории какого
типа (электронного или дырочного) они содержат.
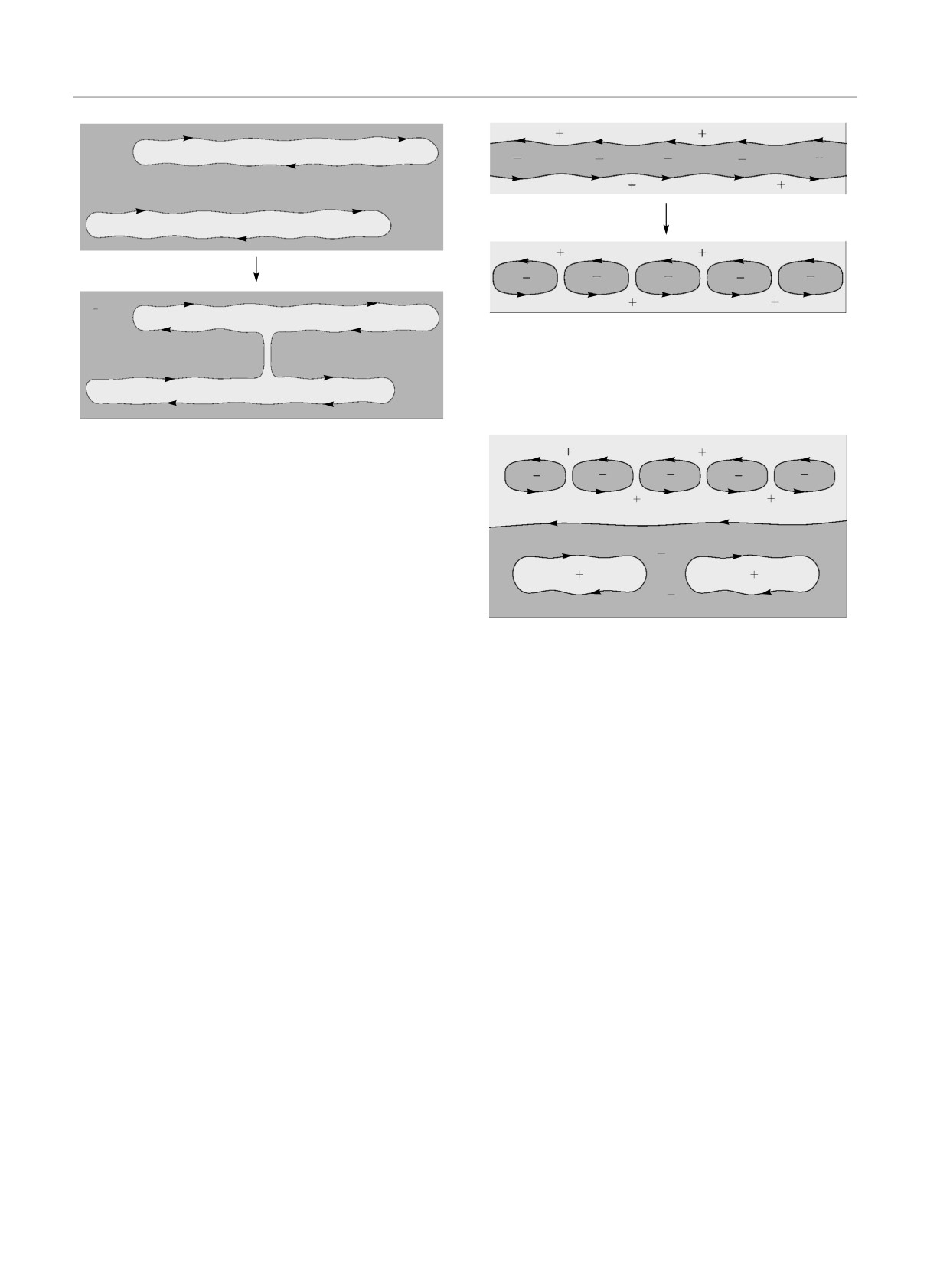
В соответствии с картиной на рис. 10, границе
зоны устойчивости Ωα должно обязательно соответ-
B
ствовать обращение в нуль высоты одного из ци-
линдров замкнутых траекторий (и последующее его
исчезновение) для соответствующих направлений B
(рис. 11). Как легко видеть, после пересечения гра-
ницы зоны устойчивости открытые траектории по-
лучают возможность «перескакивать» с одного но-
сителя открытых траекторий на другой, что изме-
няет общую структуру траекторий на поверхности
Ферми.
Можно видеть также, что общая граница зоны
устойчивости может быть при этом как «простой»,
т. е. соответствовать исчезновению одного и того же
цилиндра замкнутых траекторий во всех своих точ-
B
ках (рис. 12), так и «составной», т. е. соответствовать
исчезновению разных цилиндров замкнутых траек-
Рис. 11. Обращение в нуль высоты цилиндра замкнутых
торий на различных ее участках (рис. 13, 14). Кро-
траекторий и последующий перескок открытых траекторий
ме того, можно видеть, что в случае составной гра-
с одного носителя на другой на границе зоны устойчивости
ницы зоны устойчивости возможна как ситуация,
когда на разных ее участках происходит исчезно-
вение цилиндров замкнутых траекторий различных
мой исчезновением цилиндров различных типов на
типов (рис. 13), так и ситуация, когда на разных
разных ее участках, должно приводить при этом к
ее участках происходит исчезновение разных цилин-
наличию разных значений холловской проводимо-
дров замкнутых траекторий одного и того же типа
сти в разных областях вне зон устойчивости и, как
(рис. 14).
следствие этого, к достаточно сложной структуре
угловой диаграммы в целом.
Отметим здесь, что тип исчезающего цилиндра
замкнутых траекторий также играет важную роль в
данной ситуации в описании гальваномагнитных яв-
3. ОСОБЕННОСТИ УГЛОВЫХ ДИАГРАММ,
лений для соответствующих направлений B. Так, в
ОПРЕДЕЛЕННЫХ ДЛЯ
частности, он определяет величину холловской про-
ДИСПЕРСИОННОГО ЗАКОНА
водимости в металле вне зоны Ωα вблизи соответ-
ствующего участка границы в пределе ωBτ → ∞.
Приведем теперь общее описание диаграмм,
Как было указано в [32], наличие хотя бы одной зо-
определенных для всего дисперсионного закона
ны устойчивости с составной границей, определяе-
ϵ(p) [23]. Согласно работе [23], возможность по-
147
10*
А. Я. Мальцев
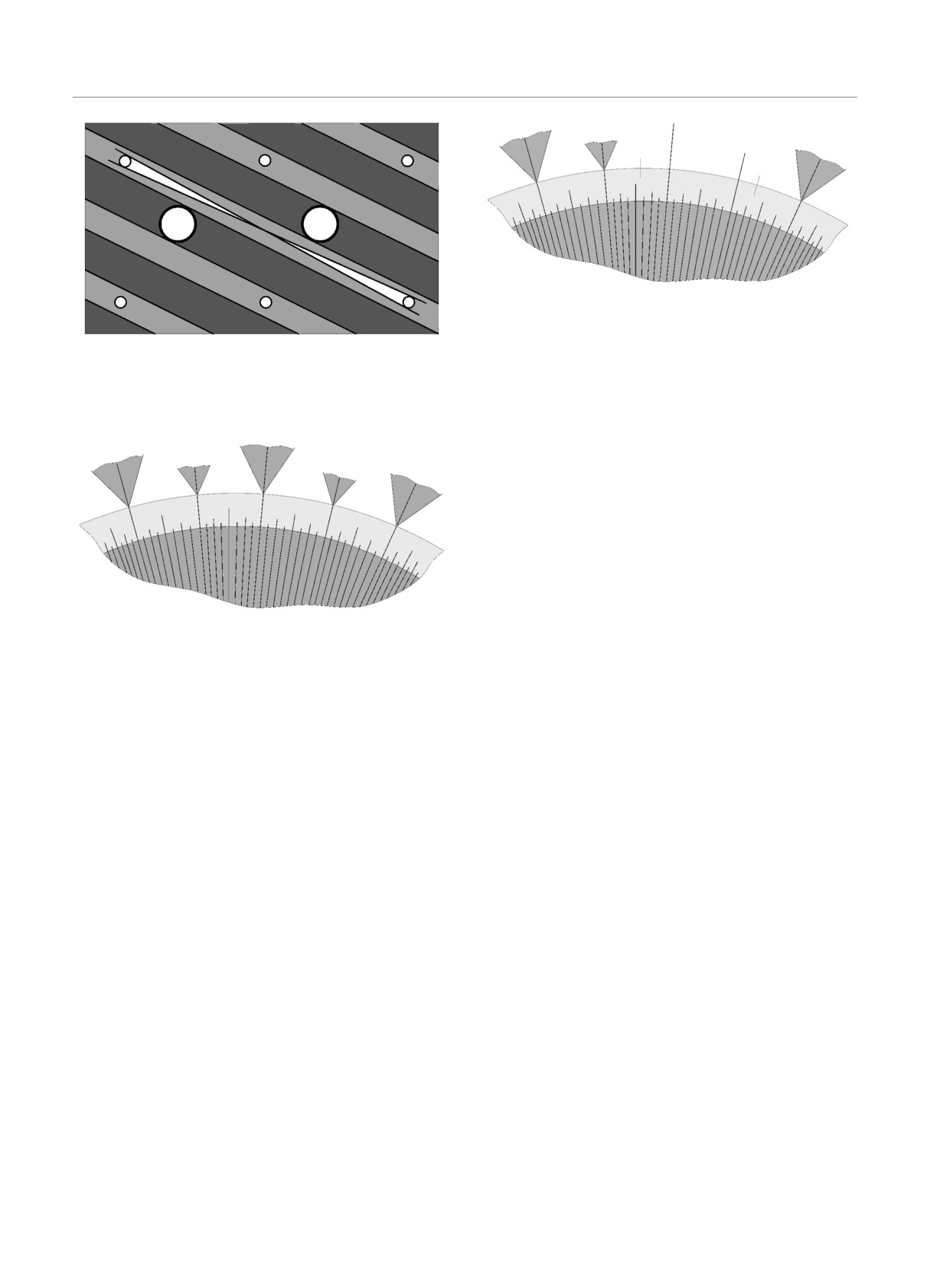
ЖЭТФ, том 156, вып. 1 (7), 2019
B
Рис. 12. Поверхность Ферми, обладающая зоной устойчивости Ωα с границей, определяемой исчезновением одного и
того же цилиндра замкнутых траекторий во всех ее точках
B
Рис. 13. Поверхность Ферми, обладающая зоной устойчивости Ωα с границей, определяемой исчезновением разных
цилиндров различных типов на разных ее участках
B
Рис. 14. Поверхность Ферми, обладающая зоной устойчивости Ωα с границей, определяемой исчезновением разных
цилиндров одного и того же типа на разных ее участках
строения таких угловых диаграмм базируется на
иррациональности) значения ϵ1(B/B) и ϵ2(B/B)
следующих важных утверждениях относительно
совпадают со значениями некоторых непрерывных
траекторий системы (1.2).
функций ϵ1(B/B) и ϵ2(B/B), определенных всюду
1) Рассмотрим произвольное периодическое дис-
на единичной сфере. Для специальных направлений
персионное соотношение
B, отвечающих появлению строго периодических
открытых траекторий системы
(1.2), значения
ϵmin ≤ ϵ(p) ≤ ϵmax
ϵ1(B/B) и ϵ2(B/B) могут отличаться от значений
и зафиксируем направление магнитного поля B.
ϵ1(B/B) и
ϵ2(B/B), при этом мы всегда имеем
Тогда все уровни энергии ϵ(p) = const, на кото-
соотношения
рых присутствуют незамкнутые траектории систе-
мы (1.2), представляют либо замкнутый интервал
ϵ1(B/B) ≤ ϵ1(B/B), ϵ2(B/B) ≥ ϵ2(B/B).
[ϵ1(B/B), ϵ2(B/B)], либо единственную точку ϵ0 =
= ϵ1(B/B) = ϵ2(B/B).
3) В случае ϵ2(B/B) > ϵ1(B/B) для направлений
2) Для направлений B общего положе-
B общего положения все несингулярные открытые
ния (в частности, направлений максимальной траектории системы (1.2) (на всех уровнях энергии)
148
ЖЭТФ, том 156, вып. 1 (7), 2019
Классы сложности угловых диаграмм проводимости металлов. ..
имеют вид, представленный на рис. 2, с одним и тем
а
б
же средним направлением, задаваемым пересечени-
ем плоскости, ортогональной B, и некоторой цело-
численной плоскости Γ.
4) Свойство ϵ2(B/B) > ϵ1(B/B), а также цело-
численная плоскость Γ являются локально устойчи-
выми по отношению к малым вращениям B и опре-
Рис. 15. Всюду плотное множество направлений B в зоне
деляют, таким образом, некоторую зону устойчивос-
Ω∗α, соответствующих появлению периодических траекто-
ти Ω∗ на угловой диаграмме. Зона Ω∗ представляет
∗
α
рий, в случаях, когда Mα/|Mα| ∈ Ωα и Mβ /|Mβ | ∈ Ω
собой открытую область с кусочно-гладкой грани-
цей на S2, при этом на границе ∂Ω∗ выполняется
соотношение ϵ2(B/B) = ϵ1(B/B).
5) Объединение всех зон устойчивости Ω∗α явля-
ется всюду плотным на единичной сфере S2, при
этом S2 может содержать либо одну зону устойчи-
вости Ω∗, либо бесконечно много зон Ω∗α.
Как легко видеть, угловые диаграммы для дис-
персионного закона можно естественно разделить
на очень простые (единственная зона устойчивости)
Рис. 16. Множество зон Ω∗β , примыкающих к границе зоны
Ω∗α в каждой из ее «рациональных» точек
и очень сложные (бесконечно много зон устойчи-
вости). Здесь нам будут интересны, главным об-
разом, диаграммы второго типа. Сложность угло-
ющая точка примыкания является при этом точкой
вых диаграмм второго типа обусловлена, в частно-
излома границы Ω∗β , а топологические числа Mα =
сти, следующими особенностями их общей структу-
= (M1α, M2α, M3α) и Mβ = (M1β, M2β, M3β), а также со-
ры (см. [23]).
ответствующее направление B связаны соотношени-
А именно, рассмотрим некоторую зону устой-
ем
чивости Ω∗α, отвечающую некоторой целочисленной
B=ηMα +θMβ,
плоскости Γα (или топологическим числам Mα =
= (M1α, M2α, M3α)) и имеющую кусочно-гладкую гра-
причем |η/θ| < 1.
ницу на S2. Как уже неоднократно указывалось, все
Можно видеть, таким образом, что структура уг-
несингулярные открытые траектории системы (1.2)
ловых диаграмм для дисперсионного соотношения,
имеют при B/B ∈ Ω∗α общее среднее направление,
содержащих более одной зоны устойчивости, явля-
задаваемое пересечением плоскости Γα и плоскости,
ется крайне сложной.
ортогональной B. Нетрудно видеть, что всякий раз,
Во избежание неоднозначности мы будем всегда
когда такое пересечение имеет целочисленное на-
обозначать здесь через Ω∗α полную (открытую) зону
правление, соответствующие траектории являются
устойчивости и через Ω∗α — зону Ω∗α вместе с грани-
периодическими в p-пространстве. Можно видеть
цей. Множество
также, что соответствующие направления B обра-
\
зуют в Ω∗α всюду плотное множество, состоящее из
D∗ = S2
∪Ω∗α
сегментов больших кругов (рис. 15). Кроме того,
можно видеть, что соответствующее множество яв-
представляет собой множество направлений B, для
ляется также всюду плотным и на границе области
которых открытые траектории системы (1.2) суще-
Ω∗α, образуя на ней подобие множества рациональ-
ствуют на единственном уровне энергии и ведут се-
ных чисел. Будем называть точки описанного мно-
бя хаотически в плоскостях, ортогональных B. Со-
жества на границе Ω∗α «рациональными» точками
гласно гипотезе Новикова [28], фрактальная размер-
границы.
ность этого множества для дисперсионных соотно-
Важной особенностью угловых диаграмм для
шений общего положения строго меньше 2. Отме-
дисперсионного закона является то обстоятельство,
тим, что исследование различных особенностей как
что в каждой «рациональной» точке границы лю-
множества D∗, так и соответствующих хаотических
бой из зон устойчивости Ω∗α к этой зоне примыкает
траекторий (1.2) представляет в настоящее время
другая зона устойчивости Ω∗β , отвечающая другой
довольно быстро развивающуюся область теории
целочисленной плоскости Γβ (рис. 16). Соответству-
динамических систем (см., например, [19-23,33-49]).
149
А. Я. Мальцев
ЖЭТФ, том 156, вып. 1 (7), 2019
Построенное в [23] и приведенное выше описание
угловых диаграмм для системы (1.2) основано на ре-
зультатах, полученных в работах [14,16] и приводя-
щих к описанному выше представлению энергетиче-
ских поверхностей (рис. 10), содержащих устойчи-
вые открытые траектории системы (1.2). Отметим
при этом, что граница зоны устойчивости Ω∗α, опре-
деленной для всего дисперсионного закона, соответ-
ствует исчезновению одновременно двух цилиндров
Рис. 17. Множество направлений B вблизи зон устойчи-
вости, соответствующих появлению (неустойчивых) пери-
замкнутых траекторий (электронного и дырочного
одических траекторий на поверхности Ферми
типа), соединяющих носители открытых траекто-
рий. Здесь можно видеть разницу с ситуацией на уг-
ловых диаграммах, определенных для фиксирован-
ного значения энергии, где каждый участок грани-
Отметим здесь сразу одну особенность зон устой-
цы зоны устойчивости соответствует исчезновению
чивости для фиксированной поверхности Ферми,
цилиндра замкнутых траекторий определенного ти-
несколько отличающую их от зон устойчивости для
па. Кроме того, как было отмечено в [23], грани-
всего дисперсионного закона. Именно, как мы уже
цы различных зон устойчивости, определенных для
сказали, зона устойчивости Ωα определяет мно-
фиксированного значения энергии, не имеют общих
жество направлений B, для которых существуют
точек в случае общего положения, что говорит в
устойчивые открытые траектории на поверхности
целом о несколько менее сложной структуре таких
Ферми, соответствующие фиксированным топологи-
диаграмм.
ческим числам (M1α, M2α, M3α). Можно, однако, ука-
В следующем разд. 4 мы проведем более по-
зать дополнительные направления B, для которых
дробное рассмотрение угловых диаграмм проводи-
на поверхности Ферми существуют открытые траек-
мости, соответствующих некоторому фиксированно-
тории системы (1.2), не являющиеся устойчивыми,
му уровню энергии (уровню Ферми) ϵF , что отвеча-
однако также связанные с зоной Ωα. Такие траек-
ет ситуации нормального металла. Как можно будет
тории являются периодическими и появляются на
видеть, наибольшую часть рассмотрения надо будет
продолжениях сегментов больших кругов, описан-
при этом посвятить анализу траекторий системы
ных выше, за пределы Ωα (рис. 17). Можно пока-
(1.2) на сложных поверхностях Ферми, обсуждав-
зать, что такие траектории всегда появляются вбли-
шихся в разд. 2. Следствием такого анализа будет,
зи границы зоны Ωα, что следует из приведенного
в частности, описание наиболее сложных диаграмм,
выше представления поверхности Ферми (рис. 10)
возникающих в этой ситуации, и исследование того,
для направлений B/B ∈ Ωα. Сеть соответствующих
насколько такие диаграммы могут приближаться к
направлений B является всюду плотной на грани-
описанным выше по уровню сложности.
це Ωα, однако, длины добавочных участков к сег-
ментам больших кругов довольно быстро убывают
с ростом целых чисел (m1, m2, m3), определяющих
направление соответствующих периодических тра-
4. СЛОЖНОСТЬ УГЛОВЫХ ДИАГРАММ,
екторий в p-пространстве. Как следствие этого, опи-
ОПРЕДЕЛЕННЫХ ДЛЯ ФИКСИРОВАННОЙ
ПОВЕРХНОСТИ ФЕРМИ, И ИХ СВЯЗЬ С
санные сети добавочных направлений B имеют ко-
ДИАГРАММАМИ ДЛЯ ДИСПЕРСИОННОГО
нечную плотность на любом конечном расстоянии
ЗАКОНА
от границы Ωα. Как было показано в [30], наличие
(неустойчивых) периодических траекторий, а также
Как мы уже указывали выше, каждая из зон
очень длинных замкнутых траекторий системы (1.2)
устойчивости Ωα, определенная для фиксированной
вблизи границ Ωα приводит в действительности к
поверхности Ферми, лежит внутри некоторой (боль-
довольно сложному поведению проводимости для
шей) зоны устойчивости Ω∗α, соответствующей пол-
соответствующих направлений B и, в частности, де-
ному дисперсионному соотношению ϵ(p). Для на-
лает невозможным наблюдение точной границы зо-
правлений B/B ∈ Ωα мы, таким образом, имеем
ны устойчивости в экспериментах по прямому изме-
устойчивые открытые траектории, лежащие на по-
рению проводимости даже в довольно сильных маг-
верхности Ферми и соответствующие топологичес-
нитных полях. Так, в действительности, «экспери-
ким числам (M1α, M2α, M3α).
ментально наблюдаемая» зона устойчивости в таких
150
ЖЭТФ, том 156, вып. 1 (7), 2019
Классы сложности угловых диаграмм проводимости металлов. ..
исследования осцилляционных явлений в сильных
магнитных полях [32].
Как можно видеть, в общем случае вторая гра-
ница зоны устойчивости может быть расположена
на произвольном расстоянии от ее первой грани-
цы. В общем случае область Ω′α может состоять
из нескольких связных компонент, ограниченных
участками первой границы зоны Ωα с «внутренней
Рис. 18. «Экспериментально наблюдаемые» зоны устой-
стороны» и участками второй границы с «внешней
чивости в экспериментах по прямому измерению проводи-
стороны» (рис. 19). Можно также отметить, что для
мости в сильных магнитных полях
каждой из связных компонент области Ω′α ее «внут-
ренняя» и «внешняя» границы соответствуют исчез-
новению цилиндров замкнутых траекторий проти-
экспериментах не совпадает с точной математичес-
воположных типов на рис. 10. При этом внутри каж-
кой зоной Ωα (рис. 18) и зависит от максимальных
дой области Ω′α лежит также граница зоны устойчи-
величин внешних магнитных полей, достижимых в
вости Ω∗α, имеющая одновременно «электронный» и
эксперименте.
«дырочный» тип (рис. 20). Общим обстоятельством
Вместе с тем, точные границы математических
является также то, что для зон устойчивости с со-
зон устойчивости Ωα являются в действительности
ставной границей, имеющей участки, соответству-
также наблюдаемыми экспериментально при специ-
ющие исчезновению цилиндров замкнутых траек-
альной постановке эксперимента. В частности, как
торий разных типов, «угловые» точки ее границы
было показано в работе [31], они могут быть опре-
(разделяющие участки, соответствующие исчезно-
делены при наблюдении картины осцилляционных
вению цилиндров замкнутых траекторий разных ти-
явлений (классических или квантовых) в сильных
пов) являются также «угловыми» точками для вто-
магнитных полях. Мы будем интересоваться распре-
рой границы зоны устойчивости, а также принадле-
делением именно точных математических зон устой-
жат границе соответствующей зоны Ω∗α (рис. 20б).
чивости на угловой диаграмме проводимости.
В то же время, для зоны устойчивости, границы ко-
Как можно заметить из приведенной выше кар-
торой целиком соответствуют исчезновению цилин-
тины, возникающей на поверхности Ферми в случае
дров замкнутых траекторий одного и того же типа,
наличия устойчивых открытых траекторий систе-
ее первая граница не пересекается со второй в слу-
мы (1.2), для каждой из зон устойчивости Ωα есте-
чае общего положения, а граница соответствующей
ственно также ввести «вторую границу» на угловой
зоны Ω∗α лежит внутри области, ограниченной пер-
диаграмме. Вторая граница зоны Ωα определяется
вой и второй границами (рис. 20а,в).
при этом исчезновением еще одного цилиндра за-
Здесь удобно ввести некоторые специальные обо-
мкнутых траекторий на рис. 10 и появлением пере-
значения для разных типов зон Ωα. А именно, ска-
скоков траекторий (1.2) между парами «сливших-
жем, что зона Ωα относится к типу (+), если все
ся» носителей открытых траекторий, определенных
точки ее границы соответствуют исчезновению ци-
для зоны Ωα. Можно видеть при этом, что в области
линдров замкнутых траекторий электронного типа.
Ω′α, заключенной между первой и второй границами
Аналогично, скажем, что Ωα относится к типу (-),
зоны устойчивости, не могут возникать открытые
если все точки ее границы соответствуют исчезно-
траектории системы (1.2), отличные от описанных
вению цилиндров замкнутых траекторий дырочного
выше неустойчивых периодических траекторий. Об-
типа. Наконец, зона Ωα относится к типу (±), если
ласть Ω′α может быть при этом названа «производ-
на разных участках ее границы происходит исчезно-
ной» зоны устойчивости Ωα, поскольку поведение
вение цилиндров замкнутых траекторий как элек-
траекторий системы (1.2) в этой области определя-
тронного, так и дырочного типа.
ется в действительности структурой этой системы
Нетрудно показать, что на участках границ Ωα,
в зоне Ωα. Заметим здесь, что картина поведения
соответствующих исчезновению цилиндров замкну-
проводимости, а также осциллляционных явлений
тых траекторий электронного типа в случае общего
в области Ω′α является в общем случае достаточно
положения имеет место соотношение
сложной (см. [32]). Как и для первой границы зоны
устойчивости Ωα, положение второй ее границы так-
же удобнее всего определять при этом с помощью
ϵF = ϵ2(B/B) > ϵ1(B/B).
151
А. Я. Мальцев
ЖЭТФ, том 156, вып. 1 (7), 2019
B
а
B
б
B
в
Рис. 19. Внутренние и внешние границы, ограничивающие области Ω′α
Аналогично, на участках границ Ωα, соответ-
2) Везде на множествах U+α\Ωα имеет место со-
ствующих исчезновению цилиндров замкнутых тра-
отношение
екторий дырочного типа, мы имеем в случае общего
ϵF > ϵ2(B/B),
(4.1)
положения соотношение
а на множествах U-β \ Ωβ — соотношение
ϵF = ϵ1(B/B) < ϵ2(B/B).
ϵF < ϵ1(B/B).
(4.2)
Особая ситуация имеет место в «угловых» (раз-
Возвращаясь к полному дисперсионному соотно-
деляющих участки границы разных типов) точках
шению, можно отметить, что каждая зона Ωα про-
зон типа (±), где мы имеем соотношение
ходит в случае общего положения все типы (-), (±)
и (+) при изменении уровня Ферми от некоторо-
ϵF = ϵ1(B/B) = ϵ2(B/B).
го минимального до некоторого максимального зна-
Можно видеть, что для поверхности Ферми об-
чения, определяемых существованием данной зоны.
щего положения все зоны устойчивости Ωα типа (+)
На рис. 21 представлена возможная схема эволюции
можно покрыть открытыми областями U+α, а зоны
зоны Ωα при изменении ϵF в интервале [ϵmin, ϵmax].
устойчивости Ωβ типа (-) — открытыми областями
Как мы уже сказали, нас будут интересовать
U-β, такими что:
вопросы сложности угловых диаграмм для прово-
1) Все области U+α и U-β не пересекаются друг
димости в металлах с произвольными (физически-
с другом, а также с зонами устойчивости Ωα типа
ми) дисперсионными соотношениями. Отметим так-
(±);
же, что в работе [32] было предложено разделить
152
ЖЭТФ, том 156, вып. 1 (7), 2019
Классы сложности угловых диаграмм проводимости металлов. ..
B
а
B
б
B
в
Рис. 20. Границы зон Ω∗α, лежащие внутри областей Ω′α
а
б
в
г
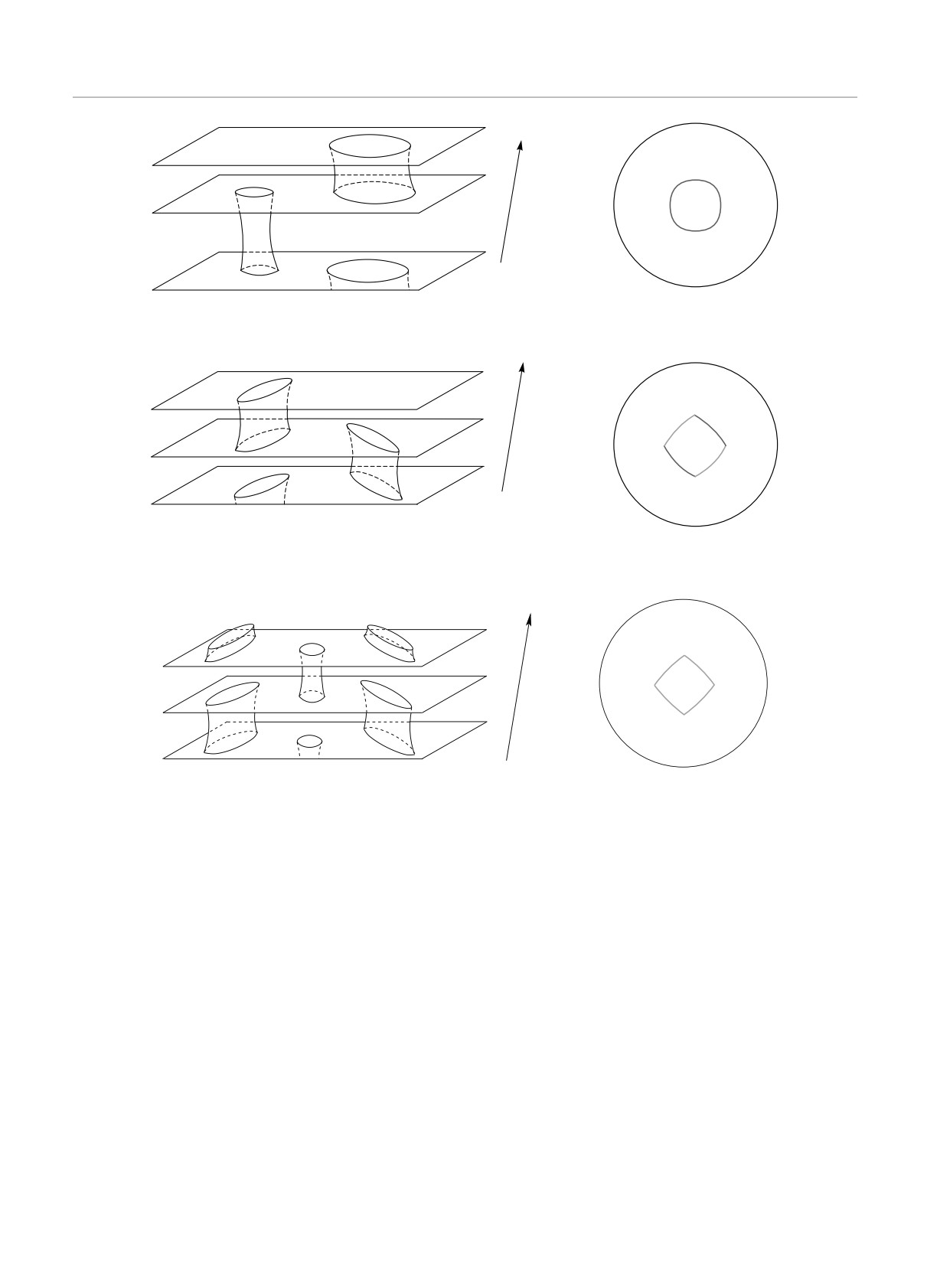
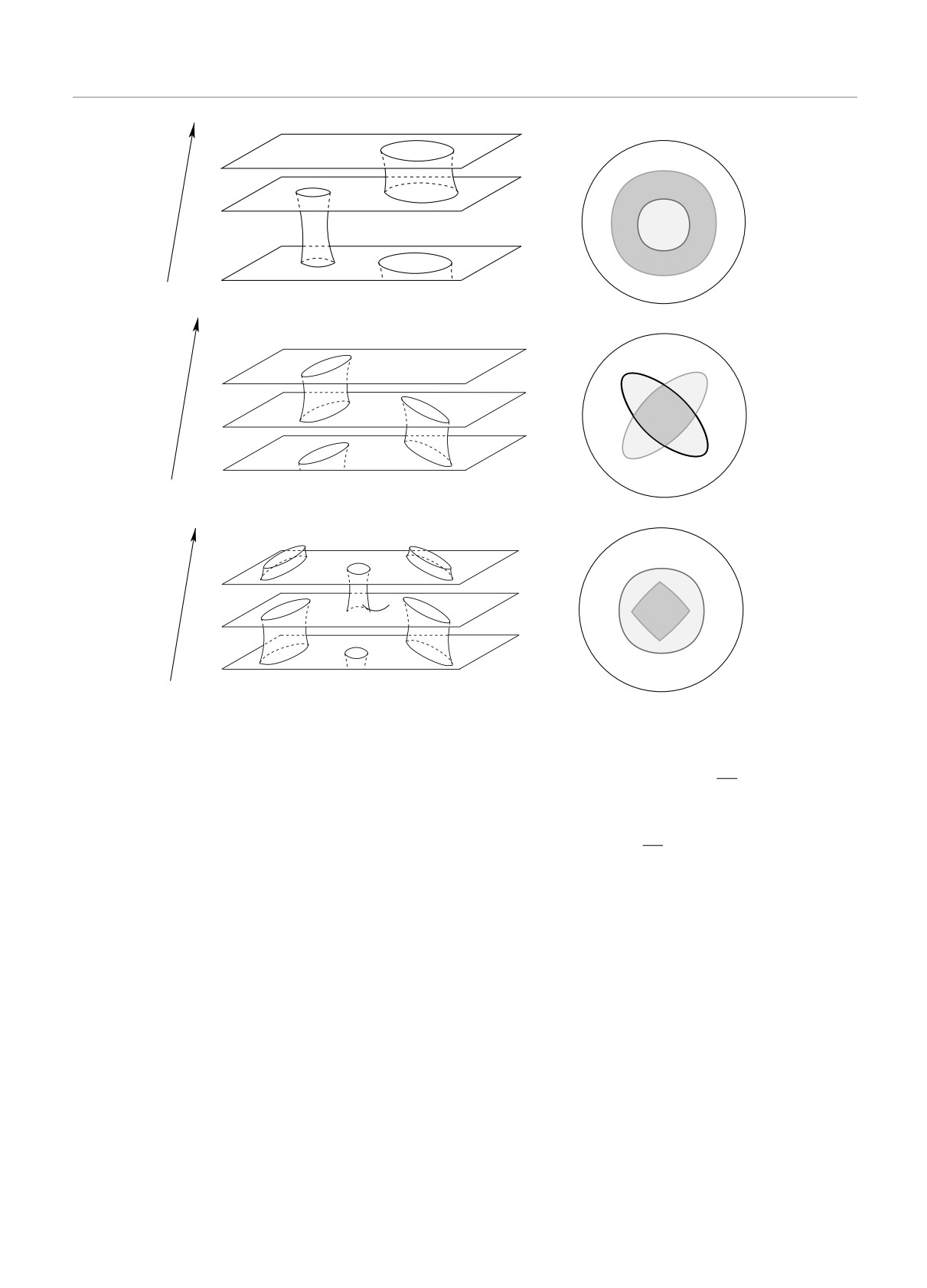
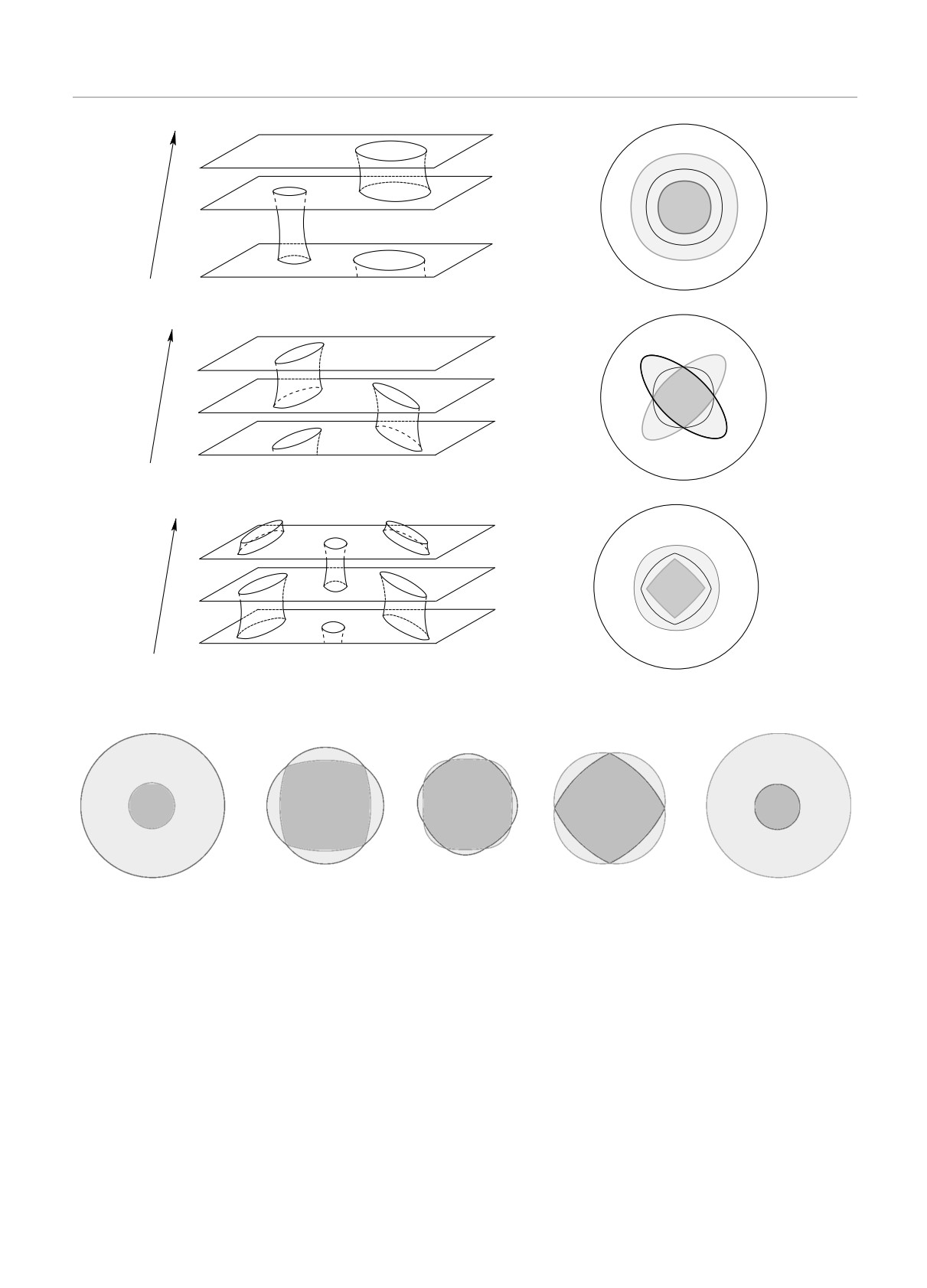
д
Рис. 21. Изменение формы зон Ωα и Ωα при возрастании значения ϵF для фиксированного дисперсионного соотноше-
ния ϵ(p): a — появление и рост зоны устойчивости Ωα, имеющей тип (-); б — смыкание первой и второй границ зоны
Ωα и образование зоны типа (±); в — эволюция зоны типа (±); г — изменение типа зоны на (+); д — уменьшение и
исчезновение зоны типа (+)
все нетривиальные (содержащие зоны устойчиво-
Более точно, для направлений B общего положе-
сти) угловые диаграммы металлов на более простые
ния, лежащих вне какой-либо зоны устойчивости, на
(тип A) и более сложные (тип B). Как было отмече-
поверхности Ферми имеются лишь замкнутые тра-
но в работе [32], данные особенности угловых диа-
ектории системы (1.2). Тензор электропроводности в
грамм связаны с поведением холловской проводимо-
плоскости, ортогональной B, может быть представ-
сти вне зон устойчивости в пределе ωBτ → ∞.
лен в этом случае в виде регулярного ряда по обрат-
153
А. Я. Мальцев
ЖЭТФ, том 156, вып. 1 (7), 2019
ным степеням параметра ωBτ в пределе ωBτ → ∞
и имеет в главном порядке следующий вид:
(
)
-1
a11 (ωBτ)-2
a12 (ωBτ)
σαβ =
,
-a12 (ωBτ)-1 a22 (ωBτ)-2
(4.3)
ωBτ → ∞.
Величина σ12
= a12(ωBτ)-1 может быть при
а
этом представлена в виде
ec
σ12 =
(ne - nh) ,
(4.4)
B
где величины ne и nh представляют «электронную
и дырочную концентрации» для заданного направ-
ления B. Величины ne и nh могут быть определены
формулами
ne = 2Ve/(2πℏ)3, nh = 2Vh/(2πℏ)3,
б
где Ve и Vh обозначают объемы, ограниченные всеми
неэквивалентными цилиндрами замкнутых траекто-
Рис. 22. Две возможные картины в плоскостях, ортого-
нальных B, в случае, когда поверхность Ферми содержит
рий (на поверхности Ферми) электронного и дыроч-
только замкнутые траектории в p-пространстве
ного типа в p-пространстве.
Важной особенностью возникающей картины
для направлений B общего положения, лежащих
вне какой-либо зоны устойчивости, является то,
В результате, величина холловской проводимос-
что во всех плоскостях, ортогональных B, воз-
ти является локально постоянной (при постоянной
никает один и тот же тип поведения траекторий
величине B) везде за пределами зон устойчивости
системы (1.2), определяемый одной из следующих
при выполнении условия ωBτ ≫ 1. (В действитель-
возможностей.
ности, условия τ ≫ T , где T — типичное время об-
I. Область больших значений энергии ϵ(p) > ϵF
ращения электрона по замкнутой траектории при
представляет собой «море» в плоскости, ортогональ-
заданном направлении B. Как указывалось в [32],
ной B, в то время как области меньшей энергии
это условие может являться более сильным.) Дан-
ϵ(p) < ϵF представляют собой конечные «острова»
ное обстоятельство, как легко видеть, дает простое
(«острова» могут содержать «озера» больших зна-
средство экспериментального определения каждой
чений энергии и т. д., рис. 22a).
из двух описанных ситуаций для направлений B, ле-
II. Область меньших значений энергии ϵ(p) < ϵF
жащих вне зон устойчивости. При этом области, от-
представляет собой «море» в плоскости, ортогональ-
вечающие различным описанным ситуациям, долж-
ной B, в то время как области большей энергии
ны быть разделены зонами устойчивости, которые
ϵ(p) > ϵF представляют собой конечные «острова»
образуют в случае общего положения «цепочки», со-
(«острова» могут содержать «озера» меньших зна-
стоящие из бесконечного числа зон.
чений энергии и т. д., рис. 22б).
Определим тип (A или B) угловой диаграммы
Как следствие, величина σ12 в этом случае опре-
проводимости металла следующим образом.
деляется в действительности одним из следующих
Скажем, что угловая диаграмма проводимости
соотношений:
металла имеет тип A, если для всех направлений
2ec
B общего положения вне зон Ωα наблюдается лишь
σ12 =
V- (ситуация I),
(4.5)
(2πℏ)3B
один тип холловской проводимости в пределе ωBτ →
→ ∞. Скажем, что угловая диаграмма проводимо-
2ec
σ12 = -
V+ (ситуация II),
(4.6)
сти металла имеет тип B, если для различных на-
(2πℏ)3B
правлений B общего положения вне зон Ωα могут
где V- и V+ обозначают объемы, определенные усло-
наблюдаться оба типа холловской проводимости в
виями ϵ(p) < ϵF и ϵ(p) > ϵF в зоне Бриллюэна.
пределе ωBτ → ∞.
154
ЖЭТФ, том 156, вып. 1 (7), 2019
Классы сложности угловых диаграмм проводимости металлов. ..
«угловой точке» границы должна при этом примы-
кать цепочка зон устойчивости, отделяющая обла-
I
II
сти с разной холловской проводимостью, возникаю-
щие вблизи соответствующих участков границы зо-
ны Ωα. При этом зона Ωβ может примыкать непо-
I
II
средственно к «угловой точке» Ωα только в том слу-
чае, если соответствующее направление B отвечает
появлению периодических траекторий (с направле-
нием, задаваемым пересечением плоскостей Γα и Γβ)
на поверхности Ферми, что соответствует случаю
Рис. 23. Области с различными значениями холловской
необщего положения. В случае же общего положе-
проводимости и цепочка уменьшающихся зон устойчиво-
ния, к «угловой точке» зоны Ωα должна примыкать
сти и «хаотических» направлений B вблизи «угловой точ-
цепочка из бесконечного числа уменьшающихся зон
ки» границы зоны устойчивости типа (±)
устойчивости Ωβ (рис. 23).
Заметим здесь, что любая точка накопления
Сделаем здесь еще одно замечание, касающе-
уменьшающихся зон устойчивости, не являющаяся
еся поверхностей Ферми реальных металлов. Как
точкой границы некоторой зоны устойчивости, соот-
мы уже сказали выше, мы предполагаем здесь для
ветствует направлению B, отвечающему появлению
простоты, что поверхность Ферми состоит из одной
хаотических траекторий (типа Царева или Дынни-
связной компоненты, на которой мы и рассматри-
кова) на поверхности Ферми. Совокупность соответ-
ваем траектории системы (1.2). В действительно-
ствующих направлений B представляет собой в об-
сти, поверхность Ферми реального металла состоит
щем случае довольно сложное множество на угловой
обычно из нескольких компонент и очень часто со-
диаграмме S2. Как можно показать (см. [23]), об-
держит компоненты рода 0 или 1 вместе со слож-
щая мера таких направлений на угловой диаграмме
ными компонентами. При вычислении холловской
равна нулю для поверхности Ферми общего положе-
проводимости мы должны в действительности сло-
ния. Согласно гипотезе Новикова [26,27], фракталь-
жить вклады от всех компонент поверхности Ферми,
ная размерность множества D таких направлений
которые также обладают описанными выше свой-
для поверхности Ферми общего положения строго
ствами. При этом может оказаться, что тип полной
меньше единицы (но может быть больше для специ-
холловской проводимости может отличаться от ти-
альных поверхностей Ферми). Отметим здесь так-
па вклада в эту проводимость от рассматриваемой
же, что, в отличие от угловых диаграмм для всего
нами компоненты. Поэтому более строго было бы
дисперсионного соотношения, на угловых диаграм-
говорить, что угловая диаграмма проводимости ме-
мах для поверхности Ферми общего положения на-
талла имеет тип A, если для всех направлений B об-
копление уменьшающихся зон устойчивости не мо-
щего положения вне зон Ωα наблюдается лишь од-
жет происходить у «регулярных» точек границ Ωα,
но значение холловской проводимости (при задан-
поскольку каждая из зон Ωα окружена здесь до-
ном значении B) при условии ωBτ
≫ 1, и угло-
полнительной областью Ω′α. Исключение составля-
вая диаграмма проводимости металла имеет тип B,
ют лишь «угловые» точки зон типа (±), где вторая
если для различных направлений B общего поло-
граница зоны Ωα примыкает к первой.
жения вне зон Ωα могут наблюдаться как минимум
Множество
два значения холловской проводимости при том же
⋃(
)
условии. Мы для большей наглядности изложения
M=D
∪Ωα
сохраним здесь, однако, введенную выше термино-
логию.
представляет собой при этом замкнутое множество
Как было также отмечено в работе [32], угловая
на S2.
диаграмма имеет тип B, в частности, если она со-
В точках множества S2\M мы всегда имеем од-
держит хотя бы одну зону устойчивости типа (±).
но из соотношений ϵF < ϵ1(B/B) или ϵF > ϵ2(B/B),
Действительно, как можно показать (см. [32]), в
при этом соответствующие подмножества на S2 раз-
разных связных компонентах соответствующей об-
делены точками множества M. Можно видеть (см.
ласти Ω′α при этом присутствуют различные типы
[23]), что первое из соотношений соответствует опи-
холловской проводимости для направлений B об-
санной выше картине (I) для направлений B общего
щего положения (рис. 23). Можно видеть, что к
положения, в то время как второе соотношение со-
155
А. Я. Мальцев
ЖЭТФ, том 156, вып. 1 (7), 2019
ответствует картине (II) для направлений B общего
мера компонент, отвечающих дырочной холловской
положения.
проводимости, растет.
Надо сказать, что точки множества D, также
Естественно ввести также величины
как и зоны устойчивости Ωα играют важную роль
ϵA1 = min ϵ1(B/B), ϵA2 = max ϵ2(B/B).
при разделении множества S2\M на компоненты с
различным поведением холловской проводимости в
Как следует из наших рассуждений, угловая
пределе ωBτ → ∞. Отметим также, что из всего
диаграмма проводимости металла принадлежит к
набора зон устойчивости Ωα для разделения таких
типу A, если уровень Ферми ϵF принадлежит од-
компонент важны лишь зоны типа (±), поскольку
ному из интервалов (ϵA1, ϵB1] или [ϵB2, ϵA2). Нетрудно
зоны типа (+) и (-) не играют роли в разделении
видеть также, что первый случай соответствует при
упомянутых компонент в силу приведенных выше
этом холловской проводимости электронного типа
свойств (1) и (2) и соотношений (4.1), (4.2).
при B/B ∈ S2\M, в то время как второй случай от-
В рассматриваемой ситуации естественно ввести
вечает холловской проводимости дырочного типа на
следующие величины:
том же множестве направлений B (общего положе-
ния).
ϵB1 = min ϵ2(B/B), ϵB2 = max ϵ1(B/B)
На рис.
24
представлено (очень схематично)
типичное изменение угловой диаграммы проводи-
для каждого дисперсионного соотношения. Отме-
мости при изменении величины ϵF в интервале
тим сразу, что для рассматриваемых нами сложных
(ϵA1, ϵA2). Так, после прохождения уровня ϵF = ϵA1
угловых диаграмм (бесконечное число зон устойчи-
можно наблюдать появление первых зон устойчи-
вости для всего дисперсионного соотношения) мы
вости и затем дальнейшее увеличение их числа и
всегда имеем соотношение
размеров, при этом всюду за пределами зон устой-
ϵB2 ≥ ϵB1,
чивости имеет место электронный тип холловской
проводимости для направлений B общего положе-
поскольку на границах зон устойчивости Ω∗α, (а так-
ния. Количество зон устойчивости стремится к бес-
же для «хаотических» направлений B) мы имеем со-
конечности при ϵF → ϵB1, и в точке ϵB1 наблюдается
отношение ϵ1(B/B) = ϵ2(B/B). Для дисперсионных
появление первых точек сгущения зон устойчивости
соотношений общего положения мы в действитель-
на угловой диаграмме. После прохождения значе-
ности будем иметь
ния ϵB1 можно наблюдать присутствие областей вне
зон устойчивости, соответствующих как электрон-
ϵB2 > ϵB1,
ной, так и дырочной холловской проводимости, и
разделенных бесконечным множеством зон устойчи-
поскольку для таких направлений B соответствую-
вости и «хаотических» направлений B (в случае об-
щие величины
F
щего положения). По мере увеличения значения ϵ
мера областей, соответствующих электронной хол-
ϵ1(B/B) = ϵ2(B/B) = ϵ0(B/B)
ловской проводимости, убывает, в то время как ме-
не принадлежат единственному уровню энергии в
ра областей, соответствующих дырочной холловс-
общем случае. Как следует из наших рассуждений,
кой проводимости, растет. В интервале (ϵB1, ϵB2) мож-
угловая диаграмма проводимости металла принад-
но также наблюдать рождение новых зон типа (-),
лежит к типу B, если уровень Ферми ϵF принадле-
образование из них зон типа (±), а затем зон типа
жит интервалу (ϵB1, ϵB2).
(+) и исчезновение зон типа (+). В точке ϵF = ϵB2
В граничных точках интервала ϵF = ϵB1 и ϵF =
области, соответствующие электронной холловской
= ϵB2 на всем множестве S2\M имеет место только
проводимости, полностью исчезают, и после прохож-
один тип холловской проводимости (соответственно,
дения значения ϵB2 мы снова имеем угловую диа-
электронный и дырочный) для направлений B об-
грамму типа A, соответствующую дырочной хол-
щего положения, при этом угловая диаграмма про-
ловской проводимости для направлений B (обще-
водимости металла содержит в случае общего по-
го положения) вне зон Ωα. Таким образом, число
ложения бесконечное число зон устойчивости Ωα.
зон устойчивости и их размеры уменьшаются с рос-
Можно видеть также, что по мере возрастания ве-
том значения ϵF и в пределе ϵF → ϵA2 зоны полно-
личины ϵF в интервале [ϵB1, ϵB2] общая мера компо-
стью исчезают. Как можно видеть, наиболее слож-
нент S2\M, соответствующих электронной холловс-
ная структура угловых диаграмм должна наблю-
кой проводимости, убывает, в то время как общая
даться в общем случае вдоль «квазиодномерных»
156
ЖЭТФ, том 156, вып. 1 (7), 2019
Классы сложности угловых диаграмм проводимости металлов. ..
e
e
h
e
e
e
e
e
e
e
h
e
e
e
e
h
h
h
h
e
e
e
e
e
h
e
e
e
e
e
e
h
а
б
в
h
h
h
h
e
e
e
e
h
h
h
h
h
e
h
e
h
h
h
h
h
h
h
e
e
h
h
h
h
h
h
e
h
e
e e
h
h
h
h
г
д
е
Рис. 24. a) Зарождение первых зон устойчивости типа (-) после прохождения значения ϵA1 уровнем Ферми ϵF ; б) уве-
личение числа зон типа (-) и появление точек сгущения мелких зон при ϵF → ϵ1; в) образование областей дырочной
холловской проводимости и зон типа (±) и (+) и появление «хаотических» направлений B после прохождения значения
ϵB1 уровнем Ферми ϵF ; г) исчезновение областей электронной холловской проводимости и зон типа (-) и (±) при ϵF → ϵ2;
д) исчезновение точек сгущения мелких зон и уменьшение числа и размеров зон типа (+) после прохождения значения
ϵB2 уровнем Ферми ϵF ; е) исчезновение зон типа (+) в пределе ϵF → ϵ2
множеств, разделяющих области различных значе-
ϵF > ϵB2. Напомним здесь также, что мы рассматри-
ний холловской проводимости.
ваем здесь угловые диаграммы сложного типа, т.е.
диаграммы, содержащие более одной зоны устойчи-
Как мы уже отмечали выше, угловая диаграм-
вости при изменении ϵF в интервале (ϵA1, ϵA2).
ма типа B общего положения содержит бесконеч-
ное число зон устойчивости со сколь угодно больши-
Как можно видеть также, оба типа сложных диа-
ми значениями топологических чисел (M1α, M2α, M3α).
грамм (A и B) представляют диаграммы общего по-
Как нетрудно показать, угловая диаграмма типа A
ложения и должны наблюдаться эксперименталь-
общего положения, напротив, содержит лишь ко-
но. При этом надо отметить, что диаграммы ти-
нечное число зон Ωα. Более точно, можно видеть,
па B должны быть, видимо, довольно редки в си-
что если ϵF ∈ (ϵA1, ϵB1) или ϵF ∈ (ϵB2, ϵA2), то соот-
лу небольшого размера отрезка (ϵB1, ϵB2) для реаль-
ветствующая угловая диаграмма проводимости ме-
ных дисперсионных соотношений. Можно отметить
талла содержит лишь конечное число зон устойчи-
также, что хотя для дисперсионных законов с близ-
вости. Действительно, наличие бесконечного числа
кими значениями ϵB1 и ϵB2 вероятность наблюдения
зон устойчивости означает наличие точки скопле-
диаграммы типа B весьма мала, соответствующие
ния таких зон на S2, в которой мы должны иметь
диаграммы при этом наиболее приближаются по
соотношение ϵ1(B/B) = ϵ2(B/B), что невозможно в
сложности к диаграммам, соответствующим полно-
указанных интервалах энергии.
му дисперсионному соотношению.
Можно видеть, таким образом, что угловая диа-
Для наиболее полного описания всех типов угло-
грамма типа A может содержать бесконечное число
вых диаграмм, возникающих в теории нормальных
зон устойчивости только в случае ϵF = ϵB1 или ϵF =
металлов, естественно ввести еще величины
= ϵB2. Нетрудно видеть также, что по той же причине
угловая диаграмма проводимости не может содер-
жать «хаотических» направлений B при ϵF < ϵB1 или
ϵA′1 = inf ϵ1(B/B), ϵA′2 = supϵ2(B/B).
157
А. Я. Мальцев
ЖЭТФ, том 156, вып. 1 (7), 2019
Отметим, что здесь мы уже не фокусируем вни-
(T1) Наиболее простые диаграммы:
мание лишь на «сложных» поверхностях Ферми и
ϵF ∈ [ϵmin, ϵA′1].
включаем в рассмотрение все их типы.
Поверхность Ферми может содержать лишь замкну-
Для значений ϵF , лежащих в интервалах (ϵA′1, ϵA1]
тые или сингулярные траектории системы (1.2) при
и [ϵA2, ϵA′2), угловая диаграмма проводимости не со-
любом направлении B. Вклад в холловскую прово-
держит конечных зон устойчивости и может со-
димость от соответствующего дисперсионного соот-
держать лишь зоны, вырождающиеся в точки при
ношения имеет электронный тип и постоянное зна-
ϵF = ϵA1 или ϵF = ϵA2. При этом для значений ϵF,
чение (при заданном значении B, ωBτ ≫ 1) при всех
лежащих в интервалах (ϵA′1, ϵA1) и (ϵA2, ϵA′2), на по-
направлениях B.
верхности Ферми появляются лишь (неустойчивые)
(T2) Достаточно простые диаграммы:
периодические траектории системы (1.2) при специ-
альных направлениях B. Соответствующие направ-
ϵF ∈ (ϵA′1, ϵA1].
ления B представлены при этом сегментами боль-
ших кругов, каждый из которых отвечает опре-
Поверхность Ферми может содержать лишь замкну-
деленному рациональному направлению открытых
тые, сингулярные или неустойчивые периодические
траекторий системы (1.2). Нетрудно видеть так-
открытые траектории системы (1.2). Множество на-
же, что в интервалах (ϵA′1, ϵA1) и (ϵA2, ϵA′2) количе-
правлений B, отвечающих появлению периодичес-
ство указанных сегментов и соответствующих им
ких открытых траекторий, представлено набором
рациональных направлений траекторий всегда яв-
сегментов больших кругов, каждый из которых от-
ляется конечным. Действительно, бесконечный на-
вечает определенному рациональному направлению
бор сегментов указанного типа должен обязатель-
периодических траекторий. При ϵF ∈ (ϵA′1, ϵA1) мно-
но содержать точки накопления на S2, в каждой
жество таких сегментов является конечным. При
окрестности которых присутствуют периодические
ϵF = ϵA1 количество сегментов и соответствующих
траектории со сколь угодно большими знаменате-
им рациональных направлений периодических от-
лями соответствующих рациональных направлений.
крытых траекторий может быть бесконечным. Для
Для соответствующих направлений B мы имеем со-
направлений B общего положения вклад в хол-
отношения ϵ1(B/B)
< ϵ1(B/B) (или ϵ2(B/B) >
ловскую проводимость от соответствующего дис-
> ϵ2(B/B)), однако величины |ϵ1(B/B) - ϵ1(B/B)|
персионного соотношения имеет электронный тип
(или |ϵ2(B/B) - ϵ2(B/B)|) довольно быстро убыва-
и постоянное значение при заданном значении B
ют с ростом знаменателей рациональных направле-
(ωB τ ≫ 1).
ний периодических траекторий. Как следствие это-
(T3) Сложные диаграммы типа A:
го, в соответствующих точках накопления мы долж-
ϵF ∈ (ϵA1, ϵB1].
ны иметь соотношения ϵ1(B/B)
= ϵ1(B/B) или
ϵ2(B/B) = ϵ2(B/B), что невозможно в указанных
Кроме замкнутых и сингулярных траекторий,
энергетических интервалах. Можно видеть также,
поверхность Ферми общего положения содержит
что при ϵF = ϵA1 или ϵF = ϵA2 множество направ-
устойчивые открытые траектории и неустойчи-
лений B, соответствующих появлению периодиче-
вые периодические траектории для определенных
ских траекторий на поверхности Ферми, может со-
направлений B. Устойчивые открытые траек-
держать бесконечное число сегментов больших кру-
тории обладают описанными выше свойствами
гов, отвечающих бесконечному числу рациональных
регулярности и возникают в специальных зонах
направлений неустойчивых открытых траекторий.
устойчивости Ωα на угловой диаграмме, отвеча-
ющих определенным значениям топологических
Наконец, в интервалах [ϵmin, ϵA′1] и [ϵA′2, ϵmax]
квантовых чисел (M1α, M2α, M3α). При ϵF ∈ (ϵA1, ϵB1)
система (1.2) не может содержать несингулярных
количество зон устойчивости на угловой диаграмме
открытых траекторий.
является конечным. Множество направлений B,
В результате, можно привести разделение всех
отвечающих появлению периодических открытых
угловых диаграмм на «классы сложности» в соот-
траекторий, представлено бесконечным набором
ветствии с положением уровня Ферми по отноше-
сегментов больших кругов, каждый из которых от-
нию к набору «реперных» точек, определенных для
вечает определенному рациональному направлению
заданного дисперсионного соотношения (общего по-
периодических траекторий. При ϵF = ϵB1 множество
ложения). А именно:
зон устойчивости Ωα становится в случае общего
158
ЖЭТФ, том 156, вып. 1 (7), 2019
Классы сложности угловых диаграмм проводимости металлов. ..
положения (т. е. для дисперсионного закона общего
общего положения вне зон Ωα вклад в холловскую
положения) бесконечным, кроме того, на угловой
проводимость от соответствующего дисперсионного
диаграмме возникают специальные направления B,
соотношения имеет дырочный тип и постоянное
отвечающие появлению хаотических открытых тра-
значение при заданном значении B (ωBτ ≫ 1).
екторий на поверхности Ферми. Для направлений B
(T6) Достаточно простые диаграммы:
общего положения вне зон Ωα вклад в холловскую
ϵF ∈ [ϵA2, ϵA′2).
проводимость от соответствующего дисперсионного
соотношения имеет электронный тип и постоянное
Поверхность Ферми может содержать лишь замкну-
значение при заданном значении B (ωBτ ≫ 1).
тые, сингулярные или неустойчивые периодические
(T4) Сложные диаграммы типа B:
открытые траектории системы (1.2). Множество на-
правлений B, отвечающих появлению периодичес-
ϵF ∈ (ϵB1, ϵB2).
ких открытых траекторий, представлено набором
Кроме замкнутых и сингулярных траекторий, по-
сегментов больших кругов, каждый из которых от-
верхность Ферми содержит устойчивые открытые
вечает определенному рациональному направлению
траектории, неустойчивые периодические траекто-
периодических траекторий. При ϵF ∈ (ϵA2, ϵA′2) мно-
рии и хаотические траектории для определенных
жество таких сегментов является конечным. При
направлений B. Множество зон устойчивости Ωα,
ϵF = ϵA2 количество сегментов и соответствующих
множество дополнительных сегментов больших кру-
им рациональных направлений периодических от-
гов, отвечающих появлению периодических откры-
крытых траекторий может быть бесконечным. Для
тых траекторий, а также множество специальных
направлений B общего положения вклад в холловс-
направлений B, отвечающих появлению хаотиче-
кую проводимость от соответствующего дисперси-
ских открытых траекторий на поверхности Ферми,
онного соотношения имеет дырочный тип и постоян-
являются в случае общего положения бесконечны-
ное значение при заданном значении B (ωBτ ≫ 1).
ми. Для направлений B общего положения вне зон
(T7) Наиболее простые диаграммы:
Ωα вклад в холловскую проводимость от соответ-
ствующего дисперсионного соотношения имеет раз-
ϵF ∈ [ϵA′2, ϵmax].
личные типы (электронный и дырочный) в различ-
Поверхность Ферми может содержать лишь замкну-
ных областях угловой диаграммы, разделенных в
тые или сингулярные траектории системы (1.2) при
случае общего положения бесконечными «цепями»
любом направлении B. Вклад в холловскую прово-
зон устойчивости и «хаотических» направлений B
димость от соответствующего дисперсионного соот-
(ωBτ ≫ 1).
ношения имеет дырочный тип и постоянное значе-
(T5) Сложные диаграммы типа A:
ние (при заданном значении B, ωBτ ≫ 1) при всех
направлениях B.
ϵF ∈ [ϵB2, ϵA2).
Таким образом, все угловые диаграммы прово-
Кроме замкнутых и сингулярных траекторий,
димости в металлах в сильных магнитных полях
поверхность Ферми общего положения содержит
могут быть отнесены к одному из представленных
устойчивые открытые траектории и неустойчи-
выше классов (T1)-(T7), определяемых положением
вые периодические траектории для определенных
уровня Ферми и дисперсионным законом ϵ(p). От-
направлений B. При ϵF
∈ (ϵB2, ϵA2) количество
метим снова, что полная картина угловых диаграмм
зон устойчивости на угловой диаграмме является
для всех значений ϵF имеет до некоторой степени
конечным. Множество направлений B, отвечающих
абстрактный характер, поскольку эксперименталь-
появлению периодических открытых траекторий,
но наблюдаемой является лишь диаграмма для нас-
представлено бесконечным набором сегментов
тоящего значения ϵF . В частности, при эксперимен-
больших кругов, каждый из которых отвечает
тальном изменении положения ϵF (например, с по-
определенному рациональному направлению пе-
мощью внешнего давления) изменение соответству-
риодических траекторий. При ϵF = ϵB2 множество
ющей диаграммы проводимости не обязано опре-
зон устойчивости Ωα является в случае общего
деляться исходным соотношением ϵ(p), поскольку
положения бесконечным, кроме того, на угловой
соответствующее внешнее воздействие меняет па-
диаграмме имеются специальные направления B,
раметры дисперсионного соотношения. Приведен-
отвечающие появлению хаотических открытых тра-
ное замечание, однако, не отменяет того обстоя-
екторий на поверхности Ферми. Для направлений B
тельства, что тип конкретной угловой диаграммы
159
А. Я. Мальцев
ЖЭТФ, том 156, вып. 1 (7), 2019
определен при этом однозначно, исходя из теорети-
(T1), (T2), (T6), (T7) в точности совпадают с опи-
ческого рассмотрения, приведенного выше. Заметим
санными выше классами, а для диаграмм классов
снова, что наше рассмотрение здесь может считать-
(T3) и (T5) надо заменить лишь слова «количество
ся совершенно общим для любого «физически ре-
зон устойчивости на угловой диаграмме является
алистичного» дисперсионного соотношения ϵ(p). В
конечным» на «мы имеем одну зону устойчивости
то же время, мы опускаем здесь некоторые теорети-
Ω, занимающую часть сферы S2». (Мы не требуем
чески возможные дополнительные особенности (на-
здесь связности зоны Ω, и, в частности, считаем од-
пример, неодносвязность зон устойчивости), кото-
ной зоной ее возможно разделенные противополож-
рые являются крайне маловероятными в реальной
ные части на S2.) Что же касается класса (T4), то
ситуации.
диаграммы этого класса содержат здесь одну зону
Еще одно замечание, которое можно здесь сде-
устойчивости Ω, занимающую всю сферу S2. Заме-
лать, относится к тому факту, что в общем слу-
тим здесь, что для класса (T4) теоретически мы мог-
чае полная поверхность Ферми представляет собой
ли бы также иметь зону устойчивости Ω, занимаю-
объединение нескольких компонент, относящихся к
щую часть сферы S2, с различными знаками хол-
различным дисперсионным соотношениям. Нетруд-
ловской проводимости в различных областях вне Ω.
но видеть, что угловая диаграмма проводимости да-
Эта ситуация, однако, соответствует неодносвязной
ется в этом случае «наложением» диаграмм, опреде-
зоне Ω и физически крайне маловероятна, так что
ляемых всеми компонентами. Важным обстоятель-
мы не приводим ее здесь.
ством является то, что если различные компоненты
Отметим также, что упомянутые выше «репер-
не пересекаются друг с другом, то пересечение соот-
ные» значения энергии связаны довольно просто с
ветствующих им зон устойчивости возможно толь-
«реперными» значениями, определяемыми для дис-
ко в том случае, когда эти зоны отвечают одним и
персионных соотношений, обладающих «сложны-
тем же топологическим числам (M1α, M2α, M3α). Как
ми» угловыми диаграммами. Так, можно в действи-
следствие, такие пересекающиеся зоны можно рас-
тельности написать соотношения
сматривать как сложные «составные» зоны с более
′
′
сложной структурой границ.
ϵA1
=ϵA′1,
ϵA1 = ϵA1,
ϵA2 = ϵA2,
ϵA2
=ϵA′2
Нам следует также сказать несколько слов об уг-
в соответствии с определением величин ϵA′1, ϵA1, ϵA2,
ловых диаграммах (для фиксированных значений
A′
ϵ
, приведенными выше.
ϵF ), возникающих для дисперсионных соотношений,
2
Что же касается величин ϵB1 и ϵB2, то для них мы
обладающих всего одной зоной устойчивости Ω (за-
имеем соотношения
нимающей всю сферу S2). Отметим, что диспер-
сионные соотношения такого типа также представ-
ϵB1 = ϵB2 = max ϵ1(B/B),
ляют собой соотношения общего положения и мо-
гут вполне встречаться в реальных кристаллах. (В
ϵB2 = ϵB1 = min ϵ2(B/B),
частности, к ним относятся соотношения, для ко-
торых в некотором интервале энергии поверхности
поскольку для дисперсионных законов рассматрива-
ϵ(p) = const представляют собой набор периодичес-
емого типа имеем в нашем случае соотношение ϵB1 >
ки деформированных («гофрированных») целочис-
> ϵB2. (Заметим снова, что теоретически здесь воз-
ленных плоскостей, не соединенных друг с другом.)
можна также ситуация ϵB1 < ϵB2 и ϵB1 = ϵB1, ϵB2 = ϵB2,
Мы опустим здесь подробный анализ возникающей
однако она крайне маловероятна согласно нашим за-
ситуации и приведем лишь общее описание классов
мечаниям выше.)
сложности угловых диаграмм, возникающих в этом
Нетрудно видеть также, что никакие угловые
случае для различных значений ϵF .
диаграммы не могут в рассматриваемом случае со-
Именно, как и в случае дисперсионных соотно-
держать направлений B, соответствующих появле-
шений со «сложными» угловыми диаграммами, в
нию «хаотических» траекторий на поверхности Фер-
рассматриваемой нами ситуации можно в случае об-
ми.
щего положения ввести также некоторые «репер-
В заключение проведем некоторое сравнение
ные» значения
сложности расположения зон устойчивости на угло-
вых диаграммах для фиксированных поверхностей
ϵmin < ϵA′1 < ϵA1 < ϵB1 < ϵB2 < ϵA2 < ϵA′2 < ϵmax
Ферми с расположением зон Ω∗α на диаграммах для
и классы диаграмм (T1)-(T7), аналогичные рас-
всего дисперсионного закона. Более конкретно, мы
смотренным выше. При этом диаграммы классов
рассмотрим аналог структуры зон, представленной
160
ЖЭТФ, том 156, вып. 1 (7), 2019
Классы сложности угловых диаграмм проводимости металлов. ..
на рис. 16, для диаграмм, определенных для фикси-
а
рованного значения ϵF .
Как мы уже видели, угловые диаграммы прово-
димости для фиксированных значений ϵF могут, в
частности, быть довольно простыми и не обладать
уровнем сложности, сопоставимым с уровнем слож-
ности для угловых диаграмм для всего соотношения
ϵ(p). Нам поэтому будут интересны диаграммы (ти-
па A или B), содержащие зоны устойчивости Ωα,
близкие по форме к соответствующим зонам устой-
чивости Ω∗α, определенным для всего дисперсионно-
го соотношения. Как нетрудно видеть, такими зо-
нами являются зоны устойчивости, первая и вторая
границы которых расположены достаточно близко
друг к другу (рис. 21б,в,г). Как мы уже указыва-
б
ли ранее, в области Ω′α, ограниченной первой и вто-
рой границами зоны Ωα, не может возникать устой-
чивых открытых траекторий системы (1.2) и, соот-
ветственно, не может быть других зон устойчивости
для данного значения ϵF . Можно видеть, таким об-
разом, что структуры, аналогичные приведенной на
рис. 16, если они возникают, должны быть связаны
в этом случае со второй границей зоны Ωα.
Для описания возникающей в нашем случае кар-
тины необходимо обратиться снова к структуре по-
верхности Ферми при B/B ∈ Ωα (рис. 10), а также
Рис. 25. a) Проекции длинных замкнутых траекторий сис-
механизму разрушения этой структуры на первой и
темы (1.2), возникающих после пересечения границы зоны
второй границах Ωα посредством «перескоков» тра-
устойчивости при иррациональном среднем направлении
екторий с одного носителя открытых траекторий на
открытых траекторий; б) проекции длинных замкнутых и
другой, представленных на рис. 11.
открытых периодических траекторий системы (1.2) после
пересечения границы зоны устойчивости при рациональ-
Для упрощения описания удобно рассмотреть
ном среднем направлении открытых траекторий
проекцию «носителей открытых траекторий» на
плоскость Π(B/B), порожденную направлением B,
а также направлением пересечения плоскости, орто-
Каждый из носителей открытых траекторий
гональной B, и плоскости Γα. Все траектории сис-
представляет собой периодически деформирован-
темы (1.2) будут представлены в этой плоскости па-
ную целочисленную плоскость в p-пространстве и,
раллельными прямыми линиями, ортогональными
таким образом, картина, возникающая в плоскости
B. После пересечения первой границы Ωα и воз-
Π(B/B), всегда является двоякопериодической. (За-
никновения перескоков траекторий с одного носи-
метим также, что отверстия (плоские диски) в носи-
теля на другой (рис. 11) для каждого носителя на
телях открытых траекторий исчезают на проекции,
проекции можно отметить «места», где происходят
будучи ортогональными B.) В частности, двоякопе-
перескоки траекторий между парами «слившихся»
риодическим является расположение описанных на-
носителей. Оба бывших носителя из каждой обра-
ми «ловушек» для каждой пары «слившихся» носи-
зовавшейся пары можно представлять одной и той
телей открытых траекторий.
же проекцией на плоскость Π(B/B), а «места», где
Прямые линии, представляющие собой траекто-
происходят перескоки, обозначать кружками мало-
рии системы (1.2), после пересечения границы Ωα
го радиуса (хотя это и не очень точно). Можно ска-
оказываются, вообще говоря, «разрезанными» на
зать, что такие кружки представляют собой «ло-
отрезки конечной длины. Нетрудно видеть, что каж-
вушки», попадая в которые траектория перескаки-
дый из таких отрезков, ограниченный «ловушками»
вает с одного бывшего носителя открытых траекто-
на обоих своих концах, представляет собой (длин-
рий (для фиксированной пары) на другой, и обрат-
ную) замкнутую траекторию системы (1.2), возни-
но.
кающую на паре бывших носителей открытых тра-
161
11
ЖЭТФ, вып. 1 (7)
А. Я. Мальцев
ЖЭТФ, том 156, вып. 1 (7), 2019
екторий после пересечения границы зоны устойчи-
вости. Можно видеть также, что если пересечение
плоскости, ортогональной B, и Γα имеет при этом
иррациональное направление, то все бывшие откры-
тые траектории превращаются в замкнутые после
пересечения границы Ωα (рис. 25a). В то же время,
если среднее направление открытых траекторий яв-
ляется рациональным, то непосредственно после пе-
ресечения первой границы Ωα на паре бывших носи-
телей открытых траекторий должны будут присут-
ствовать как длинные замкнутые траектории, так и
«неповрежденные» периодические открытые траек-
Рис. 26. Ловушки второго типа, появляющиеся после пе-
ресечения второй границы зоны Ωα
тории (рис. 25б).
Диаметры «ловушек» стремятся к нулю при при-
ближении к границе зоны Ωα с внешней стороны и
«слившихся» носителей. Как и «ловушки первого
увеличиваются при отдалении от нее (вблизи Ωα).
типа», «ловушки второго типа» образуют периоди-
Можно видеть, что для каждого рационального на-
ческую структуру в плоскости Π(B/B) (рис. 26).
правления открытых траекторий существует в дей-
ствительности критический радиус «ловушек», при
На рис. 26 мы в действительности изобразили
проекции лишь половины «ловушек второго типа»,
котором слои открытых траекторий исчезают из-
за полного их перекрытия «ловушками». Кроме то-
возникающих на паре «слившихся» носителей от-
крытых траекторий, а именно, «ловушек», лежащих
го, можно видеть также, что критический ради-
ус «ловушек» довольно быстро убывает с увеличе-
на «верхнем» носителе и отвечающих перескокам на
нием «знаменателей» соответствующих рациональ-
одну из соседних пар таких же носителей. Проекция
соседней пары «слившихся» носителей на плоскость
ных направлений траекторий. Как следствие это-
го, отрезки, примыкающие к границе зоны устой-
Π(B/B) при этом совпадает с проекцией рассматри-
ваемой нами пары, сдвинутой на некоторый вектор
чивости и соответствующие появлению неустойчи-
вых периодических траекторий на поверхности Фер-
в этой плоскости. Можно сказать поэтому, что каж-
дая из «ловушек второго типа» имеет в действитель-
ми (рис. 17), образуют всюду плотное множество
на границе Ωα, однако на любом конечном расстоя-
ности верхнее и нижнее основания, лежащие в раз-
личных частях картины, представленной рис. 25а
нии от границы количество таких отрезков является
конечным. Для нашего рассмотрения здесь важны
или рис. 25б.
будут отрезки, достигающие второй границы зоны
Диаметры «ловушек второго типа» стремятся к
устойчивости.
нулю при приближении ко второй границе зоны Ωα
Как уже отмечалось выше, в каждой связной
с внешней стороны и увеличиваются при отдалении
компоненте области Ω′α, примыкающей к опреде-
от нее (вблизи Ωα). При пересечении второй грани-
ленному участку первой границы зоны Ωα, для
цы Ωα «ловушки второго типа» возникают в виде
всех направлений B общего положения имеет ме-
точек на рис. 25a или рис. 25б, имеющих «верхнее и
сто один и тот же тип холловской проводимости,
нижнее основание» на цилиндрах замкнутых траек-
противоположный типу исчезающего цилиндра за-
торий или на слоях периодических траекторий (если
мкнутых траекторий на соответствующем участке
они имеются) системы (1.2).
первой границы Ωα. На соответствующем участке
Здесь мы будем рассматривать лишь «физи-
второй границы Ωα происходит исчезновение цилин-
ческие» дисперсионные законы, удовлетворяющие
дра замкнутых траекторий противоположного типа
требованию ϵ(p) = ϵ(-p), что влечет также инва-
(по отношению к типу цилиндра, исчезающего на
риантность поверхности Ферми относительно преоб-
первой границе) и становятся возможными переско-
разования p → -p. Нетрудно проверить при этом,
ки траекторий между парами «слившихся» бывших
что инвариантность структуры системы (1.2) отно-
носителей открытых траекторий (рис. 10). На опи-
сительно того же преобразования влечет в рассмат-
санной выше проекции бывших носителей открытых
риваемой ситуации также симметрию верхнего и
траекторий на плоскость Π(B/B) при этом появля-
нижнего оснований «ловушек второго типа». В част-
ются «ловушки второго типа», попадая в которые
ности, каждая вновь появившаяся после пересече-
траектория осуществляет перескок между парами
ния второй границы зоны Ωα (маленькая) «ловуш-
162
ЖЭТФ, том 156, вып. 1 (7), 2019
Классы сложности угловых диаграмм проводимости металлов. ..
-
+
+
-
-
+
+
-
-
+
+
Рис. 28. Перестройка траекторий системы (1.2) при пере-
-
-
сечении второй границы Ωα в случае, когда «ловушки вто-
рого типа» возникают на слоях периодических открытых
+
+
-
траекторий
Рис. 27. Перестройка траекторий системы (1.2) при пе-
ресечении второй границы Ωα в случае, когда «ловушки
второго типа» возникают на цилиндрах замкнутых траек-
торий
ка второго типа» соединяет между собой (в случае
общего положения) либо длинные замкнутые тра-
ектории системы (1.2), либо периодические откры-
тые траектории. Как можно видеть, два этих случая
соответствуют существенно различным структурам
Рис. 29. Картины I и II в плоскости, ортогональной B,
траекторий системы (1.2) на поверхности Ферми по-
разделенные открытыми траекториями (1.2)
сле пересечения второй границы зоны Ωα.
Действительно, как нетрудно видеть, перестрой-
ка второго типа соответствует картине, представ-
приведенной на рис. 28. При этом в плоскостях, ор-
ленной на рис. 27. Можно видеть, что как до пе-
тогональных B, возникают обе картины (I и II), раз-
рестройки, так и после перестройки траекторий, по-
деленные открытыми траекториями системы (1.2)
верхность Ферми содержит лишь замкнутые траек-
(рис. 29). Такая ситуация может возникать лишь
тории системы (1.2) и картины во всех плоскостях,
в случае, когда пересечение второй границы зоны
ортогональных B, имеют один и тот же тип (I или
устойчивости происходит в точке, соответствующей
II) в обоих случаях. Таким образом, после описан-
наличию периодических открытых траекторий (1.2)
ной перестройки траекторий соответствующие на-
на поверхности Ферми, т. е. в точке пересечения вто-
правления B лежат вне любой из зон устойчиво-
рой границы с дополнительным отрезком, примыка-
сти Ωβ и суммарный вклад поверхности Ферми в
ющим к границе зоны устойчивости и соответству-
холловскую проводимость не изменяется. Эта ситу-
ющим появлению неустойчивых периодических тра-
ация имеет место, в частности, при пересечении вто-
екторий на поверхности Ферми. Заметим при этом,
рой границы зоны Ωα в точках общего положения,
что даже в этом случае ситуация может также опи-
а также в точках, соответствующих рациональным
сываться картиной, представленной на рис. 27, если
направлениям пересечения Γα и плоскости, ортого-
«ловушки второго типа» возникают на цилиндрах
нальной B, в случае если диаметр «ловушек первого
замкнутых траекторий.
типа» в них превышает критический (соответству-
Замкнутые траектории, изображенные на
ющие «дополнительные отрезки» не доходят до вто-
рис. 29, разрезают поверхности Ферми на новые
рой границы).
носители открытых траекторий, соответствующие
В другом случае, когда «ловушки второго типа»
появлению новой зоны устойчивости Ωβ . Зона Ωβ ,
возникают на слоях периодических открытых тра-
определенная для фиксированной поверхности
екторий системы (1.2), соответствующая перестрой-
Ферми, принадлежит при этом одной из зон Ω∗β ,
ка траекторий может быть представлена картиной,
изображенных на рис. 16.
163
11*
А. Я. Мальцев
ЖЭТФ, том 156, вып. 1 (7), 2019
Рис. 32. Сегменты границы зоны Ωα, соответствующие по-
явлению и отсутствию новых зон устойчивости в точках
пересечения второй границы с отрезками специальных на-
Рис. 30. Допустимый угол отклонения направления пере-
правлений B
сечения Γα с плоскостью, ортогональной B, при фиксиро-
ванном диаметре «ловушек второго типа»
и не происходить даже в точках пересечения второй
границы с «дополнительными отрезками», примы-
кающими к Ωα и представляющими направления B,
отвечающие появлению неустойчивых периодиче-
ских траекторий на поверхности Ферми. Эта ситуа-
ция имеет место, если, несмотря на наличие сло-
ев периодических траекторий на поверхности Фер-
ми, появление «ловушек второго типа» происходит
на цилиндрах замкнутых траекторий системы (1.2).
Таким образом, в общем случае граница Ωα мо-
жет разделяться на сегменты, в которых происходит
Рис. 31. Зоны устойчивости Ωβ , примыкающие ко второй
рождение новых зон в описанных точках пересече-
границе зоны Ωα в части из ее «рациональных» точек
ния, и на сегменты, в которых рождения новых зон
не происходит (рис. 32). Можно отметить, что, по-
скольку высота цилиндров замкнутых траекторий
Картина, представленная на рис. 29, являет-
определяется в этом случае диаметром «ловушек
ся локально устойчивой (по отношению к малым
первого типа», общая мера сегментов второго типа
вращениям направления B) и сохраняется до тех
будет тем меньше, чем ближе вторая граница зоны
пор, пока не происходит перестройки изображенных
Ωα расположена к ее первой границе. Кроме того,
на ней замкнутых траекторий. Можно видеть, что
можно заметить также, что для сегментов второго
вблизи второй границы зоны Ωα область устойчи-
типа появление новых зон Ωβ на отрезках специаль-
вости картины, изображенной на рис. 29, определя-
ных направлений B теоретически может происхо-
ется диаметром «ловушек второго типа», который в
дить и на некотором расстоянии от второй грани-
этой ситуации мал по сравнению с диаметром «лову-
цы Ωα в результате взаимного смещения «ловушек»
шек первого типа». Так, допустимый угол отклоне-
первого и второго типов.
ния направления пересечения плоскости Γα с плос-
В целом, можно отметить, что структура уг-
костью, ортогональной B, при фиксированном ма-
ловых диаграмм для фиксированной поверхности
лом диаметре «ловушек второго типа» прямо про-
Ферми может быть довольно близка к структуре
порционален этому диаметру, что определяет допу-
диаграмм для всего дисперсионного закона вблизи
стимый угол отклонения направления B параллель-
специальных зон устойчивости, рассмотренных вы-
но второй границе Ωα (рис. 30). Поскольку величина
ше.
диаметра «ловушек второго типа» прямо пропорци-
ональна расстоянию до второй границы зоны Ωα,
5. ЗАКЛЮЧЕНИЕ
нетрудно видеть также, что границы зон Ωβ долж-
ны при этом иметь «излом» на второй границе Ωα
Мы рассмотрели угловые диаграммы для про-
(рис. 31).
водимости в металлах, имеющих произвольные
Как мы уже сказали выше, появления новой зо-
(физические) поверхности Ферми. Как оказывает-
ны устойчивости на второй границе зоны Ωα может
ся, является естественным разделение всех угловых
164
ЖЭТФ, том 156, вып. 1 (7), 2019
Классы сложности угловых диаграмм проводимости металлов. ..
диаграмм на конечное число «классов сложности»,
16.
И. А. Дынников, Математические заметки 53, 57
имеющих достаточно эффективное геометрическое
(1993).
описание. Наибольший интерес, с нашей точки
17.
С. П. Новиков, А. Я. Мальцев, Письма в ЖЭТФ
зрения, представляют при этом наиболее сложные
63, 809 (1996).
диаграммы (типа B), содержащие бесконечное
число зон устойчивости, а также направления B,
18.
С. П. Новиков, А. Я. Мальцев, УФН 168, 249
соответствующие появлению «хаотических» траек-
(1998).
торий на поверхности Ферми. В работе приведено
19.
С. П. Царев, Частное сообщение (1992-93).
также некоторое сравнение сложности таких диа-
грамм с диаграммами, определенными для всего
20.
I. A. Dynnikov, Amer. Math. Soc. Transl. Ser. 2, 179,
дисперсионного закона.
Amer. Math. Soc., Providence, RI, 45 (1997).
21.
А. Я. Мальцев, ЖЭТФ 112, 1710 (1997).
Финансирование. Работа выполнена за
счет Российского научного фонда (проект
22.
А. Я. Мальцев, С. П. Новиков, Труды МИАН 302,
№18-11-00316).
296 (2018).
23.
И. А. Дынников, УМН 54, 21 (1999).
ЛИТЕРАТУРА
24.
I. A. Dynnikov, Surfaces in 3-Torus: Geometry of
1.
Ч. Киттель, Квантовая теория твердых тел,
Plane Sections, Proc. ECM2, BuDA (1996).
Наука, Москва (1967).
25.
И. А. Дынников, А. Я. Мальцев, ЖЭТФ 112, 371
2.
Дж. Займан, Принципы теории твердого тела,
(1997).
Мир, Москва (1974).
26.
A. Ya. Maltsev and S. P. Novikov, Bulletin of Braz.
3.
А. А. Абрикосов, Основы теории металлов, Нау-
Math. Society, New Series 34, 171 (2003).
ка, Москва (1987).
27.
A. Ya. Maltsev and S. P. Novikov, J. Stat. Phys. 115,
4.
И. М. Лифшиц, М. Я. Азбель, М. И. Каганов,
31 (2004).
ЖЭТФ 31, 63 (1956).
5.
И. М. Лифшиц, В. Г. Песчанский, ЖЭТФ 35, 1251
28.
A. Ya. Maltsev and S. P. Novikov, arXiv:cond-mat/
0304471.
(1958).
6.
И. М. Лифшиц, В. Г. Песчанский, ЖЭТФ 38, 188
29.
R. De Leo, Physica B: Condensed Matter 362, 62
(1960).
(2005).
7.
И. М. Лифшиц, М. И. Каганов, УФН 69, 419
30.
А. Я. Мальцев, ЖЭТФ 151, 944 (2017).
(1959).
31.
А. Я. Мальцев, ЖЭТФ 152, 1053 (2017).
8.
И. М. Лифшиц, М. И. Каганов, УФН 78, 411
32.
А. Я. Мальцев, ЖЭТФ 154, 1183 (2018).
(1962).
33.
A. V. Zorich, Proc. Geometric Study of Foliations,
9.
И. М. Лифшиц, М. И. Каганов, УФН 87, 389
(Tokyo, November 1993), ed. by T. Mizutani et al.,
(1965).
World Scientific, Singapore (1994), p. 479.
10.
И. М. Лифшиц, М. Я. Азбель, М. И. Каганов,
34.
A. V. Zorich, Annales de l’Institut Fourier 46, 325
Электронная теория металлов, Наука, Москва
(1996).
(1971).
11.
Электроны проводимости, под ред. М. И. Кагано-
35.
Anton Zorich, Translations of the AMS, Ser. 2,
ва, В. С. Эдельмана, Наука, Москва (1985).
Vol. 179, AMS, Providence, RI (1997), p. 173.
12.
M. I. Kaganov and V. G. Peschansky, Phys. Rep. 372,
36.
Anton Zorich, Translations of the AMS, Ser. 2,
445 (2002).
Vol. 197, AMS, Providence, RI (1999), p. 135.
13.
С. П. Новиков, УМН 37, 3 (1982).
37.
Р. Де Лео, УМН 55, 181 (2000).
14.
А. В. Зорич, УМН 39, 235 (1984).
38.
Р. Де Лео, УМН 58, 197 (2003).
15.
И. А. Дынников, УМН 47, 161 (1992).
39.
R. De Leo, Exper. Math. 15, 109 (2006).
165
А. Я. Мальцев
ЖЭТФ, том 156, вып. 1 (7), 2019
40. Anton Zorich, in collect.: Frontiers in Number Theo-
45. I. Dynnikov and A. Skripchenko, Novikov’s Seminar
ry, Physics and Geometry. Vol. 1: On Random Mat-
2012-2014, Adv. Mathem. Sci., Amer. Math. Soc.
rices, Zeta Functions and Dynamical Systems; Ecole
Transl. Ser.
2,
234, ed. by V. M. Buchstaber,
de Physique des Houches, France, March 9-21 (2003);
B. A. Dubrovin, and I. M. Krichever, Amer. Math.
ed. by P. Cartier, B. Julia, P. Moussa, and P. Vanho-
Soc., Providence, RI (2014), p. 173.
ve, Springer-Verlag, Berlin (2006), p. 439.
46. I. Dynnikov and A. Skripchenko, Trans. Moscow
41. Р. Де Лео, И. А. Дынников, УМН 62, 151 (2007).
Math. Soc. 76, 287 (2015).
42. R. De Leo and I. A. Dynnikov, Geom. Dedicata 138,
47. A. Avila, P. Hubert, and A. Skripchenko, Invent. Ma-
51 (2009).
them. 206, 109 (2016).
43. A. Skripchenko, Discrete Contin. Dyn. Sys. 32, 643
48. A. Avila, P. Hubert, and A. Skripchenko, Bulletin de
(2012).
la Societe Mathematique de France 144, 539 (2016).
44. A. Skripchenko, Ann. Glob. Anal. Geom. 43, 253
49. R. De Leo, arXiv:1711.01716.
(2013).
166