ЖЭТФ, 2019, том 156, вып. 1 (7), стр. 167-175

ЦИРКУЛЯРНЫЙ ФОТОТОК В ПОЛУМЕТАЛЛАХ ВЕЙЛЯ

С ЗЕРКАЛЬНОЙ СИММЕТРИЕЙ

Н. В. Леппенен^*, Е. Л. Ивченко, Л. E. Голуб

Физико-технический институт им. А. Ф. Иоффе Российской академии наук

194021, Санкт-Петербург, Россия

Поступила в редакцию 15 февраля 2019 г.,

после переработки 15 февраля 2019 г.

Принята к публикации 27 февраля 2019 г.

Теоретически рассмотрены полуметаллы Вейля, точечная группа симметрии которых содержит плоско-

сти отражения и в которых имеются эквивалентные долины с противоположной киральностью. К ним

относятся наиболее часто исследуемые соединения — монопниктиды переходных металлов TaAs, NbAs,

TaP, NbP, а также сплавы Bi1-xSbx. Циркулярный фотогальванический ток, инвертирующий свое на-

правление при смене знака круговой поляризации, рассчитан для поглощения света при прямых оптиче-

ских переходах вблизи точек Вейля. Суммарный вклад всех долин в фототок отличен от нуля при выходе

за пределы вейлевской модели, когда дополнительно в эффективном электронном гамильтониане учи-

тывается или спин-независимый, линейный по волновому вектору k наклон (tilt), или спин-зависимые,

кубические по k слагаемые. При учете наклона конуса энергетической дисперсии в полуметалле Вейля

симметрии C4v фотогальванический ток выражен через компоненты симметричного тензора второго ран-

га, определяющего энергетический спектр носителей вблизи узла Вейля. При низкой температуре этот

вклад в фототок возбуждается в некотором ограниченном частотном интервале Δ. Фототок, обуслов-

ленный кубическими поправками, в области оптического поглощения пропорционален квадрату частоты

света и генерируется как внутри окна Δ, так и за его пределами.

DOI: 10.1134/S0044451019070162

ский ток, появляющийся при поглощении света без

приложения внешнего электрического напряжения

и меняющий свое направление на противоположное

1. ВВЕДЕНИЕ

при смене знака круговой поляризации света [3]. А

В последнее время открыты и активно изуча-

именно, было установлено, что при отсутствии плос-

ются трехмерные системы с линейным спектром —

костей отражения циркулярный фототок направлен

полуметаллы Вейля (в качестве недавних обзоров

вдоль момента фотона и темп его генерации опреде-

см. [1, 2]). Эти системы, обладающие невырожден-

ляется помимо напряженности электрического поля

ным энергетическим спектром квазичастиц (за ис-

волны мировыми постоянными [4].

ключением двукратного вырождения в узле Вей-

ля), привлекают большое внимание благодаря своим

Реальные полуметаллы Вейля TaAs, TaP, NbAs,

NbP [5-11] и Bi1-xSb_x [12] имеют точечную симмет-

необычным электрическим и оптическим свойствам

в объеме и на поверхности и расширяют представле-

рию соответственно C4v и C3v. Таким образом, в них

присутствует зеркальная симметрия, при которой

ния топологической теории в физике твердого тела.

В таких системах в простейшей модели носители то-

вклады в циркулярный фототок от двух узлов Вей-

ля, связанных отражением, в точности компенсиру-

ка описываются эффективным гамильтонианом, ко-

ют друг друга. Поэтому в направлении распростра-

торый имеет вид гамильтониана Вейля, используе-

мого для описания нейтрино, чем и обусловлено их

нения света генерируется чисто долинный фототок,

а электрический ток отсутствует. Тем не менее пе-

название.

речисленные выше точечные группы симметрии яв-

В полуметаллах Вейля замечательным образом

ляются гиротропными, так что в соответствующих

ведет себя циркулярный фототок, т. е. электриче-

материалах возможен циркулярный электрический

^* E-mail: nik-leppenen@yandex.ru

фототок, поперечный моменту фотона, при распро-

167

Н. В. Леппенен, Е. Л. Ивченко, Л. E. Голуб

ЖЭТФ, том 156, вып. 1 (7), 2019

странении света поперек поворотной оси симметрии

где i, j, l = x, y, z, определяется девятью компонен-

третьего или четвертого порядка. Такой фототок

тами матрицы

β размерности 3 × 3 и тремя компо-

микроскопически не может быть получен в рамках

нентами вектора a. Они находятся из дифференци-

чисто вейлевского гамильтониана. В работе [13] бы-

рования по q величин d_i и d₀:

ло показано, что поперечный циркулярный фото-

⁽∂d_i)

⁽∂d₀)

ток может быть обусловлен линейными по импуль-

β_ij =

a_l =

(4)

∂qjq

∂q

су спин-независимыми добавками к гамильтониану

Вейля, приводящему к «наклону» дисперсионных

Коэффициент при спин-независимом слагаемом в

конусов. В рамках такой модели была предпринята

гамильтониане (3) получил название наклона (tilt).

попытка объяснить экспериментальные результаты

В дальнейшем мы будем разность q - q_W обо-

по циркулярному фотогальваническому эффекту в

значать в виде k, т. е. будем отсчитывать волновой

арсениде тантала, наблюдавшемуся при возбужде-

вектор электрона от вейлевского узла. Тогда в ли-

нии CO₂-лазером с энергией фотонов 120 мэВ [5].

нейном приближении уравнение (2) можно предста-

В данной работе демонстрируется, что наклон

вить в виде

дисперсии приводит к фототоку лишь в ограни-

√

ченной области частот. Предложена альтернатив-

E±,k = ±

Λ_ijk_ik_j + a · k.

(5)

ная модель нелинейных спин-зависимых поправок

к гамильтониану Вейля, приводящих к фототоку,

Здесь симметричная, положительно определенная

нарастающему с частотой света. Теория построена

матрица

Λ связана с матрицей

β соотношением

для произвольной матрицы β_ij , описывающей ли-

Λ=

нейную часть эффективного электронного гамиль-

β^T

β,

(6)

тониана β_ijσ_ik_j и содержащей как диагональные,

где

β^T — матрица, транспонированная по отноше-

так и недиагональные компоненты.

ˆ. Для нахождения шести линейно незави-

нию к

симых компонент матрицы

Λ достаточно численно-

го расчета линейной дисперсии вблизи точки Вей-

2. ЭФФЕКТИВНЫЙ ГАМИЛЬТОНИАН

ля для шести различных направлений в k-простран-

Вблизи вейлевской точки q_W достаточно учиты-

стве.

вать только две зоны, вырожденные в точке Вей-

При заданной матрице

Λ уравнению (6) удовле-

ля. В общем виде эффективный гамильтониан пред-

творяет совокупность матриц

ставляет собой матрицу второго ранга, которую

β=±D(ϕ,θ,ψ

β₀ ,

(7)

можно представить в следующем виде:

где

β₀ — любое частное решение этого уравнения, а

H(q) = σ · d(q) + σ₀d₀(q),

(1)

ˆ — матрица ортогональных преобразований спино-

вых матриц Паули σ_i, которая задается тремя угла-

где q — волновой вектор, определенный в первой

зоне Бриллюэна кристалла, σ_i — спиновые матрицы

ми Эйлера, ϕ, θ и ψ, и имеет определитель +1. Дей-

ствительно, произведение

β^Tβ равно

βT0

DT Dβ0 =

Паули, σ₀ — единичная матрица размерности 2 × 2,

βT0β0, а это, по определению

β₀, есть матрица

Λ.

и при q = q_W трехкомпонентная функция d(q) и

В Приложении указан способ выбора матрицы

β₀ и

скалярная функция d₀(q) обращаются в нуль. Для

приведено выражение для нее через матрицу

Λ. За-

собственных значений энергии имеем

метим, что знак в (7) не определяется матрицей

E±,q = ±d(q) + d₀(q) ,

(2)

и является топологическим зарядом, или кирально-

стью данного узла [1]:

√

где d(q) =

|d(q)|² .

(

)

C =sign de

β .

(8)

2.1. Линейное приближение с анизотропным

Узлы Вейля, связанные несобственной операцией

спектром

симметрии σ_v, например узлы kW1 = (k_x, k_y, k_z ) и

В линейном приближении по отступлению q-q_W

kW2 = (-k_x, k_y, k_z), имеют противоположные ки-

эффективный гамильтониан

ральности. В то же время у узлов, связанных опера-

цией инверсии времени T , матрицы

β совпадают, а

H = β_ijσi (q_j - q_Wj) + σ₀al (q_l - q_Wl),

(3)

значит, совпадают и их киральности. Как и должно

168

ЖЭТФ, том 156, вып. 1 (7), 2019

Циркулярный фототок в полуметаллах Вейля. . .

быть для вещественной матрицы размерности 3 × 3,

[101] и [011]. Пользуясь этими шестью значениями,

при выбранном знаке «±» в выражении (7) множе-

мы рассчитали матрицу

Λ и вектор a, входящие в

ство матриц

β определяется девятью параметрами:

уравнение (5). Определитель полученной матрицы

шестью компонентами симметричной матрицы

Λ и

оказался отрицательным в противоречии с тем, что

тремя углами ϕ, θ, ψ.

матрица

Λ должна быть положительно определен-

Преобразование

D в (7) осуществляет переход от

ной. Если приписать значения v_±(101) не направле-

одного базиса двукратно вырожденного состояния в

нию [101], а направлению [101], матрица

Λ становит-

узле Вейля к другому при сохранении системы коор-

ся положительно определенной. Однако найденный

динат в k-пространстве. Естественно, при этом энер-

при этом модуль вектора b превышает единицу, что

гия электрона в точке k не меняется. Аналогичное

не согласуется с типом I полуметалла TaAs [2]. По-

преобразование

D в спиновом пространстве, σ_i =

этому указанная табл. S3 требует уточнения.

= D-1ii′σi′ , можно применить и для гамильтониана

общего вида (1). При этом скалярное произведение

2.2. Учет нелинейных по k слагаемых

σidi(k) перейдет в сумму σi′ di′ (k), где di′ = Di′idi.

При расчете фототоков в полуметаллах Вейля

Для дальнейшего расчета фототока важно иметь в

потребуется учесть нелинейные по k слагаемые в эф-

виду, что указанное преобразование, не вовлекаю-

фективном гамильтониане

щее k-пространство, не меняет не только энергии

электрона, но и кривизны Берри Ω_k. Для доказа-

H = β_ijσ_ik_j + σ_iP(2)i(k) + σ_iP(3)i(k)+

тельства заметим, что компоненты последней мож-

+ σ0 (a · k + ...),

(14)

но представить в виде скалярно-векторного произ-

ведения [14,15],

где учтены квадратичные и кубические спин-зави-

[

]

симые вклады

∂d

Ωk,i =

(9)

∑

2d³

∂ki+1

∂ki+2

P(2)i(k) =

C(2)ijlk_jk_l,

которое инвариантно относительно любого поворота

∑

(15)

P(3)i(k) =

C(3)ijlmk_jk_lk_m.

вектора d(k).

jlm

Полуметалл Вейля с гамильтонианом

С учетом нелинейных слагаемых энергия по-преж-

H=βσ·k+a·k

(10)

нему может быть представлена в виде (2), но с обоб-

щенным вектором d(k):

относят к типу I, если |β| > |a| ≡ a, и к типу II, если

|β| < a [16]. Для матрицы β_ij общего вида принад-

d_i(k) = β_ijk_j + P(2)i(k) + P(3)i(k) .

лежность к типу I или II определяется отсутствием

Введенные в (15) коэффициенты симметричны к

или наличием такого направления вектора k, при

перестановкам индексов при компонентах волнового

котором d(k) < |a · k|, или

вектора:

∑

Λ_ijk_ik_j <

a_ia_jk_ik_j.

(11)

C(2)ijl = C(2)ilj, C(3)ijlm = C(3)iljm = C(3)imlj.

При ортогональном преобразовании

D(ϕ, θ, ψ) мат-

Критерием выполнения этого условия является

рицы C(n) переходят в матрицы

неравенство

∑

1 < |b| ≡ b,

(12)

D_niC(2)ijl и

D_niC(3)ijlm.

где b — вектор с компонентами

Такое преобразование в (7) оставляет инвариантной

b_i = β-1jia_j

(13)

не только матрицу

Λ, но и суммы произведений:

√

∑

C_jlmn = β-1jiC(3)ilmn,

и абсолютным значением b = Λ-1ija_ia_j. В данной

работе рассматриваются полуметаллы Вейля типа I

∑

(16)

C^′jlmn =

β_ijC(3)ilmn =

β^TjiC(3)ilmn.

(b < 1).

В дополнительной информации к работе [5] (см.

в ней табл. S3) приведены значения v_±(lmn)

Матрицы

Ĉи

Ĉ^′ связаны между собой соотношени-

= ∂E±,k/∂k для шести направлений [lmn] в k-про-

ем

странстве полуметалла TaAs: [100], [010], [001], [110],

C^′jlmn = Λ_jiC_ilmn.

(17)

169

Н. В. Леппенен, Е. Л. Ивченко, Л. E. Голуб

ЖЭТФ, том 156, вып. 1 (7), 2019

3. ОБЩИЕ ФОРМУЛЫ ДЛЯ ФОТОТОКА

Для определенности мы рассматриваем узлы

= 0. Их удобно различать элементами то-

Вейля с k_z

В продолжение работ [14,15] мы исследуем цир-

чечной симметрии g и комбинациями T g элементов

кулярный фотогальванический эффект, описывае-

g и операции инверсии времени T . Тензор γ, про-

мый феноменологической формулой

суммированный по всем долинам, запишем в виде

суммы

j_λ = γ_ληκ_η|E|²,

(18)

∑

γ =2

γ(g),

где j — плотность электрического тока, E — ам-

плитуда электрического поля световой волны, κ =

= i[E × E^∗]/|E|² — векторная спиральность фотона,

где γ(g) — вклад долины gk_W , k_W — исходный узел,

равная единичному вектору в направлении распро-

например, узел с k_Wy > k_Wx > 0; множитель 2 учи-

странения света, умноженному на степень его кру-

тывает вклад долин -gk_W . Из общей формулы (19)

говой поляризации P_circ. В кристаллах гиротропных

следует выражение для парциального вклада в фо-

классов C_nv (n = 3, 4, 6) тензор γ имеет две отлич-

тогальванический тензор долины gk_W :

ные от нуля компоненты γ_xy = -γ_yx, расчет кото-

рых является целью данной работы.

Плотность циркулярного фототока, генерируе-

2πe³τ_p ∑

γ(g)λν =

v(g)so,λΩ(g)k,νδ[2d(g)(k) - ℏω] ×

мого в полуметаллах Вейля при прямых оптических

ℏ

переходах, рассчитывается по формуле [4, 14, 15]

[

]

(g)

× f₀(E_-

) - f₀(E(g)+,k)

(22)

∑

2πe

j = |E|²

v_soτ_p (κ · Ω_k)δ[2d(k) - ℏω]×

ℏ

В кристаллах симметрии C4v вклад в компоненту

γ_xy принимает вид

× [f₀(E-,k) - f₀(E+,k)] .

(19)

Здесь e — заряд электрона, vso = ℏ-1(∂d/∂k) —

2πe³τ_p ∑

∂d(gk)

спин-зависимая часть групповой скорости электро-

γ(g)xy =

ℏ²

2d³(gk)

∂k_x

на в зоне проводимости, τ_p — время релаксации но-

(

])

сителей заряда по квазиимпульсу, Ω_k — кривизна

^[∂d(gk)

∂d(gk)

× d(gk) ·

Берри (9), f₀(E) = {exp [(E - μ)/T ] + 1}-1 — равно-

∂k_z

∂k_x

весная функция распределения электронов по энер-

× [f₀(E-,gk) - f₀(E+,gk)] δ[2d(gk) - ℏω].

(23)

гии E, μ — химический потенциал, с учетом закона

сохранения энергии

С учетом закона сохранения величину 2d³(gk) мож-

ℏω

но заменить на (ℏω)³/4.

E±,k = ±

+ d₀(k).

(20)

Выполним в сумме (23) замену переменных k →

В работе [4] рассчитан циркулярный фототок

→ g-1k и учтем, что для половины операций сим-

(19) в узле Вейля с линейным по k эффективным

метрии (gk)_x = ±k_x, а для второй половины (gk)_x =

гамильтонианом (3) без наклона (a = 0) и показа-

= ±k_y, и для всех g ∈ C4v компонента волнового

но, что вклад каждого узла в циркулярный фототок

вектора k_z не меняется. Тогда для xy-компоненты

имеет универсальный вид

суммарного тензора γ получим

πe

j = CΓ₀τ_pκ|E|², Γ₀ =

(21)

4Nπe³τ_p

3h²

γ_xy =

ℏ²(ℏω)³

где h — постоянная Планка, а C = ±1 — киральность

∑

[f₀(E-,k) - f₀(E+,k)] δ[2d(k) - ℏω] ×

этого узла, определенная согласно (8). При наличии

в кристалле несобственных элементов точечной сим-

(

])

^{∂d(k)

^[∂d(k)

∂d(k)

метрии вклады узлов с противоположными кираль-

d(k) ·

∂k_x

∂k_z

∂k_x

ностями компенсируют друг друга и фототок, рас-

}

считанный в модели [4], отсутствует. Фототок, про-

+ (x → y)

(24)

суммированный по всем узлам Вейля в таких крис-

таллах, отличен от нуля при учете наклона [13] или

нелинейных слагаемых в гамильтониане (14) [14,15].

где N = 16 — число вейлевских долин.

170

ЖЭТФ, том 156, вып. 1 (7), 2019

Циркулярный фототок в полуметаллах Вейля. . .

4. ЦИРКУЛЯРНЫЙ ФОТОТОК С УЧЕТОМ

Первое слагаемое вклада в γ_xy не дает, а вклад вто-

ОБЩЕГО НАКЛОНА В ЭНЕРГЕТИЧЕСКОЙ

рого сводится к

ДИСПЕРСИИ

γ_xy =

CNΓ₀τ_pχ_xyJ,

(30)

В данном разделе учитываются только линейные

по k спин-зависимое и спин-независимое слагаемые

где C — киральность исходного узла,

в гамильтониане. В работе [13] наклонное слагае-

∑(

)

мое учитывалось в модели с изотропной матрицей

a_xΛ-1yi - a_yΛ-1xi

a_i

β, см. (10). Здесь мы обобщаем теорию на произ-

χ_xy

= i

∑

(31)

вольный вид этой матрицы.

Λ-1

a_ia_j

Матрица

β входит в выражение (24) только че-

рез

Λи C:

[

]

√

∫

∂d

(Λk)_x

∂d

d·

Δ_Λk_y,

(25)

∂k_x

d(k)

∂k_z

∂k_x

J =

(3u² - 1)F (bQu) du.

(32)

-1

где Δ_Λ = det

Λ. Используя формулы (25), можно

При a = 0 выражение для χ_xy инвариантно к

преобразовать γ_xy к виду

преобразованию (7). При изотропной матрице Λ_ij =

∫

= Λδ_ij сумма по i в числителе (31) обращается в

12CNΓ₀τ_p

^√Δ_Λ

γ_xy =

dk ×

нуль в согласии с работами [14,15], где показано, что

π(ℏω)⁴

∑

в кристаллах симметрии C_nv (n = 3, 4, 6) фототок

× (Λ_xjk_y - Λ_yjk_x) k_j F (a · k) δ[2d(k) - ℏω],

(26)

отсутствует даже при наличии наклона d₀(k), если

спин-зависимая часть гамильтониана имеет простой

где

изотропный вид (10). Однако при матрице β_ij об-

(

)

(

)

щего вида учет наклона в функциях распределения

ℏω

F (x) = f₀

-f₀

(27)

f₀(E±,k) приводит к появлению фототока. Напри-

мер, при диагональной матрице Λ_ij с различными

Переходя к переменным

компонентами Λ_xx и Λ_yy параметр χ_xy равен отно-

шению

Q_i = β_ijk_j, k_j = β-1jiQ_i, d(k) = Q ≡ |Q|

(28)

a_xa_y(Λ_xx - Λ_yy)

и выполняя интегрирование по модулю вектора Q,

Λ_yya2x + Λ_xxa2y + Λ_xxΛ_yyΛ

z a^z

получим

∫

(3u² - 1) du = 0, величину J можно

Так как

представить в следующей эквивалентной форме:

γ_xy =

CNΓ₀τ_p×

∑(

)

Q_sQ_t

∫

β_sxβ-1yt - β_syβ-1

F (b · Q)

(29)

3u² - 1

Q²

J =

exp[(-ℏω/2 - μ + bQu)/T] + 1

−1

где вектор b определен согласно (13), а угловые

+ (μ → -μ).

(33)

скобки означают усреднение по направлениям век-

тора Q. В пренебрежении наклоном разность функ-

При произвольной температуре интеграл (33) вы-

ций распределения F (a · k) = F (b · Q) не зависит

числяется аналитически, но соответствующее выра-

от Q, см. (20), и, поскольку произведение 〈Q_sQ_t〉 =

жение (содержащее полилогарифмы) довольно гро-

= δ_stQ²/3, сумма по s и t обнуляется.

моздко, и мы его не приводим. Вместо этого мы

Среднее в (29) можно преобразовать к виду

приведем выражения для J при низкой температуре

∫

(T → 0):

Q_sQ_t

δ_st

F (b · Q)

(1 - u²)F (bQu) du +

Q²

J = -θ (1 - |u₀|)u₀(1 - u²⁰),

(34)

-1

∫

и при высокой температуре (bℏω/2 ≪ T ):

b_sb_t

(3u² - 1)F (bQu) du.

4b²

b²

-1

J ≈

(ℏω)²F^′′.

(35)

171

Н. В. Леппенен, Е. Л. Ивченко, Л. E. Голуб

ЖЭТФ, том 156, вып. 1 (7), 2019

Здесь θ(x) — функция Хевисайда,

где

∑

(

)

ξ_xy =

(Ξ_sxy - Ξ_syx) ,

(40)

2|μ|

u₀ =

F (ε) = f₀(-ε) - f₀(ε),

(36)

s=x,y,z

ℏω

а штрихи означают дифференцирование при ε =

Ξ_sxy = C_yxkqΛ-1kq + 2C_kxkqΛ-1yq +

= ℏω/2.

(

-1

+C_mαβγΛ_xmΛ

Λ-1γy + 4

C_zzxsΛ-1ys -

αβ

)

5. ЦИРКУЛЯРНЫЙ ФОТОТОК С УЧЕТОМ

− C_yzxsΛ-1zs + C_xxxsΛ-1ys - C_yxxsΛ-1xs

(41)

КУБИЧЕСКОЙ НЕЛИНЕЙНОСТИ

а Ξ_syx получается из (41) заменой x ↔ y. В частном

При учете кубических слагаемых учет наклона

случае β_ij = βδ_ij,

= Cxy)yyk3y,

= Cyx)xxk3x,

не обязателен [15], поэтому в этом разделе положим

= 0 приходим к результату работы [15]:

d₀(k) ≡ 0. Считаем нелинейные вклады в гамильто-

ниан (14) малыми по сравнению с линейным вкла-

3NΓ₀τ_p

(ℏω⁾

γ_xy = C

(ℏω)²F

(C_xyyy - C_yxxx) , (42)

дом. В первом порядке по нелинейности P(3)i(k) фо-

20β²

тоток (22) можно представить в виде суммы трех

слагаемых:

где C_jlmn = C(3)jlmn/β.

j=j(3)v +j^(3)Ω +j(3)δ,

(37)

определяемых нелинейными поправками соответ-

6. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

ственно к групповой скорости v_so, кривизне Бер-

ри (9) и энергии, входящей в δ-функцию в выра-

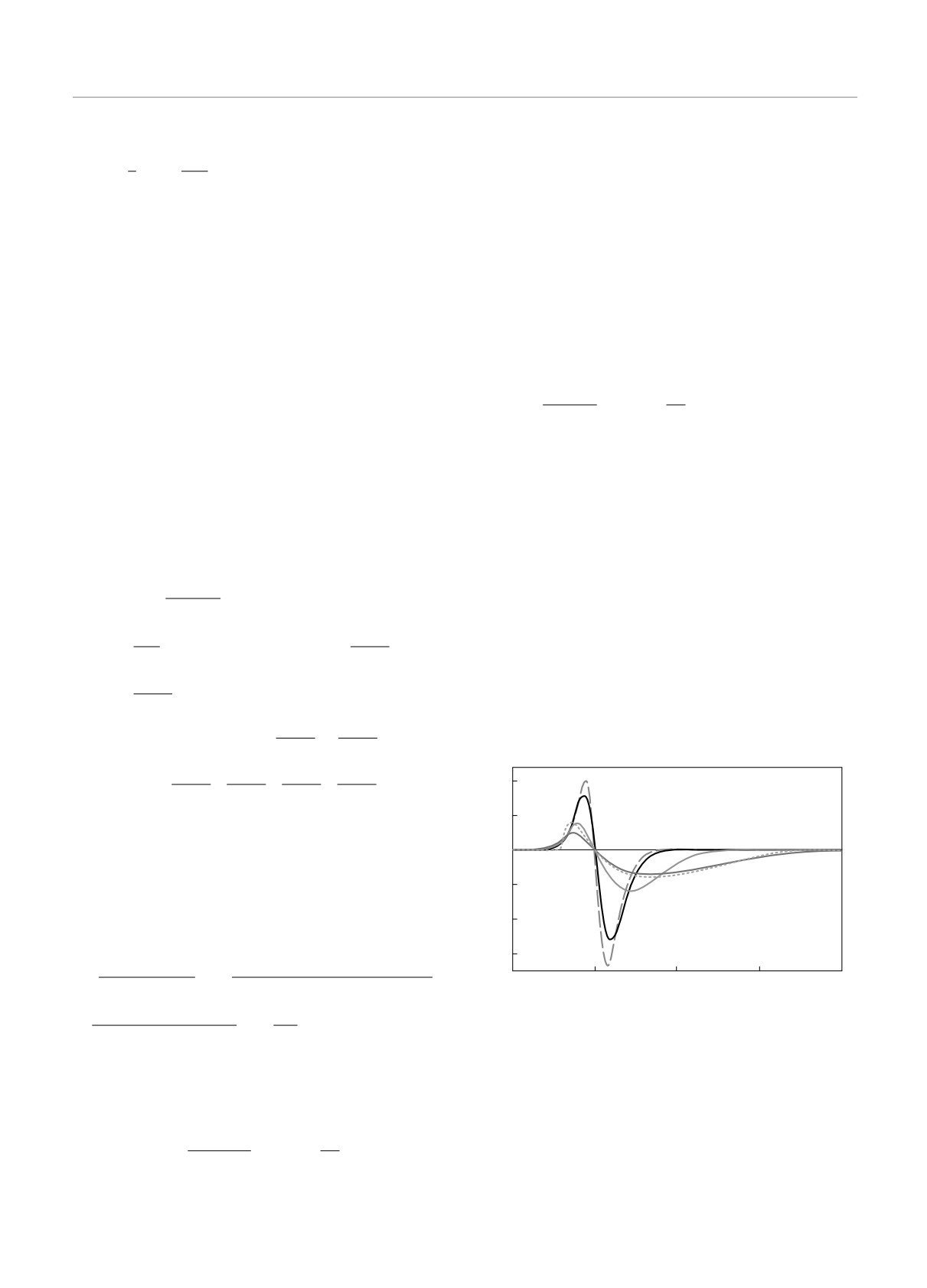
Зависимость циркулярного фототока от часто-

жении (19). Приведем эти поправки в явном виде:

ты в модели с анизотропным линейным спектром

(3)

проиллюстрирована на рис. 1. Как видно из фор-

Q·P

d ≈Q +

мул (30)-(32), фототок зависит от двух скалярных

(

)

параметров, χ_xy и b =

β-1a|. При этом первый па-

(3)

∂P_i

раметр не зависит от модуля |a|, он определяет мас-

v_so,j =

β_ijβ_ilk_l + β_ijP⁽³⁾

+β_ilk_l

ℏ²ω

∂k_j

штаб фотогальванического эффекта, но не форму

частотной зависимости фототока, и при выборе про-

Ωk,i =

(38)

(ℏω)³

извольных единиц по оси ординат выпадает. Пара-

{

[

]

∂Q

× det

β)k_i + P⁽³⁾ ·

∂ki+1

∂ki+2

/b ,² отн. ед.

[

]}

(3)

∂Q

∂P

∂Q

∂P⁽³⁾

+Q·

∂ki+1

∂ki+2

∂ki+1

В двух последних формулах величина d заменена

на ℏω/2 и для удобства введен вектор Q, определен-

ный согласно (28). Подставим нелинейные поправки

0.7

в формулу (24), перейдем от суммирования по k к

-1

0.5

интегрированию по Q и проведем усреднение по на-

правлениям вектора Q в соответствии с правилами,

-2

0.2

приведенными в работе [17]:

-3

^>Qi1Qi2Qi3Qi4 ?

i2i3

δi1i2 δi3i4 +δi1i3 δi2i4 +δi1i4 δ

Q⁴

^>Qi1Qi2Qi3Qi4Qi5Qi6 ?

(δi1i2 δi3i4 δi5i6 + . . . ) .

Рис. 1. (В цвете онлайн) Зависимость фототока от энер-

Q⁶

105

гии кванта в модели с анизотропным линейным спектром

Здесь многоточие предполагает сумму остальных 14

при T/μ = 0.1. Сплошные кривые — численный расчет

произведений трех δ-функций с парными индекса-

по формулам (30)-(32) для b = 0.2, 0.5, 0.7; штриховая

ми. В результате для компоненты γ_xy окончательно

кривая — приближенный расчет с использованием форму-

имеем

лы (35), а пунктиром показана зависимость, рассчитанная

3NCΓ₀τ_p

(ℏω⁾

при T = 0 по формуле (34)

γ_xy =

(ℏω)²F

ξ_xy,

(39)

172

ЖЭТФ, том 156, вып. 1 (7), 2019

Циркулярный фототок в полуметаллах Вейля. . .

, отн. ед.

метр b влияет как на форму, так и на «размах» зави-

0.6

симости γ_xy(ℏω). Из-за зарядовой симметрии спин-

зависимой части гамильтониана (3) интеграл J ин-

0.4

вариантен к замене μ на -μ, что явно следует из его

представления в форме (33). Для любой температу-

b = 0.5

ры один из двух вкладов в (33) при ℏω = 2|μ| обра-

0.2

щается в нуль, а другой при |μ| ≫ T мал и им мож-

но пренебречь. Поэтому интеграл J при ℏω = 2|μ|

должен менять знак, как это имеет место для всех

кривых на рис. 1. Сплошными линиями приведены

-0.2

результаты точного расчета по формулам (30)-(32),

штриховая линия отвечает расчету по формуле (35),

полученной разложением интеграла J по малому па-

раметру b. Согласно (34), при нулевой температуре

фототок генерируется в пределах интервала энергий

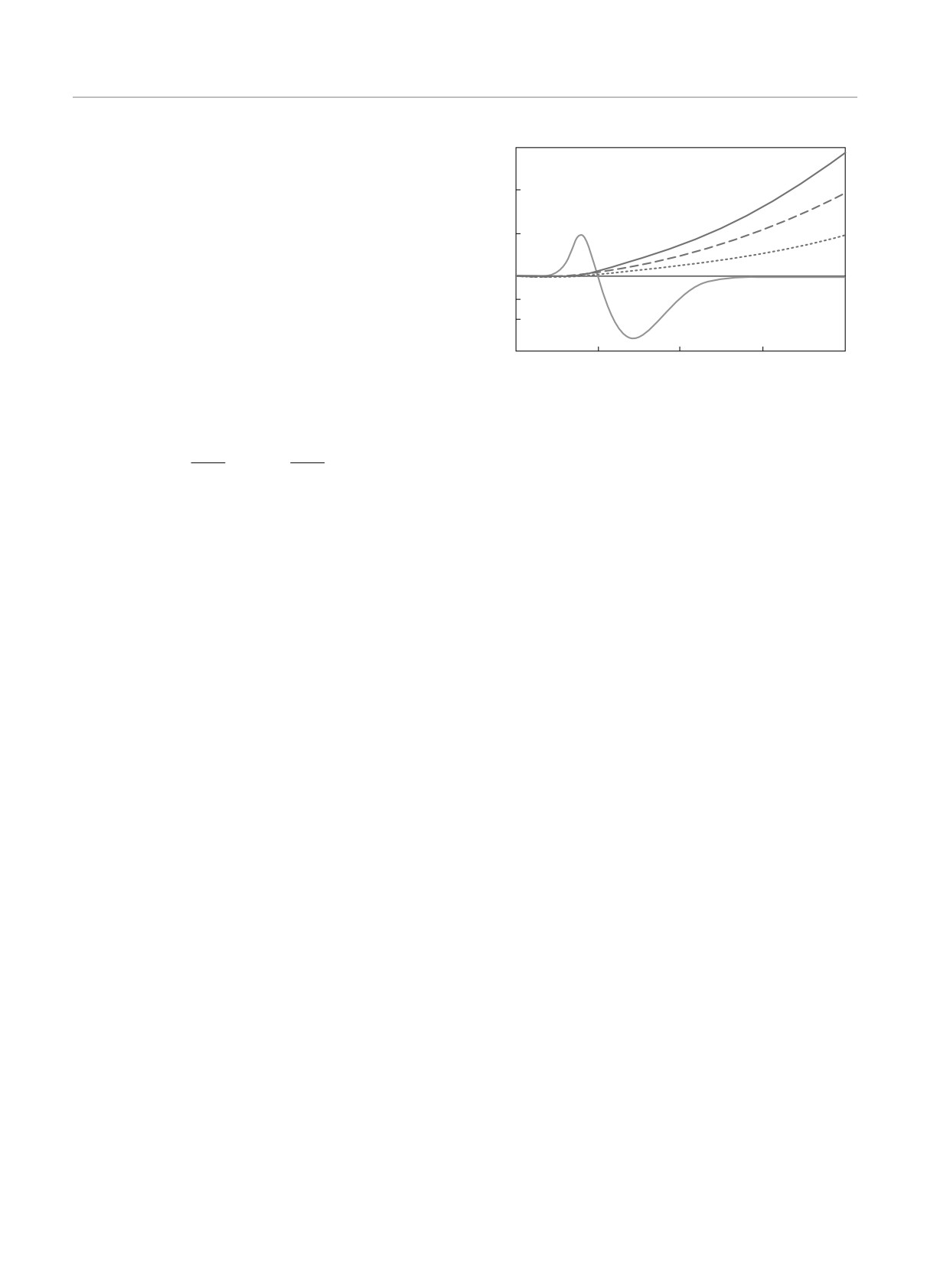
Рис. 2. (В цвете онлайн) Сравнение спектральных зависи-

мостей циркулярного фототока, рассчитанных при T /μ =

фотона [15]

= 0.1 в модели с наклоном и с учетом кубической нели-

2|μ|

< ℏω <

(43)

нейности: пунктирная, штриховая и сплошная кривые со-

1+b

1-b

= 0.03, 0.06 и 0.09

ответствуют μ²ξxy/χxy

т. е. в энергетическом окне Δ = 4|μ|b/(1 - b²). При

b = 0.7 это окно лежит в пределах от 1.18|μ| до 6.7|μ|

в согласии с пунктирной кривой на рис. 1. Следует

при анализе использована модель линейного эффек-

отметить, что такое же ограничение фототока по ча-

тивного гамильтониана (3). Наш расчет показыва-

стотам имеет место и при совместном учете накло-

ет, однако, что линейная модель дает нулевой фо-

на и квадратичной нелинейности P⁽²⁾(k) в (14). При

тоток при больших частотах, и генерацию фототока

конечной температуре спектральная область, внут-

можно объяснить нелинейным по k спин-зависимым

ри которой эффект значителен, выходит за пределы

вкладом в эффективный электронный гамильтони-

интервала (43), но в целом определяется наиболь-

ан.

шей из величин Δ и T . Заметим также, что из фор-

мулы (36) следует, что при T = 0 фототок зависит

от ℏω и μ не по отдельности, а от отношения ℏω/μ,

7. ЗАКЛЮЧЕНИЕ

тогда как при T = 0 возникает дополнительная за-

висимость от отношения T/μ.

Проанализирована связь между девятью компо-

Частотная зависимость вклада в фототок от ку-

нентами матрицы β_ij , определяющей линейный по

бической нелинейности кардинально отличается от

k гамильтониан вблизи вейлевского узла, и энерге-

поведения кривых на рис. 1. Действительно, из фор-

тической дисперсией электрона вблизи этого узла.

мулы (39) следует, что γ_xy ∝ ω²F(ℏω/2). При T ≪

Дисперсия задается шестью линейно независимыми

≪ ℏω разность заселенностей начального и конечно-

компонентами диагональной, положительно опреде-

го состояний F(ℏω/2) пренебрежимо мала при ℏω <

ленной матрицы

Λ =

β^Tβ, а матрица

β — этими

< 2|μ| и близка к единице при ℏω > 2|μ|, т.е. выше

шестью компонентами, тремя углами Эйлера орто-

порога поглощения ℏω = 2|μ| фототок пропорциона-

гонального преобразования пары базисных состоя-

лен квадрату частоты излучения (рис. 2). На рис. 2

ний в узле Вейля и киральностью C = sign(detβ).

для сравнения приведен также спектр в линейной

Построена теория циркулярного фотогаль-

модели с наклоном.

ванического эффекта в полуметаллах Вейля с

В литературе имеются две экспериментальные

зеркальной симметрией. Циркулярный фототок

статьи по циркулярному фотогальваническому эф-

рассчитан для произвольного анизотропного га-

фекту в вейлевских полуметаллах. В работе [18] из-

мильтониана, включающего как линейные, так и

мерен циркулярный фототок в TaAs. Однако энер-

нелинейные по k слагаемые. В отличие от чисто

гии фотона в ней были настолько велики (ℏω ≈

спинового тока, электрический ток выражается

≈ 2.38 эВ), что оптические переходы шли вдали

через компоненты матрицы

Λ и комбинации про-

от точек Вейля. В работе [5] циркулярный фото-

изведений компонент матрицы β_ij и матриц более

ток зарегистрирован также в полуметалле TaAs, но

высокого порядка, инвариантные к ортогональ-

при возбуждении CO₂-лазером (ℏω = 120 мэВ), а

ному преобразованию базисных состояний в узле

173

Н. В. Леппенен, Е. Л. Ивченко, Л. E. Голуб

ЖЭТФ, том 156, вып. 1 (7), 2019

Вейля. Установлено, что циркулярный фототок

где

Î — единичная матрица 3 × 3, Δ_Λ = det(Λ), а

в полуметаллах симметрии C4v отличен от нуля

I_Λ = λ²¹ +λ²² +λ²³ и I_β = λ₁ +λ₂ +λ₃ — следы матриц

в модели с наклоном, если его энергетический

Λи

β. Заметим, что, несмотря на то что матрица

β₀

спектр анизотропен в плоскости, перпендикулярной

диагональна, в совокупность матриц (7), удовлетво-

оси C₄. Линейная модель дает ненулевой фототок

ряющих уравнению (6), входят как диагональные,

лишь в конечном интервале частот, в то время как

так и недиагональные матрицы.

учет кубических по k поправок к гамильтониану

приводит к циркулярному фототоку, квадратично

растущему с частотой во всем диапазоне прямых

ЛИТЕРАТУРА

оптических переходов вблизи вейлевских узлов.

N. P. Armitage, E. J. Mele, and A. Vishwanath, Rev.

Финансирование. Работа частично поддержа-

Mod. Phys. 90, 015001 (2018).

на Российским фондом фундаментальных исследо-

ваний (грант №19-02-00095).

Hao Zheng and M. Z. Hasan, Adv. Phys. X 3, 1466661

Благодарности. Один из авторов (Л. Е. Г.) бла-

(2018).

годарит Фонд развития теоретической физики и ма-

E. L. Ivchenko, Optical Spectroscopy of Semiconduc-

тематики «БАЗИС». Другой автор (Е. Л. И.) благо-

tor Nanostructures, Alpha Science Int., Harrow, UK

дарен фонду Academy of Finland (grant No 317920)

(2005).

за поддержку участия в Международном семина-

ре Nanocarbon Photonics and Optoelectronics (NPO

F. de Juan, A. G. Grushin, T. Morimoto, and

2018).

J. E. Moore, Nature Comm. 8, 15995 (2017).

Q. Ma, S.-Y. Xu, C.-K. Chan, C.-L. Zhang, G. Chang,

ПРИЛОЖЕНИЕ

Y. Lin, W. Xie, T. Palacios, H. Lin, S. Jia, P. A. Lee,

P. Jarillo-Herrero, and N. Gedik, Nature Phys. 13,

Выбор матрицы

β по известной матрице

842 (2017).

В качестве матрицы

β₀ в выражении (7) возьмем

B. Q. Lv, N. Xu, H. M. Weng, J. Z. Ma, P. Richard,

одно из решений уравнения

X. C. Huang, L. X. Zhao, G. F. Chen, C. E. Matt,

F. Bisti, V. N. Strocov, J. Mesot, Z. Fang, X. Dai,

β² =

^Λ.

(44)

T. Qian, M. Shi, and H. Ding, Nature Phys. 11, 724

(2015).

Приведем матрицу

Λ к диагональному виду

⎡

⎤

Hongming Weng, Chen Fang, Zhong Fang, B. A. Ber-

λ²¹

nevig, and Xi Dai, Phys. Rev. X 5, 011029 (2015).

D_d Λ D-1

⎢

⎥

⎣ 0

λ²²

⎦,

Yan Sun, Shu-Chun Wu, and Binghai Yan, Phys. Rev.

λ23

B 92, 115428 (2015).

где λ²¹, λ²², λ²³ — собственные числа этой матрицы,

J. Buckeridge, D. Jevdokimovs, C. R. A. Catlow, and

D_d — матрица соответствующего ортогонально-

A. A. Sokol, Phys. Rev. B 93, 125205 (2016).

го преобразования. Тогда выбранная нами матрица

имеет вид

10.

Yonghui Zhou, Pengchao Lu, Yongping Du, Xiangde

⎡

⎤

Zhu, Ganghua Zhang, Ranran Zhang, Dexi Shao,

λ₁

Xuliang Chen, Xuefei Wang, Mingliang Tian, Jian

⎢

⎥

D-1

β₀ =

⎣ 0

λ₂

⎦ D

(45)

Sun, Xiangang Wan, Zhaorong Yang, Wenge Yang,

Yuheng Zhang, and Dingyu Xing, Phys. Rev. Lett.

λ₃

117, 146402 (2016).

где для определенности мы полагаем все три числа,

λ₁, λ₂, λ₃, положительными. Выражение (45) можно

11.

D. Grassano, O. Pulci, A. M. Conte, and F. Bech-

выразить через матрицу

Λ и ее собственные чис-

stedt, Sci. Rep. 8, 3534 (2018).

ла [19]:

12.

Yu-Hsin Su, Wujun Shi, C. Felser, and Yan Sun, Phys.

)

1⁽

Rev. B 97, 155431 (2018).

Λ2

I_β√Δ

Î+

I2β + I_Λ

^Λ-

β₀ =

(

)

(46)

13.

C.-K. Chan, N. H. Lindner, G. Refael, and P. A. Lee,

√

I_β I2β - I_Λ

∓

Δ_Λ

Phys. Rev. B 95, 041104 (2017).

174