ЖЭТФ, 2019, том 156, вып. 2 (8), стр. 195-204
© 2019
НЕЛИНЕЙНЫЕ ПОВЕРХНОСТНЫЕ ВОЛНЫ НА ГРАНИЦЕ
РАЗДЕЛА ОПТИЧЕСКИХ СРЕД С РАЗЛИЧНЫМИ
МЕХАНИЗМАМИ ИНДУЦИРОВАНИЯ НЕЛИНЕЙНОСТИ
С. Е. Савотченко*
Белгородский государственный технологический университет им. В. Г. Шухова
308012, Белгород, Россия
Поступила в редакцию 2 января 2019 г.,
после переработки 25 марта 2019 г.
Принята к публикации 26 марта 2019 г.
Описаны типы нелинейных поверхностных волн необыкновенной поляризации, возникающие на границе
раздела фоторефрактивного кристалла и среды с керровской нелинейностью. Рассмотрены случаи фо-
кусирующей и дефокусирущей нелинейности. Показано, что в такой системе могут существовать нели-
нейные поверхностные волны несимметричного профиля нескольких типов. Волны одного типа затухают
при удалении от границы раздела без осцилляций в глубину как фоторефрактивного кристалла, так и
керровского, а другого типа — с осцилляциями. Вблизи границы раздела фоторефрактивного кристалла
и среды с дефокусирующей керровской нелинейностью могут существовать по два вида локализованных
состояний, различающихся формой затухания поля, как с осцилляциями, так и без. Получены диспер-
сионные соотношения и указаны условия существования всех описанных типов волн в зависимости от
оптических характеристик кристаллов. В явном аналитическом виде найдены точные решения дисперси-
онных уравнений, описывающие зависимости константы распространения от оптических характеристик
кристаллов.
DOI: 10.1134/S0044451019080017
формами нелинейности (наиболее часто встречаю-
щийся случай — контакт двух сред с керровской
нелинейностью [13-21]) либо на границе раздела ли-
1. ВВЕДЕНИЕ
нейной и нелинейной сред [22-26].
Теоретическому описанию поверхностных элект-
В данной работе предлагается теоретическое
ромагнитных волн (плазмонов, поляритонов) на
описание новых типов нелинейных локализованных
границах различных сред посвящено большое ко-
состояний, соответствующих поверхностным вол-
личество работ [1-7]. С точки зрения технических
нам на границе двух оптических сред с различны-
приложений особую важность имеют исследования
ми по физической природе формами нелинейности:
свойств поверхностных волн в различных нелиней-
фоторефрактивного кристалла и кристалла с кер-
ных оптических средах, таких как фоторефрактив-
ровской нелинейностью. Очевидно, что такие по-
ные кристаллы [8-11] и среды с эффектом Кер-
верхностные волны будут иметь несимметричный
ра [12]. Тем не менее необходим детальный анализ
профиль относительно границы раздела сред. Кро-
многих практически важных аспектов, в частнос-
ме того, различие форм нелинейности, обусловлен-
ти, механизмов формирования нелинейных поверх-
ных различными механизмами индуцирования поля
ностных волн с несимметричным профилем, воз-
вследствие перераспределения плотности зарядов в
никающих вблизи границ между фоторефрактив-
кристаллах, приводит к возможности существова-
ными кристаллами и другими оптическими среда-
ния нелинейных поверхностных волн, амплитуда по-
ми. В основном описывалась локализация возбуж-
ля в которых убывает при удалении от границы раз-
дений электромагнитного поля вблизи границ раз-
дела сред осциллирующим образом. Также будет по-
дела сред с одинаковыми по физической природе
казано, что если считать известной амплитуду поля
поверхностной волны на границе раздела кристал-
* E-mail: savotchenkose@mail.ru
лов, то возможно найти в явном аналитическом ви-
195
С. Е. Савотченко
ЖЭТФ, том 156, вып. 2 (8), 2019
де без использования дополнительных приближений
Нелинейная добавка к показателю преломления
точные решения дисперсионных уравнений, опреде-
фоторефрактивного кристалла формируется в ре-
ляющие зависимости константы распространения от
зультате диффузионного механизма нелинейности
оптических характеристик кристаллов.
[27]. Если пренебречь темновой интенсивностью по
сравнению с интенсивностью поверхностной волны,
то нелинейную добавку к показателю преломления
2. УРАВНЕНИЯ МОДЕЛИ
фоторефрактивного кристалла можно представить
в виде [9,10,27]
Рассмотрим контакт одноосного фоторефрак-
тивного кристалла с диффузионным механизмом
1
kBT I′1
Δn1(x) =
n3
10
reff
,
формирования нелинейности и одноосного кристал-
2
e I1
ла с керровской нелинейностью (далее будем для
где штрихи здесь и далее означают производные по
краткости называть его керровским кристаллом) в
координате x, reff — эффективный электрооптичес-
отсутствие приложенного внешнего поля. Границу
кий коэффициент, kB — константа Больцмана, T —
раздела кристаллов будем считать настолько тон-
температура, e — модуль заряда электрона, Ij ∝
кой, что можно пренебречь оптическими эффекта-
∝ |Hj |2 — интенсивность светового пучка в поверх-
ми внутри нее.
ностной волне.
Будем изучать Р-поляризованные нелинейные
Нелинейная добавка к показателю преломления
поверхностные волны, для которых Ey = 0, Hx =
керровского кристалла пропорциональна интенсив-
= Hz = 0, т.е. волны с необыкновенной поляри-
ности: Δn2(x) ∝ I2. Для нее будем использовать вы-
зацией (ТМ-волны). Так как будет рассматривать-
ражение в виде Δn2(x) = α|H2|2, α — коэффициент
ся скользящее распространение светового пучка, то
керровской нелинейности (постоянный).
можно пренебречь анизотропией показателя пре-
Предполагая, что установившееся распределение
ломления и использовать одноосное приближение.
распространяющейся вдоль оси z волны представи-
Пусть полярная ось фоторефрактивного крис-
мо в виде
талла направлена вдоль оси x. ТМ-волна распрост-
{
H1(x)eiβk0z, x > 0,
раняется вдоль оси z. Граница раздела между фото-
Hy(x, z) =
рефрактивным и керровским кристаллами располо-
H2(x)eiβk0z, x < 0,
жена в плоскости x = 0. Фоторефрактивный крис-
где β — константа распространения, в рассматри-
талл занимает полупространство x > 0, а керровс-
ваемом приближении с учетом малости темновой
кий — полупространство x < 0.
интенсивности по сравнению с интенсивностью по-
Будем рассматривать только стационарное рас-
верхностной волны и малости нелинейных добавок
пределение поля поверхностной волны. Из системы
к невозмущенным показателям преломления из (1)
уравнений Максвелла в рассматриваемом случае по-
можно получить уравнения
лучается уравнение для отличной от нуля компонен-
ты вектора магнитного поля:
H′′1 + μH′1 + (n210 - β2)k20H1 = 0,
(2)
H′′2 + (n220 - β2)k20H2 + g|H2|2H2 = 0,
(3)
ΔHy + k2(x)Hy = 0,
(1)
где μ = 2k20n410reff kB T/e — коэффициент затуха-
где Δ — двумерный оператор Лапласа по координа-
ния волны в фоторефрактивном кристалле, g
=
там x и z,
= 2αk20n20 — эффективный коэффициент нелиней-
{
k0 {n10(x) + Δn1(x)} , x > 0,
ности в керровском кристалле.
k(x) =
Из условия непрерывности тангенциальных со-
k0 {n20(x) + Δn2(x)} , x < 0,
ставляющих полей на границе кристаллов вытекают
k0
= 2π/λ0, λ0 — длина волны света в вакуу-
граничные условия
ме, nj0 — невозмущенные показатели преломления,
H1(0) = H2(0) = H0,
(4)
Δnj — нелинейные добавки к ним, которые счита-
1
1
ются малыми (Δnj ≪ nj0), j = 1, 2. Здесь и далее
H′1(0) =
H′2(0),
(5)
ε1
ε2
значение индекса j = 1 соответствует величине, ха-
рактеризующей фоторефрактивный кристалл в об-
где H0 — амплитуда поля на границе раздела, εj ∝
ласти x > 0, а значение индекса j = 2 соответствует
∝ n2j0 — линейные (невозмущенные) части диэлек-
величине, характеризующей керровский кристалл в
трических проницаемостей фоторефрактивного и
области x < 0.
керровского кристаллов.
196
ЖЭТФ, том 156, вып. 2 (8), 2019
Нелинейные поверхностные волны...
Таким образом, математическая формулировка
Подстановка решений (6) и (7) в граничные усло-
модели для описания нелинейных поверхностных
вия (4) и (5) приводит к следующим выражениям
волн на границе фоторефрактивного и керровского
для параметров поля в фоторефрактивном кристал-
кристаллов сводится к уравнениям (2) и (3) с гра-
ле:
ничными условиями (4) и (5).
)
q
(ε1
μ
Нелинейные поверхностные волны в рассматри-
A=
√
q th qx0 +
+ν
,
(10)
ν
2g chqx0
ε2
2
ваемой модели представляют собой решения кра-
)
q
(ε1
μ
евой задачи
(2)-(5), удовлетворяющие условиям
B=-
√
q th qx0 +
-ν
(11)
ограниченности.
ν
2g chqx0
ε2
2
Уравнение (2) имеет два типа исчезающих на
Таким образом, нелинейная поверхностная волна
бесконечности решений в зависимости от соотноше-
с неосциллирующим профилем при положительной
ния между значениями константы распространения,
керровской нелинейности описывается распределе-
коэффициента затухания и невозмущенного показа-
ниями полей (6) и (7) с параметрами, определяемы-
теля преломления в фоторефрактивном кристалле.
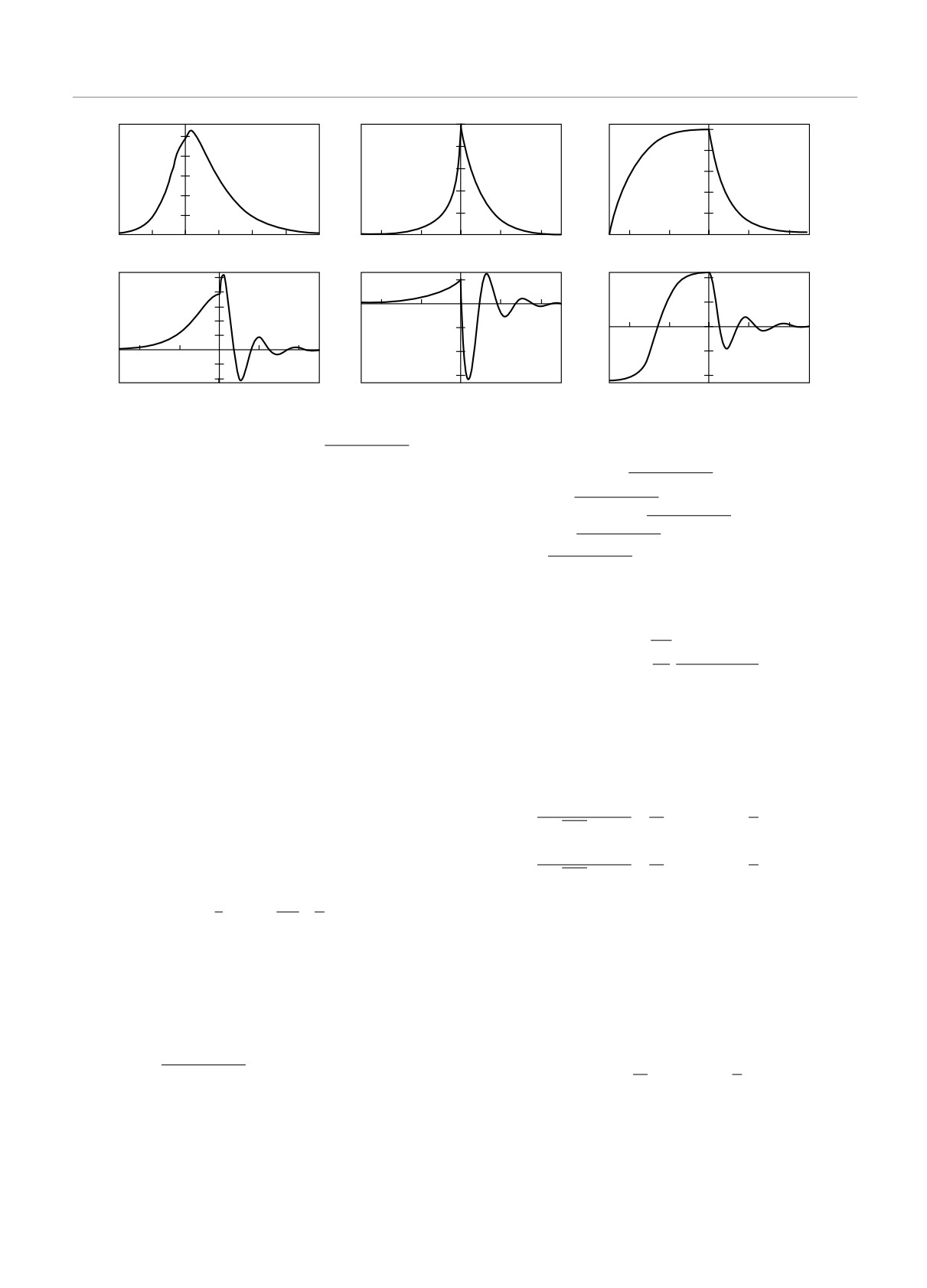
ми выражениями (8)-(11) (см. рис. а). Величина x0
Амплитуда волны первого типа затухает без осцил-
здесь играет роль свободного параметра.
ляций при удалении от границы раздела вглубь фо-
Если максимум локализации расположен в плос-
торефрактивного кристалла, а второго типа — ос-
кости границы раздела кристаллов, когда x0 = 0, то
циллирующим образом [28].
выражения (10) и (11) упрощаются:
Решения нелинейного уравнения (3) определя-
(
)
ются знаком коэффициента нелинейности g и зна-
q
μ
A=
+ν
,
(12)
ком разности n220 - β2. В зависимости от их ком-
ν
√2g
2
(
)
бинаций возникает несколько типов нелинейных по-
q
μ
B=-
-ν
(13)
верхностных волн несимметричного профиля.
ν
√2g
2
Нелинейная поверхностная волна с неосциллиру-
3. ЗАТУХАЮЩИЕ БЕЗ ОСЦИЛЛЯЦИЙ
ющим профилем (6) может затухать в глубину фо-
НЕЛИНЕЙНЫЕ ПОВЕРХНОСТНЫЕ ВОЛНЫ
торефрактивного кристалла немонотонно или моно-
тонно. Монотонное затухание волны в глубину фо-
3.1. Волны в кристалле с положительной
торефрактивного кристалла происходит в двух слу-
керровской нелинейностью
чаях:
{
√
}
В случае g > 0 и max n20,
n210 - μ2/4k2
<
1) A = 0, и тогда H0 = B,
0
или
< β < n10 решения уравнений (2) и (3) представимы
2) B = 0, и тогда H0 = A.
в виде
Далее, из (10) и (11) получается
H1(x) = e-μx/2(Aeνx + Be-νx),
(6)
(
)
ε1
μ
√2
q
ν =∓
q th qx0 +
,
(14)
H2(x) =
(7)
ε2
2
g ch q(x - x0)
где выбирается знак «-» для A = 0 и знак «+» для
Параметр ν решения (6) определяется выраже-
B = 0. В этих случаях распределение поля (6) в
нием
монотонно затухающей поверхностной волне в фо-
1
{
}
торефрактивном кристалле принимает вид
ν2 =
μ2 - 4k20(n210 - β2)
,
(8)
4
H1(x) = H0e-γx,
(15)
а решения (7) —
где амплитуда поля на границе раздела
q2 = k20(β2 - n220).
(9)
√
2
q
Величина 1/q характеризует глубину локализа-
H0 =
(16)
g ch qx0
ции поля в керровском кристалле, а x0 определяет
положение центра локализации поля.
и коэффициент затухания
Поверхностная волна с неосциллирующим про-
ε1
филем может наблюдаться только при очень малых
γ=-
q th qx0.
(17)
углах скольжения пучка, возбуждающего эту волну.
ε2
197
С. Е. Савотченко
ЖЭТФ, том 156, вып. 2 (8), 2019
HK
HP
а
HK
HP
б
HK
HP
в
0
x
0
x
0
x
HK
H
HK
г
P
д
H
HP
е
HP
K
0
x
0
x
0
x
Характерные профили распределения поля (HK — в керровском кристалле при x < 0, HP — в фоторефрактивном
при x > 0) в поверхностной волне в зависимости от расстояний x от границы раздела кристаллов при фиксированных √ }{
параметрах: a) диапазон max n20,
n210 - μ2/4k2
0
< β < n10 и g > 0, в фоторефрактивном кристалле — график
{
√
}
зависимости (6), в керровском — график зависимости (7); б) диапазон max n20,
n210 - μ2/4k2
0
< β < n10 и g < 0,
√
в фоторефрактивном кристалле — (6), в керровском — (19); в) диапазон
n210 - μ2√k20 < β < min{n10, n20} и g < 0,
в фоторефрактивном кристалле — (6), в керровском — (28); г) диапазон n√ <β <
n210 - μ2/4k20 и g > 0, в фоторе-
фрактивном кристалле — (36), в керровском — (7); д) диапазон n20 <β<
n2
и g < 0, в фоторефрактивном
{
10
- μ2/4k0}
√
кристалле — (36), в керровском — (19); е) диапазон β < min n20,
n210 - μ2/4k20 и g < 0, в фоторефрактивном
кристалле — (36), в керровском — (28)
√
Для положительности коэффициента затухания
2
q
H2(x) =
,
(19)
(17) в монотонно убывающей волне (15) должно
|g| sh q(x - x0)
быть x0 < 0. Такая монотонно убывающая волна су-
ществует при фиксированной связи константы расп-
где q определяется выражением (9) (см. рис. б). Па-
ространения, коэффициентов преломления и дру-
раметр ν решения (6) определяется выражением (8),
гих физических характеристик фоторефрактивного
а константы A и B находятся после подстановки (6)
и керровского кристаллов, определяемой выражени-
и (19) в граничные условия (4) и (5):
ем (14).
)
q
(ε1
μ
Выражение (14) можно использовать другим об-
A=
√
q cth qx0 +
+ν
,
(20)
разом, определив из него положение центра локали-
ν
2|g| sh qx0 ε2
2
)
зации поля как функцию константы распростране-
q
(ε1
μ
B=
√
q cth qx0 +
-ν
(21)
ния:
2
ν
2|g| sh qx0 ε2
))
1
( ε2 (μ
x0(β) = -
Arth
±ν
,
(18)
Как и для кристалла с положительной керровс-
q
ε1q
2
кой нелинейностью, в кристалле с отрицательной
керровской нелинейностью возможно существова-
где знаки «+» для A = 0 и «-» для B = 0.
ние монотонно затухающих в глубину фоторефрак-
тивного кристалла волн в двух случаях (A = 0 или
3.2. Волны первого типа в кристалле с
B = 0). Тогда из (20) и (21) получается дисперсион-
отрицательной керровской нелинейностью
ное уравнение
Р{ссмотрим теперь} случай g
<
0
и
)
√
(ε1
μ
max n20,
n210-μ2/4k2
< β
< n10. Тогда в
ν =∓
q cth qx0 +
,
(22)
0
2
ε2
фоторефрактивном кристалле решение уравнения
(2) определяется выражением (6), в керровском
где выбирается знак «-» для A = 0 и «+» для
кристалле решение уравнения (3) представимо в
B = 0. В этих случаях распределение поля (6) в
виде
монотонно затухающей поверхностной волне в фо-
198
ЖЭТФ, том 156, вып. 2 (8), 2019
Нелинейные поверхностные волны...
торефрактивном кристалле принимает вид (15), где
условию |H2(x)| → 0 при x → -∞), но всюду оста-
амплитуда поля на границе раздела
ется конечным и может использоваться для анализа
√
локализованных состояний в кристаллах конечной
2
q
толщины при условии, что она существенно превос-
H0 = -
(23)
|g| sh qx0
ходит характерное расстояние локализации возму-
щений поля вблизи границы раздела (см. рис. в).
и коэффициент затухания
Параметр ν решения (6) определяется выраже-
нием (8), а константы A и B находятся после под-
ε1
γ =-
q cth qx0.
(24)
становки (6) и (28) в граничные условия (4) и (5):
ε2
)
qt thqtx0
(μ
ε1
2qt
Из формулы (22) можно выразить положение
A=-
√
+ν-
,
(30)
центра локализации поля как функцию константы
ν
2|g|
2
ε2 sh2qtx0
распространения:
)
qt thqtx0
(μ
ε1
2qt
1
( ε2
(μ
))
B=
√
-ν-
(31)
x0(β) = -
Arcth
±ν
,
(25)
ν
2|g|
2
ε2 sh2qtx0
q
ε1q
2
Как и в разд. 3.2, в рассматриваемом случае воз-
где выбирается знак «+» для A = 0 и «-» для B =
можно существование монотонно затухающих в глу-
= 0.
бину фоторефрактивного кристалла волн при A = 0
В приближении qx0 ≪ 1 из (22) получается вы-
или B = 0. Тогда из (30) и (31) для таких волн по-
ражение
лучается дисперсионное уравнение
(
)
ε1
μ
ν =±
+
,
(26)
ε1
2qt
μ
ε2x0
2
ν =
∓
,
(32)
ε2 sh2qtx0
2
из которого можно найти в явном виде закон дис-
где выбирается верхний знак для A = 0 и нижний
персии — зависимость константы распространения
знак для B = 0. В этих случаях распределение поля
от параметров кристаллов:
(6) в монотонно затухающей поверхностной волне в
(
)
фоторефрактивном кристалле принимает вид (15),
ε1
ε1
β2(x0) = n210 +
+μ
(27)
где амплитуда поля на границе раздела
ε2x0k2
ε2x0
0
√
Условия существования такой поверхностной
2
H0 = -qt
th qtx0,
(33)
волны реализуются при -ε1/ε2μ < x0 < 0.
|g|
и коэффициент затухания
3.3. Волны второго типа в кристалле с
отрицательной керровской нелинейностью
ε1
2qt
γ =-
(34)
ε2 sh2qtx0
Рассмотрим теперь случай g
<
0
и
√
n210 - μ2/4k20
< β
< min{n10, n20}. Тогда в
Для положительности коэффициента затухания
фоторефрактивном кристалле решение уравнения
(34) в монотонно убывающей волне (15) должно
(2) определяется выражением (6), в керровском
быть x0 < 0.
кристалле решение уравнения (3) представимо в
Из уравнения (32) можно выразить положение
виде
центра локализации поля как функцию константы
√
распространения:
2
H2(x) = qt
th qt(x - x0),
(28)
(
)
|g|
1
2qtε1
x0(β) =
Arsh
(35)
2qt
ε2(μ/2 ± ν)
где
В приближении qx0 ≪
1 из (32) получается
k20(n220 - β2)
q2t =
(29)
выражение (26) и, соответственно, закон диспер-
2
сии (27).
Решение (28) хотя и не исчезает на бесконечности
В противоположном предельном случае, когда
(в отличие от решений (7) и (19), удовлетворяющих
qx0 ≫ 1, из (32) следует, что ν → ∓μ/2, β → n10.
199
С. Е. Савотченко
ЖЭТФ, том 156, вып. 2 (8), 2019
4. ЗАТУХАЮЩИЕ С ОСЦИЛЛЯЦИЯМИ
При x0 = 0 и меняющемся ϕ формула (38) при-
НЕЛИНЕЙНЫЕ ПОВЕРХНОСТНЫЕ ВОЛНЫ
мет вид
μ
4.1. Осциллирующие поверхностные волны в
tg ϕ = -
(42)
кристалле с положительной керровской
2p
нелинейностью
Из (42) получается закон дисперсии в виде
√
При g > 0 и n20 < β <
n210 - μ2/4k20 решение
μ2
уравнения (3) остается в виде (7), а решение урав-
β2(ϕ) = n210 -
(1 + ctg2 ϕ).
(43)
нения (2) примет вид
4k2
0
cos(px + ϕ)
Условие существования такой волны с законом
H1(x) = H0e-μx/2
,
(36)
cosϕ
дисперсии (43) определяется неравенством ctg2 ϕ <
< 4k20n210
/μ2 - 1.
где H0 определяется (16) и волновое число
При qx0 ≪ 1 и меняющемся ϕ из формулы (38)
1
{
}
получается закон дисперсии в виде
p2 = -ν2 =
4k20(n210 - β2) - μ2
(37)
4
(
)2 {
}
μ2
ε2 tg ϕ
Распределение поля (36) в поверхностной волне
β2(ϕ) = n210 -
-
1±D1/2
,
(44)
4k20
2ε1k0x0
затухает с осцилляциями при удалении от границы
раздела в глубину фоторефрактивного кристалла
D = 1 - f ctg2 ϕ,
(см. рис. г). Затухание поля в глубину керровского
]
}
4ε1x0
{ε1x0 [μ2
μ
кристалла по-прежнему происходит без осцилляций.
f =
- k20(n210 - n220) -
ε2
ε2
4
2
Подстановка решений (7) и (36) в граничные
условия (4) и (5) приводит к амплитуде поля в фо-
Условие существования такой волны с законом
торефрактивном кристалле в виде (16), а также к
дисперсии (44) определяется неравенством tg2 ϕ >
дисперсионному соотношению
>f.
)
Из (38) можно выразить положение центра лока-
(ε1
μ
p tg ϕ = -
q th qx0 +
(38)
лизации поля как функцию константы распростра-
ε2
2
нения:
Дисперсионное соотношение
(38), определяю-
)}
1
{ ε2 (μ
щее зависимость константы распространения от ко-
x0(β) = -
Arth
+ ptgϕ
(45)
q
ε1q
2
эффициентов преломления и других физических
характеристик фоторефрактивного и керровского
4.2. Осциллирующие поверхностные волны
кристаллов, можно проанализировать в различных
первого типа в кристалле с отрицательной
предельных случаях.
керровской нелинейностью
В частности, при ϕ = 0 формула (38) примет вид
με2
Рассмотрим теперь случай g < 0 и n20
< β <
√
q th qx0 = -
(39)
<
n210 - μ2/4k20. Тогда решение уравнения
(2)
2ε1
остается в виде (36), а решение уравнения (3) — в
При qx0 ≪
1 из (38) можно получить в явном
виде (19). Параметры q и p определяются формула-
виде закон дисперсии:
ми (9) и (37), а H0 — (23) (см. рис. д).
με2
Подстановка решений (19) и (36) в граничные
β2(x0) = n220 -
(40)
2ε1x0k2
условия (4) и (5) приводит к амплитуде поля в фо-
0
торефрактивном кристалле в виде (23), а также к
Волна с законом дисперсии (40) существует при
дисперсионному соотношению
x0 < 0.
ε1
μ
В противоположном предельном случае при
p tg ϕ =
q cth qx0 -
(46)
ε2
2
qx0 ≫ 1 из (39) находится значение q = -με2/2ε1,
из которого и получается закон дисперсии в явном
При ϕ = 0 дисперсионное уравнение (46) примет
виде:
вид
(
)2
με2
με2
β2(ϕ) = n220 +
(41)
q cth qx0 =
(47)
2ε1k0
2ε1
200
ЖЭТФ, том 156, вып. 2 (8), 2019
Нелинейные поверхностные волны...
При qx0 ≪ 1 из (47) можно определить положе-
5. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
ние центра x0 = 2ε1/με2. В противоположном пре-
Рассмотрим подход к решению дисперсионных
дельном случае при qx0 ≫ 1 из (47) находится зна-
уравнений, основанный на том, что известной харак-
чение q = με2/2ε1, из которого и получается закон
теристикой пусть теперь считается амплитуда поля
дисперсии в виде (41).
H0 поверхностной волны на границе раздела кри-
При qx0 ≪ 1 и меняющемся ϕ из (46) можно по-
сталлов. В этом случае дисперсионные уравнения
лучить в явном виде закон дисперсии:
будут содержать вместо параметра x0 амплитуду
{
}
(
)2
H0, и тогда возможно найти в явном аналитическом
1
ε1
β2(ϕ) = n210-
μ2+
-μ ctg2 ϕ
(48)
виде без использования дополнительных приближе-
4k20
2ε2x0
ний их точные решения, определяющие зависимости
константы распространения от характеристик крис-
Из (46) можно выразить положение центра лока-
таллов.
лизации поля как функцию константы распростра-
нения:
5.1. Затухающие без осцилляций волны
)}
1
{ ε2 (μ
x0(β) =
Arcth
+ ptgϕ
(49)
Для монотонно затухающих волн в кристалле с
q
ε1q
2
положительным коэффициентом керровской нели-
нейности дисперсионное уравнение (14) с использо-
4.3. Осциллирующие поверхностные волны
ванием выражения (16) можно представить как
второго типа в кристалле с отрицательной
(
)1/2
(
)
керровской нелинейностью
ε1
g
μ
q2 -
H20
=-
±ν
(53)
ε2
2
2
Рас{мотрим теперь сл}чай g
<
0
и β
<
√
< min n20,
n210 - μ2/4k2
. Тогда решение урав-
Точное решение дисперсионного уравнения (53)
0
имеет вид
нения (2) остается в виде (36), а решение уравнения
{
(3) — в виде (28). Параметры qt и p определяются
[ (
)1/2]}2
1
1
4hε
формулами (29) и (37) соответственно, а H0 — (33)
β2 = n210
-μ2
-
1±
1+
,
(54)
4k20
ε2
μ2
(см. рис. е).
Подстановка решений (28) и (36) в граничные
где
условия (4) и (5) приводит к амплитуде поля в фо-
ε=
(ε1)2 - 1,
торефрактивном кристалле в виде (33), а также к
ε2
дисперсионному соотношению
)2 {
}
μ2
(ε
1
g
μ2
h=
+
H20 +
+ k20(n220 - n210)
ε1
2qt
μ
4
ε2
2
4
p tg ϕ =
-
(50)
ε2 sh2qtx0
2
Если амплитуда поля на границе раздела выра-
жается через характеристики кристаллов как (по-
При ϕ = 0 дисперсионное уравнение (50) примет
лучается при h = 0)
вид
{
]}
2
(2)
μ2
[(ε1 )2
qt
με2
H20 =
k20(n210-n220)-
+1
,
(55)
=
,
(51)
g
4
ε2
sh2qtx0
4ε1
из которого в предельных случаях получаются та-
то из (53) получается величина ν = ±μ/ε и закон
кие же результаты как и в разд. 4.2.
дисперсии в виде
При qx0 ≪
1 и меняющемся ϕ из (50) получа-
(
)
μ2
4
ется закон дисперсии вида (48). При qx0 ≫
1 и
β2 = n210 -
1-
(56)
4k20
ε2
меняющемся ϕ из (50) получается закон дисперсии
вида (43).
Для существования волны с законом дисперсии
√
Из формулы (50) можно выразить положение
(56) должны выполняться условия ε1 >
5ε2 иμ2 <
центра локализации поля как функцию константы
< 4k20(n210 - n220)/[(ε1/ε2)2 + 1].
распространения:
Для кристалла с отрицательным коэффициен-
{
}
том керровской нелинейности для монотонно зату-
1
2qtε1
хающих волн первого типа дисперсионное уравне-
x0(β) =
Arsh
(52)
2qt
ε2(μ/2 + p tg ϕ)
ние (22) с использованием выражения (23) можно
201
С. Е. Савотченко
ЖЭТФ, том 156, вып. 2 (8), 2019
(
)1/2
представить в виде (53), в котором перед g ставится
μ
ε1
g
+
q2 -
H20
+ ptgϕ = 0.
(62)
противоположный знак.
2
ε2
2
Для кристалла с отрицательным коэффициен-
Точное решение дисперсионного уравнения (62)
том керровской нелинейности для монотонно зату-
имеет вид
хающих волн второго типа дисперсионное уравнение
{
(
)1/2}
(32) с использованием выражения (33) можно пред-
b
4a2c
ставить в виде
β2 = n220 +
1±
1-
,
(63)
2a2k20
b2
√
)
(
)
ε1
(g
|g|
μ
H20 - q2
=-
H0
±ν
(57)
где
t
ε2
2
2
2
)2
(ε1
Точное решение дисперсионного уравнения (57)
a=
+ tg2 ϕ, b = 2aΔ +
( με1 )2 ,
ε2
ε2
имеет вид
⎧
)2
( με1 )2 gH20
⎨
c=Δ2 +
,
1
μ2
(ε2
β2 = n210 -
-g
H0
×
ε2
2
2k20 ⎩ 2
ε1
{
}
μ2
μ2
(ε1)2 gH20
[
Δ = k20(n210-n220)-
tg2 ϕ-
+
(
)1/2]2⎫⎬
4
4
ε2
2
4htε1
× ∓1 ±
1-
,
(58)
2gε2H2
⎭
В частном случае при ϕ = 0 из дисперсионного
0
уравнения (62) можно получить более простое для
где
анализа выражение, определяющее ширину локали-
{
√
зации поля в керровском кристалле:
H0μ
μ2
ht =
2|g|
- gH20-
-k20(n220-n210)}ε1.
2
4
ε2
g
q2 =
H20 +
( με2 )2 ,
(64)
Если амплитуда поля на границе раздела вы-
2
2ε1
ражается через характеристики кристаллов в виде
из которого с помощью (9) можно получить следу-
(получается при ht = 0)
ющий закон дисперсии:
(
)1/2
{
}
)2
ε2
2
H0 =
×
1
g
( με2
ε1
|g|
β2 = n220 +
H20 +
(65)
{
k20
2
2ε1
]}
2
8
(ε1)2[μ
×
1±
+ k20(n220-n210)
,
(59)
Для кристалла с отрицательным коэффициен-
μ2
ε2
4
том керровской нелинейности для затухающих с ос-
то из (58) получается величина
цилляциями волн первого типа дисперсионное урав-
√
нение (46) с использованием выражения (23) можно
ν =∓
2|g| H0ε2/ε1,
(60)
представить в виде
(
)1/2
которой соответствует следующий закон дисперсии
μ
ε1
g
+ ptgϕ =
q2 +
H20
,
(66)
{
}
)2
2
ε2
2
2
1
μ
(ε2
β2 = n210 -
- 2g
H0
(61)
k2
4
ε1
отсюда получаются зависимости вида (63) и (65), в
0
которых перед g ставится противоположный знак.
Для существования волны с законом дисперсии
Для кристалла с отрицательным коэффициен-
(61) должно выполняться условие μ2 > 4k20(n220 -
том керровской нелинейности для затухающих с ос-
- n210)(ε1/ε2)2/[1/2 - (ε1/ε2)2].
цилляциями волн второго типа дисперсионное урав-
нение (50) с использованием выражения (33) можно
представить в виде
5.2. Затухающие с осцилляциями волны
√
Для затухающих с осцилляциями волн в кри-
)
(
)
ε1
(g
|g|
μ
H20 - q2
=
H0
+ ptgϕ
(67)
сталле с положительным коэффициентом керров-
t
ε2
2
2
2
ской нелинейности дисперсионное уравнение (38) с
использованием выражения (16) можно представить
Точное решение дисперсионного уравнения (67)
в виде
имеет вид
202
ЖЭТФ, том 156, вып. 2 (8), 2019
Нелинейные поверхностные волны...
{
1
μ
2
первого типа могут затухать монотонно при опреде-
β2 = n210 -
+
(ε2)2 g tg2 ϕ ×
2k2
2
ε1
ленных условиях связи константы распространения,
0
⎡
⎤⎫
коэффициентов преломления и других физических
(
)1/2
)
2
⎬
4Δt
(ε1
характеристик фоторефрактивного и керровского
× ⎣-1 ±
1-
ctg2 ϕ
⎦
,
(68)
g
ε2
⎭
кристаллов.
В данной работе были рассмотрены условия
где
существования таких нелинейных поверхностных
}
волн вблизи границы раздела фоторефрактивно-
√
{ε2
μ
√
μ2
Δt =
|g| H0
-
|g| H0
+k20(n220-n210)+
го кристалла и кристаллов с различными знаками
ε1 2
4
коэффициента керровской нелинейности. В случае
контакта фоторефрактивного кристалла с кристал-
Волны с законом дисперсии (68) существуют при
√
лом с положительным коэффициентом керровской
условии tg ϕ >
2|g|Δt ε1/ε2.
Если амплитуда поля на границе раздела вы-
нелинейности возникают два типа нелинейных по-
верхностных волн с различным характером зату-
ражается через характеристики кристаллов в виде
(получается при Δt = 0)
хания. В случае контакта фоторефрактивного кри-
сталла с кристаллом с отрицательным коэффициен-
{
(
(
)
2
том керровской нелинейности возникают два вида
με2
ε1
H0 =
√
1±
1-8
×
нелинейных поверхностных волн с затуханием без
2ε1
2|g|
με2
осцилляций и два вида волн, затухающих с осцил-
[
])1/2⎬
2
ляциями.
μ
×
+ k20(n220 - n210)
,
(69)
Для всех рассмотренных в работе типов нелиней-
4
⎭
ных поверхностных волн получены дисперсионные
уравнения, найдены их решения, определяющие за-
то из (67) получается волновое число
висимости константы распространения от характе-
√
p=
2|g| H0 tg ϕ ε2/ε1,
(70)
ристик фоторефрактивного и керровского кристал-
лов в явном аналитическом виде, а также указаны
которому соответствует закон дисперсии
условия их существования.
{
}
В работе приведен подход к решению дисперси-
(
)2
2
1
μ
ε2
онных уравнений, основанный на том, что известной
β2 = n210 -
+ 2g
H0 tg ϕ
(71)
k2
4
ε1
0
характеристикой считается амплитуда поля H0 по-
верхностной волны на границе раздела кристаллов.
Для существования волн с законом дисперсии
В этом случае удалось найти точные решения дис-
(71) должно выполняться условие μ2 > 4k20(n210 -
персионных уравнений в явном аналитическом виде
- n220)/[1 + (ε2/ε1)2/2].
без использования дополнительных приближений.
Из полученных выражений (58), (61), (63), (65),
Возможность существования волн с осциллирую-
(68) и (71) следует, что в основном приближении
щим затуханием принципиально отличает контакт
квадрат константы распространения линейно зави-
фоторефрактивного кристалла и нелинейной кер-
сит от квадрата амплитуды магнитного поля на гра-
ровской среды от контакта двух нелинейных кер-
нице раздела кристаллов.
ровских сред или контакта нелинейной керровской
и линейной сред, поскольку осцилляции затухающе-
го поля обусловлены фоторефрактивной нелинейно-
6. ЗАКЛЮЧЕНИЕ
стью диффузионного происхождения. Такое форми-
Таким образом, в данной работе установлено, что
рование поля демонстрировалось в поверхностных
на границе раздела фоторефрактивного кристалла
волнах, распространяющихся вдоль контакта фото-
и керровского кристалла могут существовать нели-
рефрактивного кристалла с воздухом или металли-
нейные поверхностные волны несимметричного про-
ческой пленкой (т. е. с линейными средами) [9-11],
филя двух типов, различающихся характером зату-
однако вдоль контакта нелинейных сред с иным ме-
хания. Волны первого типа затухают при удалении
ханизмом индуцирования нелинейности, керровско-
от границы раздела без осцилляций в глубину как
го типа в частности, амплитуда поля в поверхност-
фоторефрактивного кристалла, так и керровского,
ных волнах носит только апериодический или стро-
а волны второго типа затухают в глубину фото-
го монотонный характер [12-18]. В связи с этим при
рефрактивного кристалла с осцилляциями. Волны
проектировании различных оптических устройств
203
С. Е. Савотченко
ЖЭТФ, том 156, вып. 2 (8), 2019
(переключателей, сенсоров), использующих волно-
15.
И. Е. Дикштейн, Д. С. Никитов, С. А. Никитов,
водные свойства нелинейных поверхностных волн,
ФТТ 40, 1885 (1998).
существенное значение будет иметь тип нелиней-
16.
A. A. Sukhorukov and Yu. S. Kivshar, Phys. Rev.
ности контактирующих кристаллических просло-
Lett. 87, 083901 (2001).
ек [29-31].
17.
I. V. Shadrivov, A. A. Sukhorukov, Yu. S. Kivshar,
A. A. Zharov, A. D. Boardman, and P. Egan, Phys.
ЛИТЕРАТУРА
Rev. E 69, 016617 (2004).
1.
V. Tekkozyan, A. Babajanyan, and K. Nerkararyan,
18.
I. V. Shadrivov, A. A. Sukhorukov, and Yu. S. Kiv-
Opt. Comm. 305, 190 (2013).
shar, Phys. Rev. E 67, 057602 (2003).
2.
Y. V. Bludov, D. A. Smirnova, Yu. S. Kivshar,
19.
С. Е. Савотченко, Изв. вузов. Физика 47, 79 (2004).
N. M. R. Peres, and M. I. Vasilevsky, Phys. Rev. B 89,
20.
S. E. Savotchenko, Mod. Phys. Lett. B 32, 1850120
035406 (2014).
(2018).
3.
I. S. Panyaev and D. G. Sannikov, J. Opt. Soc. Amer.
B 33, 220 (2016).
21.
С. Е. Савотченко, ЖЭТФ 154, 514 (2018).
4.
A. I. Ignatov, I. A. Nechepurenko, and D. G. Baranov,
22.
Н. Н. Ахмедиев, В. И. Корнеев, Ю. В. Кузьменко,
Ann. Phys. 528, 537 (2016).
ЖЭТФ 88, 107 (1985) [N. N. Akhmediev, V. I. Kor-
neev, and U. V. Kuz’menko, J. Exper. Theor. Phys.
5.
F. Yang and H. Tian, J. Opt. 18, 1 (2016).
88, 107 (1985)].
6.
I. Haddouche and L. Cherbi, Opt. Comm. 382, 132
23.
A. D. Boardman, M. M. Shabat, and R. F. Wallis, J.
(2017).
Phys. D: Appl. Phys. 24, 1702 (1991).
7.
Y. M. Aleksandrov and V. V. Yatsishen, J. Nano- and
24.
С. Е. Савотченко, Конденсированные среды и
Electronic Phys. 9, 03039 (2017).
межфазные границы 19, 567 (2017).
8.
В. Н. Белый, Н. А. Хило, Письма в ЖТФ 23, 31
25.
С. Е. Савотченко, Вестник ВГУ, сер.: Физика. Ма-
(1997).
тематика 1, 44 (2018).
9.
Д. Х. Усиевич, Б. А. Нурлигареев, В. А. Сычугов,
26.
S. E. Savotchenko, Surfaces and Interfaces 13, 157
Л. И. Ивлева, П. А. Лыков, Н. В. Богодаев, КЭ 40,
(2018).
437 (2010).
27.
М. П. Петров, С. И. Степанов, А. В. Хоменко, Фо-
10.
Д. Х. Усиевич, Б. А. Нурлигареев, В. А. Сычугов,
торефрактивные кристаллы в когерентной опти-
Л. И. Ивлева, КЭ 43, 14 (2013).
ке, Наука, Санкт-Петербург (1992).
11.
С. А. Четкин, И. М. Ахмеджанов, КЭ 41, 980
28.
V. S. Zuev, J. Russ. Laser Res. 26, 347 (2005).
(2011).
12.
Y. S. Kivshar and G. P. Agrawal, Optical Solitons:
29.
N. Zhong, Z. Wang, M. Chen, X. Xin, R. Wu, Y. Cen,
From Fibers to Photonic Crystals, Acad. Press, San
and Y. Li, Sensors and Actuators B: Chem. 254, 133
Diego (2003).
(2018).
13.
Yu. S. Kivshar, A. M. Kosevich, and O. A. Chubykalo,
30.
D. Zhang, Z. Li, W. Hu, and B. Cheng, Appl. Phys.
Phys. Rev. A 41, 1677 (1990).
Lett. 67, 2431 (1995).
14.
F. Kh. Abdullaev, B. B. Baizakov, and B. A. Umarov,
31.
T. Strudley, R. Bruck, B. Mills, and O. L. Muskens,
Opt. Comm. 156, 341 (1998).
Light: Sci. Appl. 3, e207 (2014).
204