ЖЭТФ, 2019, том 156, вып. 2 (8), стр. 239-253

ДИНАМИЧЕСКАЯ ТЕОРИЯ ДИФРАКЦИИ РЕНТГЕНОВСКИХ

ЛУЧЕЙ В КРИСТАЛЛЕ С ПОВЕРХНОСТНОЙ РЕШЕТКОЙ

ДРУГОГО МАТЕРИАЛА

В. И. Пунегов^*

Физико-математический институт

Федерального исследовательского центра «Коми научный центр»

Уральского отделения Российской академии наук

167982, Сыктывкар, Россия

Поступила в редакцию 1 февраля 2019 г.,

после переработки 1 февраля 2019 г.

Принята к публикации 12 марта 2019 г.

Разработана общая теория динамической рентгеновской дифракции в кристалле, на поверхности которо-

го сформирована латеральная периодическая структура из тонкопленочных линий (полос) другого мате-

риала. На основе модели краевых сил вычислены поля упругих решеточных смещений в подложке, возни-

кающих в результате создания латеральной поверхностной решетки. Используя формализм дифракции

пространственно-ограниченных рентгеновских пучков, мы получили решения для амплитуд отраженных

рентгеновских волн от кристалла с поверхностной решеткой, химический состав которой отличается от

состава подложки. Выполнено численное моделирование рентгеновской дифракции в подложке кремния

с поверхностными решетками вольфрама и оксида SiO2. Показано, что угловые распределения интен-

сивностей рассеяния от кристалла кремния с одинаковыми по размеру вольфрамовыми и оксидными

линиями существенно различаются, установлена физическая природа такого различия.

DOI: 10.1134/S0044451019080030

подложки Si становится покрытой поверхностной

решеткой (ПР) оксидного материала [6, 7].

В работах [8, 9] исследована дифракция рентге-

1. ВВЕДЕНИЕ

новских лучей в кристаллах кремния, на поверх-

ности которых методом литографии была сформи-

Первые эксперименты трехосевой рентгеновской

рована решетка в виде периодически расположен-

дифрактометрии

[1] на кристаллах кремния с

ных линий золота и вольфрама. При этом в отли-

прямоугольным поверхностным рельефом [2, 3] и

чие от известных латеральных решеток [2-7], сател-

на структурах, промодулированных поверхностной

литы на картах распределения интенсивности рас-

акустической волной [4, 5], показали, что наряду

сеяния (Reciprocal Space Maps (RSM)) возникали

с основным дифракционным пиком возникают

не только в горизонтальном направлении обратного

побочные дифракционные порядки (сателлиты).

пространства, но и вдоль линий псевдопиков моно-

Латеральные порядки появляются и в случае

хроматора и анализатора. Отметим, что ранее бы-

рентгеновского рассеяния на кристаллах кремния

ла получена двумерная карта распределения ин-

с периодически повторяющимися тонкопленоч-

тенсивности рентгеновского рассеяния на системе

ными линиями (полосами) SiO₂ [6, 7]. Оксидные

Au/Si(111), ПР которой имела период 2 мкм из чере-

пленочные линии создаются термическим окисле-

дующихся золотых линий [10]. Из-за плохого угло-

нием поверхности или осаждением оксида SiO₂ из

вого разрешения и относительно большого периода

паровой фазы, при этом часть оксидной пленки

в расположении металлических полос, дифракцион-

удаляется методом литографии с последующим

ные порядки были размыты и результаты детально

химическим травлением так, что поверхность

не анализировались.

Для объяснения необычного появления диаго-

^* E-mail: vpunegov@dm.komisc.ru

нальных сателлитов вдоль направлений псевдопи-

239

В. И. Пунегов

ЖЭТФ, том 156, вып. 2 (8), 2019

q_z, мкм^-1

E₀

E_h

-2

-1

-60

-15

q_x, мкм-1

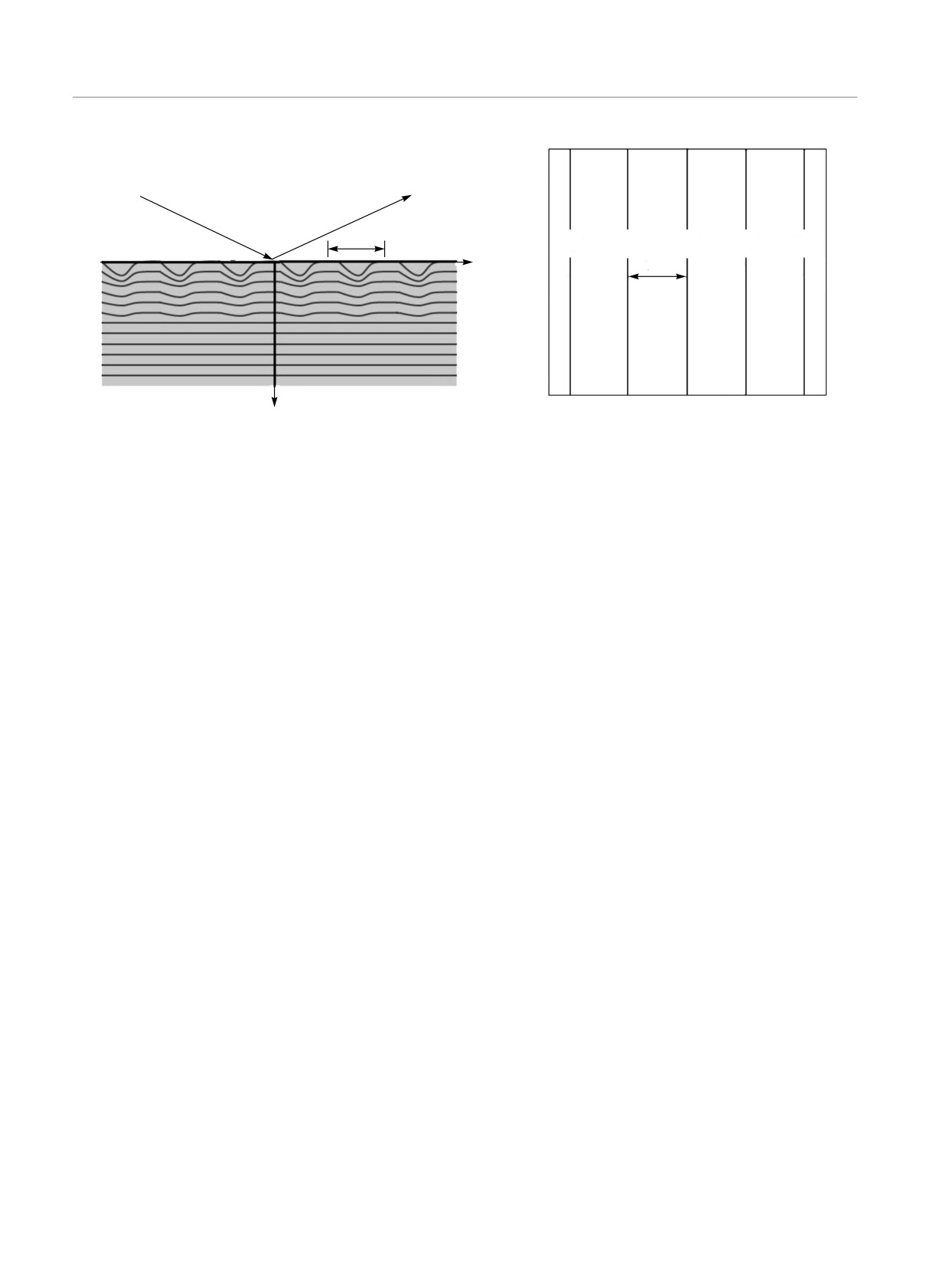
Рис. 1. Схематическое изображение дифракции плоской рентгеновской волны на кристалле с периодической латеральной

деформацией решетки (а) и соответствующая карта распределения интенсивности рассеяния в обратном пространстве (б)

ков монохроматора и анализатора в работе [9] пред-

2. ДИФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ

ложена феноменологическая модель, на основе ко-

НА КРИСТАЛЛЕ С ПЕРИОДИЧЕСКОЙ

торой выполнено численное моделирование углово-

ПОВЕРХНОСТНОЙ ДЕФОРМАЦИЕЙ.

ОСНОВНЫЕ УРАВНЕНИЯ

го распределения интенсивности рассеяния и про-

ведено сопоставление теоретических результатов с

экспериментальными данными. Однако формирова-

ние сегментальной структуры рентгеновских полей

Рассмотрим динамическую дифракцию рентге-

в объеме кристалла в рамках феноменологической

новских лучей в кристалле, который имеет перио-

модели [9] являлось лишь предположением. Стро-

дическую деформацию вдоль поверхности. Такие

гая модель динамической дифракции на кристалле с

деформации могут возникать в кристалле танта-

периодически расположенными на его поверхности

лата лития с периодически расположенными доме-

металлическими линиями без учета деформаций в

нами противоположной полярности [12] в структу-

приповерхностном слое кремния предложена в ра-

рах, промодулированных поверхностной акустиче-

боте [11]. Численные расчеты в рамках этой модели

ской волной [5] или при латеральной периодической

позволили получить ромбоидальную структуру ди-

ионной имплантации поверхности кристалла [13].

фракционного поля внутри кристалла, предсказан-

Кроме того, периодические упругие напряжения в

ную в работе [9]. С другой стороны, на расчетной

кристаллической решетке подложки появляются в

карте углового распределения интенсивности рассе-

результате нанесения на поверхность кремния пе-

яния в обратном пространстве отсутствовали неко-

риодических тонкопленочных линий SiO₂ [6, 7, 14],

торые дифракционные порядки, которые были заре-

Si₄N₃ [15], Au [10] и W [9], а также при создании

гистрированы на экспериментальных картах RSM.

на поверхности кристалла канавок, заполненных ок-

Следовательно, результаты [11] также полностью

сидным материалом [16].

не отвечают физическому явлению рентгеновской

дифракции на кристалле с вольфрамовой поверх-

Пусть на кристалл с периодической поверхност-

ностной решеткой. Кроме того, не выяснена причи-

ной деформацией под углом θ = θ_B + ω падает плос-

на разного углового распределения интенсивности

кая рентгеновская волна, где ω = θ - θ_B — откло-

рассеяния на кристалле с металлической и оксид-

нение рентгеновского пучка от угла Брэгга θ_B под-

ной поверхностной решеткой [7, 9]. Таким образом,

ложки (рис. 1a). Динамическая дифракция рентге-

данная работа посвящена более глубокому, последо-

новских лучей в деформированных кристаллах тра-

вательному и полному изучению рентгеновской ди-

диционно описывается уравнениями Такаги [17], ко-

фракции на кристаллах с поверхностной решеткой

торые в декартовой системе координат имеют вид:

из другого материала.

240

ЖЭТФ, том 156, вып. 2 (8), 2019

Динамическая теория дифракции рентгеновских лучей. . .

(

)

∂

∂ Ê₀(κ, η; z)

ctg θ_B

E₀(η; x, z) = ia₀E₀(η; x, z)+

= i(a₀ - κ ctg θ_B) Ê0(κ, η; z)+

∂x

∂z

∫

∞

+ iahφ(x, z)Eh(η; x, z),

(

)

(1)

+ iah

dκ^′

φ(κ^′, z)Êh(κ - κ^′, η; z),

∂

2π

ctg θ_B

E_h(η; x, z) =

-∞

∂x

∂z

(6)

∂ Ê_h(κ, η; z)

= i(a₀ + η)E_h(η; x, z) + ia_hφ^∗(x, z)E₀(η; x, z),

−

= i(a₀+η-κ ctg θ_B) Êh(κ, η; z)+

∂z

∫

∞

где a0 = πχ0/(λγ0); ah,h = Cπχh,h/(λγh,0); η =

+ ia_h

dκ^′

φ^∗(κ^′, z)Ê0(κ - κ^′, η; z).

= 4π cos(θ_B)ω/λ — угловой параметр, используе-

2π

мый в двухкристальной дифрактометрии в режи-

−∞

ме θ-2θ-сканирования; λ — длина волны рентгенов-

Отметим, что уравнения (6) имеют аналитическое

ского излучения в вакууме; C — поляризационный

решение в отсутствие деформаций кристалличес-

фактор; χ_g = -r₀λ²F_g/(πV_c) — фурье-компоненты

кой решетки, т. е. когда φ(x, z) = 1 и

φ(κ^′, z) =

рентгеновской поляризуемости для g = 0, h,h; V_c —

= 2πδ(κ^′) [18].

объем элементарной ячейки; r₀ = e²/(mc²) — клас-

В кристалле с чередующейся латеральной де-

сический радиус электрона; e, m — соответственно

формацией поле упругих решеточных смещений

заряд и масса электрона; F_g — структурный фак-

u_z(x, z) является периодической функцией вдоль на-

тор. В уравнениях (1) фазовый фактор φ(x, z) =

правления x, при этом u_z(x + Λ, z) = u_z(x, z), где

= exp(ihu_z(x, z)), при этом «звездочка» означает

Λ — период латеральной модуляции (рис. 1а). Сле-

комплексное сопряжение, h — величина вектора об-

довательно, присутствующий в уравнениях дифрак-

ратной решетки (h = 2π/dhkl), где dhkl — меж-

ции фазовый фактор (4) также будет периодиче-

плоскостное расстояние кристаллической подлож-

ской функцией, т. е. φ(x + Λ, z) = φ(x, z). Считая

ки, u_z(x, z) — проекция вектора упругих решеточ-

фронт падающей рентгеновской волны неограни-

ных смещений на направление вектора обратной ре-

ченным (ширина пятна засветки поверхности крис-

шетки отражающих атомных плоскостей.

талла много больше периода модуляции), фазовая

В уравнениях (1) выполним фурье-преобразова-

функция φ(x, z) представима в виде ряда Фурье:

ние для амплитуд рентгеновских полей [18, 19]:

∑

∫

∞

φ(x, z) =

B_m(z)exp(-imκ_Λx),

(7)

E0,h(η; x, z) =

dκ exp(iκx)Ê0,h(κ, η; z),

(2)

m=-∞

2π

−∞

где κ_Λ = 2π/Λ — волновое число латеральной моду-

ляции кристаллической решетки. Фурье-коэффици-

где амплитуды в фурье-пространстве имеют вид

енты в (7) зависят от координаты z, направленной

в глубь кристалла и запишутся как

∫∞

Ê0,h(κ, η; z) =

dx exp(-iκx)E0,h(η; x, z).

(3)

∫

-∞

B_m(z) =

exp[i(hu_z(x, z) + κ_Λmx)] dx =

Проведем также фурье-преобразование для фазово-

-Λ/2

го множителя φ(x, z):

∫

= (2π)-1

exp[i(hu_z(ϕ/κ_Λ, z) + mϕ)] dϕ.

(8)

∫

∞

φ(x, z) =

dκ^′ exp(iκ^′x

φ(κ^′, z),

(4)

2π

−∞

Фазовую функцию в фурье-пространстве

φ(κ^′, z) за-

пишем с учетом ее периодичности:

∫∞

∑

φ(κ^′, z) =

B_m(z)×

φ(κ^′, z) =

dx exp(-iκ^′x)φ(x, z).

(5)

m=-∞

-∞

∞

∫

× exp(-i(κ^′ + mκ_Λ)x) dx

(9)

Подставляя (2), (4) в (1), получаем одномерные ин-

тегродифференциальные уравнения

-∞

241

ЖЭТФ, вып. 2 (8)

В. И. Пунегов

ЖЭТФ, том 156, вып. 2 (8), 2019

и подставим в (6). Поскольку

Без учета взаимодействия волн соседних ди-

фракционных порядков (одномодовый режим) име-

∞

∫

ем

exp(-i(κ^′ + mκ_Λ)x) dx = δ(κ^′ + mκ_Λ)

2π

∂ˆ0,n(κ, η; z)

-∞

= i[a₀ - (κ - nκ_Λ)ctg θ_B] ×

∂z

— дельта-функция Дирака, уравнения дифракции

E0,n(κ, η; z) + ia_-hB_n(z)Êh,n(κ, η; z),

(12)

для рентгеновских амплитуд в результате простых

∂ Ê_h,n(κ, η; z)

преобразований примут вид

−

= i[a₀+η-(κ-nκ_Λ)ctg θ_B] ×

∂z

∂ Ê₀(κ, η; z)

E_h,n(κ, η; z) + ia_hB^∗n(z)Ê0,n(κ, η; z).

= i(a₀ - κ ctg θ_B) Ê0(κ, η; z)+

∂z

Как правило, система уравнений (11) используется

∑

+ iah

B_m(z)Êh(κ + mκ_Λ, η; z),

для описания дифракции в кристаллах с большим

m=-∞

периодом модуляции (Λ > 10 мкм) [21]. Поскольку

(10)

∂ Ê_h(κ, η; z)

в рассматриваемом случае период продольной упру-

= i(a₀+η-κ ctg θ_B) Êh(κ, η; z)+

гой деформации Λ ∝ 1 мкм, достаточно исходить из

∂z

∑

более простых уравнений (12).

+ ia_h

B^∗m(z)Ê0(κ + mκ_Λ, η; z).

m=-∞

3. ДИФРАКЦИЯ ПЛОСКОЙ

РЕНТГЕНОВСКОЙ ВОЛНЫ

Система связанных дифференциальных уравнений

(10) соответствует описанию многоволновой диф-

Сначала рассмотрим общеизвестную трактовку

ракции рентгеновских лучей в кристаллах

[20],

рентгеновской дифракции, согласно которой фронт

включая структуры с периодической упруго дефор-

рентгеновской волны неограничен в латеральном

мированной кристаллической решеткой вдоль по-

направлении вдоль оси x (рис. 1a). В этом слу-

верхности [5,21], при этом отличную от нуля ампли-

чае справедливы следующие граничные условия в

туду

E0,h(κ, η; z) получаем при значениях κ, крат-

прямом пространстве: для амплитуды рентгеновс-

ных волновому числу латеральной модуляции κ_Λ,

кой волны, падающей на поверхность кристал-

т. е. при κ = nκ_Λ, где n = 0, ±1, ±2, . . . Следователь-

ла, примем E0,n(η; x, z

= 0) = 1. Пусть толщи-

но, система уравнений (10) может быть представ-

на кристалла l_z, тогда для дифракционной волны

лена в виде отдельных уравнений для разных ди-

E_h,n(η; x, z = l_z) = 0. В фурье-пространстве, в кото-

фракционных порядков. Например, для произволь-

ром представлены уравнения (12), граничные усло-

ного порядка с номером n можно записать

вия запишутся как

E0,n(κ, η; z

= 0) = 2πδ(κ) и

E_h,n(κ, η; z = l_z) = 0. Здесь δ(κ) — дельта-функция

∂ Ê0,n(κ, η; z)

= i[a₀ - (κ - nκ_Λ)ctg θ_B] ×

Дирака.

∂z

В уравнениях (12) присутствуют фурье-коэффи-

E0,n(κ, η; z)+

циенты B_n(z), зависящие от координаты z в глубь

∑

кристалла. Эта система уравнений в общем случае

+ iah

B_m(z)Êh,n-m(κ, η; z),

не имеет аналитического решения, поэтому, как пра-

m=-∞

вило, применяются численные методы [5]. С другой

(11)

∂ Ê_h,n(κ, η; z)

= i[a₀+η-(κ-nκ_Λ)ctg θ_B] ×

стороны, если коэффициенты B_n(z) для всех ди-

∂z

фракционных порядков не зависят от z, т. е. B_n(z) =

E_h,n(κ, η; z)+

= B_n, то система (12) решается аналитически. Та-

∑

ким образом, если разбить кристалл на отдельные

+ ia_h

B^∗m(z)Ê0,n-m(κ, η; z).

элементарные слои толщиной z^p-zp-1 = l^pz, в преде-

m=-∞

лах которых коэффициенты B^pn = B_n(z^p-zp-1 = l^pz)

Наличие суммы в правой части (11) указывает на

можно считать постоянными величинами, то реше-

то, что для углового положения основного максиму-

ние находится в виде рекуррентных соотношений.

ма (n = 0) или сателлита с номером n имеет место

Здесь z^p, zp-1 — координаты верхней и нижней гра-

не только динамическое взаимодействие отражен-

ницы слоя с номером p, при этом нумерация слоев

ной

Ê0,n(κ, η; z) и дифракционной

Ê_h,n(κ, η; z) вол-

выполнена снизу вверх (p = 0, 1, 2, . . . , P ). В рам-

ны данного порядка, но и взаимодействие с волнами

ках данной модели рассмотрим неоднородную по

других дифракционных сателлитов.

глубине кристаллическую систему, состоящую из P

242

ЖЭТФ, том 156, вып. 2 (8), 2019

Динамическая теория дифракции рентгеновских лучей. . .

слоев. Для произвольного элементарного слоя, на-

где коэффициенты Mp1,2, ψ_n, ξ^pn, ξpn,1,2, Q^pn, σ₀ сле-

пример, с номером p, находящегося внутри много-

дуют из соответствующих параметров, присутству-

слойной структуры решение уравнений (12) пред-

ющих в решениях (13) и (14) при κ = 0. Отме-

ставим в виде

тим, что в случае падающей на кристалл плоской,

(

)

пространственно-неограниченной волны, амплиту-

Ê^p

(κ, η; z) =

M^p

exp

ξ^pnz

+Mˆp2

ды проходящего (17) и отраженного (18) рентгенов-

0,n

( [

]

)

ского полей не зависят о продольной координаты x.

× exp i

σp0 +

ξ^p

(13)

n,2

Трехосевая регистрация рентгеновских полей в

обратном пространстве определяется параметрами

(

)

ω и ε, фиксирующими угловое положение образца

Ê^p

M^p

(κ, η; z) =

exp

ξ^pnz

+bp2 Mˆp2

и анализатора [1]. В симметричной брэгговской гео-

h,n

( [

]

)

метрии эти параметры связаны с проекциями откло-

× exp i

σp0 +

ξ^p

(14)

n,2

нения вектора дифракции от узла обратной решетки

соотношениями [18]

где

ψ_n = 2a₀ + η - 2(κ - nκ_Λ)ctg θ_B,

q_x = k sinθ_B(2ω - ε),

√

ξ^pn =

ψ_n)² - 4BⁿBn∗a_ha¯_h,

q_z = -k cosθ_Bε.

Переход к трехосевой дифракционной схеме выпол-

ξpn,1,2 = (

ψ^pn ±

ξ^pn)/2,

ξpn,1 exp(

ξ^pnl^pz)

ξpn,2,

няется фурье-преобразованием (17) и (18):

σ₀ = a₀ - (κ - nκ_Λ)ctg θ_B,

ξp1,2/[B^pna_-h].

1,2

E₀

(q_x + nκ_Λ, q_z; z) =

,h,n

Коэффициенты

M^p

находятся из граничных усло-

1,2

∞

∫

вий на интерфейсах, где амплитуда рентгеновской

= dx exp (-i[q_x + nκ_Λ]x) Ep0,h,n(η; z).

(19)

волны, падающей на элементарный слой с номером

Ê^p

-∞

p, задается сверху этого слоя

(κ, η; z_p) и ампли-

0,n

туда дифракционной волны фиксируется на нижней

Таким образом, в случае падающей плоской вол-

границе

Êp

(κ, η; zp-1):

ны получаем математические решения для ампли-

h,n

(

[

]

)

туд рентгеновских полей в обратном пространстве:

exp

-i σp0

ξ^p

n,1

z_p

M^p

= -Êp0,n(κ, η; z_p)

(15)

Ep0,h,n(q_x + nκ_Λ, η; z) =

Sp1 -

S^p

= 2πδ(q_x + nκ_Λ)Ep0,h,n(η; z),

(20)

(

[

]

)

где Ep0,h,n(η; z) — амплитуды полей в прямом прост-

exp

-i σp0

ξ^p

z_p

n,2

M^p

= Êp0,n(κ, η; z_p)

(16)

ранстве (17) и (18). Угловая переменная η, использу-

Sp1 -

S^p

емая в двухкристальной дифракционной схеме, те-

перь представима в виде η = (q_x + nκ_Λ) ctg θ_B - q_z,

Rp-1

Здесь

Sp1 = (Rp-1n -bp1)exp(

ξ^pnl^pz),

Sp2 =

-bp2;

параметр ψ_n = 2a₀ +(q_x +nκ_Λ) ctg θ_B -q_z. Соотноше-

ние (20) имеет совершенно прозрачную физическую

Rp-1

= Êp-1h,n(κ, η; zp-1)/Êp-10,n(κ, η; zp-1)

интерпретацию. В рамках трехосевой дифракци-

— амплитудный коэффициент отражения от (p - 1)

онной схемы угловое распределение интенсивности

рассеяния в обратном пространстве представимо в

нижних слоев многослойной структуры. Решения

для дифракционного порядка с номером n в прямом

виде чередующихся бесконечно узких полос (дельта-

функций) соответствующих дифракционных поряд-

пространстве находится обратным преобразованием

Фурье выражений (13) и (14) и запишутся как

ков в латеральном направлении (рис. 1б). Распреде-

ление интенсивностей в вертикальном направлении

Ep0,n(η; z) = (Mp1 exp(iξ^pnz) + Mp2) ×

определяется соотношениями (17), (18) и зависит от

(

)

угловой переменной η = -q_z при q_x = -nκ_Λ, что

× exp

i[σ₀ + ξpn,2]z

(17)

соответствует (ω - 2θ)-сканированию в трехосевой

дифрактометрии [18]. Амплитуда отраженной вол-

ны на входной поверхности кристалла (z = z_P = 0)

E^ph,n(η; z) = (bp1Mp1 exp(iξ^pnz) + bp2Mp2) ×

(

)

вычисляется на последнем этапе рекуррентной про-

× exp

i[σ₀ + ξpn,2]z

(18)

цедуры:

243

В. И. Пунегов

ЖЭТФ, том 156, вып. 2 (8), 2019

)

⁽bP2SP1-bP1SP2

S₁

S₂

ÊP

h,n

(q_x, q_z) = 2πδ(q_x+nκ_Λ)

(21)

SP1 - S^P

E₀

E_h

l_x(in)

Если многослойная структура — конечной толщи-

ны, то при p = 0 амплитуда дифракционной волны

на ее нижней границе E0h,n(q_z ; z = z₀) = 0. В случае,

когда многослойная структура лежит на полубеско-

нечной подложке, начальная амплитуда имеет вид

a_h

E0h,n(q_z; z = z₀) =

;

Im(ξ0n) < 0,

ξ⁰

n,1

(22)

l_x

(ex)

a_h

E0h,n(q_z; z = z₀) =

;

Im(ξ0n) > 0,

ξ⁰

n,2

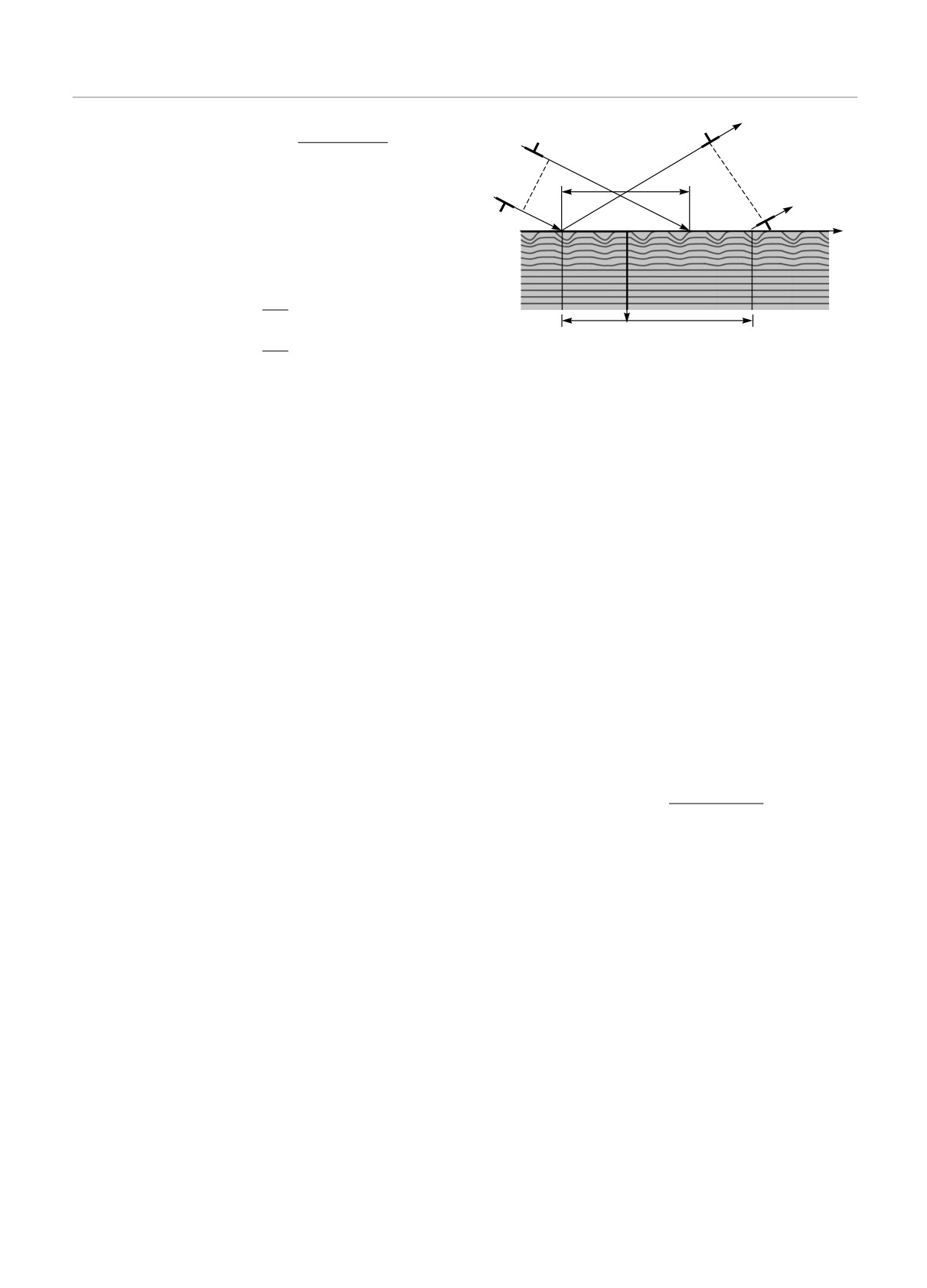
Рис.

2. Схематическое изображение дифракции огра-

ниченного рентгеновского пучка на кристалле с пери-

где коэффициенты ξ0n и ξ0n,1,2 такие же, что и в со-

одической латеральной деформацией решетки; w

отношениях (13), (14), и зависят от характеристик

= lxin) sin(θB) — ширина падающего пучка, ограниченного

рентгеновского излучения и материала подложки.

щелью S1

Полная амплитуда рентгеновской волны, отражен-

ной от кристалла с периодической латеральной де-

Уравнения дифракции (12) для пространствен-

формацией, находится суммированием по всем ди-

но-ограниченных пучков должны быть дополне-

фракционным порядкам:

ны новыми граничными условиями. Наличие ще-

∑

ли S₁ позволяет записать в прямом пространстве

ÊP

(q_x, q_z ) =

ÊP

(q_x, q_z).

(23)

h,n

следующее выражение для амплитуды рентгеновс-

n=-∞

кого пучка, падающего на поверхность кристалла:

E0,n(η; x, z = 0) = Y (x, lxin)), где

{

4. ДИФРАКЦИЯ

1, x ∈ ±lxin)/2,

ПРОСТРАНСТВЕННО-ОГРАНИЧЕННОГО

Y (x, l(in)x) =

(24)

0, x ∈ ±lxin)/2.

РЕНТГЕНОВСКОГО ПУЧКА НА

КРИСТАЛЛЕ С ПЕРИОДИЧЕСКОЙ

Это граничное условие в фурье-пространстве зада-

ЛАТЕРАЛЬНОЙ ДЕФОРМАЦИЕЙ

ется равенством

Ê^p

(κ, η; z = 0) =

Y (κ, lxin)), при

0,n

этом фурье-образ функции (24) имеет вид

Устоявшийся формализм плосковолновой дина-

(

)

мической теории дифракции [22] не отвечает опи-

(

) sin κlxin)/2

санию реальных экспериментальных условий. Бо-

Y κ, l(in)

(25)

лее того, как показано выше, становится затруд-

κ/2

нительным анализ карт распределения интенсив-

Второе граничное условие для кристалла толщи-

ности рассеяния вблизи узла обратной решетки

ной l_z:

(рис. 1б), поэтому следующим шагом является пе-

реход к рассмотрению дифракции пространственно-

E_h,n(η; x, l_z) =

Ê_h,n(κ, η; l_z) = 0.

ограниченных рентгеновских пучков на кристалле с

периодической латеральной деформацией.

Полагая, что периодическая латеральная деформа-

ция кристаллической решетки изменяется с глуби-

Пусть на кристалл с периодической латераль-

ной z, в рамках рекуррентной процедуры получаем

ной деформацией решетки падает рентгеновский пу-

соотношения, по структуре аналогичные (13), (14).

чок шириной w, ограниченный щелью S₁ (рис. 2).

Линейный размер засветки этим пучком поверхнос-

Отличие заключается в том, что для плоской волны

граничные коэффициенты

M^p

∝ δ(κ), для ограни-

ти кристалла в направлении оси x равен lxin) =

1,2

M^p

= w/ sin(θ_B). Наличие щели S₂ в дифракционном

ченного падающего пучка

1,2

∝

Y (κ, lxin)).

направлении задает ширину отраженного пучка на

Переход к решениям, описывающим трехосевую

входной поверхности кристалла (рис. 2). Дифракци-

регистрацию рентгеновских полей, требует выпол-

ей рентгеновских лучей на краях щелей падающего

нить фурье-преобразования (19). Для амплитуды

S₁ и отраженного S₂ пучков пренебрегаем (прибли-

отраженного рентгеновского пучка n-го дифракци-

жение геометрической оптики).

онного порядка на поверхности кристалла (z = z_P =

244

ЖЭТФ, том 156, вып. 2 (8), 2019

Динамическая теория дифракции рентгеновских лучей. . .

= 0) в трехосевой геометрии с щелями S₁ и S₂ по-

S₁

S₂

лучаем

(in)

E_h

∞

)

E₀

l_x

∫

⁽ˆ_bPSP1 -bP1

SP2

ÊP

(q_x, q_z) =

dκ

h,n

l_f

2π

SP1 -

S^P

-∞

h_f

(

)

(

)

Y κ, l(in)x

Y κ - nκ_Λ - q_x,l(ex)

(26)

где

(

)

(ex)

l_x

Y κ - nκ_Λ - q_x,l(in)

(

)

sin

[κ - nκ_Λ - q_x]lxex)/2

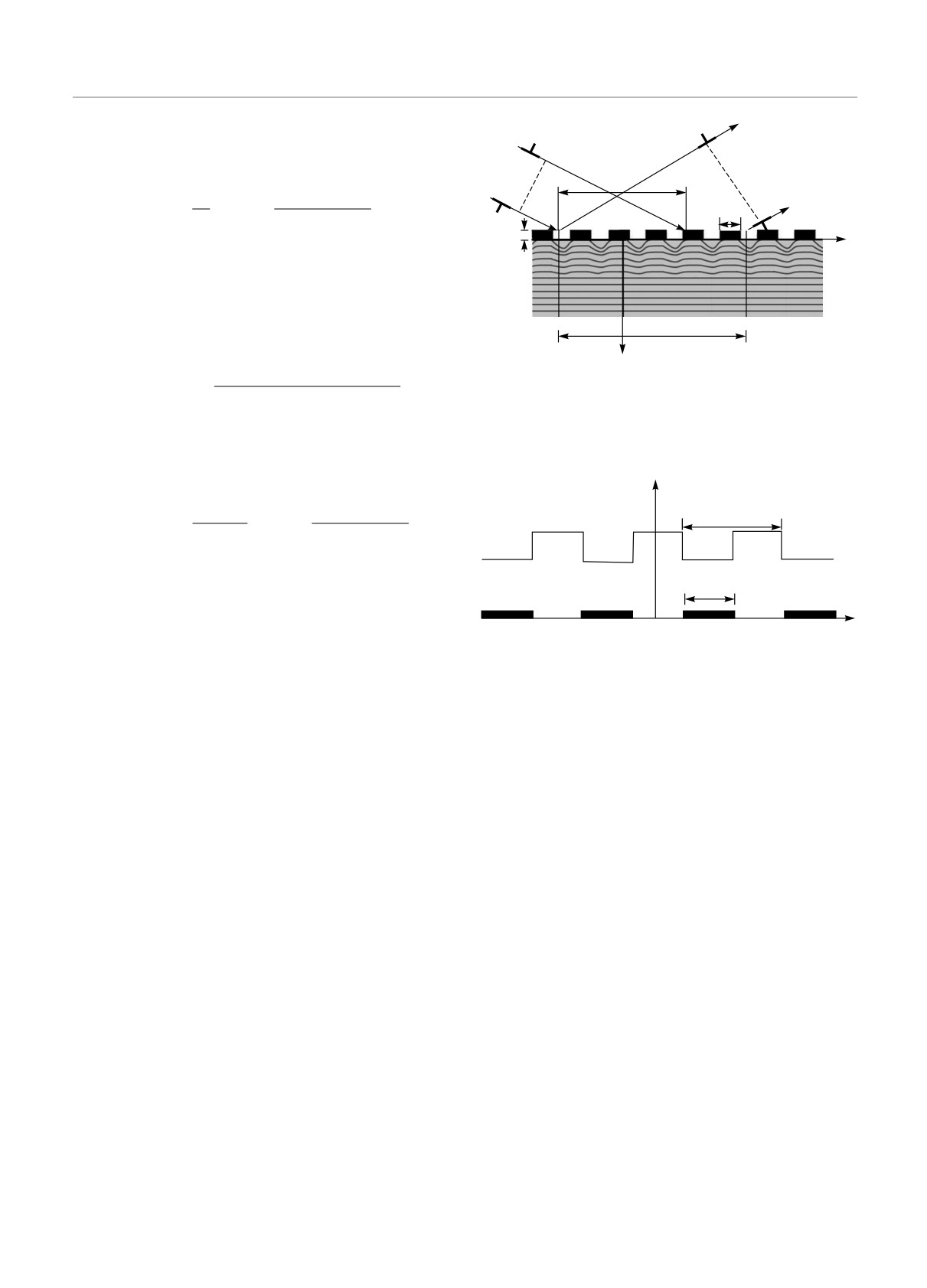
Рис. 3. Схема дифракции ограниченных рентгеновских

(27)

[κ - nκ_Λ - q_x]/2

пучков на кристалле с поверхностной решеткой другого

материала

Коэффициенты в (26) зависят от угловой перемен-

ной

ψ^pn = 2a₀ + (q_x + nκ_Λ - 2κ)ctg θ_B - q_z. Ампли-

тудный коэффициент отражения запишется как

Y (x)

∞

)

∫

⁽ˆ_bP

SP1 -bP1

SP2

R_h,n(q_x, q_z) =

dκ

2πl_norm

SP1 -

S^P

-∞

(

)

(

)

Y κ, l(in)x

Y κ - nκ_Λ - q_x,l(ex)

(28)

l_f

Величина l_norn равна наименьшему из значений lxin)

и lxex).

Рис. 4. Функция модуляции интенсивности падающего

рентгеновского излучения: γ — доля пропускаемого из-

лучения через периодически расположенные поглотители,

5. ДИФРАКЦИЯ

lf — ширина поглощающей тонкопленочной линии, Λ —

ПРОСТРАНСТВЕННО-ОГРАНИЧЕННОГО

период модуляции

РЕНТГЕНОВСКОГО ПУЧКА НА

КРИСТАЛЛЕ С ПОВЕРХНОСТНОЙ

РЕШЕТКОЙ ДРУГОГО МАТЕРИАЛА

Рассмотрим симметричную брэгговскую диф-

Если на поверхности кристалла находится сис-

ракцию ограниченных рентгеновских пучков в крис-

тема тонкопленочных линий другого материала, то

талле, на поверхности которого, например, методом

в общем случае падающий рентгеновский пучок,

литографии сформирована поверхностная решетка

прежде чем он достигнет поверхности подложки, бу-

из другого материала в виде периодически располо-

дет испытывать поглощение на участках, где эти ли-

женных латерально-ограниченных тонкопленочных

нии присутствуют. Кроме того, наличие линий при-

линий одинаковой высоты h_f и ширины l_f . Эти ли-

водит к периодической деформации приповерхност-

нии могут быть кристаллическими, аморфными или

ной области кристалла, поэтому динамическая диф-

поликристаллическими и, в отличии от кристалла,

ракция для произвольного сателлита будет описы-

на котором они размещены, находятся вне дифрак-

ваться системой уравнений (12). На участках между

ционного условия. Из-за различия в коэффициен-

линиями поглощение отсутствует, тем самым возни-

тах термического расширения при комнатной тем-

кает периодическая модуляция интенсивности пада-

пературе, в тонкопленочных линиях и в подложке

ющего излучения в латеральном направлении. Для

возникают упругие напряжения, приводящие к воз-

описания динамической дифракции на кристалле

никновению деформаций кристаллической решетки

с такой модуляцией падающего излучения примем

подложки. Период в расположении линий другого

следующую модель граничных условий в прямом

материала Λ совпадает с периодом деформаций в

пространстве: E0,n(η; x, z = 0) = Y_γ (x, M), где моду-

подложке, (Λ - l_f ) — расстояние между соседними

ляция падающего рентгеновского излучения задает-

линиями (рис. 3).

ся функцией вида (рис. 4):

245

В. И. Пунегов

ЖЭТФ, том 156, вып. 2 (8), 2019

Λ-l_f

MΛ

Y_γ(x, M) = 1, x ∈ ±

, -

≤x≤

6. ПОЛЕ УПРУГИХ ДЕФОРМАЦИЙ

Λ-l_f

MΛ

Тонкопленочные линии одного материала на по-

Y_γ(x, M) = γ, x ∈ ±

, -

≤ x ≤ MΛ,

(29)

верхности кристаллической подложки другого ма-

MΛ

териала имеют широкое применение в приборах

Y_γ(x, M) = 0, x < -

микро- и наноэлектроники, например, в техноло-

Здесь γ — доля излучения, пропускаемого через

гии интегральных схем [23]. Известно, что пленки,

осажденные на подложке, находятся в напряжен-

поглотитель (тонкопленочную линию), M — чис-

ном состоянии. Эти напряжения являются резуль-

ло периодов модуляции, lxin)

= MΛ — шири-

татом различий коэффициентов теплового расши-

на засветки поверхности кристалла с ПР падаю-

рения пленки и подложки [24]. Когда тонкая плен-

щим рентгеновским пучком. Для кристалла тол-

ка покрывает всю поверхность толстой подложки,

щиной l_z справедливо второе граничное условие:

то упругие напряжения в основном присутствуют

E_h,n(η; x, z = l_z) = 0. Поскольку система уравнений

в пленке. Если при этом система пленка-подлож-

(12) представлена в фурье-пространстве, граничные

ка испытывает упругий изгиб, эти напряжения мо-

условия имеют вид

Ê0,n(κ, η; z = 0) =

Y_γ(κ, M) и

гут быть вычислены с использованием классичес-

E_h,n(η; x, z = l_z) = 0, где

кой формулы Стони [25]. В случае, когда пленка,

sin(κMΛ/2)

например, методом литографии трансформируется

Y_γ(κ, M) =

в систему из периодически расположенных линий,

sin(κΛ/2)

[

]

напряженное состояние накапливается в подложке

sin(κ(Λ - l_f )/2)

sin(κΛ/2)

× (1 - γ)

+γ

(30)

и усиливается преимущественно у краев тонкопле-

κ/2

ночных линий. Такое усиление упругих напряжений

Отметим, что при γ = 1, т.е. когда материал ПР

в ряде случаев приводит к генерации дислокаций в

является непоглощающим, выражение (30) сводит-

подложке [26].

ся к (25):

Анализ упругих деформаций кристаллической

решетки на краях пленки впервые выполнен в рабо-

Y_γ(κ, M) = sin(κMΛ/2)/(κ/2).

те [27]. Позже предложено несколько различных мо-

делей для изучения упругих напряжений в системе

Пусть отраженный рентгеновский пучок, выхо-

пленка-подложка [28-31]. На основе этих моделей

дящий с нижней границы поверхности подложки,

[32-35], а также расчетов с использованием метода

засвечивает L полос ПР. В режиме трехосевой реги-

конечных элементов [36, 37] спрогнозированы крае-

страции амплитудный коэффициент отражения n-го

вые эффекты в системе тонкопленочная линия-под-

дифракционного порядка от кристалла с поверх-

ложка.

ностной решеткой другого материала запишется как

Для простоты будем исходить из первой, наибо-

∞

)

лее простой модели краевых сил [28]. Согласно этой

∫

⁽ˆ_bPSP1 -bP1

SP2

модели, на краю пленки, лежащей на полубесконеч-

R_h,n(q_x, q_z) =

dκ

2πl_norm

SP1 -

S^P

ной подложке из другого материала, концентриру-

-∞

ется сила в направлении, параллельном интерфейсу

Y_γ (κ, M)Yγ (κ - nκΛ - qx, L),

(31)

между пленкой и подложкой. Величина этой силы

равна F_f = σ_fxxh_f , где σ_fxx — компонента напряже-

где

ния, присутствующая у края пленки, h_f — толщина

пленки. В результате действия этой силы в подлож-

sin([κ - nκ_Λ - q_x]ΛL/2)

Y_γ (κ-nκ_Λ-q_x, L) =

ке возникают упругие напряжения, компоненты ко-

sin([κ - nκ_Λ - q_x]Λ/2)

[

торых в плоскости дифракции xz имеют вид [28]

sin([κ - nκ_Λ - q_x](Λ - l_f )/2)

× (1 - γ)

(

)

[κ - nκ_Λ - q_x]/2

2F_f

x³

]

σ_xx = -

sin([κ - nκ_Λ - q_x]Λ/2)

π (x² + z²)²

+ γ

(32)

(

)

(33)

[κ - nκ_Λ - q_x]/2

2F_f

xz²

σ_zz = -

π (x² + z²)²

При γ = 1, т. е. в отсутствие модуляции падающего

рентгеновского пучка, соотношение (32) непосред-

Строго говоря, величина σ_fxx зависит от ширины

ственно сводится к формуле (28), при этом lxex) =

тонкопленочной линии l_f, — чем уже линия, тем

= LΛ.

меньше ее значение. Имеются теоретические моде-

246

ЖЭТФ, том 156, вып. 2 (8), 2019

Динамическая теория дифракции рентгеновских лучей. . .

ли и эксперименты по нахождению величины σ_fxx

Следующим шагом в рассмотрении является вычис-

[33, 37]. Так, в работе [37] получена универсальная

ление фурье-коэффициентов B_n(z). Формула (8) да-

кривая среднего напряжения в пленке, латераль-

ет связь этих коэффициентов с полем решеточных

ный размер которой существенно меньше поверхнос-

смещений u_z,line(ϕ/κ_Λ, z_p) для отдельной линии:

ти подложки:

= (2π)-1 ×

B^pn

σ_fxx = σ₀

(34)

∫

X+a

exp[i (hu_z,st(ϕ/κ_Λ, z_p) + nϕ)] dϕ,

(39)

где X = K_hul_f /h_f , K_hu = E_s(1 - ν2f)/E_f (1 - ν2s),

a = 5.545, σ₀ — однородное напряжение в пленке

где u_z,line(ϕ/κ_Λ, z_p) задается соотношением (37) за-

больших латеральных размеров, E_f,s, ν_f,s — модули

меной x → ϕ/κ_Λ и при значении координаты z = z_p.

Юнга и коэффициенты Пуассона пленочной линии

(индекс «f») и подложки (индекс «s»).

Фурье-коэффициенты B_n(z), присутствующие в

7. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ

решениях для амплитуд полей рентгеновских пуч-

Численное моделирование углового распределе-

ков, определяются упругими смещениями атомов из

ния интенсивности рентгеновского рассеяния вы-

узлов кристаллической решетки (см. Приложение,

формула (A.4))

полнено для кристалла кремния с поверхностными

решетками из вольфрама и оксида SiO₂. В обоих

(

)

1-ν_s

случаях период ПР составлял 1 мкм, ширины ме-

u_z(x, z) = u₀

arctg

(35)

x² + z²

1+ν_s

таллической и оксидной линий 0.5 мкм, их толщины

равны 100 нм.

где максимальное значение решеточных смещений

Использованы табличные данные для симмет-

u₀ = F_f (1+ν_s)/(πE_s) зависит от характеристик тон-

ричного (111) отражения σ-поляризованного рент-

копленочной линии (краевой силы F_f ), а также от

геновского Kα1-излучения Cu с длиной волны λ =

коэффициента Пуассона и модуля Юнга подложки.

= 1.54Å (см. ссылку [39] и указанный в ней адрес

Для численных расчетов поле решеточных смеще-

сайта “X-Ray Server”). Длина первичной экстинкции

ний вдоль вектора обратной решетки удобно пред-

составляет l_ext = 1.51 мкм. Угол Брэгга для выбран-

ставить в виде

ного отражения равен 14.221^◦, межплоскостное рас-

(

)

стояние d₁₁₁ = 3.1355Å.

u_z

В численных расчетах значения модулей Юнга и

κ_Λ

коэффициентов Пуассона для кремния, вольфрама

(

)

z(ϕ/κ_Λ)

1-ν_s

и оксида SiO₂ взяты из работ [33,40,41]. Несмотря на

=u₀

arctg

(36)

(ϕ/κ_Λ)² + z²

1+ν_s

ϕ/κ_Λ

то что однородные напряжения в пленках больших

латеральных размеров для вольфрама (1300 МПа)

Выражения (35), (36) записаны для одного края

и оксида SiO₂ (400 МПа) сильно разнятся, компо-

пленки, латеральный размер которой меньше по-

ненты напряжений, присутствующие у краев пленок

верхности подложки, поэтому для одной линии

вольфрама (360 МПа) и SiO₂ (300 МПа) различают-

упругие решеточные смещения запишутся как

ся незначительно. Это связано с тем, что коэффи-

циенты K_hu в (34) для вольфрама (0.427) и оксида

u_z,line(x, z) = u_z(x - l_f /2, z) - u_z(x + l_f /2, z).

(37)

кремния (2.608) имеют заметное различие. Макси-

мальные решеточные смещения на краю пленки u₀ в

Аналогичная запись справедлива и для упругих ре-

(35) и (36) имеют значения 0.064 нм для вольфрама

шеточных напряжений, а также деформаций кри-

и 0.051 нм для SiO₂. Для периодически расположен-

сталлической решетки [38]. В случае периодического

ных тонкопленочных линий максимальные значе-

расположения M линий общее поле упругих реше-

ния смещений равны 0.053 нм для W и 0.042 нм для

точных смещений в подложке запишется как супер-

SiO₂. Карты равнозначных контуров упругих реше-

позиция смещений для одной изолированной тонко-

точных смещений для вольфрама и оксида SiO₂ вы-

пленочной линии:

числены на основе формул (36)-(38) и показаны на

∑

рис. 5.

u_z,gr(x, z) =

u_z,line(x + mΛ, z).

(38)

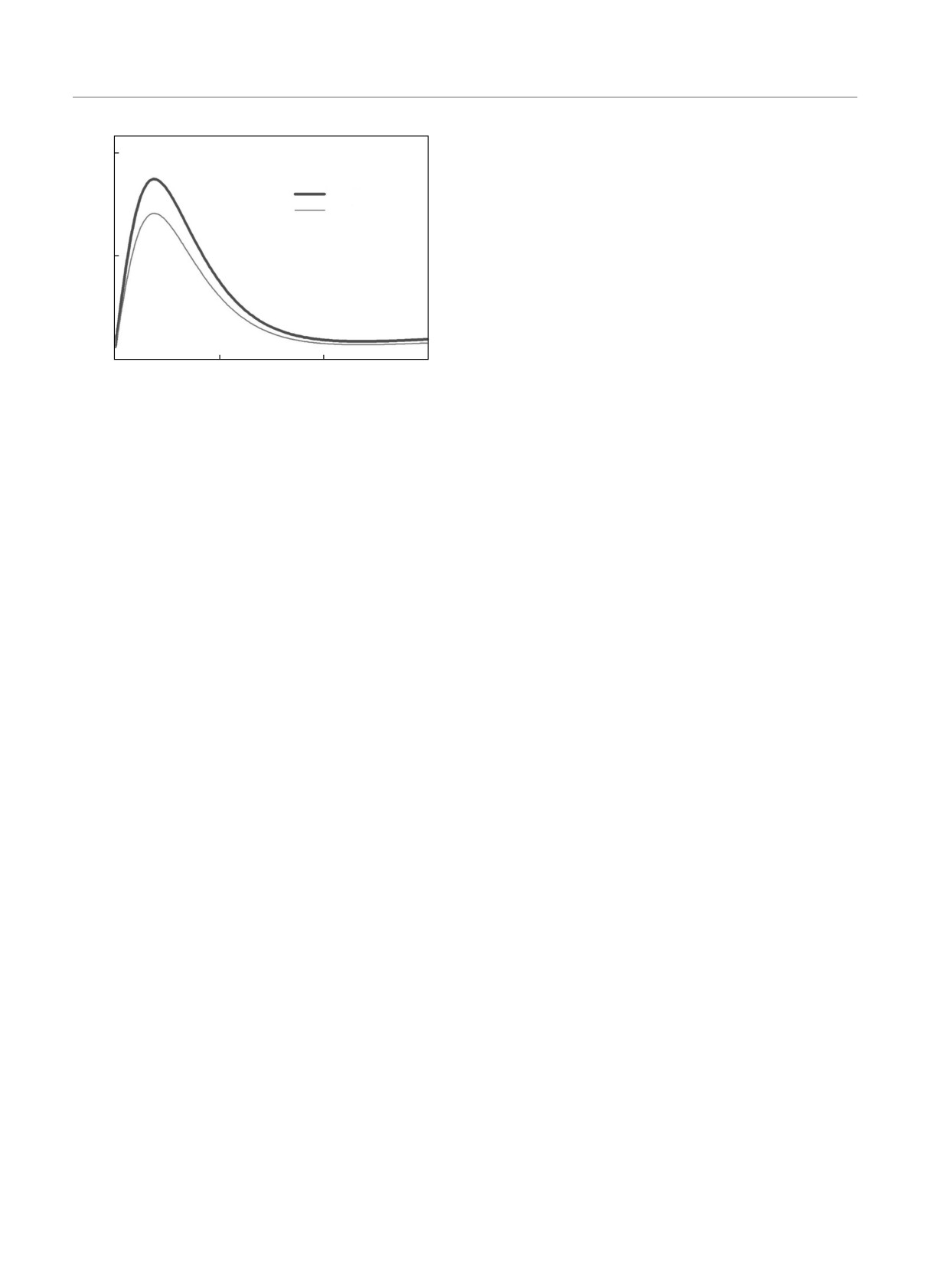
На рис. 6 представлены профили (горизонталь-

m=-M/2

ные сечения на картах рис. 5) упругих решеточных

247

В. И. Пунегов

ЖЭТФ, том 156, вып. 2 (8), 2019

SiO₂

1.5

–3

-3

x, мкм

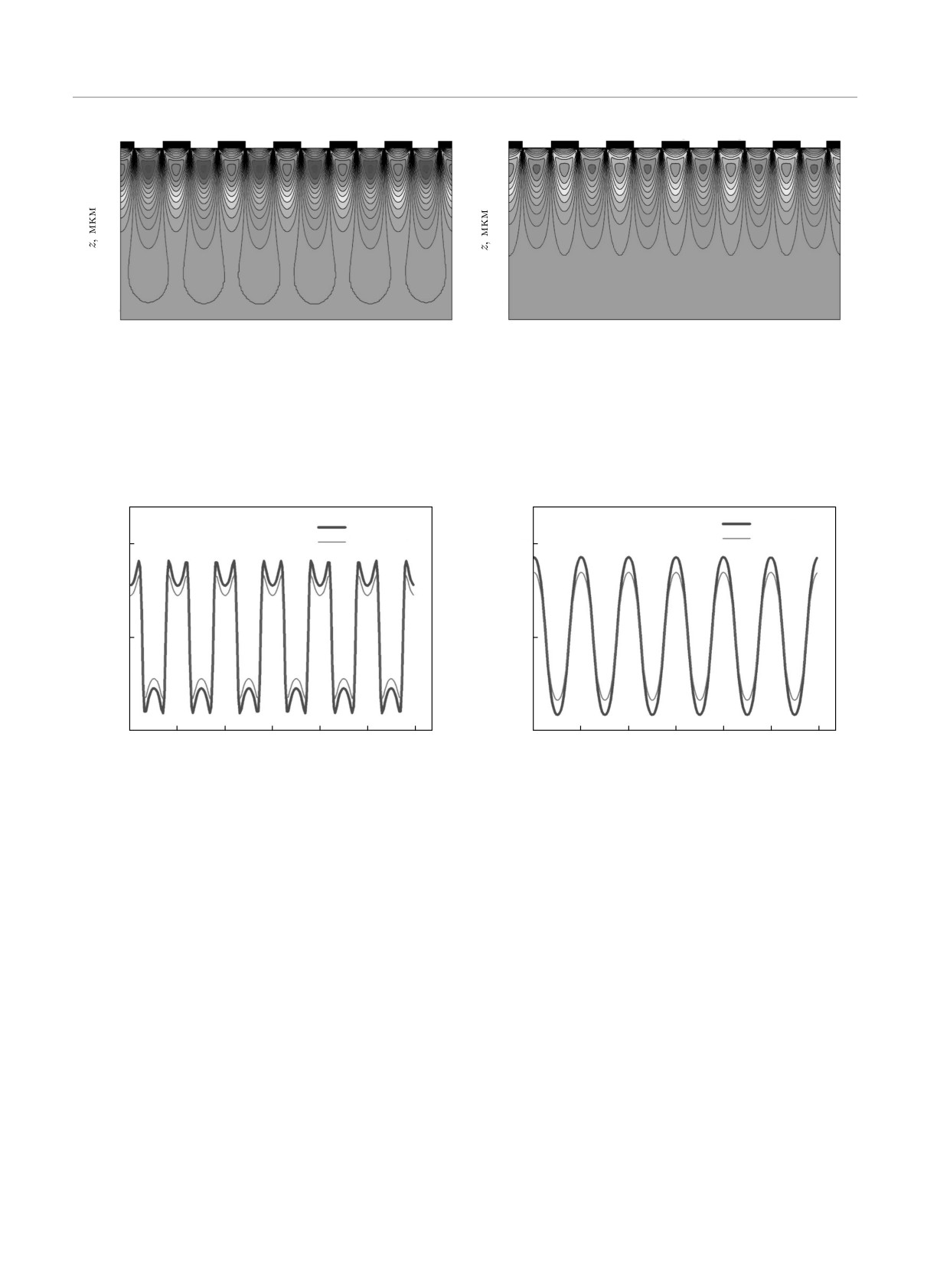
Рис. 5. (В цвете онлайн) Поля упругих решеточных смещений в кристалле кремния uz,gr(x, z), вызванные поверхност-

ными решетками вольфрама (а) и SiO2 (б). Ширина каждой тонкопленочной линии обоих материалов 0.5 мкм, толщина

0.1 мкм. Период решетки 1.0 мкм. Контуры равных смещений представлены в линейном масштабе, максимальное значе-

ние uzmax) = 0.06 нм (красный цвет), минимальное значение uzmin) = -0.06 нм (синий цвет). Разность между соседними

контурными линиями 0.005 нм

u_z, нм

W/Si(111)

SiO /Si(111)₂

0.05

SiO /Si(111)₂

0.06

–0.05

-0.06

-3

-2

-1

-3

-2

-1

x, мкм

Рис. 6. (В цвете онлайн) Профили упругих решеточных смещений uz,gr (x) кристалла кремния вдоль латеральной оси x

на глубине z = 0.06 мкм (а) и z = 0.23 мкм (б) для поверхностных решеток вольфрама (жирная синяя линия) и SiO2

(красная тонкая линия)

смещений u_z,gr(x) подложки кремния вдоль лате-

вольфрама и SiO₂ выполнялись на основе соотноше-

ральной оси на разной глубине кристалла. Нетрудно

ния

видеть, что максимальные значения упругих смеще-



∑



ний локализуются не на поверхности подложки, а



I_h(q_x, q_z) =



R_h,n(q_x, q_z)

(40)

на глубине 0.23 мкм. При этом вблизи интерфейса



n=-∞

(рис. 5, 6a) смещения максимальны у краев тонко-

пленочных линий, с увеличением глубины максиму-

где R_h,n(q_x, q_z) — амплитудный коэффициент отра-

мы упругих деформаций концентрируются под цен-

жения (31). Результаты вычислений представлены в

тром линии (рис. 5, 6б). Более наглядно распреде-

виде карт распределения интенсивности рассеяния

ления упругих смещений по глубине подложки для

в обратном пространстве (RSM). Поскольку в экс-

ПР разных материалов показаны на рис. 7. Вычис-

перименте, как правило, ширина падающего пучка,

ления углового распределения интенсивности рент-

ограниченного щелью S₁, составляет порядка w =

геновского рассеяния вблизи узла обратной решетки

= 100 мкм, получаем lxin) = MΛ = 400 мкм. Это

на кристалле кремния с поверхностными решетками

значение для lxin), а также lxex) = LΛ = 400 мкм

248

ЖЭТФ, том 156, вып. 2 (8), 2019

Динамическая теория дифракции рентгеновских лучей. . .

u_z, нм

фрамовая поверхностная решетка периодически мо-

0.06

дулирует падающее на кристалл кремния рентге-

новское излучение, в то время как оксидная ПР

W/Si(111)

пропускает падающее излучение к поверхности под-

SiO /Si(111)₂

ложки практически без поглощения. Таким обра-

зом, периодическая модуляция падающего на крис-

талл излучения с ПР сильно поглощающего мате-

риала приводит к возникновению дополнительных

диагональных дифракционных порядков, которые

могут быть более интенсивными по сравнению с са-

теллитами, вызванными периодической деформаци-

ей приповерхностной области подложки (рис. 8a,

0.5

1.0

1.5

9a). Латеральные дифракционные порядки на всех

z, мкм

расчетных RSM обозначены нулем, положительны-

Рис. 7. (В цвете онлайн) Профили упругих решеточных

ми и отрицательными целыми числами. Диагональ-

смещений uz,gr (z) кристалла кремния вдоль вертикальной

ные сателлиты имеют два цифровых значения, пер-

оси z для поверхностных решеток вольфрама (жирная си-

вое число указывает на латеральное положение, вто-

няя линия) и SiO2 (красная тонкая линия) при x = 0

рое — на вертикальную координату на картах RSM.

Ранее была рассмотрена модель рентгеновской

(M = L = 400), было использовано в численном

дифракции от системы W/Si(111) без учета перио-

моделировании рентгеновской дифракции на кри-

дических упругих деформаций в приповерхност-

сталле кремния с ПР обоих материалов. Вычисле-

ной области подложки [11]. Теоретические расче-

ния карт RSM проводились непосредственно с при-

ты RSM показали наличие диагональных дифрак-

менением формулы (40). Чтобы полученные теоре-

ционных порядков, однако отсутствовали некото-

тические результаты визуально были похожи на ре-

рые латеральные сателлиты, наблюдаемые на экс-

зультаты экспериментальных измерений, выполне-

периментальных картах интенсивности рассеяния

но численное моделирование с учетом инструмен-

[9]. Здесь в рамках этой модели с целью сравне-

тальной функции [18, 42] для дифракционной схе-

ния результатов выполнено численное моделиро-

мы с четырехкратно отражающим монохроматором

вание для кристалла кремния с ПР вольфрама и

Ge(022) и двукратно отражающим анализатором

оксида SiO₂. Расчетные карты RSM представлены

Ge(022).

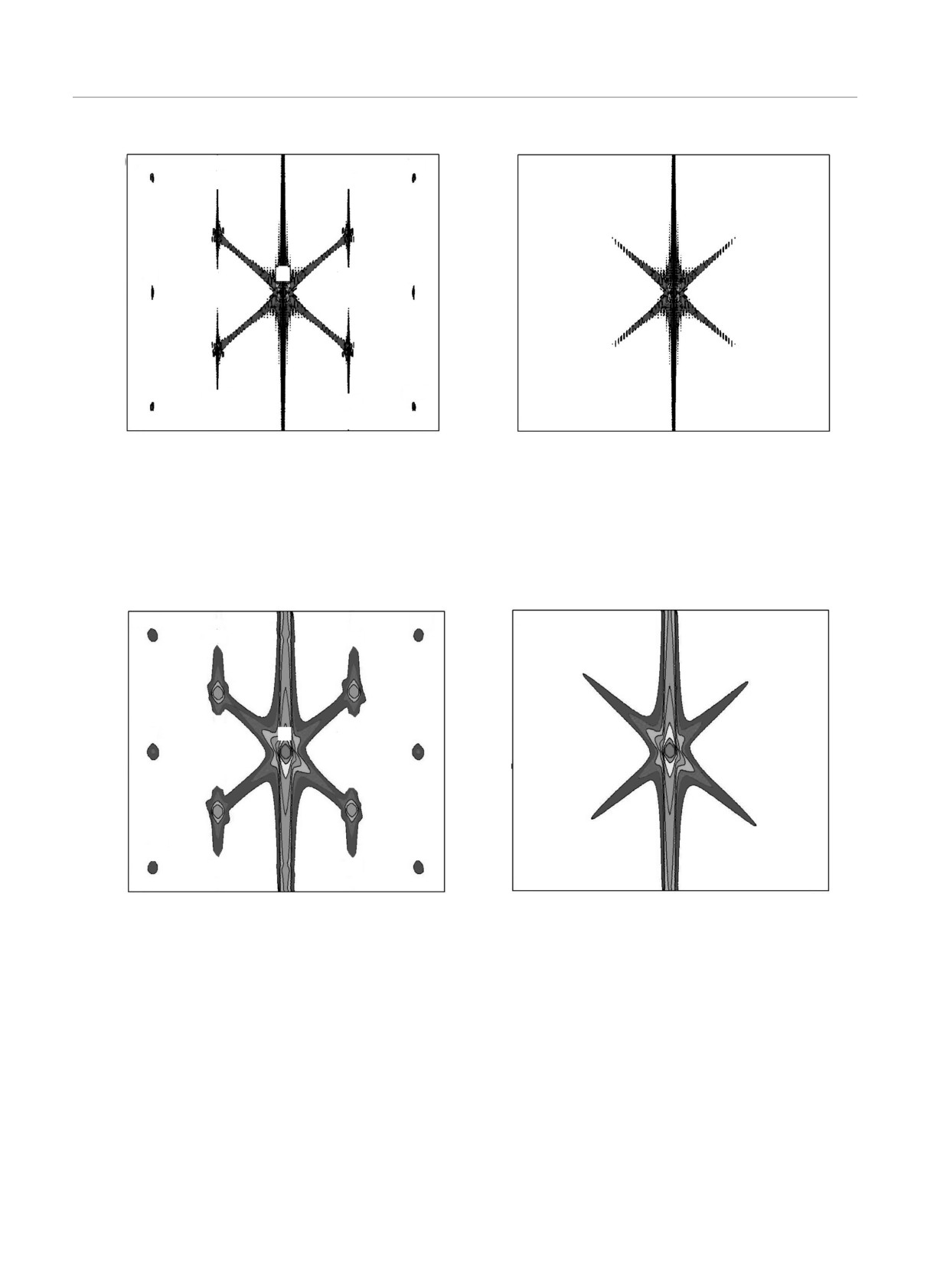
на рис. 10 и 11. В отсутствие периодических де-

На рис. 8 показаны карты RSM от кристалла

формаций в подложке с вольфрамовой ПР на кар-

кремния с вольфрамовой (a) и оксидной (б) по-

тах RSM присутствуют диагональные дифракцион-

верхностной решеткой, а на рис. 9 то же самое,

ные порядки, при этом отсутствуют ±1 сателлиты

но с учетом инструментальной функции. Нетруд-

(рис. 10a, рис. 11a). Кроме того, отсутствуют сател-

но видеть, что угловые распределения интенсивно-

литные пики с номерами (±2, ±1), наблюдаемые на

стей рассеяния вблизи узла обратной решетки для

картах рис. 8a и 9a, поскольку на дифракционных

систем W/Si(111) и SiO₂/Si(111) существенно раз-

картинах (рис. 10a, рис. 11a) нет латеральных са-

личаются. В случае вольфрамовой ПР на картах

теллитов ±1. Что касается оксидной ПР, то без пе-

RSM, помимо традиционных латеральных дифрак-

риодических латеральных деформаций в подложке,

ционных порядков, возникают диагональные сател-

дифракционные порядки вовсе отсутствуют. В дан-

литы. Причина такого различия в дифракционных

ном случае угловое распределение интенсивности

картинах сводится к следующему. Мнимые части

рассеяния в обратном пространстве соответствует

фурье-коэффициентов рентгеновской поляризуемо-

дифракции пространственно-ограниченного рентге-

сти вольфрама χim0,W = i0.684 · 10-5 и SiO₂ χ^im

новского пучка в совершенном кристалле (рис. 10б,

0,SiO2

= i0.0116 · 10-5 [39] различаются в 41 раз, на эту

рис. 11б) [18].

же величину различаются линейные коэффициен-

ты поглощения. Таким образом, параметр γ в (29)

и (30), определяющий долю пропускаемого излуче-

8. ЗАКЛЮЧЕНИЕ

ния через периодически расположенные тонкопле-

ночные линии, для вольфрама γ = 0.87, для окси-

Суммируя изложенное выше, можно сделать вы-

да кремния γ = 0.99. Из этого следует, что воль-

вод, что разработанная теория полностью объясняет

249

В. И. Пунегов

ЖЭТФ, том 156, вып. 2 (8), 2019

q_z, мкм^-1

–2,2

2,2

-1,1

1,1

–2,1

2,1

-1

-2

–2,-1

2,-1

–2,-2

2,-2

-1,-1

1,-1

–60

-60

-15

q_x, мкм^-1

q_x, мкм-1

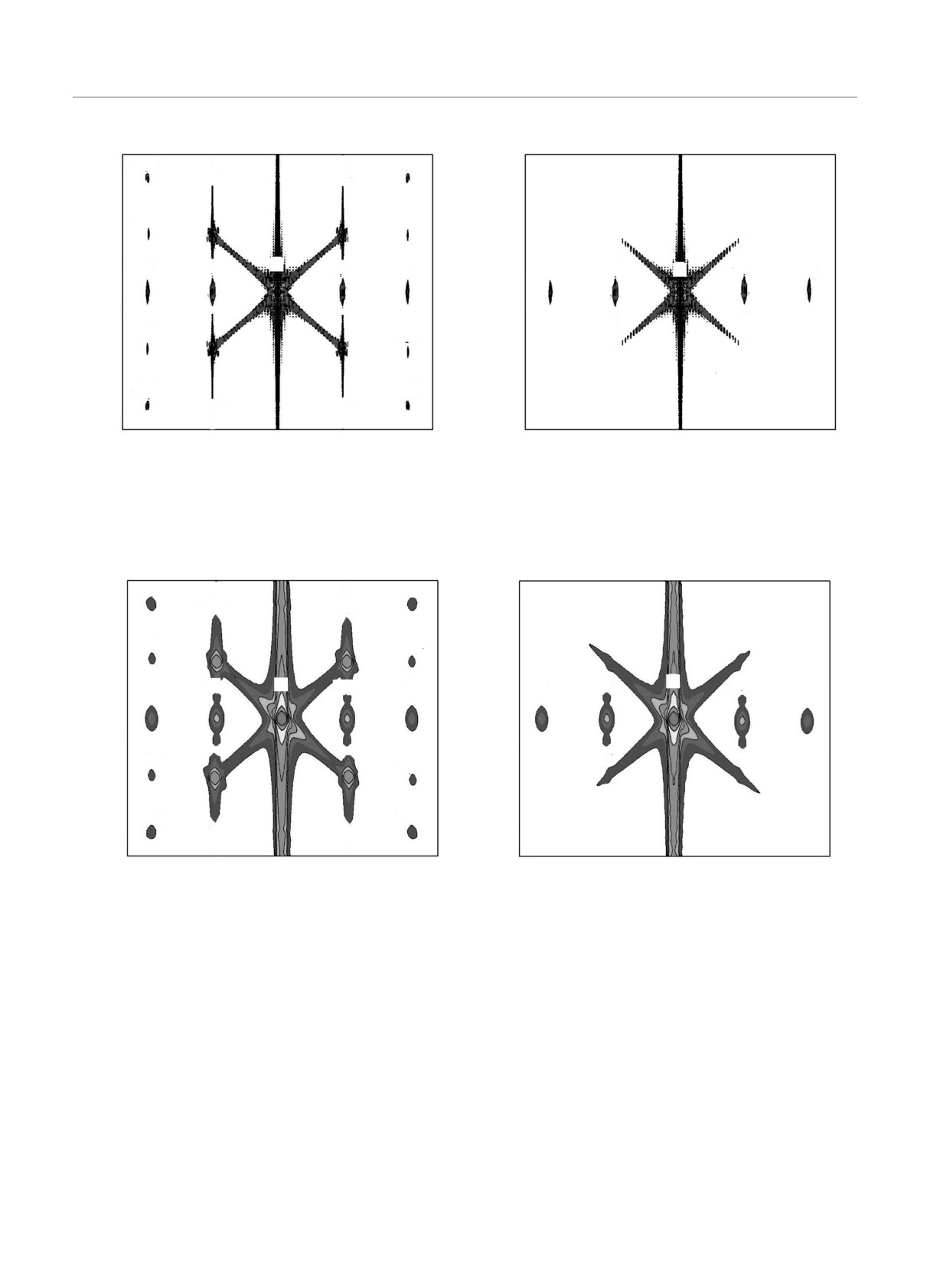
Рис. 8. Карты распределения интенсивности рассеяния от кристалла кремния с вольфрамовой (а) и оксидной (б) поверх-

ностными решетками. Ширина падающего и отраженного рентгеновских пучков 100 мкм

q_z, мкм^-1

–2,2

2,2

-1,1

1,1

–2,1

2,1

–2

-1

-2

–2,-1

2,-1

–2,-2

2,-2

-1,-1

1,-1

–60

-60

-15

q_x, мкм^-1

q_x, мкм-1

Рис. 9. Карты распределения интенсивности рассеяния от кристалла кремния с вольфрамовой (а) и оксидной (б) поверх-

ностными решетками с учетом инструментальной функции. Ширина падающего и отраженного рентгеновских пучков

100 мкм

наблюдаемое в эксперименте различие в угловых

дулированных поверхностной акустической волной

распределениях интенсивности рассеяния от кри-

[4, 5, 21], доменных структурах [12], системах с

сталла кремния с вольфрамовой [9] и оксидной [7]

поверхностным рельефом с канавками, заполнен-

поверхностной решеткой. В зависимости от гранич-

ными, другим материалом [16], и т. д. Следует также

ных условий и вида периодических полей упругих

подчеркнуть, что разработанный подход оперирует

деформаций теория может быть использована для

с пространственно-ограниченными рентгеновскими

описания динамической дифракции рентгеновских

пучками, что может существенно облегчить ана-

лучей и тепловых нейтронов в кристаллах, промо-

лиз экспериментальных данных, сопровождаемый

250

ЖЭТФ, том 156, вып. 2 (8), 2019

Динамическая теория дифракции рентгеновских лучей. . .

q_z, мкм^-1

–2,2

2,2

-1,1

1,1

-2

–2,-2

2,-2

-1,-1

1,-1

–60

-60

-15

q_x, мкм^-1

q_x, мкм-1

Рис. 10. Карты распределения интенсивности рассеяния от кристалла кремния с вольфрамовой (а) и оксидной (б) по-

верхностными решетками без учета деформаций в подложке. Ширина падающего и отраженного рентгеновских пучков

100 мкм

q_z, мкм^-1

–2,2

2,2

-1,1

1,1

-2

–2,-2

2,-2

-1,-1

1,-1

–60

-60

-15

q_x, мкм^-1

q_x, мкм-1

Рис. 11. Карты распределения интенсивности рассеяния от кристалла кремния с вольфрамовой (а) и оксидной (б) по-

верхностными решетками без учета деформаций в подложке и с учетом инструментальной функции. Ширина падающего

и отраженного рентгеновских пучков 100 мкм

численным моделированием или в рамках строгого

тичной финансовой поддержке программы фун-

решения обратных задач рентгеновской дифрак-

даментальных исследований Уральского отделения

ции [43].

Российской академии наук (проект № 18-10-2-23) и

Российского фонда фундаментальных исследований

Финансирование. Работа выполнена при час- (проект № 17-02-00090-а).

251

В. И. Пунегов

ЖЭТФ, том 156, вып. 2 (8), 2019

ПРИЛОЖЕНИЕ

D. V. Irzhak, M. A. Knyasev, V. I. Punegov et al., J.

Appl. Cryst. 48, 1159 (2015).

Возникающие в подложке упругие деформа-

10.

A. Erko and A. Firsov, Proc. SPIE 5539, 148 (2004).

ции можно рассчитать с использованием соотноше-

ний (33)

11.

В. И. Пунегов, С. И. Колосов, Письма в ЖЭТФ

102, 159 (2015).

ε_xx =

[σ_xx - ν_sσ_zz ] =

12.

M. Bazzan, C. Sada, N. Argiolas et al., J. Appl. Phys.

E_s

106, 104121 (2009).

(

)

13.

V. V. Aristov, V. N. Mordkovich, A. Yu. Nikulin et

2F_f

xz²

-ν_s

(A.1)

al., Phys. Stat. Sol. (a) 120, K1 (1990).

πE_s

(x² + z²)²

14.

A. Daniel, Y. Zhuang, J. Stangl et al., Proceedings

GMe Forum (2001), p. 165.

ε_zz =

[σ_zz - ν_sσ_xx] =

15.

Y. Ezzaidi, G. Gaudeau, S. Escoubas et al., Nucl.

E_s

(

)

Instr. Meth. Phys. Res. B 284, 23 (2012).

2F_f

x³

-ν_s

(A.2)

πE_s

(x² + z²)²

16.

M. Eberlein, S. Escoubas, M. Gailhanou et al., Phys.

Stat. Sol. (a) 204, 2542 (2007).

Зная связь деформаций с полями атомных смеще-

17.

S. Takagi, Acta Cryst. 15, 1311 (1962).

ний ε_xx = du_x/dx, ε_zz = du_z/dz, получаем

)

18.

V. I. Punegov, K. M. Pavlov, A. V. Karpov et al., J.

2F_f

⁽x² +ν_sz

Appl. Cryst. 50, 1256 (2017).

u_x = -

ln |x² + z²|

(A.3)

πE_s

2(x² + z²)

19.

В. И. Пунегов, ЖЭТФ 154, 248 (2018).

20.

Shin-Lin Chang, Multiple Diffraction of X-Rays in

2F_f

Crystals, Springer-Verlag, Berlin (1984).

u_z =

πE_s

(

)

21.

В. И. Пунегов, Д. В. Рощупкин, Кристаллография

× (1 + ν_s)

- (1 - ν_s)

arctg

(A.4)

57, 29 (2012).

2(x² + z²)

22.

A. Authier, Dynamical Theory of X-Ray Diffraction,

Oxford University Press, New York (2001).

ЛИТЕРАТУРА

23.

T. Arai, H. Nakaie, K. Kamimura et al., J. Mat. Sci.

Chem. Engin. 4, 29 (2016).

1. A. Iida and K. Kohra, Phys. Stat. Sol. (a) 51, 533

(1979).

24.

S. C. Jain, H. E. Maes, K. Pinardi et al., J. Appl.

Phys. 79, 8145 (1996).

2. V. V. Aristov, A. I. Erko, A. Yu. Nikulin et al., Opt.

Commun. 58, 300 (1986).

25.

G. G. Stoney, Proc. R. Soc. London, Ser. A 82, 172

(1909).

3. V. V. Aristov, A. Yu. Nikulin, A. A. Snigirev et al.,

26.

Z. Zhang, J. Yoon, and Z. Suo, Appl. Phys. Lett. 89,

Phys. Stat. Sol. (a) 95, 81 (1986).

261912 (2006).

4. R. Tucoulou, R. Pascal, M. Brunel et al., J. Appl.

27.

A. Blech and E. S. Meieran, J. Appl. Phys. 38, 2913

Cryst. 33, 1019 (2000).

(1967).

5. V. I. Punegov, Ya. I. Nesterets, and D. V. Roshchup-

28.

S. M. Hu, Appl. Phys. Lett. 32, 5 (1978).

kin, J. Appl. Cryst. 43, 520 (2010).

29.

S. M. Hu, J. Appl. Phys. 50, 4661 (1979).

6. V. V. Aristov, S. M. Kuznetsov, A. V. Kouyumchyan

et al., Phys. Stat. Sol. (a) 125, 57 (1991).

30.

S. Isomae, J. Appl. Phys. 52, 2782 (1981).

31.

E. Suhir, J. Appl. Mech. 53, 657 (1986).

7. P. Ershov, S. Kuznetsov, I. Snigireva et al., J. Appl.

Cryst. 46, 1475 (2013).

32.

A. Atkinson, T. Johnson, A. H. Harker et al., Thin

Solid Films 274, 106 (1996).

8. D. V. Roshchupkin, D. V. Irzhak, S. L. Shabel’nikova

et al., J. Surface Investigation. X-ray, Synchrotron

33.

I. De Wolf, M. Ignat, G. Pozza et al., J. Appl. Phys.

and Neutron Techniques 7, 663 (2013).

85, 6477 (1999).

252