ЖЭТФ, 2019, том 156, вып. 2 (8), стр. 355-370
© 2019
ВОЗБУЖДЕНИЕ ПОВЕРХНОСТНЫХ ВОЛН ПРИ ПАДЕНИИ
НЕОДНОРОДНОЙ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ
НА ГРАНИЦУ ПЛАЗМЫ
И. Н. Карташов*, М. В. Кузелев**
Физический факультет, Московский государственный университет им. М. В. Ломоносова
119991, Москва, Россия
Поступила в редакцию 21 февраля 2019 г.,
после переработки 21 февраля 2019 г.
Принята к публикации 18 марта 2019 г.
Исследовано возбуждение поверхностных плазменных волн при распространении цилиндрической элект-
ромагнитной волны в слоистой плазменно-диэлектрической среде. Рассмотрены слои диэлектрик-ваку-
ум-плазма и вакуум-плазма-плазма. Показано, что на границе диэлектрик-плазма поверхностные вол-
ны цилиндрической электромагнитной волной не возбуждаются (аналогично случаю плоской волны). В
слоистой среде возбуждение поверхностной волны происходит в достаточно узком диапазоне частот и
углов распространения. Вычислены структуры электромагнитного поля, потока электромагнитной энер-
гии, найдены интегральные коэффициенты отражения и прохождения. Использованы как численные, так
и аналитические асимптотические методы. Показано, что во всех случаях вклад поля от боковой волны
пренебрежимо мал.
DOI: 10.1134/S0044451019080145
волн [14-18]. Подобные системы представляют собой
металлические волноводы, в которых создана плаз-
1. Исследование поверхностных электромагнит-
ма со свободной поверхностью и вдоль которых рас-
ных волн имеет давнюю историю и продолжается
пространяется мощный релятивистский электрон-
до настоящих дней. Интерес к поверхностным вол-
ный пучок. В плазменных волноводах существуют
нам в значительной степени вызван широким кру-
замедленные поверхностные волны E-типа, которые
гом практических приложений во многих областях
могут эффективно взаимодействовать с электрон-
физики. Впервые задача о поверхностных электро-
ным пучком, забирая от него энергию. Таким обра-
магнитных волнах возникла при исследовании рас-
зом, в зависимости от конкретной реализации систе-
пространения радиоволн вблизи поверхности Зем-
мы, возможно или усиление сигнала, подаваемого на
ли Зоммерфельдом и Ценнеком [1-3]. Несмотря на
вход волновода, или его генерация за счет создания
то что некоторые их результаты вскоре были уточ-
обратной связи. Заметим, что при эксперименталь-
нены другими авторами [4-7], вопросы о возмож-
ной реализации плазменных усилителей и генерато-
ности возбуждения так называемой поверхностной
ров на поверхностных волнах используется внешнее
волны Ценнека считаются дискуссионными и по сей
продольное магнитное поле, существенно влияющее
день [8-13].
как на свойства поверхностных плазменных волн,
Поверхностные электромагнитные волны возни-
так и на механизм их взаимодействия с пучком элек-
кают и в других частотных диапазонах, в частности,
тронов [19-21]. В настоящей работе наличие внеш-
в СВЧ-диапазоне. Именно на возбуждении поверх-
него магнитного поля не учитывается.
ностных плазменных волн электронным пучком ос-
Поверхностные
электромагнитные
волны
нованы успешные реализации мощных плазменных
СВЧ-диапазона возникают также при реализа-
источников электромагнитного излучения (усилите-
ции поверхностного газового разряда, т. е. разряда,
лей и генераторов) микроволнового диапазона длин
в котором вложение энергии для его поддержания
* E-mail: igorkartashov@mail.ru
осуществляется поверхностной электромагнитной
** E-mail: kuzelev@mail.ru
волной. Этот безэлектродный разряд локализован в
355
11*
И. Н. Карташов, М. В. Кузелев
ЖЭТФ, том 156, вып. 2 (8), 2019
непосредственной близости от поверхности. В отли-
и решеточного ввода излучения. По сути же приз-
чие от объемного разряда он позволяет создавать
менный ввод излучения означает возбуждение не
плазму со сверхкритической концентрацией элек-
поверхностной волны на границе раздела двух сред,
тронов. Перечисленные свойства поверхностного
а одной из мод более сложной структуры, содержа-
разряда в ряде технологических применений явля-
щей две границы раздела. В работе [33] численно ис-
ются его преимуществами по сравнению с другими
следуется задача рассеяния падающей плоской элек-
формами газовых разрядов. К таким применениям
тромагнитной волны оптического диапазона на си-
можно отнести модификацию свойств поверхности,
стеме параллельно расположенных металлических
управление обтеканием поверхности в потоке газа,
цилиндров, погруженных в диэлектрическую среду.
повышение эффективности воспламенения топлива
Волна падает из другого диэлектрика с большим по-
в высокоскоростных потоках топливовоздушной
казателем преломления, так что реализуется режим
смеси [22, 23].
полного внутреннего отражения. Возможно также
Задача возбуждения поверхностных электромаг-
возбуждение поверхностных плазмонов в нелиней-
нитных волн примыкает и к проблеме создания из-
ной среде без дополнительного согласования [34,35].
лучающих антенн с динамически перестраиваемой
В плазмонике традиционным является предполо-
диаграммой направленности [24,25]. Как хорошо из-
жение о плоской падающей волне. В то же время для
вестно, диаграмма направленности антенны опреде-
возбуждения поверхностных волн в газоразрядной
ляется ее геометрией. Причем традиционно исполь-
плазме, при использовании существенно более длин-
зуемые металлические элементы антенны во мно-
новолнового излучения, более привлекательным мо-
гих случаях могут быть успешно заменены прово-
жет оказаться излучение штыревой антенны. В этом
дящими каналами газоразрядной плазмы. Таким об-
случае возбуждающая волна по своей структуре бу-
разом, управляя структурой проводящих областей,
дет близка к цилиндрической. В настоящей работе
возможно формирование антенн различных конфи-
мы рассмотрим возбуждение поверхностных плаз-
гураций. Плазменные области при этом демонстри-
менных волн падающей цилиндрической волной.
руют резонансные свойства, связанные с возбужде-
2. Рассмотрим взаимодействие неоднородной
нием поверхностных плазмонов [26, 27].
электромагнитной волны частоты ω с плоским
Значительное место поверхностным волнам от-
диэлектрическим слоем, соседствующим с двумя
водится в проблеме повышения скорости работы
различными диэлектрическими средами. Диэлект-
электронных устройств. Сформировалась новая об-
рики считаем изотропными, пространственную
ласть физики — плазмоника [28-30], объектом ис-
дисперсию не учитываем, поэтому пространствен-
следования которой являются поверхностные плаз-
ное распределение диэлектрической проницаемости
мон-поляритоны и поверхностные плазмоны. Воз-
зададим в виде
можность локализации поля на субволновых масш-
⎧
табах даже для излучения оптического диапазо-
⎨
ε1(ω),
x < 0,
на длин волн является перспективной с точки зре-
ε(ω, x) =
ε0(ω),
0<x<L0,
(1)
⎩
ния миниатюризации вычислительных устройств.
ε2(ω),
x>L0.
По сути, поверхностный плазмон-поляритон и по-
верхностный плазмон ничем не отличаются от по-
Здесь L0
— толщина диэлектрического слоя, а
верхностных плазменных волн, исследование кото-
ε1,2(ω) и ε0(ω) — некоторые функции частоты (во-
рых началось еще на заре XX века. В теории плаз-
обще говоря, комплексные). Ниже будет рассмот-
мы поверхностные плазмон-поляритоны называют
рен случай, когда среда с диэлектрической прони-
также поверхностными фотонами [31], что вполне
цаемостью ε2 является холодной электронной плаз-
естественно, поскольку в длинноволновой области
мой. Значительный интерес представляет также
законы дисперсии фотонов и плазмон-поляритонов
случай, когда плазмой (другой плотности) являет-
практически совпадают [32].
ся среда с проницаемостью ε0. На границах раздела
Одним из ключевых вопросов в плазмонике яв-
плазма-вакуум, плазма-диэлектрик и плазма-плаз-
ляется вопрос о возбуждении поверхностных волн.
ма существуют поверхностные волны различного
Невозможность согласования частоты и компонен-
типа: поверхностные плазмон-поляритоны (поверх-
ты волнового вектора вдоль поверхности у падаю-
ностные фотоны) и поверхностные плазмоны. Ос-
щей объемной волны и у поверхностной волны
новное внимание в настоящей работе сосредоточено
требует использования специальных согласующих
на границе слоя с плазмой x = L0 и на возбужде-
схем. Традиционными являются схемы призменного
нии на этой границе указанных выше поверхност-
356
ЖЭТФ, том 156, вып. 2 (8), 2019
Возбуждение поверхностных волн. . .
ных волн. Казалось бы, что слой при таком под-
кую волну (она определяется решением волнового
ходе вообще не нужен, т. е. в (1) можно положить
уравнения (2) [37]):
L0 = 0. Оказывается, однако, что без слоя поверх-
(
√
)
ностные волны вообще не возбуждаются. Для слу-
Πz(x, z) = Π0H(1)
k1
(x - x0)2 + z2
=
0
чая плоских волн это обстоятельство хорошо извест-
(
)
√
∞
∫
но [28-30].
exp i
k21 - k2z (x - x0) + ikzz
1
=Π0
dkz
√
,
(4)
Предположим, что электромагнитная волна со-
π
k21 - k2
z
здается бесконечно длинным линейным внешним ис-
-∞
точником, перпендикулярным плоскости xz и распо-
ложенным в точке x = x0 < 0, z = 0. Таким источни-
где k21 = ε1ω2/c2, H(1)0 — функция Ганкеля первого
ком может быть линейный диполь с дипольным мо-
рода, а Π0 ∼ d — постоянная амплитуда, которую во
ментом P = d exp(-iωt)δ(x-x0)δ(z), где d — вектор,
всех последующих формулах полагаем равной еди-
определяющий направление и величину дипольно-
нице. Формула (4) дает разложение цилиндрической
го момента. Поскольку зависимости источника, а
волны по плоским волнам при x > x0. При вычис-
значит, и создаваемого им электромагнитного поля,
лении интеграла в (4) выбирается та ветвь квадрат-
от координаты y нет, ограничимся рассмотрением
ного корня, которая обеспечивает сходимость интег-
только электромагнитных волн с отличными от ну-
рала.
ля компонентами электромагнитного поля Ez, Ex,
Рассмотрим сначала падение на границу x = 0 не
By (волны, поляризованные в плоскости падения,
суперпозиции (4), а одной плоской волны с некото-
или волны E-типа). Волны, поляризованные перпен-
рым фиксированным kz. Для этого запишем извест-
дикулярно плоскости падения (или волны B-типа с
ное решение задачи Френеля для диэлектрического
отличными от нуля Bz , Bx, Ey) к возбуждению по-
слоя [36]:
верхностной волны не приводят.
Для описания электромагнитного поля удоб-
Ez =
⎧
но использовать электрический вектор Герца
⎨A exp(ikx1x) + B exp(-ikx1x), x < 0,
Πe [36,37]. Функция Πe (без общего множителя
C exp(ikx0x)+D exp(-ikx0x),
0<x<L0,
(5)
exp(-iωt)) в областях постоянства диэлектричес-
=⎪⎩
F exp(ikx2x),
L0 < x,
ких проницаемостей удовлетворяет следующему
волновому уравнению:
где
√
√
∂2Πe
∂2Πe
ω2
kx1 = k21 - k2z, kx0 = k20 - k2z,
+
+
ε(ω, x)Πe =
√
(6)
∂z2
∂x2
c2
kx2 = k22 - k2z,
= -4πd δ(x - x0)δ(z),
(2)
k20 = ε0ω2/c2, k22 = ε2ω2/c2, а kz — тангенциальная
а компоненты электромагнитного поля определяют-
к границе раздела компонента волнового вектора.
ся формулами
Она определяется падающей волной и может быть
)
ω
(∂Πz
∂Πx
выражена через угол падения α по формуле
By = i
ε
-
,
c
∂x
∂z
)
kz = k1 sinα.
(7)
2
∂2Πz
(ω
∂2
Ex =
+
ε+
Πx,
(3)
∂z∂x
c2
∂x2
Амплитуда отраженной волны B, амплитуда про-
)
2
(ω
∂2
∂2Πx
шедшей волны F , а также C и D выражаются через
Ez =
ε+
Πz +
c2
∂z2
∂z∂x
амплитуду падающей волны A по формулам
Волна E-типа определяется только двумя компонен-
A
B =
[(ε1kx0 - ε0kx1)(ε0kx2 + ε2kx0) +
тами вектора Герца Πz и Πx, а они, в свою оче-
S
редь — соответствующими компонентами дипольно-
+ (ε1kx0+ε0kx1)(ε0kx2-ε2kx0) exp(2kx0L0)] ,
го момента (и тока). Мы рассмотрим случай дипо-
A
ля, параллельного границам слоя, т. е. d = {0, 0, d}.
C =
2ε1kx0(ε0kx2 + ε2kx0),
(8)
S
На границах раздела x = 0 и x = L0 должны быть
A
непрерывны Ez и By (и εEx).
D=
2ε1kx0(ε0kx2 - ε2kx0)exp(2ikx0L0),
S
3. Линейный источник в среде с проницаемостью
A
ε1 создает следующую расходящуюся цилиндричес-
F =
4ε1kx0ε0kx2 exp[i(kx0 - kx2)L0] .
S
357
И. Н. Карташов, М. В. Кузелев
ЖЭТФ, том 156, вып. 2 (8), 2019
Здесь
где угловые скобки обозначают усреднение по
периоду 2π/ω. Начнем со случая плоских волн
S(ω, kz) = (ε1kx0 + ε0kx1)(ε0kx2 + ε2kx0) +
(5). Заметим, что в плоском случае имеет смысл
только подынтегральное выражение в (12), P0 =
+ (ε1kx0 - ε0kx1)(ε0kx2 - ε2kx0) exp(2ikx0L0).
(9)
=
-c〈Ez(x)By(x)〉/4π, определяющее плотность
потока энергии. В области постоянства диэлект-
Чтобы связать решение (5) и формулы (8) с зада-
рической проницаемости с учетом (5) и второй
чей о волнах от линейного внешнего источника, сле-
формулы (3) имеем
дует, используя разложение по плоским волнам (4) и
третью формулу (3), определить амплитуду падаю-
1
Ez =
[G exp(-iϕ) + G∗ exp(iϕ)] ,
щей плоской волны в (5) и (8). Сравнивая подынтег-
2
ральное выражение в (4) и самый первый член в
1 ω
By = -
[H exp(-iϕ) + H∗ exp(iϕ)] ,
решении (5), имеем (множитель exp(ikzz) в (5) от-
2 c
(13)
сутствует, потому что на него было сделано сокра-
G = A(+) exp(ikxx) + A(-) exp(-ikxx),
щение)
ε [
]
H =
A(+) exp(ikxx) - A(-) exp(-ikxx)
√
(
√
)
kx
1
A = A(kz) =
k21-k2z exp
-i k21-k2z x0
(10)
π
Здесь символ «∗» обозначает комплексное сопряже-
ние, ϕ = ωt - kzz, а ε и kx — любая из величин (1) и
Выражение (10) есть не что иное, как угловой (про-
(6). Записывая выражения (13), мы учли, что может
странственный) спектр излучения линейного источ-
быть ε = ε∗ и kx = k∗x, а общее комплексное решение
ника в плоскости x = 0. Полное решение задачи,
уравнения (2) взяли в виде
очевидно, дается суперпозицией плоских волн (5) с
[
]
угловым спектром (10), а именно:
A(+) exp(ikxx) + A(-) exp(-ikxx)
exp(-iϕ).
∫∞
Используя (13), находим следующее выражения для
Ez(x < 0, z) =
dkz A exp(ikx1x + ikzz) +
плотности потока электромагнитной энергии в плос-
-∞
кой волне:
∫∞
ω [
(
+ dkz B exp(-ikx1x + ikzz),
P0 =
Re(ε/kx)
exp[-2 Im(kx)x]|A(+)|2 -
8π
-∞
)
− exp[2 Im(kx)x]|A(-)|2
- 2Im(ε/kx)×
Ez(0 < x < L0, z) =
(
)]
∫∞
× Im A(+)A∗(-) exp[2i Re(kx)x]
≡
(11)
= dkz C exp(ikx0x + ikzz) +
≡ P0(A(+), A(-), kx, ε).
(14)
-∞
∫∞
Обратим внимание, что при комплексных ε и kx по-
+ dkz D exp(-ikx0x + ikzz),
ток энергии не сводится просто к разности |A(+)|2 -
- |A(-)|2, имеется еще перекрестный член, пропор-
-∞
циональный A(+)A∗(-) .
∫∞
Используя введенное в (14) обозначение, запи-
Ez(x > L0, z) =
dkzF exp(ikx2x + ikzz).
шем плотность потока электромагнитных волн (5) в
-∞
виде
Волновое число kz в (10) является переменной ин-
тегрирования и никак не связано с формулой (7).
P0(x, kz) =
⎧
Для перехода к плоской волне и обычной задаче
⎨
P0(A, B, kx1, ε1), x < 0,
Френеля для слоя в (11) следует подставить A =
P0(C, D, kx0, ε0),
0<x<L0,
(15)
= δ(kz - k1 sinα).
=⎪⎩
P0(F, 0, kx2, ε2), L0 < x,
4. Вычислим полный поток энергии неоднород-
ной электромагнитной волны (11) в направлении
где величины A, B, C, D и F определены в (8). В
оси x:
формуле (15) специально подчеркнута зависимость
∞
∫
c
плотности потока энергии плоской волны от компо-
Px(x) = -
〈Ez (x)By (x)〉 dz,
(12)
ненты волнового вектора kz. Учитывая далее равен-
4π
−∞
ство Парсеваля [38]
358
ЖЭТФ, том 156, вып. 2 (8), 2019
Возбуждение поверхностных волн. . .
∞
∫
Помимо локализованных поверхностных волн
1
〈Ez (x, z)By(x, z)〉 dz =
×
уравнение (18) определяет и частоты частично ло-
4π
−∞
кализованных волн. Действительно, слой среды 0 <
∫∞
< x < L0 является резонатором Фабри-Перо с по-
[
×
Ez(x, kz)B∗y(x, kz) +
лупрозрачными стенками x = 0 и x = L0. Излучение
-∞
может уходить через эти стенки на бесконечность,
чему соответствует нарушение хотя бы одного из
+ E∗z(x, kz)By(x, kz)] dkz,
(16)
неравенств (19). Поскольку излучение уносится на
получаем окончательно следующее выражение для
бесконечность, поле в слое должно затухать. Поэто-
му частоты частично локализованных волн должны
полного потока энергии электромагнитного поля
быть комплексными даже тогда, когда любые дис-
(11) в полупространство x > 0:
сипативные эффекты отсутствуют, т. е. диэлектри-
∫∞
ческие проницаемости ε1, ε0, ε2 вещественны. За-
Px(x) =
P0(x, kz)dkz,
(17)
метим, что частоты поверхностных волн в недисси-
−∞
пативной системе всегда вещественны. Исследова-
ние возможности возбуждения частично локализо-
где подынтегральное выражение определено форму-
ванных волн диэлектрического слоя падающей на
лами (14) и (15).
него неоднородной волной (4) также представляет-
5. Из формул (8) следует, что при отсутствии па-
ся интересным.
дающей волны, т. е. при A = 0, решение (5) тождест-
В случае, когда k2x0 < 0 (а этот случай и будет
венно равно нулю. Исключением является случай
нами исследоваться ниже) и выполнено неравенство
2|kx0|L0 ≫ 1, с точностью до экспоненциально ма-
S(ω, kz) = 0.
(18)
лой величины дисперсионное уравнение (18) распа-
дается на произведение дисперсионных уравнений
Равенство (18) есть дисперсионное уравнение для
S10(ω, kz) = ε1kx0 + ε0kx1 = 0,
определения спектров частот собственных волн ди-
(20)
электрического слоя1). Эти волны распространяют-
S02(ω, kz) = ε0kx2 + ε2kx0 = 0,
ся вдоль оси z и локализованы или частично локали-
первое из которых определяет спектры поверхност-
зованы в направлении x. Локализованными волнами
ных волн на границе x = 0, второе — на границе
являются поверхностные волны, которые возможны
x = L0. В другом частном случае L0 = 0 (т.е. ди-
не при любом сочетании диэлектрических проница-
электрического слоя нет) дисперсионное уравнение
емостей ε1, ε0, ε2. Поле поверхностных волн убывает
(18) преобразуется к виду
при удалении от слоя, т. е. при x → ±∞. Поэтому,
как видно из (5) и (6), для существования поверх-
S(ω, kz) = ε1kx2 + ε2kx1 = 0.
(21)
ностных волн необходимо выполнение неравенств2)
Уравнение (21) определяет спектры поверхностных
волн на границе диэлектриков ε1 и ε2.
k2x1 = k21 - k2z < 0, k2x2 = k22 - k2z < 0,
(19)
6. Перейдем теперь к рассмотрению конкретных
систем. Положим
записанных для простоты для случая вещественной
диэлектрической проницаемости. Что касается зна-
ω2p
ε1 > 1, ε0 = 1, ε2 = 1 -
(22)
ка величины k2x0, то он может быть любым, т. е.
ω(ω + iν)
внутри диэлектрического слоя поле волны может
Таким образом, диэлектрическая среда без диспер-
быть как поверхностным, так и объемным. Очевид-
сии в области x < 0 и холодная электронная плаз-
но, что в интегралах (11) есть спектральные состав-
ма в области x > L0 разделены вакуумным зазо-
ляющие, для которых неравенства (19) выполнены.
ром (ωp — электронная ленгмюровская частота, ν —
Поэтому возникает закономерный вопрос о возмож-
частота столкновений электронов с нейтральными
ности возбуждения поверхностных волн при облу-
атомами). В простейшем случае, когда вакуумно-
чении слоя цилиндрической волной (4).
го зазора нет (L0 = 0), имеем границу диэлект-
рик-плазма. Напомним, что известно о волнах гра-
1) Заметим, что уравнение (18) удовлетворяется тождест-
ницы диэлектрик-плазма и о падении электромаг-
венно при kx0 = 0. Однако из решения (8) следует, что поле
в этом случае при A = 0 является тождественным нулем.
нитной волны из области диэлектрика на эту грани-
√
2) Считается, что
-1 ± i0 = ±i.
цу.
359
И. Н. Карташов, М. В. Кузелев
ЖЭТФ, том 156, вып. 2 (8), 2019
Известно, что на плоской границе диэлектрика
числом, определяемым формулой (24). Таким обра-
с плазмой имеется сильно непотенциальная поверх-
зом, в схеме (22) резонанс между падающей и по-
ностная волна, волновое число которой определяет-
верхностной волнами возможен. Правда, в описан-
ся из уравнения (21) и при ν = 0 дается форму-
ной схеме имеется вакуумный зазор, в котором про-
лой [39]
исходит ослабление волны из-за полного внутренне-
ω
2
ω2p - ω2
го отражения. Но при достаточно малой толщине
k2z =
c2
ε1 ω2p - (ε1 + 1)ω2,
(23)
зазора L0 эффект ослабления волны незначителен.
(
Кроме того, наличие зазора меняет закон дисперсии
ω∈
0, ωp/√ε1 + 1) .
поверхностной волны, что будет учтено в дальней-
Именно эту волну в длинноволновой области kz c ≪
шем.
≪ ωp называют поверхностным плазмон-полярито-
Рассмотрим основные соотношения для схемы
ном (поверхностным фотоном), а в коротковолновой
(22) в случае падения на границу x = 0 плоской
области — поверхностным плазмоном. Падающей из
волны. Приравнивая (7) и (24), находим резонанс-
диэлектрика на границу плазмы плоской электро-
ную частоту возбуждения поверхностной волны в
магнитной волной нельзя возбудить поверхностную
схеме (22):
волну плазмы [28-30]. Действительно, для возмож-
ности такого возбуждения необходимо, чтобы у обе-
ε1(sin α)2 - 1
ω2 = ω2
(25)
их волн совпадали и частоты, и тангенциальные вол-
p 2ε1(sin α)2 - 1
новые числа kz. Но, как видно из (7), у волны в
Встает вопрос о ширине резонанса, т. е. о том, на-
диэлектрике kz <
√ε1 ω/c, а у поверхностной вол-
сколько точно частота падающей под углом α вол-
ны (23) kz >
√ε1 ω/c. Невозможность возбуждения
ны должна совпадать со значением (25). Для отве-
поверхностной волны следует и из формул (5), (8),
та на этот вопрос исследуем резонансные свойства
которые при L0 = 0 превращаются в обычные фор-
коэффициента отражения R = |B/A|, где величина
мулы Френеля [36]. В частности, коэффициенты B,
B определена в (8). Но для этого необходим учет
F в формулах (8) превращаются в обычные коэффи-
столкновений в плазме. Действительно, на частоте
циент отражения и коэффициент прохождения (по
ω < ωp плазма экранирует электромагнитное поле,
амплитуде) на плоской границе раздела, не содержа-
т. е. любые волны при x > L0 экспоненциально зату-
щие никаких особенностей, кроме связанных с явле-
хают, а поэтому коэффициент отражения, если нет
ниями полного внутреннего отражения и Брюстера.
поглощения, строго равен единице. Учитывая ска-
В случае падающей неоднородной волны волно-
занное, при расчетах используем диэлектрическую
вое число kz уже не связано соотношением (7), а
проницаемость плазмы, приведенную в (22), но ча-
является переменной интегрирования в (11). Поэто-
стоту столкновений считаем достаточно малой. При
му обязательно существует значение, совпадающее
выполнении неравенства ν/ω ≪ 1 формула (25) при-
с (23). Оказывается, однако, что и в этом случае
менима, хотя и является приближенной.
возбуждение поверхностной волны отсутствует, что
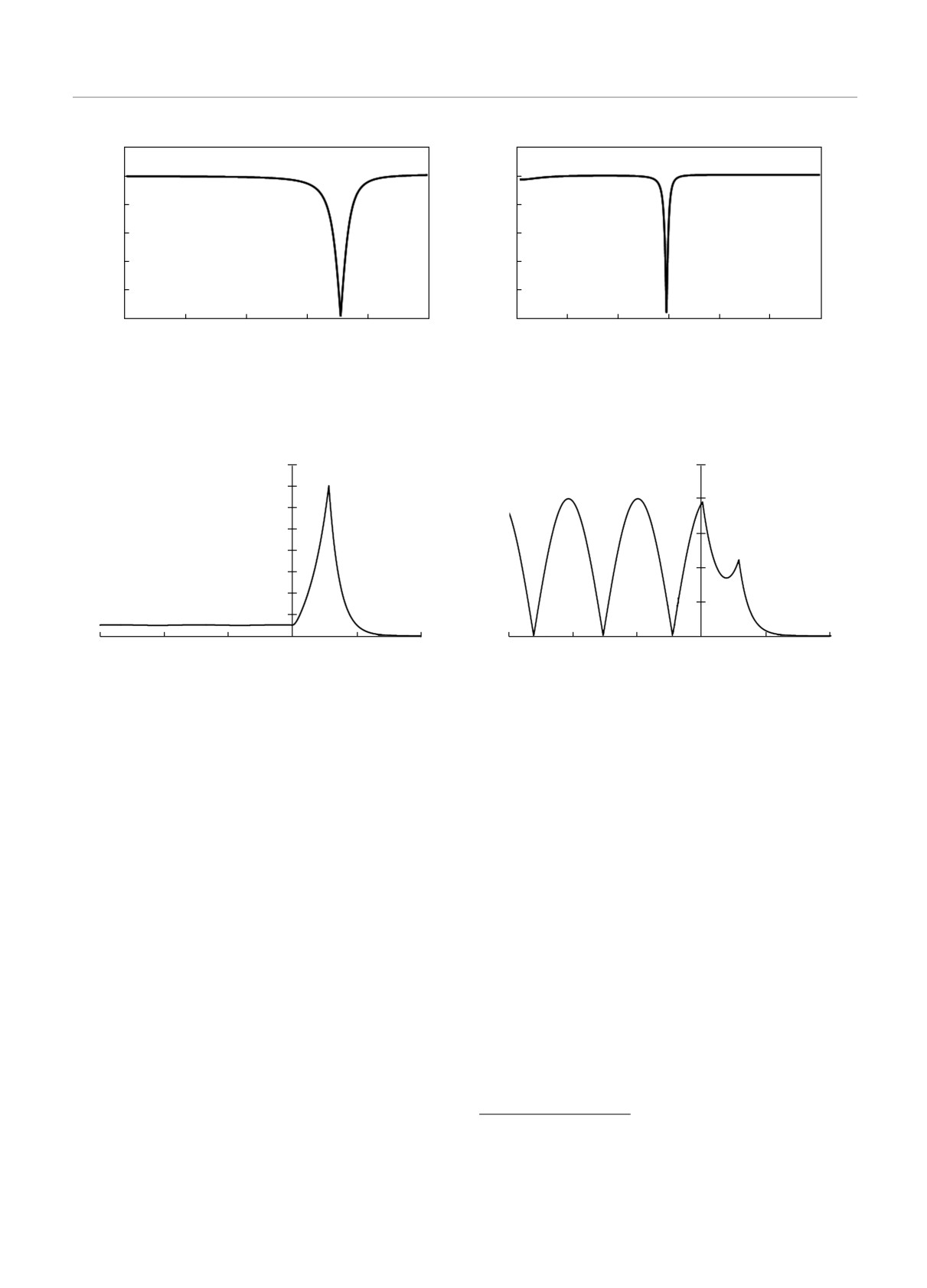
Коэффициент отражения R для схемы (22) в
следует из асимптотических оценок интегралов (11)
зависимости от угла падения α представлен на
(см. далее) и подтверждается численными расчета-
рис. 1а (ε1
= 3, ω/ωp
= 0.592, ν/ωp
= 0.01,
ми. Ситуация не меняется и при учете столкновений
(ωp/c)L0 = 2.8). Виден резко выраженный резонанс-
в плазме. Поэтому были разработаны специальные
ный характер представленной на рисунке зависимо-
схемы возбуждения поверхностной плазменной вол-
сти. В резонансной точке коэффициент отражения
ны при падении электромагнитной волны на грани-
мал по сравнению с единицей, хотя строго в нуль не
цу плазмы.
обращается. Поскольку частота ω задана, по фор-
7. Одна из таких схем — схема Отто [28-30] —
муле (25) можно вычислить значение резонансного
описывается формулами (1) и (22). Поскольку в этой
угла падения:
схеме плазма граничит с вакуумным зазором, вол-
√
новое число поверхностной плазменной волны опре-
1
ω2p - ω2
деляется формулой
α = arcsin
(26)
ε1 ω2p - 2ω2
2
(
ω
ω2p - ω2
√ )
k2z =
,
ω∈
0, ωp/
2
(24)
Значение, вычисленное по формуле (26), хорошо со-
c2 ω2p
- 2ω2
гласуется с тем, которое следует из рис. 1. Коэффи-
При ε1 > 1, начиная с некоторых углов падения
циент отражения для схемы (22) в зависимости от
α, волновое число (7) может совпасть с волновым
частоты ω при α = 1.0724 представлен на рис. 1б.
360
ЖЭТФ, том 156, вып. 2 (8), 2019
Возбуждение поверхностных волн. . .
R
R
1.2
1.2
а
б
1.0
1.0
0.8
0.8
0.6
0.6
0.4
0.4
0.2
0.2
0
0.3
0.6
0.9
1.2
1.5
0
0.2
0.4
0.6
0.8
1.0
1.2
/ p
Рис. 1. Коэффициент отражения по амплитуде в схеме (22) в зависимости от угла падения (а) и от частоты (б)
|E |, отн. ед.z
|E |, отн. ед.z
16
2.5
а
б
14
2.0
12
10
1.5
8
1.0
6
4
0.5
2
-15
-10
-5
0
5
10
-15
-10
-5
0
5
10
x /cp
x /cp
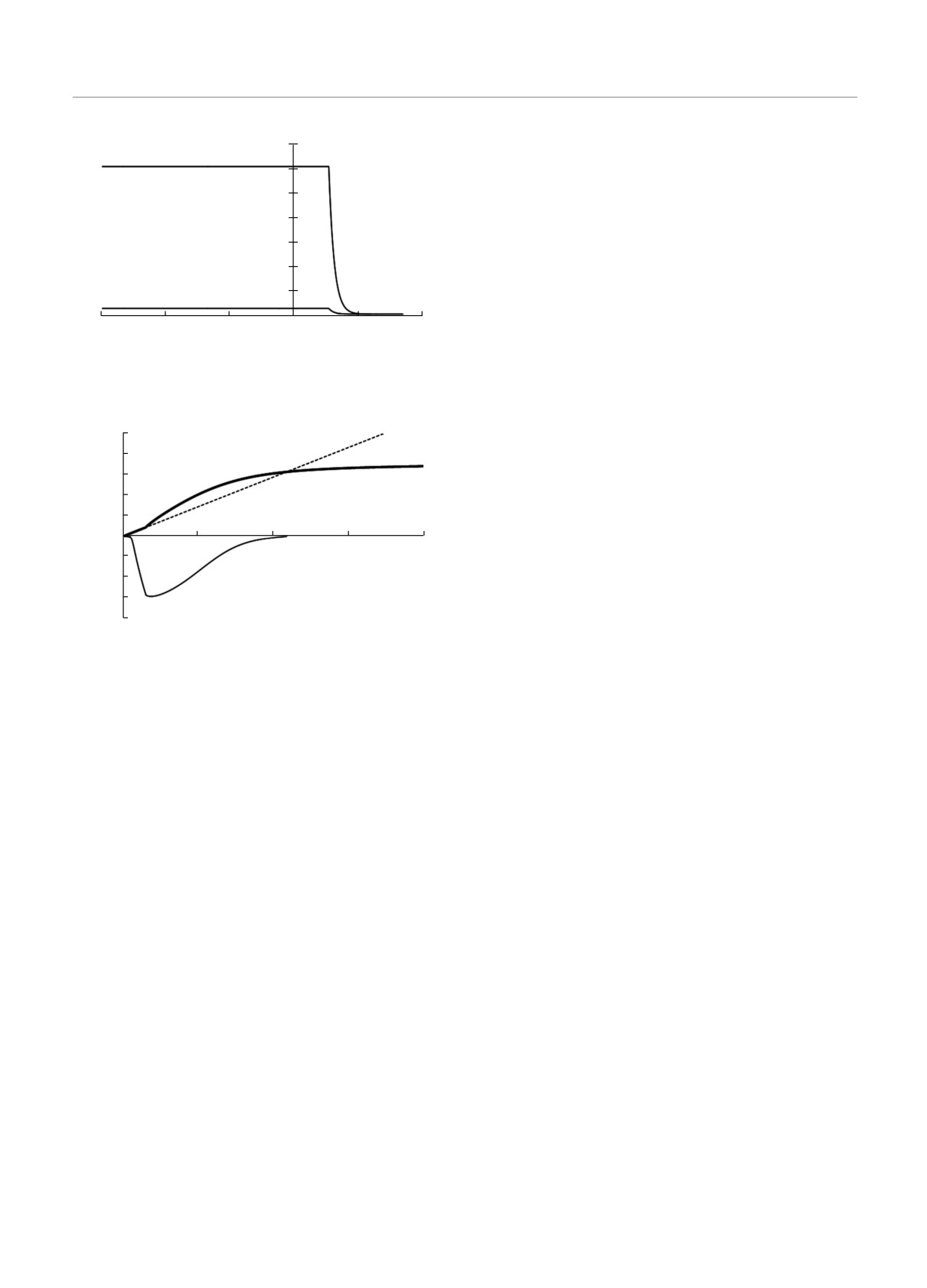
Рис. 2. Пространственное распределение поля волны при ω/ωp = 0.592 (а), 0.53 (б)
Коэффициент отражения по-прежнему имеет ярко
жения (рис. 1б)3). В случае рис. 2б незначительно
выраженный резонансный характер. Заметим, что
изменена частота (уменьшена всего на 10 %). Вид-
рис. 1 является результатом оптимизации системы
но, что резонанс пропал, поскольку амплитуда от-
по углу падения α и частоте ω. В частности, при
раженной волны практически совпала с амплитудой
любой частоте из области существования поверх-
падающей волны.
ностной волны можно подобрать угол, при котором
На рис. 3 показано пространственное распре-
коэффициент отражения достигает локального ми-
деление потока энергии для резонансного случая
нимума. Меняя далее частоту и подбирая при этом
(верхняя кривая) и нерезонансного случая (нижняя
угол, можно достичь абсолютного минимума коэф-
кривая). Обратим внимание, что нижняя кривая
фициента отражения.
построена в десятикратно увеличенном масштабе.
В резонансном случае в области вне плазмы поток
На рис. 2 изображен модуль комплексной функ-
энергии большой, что обусловлено отсутствием от-
ции (5) в зависимости от безразмерной координа-
раженной волны. Уменьшение потока вглубь плаз-
ты xωp/c. В случае рис. 2а имеет место резонанс-
мы связано с поглощением энергии за счет столкно-
ное возбуждение поверхностной плазменной волны:
вений. В нерезонансном случае поток энергии суще-
амплитуда достигает резкого максимума на границе
плазмы при xωp/c = 2.8 и экспоненциально убывает
в обе стороны от границы. Видно также отсутствие
3) Модуль первого выражения в (5) изменяется от |A| - |B|
отраженной от границы xωp/c = 0 волны, что со-
до |A| + |B|, т. е. постоянен при B = 0 и может обращаться в
гласуется с обращением в нуль коэффициента отра- нуль при |A| = |B|.
361
И. Н. Карташов, М. В. Кузелев
ЖЭТФ, том 156, вып. 2 (8), 2019
ственно меньше (примерно в 260 раз), что обуслов-
для вычисления интегралов в решении (11). Ограни-
лено почти полным отражением падающей волны.
чимся областью низких частот, ω2 < ω2p. Низкочас-
В любом случае поглощение волны в плазме проис-
тотные волны в системе (22) оказываются частично
ходит в слое толщиной порядка δν = |kx2|-1. При
локализованными волнами. Поскольку такие волны
малой частоте столкновений величина δν определя-
представляют самостоятельный интерес, будем ре-
ется скинированием поперечного поля в плазме в
шать уравнение (18) относительно частоты ω(kz).
области частот ω < ωp, а поглощение определяет-
Решения этого уравнения относительно волнового
ся столкновениями. При ν = 0 проникновение поля
числа kz (ω) находятся аналогично (они потребуются
в плазму на конечную глубину δν есть, а поглощения
в дальнейшем при аналитическом вычислении инте-
нет. При этом поток (14) тождественно равен нулю,
гралов в (11)).
а при ν = 0 на резонансной частоте поток достигает
В коротковолновом пределе k2z ≫ ω2p/c2 при-
максимального значения.
менимо потенциальное приближение. При этом из
уравнения (18) имеем
8. Обсуждая резонансный характер возбужде-
√
ния поверхностной плазменной волны плоской элек-
ωp
ε1 - 1
ω=
√
1-
exp(-2kzL0) .
(27)
тромагнитной волной, падающей на границу плаз-
2
ε1 + 1
мы, мы допустили существенную неточность. Дело
в том, что формула (24) справедлива для границы
Потенциальная волна (27) является полностью ло-
плазменного и вакуумного полупространств. В схе-
кализованной поверхностной волной (поверхност-
ме (22) плазменное полупространство граничит не с
ным плазмоном), поскольку выполнены не только
вакуумным полупространством, а с вакуумным за-
неравенства (19), но и неравенство k2x0 < 0. Для нас
зором. При этом волновое число поверхностной вол-
волна со спектром (27) интереса не представляет. В
ны должно определяться не из второго уравнения
длинноволновом пределе ω ∼ kzc ≪ ωp ситуация
(20), а из существенно более сложного дисперсион-
существенно усложняется, что видно из следующих
ного уравнения (18). Рассмотрим решения уравне-
соображений. При L0 = 0 и L0 = ∞ уравнение (18)
ния (18), тем более что они будут необходимы нам
имеет следующие точные решения [39]:
√
√
1
1
L0 = ∞: ω =
ω2p + k2zc2 -
ω4p + k4zc4 ,
(28a)
2
4
;
<
√
<
)
2
√1
ε1 + 1
1
(ε1 +1
ε1 - 1
L0 = 0: ω =
ω2p +
k2zc2-
ω4p +
k4zc4 +
ω2pk2zc2 .
(28b)
2
2ε1
4
2ε1
2ε1
Волны (28a), (28b) являются полностью локализо-
При этом первое неравенство (19) оказывается нару-
ванными поверхностными волнами. В длинноволно-
шенным и волна не является локализованной: энер-
вом пределе из (28a), (28b) имеем (это случай по-
гия волны излучается в область x < 0. В связи с
верхностных фотонов)
имеющимся в этом случае оттоком энергии, коле-
⎧
(
)
бания в области вакуумного зазора затухают, чему
⎪
k2zc2
⎨
kzc
1-
,
L0 = ∞,
соответствует появление у частоты ω отрицательной
2ω2
p
мнимой части.
(
)
(29)
ω=⎪
⎪
c
k2zc2
Аналитическое решение уравнения (18) затруд-
⎩ kz
1-
,
L0 = 0.
√ε1
2ω2
нительно. Поэтому приведем характерное численное
p
решение (рис. 4, L0ωp/c = 2.8, ν = 0). Пунктиром на
Очевидно, что при промежуточном значении ваку-
рисунке проведена «световая» прямая ω = kzc/√ε1.
умного зазора в длинноволновом пределе должны
Видно, что затухание имеется именно в той области
выполняться неравенства
kz, где выполнено первое неравенство (19)4).
c
ω
<
< c.
(30)
√ε1
kz
4) В окрестности точки ω = 0, kz = 0 решение уравнения (18) подробно не исследовалось.
362
ЖЭТФ, том 156, вып. 2 (8), 2019
Возбуждение поверхностных волн. . .
P0, отн. ед.
щей из -∞ волной, в случае рис. 5 объемный ха-
14
рактер поля при x < 0 связан с излучением волны
12
на -∞.
10
9. Возбуждение поверхностных волн в схеме (22)
цилиндрической волной (4) описывается формула-
8
ми (8)-(11). Рассмотрим результаты компьютерных
6
расчетов по этим формулам. Выберем те же пара-
4
метры, что были взяты для случая падения плос-
2
P0. 10
кой волны: ω/ωp = 0.592, (ωp/c)L0 = 2.8, ε1 = 3,
ν/ω
p
= 0.01. Расстояние от линейного источника
-15
-10
-5
0
5
10
до плоскости x = 0 положим равным (ωp/c)x0 =
x /cp
= -60 (примерно 10 длин волн). На рис. 6 представ-
Рис. 3. Пространственное распределение потока энергии
лено пространственное распределение компоненты
поля Ez вдоль границы раздела плазма-вакуум.
Видим, что при удалении от центральной точки
Re
/ p
1.0
z = 0 амплитуда высокочастотного электромагнит-
0.8
ного поля сначала возрастает, а затем значитель-
0.6
но уменьшается. Если координату точки максиму-
0.4
ма плотности энергии (zωp/c ≈ 120 . . . 140) разде-
0.2
лить на расстояние от источника до границы плаз-
0
мы ((ωp/c)(|x0| + L0) = 62.8), то получится тангенс
0.5
1.0
1.5
2.0
-0.2
угла в направлении наиболее сильного возбуждения
kcz
/
p
-0.4
волн на границе плазмы. В нашем случае этот угол
–0.6
составляет порядка 1.09 рад, что весьма близко к
-0.8
значению угла (α = 1.0724 рад), при котором имеет
Im
/
10
p
место резонансное возбуждение поверхностной вол-
ны падающей на границу плазмы плоской волной в
Рис. 4. Комплексная дисперсионная кривая нелокализо-
схеме Отто (рис. 1а). Это указывает на то, что при
ванной поверхностной волны
падении на границу плазмы неоднородной волны от
линейного источника также имеет место резонанс-
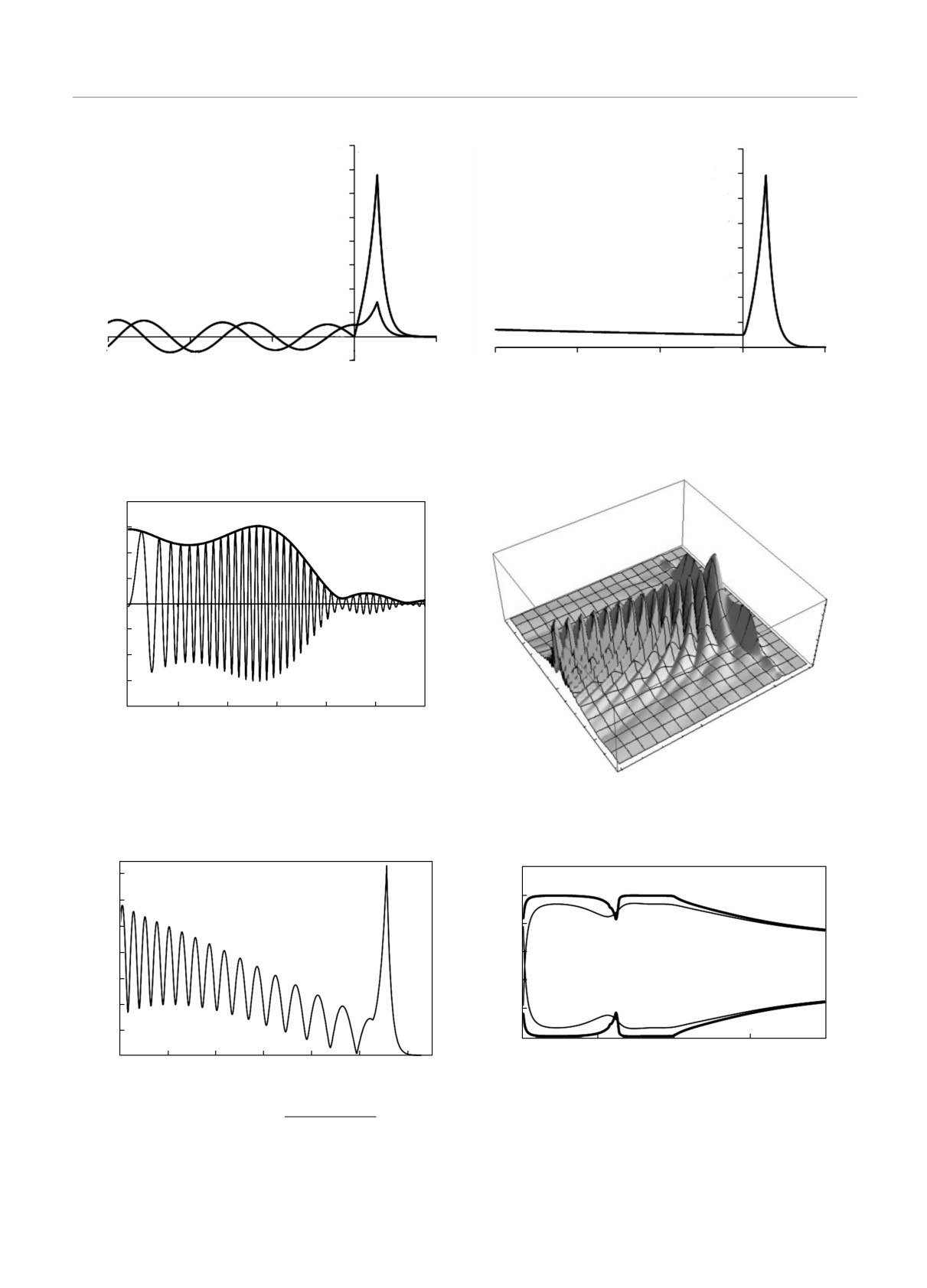
На рис. 5 для одной из точек дисперсионной
ное возбуждение поверхностной плазменной волны.
кривой, показанной на рис.
4, (kzc/ωp
=
0.9,
Бесспорным доказательством того, что речь идет
ω/ωp = 0.592 - 0.0033i) представлено распределе-
именно о резонансном возбуждении поверхностной
ние поля в системе (собственная функция). Модуль
волны, служит рис. 7, на котором показано рас-
поля, изображенный на рис. 5б, мало отличается от
пределение модуля поля вдоль луча от источника
распределения, представленного на рис. 2а. Следо-
к максимуму плотности электромагнитной энергии
вательно, в этом случае при падении плоской вол-
на границе плазмы. Наблюдается типичная карти-
ны в схеме (22) правильнее говорить не о резонанс-
на распределения поля в поверхностной волне, при-
ном возбуждении поверхностной волны на грани-
чем очень похожая на представленные на рис. 2а и
це плазма-вакуум, а о резонансном возбуждении
рис. 5. Отличие обусловлено неоднородностью (ци-
частично локализованной волны резонатора Фаб-
линдричностью) падающей волны и связанной с
ри - Перо. Эта волна является низшей по частоте мо-
этим интерференцией отраженных в сторону источ-
дой резонатора. Ее отличительной особенностью яв-
ника волн. На рис. 8 показано пространственное рас-
ляется поверхностный характер распределения поля
пределение амплитуды поля. Хорошо виден узкий
в областях 0 < x < L0 и x > L0, а также рост ее
пик в той области плоскости xz, где имеет место ре-
амплитуды в области x < 0. Этот рост следует из
зонансное возбуждение поверхностной волны.
принципа причинности, в соответствии с которым
Тот факт, что интенсивное возбуждение поверх-
при Im ω < 0 амплитуда волны в направлении рас-
ностной плазменной волны происходит в достаточ-
пространения (излучения) возрастает. Заметим, что
но узком диапазоне направлений от источника к
между полями, изображенными на рис. 2а и рис. 5,
плазменной границе (или в достаточно узком диапа-
имеется существенное различие: в случае рис. 2 объ-
зоне координаты вдоль границы плазмы, см. рис. 7),
емный характер поля при x < 0 обусловлен падаю-
означает, что только небольшая часть потока энер-
363
И. Н. Карташов, М. В. Кузелев
ЖЭТФ, том 156, вып. 2 (8), 2019
Ez, отн. ед.
|E |, отн. ед.z
16
16
14
14
а
б
12
12
10
10
8
8
1
6
6
4
4
2
2
2
–30
–20
–10
0
10
-2
–30
–20
-10
0
10
x /cp
x /cp
Рис. 5. Распределение поля нелокализованной поверхностной волны: Re Ez (1), Im Ez (2)
E ,|Ezz|, отн. ед.
0.20
0.15
0.10
0.05
|E |z
0
0.2
-0.05
0.1
200
-0.10
0
-0.15
0
0
-0.20
0
50
100
150
200
250
300
z
p
/c
z
/c
–20
p
-200
x /cp
Рис. 6. Распределение поля вдоль границы раздела ва-
-40
куум-плазма: Re Ez — нежирная линия, |Ez | — жирная
линия
Рис. 8. Поверхность |Ez (zωp/c, xωp/c)|
|E |, отн. ед.z
R, T
1.2
0.14
0.12
1.0
0.10
0.8
0.08
0.6
0.06
0.4
0.04
0.2
0.02
0
0
0.5
1.0
1.5
2.0
20
40
60
80
100
120
140
/ p
Рис. 9. Коэффициенты отражения (нижние кривые) и ко-
Рис. 7. Распределение поля |√| в зависимости от ради-
эффициенты прохождения (верхние кривые): жирные ли-
альной координаты ρ = (ωp/c)
(x - x0)2 + z2 вдоль луча
α = 1.07
нии — ν/ωp = 0.01, нежирные линии — ν/ωp = 0.1
364
ЖЭТФ, том 156, вып. 2 (8), 2019
Возбуждение поверхностных волн. . .
гии цилиндрической волны источника поглощается
в плазме. На рис. 9 представлены интегральные ко-
эффициенты отражения от границы плазмы и про-
хождения в плазму потока энергии источника, по-
s
считанные по формулам (14) и (15) для двух значе-
2
ний частоты столкновений. Видно, что коэффици-
ент отражения заметно меньше единицы только в
достаточно узком диапазоне частот. При этом абсо-
лютный минимум коэффициента отражения (≈ 0.8)
- /2
0
/2
0
и абсолютный максимум коэффициента прохожде-
ния в плазму (≈ 0.2) достигаются при ω/ωp ≈ 0.6,
–2
что коррелирует с результатом, представленным на
рис. 1а.
10. Рассмотрим теперь некоторые аналитиче-
ские результаты, основанные на асимптотической
оценке интегралов, входящих в (11), при помощи
метода перевала в дальней зоне [40,41]. Представим
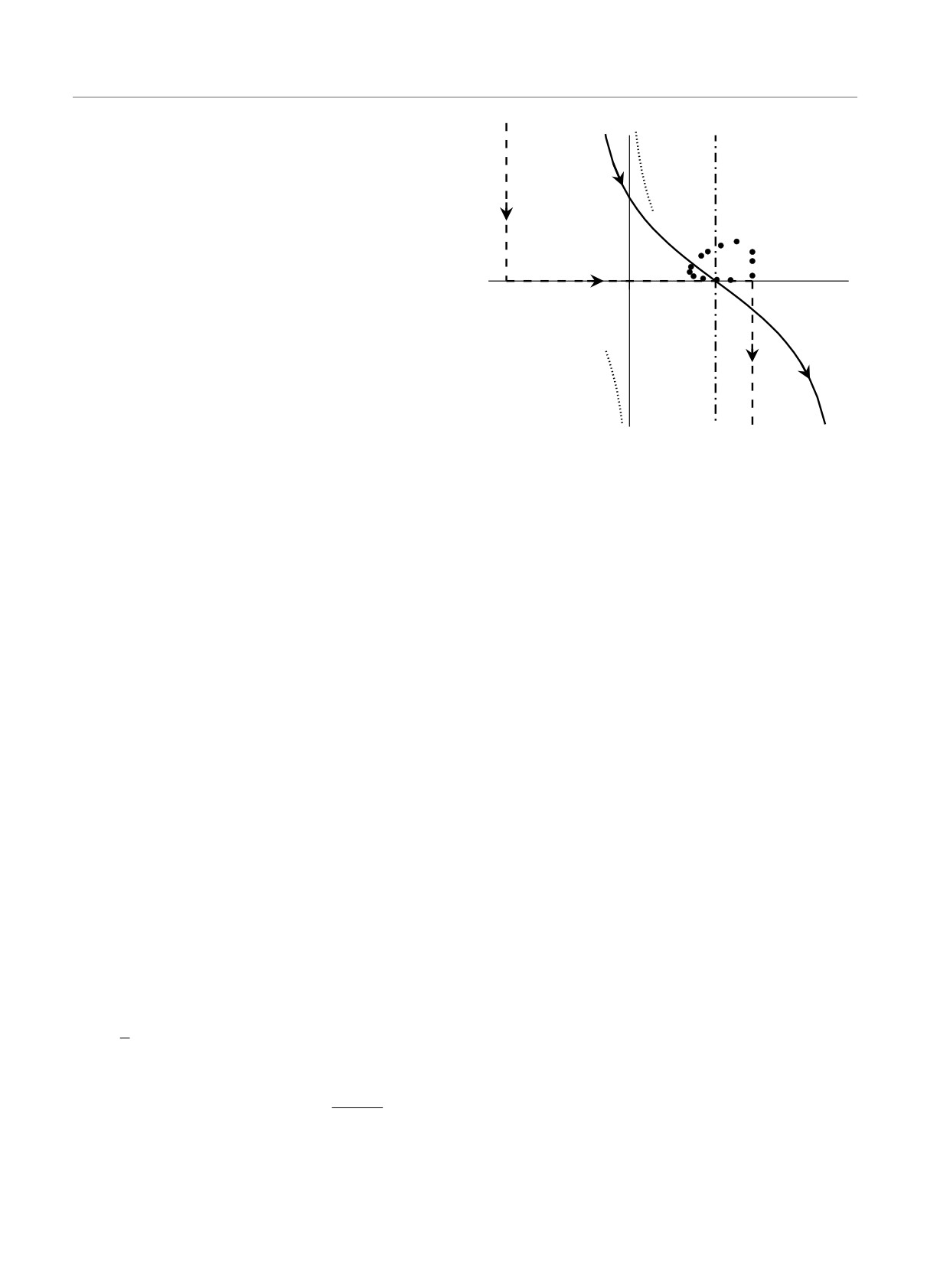
Рис. 10. Комплексная плоскость переменной θ
интегралы в (11) в следующем обобщенном виде:
∫∞
быть определена из формул (11) и (8), в которых
I = f(kx0,kx1,kx2)exp(ikx1|x0| + ikzz)dkz.
(31)
следует положить A = k21 cos2 θ. Второй аргумент
-∞
предэкспоненциальной функции в (32) определяет
полностью аналитическую часть зависимости от θ,
В (31) выделен экспоненциальный множитель, оди-
другие два определяют зависимость через радикалы
наковый для всех интегралов в (11), а функция
вида (6). Путь интегрирования Γ по новой перемен-
f (kx0, kx1, kx2) для каждого из интегралов своя.
ной выбираем из тех соображений, что kz = k1 sinθ
Подынтегральное выражение
(31) содержит ряд
изменяется в пределах от -∞ до +∞ и интеграл схо-
особых точек, которые необходимо учитывать при
дится. А именно, от значения -π/2 + i∞ комплекс-
использовании метода перевала. В частности, это
ной плоскости θ спускаемся по вертикальной прямой
точки ветвления kz = ±k1. При вещественной ε1
до значения -π/2, далее путь интегрирования про-
эти точки лежат на вещественной оси, по которой
ходит по вещественной оси до значения π/2, а затем
проходит и контур интегрирования в (31). Чтобы
по вертикальной прямой до значения π/2 - i∞ (см.
устранить неоднозначность при интегрировании, до-
рис. 10).
статочно считать, что первая среда, хотя и является
При достаточно больших значениях R интеграл
в нашем рассмотрении недиссипативной, тем не ме-
(32) может быть оценен методом перевала. Из (32)
нее имеет исчезающе малую положительную мни-
нетрудно определить точку перевала
мую часть в диэлектрической проницаемости, что
соответствует предельно малому поглощению волн.
θs = θ0
(33)
Этот прием задает направление обхода особенностей
на вещественной оси: точка ветвления +k1 обходит-
и значения показателя экспоненты в (32) в этой точ-
ся снизу, а точка ветвления -k1 обходится сверху.
ке ik1R. Преобразуя контур интегрирования так,
Для удобства рассмотрения часто вместо пере-
чтобы значения подынтегральной экспоненты убы-
менной интегрирования kz вводят новую перемен-
вали от точки перевала наиболее быстрым образом,
ную, определяемую соотношением kz = k1 sin θ [40],
запишем показатель экспоненты в (32) в виде
и тогда интеграл (31) можно переписать в виде
ik1R cos(θ - θ0) = ik1R - s2,
(34)
∫
1
I =
f (kx0(θ), k1 cosθ, kx2(θ)) ×
где s пробегает вещественные значения от -∞ до
π
Γ
+∞. Значение s = 0 соответствует значению θ в точ-
ке перевала (33), соответствие других значений s и θ
× exp{ik1R cos(θ - θ0)} dθ.
(32)
на перевальном контуре определяется вещественной
√
В (32) введены обозначения R =
z2 + x20 и tg θ0 =
частью соотношения (34). Мнимая часть (34) опре-
= z/|x0|. Функция f (kx0(θ), k1 cosθ, kx2(θ)) опреде-
деляет форму перевального контура Γs, а именно,
ляет зависимость от новой переменной θ и может
cos(θ′ - θ0)chθ′′ = 1, где θ′ = Re θ, θ′′ = Imθ. Левая
365
И. Н. Карташов, М. В. Кузелев
ЖЭТФ, том 156, вып. 2 (8), 2019
его часть уходит на -π/2 + θ0 + i∞, правая часть —
регам разреза. Этот интеграл, как известно, отвеча-
на π/2 + θ0 - i∞. В точке перевала перевальный
ет за так называемую боковую волну [40,41].
контур пересекает ось абсцисс под углом -π/4 (см.
Интеграл вида (32) по петле, идущей по берегам
рис. 10). При достаточно больших R значение инте-
разреза вокруг точки ветвления θ = θ2, может быть
грала (в отсутствие особых точек подынтегральной
сведен к интегралу по правому берегу разреза в на-
функции) определяется малой окрестностью пере-
правлении от точки ветвления до +i∞:
вальной точки, что в соответствии с методом пере-
∫
1
вала дает
I2 =
(f (kx0(θ), k1 cos θ, kx2(θ)) -
π
Γ2
√
2
- f (kx0(θ),k1 cosθ,-kx2(θ))) ×
Is =
e-iπ/4f (kx0(θ0), k1 cosθ0, kx2(θ0)) ×
πk1R
× exp{ik1Rcos(θ - θ0)} dθ.
(36)
×eik1R.
(35)
Для вычисления интеграла (36) применим одну
из модификаций метода наискорейшего спуска. А
Выражение (35) в зависимости от выбора функции
именно, деформируем контур интегрирования та-
f описывает падающую, отраженную и прошедшую
ким образом, что при удалении от точки ветвле-
волны.
ния значения подынтегральной экспоненты убывали
наиболее быстрым образом, т. е. представим
При переходе к новой переменной в комплекс-
ной плоскости θ точка ветвления, соответствующая
ik1R cos(θ - θ0) = ik1R cos(θ2 - θ0) - s,
(37)
kz = ±k1, уже отсутствует, но имеются радикалы
где s пробегает вещественные значения от 0 до +∞.
kx0 и kx2. Легко проверить, что при изменении зна-
Значение s = 0 соответствует значению θ = θ2 =
ка у kx0 выражения в (11), обобщенно обозначен-
= θ′2 + iθ′′2, а контур интегрирования определяется
ные в (32) через f, не меняются. Это значит, что
уравнением
подынтегральная функция в (32) не имеет точек
ветвления kz = ±k0, несмотря на наличие ради-
cos(θ′ - θ0)chθ′′ = cos(θ′2 - θ0)chθ′′2
кала kx0. Радикал kx2 определяет точки ветвления
и подходит к точке θ2 под углом, тангенс которо-
kz = ±k2. На комплексной плоскости θ им соответ-
го равен tg(θ′2 -θ0)/ thθ′′2. С другой стороны контур
ствуют значения θ = ±θ2 = ± arcsin(k2/k1). Если
интегрирования уходит к значению -π/2 + θ0 + i∞.
под средой с индексом «2» подразумевать плазму,
Применение к (36) модификации метода перевала
то при ω < ωp одна из точек ветвления (верхняя)
на случай, когда на одном из концов контура инте-
лежит в области θ′ > 0 и θ′′ > 0. Другая (ниж-
грирования достигается наибольшее значение веще-
няя) расположена симметрично относительно нача-
ственной части показателя экспоненты, приводит к
ла координат (в бесстолкновительном пределе обе
оценке
точки ветвления при ω < ωp лежат на мнимой оси
√
комплексной плоскости θ). Для выбора однознач-
sin2θ2
I2 =
f′3 (kx0(θ2), k1 cosθ2, 0) ×
ного решения следует провести разрезы на комп-
iπk1R3 sin(θ2-θ0)
лексной плоскости θ и при интегрировании оста-
exp{ik1Rcos(θ2 - θ0)}
ваться на одном листе римановой поверхности. Про-
×
,
(38)
sin(θ2 - θ0)
ведем разрезы исходя из условия отсутствия воз-
мущений при x → +∞, т. е. линия разреза будет
где f′3 означает производную по третьему аргументу,
определяться условием Im kx2 = 0, а на выбран-
а знак корня выбирается таким, что вещественная
ном листе римановой поверхности Im kx2 > 0. Лег-
его часть положительна. Боковая волна (38) порож-
ко получить уравнение, определяющее линию раз-
дается плазменным полупространством и согласно
реза: sin 2θ′ sh 2θ′′ = 2Imε2/ε1, она идет от точки
выражению (38) является сильно затухающей вдоль
ветвления до значения ±i∞ для верхней и нижней
границы плазмы даже в бездиссипативном случае
точек ветвления соответственно (пунктирные линии
ввиду наличия значительной мнимой части у вели-
на рис. 10). При деформации исходного контура ин-
чины θ2.
тегрирования в перевальный верхняя из точек ветв-
Кроме точек ветвления, подынтегральные выра-
ления может зацепляться за контур интегрирования
жения в (11) содержат полюсы — корни дисперсион-
(на рис. 10 этот случай не показан) и к выраже-
ного уравнения (18). Если при деформации конту-
нию (35) мы должны добавить интеграл по «петле»,
ра интегрирования к перевальному произойдет за-
охватывающей эту точку ветвления и идущей по бе-
цепление за полюс подынтегрального выражения,
366
ЖЭТФ, том 156, вып. 2 (8), 2019
Возбуждение поверхностных волн. . .
то оценка исходного интеграла помимо (35) и (38)
этим корням частоты отвечают условиям резонанс-
должна содержать вклад от этого полюса. Именно
ного возбуждения поверхностной волны.
этот полюс и отвечает за поверхностную волну. За-
В случае, когда полюс (корень дисперсионного
пишем предэкспоненциальный множитель в (32) в
уравнения) оказывается вблизи перевальной точки,
виде
требует уточнения и основная формула метода пе-
ревала (35) [40]. Запишем (39) в виде
f1(θ)
f =
,
(39)
S(ω, θ)
f1 (θ(s))
f =
,
(42)
S (ω, θ(s))
где S(ω, θ) — дисперсионная функция S(ω, kz), вы-
(s2 - s2p)
s2 - s2
p
раженная через новую переменную θ. Равенство
S(ω, θ) = 0 представляет собой дисперсионное урав-
выделив полюсы s = ±sp, соответствующие при за-
нение и, если θ = θp — его решение (вообще говоря,
мене (34) полюсу θ = θp. Первый множитель в зна-
комплексное), то вблизи θp выражение (39) можно
менателе (42) уже не содержит нулей при s = ±sp.
представить в виде
Так приходим к асимптотической оценке интеграла
вблизи перевальной точки:
f1(θp)
f =
(40)
S′(ω, θp)(θ - θp)
(√
)√
2
Is = J0
2sp
e-iπ/4 ×
В итоге полюс, который зацепляется за перевальный
πk1R
контур при деформации, дает вклад в интеграл (32)
× f (kx0(θ0),k1 cosθ0,kx2(θ0))eik1R,
(43)
2if1(θp)
где
Ip = ±
exp{ik1R cos(θp - θ0)}.
(41)
S′(ω, θp)
∫
∞
x
e-ξ2/2
Знак в правой части (41) определяется направле-
J0(x) =
√
dξ.
(44)
2π
x-ξ
нием обхода полюса при деформации контура. При
−∞
θ0 < Re θp < π/2 следует взять знак «-», в осталь-
ных случаях — знак «+».
Формула (43) отличается от (35) только наличием
(√
)
Среди множества корней дисперсионного урав-
множителя J0
2sp
. Область значений s, при ко-
торых этот множитель еще существен, составляет
нения (18) не все будут давать сколь-нибудь сущест-
венный вклад в оценку интеграла (32), даже если
диапазон -1 < s < 1. Если |sp| значительно превы-
шает единицу, то можно использовать асимптотиче-
они лежат на рассматриваемом листе римановой по-
верхности и зацепляются за перевальный контур.
ское выражение для J0(x):
На рис. 10 штрихпунктирной линией представлена
1
одна из линий уровня подынтегральной экспонен-
J0(x) ≈ 1 +
при
|x| ≫ 1.
(45)
x2
ты, вторая из этих линий совпадает с веществен-
ной осью. Линии уровня делят комплексную плос-
В итоге мы возвращаемся к формуле (35). Похо-
кость на четыре сектора: два из них соответствуют
жая на J0(x) функция (обозначаемая иногда J+(x))
убыванию подынтегрального выражения (те, через
часто используется в кинетической теории плазмы
которые проходит перевальный контур), два дру-
[32]. В отличие от (44) функция J+(x) задается не
гих — возрастанию. Зацепиться за перевальный кон-
определенным интегралом, а контурным, при этом
тур могут только полюсы, лежащие в секторах, где
контур интегрирования проходит по вещественной
он проходит. Причем не пренебрежимо малый вклад
оси, огибая особую точку ξ
= x снизу. То есть
по сравнению с вкладом от точки перевала будут
при Im x > 0 функции J0(x) и J+(x) совпадают, а
√
давать только те из них, которые находятся вбли-
при Im x < 0 различаются на
2π ixe-x2/2. Функ-
зи линий уровня, точнее, той линии уровня, ко-
ция J+(x) аналитически продолжается из области
торая совпадает с вещественной осью. На рис. 10
Im x > 0 в область Im x < 0, а функция J0(x) имеет
для параметров системы, использованных выше, от-
разрыв при переходе вещественной оси.
дельными точками представлены положения кор-
Приведенные выше решения представлены на
ней дисперсионного уравнения для набора частот из
рис. 11 в зависимости от координаты вдоль поверх-
диапазона ω/ωp = 0.65 . . . 0.05. Наибольший вклад
ности на границе плазма-вакуум при x = L0 для
в интеграл дают корни дисперсионного уравнения,
частот столкновений ν/ωp = 0 и ν/ωp = 0.01 при
лежащие вблизи точки перевала. Соответствующие
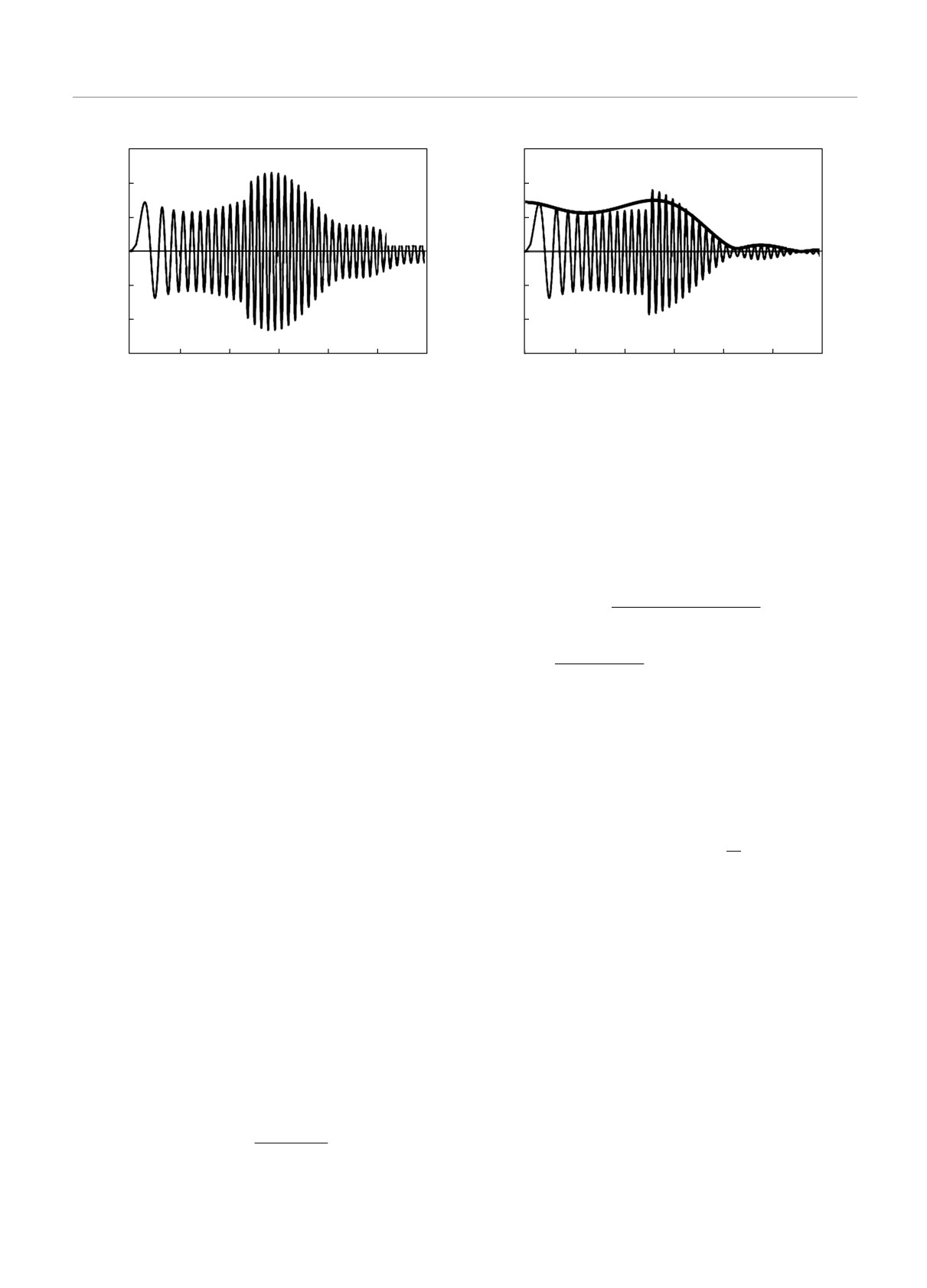
тех же остальных параметрах. Жирной линией на
367
И. Н. Карташов, М. В. Кузелев
ЖЭТФ, том 156, вып. 2 (8), 2019
Ez, отн. ед.
Ez, отн. ед.
0.3
0.3
а
б
0.2
0.2
0.1
0.1
0
0
–0.1
-0.1
–0.2
-0.2
-0.3
-0.3
0
50
100
150
200
250
300
0
50
100
150
200
250
300
z
/c
z
/c
p
p
Рис. 11. Зависимость поля Re Ez от координаты вдоль поверхности на границе плазма-вакуум при ν/ωp = 0 (а), 0.01 (б)
рис. 11б изображена огибающая с рис. 6. В целом
Положим также ε1 = 1, т. е. будем рассматривать
результаты аналитического исследования с доста-
систему вакуум-плазма-плазма. Как известно [39],
точной степенью точности соответствуют полному
на границе раздела слоев плазмы разной плотнос-
численному нахождению интегралов в (11). Из ри-
ти возможно распространение поверхностной вол-
сунков видно, что начиная со значения zωp/c ≈
ны, волновое число которой определяется формулой
≈ 120 . . .130 амплитуда поля увеличивается. Эти
|(ω2p - ω2)(ω2 - ω2p0)|
значения координаты соответствуют пересечению
k2z =
,
2c2(Ω2 - ω2)
(47)
полюсом (нулем дисперсионного уравнения) пере-
ω ∈ (min(ωp,ωp0),Ω),
вального контура и, следовательно, возбуждению
√
поверхностной волны. С ростом частоты столкнове-
где Ω = (ω2p + ω2p0)/2. Случай ωp0 < ωp практичес-
ний в плазме эффективность возбуждения поверх-
ки не отличается от уже рассмотренного, а все ре-
ностной волны снижается. При значениях zωp/c,
зультаты в целом сохраняют свою силу. В частности,
меньших указанных выше, поверхностная волна от-
расположение характерных точек на комплексной
сутствует и поле Ez определяется суперпозицией по-
плоскости θ аналогично показанному на рис. 11. Ес-
лей падающей и отраженной волн. При этом, как
ли ωp0 > ωp, то волна с частотой ωp < ω < Ω, падаю-
и следовало ожидать, значения Ez в этом диапа-
щая из среды с индексом «1», оказывается непрони-
зоне zωp/c слабо зависят от частоты столкновений
кающей в плазму с диэлектрической проницаемос-
в плазме.
тью ε0 при любом угле падения. Кроме того, точки
(√
)
Таким образом, при некотором значении z0, со-
ветвления θ = ±θ2 = ± arcsin
ε2
в бесстолкно-
ответствующем углу падения плоской волны, при
вительном пределе лежат уже на вещественной оси
котором наблюдается минимум коэффициента отра-
комплексной плоскости θ, а при учете слабых столк-
жения, происходит возбуждение поверхностной вол-
новений в первом и третьем квадрантах вблизи ве-
ны и с этого значения z0 начинается ее распрост-
щественной оси θ. Причем во многих практически
ранение вдоль поверхности. При других значениях
важных случаях расположение характерных точек
z поверхностная волна падающей цилиндрической
на комплексной плоскости θ таково, что точка пе-
волной уже не возбуждается.
ревала оказывается вблизи как полюса, так и точ-
11. Аналогично можно рассмотреть возбужде-
ки ветвления. В связи с этим получение каких-либо
ние поверхностной волны на границе раздела двух
аналитических выражений для поля возбуждаемой
слоев плазмы разной плотности. В этом случае ди-
поверхностной волны затруднено.
электрическую проницаемость среды с индексом
12. В работе исследовано возбуждение поверх-
«0» в (1) следует определить формулой
ностных плазменных волн цилиндрической элек-
тромагнитной волной. Волны по структуре близ-
ω2p0
кой к цилиндрической возникают при использова-
ε0 = 1 -
(46)
ω(ω + iν0)
нии штыревых дипольных антенн. Как и в случае
368
ЖЭТФ, том 156, вып. 2 (8), 2019
Возбуждение поверхностных волн. . .
плоской падающей волны, возбуждения поверхност-
8.
Ю. Б. Башкуев, В. Б. Хаптанов, М. Г. Дембелов,
ных волн на границе двух полупространств не про-
Письма в ЖТФ 36(3), 88 (2010) [Yu. B. Bashkuev,
исходит и поэтому в работе рассмотрена слоистая
V. B. Khaptanov, and M. G. Dembelov, Tech. Phys.
Lett. 36(2), 136 (2010)].
плазменно-диэлектрическая структура. В частнос-
ти, проанализированы структуры: диэлектрик-ва-
9.
В. И. Байбаков, В. Н. Дацко, Ю. В. Кистович,
куум-плазма и вакуум-плазма-плазма. При паде-
УФН 157, 722 (1989) [V. I. Baibakov, V. N. Datsko,
нии цилиндрической волны на слоистую структуру
and Yu. V. Kistovich, Sov. Phys. Usp. 32, 378 (1989)].
возбуждение поверхностной волны происходит в до-
10.
В. Н. Дацко, А. А. Копылов, УФН 178, 109 (2008)
статочно узком диапазоне частот и углов распро-
[V. N. Datsko and A. A. Kopylov, Phys.-Usp. 51, 101
странения, соответствующих условию возбуждения
(2008)].
поверхностной плазменной волны плоской электро-
магнитной волной. В работе получены аналитиче-
11.
А. В. Кукушкин, УФН 179, 801 (2009) [A. V. Ku-
ские интегральные выражения для электромагнит-
kushkin, Phys.-Usp. 52, 755 (2009)].
ного поля в каждой из областей слоистой структу-
12.
А. В. Кукушкин, А. А. Рухадзе, К. З. Рухадзе,
ры. На основе этих выражений вычислены структу-
УФН 182, 1205 (2012) [A. V. Kukushkin, A. A. Ru-
ры поля, потока электромагнитной энергии, найде-
khadze, and K. Z. Rukhadze, Phys.-Usp. 55, 1124
ны интегральные коэффициенты отражения и про-
(2012)].
хождения. Однако такой численный анализ не поз-
13.
И. Н. Карташов, М. В. Кузелев, Физика плазмы
воляет выделить различные составляющие полного
40, 749 (2014) [I. N. Kartashov and M. V. Kuzelev,
электромагнитного поля, такие как поверхностная
Plasma Phys. Rep. 40, 650 (2014)].
волна на границе раздела, боковая волна и т. п. Для
этих целей были использованы асимптотические ме-
14.
K. S. Bekhovskaya, I. L. Bogdankevich, P. S. Strelkov,
тоды — метод перевала и его модификации, при-
V. P. Tarakanov, and D. K. Ul’yanov, Plasma Phys.
мененные к выражению для поля в виде фурье-ин-
Rep. 37, 1119 (2011).
теграла. Падающая, отраженная и прошедшая вол-
15.
П. С. Стрелков, И. Е. Иванов, Д. В. Шумейко, Фи-
ны определяются вкладом в интеграл от окрестнос-
зика плазмы 38, 536 (2012) [P. S. Strelkov, I. E. Iva-
ти перевальной точки. Боковая волна определяется
nov, and D. V. Shumeiko, Plasma Phys. Rep. 38, 488
вкладом в интеграл при интегрировании по берегам
(2012)].
разреза вблизи точек ветвления подынтегральной
функции. Во всех случаях вклад от боковой волны
16.
П. С. Стрелков, В. П. Тараканов, И. Е. Иванов,
Д. В. Шумейко, Физика плазмы 40, 738 (2014)
пренебрежимо мал. Поверхностная волна определя-
[P. S. Strelkov, I. E. Ivanov, D. V. Shumeiko, and
ется вкладом от полюса подынтегрального выраже-
V. P. Tarakanov, Plasma Phys. Rep. 40, 640 (2014)].
ния (корня дисперсионного уравнения). Этот вклад
возникает при пересечении полюсом перевального
17.
И. Н. Карташов, М. В. Кузелев, П. С. Стрелков,
контура.
В. П. Тараканов, Физика плазмы 44, 250 (2018)
[I. N. Kartashov, M. V. Kuzelev, P. S. Strelkov, and
V. P. Tarakanov, Plasma Phys. Rep. 44, 289 (2018)].
ЛИТЕРАТУРА
18.
М. В. Кузелев, А. А. Рухадзе, П. С. Стрелков,
Плазменная релятивистская СВЧ-электроника,
1. A. Sommerfeld, Math. Ann. 47, 317 (1896).
Ленанд, Москва (2018).
2. J. Zenneck, Ann. Physik. 328, 846 (1907).
19.
М. В. Кузелев, Н. Г. Орликовская, ЖЭТФ 150,
1252 (2016) [M. V. Kuzelev and N. G. Orlikovskaya,
3. A. Sommerfeld, Ann. Physik. 333, 665 (1909).
JETP 123, 1090 (2016)].
4. H. Weyl, Ann. Physik. 365, 481 (1919).
20.
И. Н. Карташов, М. В. Кузелев, А. А. Рухад-
зе, Физика плазмы 30, 60 (2004) [I. N. Kartashov,
5. V. Fock, Ann. Physik. 409, 401 (1933).
M. V. Kuzelev, and A. A. Rukhadze, Plasma Phys.
Rep. 30, 56 (2004)].
6. B. Van der Pol, Physica 2, 843 (1935).
21.
И. Н. Карташов, М. В. Кузелев, А. А. Рухадзе,
7. Ф. Франк, Р. Мизес, Дифференциальные и интег-
Физика плазмы 35, 194 (2009) [I. N. Kartashov,
ральные уравнения математической физики, ч. 2,
M. V. Kuzelev, and A. A. Rukhadze, Plasma Phys.
ОНТИ (1937).
Rep. 35, 169 (2009)].
369
12
ЖЭТФ, вып. 2 (8)
И. Н. Карташов, М. В. Кузелев
ЖЭТФ, том 156, вып. 2 (8), 2019
22.
А. Ф. Александров, В. М. Шибков, Л. В. Шибкова,
er, Plasmonics: Fundamentals and Applications,
ТВТ 48, 643 (2010) [A. F. Aleksandrov, V. M. Shib-
Springer (2007)].
kov, and L. V. Shibkova, High Temp. 48, 611 (2010)].
31.
М. В. Кузелев, Физика плазмы 44, 430 (2018)
23.
В. М. Шибков, Л. В. Шибкова, В. Г. Громов,
[M. V. Kuzelev, Plasma Phys. Rep. 44, 498 (2018)].
А. А. Карачев, Р. С. Константиновский, ТВТ 49,
32.
А. Ф. Александров, Л. С. Богданкевич, А. А. Ру-
163 (2011) [V. M. Shibkov, L. V. Shibkova, V. G. Gro-
хадзе, Основы электродинамики плазмы, Высш.
mov, A. A. Karachev, and R. S. Konstantinovskii,
школа, Москва (1988) [A. F. Alexandrov, L. S. Bog-
High Temp. 49, 155 (2011)].
dankevich, and A. A. Rukhadze, Principles of
24.
Г. П. Кузьмин, И. М. Минаев, К. З. Рухадзе,
Plasma Electrodynamics, Springer-Verlag, Heidelberg
В. П. Тараканов, О. В. Тихоневич, Радиотехн. и
(1984)].
электр. 57, 590 (2012) [G. P. Kuzmin, I. M. Minaev,
33.
А. В. Немыкин, С. В. Перминов, Л. Л. Фрумин,
K. Z. Rukhadze, V. P. Tarakanov, and O. V. Tikho-
Д. А. Шапиро, КЭ 45, 240 (2015).
nevich, J. Comm. Technol. Electron. 57, 536 (2012)].
34.
И. М. Ахмеджанов, КЭ 42, 934 (2012) [I. M. Akh-
25.
Н. Н. Богачев, И. Л. Богданкевич, Н. Г. Гусейн-за-
medzhanov, Quant. Electr. 42, 934 (2012)].
де, А. А. Рухадзе, Физика плазмы 41, 860 (2015)
[N. N. Bogachev, I. L. Bogdankevich, N. G. Gu-
35.
С. А. Урюпин, А. А. Фролов, КЭ 43, 1132 (2013)
sein-zade, and A. A. Rukhadze, Plasma Phys. Rep.
[S. A. Uryupin and A. A. Frolov, Quant. Electr. 43,
41, 792 (2015)].
1132 (2013)].
26.
В. А. Еськин, А. В. Ивонинский, А. В. Кудрин,
36.
М. Борн, Э. Вольф, Основы оптики, Наука, Моск-
Л. Л. Попова, ЖЭТФ 151, 236 (2017) [V. A. Es’kin,
ва (1973) [M. Born and E. Wolf, Principles of Optics,
A. V. Ivoninsky, A. V. Kudrin, and L. L. Popova,
Pergamon Press (1968)].
JETP 124, 202 (2017)].
37.
М. Б. Виноградова, О. В. Руденко, А. П. Сухору-
27.
В. А. Еськин, А. В. Ивонинский, А. В. Кудрин, Фи-
ков, Теория волн, Наука, Москва (1979).
зика плазмы 44, 203 (2018) [V. A. Es’kin, A. V. Ivo-
ninsky, and A. V. Kudrin, Plasma Phys. Rep. 44, 245
38.
В. А. Ильин, Э. Г. Позняк, Основы математичес-
(2018)].
кого анализа, ч. 2, Физматлит, Москва (2002).
28.
H. Raether, Surface Plasmons on Smooth and Rough
39.
М. В. Кузелев, Волновые явления в средах с дис-
Surface and on Gratings, Springer-Verlag (1988).
персией, Ленанд, Москва (2017).
29.
В. В. Климов, Наноплазмоника, Физматлит, Моск-
40.
Л. М. Бреховских, Волны в слоистых средах, Изд.
ва (2009).
АН СССР, Москва (1957).
30.
С. А. Майер, Плазмоника. Теория и приложения,
41.
Л. Д. Ландау, Е. М. Лифшиц, Гидродинамика,
R&C Dynamics, Москва, Ижевск (2011) [S. A. Mai-
Наука, Москва (1986).
370