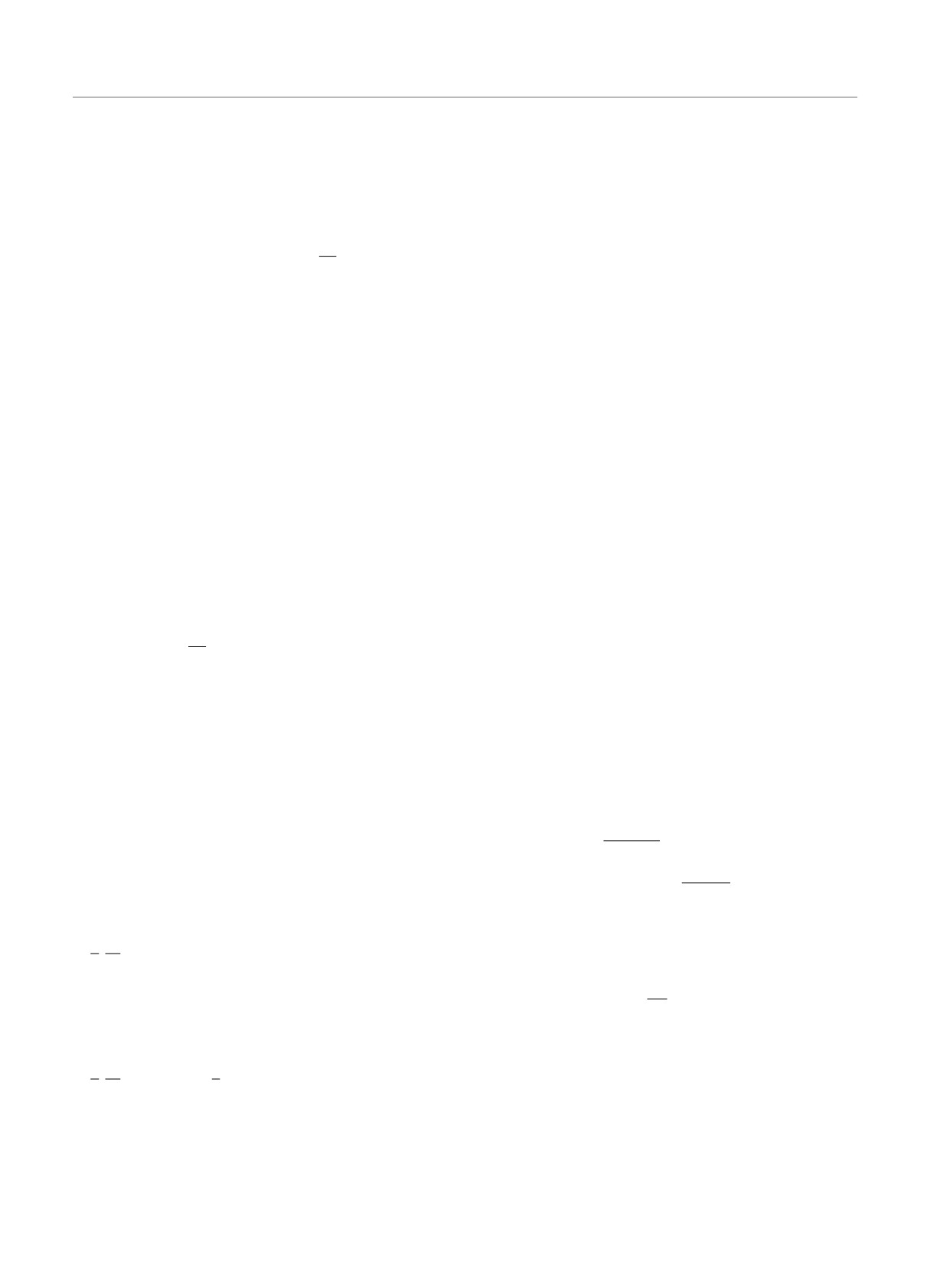ЖЭТФ, 2019, том 156, вып. 3 (9), стр. 387-395

НЕСТАЦИОНАРНОЕ ПРОСТРАНСТВЕННО-ЭНЕРГЕТИЧЕСКОЕ

РАСПРЕДЕЛЕНИЕ КАСКАДА ВЫБИТЫХ АТОМОВ

В ТВЕРДОМ ТЕЛЕ

Е. В. Метелкинa*, В. А. Акатьев^b, В. И. Шмырев^a, Е. Ю. Барышева^b

^a Российский государственный социальный университет

129226, Москва, Россия

^b Московский государственный технический университет им. Н. Э. Баумана

105005, Москва, Россия

Поступила в редакцию 8 февраля 2019 г.,

после переработки 8 февраля 2019 г.

Принята к публикации 29 марта 2019 г.

Рассматривается развитие каскада атомных столкновений в твердом теле, состоящем из одинаковых ато-

мов. Найдено решение кинетического уравнения Больцмана, описывающее нестационарное пространст-

венно-энергетическое распределение замедляющихся атомов с учетом их размножения. Предполагается,

что рассеяние атомов является упругим, сферически-симметричным в системе центра масс, а сечение

рассеяния постоянно. Отдельные частные случаи этого решения совпадают с результатами, полученными

ранее.

DOI: 10.1134/S0044451019090013

в твердом теле образуются первичные точечные де-

фекты: вакансии и межузельные атомы, определяю-

щие степень повреждения материала и его дальней-

1. ВВЕДЕНИЕ

шие физические свойства [1, 2]. В связи с этим ис-

следование энергетического распределения каскада

Создание ядерных реакторов и проектирование

атомных столкновений и его развития во времени

будущих термоядерных установок тесно связано с

представляет большой интерес.

проблемой выбора для них радиационно-стойких

материалов, поскольку их корпуса и отдельные

Исследованию развития каскадов атомных

элементы должны выдерживать продолжительное

столкновений в твердом теле было посвящено до-

воздействие радиации. Именно радиационная стой-

статочно большое количество работ [3-9]. В работе

кость материала во многом определяет время жизни

[3] с помощью построенной модельной индикатрисы

установок и многие другие их физические характе-

рассеяния было получено приближенное стаци-

ристики.

онарное энергетическое распределение каскада

Облучение твердых тел быстрыми частицами

движущихся атомов для произвольных потен-

(особенно нейтронами) приводит к тому, что ато-

циалов межатомного взаимодействия. В работах

мы кристаллической решетки, получившие от нале-

[4, 5] анализировалась возможность образования

тающей частицы энергию, большую некоторой по-

субкаскадов

— ряда неперекрывающихся меж-

роговой величины, вылетают из своих равновес-

ду собой областей в процессе развития каскада

ных положений. Дальнейший обмен энергией меж-

атомных столкновений. Оценка пороговой энергии

ду движущимися атомами и атомами, находящи-

образования субкаскадов была проведена в работе

мися в узлах кристаллической решетки, приводит

[6]. В работе [7] была разработана теоретическая

к появлению новых поколений выбитых атомов. В

модель для исследования образования каскадов и

результате возникает так называемый каскад атом-

субкаскадов атомных столкновений в облучаемых

ных столкновений. В результате развития каскада

твердых телах, основанная на использовании ли-

нейного кинетического уравнения Больцмана. На

^* E-mail: sitech47@mail.ru

основе расширенного толкования понятия первично

387

Е. В. Метелкин, В. А. Акатьев, В. И. Шмырев, Е. Ю. Барышева

ЖЭТФ, том 156, вып. 3 (9), 2019

выбитый атом (ПВА) в работе [7] был сформулиро-

Преимущество использованных приближений со-

ван критерий для определения пороговой энергии

стоит в том, что в этом случае удается найти ре-

образования субкаскадов в твердом теле и получе-

шение кинетического уравнения и получить про-

ны формулы для определения их числа и средних

стые аналитические формулы для функции распре-

размеров в зависимости от энергии ПВА. На основе

деления, позволяющие проанализировать основные

результатов, представленных в [7], в работе [8] были

особенности развития каскада атомных столкнове-

проведены численные расчеты для конкретных

ний. Кроме того, с помощью полученных результа-

материалов, согласующиеся с экспериментальными

тов можно оценивать точность различных прибли-

данными.

женных решений.

Следует отметить, что в работе [7] была найдена

функция распределения, описывающая стационар-

2. ПОСТАНОВКА ЗАДАЧИ

ное энергетическое распределение каскада движу-

щихся атомов с учетом их размножения для наибо-

Рассмотрим распространение каскада выбитых

лее простого частного случая упругого, сферичес-

атомов в твердом теле. Будем предполагать, что

ки-симметричного рассеяния в системе центра масс

твердое тело состоит из одинаковых атомов, энер-

без учета энергии связи атомов в узлах решетки. В

гией связи которых в узлах решетки (ε_d) будем пре-

работе [9] на основе решения кинетического уравне-

небрегать (ε_d = 0). Будем, кроме того, предпола-

ния Больцмана была рассчитана функция распре-

гать, что рассеяние движущихся атомов на атомах,

деления по энергиям, описывающая стационарное

находящихся в узлах решетки, является сферичес-

энергетическое распределение каскада движущихся

ки-симметричным в системе центра масс, а полное

атомов при степенном потенциале взаимодействия

сечение рассеяния является постоянным.

(U ∝ 1/rⁿ [10]) с учетом энергии связи атомов в уз-

Кинетическое уравнение Больцмана, описываю-

лах решетки.

щее этот процесс, имеет следующий вид [7,14]:

Кроме того, на основе представлений, развитых в

[7], в работе [11] были определены пространственные

1 ∂

и временные характеристики первично выбитых ре-

Φ(r, E, Ω, t) + Ω∇Φ(r, E, Ω, t) +

v ∂t

∫

лятивистских электронов (ПВЭ), замедляющихся в

веществе за счет ионизационных потерь: зависи-

+ Σ(E)Φ(r, E, Ω, t) = dΩ^′ dE^′Σ(E^′) ×

мость энергии ПВЭ от времени, зависимость энер-

× P(E^′ → E,Ω^′Ω)Φ(r,E^′,Ω^′,t)+

гии замедляющегося ПВЭ от пройденного пути и

∫

зависимость пути, проходимого ПВЭ, от времени за-

+ dΩ^′ dE^′Σ(E^′)P (E^′ → E^′ - E, Ω^′Ω) ×

медления. В работе [12] эти представления были ис-

пользованы для вычисления стационарного энерге-

× Φ(r, E^′, Ω^′, t) + S(r, E, Ω, t),

(1)

тического распределения релятивистских электро-

нов, замедляющихся в веществе за счет ионизаци-

где Φ(r, E^′, Ω, t) = vf(r, E^′, Ω, t) — поток атомов,

онных потерь с учетом их размножения.

f (r, E^′, Ω, t) — функция распределения движущихся

атомов, v — скорость атома, Ω — единичный вектор

В работе [13] было получено точное решение

в направлении его движения, P (E^′ → E, Ω^′Ω) =

кинетического уравнения Больцмана, описывающее

= Σ(E^′ → E, Ω^′Ω)/Σ(E^′) — индикатриса рассея-

нестационарное энергетическое распределение кас-

ния, Σ(E^′

→ E, Ω^′Ω) — макроскопическое сече-

када движущихся атомов с учетом их размножения.

ние рассеяния атома с энергией E^′ и направлени-

Предполагалось, что рассеяние движущихся атомов

ем движения Ω^′ в интервал энергий и углов [E, E +

является упругим и сферически-симметричным в

+ dE, Ω, Ω+dΩ], Σ(E^′) — полное сечение рассеяния,

системе центра инерции, сечение взаимодействия —

S(r, E, Ω, t) — функция источника.

постоянная величина, а энергии связи атомов в уз-

В случае упругого сферически-симметричного в

лах решетки не учитывалась.

системе центра масс рассеяния движущихся атомов

В настоящей работе на основе использования та-

на покоящихся свободных (ε_d = 0) атомах твердого

ких же предположений определяется решение кине-

тела индикатриса рассеяния имеет вид [14]

тического уравнения Больцмана для функции рас-

[

√

]

пределения, описывающей нестационарное прост-

ранственно-энергетическое распределение каскада

P (E^′ → E, Ω^′Ω) =

δ (Ω^′Ω) -

(2)

2πE^′

E^′

движущихся атомов с учетом их размножения.

388

ЖЭТФ, том 156, вып. 3 (9), 2019

Нестационарное пространственно-энергетическое распределение.. .

где δ(z) — дельта-функция Дирака. Интегрирова-

где

∫

ние выражения (2) по dΩ приводит к следующему

результату [14]:

P₀(E^′ → E) = dΩ P(E^′ → E, Ω^′Ω),

∫

(8)

P₀(E^′ → E) = dΩ P(E^′ → E, Ω^′Ω) =

P₁(E^′ → E) = dΩ(Ω^′Ω)P(E^′ → E, Ω^′Ω),

θ(E^′ - E),

(3)

∫

E^′

S₀(r, E, t) = dΩ S(r, E, Ω, t),

где θ(z) — единичная функция Хевисайда.

∫

(9)

Первый интеграл, стоящий в правой части кине-

S₁(r, E, t) = dΩ Ω S(r, E, Ω, t).

тического уравнения (1), описывает переход движу-

щегося атома с энергией E^′ в состояние с энергией

Система уравнений (6), (7) совместно с выражени-

E. При этом выбитый атом получает кинетическую

ем (3) представляет собой «строгое» P₁-приближе-

энергию E^′ - E. Второй интеграл учитывает обра-

ние [14].

зование выбитого атома с энергией E, когда движу-

Несмотря на использование довольно сильного

щийся атом перешел из состояния с энергией E^′ в

упрощающего предположения (4), решение системы

состояние с энергией E^′ - E. Если второй интеграл

(6), (7) остается достаточно сложной задачей, требу-

в правой части уравнения (1) не учитывать, то по-

ющей дальнейших упрощений. Следующим прибли-

лучим обычное уравнение замедления частиц [14].

жением, значительно облегчающим решение постав-

Решение кинетического уравнения

(1) будем

ленной задачи, является отбрасывание производной

определять в P₁-приближении, предполагая, что

по времени от тока частиц в уравнении (7) (подроб-

в разложении функции распределения в ряд по

ное обсуждение см. в [14]) и использование транс-

сферическим гармоникам относительно вектора

портного приближения [14], основанного на предпо-

Ω можно ограничиться лишь двумя первыми

ложении, что можно пренебречь изменением энер-

членами [14]:

гии частиц за счет первого углового момента инди-

катрисы рассеяния, т. е. что можно положить

Φ(r, E, Ω, t) =

[Φ₀(r, E, t) + 3Ω · Φ₁(r, E, t)] . (4)

4π

P₁(E^′ → E) = μ_lδ(E - E^′),

(10)

Здесь функции Φ₀(r, E, t) и Φ₁(r, E, t) представляют

собой поток и ток частиц:

где μ_l — средний косинус угла рассеяния частицы

∫

в лабораторной системе координат (в нашем случае

Φ₀(r, E, t) = dΩ Φ(r, E, Ω, t),

μ_l = 2/3, см. (2)).

∫

(5)

При использовании перечисленных предположе-

Φ₁(r, E, t) = dΩ ΩΦ(r, E, Ω, t).

ний второй интеграл в правой части уравнения (7)

обращается в нуль, и мы получаем

Возможность и оправданность этого приближения

подробно проанализированы в [14].

Φ₁(r, E, t) = -

∇Φ₀(r, E, t) +

Подставив выражение (4) в уравнение (1) и про-

3Σ_tr(E)

интегрировав полученное уравнение по dΩ с весом

S₁(r, E^′, t),

(11)

1 и Ω, получим систему уравнений для определения

Σ_tr(E)

функций Φ₀(r, E, t) и Φ₁(r, E, t):

где Σ_tr(E) = (1 - μ_l)Σ(E) — транспортное сечение.

1 ∂

В случае точечного импульсного изотропного мо-

Φ₀(r, E, t)+div Φ₁(r, E, t)+Σ(E)Φ₀(r, E, t) =

v ∂t

ноэнергетического источника,

∫

= dE^′Σ(E^′)P₀(E^′ → E)Φ₀(r, E^′, t)+ dE^′Σ(E^′) ×

N₀

S(r, E, Ω, t) =

δ(r)δ(t)δ(E - E₀)

(12)

4π

× P₀(E^′ → E^′ - E)Φ₀(r, E^′, t) + S₀(r, E, t),

(6)

(N₀ — число ПВА), с которым мы будем иметь дело

в дальнейшем, функции S₀ и S₁

принимают вид

1 ∂

Φ₁(r, E, t)+

∇Φ₀(r, E, t)+Σ(E)Φ₁(r, E, t) =

S₀(r, E, t) = N₀δ(r)δ(t)δ(E - E₀),

v ∂t

∫

(13)

S₁(r, E, t) = 0,

= dE^′Σ(E^′)P₁(E^′ → E)Φ₁(r, E^′, t)+ dE^′Σ(E^′) ×

а соотношение (11) совпадает с известным законом

× P₁(E^′ → E^′ - E)Φ₁(r, E^′, t) + S₁(r, E, t),

(7)

Фика.

389

Е. В. Метелкин, В. А. Акатьев, В. И. Шмырев, Е. Ю. Барышева

ЖЭТФ, том 156, вып. 3 (9), 2019

Подставляя соотношение (11) в уравнение (6)

Выделим из уравнения (17) член, описывающий

и учитывая (13), получим кинетическое уравнение

нерассеянное излучение:

для определения нестационарного пространствен-

но-энергетического распределения потока замедля-

N₀δ(E - E₀)

Ψ(p, k, E) =

Ψ₀(p, k, E) +

(18)

ющихся атомов с учетом их размножения:

k²

1 ∂

v₀Σ

3ΣΣ_tr

Φ₀(r, E, t) -

ΔΦ₀(r, E, t) +

v ∂t

3Σ_tr

∫

Подставив (18) в (17), найдем

+ Σ(E)Φ₀(r, E, t) = dE^′Σ(E^′)P₀(E^′ → E) ×

(

)

∫

k²

× Φ₀(r, E^′, t) + dE^′Σ(E^′)P₀(E^′ → E^′ - E)×

Ψ₀(p, k, E) =

vΣ

3ΣΣ

× Φ₀(r, E^′, t) + N₀δ(r)δ(t)δ(E - E₀).

(14)

2N₀

(

k²

E₀

v₀Σ

3ΣΣ_tr

3. РЕШЕНИЕ КИНЕТИЧЕСКОГО

УРАВНЕНИЯ

∫

dE^′

Рассматривая сферически-симметричное рассея-

Ψ₀(p, k, E^′).

(19)

ние в системе центра масс и используя (3), уравне-

E^′

ние (14) можно привести к следующему виду:

∂

Учитывая, что сечение рассеяния постоянно

Ψ(r, E, t) -

ΔΨ(r, E, t)+Ψ(r, E, t) =

vΣ ∂t

3ΣΣ_tr

(Σ(E) = const), и дифференцируя уравнение (19)

∫E0

по энергии, получим дифференциальное уравнение

dE^′

для функции

Ψ₀(p, k, E):

Ψ(r, E^′, t) + N₀δ(r)δ(t)δ(E - E₀),

(15)

E^′

где Ψ(r, E, t) = ΣΦ₀(r, E, t) — плотность соударений.

Ψ₀(p, k, E) =

Применяя к уравнению

(15) преобразование

Лапласа по времени и преобразование Фурье по про-

2vΣ

(

) Ψ₀(p, k, E).

(20)

странственным координатам,

k²

∞

∫∞

∫∫

∫

vΣ

3ΣΣ_tr

Ψ(p, k, E) = dt e^-pt

dx dy dz ×

-∞

Решение этого уравнения должно (см. (19)) удовлет-

× exp(-ik · r)Ψ(r, E, t),

(16)

ворять следующему «начальному» условию:

получим

2N₀

(

)

Ψ₀(p, k, E₀) =

(

)₂ .

(21)

k²

Ψ(p, k, E) =

E₀

vΣ

3ΣΣ_tr

v₀Σ

3ΣΣ_tr

∫E0

dE^′

Ψ(p, k, E^′) + N₀δ(E - E₀).

(17)

Решение уравнения (20) с учетом начального

E^′

условия (21) имеет следующий вид:

)∕(

)

[

(

)](3- k²

k²

3ΣΣ_tr

k²

p+v₀Σ

2N₀

3ΣΣ_tr

Ψ₀(p, k, E) ==

Σ²v₀v

)∕(

) .

(22)

E₀

[

(

)](5- k2

k²

3ΣΣ_tr

k²

p+vΣ

3ΣΣ_tr

Отсюда найдем функцию распределения

f (p, k, t):

390

ЖЭТФ, том 156, вып. 3 (9), 2019

Нестационарное пространственно-энергетическое распределение.. .

)∕(

)

[

(

)](3- k²

k²

3ΣΣ_tr

k²

p+v₀Σ

2N₀

3ΣΣ_tr

N₀δ(E - E₀)

f (p, k, E)

Σv₀

)∕(

)

(

(23)

E₀

[

(

)]⁽

5-k23ΣΣtr

1+k2

k²

3ΣΣ_tr

k²

p+v₀Σ

p+vΣ

3ΣΣ_tr

где

f =

^Ψ/vΣ.

4. АНАЛИЗ ПОЛУЧЕННОГО РЕШЕНИЯ

Воспользовавшись, как и прежде, выражением (23)

получим

В случае стационарного, равномерно распреде-

ленного в пространстве монохроматического источ-

∫

ника положим в выражении (23) p = k = 0 и най-

E(p) = dE

f (E, p, k = 0) =

N₀E₀,

(29)

дем стационарное распределение атомов с учетом их

размножения (без учета нерассеянного излучения):

откуда вытекает, что полная энергия движущихся

)₂

2N₀

⁽E₀

атомов со временем не изменяется и равна началь-

Ψ(E) = vΣf(E) =

(24)

E₀

ной:

что совпадает с аналогичным результатом рабо-

E(t) = N₀E₀ = const.

(30)

ты [7].

Проанализируем законы сохранения. Найдем из-

Из соотношения (30) следует, что, несмотря на

менение со временем полного числа движущихся

рост числа движущихся атомов, их полная энергия

атомов:

со временем сохраняется. Это объясняется тем, что

∞

мы не учитываем энергию связи покоящихся ато-

∫∫

∫

мов. В таком случае энергия, с которой начал дви-

N (t) =

dx dy dz dE f(r, E, t).

(25)

гаться после соударения покоящийся атом, целиком

-∞

равна энергии, переданной ему движущимся ато-

Для этого получим сначала с помощью соотношения

мом.

(23) образ Лапласа искомой функции:

Из полученных соотношений (27) и (30) прове-

дем оценку промежутка времени, в течение которо-

∫E0

го результат (23) будет справедлив без учета энергии

^Ń (p) = dE

f (E, p, k = 0) =

связи атомов в твердом теле (ε_d). Поскольку на соз-

дание одного выбитого атома тратится энергия ε_d,

)

⁽1

v₀Σ

v²⁰Σ²

с ростом времени затраченная на выбивание атомов

=N₀

(26)

p²

3p³

энергия E_d возрастает (см. (27)):

Применяя к (26) обратное преобразование Лапласа

E_d ≈

N₀τ²ε_d.

(31)

[15], получим, как и следовало ожидать, что число

движущихся атомов в каскаде со временем возрас-

В таком случае результат (23) будет справедлив и

тает:

(

)

при учете энергии связи до тех пор, пока величина

N (t) = N₀

1+τ +

τ²

(27)

(31) будет значительно меньше величины (30), т. е.

при временах (см. также [13])

где τ = v₀Σt — безразмерное время. В данном слу-

√

6E₀

чае этот рост будет продолжаться неограниченно,

τ ≪

(32)

поскольку мы не учитываем энергию связи атомов

ε_d

в твердом теле.

Положив в (23) k = 0 и применив далее к полу-

Теперь найдем изменение со временем полной

ченному выражению обратное преобразование Ла-

энергии движущихся атомов:

пласа, найдем нестационарное энергетическое рас-

∫∫

∞

∫

пределение каскада атомных столкновений в случае

E(t) =

dx dy dz dE Ef(r, E, t).

(28)

равномерно распределенного в пространстве источ-

ника в универсальном безразмерном виде:

−∞

391

Е. В. Метелкин, В. А. Акатьев, В. И. Шмырев, Е. Ю. Барышева

ЖЭТФ, том 156, вып. 3 (9), 2019

При использовании обратного преобразования

Фурье будем предполагать, что основной вклад в

f( , )

интеграл дают малые значения k² (k2 < 3ΣΣtr)

4000

[14]. Далее, рассматривая случай v ≪ v₀ и пола-

гая v₀Σt ≫ 1, воспользуемся асимптотическим пред-

3000

ставлением гипергеометрической функции [16]:

2000

1000

Γ(γ)

F₁(α; γ; z) ≈

z^α-γe^z,

(35)

0.10

Γ(α)

0.08

0.06

10 20 30 40

0.04

где Γ(x) — гамма-функция [16].

50 60 70

0.02

Учитывая сказанное выше и воспользовавшись

80 90 100

выражением (35), найдем

Рис. 1. Функция распределения замедляющихся атомов

от однородно распределенного в пространстве источни-

⎡⎛

⎞

⎤

ка с учетом их размножения (в пределах 0 ≤ τ ≤ 100,

k²

(

0.01 ≤ ε ≤ 0.1)

⎢⎜5+

⎟

)⎥

3ΣΣ_tr

k²

F₁

⎢⎜

⎟;2; (v0-v)Σt

⎥

⎣⎝

⎠

⎦^≈

k²

3ΣΣ_tr

{

3ΣΣ_tr

[(

(

)(

)

f (E, t) = 2τ

√ε⁾ τ^] +

k²

≈ (v₀Σt)31-3

3ΣΣ_tr

1+3

}

3ΣΣ_tr

[(

[

(

)]

√ε⁾ τ]2 +

√ε⁾ τ]3

e^-τ

√ε +

× exp (v₀ - v)Σt

(36)

3ΣΣ

N₀

e^-τ δ(ε - 1),

(33)

E₀

поскольку

где ε = E/E₀ — безразмерная энергия, f^′ = fE₀/N₀.

⎛

⎞

k²

Это выражение совпадает с точным решением, по-

[ (

)]

⎜5+3ΣΣtr

⎟

k²

⎜

⎟

лученным ранее в работе [13], где были проведены

Γ 5

≈ Γ(5),

⎝

⎠^≈

k²

5 3ΣΣ_tr

его подробный анализ и сопоставление с результа-

3ΣΣ_tr

том, не учитывающим процесс размножения замед-

ляющихся атомов. На рис. 1 представлена функция

(33) при E < E₀ (рассеянное излучение).

(

)

[

(

)]31- 4

k²

3 3ΣΣ_tr

k²

(v₀-v)Σt

≈

3ΣΣ_tr

5. НЕСТАЦИОНАРНОЕ

(

)(

)

k²

ПРОСТРАНСТВЕННО-ЭНЕРГЕТИЧЕСКОЕ

3ΣΣ_tr

≈ (v₀Σt)31-3

1+3

РАСПРЕДЕЛЕНИЕ КАСКАДА

3ΣΣ_tr

ЗАМЕДЛЯЮЩИХСЯ АТОМОВ

Подставив соотношение (36) в (34), получим

Применяя к первому слагаемому в выраже-

нии (23), описывающему рассеянное излучение, об-

2N₀ 1

(

ратное преобразование Лапласа по времени, полу-

f (E, t, k) =

τ⁴ exp

-τ

√ε⁾ ×

E₀

чим [15]

(

)

[

]

k²

(

[

(

)]

× 1+3

exp -

√ε+4 ln τ⁾

(37)

2N₀

k²

3ΣΣ_tr

f (E, t, k) =

v₀Σt exp -v0Σt

E₀

3ΣΣ_tr

⎡

⎤

При k = 0 выражение (37) совпадает с асимп-

k²

(

тотикой (τ ≫ 1, ε ≪ 1) нестационарного энергети-

⎢5+3ΣΣtr

k²

)⎥

⎢

⎥

×F₁

;2; (v₀-v)Σt

(34)

ческого распределения каскада атомных столкнове-

⎣

⎦

k²

3ΣΣ_tr

ний от однородно распределенного в пространстве

3ΣΣ_tr

источника (см. (33)).

где F₁(α; γ; z) — вырожденная гипергеометрическая

Применяя к (37) обратное преобразование Фу-

функция [16].

рье, получим окончательное выражение для неста-

392

ЖЭТФ, том 156, вып. 3 (9), 2019

Нестационарное пространственно-энергетическое распределение.. .

ционарного пространственно-энергетического рас-

6. АНАЛИЗ ПРОСТРАНСТВЕННОГО

пределения каскада движущихся атомов:

РАСПРЕДЕЛЕНИЯ КАСКАДА

ЗАМЕДЛЯЮЩИХСЯ АТОМОВ

2N₀ 1

(

f (E, r, t) =

τ⁴ exp

-τ

√ε⁾ ×

Проанализируем нестационарное пространствен-

E₀

⎧

⎡

⎤⎫

но-энергетическое распределение каскада замедля-

⎪

⎨

⎬

ющихся атомов (39). Исходя из сделанных предпо-

⎢

r²

⎥

⎢

−

⎥

⎣¹

⎦

ложений это выражение будет справедливо и при

^×⎪⎪

2 ξ(E, t)

ξ(E, t)

⎪

⎩

⎭

учете энергии связи атомов в узлах решетки, если

3ΣΣ_tr

(

)

ε ≪ 1 в моменты времени, лежащие в интервале

r²

exp

(см. (32))

4ξ(E, t)/3ΣΣ_tr

(38)

√

⁽4πξ(E, t))3/2

1≪τ ≪

6E₀/ε_d .

(41)

3ΣΣ_tr

На рис. 2а представлены пространственные рас-

где ξ(E, t) = τ

√ε + 4 lnτ.

пределения атомов (39) в момент времени τ = 10

Функцию (38) можно представить в универсаль-

при различных значениях энергии. Из этих резуль-

ном безразмерном виде:

татов следует, что в фиксированный момент време-

ни с уменьшением энергии число атомов в каска-

(

f^′(ε, ρ, τ) =

τ⁴ exp

-τ

√ε⁾ ×

де увеличивается. Это происходит как за счет за-

{

[

]}

медления, так и за счет размножения. Для сравне-

ρ²

× 1+

ния на рис. 2б представлены аналогичные результа-

2ξ(ε, τ)

6ξ(ε, τ)

ты без учета размножения замедляющихся атомов

[

]

exp

-ρ²/4ξ(ε, τ)

(см. (40)). В данном случае рост функции обуслов-

(39)

лен тем, что за счет замедления увеличивается чис-

[4πξ(ε, τ)]3/2

ло атомов с меньшими энергиями. Сами значения

где

функции меньше аналогичных на рис. 2а, посколь-

(

)3/2

ку размножение атомов здесь не учитывается.

E₀

f^′ = f

ξ(ε, τ) = τ

√ε + 4 lnτ,

На рис. 3а представлены пространственные рас-

N₀

3ΣΣ_tr

пределения атомов (39) при фиксированном значе-

√

нии энергии в различные моменты времени. Эти ре-

ρ=r

3ΣΣ_tr.

зультаты показывают, что число атомов с данной

Проделав вычисления, аналогичные проведен-

энергией со временем уменьшается за счет замедле-

ным выше, для нестационарного пространствен-

ния. Без учета размножения (см. (40)) наблюдается

но-энергетического распределения замедляющихся

аналогичная тенденция при значительно меньших

атомов без учета их размножения (второй интеграл

значениях самой функции распределения (рис. 3б).

в уравнении (1) равен нулю), получим следующий

Следует отметить, что результаты, приведенные

результат (см. также [14]):

на рис. 2, 3, правильно описывают функцию рас-

пределения и при учете энергии связи атомов в уз-

(

f^′n(ε, ρ, τ) =

τ² exp

-τ

√ε⁾ ×

лах решетки, так как соответствующие им значения

{

[

]}

энергии и времени удовлетворяют условию приме-

ρ²

нимости (41), сформулированному выше. Действи-

2ξ₀(ε, τ)

6ξ₀(ε, τ)

[

]

тельно, при E₀

≈ 1 МэВ и ε_d ≈ 15 эВ имеем

√

exp

-ρ²/4ξ0(ε, τ)

6E₀/ε_d ≈ 6 · 10².

(40)

[4πξ₀(ε, τ)]3/2

7. ВЫВОДЫ

где ξ₀(ε, τ) = τ

√ε + 2 lnτ.

Следует отметить, что оба результата, (39) и

На основе решения кинетического уравнения

(40), представляют собой произведение нестацио-

Больцмана получена функция распределения, опи-

нарной функции распределения в среде с равномер-

сывающая нестационарное пространственно-энер-

но распределенным по пространству источником и

гетическое распределение каскада замедляющихся

нормированного на единицу множителя, учитываю-

атомов с учетом их размножения (см. (38), (39)).

щего пространственную зависимость.

При решении предполагалось, что рассеяние движу-

393

Е. В. Метелкин, В. А. Акатьев, В. И. Шмырев, Е. Ю. Барышева

ЖЭТФ, том 156, вып. 3 (9), 2019

f , 10^-1

f , 10^-2

= 0.001

0.01

0.1

Рис. 2. Пространственные распределения атомов в момент времени τ = 10 при энергиях ε =

0.1,

0.01,

0.001 c учетом (а)

и без учета (б) их размножения

f , 10^-2

f , 10^-3

2.5

2.8

2.4

2.0

= 10

1.5

1.6

1.2

1.0

0.8

0.5

0.4

Рис. 3. Пространственные распределения атомов при энергии ε = 0.1 в моменты времени τ = 10, 20, 30 с учетом (а) и

без учета (б) их размножения

щихся атомов является упругим и сферически-сим-

тывалась. На основе законов сохранения был сфор-

метричным в системе центра инерции, а сечение вза-

мулирован критерий (41), указывающий, при каких

имодействия является постоянной величиной. Кро-

временах и энергиях этот результат будет справед-

ме того, предполагалось, что твердое тело состоит из

лив и при учете энергии связи атомов в узлах ре-

атомов одного сорта, энергия связи которых не учи-

шетки.

394

ЖЭТФ, том 156, вып. 3 (9), 2019

Нестационарное пространственно-энергетическое распределение.. .

Проанализированы особенности, присущие

7. Е. В. Метелкин, А. И. Рязанов, Е. В. Семенов,

функции распределения, имеющие общий характер.

ЖЭТФ 134, 469 (2008).

Кроме того, проведено сопоставление этой функции

8. A. I. Ryazanov, E. V. Metelkin, and E. V. Semenov,

распределения с аналогичным результатом (40), не

J. Nucl. Mater. 386-388, 132 (2009).

учитывающим размножение атомов, и отмечены их

характерные различия, обусловленные ростом чис-

9. А. А. Александров, В. А. Акатьев, Е. В. Метел-

ла атомов в каскаде за счет размножения. Следует

кин и др., Вестник МГТУ им. Н. Э. Баумана, сер.

отметить, что на основе полученных результатов

Естественные науки 1, 27 (2019).

можно оценивать точность различных приближен-

10. J. Lindhard, V. Nielsen, and M. Scharff, Mat. Fys.

ных решений.

Medd. Dan. Vid. Selsk. 36, 1 (1968).

11. В. А. Акатьев, Е. В. Метелкин, А. М. Савинов,

ЛИТЕРАТУРА

Атомная энергия 122, 295 (2017).

1. К. Лейман, Взаимодействие излучения с твер-

12. Е. В. Метелкин, М. В. Лебедева, А. В. Черняев,

дым телом и образование элементарных дефек-

Атомная энергия 125, 184 (2018).

тов, Атомиздат, Москва (1979).

13. А. А. Александров, В. А. Акатьев, Е. В. Метел-

2. С. Вас Гэри, Основы радиационного материало-

кин и др., Вестник МГТУ им. Н. Э. Баумана, сер.

ведения. Металлы и сплавы, Техносфера, Москва

Естественные науки (2019), в печати.

(2014).

14. А. И. Исаков, М. В. Казарновский, Ю. А. Мед-

3. A. I. Ryazanov and E. V. Metelkin, Radiat. Effects

ведев, и др., Нестационарное замедление нейтро-

and Defects in Solids 52, 15 (1980).

нов. Основные закономерности и некоторые при-

ложения, Наука, Москва (1984).

4. Y. Sato, S. Kojimo, T. Yoshiie et al., J. Nucl. Mater.

179-181, 901 (1991).

15. Г. Бейтман, А. Эрдейи, Таблицы интегральных

5. Y. Sato, T. Yoshiie, and M. Kiritani, J. Nucl. Mater.

преобразований, т. 1, Наука, Москва (1969).

191-194, 1101 (1992).

16. И. С. Градштейн, И. М. Рыжик, Таблицы интегра-

6. Е. В. Метелкин, А. И. Рязанов, Атомная энергия

лов, сумм, рядов и произведений, Наука, Москва

83, 183 (1997).

(1971).

395