ЖЭТФ, 2019, том 156, вып. 3 (9), стр. 396-406
© 2019
РАССЕЯНИЕ СВЕТА ПРОФИЛИРОВАННОЙ ГРАНИЦЕЙ
ГИПЕРБОЛИЧЕСКОЙ СРЕДЫ
Н. А. Жароваa*, А. А. Жаровb, А. А. Жаров, мл.b
a Институт прикладной физики Российской академии наук
603950, Нижний Новгород, Россия
b Институт физики микроструктур Российской академии наук
603950, Нижний Новгород, Россия
Поступила в редакцию 5 марта 2019 г.,
после переработки 2 апреля 2019 г.
Принята к публикации 2 апреля 2019 г.
Проведено численное исследование особенностей рассеяния падающего излучения на периодически мо-
дулированной границе среды гиперболического типа. Найдена оптимальная (на определенном классе
функций) — пилообразная — форма профиля, обеспечивающая минимум отражения в широком диапа-
зоне длин волн. Показано, что при определенной ориентации оптических осей гиперболической среды на
пилообразной границе возникают «горячие точки», отвечающие субволновой локализации поля. Прове-
дено обобщение численного метода расчета полей, основанного на применении второго тождества Грина.
DOI: 10.1134/S0044451019090025
В видимом и ближнем ИК-диапазонах ГС мо-
жет быть реализована, например, как метаматери-
ал с элементарной ячейкой специального дизайна
1. ВВЕДЕНИЕ
(металло-диэлектрическая планарная нанострукту-
ра либо решетка металлических нанопроволок или
Возникший в последние годы большой интерес
металлических наночастиц с анизотропной поляри-
исследователей к так называемым гиперболическим
зуемостью в диэлектрической матрице).
средам (ГС) [1-7] обусловлен их необычными и по-
лезными для приложений электромагнитными свой-
Гиперболический тип дисперсии метаматериала
ствами. ГС — это анизотропная среда, которая ха-
достигается лишь при достаточно высокой объемной
рактеризуется изочастотной поверхностью гипер-
доле металла в композите, что неизбежно приводит
болического типа, а не эллипсоидальной, как для
к омическим потерям. Поглощение излучения ста-
диэлектрических анизотропных сред. Гиперболиче-
новится существенным для мелкомасштабных мод,
ский характер изочастотной поверхности (поверхно-
фазовая скорость которых направлена вдоль обра-
сти волновых векторов) обусловлен разными знака-
зующей резонансного конуса. Для оптической лито-
ми компонент тензора диэлектрической проницае-
графии и создания изображений с субволновым раз-
мости вдоль и поперек оси анизотропии.
решением омические потери нежелательны, с дру-
Уникальные свойства ГС могут найти множе-
гой стороны, сильное поглощение в гиперболиче-
ство приложений, среди которых отрицательная ре-
ских метаматериалах может быть использовано для
фракция [8, 9], создание субволновых изображений
дизайна поглощающих покрытий. В работе [21] был
[10-15], локализация света в широком частотном
предложен дизайн поглощающего покрытия на ос-
диапазоне [16,17]. Высокая плотность фотонных со-
нове неоднородного гиперболического метаматериа-
стояний в ГС [18-20] обеспечивает эффективный из-
ла. Оказывается, что почти полное поглощение све-
лучательный теплообмен [4-6], что может использо-
та в широкой полосе частот видимого спектра мож-
ваться в дизайне наноразмерных устройств нагре-
но реализовать в тонком слое гиперболического ме-
ва/охлаждения.
таматериала при условии плавно меняющейся ори-
ентации оптической оси от параллельной к нор-
* E-mail: zhani@appl.sci-nnov.ru
мальной по отношению к границе раздела. Однако
396
ЖЭТФ, том 156, вып. 3 (9), 2019
Рассеяние света профилированной границей. . .
при изготовлении такого покрытия трудно на на-
E
номасштабе контролировать заданным образом ме-
Hz
kinc
няющееся направление оптической оси метаматери-
Lx = 2 /
ала (например, ориентацию металлических прово-
inc
A
лочных включений).
Идеальный поглотитель должен обеспечивать
X
y
минимальное отражение излучения. Одним из воз-
можных способов снижения коэффициента отраже-
Y
ния является структурирование поверхности погло-
x
щающего материала, иными словами, профилирова-
ние его границы раздела. В данной работе мы изу-
Рис. 1. (В цвете онлайн) Геометрия задачи: периодически
модулированная граница разделяет свободное пространст-
чаем особенности рассеяния падающего электромаг-
во (вверху) и гиперболическую среду (внизу). Рассеяние
нитного излучения слоем ГС с периодически про-
падающего излучения на такой границе зависит от фор-
филированной границей. Рассматривается влияние
мы профиля, периода модуляции Lx = 2π/κ и амплиту-
формы профиля, а также амплитуды и периода мо-
ды модуляции A. Кроме того, на результат рассеяния су-
дуляции на коэффициент отражения.
щественно влияет ориентация оси анизотропии среды, ко-
торая определяется ориентацией металлических проволок
в так называемой «проволочной среде» или направлени-
2. ПОСТАНОВКА ЗАДАЧИ
ем нормали к слоям в слоистом металло-диэлектрическом
метаматериале (схематически совпадает с направлением
Дисперсионное уравнение для электромагнитно-
штриховки и направлена под углом θ к вертикали). При
го излучения в одноосной анизотропной среде,
θ = 0 тензор диэлектрической проницаемости диагона-
(
)
лен в системе координат (X, Y ), где X = x cos θ + y sin θ,
(
)
k2∥
k2⊥
Y = y cosθ - xsinθ
k2∥ + k2⊥ - ε⊥k2
0
+
-k2
0
= 0,
ε⊥
ε∥
описывает две взаимно ортогональные поляризации
Линейная трансформация может оказаться суще-
поля, отвечающие двум собственным (нормальным)
ственной, в частности, при рассеянии электромаг-
модам среды — обыкновенной и необыкновенной.
нитных волн в ГС с гофрированной поверхностью.
Здесь индексы ∥ и ⊥ определяют направления вдоль
Учет эффектов линейной трансформации чрезвы-
и поперек оси анизотропии, а k∥,⊥ и ε∥,⊥ обозначают
чайно усложняет аналитические и численные рас-
проекции волнового вектора на эти направления и
четы процессов рассеяния излучения. Значительные
соответствующие компоненты тензора диэлектриче-
трудности возникают также при оптимизации фор-
ской проницаемости.
мы гофрировки в дизайне поглотителя. Поэтому ни-
Гиперболическая среда характеризуется разны-
же мы ограничимся изучением рассеяния оптиче-
ми знаками продольной и поперечной компонент ди-
ского излучения двумерно-гофрированной границей
электрического тензора, ε∥ε⊥ < 0. Если ε⊥ > 0 и
гиперболической среды в двумерной постановке, т.е.
ε∥ < 0, то изочастотная поверхность является сфе-
будем полагать, что все поля зависят лишь от коор-
рой для обыкновенных волн и представляет собой
динат x, y и оптическая ось также лежит в плоскос-
двухполостный гиперболоид вращения для необык-
ти (x, y).
новенных волн. В случае ε∥ > 0 и ε⊥ < 0 среда
оказывается непрозрачной для обыкновенных волн,
В этом случае линейная трансформация обыкно-
распространяться могут лишь необыкновенные вол-
венной (Ho = x0Hx + y0Hy, Eo = z0Ez, TE-поляри-
ны, и изочастотная поверхность для них имеет фор-
зация) и необыкновенной (Ee = x0Ex + y0Ey, He =
му однополостного гиперболоида вращения. Во всех
= z0Hz, TM-поляризация) волн на границе отсут-
этих случаях осевая симметрия изочастотной по-
ствует. В дальнейшем мы ограничимся физически
верхности определяется осью анизотропии среды.
более содержательным случаем излучения TM-по-
ляризации.
В силу ортогональности нормальные волны в од-
нородной среде являются независимыми. Однако в
Геометрия задачи иллюстрируется на рис. 1. Па-
неоднородной среде (например, при наличии гра-
дающее из свободного пространства излучение рас-
ниц раздела) ортогональность нормальных мод мо-
сеивается на границе гиперболической среды, кото-
жет нарушиться, что приводит к их линейной транс-
рая характеризуется формой профиля, периодом Lx
формации, сопровождающейся обменом энергией.
(можно также ввести характерное волновое число
397
Н. А. Жарова, А. А. Жаров, А. А. Жаров, мл.
ЖЭТФ, том 156, вып. 3 (9), 2019
P = -1.2
модуляции профиля κ = 2π/Lx) и амплитудой A
модуляции. Для случая TM-поляризации магнитное
-0.2
поле H направлено по оси z, а у электрического по-
0.8
ля есть компоненты Ex, Ey.
1.8
Гиперболическая среда описывается диэлектри-
2.8
ческим тензором
(
)
3.8
ε⊥
0
ε=
0
ε∥
с компонентами ε⊥, ε∥ (ε∥ε⊥ < 0 ) в направлении
оптических осей. Если направление оптических осей
совпадает с осями x, y, то тензор εв этой системе ко-
Рис. 2. (В цвете онлайн) Форма профиля yB (xB) перио-
ординат диагонален, εxx = ε⊥, εyy = ε∥, и уравнение
дической границы (элементарная ячейка) для различных
для магнитного поля H в такой среде имеет вид
значений параметра P
1
∂2H
1
∂2H
+
+ k20H = 0,
Граница xB (τ), yB (τ), разделяющая свободное
εyy ∂x2
εxx ∂y2
пространство и ГС, является периодической функ-
где k0 = ω/c — волновое число в свободном прост-
цией параметра τ (длина вдоль границы) и харак-
ранстве. При этом компоненты электрического поля
теризуется масштабом вдоль границы Lx, амплиту-
выражаются как
дой модуляции A и формой профиля. В дальней-
шем мы будем полагать, что период модуляции Lx
1
∂H
1
∂H
Ex = -
,
Ey =
меньше вакуумной длины волны, так что все выс-
ik0εxx ∂y
ik0εyy ∂x
шие пространственные гармоники рассеянного поля
В случае, когда оптические оси не совпадают с
являются неизлучающими и отражение от границы
осями x, y и повернуты относительно них на угол θ
оказывается зеркальным.
(см. рис. 1), компоненты диэлектрического тензора
Параметрическое задание формы профиля поз-
(в осях x, y) становятся функциями θ:
воляет рассматривать в том числе и неоднозначные
функции yB(xB) (см. рис. 2). Выбрав для анали-
εxx = ε⊥ cos2 θ+ε∥ sin2 θ, εyy = ε⊥ sin2 θ+ε∥ cos2 θ,
за конкретную зависимость xB(τ), yB(τ) с характер-
ным масштабом L0 и амплитудой A0, можно изме-
εxy = εyx = (ε⊥ - ε∥)sinθ cosθ.
нять период и амплитуду профиля простым мас-
Соответственно модифицируются также уравнение
штабированием, xB (τ) → (Lx/L0)xB (τ), yB(τ) →
для H:
→ (A/A0)yB(τ). Задачу выбора формы также мож-
но свести к перебору значений некоторого парамет-
∂2H
∂2H
∂2H
ра P , задающего зависимости xB(τ, P ), yB(τ, P ) ма-
εxx
+ 2εxy
+εyy
+ ε∥ε⊥k20H = 0,
∂x2
∂x∂y
∂y2
тематической формулой. В дальнейшем мы исполь-
и связь компонент электрического поля с магнит-
зуем следующий алгоритм, параметрически задаю-
ным:
щий профиль xB, yB в виде функции τ:
(
)
Fx(τ, P)
Fy(τ)
1
∂H
∂H
xB =
,
yB =
,
(1)
Ex = -
εyy
-εxy
,
Fx(3π/2, P)
Fy(3π/2)
ik0ε∥ε⊥
∂y
∂x
где
(
)
1
∂H
∂H
Ey = -
εxy
-εxx
∫
τ
ik0ε∥ε⊥
∂y
∂x
P sin(2τ)
Fx(τ, P ) =
cosα(τ′)dτ′ -
,
π
Следует заметить, что в такой постановке эф-
−π/2
фект рассеяния симметричен по отношению к выбо-
τ
(2)
∫
ру знака компонент тензора проницаемости ε∥ и ε⊥
Fy(τ) =
sinα(τ′)dτ′,
и, соответственно, к типу возникающей изочастот-
-π/2
ной поверхности. Действительно, изменение знаков
ε∥ и ε⊥ на противоположные отвечает повороту оп-
α = -0.4πcosτ и элементарная ячейка профиля по-
тической оси на π/2.
лучается при изменении τ от -π/2 до 3/2π. Управ-
398
ЖЭТФ, том 156, вып. 3 (9), 2019
Рассеяние света профилированной границей. . .
ляющий параметр P меняет форму профиля от по-
y/
а
y/
б
y/
в
2.2
чти пилообразной к синусоидальной и до профиля,
2.4
1.8
1.0
1.0
1.0
напоминающего греческую букву Ω. На рис. 2 при-
2.0
2.2
1.6
ведены в качестве иллюстрации кривые yB(xB) для
2.0
1.8
набора значений P .
0.5
0.5
0.5
1.4
1.8
1.6
Перебирая различные значения параметра P,
1.2
1.6
масштаба элементарной ячейки вдоль границы Lx и
1.4
1.0
амплитуды профиля A, можно найти такое их соче-
0
1.4
0
0
1.2
тание, которое обеспечивает слабое отражение пада-
1.2
0.8
1.0
ющего излучения от границы ГС. Дополнительным
1.0
0.6
–0.5
-0.5
-0.5
параметром может служить также угол θ ориента-
0.8
0.8
0.4
ции главных (оптических) осей ГС по отношению к
0.6
0.6
осям x, y.
–1.0
-1.0
-1.0
0.2
0.4
0.4
Задача об отражении падающего излучения от
полупространства ГC с профилированной границей
-0.2 0
0.2
-0.2 0
0.2
-0.2 0
0.2
x/
x/
x/
может быть решена численно методом конечных
элементов (FEM). Однако при расчетах с помощью
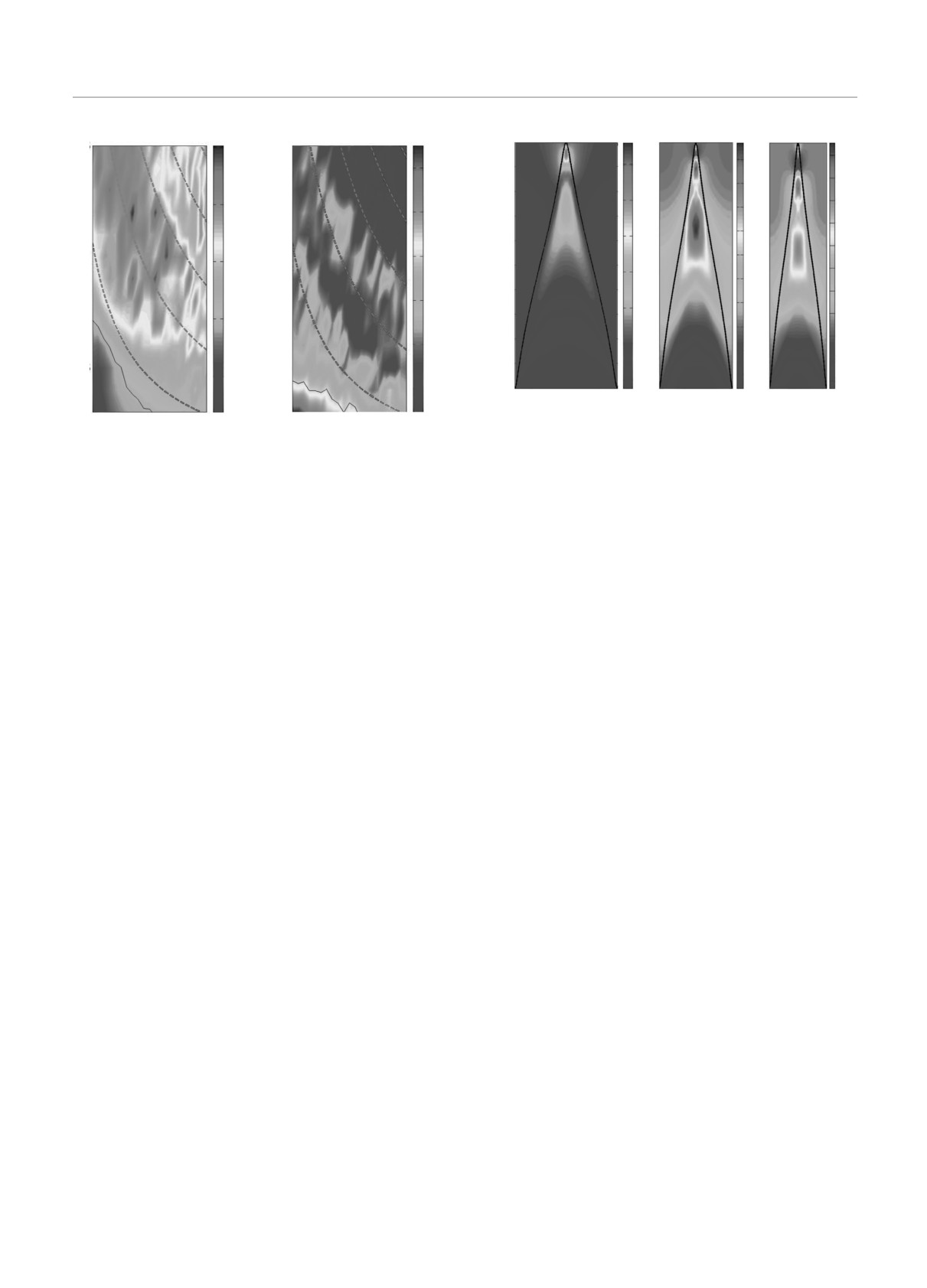
Рис. 3. (В цвете онлайн) Распределение модуля магнит-
доступного коммерческого FEM-кода мы столкну-
ного поля |H(x, y)| (показан один период структуры) при
лись, в частности, с тем, что в нем нет опции за-
нормальном падении плоской волны Hinc = exp(-ik0y) на
дания периодических по x граничных условий, при-
периодически модулированную границу гиперболической
чем от границ расчетного интервала происходит за-
среды. Амплитуда модуляции A = 0.8λ0, период структу-
метное отражение излучения, что вносит ошибки в
ры в x-направлении λ0/1.5, (вакуумная) длина волны из-
лучения λ = λ0 = 0.6 мкм, угол ориентации оптической
результаты расчета коэффициента отражения. Бо-
оси ГС θ = 0, параметр P , контролирующий форму моду-
лее удобным оказался поэтому другой подход, осно-
ляции (см. формулу (1)), P = -1.2 (а), 0.5 (б), 3.5 (в).
ванный на использовании второго тождества Грина
Рассчитанный для этих трех вариантов коэффициент от-
(Green’s second identity), подробное описание кото-
ражения R = 0.01 (а), 0.057 (б), 0.148 (в)
рого дается в Приложении.
трическую матрицу с металлическими проволочны-
3. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО
ми включениями. В приближении эффективной сре-
ИССЛЕДОВАНИЯ
ды компоненты диэлектрического тензора ε вдоль
) находятся по фор-
проволок (ε∥) и поперек них (ε⊥
Тестирование метода и соответствующей расчет-
мулам гомогенизации [22]:
ной программы проводилось для предельных слу-
εM(1 + ρM ) + εD(1 - ρM )
чаев (1) слабой модуляции границы, (2) одинаковых
ε∥ = εD
,
диэлектрических характеристик двух сред и (3) ма-
εD(1 + ρM ) + εM (1 - ρM )
(3)
лого характерного периода модуляции, когда при-
ε⊥ = εMρM + εD(1 - ρM),
менимо приближение эффективной среды. Расчет-
где εM — диэлектрическая проницаемость метал-
ные и теоретические значения коэффициента отра-
ла, εD — проницаемость диэлектрической матрицы,
жения совпали в этих случаях с точностью порядка
ρM — объемная доля металла в составе композита.
1% (ошибка обусловлена дискретизацией вычисле-
Далее мы используем для расчетов параметры стек-
ний)1). Кроме того, проводилось сравнение распре-
ла (εD = 2.1590) и серебра с объемной долей ρM =
деления полей, полученного этим методом и рассчи-
= 0.25. Дисперсионная зависимость проницаемости
танного стандартной FEM-программой, и это срав-
серебра εM(λ) бралась из базы данных [23]. Для ва-
нение показало хорошее совпадение.
куумной длины волны излучения λ0 = 0.6 мкм вели-
Параметры гиперболической среды, использо-
чина εM = -15.9822 + 0.5899i, и расчеты по форму-
ванные в численном моделировании, были найдены
лам (3) дают значения ε∥ = -2.3763 + 0.1475i, ε⊥ =
для метаматериала, представляющего собой диэлек-
= 4.2660 + 0.0318i.
Все последующие рисунки иллюстрируют ре-
1) Коэффициент отражения R вычислялся как R
=
зультаты расчета рассеяния излучения на периоди-
= Psct/Pinc, где Pinc (Psct) — интеграл по периоду Lx от
y-компоненты вектора Пойнтинга падающего (рассеянного)
чески профилированной границе ГС с помощью ме-
излучения.
тода, описанного в Приложении. В качестве приме-
399
Н. А. Жарова, А. А. Жаров, А. А. Жаров, мл.
ЖЭТФ, том 156, вып. 3 (9), 2019
а
б
в
/2
/2
y/
y/
y/
0
а
0
б
5.5
5.5
2.0
1.0
5.5
1.0
3.0
1.0
0.26
0.9
1.8
5.0
5.0
5.0
0.24
1.6
0.8
4.5
2.5
4.5
4.5
0.5
0.5
0.5
0.22
4.0
1.4
0.7
2.0
0.20
3.5
4.0
4.0
1.2
0.6
0.18
0
3.0
0
0
1.0
3.5
3.5
1.5
0.5
2.5
0.16
0.8
3.0
3.0
0.4
2.0
0.14
1.0
-0.5
–0.5
-0.5
0.6
1.5
0.3
2.5
0.12
2.5
0.4
1.0
0.5
0.10
0.2
0.2
2.0
2.0
–1.0
0.5
-1.0
-1.0
0.08
0.1
–0.2 0
0.2
-0.2 0
0.2
-0.2 0
0.2
–1
0
1
2
3
4
-1
0
1
2
3
x/
x/
x/
P
P
Рис. 4. (В цвете онлайн) To жe, что на рис. 3, но угол ори-
Рис. 5. (В цвете онлайн) Коэффициент отражения от про-
ентации оптической оси ГС θ = π/2. Рассчитанный для
филированной границы как функция параметра формы P
этих трех вариантов коэффициент отражения R = 0.14 (а),
и нормированного волнового числа модуляции κλ0/2π =
0.22 (б), 0.84 (в)
= (Lx/λ0)-1. Угол поворота осей анизотропии θ = 0 (а),
π/2 (б), длина волны излучения λ = λ0 = 0.6 мкм, ампли-
туда модуляции A = 0.3λ0 = 0.18 мкм. Данные усреднены
ра на рис. 3 приведены рассчитанные распределе-
по углам падения φinc = 0 : 80◦. Штриховые линии отве-
чают значению 〈R〉 = 0.2
ния поля для трех различных типов профиля гра-
ницы гиперболической среды при нормальном па-
ется для пилообразного профиля, а максимальное —
дении излучения. Для этих вариантов расчета ва-
для Ω-профиля.
куумная длина волны λ = λ0 = 0.6 мкм, угол ори-
Следует отметить, что при нормальном падении
ентации оптической оси ГС θ = 0. Коэффициент от-
ражения плоской волны Hinc = exp(-ik0y) оказы-
на плоскую границу гиперболическая среда ведет
себя как диэлектрик (εxx = ε⊥ > 1) для случая θ =
вается равным R = 0.01, 0.057, 0.148. Оптимальной
формой границы, обеспечивающей минимум отра-
= 0 и как металл (εxx = ε∥ < 0) для θ = π/2. Мо-
дуляция границы приводит к тому, что на процесс
жения, является пилообразный профиль (a). В слу-
рассеяния начинает влиять компонента εyy тензора
чае (б) (квазисинусоидальный профиль) отражение
проницаемости. Поэтому неудивительно, что гофри-
примерно вдвое меньше, чем от плоской границы по-
ровка улучшает согласование при θ = π/2 и ухудша-
лупространства с ε = ε⊥, но максимальное отраже-
ет при θ = 0.
ние наблюдается от Ω-подобного профиля (в), и ко-
эффициент отражения в этом случае заметно боль-
Более информативной для выбора формы (пара-
ше, чем от плоской границы.
метра P ) является зависимость коэффициента отра-
жения от нескольких параметров, например, функ-
Отражение существенно зависит от ориентации
ция R(P, κλ0/2π), которая приведена на рис. 5 для
осей анизотропии ГС по отношению к границе. При
двух ориентаций (θ = 0, π/2) оптической оси ГС и
повороте осей на 90◦ (θ = π/2), когда отрицатель-
фиксированных амплитуде модуляции A = 0.3λ0 =
ной становится компонента тензора проницаемости
= 0.18 мкм и длине волны излучения λ = λ0 =
вдоль границы, εxx = ε∥ = -2.3763 + 0.1475i, ко-
= 0.6 мкм2). Анализ этой зависимости, а также дан-
эффициент отражения от плоской границы близок
ных, полученных при других амплитудах модуля-
к единице, и профилирование границы уменьшает
ции и других частотах, показал преимущество пило-
отражение. Соответствующая структура поля для
образного профиля, и для дальнейшего исследова-
ориентации θ = π/2 оптической оси ГС и таких же,
ния мы остановились на форме модуляции профиля
как на рис. 3, параметров границы, приведена на
рис. 4. Несмотря на значительный рост отражения
2) С целью уменьшить число параметров значения коэф-
при такой ориентации оптических осей, зависимость
фициента отражения, приведенные на рис. 5 и всех после-
коэффициента отражения от параметра формы ока-
дующих рисунках, усреднены по углам падения излучения в
зывается похожей: минимальное отражение достига-
интервале φinc = 0 : 80◦.
400
ЖЭТФ, том 156, вып. 3 (9), 2019
Рассеяние света профилированной границей. . .
A/0
A/0
0
/2
0
/2
а
б
а
б
1.5
1.5
5.5
5.5
0.40
0.35
0.55
0.55
5.0
5.0
0.35
0.50
0.50
0.30
4.5
4.5
0.45
0.30
0.45
0.40
4.0
4.0
0.25
0.40
0.25
0.35
1.0
1.0
3.5
3.5
0.30
0.35
0.20
0.20
0.25
0.30
3.0
3.0
0.15
0.20
0.25
2.5
0.15
2.5
0.15
0.10
0.20
0.10
0.5
0.5
2.0
2.0
0.05
0.10
0.15
0.05
0.5
0.6
0.7
0.5
0.6
0.7
2
3
4
5
2
3
4
5
, нм
, нм
/2
/2
0
0
Рис. 7. (В цвете онлайн) Коэффициент отражения от про-
Рис. 6. (В цвете онлайн) Коэффициент отражения от про-
филированной границы с параметром формы P = -1.2
филированной границы с параметром формы P = -1.2
как функция параметров κλ0/2π и λ. Данные усреднены
как функция амплитуды модуляции A/λ0 и нормирован-
по углам падения φinc = 0 : 80◦. Угол поворота осей ани-
ного волнового числа модуляции κ/k0 = (Lx/λ0)-1. Угол
зотропии θ = 0 (а), π/2 (б), амплитуда модуляции A =
поворота осей анизотропии θ = 0 (а), π/2 (б), длина волны
= 0.5λ0 = 0.3 мкм. Контур отвечает значению 〈R〉 = 0.2
излучения λ = λ0 = 0.6 мкм. Штриховые линии отвечают
постоянным значениям произведения Aκ
ется как при относительно длинноволновой модуля-
ции с большой амплитудой, так и при слабой, но
с параметром P = -1.2 (форма профиля изображе-
мелкомасштабной модуляции.
на на рис. 3a, 4a).
Оптимальный поглотитель должен быть широ-
Зафиксировав параметр формы, мы сущест-
кополосным, т. е. должен, кроме прочего, обеспе-
венно упростим задачу, поскольку теперь выбор
чивать минимум отраженной мощности при паде-
структуры поглощающей поверхности ограничива-
нии излучения в широком диапазоне длин волн, где
ется лишь двумя параметрами: амплитудой модуля-
диэлектрическая проницаемость металла (здесь се-
ции A и волновым числом модуляции κ. На рис. 6
ребра) обладает заметной дисперсией. Частотно-за-
приведены зависимости R(A/λ0, κλ0/2π), вычислен-
висимый характер коэффициента отражения иллю-
ная для λ = λ0 = 0.6 мкм, P = -1.2 и двух ори-
стрируется рис. 7, где приведены результаты вычис-
ентаций θ = 0, π/2. Результаты расчетов показы-
ления R(λ, κλ0/2π) при фиксированной амплитуде
вают, что рост как амплитуды A, так и волново-
модуляции A = 0.5λ0 = 0.3 мкм. Поэтому при выбо-
го числа модуляции κ одинаковым образом влияет
ре оптимальных параметров границы имеет смысл
на коэффициент отражения, увеличивая его в сред-
сравнивать коэффициенты отражения, усредненные
нем для случая θ = 0 (а) и уменьшая для ориен-
не только по углам падения φinc, но также и по дли-
тации θ = π/2 (б). Анализ полученных результа-
нам волн λ. Данные, полученные при усреднении ко-
тов позволяет заключить, что основным парамет-
эффициента отражения по углам φinc = 0 : 80◦ и
ром, определяющим отражение (по крайней мере,
длинам волн λ = 0.45 : 0.8 мкм (в этом диапазоне λ
при достаточно сильной модуляции границы), явля-
выполняются условия гиперболичности среды, т. е.
ется отношение поперечного (амплитуды модуляции
Re ε∥ Re ε⊥ < 0 для компонент эффективного тен-
A) и продольного (Lx = 2π/κ) масштабов модуля-
зора диэлектрической проницаемости, вычисленных
ции, т. е. параметр g = Aκ/2π. Линии уровня функ-
по формулам (3)), приведены на рис. 8. Штрихо-
ции g (штриховые на рис. 6) практически ложат-
выми линиями отмечены на плоскости параметров
ся на последовательность максимумов коэффициен-
(κλ0/2π, A/λ0) линии уровня функции Aκ, и можно
та отражения для обеих ориентаций оси анизотро-
заметить, что тенденция зависимости коэффициен-
пии ГС. Таким образом, для пилообразного профи-
та отражения от произведения Aκ сохраняется (см.
ля одинаковый коэффициент отражения наблюда-
рис. 6) и после усреднения по длинам волн.
401
2
ЖЭТФ, вып. 3 (9)
Н. А. Жарова, А. А. Жаров, А. А. Жаров, мл.
ЖЭТФ, том 156, вып. 3 (9), 2019
A/0
A/0
а
б
в
а
б
y/
1.5
0.35
1.5
2.4
2.2
0.30
0.08
3.5
2.2
2.0
0.06
3.0
2.0
0.30
1.8
0.25
0.04
1.8
1.6
0.02
2.5
1.6
1.0
1.0
0.20
1.4
0.25
0
1.4
2.0
1.2
-0.02
1.2
0.15
1.0
1.5
–0.04
1.0
0.20
0.8
-0.06
0.8
0.10
1.0
0.6
0.6
-0.08
0.5
0.5
0.15
0.4
0.5
0.4
0.05
–0.10
–0.1
0
-0.1
0
-0.1
0
x/
x/
x/
2
3
4
5
2
3
4
5
/2
/2
0
0
Рис. 9. (В цвете онлайн) Распределение модуля магнит-
Рис. 8. (В цвете онлайн) Коэффициент отражения от про-
ного поля |H(x, y)| (показан один период структуры) при
филированной границы с параметром формы P = -1.2
нормальном падении плоской волны Hinc = exp(-ik0y)
как функция параметров κλ0/2π и A/λ0 (λ0 = 0.6 мкм).
на периодически модулированную границу гиперболиче-
Данные усреднены по углам падения φinc = 0 : 80◦ и дли-
ской среды. Амплитуда модуляции A = 0.2λ0, параметр P ,
нам волн λ = 0.45 : 0.8 мкм. Угол поворота осей ани-
контролирующий форму модуляции, P = -1.2, волновое
зотропии θ = 0 (а), π/2 (б). Контур отвечает значению
число модуляции κ = 5 · 2π/λ0 (а), 7 · 2π/λ0 (б), 9 · 2π/λ0
〈R〉 = 0.2. Штриховые линии отвечают постоянным зна-
(в). Угол поворота осей анизотропии θ = π/2. Коэффи-
чениям произведения Aκ
циент отражения для этих вариантов 0.01 (а), 0.043 (б),
0.009 (в)
Результаты расчетов показывают, что минимум
отражения обеспечивает ориентация оси анизотро-
однородные изотропную и анизотропную гипербо-
пии ГС с θ = π/2, причем одинаковый эффект до-
лическую среды для случая, когда профиль грани-
стигается как для крупномасштабной модуляции по-
цы является произвольной периодической функци-
верхности с большой амплитудой, так и для мелко-
ей координаты вдоль границы. Естественное обоб-
масштабной модуляции с малой амплитудой.
щение второго тождества Грина (см. Приложение)
Интересный эффект имеет место для угла пово-
позволило рассмотреть нетривиальный случай, ко-
рота осей анизотропии θ = π/2 при рассеянии па-
гда одна из сред представляет собой среду ги-
дающего излучения на пилообразом профиле. При
перболического типа, характеризующуюся условием
достаточно узких зубцах «пилы» поле локализует-
εXXεYY < 0. В этом случае перенормировка коор-
ся в ГС и представляет собой последовательность
динат превращает уравнение гиперболического типа
нескольких максимумов, расположенных вдоль оси
в (эллиптическое) уравнение Гельмгольца, записан-
клина, причем расстояние между максимумами и их
ное, однако, в комплексных пространственных пере-
ширина растут при удалении от вершины клина. Ха-
менных. Метод применим и в поглощающей/актив-
рактерные распределения поля приведены на рис. 9.
ной среде, когда сами компоненты диэлектрического
Эти «горячие точки» имеют субволновой характер-
тензора являются комплексными величинами.
ный масштаб и напоминают распределения поля, по-
C помощью развитого метода численно ис-
лученные в численном эксперименте [16], где также
следованы особенности рассеяния падающего
указывалось на субволновую локализацию и эффек-
излучения слоем ГС с периодически профилиро-
тивное поглощение излучения в малом объеме.
ванной границей, в частности, влияние формы,
продольного и поперечного характерного мас-
штаба неоднородности профиля на коэффициент
4. ЗАКЛЮЧЕНИЕ
отражения. Численное моделирование показало,
что достаточно мелкомасштабное профилирование
В работе предложен метод расчета полей, рас-
границы приводит к уменьшению отражения по
сеянных профилированной границей, разделяющей
сравнению с плоской границей практически для
402
ЖЭТФ, том 156, вып. 3 (9), 2019
Рассеяние света профилированной границей. . .
всех рассмотренных форм профиля (при изменении
Для излучения TM-поляризации уравнение
управляющего параметра форма профиля меняется
Гельмгольца в свободном пространстве имеет вид
от почти пилообразной до почти синусоидальной
Δh + k20h = 0,
(5)
и напоминающей греческую букву Ω). Однако
оптимальной формой оказывается пилообразная,
где h ≡ hz — (единственная) z-компонента магнит-
и чем сильнее форма профиля отклоняется от
ного поля. Для функции Грина, удовлетворяющей
пилообразной, тем в среднем большим оказывается
уравнению
коэффициент отражения.
ΔG + k20G = δ(x - x0)δ(y - y0) ≡ δ(r - r0),
(6)
Финансирование. Работа выполнена при под-
известно аналитическое выражение G(r, r0)
=
держке Российского фонда фундаментальных ис-
= i/4H10(k0ρ), где H10 — функция Ханкеля нулевого
следований (грант № 16-02-00556), разработка чис-
√
порядка и ρ =
(x - x0)2 + (y - y0)2.
ленного метода (Приложение) проводилась при под-
Нетрудно заметить, что при таком выборе φ и ψ
держке государственного контракта с Федераль-
интеграл в левой части равенства (4) равен нулю,
ным исследовательским центром Институт при-
а правая часть задает соотношение между значени-
кладной физики Российской академии наук (проект
ями рассеянного магнитного поля hsct и его произ-
№0035-2019-0004).
водной по нормали ∂hsct/∂n в точках на границе
(xB (τi), yB(τi)), причем аналогичное соотношение
можно записать для каждой i-й из N граничных
ПРИЛОЖЕНИЕ
точек, используя соответствующие функции Грина,
Метод расчета полей при рассеянии плоской
Gij ≡ G(k0ρij), где
волны на периодически модулированной
√
границе гиперболической среды
ρij =
[xB (τi) - xB (τj )]2 + [yB(τi) - yB(τj )]2.
Метод основан на использовании второго тожде-
Таким образом, для 2N неизвестных (значения
ства Грина (Green’s second identity) и сводит зада-
hsct и ∂hsct/∂n) имеем N уравнений, полученных из
чу рассеяния падающего излучения на границе од-
соотношений (4),
нородной среды к вычислению поверхностных (для
двумерного случая контурных) интегралов от функ-
∂Gij
∂hsctj
hsctj
dτj - Gij
dτj = 0,
(7)
ции Грина и ее производной по нормали к поверхно-
∂nj
∂nj
сти. Похожая методика применялась в публикации
√
[24] для решения уравнения Гельмгольца в акустике,
где dτj = dx2j + dy2j и, как обычно, предполагается
но в данной работе проведено обобщение, позволя-
суммирование по повторяющимся индексам. Недо-
ющее рассматривать анизотропную среду гипербо-
стающие N уравнений находятся из условий непре-
лического типа, в которой обычное (эллиптическое)
рывности тангенциальных компонент электрическо-
уравнение Гельмгольца фактически становится ги-
го и магнитного полей на границе xB(τi), yB(τi).
перболическим уравнением.
В простейшем случае, когда падающее излучение
Второе тождество Грина формулируется следу-
рассеивается на идеально отражающем металле, эти
ющим образом. Если ψ и φ дважды непрерывно
условия сводятся к равенству нулю нормальной про-
дифференцируемы в области U ∈ R3, тогда
изводной полного (рассеянное плюс падающее) маг-
∫
∮
(
)
нитного поля, ∂hsct/∂n = -∂hinc/∂n.
∂φ
∂ψ
(ψΔφ - φΔψ) dV =
ψ
-φ
dS.
(4)
Если граница xB (τ), yB(τ) разделяет свободное
∂n
∂n
U
∂U
пространство и диэлектрик характеризуется прони-
цаемостью εD, то в области диэлектрика волновое
В рассматриваемом двумерном случае лапласиан
число k =
√εDk0 и функция Грина перенормиру-
Δ = ∂2/∂x2 +∂2/∂y2, интегрирование по объему за-
ется как
G= G(kρ/k0). Прошедшее магнитное поле
меняется на интегрирование по x-, y-координатам,
htr и его нормальная производная на границе удо-
а граница области ∂U представляет собой (парамет-
влетворяет уравнению
(4) с этой новой функцией
рически заданную) линию xB (τ), yB(τ) (см. (1)).
Грина
G, а условия непрерывности полей записыва-
Возьмем в качестве φ рассеянное магнитное поле
ются как
hsct, а в качестве ψ функцию Грина G двумерной за-
)
дачи, в которой точка особенности расположена на
∂htr
(∂hsct
∂hinc
htr = hsct + hinc
,
= -εD
+
границе области U.
∂n
∂n
∂n
403
2*
Н. А. Жарова, А. А. Жаров, А. А. Жаров, мл.
ЖЭТФ, том 156, вып. 3 (9), 2019
0.20
водной в области диэлектрика) возникает проблема
и ее производ-
сингулярности функции Грина Gii
0.15
ной ∂Gii/∂ni. Очевидно, что требуется более точное
вычисление диагональных коэффициентов в урав-
0.10
нении (7). Правильный результат дает сдвиг кон-
тура интегрирования таким образом, чтобы точка
0.05
Свободное
особенности оставалась вне области U, как это ил-
пространство
0
люстрируется на рис. 10. Соответственно, интеграл
вычисляется вдоль верхней полуокружности для
-0.05
полей в области свободного пространства и вдоль
нижней полуокружности для полей в диэлектрике
-0.10
(см. рис. 10).
Задача усложняется в случае, когда рассеяние
-0.15
происходит на границе среды с тензорной прони-
а
цаемостью ε, например, метаматериала. Уравнение
-0.20
-0.2
–0.1
0
0.1
0.2
Гельмгольца для магнитного поля в такой среде
имеет вид
0.20
1
∂2htr
1
∂2htr
+
+k20htr
= 0,
(8)
εYY
∂X2
εXX
∂Y2
б
0.15
где X и Y
— главные оси, в которых диэлект-
рический тензор диагонален (в общем случае оси
0.10
Анизотропная
X, Y повернуты на некоторый угол θ относительно
среда
0.05
осей x, y, определяющих ориентацию границы: X =
= xcosθ + y sinθ, Y = ycosθ - xsinθ), εXX = ε⊥,
0
εYY = ε∥.
Нетрудно заметить, что заменой
-0.05
ξ=
√εYY X, η =√εXX Y
(9)
–0.10
уравнение (8) приводится к каноническому виду (5),
и функция Грина в этих переменных по-прежнему
-0.15
выражается через функцию Ханкеля нулевого по-
рядка,
–0.20
i
-0.4
-0.3
-0.2
-0.1
0
G=
,
4H10(k0 ρ)
Рис. 10. (В цвете онлайн) Геометрия задачи. a) Замкну-
где
тый контур, используемый для расчета рассеянных полей
√
в свободном пространстве; показано направление норма-
ρ=
(ξ - ξ0)2 + (η - η0)2 =
лей, стрелки указывают направление обхода контура. На
√
синей части контура применяются условия радиационного
=
εYY (X - X0)2 + εXX(Y - Y0)2.
излучения (см. текст). б) То же для области анизотропной
Поэтому естественным для решения задачи пред-
среды
ставляется следующий алгоритм: в области расче-
та, относящейся к анизотропной среде, вводятся по
формулам (9) координаты ξ, η, определяются гра-
(знак «-» здесь учитывает противоположное на-
ничные точки ξB , ηB, соответствующие реальным
правление векторов нормали для области свободно-
граничным точкам xB , yB в свободном простран-
го пространства и области диэлектрика, см. рис. 10)
стве, и векторы нормали ñ (ñξ
= dη/dτ, ñη
=
√
в каждой из N граничных точек. Таким образом,
= -dξ/dτ, где dτ =
dξ2 + dη2) в этом норми-
мы имеем 4N уравнений для 4N неизвестных, что
рованном пространстве. Интегрирование уравнений
единственным образом определяет решение.
(4) в пространстве ξ, η дает, как и раньше, N урав-
Следует отметить, что при вычислении коэффи-
нений, связывающих htr и ∂htr/∂ñ = ñξ∂htr/∂ξ +
циентов матричного уравнения (7) (и аналогично-
+ ñη∂htr/∂η. Заключительным шагом является ис-
го уравнения для поля и его нормальной произ-
пользование условий непрерывности магнитного и
404
ЖЭТФ, том 156, вып. 3 (9), 2019
Рассеяние света профилированной границей. . .
тангенциального электрического полей на границе
и аналогичное соотношение записывается для рас-
между областями.
сеянного поля в свободном пространстве:
Нас интересует случай, когда диэлектрическая
∑
[G′ijk0
среда является гиперболической средой, в которой
(rj - ri) · nj hsctjdτj -
продольная и поперечная компоненты диэлектриче-
ρij
j
]
ского тензора имеют разные знаки (для определен-
ности будем считать, что εXX > 0, εYY < 0). При
- ik0Gij(Esct)jdτj
= 0.
(11)
τ
этих условиях нормированные координаты ξ ока-
зываются мнимыми, понятие вектора нормали как
Условие непрерывности тангенциальных электриче-
вектора единичной длины теряет смысл. Что бо-
ского и магнитного полей приводит к равенствам
лее важно, эффективное расстояние до источника
в функции Грина ρ стремится к нулю в направле-
htrj = hsctj + hincj, (Etrτ)j = (Esctτ)j + (Eincτ)j.
(12)
нии резонансного конуса (при (X - X0)/(Y - Y0) =
√
Описанная выше постановка задачи непосред-
=
-εXX/εYY ), а поле в этом направлении беско-
ственно применима для расчета рассеяния плоской
нечно велико. Ситуацию, как всегда, спасает учет
волны на диэлектрическом/метаматериальном объ-
затухания в среде, однако при этом комплексными
екте конечных размеров. В этом случае граница
становятся как ξ, так и η, и интегрирование уравне-
двух сред является замкнутым контуром ∂U в фор-
ния (4) приходится проводить в комплексном про-
муле (4) для ГС, а бесконечно удаленная граница
странстве.
свободного пространства не влияет на процесс рас-
Однако можно свести вычисление коэффициен-
сеяния. Если же мы рассматриваем рассеяние пада-
тов матричного уравнения (7) к интегрированию в
ющего излучения на периодическом профиле и хо-
обычном пространстве. Действительно, учтем, что
тим ограничиться численными расчетами полей в
G′
пределах элементарной ячейки, имея в виду при-
∂Gij
ij
k0
dτj =
[(ξj - ξi) dηj - (ηj - ηi) dξj ] =
∂ñj
менение в дальнейшем теоремы Блоха, то замкну-
ρij
тый контур ∂U в формуле (4), ограничивающий об-
√
G′
k0
ij
=
εXXεYY
[(xj - xi) dyj - (yj - yi) dxj ] =
ласть свободного пространства, необходимо содер-
ρij
жит участки, которые не граничат с областью ГС и
G′
k0
для которых поэтому неприменимо граничное усло-
√
ij
=
ε∥ε⊥
(rj - ri) · nj dτj ,
вие (12). Соответствующие участки имеются так-
ρij
же на замкнутом контуре, ограничивающем область
где G′ означает производную от функции Грина по
ГС (см. рис. 10). На этих участках границы следу-
аргументу. Аналогично можно записать выражение
ет использовать условия радиационного излучения
для величины
(условия излучения Зоммерфельда), которые свя-
∂htrj
∂htrj
∂htrj
зывают между собой тангенциальные компоненты
dτj =
dηj -
dξj =
∂ñj
∂ξ
∂η
электрического и магнитного полей (для свободного
)
пространства магнитное поле и его нормальную про-
(∂htr
1
∂htrj
1
√
j
=
ε∥ε⊥
dYj
-
dXj
=
изводную). Учет этой связи позволяет полностью
∂X
εYY
∂Y
εXX
рассчитать задачу и найти распределение тангенци-
=
√εXXεYY ik0 (EtrXdXj + EtrYdYj) =
альных компонент полей на границе ∂U и тем самым
=
√ε∥ε⊥ik0Etrτdτj ,
коэффициент отражения.
Если же кроме коэффициента отражения нас ин-
где Etrτ — тангенциальная компонента электричес-
тересует распределение полей внутри этого замкну-
кого поля в прошедшей волне в граничных точках.
того контура, то необходимо найти амплитуды эф-
Таким образом, уравнение (7) модифицируется
фективных источников Vi, которые мы должны рас-
для случая среды с тензорной диэлектрической про-
положить лишь на части контура ∂U, разделяю-
ницаемостью следующим образом:
щей свободное пространство и ГС и которые долж-
[
∑
G′
ны создавать на этой части контура рассчитанное
ij
k0
(rj - ri) · nj htrjdτj -
выше распределение полей. Математически задача
ρ
ij
j
сводится к решению матричного уравнения
]
− ik0
Gij(Etrτ)jdτj
= 0,
(10)
ViGij = hsctj
405
Н. А. Жарова, А. А. Жаров, А. А. Жаров, мл.
ЖЭТФ, том 156, вып. 3 (9), 2019
и аналогично
10.
Z. Jacob, L. V. Alekseyev, and E. Narimanov, Opt.
Express 14, 8247 (2006).
Vi
Gij = htrj,
11.
J. Sun, M. Shalaev, and N. Litchinitser, Nat. Com-
где ri, rj принадлежат граничной части контура ∂U.
mun. 6, 7201 (2015).
Соответственно поля в части свободного простран-
12.
T. U. Tumkur, L. Gu, J. K. Kitur, E. E. Narimanov,
ства и ГС, ограниченных контурами ∂U и ∂Ũ вы-
and M. A. Noginov, Appl. Phys. Lett. 100, 161103
числяются как
(2012).
(
)
√
h(x, y) = ViG k0
(x-xi)2+(y-yi)2
+hinc(x, y),
13.
T. U. Tumkur, J. K. Kitur, B. Chu et al., Appl. Phys.
Lett. 101, 091105 (2012).
(
√
)
h(X, Y ) =
ViG k0
εYY (X-Xi)2+εXX(Y -Yi)2
,
14.
Z. Liu, H. Lee, Y. Xiong, C. Sun, and X. Zhang,
Science 315, 1686 (2007).
где hinc(x, y) — магнитное поле в падающей плоской
волне.
15.
K. Mantel, D. Bachstein, and U. Peschel, Opt. Lett.
36, 199 (2011).
16.
Y. Cui, K. H. Fung, J. Xu et al., Nano Lett. 12, 1443
ЛИТЕРАТУРА
(2012).
1. A. Poddubny, I. Iorsh, P. Belov, and Y. Kivshar, Nat.
17.
H. Hu, D. Ji, X. Zeng, K. Liu, and Q. Gan, Sci. Rep.
Photon. 7, 948 (2013).
3, 1249 (2013).
2. D. Lu and Z. Liu, Nat. Commun. 3, 1205 (2012).
18.
Z. Jacob, J.-Y. Kim, G. V. Naik et al., Appl. Phys.
B 100, 215 (2010).
3. I. V. Iorsh, I. S. Mukhin, I. V. Shadrivov, P. A. Belov,
and Y. S. Kivshar, Phys. Rev. B 87, 075416 (2013).
19.
P. Shekhar, J. Atkinson, and Z. Jacob, Nano Conver-
4. Y. Guo, C. L. Cortes, S. Molesky, and Z. Jacob, Appl.
gence 1, 1 (2014).
Phys. Lett. 101, 131106 (2012).
20.
N. A. Zharova, A. A. Zharov, and A. A. Zharov, J.
5. S. M. Hashemi and I. S. Nefedov, Phys. Rev. B 86,
Opt. Soc. Amer. B 33, 594 (2016).
195411 (2012).
21.
N. A. Zharova, A. A. Zharov, and A. A. Zharov Jr.,
6. I. S. Nefedov, C. A. Valagiannopoulos, S. M. Hashe-
Adv. Cond. Mat. Phys.
2018,
4578148
(2018);
mi, and E. I. Nefedov, Sci. Rep. 3, 2662 (2013).
7. I. S. Nefedov, C. A. Valagiannopoulos, and L. A. Mel-
22.
L. Ferrari, C. Wu, D. Lepage, X. Zhang, and Z. Liu,
nikov, J. Opt. 15, 114003 (2013).
Prog. Quant. Electron. 40, 1 (2015).
8. J. Yao, Z. Liu, Y. Liu et al., Science 321, 930 (2008).
23.
9. A. J. Hoffman, L. Alekseyev, S. S. Howard,
24.
Q. Sun, E. Klaseboer et al., Roy. Soc. Open Sci. 2,
K. J. Franz et al., Nat. Mater. 6, 946 (2007).
140520 (2015).
406