ЖЭТФ, 2019, том 156, вып. 3 (9), стр. 502-506

ФАЗОВЫЕ ПЕРЕХОДЫ И ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА

МОДЕЛИ ПОТТСА С ЧИСЛОМ СОСТОЯНИЙ СПИНА q = 4

НА ГЕКСАГОНАЛЬНОЙ РЕШЕТКЕ

А. К. Муртазаев, М. К. Рамазанов^*, М. К. Мазагаева, М. А. Магомедов

Институт физики Дагестанского научного центра Российской академии наук

367003, Махачкала, Республика Дагестан, Россия

Поступила в редакцию 14 марта 2019 г.,

после переработки 14 марта 2019 г.

Принята к публикации 8 апреля 2019 г.

На основе алгоритма Ванга - Ландау методом Монте-Карло выполнены исследования фазовых перехо-

дов и термодинамических свойств двумерной ферромагнитной модели Поттса с числом состояний спина

q = 4 на гексагональной решетке. С использованием метода кумулянтов Биндера четвертого порядка

и гистограммного анализа данных проведен анализ характера фазовых переходов. Установлено, что в

исследуемой модели наблюдается фазовый переход первого рода.

DOI: 10.1134/S004445101909013X

области значений q > 4, в которой ФП происходит

как переход первого рода [14]. Согласно результатам

работ [4,11,12], для модели Поттса с числом состоя-

1. ВВЕДЕНИЕ

ний спина q = 2, 3, 4 наблюдается ФП второго рода.

Однако при q = 4 в рассматриваемой модели были

Исследование фазовых переходов (ФП), крити-

обнаружены особенности термодинамического пове-

ческих, магнитных и термодинамических свойств

дения. Кроме того, при исследовании модели Поттса

магнетиков, описываемых двумерными решеточны-

основное внимание до сих пор уделялось спиновым

ми моделями Изинга и Поттса, имеет большой науч-

системам на квадратной и треугольной решетках.

ный интерес и открывает широкие перспективы для

ФП и термодинамические свойства модели Поттса

практического применения [1-3]. Такой интерес обу-

с числом состояний спина q = 4 на гексагональной

словлен тем, что низкоразмерные решеточные моде-

решетке практически не изучены.

ли описывают большой класс реальных физических

систем: слоистые магнетики, пленки жидкого гелия,

В связи с этим в данной работе нами предпри-

сверхпроводящие пленки, адсорбированные пленки

нята попытка на основе метода Монте-Карло (МК)

и др. [1, 4, 5].

провести исследование ФП и термодинамических

В настоящее время двумерная модель Изинга

свойств двумерной ферромагнитной модели Поттса

изучена достаточно хорошо и известны практически

с числом состояний спина q = 4 на гексагональной

все ее свойства [6-10]. Для двумерной модели Потт-

решетке.

са с различным числом состояний спина q существу-

ет совсем немного надежно установленных фактов.

Из данных, полученных на сегодняшний день,

Большинство имеющихся результатов получены для

нельзя однозначно определить характер ФП и зако-

двумерной модели Поттса с числом состояний спина

номерности изменения термодинамического поведе-

q = 2 и q = 3 [4,11-13]. Двумерная модель Поттса

ния данной модели, и эти вопросы до сих пор оста-

с числом состояний спина q = 4 до сих пор изуче-

ются открытыми. Исследование двумерной модели

на мало. Данная модель интересна тем, что значе-

Поттса с числом состояний спина q = 4 на основе со-

ние q = 4 является граничным значением интерва-

временных методов и идей позволит получить ответ

ла 2 ≤ q ≤ 4, где наблюдается ФП второго рода, и

на ряд вопросов, связанных с ФП и термодинамиче-

скими свойствами низкоразмерных решеточных си-

^* E-mail: shikh77@mail.ru

стем.

502

ЖЭТФ, том 156, вып. 3 (9), 2019

Фазовые переходы и термодинамические свойства. ..

2. МОДЕЛЬ И МЕТОД ИССЛЕДОВАНИЯ

мы). При этом вероятность перехода из состояния с

определяется

энергией E₁ в состояние с энергией E₂

Гамильтониан модели Поттса с числом состоя-

по формуле

ний q = 4 может быть представлен в следующем

p = g(E₁)/g(E₂).

виде:

∑

Если переход в состояние с энергией E₂ состоялся,

H = -J cosθ_i,j,

(1)

то

i,j

) + 1,

g(E₂) → fg(E₂), H(E₂) → H(E₂

где J — параметр обменного ферромагнитного взаи-

модействия для ближайших соседей, θi,j — угол

иначе

между взаимодействующими спинами S_i и S_j .

В настоящее время такие системы на основе мик-

g(E₁) → fg(E₁), H(E₁) → H(E₁) + 1.

роскопических гамильтонианов успешно изучаются

на основе метода МК [6, 7, 15, 16]. В последнее вре-

Если гистограмма стала плоской, то обнуляем гисто-

мя разработано много новых вариантов алгоритмов

грамму, H(E) → 0, уменьшаем модификационный

метода МК. Одним из наиболее эффективных для

фактор, f →

√f, и продолжаем снова, пока f ≥

исследования подобных систем является алгоритм

≥ f_min. В нашем случае f_min = 1.000000000. Более

Ванга - Ландау [13,17], особенно в низкотемператур-

подробно алгоритм Ванга - Ландау изложен в рабо-

ной области. Поэтому мы в данном исследовании ис-

тах [17,18]. Таким образом, определив плотность со-

пользовали этот алгоритм.

стояний системы, можно рассчитать значения тер-

В стандартный алгоритм Ванга - Ландау нами

модинамических параметров при любой температу-

были внесены дополнения, которые позволяют вы-

ре. В частности, внутреннюю энергию U, свободную

яснить магнитную структуру основного состояния

энергию F , теплоемкость C и энтропию S можно вы-

системы. Данный алгоритм является реализацией

числить, используя следующие выражения:

метода энтропийного моделирования и позволяет

∑

вычислить функцию плотности состояний системы.

Eg(E)exp(-E/k_BT)

Алгоритм Ванга - Ландау основан на том, что, со-

∑

≡ 〈E〉_T ,

(2)

вершая случайное блуждание в пространстве энер-

g(E) exp(-E/k_BT )

гий с вероятностями, обратно пропорциональными

плотности состояний g(E), мы получаем равномер-

ное распределение по энергиям. Подобрав вероятно-

]

[∑

сти перехода такими, что посещение всех энергети-

F (T ) = -k_BT ln

g(E) exp(-E/k_BT )

(3)

ческих состояний стало бы равномерным, мы можем

получить изначально неизвестную плотность состо-

яний g(E), зная которую можно вычислить значе-

(

)

C =NK²

〈U²〉 - 〈U〉²

(4)

ния необходимых термодинамических параметров

при любой температуре. Так как плотность состо-

яний g(E) очень быстро растет с увеличением раз-

U (T ) - F (T )

меров исследуемых систем, для удобства хранения

S(T ) =

(5)

и обработки больших чисел пользуются величи-

ной ln g(E).

где K = |J|/k_BT , N — число частиц, T — темпе-

Алгоритм Ванга - Ландау был использован нами

ратура (здесь и далее температура дана в единицах

в следующем виде.

|J|/k_B), U — внутренняя энергия (U является нор-

Задается произвольная начальная конфигура-

мированной величиной).

ция спинов. Стартовые значения плотности состо-

Для анализа характера ФП мы использова-

яний g(E)=1, гистограммы распределений по энер-

ли метод кумулянтов Биндера четвертого поряд-

гиям H(E) = 0, стартовый модификационный фак-

ка и гистограммный метод анализа данных метода

тор f = f₀ = e¹ ≈ 2.71828. Многократно совершаем

МК [18, 19].

шаги в фазовом пространстве, пока не получим от-

Расчеты проводились для систем с периодичес-

носительно «плоскую» гистограмму H(E) (т. е. пока

кими граничными условиями (ПГУ) и линейными

не будут посещены примерно одинаковое количество

размерами L × L = N, L = 12-120, где L измеря-

раз все возможные энергетические состояния систе-

ется в размерах элементарной ячейки.

503

А. К. Муртазаев, М. К. Рамазанов, М. К. Мазагаева, М. А. Магомедов

ЖЭТФ, том 156, вып. 3 (9), 2019

C/k_B

ln 4

1.4

L = 120

L = 60

1.2

1.0

120

0.8

0.6

0.4

0.2

0.5

1.0

1.5

2.0

00.610

0.615

0.620

0.625

0.630

k T/|J_B|

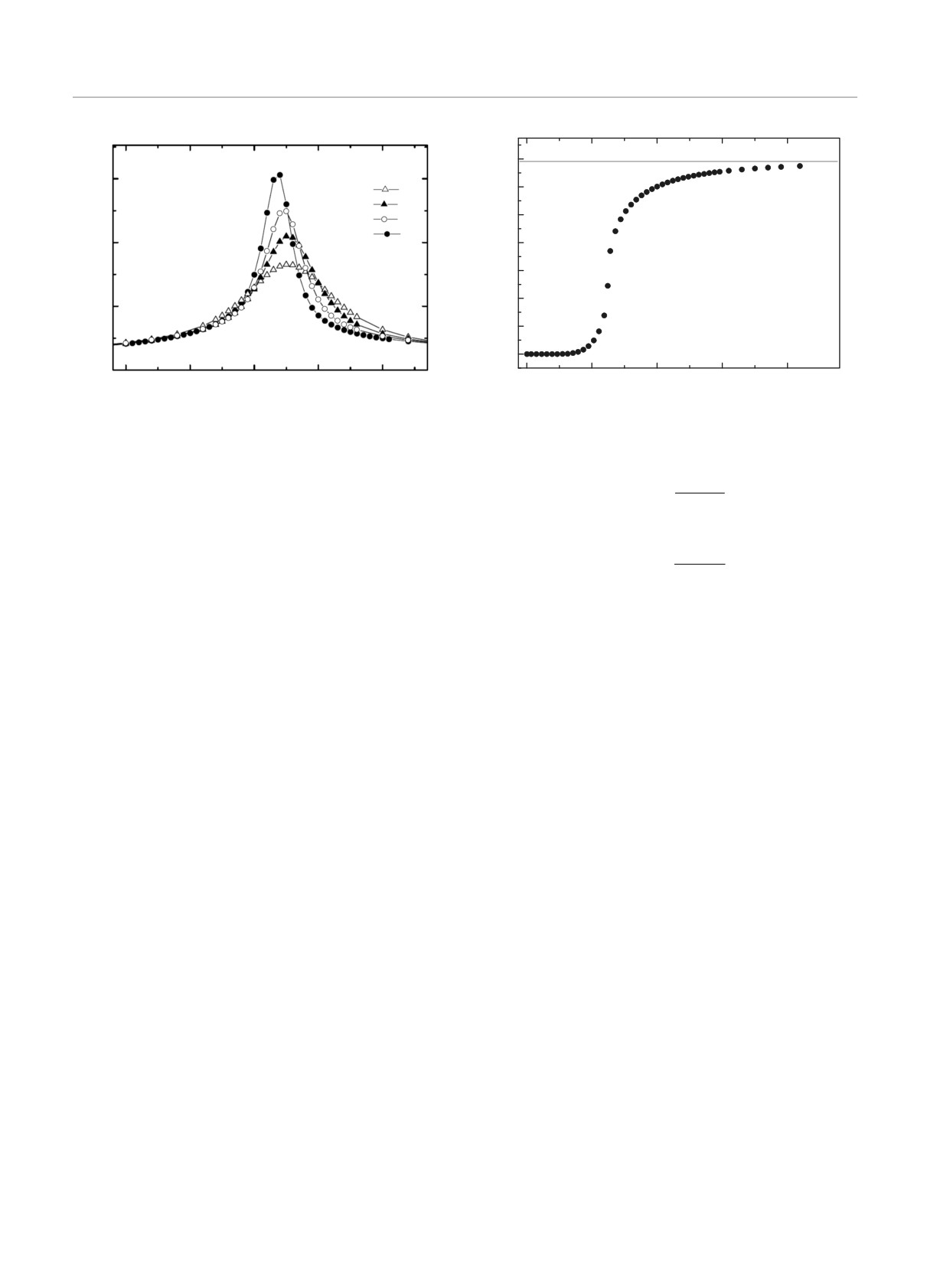
Рис. 1. Температурные зависимости теплоемкости C

Рис. 2. Температурная зависимость энтропии S

3. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

〈U⁴〉_L

V_L = 1 -

(6)

3〈U²〉2L

На рис. 1 представлены характерные зависимо-

сти теплоемкости C от температуры для систем с

линейными размерами L = 60, 72, 96, 120 (здесь

〈m⁴〉_L

V_L = 1 -

(7)

и далее статистическая погрешность не превыша-

3〈m²〉²

ет размеров символов, использованных для построе-

где V_L — энергетический кумулянт, U_L — магнитный

ния зависимостей). Отметим, что в температурных

кумулянт.

зависимостях теплоемкости C для всех систем вбли-

Выражения (6) и (7) позволяют определить кри-

зи критической температуры наблюдаются хорошо

тическую температуру T_c с большой точностью для

выраженные максимумы, которые увеличиваются с

ФП соответственно первого и второго рода. Следу-

ростом числа спинов в системе, причем эти макси-

ет отметить, что применение кумулянтов Биндера

мумы в пределах погрешности приходятся на одну

позволяет также хорошо тестировать тип ФП в сис-

и ту же температуру даже для систем с наимень-

теме. Известно, что ФП первого рода характеризу-

шим значением L. Это свидетельствует, во-первых,

ется тем, что величина V_L стремится к некоторому

о высокой эффективности использованного способа

нетривиальному значению V^∗ согласно выражению

добавления ПГУ, а во-вторых, о достижении насы-

щения по N для многих исследуемых нами парамет-

V_L = V^∗ + bL^-d,

(8)

ров.

Температурная зависимость энтропии S для сис-

при L → ∞ и T = T_c(L), где величина V^∗ отлична

темы с L = 120 приведена на рис. 2. На рисун-

от 2/3, а минимальная величина U_Lmin(T = T_min)

ке видно, что с увеличением температуры энтро-

расходится, U_Lmin(T = T_min) → -∞ при L → ∞.

пия системы стремится к теоретически предсказан-

В случае ФП второго рода кривые температур-

ному значению ln 4 = 1.38629. При низких темпера-

ных зависимостей кумулянтов Биндера U_L имеют

турах, близких к абсолютному нулю, энтропия сис-

четко выраженную точку пересечения [19].

темы стремится к нулю. Аналогичные зависимости

На рис. 3 представлены характерные зависимо-

наблюдаются для всех рассмотренных значений L.

сти U_L от температуры для разных значений L. Вид-

Такое поведение энтропии позволяет говорить о том,

но, что в критической области отсутствует четко вы-

что в данной модели вырождение основного состоя-

раженная точка пересечения, что свидетельствует в

ния отсутствует.

пользу наличия в системе ФП первого рода.

Для анализа характера ФП, особенностей пове-

Температурные зависимости энергетических ку-

дения тепловых характеристик вблизи критической

мулянтов V_L для разных значений L представлены

точки и определения критической температуры T_c

на рис. 4. Видно, что величина V_L стремится к 2/3,

наиболее эффективным является метод кумулянтов

а величина V ^∗ = 2/3, что характерно для ФП второ-

Биндера четвертого порядка [19]:

го рода. Эта величина рассчитана с использованием

504

ЖЭТФ, том 156, вып. 3 (9), 2019

Фазовые переходы и термодинамические свойства. ..

U_L

0.65

L = 60

1.0

L = 60

0.60

0.8

120

0.6

0.55

0.4

0.50

0.2

0.45

0.618

0.619

0.620

0.621

0.622

0.623

-1.28

-1.24

-1.20

-1.16

-1.12

k T/|J_B|

Рис. 5. Гистограммы распределения энергии для L = 60,

Рис. 3. Температурные зависимости магнитного кумулянта

72, 96

Биндера UL

V_L

L = 120

1.0

T = 0.6218

0.6666

0.6219

0.6220

0.8

0.6223

0.6

0.6660

L = 60

0.4

0.6654

120

0.2

-1.24

-1.20

-1.16

-1.12

0.6648

0.610

0.615

0.620

0.625

0.630

k T/|J_B|

Рис. 6. Гистограммы распределения энергии для L = 120

при различных температурах

Рис. 4. Температурные зависимости энергетического ку-

мулянта Биндера VL

сти W от энергии E для всех систем наблюдаются

выражения (8). На рис. 4 видно, что для исследуе-

два максимума, которые свидетельствуют в пользу

мой модели V^∗ = 0.6660(1).

ФП первого рода. Наличие двойного пика на гисто-

Для более подробного анализа рода ФП мы ис-

граммах распределения энергии является достаточ-

пользовали гистограммный анализ данных метода

ным условием для ФП первого рода. Отметим, что

МК. Этот метод позволяет надежно определить род

двойные пики для исследуемой модели наблюдают-

ФП. Методика определения рода ФП этим методом

ся только для систем с большими линейными раз-

подробно описана в работах [20, 21].

мерами (L > 60). Кроме того, двойные пики в дан-

Результаты нашей работы, полученные на осно-

ной модели наблюдаются вблизи критической обла-

ве гистограммного анализа, показывают, что ФП в

сти только в очень узком температурном интервале.

данной модели является переходом первого рода.

Это продемонстрировано на рис. 6. На этом рисун-

Это продемонстрировано на рис. 5. На этом рисунке

ке представлены гистограммы распределения энер-

представлены гистограммы распределения энергии

гии для системы с линейными размерами L = 120.

для систем с линейными размерами L = 60, 72, 96.

Графики построены при различных температурах,

Графики построены вблизи критической температу-

близких к критической. Как видно на рисунке, двой-

ры. На рисунке видно, что в зависимости вероятно-

ные пики наблюдаются в маленьком интервале тем-

505

А. К. Муртазаев, М. К. Рамазанов, М. К. Мазагаева, М. А. Магомедов

ЖЭТФ, том 156, вып. 3 (9), 2019

ператур 0.6217 < T < 0.6223. Ниже и выше указан-

A. K. Murtazaev, M. K. Ramazanov, and M. K. Ba-

ного интервала один пик исчезает, что усложняет

diev, Physica B 476, 1 (2015).

определение типа ФП в таких системах. Такое пове-

F. A. Kassan-Ogly, A. K. Murtazaev, A. K. Zhurav-

дение характерно для систем, в которых происходят

lev, M. K. Ramazanov, and A. I. Proshkin, J. Magn.

ФП первого рода, близкие к переходам второго ро-

Magn. Mater. 384, 247 (2015).

да.

M. K. Ramazanov, A. K. Murtazaev, and M. A. Ma-

gomedov, Sol. St. Comm. 233, 35 (2016).

4. ЗАКЛЮЧЕНИЕ

10.

M. K. Ramazanov, A. K. Murtazaev, M. A. Mago-

Исследование фазовых переходов и термоди-

medov, and M. K. Badiev, Phase Transitions 91, 610

(2018).

намических свойств двумерной ферромагнитной

модели Поттса с числом состояний спина q = 4 на

11.

M. Nauenberg and D. J. Scalapino, Phys. Rev. Lett.

гексагональной решетке выполнено с использовани-

44, 837 (1980).

ем алгоритма Ванга - Ландау метода Монте-Карло.

12.

J. L. Cardy, M. Nauenberg, and D. J. Scalapino,

На основе гистограммного метода и метода ку-

Phys. Rev. B 22, 2560 (1980).

мулянтов Биндера проведен анализ характера

фазовых переходов. Показано, что в системе на-

13.

M. K. Ramazanov, A. K. Murtazaev, and M. A. Ma-

блюдается фазовый переход первого рода.

gomedov, Physica A 521, 543 (2019).

14.

H. Feldmann, A. J. Guttmann, I. Jensen, R. Shrocк,

Финансирование. Исследование выполнено

and S.-H. Tsai, J. Phys. A 31, 2287 (1998).

при финансовой поддержке Российского фонда

фундаментальных исследований в рамках научных

15.

А. К. Муртазаев, М. К. Рамазанов, Ф. А. Ка-

проектов №№ 19-02-00153-а, 18-32-20098-мол-а-вед.

сан-Оглы, Д. Р. Курбанова, ЖЭТФ

147,

127

(2015).

16.

М. К. Бадиев, А. К. Муртазаев, М. К. Рамазанов,

ЛИТЕРАТУРА

ЖЭТФ 150, 722 (2016).

1. H. T. Diep, Frustrated Spin Systems, World Sci., Sin-

17.

F. Wang and D. P. Landau, Phys. Rev. E 64, 056101

gapore (2004).

(2001).

2. Р. Бэкстер, Точно решаемые модели в статисти-

18.

F. Wang and D. P. Landau, Phys. Rev. Lett. 86, 2050

ческой механике, Мир, Москва (1985).

(2001).

3. F. Y. Wu, Exactly Solved Models: A Journey in Sta-

19.

К. Биндер, Д. В. Хеерман, Моделирование ме-

tistical Mechanics, World Sci., New Jersey (2008).

тодом Монте-Карло в статистической физике,

4. F. Y. Wu, Rev. Mod. Phys. 54, 235 (1982).

Наука, Москва (1995).

5. W. Zhang and Y. Deng, Phys. Rev. E 78, 031103

20.

М. К. Рамазанов, А. К. Муртазаев, Письма в

(2008).

ЖЭТФ 103, 522 (2016).

6. А. К. Муртазаев, М. К. Рамазанов, Ф. А. Кас-

21.

М. К. Рамазанов, А. К. Муртазаев, Письма в

сан-Оглы, М. К. Бадиев, ЖЭТФ 144, 1239 (2013).

ЖЭТФ 106, 72 (2017).

506