ЖЭТФ, 2019, том 156, вып. 3 (9), стр. 566-572

АМПЛИТУДНАЯ НЕУСТОЙЧИВОСТЬ ЗАРЯЖЕННЫХ ЧАСТИЦ

В ОБЪЕМНО-ЦЕНТРИРОВАННОЙ КУБИЧЕСКОЙ ЯЧЕЙКЕ

О. С. Ваулина^*

Объединенный институт высоких температур Российской академии наук

125412, Москва, Россия

Московский физико-технический институт

141700, Долгопрудный, Московская обл., Россия

Поступила в редакцию 5 апреля 2019 г.,

после переработки 5 апреля 2019 г.

Принята к публикации 23 апреля 2019 г.

Выполнены исследования условий формирования амплитудных неустойчивостей в трехмерных системах

Юкавы, состоящих из девяти заряженных частиц в объемно-центрированной кубической (ОЦК) ячейке.

Для поиска критерия формирования амплитудной неустойчивости использовался аналитический подход,

основанный на определении точки перегиба потенциальной энергии системы при отклонении частиц от

своего равновесного положения. Приведено сравнение полученных результатов с критериями плавления

для протяженных ОЦК-решеток.

DOI: 10.1134/S0044451019090207

положения, второй же является более фундамен-

тальным и зачастую используется для определения

критериев плавления и условий формирования

1. ВВЕДЕНИЕ

различных кристаллических решеток [11, 17-20].

Вопросы о формировании различных неустой-

Невозможность корректного применения лине-

чивостей в неидеальных средах вызывают постоян-

аризованных уравнений движения для описания

ный интерес в различных областях науки и техники

нелинейных процессов (возникающих, например, с

[1-9]. Небольшое изменение управляющих парамет-

ростом температуры частиц) привела к широкому

ров в изначально равновесных системах способно

использованию разнообразных феноменологичес-

ких критериев в теории плавления кристаллических

вызвать существенное изменение их физических ха-

рактеристик за счет развития диссипативных и/или

решеток: критерия Лидемана, критерия Хансена

и т. д. [1, 2, 20, 21]. Однако использование таких

дисперсионных неустойчивостей [7-14]. Кроме того,

системы взаимодействующих частиц могут терять

критериев для малоразмерных кластерных систем

устойчивость с ростом амплитуды их отклонений от

зачастую не является возможным [20, 22].

изначально равновесных позиций (за счет развития

В настоящей работе для анализа условий изме-

амплитудной неустойчивости), например, при уве-

нения физических характеристик объемно-центри-

личении температуры частиц.

рованных кубических (ОЦК) кластеров с ростом

Большинство методов для поиска критери-

температуры частиц исследовалась их амплитудная

ев формирования различных неустойчивостей в

устойчивость, т. е. устойчивость к любым (а не толь-

неидеальных средах опирается либо на анализ

ко к малым) отклонениям частиц от их равновес-

линеаризованных уравнений движения взаимо-

ного положения. Данный подход основан на поис-

действующих частиц, либо на поиск минимума

ке точки перегиба потенциальной энергии системы с

потенциальной энергии системы [10-20]. Первый из

ростом смещений взаимодействующих частиц и ра-

подходов ограничен необходимым условием малости

нее успешно использовался для систем Юкавы из

отклонения (смещения) частиц от их равновесного

двух частиц [23], а также для двумерных гексаго-

нальных кластеров, состоящих из семи заряженных

^* E-mail: olga.vaulina@bk.ru

частиц [24, 25].

566

ЖЭТФ, том 156, вып. 3 (9), 2019

Амплитудная неустойчивость заряженных частиц. . .

2. УСЛОВИЯ ФОРМИРОВАНИЯ

АМПЛИТУДНОЙ НЕУСТОЙЧИВОСТИ В

l₀

ОЦК-ЯЧЕЙКЕ

Для исследования амплитудной устойчивости

ОЦК-ячейки, состоящей из девяти частиц, взаимо-

действующих с экранированным кулоновским по-

тенциалом, анализировалось изменение ее потенци-

альной энергии при отклонениях частиц от их рав-

новесного положения. Расчеты выполнялись в ши-

роком диапазоне параметров экранирования κ =

/λ (от κ = 0 до κ = 8). Рассматривались две

= l_p

Рис. 1. Иллюстрация положения частиц в трехмерной объ-

задачи: 1) отклонение центральной частицы ячейки

емно-центрированной кубической ячейке. Здесь a — шаг

при неподвижных частицах на периферии; 2) вза-

ОЦК-решетки, l0 — наиболее вероятное межчастичное рас-

имные отклонения всех девяти частиц ячейки (см.

стояние

рис. 1). Отметим, что здесь мы приводим результа-

ты только для смещений частиц в ортогональном

Расчеты проводились для трехмерных систем,

направлении к грани ячейки, поскольку все дру-

представляющих собой ОЦК-ячейку из девяти за-

гие варианты смещений дают большую глубину по-

ряженных частиц, взаимодействующих с экраниро-

тенциальной ямы при приращении потенциальной

ванным кулоновским потенциалом (типа Юкавы):

энергии в анализируемых системах и, соответствен-

ϕ = Qexp(-l/λ)/l, где Q — заряд частиц, l — рас-

но, требуют большей тепловой энергии для разру-

стояние между двумя частицами, λ — длина экрани-

шения ОЦК-ячейки и не могут определять критерий

рования. Найдена величина параметра Γ₀ = Q²/T l₀

развития амплитудной неустойчивости.

вблизи линии формирования амплитудной неустой-

Тогда, в первом случае 1) при смещении одной

чивости; здесь T — температура частиц в энерге-

центральной частицы для приращения U потенци-

√

тических единицах, l₀ =

3a/2 — наиболее веро-

альной энергии в анализируемой системе (с точно-

ятное межчастичное расстояние, a — шаг решетки

стью до постоянной величины) имеем

(см. рис. 1). Здесь и далее под температурой час-

]

Qαδr²

Q²

^[exp(-κ^∗l₁)

exp(-κ^∗l₂)

тиц принимается средняя кинетическая энергия их

U =

(2)

a³

l₁

l₂

стохастического движения [1-3].

Выполнено сравнение полученных результатов

где κ∗ = a/λ ≡ aκ/lp, δr — отклонение части-

с кулоновским параметром неидеальности, Γ

цы от ее равновесного положения, α

— вели-

= Q²/Tl_p (Γ

≡ Γ₀l₀/l_p), определяющим крите-

чина градиента внешнего электрического поля

рий плавления ОЦК-решетки для систем Юкавы

в точке равновесного положения центральной

[26-28]:

частицы, l₁

= {0.5 + (0.5 + δr/a)²}1/2, а l₂

= {0.5 + (0.5 - δr/a)²}1/2.

exp(κ)

Γ_m = C

(1)

Во втором случае 2) для взаимного отклонения

1 + κ + κ²/2

всех частиц в ячейке

где λ = l_p/λ — параметр экранирования, а l_p =

√

Qαδr²

Qα^∗δr²⁸

Q²

= (3

3/4)-1/3l₀ — среднее межчастичное расстоя-

U =

a³

ние для кристаллических систем с ОЦК-решеткой.

]

^[ exp(-κ^∗l₃)

exp(-κ^∗l₄)

Величина коэффициента C несколько различается

(3)

l₃

l₄

в зависимости от способа, выбранного для иденти-

фикации фазового перехода, а также от величины

где α^∗ — величина градиента внешнего поля в точ-

параметра экранирования κ и варьируется в пре-

ках равновесного положения периферийных частиц

делах приблизительно от 98 до 114 [26-34]. При

ячейки (частиц «оболочки»), δr₈ — отклонение час-

этом C ≈ 104 ± 6 для κ < 6 и несколько растет

тиц от равновесного положения, l₃ = {0.5 + (0.5 +

при κ → κ = 6.9, т. е. при приближении к точ-

+ Δr/a)²}1/2, l₄ = {0.5 + (0.5 - Δr/a)²}1/2, а Δr =

ке формирования полиморфного фазового перехода

= δr - δr₈ — величина взаимного смещения цент-

ОЦК-структуры в гранецентрированную кубичес-

ральной частицы, δr, и периферийных частиц, δr₈

кую (ГЦК) решетку [29, 30].

(см. рис. 1).

567

О. С. Ваулина

ЖЭТФ, том 156, вып. 3 (9), 2019

10^-1

10^-2

-3

-1

-0.05

0.05

0.10

0.15

0.20

0.25

0.30

r/l₀

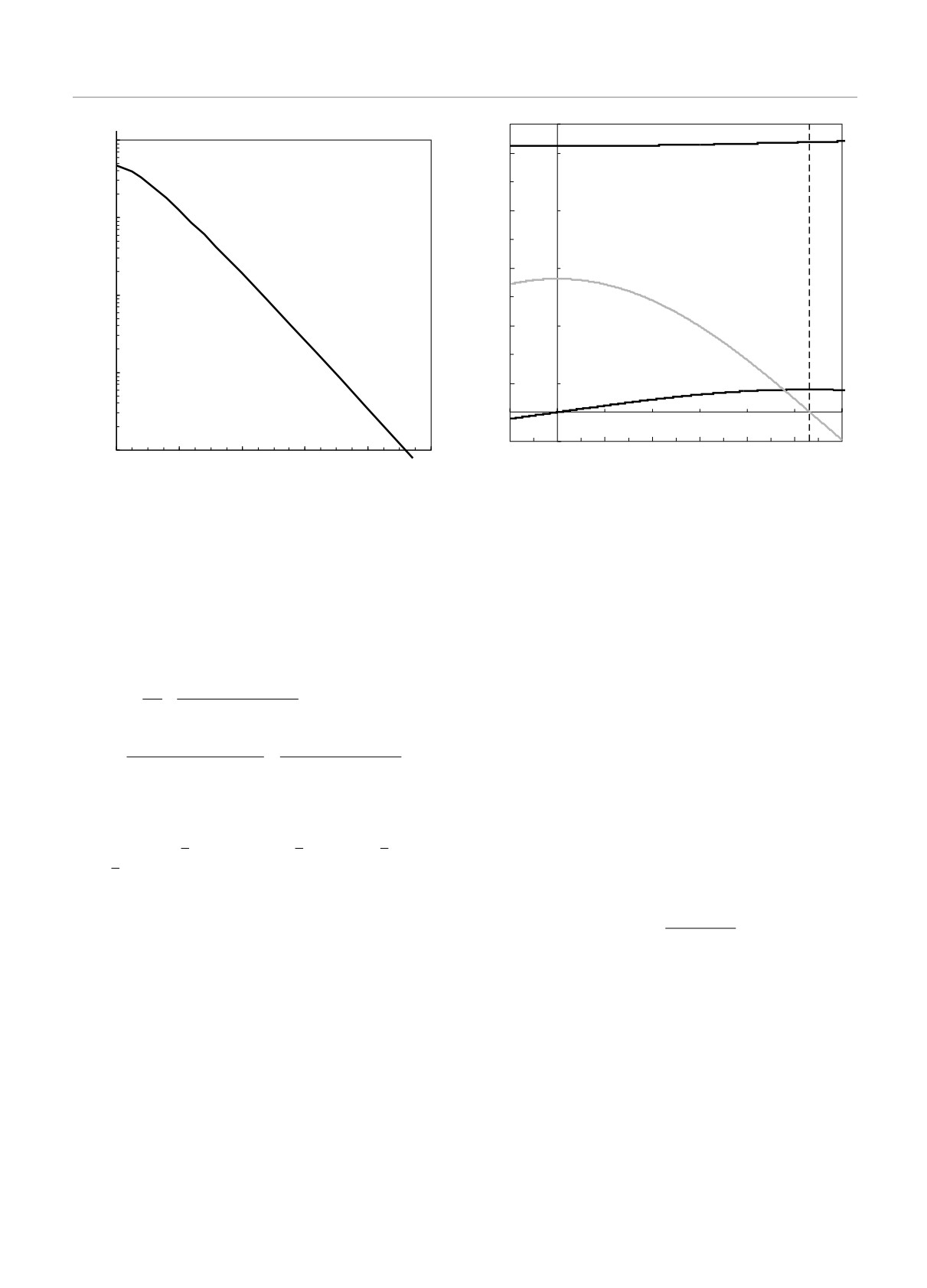
Рис.

2. Зависимость относительного значения α^∗

Рис. 3. Зависимости U^∗ (1), U∗′ (2), U∗′′ (3) от δr/l0 для

= α/(Ql-30) от параметра экранирования κ

κ = 0. Штриховой линией показано положение точки пе-

региба δr0/l0

В приближении линейности внешней силы в на-

правлении главных осей ОЦК-ячейки α^∗ = α и вели-

чину градиента внешнего электрического поля мож-

Развитие амплитудной неустойчивости в анализиру-

но найти из уравнения баланса сил, действующих в

емой ячейке будет происходить, когда минимальное

системе:

(среди всех возможных) значение ΔU = Δ_minU на

одну подвижную частицу системы будет меньше ее

^[ exp(-κ₁)(1 + κ₁)

Qα = 2

кинетической энергии, равной K = 3T/2 для трех-

a³

l₅

мерной системы. В случае взаимного смещения всех

частиц системы (3) условие минимальности глубины

exp(-2κ₁)(1 + 2κ₁)

exp(-κ₂)(1 + κ₂)

потенциальной ямы достигается при контрсмещени-

l₅

l₆

ях центральной частицы и частиц оболочки, когда

]

δr = δr₈ (Δr = 2δr), см. рис. 1. В обоих случаях дан-

+ exp(-κ^∗)(1 + κ^∗) ,

(4)

ное условие можно записать как Δ_minU/N < 3T/2,

где N — количество подвижных частиц (N = 1 и

√

где κ1 = κ∗

3/2, κ2 = κ∗

2, l5 = 3

3/4, l6 =

N = 9). Таким образом, условие развития ампли-

√

2. Зависимость относительного значения α^∗ =

тудной неустойчивости можно представить в виде

= α/(Qa-3) от параметра экранирования κ показа-

на на рис. 2.

3NQ²

Γ<Γ_c =

(5)

Первая производная, U^′, приращения потенци-

2l_pΔ_minU

альной энергии U по δr в точке δr ≡ 0 равна нулю

и соответствует равновесному состоянию системы,

Зависимости параметра Γ_c вблизи линии разви-

а ее вторая производная, U^′′ = 0, в точке переги-

тия амплитудной неустойчивости в рассматривае-

ба (δr = δr₀) отвечает за устойчивость системы при

мых системах от κ представлены на рис. 4, приве-

различных смещениях частиц. Зависимости от δr/l₀

дены значения Γ_c = Γc1 для N = 1 и Γ_c = Γc9 для

относительных значений U^∗ = U/(Q²a-1), а также

N = 9. Там же показаны кривые плавления для про-

первой U∗′ и второй U∗′′ производных представлены

тяженных ОЦК-систем, Γ_m(κ), усредненные по ре-

на рис. 3 для параметра экранирования κ = 0 для

зультатам различных работ [26-34], см. [29,34]. Лег-

случая смещения одной центральной частицы.

ко увидеть, что полученные кривые Γc1(κ) и Γc9(κ) с

Глубина потенциальной ямы рассматриваемой

хорошей точностью пропорциональны зависимости

системы определяется как ΔU = U(δr₀)-U(δr = 0).

Γ_m(κ), см. рис. 4.

568

ЖЭТФ, том 156, вып. 3 (9), 2019

Амплитудная неустойчивость заряженных частиц. . .

10⁴

0.32

0.28

10³

0.24

10²

0.20

0.16

0.12

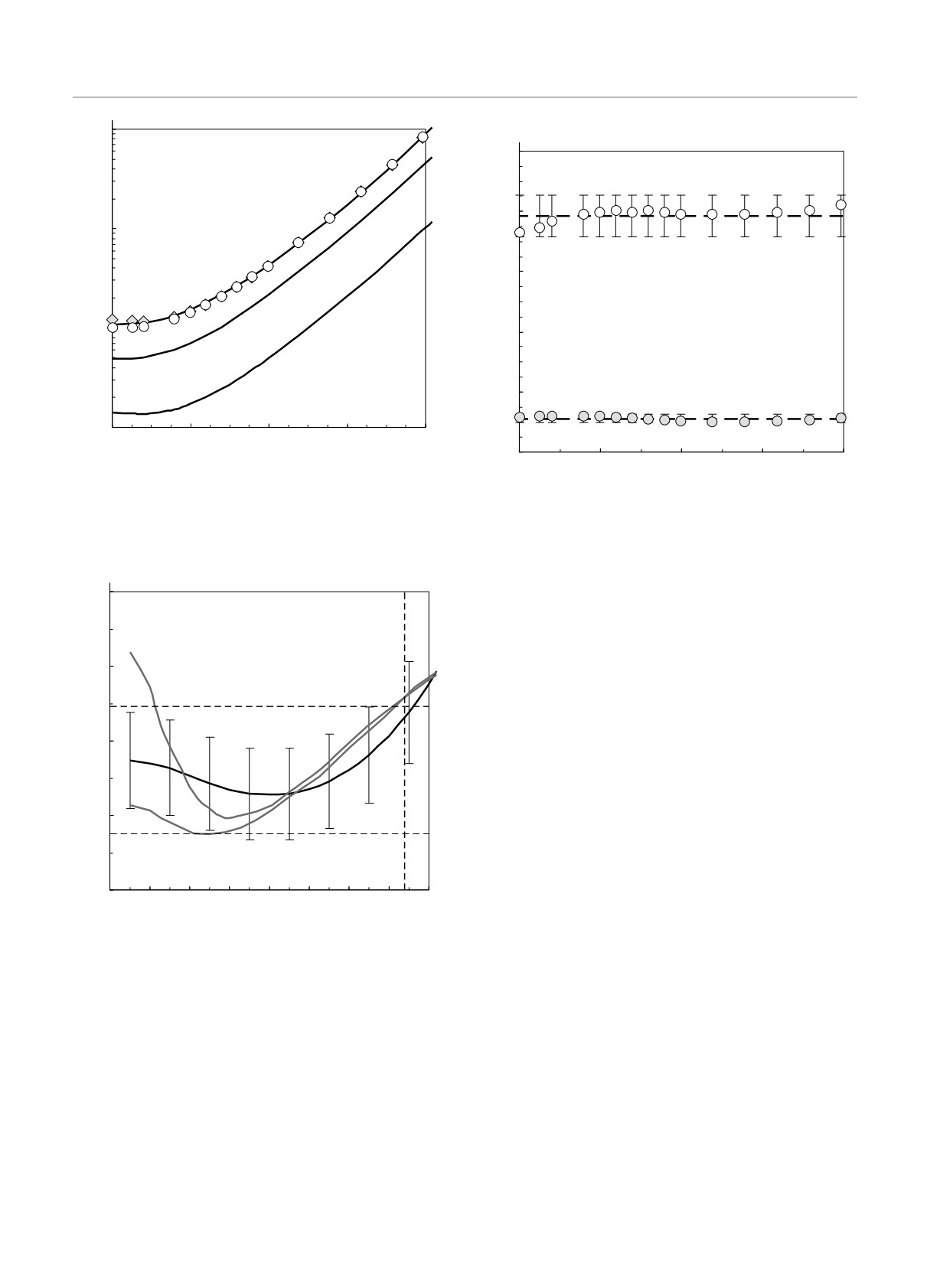
Рис. 4. Зависимости Γc1(κ), Γc9(κ) и Γm(κ) (сплошные

линии). Символы: ♦ — 8.6Γc1(κ), ◦ — 2Γc9(κ)

Рис. 6. Зависимости отношения δr0/l0 от параметра экра-

нирования κ для случаев смещения одной центральной

частицы в ОЦК-ячейке (1), взаимного смещения девяти

частиц в ОЦК-ячейке (2). Средние значения δr0/l0 показа-

ны штриховыми линиями. На рисунке обозначены отклоне-

130

ния в 4 % от среднего значения для кривой 1 и отклонения

от среднего значения в 2 % для кривой 2

120

= Γ_m/B, Γ∗c1 = 8.6Γc1/B и Γ∗c9 = 2Γc9/B, где B =

= exp(κ)(1 + κ + κ²/2)-1. Легко увидеть, что зна-

чения Γ^∗m, Γ∗c1 и Γ∗c9 различаются не более чем на

110

∼ 5%, за исключением Γ∗c1 для κ < 1. Причины

таких различий могут быть связаны как с погреш-

ностью численного моделирования при определении

100

величины Γ_m, так и с наличием используемых при-

ближений, а именно, приближения «ближайших со-

седей» и линейности внешней силы.

Зависимость относительных смещений частиц,

-0.5

0.5

1.5

2.5

3.5

4.5

5.5

6.5

7.5

δr₀/l₀, в точке перегиба, соответствующей случаю

минимальной глубины потенциальной ямы, от пара-

метра экранирования κ показана ни рис. 6. Для всех

Рис. 5. Зависимости Γ^∗m (1), 8.6Γ∗c1 (2) и 2Γ∗c9 (3) от пара-

анализируемых параметров экранирования δr₀/l₀ ≈

метра экранирования κ. На рисунке обозначены отклоне-

≈ 0.27 ± 4 % для случая отклонений центральной

ния в 5 % от величины Γ^∗m. Вертикальная штриховая линия

соответствует κ = 6.9. Горизонтальные штриховые линии

частицы в ОЦК-ячейке и δr₀/l₀ ≈ 0.14 ± 2 % для

ограничивают диапазон от Γ^∗m = 97.5 до Γ^∗m = 114.5

случая смещений всех девяти частиц. Для откло-

нений центральной частицы полученный результат

с точностью до постоянного коэффициента, при-

близительно равного 2, согласуется с параметром

Для более подробного сравнения отклонения

Лидемана для протяженных ОЦК-систем: δ_L

формы полученных кривых (Γc1(κ) и Γc9(κ)) от

= δr_p/l_p ≈ 0.136 ± 2 % [34,35]. Результаты, получен-

зависимости Γ_m(κ) относительные значения Γ^∗m,

ные для случая смещений всех девяти частиц ячей-

8.6Γ∗c1 и 2Γ∗c9 приведены на рис. 5. Здесь Γ∗m =

ки, хорошо соответствуют значениям δ_L.

569

О. С. Ваулина

ЖЭТФ, том 156, вып. 3 (9), 2019

Обратимся к проблеме корректности использова-

ния приближения ближайших соседей для анализа

линий плавления протяженных систем. Здесь сле-

дует отметить, что указанное приближение успешно

использовалось ранее для определения линий плав-

ления протяженных ОЦК- и ГЦК-решеток в си-

стемах Юкавы при κ > 1 ÷ 2 с учетом нелиней-

ности (ангармонизма) сил взаимодействия между

центральной частицей и ее 8 ближайшими соседя-

ми в ОЦК-кластере или 12 соседями в ГЦК-ячейке

[20, 34].

Что касается предположения о линейности внеш-

него поля, следует отметить, что формирование

ОЦК-кластера (состоящего из девяти частиц) в ли-

10^-1

нейном изотропном поле ловушки не соответству-

ет критерию минимума потенциальной энергии си-

стемы [35]. Минимуму потенциальной энергии клас-

Рис.

7. Зависимости (ω^∗E )²

= M(ωE)²/(Q²a-3) (1),

тера из девяти частиц, взаимодействующих с экра-

(ω∗0)²

= M(ω0)²/(Q²a-3)

(2)

2(ω^∗bcc)²

нированным кулоновским потенциалом, в линейном

2M(ω_bcc)²/(Q²a-3)

(3) от параметра экранирова-

изотропном поле соответствует конфигурация «тре-

ния κ показаны сплошными линиями. Символы ◦

—

угольной призмы с тремя дополнительными верши-

= (ω∗0)² + 2Mω2t/(Q²a-3), символы •

— S2

нами». Несколько большей энергией (в пределах ме-

= (ω∗0)² + Mω2t/(Q²a-3). Штриховая линия соответствует

нее 2 % для κ < 7) обладает «квадратная антиприз-

величине κ = 6.9

ма» [35], потенциальная энергия которой, в свою

очередь, несущественно меньше энергии ОЦК-клас-

тера [28,32]. Отметим, что приближение изотропнос-

но предположить, что в случае корректности ис-

ти и линейности электрического поля в кристалли-

пользуемых приближений ω2E - ω²⁰ ∝ ω2t. Результа-

ческих ОЦК- и ГЦК-структурах (включая незави-

ты сравнения упомянутых выше частот показывают,

симость характерных частот системы от числа со-

что ω2E - ω²⁰ ≈ 2ω2t, см. рис. 7. Некоторые отклоне-

ставляющих ее частиц) может иметь место только

ния (менее 10 % для κ < 1 и менее 5 % для κ > 6)

при их значительных размерах R_c ≫ l_p, т. е. когда

могут быть связаны с погрешностью линейного при-

упомянутые системы можно характеризовать одно-

ближения для внешних сил ловушки; на участке от

родной концентрацией.

κ = 1 до κ = 6 отклонения величины (ω2E - ω²⁰) от

значения 2ω2t не превышали 2.5 %.

Для анализа корректности сопоставления ре-

Вторая характерная частота, ω_bcc, является

зультатов, полученных для ОЦК-ячейки, с данными

полуэмпирической аппроксимацией численных

для протяженных систем введем две характерные

данных и хорошо описывает критерий плавле-

частоты ω_E и ω_bcc. Первая из них — частота Эйн-

ния ОЦК-решетки для систем Юкавы; ω2bcc

штейна ω_E, которая отвечает за частоту колебаний

= (2Q)² exp(-κ)(1+κ+κ²/2)/(πl3pM) [37]. Отметим,

частиц в протяженной системе [33, 36]:

что удвоенный квадрат этой частоты 2ω2bcc от-

вечает за отклонения частиц от их положения

2U_t

ω2E =

(6)

равновесия, а также за процессы массопереноса на

3Mλ²

малых временах наблюдения [38, 39]. Результаты

где M — масса частицы, U_t — внутренняя (потенци-

сравнения величин U^′′(δr = 0)/M = (ω20 + ω2t) и

альная) энергия бесконечной решетки на одну час-

ω2bcc показывают, что (ω²⁰ + ω2t) ≈ 2ω2bcc, см. рис. 7.

тицу для систем Юкавы при κ > 0. В случае при-

Отклонения (менее 10 % для κ < 2 и менее 5 %

ближения «ближайших соседей» величина ω2E →

для κ

> 6) в этом случае могут быть связаны

→ ω²⁰ = 8Q²/(3Mλ²l₀). Отметим, что вторая про-

как с погрешностью линейного приближения для

изводная U^′′ потенциальной энергии U (2) по δr в

внешних сил ловушки, так и с использованием

точке δr ≡ 0 для смещения одной центральной час-

приближения «ближайших соседей». На участке от

тицы записывается как U^′′(δr = 0) = M(ω²⁰ + ω2t),

κ = 2 до κ = 6 отклонения величины ω²⁰ + ω2t от

где ω2t = Qα/M — квадрат частоты ловушки. Мож-

значения 2ω2bcc не превышали 2.5 %.

570

ЖЭТФ, том 156, вып. 3 (9), 2019

Амплитудная неустойчивость заряженных частиц. . .

3. ЗАКЛЮЧЕНИЕ

B. Pullman, Intermolecular Interactions: from Di-

atomics to Biopolymers, Wiley Intersci., Chichester

Выполнены исследования условий формирова-

(1978).

ния амплитудных неустойчивостей в трехмерных

R. K. Dodd, J. C. Eilbeck, J. D. Gibbon, and

ОЦК-кластерах, состоящих из девяти заряженных

H. C. Morris, Solitons and Nonlinear Wave Equati-

частиц. Расчеты выполнялись для экранированного

ons, Acad. Press, London-New York (1982).

кулоновского взаимодействия частиц (типа Юкавы)

в широком диапазоне параметров экранирования κ.

R. Balescu, Equilibrium and Nonequilibrium Statis-

Для поиска критерия формирования амплитудной

tical Mechanics, Wiley Intersci., Chichester (1975).

неустойчивости использовался аналитический под-

E. M. Lifshitz and L. P. Pitaevskii, Physical Kinetics,

ход, основанный на определении точки перегиба по-

Pergamon Press, Oxford (1981).

тенциальной энергии системы при отклонении час-

тиц от своего равновесного положения.

10.

O. S. Vaulina, X. G. Adamovich, and S. V. Vladimi-

rov, Phys. Scripta 79, 035501 (2009).

Получена зависимость параметров Γc1 (при сме-

щении одной центральной частицы в ОЦК-ячейке) и

11.

I. I. Lisina and O. S. Vaulina, Europhys. Lett. 103,

Γc9 (для взаимного смещения девяти частиц) от ве-

55002 (2013).

личины параметра экранирования κ вблизи линий

12.

О. С. Ваулина, И. И. Лисина, К. Г. Косс, Физика

развития амплитудной неустойчивости. Выполнено

плазмы 39, 455 (2013).

сравнение полученных результатов с фазовыми кри-

выми, Γ_m(κ), для протяженных трехмерных систем

13.

О. С. Ваулина, А. П. Нефедов, О. Ф. Петров,

с ОЦК-решеткой.

В. Е. Фортов, ЖЭТФ 118, 1325 (2000).

Результаты настоящей работы могут быть адап-

14.

O. S. Vaulina, Europhys. Lett. 115, 10007 (2016).

тированы для структур с любым типом взаимо-

действий, а также могут быть полезны для анализа

15.

A. V. Ivlev, A. G. Khrapak, S. A. Khrapak, B. M. An-

условий плавления малоразмерных систем различ-

naratone, G. Morfill, and K. Yoshino, Phys. Rev.

ной конфигурации, которые представляют интерес

E 68, 026403 (2003).

в физике плазмы, медицине, биологии, физике по-

16.

I. Lisina, E. Lisin, and О. Vaulina, Phys. Plasmas 23,

лимеров и коллоидных систем.

033704 (2016).

Финансирование. Работа частично поддержа-

17.

S. Hamaguchi, R. T. Farouki, and D. H. E. Dubin,

Phys. Rev. E 56, 4671 (1997).

на Российским фондом фундаментальных исследо-

ваний (грант №18-38-20175), а также Программой

18.

D. H. Dubin and H. Dewitt, Phys. Rev. B 49, 3043

Президиума РАН.

(1994).

19.

W. G. Hoover, D. A. Young, and R. Grover, J. Chem.

Phys. 56, 2207 (1972).

ЛИТЕРАТУРА

20.

O. S. Vaulina and X. G. Koss, Phys. Rev. E 92,

1. О. С. Ваулина, О. Ф. Петров, В. Е. Фортов,

042155 (2015).

А. Г. Храпак, С. А. Храпак, Пылевая плазма (экс-

перимент и теория), Физматлит, Москва (2009).

21.

O. S. Vaulina and S. V. Vladimirov, Plasma Phys. 9,

835 (2002).

2. Complex and Dusty Plasmas, ed. by V. E. Fortov and

G. E. Morfill, CRC Press (2010).

22.

К. Г. Косс, О. Ф. Петров, М. И. Мясников,

К. Б. Стаценко, М. М. Васильев, ЖЭТФ 149, 1

3. A. Ivlev, G. Morfıll, H. Lowen, and C. P. Royall,

(2016).

Complex Plasmas and Colloidal Dispersions: Partic-

le-Resolved Studies of Classical Liquids and Solids,

23.

I. I. Lisina, О. S. Vaulina, and Е. А. Lisin, Phys.

World Sci., Singapore (2012).

Plasmas 24, 113705 (2017).

4. Photon Correlation and Light Beating Spectroscopy,

24.

О. С. Ваулина, ЖЭТФ 154, 588 (2018).

ed. by H. Z. Cummins and E. R. Pike, Plenum, New

York (1974).

25.

O. S. Vaulina, I. I. Lisina, and E. A. Lisin, Plasma

Phys. Rep. 44, 270 (2018).

5. А. А. Овчинников, С. Ф. Тимашев, А. А. Белый,

Кинетика диффузионно-контролируемых хими-

26.

O. S. Vaulina and S. A. Khrapak, Zh. Eksp. Teor.

ческих процессов, Химия, Москва (1986).

Fiz. 117, 326 (2000) [JETP 90, 287 (2000)].

571