ЖЭТФ, 2019, том 156, вып. 4 (10), стр. 711-720

ВЗРЫВНОЕ РАЗВИТИЕ КВАНТОВОЙ НЕУСТОЙЧИВОСТИ

КЕЛЬВИНА - ГЕЛЬМГОЛЬЦА СВОБОДНОЙ

ПОВЕРХНОСТИ He-II

Н. М. Зубаревa,b*, П. М. Лушниковc,d**

^a Институт электрофизики Уральского отделения Российской академии наук

620016, Екатеринбург, Россия

^b Физический институт им. П. Н. Лебедева Российской академии наук

119991, Москва, Россия

^c Институт теоретической физики им. Л. Д. Ландау Российской академии наук

142432, Черноголовка, Московская обл., Россия

^d Department of Mathematics and Statistics, University of New Mexico

87131-0001 NM, USA

Поступила в редакцию 12 мая 2019 г.,

после переработки 12 мая 2019 г.

Принята к публикации 15 мая 2019 г.

Исследуется нелинейная динамика квантовой неустойчивости Кельвина - Гельмгольца свободной поверх-

ности He-II, развивающейся при встречном движении нормальной и сверхтекучей компонент жидкого

гелия. Продемонстрировано, что вблизи порога линейной устойчивости эволюция границы описывается

моделью |φ|⁴ — уравнением Клейна - Гордона для комплексной амплитуды возбуждаемой волны с куби-

ческой нелинейностью. Важно, что при любых соотношениях плотностей компонент гелия нелинейность

играет дестабилизирующую роль, ускоряя развитие линейной неустойчивости границы. В рамках метода

интегральных неравенств сформулированы условия взрывного роста возмущений свободной поверхности.

Обсуждается аналогия между квантовой неустойчивостью Кельвина - Гельмгольца и электрогидродина-

мической неустойчивостью заряженной электронами свободной поверхности жидкого гелия.

Статья для специального выпуска ЖЭТФ, посвященного 100-летию И. М. Халатникова

DOI: 10.1134/S0044451019100134

вый случай, реализующийся для³He, наиболее бли-

зок к классической НКГ (фазы находятся по раз-

ные стороны границы), в то время как второй слу-

1. ВВЕДЕНИЕ

чай принципиально отличен — неустойчивость воз-

никает из-за разнонаправленного движения сверх-

Тангенциальный разрыв скоростей как внутри

текучей и нормальной компонент⁴He под свобод-

одной жидкости, так и на границе раздела двух

ной поверхностью. В настоящей работе рассматри-

жидкостей приводит к возникновению классической

вается второй случай, который естественно назвать

неустойчивости Кельвина - Гельмгольца (НКГ) [1].

квантовой НКГ, поскольку обе компоненты нахо-

В последние годы НКГ активно изучалась в сверх-

дятся по одну сторону свободной поверхности и их

текучих жидкостях, включая неустойчивость грани-

сосуществование в одном объеме является кванто-

цы раздела различных сверхтекучих фаз³He [2-6]

вым эффектом, не имеющим классического анало-

и неустойчивость свободной поверхности ⁴He [7-9] в

га. Типичная экспериментальная ситуация, в кото-

сверхтекучей фазе (так называемая фаза He-II, воз-

рой реализуется такое относительное движение ком-

никающая при температуре ниже 2.17 K [10]). Пер-

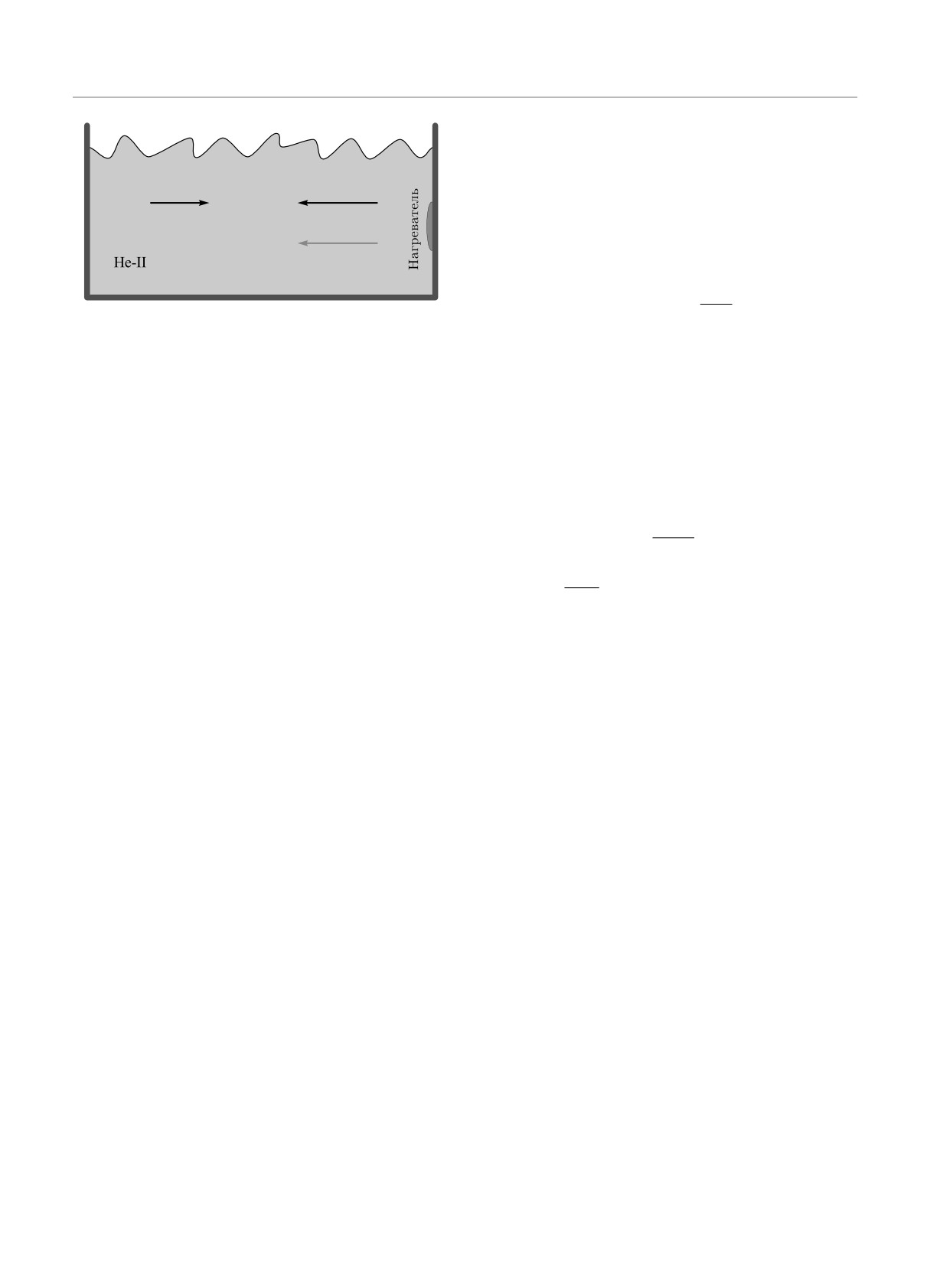
понент, проиллюстрирована на рис. 1. Эксперимен-

тальные исследования возникновения неустойчиво-

^* E-mail: nick@iep.uran.ru

стей свободной плоской поверхности сверхтекучего

^** E-mail: lushniko@itp.ac.ru

711

Н. М. Зубарев, П. М. Лушников

ЖЭТФ, том 156, вып. 4 (10), 2019

считается потенциальным. В таком случае скорости

фаз можно представить в виде v_n,s = ∇Φ_n,s, где

Φ_n,s — потенциалы скоростей, которые удовлетво-

ряют (в силу ρ_n = const и ρ_s = const) уравнениям

v_s

v_n

Лапласа

∇²Φ_n = 0,

∇²Φs = 0,

(3)

Тепловой поток

а дисперсионное соотношение (1) сводится к виду

ρ_sρ_n

(ω - V_m·k)

² =ω2k -

(V·k)²,

(4)

Рис. 1. Встречное движение (со скоростями vs,n) сверхте-

кучей и нормальной компонент сверхтекучего⁴He, вызван-

где V_m ≡ (ρ_nV_n + ρ_sV_s)/ρ — средняя скорость дви-

ное потоком тепла от нагревательного элемента, переноси-

жения центра масс жидкости и V ≡ V_s -V_n — сред-

мого нормальной компонентой. Обе компоненты находятся

няя относительная скорость компонент жидкости.

в одном и том же объеме ⁴He и перемещаются по касатель-

Ниже без потери общности мы полагаем V_m = 0,

ной к общей свободной поверхности

подразумевая переход в соответствующую движу-

щуюся систему отсчета.

He-II при протекании теплового потока в объеме

Дисперсионное соотношение (4) позволяет найти

жидкости были поставлены и активно проводятся

[15, 16] пороговое значение относительной скорости

в Лаборатории квантовых кристаллов ИФТТ РАН

)1/4

по инициативе И. М. Халатникова, см., например,

⁽4ρ³gα

Vc =

(5)

работы [8, 11-14].

ρ2nρ²

Мы используем двухжидкостное приближение

которое соответствует значению волнового числа

√

для описания динамики⁴He [10] с плотностями

k =k₀ ≡

ρg/α. Линейная НКГ возникает при от-

сверхтекучей ρ_s и нормальной ρ_n компонент (общая

носительной скорости V ≡ |V| > V_c.

плотность жидкости есть ρ = ρ_n + ρ_s). Обе компо-

Заметим, что закон дисперсии квантовой НКГ

ненты рассматриваются как несжимаемые жидкос-

примет такой же вид, что и обычный закон дис-

ти (ρ_n = const и ρ_s = const).

персии НКГ для границы раздела двух идеаль-

Инкремент квантовой НКГ для линейных возму-

ных несмешивающихся жидкостей (см., например,

щений, пропорциональных eik·r⊥^-i^ωt, плоской гори-

[1], стр. 346), если в уравнении (4) для ωk вмес-

зонтальной поверхности при наличии гравитации и

то (2) будет использовано классическое дисперсион-

капиллярности, дается следующим дисперсионным

ное соотношение ω2k,classical = (ρ_s - ρ_n)gk/ρ + αk³/ρ

соотношением, найденным в работах [15,16]:

для гравитационно-капиллярных волн в отсутствие

(

)₂

среднего движения компонент жидкости (в этом

ω2k = ρ_s(ω-V_s·k)²+ρ_n

ω - V_n · k + i2ν_nk²

случае подразумевается, что жидкость с плотно-

+ 4ρ_nν2nk³m_n,

(1)

стью ρ_n находится выше границы раздела, а с плот-

ностью ρ_s — ниже). Чтобы вернуться от ω_k,classical к

где V_s и V_n — средние скорости сверхтекучей и

(2) достаточно произвести замену ρ_n → -ρ_n (без из-

нормальной компонент, r_⊥

— горизонтальная ко-

менения полной плотности ρ) в ω_k,classical. Осталь-

ордината, t — время, ν_n — кинематическая вязкость

ные члены в (4) не зависят от g и поэтому не ме-

нормальной компоненты, определяемая как динами-

няются вне зависимости от того, расположена ли

ческая вязкость, нормализованная на ρ_n, k и ω —

вторая жидкость с плотностью ρ_n под свободной

волновой вектор и частота возмущения, k = |k| и

[

]1/2

поверхностью (квантовый случай) или выше грани-

m_n =

k² - i(ω - V_n·k)/ν_n

. Так же

цы раздела (классический случай). Описанное отли-

чие между линейными законами дисперсии класси-

ω2k ≡ gk + αk³/ρ

(2)

ческой и квантовой НКГ носит только количествен-

— закон дисперсии гравитационно-капиллярных

ный характер. Качественное различие между клас-

волн в отсутствие среднего движения компонент

сической и квантовой НКГ возникает на нелиней-

жидкости, g

— ускорение поля тяжести, α

—

ных стадиях развития неустойчивости. Так, в част-

коэффициент поверхностного натяжения.

ности, в пределе V

≫ V_c для классической НКГ

В рамках простейшего бездиссипативного двух-

возникает тенденция к формированию на границе

жидкостного описания [15, 16] течение обоих фаз

раздела жидкостей слабых корневых особенностей,

712

ЖЭТФ, том 156, вып. 4 (10), 2019

Взрывное развития квантовой неустойчивости. . .

для которых поверхность остается гладкой, а беско-

ных неравенств с использованием аналогии с движе-

нечной за конечное время становится ее кривизна

нием эффективной ньютоновской частицы в некото-

[17, 18]. При аналогичных условиях для квантовой

ром потенциале сформулированы достаточные усло-

НКГ возникает тенденция к образованию сильных

вия взрывного роста возмущений свободной поверх-

особенностей — точек заострения [19].

ности. В заключительном разд. 7 обсуждается жест-

В настоящей работе рассматриваются нелиней-

кий характер возбуждения сильно нелинейных ре-

ные стадии развития квантовой НКГ вблизи поро-

шений и их применимость для полной двухжидкост-

га устойчивости, т. е. при |V - V_c|/V_c ≪ 1. В этой

ной гидродинамики.

ситуации возбуждается узкий в фурье-пространстве

пакет поверхностных волн, что позволяет сформу-

2. ИСХОДНЫЕ УРАВНЕНИЯ

лировать уравнение для огибающей этого волно-

вого пакета. Показано, что влияние нелинейности

Мы ограничимся рассмотрением плоских тече-

при любых соотношениях плотностей компонент ге-

ний, когда все величины зависят от пары перемен-

лия оказывает дестабилизирующую роль, т. е. уско-

ных r = (x, y), где x и y — соответственно горизон-

ряет развитие линейной неустойчивости границы и

тальная и вертикальная координаты. В таком слу-

приводит к взрывной неустойчивости с достижени-

чае имеем ∇ = (∂/∂x, ∂/∂y).

ем сингулярности за конечное время в уравнении

В невозмущенном состоянии поверхность ге-

для огибающей. В рамках полных гидродинамичес-

лия — плоскость y = 0, а движение компонент ге-

ких уравнений это означает, что решение становит-

лия вдоль оси x является однородным, т. е. для по-

ся сильно нелинейным (характерные углы наклона

тенциалов скорости справедливо Φ_n,s = V_n,sx, где

укручаются до значений порядка единицы) за ко-

Vn,s — горизонтальные скорости компонент. Как

нечное время.

уже указывалось, без потери общности можно счи-

План статьи следующий: в разд. 2 приводятся

тать ρ_nV_n + ρ_sV_s = 0, что соответствует рассмот-

основные уравнения двухжидкостной гидродинами-

рению задачи в системе центра масс. Тогда компо-

ки с кинематическими и динамическими граничны-

ненты скорости выражаются через среднюю относи-

ми условиями на свободной поверхности. В разд. 3

тельную скорость компонент V = V_s - V_n > 0 как

для двумерных течений проводится переход к эф-

V_n,s = ∓ρ_s,nV/ρ.

фективному одножидкостному описанию с исполь-

Будем считать, что возмущенная свободная по-

зованием гармонически сопряженных потенциалов

верхность жидкого гелия задается уравнением y =

(функций тока). В разд. 4 продемонстрировано, что

= η(x, t), т.е. жидкость занимает область

в итоге наших преобразований исходная задача опи-

сания нелинейного развития квантовой НКГ, возни-

-∞ < x < ∞,

-∞ < y < η(x, t).

кающей за счет относительного движения нормаль-

ной и сверхтекучей фаз, становится эквивалентной

Возмущения потенциалов скорости, возникающие

из-за деформации границы, затухают на глубине:

(с точностью до устранимых заменами постоянных)

задаче о динамике заряженной электронами грани-

Φ_n,s → V_n,sx, y → -∞.

(6)

це жидкого гелия в электрическом поле (предел,

когда заряд полностью экранирует поля над жид-

Движение границы определяется динамическим и

костью). Эта аналогия позволила использовать для

кинематическим граничными условиями. Динами-

рассматриваемой проблемы ряд результатов, полу-

ческое условие (нестационарное уравнение Бернул-

ченных ранее при анализе поведения жидкого гелия

ли для двухкомпонентной жидкости) имеет вид

в электрическом поле. В разд. 5 с использованием

)

результатов работ [20,21] получено, что вблизи поро-

⁽∂Φ_n

(∇Φ_n)²

⁽∂Φ_s

(∇Φ_s)²

ρ_n

+ρ_s

га устойчивости эволюция границы описывается мо-

∂t

делью |φ|⁴ — релятивистски-инвариантным уравне-

αη_xx

= -ρgη +

+ Γ, y = η,

(7)

нием Клейна - Гордона с нелинейным притяжением

(1 + η2x)3/2

для комплексной огибающей возбуждаемой волны.

Важно, что при любых соотношениях плотностей

где η_x ≡ ∂η/∂x, η_xx ≡ ∂²η/∂x²; первое слагаемое в

компонент гелия нелинейность играет дестабилизи-

правой части ответственно за силу тяжести, а вто-

рующую роль, ускоряя развитие линейной неустой-

рое — за капиллярные силы. Эти силы стремятся

чивости границы. В разд. 6 в рамках уравнения

вернуть возмущенную границу жидкости в исход-

Клейна - Гордона на основании метода интеграль-

ное плоское состояние. Величина Γ — постоянная

713

Н. М. Зубарев, П. М. Лушников

ЖЭТФ, том 156, вып. 4 (10), 2019

Бернулли; ее значение, обеспечивающее выполнение

Кинематическое условие для потенциала Φ, как

условия (7) в невозмущенном состоянии Φ_n,s = V_n,sx

несложно получить из (8), примет форму

и η = 0, задается выражением

η_t

√

= ∂_nΦ, y = η.

(14)

ρ_nV2n + ρ_sV2s

ρ_nρ_sV

1+η²

Γ=

2ρ

Наконец, кинематическое условие для потенциала φ

Наконец, согласно кинематическому условию, нор-

имеет, очевидно, тривиальный вид:

мальная скорость границы должна совпадать с нор-

мальной компонентой скорости каждой из фаз:

∂_nφ = 0, y = η.

(15)

η_t

√

= ∂_nΦ_n = ∂_nΦ_s, y = η(x, t),

(8)

Таким образом, исходные уравнения для движения

1+η²

двух компонент жидкого гелия в бездиссипативном

где η_t ≡ ∂η/∂t, а ∂_n ≡ n · ∇ обозначает производную

приближении сводятся к классическим уравнениям

по внешней нормали

для потенциального движения единственной несжи-

маемой жидкости со свободной границей, учитыва-

n = (-η_x,1)

√

ющим капиллярные и гравитационные силы, с до-

1+η2x

полнительным слагаемым ρ(∇φ)²/2 в правой части

к границе жидкости.

нестационарного уравнения Бернулли (13). Оно от-

ветственно за влияние встречного движения компо-

нент жидкого гелия и, как следствие, за развитие

3. ПЕРЕХОД К ЭФФЕКТИВНОМУ

квантовой неустойчивости Кельвина - Гельмгольца.

ОДНОЖИДКОСТНОМУ ОПИСАНИЮ

Обсудим это слагаемое более подробно.

Введем среднюю скорость среды как

Введем вспомогательную функцию ψ, гармони-

чески сопряженную с потенциалом φ, т. е. ψ и φ свя-

ρ_nv_n + ρ_sv_s

v≡

(9)

заны соотношениями Коши- Римана

∂φ

∂ψ

∂φ

∂ψ

Уравнения движения можно переписать в терминах

∂x

∂y

∂x

одной эффективной жидкости с плотностью ρ, дви-

жущейся со скоростью v. Скорости (9) соответству-

Поясним физический смысл величины ψ. Ее можно

ет потенциал

по аналогии с (11) представить в виде

ρ_nΦ_n + ρ_sΦ_s

Φ=

(10)

ψ=

√ρ_sρ_n (Ψ_n - Ψ_s)/ρ,

(16)

т. е. v = ∇Φ. Введем также вспомогательный потен-

где Ψ_n,s — функции тока для нормальной и сверх-

текучей компонент He-II, которые связаны с потен-

циал скорости

циалами Φ_n,s соотношениями

φ=

√ρ_sρ_n (Φ_n - Φ_s)/ρ.

(11)

∂Φ_n,s

∂Ψ_n,s

∂Φ_n,s

∂Ψ_n,s

Потенциалы Φ и φ являются линейными комбинаци-

∂x

∂y

∂x

ями гармонических потенциалов Φ_s,n, поэтому они

удовлетворяют уравнениям Лапласа

Таким образом, гармоническая функция ψ является

(с точностью до постоянного множителя) разностью

∇²Φ = 0,

∇²φ = 0.

функций тока различных компонент гелия.

Как следствие соотношений Коши- Римана име-

Условия на глубине (6) запишутся как

ем

Φ → 0, φ → -V x√ρsρn/ρ, y → -∞.

(12)

∂_nφ|y=η = - ∂_τ ψ|y=η ,

Динамическое граничное условие (7) перепишется

где

как

∂_τ ≡

√

(1, η_x) · ∇

)

1+η²

⁽∂Φ

(∇Φ)

αη_xx

= -ρgη +

— тангенциальная производная. Тогда граничное

∂t

(1 + η2x)3/2

условие (15) перепишется как

ρ(∇φ)

+Γ-

y=η.

(13)

∂_τ ψ = 0, y = η,

714

ЖЭТФ, том 156, вып. 4 (10), 2019

Взрывное развития квантовой неустойчивости. . .

т. е. величина ψ не меняется вдоль границы. Можно

Φ → 0, ϕ_i,o → -E_i,oy, y → -∞,

)

без потери общности положить ψ|y=η = 0.

⁽∂Φ

(∇Φ)²

αη

С использованием ψ уравнения движения при-

= -ρgη +

∂t

(1 + η2x)3/2

мут окончательный вид:

(∇ϕ_i)² - (∇ϕ_o)²

+γ-

y=η,

8π

∇²Φ = 0,

∇²ψ = 0,

(17)

√

= ∂_nΦ, ϕ_i = ϕ_o = 0, y = η,

1+η²

Φ → 0, ψ → -V y√ρsρn/ρ, y → -∞,

(18)

- E2o)/8π, а

где постоянная Бернулли есть γ = (E2i

)

⁽∂Φ

(∇Φ)

αη_xx

потенциал границы y = η принят за нуль. Послед-

= -ρgη +

∂t

(1 + η2x)3/2

нее слагаемое в нестационарном уравнении Бернул-

ли ответственно за электростатическое давление на

ρ(∇ψ)

+Γ-

y=η,

(19)

свободной границе; оно включает в себя давления

над и под поверхностью.

η_t

√

= ∂_nΦ, ψ = 0, y = η.

(20)

Приведенные уравнения оказываются идентич-

1+η²

ными выведенным нами уравнениям для квантовой

Важно, что задача на определение функции ψ и, как

неустойчивости Кельвина - Гельмгольца (17)-(20) в

следствие, ключевого слагаемого ρ(∇ψ)²/2 в дина-

частном случае, когда Eo = 0 и, соответственно,

мическом граничном условии отщепляется от общей

ϕ_o ≡ 0 и E_i = -4πσ. Этот случай (поверхностный

задачи о движении границы. Действительно, из этих

заряд полностью экранирует поле над жидкостью)

уравнений видно, что величина ψ полностью опреде-

реализовывался, например, в экспериментах [22,24].

ляется формой границы η и не зависит от характера

В рамках этой аналогии вспомогательная функция

ее движения (т. е. от потенциала Φ). Именно это и

тока ψ и потенциал электрического поля в жидкости

определяет возможность перехода к одножидкост-

ϕ_i, а также разность скоростей V и напряженность

ному описанию для рассматриваемой проблемы.

поля E_i связаны соотношениями

√

4πρ ≡ ϕ_i, V

4πρ_nρ_s/ρ ≡ E_i.

4. АНАЛОГИЯ С ДИНАМИКОЙ ЖИДКОГО

ГЕЛИЯ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ

Отметим, что тогда совпадают и постоянные Бер-

нулли: Γ ≡ γ.

Продемонстрируем, что уравнения

(17)-(20)

Выявленная аналогия позволяет использовать

идентичны уравнениям, возникающим в описании

результаты, полученные ранее при анализе разви-

неустойчивости заряженной электронами свободной

тия электрогидродинамической неустойчивости за-

границы жидкого гелия во внешнем электрическом

ряженной поверхности жидкого гелия [20, 21, 25-27],

поле. Пусть жидкий гелий находится при доста-

для анализа квантовой неустойчивости Кельви-

точно низкой температуре, так что можно считать,

на - Гельмгольца.

что нормальная фаза отсутствует (ρ_n ≈ 0 и ρ ≈

В заключение раздела отметим, что эта аналогия

≈ ρ_s). Невозмущенная (плоская) граница заряжена

не распространяется на общий, трехмерный случай.

электронами с поверхностной плотностью электри-

Для НКГ имеется выделенное направление — на-

ческого заряда σ. Как известно, электроны могут

правление течения жидкостей (ось x в нашем слу-

свободно перемещаться вдоль границы, обеспечивая

чае). Для электрогидродинамической неустойчиво-

ее эквипотенциальность [22, 23]. В приложенном

сти выделенного направления не существует — зада-

вертикальном однородном электрическом поле на-

ча инвариантна относительно вращения вокруг вер-

пряженности поля над (E_o) и внутри (E_i) жидкости

тикальной оси y, вдоль которой направлено внешнее

связаны соотношением E_o - E_i = 4πσ.

электрическое поле.

Потенциал скорости жидкости (единственной) Φ

и потенциалы электрического поля над (ϕ_o) и внут-

ри (ϕ_i) жидкости удовлетворяют уравнениям Ла-

5. АМПЛИТУДНОЕ УРАВНЕНИЕ ДЛЯ

пласа

ДИНАМИКИ СВОБОДНОЙ ГРАНИЦЫ

∇²Φ = 0,

∇²ϕ_i,o = 0.

Анализ, проведенный в работе [20] показал, что

Их следует решать совместно со следующими усло-

граница жидкого гелия в электрическом поле ста-

виями на глубине и на свободной границе:

новится неустойчивой при выполнении условия

715

Н. М. Зубарев, П. М. Лушников

ЖЭТФ, том 156, вып. 4 (10), 2019

E2i + E2o > E2c,

где критическая скорость определяется уравнени-

ем (5).

где

За счет дестабилизирующего влияния нелиней-

E2c = 8π√ρgα.

ности возникает тенденция к взрывному росту амп-

Вблизи порога устойчивости нарастают гармоники

литуды границы He-II при развитии НКГ прост-

√

с волновыми числами близкими к k₀ =

ρg/α. Вве-

ранственно-однородного решения: она неограничен-

дем параметр надкритичности как

но увеличивается за конечное время как

E2i + E2o - E2c

u∝

t→t_c,

δ=

t-t_c

E²

— момент «взрыва». Любопытно, что этот ре-

где t_c

Если |δ| ≪ 1, то при описании динамики границы

зультат не зависит от отношения плотностей нор-

естественно построить уравнение для огибающей.

мальной и сверхтекучей компонент гелия. Коэффи-

Для двумерного случая (в трехмерном возникает

циент перед нелинейным слагаемым в уравнении

необходимость рассмотрения взаимодействия трех

(21) оказывается универсальным. В рамках разви-

плоских волн, волновые векторы которых поверну-

ваемой модели единственной величиной, зависящей

ты на 2π/3 [28,29]) форма границы ищется в виде

от отношения плотностей, является пороговое для

[

]

(

)

развития НКГ значение разности скоростей компо-

η(x, t) =

u(x, t)eik0x+u^∗(x, t)e-ik0

|u|²

нент (5), входящее в надкритичность (22).

2k₀

После масштабирования

где u — безразмерная комплексная амплитуда (оги-

бающая) волны, а знак «∗» обозначает комплексное

t→

x→

√

u→

√

^√2gk₀ ,

2k₀

сопряжение. Как показано в работе [21], эволюция

границы описывается уравнением Клейна - Гордона

амплитудное уравнение (21) для огибающей u при-

с кубической нелинейностью:

нимает компактный вид:

(

)

∂²u

= δu +

+ Δ² -

u |u|² ,

= δu +

+ |u|² u.

(23)

2gk₀ ∂t²

2k²

∂x²

∂t²

∂x²

Ему соответствует гамильтониан

где обозначено

)

∫ (



_∂u2

|u|⁴

E2i - E2o

H =



- δ|u|²

dx,

(24)

Δ=



∂t

^∂x

E²

который является интегралом движения.

Видно, что в линейном приближении (в простран-

ственно однородном случае) амплитуда будет экс-

поненциально нарастать при δ > 0. При этом нели-

6. УСЛОВИЯ ВЗРЫВНОГО РАЗВИТИЯ

нейность будет сдерживать развитие неустойчивос-

КВАНТОВОЙ НЕУСТОЙЧИВОСТИ

ти для 0 < Δ² < 5/16 и ускорять ее развитие для

КЕЛЬВИНА - ГЕЛЬМГОЛЬЦА

Δ² > 5/16.

В интересующем нас случае, когда E_o = 0, при

Итак, мы установили, что при развитии кванто-

малых надкритичностях δ ≈ 0 имеем E_i ≈ E_c и,

вой НКГ огибающая волнового пакета u подчиня-

как следствие, Δ ≈ 1. В таком случае амплитудное

ется комплексному нелинейному уравнению Клей-

уравнение принимает вид

на - Гордона с кубической нелинейностью, называе-

мой моделью |φ|⁴. Особенностью уравнения (23) яв-

∂²u

ляется то, что нелинейность не стабилизирует ли-

= δu +

u |u|² ,

(21)

2gk₀ ∂t²

2k²

∂x²

нейную неустойчивость, а, наоборот, усиливает ее,

приводя при определенных условиях к взрывному

т. е. нелинейность — дестабилизирующая. Как сле-

росту амплитуд. Действительно, полагая возмуще-

дует из анализа разд. 4, это уравнение будет описы-

ние границы η(x, t) и, следовательно, амплитуду

вать и развитие неустойчивости Кельвина - Гельм-

u(x, t) локализованными в пространстве, рассмот-

гольца границы He-II. Для этого случая надкритич-

рим, аналогично [30], временную эволюцию квадра-

ность задается выражением

та L² нормы

∫

V -V_c

δ=

(22)

B(t) ≡

|u|² dx.

(25)

V_c

716

ЖЭТФ, том 156, вып. 4 (10), 2019

Взрывное развития квантовой неустойчивости. . .

Уравнения (23)-(25) позволяют написать

∫

[

]

> 0

B_tt =

2|u_t|² + u_ttu^∗ + uu^∗tt

dx =

4H²

–

< 0

∫

[

]

H < 0,

= -4H +

6|u_t|² - 2δ|u|² + 2|u_x|²

dx,

(26)

или

где мы использовали интегрирование по частям по

x с учетом убывающих граничных условий при

∫

|x| → ∞. Отметим, что вклад от 2

|u|⁴dx был

Рис. 2. Качественный вид потенциала U(A) (32) в зависи-

полностью поглощен членом -4H. Нижние индек-

мости от H и δ при Q = 0

сы в уравнении (26) и далее означают диффе-

ренцирование: u_t

= ∂u/∂t, u_x

= ∂u/∂x, B_tt

= ∂²B/∂t² = d²B/dt² и т. д.

Для оценки снизу члена

∫

Замена переменных B = A-2 позволяет предста-

6|u_t|²dx = 6 R2tdx + 6 φ2tR²dx

(27)

вить (30) в виде

∂U(A)

в уравнении (26) мы представляем комплексную ам-

A_tt ≤ -

(31)

∂A

плитуду u в форме u ≡ Re^iφ, где R = |u| — ампли-

где

туда и φ — фаза. Используя неравенство Коши - Бу-

HA⁴

A²

A⁶Q²

няковского

U (A) = -

-δ

(32)

∫



(∫

)1/2 (∫

)1/2



Дифференциальное неравенство

(31) может



fgdx

≤

|f|²dx

|g|²dx



быть переписано в эквивалентном виде обыкновен-

ного дифференциального уравнения

справедливого для комплексных функций f и g, мы

∂U(A)

получаем неравенства

A_tt = -

- h²(t),

(33)

∂A

∫



(∫

)1/2



|B_t| = 2



R_tdx

2B1/2

R2tdx

(28)

где -h²(t) является неположительной неизвестной

 R

^≤

силой.

Анализ образования сингулярности в уравнении

∫



(∫

)1/2

(23) может быть проведен на основании метода,



|Q| = 2



2B1/2

φ2tR²dx

(29)

предложенного в работе [33] (дальнейшее разви-

 φ

tR²dx≤

тие метода см. [34-36]). Метод основан на аналогии

∫

где Q ≡ i

[u_tu^∗ - uu^∗t]dx является интегралом дви-

уравнения (33) с движением эффективной ньюто-

жения (Q_t ≡ 0) уравнения (23). При использовании

новской «частицы» с координатой A в потенциале

уравнения (23) в квантовой теории поля и теории

(32) под воздействием дополнительной (вообще го-

солитонов этот интеграл иногда называется зарядом

воря непотенциальной) силы -h(t)², тянущей части-

(см., например, [31, 32]), мы однако ниже не будем

цу в начало координат. Достижение этой частицей

использовать подобную терминологию, поскольку

нуля A = 0 соответствует образованию сингуляр-

понятие заряда уже использовалось в разд. 4 и 5

ности B = ∞ в уравнении (23). В зависимости от

в другом контексте.

значений H и δ, качественный вид потенциала U(A)

Используя неравенства (28), (29) мы получаем из

(32) показан на рис. 2 при Q = 0. (Частный случай

(27) следующее неравенство:

Q = 0 рассматривается аналогично, см. также [30]).

∫

Удобно ввести энергию частицы

3B2t

3Q²

6|u_t|²dx ≥

W (t) ≡

+ U(A),

(34)

Подставляя это выражение в (26), а также опус-

∫

которая зависит от времени в силу наличия силы

кая член

2|u_x|²dx (пренебрежение этим неотрица-

-h(t)² как

тельным членом совместимо со знаком неравенства)

приходим к дифференциальному неравенству

[

]

dW (t)

∂U(A)

=A_t A_tt +

= -h(t)²A_t.

(35)

3 B²

3 Q

∂A

B_tt ≥

- 4H - 2δB.

(30)

2 B

717

Н. М. Зубарев, П. М. Лушников

ЖЭТФ, том 156, вып. 4 (10), 2019

Полная классификация достаточных условий об-

в этих случаях достаточное условие коллапса не мо-

разования сингулярности за конечное время (назы-

жет быть сформулировано (хотя коллапс все равно

ваемое также волновым коллапсом или просто кол-

не исключен: для его полного описания требуется

лапсом [37]) может быть получена и при необходи-

полное знание зависимости -h(t)²).

мости легко сформулирована как точная теорема на

Если одно из приведенных выше достаточных

основании следующих соображений, которые долж-

условий взрывного развития НКГ выполняется и

ны рассматриваться отдельно для случаев A_t(0) > 0

A_t(0) ≤ 0, то для времени возникновения особен-

и A_t(0) ≤ 0:

ности t_c справедливо неравенство

(A) Если при данных начальных условиях A(0)

∫

и A_t(0) ≤ 0 частица достигла бы начала координат

t_c ≤

√

A = 0 в уравнении (33) под воздействием только

2[W (0) - U(A)]

консервативной силы -∂U(A)/∂A, то она заведомо

достигнет начала координат за такое же или мень-

следующее из уравнений (33) и (34).

шее время при учете силы -h(t)². Это связано с тем,

Также заметим, что для пространственно-одно-

что, в соответствии с (35), в рассматриваемом слу-

родных начальных условий -h²(t) ≡ 0 (все интег-

чае с A_t ≤ 0, для энергии имеем W (t) ≥ W (0). В

ралы в этом случае должны пониматься в смысле

случае рис. 2a для коллапса требуется, чтобы было

их значений на единицу длины вдоль x), все нера-

W (0) > 0, т. е. частица имела достаточную началь-

венства этого раздела превращаются в равенства, в

ную энергию для достижения нуля за конечное вре-

том числе дифференциальное неравенство (31) ста-

мя. В случае рис. 2б необходимо, чтобы либо A(0)

новится обыкновенным дифференциальным уравне-

находилось левее барьера (при любом W (0)), либо

нием для ньютоновской частицы. Таким образом, на

значение W (0) было выше барьера (при A(0) правее

классе однородных решений достаточные критерии

барьера). Случай рис. 2в наиболее простой, посколь-

коллапса этого раздела становятся достаточными и

ку для него коллапс возникает при любых значениях

необходимыми критериями коллапса, что обобщает

A(0), A_t(0) и W (0).

критерии коллапса работы [30], где не был учтен

(B) При A_t(0) > 0 достаточные условия коллап-

вклад от интеграла движения Q. При этом асимп-

са могут быть сформулированы для случаев, по-

тотика падения частицы в нуль A = 0 соответствует

казанных на рис. 2б и 2в. В случае рис. 2в кол-

постоянной скорости A_t, поэтому для B = A-2 и,

лапс возникнет при любых значениях A(0), A_t(0)

соответственно, для квадрата амплитуды |u|² оги-

и W(0), поскольку монотонность потенциала U(A)

бающей поверхностной волны асимптотика коллап-

заставит частицу перестать двигаться вправо за ко-

са соответствует закону (t_c - t)-2.

нечное время (ненулевая сила -h(t)² только ускорит

этот процесс), после чего частица упадет в нуль за

конечное время (опять же, ненулевая сила -h(t)²

7. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ

только ускорит этот процесс). При этом, к примеру,

для обеспечения условия H < 0 при δ < 0 необходи-

Отметим, что часть достаточных критериев

мо, чтобы нелинейность была достаточно сильной,

взрывного роста амплитуд, полученных в разд. 6,

∫

так чтобы отрицательный вклад от -

(1/2)|u|⁴dx в

применима к случаю, когда плоская поверхность

гамильтониане (24) перевесил вклад от всех осталь-

устойчива по отношению к малым возмущениям

ных положительных членов. В случае рис. 2б с

(δ < 0). Это означает, что возбуждение неустойчи-

A_t(0) > 0 коллапс заведомо возникает, если A(0)

вости будет носить жесткий характер и достаточно

находится левее барьера и начальная энергия W (0)

большое начальное возмущение линейно устойчиво-

недостаточна для его преодоления даже без учета

го режима может приводить к образованию сингу-

силы -h²(t). Тогда с учетом силы -h²(t) частица

лярности за конечное время. Во всех случаях вбли-

заведомо остановится левее барьера и далее упа-

зи сингулярности уравнение (23) теряет свою при-

дет в нуль за конечное время. В остальных случаях

менимость: следующие порядки теории возмущений

рис. 2а и 2б (A(0) правее барьера) частица может

начинают давать вклад такого же порядка, как и

застрять в окрестности минимума потенциала, по-

нелинейность в (23). Тогда можно заключить, что за

скольку, как следует из уравнения (35) при A_t(0) >

конечное время t_c решение становится сильно нели-

> 0, имеем W(t) ≤ W(0), т.е. частица теряет энер-

нейным, т. е. характерные углы наклона поверхно-

гию и после отражения от стенки ее может оказать-

сти становятся порядка единицы за счет действия

ся недостаточной для преодоления барьера, поэтому

ведущей нелинейности уравнения Клейна - Гордона.

718

ЖЭТФ, том 156, вып. 4 (10), 2019

Взрывное развития квантовой неустойчивости. . .

После этого в ситуации общего положения можно

S. Babuin, V. S. Lvov, A. Pomyalov, L. Skrbek, and

ожидать обрушения волн. В этой области необходи-

E. Varga, Phys. Rev. B 94, 174504 (2016).

мо рассматривать полные гидродинамические урав-

10.

И. М. Халатников, Теория сверхтекучести, Нау-

нения разд. 3, что выходит за рамки настоящей ра-

ка, Москва (1971).

боты.

Заметим, что в работе [19] в пренебрежении

11.

L. V. Abdurahimov, A. A. Levchenko, L. P. Mezhov-

Deglin, and I. M. Khalatnikov, Low Temp. Phys. 38,

гравитацией и капиллярностью были исследованы

1013 (2012).

сколько угодно сильнонелинейные стадии кванто-

вой НКГ: была показана полная интегрируемость

12.

А. А. Левченко, Л. П. Межов-Деглин, А. А. Пель-

уравнений движения в смысле сведения точной ди-

менев, Письма в ЖЭТФ 106, 233 (2017).

намики к уравнению лапласовского роста, которое

13.

А. А. Левченко, Л. П. Межов-Деглин, А. А. Пель-

имеет бесконечное число интегралов движения и

менев, ФНТ 44, 1284 (2018).

связано с бездисперсионным пределом интегрируе-

мой иерархии Тоды [38]. Интересным вопросом для

14.

L. Mezhov-Deglin, A. Pel’menev, and A. Levchenko,

будущих исследований будет изучение возможности

Mat. Lett. 238, 226 (2019).

интегрируемости полных гидродинамических урав-

15.

S. E. Korshunov, Europhys. Lett. 16, 673 (1991).

нений разд. 3.

16.

S. E. Korshunov, Письма в ЖЭТФ 75, 496 (2002).

Финансирование. Работа Н. М. З. выполня-

17.

D. W. Moore, Proceed. Royal Soc. London A: Math.,

лась при частичной поддержке Российской акаде-

Phys. and Eng. Sci. 365(1720), 105 (1979).

мии наук (программа Президиума РАН № 2), Ураль-

ского отделения Российской академии наук (про-

18.

Н. М. Зубарев, Е. А. Кузнецов, ЖЭТФ 146, 194

ект № 18-2-2-15) и Российского фонда фундамен-

(2014).

тальных исследований (проект № 19-08-00098). Ра-

19.

P. M. Lushnikov and N. M. Zubarev, Phys. Rev. Lett.

бота П. М. Л. по анализу взрывной неустойчивости

120, 204504 (2018).

была выполнена в рамках госзадания «Динамика

сложных сред». Работа П. М. Л. выполнялась при

20.

Д. М. Черникова, ФНТ 2, 1374 (1976).

частичной поддержке Nationаl Science Foundation

21.

Л. П. Горьков, Д. М. Черникова, ДАН СССР 228,

(grant number DMS-1814619).

829 (1976).

22.

В. С. Эдельман, УФН 130, 675 (1980).

ЛИТЕРАТУРА

23.

В. Б. Шикин, УФН 181, 1241 (2011).

1. Л. Д. Ландау, И. М. Лифшиц, Гидродинамика,

24.

А. П. Володин, М. С. Хайкин, В. С. Эдельман,

Наука, Москва (1988).

Письма в ЖЭТФ 26, 707 (1977).

2. G. E. Volovik, Письма в ЖЭТФ 75, 491 (2002).

25.

Н. М. Зубарев, Письма в ЖЭТФ 71, 534 (2000).

3. R. Blaauwgeers, V. B. Eltsov, G. Eska, A. P. Finne,

26.

Н. М. Зубарев, ЖЭТФ 121, 624 (2002).

R. P. Haley, M. Krusius, J. J. Ruohio, L. Skrbek, and

27.

Н. М. Зубарев, ЖЭТФ 134, 779 (2008).

G. E. Volovik, Phys. Rev. Lett. 89, 155301 (2001).

28.

Е. А. Кузнецов, М. Д. Спектор, ЖЭТФ 71, 262

4. G. E. Volovik, The Universe in a Helium Droplet,

(1976).

Oxford Univ. Press, Oxford (2003).

29.

N. M. Zubarev, O. V. Zubareva, Phys. Lett. A 272,

5. A. P. Finne, V. B. Eltsov, R. Hanninen, N. B. Kopnin,

119 (2000).

J. Kopu, M. Krusius, M. Tsubota, and G. E. Volovik,

Rep. Progr. Phys. 69, 3157 (2006).

30.

Е. А. Кузнецов, П. М. Лушников, ЖЭТФ 108, 614

(1995).

6. Г. Е. Воловик, УФН 185, 970 (2015).

31.

Н. Н. Боголюбов, Д. В. Ширков, Квантовые поля,

7. R. Hänninen and A. W. Baggaley, Proceeding of the

Наука, Москва (1993).

National Academy of Sciences USA 111, 4667 (2014).

32.

V. G. Makhankov, Phys. Rep. 35, 1 (1978).

8. I. A. Remizov, A. A. Levchenko and L. P. Me-

zhov-Deglin, J. Low Temp. Phys. 185, 324 (2016).

33.

П. М. Лушников, Письма в ЖЭТФ 62, 447 (1995).

719