ЖЭТФ, 2019, том 156, вып. 4 (10), стр. 742-749

РАЗЛОЖЕНИЕ НЕРЕГУЛЯРНОГО РЕШЕНИЯ В ТЕОРИИ

ЭФФЕКТА ШТАРКА В РИДБЕРГОВСКИХ СОСТОЯНИЯХ

ВОДОРОДОПОДОБНЫХ АТОМОВ

В. Г. Ушаков^*, В. И. Ошеров , Э. С. Медведев^**

Институт проблем химической физики Российской академии наук

142432, Черноголовка, Московская обл., Россия

Поступила в редакцию 6 марта 2019 г.,

после переработки 6 марта 2019 г.

Принята к публикации 7 марта 2019 г.

Получено разложение нерегулярного физического решения по сферическим функциям при отрицатель-

ных энергиях, необходимое для вывода S-матрицы. Прослежена взаимосвязь этого разложения с теорией,

развитой в работе [6]. В частности, показано, что отсутствующее в этой теории разложение нерегулярно-

го решения может быть получено из ее постулатов. Полученное таким образом разложение оказывается

численно эквивалентным нашему разложению, в том числе и при больших значениях углового момента.

Выведены аналитические выражения для матриц обоих разложений.

Статья для специального выпуска ЖЭТФ, посвященного 100-летию И. М. Халатникова

DOI: 10.1134/S0044451019100171

туры остова и внешнего поля мало по сравнению

с кулоновским притяжением остова. В процедуре

сшивки используются взаимные разложения регу-

1. ВВЕДЕНИЕ

лярных и нерегулярных параболических и сфериче-

Для количественного описания спектров фото-

ских решений, которые необходимы для расчета на-

поглощения атомов щелочных металлов в электри-

блюдаемых величин. Теория Хармина была с успе-

ческом поле Хармин [1] использовал идею Фано [2]

хом применена к расчетам сечения фотоионизации

о локальном преобразовании (ЛП) волновых функ-

атомов натрия и для интерпретации экспериментов

ций. В рамках этого подхода физические, т. е. огра-

по фотоионизации. Однако ее применение к расче-

ниченные на бесконечности решения, записанные

там дифференциального сечения в экспериментах

в параболических координатах, необходимо сшить

по ионизационной микроскопии и сравнение с ре-

вблизи остова со сферическими решениями, удовле-

зультатами высокоточных экспериментов [5] оказа-

творяющими граничным условиям, определяемым в

лись неудовлетворительными. Более того, было по-

теории квантового дефекта [3,4]. Согласно этой тео-

казано, что ЛП для нерегулярной волновой функ-

рии, решения вне остова представляют собой линей-

ции, определенное в теории Хармина, не удовлетво-

ные комбинации регулярной и нерегулярной сфери-

ряет некоторым необходимым требованиям [5-8].

ческих кулоновских функций. Поэтому, чтобы по-

Недавно Джаннакис и др., используя формаль-

лучить решение, справедливое при любых значе-

ную операторную алгебру и вводя эффективный од-

ниях радиальной координаты r вне остова, необ-

ночастичный потенциал, предложили обобщенную

ходимо сшить физическое параболическое решение

теорию локального преобразования (ОЛП) [6]. В

со сферическими функциями, отвечающими опреде-

теории ОЛП сделана попытка не использовать ЛП

ленным значениям орбитального углового момента

нерегулярного решения, но оно тем не менее присут-

l. Такая сшивка возможна лишь локально в проме-

ствует неявно и может быть выведено из ее посту-

жуточной области расстояний, где влияние струк-

латов. В данной работе мы, во-первых, даем свой

^* E-mail: uvg@icp.ac.ru

вывод ЛП нерегулярного решения и приводим яв-

^** E-mail: medvedev@icp.ac.ru

ное аналитическое выражение для матрицы этого

742

ЖЭТФ, том 156, вып. 4 (10), 2019

Разложение нерегулярного решения в теории эффекта Штарка. . .

преобразования (разд. 2). Во-вторых, мы сравнива-

В [9] матрица γ_l,l′ вычислялась численно. В этом

ем наше ЛП нерегулярного решения с тем, которое

разделе будет выведено ее явное аналитическое вы-

мы вывели из теории Джаннакиса и др. (разд. 3), и

ражение. Определения ненормированных радиаль-

находим, что численно они эквивалентны.

ных сферических функций, принятые в [9], имеют

вид

⁽r

2. РАЗЛОЖЕНИЕ НЕРЕГУЛЯРНОГО

F_l (r) =

)^l e-r/nΦ (-n + l + 1, 2l + 2, 2r/n) ,

(2)

РЕШЕНИЯ

В пределе слабого поля F ≪ 1 (используются

)_l

⁽r

атомные единицы) можно выделить область остова

Gl (r) =

e^-r/nΨ (-n + l + 1, 2l + 2, 2r/n),

(3)

(r ≲ 1) и промежуточную (кулоновскую) область

√

расстояний 1 ≪ r ≪ F-1/2, в которой внешнее по-

где n

-2E, E

— энергия, Φ (a, b, x) и

ле слабо, F r ≪ 1/r, и потенциал является кулонов-

Ψ (a, b, x)

— функции Куммера соответственно

ским, -1/r. В кулоновской области внешнее поле,

M (a, b, x) и U (a, b, x) [10]. Мы рассматриваем слу-

несмотря на его слабость, может смешивать состо-

чай n ≫ 1, что соответствует высоковозбужденным

яния с разными значениями орбитального момента

ридберговским состояниям.

на расстояниях, где полевая энергия электрона пре-

Функции в правой части уравнения (1) — это

вышает разность его центробежных энергий между

нерегулярные решения штарковской задачи в пара-

соседними состояниями l и l-1, F r ≥ 2l/r². Поэтому

болических координатах. Они имеют вид

смешиванием можно пренебречь не во всей кулонов-

ской области, а только в ее части, «ближней куло-

ψ_k (ξ, η) = χ_ν

(ξ) ψμk (η) ,

(4)

новской области» 1 ≪ r ≪ F-1/3, которая намно-

где χνk (ξ) — нормированные на единицу решения

го уже. При малых r, т. е. в ближней кулоновской

задачи на собственные значения для финитного дви-

области, существуют одновременно сферические и

жения вдоль координаты ξ и ψμk (η) — нерегуляр-

параболические решения, и поэтому можно выпол-

ные в нуле решения штарковской задачи для ин-

нить ЛП между ними, тогда как при больших r, т. е.

финитного движения по η. Нецелые квантовые чис-

вне ее, имеются только параболические функции.

ла ν_k = nβ_k - (m + 1)/2 и μ_k = n - ν_k - m - 1

Как следствие l-смешивания в кулоновской обла-

пробегают ряд дискретных значений, соответствую-

сти, пришитые сферические функции должны неиз-

щих собственным значениям β_k константы разделе-

бежно включать линейную комбинацию состояний с

ния β (парциального заряда) сепарабельного урав-

разными l. Результирующее уравнение сшивки име-

нения Шредингера в параболических координатах.

ет вид

При малых r, т. е. в ближней кулоновской области,

∑

эти функции примерно совпадают с параболически-

P^ml (cosθ) G_l(r) +

′

(cos θ) F_l′ (r) =

ми кулоновскими функциями,

l^′=m

∑

χνk (ξ) ≈ c_k f_ν

(ξ), ψμk (η) ≈ gμk (η),

(5)

= Υ_l,kψ_k (ξ, η) ,

(1)

k=1

где c_k — нормировочные постоянные. Регулярные

и нерегулярные параболические кулоновские функ-

где P^ml (cos θ) — полиномы Лежандра, Fl′ (r) и

ции соответственно определены как

G_l(r) — регулярное и нерегулярное в нуле решения

радиального уравнения Шредингера в чисто куло-

⁽ζ)m/2

f_κ(ζ) =

e-ζ/2nΦ (-κ, m + 1, ζ/n)

(6)

новском потенциале и ψ_k (ξ, η) — физические, огра-

ниченные на бесконечности нерегулярные решения в

чисто штарковском потенциале. Коэффициенты γ_l,l′

(где либо ζ = ξ и κ = ν, либо, как требуется ниже в

и Υ_l,k однозначно определяются условиями сшив-

выражении (10), ζ = η и κ = μ) и соответственно

ки. Правая часть уравнения (1) представляет собой

)m/2

⁽η

нерегулярное физическое решение вне остова, кото-

g_μ(η) =

e-η/2n Ψ (-μ, m + 1, η/n).

(7)

рое в ближней кулоновской области должно пере-

ходить в линейную комбинацию сферических функ-

Нерегулярные сферические и параболические функ-

ций, стоящую слева, что и выражает формула (1).

ции (3) и (7) выбраны из условия ограниченности

Подробности вывода приведены в [9].

решения на бесконечности.

743

В. Г. Ушаков, В. И. Ошеров, Э. С. Медведев

ЖЭТФ, том 156, вып. 4 (10), 2019

Коэффициенты γ_l,l′ и Υ_l,k однозначно определя-

Матрица Υ_l,k имеет вид [9]

ются условием сшивки физического параболическо-

W_l

го решения со сферическими функциями в ближней

Υ_l,k =

A_ν

(8)

k μk ,l ckΓ(-μk),

m! N_lm

кулоновской области и выбором функций (3) и (7).

где

∑

(-1)p+m2^l (l - m)!l!Γ (1 + ν) Γ (1 + μ) (m!)²

A_νμ,l =

(9)

(2l)!Γ (1 + ν - p) Γ (1 + μ + m - l + p)(l - p)!(l - m - p)!(m + p)!p!

p=0

— матрица ЛП для регулярных решений. Последние

любом фиксированном η = 0 можно разложить по

имеют вид произведения функций, определенных в

базису функций fn1 (ξ). Коэффициенты этого разло-

(6); ЛП для них определяется формулой (см. [1], а

жения пропорциональны затухающему на бесконеч-

также Приложение A в [9])

ности параболическому решению (7) с μ = n₂. От-

метим, что любая другая нерегулярная радиальная

∑

функция, отличная от G_l (r), является экспоненци-

f_ν (ξ) f_μ (η) =

A_νμ,lP^ml (cosθ)F_l(r).

(10)

ально растущей и соответствующая ей сферическая

l=m

функция не может быть разложена по параболиче-

ским решениям.

В формуле (8) W_l и N_lm — вронскиан и норми-

ровочная постоянная для сферических кулоновских

Физическая нерегулярная штарковская волновая

функций,

функция в правой части формулы (1) с коэффици-

ентами Υ_l,k, определяемыми по формуле (8), при ко-

n (2l + 1)!

2l+1 (l-m)!

нечном r сходится к регулярной функции от θ, тогда

W_l =

N_lm =

(11)

22l+1Γ (1+l-n)

(l + m)!

как сингулярная часть этой функции при r = 0 сов-

падает с сингулярной частью G_l (r, θ) [9]. Поэтому

Наш метод вывода формулы (1) основан на точ-

разность между ними есть регулярная функция от

ном разложении нерегулярных сферических функ-

r и θ, которую можно разложить в ряд по регуляр-

ций по нерегулярным параболическим кулоновским

ным сферическим функциям:

функциям,

∑

G_l (r, θ) ≡ P^ml (cosθ)G_l(r) =

Ψ_l,reg (ξ, η) =

Υ_l,kχνk (ξ)ψμk (η) - G_l (r, θ) =

k=1

∑

= Bl,n1 fn1 (ξ) gn2 (η) ,

(12)

∑

n1=0

′

(cos θ) F_l′ (r),

(15)

l^′=m

в котором матрица преобразования имеет вид

что приводит к формуле (1).

W_l

Bl,n1 =

Γ (-n₂)

(13)

В работе [9] матрица γ была найдена числен-

An1n2,l

m! N_lm

но, здесь же мы дадим ее аналитическое выраже-

и n₂ = n - n₁ - m - 1. Параметр Nn1 есть норми-

ние. Для начала заметим, что основная трудность

ровочная постоянная регулярного решения fn1 (ξ):

при вычислении матричных элементов γ_l,l′ связа-

на с неравномерной сходимостью суммы в левой ча-

√

сти уравнения (15), см. [9]. Почленное проектирова-

(m + n₁)!

Nn1 =

(14)

ние этой суммы на полиномы Лежандра невозмож-

n₁!n

но, так как приводит к расходящемуся ряду. Обре-

занная сумма имеет особенность при η = 0, причем

Разложение (12) было получено в [9] для произ-

вольных целых и нецелых n при специальном выбо-

вклад этой особенности в интеграл не исчезает при

ре (3) нерегулярной радиальной сферической функ-

стремлении верхнего предела суммирования в бес-

ции G_l (r), удовлетворяющей требованию затухания

конечность.

на бесконечности. Благодаря такому выбору, сфери-

Чтобы найти матрицу γ_l,l′, преобразуем Ψ_l,reg с

ческую функцию в левой части выражения (12) при

помощью соотношений (8), (12) и (13) к виду

744

ЖЭТФ, том 156, вып. 4 (10), 2019

Разложение нерегулярного решения в теории эффекта Штарка. . .

∑

Ψ_l,reg (ξ, η) =

Υ_l,kχ_ν

(ξ) ψ_μ

(η) -

∑

k=1

F_St (ν_k) A_ν

k μk,l c^k Γ (-μk) fνk (ξ)gμk (η) =

∑

W_l

Bl,n1 fn1 (ξ)gn2 (η) =

k=kmax

N_lmm!

∞

∫

n1=0

[

F_St (ν)A_νμ,lc2kΓ (-μ)f_ν(ξ)g_μ(η)

dν.

(19)

∑

dν

× A_ν

k μk,l c^k Γ (-μk) fνk (ξ)gμk (η) -

kmax

k=1

]

∑

Здесь F_St (ν_k) и F_Coul (n₁) — обрезающие множители

- An1n2,l

Γ (-n₂) fn1(ξ)gn2 (η)

(16)

для штарковской и кулоновской сумм. При больших

n1=0

значениях k и n₁ имеем

Обе суммы в правой части формулы (16) сходятся

N2n

неравномерно при η = 0, и их разность при произ-

(20)

dν

c²

вольно выбранных конечных верхних пределах сум-

мирования является сингулярной функцией, кото-

где n₁

= ν. Тогда, выбирая n1,max

= νkmax и

рую нельзя разложить по сферическим гармоникам.

F_Coul (z) = F_St (z) = F_cut (z), получаем, что два ин-

Однако эту сингулярность можно устранить, вводя

теграла равны друг другу.

в суммы специальным образом подобранные обреза-

Сингулярное поведение функций gμk и gn2 в фор-

ющие функции.

муле (16) определяется вырожденной гипергеомет-

При асимптотически больших значениях k и n₁

рической функцией Ψ (a, b, x), которую можно пред-

коэффициенты Aνkμ_k,l и An1n2,l являются гладкими

ставить в виде суммы равномерно сходящегося ря-

функциями индексов,

да по возрастающим степеням η и конечного числа

2^l (m!)

сингулярных членов. После введения универсальной

A_νμ,l ≈ (-1)^lν^l-m

(17)

(l!)² (l + m)!

обрезающей функции в формулу (16) сингулярные

члены взаимно уничтожаются и остающуюся функ-

Произведение Γ (-μ) g_μ(η) при больших отрица-

цию можно разложить в ряд по полиномам Лежанд-

тельных значениях μ — также гладкая функция μ.

ра. Разложение регулярных членов сумм проводит-

Благодаря гладкой зависимости членов сумм от ин-

ся так же, как это делалось в [9] для регулярных

дексов, суммирования по большим значениям ин-

функций. Окончательно получаем

дексов могут быть заменены интегрированиями:

[

∑

Γ (-n₂) ×

W_l

F_Coul (n₁)An1n2,l

γ_l,l′

F_cut(n₁)An1n2,l

An1n2,l^′ -

n1=n1,max

lm n1=0

∫∞

]

∑

× fn1(ξ)gn2(η) =

F_Coul (n₁) An1n2,l Nⁿ

- F_cut(ν_k)A_ν

(21)

k μk ,l c^k

Aνkμ_k,l′

n1,max

k=1

× Γ(-n₂)fn1(ξ)gn2(η)dn₁,

(18)

где

∑

(-1)p+m 2^l (l - m)!l!Γ (1 + ν) Γ (1 + μ + m) Ψ (μ, l - m - p)

A_νμ,l =

(22)

(2l)!Γ (1 + ν - p) Γ (1 + μ + m - l + p) (l - p)!(l - m - p)!(m + p)!p!

p=0

Ψ (μ, s) = ψ (-μ + s)-ψ (1 + m + s)-ψ (1 + s) (23)

вследствие полного пренебрежения полем в ближ-

ней кулоновской области. На точность сшивки вли-

(ψ — это дигамма-функция).

яет также важный физический параметр

Следует отметить, что сходимость сумм в фор-

δ = 16Fn⁴,

(24)

муле (21) обеспечивается обрезающими функция-

ми, которые в обеих суммах имеют один и тот же

определяющий высоту потенциального барьера для

функциональный вид. Отметим также, что точная

ионизации; значение δ = 1 соответствует классиче-

сшивка штарковской волновой функции со сфериче-

скому порогу ионизации. На практике, когда δ ∼ 1,

скими кулоновскими решениями происходит толь-

высокой точности сшивки можно добиться уже при

ко в асимптотическом пределе n → ∞. Это обстоя-

n > 10, если правильно выбрать обрезающую функ-

тельство отражает приближенный характер сшивки

цию.

745

В. Г. Ушаков, В. И. Ошеров, Э. С. Медведев

ЖЭТФ, том 156, вып. 4 (10), 2019

Новым по сравнению с разложением Хармина [1]

по базису сферических функций (формула G10), мы

в нашем локальном преобразовании (1) является то,

получим разложение нерегулярной функции в виде

что сшивка параболических функций со сферичес-

∑[

]

кими проводится в более узкой ближней области, а

g_ϵlm (r) =

U^T (ϵ)

lβ^F m

χ_ϵβF m (r) -

не во всей кулоновской области и что в левой части

β^F

∑

уравнения сшивки (1) добавилась сумма по регуляр-

γl,l′ fϵ l′m (r) ,

(26)

ным сферическим функциям. Вне ближней куло-

l^′

новской области происходит смешивание состояний

где

с разными l, и поэтому физическое решение, про-

долженное в область сферической симметрии, обя-

γl,l′

= J_l,l′ + ctg (πn) ,

(27)

зательно должно включать вклады состояний с раз-

а J_l,l′ дается формулой G22. Подставляя в (26) на-

ными l. Это радикально отличается от харминовско-

ши функции и обозначения, получаем окончатель-

го уравнения сшивки, в котором физическое реше-

ный результат в виде формулы (1), в которой

ние сшивается со сферической функцией с опреде-

[

ленным l во всей кулоновской области. Преимуще-

∑

W_l

ство нашего разложения было численно продемон-

γ_l,l′

An1n2,l

Ω(n₂)An1n2,l^′ -

N_lm

(m!)²

стрировано в работе [9] для l = 1, 3, 5, r = 10 - 80 и

n1=0

]

-1 < cosθ < 1 путем сравнения с точным решением.

∑

- A_ν

Ω(μ_k) Aνkμ_k ,l′

(28)

Используя разложение (1) нерегулярного реше-

k μk,l c^k

k=1

ния и известное аналогичное разложение регуляр-

ного решения [1, 6, 9], мы получили в [9] выражение

где

для S-матрицы, пригодное для расчета наблюдае-

мых величин, таких как сечения фотоионизации. В

Γ (1 + m + μ)

Ω(μ) =

альтернативном методе ОЛП, развитом Джаннаки-

Γ (1 + μ)

[

]

сом и др. [6], разложение нерегулярного решения в

ψ (1+m+μ) +ψ (1+μ) -2 ln n

+π ctg (πμ)

(29)

явном виде не фигурирует. Тем не менее, используя

основные предположения теории ОЛП, это разложе-

ние можно вывести в явном виде и сравнить его с

Обе суммы в (28) расходятся, однако суммирова-

полученным в данной работе. Это делается в следу-

ние проводится до некоторого общего максимально-

ющем разделе.

го значения β с использованием подходящей обреза-

ющей функции.

Несмотря на очевидное различие выражений

(21) и (28) для γ, они оказываются численно экви-

3. СРАВНЕНИЕ С ТЕОРИЕЙ ОЛП

валентными вплоть до больших значений углово-

го момента. Чтобы сравнить эти две формулы для

В этом разделе мы используем обозначения ра-

γ, мы использовали обрезающую функцию из ра-

боты [6], а ссылки на формулы в ней снабжены пре-

боты [6]. Две матрицы, (21) и (28), определяют

фиксом «G». Одним из основных сильных утверж-

приближенные нерегулярные сферические решения

дений теории ОЛП является равенство двух гринов-

G_l,matched(r, θ), пришитые к физическому нерегуляр-

ских функций на малых расстояниях (см. формулы

ному параболическому решению двумя разными ме-

G18-G21 и последующий текст в [6]):

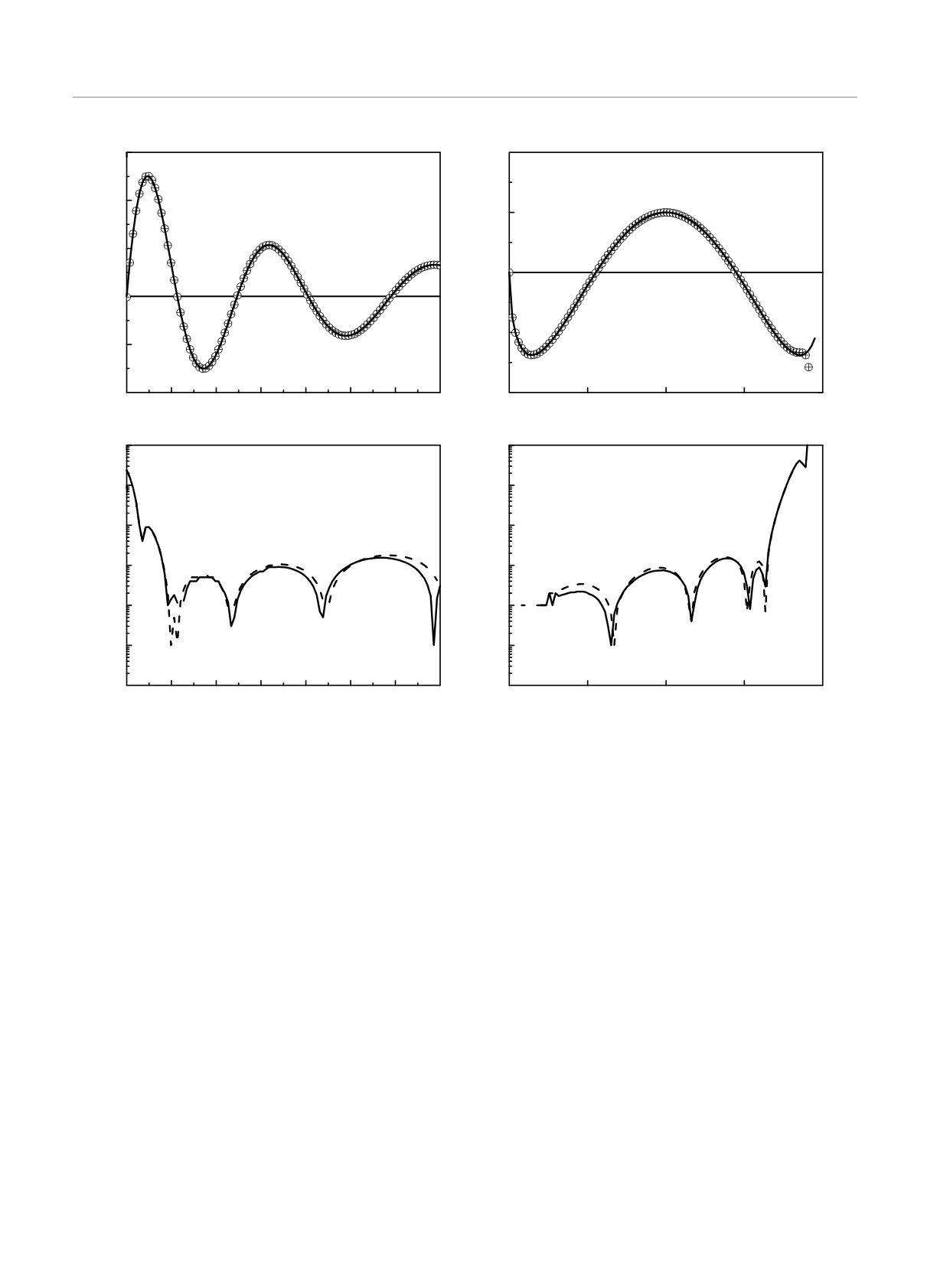
тодами. На рис. 1а,б и 2а,б показано их наложение

на точное решение, а на рис. 1в,г и 2в,г — их раз-

G^C-S,smooth (r, r^′) = G^C,smooth (r, r^′).

(25)

ности с точным решением. На рис. 1 видно, что обе

приближенные функции идеально совпадают с точ-

Обе функции определены как расходящиеся сум-

ной, а их разность с точной функцией составляет

мы по бесконечному набору дискретных значений

величину порядка 10-3 в широкой области измене-

константы разделения β (парциального заряда), но

ния переменных.

фактическое суммирование выполняется до некото-

Процедура сшивки справедлива, строго говоря,

рого общего максимального значения β. Подставляя

лишь в асимптотическом пределе n → ∞, т. е. в пре-

явные выражения для соответствующих функций,

деле F

→ 0 при фиксированном значении δ (см.

приведенные в формулах G13, G15, G18, G19 и G22,

(24)). Рисунок 2 иллюстрирует быструю сходимость:

и разлагая все регулярные параболические функции

при увеличении n от 10.5 до 28.5 разность между

746

ЖЭТФ, том 156, вып. 4 (10), 2019

Разложение нерегулярного решения в теории эффекта Штарка. . .

(r,

)

(r,

)

= /2

r = 30

–1

-1

-2

-1.0

-0.5

0.5

1.0

cos

l,matched

10^-1

= /2

r = 30

10^-2

10^-3

10^-4

10^-5

-1.0

-0.5

0.5

1.0

cos

Рис. 1. Сравнение двух пришитых нерегулярных сферических функций с точным решением при n = 10.5, m = 1, l = 3 и

δ = 1.3: а,б — сплошные линии соответствуют точным решениям, символы — приближенным функциям G_l,matched(r,θ),

полученным двумя методами; в,г — поскольку две приближенные функции почти совпадают и их символы неразличимы,

показана разность между точным решением и приближенными функциями, отвечающими матрицам (21) (сплошные

линии) и (28) (штриховые линии). Все функции поделены на G_l (r = 30, cos θ = 0)

точной и приближенными функциями уменьшается

функции с нерегулярным сферическим решением,

на порядок.

отвечающим определенному значению орбитально-

Отметим, что разность приближенной и точной

го углового момента l. Однако, строго говоря, такая

функций возрастает при малых η (cosθ ≈ +1). Это

сшивка физически невозможна, потому что в ши-

обусловлено не погрешностями сшивки, как тако-

рокой области малых r внешнее поле сильно сме-

вой, а использованием конечного базиса при вычис-

шивает состояния с разными l, несмотря на то, что

лении суммы в правой части формулы (1) и неравно-

оно мало по сравнению с кулоновским. Джанна-

мерной сходимостью этой суммы при η = 0.

кис и др. вывели общее выражение для K-матрицы

(т. е. вещественной матрицы рассеяния, связываю-

щей стоячие волны на бесконечности, см. форму-

лу G6 в [6]), не прибегая явно к процедуре сшивки

4. ОБСУЖДЕНИЕ

нерегулярного решения. Они ввели одночастичный

Основным источником неточностей теории Хар-

потенциал, имитирующий соответствующее теории

квантового дефекта граничное условие на остове,

мина является сшивка на малых расстояниях r

физической нерегулярной штарковской волновой

и применили формализм Липпмана - Швингера. На

747

В. Г. Ушаков, В. И. Ошеров, Э. С. Медведев

ЖЭТФ, том 156, вып. 4 (10), 2019

(r,

)

(r,

)

r = 40

= /2

–1

-1

-2

-1.0

-0.5

0.5

1.0

cos

l,matched

10^-1

r = 40

= /2

10^-2

10^-3

10^-4

10^-5

-1.0

-0.5

0.5

1.0

cos

Рис. 2. То же, что на рис. 1, при n = 28.5, m = 1, l = 3, и δ = 1.3. Все функции поделены на G_l (r = 40, cos θ = 0)

самом же деле, как показано в настоящей работе,

зультирующая формула (21) для матрицы γ внешне

сшивка нерегулярных штарковской и кулоновской

отличается от (28), однако численные расчеты пока-

функций все равно неявно присутствует в теории

зали, что две формулы имеют одинаковую точность

Джаннакиса и др., и здесь дан прямой вывод усло-

и одинаковые пределы применимости.

вия сшивки на основе одного из ее главных посту-

латов — формулы G22; результирующее разложе-

ние нерегулярной функции приведено в (26) и (27).

5. ЗАКЛЮЧЕНИЕ

Используя эти формулы и аналогичное разложение

регулярного решения, приведенное в формуле G10,

В области сферической симметрии выполнена

можно получить ту же K-матрицу, что и в работе

аналитическая сшивка физического нерегулярного

[6], безо всякого одночастичного потенциала. Мат-

решения штарковской задачи для ридберговских

рица сшивки — матрица γ — в наших обозначениях

состояний водородоподобных атомов с линейной

имеет вид (28). Альтернативный подход, развитый

комбинацией нерегулярной и регулярных сфери-

в данной работе, основан на полученном в работе

ческих функций в чисто кулоновском поле. Был

[9] точном разложении нерегулярной сферической

принят во внимание тот факт, ранее ускользавший

кулоновской функции по нерегулярным параболи-

от внимания исследователей, что на малых рассто-

ческим кулоновским функциям (формула (12)). Ре-

яниях, где внешнее поле уже слабо по сравнению с

748

ЖЭТФ, том 156, вып. 4 (10), 2019

Разложение нерегулярного решения в теории эффекта Штарка. . .

кулоновским (кулоновская область), поле все еще

ЛИТЕРАТУРА

может эффективно смешивать состояния с разными

значениями орбитального момента. Другими сло-

1. D. A. Harmin, Phys. Rev. A 24, 2491 (1981).

вами, область сферической симметрии оказывается

намного уже кулоновской области, что приводит

2. U. Fano, Phys. Rev. A 24, 619 (1981).

к значительной перестройке волновой функции.

Используя полученную здесь сшивку и аналогич-

3. M. J. Seaton, Prog. Phys. Soc. 88, 801 (1966).

ную сшивку для регулярного решения, можно

4. M. J. Seaton, Rep. Prog. Phys. 46, 167 (1983).

стандартными методами получить S-матрицу [9],

необходимую для расчета наблюдаемых величин.

5. G. D. Stevens, C.-H. Iu, T. Bergeman, H. J. Metcalf,

I. Seipp, K. T. Taylor, and D. Delande, Phys. Rev.

Мы посвящаем эту работу столетнему юбилею

A 53, 1349 (1996).

выдающегося ученого, основателя и многолетнего

6. P. Giannakeas, Chris H. Greene, and F. Robicheaux,

директора Института теоретической физики им.

Phys. Rev. A 94, 013419 (2016).

Л. Д. Ландау и просто замечательного человека

7. P. Giannakeas, F. Robicheaux, and Chris H. Greene,

академика Исаака Марковича Халатникова, «Ха-

Phys. Rev. A 91, 043424 (2015).

лата» для его коллег и учеников. Один из нас

(Э. С. Медведев) хранит теплые воспоминания о

8. L. B. Zhao, I. I. Fabrikant, M. L. Du, and C. Bordas,

1957-1963 гг. учебы в Московском физико-техни-

Phys. Rev. A 86, 053413 (2012).

ческом институте и Институте физических проблем

им. П. Л. Капицы, когда Халат был куратором

9. V. G. Ushakov, V. I. Osherov, and E. S. Medvedev,

722 группы.

submitted to J. Phys. A: Math. Theor. 52, 385302

(2019).

Финансирование. Работа выполнена по теме

10. Г. Бейтмен, А. Эрдейи, Высшие трансцендентные

Государственного задания, номер государственной

функции, т. 1, Наука, Москва (1973).

регистрации 0089-2019-0002.

749