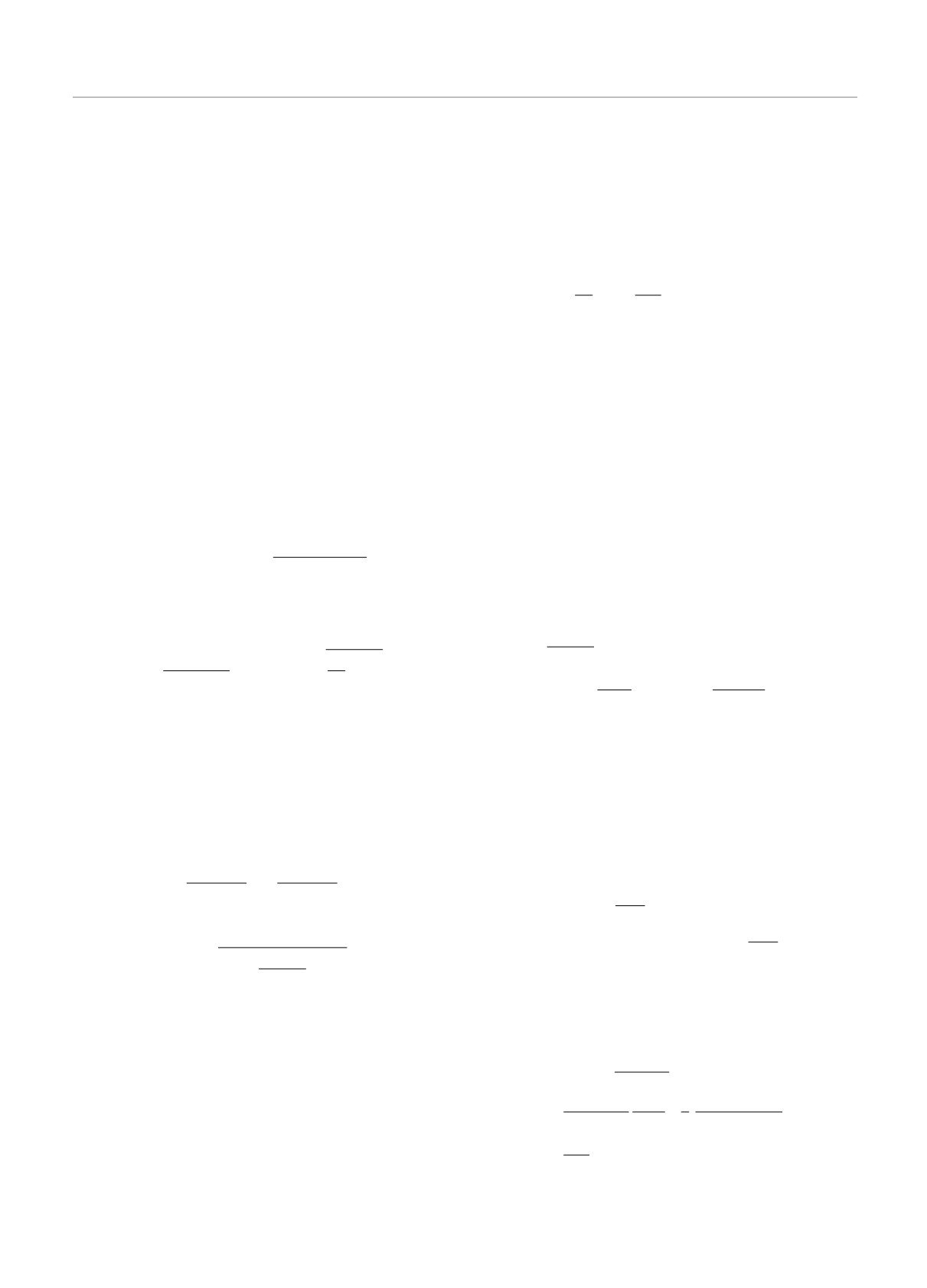ЖЭТФ, 2019, том 156, вып. 4 (10), стр. 750-760

КИНЕТИЧЕСКИЕ СВОЙСТВА МЕТАЛЛОВ БЕЗ ЦЕНТРА

ИНВЕРСИИ ПРИ НИЗКИХ ТЕМПЕРАТУРАХ

В. П. Минеев^*

Univ. Grenoble Alpes, CEA, IRIG, PHELIQS

F-38000, Grenoble, France

Институт теоретической физики им. Л. Д. Ландау Российской академии наук

142432, Черноголовка, Московская обл., Россия

Поступила в редакцию 12 марта 2019 г.,

после переработки 24 мая 2019 г.

Принята к публикации 24 мая 2019 г.

Развита теория низкотемпературных кинетических явлений в металлах без центра инверсии. Кинетичес-

кие свойства металлов без центра инверсии описываются четырьмя кинетическими уравнениями для

диагональных (внутризонных) и недиагональных (межзонных) элементов матричной функции распреде-

ления электронов по состояниям из двух зон проводимости, расщепленных спин-орбитальным взаимо-

действием. Выведены интегралы столкновений для рассеяния электронов на примесях и парных столк-

новений. Рассмотрены электрический и спиновый токи и поток тепла в бесстолкновительном режиме

и в случае слабого рассеяния на примесях. Показано, что в трехмерных средах недиагональные члены

функции распределения дают вклад в транспорт заряда, спина и тепла не только благодаря процессам

межзонного рассеяния, но и в бесстолкновительном режиме, порождая необычные диссипативные токи.

Показано, что остаточное сопротивление и остаточное тепловое сопротивление при нулевой температуре

определяются не только рассеянием электронов на примесях, но и электрон-электронными столкновени-

ями.

Статья для специального выпуска ЖЭТФ, посвященного 100-летию И. М. Халатникова

DOI: 10.1134/S0044451019100183

ε = ε_σσ′, n = n_σσ′ по спиновым индексам. Времен-

ное поведение матричной функции распределения

в (k, r)-пространстве в квазиклассическом при-

1. ВВЕДЕНИЕ

ближении определяется выведенным Силиным [5]

кинетическим уравнением

Уже много лет спиновая электроника систем с

)

сильным спин-орбитальным взаимодействием вызы-

∂n

⁽∂ε ∂n

∂n ∂ε

вает значительный интерес. В частности, изучались

∂t

∂k ∂r

∂r ∂k

кинетические свойства двумерных полупроводни-

)

⁽∂ε∂n

∂n ∂ε

ковых структур с нарушенной пространственной

−

- i[ε, n] =

Ist,

(1)

∂r ∂k

∂k ∂r

четностью, с характерным спин-орбитальным вза-

имодействием типа Рашба и Дрессельхауза

[1-4].

где [ε, n] — коммутатор матриц ε = ε(k, r) и n =

Спин-орбитальное взаимодействие электронов с

= n(k, r). Здесь и далее ℏ = 1. Интеграл столкнове-

кристаллической решеткой без центра инверсии

ний в правой части уравнения определяет релакса-

снимает спиновое вырождение электронных со-

ционные процессы.

стояний. Каждая электронная зона расщепляется

Представляется естественным переписать кине-

на две зоны с разной величиной квазиимпульса

тическое уравнение в зонном представлении, где га-

при равной энергии. Закон дисперсии и функция

мильтониан имеет диагональный вид. Можно ду-

распределения электронов становятся матрицами

мать, что после этого преобразования мы придем

к системе двух кинетических уравнений для функ-

^* E-mail: vladimir.mineev@cea.fr

ций распределения электронов в каждой из зон,

750

ЖЭТФ, том 156, вып. 4 (10), 2019

Кинетические свойства металлов. ..

взаимодействующих между собой через интегралы

Роль парных столкновений в происхождении

столкновений, включающие процессы межзонного

остаточного сопротивления и теплового сопротивле-

рассеяния, и теория будет выглядеть как соответ-

ния при нулевой температуре обсуждается в разд. 4.

ствующая кинетическая теория обычного двухзон-

В Заключении перечислены основные результаты

ного металла с центром инверсии. Однако, это не

работы. Вывод интегралов столкновений для рассе-

так. Кинетические процессы в металлах без цен-

яния электронов на примесях и друг на друге дан в

тра инверсии описываются четырьмя кинетически-

двух Приложениях. Полученные результаты отно-

ми уравнениями для диагональных (внутризонных)

сятся как к трехмерным, так и к двумерным сис-

и недиагональных (межзонных) элементов матрич-

темам без центра инверсии. Выявлены принципи-

ной функции распределения электронов по состо-

альные отличия между кинетическими свойствами

яниям из двух зон проводимости, расщепленных

в двух и трех измерениях.

спин-орбитальным взаимодействием. Недиагональ-

ные члены дают вклад в транспортные свойства да-

же в бесстолкновительном режиме. В работе показа-

2. ЭЛЕКТРОННЫЕ СОСТОЯНИЯ В

но, что в трехмерных веществах без центра инверсии

МЕТАЛЛАХ БЕЗ ЦЕНТРА ИНВЕРСИИ

электрическое поле не только ускоряет электроны,

но также передает энергию электронному газу, со-

Энергетический спектр электронов в металле без

здавая неравновесные состояния с недиагональной

центра инверсии имеет вид

матричной функцией распределения. Это новое яв-

ление полностью специфично для трехмерных сред

ε(k) = ε(k)^δ + γ(k) · σ,

(2)

без центра инверсии.

где ε(k) — скалярная часть спектра,

δ — единич-

Выражения для интеграла столкновений элект-

ная 2 × 2-матрица в спиновом пространстве, σ =

ронов с примесями в металлах и полупроводниках

= (σ_x, σ_y, σ_z) — матрицы Паули. Второе слагаемое в

без центра инверсии можно найти в работах [6, 7].

уравнении (2) описывает спин-орбитальное взаимо-

Авторы не приводят вывода этих выражений, но пи-

действие. Его вид зависит от конкретной кристал-

шут: «Вывод интеграла столкновений можно найти

лической симметрии вещества. Псевдовектор γ(k)

во многих работах», — отсылая к соответствующей

обладает следующими свойствами γ(-k) = -γ(k) и

литературе. В этих ссылках, однако, вывода инте-

gγ(g-1k) = γ(k), где g — любое преобразование сим-

грала столкновений не содержится. Вывод интегра-

метрии точечной группы G кристалла. Более деталь-

лов столкновений для столкновений электронов с

ное описание свойств металлов без центра инверсии

примесями, а также электрон-электронных столкно-

в нормальном и сверхпроводящем состоянии изло-

вений в металлах без центра инверсии дан в насто-

жено в работе [8]. В кристаллах CePt₃Si, CeRhSi₃ и

ящей работе. Показано, что остаточное сопротивле-

CeIrSi₃ с тетрагональной симметрией G = C4v век-

ние и остаточное тепловое сопротивление при нуле-

тор

вой температуре определяются не только рассеяни-

ем электронов на примесях, но и парными электрон-

γ(k) = γ(k_y x - k_x ŷ) + γ_∥k_xk_yk_z (k2x - k2y)z.

(3)

ными столкновениями.

Статья состоит из трех разделов, Введения и За-

В двумерном случае, полагая γ_∥ = 0, мы приходим

ключения. В разд. 2 приведены основные сведения

к спин-орбитальному взаимодействию Рашба [9], ко-

о спектре и равновесных функциях распределения

торое часто используется для описания нарушен-

в металлах без центра инверсии. В разд. 3 выведе-

ной зеркальной симметрии в пленках. В изотроп-

ны кинетические уравнения и получены общие вы-

ном случае, соответствующем кубической симмет-

ражения для нахождения электрического и спино-

рии, ε(k) = k²/2m и

вого токов и потока тепла. Рассмотрены транспорт-

ные явления в бесстолкновительном режиме и в слу-

γ(k) = γk.

(4)

чае слабого рассеяния на примесях. Показано, что

в трехмерных средах недиагональные члены функ-

Здесь γ — постоянная с размерностью скорости.

ции распределения дают вклад в транспорт заряда,

Собственные значения и собственные векторы

спина и тепла не только благодаря процессам меж-

матрицы (2) выглядят следующим образом:

зонного рассеяния, но и в бесстолкновительном ре-

жиме, порождая необычные диссипативные токи.

ε_±(k) = ε(k) ± |γ(k)|,

(5)

751

В. П. Минеев

ЖЭТФ, том 156, вып. 4 (10), 2019

(

)

γkz + 1

3. ТРАНСПОРТНЫЕ СВОЙСТВА.

Ψ⁺

(k) = C_k

РАССЕЯНИЕ НА ПРИМЕСЯХ

γkx + iγky

(

)

-γkx + iγky

(6)

3.1. Кинетическое уравнение

Ψ^-(k) = C

γkz + 1

При наличии внешнего электрического поля

E(t)

= E_ωe^-iωt линеаризованное кинетическое

C_k = (2(γkz + 1))-1/2.

уравнение (1) имеет вид

Здесь, γkx, γky, γkz — компоненты единичного век-

∂ĝ

∂n⁰

тора γ(k)/|γ(k)|. Собственные векторы удовлетво-

+ eE

- i[ε, ĝ] =

Ist,

(15)

∂t

∂k

ряют соотношениям ортогональности

где ĝ = n-n⁰ — отклонение функции распределения

Ψ^α⋆σ(k)Ψ^βσ(k) = δ_αβ, Ψ^ασ

(k)Ψ^α⋆σ

(7)

(k) = δσ1σ2 .

от равновесной функции распределения n⁰.

Эрмитовские матрицы функций неравновесного

В этих выражениях и всюду далее подразумевается

распределения в зонном и спиновом представлениях

суммирование по повторяющимся спиновым индек-

связаны между собой преобразованием

сам σ =↑, ↓ или зонным индексам α = +, -.

Имеются две ферми-поверхности, определяемые

f_αβ(k) = Ψ^α⋆σ

(k).

(16)

(k)nσ1σ2 Ψ^σ

уравнениями

В зонном представлении равновесная функция рас-

ε_±(k) = μ,

(8)

пределения (11) суть диагональная матрица

с различными импульсами Ферми k_F±. В изотроп-

(

)

n₊

ном случае они равны

f0αβ(k) = Ψ^α⋆σ(k)n0σ

Ψ^βσ

(k) =

(17)

1 σ2

√

- αβ

k_F± = ∓mγ +

2mμ + (mγ)²,

(9)

Однако ее производная недиагональна и определя-

а скорость Ферми одинакова на обеих ферми-по-

ется уравнением

верхностях

∂n0σ

1 σ2



√

Ψ^α⋆σ(k)

Ψ^β (k) =_σ

∂(ε ± γk)



2μ

∂k



[

]

v_F± =

= k

+γ².

(10)



∂f⁰

∂k

αβ

∂Ψ^γσ(k)

k=kF ±

+ Ψ^α⋆σ(k)

,f⁰

(18)

γβ

∂k

Здесь

k — единичный вектор в направлении им-

где квадратные скобки означают коммутатор. Та-

пульса k. Равенство скоростей Ферми при разных

ким образом, матричное кинетическое уравнение

ферми-импульсах — специфическое свойство моде-

для зависящей от частоты амплитуды Фурье нерав-

лей с изотропным спектром (4) в трехмерном случае

новесной части функции распределения g_αβ (k, t) =

и взаимодействием Рашба в двумерном случае.

= g_αβ(k,ω)e^-iωt принимает вид

Матричная функция равновесного распределе-

(

)

ния электронов по импульсам имеет вид

g₊ g_±

- iω

n₊ + n_-

n₊ - n_-

g∓ g-

n⁰ =

^δ+

γ·σ,

(11)

⎛

⎞

2|γ|

∂n₊

(v₊E)

(v_±E)(n_- - n₊)

⎜

∂ξ₊

⎟

где

+e⎝

⎠ +

∂n

(v_∓E)(n₊ - n_-)

(v_-E)

n_± =

(12)

∂ξ_-

⁽ε_± -μ⁾

(

)

exp

ig_±(ε_- - ε₊)

=I_αβ.

(19)

— функции Ферми. В изотропном случае вблизи

ig_∓(ε₊ - ε_-)

соответствующих ферми-поверхностей законы дис-

Здесь

персии выглядят особенно просто:

∂Ψ^-σ(k)

v_± = Ψ+⋆σ(k)

ξ_± = ε_± - μ ≈ v_F (k - k_F±) = ϵ - μ_±,

(13)

∂k

γkx-iγky

∂γkz

1 ∂(γkx-iγky)

(20)

здесь

2(γkz+1) ∂k

∂k

∂ε_α

ϵ = v_Fk, μ_± = v_Fk_F±, μ+ -μ_- = -2mv_Fγ. (14)

v_α =

v_∓ = -v^⋆±.

∂k

752

ЖЭТФ, том 156, вып. 4 (10), 2019

Кинетические свойства металлов. ..

∫

Интеграл столкновений для рассеяния электронов

d³k

j=e²

{v₊(w₊E) + v_-(w_-E) +

на примесях выведен в Приложении А. Ненулевой

(2π)³

вклад в интеграл столкновений дает лишь неравно-

+ [v_±(w_∓E) - v_∓(w_±E)] (ε_- - ε₊)} .

(26)

весная часть функции распределения. Таким обра-

зом,

Поскольку функции w₊, w_-, w_±, w_∓ зависят от ве-

личины и направления импульса k, направление то-

∫

d³k^′

ка, вообще говоря, не совпадает с направлением

Iαβ (k) = 2πnimp

|V (k - k^′)|² ×

(2π)³

электрического поля.

1. Баллистический режим. В пренебрежении

× {O_αν (k, k^′) [g_νμ(k^′)O_μβ (k^′, k) -

процессами рассеяния, т. е. при ωτ > 1, где τ — ти-

- O_νμ(k^′, k)g_μβ(k)] δ(ε^′ν - ε_β) +

пичное время рассеяния, определяемое различными

+ [O_αν (k, k^′)g_νμ(k^′) - g_αν (k)O_νμ(k, k^′)] ×

слагаемыми, входящими в интеграл столкновений,

}

× O_μβ(k^′,k)δ(ε^′μ - ε_α)

(21)

уравнение (19) имеет решение

O_αβ(k, k^′) = Ψ^α⋆σ(k)Ψ^βσ(k^′).

(22)

∂n₊

g₊ = e(w₊E) =

(v₊E)

(27)

iω

∂ξ₊

Здесь и во всех последующих формулах, в двумер-

∫

ном случае

d³k^′/(2π)³ должно быть заменено на

∫

∂n_-

d²k^′/(2π)².

g_- = e(w_-E) =

(v_-E)

(28)

Решение уравнений (19) имеет вид

iω

∂ξ_-

(

)

(

)

g₊ g_±

(w₊E) (w_±E)

e(v_±E)(n_- - n₊)

g_αβ =

(23)

g_± = e(w_±E) =

(29)

g_∓ g_-

(w_∓E) (w_-E)

iω - i(ε_- - ε₊)

После подстановки этой матрицы в уравнение (19)

и в интеграл столкновений (21) мы получим четы-

e(v_∓E)(n₊ - n_-)

g_∓ = e(w_∓E) =

(30)

ре скалярных уравнения, соответствующие матрич-

iω - i(ε₊ - ε_-)

ным элементам матрицы (19) для зависящих от ве-

Подставляя эти выражения в (26) получим

личины и направления импульса k скалярных функ-

ций (w₊E), (w_±E), (w_∓E), (w_-E). В общем случае

∫

d³k

^{v₊(v₊E) ∂n₊

v_-(v_-E) ∂n_-

эти функции могут быть найдены посредством чис-

j=e²

(2π)³

iω

∂ξ₊

iω

∂ξ_-

ленного решения уравнений. Решения для бесстолк-

(n₊ - n_-)(ε_- - ε₊)

[

новительного режима и случая слабого рассеяния на

+ 2

iω Re(v_±(v^⋆±E)) +

ω² - (ε₊ - ε_-)²

примесях рассмотрены ниже.

]}

+ (ε_- - ε₊)] Im(v_±(v^⋆±E))

(31)

3.2. Электрический ток

Последний член в этой формуле представляет дис-

Выражение для плотности электрического тока

сипативный ток. Он зависит от

во внешнем поле имеет вид

∫

Im(v_±(v^⋆±E)) =

d³k ∂εσσ1(k)

4(γkz + 1)

j=e

gσ1σ(k, ω).

(24)

{

[

(

)

(

)]

(2π)³

∂k

∂γkz

∂γky

∂γkx

-γkx

+γky

∂k

Переходя к зонному представлению, получаем

(

)[

]}

∂γkz

∂γkx

∂γky

∫

-γky

+γkx

(32)

d³k

∂εσσ1(k)

∂k

j=e

Ψ^α⋆σ(k)

Ψ^γσ

(k)Ψ^γ⋆(k) ×_σ

(2π)³

∂k

В двумерном случае z-компонента вектора γ_k

отсут-

× gσ2σ3(k, ω)Ψ^σ (k) =3

ствует, и Im(v_±(v^⋆±E)) = 0. Следовательно, в дву-

∫

{

[

]}

d³k

∂ε_αγ(k)

∂Ψ^βσ

мерных средах высокочастотное электрическое поле

+ Ψ^α⋆σ(k)

,ε_βγ

(2π)³

∂k

в отсутствие релаксации из-за рассеяния электронов

на примесях не вызывает диссипативных токов, как

× g_γα(k, ω),

(25)

и в любых металлах с центром инверсии.

где квадратные скобки означают коммутатор. Окон-

В отличие от этого, в трехмерных средах послед-

чательно приходим к выражению

ний член в уравнении (31), вообще говоря, не равен

753

ЖЭТФ, вып. 4 (10)

В. П. Минеев

ЖЭТФ, том 156, вып. 4 (10), 2019

нулю. Например, можно проверить прямым вычис-

распределения, которые оказываются в γk_F τ ≫ 1

лением, что этот член дает ненулевой диссипатив-

раз меньше чем столкновительные члены, завися-

ный вклад в ток, направленный перпендикулярно

щие от диагональных элементов функции распреде-

приложенному электрическому полю в металлах с

ления. Видно, что даже в пределе слабого рассеяния

симметрией C4v с вектором γ_k, задаваемым урав-

на примесях релаксация диагональной части функ-

нением (3). Таким образом, мы приходим к выво-

ции распределения к равновесию определяется че-

ду, что в трехмерных средах электрическое поле не

тырьмя разными столкновительными членами.

только ускоряет электроны, но также передает энер-

Было предпринято несколько попыток [2-4] ре-

гию электронному газу, создавая неравновесные со-

шить эти уравнения для двумерной модели Рашба

стояния с недиагональной матричной функцией рас-

в борновском приближении. В этом случае произве-

пределения. Это необычное явление — специфичное

дения

для трехмерных материалов без центра инверсии.

Интегралы в двух последних членах уравнения

O₊₊(kk^′)O₊₊(k^′k) = O_--(kk^′)O_--(k^′k) =

(31) берутся по области обратного пространства

ϕ-ϕ^′

= cos²

между kF+ и k_F-, где ε₊ - ε_- ≈ 2γk_F . При срав-

нительно низких частотах ω ≪ 2γk_F , но все еще

в бесстолкновительной области ω > τ-1 уравнение

O+-(kk^′)O-+(k^′k) = O-+(kk^′)O+-(k^′k) =

(31) принимает вид

ϕ-ϕ^′

∫

= -sin²

d³k

^{v₊(v₊E) ∂n₊

v_-(v_-E) ∂n_-

j=e²

(2π)³

iω

∂ξ₊

iω

∂ξ_-

зависят от разности азимутальных углов началь-

}

ного и конечного импульсов. В борновском при-

- 2(n₊ - n_-)Im(v_±(v^⋆±E))

(33)

ближении интеграл столкновений выражается через

фурье-компоненту потенциала примеси, зависящую

2. Слабое рассеяние на примесях. Режим слабо-

от переданного импульса V (k-k^′), т. е. тоже зависит

го рассеяния на примесях реализуется при τ-1 ≪

от ϕ - ϕ^′. Это позволяет искать решение уравнений

≪ 2γk_F . В этом случае можно пренебречь столк-

(34), (35) в следующем виде:

новительными членами в кинетических уравнениях

∂n₊

для недиагональных элементов функции распреде-

g₊ = -ea₊

(v₊E),

∂ξ₊

ления. Таким образом, решения для недиагональ-

(36)

ных матричных элементов по-прежнему задаются

∂n_-

g_- = -ea_-

(v_-E),

формулами (29) и (30). После подстановки этих ре-

∂ξ_-

шений в интеграл столкновений в уравнениях для

диагональных элементов функции распределения

как это было сделано в работе [4], где были най-

мы придем к уравнениям

дены коэффициенты a_±. В этом случае выражение

для тока имеет вид

∫

∂n₊

d³k

∫

- iωg₊+e(v₊E))

= 4πn_i

|V (k-k^′)|² ×

d²k

∂ξ₊

2π³

j=e²

{

(2π)

O₊₊(kk^′)O₊₊(k^′k)[g₊(k^′)-g₊(k)]δ(ε′+-ε₊) +

{

}

+ O+-(kk^′)O-+(k^′k)[g_-(k^′)-

∂n₊

∂n_-

}

× a₊v₊(v₊E)

+a_-v_-(v_-E)

(37)

∂ξ₊

∂ξ_-

- g₊(k)]δ(ε^′- - ε₊)

(34)

Этот подход легко обобщается на случай конечной

∫

частоты.

∂n_-

d³k

- iωg_-+e(v_-E))

= 4πn_i

|V (k-k^′)|² ×

Аналогичные вычисления можно проделать для

∂ξ_-

2π³

другой двумерной модели — модели Дрессельхауза

{

O-+(kk^′)O+-(k^′k)[g₊(k^′)-g_-(k)]δ(ε′+-ε_-) +

[10], где γ(k) = γ_D(k_y ŷ - k_x x), но не для модели,

+ O_--(kk^′)O_--(k^′k)[g_-(k^′)-

где вектор γ(k) представляет сумму этих векторов

}

в моделях Рашба и Дрессельхауза.

- g_-(k)]δ(ε^′- - ε_-)

(35)

Решения уравнений (34) и (35) для других дву-

полученным в пренебрежении столкновительными

мерных и трехмерных моделей можно искать лишь

членами, с недиагональными элементами функции

численными методами.

754

ЖЭТФ, том 156, вып. 4 (10), 2019

Кинетические свойства металлов. ..

∫

В трехмерном случае в условиях слабого рассе-

d³k

j_zi = e

{[v+i(w₊E) - v_-i(w_-E)] +

яния на примесях выражение для плотности тока

(2π)³

имеет вид

+ [v_±i(w_∓E) + v_∓i(w_±E)] (ε_- - ε₊)} .

(42)

∫

d³k

j=e²

{v₊(w₊E) + v_-(w_-E) -

(2π)³

В бесстолкновительном режиме решения кинети-

}

ческого уравнения даются формулами (27)-(30). В

- 2(n₊ - n_-)Im(v_±(v^⋆±E))

(38)

двумерном случае выражения для скоростей (20)

Здесь два первых члена определяются решениями

имеют вид

уравнений (34) и (35), а последний член — дополни-

∂ε_α

1 ∂(γkx - iγky)

тельный диссипативный ток, определяемый недиа-

v_α =

v_± = -

(43)

∂k

гональными элементами матричной функции рас-

пределения, как и в бесстолкновительном случае.

Очевидно, «диагональные» скорости — нечетные

3. Сильное рассеяние на примесях. Режим силь-

функции волнового вектора v_α(-k) = -v_α(k), тог-

ного рассеяния на примесях реализуется, когда ти-

да как «недиагональные» скорости — четные функ-

пичное обратное время рассеяния оказывается по-

ции волнового вектора v_±(-k)

= v_±(k). Таким

рядка энергии спин-орбитального расщепления зон

образом, баллистические спиновые токи (40), (41)

τ-1 ≈ γk_F . В этом случае при выполнении усло-

тождественно равны нулю:

вия γk_F ≪ ε_F квазиклассическая теория остается

применимой к описанию кинетических явлений, но

j_xi = j_yi = 0.

(44)

необходимо решать полную систему из четырех ки-

нетических уравнений для диагональных и недиаго-

Чтобы найти спиновый ток в случае слабого рас-

нальных матричных элементов функции распреде-

сеяния на примесях, можно использовать недиаго-

ления.

нальные матричные элементы функции распреде-

ления (29), (30), но для нахождения диагональных

3.3. Спиновый ток

элементов надо решать уравнения (34), (35). Для

Электрическое поле в кристаллах без центра ин-

модели Рашба в борновском приближении решения

версии порождает спиновый ток. Плотность спино-

этих уравнений имеют вид (36). Таким образом, в

вого тока имеет вид

этом случае спиновый ток также обращается в нуль

∫

d³k

∂εσ1σ2(k)

в силу симметрийных свойств «диагональных» и

j_i = e

σσσ1

gσ2σ(k, ω).

(39)

(2π)³

∂k_i

«недиагональных» скоростей.

Переходя к зонному представлению, так же как это

В трехмерном случае недиагональные скорости

было сделано для электрического тока, получим вы-

(20) не есть четные функции волнового вектора.

ражения для проекций плотности спинового тока на

Спиновый ток, вызванный электрическим полем,

оси координат

приобретает конечную величину. Так же как и элек-

трический ток, спиновый ток даже в баллистиче-

∫

d³k

ском режиме состоит из реактивной и диссипатив-

j_xi = e

{[v+i(w_±E) + v_-i(w_∓E)] +

(2π)³

ной составляющих.

+ [v_±i(w_-E) - v_∓i(w₊E)] (ε_- - ε₊)} ,

(40)

3.4. Поток тепла

∫

d³k

j_yi = ie

{[v+i(w_±E) - v_-i(w_∓E)] +

При наличии градиента температуры матричное

(2π)³

кинетическое уравнение для неравновесной функ-

+ [v_±i(w_-E) + v_∓i(w₊E)] (ε_- - ε₊)} ,

(41)

ции распределения g_αβ есть

⎛

(

)

⎞

∂n

∂n₊

∂n_-

(v₊∇T )ξ₊

(v_±∇T )(ε_- - ε₊) ξ₊

+ξ_-

⎜

∂ξ₊

∂ξ_-

⎟

⎜

(

)

⎟

⎝

⎠⁺

∂n₊

∂n_-

(v_∓∇T )(ε₊ - ε_-) ξ₊

+ξ_-

(v_-∇T )ξ_-

∂ξ₊

∂ξ_-

(

)

ig_±(ε_- - ε₊)

=I_αβ.

(45)

ig_∓(ε₊ - ε_-)

755

12*

В. П. Минеев

ЖЭТФ, том 156, вып. 4 (10), 2019

∫

Решение этого уравнения имеет вид

∂n_-

d³k

(v_-∇T )ξ_-

= 4πn_i

|V (k - k^′)|² ×

∂ξ_-

2π³

(

)

{

g₊ g_±

O-+(kk^′)O+-(k^′k)[g₊(k^′) - g_-(k)]δ(ε′+

-ε_-) +

g_αβ =

g_∓ g_-

+ O_--(kk^′)O_--(k^′k)[g_-(k^′)-

}

(

)

- g_-(k)]δ(ε^′- - ε_-)

(53)

(u₊∇T ) (u_±∇T )

(46)

T (u_∓∇T ) (u_-∇T )

4. РОЛЬ ЭЛЕКТРОН-ЭЛЕКТРОННЫХ

После подстановки этой матрицы в уравнение (45)

СТОЛКНОВЕНИЙ

и в интеграл столкновений (21) мы получим четыре

уравнения, соответствующие каждому матричному

Задача о рассеянии электронов на электронах

элементу матрицы (46) для четырех зависящих от

в металлах без центра инверсии решалась в рабо-

k скалярных функций (u₊∇T ) , (u_±∇T ), (u_∓∇T ),

те автора [11]. Вычисления проводились с использо-

(u_-∇T ).

ванием электрон-электронного интеграла столкно-

вений для матричной спиновой функции распреде-

Плотность потока тепла есть

ления, выведенного в работах [12,13] (см. уравнения

∫

d³k

(B.1), (B.2) в Приложении B). Этот интеграл столк-

∂εσ1σ2(k)

ξσσ1 (k)

gσ2σ(k).

(47)

(2π)³

∂k

новений, давая правильное описание релаксацион-

ных процессов для установления равновесия в спи-

Преобразуя это выражение к зонному представле-

новом распределении ферми частиц в средах с нена-

нию, получим

рушенной зеркальной симметрией, не годится для

описания релаксации в системах без центра инвер-

∫

d³k

сии. Таким образом, подход, использованный в ра-

{ξ₊v₊g₊ + ξ_-v_-g_- +

(2π)³

боте [11], неверен. Электрон-электронный интеграл

столкновений в средах без центра инверсии имеет

+ [ξ₊v_±g_∓ - ξ_-v_∓g_±](ε_- - ε₊)} .

(48)

значительно более сложный вид (B.1), (B.3). Тем не

менее, главное утверждение работы [11] о том, что

Подставляя в это выражение g_αβ из (46), приходим к

характерное время рассеяния электронов на элект-

∫

ронах оказывается конечным при нулевой темпера-

d³k

q=-

{ξ₊v₊(u₊∇T)+ξ_-v_-(u_-∇T) +

туре, остается справедливым.

(2π)³

В равновесном состоянии интеграл (B.1), (B.3)

+ [ξ₊v_±(u_∓∇T) - ξ_-v_∓(u_±∇T)](ε_- - ε₊)}.

(49)

обращается в нуль. При отклонении от равновесно-

го распределения столкновительный член отличен

Чтобы найти поток тепла в случае слабого рас-

от нуля даже при нулевой температуре. Дело в том,

сеяния на примесях, можно использовать недиаго-

что даже при нулевой температуре квазичастицы

нальные матричные элементы функции распределе-

имеют возможность рассеяться в незанятые состо-

ния, полученные в пренебрежении столкновениями

яния между двумя ферми-поверхностями, соответ-

(

)

ствующими двум зонам, расщепленным спин-орби-

∂n₊

∂n_-

тальным взаимодействием. Аналогичная ситуация

g_± = -

(v_±∇T ) ξ₊

+ξ_-

(50)

∂ξ₊

∂ξ_-

имеет место в поляризованном жидком³He, где вре-

(

)

∂n₊

∂n_-

мя релаксации для спиновой диффузии в направле-

g_∓ = -

(v_∓∇T ) ξ₊

+ξ_-

(51)

∂ξ₊

∂ξ_-

нии, перпендикулярном внешнему магнитному по-

лю, имеет конечную величину и при T = 0, бла-

Тогда как диагональные матричные элементы

годаря возможности рассеяния в состояния меж-

должны быть найдены из уравнений

ду ферми-поверхностями частиц со спином вверх и

вниз, имеющими разные радиусы [13-15]. Здесь бу-

∫

∂n₊

d³k

дет уместно напомнить также замечание Херринга

(v₊∇T )ξ₊

= 4πn_i

|V (k - k^′)|² ×

∂ξ₊

2π³

[16] в отношении релаксации в ферромагнетиках: «В

{

O₊₊(kk^′)O₊₊(k^′k)[g₊(k^′)-g₊(k)]δ(ε′+-ε₊) +

любом ферромагнитном металле. . . , если спин ква-

зичастицы на ферми-поверхности будет перевернут,

+ O+-(kk^′)O-+(k^′k)[g_-(k^′)-

}

соответствующее квазичастичное состояние не бу-

- g₊(k)]δ(ε^′- - ε₊)

(52)

дет оставаться вблизи ферми-поверхности, но будет

756

ЖЭТФ, том 156, вып. 4 (10), 2019

Кинетические свойства металлов. ..

иметь конечную, а не бесконечно малую скорость

Металл без центра инверсии

распада».

Конечная скорость распада при нулевой темпе-

ратуре вызывает сомнения в применимости фер-

ми-жидкостного описания электронов в металлах

без центра инверсии. Оценка, сделанная в работе

(T = 0)

Металл с центром инверсии

[11], а также более тщательные вычисления для по-

ляризованного ферми-газа [17] позволяют выразить

n_imp

уверенность в применимости теории ферми-жидкос-

ти при условии, что расщепление ферми-поверхнос-

Остаточное сопротивление

тей в импульсном пространстве мало по сравнению

с энергией Ферми:

По той же причине остаточное тепловое сопро-

v_F (k_F- - kF+) ≪ ε_F .

(54)

тивление в металлах без центра инверсии складыва-

Спин-орбитальное расщепление зон v_F Δk_F прямо

ется из теплового сопротивления за счет рассеяния

выражается через соответствующее расщепление

электронов на примесях и теплового сопротивления,

частот в осцилляциях намагниченности [18] (эф-

обусловленного электрон-электронным рассеянием:

фект де Гааза-ван Альфена). Измеренная экспери-

T/κ = d_imp + d_ee(T = 0).

(57)

ментально типичная величина зонного расщепления

в ряде металлических соединений без центра инвер-

Здесь κ — коэффициент теплопроводности. Отноше-

ние теплового сопротивления к сопротивлению при

сии порядка нескольких сот Кельвин [19-21], что

низких температурах пропорционально температу-

значительно меньше типичной энергии Ферми.

ре в соответствии с законом Видемана - Франца

Из-за конечного времени релаксации, определяе-

мой электрон-электронными столкновениями, оста-

κ/σ = AT.

(58)

точное сопротивление в металлах без центра ин-

Однако коэффициент пропорциональности не есть

версии складывается из двух частей, определяемых

универсальное число Лоренца, но может быть раз-

рассеянием электронов на примесях и рассеяния

ным даже для образцов одного и того же соединения

электронов на электронах:

разной чистоты .

ρ = ρ_ee(T = 0) + ρ_imp.

(55)

Мы игнорируем здесь тензорный характер удельно-

5. ЗАКЛЮЧЕНИЕ

го сопротивления. Примесное сопротивление про-

порционально концентрации примесей ρ_imp ∝ n_imp.

Спин-орбитальное взаимодействие в металлах

Следовательно, остаточное сопротивление из-за

без центра инверсии снимает спиновое вырожде-

электрон-электронного рассеяния ρ_ee(T

= 0) мо-

ние электронных состояний и расщепляет каж-

жет быть найдено измерением сопротивления при

дую зону проводимости на две зоны c разными

низкой температуре при разных концентрациях

ферми-импульсами. Кинетика металлов без цен-

примесей с последующим нахождением формально-

тра инверсии описывается четырьмя кинетически-

го предела

ми уравнениями для диагональных (внутризонных)

и недиагональных (межзонных) элементов матрич-

ρ_ee(T = 0) = ρ(n_imp → 0).

(56)

ной функции распределения. В отличие от матери-

Соответствующее поведение изображено на рисун-

алов, обладающих центром инверсии, в веществах с

ке. Разумеется, кристалл должен быть как мож-

нарушенной зеркальной симметрией внешние силы

но ближе к идеальному, ибо наличие дислока-

не только ускоряют электроны, но и передают энер-

ций, двойников и дефектов упаковки может пол-

гию электронному газу, создавая неравновесные со-

ностью скрыть роль электрон-электронного рас-

стояния с недиагональной матричной функцией рас-

сеяния в формировании остаточного сопротивле-

пределения, что порождает диссипативные потоки

ния. Насыщение электрон-электронного вклада в

заряда, спина и тепла даже в бесстолкновительном

сопротивление возможно служит объяснением от-

режиме. Это чисто трехмерное явление, отсутству-

сутствия обычной зависимости сопротивления про-

ющее в двумерных средах. Теория транспорта за-

порциональной T², наблюденного в недавних экспе-

ряда, спина и тепла сильно упрощается в преде-

риментах [22].

ле слабого рассеяния на примесях, когда типичное

757

В. П. Минеев

ЖЭТФ, том 156, вып. 4 (10), 2019

обратное время рассеяния не превышает энергию

Чтобы преобразовать интеграл столкновений из ко-

спин-орбитального расщепления зон. В этом случае

ординатного в импульсное представление и в то же

можно пользоваться недиагональными элементами

время из спинового в зонное представление нужно

функции распределения, полученными в пренебре-

сосчитать матричный элемент от выражения (A.2)

жении столкновениями, и решать лишь уравнения

∫

для диагональных матричных элементов. Проделан

d³k^′

Ψ^α⋆σ(k)〈k|A_σσ′ (τ, t)|k^′〉Ψ^βσ′ (k) =

вывод интегралов столкновений электронов с при-

(2π)³

{

месями и друг с другом. Показано, что наряду с

× Ψ^α⋆σ(k)〈k| exp(iĥσσ1τ)eiqrρσ1σ2(r, t) ×

рассеянием на примесях рассеяние электронов на

электронах дает вклад в остаточное сопротивление

× exp(-iĥσ2σ′ τ)|k^′〉Ψ^μσ′ (k^′)Ψσ⋆3(k^′)〈k^′|e-iqr|k〉Ψ^σ

(k) -

и в остаточное тепловое сопротивление при нулевой

- Ψ^α⋆σ(k)〈k| exp(iĥσσ1τ)ρσ1σ2(r, t)eiqr ×

температуре.

× exp(-i^ˆσ2σ′ τ)|k′〉Ψσ′ (k′)Ψσ⋆3(k′)〈k′|e-iqr|k〉Ψσ3 (k) -

- Ψ^α⋆σ(k)〈k|e-iqr|k′〉Ψνσ

(k^′)Ψ^ν⋆σ(k^′)〈k| ×

ПРИЛОЖЕНИЕ A

×exp(iĥσσ1 τ)eiqrρσ1σ2 (r, t)exp(-iĥσ2σ′ τ)|k〉Ψ^σ′ (k) +

Интеграл столкновений электронов с

+ Ψ^α⋆σ(k)〈k|e-iqr|k′〉Ψνσ

(k^′)Ψ^ν⋆σ(k^′)〈k| ×

}

примесями

× exp(iĥσσ1 τ)ρσ1 σ2 (r, t)eiqr exp(-iĥσ2σ′ τ)|k〉Ψ^σ′ (k)

+ h.c. (A.5)

Интеграл столкновений электронов с примесями

в операторной форме [23] для пространственно-од-

Воспользуемся теперь уравнением (A.4) и условия-

нородных систем имеет вид

ми ортогональности (7). Для первого члена в выра-

∫

жении (A.5) это дает

d³q

Iσσ′ = nimp

|V (q)|² ×

∫

(2π)³

d³k^′

∫⁰

Ψ^α⋆σ(k)〈k| exp(iĥσσ1 τ)eiqrρσ1σ2 (r, t)×

(2π)³

× dτe^λτ Aˆ_σσ′ (τ, t), (A.1)

× exp(-iĥσ2σ′ τ)|k^′〉Ψ^μσ′ (k^′) Ψ

^μ⋆(k′)〈k′|e-iqr|k〉×

σ3

-∞

∫

d³k^′

×Ψ^βσ

(k) + h.c. =

Ψ^α⋆σ(k)〈k| exp(iε_ατ)×

где λ → +0 и подынтегральное выражение в линей-

(2π)³

ном приближении по медленноменяющейся во вре-

×Ψ^νσ

(k^′)Ψ^ν⋆σ

(k^′)eiqrρσ3σ2 (r, t) exp(-iε^μτ)|k^′〉 ×

мени матрице плотности ρσ1σ2 (r, t) дается формулой

×Ψ^μσ

(k^′)Ψ^μ⋆σ

(k^′)δ(k^′ + q - k)Ψβ (

k) + h.c. (A.6)

σ3

[

Подставляя эту формулу в уравнение (A.1) и выпол-

A_σσ′ (τ, t) = exp(iĥσσ1 τ)[eiqr, ρσ1σ2 (r, t)] ×

]

няя интегрирования по d³q и по τ, приходим к

× exp(-iĥσ2σ′τ), e-iqr

(A.2)

∫

³k^′

2πn_imp

|V (k - k^′)|²O_αν (k, k^′)f_νμ(k^′) ×

Здесь квадратные скобки означают коммутатор,

(2π)³

σ, σ₁, . . . — спиновые индексы,

× O_μβ(k^′,k)δ(ε^′ν - ε_β), (A.7)

(

)

∂

ĥ_σσ

= εσσ1

-i

(A.3)

где

∂r

f_αβ(k) = Ψ^α⋆σ

(A.8)

(k)〈k|ρσ1 σ2 (r, t)|k〉Ψσ (k),

— гамильтониан не взаимодействующих электро-

нов, определяемый выражением (2) в координатном

ε_± = ε_±(k), ε^′± = ε_±(k^′) и

представлении. Его собственные функции удовле-

творяют уравнению

O_αβ(k, k^′) = Ψ^α⋆σ(k)Ψ^βσ(k^′),

(A.9)

ĥ_σσ

так что O_αβ (k, k^′) = O^⋆βα(k^′, k). Выполняя анало-

eikrΨ^ασ

(k) = ε_αeikrΨ^ασ(k).

(A.4)

гичные преобразования с остальными членами в

В обозначениях Дирака они записываются как

(A.5), приходим к выражению для интеграла столк-

новений электронов с примесями в зонном представ-

eikrΨ^ασ(k) = |k〉Ψ^ασ(k).

лении:

758

ЖЭТФ, том 156, вып. 4 (10), 2019

Кинетические свойства металлов. ..

∫

d³k^′

ПРИЛОЖЕНИЕ B

Iαβ (k) = 2πnimp

|V (k - k^′)|² ×

(2π)³

Интеграл парных столкновений электронов

× {O_αν(k, k^′)[f_νμ(k^′)O_μβ(k^′, k)-O_νμ(k^′, k)f_μβ(k)] ×

Интеграл парных столкновений ферми частиц

в Борновском приближении был выведен Силиным

× δ(ε^′ν - ε_β) +

[12] и в работе [13] в приложении к жидкому³He. В

металле с учетом процессов переброса он имеет вид

+ [O_αν (k, k^′)f_νμ(k^′) - f_αν (k)O_νμ(k, k^′)] ×

}

∫

× O_μβ(k^′,k)δ(ε^′μ - ε_α)

(A.10)

d³k^′′ d³k₂

I = 2π d³k^′

(2π)³ (2π)³

Интеграл столкновений для функций распределе-

(

)

∑

ния, меняющихся в пространстве на масштабах,

2πm

δ k₁ +k₂ -k^′ -k^′′ -

F, (B.1)

больших по сравнению с межэлектронными рассто-

яниями, имеет такой же вид.

Можно переписать интеграл столкновений для

где 2πm/a — вектор обратной решетки,

матричной функции распределения в виде интегра-

ла для функции распределения в «векторной» фор-

^{1

{

F =

W₁

[n^′, (1 - n₁)]₊Tr((1 - n₂)n^′′) -

ме:

f^j(k) =

f_αβ(k)σ^jβα,

(A.11)

}

− [(1 - n^′), n₁]₊Tr(n₂(1 - n^′′))

где σ^jβα = (δ_βα, σ^xβα, σ^yβα, σ^zβα) — матричный вектор с

компонентами из базиса двухкомпонентных матриц

{

W₂

[n^′(1 - n₂)n^′′, (1 - n₁)]₊ -

Паули и единичной матрицы. В результате полу-

чим интеграл столкновений, удивительно похожий

}

на стандартное диагональное по спиновым индек-

−[(1-n^′)n₂(1-n^′′), n₁]₊

δ(ε₁+ε₂-ε^′-ε^′′). (B.2)

сам выражение

∫

d³k^′

Здесь

^B]₊ означает антикоммутатор матриц

Iαβ (k) = 2πnimp

|V (k - k^′)|² ×

(2π)³

A и B и использованы следующие обозначения:

n′ = n(k′), ε′ = ε(k′) и т.п. В изотропной ферми-

{

жидкости типа жидкого³He

× O_αν(k,k^′)R^jνβ(k^′,k)δ(ε^′ν - ε_β) +R^jαν(k,k^′)×

[

]

W₁ = [V (|k₁-k^′|)]²,

× O_νβ(k^′,k)δ(ε^′ν - ε_α)}

f^j(k^′) - f^j(k)

(A.12)

Здесь

W₂ = -V (|k₁-k^′|)V (|k₁-k^′′|)

R0νβ(k^′, k) = O⁰(k^′, k)δ_νβ + O^x(k^′, k)σ^xνβ +

выражаются через фурье-преобразования потенци-

ала взаимодействия квазичастиц. В металле, ввиду

+ O^y(k^′,k)σ^yνβ + O^z(k^′,k)σ^zνβ,

экранировки заряда, можно положить их постоян-

ными, не зависящими от передаваемого импульса.

R^xνβ(k^′, k) = O^x(k^′, k)δ_νβ + O⁰(k^′, k)σ^xνβ +

Интеграл парных столкновений может быть так-

же получен из интеграла парных столкновений

+ iO^y(k^′, k)σ^zνβ - iO^z(k^′, k)σ^yνβ,

(A.13)

в операторной форме, выведенного в книге [23],

где продемонстрировано, что в случае неравновес-

R^yνβ(k^′, k) = O^y(k^′, k)δ_νβ + O⁰(k^′, k)σ^yνβ +

ных распределений, диагональных по спиновым ин-

дексам, интеграл парных столкновений принимает

+ iO^z(k^′, k)σ^xνβ - iO^x(k^′, k)σ^zνβ,

стандартный вид.

R^zνβ(k^′, k) = O^z(k^′, k)δ_νβO⁰(k^′, k)σ^zνβ +

Матрица

F для электрон-электронных столкно-

+ iO^x(k^′, k)σ^yνβ - iO^y(k^′, k)σ^xνβ,

вений, соответствующая формуле (B.1), в металлах

без центра инверсии для матричной функции рас-

и O^j(k^′,k) = (1/2)O_αβ(k)σ^jβα.

пределения в зонном представлении имеет вид

759

В. П. Минеев

ЖЭТФ, том 156, вып. 4 (10), 2019

F_αβ =

W₁ {[O_αν(k₁, k^′)f_νμ(k^′)O_μλ(k^′, k₁)(δ_λβ - f_λβ(k₁))(δ_ξη - f_ξη(k₂))O_ηζ(k₂, k^′′)f_ζρ(k^′′)O_ρξ(k^′′, k₂) -

− O_αν(k₁,k^′)(δ_νμ-f_νμ(k^′))O_μλ(k^′,k₁)f_λβ(k₁)f_ξη(k₂)O_ηζ(k₂,k^′′)(δ_ζρ-f_ζρ(k^′′))O_ρξ(k^′′,k₂)] δ(ε^′ν-ε1β-ε2ξ+ε^′′ζ)+

+ [(δ_αν - f_αν (k₁))O_νμ(k₁, k^′)(δ_μλ - f_μλ(k^′))O_λβ (k^′, k₁)(δ_ξη - f_ξη(k₂))O_ηζ (k₂, k^′′)f_ζρ(k^′′)O_ρξ (k^′′, k₂) -

}

- f_αν(k₁))O_νμ(k₁,k^′)f_μλ(k^′)O_λβ(k^′,k₁)f_ξη(k₂)O_ηζ(k₂,k^′′)(δ_ζρ - f_ζρ(k^′′))O_ρξ(k^′′,k₂)] δ(ε1α - ε^′μ + ε2ξ - ε^′′ζ)

W₂ {[O_αν(k₁, k^′)f_νμ(k^′)O_μλ(k^′, k₂)(δ_λϕ - f_λϕ(k₂))O_ϕψ(k₂, k^′′)f_ψρ(k^′′))O_ρω(k^′′, k₁)(δ_ωβ - f_ωβ(k₁) -

- O_αν(k₁,k^′)(δ_νμ - f_νμ(k^′))O_μλ(k^′,k₂)f_λϕ(k₂)O_ϕψ(k₂,k^′′)(δ_ψρ - f_ψρ(k^′′))O_ρω(k^′′,k₁)f_ωβ(k₁] ×

× δ(ε^′ν - ε1β - ε2ϕ + ε^′′ψ) + [(δ_αν - f_αν(k₁)O_νμ(k₁, k^′)f_μλ(k^′)O_λϕ(k^′, k₂)(δ_ϕψ - f_ϕψ(k₂))O_ψρ(k₂, k^′′) ×

× f_ρω(k^′′))O_ωβ(k^′′,k₁)-f_αν(k₁)O_νμ(k₁,k^′)(δ_μλ-f_μλ(k^′))O_λϕ(k^′,k₂)f_ϕψ(k₂)O_ψρ(k₂,k^′′)(δ_ρω-f_ρω(k^′′)) ×

}

× O_ωβ(k^′′,k₁)]δ(ε1α - ε^′μ + ε2ψ - ε^′′ρ)

(B.3)

ЛИТЕРАТУРА

14.

A. E. Meyerovich, in Helium Three, ed. by W. P. Hal-

perin and L. P. Pitaevskii, Elsevier Sc. Publ., Ams-

E. G. Mishchenko and B. I. Halperin, Phys. Rev.

terdam (1990), p. 757.

B 68, 045317 (2003).

15.

V. P. Mineev, Phys. Rev. B 69, 144429 (2004).

J. Schliemann and D. Loss, Phys. Rev. 68, 165311

(2003).

16.

C. Herring, in: Magnetism, Vol. IV, ed. by G. T. Rado

Zhian Huang and Liangbin Hu, Phys. Rev. B 73,

and H. Suhl, Academic Press, New York and London

113312 (2006).

(1966), p. 345.

V. Brosco, L. Benfatto, E. Cappelutti, and C. Gri-

17.

D. I. Golosov and A. E. Ruckenstein, J. Low Temp.

maldi, Phys. Rev. Lett. 116, 166602 (2016).

Phys. 112, 265 (1998).

В. П. Силин, ЖЭТФ 33, 1227 (1957) [Sov. Phys.

18.

V. P. Mineev and K. V. Samokhin, Phys. Rev. B 72,

JETP 6, 945 (1958)].

212504 (2005).

A. Е. Кошелев, В. Я. Кравченко, Д. Е. Хмельниц-

19.

T. Terashima, M. Kimata, S. Uji, T. Sugawara, N. Ki-

кий, ФТТ 30, 246 (1988).

mura, H. Aoki, and H. Harima, Phys. Rev. B 78,

A. Khaetskii, Phys. Rev. Lett. 96, 056602 (2006).

205107 (2008).

V. P. Mineev and M. Sigrist, in: Non-Centrosym-

20.

Y. Onuki, A. Nakamura, T. Uejo, A. Teruya, M. He-

metric Superconductors: Introduction and Overview,

do, T. Nakama, F. Honda, and H. Harima, J. Phys.

Lecture Notes in Physics, ed. by E. Bauer and

Soc. Jpn. 83, 061018 (2014).

M. Sigrist, Vol. 847, Springer, Heidelberg (2012),

p. 129.

21.

A. Maurya, H. Harima, A. Nakamura, Y. Shimizu,

Y. Homma, DeXin Li, F. Honda, Y. J. Sato and

Э. И. Рашба, ФТТ 2, 1109 (1960).

D. Aoki, J. Phys. Soc. Jpn. 87, 044703 (2018).

10.

G. Dresselhaus, Phys. Rev. 100, 580 (1955).

22.

Darren C. Peets, Tianping Ying, Xiaoping Shen,

11.

V. P. Mineev, Phys. Rev. B 98, 165121 (2018).

Yunjie Yu, Maxim Avdeev, Shiyan Li, and Donglai

Feng, Phys. Rev. Mater. 2, 103403 (2018).

12.

В. П. Силин, Введение в кинетическую теорию

газов, Наука, Moсква (1971).

23.

F. T. Vasko and O. E. Raichev, Quantum Kinetic

13.

J. W. Jeon and W. J. Mullin, J. Phys. France 49,

Theory and Applications, Springer Science+Buisness

1691 (1988).

Media, Inc, New York (2005).

760