ЖЭТФ, 2019, том 156, вып. 4 (10), стр. 761-774

ТЕОРИЯ ДИНАМИЧЕСКИХ СИСТЕМ И ТРАНСПОРТНЫЕ

ЯВЛЕНИЯ В НОРМАЛЬНЫХ МЕТАЛЛАХ

С. П. Новиков^a,b, Р. Де Леоc*, И. А. Дынников^b, А. Я. Мальцевa**

^a Институт теоретической физики им. Л. Д. Ландау Российской академии наук

142432, Черноголовка, Московская обл., Россия

^b Математический институт им. В. А. Стеклова Российской академии наук

119991, Москва, Россия

^c Department of Mathematics, Howard University

DC 20059, Washington

Поступила в редакцию 18 марта 2019 г.,

после переработки 18 марта 2019 г.

Принята к публикации 19 марта 2019 г.

Представлены результаты последних исследований в теории динамических систем, связанных с движени-

ем электронов на сложных поверхностях Ферми в нормальных металлах. Рассматриваемая задача тесно

связана с задачей описания электронных транспортных явлений в сильных магнитных полях и вместе

с тем представляет огромный интерес с точки зрения топологии и теории динамических систем. Мы

постараемся дать краткий общий обзор современного состояния данной области исследований, а также

указать ряд интересных вопросов, активно изучаемых в настоящее время.

Статья для специального выпуска ЖЭТФ, посвященного 100-летию И. М. Халатникова

DOI: 10.1134/S0044451019100195

ближении для электронной динамики в кристалле.

Как оказывается, квазиклассическое описание дина-

мики электронных состояний в пространстве квази-

1. ВВЕДЕНИЕ

импульсов может быть крайне нетривиальным для

Мы хотели бы представить обзор современного

металлов со сложными поверхностями Ферми. Здесь

состояния области исследований, зарождение кото-

мы хотели бы представить результаты исследова-

рой произошло в 1950-х-1960-х гг. в работах научной

ний соответствующей динамической задачи, прово-

школы И. М. Лифшица, тесно связанной в эти годы

димых в течение последних десятилетий и исполь-

с Институтом теоретической физики им. Л. Д. Лан-

зующих наиболее современные методы топологии и

дау. А именно, мы рассмотрим вопросы, связанные

теории динамических систем. Как будет видно из

с особенностями транспортных явлений в металлах

приведенных результатов, на настоящее время боль-

со сложными поверхностями Ферми в присутствии

шинство важнейших аспектов рассматриваемой за-

сильных магнитных полей. Как правило, в качестве

дачи являются изученными весьма детально, что

главного примера таких явлений рассматриваются

позволяет также дать весьма детальное описание

гальваномагнитные явления в нормальных метал-

связанных с ней физических явлений. Вместе с тем,

лах, хотя все рассматриваемое ниже имеет отноше-

можно также указать ряд интереснейших проблем,

ние также и к другим типам таких явлений (на-

связанных с рассматриваемой задачей и активно ис-

пример, термотранспортным). В качестве главного

следуемых в настоящее время.

приближения к описанию рассматриваемых явле-

Все приводимое ниже будет относиться к метал-

ний выступает кинетическое описание электронных

лам со сложными поверхностями Ферми, при этом

процессов, основанное на квазиклассическом при-

металлические образцы будут полагаться монокри-

^* R. De Leo

сталлическими, а также достаточно чистыми и име-

^** E-mail: maltsev@itp.ac.ru

ющими достаточно низкую температуру, так что

761

С. П. Новиков, Р. Де Лео, И. А. Дынников, А. Я. Мальцев

ЖЭТФ, том 156, вып. 4 (10), 2019

время свободного пробега электронов в металле τ

может полагаться довольно большим. Металличес-

кий образец будет предполагаться помещенным в

постоянное внешнее магнитное поле, величина ко-

торого удовлетворяет условию ω_Bτ ≫ 1, где ω =

= eB/m^∗c играет роль электронной циклотронной

частоты в металле. Надо сказать, в действительно-

сти, что как величина m^∗ ≈ p_F /v_F , так и величина

ω_B имеют здесь несколько формальный смысл, по-

скольку спектр электрона в кристалле задается в

общем случае произвольной 3-периодической функ-

Рис. 1. Замкнутые (а) и периодические (б) траектории сис-

цией ϵ(p) с периодами, равными периодам обратной

темы (1.1), возникающие на поверхностях Ферми различ-

решетки. Изменение электронного состояния в при-

ной формы

сутствии магнитного поля задается адиабатической

системой в пространстве квазиимпульсов (см., на-

Главную роль при рассмотрении транспортных

пример, [1-3])

электронных явлений в металлах играет поверх-

ность Ферми, определяемая уравнением

[v_gr (p) × B] ≡

[∇ϵ(p) × B],

(1.1)

ϵ(p) = ϵ_F

имеющей, вообще говоря, траектории самой различ-

и представляющая собой 3-периодическую поверх-

ной геометрии (что и будет главной тематикой, об-

ность в p-пространстве. Можно видеть, таким обра-

суждаемой в данной работе). Можно говорить при

зом, что сложность поведения транспортных явле-

этом, что магнитное поле B является достаточно

ний в сильных магнитных полях определяется во

сильным, если электрон успевает пройти много раз

многом сложностью поверхности Ферми металла.

по типичным замкнутым траекториям системы (1.1)

Это важнейшее свойство транспортных явлений в

или проходит достаточно большое расстояние (мно-

сильных магнитных полях было впервые отмечено

го больше p_F ) по открытым траекториям той же си-

в пионерской работе [4], где были рассмотрены два

стемы между двумя актами рассеяния на примесях.

принципиально различных типа траекторий систе-

Как нетрудно видеть, система (1.1) сохраняет

мы (1.1) на различных поверхностях Ферми. А имен-

как значение энергии электронного состояния ϵ(p),

но, в работе [4] были рассмотрены вклады в магни-

так и проекцию квазиимпульса вдоль направления

топроводимость, возникающие от замкнутых и пе-

магнитного поля. Как следствие этого, траектории

риодических траекторий системы (1.1) (рис. 1), и

системы (1.1) в p-пространстве геометрически зада-

показано, что в главном порядке по значению па-

ются пересечениями поверхностей постоянной энер-

раметра ω_Bτ ≫ 1 они могут быть предсталены в

виде

гии ϵ(p) = const с плоскостями, ортогональными

магнитному полю.

ne²τ

σ^kl ≈

Можно также выписать квазиклассическую си-

m^∗

⎛

⎞

стему, описывающую движение электронного вол-

(ω_Bτ)-2

(ω_Bτ)-1

⎜

⎟

(1.3)

нового пакета в координатном пространстве

×⎝ (ωBτ)-1 (ωBτ)-2 (ωBτ)-1

⎠,

(ω_Bτ)-1

∗

x = v_gr(p) ≡ ∇ϵ(p).

(1.2)

ω_Bτ → ∞

Как также нетрудно видеть, траектории систе-

(замкнутые траектории),

мы (1.2) определяются в действительности траекто-

σ^kl ≈

риями системы (1.1), в частности, их проекции на

⎛

⎞

(ω_Bτ)-2

(ω_Bτ)-1

(ω_B τ)-1

плоскость, ортогональную B, подобны траекториям

ne²τ

⎜

⎟

≈

⎝ (ω_Bτ)-1

∗

⎠,

(1.4)

системы (1.1), повернутым на 90^◦. Траектории си-

m^∗

стемы (1.2) не являются, вообще говоря, плоскими

(ω_Bτ)-1

∗

и описывают также движение вдоль направления B,

ω_Bτ → ∞

определяемое соответствующими значениями груп-

повой скорости v_gr(p).

(открытые периодические траектории).

762

ЖЭТФ, том 156, вып. 4 (10), 2019

Теория динамических систем. . .

Формулы (1.3), (1.4) представляют собой поря-

ственно наблюдаемыми в транспортных явлениях в

док величин σ^kl(B) в пределе ω_Bτ → ∞. В част-

сильных магнитных полях. Соответствующие топо-

ности, предполагается, что каждый из матричных

логические характеристики выражаются при этом

элементов имеет в действительности некоторый по-

целыми числами и являются локально устойчивы-

стоянный безразмерный коэффициент, так же как

ми при малых изменениях направления магнитного

обозначения «∗» представляют некоторые безраз-

поля. В самом общем случае, все устойчивые откры-

мерные величины порядка единицы. Как нетрудно

тые траектории для заданной поверхности Ферми

видеть, главным различием вклада замкнутых и пе-

(или всего дисперсионного закона [19]) могут быть в

риодических траекторий в пределе ω_Bτ → ∞ явля-

действительности разделены на семейства, соответ-

ется сильная анизотропия проводимости в плоско-

ствующие различным значениям указанных топо-

сти, ортогональной B, возникающая во втором слу-

логических характеристик и представленные опре-

чае. Здесь и далее мы всегда будем полагать, что

деленными зонами устойчивости на диаграмме на-

ось z выбрана вдоль направления магнитного поля.

правлений магнитного поля. Общая структура зон

В формуле (1.4) мы также предполагаем, что ось

устойчивости на угловой диаграмме проводимости

x выбрана вдоль среднего направления периодиче-

металла может быть при этом крайне нетривиаль-

ских открытых траекторий в p-пространстве.

ной, что приводит в общем случае к большому

В работах [5, 6] были рассмотрены более общие

разнообразию эффектов, наблюдаемых эксперимен-

примеры открытых траекторий системы (1.1), так-

тально (см., например, [19-32]). В следующем раз-

же обладающие сильно анизотропными свойствами.

деле мы постараемся привести по возможности наи-

Множество вопросов, связанных с геометрией по-

более детальный обзор вопросов, связанных с пове-

верхности Ферми и связанных с ней физических яв-

дением устойчивых открытых траекторий системы

лений, рассматривавшихся в указанный (а также бо-

(1.1), а также физических явлений, обусловленных

лее поздний) период, представлено в работах [7-10],

различной структурой угловых диаграмм для ме-

а также в книгах [1-3, 11, 12].

таллов с произвольными поверхностями Ферми.

В настоящей работе мы приведем обзор бо-

Устойчивые открытые траектории, однако, не

лее поздних результатов, основанных на деталь-

являются единственным примером нетривиальных

ных топологических исследованиях структуры си-

траекторий системы (1.1), и на достаточно сложных

стемы (1.1) для произвольного дисперсионного за-

поверхностях Ферми могут возникать также тра-

кона ϵ(p) и направления магнитного поля. Задача

ектории совершенно другого типа, обладающие го-

полной классификации всевозможных траекторий

раздо более сложным («хаотическим») поведением

системы (1.1) была впервые поставлена Новиковым

как на поверхности Ферми, так и в накрывающем

в работе [13], где также были проведены первые ее

p-пространстве. Первый пример таких траекторий

исследования в общей постановке. В течение после-

был построен Царевым [33]. Надо сказать, что тра-

дующих десятилетий эта задача интенсивно иссле-

ектории, построенные Царевым, также имеют свои

довалась в топологической школе С. П. Новикова

особенные свойства и образуют в действительно-

(С. П. Новиков, А. В. Зорич, С. П. Царев, И. А. Дын-

сти отдельный класс открытых траекторий системы

ников), что привело к ряду довольно глубоких мате-

(1.1), представляющий существенную часть общей

матических результатов, позволивших, в конечном

классификации ее траекторий.

итоге, получить к настоящему моменту ответы на

Еще более сложные примеры хаотических тра-

большинство связанных с ней важнейших вопросов.

екторий, появляющихся на достаточно сложных по-

При описании траекторий системы (1.1) важней-

верхностях Ферми, были построены Дынниковым

шую роль играет описание ее устойчивых откры-

[34]. Траектории типа траекторий Дынникова об-

тых траекторий, полученное в работах [14-16]. Осо-

ладают наиболее сложным поведением, что имеет

бенно важную роль при этом играет в действитель-

также яркое проявление в поведении транспортных

ности топологическая структура поверхности Фер-

электронных явлений в сильных магнитных полях

ми, возникающая на ней при появлении устойчивых

(см. [35, 36]). Общие свойства хаотических траекто-

открытых траекторий системы (1.1) и приводящая

рий Дынникова, а также структура множеств, на

к наличию замечательных геометрических свойств

которых они возникают, представляют в настоящее

у таких траекторий. Как было отмечено в рабо-

время предмет интенсивных исследований в теории

тах [17, 18], устойчивые открытые траектории (1.1)

динамических систем (см. [37-53]). Так же как и тра-

обладают также важными топологическими харак-

ектории Царева, траектории Дынникова могут быть

теристиками (топологическими числами), непосред-

отнесены к специальному классу траекторий систе-

763

С. П. Новиков, Р. Де Лео, И. А. Дынников, А. Я. Мальцев

ЖЭТФ, том 156, вып. 4 (10), 2019

мы (1.1), представляющему важную составляющую

общей классификации всех ее траекторий. В разд. 3

мы постараемся дать обзор результатов, относящих-

ся к хаотическим траекториям системы (1.1) и свя-

занным с ними физическими явлениями в сильных

Рис. 2. Канонические компактные поверхности, имеющие

магнитных полях.

род 0 (а), 1 (б), 2 (в) (и т. д.)

2. УСТОЙЧИВЫЕ ОТКРЫТЫЕ

ТРАЕКТОРИИ И УГЛОВЫЕ ДИАГРАММЫ

ПРОВОДИМОСТИ МЕТАЛЛОВ

Мы начнем данную главу с описания структу-

ры поверхности Ферми при возникновении на ней

устойчивых открытых траекторий системы (1.1).

Отметим прежде всего, что поверхность Ферми мо-

жет рассматриваться двояким образом. А именно, с

одной стороны, поверхность Ферми может рассмат-

риваться как 3-периодическая поверхность в p-про-

странстве, задаваемая уравнением ϵ(p) = ϵ_F . При

этом мы должны помнить, однако, что точки по-

верхности Ферми, различающиеся на векторы об-

ратной решетки, задают одно и то же электрон-

Рис. 3. Примеры поверхностей Ферми в p-пространстве

ранга 0 (а), 1 (б), 2 (в), 3 (г)

ное состояние. С другой стороны, p-пространство и

поверхность Ферми могут быть профакторизованы

по векторам обратной решетки и могут рассматри-

ваться как компактные многообразия. Полная зо-

ограниченных сингулярными траекториями (1.1) на

на Бриллюэна будет представлять собой при этом

своих основаниях (частным случаем такого основа-

трехмерный тор T³, а поверхность Ферми — глад-

ния может быть также единственная узловая особая

кую компактную двумерную поверхность S_F , вло-

точка системы (1.1)). После такого удаления остав-

женную в T³. Как абстрактная компактная поверх-

шаяся часть поверхности Ферми также будет пред-

ность поверхность Ферми обладает при этом фикси-

ставлена конечным числом (неэквивалентных) ком-

рованным родом g ≥ 0 и диффеоморфна канониче-

понент с отверстиями, ограниченными сингулярны-

ской двумерной поверхности соответствующего рода

ми траекториями системы (1.1). Мы можем назы-

(рис. 2). Кроме того, вложение поверхности Ферми

вать получаемую таким образом совокупность дву-

в T³ (или ее представление в виде периодической

мерных компонент с отверстиями редуцированной

поверхности в p-пространстве) может быть охарак-

поверхностью Ферми, соответствующей заданному

теризовано топологическим рангом, могущим при-

направлению магнитного поля.

нимать значения 0, 1, 2 или 3 (рис. 3). Нам здесь

При описании устойчивых открытых траекто-

будут интересны, прежде всего, наиболее сложные

рий системы (1.1) мы можем полагать, что направ-

поверхности Ферми, поэтому мы будем, как пра-

ление B является полностью иррациональным, т.е.

вило, подразумевать, что рассматриваемая поверх-

плоскость, ортогональная B, не содержит векторов

ность Ферми имеет ранг 3. Можно также показать,

обратной решетки. Важнейшим свойством редуци-

что род такой поверхности должен удовлетворять

рованной поверхности Ферми при наличии устой-

соотношению g ≥ 3.

чивых открытых траекторий системы (1.1) явля-

Начнем с того, что удалим из поверхности Фер-

ется то, что каждая ее связная компонента пред-

ми все замкнутые (сингулярные и несингулярные)

ставляет собой двумерный тор с отверстиями, вло-

траектории системы (1.1) и рассмотрим оставшую-

женный в T³ [14, 16]. Возвращаясь к расширенному

ся ее часть, несущую открытые траектории. В об-

p-пространству, можно также сформулировать эти

щем случае, все несингулярные замкнутые траек-

свойства так, что каждая связная компонента реду-

тории (1.1) на поверхности Ферми будут образовы-

цированной поверхности Ферми представляет собой

вать конечное число (неэквивалентных) цилиндров,

целочисленную (порожденную двумя векторами об-

764

ЖЭТФ, том 156, вып. 4 (10), 2019

Теория динамических систем. . .

Рис. 6. Вид устойчивой открытой траектории в плоскости,

ортогональной B, в расширенном p-пространстве

1) каждая устойчивая открытая траектория систе-

Рис. 4. Связная компонента редуцированной поверхности

мы (1.1) (в p-пространстве) лежит в прямой поло-

Ферми в p-пространстве, несущая устойчивые открытые

се конечной ширины в плоскости, ортогональной B,

траектории системы (1.1)

проходя ее насквозь (рис. 6) (см. также [15]);

2) среднее направление всех устойчивых открытых

траекторий одинаково при заданном направлении B

и дается пересечением плоскости, ортогональной B,

и некоторой (локально) фиксированной целочислен-

ной плоскости Γ в p-пространстве.

Геометрические свойства устойчивых открытых

траекторий системы (1.1) имеют самое непосред-

ственное отношение к транспортным явлениям в ме-

талле в сильных магнитных полях. Так же, как и в

случае периодических открытых траекторий, тензор

проводимости в плоскости, ортогональной B, обла-

дает здесь сильной анизотропией в пределе ω_Bτ ≫

≫ 1. Общее свойство полного тензора проводимости

⎛

⎞

o(1) o(1) o(1)

ne²τ

⎜

⎟

σ^ik ≈

⎝ o(1)

∗

⎠,

Рис. 5. Общая структура поверхности Ферми в p-простран-

m^∗

(2.1)

стве, несущей устойчивые открытые траектории системы

o(1)

∗

(1.1) (схематично)

ω_Bτ → ∞,

позволяет при этом определить среднее направле-

ратной решетки) периодически деформированную

ние открытых траекторий в p-пространстве как на-

плоскость с отверстиями, вложенную в R³ (рис. 4).

правление наибольшего подавления проводимости

В целом, полная поверхность Ферми в описанной

(в x-пространстве) в пределе ω_Bτ → ∞. Устойчи-

ситуации может быть представлена в случае обще-

вость открытых траекторий по отношению к малым

го положения в виде набора четного числа (неэк-

вращениям направления B позволяет определить

вивалентных) целочисленных плоскостей в p-про-

также целочисленную плоскость Γ как плоскость,

странстве, соединенных компонентами, состоящими

содержащую направления наибольшего подавления

из цилиндров замкнутых траекторий системы (1.1)

проводимости для всех направлений B, лежащих в

конечной высоты (рис. 5). Такая структура поверх-

соответствующей зоне устойчивости Ω (на единич-

ности Ферми является локально устойчивой по от-

ной сфере).

ношению к малым вращениям направления B, а так-

Наблюдаемая экспериментально плоскость Γ по-

же к малым вариациям уровня Ферми ϵ_F . При этом

рождена некоторыми двумя векторами обратной

поверхность Ферми будет иметь различные описан-

решетки и, в частности, не обязана совпадать с

ные выше представления для направлений B, ле-

какой-либо из кристаллографических плоскостей.

жащих в различных зонах устойчивости на угловой

Вместо этого она ортогональна одному из кристал-

диаграмме (на единичной сфере S²).

лографических направлений образца и может, та-

Что касается устойчивых открытых траекторий

ким образом, быть задана несократимой тройкой це-

системы (1.1), можно видеть, что они в описанной

лых чисел (M¹, M², M³). Целочисленные парамет-

ситуации должны обладать следующими двумя за-

ры (M1α, M2α, M3α) плоскостей Γ_α для каждой из зон

мечательными свойствами:

устойчивости Ω_α были введены в работе [17] как

765

С. П. Новиков, Р. Де Лео, И. А. Дынников, А. Я. Мальцев

ЖЭТФ, том 156, вып. 4 (10), 2019

важные топологические характеристики, наблюдае-

мые в проводимости нормальных металлов. Полный

набор топологических чисел (M1α, M2α, M3α), а также

геометрия соответствующих зон устойчивости пред-

ставляют собой важные характеристики электрон-

ного спектра в кристалле. Отметим здесь, что зо-

на устойчивости Ω_α может быть определена либо

как связная область (на S²), отвечающая заданному

Рис. 7. «Экспериментально наблюдаемые» зоны устойчи-

семейству устойчивых открытых траекторий (1.1),

вости в экспериментах по прямым измерениям проводи-

либо как полный набор всех таких областей, соот-

мости в сильных магнитных полях

ветствующих одной и той же целочисленной тройке

(M1α, M2α, M3α). Довольно часто бывает удобным вто-

рое определение, которое, в частности, относит к од-

ной и той же зоне диаметрально противоположные

этого, угловая зависимость тензора проводимости

области на единичной сфере.

при B/B ∈ Ω_α имеет некоторую иррегулярность,

что может вносить определенный элемент случай-

Возвращаясь к полной структуре поверхности

ности в экспериментальные данные при измерении

Ферми при наличии на ней устойчивых открытых

проводимости. Кроме того, как можно также по-

траекторий системы (1.1), можно утверждать, как

казать, при описанной структуре поверхности Фер-

мы уже сказали, что для направлений B/B ∈ Ω_α

ми периодические открытые траектории системы

общего положения поверхность Ферми может быть

представлена в виде четного набора (неэквивалент-

(1.1) существуют также на продолжениях указан-

ных выше сегментов больших кругов за пределы зо-

ных) деформированных целочисленных плоскостей

с отверстиями, соединенных компонентами конеч-

ны устойчивости. Последнее обстоятельство, вместе

с появлением длинных замкнутых траекторий для

ной высоты, несущими замкнутые траектории си-

близких направлений B, приводит к тому, что «экс-

стемы (1.1). Как можно также видеть, в «физиче-

периментально наблюдаемая» зона устойчивости

Ω_α

ски реалистичной» ситуации каждая из таких ком-

при прямых измерениях проводимости оказывается

понент должна представлять собой в действитель-

несколько больше точной математической зоны да-

ности простой цилиндр, состоящий из замкнутых

же в достаточно сильных магнитных полях (рис. 7).

траекторий и ограниченный сингулярными траекто-

риями на своих основаниях (рис. 5). Такая структу-

В общем и целом, аналитические свойства тензора

проводимости в «экспериментально наблюдаемой»

ра позволяет в действительности сказать несколь-

ко больше о траекториях системы (1.1) для на-

зоне устойчивости могут быть достаточно сложны-

ми (см. [29]).

правлений B, лежащих внутри какой-либо из зон

устойчивости, а также вблизи нее (см., например,

Вместе с тем, границы точных математических

[19, 29-31]).

зон устойчивости Ω_α являются также эксперимен-

Действительно, можно отметить, прежде всего,

тально наблюдаемыми при соответствующей поста-

что указанная структура на поверхности Ферми

новке эксперимента. Данное обстоятельство связано

должна приводить к появлению периодических от-

с тем, что граница зоны Ω_α связана с определенной

крытых траекторий при B/B ∈ Ω_α всякий раз, ко-

перестройкой траекторий системы (1.1) и разруше-

гда пересечение плоскости, ортогональной B и соот-

нием структуры, показанной на рис. 5, при соответ-

ветствующей плоскости Γ_α, имеет рациональное на-

ствующих направлениях B. А именно, на границе

правление в p-пространстве. Как следствие этого, в

любой из зон Ω_α происходит обращение в нуль высо-

каждой зоне Ω_α можно в действительности указать

ты одного из цилиндров замкнутых траекторий, со-

всюду плотное множество (состоящее из сегментов

единяющего носители открытых траекторий, и его

больших кругов) направлений B, соответствующее

последующее исчезновение после пересечения гра-

появлению периодических открытых траекторий си-

ницы Ω_α. Исчезновение любого из таких цилиндров

стемы (1.1). Периодические траектории, в отличие

замкнутых траекторий может быть при этом обна-

от траекторий общего положения, не являются всю-

ружено экспериментально, например, при исследо-

ду плотными на носителях открытых траекторий,

вании осцилляционных явлений (классических или

что приводит в действительности к несколько дру-

квантовых) в металле в сильных магнитных полях

гим значениям проводимости для соответствующих

(см., например, [30]). Как мы увидим ниже, именно

направлений B в пределе ω_Bτ → ∞. Как следствие

структура точных математических зон устойчивос-

766

ЖЭТФ, том 156, вып. 4 (10), 2019

Теория динамических систем. . .

001

010

112

111

110

100

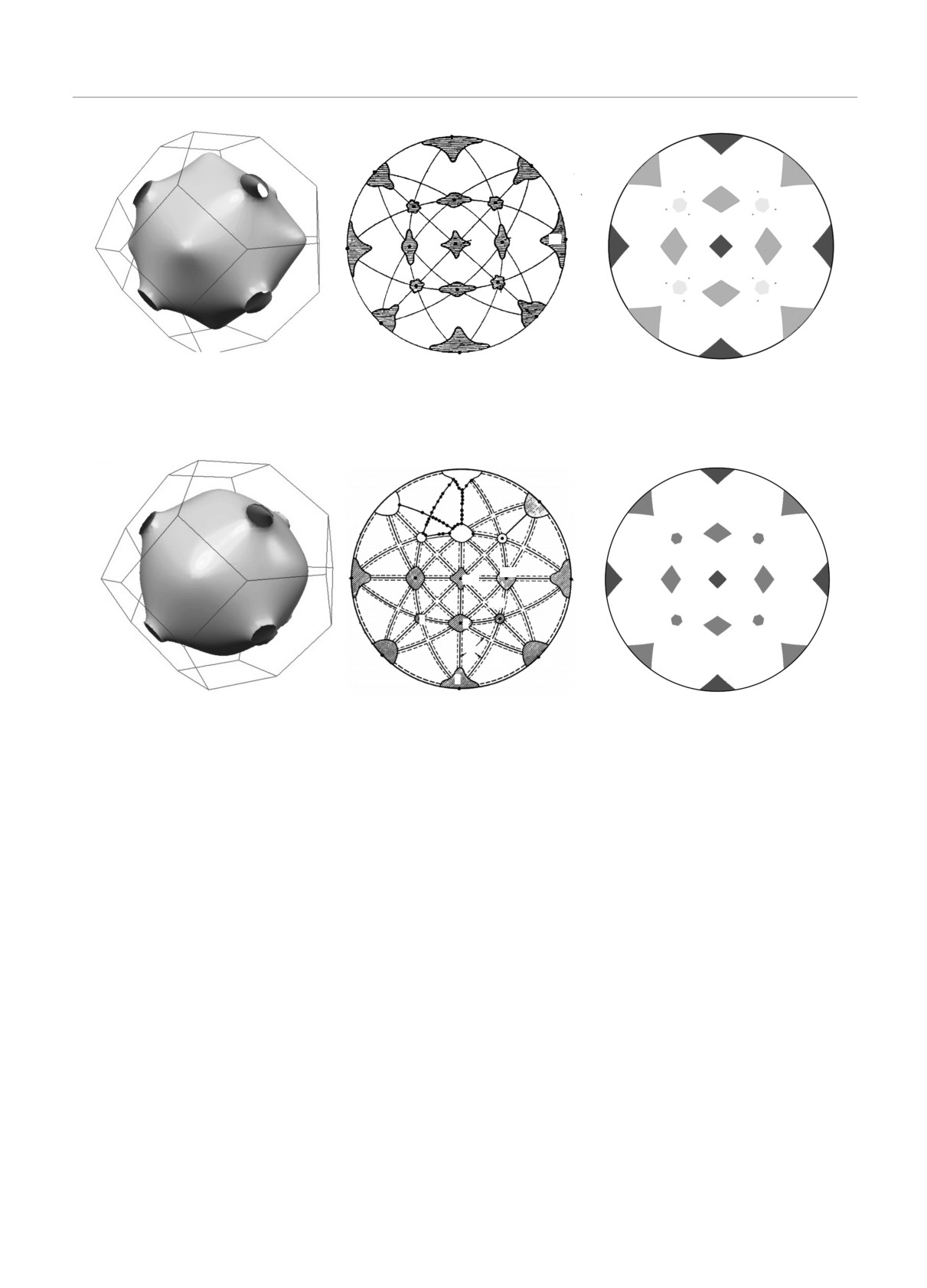
Рис. 8. Форма поверхности Ферми золота, экспериментально измеренные зоны устойчивости [54] и зоны устойчивости,

полученные в результате прецизионных численных вычислений [25, 26]

011

001

010

112

111

III

110

Рис. 9. Форма поверхности Ферми серебра, экспериментально измеренные зоны устойчивости [55] и зоны устойчивости,

полученные в результате прецизионных численных вычислений [25, 26]

ти является наиболее интересной для металлов со

бывших носителей. Можно видеть, таким образом,

сложными поверхностями Ферми с точки зрения ее

что для каждой из зон Ω_α естественно ввести еще

математического описания.

одну (вторую) границу (вообще говоря, не совпада-

ющую с границей «экспериментально наблюдаемой»

Еще одной важной особенностью структуры,

зоны

Ω_α), соответствующую полному исчезновению

приведенной на рис. 5, является то, что пересече-

описанной структуры. В области Ω^′α, ограниченной

ние границы зоны Ω_α приводит в действительности

первой и второй границами зоны Ω_α, траектории си-

лишь к частичному ее разрушению. Действитель-

стемы (1.1) также поддаются эффективному описа-

но, можно видеть, что исчезновение лишь одного

нию на основе структуры, возникающей в зоне Ω_α,

из цилиндров замкнутых траекторий не дает полно-

что позволяет также дать описание основных физи-

го исчезновения этой структуры, поскольку поверх-

ческих явлений, связанных с геометрией траекторий

ность Ферми остается при этом разбитой на разде-

системы (1.1) [31]. Отметим здесь, что, в отличие от

ленные оставшимися цилиндрами замкнутых траек-

зон Ω_α, различные зоны Ω^′α, Ω^′β могут пересекаться

торий пары «слившихся» бывших носителей откры-

друг с другом.

тых траекторий. Таким образом, для полного исчез-

новения структуры, представленной на рис. 5, необ-

Описанная структура системы (1.1) на поверхно-

ходимо исчезновение хотя бы еще одного цилиндра

сти Ферми при наличии устойчивых открытых тра-

замкнутых траекторий, делающее возможными «пе-

екторий явилась также основой для построения чис-

рескоки» траекторий между парами «слившихся»

ленных методов исследования этой системы в об-

767

С. П. Новиков, Р. Де Лео, И. А. Дынников, А. Я. Мальцев

ЖЭТФ, том 156, вып. 4 (10), 2019

Рис. 10. Пример диаграммы типа A (очень схематично) с

Рис. 11. Пример диаграммы типа B (очень схематично,

одним и тем же типом поведения холловской проводимо-

показано лишь конечное число зон устойчивости и «хао-

сти (электронным) вне зон устойчивости

тических» направлений B) с различными типами холлов-

ской проводимости (электронным и дырочным) в различ-

ных областях вне зон устойчивости

щем случае и вычисления структуры зон устойчи-

вости в особенно сложных примерах (см., например,

[20,24-26]). А именно, исследование топологии цик-

вает, как правило, наиболее важное влияние на об-

лов, задаваемых замкнутыми траекториями (1.1) на

щую сложность угловой диаграммы. Более точно,

поверхности Ферми, позволяет эффективно описать

диаграммы, для которых холловская проводимость

глобальную структуру траекторий даже при весь-

имеет одно и то же значение везде вне зон устойчи-

ма сложной геометрии поверхности Ферми и нали-

вости (при заданной величине B, ω_Bτ ≫ 1), мож-

чии зон устойчивости весьма малых размеров. На

но отнести к типу A. Напротив, диаграммы, на ко-

рис. 8, 9 приведены картины зон устойчивости для

торых существуют области вне зон устойчивости с

поверхностей Ферми золота и серебра, полученные

различными значениями холловской проводимости

экспериментально и вычисленные на основе тополо-

(часто с различными типами проводимости, элек-

гических методов, приведенных выше. Как можно

тронной и дырочной), относятся к типу B (рис. 10,

видеть, численные методы существенно уточняют

11). Предположительно, диаграммы типа A явля-

картину зон устойчивости, в частности, существен-

ются наиболее распространенными среди всех диа-

но уточняют границы экспериментально измерен-

грамм для реальных веществ, однако, они являются

ных зон. На диаграмме рис. 8 можно, кроме точ-

априори более простыми, нежели диаграммы типа

ных зон устойчивости, обнаруженных эксперимен-

B. В частности, диаграмма типа B содержит в слу-

тально, видеть также наличие (весьма малых) до-

чае общего положения бесконечное число зон устой-

полнительных зон, не обнаруженных ранее в экспе-

чивости со сколь угодно большими значениями то-

риментах.

пологических чисел, в то время как для диаграмм

Отмечая возможную сложность угловых диа-

типа A наличие бесконечного числа зон устойчиво-

грамм для проводимости, можно специально от-

сти является исключительным случаем (см. [32]).

метить, что все нетривиальные (содержащие зоны

Рассматривая устойчивые открытые траектории

устойчивости) угловые диаграммы для нормальных

системы (1.1) и соответствующие им зоны устой-

металлов можно в действительности разделить на

чивости в пространстве направлений B, нельзя не

2 различных типа [31, 32]. Тип диаграммы опреде-

сказать здесь о возможности введения общей уг-

ляется при этом, исходя из поведения холловской

ловой диаграммы для всего дисперсионного соот-

проводимости для направлений B, лежащих вне зон

ношения ϵ(p), описывающей поведение открытых

устойчивости, однако, именно это поведение оказы-

траекторий (1.1) на всех энергетических уровнях

768

ЖЭТФ, том 156, вып. 4 (10), 2019

Теория динамических систем. . .

ϵ(p) = const одновременно [19]. Возможность вве-

дения такой диаграммы базируется на следующих

важных утверждениях о траекториях системы (1.1),

доказанных в работе [19].

Рассмотрим произвольное 3-периодическое дис-

персионное соотношение ϵ(p) и соответствующие

ему системы (1.1), возникающие для различных на-

правлений B. Тогда верны следующие утверждения:

1) для каждого направления B открытые траек-

тории системы (1.1) существуют либо в замкнутом

энергетическом интервале ϵ ∈ [ϵ₁(B/B), ϵ₂(B/B)],

либо на единственном энергетическом уровне ϵ =

= ϵ₀(B/B) = ϵ₁(B/B) = ϵ₂(B/B);

2) всякий раз, когда открытые траектории систе-

мы (1.1) возникают в конечном энергетическом ин-

тервале [ϵ₁(B/B), ϵ₂(B/B)], все несингулярные от-

крытые траектории лежат в прямых полосах конеч-

ной ширины в плоскостях, ортогональных B, прохо-

Рис.

12. (В цвете онлайн) Пример сложной угловой

дя их насквозь;

диаграммы для дисперсионного соотношения ϵ(p)

= cos x cos y + cos y cos z + cos z cos x (показано лишь ко-

3) для направлений B общего положения значе-

нечное число зон устойчивости (цветом) в порядке возрас-

ния функций ϵ₁(B/B) и ϵ₂(B/B) совпадают со зна-

тания соответствующих топологических чисел [51])

чениями некоторых непрерывных функций ϵ₁(B/B)

и ϵ₂(B/B), определенных всюду на единичной сфе-

ре S². Для специальных направлений B, таких что

5) Совокупность всех зон устойчивости Ω_α обра-

плоскость, ортогональная B, содержит вектор об-

зует всюду плотное открытое множество на единич-

ратной решетки, значения ϵ₁(B/B) и ϵ₂(B/B) могут

ной сфере S².

не совпадать с ϵ₁(B/B) и ϵ₂(B/B) (если данное на-

Можно также отметить, что все угловые диа-

правление B соответствует появлению периодичес-

граммы для дисперсионного соотношения можно

ких траекторий системы (1.1)). При этом мы всегда

разделить на два класса, а именно:

имеем соотношения

1) сложные диаграммы, содержащие бесконечное

ϵ₁(B/B) ≤ ϵ₁(B/B), ϵ₂(B/B) ≥ ϵ₂(B/B).

число зон устойчивости (рис. 12);

2) простые диаграммы, содержащие единственную

4) Для направлений B общего положения, та-

зону устойчивости, заполняющую всю сферу S².

ких что ϵ₁(B/B) < ϵ₂(B/B), все несингулярные от-

Для сложных угловых диаграмм, описанных вы-

крытые траектории (1.1) имеют одно и то же сред-

ше, большой интерес представляет также структура

нее направление в p-пространстве, задаваемое пе-

множества

ресечением плоскости, ортогональной B, и неко-

S²\ ∪ Ω_α.

торой целочисленной (порожденной двумя векто-

рами обратной решетки) плоскости Γ, неизменной

Данное множество представляет собой множест-

при малых вращениях направления B. Плоскость

во направлений B, для которых возникают «хаоти-

Γ, таким образом, является постоянной для лю-

ческие» траектории системы (1.1), которые мы обсу-

бой связной области на S², где выполняется соот-

дим в следующей главе. Структура данного множе-

ношение ϵ₁(B/B) < ϵ₂(B/B). Максимальные (от-

ства, в действительности, является весьма сложной

крытые) связные области Ω_α, удовлетворяющие

(фрактальной, рис. 13). Согласно гипотезе Новикова

указанному выше условию, можно назвать зона-

[23], для дисперсионных законов общего положения

ми устойчивости для всего дисперсионного зако-

Хаусдорфова размерность этого множества строго

на ϵ(p). Каждая зона устойчивости имеет кусоч-

меньше двух.

но-гладкую границу, на которой выполняются соот-

Как можно видеть, структура угловых диаграмм

ношения ϵ₁(B/B) = ϵ₂(B/B). Каждой из зон устой-

для всего дисперсионного закона является в боль-

чивости Ω_α соответствует при этом некоторая цело-

шинстве случаев гораздо более сложной, нежели

численная плоскость Γ_α, определяемая приведенны-

структура угловых диаграмм для фиксированной

ми выше условиями.

поверхности Ферми. Интересно обратить внимание,

769

ЖЭТФ, вып. 4 (10)

С. П. Новиков, Р. Де Лео, И. А. Дынников, А. Я. Мальцев

ЖЭТФ, том 156, вып. 4 (10), 2019

Рис. 13. Фрактальная структура множества «хаотичес-

ких» направлений B (дополнение к зонам устойчивости)

на угловой диаграмме

однако, на то, что существуют также специальные

поверхности Ферми, угловые диаграммы для кото-

рых совпадают с угловыми диаграммами для все-

го дисперсионного закона [20]. Например, такой по-

верхностью является поверхность

cosx + cosy + cosz = 0,

угловая диаграмма для которой (частично) приве-

дена на рис. 14.

Отметим здесь также, что угловые диаграммы

для всего дисперсионного закона являются до неко-

торой степени абстрактными с точки зрения тео-

рии нормальных металлов. Не исключено, однако,

Рис. 14. Форма поверхности cos x + cos y + cos z = 0 (род

что существует некоторая возможность наблюде-

3) и соответствующие зоны устойчивости на угловой диа-

ния таких диаграмм в полупроводниковых монокри-

грамме [25, 26]

сталлах в присутствии сверхсильных магнитных по-

лей [56].

найдено, например, в работах [34,52]. Отметим сра-

зу, что траектории типа траекторий Царева пред-

3. ХАОТИЧЕСКИЕ ОТКРЫТЫЕ

ставляют собой отдельный класс неустойчивых от-

ТРАЕКТОРИИ СИСТЕМЫ (1.1)

крытых траекторий системы (1.1), они появляются

Мы рассмотрим здесь открытые траектории си-

при «частично иррациональных» направлениях B

стемы

(1.1), отличающиеся от рассмотренных в

(плоскость, ортогональная B, содержит вектор об-

предыдущем разделе, и связанные с ними физичес-

ратной решетки). Можно сразу отметить, что носи-

кие явления.

тель (замыкание) каждой траектории, построенной

Как мы уже указывали во Введении, первые при-

Царевым, представляет собой топологически более

меры такого типа были построены Царевым в 1992 г.

сложную часть поверхности Ферми, нежели описан-

Мы здесь опишем лишь общие свойства траекторий

ные в предыдущем разделе двумерные торы с отвер-

Царева, более подробное их описание может быть

стиями. Как следствие этого, поведение траекторий

770

ЖЭТФ, том 156, вып. 4 (10), 2019

Теория динамических систем. . .

Рис. 15. Вид хаотической траектории Дынникова в плоскости, ортогональной B, в расширенном p-пространстве

Царева на поверхности Ферми более хаотично, а са-

рева приводит к тому, что вклад части поверхности

ми траектории можно отнести уже к классу «хаоти-

Ферми, несущей такие траектории, также является

ческих» траекторий.

сильно анизотропным в пределе ω_Bτ ≫ 1, как и для

случая устойчивых открытых траекторий системы

Что касается формы траекторий типа траекто-

рий Царева в расширенном p-пространстве, то они,

(1.1). В частности, здесь мы также имеем соотно-

в действительности, обладают здесь в некоторой

шение (2.1) для тензора проводимости в правильно

выбранной системе координат. Надо отметить, од-

степени как свойствами устойчивых открытых тра-

екторий, так и свойствами, не присущими устойчи-

нако, что соотношения (1.4) в данном случае уже

не выполняются и поведение тензора проводимости

вым открытым траекториям. Так, в частности, от-

крытая траектория Царева не может быть заключе-

в случае появления траекторий Царева становится

несколько более сложным. Можно отметить также,

на ни в какую прямую полосу конечной ширины в

плоскости, ортогональной B. Вместе с тем, все от-

что в силу неустойчивости описанных траекторий

структура тензора проводимости не связана здесь

крытые траектории Царева при заданном направ-

лении магнитного поля обладают одним и тем же

с топологическими числами, аналогичными введен-

асимптотическим направлением в плоскостях, ор-

ным выше для устойчивых открытых траекторий

тогональных B, что делает их несколько похожи-

системы (1.1).

ми на устойчивые открытые траектории системы

Второй класс хаотических открытых траекто-

(1.1). Данное свойство, в действительности, присуще

рий системы (1.1) составляют неустойчивые откры-

всем неустойчивым открытым траекториям, возни-

тые траектории, возникающие при направлениях

кающим при частично иррациональных направле-

B максимальной иррациональности. Такие траек-

ниях B [34], что позволяет отнести все такие при-

тории были впервые построены Дынниковым в ра-

меры к классу траекторий, имеющих один и тот же

боте [34], они обладают максимально хаотическим

тип. Кроме того, указанное свойство траекторий Ца-

поведением как на поверхности Ферми, так и в на-

771

13*

С. П. Новиков, Р. Де Лео, И. А. Дынников, А. Я. Мальцев

ЖЭТФ, том 156, вып. 4 (10), 2019

крывающем p-пространстве (рис. 15). Данное свой-

дорфа указанного множества в этом случае стро-

ство траекторий Дынникова приводит также к весь-

го меньше единицы для поверхности Ферми общего

ма нетривиальному поведению тензора магнитопро-

положения (хотя может быть больше для специаль-

водимости в пределе ω_Bτ

≫ 1 при возникнове-

ных поверхностей Ферми). Можно здесь также от-

нии таких траекторий на поверхности Ферми. Од-

метить, что появление хаотических траекторий на

ной из наиболее интересных особенностей такого по-

поверхности Ферми свойственно в общем случае уг-

ведения является резкое подавление проводимости

ловым диаграммам типа B (рис. 11), упомянутым

вдоль направления магнитного поля при ω_Bτ → ∞

в предыдущем разделе, в то время как для угло-

[35]. Другой особенностью здесь является появление

вых диаграмм типа А их появление может проис-

дробных степеней параметра ω_Bτ в асимптотиках

ходить лишь в исключительных случаях (см. [32]).

компонент тензора проводимости [35, 36], что так-

Как мы уже сказали, исследования структуры мно-

же отражает специфику хаотической динамики та-

жества направлений B, отвечающих появлению хао-

ких траекторий. В целом, вклад носителей хаоти-

тических траекторий как на фиксированной поверх-

ческих траекторий Дынникова во все компоненты

ности Ферми, так и на любой поверхности посто-

тензора проводимости стремится к нулю в пределе

янной энергии для данного дисперсионного закона,

ω_Bτ → ∞.

представляют на данный момент довольно активно

В исследовании хаотических режимов, возника-

развивающуюся область топологии и теории дина-

ющих в системе (1.1), можно (несколько упрощен-

мических систем.

но) выделить два основных направления, а именно,

Исследование особенностей динамики хаотичес-

исследование множества параметров системы (1.1),

ких траекторий является наиболее актуальным в

при которых возникают такие режимы, а также

случае траекторий типа траекторий Дынникова, об-

исследование особенностей динамики соответствую-

ладающих наиболее сложным поведением как на по-

щих хаотических траекторий и связанных с ними

верхности Ферми (в T³), так и в расширенном p-про-

особенностей транспортных явлений в металлах.

странстве. Специальные примеры таких траекторий

К пространству параметров системы (1.1) мож-

могут при этом обладать весьма замечательными

но отнести параметры дисперсионного соотношения

свойствами. Так, например, траектории, построен-

ϵ(p), значение энергии Ферми ϵ_F , а также направ-

ные в работе [34], обладают свойством «самоподоб-

ление магнитного поля B. Для наиболее полного

ности» в p-пространстве. А именно, каждая из та-

теоретического описания системы (1.1) при задан-

ких траекторий совпадает сама с собой после рас-

ном дисперсионном соотношении ϵ(p) при этом яв-

тяжения вдоль некоторых двух векторов в соответ-

ляется естественной постановка вопроса о множе-

ствующей плоскости, ортогональной B, с некоторы-

стве направлений B, соответствующих появлению

ми собственными числами, и последующей конеч-

хаотических траекторий на любом из энергетиче-

ной деформации, получившейся после растяжения

ских уровней. Как мы уже отмечали в предыдущей

траектории (изотопии траектории в плоскости, при

главе, данное множество является достаточно слож-

которой расстояние между начальной точкой траек-

ным и может описываться некоторой фрактальной

тории и любым ее образом в процессе изотопии не

структурой на сфере S². Как мы также уже отме-

превышает фиксированной константы).

чали, согласно гипотезе Новикова (верхняя) фрак-

Замечательное свойство, описанное выше, к со-

тальная размерность этого множества строго мень-

жалению, не присуще хаотическим траекториям

ше 2 для дисперсионных соотношений общего по-

Дынникова в общем случае. Для исследования ди-

ложения. Исследования структуры указанного мно-

намики таких траекторий, однако, оказались весьма

жества (как аналитические, так и численные) в на-

эффективными методы, возникшие первоначально

стоящее время являются довольно интенсивными и

в абстрактной теории динамических систем и сло-

можно сказать, что гипотеза Новикова в целом под-

ений на двумерных поверхностях (см., например,

тверждается на настоящий момент (см., например,

[36,38-40,45-49]). В частности, весьма важными ха-

[41, 42, 44, 50, 53]). Возвращаясь к теории нормаль-

рактеристиками хаотических траекторий оказались

ных металлов, мы должны также поставить вопрос

так называемые индексы Зорича - Концевича - Фор-

о структуре указанного множества для фиксирован-

ни (см., например, [40]), описывающие важные ас-

ного уровня Ферми ϵ_F . Можно показать [19], что

пекты поведения таких траекторий как на поверх-

мера Лебега такого множества равна нулю для по-

ности Ферми, так и в расширенном p-пространстве.

верхности Ферми общего положения. Согласно ги-

Здесь мы не можем привести подробного описания

потезе Новикова [21,22], верхняя размерность Хаус-

указанных характеристик, отметим, однако, что они

772

ЖЭТФ, том 156, вып. 4 (10), 2019

Теория динамических систем. . .

играют, в действительности, весьма важную роль

И. М. Лифшиц, В. Г. Песчанский, ЖЭТФ 35, 1251

в появлении дробных степеней параметра ω_Bτ в

(1958).

асимптотиках компонент тензора проводимости при

И. М. Лифшиц, В. Г. Песчанский, ЖЭТФ 38, 188

возникновении хаотических траекторий типа Дын-

(1960).

никова на поверхности Ферми в общем случае (см.

[36]). Можно также отметить, что наиболее полное

И. М. Лифшиц, М. И. Каганов, УФН 69, 419

возможное описание поведения хаотических траек-

(1959).

торий Дынникова с точки зрения общей теории

И. М. Лифшиц, М. И. Каганов, УФН 78, 411

динамических систем является на данный момент

(1962).

весьма актуальной задачей, представляющей инте-

рес для многих исследователей.

И. М. Лифшиц, М. И. Каганов, УФН 87, 389

(1965).

10.

M. I. Kaganov and V. G. Peschansky, Phys. Rep. 372,

4. ЗАКЛЮЧЕНИЕ

445 (2002).

Представлены последние результаты исследо-

11.

И. М. Лифшиц, М. Я. Азбель, М. И. Каганов,

ваний задачи динамики электронных состояний на

Электронная теория металлов, Наука, Москва

сложных поверхностях Ферми в присутствии внеш-

(1971).

него магнитного поля и их связь с электронными

транспортными явлениями в металлах в сильных

12.

Электроны проводимости, под ред. М. И. Кагано-

магнитных полях. Рассмотрение транспортных

ва, В. С. Эдельмана, Наука, Москва (1985).

явлений в металлах проводится в главном (квази-

13.

С. П. Новиков, УМН 37:5, 3 (1982).

классическом) приближении, что непосредственно

связывает особенности динамики электронов с

14.

А. В. Зорич, УМН 39, 235 (1984).

различными режимами электронного транспорта в

15.

И. А. Дынников, УМН 47, 161 (1992).

пределе ω_Bτ ≫ 1. Результаты основаны на общих

теоремах топологического характера и включают

16.

И. А. Дынников, Математические заметки 53, 57

в себя описание всех возможных типов электрон-

(1993).

ной динамики и соответствующих им режимов

17.

С. П. Новиков, А. Я. Мальцев, Письма в ЖЭТФ

электронного транспорта в металле при самых

63, 809 (1996).

общих предположениях относительно электронного

спектра. Вместе с тем, в работе обсуждаются также

18.

С. П. Новиков, А. Я. Мальцев, УФН 168, 249

вопросы, интересные для дальнейшего развития

(1998).

данной области исследований.

19.

И. А. Дынников, УМН 54, 21 (1999).

Финансирование. Работа одного из соавто-

20.

I. A. Dynnikov, Surfaces in 3-Torus: Geometry of Pla-

ров (Р. Д. Л.) выполнена при поддержке National

ne Sections, Proc. of ECM2, BuDA (1996).

Science Foundation (грант №DMS-1832126), другого

21.

A. Ya. Maltsev and S. P. Novikov, Solid State Phys.,

(А. Я. М.) — при поддержке Российского научного

Bulletin of Braz. Math. Society, New Series 34, 171

фонда (грант №18-11-00316).

(2003).

22.

A. Ya. Maltsev and S. P. Novikov, J. Stat. Phys. 115,

ЛИТЕРАТУРА

31 (2004).

1. Ч. Киттель, Квантовая теория твердых тел,

23.

A. Ya. Maltsev and S. P. Novikov, arXiv:cond-mat/

Наука, Москва (1967).

0304471.

2. Дж. Займан, Принципы теории твердого тела,

24.

R. De Leo, SIAM J. Appl. Dynam. Syst. 2, 517

Мир, Москва (1974).

(2003).

3. А. А. Абрикосов, Основы теории металлов, Нау-

25.

R. De Leo, Phys. Lett. A 332, 469 (2004).

ка, Москва (1987).

26.

R. De Leo, Physica B: Cond. Matt. 362, 62 (2005).

4. И. М. Лифшиц, М. Я. Азбель, М. И. Каганов,

ЖЭТФ 31, 63 (1956).

27.

R. De Leo, Exper. Math. 15, 109 (2006).

773

С. П. Новиков, Р. Де Лео, И. А. Дынников, А. Я. Мальцев

ЖЭТФ, том 156, вып. 4 (10), 2019

28.

R. De Leo and I. A. Dynnikov, Geom. Dedicata 138,

Functions and Dynamical Systems, Ecole de Physique

51 (2009).

des Houches, France, March 9-21 (2003), Sprin-

ger-Verlag, Berlin (2006), p. 439.

29.

А. Я. Мальцев, ЖЭТФ 151, 944 (2017).

44.

Р. Де Лео, И. А. Дынников, УМН 62, 151 (2007).

30.

А. Я. Мальцев, ЖЭТФ 152, 1053 (2017).

45.

A. Skripchenko, Discrete Contin. Dyn. Sys. 32, 643

31.

А. Я. Мальцев, ЖЭТФ 154, 1183 (2018).

(2012).

32.

А. Я. Мальцев, ЖЭТФ 156, 140 (2019).

46.

A. Skripchenko, Ann. Glob. Anal. Geom. 43, 253

(2013).

33.

С. П. Царев, Частное сообщение (1992-93).

47.

I. Dynnikov and A. Skripchenko, Amer. Math. Soc.

34.

I. A. Dynnikov, Amer. Math. Soc. Transl. Ser. 2,

Transl., Ser. 2, Vol. 234, AMS, Providence, RI (2014),

Vol. 179, AMS, Providence, RI (1997), p. 45.

p. 173, arXiv:1309.4884.

35.

А. Я. Мальцев, ЖЭТФ 112, 1710 (1997).

48.

I. Dynnikov and A. Skripchenko, Trans. Moscow

36.

А. Я. Мальцев, С. П. Новиков, Труды МИАН 302,

Math. Soc. 76, 287 (2015).

296 (2018).

49.

A. Avila, P. Hubert, and A. Skripchenko, Invent.

37.

A. V. Zorich, in: Proc. Geometric Study of Foliations,

Math. 206, 109 (2016).

(Tokyo, November 1993), ed. by T. Mizutani et al.,

50.

A. Avila, P. Hubert, and A. Skripchenko, Bulletin de

World Scientific, Singapore (1994), p. 479.

la Société Mathématique de France 144, 539 (2016).

38.

A. V. Zorich, Ann. de l’Institut Fourier 46,

325

51.

R. De Leo, in: Advanced Mathematical Methods in

(1996).

Biosciences & Applications, ed. by F. Berezovskaya

and B. Toni, Springer (2018); arXiv:1711.01716.

39.

A. Zorich, Amer. Math. Soc. Transl., Ser. 2, Vol. 179,

AMS, Providence, RI (1997), p. 173.

52.

А. Я. Мальцев, С. П. Новиков, УМН 74, 149 (2019).

40.

A. Zorich, Amer. Math. Soc. Transl., Ser. 2, Vol. 197,

53.

R. Gutiérrez-Romo and C. Matheus, arXiv:1902.

AMS, Providence, RI (1999), p. 135.

04516 [math.DS].

54.

Ю. П. Гайдуков, ЖЭТФ 37, 1281 (1959).

41.

Р. Де Лео, УМН 55, 181 (2000).

55.

Н. Е. Алексеевский, Ю. П. Гайдуков, ЖЭТФ 42,

42.

Р. Де Лео, УМН 58, 197 (2003).

69 (1962).

43.

A. Zorich, in: Frontiers in Number Theory, Physics

56.

И. А. Дынников, А. Я. Мальцев, ЖЭТФ 112, 371

and Geometry, Vol. 1: On Random Matrices, Zeta

(1997).

774