ЖЭТФ, 2019, том 156, вып. 4 (10), стр. 775-787

СИНХРОНИЗАЦИЯ ПРОЦЕССОВ ПРИ ПАРАЛЛЕЛЬНОМ

МОДЕЛИРОВАНИИ ДИСКРЕТНЫХ СОБЫТИЙ

Л. Н. Щурa,b*, Л. Ф. Зигануроваb,c**

^a Институт теоретической физики им. Л. Д. Ландау Российской академии наук

142432, Черноголовка, Московская обл., Россия

^b Национальный исследовательский университет Высшая школа экономики

101000, Москва, Россия

^c Научный центр Российской академии наук в Черноголовке

142432, Черноголовка, Московская обл., Россия

Поступила в редакцию 22 апреля 2019 г.,

после переработки 22 апреля 2019 г.

Принята к публикации 23 апреля 2019 г.

Метод параллельного моделирования дискретных событий (ПМДС) является одним из перспективных

методов эффективного использования суперкомпьютерных систем. В работе приводятся результаты ана-

лиза моделей синхронизации процессорных элементов при выполнении вычислений методом ПМДС. Для

классификации моделей синхронизации используется аналогия между изменением профиля локальных

времен процессорных элементов и ростом поверхности образца при молекулярной эпитаксии. Два важных

класса таких моделей — это модели консервативного ПМДС и оптимистического ПМДС. Консервативная

модель принадлежит к классу универсальности уравнения Кардара - Паризи - Жанга, а оптимистическая

модель — к классу универсальности задач направленного протекания. Мы приводим результаты анализа

моделей синхронизации в случае, если граф обмена сообщениями между процессорными элементами

принадлежит к классу сетей малого мира.

Статья для специального выпуска ЖЭТФ, посвященного 100-летию И. М. Халатникова

DOI: 10.1134/S0044451019100201

чены возможные интересные физические приложе-

ния, они понимали перспективность нового направ-

ления исследований, основанных на использовании

1. ВВЕДЕНИЕ

ЭВМ [2], но известные трагические события прерва-

ли их совместную работу. Предложенная ими схе-

Начало развитию вычислительной физики поло-

ма бегущего счета, известная как «метод прогон-

жили научно-практические работы по разработке

ки», вошла в учебники, она широко используется

ракетно-ядерного щита. С этой целью были созда-

специалистами по вычислительной физике во всем

ны ЭВМ в США и в СССР. Основной круг решае-

мире, хотя большинство из них и не знает о су-

мых задач находился в области гидродинамики экс-

ществовании основополагающей работы [1], вошед-

тремального состояния вещества. В процессе работ

шей во второй том Собрания трудов Ландау. В этом

над такими вычислениями была предложена очень

мы имели возможность убедиться на прошедшей в

красивая и эффективная схема решения уравнений

2013 г. в Москве международной конференции по

гиперболического и параболического типов. Это бы-

вычислительной физике IUPAP CCP2013 [3], на ко-

ло сделано Л. Д. Ландау и И. М. Халатниковым

торой И. М. Халатников впервые представил до-

в соавторстве с математиком Н. Н. Мейманом [1].

клад по материалам этой работы шестидесятилет-

Ландау и Халатников разработали программу раз-

ней давности.

вития методов вычислений, в которую были вклю-

Первые вычислительные системы были скаляр-

^* E-mail: lev@landau.ac.ru

ными и проводили в единицу времени одно вычис-

^** E-mail: ziganurova@gmail.com

ление. В настоящее время процесс развития вычис-

775

Л. Н. Щур, Л. Ф. Зиганурова

ЖЭТФ, том 156, вып. 4 (10), 2019

лительных технологий находится на очередном вит-

вычисления в одной из подобластей. Свою часть

ке, которое состоит в переходе на иерархическую

вычислений логические процессы могут проводить

структуру вычислительных устройств. Если цен-

независимо друг от друга, а взаимодействие логиче-

тральный процессор ранних ЭВМ состоял из одного

ских процессов происходит только на границах об-

арифметически-логического устройства, то совре-

ластей с целью обмена обновленными значениями

менный процессор имеет несколько таких устройств

сеточных переменных.

в одном процессорном элементе, называемом ядром.

Первые принципы параллельного моделирова-

Более того, процессор может иметь до нескольких

ния дискретных событий были описаны Любачевс-

десятков таких ядер. Каждое ядро может выпол-

ким в 1987 г. [6] на примере модели Изинга. Главная

нять свой независимый процесс вычислений. Для

особенность метода состоит в том, что он не изме-

эффективного использования в вычислениях ЭВМ

няет динамику физической системы при моделиро-

с такой конструкцией необходим особый подход к

вании [7]. Например, в спиновых системах перево-

организации вычислений.

роты спинов происходят в случайные моменты вре-

ЭВМ с иерархической структурой можно ис-

мени в разных узлах системы. Если моделировать

пользовать как большой набор традиционных ЭВМ,

спиновую систему традиционным синхронным спо-

каждая из которых выполняет свою задачу на од-

собом, то расчеты переворота спина будут происхо-

ном из ядер. При этом процесс выполнения задач

дить в моменты времени 0, Δt, 2Δt, . . ., где Δt — за-

каждым ядром не будет зависеть от процессов, вы-

ранее заданный временной шаг моделирования. Ме-

полняемых другими ядрами. Если же требуется ис-

тод параллельного моделирования дискретных со-

пользовать всю мощность современной супер-ЭВМ

бытий (ПМДС) позволяет моделировать асинхрон-

для решения одной большой задачи, то нам надо со-

ную динамику системы: время при моделировании

ставить процесс вычислений таким образом, чтобы

течет непрерывно, но изменения в частях системы

синхронизировать работу большого числа процессов

(т. е. перевороты спинов) происходят в случайные

вычислений, выполняемых всеми ядрами ЭВМ. Со-

моменты времени. Эти изменения называются собы-

временные суперкомпьютерные системы насчитыва-

тиями, и времена между событиями распределены

ют несколько миллионов вычислительных ядер¹⁾ и

по закону Пуассона. Параллельное моделирование

обеспечить их синхронную работу таким образом,

таких дискретных событий при правильной синхро-

чтобы минимизировать простой каждого из ядер,

низации множества логических процессов дает ту

является актуальной и в общем случае нерешенной

же последовательность событий, что и при последо-

задачей.

вательном моделировании, но процесс вычислений

Один из методов загрузки суперкомпьютера на

можно значительно ускорить за счет параллелизма

полную мощность одной задачей (а это и есть основ-

вычислений ядрами.

ное предназначение супер-ЭВМ) — это метод парал-

Локальное время [8] каждого логического про-

лельного моделирования дискретных событий [5].

цесса изменяется при наступлении события в моде-

Его назначение состоит в синхронизации вычисле-

лируемой этим процессом части общей системы, по-

ний одной задачи, которая предварительно разбива-

этому времена всех логических процессов в системе

ется на части (логические процессы), каждая из ко-

различны. Локальные виртуальные времена про-

торых выполняется отдельным процессорным эле-

цессов составляют профиль локальных виртуаль-

ментом (например, ядром). В случае решения упо-

ных времен (ЛВВ). Виртуальное время процесса —

мянутых выше дифференциальных уравнений об-

это неубывающая локальная переменная логическо-

ласть вычислений может быть разбита на подоблас-

го процесса, и профиль таких времен может быть

ти и каждый логический процесс будет проводить

использован для характеристики степени синхрони-

зации параллельных вычислений [5].

¹⁾ Мы не углубляемся в основном тексте статьи в реаль-

В процессе моделирования профиль локальных

ную схему современных суперкомпьютеров, которые допол-

времен растет, что делает его схожим с процессом

нительно к центральным процессорам имеют устройства для

случайного роста поверхности в физике [9,10]. Рост

выполнения вычислений, так называемые ускорители вычис-

локальных времен в консервативном алгоритме в

лений, например, графические процессоры. Каждый такой

графический процессор имеет свою иерархическую структу-

одномерном случае имеет аналогию с ростом по-

ру, в которой насчитываются тысячи ядер, и которые имеют

верхности, описываемым уравнением Кардара - Па-

иную схему организации вычислений, чем ядра классичес-

ризи - Жанга (KPZ [11]), а в оптимистическом ал-

ких центральных процессоров [4]. Общее число таких ядер

в современных суперкомпьютерах намного превышает общее

горитме — с ростом поверхности в модели SOS (So-

число ядер центральных процессоров.

lid-on-Solid [12]). Аналогия между эволюцией про-

776

ЖЭТФ, том 156, вып. 4 (10), 2019

Синхронизация процессов при параллельном моделировании...

филя локальных виртуальных времен в консерва-

тивном алгоритме и ростом поверхности по уравне-

нию KPZ дает возможность классифицировать ал-

горитмы синхронизации на три класса: консерватив-

ный, оптимистический и FaS. Эти классы соответ-

ствуют периодическим, свободным и фиксирован-

ным граничным условиям уравнения Кардара - Па-

ризи - Жанга [13].

Сделать выводы о фундаментальных свойствах

этих алгоритмов возможно, исследуя поведение ло-

кальных виртуальных времен процессов. Для это-

го мы используем модели роста профиля локаль-

ных времен для оптимистического [10] и консерва-

тивного [9] алгоритмов синхронизации. Эти модели

учитывают такие свойства реальных систем, как ко-

личество логических процессов, граф их взаимодей-

ствия, среднее время между событиями и другие.

Рис. 1. Пример топологии малого мира

Мы исследовали поведение моделей на графах двух

типов: регулярных графах и графах с топологией

чах иногда могут возникать и связи дальнего по-

малого мира. Регулярные графы содержат только

рядка [18], поэтому в моделях мы организуем ло-

локальные взаимодействия между узлами, в то вре-

гические процессы как в регулярный граф, так и в

мя как сети малого мира учитывают также и уда-

граф малого мира [19]. В этих графах вершинами

ленные взаимодействия.

являются логические процессы (ЛП), а ребрами —

В статье мы описываем результаты моделирова-

взаимодействия между ними. Если два ЛП не соеди-

ния профиля локальных виртуальных времен для

нены ребром, это означает, что они независимы друг

консервативного и оптимистического алгоритмов

от друга и синхронизация между ними не требуется.

ПМДС и приводим основания для соотнесения мо-

Мы описываем коммуникационный граф матрицей

делей с известными классами универсальности.

смежности D. Если ЛП_i зависит от ЛП_j, то элемент

матрицы D(i, j) = 1, если процессы ЛП_i и ЛП_j неза-

висимые, то D(i, j) = 0.

2. МОДЕЛЬ РОСТА ПРОФИЛЯ

Регулярная топология представляет собой коль-

ЛОКАЛЬНЫХ ВРЕМЕН В АЛГОРИТМАХ

цо, где каждый ЛП взаимодействует только с дву-

СИНХРОНИЗАЦИИ ПМДС

мя соседними ЛП. Топология малого мира получа-

ется из регулярного графа путем добавления даль-

В этом разделе мы опишем модели роста про-

филя ЛВВ для консервативного и оптимистическо-

них связей между двумя случайно выбранными ло-

гическими процессами (рис. 1). Количество таких

го алгоритмов ПМДС [9, 10, 14, 15]. Отметим, что

дальних связей в наших моделях регулируется па-

существует множество различных реализаций ал-

раметром p ∈ [0; 1], фиксированным числом даль-

горитмов обоих классов. Мы не учитываем част-

них связей, равным pN. Случай p = 0 соответствует

ные особенности конкретных реализаций, а фоку-

регулярной топологии.

сируемся на поведении профиля локальных времен.

При топологии малого мира средний кратчай-

Поведение профиля содержит информацию о сте-

пени синхронизации процессорных элементов и об

ший путь l(N, p) в графе растет логарифмически с

количеством вершин N [20]:

эффективности использования процессорного вре-

мени [16, 17].

∑

l(N, p) =

d_ij ∝ ln(N),

(1)

Степень синхронизации процессорных элементов

N (N - 1)

i=j

и эффективность параллельного моделирования за-

висят не только от выбранного алгоритма синхро-

где расстояние d_ij измеряется как минимальное ко-

низации, но и от топологии взаимодействия логиче-

личество вершин, через которые нужно пройти, что-

ских процессов. При моделировании реальных фи-

бы попасть из вершины i в вершину j (также для

зических процессов чаще всего элементы системы

d_ij используется название chemical distance). Напом-

взаимодействуют локально, но в некоторых зада-

ним, что на регулярном графе средний кратчайший

777

Л. Н. Щур, Л. Ф. Зиганурова

ЖЭТФ, том 156, вып. 4 (10), 2019

путь растет линейно с N. Соотношение (1) выполня-

Обозначим локальное время одного логического

ется в тех графах, которые мы строим и использу-

процесса на шаге моделирования t как τ_i(t), тогда

ем при моделировании на сетях малого мира. Мы

профиль ЛВВ — это набор {τ₁(t), τ₁(t), . . . , τ_N (t)}.

численно проанализировали зависимость среднего

Мы начинаем моделирование эволюции ЛВВ с

кратчайшего пути в этих графах от размера систе-

плоского профиля: τ_i(t = 0) = 0, i = 1, 2, . . . , N.

мы и параметра p. Результаты численных экспери-

Далее увеличиваем локальное время только у тех

ментов хорошо аппроксимируются функцией [14]

процессов, чье время меньше или равно локально-

му времени соседей. Если его время больше, чем у

ln(pN)

его соседей, то на данном шаге моделирования его

l(p) = A

+ C,

(2)

локальное время не изменяется. Учитывая, что со-

бытия в системе распределены экспоненциально, мы

где A, C — константы.

обновляем профиль локальных времен на каждом

Взаимодействие между ЛП реализуется с помо-

шаге моделирования t согласно следующему прави-

щью обмена сообщениями (messages). При наступле-

лу:

нии события (т. е. при изменении состояния в моде-

{

лируемой логическом процессом подобласти) логи-

τ_i(t)+η_i, τ_i(t) ≤ {τ_j(t)}D(i,j)=1,

τ_i(t + 1) =

(3)

ческий процесс создает сообщение с указанием сущ-

τ_i(t),

τ_i(t) > {τ_j(t)}D(i,j)=1,

ности события и времени события (ЛВВ), измерен-

ного в единицах глобального времени моделируемо-

где η_i — это случайная величина, распределенная

го события [8]. Сравнение времени в полученном со-

по закону Пуассона с единичным математическим

общении с текущим локальным временем дает воз-

ожиданием, {τ_j (t)}D(i,j)=1 — это локальные време-

можность каждому ЛП делать вывод о сохранении

на логических процессов, которые соединены с ЛП_i

причинности в процессе моделирования. Если полу-

локальной либо дальней связью, i = 1, . . . , N.

ченное логическим процессом сообщение содержит

время меньшее, чем локальное время процесса, то

2.2. Модель для оптимистического

это означает нарушение причинности. Способ обра-

алгоритма

ботки нарушения причинности и отличает классы

алгоритмов [13, 21].

Идея оптимистического алгоритма заключается

в том, что вместо блокирующих конструкций (как

в консервативных алгоритмах) используется меха-

2.1. Модель для консервативного алгоритма

низм обнаружения и исправления ошибок [23]. ЛП

параллельно обрабатывают события в течение неко-

Консервативный алгоритм полностью избегает

торого установленного временного окна, а затем

ошибки причинности, т.е. такие ситуации, при ко-

происходит проверка причинности вычислений. Ес-

торых логический процесс получает сообщение «из

ли ЛП получил сообщение с меткой меньшей, чем

прошлого» — с временной меткой меньшей, чем его

его ЛВВ, то состояние этого ЛП «откатывается» до

текущее локальное время. Это осуществляется пу-

того времени, когда получение этого события бы-

тем обмена сообщениями, содержащими времена на-

ло бы безопасным. Если при этом ЛП отправлял

ступления событий в логических процессах [5, 22].

сообщения другим ЛП, то для отмены этих преж-

Говоря на языке локальных времен, в консерватив-

девременно отправленных сообщений рассылаются

ном алгоритме обработка событий логическим про-

так называемые антисообщения. Антисообщения от-

цессом будет безопасна, если его локальное время

личаются от обычных сообщений только наличием

меньше или равно локальному времени соседей, а

отрицательного знака. При попадании в одну оче-

также других ЛП, от которых он зависит в соответ-

редь двух одинаковых сообщений с разными знака-

ствии с графом взаимодействия. Если это условие

ми, происходит аннигиляция, оба сообщения унич-

не выполняется, то ЛП остается заблокированным

тожаются.

и ждет, пока соседние ЛП не «догонят» его во вре-

Поскольку в оптимистическом алгоритме ло-

мени.

кальное время логических процессов может как уве-

Рассмотрим систему из N логических процес-

личиваться, так и уменьшаться, мы разбиваем один

сов, объединенных в коммуникационную тополо-

шаг моделирования на две части: продвижение впе-

гию. Пусть p — средняя доля дальних связей на один

ред и откат назад. Во время продвижения вперед

ЛП, тогда общее число дальних связей равно pN.

каждый ЛП_i увеличивает свое ЛВВ на случайную

778

ЖЭТФ, том 156, вып. 4 (10), 2019

Синхронизация процессов при параллельном моделировании...

величину η_i, распределенную по закону Пуассона со

Для оптимистического алгоритма средняя ско-

средним значением, равным единице:

рость также отображает эффективность обработки

событий, но рассчитывается по другой формуле:

τ_i(t + 1) = τ_i(t) + η_i, i = 1, 2, . . ., N.

(4)

v(t) = 〈τ(t) - τ(t - 1)〉,

(8)

Откат происходит в том случае, когда наруше-

на причинность вычислений. Будем считать, что ко-

где τ(t) — это среднее по логическим процессам вре-

личество откатов во время одного шага моделиро-

мя на шаге t, а τ(t-1) — среднее по логическим про-

вания — это пуассоновская случайная величина со

цессам время на предыдущем шаге. В случае, когда

средним b. Во время каждого отката случайным об-

в модели оптимистического алгоритма нет откатов,

разом выбирается один ЛП_j. Считаем, что причин-

т. е. параметр b = 0, средняя скорость будет равна

ность может быть нарушена равновероятно любым

единице.

ЛП, от которого зависит j-й ЛП. Выбираем равнове-

Средняя квадратичная ширина профиля

роятно ЛП_r из числа тех, для которых D(j, r) = 1.

отражает степень синхронизации процессорных эле-

Далее τ_j сравнивается со временем τ_r и в случае,

ментов и рассчитывается по формуле

если τ_j больше ЛВВ ЛП_r, τ_j уменьшается до τ_r [10]:

∑

{

w²(t) =

[τ_i(t) - τ(t)]2

(9)

τ_r, τ_j > τ_r,

τ_j =

(5)

i=1

τ_j, τ_j < τ_r.

Чем меньше разброс локальных времен, тем лучше

ЛП синхронизированы. Большая дисперсия локаль-

2.3. Наблюдаемые величины

ного времени процессов указывает на то, что часть

ЛП отстает, а часть — слишком торопится. Это уве-

По описанным выше правилам мы моделиру-

личивает время ожидания для тех ЛП, которые на-

ем рост профиля локальных времен в течение t =

ходятся впереди по времени.

= 10⁴-10⁶ дискретных шагов моделирования. После

Мы изучаем изменение средней скорости профи-

каждого шага t, т. е. после каждого обновления про-

ля локальных времен v и средней квадратичной ши-

филя, мы рассчитываем среднее значение локально-

рины профиля локальных времен w² как функций

го времени по всем логическим процессам τ(t), сред-

шага моделирования t, количества логических про-

нюю скорость профиля v(t) и среднюю квадратич-

цессов N и концентрации дальних связей между ло-

ную ширину профиля w²(t).

гическими процессами p.

Среднее локальное виртуальное время ино-

гда называют средней высотой профиля. Оно пред-

ставляет собой среднее арифметическое по локаль-

3. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

ным временам всех логических процессов:

В этом разделе мы описываем поведение моде-

∑

ли для консервативного алгоритма синхронизации и

τ (t) =

τ_i(t)

(6)

модели для оптимистического алгоритма синхрони-

i=1

зации. Акцент сделан на аналогии моделей динами-

Угловые скобки в этом уравнении и далее озна-

ки локальных времен с моделями роста поверхности

чают усреднение по независимым реализациям про-

в физике. Таким образом, исследуемые нами свой-

филя на шаге моделирования t.

ства профиля ЛВВ в алгоритмах ПМДС могут быть

Средняя скорость профиля показывает за-

интерпретированы как в терминах степени синхро-

груженность процессорных элементов, или эффек-

низации и эффективности этих алгоритмов, так и в

тивность работы алгоритма. Для консервативно-

терминах случайного роста поверхности.

го алгоритма средняя скорость рассчитывается по

формуле

3.1. Консервативный алгоритм

^;N_акт(t)^<

v(t) =

(7)

3.1.1. Класс универсальности

Кардара - Паризи - Жанга

где N_акт(t) — это количество активных ЛП, т. е. тех

ЛП, которые изменили свое время на данном шаге

Эволюцию профиля ЛВВ в консервативном ал-

моделирования.

горитме ПМДС на одномерной топологии можно

779

Л. Н. Щур, Л. Ф. Зиганурова

ЖЭТФ, том 156, вып. 4 (10), 2019

отнести к классу универсальности Кардара - Пари-

зи- Жанга (KPZ) [9]. Класс универсальности KPZ

описывается уравнением [11]

∂

h(x, t) = ν₀ + ν∇²h +

(∇h)² + η(x, t),

(10)

∂t

где h(x, t) — это высота поверхности в точке x в

момент времени t, а η(x, t) — это гауссовский шум

(дельта-коррелированный), который задается урав-

нением

〈η(x, t)〉 = 0,

(11)

〈η(x, t)η(x^′, t^′)〉 = Dδ(x - x^′)δ(t - t^′).

Угловые скобки означают усреднение по ансамблю,

ν₀, ν, λ, D — константы.

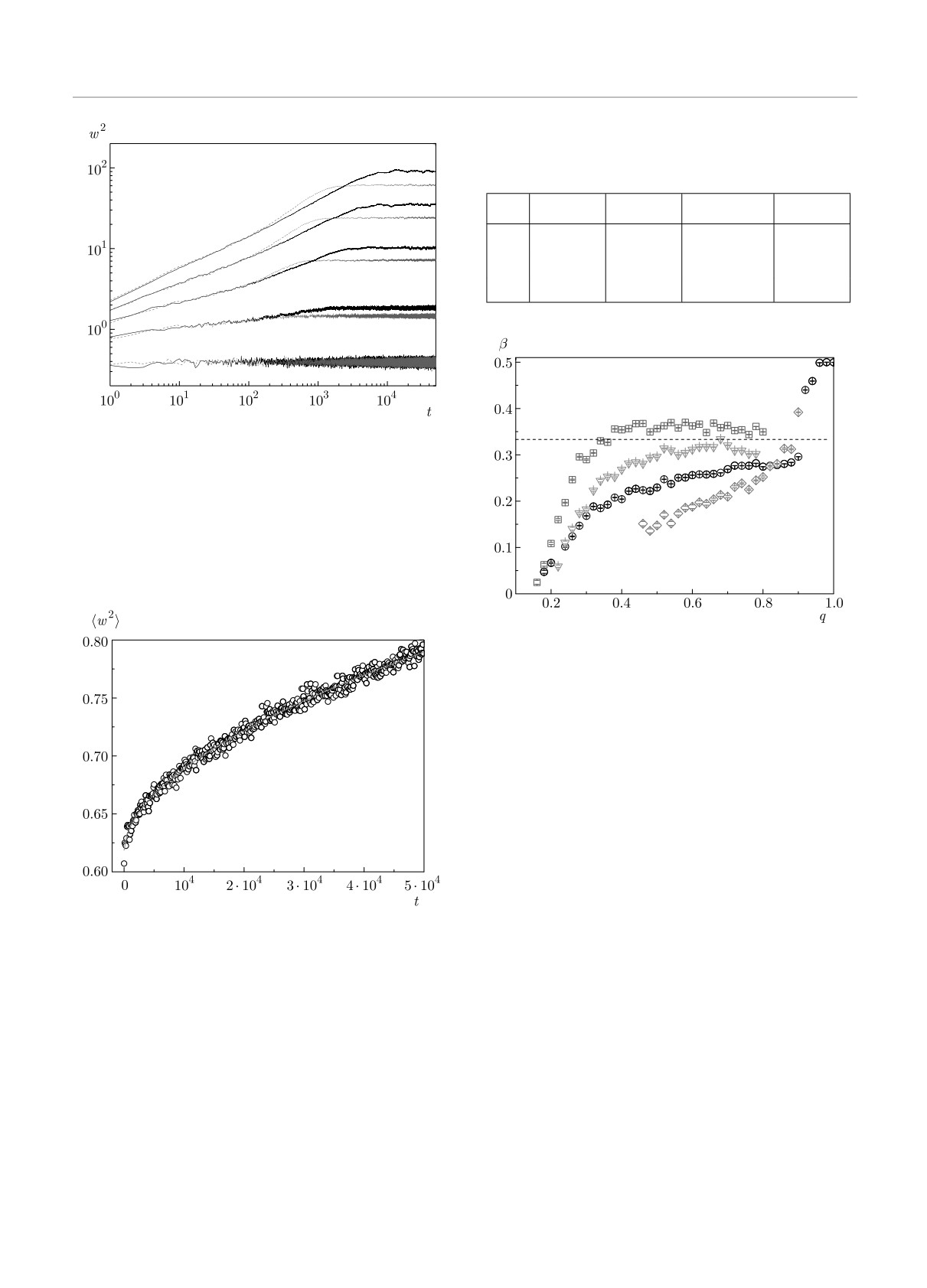
Рис. 2. Средняя квадратичная ширина w² как функция

Первый член уравнения ν₀ — это постоянная

времени для системы из N = 10⁴ логических процессов и

действующая сила. Второй член уравнения соот-

для различных значений p. Усреднение взято по 1500 неза-

ветствует поверхностному натяжению и отвечает за

висимым реализациям. Пунктиром обозначена кривая для

сглаживание поверхности. Нелинейность возникает

регулярной топологии p = 0. Из статьи [14]

из геометрических соображений: поверхность растет

в каждой точке перпендикулярно краю, а высота

w²

h(x, t) измеряется вдоль оси y. Это лишь один из

источников нелинейности, среди прочих причин мо-

10³

p = 0.002

жет быть также нелинейное взаимодействие частиц,

0.004

0.006

из которых состоит поверхность.

0.008

Известно, что квадратичная ширина поверхнос-

0.01

0.02

ти w²(L, t) масштабируется как [24]

0.04

10²

{

0.06

0.08

N2α, L ≪ ξ(t),

0.1

w²(L, t) ∝ t2βF(Lt-1/z) ∝

(12)

t2β,

L ≫ ξ(t),

10¹

где L — линейный размер системы, ξ(t) ∝ t1/z — кор-

реляционная длина, z = α/β. Критический показа-

тель α называется показателем роста, β — показате-

лем шероховатости, z — динамическим критическим

10³

10⁴

10⁵

показателем. В одномерном случае для класса уни-

версальности KPZ известны точные значения кри-

Рис. 3. Зависимость средней величины насыщения w2∞ от

тических показателей: α = 1/2, β = 1/3, z = 3/2.

количества N логических процессов при разных p [14]

3.1.2. Результаты численных экспериментов

Значения показателей α и β, полученные пу-

В модели консервативного алгоритма на регу-

тем аппроксимации данных, равны соответственно

лярной топологии квадратичная ширина профиля

0.49(1) и 0.326(5). Значения этих показателей близ-

растет со временем логарифмически:

ки к критическим индексам класса KPZ.

Средняя скорость роста профиля ЛВВ в пределе

w²(t) ∝ t2β,

(13)

бесконечного размера системы v₀ равна 0.246410(7)

[13]. Из этого следует, что при использовании кон-

а затем насыщается (рис. 2). Величина насыщения

сервативной синхронизации с локальными взаимо-

(максимальная ширина профиля ЛВВ) зависит от

действиями только четверть логических процессов

количества логических процессов линейно (рис. 3):

активна в один момент времени. Степень рассинхро-

w2∞(N) ∝ N2α.

(14)

низации между логическими процессами увеличива-

ется пропорционально их числу (w² ∝ N).

780

ЖЭТФ, том 156, вып. 4 (10), 2019

Синхронизация процессов при параллельном моделировании...

Таблица 1. Сводная таблица поведения скорости

Добавление дальних взаимодействий между ло-

v и квадратичной ширины w² профиля локальных

гическими процессами кардинально меняет пове-

времен в модели консервативного алгоритма

дение профиля ЛВВ в консервативном алгорит-

ме [14,15]. Синхронизация между ЛП в модели кон-

сервативного алгоритма становится лучше на топо-

Регулярная

Топология малого

логии малого мира. Ширина профиля растет со вре-

топология p = 0

мира p > 0

менем как t2β и насыщается (рис. 2), как и в случае

w²(t) ∝ t2β, t < t_×

w² ∝ t2β

локальной топологии, однако величина насыщения

w²(t)

β = 0.326(5)

β ∼ ln(p)

не увеличивается с ростом количества ЛП (рис. 3).

Критический показатель шероховатости α в этом

w2∞(N) ∝ N2α

w2∞(N) ∼ const

случае равен 0. Это означает, что степень синхрони-

w2∞(N)

α = 0.49(1)

α=0

зации остается одинаковой для систем любого раз-

мера.

v₀ = 0.246410(7)

v = v₀ - Δv

Средняя скорость профиля на топологии мало-

Δv ∝ p0.306(4)

го мира незначительно снижается. Так, например,

при значении параметра p = 0.01 (p — доля случай-

ных добавленных дальних связей) средняя скорость

ля снижается незначительно. Основные результа-

равна 0.221370(7). Обозначим разность между ско-

ты для консервативного алгоритма ПМДС кратко

ростью роста профиля на регулярной топологии v₀

представлены в табл. 1.

и на топологии малого мира v как Δv [14],

Δv = v₀ - v.

3.2. Оптимистический алгоритм

В этом разделе мы опишем результаты исследо-

Эта разность изменяется как

вания модели для оптимистического алгоритма и

Δv(p, N) ∝ pB(N).

(15)

покажем связь нашей модели с классами универ-

сальности KPZ с коррелированным шумом (Quen-

Степень B(N) уменьшается с ростом количества ло-

ched KPZ, qKPZ) [25] и классом направленной пер-

гических процессов:

коляции (Directed Percolation, DP) [26].

ln N

B(N) ≈ B + A

√

(16)

3.2.1. Класс универсальности направленной

перколяции

асимптотически она равна B = 0.306(4).

Уравнение KPZ с коррелированным шумом от-

Уменьшение скорости профиля ЛВВ на тополо-

личается от обычного KPZ

(10) тем, что шум

гии малого мира происходит потому, что добавляет-

η_q(x, h(x, t)) теперь является функцией x и h и не

ся число связей, потенциально тормозящих процесс.

зависит от времени:

Однако малое число добавочных связей приводит

∂

к небольшому замедлению эволюции профиля вре-

h(x, t) = F +ν∇²h+

(∇h)²+η_q(x, h(x, t)).

(17)

∂t

мен. Иными словами, дальние связи незначительно

уменьшают эффективность параллельного модели-

Такая модель описывает рост поверхности в некото-

рования, но подавление рассинхронизации дает об-

рой гетерогенной среде (например, распространение

щий выигрыш в предсказуемости процесса вычисле-

влажного края при намокании бумаги). F в уравне-

ния.

нии (17) может быть интерпретирована как сила,

Таким образом, консервативная модель роста

заставляющая поверхность расти.

профиля ЛВВ на регулярной топологии может быть

В qKPZ (17) есть фазовый переход в точке F_c.

отнесена к классу универсальности KPZ. Рассинхро-

Когда сила достаточно большая, поверхность рас-

низация локальных времен в этом алгоритме растет

тет непрерывно и в этом случае шум эквивалентен

с размером системы, а средняя скорость роста про-

шуму в обычном KPZ. Когда же сила F маленькая,

филя постоянна и примерно равна 1/4. Добавление

появляется часть поверхности, где рост подавляет-

случайных дальних взаимодействий между логиче-

ся сильным негативным шумом. Фазовый переход к

скими процессами улучшает синхронизацию. Ши-

шероховатости (вблизи F_c ) относится к классу уни-

рина профиля остается постоянной вне зависимос-

версальности направленной перколяции. В одномер-

ти от размера системы. При этом скорость профи-

ном случае универсальные критические показатели

781

Л. Н. Щур, Л. Ф. Зиганурова

ЖЭТФ, том 156, вып. 4 (10), 2019

Рис. 4. Средняя скорость v профиля как функция пара-

Рис. 5. (В цвете онлайн) Средняя скорость v профиля как

метра q для системы из N = 1000 логических процессов

функция параметра (q - qc) в системах разного разме-

на регулярной топологии p = 0

ра на регулярной топологии p = 0. Зеленые ромбы для

N = 5000; черные кружки для N = 1000; синие треуголь-

ники для N = 500; красные квадраты для N = 250

поверхности выражаются через критические пока-

затели класса универсальности одномерной направ-

ленной перколяции: α = β = ν^DP⊥ /ν^DP∥ ≈ 0.633 и

Для нахождения зависимости v(q) при каждом

z = 1, где ν^DP⊥ и ν^DP∥ — это критические показате-

значении параметра q проводится усреднение функ-

ли, соответственно описывающие расхождение кор-

ции v(t) по шагам моделирования, при этом в усред-

реляционной длины и времени в классе DP.

нении не учитываются значения для шага времени,

К классу направленной перколяции, согласно ги-

меньшего типичного интервала релаксации скоро-

потезе Грассбергера, относятся системы, соверша-

сти. График зависимости средней скорости v от па-

ющие непрерывный фазовый переход в одно аб-

раметра q представлен на рис. 4. Предполагая, что

сорбирующее состояние (состояние, которое систе-

v ∼ ξ-1∥ ∼ (q-q_c)ν∥ [26,28,29], мы аппроксимировали

ма не может покинуть) [27]. Эта гипотеза была под-

график функцией вида

тверждена множеством численных экспериментов.

Обсуждаемая нами модель для оптимистического

v(q) = v₀(q - q_c)ν∥ .

(18)

алгоритма демонстрирует аналогичное поведение.

Полученные значения параметров подгонки: v₀ =

= 1.26(2), q_c = 0.136(1), ν_∥ = 1.78(2).

3.2.2. Результаты численных экспериментов

На рис. 5 показана зависимость средней скорос-

Удобно ввести параметр q = 1/(1 + b), который

ти v от (q - q_c) в дважды логарифмической шкале.

может быть интерпретирован как интенсивность ро-

В целом результаты численного моделирования хо-

ста поверхности (growth rate).

рошо попадают на кривую (q - q_c)1.78(2), но вблизи

Определение критического индекса ν_∥.

критической точки данные отклоняются. Это мож-

Средняя скорость роста профиля ЛВВ v(t) — это

но объяснить недостаточной точностью вычислений

среднее приращение высоты профиля за один шаг

и эффектом конечного размера системы. Для то-

моделирования (8). Средняя скорость не зависит от

го чтобы проверить влияние конечного размера, мы

времени, но зависит от параметра q, интенсивности

провели моделирование систем из 250, 500, 1000 и

роста. С ростом b при некотором значении q = q_c

5000 логических процессов.

скорость профиля снижается до нуля, т. е. слишком

На рис. 6 изображен график зависимости значе-

большое количество откатов не позволяет профилю

ний скорости v от количества логических процессов

ЛВВ продвигаться вперед. Система оказывается

N вблизи точки перехода (q - q_c = 0.034). При уве-

в поглощающем состоянии. Мы можем ожидать,

личении размера системы средняя скорость профи-

согласно гипотезе Грассбергера, что модель будет

ля снижается. Мы аппроксимировали график функ-

принадлежать к классу универсальности направ-

цией v(N) = v_N→∞ + A/N^C . Полученные значения

ленной перколяции.

v_N→∞ для различных q вблизи критического зна-

782

ЖЭТФ, том 156, вып. 4 (10), 2019

Синхронизация процессов при параллельном моделировании...

Таблица 2. Значения параметров функции (18) для

регулярной топологии и топологий малого мира с

различными значениями параметра p

v₀

q_c

1.26(2)

0.136(1)

1.78(2)

0.001

1.27(4)

0.140(2)

1.80(3)

0.01

1.32(4)

0.158(2)

1.82(3)

0.1

1.64(7)

0.213(3)

1.96(5)

топологии имеет фазовый переход между активной

Рис. 6. (В цвете онлайн) Средняя скорость профиля v

фазой (когда скорость роста профиля ненулевая) и

как функция количества логических процессов N для

состоянием пиннинга (когда профиль не растет) в

q - qc = 0.034 на регулярной топологии p = 0. Крас-

точке q_c = 0.136(1). Найденная нами критическая

ной штриховой линией показана аппроксимация вида

экспонента ν_∥ = 1.78(2) близка к экспоненте в клас-

v(N) = vN→∞ + A/N^C. Найденное значение vN→∞ =

се направленной перколяции, ν^DP∥ ≈ 1.73. К клас-

= 0.0016 ± 1.5 · 10-8, χ² = 1.61894

су направленной перколяции также относятся кон-

тактные процессы [30, 31], модели распространения

эпидемий без иммунизации [32], каталитические ре-

0.004

акции [33-35], модели случайного блуждания (bran-

ching-annihilating random walks) [36, 37], модели ро-

0.003

ста поверхностей [12, 38] и другие [26].

Поведение скорости роста профиля для модели

0.002

оптимистического алгоритма на сетях малого мира

изменяется несущественно. Поскольку дополнитель-

ные зависимости между ЛП провоцируют больше

откатов, в среднем скорость профиля снижается, по-

ложение критической точки q_c и критический пока-

0.001

затель ν_∥ при этом смещаются в сторону больших

значений (табл. 2).

Ширина профиля локальных времен. В мо-

0.02

0.03

0.04

делях роста ширина характеризуется t_×, типичным

q- q_c

значением шага моделирования для выхода на на-

сыщение. Известно, что t_× ∝ N^z, где z — динами-

Рис. 7. (В цвете онлайн) Средняя скорость профиля v как

ческая экспонента. В нашей модели в период t < t_×

функция параметра (q - qc) в системах разного разме-

ширина растет степенным образом:

ра на регулярной топологии p = 0. Зеленые ромбы для

N = 5000; черные кружки для N = 1000; синие треуголь-

w²(t) ∝ t2β.

ники для N = 500; красные квадраты для N = 250. Чер-

ными звездочками показаны рассчитанные значения ско-

График изменения ширины профиля ЛВВ со

рости в пределе бесконечного размера системы (рис. 6)

временем для разных топологий представлен на

рис. 8. Чем меньше параметр q, тем меньше ширина

профиля ЛВВ. Поскольку откаты выравнивают вре-

чения изображены на рис. 7. Чем больше модели-

мена логических процессов, увеличение их количе-

руемая система, тем ближе полученные значения к

ства, т. е. уменьшение параметра q, делает профиль

предсказанной кривой, однако даже для достаточно

ЛВВ более гладким. Добавление небольшого числа

больших систем (N = 5000) заметно влияние конеч-

дальних связей также улучшает синхронизацию —

ности системы.

ширина профиля при одинаковом параметре q на

Таким образом, скорость роста профиля ЛВВ в

сетях малого мира ниже, чем на регулярной топо-

модели оптимистического алгоритма на регулярной

логии.

783

Л. Н. Щур, Л. Ф. Зиганурова

ЖЭТФ, том 156, вып. 4 (10), 2019

Таблица 3. Результаты аппроксимации ширины в

области t < t× функцией w²(t) = A+Bt2β для сис-

тем разного размера N в критической точке qc

t_×

10³

< 100

0.42(2)

0.17(2)

0.016(9)

10⁴

≈ 20000

0.600(6)

0.006(2)

0.13(3)

10⁵

> 50000

0.618(2)

0.00043(5)

0.277(9)

Рис. 8. (В цвете онлайн) Зависимость средней ширины

профиля ЛВВ от времени для разных значений парамет-

ра q снизу вверх: [0.1, 0.2, 0.3, 0.4, 0.5]. Черной линией обо-

значена ширина для регулярной топологии p = 0, синей

штриховой — для топологии малого мира с параметром

p = 0.01. Результаты усреднены по 1000 независимым ре-

ализациям

Рис. 10. (В цвете онлайн) Зависимость критического ин-

декса β от параметра q на различных топологиях для

системы из N

= 10³ логических процессов. Черными

кружками обозначены результаты на регулярной тополо-

гии p = 0, синими квадратами — результаты для тополо-

гии малого мира с p = 0.001, красными треугольниками —

для p = 0.01, зелеными ромбами — для p = 0.1. Чер-

ной штриховой линией приведено значение критического

индекса для класса KPZ β = 1/3

В критической точке q ≈ 0.136 в системе из N =

= 10⁵ логических процессов на регулярной тополо-

гии (p = 0) ширина профиля в области t < t_× растет

по степенному закону (рис. 9):

Рис.

9. (В цвете онлайн) Рост ширины w² профиля

w²(t < t_×) = 0.618(2) + 0.00043(5)t0.553(9),

ЛВВ со временем в модели оптимистического алгорит-

ма для системы из N

= 10⁵ логических процессов в

т. е. показатель β ≈ 0.277. В табл. 3 приведено зна-

критической точке при p

= 0. Каждая точка на гра-

чение показателя β в критической точке q_c для регу-

фике — это усреднение по бину в 100 временных ша-

лярной топологии (p = 0) в зависимости от количе-

гов моделирования t. Красная линия показывает функцию

ства логических процессов. По таблице видно, что β

w²(t) = 0.618(2) + 0.00043(5)t0.553(9)

увеличивается с количеством логических процессов.

Нас интересует показатель β в термодинамическом

пределе бесконечного размера системы, N → ∞.

Мы также исследовали, как изменяется показа-

На рис. 10 изображен график зависимости кри-

тель роста β в зависимости от параметра q, доли

тического индекса роста β от параметра q для раз-

дальних связей p и размера системы N.

личных топологий взаимодействия логических про-

784

ЖЭТФ, том 156, вып. 4 (10), 2019

Синхронизация процессов при параллельном моделировании...

Таблица 4. Результаты аппроксимации ширины в

области t > t× функцией w^∞(N) = A + BN2α

q=q_c

0.57(2)

0.009(6)

0.13(5)

q - q_c = 0.05

0.629(5)

0.0007(3)

0.29(5)

q - q_c = 0.1

0.671(6)

0.0003(1)

0.36(5)

q - q_c = 0.15

0.710(7)

0.0002(1)

0.39(5)

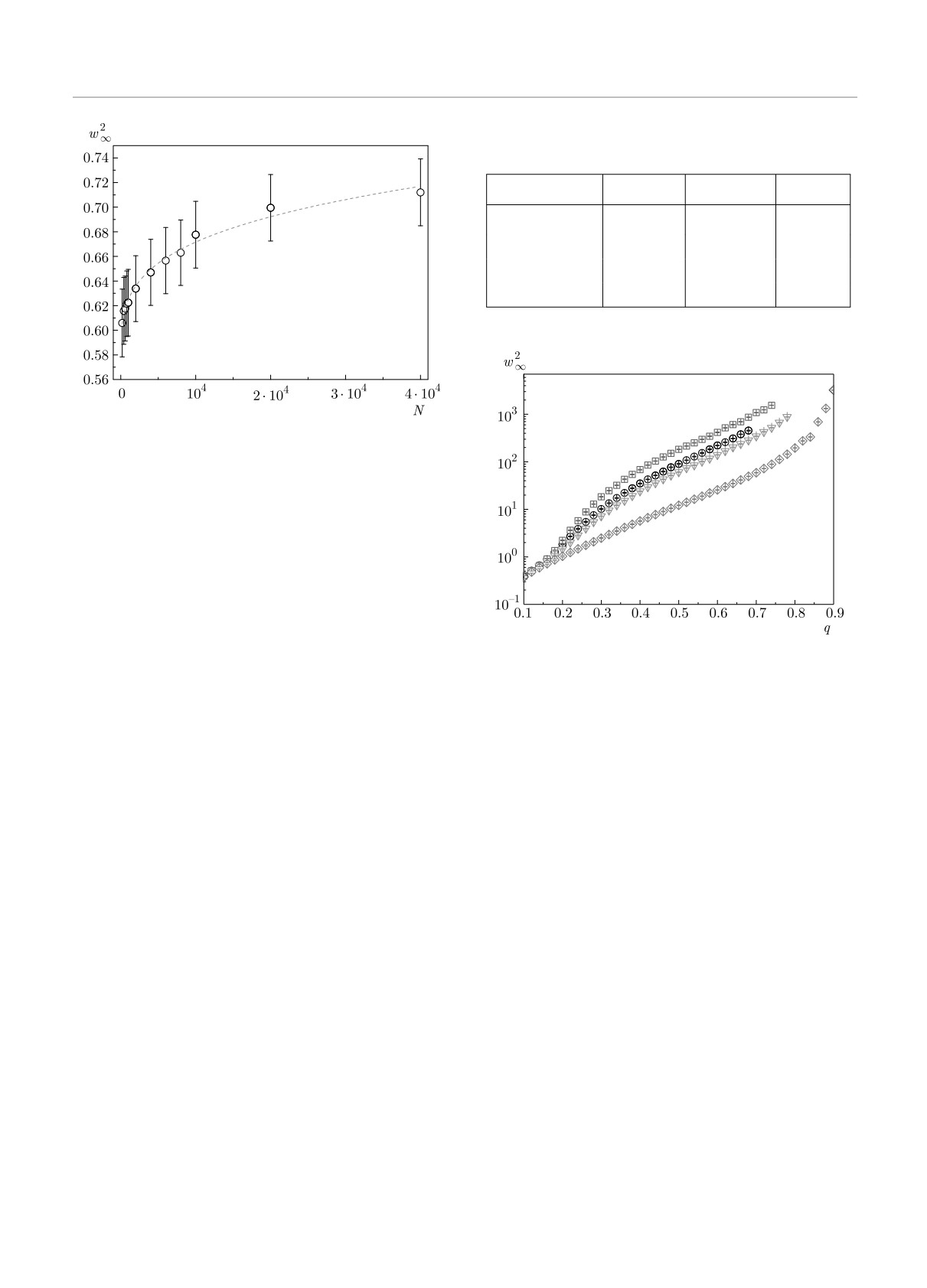
Рис. 11. Величина насыщения ширины профиля ЛВВ w2∞

в зависимости от количества логических процессов N

в точке qc = 0.136. Каждая точка на графике получе-

на усреднением функции w²(t) по диапазону [t×, tmax],

где t× — точка, где ширина равна значению насыщения,

tmax — максимальное время моделирования

цессов. Поведение критического индекса можно раз-

делить на три режима: при малых, умеренных и

больших значениях параметра q. При малых q, т.е.

в фазе пиннинга, профиль локальных времен прак-

Рис. 12. (В цвете онлайн) Зависимость ширины профи-

тически не растет, поэтому и ширина профиля w²

ля ЛВВ w2∞ от параметра q на различных топологиях

не растет и остается близкой к нулю. Для умерен-

для системы из N = 10³ логических процессов. Черными

ных q ∈ [0.4; 0.8], или в активной фазе, где профиль

кружками обозначены результаты на регулярной тополо-

растет с ненулевой скоростью v и имеется ненулевое

гии p = 0, синими квадратами — результаты для тополо-

количество откатов, во всех топологиях показатель

гии малого мира с p = 0.001, красными треугольниками —

для p = 0.01, зелеными ромбами — для p = 0.1

β либо равен константе, близкой к 1/3, либо стре-

мится к этому значению. Для точного определения

показателей β к рис. 10 необходимы поправки на ко-

нечный размер системы. При q > 0.8 наблюдается

Мы также изучили, как изменяется величина

режим, при котором профиль растет практически

насыщения w2∞ с размером системы. Мы усред-

свободно, без откатов (q = 1 соответствует чистому

нили функцию w²(t) по диапазону [t_×, t_max], где

свободному росту). В этом случае ширина профи-

t_× — точка, где ширина равна значению насыще-

ля растет быстрее всего, показатель β стремится к

ния, t_max — максимальное время моделирования.

значению 1/2.

График w2∞(N) в критической точке для регулярной

топологии представлен на рис. 11. Мы аппроксими-

По-видимому, в активной фазе, при q значитель-

но большем q_c, но несколько меньшем 1, показатель

ровали график функцией w2∞(N) = A + BN2α. Зна-

чения показателя шероховатости α в области кри-

β совпадает с показателем из класса KPZ, как в

консервативном алгоритме. При q вблизи единицы,

тической точки приведены в табл. 4. В самой кри-

система растет по закону случайного роста. Таким

тической точке показатель α намного ниже, чем в

ее окрестности.

образом, модель оптимистического алгоритма в од-

номерном случае (p = 0) демонстрирует несколько

Ширина насыщения w2∞ также имеет несколько

режимов поведения в зависимости от значения q —

режимов в зависимости от параметра q. Для малых

она имеет две критические точки (q = q_c и q = 1) и

q w2∞ близка к нулю. В области q ∈ [0.4;0.7] шири-

поведение в классе KPZ для промежуточных значе-

на насыщения w2∞ растет с параметром q примерно

ний q.

одинаково для всех видов топологий (рис. 12). Для

785

ЖЭТФ, вып. 4 (10)

Л. Н. Щур, Л. Ф. Зиганурова

ЖЭТФ, том 156, вып. 4 (10), 2019

больших значений q определить значение ширины

Conference on Computational Physics, 20-24 August,

сложно из-за очень большого времени выхода на на-

Moscow (2013), http://ccp2013.ac.ru/.

сыщение t_×.

Nvidia-V100. https://www.nvidia.com/ru-ru/data-

center/tesla-v100/.

4. ЗАКЛЮЧЕНИЕ

R. M. Fujimoto, Comm. ACM 33, 30 (1990).

B. D. Lubachevsky, Complex Syst. 1, 1099 (1987).

В работе обсуждаются модели синхронизации

при параллельном моделировании дискретных со-

B. D. Lubachevsky, J. Comput. Phys. 75, 103 (1988).

бытий. Оказывается, эволюция локальных времен

параллельных процессов имеет аналогию с ростом

D. R. Jefferson, ACM Transactions on Programming

поверхности. Это дает возможность применить для

Languages and Systems (TOPLAS) 7, 404 (1985).

анализа синхронизации и эффективности вычисле-

G. Korniss, Z. Toroczkai, M. A. Novotny, and

ний язык и аппарат статистической механики. Для

P. A. Rikvold, Phys. Rev. Lett. 84, 1351 (2000).

консервативного алгоритма модель может быть све-

дена к модели роста по уравнению Кардара - Па-

10.

L. Ziganurova, M. Novotny, and L. Shchur, J. Physics:

ризи - Жанга. Для оптимистического алгоритма мо-

Conf. Ser. 681, 012047 (2016).

дель по формулировке похожа на модель роста SOS.

11.

M. Kardar, G. Parisi, and Y. C. Zhang, Phys. Rev.

При этом, однако, у нее есть три режима — режим в

Lett. 56, 889 (1986).

классе направленной перколяции, режим случайно-

го роста и промежуточный режим, близкий к классу

12.

U. Alon, M. R. Evans, H. Hinrichsen, and D. Muka-

универсальности KPZ. Такое поведение может быть

mel, Phys. Rev. Lett. 76(15), 2746 (1996).

также сопоставлено с поведением поверхности роста

13.

L. N. Shchur and M. A. Novotny, Phys. Rev. E 70,

в qKPZ.

026703 (2004).

С точки зрения проведения параллельных

вычислений введение связей типа малого мира

14.

L. Ziganurova and L. N. Shchur, Phys. Rev. E 98,

улучшает синхронизацию процессорных элементов

022218 (2018).

при небольшом замедлении вычислений. Кон-

15.

G. Korniss, M. Novotny, H. Guclu, Z. Toroczkai, and

сервативный алгоритм свободен от блокировок

P. A. Rikvold, Science 299, 677 (2003).

(deadlock), тогда как в оптимистическом алгоритме

при увеличении частоты нарушения причинности

16.

L. Ziganurova and L. Shchur, in: Lecture Notes in

возможен переход шероховатости в абсорбирующее

Computer Science 10421, Springer (2017), p. 246.

состояние с нулевой общей производительностью.

17.

L. Shchur and L. Ziganurova, Lobachevskii J. Math.

При умеренных значениях частоты нарушения при-

38(5), 967 (2017).

чинности общая производительность положительна

и десинхронизация насыщается с ростом числа

18.

P. Crawford, S. J. Eidenbenz, P. D. Barnes, and

параллельных процессов.

P. A. Wilsey, in Proc. Winter Simulation Conference,

IEEE Press, Las Vegas (2017), p. 1025.

Финансирование. Работа инициирована при

выполнении гранта № 14-21-00158 Российского науч-

19.

D. J. Watts and S. H. Strogatz, Nature 393, 440

(1998).

ного фонда и завершена в рамках государственного

задания 0236-2019-0001.

20.

A. Barrat and M. Weigt, Eur. Phys. J. B 13, 547

(2000).

ЛИТЕРАТУРА

21.

R. M. Fujimoto, C. Carothers, A. Ferscha, D. Jeffer-

son, M. Loper, M. Marathe, and S. J. Taylor, in Proc.

1. Л. Д. Ландау, И. Н. Мейман, И. М. Халатников,

Winter Simulation Conference, IEEE Press, Las Ve-

в книге: Л. Д. Ландау, Собрание трудов, Т. 2, под

gas, USA (2017).

ред. Е. М. Лифшица, И. М. Халатникова, Физмат-

лит, Москва (2008), с. 357.

22.

V. Y. Vee and W. J. Hsu, Parallel Discrete Event

Simulation: A Survey, Technical Report. Nanyang

2. И. М. Халатников, частное сообщение.

Technological Univ., Singapore (1999).

786