ЖЭТФ, 2019, том 156, вып. 4 (10), стр. 794-798
© 2019
NON-SELF-AVERAGING IN THE CRITICAL POINT
OF A RANDOM ISING FERROMAGNET
Vic. Dotsenko*
Sorbonne Université, LPTMC
F-75005, Paris, France
Landau Institute for Theoretical Physics, Russian Academy of Sciences
142432, Chernogolovka, Moscow Region, Russia
Received January 31, 2019,
revised version February 22, 2019
Accepted for publication February 22, 2019
Contribution for the JETP special issue in honor of I. M. Khalatnikov’s 100th anniversary
DOI: 10.1134/S0044451019100225
ations for a weakly disordered Ising ferromagnet was
derived for D < 4 and its universal shape was obtained
at D = 3 [12]. Away from the critical point, at scales
much bigger than the correlation length Rc, the situ-
1. INTRODUCTION
ation is sufficiently simple: here, the system could be
considered as a set of essentially independent regions
After intensive studies during last several decades,
with the size Rc, and for that reason one could naively
it is well established now that the presence of weak
expect that the free energy distribution function must
quenched disorder in a ferromagnetic system can es-
be Gaussian. In fact, besides the central Gaussian part
sentially modify its critical behavior in the vicinity of
(the “body”), this distribution has asymmetric and es-
the phase transition point such that new universal criti-
sentially non-Gaussian tails [11]. Approaching the cri-
cal exponents may set [1-7]. According to the so called
tical point, one finds that the range of validity of the
Harris criteria [1], weak disorder is relevant for the criti-
Gaussian body shrinks while the tails are getting of
cal behavior only if the specific heat of the pure system
the same order as the body. Finally, when the correla-
is divergent, i. e., the corresponding critical exponent
tion length becomes of the order of the system size (in
α > 0. The critical behavior is then governed by a
the critical point) the free energy distribution function
new, random renormalization-group fixed point, and
turns into a universal non-Gaussian curve.
the pure fixed point becomes unstable.
A system of particular interest is the Ising model in
On the other hand, in recent years, it is argued that
two dimensions, where exact results are available both
due to the presence of disorder, the statistical proper-
for the pure [13] and for the weakly disordered [6, 7]
ties of some thermodynamical quantities at the critical
cases. Here, the Harris criterion is unable to decide the
point can become non-self-averaging [8-11], i.e., the
significance of weak disorder as α = 0, and the system
behavior of a large sample with a specific realization of
hence provides a marginal case. Still, it is now well
impurities will not be well described by the ensemble
established that such weak disorder “marginally” modi-
average normally calculated in an analytical or numer-
fies the critical behavior of this system so that the loga-
ical approach. This clearly has profound consequences
rithmic singularity of the specific heat is changed into
for the physical interpretation of the outcomes and the
a double logarithmic one. While a number of further
possibilities for comparing theoretical and experimen-
aspects of this problem have also been investigated,
tal results.
the question of the disorder distribution of measurable
Recently, an explicit expression for the probability
quantities and their (lack of) self-averaging behavior
distribution function of the critical free-energy fluctu-
was less studied. In the recent paper [14], it was shown
* E-mail: dotsenko@lptlc.jussieu.fr
that in the critical point the internal energy of this
794
ЖЭТФ, том 156, вып. 4 (10), 2019
Non-self-averaging in the critical point...
system is not self-averaging. Namely, both its typi-
In fact if we are interested not just in the average
cal sample-to-sample fluctuations and its average value
free energy of the system but in the properties of its
scale with the system size L like ∼ L lnln(L). In con-
distribution function, the situation even with weak dis-
trast, the specific heat is shown to be self-averaging
order turns out to be rather nontrivial. Considering the
with a distribution function that tends to a δ-peak in
system away from the critical point, one would naively
the thermodynamic limit L → ∞.
expect that at least at scales greater than the correla-
tion length (where the system is expected to split into
a set of more or less independent “cells” of the size of
2. REPLICA FORMALISM
the correlation length), “everything must be Gaussian
distributed”. One can easily prove that this is not true.
Present investigation of the sample-to-sample fluc-
First of all, it can be easily shown that all moments
tuations of the free energy will be performed in terms of
of the partition function Z(N) with N > g/u are di-
the replica method. This approach was already success-
vergent, and this automatically indicates that the free
fully used for the study of the free energy distribution
energy distribution function of the considered system
functions in mean-field spin-glasses and others strongly
cannot be Gaussian. Moreover, we can easily derive
disordered systems [15, 16] (see also [17]). Here, it will
that the left asymptotic of the distribution function
be applied for the Ising systems containing weak dis-
P (F ) has the following simple form:
order. As a matter of a general demonstration of how
(
)
the replica method can be used for the study of the free
g
P (F → -∞) ∝ exp -
F
energy probability distribution function, let us consider
u
the Ising ferromagnet with quenched disorder in terms
It should be stressed that this phenomenon is quite ge-
of the scalar field random temperature D-dimensional
neral: it takes place for any dimension of the system
Ginzburg-Landau Hamiltonian:
independently of the value of the temperature parame-
∫
ter τ (except for the critical point) both in the para-
H [φ, ξ] = dDx ×
magnetic and ferromagnetic phases.
]
[1(
)2
1
1
×
∇φ(x)
+
(τ-ξ(x))φ2(x)+
gφ4(x)
(1)
2
2
4
3. TOY MODEL
Here, the independent random quenched parameters
ξ(x) are Gaussian distributed with ξ2 = 2u, where u
To analyze the properties of the free energy distri-
is the parameter which describes the strength of the
bution function of a random ferromagnet, one can start
disorder. In what follows, it will be supposed that the
with very simple “toy” model [11] containing only one
disorder is weak, namely, u ≪ τ2 and u ≪ g. For a
degree of freedom:
given realization of the disorder, the partition function
1
1
of the considered system is
H(φ, ξ) =
(τ - ξ)φ2 +
gφ4,
(3)
2
4
∫
(
[
])
(
[
])
Z[ξ] = Dφ exp
-H
φ, ξ
= exp
-F
ξ
,
(2)
where ξ2 = 2u, and it is supposed that u ≪ τ2 and
∫
u ≪ g. It can be shown by sufficiently simple calcula-
where
Dφ denotes the integration over all configura-
tions that the free energy distribution function of this
[
]
tions of the fields φ(x) and F
ξ
is the random (disorder
system is strongly non-symmetric and essentially non-
dependent) free energy of the system. The distribu-
Gaussian. Namely, the right tail of this distribution (at
[
]
tion function of the random quantity F
ξ
can be ana-
large positive values of the free energy),
lyzed by studying the moments of the partition function
[
]
ZN [ξ] ≡ Z(N). Usually the replica partition function
1
P (F → +∞) ∝ exp -
exp(4F ) ,
(4)
Z(N) is studied for deriving the average value of the
4u
free energy. The heuristic (not well justified) procedure
of the replica calculations requires performing the ana-
goes to zero much faster than the Gaussian curve, while
its left tail (at large negative values of the free energy),
lytic continuation of the function Z(N) from integer
to arbitrary values of the replica parameter N. Then,
(
)
g
taking the limit N → 0, we formally get
P (F → -∞) ∝ exp -
|F |
,
(5)
u
lim
[Z(N) - 1]/N = F .
goes to zero much slower that the Gaussian one.
N →0
795
Vic. Dotsenko
ЖЭТФ, том 156, вып. 4 (10), 2019
P
4. GINZBURG-LANDAU MODEL IN
DIMENSIONS D < 4
0.5
In this section, we consider the continuous version
0.4
of the Ising ferromagnet in terms of the random tem-
perature D-dimensional scalar field Ginzburg-Landau
0.3
(GL) Hamiltonian, Eq. (1), where τ = (T - Tc)/T is
the reduced temperature. Applying the renormaliza-
0.2
tion group (RG) method to analyze the corresponding
replica Hamiltonian in dimensions D = 4 - ϵ, one does
0.1
not encounter in the one-loop approximation the fixed
point (FP) with both non-zero coordinates u∗ = 0 and
-2.5
-2.0
-1.5
-1.0
-0.5
0
g∗ = 0: this is because the system of equations for the
f
fixed points is degenerate on the one-loop level [2,4,5].
This fixed point appears in the next, two-loop approx-
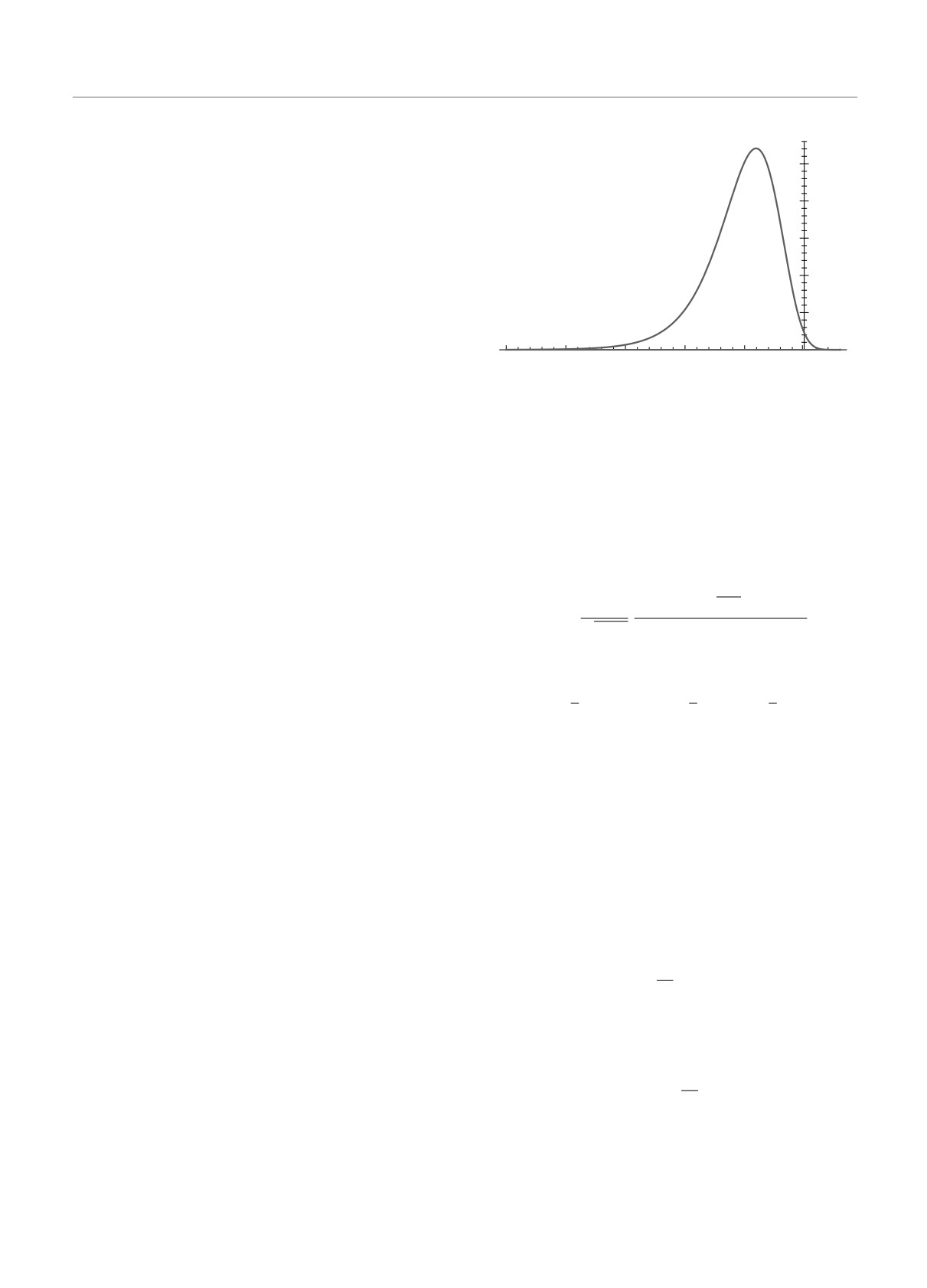
Critical free energy distribution function P (f) of the disordered
imation.
Ising ferromagnet in dimension D = 3
Alternatively, RG equations have been analyzed di-
rectly at D = 3 using the minimal subtraction [18] and
part of the free energy f ∼ L(Dν+α-2)/ν ∼ O(ln L) is
massive [19] RG schemes. To evaluate the divergent
not proportional to the volume of the system. It is the
perturbation series in the renormalized couplings, ap-
distribution function of the random fluctuating part f
propriate resummation technique has been used. Re-
of the free energy in the critical point which is derived
sults of the five loop calculations based on the minimal
in this section:
subtraction scheme at D = 3 are given in Ref. [20].
{
}
In the massive RG scheme, the most accurate results
1
exp
-f -
η2(-f)
are obtained within accuracy of six loops in Ref. [21].
1
4u∗
P (f) =
√
,
(6)
In particular, using two different resummation schemes
8πu∗
G′[η(-f)]
based on the (i) conformal mapping and (ii) Padé ap-
where the functional
proximants the following estimates for the FP values
∫
∞
}
were obtained, respectively: (i) u∗ ≃ 2.14, g∗ ≃ 6.28
1
{1
1
G′(η(t)) =
dφ φ2 exp
η(t) φ2 -
g∗φ4
(7)
and (ii) u∗ ≃ 1.98, g∗ ≃ 6.12. For further calculations
2
2
4
of the critical free energy distribution function, we take
−∞
just the average of these two FP values: u∗ ≃ 2.06 and
and the function η(t) is defined by the equation
g∗ ≃ 6.20.
ln G(η) = t. The universal curve for this distribution
According to the general approach of the RG theo-
function is represented in the Figure. We see that,
ry of critical phenomena in the vicinity of the phase
like in all the other systems, where the free energy
transition point the total free energy F of the system
probalitity distribution functions have been calculated
can be decomposed into two essentially different con-
[11, 22, 23], this function is essentially non-symmetric:
tributions:
the left tail is much more slow than the right one.
F =Vf0 +f,
Note that both the left and the right tails of the
where V = LD is the volume of the system (L is its
probability distribution function P (f) can be derived
linear size), f0 is the regular (background) free energy
explicitly:
density (which remains finite and non-singular at T =
{
}
g∗
= Tc). The second term, f ∼ LD|τ|2-α (where α is
P (f → -∞) ∝ exp
-
|f|
≃
u∗
the specific heat critical exponent), represents the fluc-
tuating part of the free energy which is singular at the
≃ exp{-3.01|f|},
(8)
critical point τ = 0, and it is this part which is cal-
culated in terms of the RG theory. Taking into ac-
{
}
count the standard relation among the critical expo-
π2
P (f → +∞) ∝ exp
2f -
exp(4f)
≃
nents, Dν = 2 - α (where ν is the critical exponent of
u∗
the correlation length), one notes that at the critical
point, when the correlation length becomes of the or-
≃ exp{2f - 4.79 exp(4f)}.
(9)
der of the system size, Rc ∼ |τ|-ν ∼ L, the fluctuating
796
ЖЭТФ, том 156, вып. 4 (10), 2019
Non-self-averaging in the critical point...
We see that the left tail of the probability distribution
internal energy E can be written as a sum of its mean
function P (f) is indeed much more slow than the right
value and a fluctuating part:
one. Note also that these asymptotics are quite similar
1
1
E∼-
L ln ln(L) +
√ L lnln(L) · f,
(12)
to the ones of the toy model considered in the previous
u0
u0
section, Eqs. (4) and (5).
where the random quantity f does not scale with L,
f ∼ 1, and is described by a standard normal distribu-
tion
(
)
5. TWO-DIMENSIONAL ISING MODEL
1
1
Pc(f) =
√
exp
-
f2
2π
2
A system of particular interest is the Ising model
This result demonstrates that at criticality, the inter-
in two dimensions, where exact results are available
nal energy of the two-dimensional random-bond Ising
both for the pure [13] and weakly disordered [6, 7]
ferromagnet is not self-averaging as the typical value of
cases. It is well known that the critical behavior of
the sample-to-sample fluctuations,
the two-dimensional ferromagnetic Ising model can be
described in terms of free two-component Grassmann-
E∗c(L) ∼ u-1/20L lnln(L),
(
)
Majorana spinor fields ψ(r) =
ψ1(r), ψ2(r)
, see, e. g.,
scales with the system size in the same way as its av-
Ref. [24]. Correspondingly, the critical behavior of the
erage value,
weakly disordered two-dimensional Ising model can be
described by the spinor Hamiltonian
Ec(L) ∼ u-10L lnln(L).
∫
On the other hand, unlike the singular part of the
1
internal energy, the specific heat in the vicinity of the
H[ψ; τ, δτ] =
d2r ×
2
critical point is a self-averaging quantity, as its distri-
[
]
(
)
× ψ(r)∂ψ(r) +
τ + δτ(r)
ψ(r)ψ(r) ,
(10)
bution function turns out to be the δ-function:
(
)
Pτ (C) = δ C - C(τ, L) ,
where τ = (T - Tc)/Tc ≪ 1 and the random function
where
δτ(r) is characterized as a spatially uncorrelated Gaus-
(
)
sian distribution with zero mean and the variance
1
2
1
C(τ, L) =
L2 ln
1+
u0 ln
2g0
π
|τ|
δτ(r)δτ(r′) = 2u0 δ(r - r′),
In particular, at large but finite value of the system size
L ≫ L∗ ∝ exp(2/πu0) at the critical point at τc
∝ 1/L,
where the parameter u0
≪ 1 defines the disorder
the critical specific heat C(L) scales with the system
strength. For a given realization of the quenched func-
size as
tion δτ(r), the partition function of the considered sys-
1
C(L) ∝
L2 lnln(L).
tem is
2u0
∫
{
}
Z[τ; δτ] = Dψ exp
-H[ψ; τ, δτ]
=
6. CONCLUSIONS
{
}
= exp
-F[τ; δτ]
,
(11)
In this brief review, we have presented recent stud-
ies of non-self-averaging phenomena in the critical point
where F [τ; δτ] is a random free-energy function. The
of weakly disordered ferromagnetic Ising model. In the
internal energy of a given realization is the first deriva-
case of the three-dimensional Ising system, we have
tive of this free energy with respect to the temperature
derived the explicit expression for the probability dis-
parameter:
tribution function of the critical free energy fluctua-
∂
E[τ; δτ] =
F [τ; δτ].
tions. It should be stressed that the mere existence
∂τ
of such non-trivial distribution function (which is not
It is clear that E[τ; δτ] must be a singular function
the δ-function) in the thermodynamic limit means that
of τ in the limit τ → 0 (in the pure system E0(τ) ∝
the critical free energy fluctuations in the considered
∝ τ ln(1/|τ|)). Additionally, E[τ;δτ] also must be a
system are non-self-averaging. This, of course, is not
random function exhibiting sample-to-sample fluctua-
surprising as the values of these critical fluctuations are
tions. In this section, it is shown that in close vicinity
not extensive with volume of the system. In more spe-
of the critical point, at τ ≪ exp(-π/2u0), and at suffi-
cific case of weakly disordered two-dimensional Ising
ciently large system size, L ≫ exp(π/2u0), the critical
model, we have presented the derivation of an explicit
797
Vic. Dotsenko
ЖЭТФ, том 156, вып. 4 (10), 2019
expression for the probability distribution function of
10.
S. Wiseman and E. Domany, Phys. Rev. Lett. 81, 22
the sample-to-sample fluctuations of the internal en-
(1998).
ergy. This result shows that the internal energy of this
11.
V. Dotsenko and B. Klumov, J. Stat. Mech. P05027
system is not self-averaging. In the thermodynamic
(2002).
limit, as the system size L tends to infinity, the typical
value of the internal energy sample-to-sample fluctua-
12.
V. Dotsenko and Yu. Holovatch, Phys. Rev. E 90,
tions scales in the same way as its average, proportional
052126 (2014).
to L ln ln(L). On the other hand, the specific heat was
13.
L. Onsager, Phys. Rev. 65, 117 (1944).
shown here to exhibit self-averaging with a distribution
function that converges to a δ-function.
14.
V. Dotsenko, Y. Holovach, M. Dudka, and M. Weigel,
Phys. Rev. E 95, 032118 (2017).
The full text of this paper is published in the English
15.
A. Crisanti, G. Paladin, H.-J. Sommers, and A. Vulpi-
version of JETP.
ani, J. de Phys. 2, 1325 (1992).
16.
G. Parisi and T. Rizzo, Phys. Rev. B 79, 134205
REFERENCES
(2009).
17.
V. Dotsenko, Introduction to the Replica Theory
1. A. B. Harris, J. Phys. C 7, 1671 (1974).
of Disordered Statistical Systems, Cambridge Univ.
2. A. B. Harris and T. C. Lubensky, Phys. Rev. Lett.
Press (2001).
33, 1540 (1974).
18.
R. Schloms and V. Dohm, Europhys. Lett. 3, 413
3. D. E. Khmel’nitskii, Sov. Phys. JETP 41, 981 (1975).
(1987); Nucl. Phys. B 328, 639 (1989).
4. T. C. Lubensky, Phys. Rev. B 11, 3573 (1975).
19.
G. Parisi, in: Proceedings of the Cargrése Summer
School (unpublished, 1973); G. Parisi, J. Stat. Phys.
5. G. Grinstein and A. Luther, Phys. Rev. B 13, 1329
23, 49 (1980).
(1976).
20.
R. Folk, Yu. Holovatch, and T. Yavors’kii, Phys. Rev.
6. Vik. S. Dotsenko and Vl. S. Dotsenko, J. Phys. C 15,
B 61, 15114 (2000).
495 (1982); Sov. Phys. JETP Lett. 33, 37 (1981).
21.
A. Pelissetto and E. Vicari, Phys. Rev. B62, 6393
7. Vik. S. Dotsenko and Vl. S. Dotsenko, Adv. Phys. 32,
(2000).
129 (1983).
22.
V. Dotsenko, Physics-Uspekhi 54, 259 (2011).
8. S. Wiseman and E. Domany, Phys. Rev. E 52, 3469
(1995).
23.
V. Dotsenko, Phil. Mag. 92, 16 (2012).
9. A. Aharony and A. B. Harris, Phys. Rev. Lett. 77,
24.
C. Itzykson and J.-M. Drouffe, Statistical Field Theo-
3700 (1996).
ry, Cambridge Univ. Press (1989).
798