ЖЭТФ, 2019, том 156, вып. 5 (11), стр. 905-917
© 2019
ПОСТНЬЮТОНОВСКИЙ ПРЕДЕЛ ГИБРИДНОЙ
f (R)-ГРАВИТАЦИИ
П. И. Дядинаa*, С. П. Лабазоваb**, С. О. Алексеевa,c***
a Государственный астрономический институт им. П. К. Штернберга,
Московский государственный университет им. М. В. Ломоносова
119234, Москва, Россия
b Кафедра астрофизики и звездной астрономии, Физический факультет,
Московский государственный университет им. М. В. Ломоносова
119234, Москва, Россия
c Кафедра квантовой теории и физики высоких энергий, Физический факультет,
Московский государственный университет им. М. В. Ломоносова
119234, Москва, Россия
Поступила в редакцию 19 июня 2019 г.,
после переработки 1 июля 2019 г.
Принята к публикации 3 июля 2019 г.
На основании последних, наиболее точных значений постньютоновских параметров γ и β, получен-
ных АМС «Мессенджер», накладываются ограничения на недавно предложенную модель гибридной
f(R)-гравитации в ее скалярно-тензорном представлении. Явно показано, что наличие легкого скалярно-
го поля не противоречит экспериментальным данным не только по параметру γ (что уже было показано
ранее), но и по всем остальным постньютоновским параметрам. Помимо этого, в работе обсуждается
вопрос применения параметризованного постньютоновского формализма к теориям гравитации с мас-
сивными полями.
DOI: 10.1134/S0044451019110087
рой путь приводит к появлению модифицированных
моделей гравитации, которые основываются на из-
менении ОТО.
1. ВВЕДЕНИЕ
В настоящее время общая теория относительнос-
Среди различных способов расширения ОТО вы-
ти (ОТО) является общепризнанной теорией грави-
деляется f(R)-гравитация [6-9]. Действие этой тео-
тации, так как в течение последнего столетия мно-
рии строится путем обобщения гравитационной час-
гие проблемы физики были решены с ее помощью.
ти действия ОТО как произвольной функции скаля-
При этом с ростом количества и качества наблю-
ра Риччи R. Такие модели получили широкое рас-
дений обнаружены явления, пока необъяснимые в
пространение после того, как f(R)-гравитация была
рамках ОТО. Например, в конце XX столетия бы-
успешно применена в теориях инфляции [10]. При-
ло установлено, что наша Вселенная ускоренно рас-
влекательны f(R)-модели тем, что ускоренное рас-
ширяется, но природа этого явления до сих пор до
ширение Вселенной может возникать здесь естест-
конца не раскрыта [1-3]. Другой загадкой современ-
венным образом как следствие гравитационной тео-
ной физики является темная материя, проявляюща-
рии. Помимо этого, f(R)-гравитация интересна как
яся на масштабах галактик и их скоплений [4, 5].
альтернатива модели ΛCDM, поскольку она способ-
Поиск решения этих проблем ведется различными
на одновременно описывать инфляцию на ранних
способами: с помощью введения новых частиц или
этапах и ускоренное расширение Вселенной, наблю-
изменением геометрии пространства-времени. Вто-
даемое в данный момент [11-18]. Более того, f(R)-
модели могут обеспечивать хорошее согласие с дан-
* E-mail: guldur.anwo@gmail.com
** E-mail: sp.labazova@physics.msu.ru
ными наблюдений, будучи почти неотличимыми от
*** E-mail: alexeyev@sai.msu.ru
модели ΛCDM [19].
905
5
ЖЭТФ, вып. 5 (11)
П. И. Дядина, С. П. Лабазова, С. О. Алексеев
ЖЭТФ, том 156, вып. 5 (11), 2019
Существуют два различных способа получения
особенностям в эволюции космологических возму-
уравнений поля в рамках моделей f(R)-гравитации:
щений [29,30].
метрический и Палатини. В метрическом подхо-
Недавно в работе [31] была предложена теория,
де gμν — единственная динамическая переменная и
состоящая из суперпозиции метрического лагран-
действие варьируется только по ней. Метод Пала-
жиана Эйнштейна - Гильберта с f(R)-членом, по-
тини основывается на том, что символы Кристоф-
строенным по методу Палатини. Модель получила
феля объявляются независимыми от метрики вели-
название гибридной f(R)-гравитации. Она исследо-
чинами. Таким образом, варьирование происходит
валась в скалярно-тензорном представлении. Было
относительно и метрики, и символов Кристоффеля.
показано, что теория позволяет описывать космоло-
Помимо этого, метод Палатини обеспечивает второй
гическую крупномасштабную структуру, не влияя
порядок для уравнений поля, тогда как в метриче-
при этом на динамику Солнечной системы. Такие
ском подходе они имеют четвертый порядок [20,21].
результаты вызвали многочисленные исследования
Однако некоторые недостатки теории проявля-
гибридной f(R)-гравитации. Космологические след-
ются как в метрическом подходе, так и в мето-
ствия теории рассматривались во многих работах:
де Палатини. Одной из основных проблем мет-
были исследованы статическая Вселенная Эйнштей-
рической f(R)-гравитации является то, что эти
на [32] и различные космологические модели [33,34];
модели имеют сложности с прохождением стан-
в работе [35] получены космологические решения и
дартных тестов в Солнечной системе [22-24]. Ко-
описано ускоренное расширение Вселенной. Более
нечно, ограниченный класс жизнеспособных моде-
того, гибридная f(R)-гравитация была изучена на
лей в метрическом подходе существует и был де-
астрофизических масштабах от звезд до скоплений
тально изучен в работах [15, 18, 19]. Наиболее яр-
галактик. В результате было показано, что различие
ко особенности f(R)-гравитации проявляются в ее
вириальных и визуальных масс скоплений галактик
скалярно-тензорном представлении. В частности, ее
может быть объяснено через геометрические чле-
метрическую модель можно интерпретировать как
ны в обобщенной теореме вириала [36]. Гибридная
скалярно-тензорную теорию Бранса - Дикке с пара-
f (R)-гравитация также позволяет объяснить скоро-
метром ωBD = 0 (ωBD — параметр Бранса - Дикке)
сти вращения пробных частиц, движущихся вокруг
и нетривиальным потенциалом V (φ). Чтобы теория
галактик. Этот подход предоставляет возможность
удовлетворяла ограничениям, наложенным лабора-
избежать введения большого количества темной ма-
торными экспериментами и наблюдениями в Сол-
терии [37]. Помимо этого, получены решения типа
нечной системе, скалярное поле должно быть мас-
кротовая нора [38]. Позднее были рассмотрены свой-
сивным, с диапазоном взаимодействия, не превы-
ства нейтронных и кварковых звезд в данной моде-
шающим нескольких миллиметров. Такое скаляр-
ли [39]. Все это наводит на мысль о перспективности
ное поле, очевидно, не может влиять на космоло-
гибридной f(R)-гравитации.
гию [25, 26]. Таким образом, метрические f(R)-тео-
Основная концептуальная причина для вве-
рии жизнеспособны только тогда, когда скалярное
дения гибридной f(R)-гравитации заключается
поле каким-то образом можно «скрыть» в локаль-
в следующем. Как подробно обсуждалось ранее,
ных экспериментах, при этом на космологических
если f(R)-гравитация представлена в скалярно-
масштабах оно будет вести себя как дальнодейству-
тензорном виде, то метрическая f(R)-модель
ющее поле, что достигается с помощью хамелеонно-
соответствует теории Бранса - Дикке с параметром
го механизма [14,25,27,28].
ωBD = 0, тогда как f(R)-гравитация Палатини —
С другой стороны, f(R)-модель Палатини можно
модели с ωBD = -3/2. Оба варианта несовместимы
представить как скалярно-тензорную теорию Бран-
с ограничениями, накладываемыми наблюдениями
са - Дикке с ωBD
= -3/2 и тем же потенциа-
в Солнечной системе, так как оригинальная теория
лом V (φ), что и в метрической формулировке. Та-
Бранса - Дикке предсказывает, что ωBD
→ ∞.
кая теория характеризуется нединамическим ска-
Это несоответствие преодолевается, если рас-
лярным полем — превращением вакуумной моде-
смотреть такое действие, в котором стандартная
ли в ОТО с эффективной космологической посто-
часть ОТО, т. е. R, определяется согласно метри-
янной Λeff . Это свойство позволяет описать совре-
ческому подходу, тогда как дальнейшие степени
менное ускоренное расширение Вселенной, если Λeff
свободы гравитационного поля, т.е. f(R) задаются
мало. Несмотря на это привлекательное свойство,
по методу Палатини. В этом случае скалярное
все изученные к настоящему моменту f(R)-модели
поле является динамическим и устраняются недо-
Палатини с малым Λeff приводят к неприемлемым
статки как метрических моделей, так и моделей
906
ЖЭТФ, том 156, вып. 5 (11), 2019
Постньютоновский предел гибридной f(R)-гравитации
Палатини. Привлекательной особенностью теории
ко необходимо обеспечить их связь со стандартными
является то, что она допускает нестандартное
ППН-параметрами и с экспериментами в Солнеч-
скалярно-тензорное представление в терминах
ной системе [50]. Второй способ подразумевает со-
динамического скалярного поля (в отличие от
хранение стандартной формы ППН-потенциалов, но
моделей Палатини), которое не обязано иметь
ППН-параметры становятся функциями, зависящи-
большую массу, чтобы соответствовать данным,
ми от пространственной переменной [51]. При этом
полученным из лабораторных экспериментов и из
ППН-параметры перестают быть константами, те-
наблюдений в Солнечной системе. Особенностей в
ряя свою универсальность, а их измеренное в экс-
эволюции космологических возмущений, которые
перименте значение теперь зависит от расстояния,
появляются в моделях Палатини, здесь также
на котором проводился эксперимент. Тем не менее,
не возникает, потому что скалярное поле слабо
этот метод также применим для проверки и огра-
связано с веществом. Следовательно, в этой теории
ничения моделей гравитации с массивными полями
скалярное поле может играть активную роль в
на конкретном расстоянии. В настоящей работе мы
космологии, не вступая в противоречие с локаль-
используем второй способ модификации ППН-фор-
ными экспериментами. Мы отсылаем читателя к
мализма и накладываем ограничения на гибридную
работе [40] для обзора мотиваций для введения
f (R)-гравитацию в режиме слабого поля.
гибридной f(R)-гравитации.
Статья имеет следующую структуру. В разд. 2
Ранее следствия гибридной f(R)-гравитации
рассматриваются действие и уравнения поля ги-
изучались как на космологических масштабах, так
бридной f(R)-гравитации в общем виде и в скаляр-
и в пределе слабого поля. На теорию были нало-
но-тензорном представлении. В разд. 3 обсужда-
жены ограничения на основе экспериментальных
ется ППН-формализм, решаются постньютоновские
данных по определению гравитационной постоян-
уравнения и выводятся аналитические выражения
ной и отклонению луча света в гравитационном
для эффективных ППН-параметров в рамках гиб-
поле Солнца (эксперимент «Кассини») [34]. Однако
ридной f(R)-гравитации. В разд. 4 рассматривают-
наиболее полным тестом теории гравитации в
ся ограничения на гибридную f(R)-гравитацию с
Солнечной системе является ee рассмотрение в
использованием наблюдаемых значений ППН-пара-
рамках параметризованного постньютоновского
метров. В разд. 5 представлены краткое изложение
формализма. Этому вопросу и посвящена данная
основных результатов работы и их обсуждение.
работа. Основной нашей целью является ограни-
В работе греческие индексы (μ, ν, . . .) пробе-
чение теории с учетом последних наиболее точных
гают значения 0, 1, 2, 3 и используется сигнатура
значений постньютоновских параметров (γ и β),
(-, +, +, +). Все вычисления выполнены в системе
полученных из данных АМС «Мессенджер» [41-44].
единиц СГС.
Параметризованный постньютоновский (ППН)
формализм был создан Уиллом и Нордтведтом
[45-48]. В рамках ППН-формализма метрики раз-
2. ГИБРИДНАЯ f(R)-ГРАВИТАЦИЯ
личных гравитационных теорий представляют
в виде обобщенной ППН-метрики, включающей
Действие гибридной f(R)-гравитации имеет сле-
ППН-потенциалы и ППН-параметры. Различия
дующий вид [40]:
между гравитационными моделями и наблюдения-
∫
ми выражаются через набор из 10 ППН-параметров,
c4
S=
d4x√-g [R + f(R)] + Sm,
(1)
в то время как форма ППН-потенциалов в различ-
2k2
ных теориях остается неизменной.
Картина меняется, когда в теории есть массив-
где c — скорость света, k2 = 8πG, R — скаляр-
ные поля. В этом случае метрика содержит не толь-
ная кривизна, R = gμν Rμν — кривизна Палатини,
ко стандартные ППН-потенциалы, но и потенциалы
g — определитель метрики, Sm — действие мате-
юкавского типа. Таким образом, ППН-формализм
рии. Здесь кривизна Палатини R определяется как
нельзя напрямую применить к моделям гравитации
функция gμν и символов Кристоффеля, не завися-
с массивными полями [49]. Существуют два способа
щих от метрики
Γα
:
μν
модифицировать ППН-формализм. Первый заклю-
чается во введении новых ППН-потенциалов, вклю-
R=gμνRμν =
чая потенциалы юкавского типа. В этом случае но-
)
(Γα
Γα
Γλ
=gμν
μν,α
-Γαμα,ν +
αλ
μν
-ΓαμλΓλαν
(2)
вые ППН-параметры остаются постоянными, одна-
907
5*
П. И. Дядина, С. П. Лабазова, С. О. Алексеев
ЖЭТФ, том 156, вып. 5 (11), 2019
Как и другие f(R)-теории, гибридную f(R)-гра-
Для рассмотрения гибридной f(R)-гравитации в
витацию (1) можно представить как скалярно-тен-
пределе слабого поля разложим скалярное φ и тен-
зорную модель:
зорное gμν поля относительно их фоновых значений:
∫
4
φ = φ0 + ϕ, gμν = ημν + hμν,
(6)
c
S =
d4x√-g ×
2k2
[
]
где φ0 — асимптотическое значение скалярного по-
3
ля вдали от источника, ημν — метрика Минковского,
× (1 + φ)R +
∂μφ∂μφ - V (φ) +Sm,
(3)
2φ
hμν и ϕ — малые возмущения соответственно тензор-
ного и скалярного полей. В общем случае φ0 не яв-
где φ — скалярное поле, V (φ) — скалярный потенци-
ляется константой, а представляет собой функцию,
ал. Здесь и ниже мы используем представление Йор-
зависящую от времени, φ(t). Однако этой зависи-
дана. После варьирования и нескольких преобразо-
мостью можно пренебречь, если характерная шкала
ваний можно получить уравнения поля в скаляр-
времени велика по сравнению с динамической шка-
но-тензорном представлении [31, 40]:
лой времени, связанной с локальной системой. Та-
(
)
ким образом, φ0 предполагается постоянной вели-
2
k
1
3
(1 + φ)Rμν =
Tμν -
gμνT
-
∂μφ∂νφ+
чиной.
c4
2
2φ
[
]
Полный постньютоновский предел требует оцен-
1
ки различных компонент возмущений метрики и
+
gμν V (φ) + ∇α∇αφ + ∇μ∇νφ,
(4)
2
скалярного поля до следующих порядков: h00
∼
∼ O(2) + O(4), h0j ∼ O(3), hij ∼ O(2) и ϕ ∼ O(2) +
+ O(4) [48]. Тогда скалярный потенциал V (φ) пред-
1
φ[2V (φ) - (1 + φ)Vφ]
∇μ∇μφ -
∂μφ∂μφ -
=
ставим в виде разложения Тейлора относительно
2φ
3
в следую-
фонового значения скалярного поля φ0
2
k
щем виде:
=-
φT.
(5)
3c4
V′′ϕ2
V′′′ϕ3
V (φ) = V0 + V ′ϕ +
+
+...
(7)
В отличие от моделей Палатини, в гибридной
2!
3!
f (R)-гравитации скалярное поле является дина-
Eго производная по ϕ примет вид Vφ = V′ + V′′ϕ +
мическим. Таким образом, теория не подвержена
+ V ′′′ϕ2/2.
неустойчивостям, проявляющимся на малых мас-
Тензор энергии-импульса для системы точечных
штабах в моделях Палатини [31, 40].
гравитирующих масс определяется как
∑
c
u
μuν
3. ППН-ПРЕДЕЛ ГИБРИДНОЙ
Tμν =
ma
δ3(r - ra),
(8)
√-g
u0
a
f (R)-ГРАВИТАЦИИ
где ma — масса a-й частицы, ra — радиус-вектор a-й
ППН-формализм был создан для сравнения раз-
частицы, uμ = dxμa/dτa — четырехскорость a-й час-
√
личных теорий гравитации между собой и с экспе-
тицы, dτ =
-ds2/c, ds2 = gμν dxμdxν — интервал,
риментом [48]. Постньютоновский (ПН) предел до-
uμuμ = -c2, δ3(r-ra(t)) — трехмерная дельта-функ-
стигается в пределе малых скоростей, асимптоти-
ция Дирака.
чески плоского пространственно-временного фона
В постньютоновском приближении компоненты
и слабых гравитационных полей. Таким образом,
тензора энергии-импульса (8) и его след принимают
ППН-формализм позволяет проверять теории гра-
вид
витации в Солнечной системе с высокой точностью.
[
]
Изначально Уилл и Нордтведт (создатели
∑
3
1 v2
1
a
T00
=c2
maδ3(r-ra) 1-
h00+
-
h ,
(9)
ППН-формализма) развивали несколько разные
2
2 c2
2
a
подходы
[45, 46]: Нордтведт исследовал пост-
ньютоновскую метрику для системы точечных
∑
T0i = -c maviaδ3(r - ra),
(10)
гравитирующих масс, тогда как Уилл рассматри-
a
вал материю системы в приближении идеальной
жидкости [45, 46]. Позднее было показано, что оба
∑
метода эквиваленты [47]. Мы применяем подход
Tij =
maviavjaδ3(r - ra),
(11)
Нордтведта.
a
908
ЖЭТФ, том 156, вып. 5 (11), 2019
Постньютоновский предел гибридной f(R)-гравитации
∑
T = -c2
maδ3(r - ra)×
где M — масса Солнца. Здесь V0/(φ0 +1) — космоло-
a
гическая постоянная. Этот член пренебрежимо мал
[
]
1
1 v2
1
на масштабах Солнечной системы, поэтому ниже мы
a
× 1-
h00 -
-
h ,
(12)
2
2 c2
2
его не учитываем.
Из (17) можно выразить эффективную гравита-
где va — скорость a-й частицы.
ционную постоянную [31, 40]:
Для вывода уравнений поля (4) и (5) в пределе
(
)
слабого поля (6) применим калибровку Натку [52]:
k2
φ0
Geff =
1-
e-mϕr
(18)
8π(1 + φ0)
3
1
ϕ,β
hαβ,α -
δαβhμμ,α =
(13)
2
1+φ0
Отметим, что верхним индексом «eff» мы обознача-
ем ППН-параметры, которые рассматриваются как
функции, зависящие от расстояния. Верхний индекс
3.1. Решения для ϕ(2), h(2)00, h(2)ij
«exp» используется для обозначения эксперимен-
Начнем с ньютоновского предела гибридной
тальных значений ППН-параметров. Для ППН-па-
f (R)-гравитации. Уравнение поля
(5) в терми-
раметров оригинального ППН-формализма верхний
нах возмущений (6), в ведущем порядке (O(2))
индекс не используется. То же самое верно и для
принимает вид
гравитационной постоянной.
В гибридной f(R)-гравитации эффективная гра-
(
)
k2φ0 ∑
∇2 - m2ϕ
ϕ(2) =
maδ3(r - ra),
(14)
витационная постоянная не является константой, а
3c2
a
представляет собой функцию, зависящую от рассто-
яния. Ньютоновский предел воспроизводится дву-
где
мя путями: φ0 ≪ 1 или mϕr ≫ 1. Первый способ
m2ϕ = [2V0 - V′ - (1 + φ0)φ0V′′]/3
подразумевает возможность существования легко-
— масса скалярного поля. Член нулевого порядка
го скалярного поля, следовательно, в этом случае
φ0[2V0 - (1 + φ0)V′]/3, появляющийся в уравнении,
нет необходимости использовать экранирующие ме-
может быть поглощен переопределением координат.
ханизмы для описания динамики Солнечной систе-
Верхний индекс «(2)» обозначает порядок возмуще-
мы в гибридной f(R)-гравитации [31, 40].
ний.
Выразим ij-компоненты уравнений поля (4) в ве-
Используя общее решение экранированного
дущем порядке O(2):
уравнения Пуассона и свойства дельта-функции
(
)
(
Дирака, можно получить решение уравнения (14):
ϕ(2)
k2
∇2
h(2)
+δij
=-
×
ij
1+φ0
(1 + φ0)c2
∑
k2φ0
e-mϕra
)
ϕ(2) = -
ma
,
(15)
∑
V0
12πc2
ra
×
maδ3(r - ra) -
δij,
(19)
a
0
1+φ
a
где ra = |r - ra|.
где δij — дельта-символ Кронекера. Получим урав-
Выразим 00-компоненту уравнения (4) в веду-
нение, аналогичное h(2)00:
щем порядке O(2):
(
)
(
)
δijk2
M
φ0
ϕ(2)
k2
h(2)ij =
1+
e-mϕr
-
∇2
h(2)00 -
=-
×
4π(1 + φ0)c2 r
3
1+φ0
c2(1 + φ0)
V0
r2
∑
V0
-δij
(20)
×
maδ3(r - ra) +
(16)
1+φ0 6
1+φ0
a
Для нахождения значений модифицированных
Используя полученное выражение для ϕ(2) (15) и
ППН-параметров необходимо сравнить полученную
предполагая, что главный вклад в метрику Солнеч-
метрику с общей ППН-метрикой для системы точеч-
ной системы дает Солнце, находим решение для h(2)00:
ных гравитирующих масс (34), введенной Нордтвед-
том [47] (см. Приложение A).
(
)
2
k
M
φ0
После сравнения
(20) с
(34) эффективный
h(2)00 =
1-
e-mϕr
+
4π(1 + φ0)c2 r
3
ППН-параметр γeff можно выразить как [31,40]
2
V0
r
1 + φ0e-mϕr/3
+
,
(17)
1+φ0
6
γeff =
(21)
1 - φ0e-mϕr/3
909
П. И. Дядина, С. П. Лабазова, С. О. Алексеев
ЖЭТФ, том 156, вып. 5 (11), 2019
Заметим, что γeff является функцией, зависящей от
и плотность энергии космологической постоян-
расстояния, а не константой. Современные наблю-
ной. Дополнительно будем ожидать, что V′(φ0) —
дения предсказывают, что γexp ≈ 1 (в ОТО γ = 1)
достаточно малая величина и ее вкладом мож-
с высокой точностью [41-44, 53,54]. Один из спосо-
но пренебречь. Причина заключается в том, что
бов получить этот результат из γeff — рассмотреть
либо скалярное поле приближается к минимуму
случай φ0 ≪ 1. Таким образом, итоговое выраже-
на поздних временах, либо потенциал принимает
ние для γeff не противоречит предположению, что
вид V
= V0e-akφ (где a порядка единицы), по-
скалярное поле может быть легким [31, 40].
этому V′(φ0) ∼ kV0. Это предположение кажется
Помимо этого, есть и другой способ получения
правдоподобным во всех разумных моделях [55].
выражения для γ из решения уравнения распро-
Следовательно, пренебрежем вкладами, содержа-
странения света. В работе [49] этот подход в дета-
щими V0, V′, умноженные на возмущения любого
лях рассмотрен для массивной теории Бранса - Дик-
порядка (например, V0h00), так как эти члены не
ке. Ключевым моментом является учет неравенства
должны приводить к наблюдательным следствиям
наблюдаемой кеплеровской массы и массы, кото-
на масштабах Солнечной системы.
рая приводит к эффекту Шапиро. Поскольку гиб-
Для решения (22) и (23) удобно использовать
ридную f(R)-гравитацию можно представить как
следующие выражения:
скалярно-тензорную модель, выражение для γ мо-
(
)
1
m2ϕ
жет быть найдено тем же способом. Результат иден-
(∇ϕ)2 =
(∇2 - m2ϕ)ϕ2 - ϕ ∇2 -
ϕ,
(24)
тичен выражению (21), что означает эквивалент-
2
2
ность двух подходов.
1
(∇h00)2 =
∇2h200 - h00∇2h00.
(25)
2
3.2. Решения для ϕ(4), h(4)00
Далее, из (22) для ϕ(4) находим
После подстановки возмущений (6) до порядка
O(4) уравнения поля (4) и (5) принимают вид
k2φ0 ∑
e-mϕra
k4φ0(1 + 3φ0)
ϕ(4) =
ma∂t∂t
+
×
24πc
2
mϕ
576π2c4(1 + φ0)
a
∑
k2φ0
∑
∑
(∇2 - m2ϕ)ϕ(4) =
maδ3(r - ra)×
e-mϕra
e-mϕrb
k4φ0
3c2
×
ma
mb
+
×
a
ra
rb
96π2c4(1 + φ0)
[
]
a
b
1
1v2
k2
(
)
∑∑
× -
h(2)jj -
+h(2)ijϕ(2),ij +
ϕ(2) ×
mamb
φ0
2
2c2
3c2
×
e-mϕra
1+
e-mϕrab
-
∑
rarab
3
a b=a
× maδ3(r - ra) + ϕ(2),00 +
∑∑
a
k4φ0(φ0 - 1)
mamb
−
e-mϕrae-mϕrab +
2
288π2c4(1 + φ0)
3φ0 + 1
(ϕ(2))
rarab
a b=a
+
(∇ϕ(2))2 -
×
2φ0(1 + φ0)
3
∑
k2φ0
ma
k4φ0mϕ
]
v2
e-mϕra -
×
[V′′′
φ0(φ0 + 1)
+ 24πc4
a ra
96π2c4(1 + φ0)
×
+ V ′′(φ0 + 1) ,
(22)
a
2
[
∑∑
mamb
×
- Ei(-2mϕra)e-mϕrabemϕra +
rab
(
)
a b=a
ϕ(4)
k2
]
∇2
h(4)00 -
=-
×
1+φ0
c2(1 + φ0)
+Ei(-2mϕrb)emϕrb- ln(ra)e-mϕrb+ ln(rb)e-mϕrb -
[
]
∑
3v2a
1
(
)]
×
maδ3(r - ra)
-h(2)00 +
-
hj
j
+
[k4φ0(1 + 7φ0)mϕ
k4φ20(1+φ0)
V′′′
2c2
2
-
+
V′′
+φ0
×
a
1152π2c4(1+φ0)
864π2c4mϕ
2
1
[
∑∑
+ h(2)00,00-(∇h(2)00 )2+h(2)ijh(2)00,ij-
h(2)ijϕ(2),ij -
mamb
1+φ0
×
Ei(-3mϕrb)e4mϕrab emϕra -
rab
(2)
a b=a
ϕ
,00
1
ϕ(2)
-
-
h00δϕ(2) -
δh(2)00 -
− Ei(-3mϕra)emϕrabemϕra-Ei(-mϕrb)e-mϕra +
1+φ0
1+φ0
1+φ0
]
1
-
(∇ϕ)2.
(23)
+ Ei(-mϕra)e-mϕrb .
(26)
(1 + φ0)2
Чтобы обеспечить адекватную космологическую
Здесь Ei обозначает экспоненциальный интеграл,
картину, V0 должен быть того же порядка, что
который определяется как
910
ЖЭТФ, том 156, вып. 5 (11), 2019
Постньютоновский предел гибридной f(R)-гравитации
∫∞
естественного предположения, что Солнце обеспечи-
e-t
Ei(-x) = -
dt.
(27)
вает главный вклад в гравитацию Солнечной систе-
t
x
мы, βeff принимает вид
Таким образом, используя решение (26) и выра-
r
φ0(φ0 + 1)e-2mϕ
жения для ϕ(2), h(2)00, h(2)ij, из уравнения (23) получа-
βeff = 1 -
(29)
(
)2 .
ем
φ0
18
1-
e-mϕr
(
)
3
4
∑
k
ma
φ0
h(4)00 = -
1-
e-mϕra
×
32π2c4(1 + φ0)2
ra
3
a
Таким образом, параметр βeff (так же, как и γeff )
(
)
∑
mb
φ0
k4φ0(1 + φ0)
предполагает наличие двух вариантов, при которых
×
1-
e-mϕrb
+
×
3
576π2c4(1 + φ0)2
достигается значение βeff ≈ 1: φ0 ≪ 1 или mϕr ≫ 1.
rb
b
∑
∑
∑
Рассматривая члены видаa v2ama/ra, можно
e-mϕra
e-mϕrb
k4
×
ma
mb
-
×
получить эффективные ППН-параметры αeff3
=
ra
rb
32π2c4(1 + φ0)2
eff
∑ ∑
a
b
= ζ1
= 0. Члены видаab=a mamb/rarab свя-
(
)(
)
∑∑
mamb
φ0
φ0
×
1-
e-mϕra
1-
e-mϕrab
+
заны с комбинацией параметров -2βeff + 1 + ζeff2 в
rarab
3
3
a b=a
оригинальной метрике (34). После выделения всех
∑∑
членов с уже известными эффективными ППН-па-
k4φ0(φ0 + 1)
mamb
+
e-mϕrae-mϕrab +
раметрами остаются только слагаемые с множите-
288π2c4(1 + φ0)2
rarab
a b=a
лями, содержащими mϕ, V′′, V′′′. Все они должны
(
)
2
∑
k
ma
φ0
вкладываться в ζeff2 . Здесь важно подчеркнуть, что
+
v2
1-
e-mϕra
+
8πc4(1 + φ0)
a ra
3
в гибридной f(R)-гравитации параметры α3 = ζ1 =
a
(
)
2
∑
= ζ2 = ζ3 = ζ4 равны нулю [56], потому что вы-
k
ma
φ0
+
v2
1+
e-mϕra
-
полняется полный набор постньютоновских законов
4πc4(1 + φ0)
a ra
3
a
сохранения (энергии, импульса, момента импульса и
∑∑
k4φ0mϕ
mamb
движения центра масс) [31, 40]. Таким образом, все
-
×
96π2c4(1 + φ0)2
rarab
вклады, умноженные на mϕ, V′′, V′′′, должны про-
a b=a
[
являться лишь в следующем ПН-порядке, поэтому
× - Ei(-2mϕra)rae-mϕrabemϕra +
ими можно пренебречь.
В (28) нерассмотренными остались только чле-
+ Ei(-2mϕrb)raemϕrb - ln(ra)rae-mϕrb +
ны, содержащие производные по времени. Обсудим
]
[
k4φ0(1 + 7φ0)mϕ
их вклад отдельно.
+ ln(rb)rae-mϕrb
-
+
1152π2c4(1 + φ0)2
(
)] ∑∑
k4φ20
V′′′
mamb
+
V′′
+φ0
×
864π2c4mϕ
2
rarab
3.3. Решения для h(3)0i
a b=a
[
× Ei(-3mϕrb)rae4mϕrabemϕra -
Решение для 0i-компоненты уравнения поля (4)
до порядка O(3) имеет следующий вид:
- Ei(-mϕrb)rae-mϕra + Ei(-mϕra)rae-mϕrb -
]
k2
k2
∑
- Ei(-3mϕra)raemϕrabemϕra
+
×
h(3)0i = -
ma via.
(30)
4πc2(1 + φ0)
2(1 + φ0)c3
ra
a
∑
(ra)
k2φ0
×
ma∂t∂t
+
×
2
24πc2(1 + φ0)
a
Мы используем конформную гармоническую ка-
)
∑
либровку (13). Чтобы привести ее к стандартной
(e-mϕra
×
ma∂t∂t
(28)
постньютоновской калибровке, проведем координат-
mϕ
a
ные преобразования t = ¯+∂tX/2c4 и xj = xj. Здесь
Сравнивая ППН-метрику гибридной f(R)-гравита-
X — суперпотенциал, определяемый как ∇2X =
ции с обобщенной метрикой Нордтведта (34), можно
= 2Geff M/r. Переходя к новым координатам в мет-
выразить оставшиеся эффективные ППН-парамет-
рике (t, xj ) и отбрасывая верхнюю черту у новых пе-
ры. Аналитическое выражение для βeff получается
ременных, получаем, что решение для ij-компонен-
из первых двух слагаемых (28). После добавления
ты останется прежним. В 00-компоненте все слагае-
911
П. И. Дядина, С. П. Лабазова, С. О. Алексеев
ЖЭТФ, том 156, вып. 5 (11), 2019
мые с производными по времени уходят, в то время
Параметр ζeff4 может быть выражен через комбина-
как 0i-компонента принимает вид [57]
цию других ППН-параметров: 6ζ4 = 3α3 + 2ζ1 - 3ζ3
[54]. Все параметры в этой комбинации равны нулю,
2
∑
3k
mavia
следовательно, ζeff4 = 0.
h(3)0i = -
×
16πc3(1 + φ0)
ra
a
(
)
φ0
k2
4. НАБЛЮДАТЕЛЬНЫЕ ОГРАНИЧЕНИЯ
× 1-
e-mϕra
-
×
3
4πc3(1 + φ0)
(
)
∑
Главной целью данной работы является нало-
mavia
φ0
k2
×
1+
e-mϕra
+
×
жение дополнительных ограничений на гибридную
ra
3
16πc3(1 + φ0)
a
f (R)-гравитацию и изучение поведения этой модели
(
)
∑
maria
φ0
в Солнечной системе. Чтобы найти ограничения на
×
(va · ra)
1-
e-mϕra
(31)
r3a
3
φ0 и mϕ, используем данные проекта «Мессенджер»
a
для γ и β [43]. В этом проекте недавно были получе-
После сравнения этого выражения с обобщенной
ны новые наблюдательные данные для β [58]. Одна-
метрикой Нордтведта (34) получаем, что αeff1 =
ко в работе [58] авторы комбинировали γexp, полу-
= αeff2 = 0. Таким образом, в гибридной f(R)-гра-
ченную из наблюдений аппарата «Кассини», с дан-
витации нет эффектов привилегированной системы
ными измерений вековой и периодической прецессии
отсчета.
орбиты Меркурия, что позволяет оценить совместно
βexp и J2. Таким образом, значение βexp было най-
дено с использованием значения γexp, полученного
3.4. ППН-метрика в приближении идеальной
на расстоянии от гравитирующего источника (Солн-
жидкости
ца), отличном от того, на котором проводился экспе-
Помимо метрики для системы точечных гра-
римент «Мессенджера». Поэтому самые новые зна-
витирующих масс, нами была также получена
чения для β из работы [58] некорректно использо-
ППН-метрика в приближении идеальной жидкости
вать для проверки массивных скалярно-тензорных
для гибридной f(R)-гравитации (37). Мы приво-
теорий, так как ППН-параметры являются функци-
дим конечное выражение в Приложении B, здесь
ями r и их значения могут меняться в зависимости
же представлено только обсуждение полученной
от расстояния, на котором они измерены.
метрики.
В нашей работе мы ограничиваем гибридную
В первоначальном варианте ППН-формализма
f (R)-гравитацию, используя следующие экспери-
все ППН-параметры являются константами, так как
ментальные значения параметров γexp и βexp [41,43]:
изначально формализм создавался для теорий гра-
γexp = 1-0.3·10-5±2.5·10-5 и βexp = 1+0.2·10-5 ±
витации без массивных полей. Однако примене-
± 2.5 · 10-5. Ограничения на φ0 и mϕ, полученные
ние ППН-формализма к гравитационным моделям
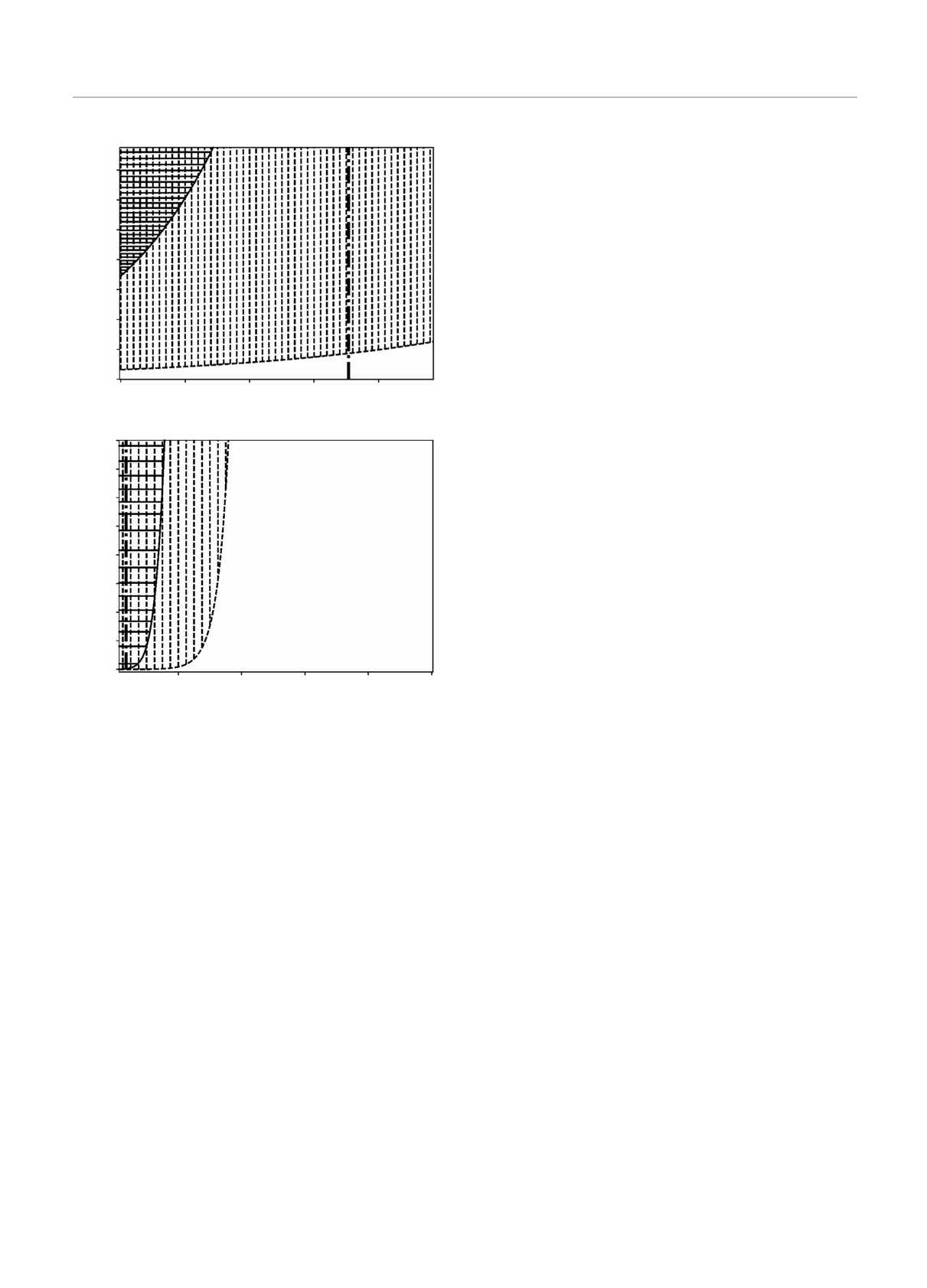
из этих данных, показаны на рисунке. Закрашенные
с массивными полями привело к тому, что ППН-па-
области отражают исключенные значения парамет-
раметры больше не являются постоянными, став
ров. Очевидно, что γexp дает лучшие ограничения
функциями, зависящими от расстояния. Более то-
по сравнению с βexp. Показано, что для всех малых
го, мы обнаружили, что в приближении идеальной
значений φ0 масса скалярного поля может прини-
жидкости ППН-параметры становятся неотделимы-
мать любое значение, включая самые малые. При
ми от ППН-потенциалов. Поэтому их выделение яв-
больших значениях массы скалярного поля значе-
ляется трудновыполнимой задачей, а их физический
ния φ0 могут быть любыми. Далее рассмотрим два
смысл утрачивается. Однако некоторые детали из
предельных случая, которые позволяют ограничить
этой метрики извлечь можно.
значение φ0.
В оригинальном варианте ППН-метрика в при-
Сначала рассмотрим случай очень легкого ска-
ближении идеальной жидкости (35) включает в себя
лярного поля: mϕr
≪ 1. Тогда можно ограни-
10 ППН-параметров: γ, β, ξ, ζ1,2,3,4, α1,2,3. Они экви-
чить φ0:
валентны ППН-параметрам, появляющимся в при-
-8 · 10-5 < φ0 < 7 · 10-5
(32)
ближении системы точечных гравитирующих масс
из γexp и
(34), но ξ и ζ3,4 не включены в метрику Нордтведта.
-9 · 10-4 < φ0 < 9 · 10-4
(33)
Однако, сравнивая полученную метрику (37) с обоб-
щенной метрикой Уилла (35), можно определить,
из βexp с точностью до 2σ. Ограничения, получен-
что ξeff = 0, ζeff3 = 0 в гибридной f(R)-гравитации.
ные из γexp, более строгие, чем полученные из βexp.
912
ЖЭТФ, том 156, вып. 5 (11), 2019
Постньютоновский предел гибридной f(R)-гравитации
0
момент. Однако ограничения на mϕ были получены
10-5
из других локальных систем, например, из двойных
175
систем с пульсаром [60].
150
125
5. ЗАКЛЮЧЕНИЕ
100
В настоящей работе рассмотрен постньютонов-
75
ский предел гибридной f(R)-гравитации. Так как
эта теория представима в скалярно-тензорном ви-
50
де с массивным скалярным полем [31, 40], ори-
25
гинальный параметризованный постньютоновский
формализм [45-48, 57] не применим напрямую [49].
0
1
2
3
4
10-36
В этом случае возможны два пути использования
m , эВ
ППН-формализма. Первый заключается в модифи-
0
цировании ППН-формализма таким образом, чтобы
2.00
включить в него не только стандартные ППН-по-
1.75
тенциалы, но и дополнительно потенциалы юкав-
ского типа. При таком подходе модифицированные
1.50
ППН-параметры остаются константами, но требу-
1.25
ют переопределения [50]. Второй способ заключает-
1.00
ся в сохранении ППН-потенциалов в их оригиналь-
ной форме и включении модификаций, связанных с
0.75
присутствием массивных полей, в ППН-параметры.
0.50
В этом случае последние уже будут не константами,
а зависящими от расстояния функциями [51]. Мы
0.25
использовали второй способ.
Модифицированная ППН-метрика гибридной
0
0.2
0.4
0.6
0.8
1.0
f (R)-гравитации получена нами в двух различных
10-34
m , эВ
приближениях: системы точечных гравитирующих
масс и идеальной жидкости [47]. Первый подход
Зависимости фонового значения скалярного поля от его
использован для выделения эффективных ППН-па-
массы. Два графика соответствуют разным масштабам.
раметров. Помимо этого, показано, что во втором
Вертикальные штриховые линии соответствуют исключен-
случае ППН-параметры не только являются зави-
ным значениям, полученным из данных γexp; горизонталь-
сящими от расстояния функциями, но и становятся
ные сплошные линии соответствуют исключенным значе-
частью ППН-потенциалов. Таким образом, чтобы
ниям, полученным из βexp; вертикальная штрихпунктир-
использовать приближение идеальной жидкости
ная линия соответствует критическому значению массы
для проверки моделей гравитации с массивными
скалярного поля mϕ = 1/r0, где r0 — расстояние от Солн-
ца до Меркурия
полями в пределе слабого поля, необходимо мо-
дифицировать оригинальные ППН-потенциалы,
оставляя ППН-параметры константами, при этом
В случае массивного скалярного поля γeff ≈ 1 и
переопределяя их.
βeff ≈ 1. Тогда φ0 может быть ограничено из Geff и
Мы получили выражения для 10 эффективных
его экспериментального значения [59]. В [34] показа-
ППН-параметров в гибридной f(R)-гравитации. Из
но, что в таком случае φ0 имеет также очень малое
них только γeff и βeff не равны нулю. Параметр
значение (|φ0| < 5 · 10-4).
γeff был получен ранее [31, 40], тогда как выраже-
Таким образом, экспериментальные данные, по-
ние для βeff представлено впервые. Так же, как и
лученные в рамках Солнечной системы, показыва-
в случае с γeff , ожидаемое значение βeff ≈ 1 до-
ют, что параметр φ0 близок к нулю. В этом случае
стигается при двух условиях: φ0 ≪ 1 или mϕr ≫ 1.
mϕ может принимать любые значения, поэтому нет
Первый позволяет скалярному полю быть очень лег-
возможности установить ограничения на массу ска-
ким, оставляя поведение в Солнечной системе без
лярного поля в слабополевом пределе в настоящий
изменений, но модифицируя космологическую и га-
913
П. И. Дядина, С. П. Лабазова, С. О. Алексеев
ЖЭТФ, том 156, вып. 5 (11), 2019
лактическую динамики без необходимости введения
ПРИЛОЖЕНИЕ A
экранирующих механизмов. Более того, ранее было
Метрики ППН-формализма
показано, что даже в случае очень массивного ска-
Метрика для системы точечных гравитирующих
лярного поля фоновое значение φ0 должно оставать-
масс имеет вид [47]
ся малым (|φ0| < 5 · 10-4) [34]. Эта проверка основы-
)2
∑
(∑
вается на эффективной гравитационной постоянной
Gmk
G mk
g00 = -1 + 2
- 2β
+
гибридной f(R)-гравитации. В предположении, что
c2 rk
c2 rk
k
k
скалярное поле легкое, мы наложили ограничения
∑
G mk ∑
G mj
на фоновое значение φ0 из γeff и βeff , используя
+ 2(1 - 2β + ζ2)
+
c2
rk
c2 rjk
данные «Мессенджера» [41-44] с точностью 2σ. По-
k
j=k
казано, что ограничения, полученные из γexp, более
∑
G mkv2k
+ (2γ + 1 + α3 + ζ1)
-
строгие: -8 · 10-5 < φ0 < 7 · 10-5.
c4
rk
k
Ранее было показано, что легкое скалярное по-
∑
G mk
ле в гибридной f(R)-гравитации не противоречит
-ζ1
(vk · rk)2-(α1-α2-α3)w2 ×
c4 r3
k
наблюдательным данным, полученным в Солнечной
k
∑
G mk
∑
Gmk
системе. Вывод был сделан на основании единствен-
×
-α2
(w · rk)2 +
ного ППН-параметра γ [34, 40]. В нашей работе мы
c4 r3
c4 rk
k
k
k
провели полный постньютоновский анализ и явно
∑
G mk
+ (2α3 - α1)
(w · vk),
(34)
показали, что легкое скалярное поле в гибридной
k
c4 r
k
f (R)-гравитации не противоречит эксперименталь-
∑
ным данным не только по параметру γ, но и по всем
1
G mkvjk
g0j = -
(4γ+3+α1-α2+ζ1)
-
остальным параметрам постньютоновского форма-
2
c3
rk
k
лизма.
∑
1
G mk
j
-
(1 + α2 - ζ1)
(vk · rk)rk
−
Несмотря на тот факт, что гибридная f(R)-гра-
2
c3 r3
k
k
витация согласуется с данными наблюдений в пре-
∑
1
G mk
деле слабого поля, интересно проверить следствия
−
(α1 - 2α2)wj
+
2
c3 rk
теории и в режиме более сильного поля, реализу-
k
∑
ющегося в двойных системах с пульсаром. Некото-
G mk
+α2
(w · rk)rjk,
рые ограничения уже были получены с помощью
c3 r3
k
k
проверки гибридной f(R)-гравитации на наблюда-
(
)
∑
G mk
тельных данных изменения орбитального периода в
gij =
1 + 2γ
δij,
c2 rk
системах PSR J1738+0333, PSR J0737-3039 [60]. Для
k
завершения работы требуется полный посткеплеров-
здесь wi — координатная скорость системы отсчета
ский тест с учетом всех посткеплеровских парамет-
ППН относительно системы покоя Вселенной.
ров, так как массы компонент двойных систем с
Метрика в приближении идеальной жидкос-
пульсаром, предсказанные теорией, могут отличать-
ти [57]:
ся от масс, предсказанных ОТО, что влияет на ко-
1
1
нечные ограничения, накладываемые на модель [39].
g00 = -1 + 2
U - 2β
U2 +
c2
c4
Развитием данной работы может стать создание
1
+ (2γ + 1 + α3 + ζ1 - 2ξ)
Φ1 -
универсального аппарата для проверки теорий
c4
гравитации с массивными полями в пределе слабого
1
1
- 2(2β-1-ζ2-ξ)
Φ2+2(1+ζ3)
Φ3 +
поля (аналога оригинального ППН-формализма
c4
c4
для безмассовых моделей), но эта тема требует
1
1
+
ΦPF + 2(3γ + 3ζ4 - 2ξ)
Φ4 -
более обширных исследований.
c4
c4
(35)
1
1
− (ζ1 - 2ξ)
Φ6 - 2ξ
ΦW ,
c4
c4
Благодарности.
Авторы
признательны
1
1
Н. А. Авдееву и В. В. Колыбасовой за полез-
g0j = -
(4γ + 3 + α1 - α2 + ζ1 - 2ξ)
Vj -
2
c3
ные обсуждения.
1
1
1
−
(1 + α2 - ζ1 + 2ξ)
Wj +
ΦPFj ,
Финансирование. Работа выполнена при фи-
2
c3
c3
(
)
нансовой поддержке Российского фонда фундамен-
1
gij =
1 + 2γ
U δij,
тальных исследований (грант №18-32-00785).
c2
914
ЖЭТФ, том 156, вып. 5 (11), 2019
Постньютоновский предел гибридной f(R)-гравитации
где ППН-потенциалы представлены как
∫
∫
ρ′
ρ′v′2
U = G
dr′, Φ1 = G
dr′,
|r - r′|
|r - r′|
∫
∫
ρ′U′
ρ′Π′
Φ2 = G
dr′, Φ3 = G
dr′,
|r - r′|
|r - r′|
∫
∫
p′
ρvj
Φ4 = G
dr′, Vj = G
dr′,
|r - r′|
|r - r′|
∫
(r - r′)j (r - r′)k
Φ6 = Gρ′v′jv′
dr′,
k
|r - r′|3
1
(36)
ΦPFj = -
α1wjU + α2wkUij,
2
∫
]
(r - r′)j
[ (r′ - r′′)j
(r - r′′)j
ΦW = G2ρ′ρ′′
-
dr′dr′′,
|r - r′|3
|r - r′′|
|r′ - r′′|
∫
ρ′v′(r - r′)(r - r′)j
Wj = G
dr′,
|r - r′|3
∫
ρ′(r - r′)i(r - r′)j
Uij = G
dr′,
|r - r′|
ΦPF = (α3 - α1)w2U + α2wjwkUij + (2α3 - α1)wjVj.
Здесь индекс «PF» обозначает потенциалы, ответственные за наличие привилегированной системы отсчета.
ПРИЛОЖЕНИЕ B
5.1. ППН-метрика гибридной f(R)-гравитации в приближении идеальной жидкости
∫
(
)
2
k
ρ′
φ0
k4
g00 = -1 +
1-
e-mϕ|r-r′| dr′ -
×
4π(1 + φ0)c2
|r - r′|
3
32π2(1 + φ0)2c4
∫
(
)
(
)
′
ρ
φ
0
ρ′′
φ0
k4
φ0(1 + φ0)
×
1-
e-mϕ|r-r′|
1-
e-mϕ|r-r′′| dr′′dr′+
×
|r-r′|
3
|r-r′′|
3
32π2(1+φ0)2c4
18
∫
∫
(
)
′
ρ
k2
Π′ρ′
φ0
×
e-mϕ|r-r′|ρ′′
e-mϕ|r-r′′|dr′′dr′ +
1-
e-mϕ|r-r′| dr′ +
|r - r′|
|r - r′′|
4π(1 + φ0)c4
|r - r′|
3
∫
∫
(
)
2
k
ρ′v′2
3k2
p′
φ0
+
dr′ +
1+
e-mϕ|r-r′| dr′ +
2π(1 + φ0)c4
|r - r′|
4π(1 + φ0)c4
|r - r′|
3
∫
[
]
∫
(
)
4
k
ρ′
φ
0
ρ
φ0
+
1-
e-mϕ|r-r′| dr′
1-
e-mϕ|r′-r| dr+
32π2(1 + φ0)2c4
|r - r′|
3
|r′ - r|
3
∫
[
]
∫
(
)
4
3k
ρ′
φ
0
ρ
φ0
+
1-
e-mϕ|r-r′| dr′
1+
e-mϕ|r′-r| dr-
(37)
32π2(1 + φ0)2c4
|r - r′|
3
|r′ - r|
3
∫
[
]
∫
(
)
4
k
ρ′
φ
0
ρ
φ0
-
1-
e-mϕ|r-r′| dr′
1-
e-mϕ|r′-r| dr+
16π2(1 + φ0)2c4
|r - r′|
3
|r′ - r|
3
∫
∫
4
k
φ0(1 + φ0)
ρ′
ρ
+
e-mϕ|r-r′|dr′
e-mϕ|r′-r|dr+
16π2(1 + φ0)2c4
18
|r - r′|
|r′ - r|
∫
(∫
)
−mϕ|r-r′|
(7φ0 + 1)k4φ0
e
ρ
+
m2
ϕ
dr′
e-mϕ|r′-r| ρ′′
e-mϕ|r′-r′′|drdr′′
+
2304π3(1 + φ0)2c4
|r - r′|
|r′ - r|
|r′ - r′′|
∫
(∫
)
−mϕ|r-r′|
k4φ0
e
ρ
+
mϕ
dr′
e-mϕ|r′-r| ρ′′
e-mϕ|r′-r′′|drdr′′
+
192π3(1 + φ0)2c4
|r - r′|
|r′ - r|
|r′ - r′′|
[
]∫
(∫
)
k4φ20
φ0
e-mϕ|r-r′|
ρ
+
V′′ -
V′′′
dr′
e-mϕ|r′-r| ρ′′
e-mϕ|r′-r′′|drdr′′
,
1728π3c4
2
|r - r′|
|r′ - r|
|r′ - r′′|
915
П. И. Дядина, С. П. Лабазова, С. О. Алексеев
ЖЭТФ, том 156, вып. 5 (11), 2019
∫
(
)
∫
(
)
2
k
ρ′v′i
φ0
3k2
ρ′v′i
φ0
g0i = -
1+
e-mϕ|r-r′| dr′ -
1-
e-mϕ|r-r′| dr′ -
4π(1+φ0)c3
|r-r′|
3
16π(1+φ0)c3
|r-r′|
3
∫
[
]
2
k
ρ′x′i(v′ · r′)
φ
0
-
1-
e-mϕ|r-r′| dr,
16π(1 + φ0)c3
|r - r′|3
3
(
∫
(
)
)
k2
ρ′
φ0
gij = δij
1+
1+
e-mϕ|r-r′|
dr′
4π(1 + φ0)c2
|r - r′|
3
ЛИТЕРАТУРА
21.
T. P. Sotiriou and V. Faraoni, Rev. Mod. Phys. 82,
451 (2010).
1.
S. Perlmutter et al., Astrophys. J. 517, 565 (1999).
22.
T. Chiba, Phys. Lett. B 575, 1 (2003).
2.
A. G. Riess et al., Astron. J. 116, 1009 (1998).
23.
G. J. Olmo, Phys. Rev. Lett. 95, 261102 (2005).
3.
A. G. Riess et al., Astrophys. J. 607, 665 (2004).
24.
G. J. Olmo, Phys. Rev. D 75, 023511 (2007).
4.
F. Zwicky, Helvetica Phys. Acta 6, 110 (1933).
25.
J. Khoury and A. Weltman, Phys. Rev. Lett. 93,
5.
J. H. Oort, Bull. Astron. Inst. Netherlands 6, 249
171104 (2004).
(1932).
26.
S. Capozziello and S. Tsujikawa, Phys. Rev. D 77,
6.
P. G. Bergmann, Int. J. Theor. Phys. 1, 25 (1968).
107501 (2008).
7.
A. De Felice and S. Tsujikawa, Living Rev. Rel. 13,
27.
J. Khoury and A. Weltman, Phys. Rev. D 69, 044026
3 (2010).
(2004).
8.
S. Nojiri, S. D. Odintsov, and V. K. Oikonomou,
28.
W. Hu and I. Sawicki, Phys. Rev. D 76, 064004 (2007)
Phys. Rep. 692, 1 (2017).
29.
T. Koivisto and H. Kurki-Suonio, Class. Quant. Grav.
9.
S. Nojiri and S. D. Odintsov, Phys. Rep. 505, 59
23, 2355 (2006).
(2011).
30.
T. Koivisto, Phys. Rev. D 73, 083517 (2006).
10.
A. A. Starobinsky, Phys. Lett. B 91, 99 (1980).
31.
T. Harko, T. S. Koivisto, F. S. N. Lobo, and G. J. Ol-
11.
S. Nojiri and S. D. Odintsov, Phys. Rev. D 68, 123512
mo, Phys. Rev. D 85, 084016 (2012).
(2003).
32.
C. G. Böhmer, F. S. N. Lobo, and N. Tamanini, Phys.
12.
F. Briscese, E. Elizalde, S. Nojiri, and S. D. Odintsov,
Rev. D 88, 104019 (2013).
Phys. Lett. B 646, 105 (2007).
33.
N. A. Lima and V. Smer-Barreto, Astrophys. J. 818,
13.
D. Saez-Gomez, Gen. Rel. Grav. 41, 1527 (2009).
186 (2016).
14.
S. Nojiri and S. D. Odintsov, Phys. Lett. B 657, 238
34.
I. Leanizbarrutia, F. S. N. Lobo, and D. Sáez-Gómez,
(2007).
Phys. Rev. D 95, 084046 (2017).
15.
S. Nojiri and S. D. Odintsov, Phys. Rev. D 77, 026007
35.
S. Capozziello, T. Harko, T. S. Koivisto, F. S. N. Lo-
(2008).
bo, and G. J. Olmo, JCAP 04, 011 (2013).
16.
S. Nojiri, S. D. Odintsov, and D. Saez-Gomez, Phys.
36.
S. Capozziello, T. Harko, T. S. Koivisto, F. S. N. Lo-
Lett. B 681, 74 (2009).
bo, and G. J. Olmo, JCAP 07, 024 (2013).
17.
G. Cognola, E. Elizalde, S. D. Odintsov, P. Tretyakov,
37.
S. Capozziello, T. Harko, T. S. Koivisto, F. S. N. Lo-
and S. Zerbini, Phys. Rev. D 79, 044001 (2009).
bo, and G. J. Olmo, Astropart. Phys. 50-52C, 65
(2013).
18.
G. Cognola, E. Elizalde, S. Nojiri, S. D. Odintsov,
L. Sebastiani, and S. Zerbini, Phys. Rev. D 77,
38.
S. Capozziello, T. Harko, T. S. Koivisto, F. S. N. Lo-
046009 (2008).
bo, and G. J. Olmo, Phys. Rev. D 86, 127504 (2012).
19.
S. D. Odintsov, D. Saez-Gomez, and G. S. Sharov,
39.
B. Danila, T. Harko, F. S. N. Lobo, and M. K. Mak,
Eur. Phys. J. C 77, 862 (2017).
Phys. Rev. D 95, 044031 (2017).
20.
S. Capozziello and M. Francaviglia, Gen. Rel. Grav.
40.
S. Capozziello, T. Harko, T. S. Koivisto, F. S. N. Lo-
40, 357 (2008).
bo, and G. J. Olmo, Universe 1, 199 (2015).
916
ЖЭТФ, том 156, вып. 5 (11), 2019
Постньютоновский предел гибридной f(R)-гравитации
41. C. M. Will, Phys. Rev. Lett. 120, 191101 (2018).
51. L. Perivolaropoulos, Phys. Rev. D 81, 047501 (2010).
42. A. Fienga, J. Laskar, P. Kuchynka, H. Manche,
52. Y. Nutku, Astrophys. J. 155, 999 (1969).
G. Desvignes, M. Gastineau, I. Cognard, and
G. Theureau, Celestial Mech. Dyn. Astron. 111, 363
53. B. Bertotti, L. Iess, and P. Tortora, Nature 425, 374
(2011).
(2003).
43. A. Verma, A. Fienga, J. Laskar, H. Manche, and
54. C. M. Will, Living Rev. Rel. 17, 4 (2014).
M. Gastineau, Astron. Astrophys. 561, A115 (2014).
55. T. P. Sotiriou and E. Barausse, Phys. Rev. D 75,
44. A. Fienga, J. Laskar, P. Exertier, H. Manche, and
084007 (2007).
M. Gastineau, Celestial Mech. Dyn. Astron. 123, 325
(2015).
56. D. L. Lee, Phys. Rev. D 10, 2374 (1974).
45. K. Nordtvedt, Phys. Rev. 169, 1017 (1968).
57. E. Poisson and C. M. Will, Gravity: Newtonian,
46. C. M. Will, Astrophys. J. 163, 611 (1971).
Post-Newtonian, Relativistic, Cambridge Univ. Press,
Cambridge, UK (2014).
47. C. M. Will and K. Nordtvedt, Astrophys. J. 177, 757
(1972).
58. R. S. Park, W. M. Folkner, A. S. Konopliv, J. G. Wil-
liams, D. E. Smith, and M. T. Zuber, Astron. J. 153,
48. C. M. Will, Theory and Experiment in Gravitational
3, 121 (2017).
Physics, Cambridge Univ. Press, Cambridge, UK
(1993).
59. P. J. Mohr, D. B. Newell, and B. N. Taylor, Rev.
Mod. Phys. 88, 035009 (2016).
49. J. Alsing, E. Berti, C. M. Will, and H. Zaglauer, Phys.
Rev. D 85, 064041 (2012).
60. P. I. Dyadina, N. A. Avdeev, and S. O. Alexeyev,
50. T. Helbig, Astrophys. J. 382, 223 (1991).
Month. Not. Roy. Astron. Soc. 483, 947 (2019).
917