ЖЭТФ, 2019, том 156, вып. 5 (11), стр. 950-971

РАСПРЕДЕЛЕНИЕ КОНДАКТАНСОВ В ОДНОМЕРНЫХ

СИСТЕМАХ: ЗАВИСИМОСТЬ ОТ УРОВНЯ ФЕРМИ

И ИДЕАЛЬНЫХ КОНТАКТОВ

И. М. Суслов^*

Институт физических проблем им. П. Л. Капицы Российской академии наук

119334, Москва, Россия

Поступила в редакцию 10 марта 2019 г.,

после переработки 10 марта 2019 г.

Принята к публикации 23 апреля 2019 г.

Корректное определение проводимости конечных систем предполагает присоединение к системе мас-

сивных идеальных контактов. Влияние последних на свойства системы оказывается существенным и

исследуется на простейшем примере одномерных систем. В логнормальном режиме оно сводится к из-

менению абсолютного масштаба кондактанса, но в общем случае изменяет всю функцию распределения.

При изменении длины системы могут возникать периодические или апериодические осцилляции в ее

сопротивлении. При изменении уровня Ферми распределение кондактансов одномерной системы претер-

певает качественные изменения, напоминающие сглаженный переход Андерсона.

DOI: 10.1134/S0044451019110129

ме остается открытым. В работе [11] для решения

этого вопроса предлагается введение слабопроница-

емых границ, отделяющих систему от идеальных

1. ВВЕДЕНИЕ И ОСНОВНЫЕ РЕЗУЛЬТАТЫ

контактов. Вопрос о влиянии последних на свойства

Вопрос о правильном определении проводимости

системы заведомо актуален вблизи перехода Андер-

конечных систем является нетривиальным и в нача-

сона [12], но обсуждался в работах [11,12] лишь на

ле 1980-х гг. был предметом оживленной дискуссии

абстрактном уровне. Ниже показано, что этот во-

[1-9] (см. обзор [10]). Причина разногласий состоя-

прос может быть предметом конструктивного ана-

ла в том, что проводимость конечных систем явля-

лиза, который мы проиллюстрируем на простейшем

ется плохо определенной величиной. Это связано со

примере одномерных систем.

спецификой формул теории линейного отклика: вхо-

В теоретических работах обычно предполагает-

дящие в них δ-функции должны быть уширены на

ся, что в системе имеется единый уровень Ферми, а

величину Γ, которая устремляется к нулю лишь по-

отличие идеальных контактов от изучаемого образ-

сле перехода к термодинамическому пределу; такая

ца определяется лишь наличием в последнем слу-

процедура, очевидно, невозможна в конечных систе-

чайного потенциала (рис. 2а). В практическом плане

мах. Для преодоления этой трудности предложен

такая ситуация не очень реалистична: обычно в экс-

довольно элегантный трюк [3]: конечная система

перименте подводящие провода изготовляются из

присоединяется к идеальным контактам (рис. 1), ко-

хорошего металла с большой энергией Ферми (так

торые предполагаются достаточно массивными, так

что переход к термодинамическому пределу факти-

чески производится в этих контактах. Такая кон-

Идеальный

струкция решает вопрос об интерпретации формулы

проводник

Кубо, но порождает новые проблемы: соответству-

ющее ей определение проводимости относится к со-

Рис. 1. Корректное определение проводимости конечных

ставной системе «образец + идеальные провода», то-

систем предполагает присоединение к системе массивных

гда как вопрос о его отношении к изучаемой систе-

идеальных контактов. Для обсуждения роли последних по-

лезно введение полупроницаемых границ [11]

^* E-mail: suslov@kapitza.ras.ru

950

ЖЭТФ, том 156, вып. 5 (11), 2019

Распределение кондактансов в одномерных системах. . .

Идеальный

Образец

Идеальный

(рис. 2в). При этом в распределении кондактансов

контакт

одномерной системы происходят качественные

E_F

изменения, напоминающие сглаженный переход

Андерсона.

Если g — безразмерный кондактанс (полная про-

водимость G системы в квантовых единицах e²/h),

то эволюция распределения P(ρ) безразмерных со-

E_F

противлений ρ = 1/g при изменении длины L систе-

мы описывается уравнением

[

]

∂P(ρ)

∂

∂P(ρ)

=α

ρ(1 + ρ)

(1)

∂L

∂ρ

которое получено во многих работах [13-18] и счи-

E_F

тается достаточно универсальным. Однако, как по-

казано в работе [12], для одномерных систем спра-

ведливо более общее уравнение

∂P(ρ)

∂

= α

∂L

∂ρ

Рис. 2. а) В теоретических работах обычно предполагает-

[

]

∂P(ρ)

ся, что отличие идеальных контактов от изучаемой систе-

× -γ(1 + 2ρ)P(ρ) + ρ(1 + ρ)

(2)

мы определяется лишь наличием в последней случайного

∂ρ

потенциала. б) Практически в эксперименте подводящие

которое в приближении случайных фаз сводится к

провода изготовляются из хорошего проводника с большой

уравнению (1). Последнее приближение хорошо ра-

энергией Ферми. в) Явное введение идеальных контактов

ботает в глубине разрешенной зоны при «естествен-

оказывается неизбежным, если уровень Ферми в изучае-

ных» идеальных контактах (рис. 2а), что обычно и

мой системе соответствует запрещенной зоне идеального

кристалла

предполагается в теоретических работах (см. ссыл-

ки в [19, 20]); ситуация внутри запрещенной зоны

рассматривается сравнительно редко [21-23] и лишь

на уровне волновых функций. Основная мотивация

что примеси эффективно экранируются), тогда как

работы [12] состояла в том, что конечное значение

изучаемая система является полуметаллом или ле-

параметра γ появляется в результате введения полу-

гированным проводником, в которых эффекты бес-

проницаемых границ (рис. 1), даже если приближе-

порядка проявляются наиболее ярко (рис. 2б). Тем

ние случайных фаз применимо к изучаемой системе.

не менее отличие от предыдущего случая (рис. 2а)

При явном введении идеальных контактов полу-

выглядит непринципиальным и обычно игнориру-

чается еще более общее уравнение (см. разд. 7):

ется в теоретических работах. Однако введение чу-

жеродных контактов оказывается неизбежным, если

[

∂P(ρ)

∂

уровень Ферми в изучаемой системе соответствует

= α

- γ₁(1 + 2ρ)P(ρ) -

∂L

∂ρ

запрещенной зоне идеального кристалла (рис. 2в),

]

√

∂P(ρ)

в которой разрешенные состояния возникают лишь

− 2γ₂

ρ(1 + ρ)P (ρ) + ρ(1 + ρ)

(3)

∂ρ

из-за наличия случайного потенциала: попытка из-

готовить подводящие провода из того же материала,

которое сводится к уравнению (2) в области малых

но без примесей, приведет к тому, что «идеальные

и больших L, когда типичные значения ρ соответ-

контакты» окажутся непроводящими.

ственно малы и велики (при этом γ = γ₁ в первом

Явное введение идеальных контактов (рис. 2б,в)

и γ = γ₁ + γ₂ во втором случае), так что уравнение

осуществляется с помощью краевых трансфер-

(3) можно интерпретировать как уравнение (2) с пе-

матриц (см. разд. 2) и приводит к интересной физи-

ременным коэффициентом γ. Возможность измене-

ческой задаче: путем небольшого изменения уровня

ния γ в процессе эволюции изначально допускалась

Ферми (не ощутимого для идеальных контактов)

в работе [12] и систематически исследуется в разд. 3.

можно переходить от квазиметаллического режима

Предельное значение γ в области больших L опре-

в изучаемой системе (рис. 2б) к флуктуационным

деляется внутренними свойствами изучаемой систе-

состояниям, лежащим в глубине запрещенной зоны

мы и не зависит от идеальных контактов; на рис. 3

951

И. М. Суслов

ЖЭТФ, том 156, вып. 5 (11), 2019

4/3

< 1)

III

(

II (

>> 1)

–4

-2

/W^4/3

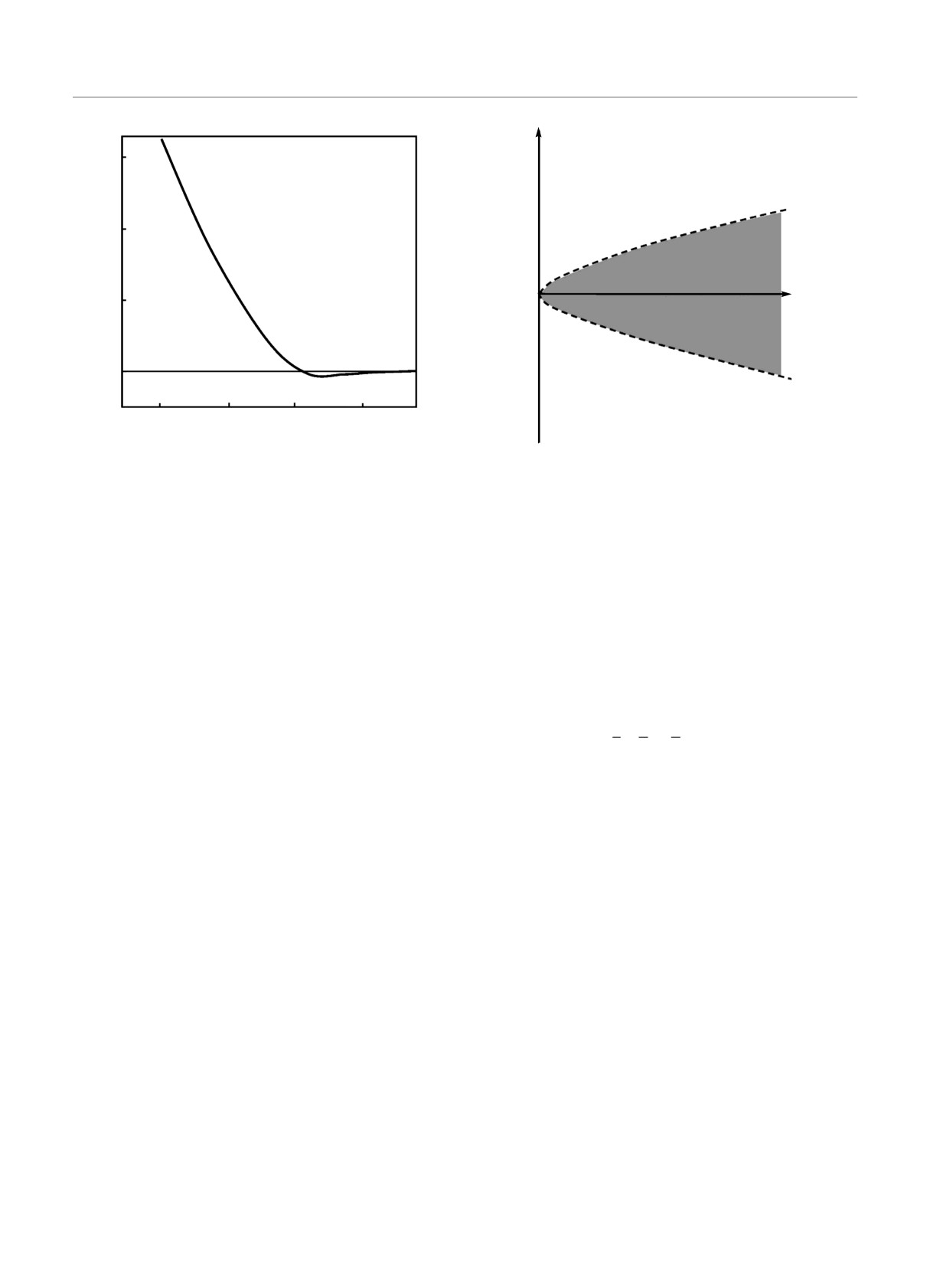
Рис. 3. Зависимость параметра γ в уравнении (2), относя-

Рис. 4. В плоскости (E, W²) можно выделить три характер-

щегося к пределу больших L, от энергии E, отсчитанной

ные области: I — квазиметаллическую (γ ≪ 1); II — силь-

от нижнего края исходной зоны

нолокализованную (γ ≫ 1); III — «критическую» (γ ∼ 1).

При изменении энергии E для фиксированной амплитуды

W случайного потенциала в распределении кондактансов

происходят качественные изменения, напоминающие сгла-

показана его зависимость от E/W4/3, где E — энер-

женный переход Андерсона. В пределе W → 0 возникает

гия Ферми, отсчитанная от нижнего края зоны, и

настоящий фазовый переход

W — амплитуда случайного потенциала (все энергии

измеряются в единицах интеграла перекрытия для

одномерной модели Андерсона, см. ниже уравнение

числяя амплитуды прохождения (t) и отражения

(14)). Нетрудно видеть, что параметр γ формально

(r), легко найти ландауэровское сопротивление ρ =

всегда отличен от нуля, но принимает малые значе-

= |r|²/|t|² такой системы:

ния в глубине разрешенной зоны в согласии с при-

)₂

⁽k

ближением случайных фаз. Таким образом, конеч-

ρ=

sh² κL,

(4)

ность параметра γ определяется внутренними свой-

ствами системы и введение полупроницаемых гра-

где k — фермиевский импульс в идеальных контак-

ниц [12] не является для этого необходимым.

тах, κ — декремент затухания волновых функций

В плоскости (E, W²) можно выделить три харак-

под барьером. Если зависимость ρ(L) определяет-

терные области (рис. 4): квазиметаллическую (|γ| ≪

ся только параметром κ, т. е. внутренними свойства-

≪ 1); сильнолокализованную (γ ≫ 1) и «крити-

ми изучаемой системы, то коэффициент пропорци-

ческую» (γ ∼ 1). При изменении энергии E для

ональности зависит от импульса k, т. е. от свойств

фиксированной амплитуды случайного потенциала

идеальных контактов.

W происходит что-то вроде сглаженного перехода

Этот результат противоречит физической инту-

Андерсона, который превращается в настоящий фа-

иции, поэтому рассмотрим вопрос о его интерпре-

зовый переход в пределе W → 0, когда γ → 0 и

тации. Наша физическая интуиция сформирована

γ → ∞ соответственно в металлической и диэлект-

на привычном омическом режиме, когда сопротив-

рической фазах, тогда как ширина критической об-

ление ρ пропорционально длине системы L или пол-

ласти (γ ∼ 1) неограниченно уменьшается.

ному числу n рассеивателей в ней; следовательно,

Перейдем к зависимости результатов от свойств

каждый рассеиватель дает аддитивный вклад в соп-

идеальных контактов. Начнем с простого примера,

ротивление. Однако известно существование и лока-

чтобы продемонстрировать наличие предмета для

лизованного режима, когда зависимость ρ(L) экспо-

обсуждения. Если в ситуации рис. 2в устранить из

ненциальна, так что ln ρ ∝ L ∝ n и каждый рассеи-

системы случайный потенциал, то возникает прос-

ватель дает мультипликативный вклад в сопротив-

тейшая квантовомеханическая задача о прохожде-

ление. Поскольку сами по себе идеальные контакты

нии частицы через потенциальный барьер [24]. Вы-

не приводят к диссипации, их вклад в сопротивле-

952

ЖЭТФ, том 156, вып. 5 (11), 2019

Распределение кондактансов в одномерных системах. . .

ние обусловлен лишь границами раздела, который

области не слишком больших L. В последнем слу-

в экспоненциальном режиме является мультиплика-

чае при «естественных» идеальных контактах (см.

тивным и влияет на коэффициент пропорциональ-

рис. 2а) реализуется распределение

ности в выражении (4). Последний при изменении k

ρ^γ exp(-ρ/t)

меняется от единицы (при k = κ) до бесконечности,

P (ρ) =

(7)

так что влияние идеальных контактов оказывается

Γ(γ + 1)

tγ+1

очень существенным.

которое является решением уравнения (2) при ма-

Уже из сказанного ясно, что в общем случае си-

лых ρ, когда 1 + 2ρ ≈ 1, ρ(1 + ρ) ≈ ρ. В критической

туация нетривиальна и вклад границ раздела не

области реализуется значение γ = -1/2, а параметр

является ни аддитивным, ни мультипликативным

A в формуле (6) равен 1/(Δ₂ - Δ₁)², где Δ₁ и Δ₂

(см. разд. 8). Кроме того, кондактанс конечной сис-

определены ниже выражениями (9).

темы является сильнофлуктуирующей величиной

4. В глубине разрешенной зоны ситуация еще

[25,26] и нужно рассматривать его функцию распре-

более усложняется и идеальные контакты изменя-

деления. Зависимость же последней от граничных

ют всю функцию распределения в области не слиш-

условий проявляется уже в металлическом режиме,

ком больших L. Если для «естественных» контактов

где она может быть исследована как аналитически

(рис. 2а) реализуется распределение (7) с γ = 0, то

[27, 28], так и численно [29].

при введении чужеродных контактов (рис. 2б) его

Зависимость распределения кондактансов одно-

форма существенно изменяется. В частности, при

мерной системы от свойств идеальных контактов

формальном пределе L → 0 возникает универсаль-

подробно исследована ниже (см. разд. 6). Отметим

ное распределение¹⁾

некоторые простые утверждения.

√

1. При больших L для P(ρ) справедливо логнор-

мальное распределение

P (ρ) =

Θ(ρ_c - ρ) ,

(8)

π ρ(ρ_c - ρ)

{

}

[ln ρ - (2γ + 1)t]²

P (ρ) =

√

exp

эволюция которого при увеличении L показана на

4πt

(5)

рис. 5а и 5б; последние различаются значениями па-

t= αL,

раметров

)

в которое входит предельное значение γ при L → ∞.

⁽k

Δ₁ =

Δ₂ =

(9)

Оно является решением уравнения (2) при больших

ρ, когда 1 + 2ρ ≈ 2ρ, ρ(1 + ρ) ≈ ρ². Параметры α и γ

устанавливаются (см. разд. 5) путем исследования

Параметры (9) определены для запрещенной зоны,

эволюции вторых и четвертых моментов для эле-

но в разрешенной зоне сохраняют тот же вид, ес-

ментов трансфер-матрицы (см. разд. 4); они опре-

ли формально положить

k = κ для фермиевского

деляются внутренними свойствами исследуемой сис-

импульса

k изучаемой системы; они связаны соот-

темы и не зависят от свойств идеальных контактов.

ношением

Последние оказывают влияние лишь на абсолютный

Δ²² - Δ²¹ = 1 ,

(10)

масштаб кондактанса.

2. Для уровня Ферми в глубине запрещенной

которое имеет принципиальное значение для сохра-

зоны (рис. 2в) последнее утверждение справедливо

нения нормировки. В дальнейшем считаем Δ₁ сво-

и за пределами логнормальной области: идеальные

бодным параметром, изменяющимся от -∞ до ∞,

контакты не влияют на форму распределения P (ρ),

тогда как положительный параметр Δ₂ определяет-

но изменяют абсолютный масштаб ρ на постоянный

ся соотношением (10).

множитель,

Среднее значение ρ в одномерных системах, как

правило, не репрезентативно, но при этом вполне

P (ρ) → AP (Aρ) , A = 1/Δ²² ,

(6)

наблюдаемо (см. разд. 8). Его эволюция допускает

полное описание при произвольных L, что позволяет

где параметр Δ₂ определен ниже в формуле (9).

наглядно продемонстрировать влияние идеальных

3. В критической области ситуация усложняется:

идеальные контакты изменяют лишь общий масш-

¹⁾ Подчеркнем, что речь идет именно о формальном пре-

таб кондактанса, но значение параметра A в выра-

деле L → 0, так как фактически применимость результатов

жении (6) различно в логнормальном режиме и в

(7) и (8) ограничена условием L ≳ 1/κ.

953

ЖЭТФ, вып. 5 (11)

И. М. Суслов

ЖЭТФ, том 156, вып. 5 (11), 2019

t = 0

t = 0.002

t = 0.3

0.05

0.10

0.15

0.05

0.10

0.15

0.20

0.5

1.0

1.5

0.4

0.010

0.008

0.3

t = 0.01

0.3

t = 3

t = 100

0.006

0.2

0.004

0.1

0.002

100

200

300

400

500

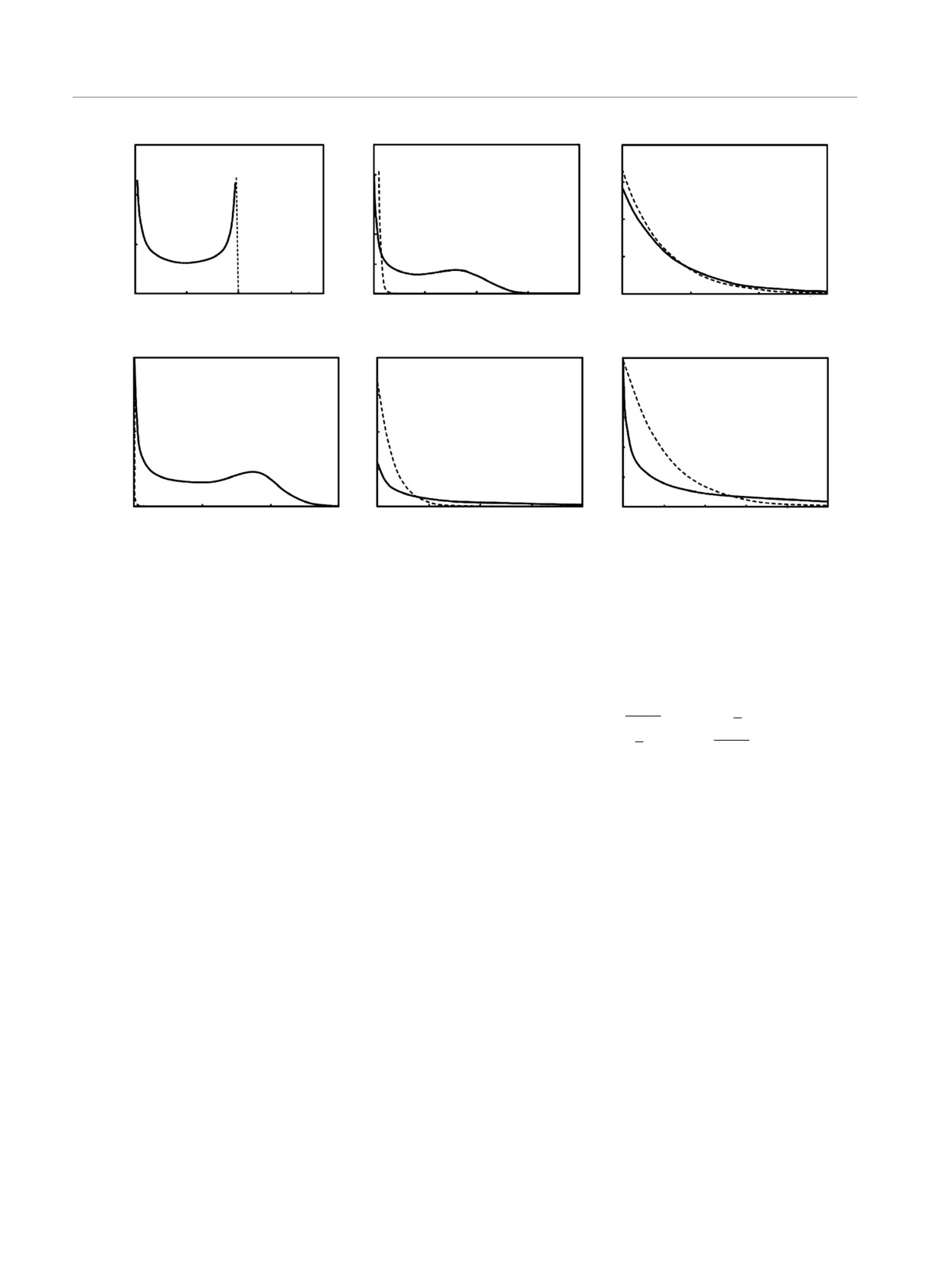
Рис. 5. Эволюция распределения P (ρ) в металлическом режиме (а) для слабого (Δ²¹ = 0.1) и (б) для сильного (Δ²¹ = 10)

различий уровней Ферми в изучаемом образце и в идеальных контактах. Штриховая линия показывает распределение

(7) с γ = 0

(

)

контактов. При изменении L как 〈ρ〉, так и высшие

1/t

-r/t

T =

моменты могут испытывать осцилляции с несоиз-

−r^∗/t^∗

1/t^∗

меримыми периодами, что обеспечивает апериоди-

)

( √

ρ+1e^iϕ

√ρe^iθ

ческий характер осцилляций ρ для конкретного об-

(12)

разца (см. разд. 8).

√ρ e^-iθ

√ρ + 1 e^-iϕ

где ρ = |r/t|² — сопротивление по Ландауэру [2].

При последовательном расположении рассеивателей

их трансфер-матрицы перемножаются. Для слабого

2. РАЗЛИЧНЫЕ ВИДЫ ТРАНСФЕР-МАТРИЦ

рассеивателя матрица T близка к единичной, что

позволяет выводить дифференциальные уравнения

Использование трансфер-матриц является есте-

эволюции для ее элементов и для ландауровского

ственным методом для исследования одномерных

сопротивления ρ.

систем. Наиболее удобна трансфер-матрица T в

Для энергии внутри запрещенной зоны решения

волновом представлении, связывающая амплитуды

слева (Ae^κx + Be^-κx) и справа (Ce^κx + De^-κx) от

волн слева (Ae^ikx+Be^-ikx) и справа (Ce^ikx+De^-ikx)

рассеивателя являются суперпозицией растущей и

от рассеивателя:

затухающей экспонент и могут быть связаны псев-

до-трансфер-матрицей:

(

)

(

)

(

)

(

)

(11)

(

)(

)

t₁₂

(13)

Она определяется амплитудами прохождения (t) и

t₂₁

t₂₂

отражения (r) и при наличии инвариантности отно-

сительно обращения времени допускает параметри-

для которой не справедлива параметризация (12) и

зацию [1]:

не очевидна связь с ландауэровским сопротивлени-

954

ЖЭТФ, том 156, вып. 5 (11), 2019

Распределение кондактансов в одномерных системах. . .

Таблица. Достоинства и недостатки различных трансфер-матриц

Матрица

Недостатки

Достоинства

Определяется внутренними свойствами системы

Ограничена разрешенной зоной

Прямая связь с ρ

Близка к единичной для слабого рассеивателя

Определяется внутренними свойствами системы

Ограничена запрещенной зоной

Близка к единичной для слабого рассеивателя

Нет прямой связи с ρ

Действительные матричные элементы

Нет прямой связи с ρ

Определяется внутренними свойствами системы

Применима при всех энергиях

Не близка к единичной для

слабого рассеивателя

Действительные матричные элементы

Применима при всех энергиях

Зависит от идеальных контактов

Прямая связь с ρ

Близка к единичной для слабого рассеивателя

ем. Элементы матрицы T действительны, а ее де-

нужными свойствами, но непосредственно примени-

терминант равен единице, как и в случае (12).

ма лишь в разрешенной зоне; в запрещенной зоне ее

Наконец, можно ввести трансфер-матрицу в

роль переходит к псевдоматрице T , которая не име-

координатном представлении, что удобно проде-

ет прямой связи с ландауэровским сопротивлением

монстрировать для одномерной модели Андерсона,

ρ. Матрица τ применима при всех энергиях, но не

определяемой дискретным уравнением Шредингера

имеет прямой связи с ρ и не близка к единичной

для слабого рассеивателя. Матрицы T и τ состоят

Ψn+1 + Ψn-1 + V_nΨ_n = EΨ_n ,

(14)

из действительных элементов, что дает некоторые

технические преимущества²⁾.

где E — энергия, отсчитанная от центра зоны, а ин-

Для преодоления указанных трудностей опреде-

теграл перекрытия принят за единицу. Переписывая

лим «внешнюю» трансфер-матрицу

T, которая учи-

(14) в виде

(

)

(

) (

)

тывает наличие чужеродных контактов (рис. 2б) и

Ψn+1

E-V_n

-1

Ψ_n

связана с матрицей T изучаемой системы с помо-

(15)

Ψ_n

Ψn-1

щью краевых матриц T_a и T_b:

и итерируя n раз, легко получить

(

)

(

)

Ψn+1

Ψ₁

T =T_aTT_b =

=τ

(

)(

)

Ψ_n

Ψ₀

a a₁

T₁₁

T₁₂

b b₁

(

)(

)

a₁

T₂₁

T₂₂

b₁

τ₁₁

τ₁₂

Ψ₁

(16)

(

(17)

τ₂₁

τ₂₂

Ψ₀

k⁾

a₁ =

где матрица τ является произведением n матриц ти-

(

)

(

)

па (15).

b₁ =

Матрицы T , T , τ определяются внутренними

свойствами системы; каждая из них обладает сво-

им набором достоинств и недостатков (см. табли-

²⁾ В частности, исследование эволюции четвертых момен-

цу). Нетрудно видеть, что эти три матрицы не поз-

тов для матриц с комплексными элементами представляет-

воляют получить уравнение эволюции для ρ, при-

ся практически нереальным, так как требует диагонализации

менимое при всех энергиях. Матрица T обладает

матрицы большого размера.

955

И. М. Суслов

ЖЭТФ, том 156, вып. 5 (11), 2019

Краевые матрицы имеют простой смысл: например,

Нетрудно проверить, что точечному рас-

T_a связывает амплитуды волн слева от границы раз-

сеивателю с потенциалом V δn0 соответствует

дела (Ae^ikx + Be^-ikx) с амплитудами волн справа

трансфер-матрица

(

)

от нее (A₁e^ikx + B₁e^-ikx). Очевидно, T_a T_b = 1, т. е.

1 - iϵ

-iϵ

краевые матрицы являются взаимно обратными.

(20)

iϵ

1 + iϵ

Для энергии внутри запрещенной зоны (рис. 2в)

явное введение идеальных контактов является необ-

где ϵ = V/2ka₀. Если два точечных рассеивателя с

ходимым и также осуществляется путем использо-

амплитудами V₀ и V₁ находятся на расстоянии L, то

вания краевых матриц, позволяющих превратить

они описываются трансфер-матрицей

псевдоматрицу T в истинную трансфер-матрицу

(

) (

)

1 - iϵ₀

-iϵ₀

e^-ikL

T =T_aT T_b =

(

) (

)(

)

iϵ₀

1 + iϵ₀

e^ikL

∗

a a

t₁₁

t₁₂

b b^∗

(

)

1 - iϵ₁

-iϵ₁

a^∗ a

t₂₁

t₂₂

b^∗ b

(18)

(21)

(

)

iϵ₁

1 + iϵ₁

(

κ⁾

Наконец, если рассеиватели с амплитудами V₀, V₁,

V₂, . . ., V_n находятся в точках 0, L₁, L₁ + L₂, . . ., то

Соотношения (18) получаются из (17) заменой

k→

соответствующая трансфер-матрица имеет вид

→ -iκ.

Использование краевых матриц позволяет свя-

T(n) = Tϵ0 Tδ1 Tϵ1 Tδ2 Tϵ2 . . . Tδn Tϵn ,

(22)

зать также

T и τ:

где

(

)

(

)

1 - iϵ_s

-iϵ_s

- exp(-ika₀)

Tϵs =

T =

iϵ_s

1 + iϵ_s

2i sinka₀

-1

exp(ika₀)

(

)

(

)(

)

exp(-iδ_s)

(23)

τ₁₁

τ₁₂

exp(ika₀) exp(-ika₀)

Tδs =

(19)

exp(iδ_s)

τ₂₁

τ₂₂

V_s

ϵ_s =

δ_s = kL_s.

где a₀ — межатомное расстояние для модели (14).

2ka₀

Таким образом, явное введение идеальных контак-

При изменении числа рассеивателей на единицу

тов приводит к линейному преобразованию элемен-

справедливо рекуррентное соотношение

тов трансфер-матрицы. Линейное преобразование

(

)

u_n v_n

не изменяет показателей роста для вторых и четвер-

T(n) = T(n-1)

тых моментов, которые определяются внутренними

v^∗n u^∗

(24)

свойствами системы и не зависят от идеальных кон-

u_n = (1 - iϵ_n)exp(-iδ_n),

тактов (см. разд. 4). Как ясно из таблицы, матри-

v_n = -iϵ_n exp(-iδ_n).

ца

T обладает всеми необходимыми свойствами, но

содержит зависимость от идеальных контактов; по-

Для удобства будем полагать ϵ₀ = 0, чтобы в каче-

следнее можно считать недостатком, но фактически

стве начального условия для T⁽⁰⁾ использовать еди-

это отражение объективной реальности.

ничную матрицу. Если все ϵ_n малы, то при не слиш-

ком больших n можно ограничиться двумя первы-

3. ПОСЛЕДОВАТЕЛЬНОСТЬ ТОЧЕЧНЫХ

ми порядками по v_n. Проводя прямое перемножение

РАССЕИВАТЕЛЕЙ

матриц, получим

∑

Коэффициенты α, γ₁, γ₂ уравнения (3) не явля-

T(n)11 = u₁u₂ . . . u_n +

u₁u₂ . . .ui-1v_i ×

ются постоянными и испытывают изменения в про-

i=1 j=i+1

цессе эволюции. Чтобы получить представление об

×u∗i+1...u∗j-1v^∗juj+1...u_n,

(25)

этой эволюции, рассмотрим последовательность из

∑

точечных рассеивателей. Для определенности будем

T(n)12 =

u₁u₂ . . . ui-1v_iu∗i+1 . . .u^∗

рассматривать модель Андерсона (14) вблизи края

i=1

зоны, где она соответствует дискретизации обычно-

го уравнения Шредингера.

и T₂₁ =T∗12,T₂₂ =T∗11.

956

ЖЭТФ, том 156, вып. 5 (11), 2019

Распределение кондактансов в одномерных системах. . .

В модели Андерсона (14) рассеиватели находят-

случайных фаз и исчезновения параметра γ, так

ся на каждом узле решетки, поэтому все δ_s одина-

как в уравнение эволюции входит лишь комбинация

ковы, δ_s = ka₀. Выражения (25) можно привести к

ψ = θ - ϕ (см. разд. 7). Решение уравнения (2) при

виду

малых ρ имеет вид (7), который согласуется с (32)

√

при γ = 0 и t = ϵ²n. Справедливость последних соот-

T(n)11 =

1+S²¹+S²² exp(-iS - inδ),

ношений следует из формул (93) в разд. 7. При боль-

(26)

ших n экспоненциальный рост элементов T_ij опре-

T(n)12 = S₁-iS₂,

деляется произведением |u₁||u₂| . . . |u_n| ≡ exp(w_n),

где в низшем порядке по ϵ имеем

которое содержится как во всех членах выражений

(25), так и членах высших порядков. Величина w_n

∑

S = ϵs , S₁ = ϵs sin(n - 2s)δ ,

имеет среднее значение ϵ²n/2, что (ввиду ρ = |T₁₂|²)

s=1

согласуется с результатом a = ϵ² для параметра a

(27)

∑

в логнормальном распределении (см. разд. 5). От-

S₂ = ϵ_s cos(n - 2s)δ .

брошенные члены не дают вкладов O(ϵ²) в среднее

s=1

значение величины w_n, но изменяют ее дисперсию.

Принимая, как обычно, для модели Андерсона

Изложенное справедливо в глубине разрешен-

ной зоны при «естественных» идеальных контактах

〈V_n〉 = 0 ,

〈V2n〉 = W² ,

(28)

(рис. 2а). При переходе в запрещенную зону имеем

T(n) = T_a T(n) T_b, где псевдоматрица T(n) определя-

получим нулевые средние значения для всех сумм в

ется теми же соотношениями, что и выше, с заменой

(27), тогда как для вторых моментов

k → -iκ. В частности,

(

)

〈S²〉 = 2〈S²¹〉 = 2〈S²²〉 = ϵ²n ,

(29)

u_n v_n

〈SS₁〉 ∼ 〈SS₂〉 ∼ 〈S₁S₂〉 ∼ ϵ² ,

T(n) =T(n-1)

∗

v^∗n u

(33)

где ϵ² = W²/4k²a²⁰. Приведенные выражения верны

u_n = (1 + ϵ_n)exp(-δ_n), v_n = ϵ_n exp(-δ_n),

при условии

ϵ_n = V_n/2κa₀ , δ_n = κL_n ,

1/δ ≪ n ≪ 1/ϵ² ,

(30)

где звездочка отмечает не комплексное сопряжение,

. С учетом этой модифи-

а изменение знаков ϵ_n и δ_n

где левое неравенство обеспечивает большое чис-

кации соотношения (25) формально сохраняются.

ло осцилляций синуса и косинуса в суммах (27), а

Вынося из сумм множитель u∗1u∗2 . . . u^∗n ≡ exp (w_n),

правое необходимо для возможности пренебрежения

имеем

высшими порядками по ϵ. При больших n все сум-

мы в (27) распределены по Гауссу и практически

T(n) =

(

)

независимы, так что их совместное распределение

exp(- w_n)- exp( w_n)S₁S₂ exp( w_n)S₁

вероятностей имеет вид

- exp( w_n)S₂

exp(wn)

{

}

S²

S²¹

S²²

∑

P (S, S₁, S₂) ∼ exp

(31)

(34)

2nϵ²

nϵ²

S₁ = ϵ_s exp(-2sδ),

s=1

Учитывая, что ρ = S²¹ + S²², ϕ = -S - nδ, имеем сле-

∑

дующее распределение вероятностей для парамет-

S₂ = ϵ_n-s exp(-2sδ),

ров трансфер-матрицы (12):

s=0

{

}

где w_n отличается от w_n на вклад O(ϵ²) с нулевым

(ϕ + nδ)²

P (ρ, ϕ, θ) ∼ exp

(32)

средним, а S₁ и S₂ приведены в низшем порядке по

2nϵ²

nϵ²

ϵ. Подстановка в (18) дает для фазовых переменных

Мы видим, что при δ ≫ ϵ², т. е. в глубине разре-

S₁ - S₂

шенной зоны, фаза θ полностью стохастизируется

tg ϕ = -Δ₁ - Δ₂(S₁ + S₂) , ctg θ =

(35)

Δ₂

на масштабе n ∼ 1/δ. Стохастизация фазы ϕ проис-

ходит на масштабе n ∼ 1/ϵ², но ее равномерное рас-

где Δ₁ и Δ₂ определены в (9). Замечая, что при

пределение возникает уже на масштабе 1/δ за счет

условии (30)

регулярных изменений. Так или иначе, стохастиза-

〈S²¹〉 = 〈S²²〉 = ϵ²/4δ,

〈S₁S₂〉 ≈ 0,

(36)

ции θ достаточно для применимости приближения

957

И. М. Суслов

ЖЭТФ, том 156, вып. 5 (11), 2019

видим, что флуктуации ϕ и θ являются ограничен-

и такие же уравнения для t(n)21 и t(n)22; существенно,

ными и не возрастают с увеличением n. Случай

что величины t(n-1)ij не содержат ϵ_n и статистически

k = κ является особым; при этом Δ₁ = 0 и Δ₂ = 1,

независимы от u_n, v_n. Вводя обозначения для вто-

так что

рых моментов,

ϕ = -(S₁ + S₂), θ = π/2 + (S₂ - S₁),

(37)

)[

]₂

z(n)1 = t(n)11

z(n)2 = t(n)11t(n)

а переменная ψ = θ - ϕ не имеет существенной эво-

(42)

люции, оставаясь локализованной вблизи π/2 при

)[

]₂

всех n ≲ 1/ϵ². Как мы увидим в разд. 7, это свой-

z(n)3 = t(n)12

ство сохраняется и при n ≳ 1/ϵ². При больших n

exp( w_n) обеспечивает рост элементов t_ij и соответ-

получим систему линейных разностных уравнений с

ственно ρ ∼ exp(2 w_n); величина 2 w_n имеет среднее

постоянными коэффициентами,

значение (2δ - ϵ²)n и дисперсию 4ϵ²n, что согласу-

⎛

⎞

ется с результатами (56) в разд. 5.

z(n)1

Перейдем к критической области, определяемой

⎜

⎟

⎝ z(n)2

⎠ =

условием δ ≪ ϵ². Тогда при достаточно малых n

z(n)

можно положить δ_s = 0 в (23) и получить

(

)

⎛

⎞

∑

1 - iS

-iS

1 - 2δ + ϵ²

-2ϵ²

T(n) =

S = ϵ_s,

(38)

⎜

⎟

1 + iS

⎝

ϵ²

1 - 2ϵ²

ϵ²

⎠×

s=1

ϵ²

-2ϵ²

1 + 2δ + ϵ²

где сумма S распределена по Гауссу аналогично

(31). Совместное распределение ρ, ϕ, θ определяется

⎛

⎞

соотношением

z(n-1)1

(

)

⎜

(n-1)

⎟

∫

⎝ z

⎠,

(43)

S²

P (ρ, ϕ, θ) = dS√

exp

2nϵ²

z(n-1)

2πnϵ²

(

)

π⁾

×δ

ρ-S²

δ (ϕ + arctg S) δ θ +

(39)

решение которой ищется в экспоненциальной фор-

(n)

ме, z_i

∼ λⁿ [30]. Нетрудно видеть, что λ есть соб-

и интегрирование по ϕ и θ приводит к результату

ственное значение матрицы в (43). Полагая λ = 1+x,

(

)

получим уравнение для определения x:

P (ρ) =

√

exp

(40)

√ρ

2πnϵ²

2nϵ²

(

)

x² - 4δ²

= 8ϵ²δ² .

(44)

что согласуется с (7) при γ = -1/2, t = 2nϵ²; по-

следнее следует из формулы (93) в разд. 7 при усло-

В (43), (44) мы имеем в виду предел

вии локализации ψ вблизи ±π/2. Такая локализация

δ → 0, ϵ → 0, δ/ϵ² = const,

(45)

действительно имеет место при малых ρ, когда ϕ ∼

∼

√ρ ≪ 1, θ = -π/2, а (40) является решением урав-

актуальный вблизи края зоны идеального кристал-

нения (2). Однако результат (40) справедлив в более

ла, когда не существенны эффекты соизмеримости

широкой области n ≲ (ϵ²δ²)-1/3 (см. разд. 8), когда

[31, 32], затрудняющие анализ. Поэтому в матрице

значение ρ ∼ nϵ² может быть велико; при этом ϕ ло-

(43) мы сохраняем члены первого порядка по δ и

кализуется вблизи ±π/2, а sin ψ становится малым

второго по ϵ.

в соответствии с результатами для логнормального

Аналогично для четвертых моментов положим

режима (см. разд. 5, 7).

)[

]₄

)[

]₃

(n)

z₁

= t(n)11

z(n)2 = t(n)11

t(n)

4. ЭВОЛЮЦИЯ МОМЕНТОВ

)

[

]₂ [

]₂

Согласно (33), для элементов псевдо-трансфер-

z(n)3 = t(n)11

t(n)12

(46)

матрицы в запрещенной зоне справедливы уравне-

)

ния эволюции

[

]₃

)[

]₄

(n)

z(n)4 = t(n)

t(n)12

z(n)5 = t

t(n)11 = u_nt(n-1)11 + v^∗nt(n-1)12,

(41)

(n-1)

и получим систему разностных уравнений

t(n)12 = v_nt(n-1)11 + u^∗nt

958

ЖЭТФ, том 156, вып. 5 (11), 2019

Распределение кондактансов в одномерных системах. . .

⎛

⎞

⎛

⎞

⎛

⎞

z(n)1

1 - 4δ + 6ϵ²

-12ϵ²

6ϵ²

z(n-1)1

⎜

⎟

⎜

⎟

⎜

⎟

⎜

z(n)2

⎟

⎜

3ϵ²

1 - 2δ - 3ϵ²

-3ϵ²

3ϵ²

⎟

⎜

z(n-1)2

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

z(n)3

ϵ²

2ϵ²

1 - 6ϵ²

2ϵ²

ϵ²

z(n-1)3

(47)

⎜

⎟

⎜

⎟

⎜

⎟.

⎜

⎟

⎜

⎟

⎜

⎟

⎝ z(n)4

⎠

⎝

3ϵ²

-3ϵ²

1 + 2δ - 3ϵ²

3ϵ²

⎠

⎝ z(n-1)4

⎠

(n-1)

z(n)

6ϵ²

-12ϵ²

1 + 4δ + 6ϵ²

z₅

Принимая z(n)i ∼ λⁿ и полагая λ = 1 + x, получим

Уравнения (49) получены при E < 0, но ввиду ре-

уравнение для x:

гулярности по E могут быть аналитически продол-

жены на произвольные E. Эти уравнения можно

(

)(

)

(

)

x² - 4δ²

x²-16δ²

= 24ϵ²

7δ²x² - 16δ⁴

(48)

также вывести, рассматривая эволюцию координат-

ной трансфер-матрицы (см. Приложение A), кото-

Заметим, что уравнения (44) и (48) можно по-

рая применима при произвольных E и не требует

лучить, составляя произведение диагональных эле-

аналитического продолжения. Один из корней для

ментов в матрицах (43), (47) и ограничиваясь вто-

каждого из уравнений (49) остается положительным

рым порядком по ϵ. Дело в том, что недиагональ-

при всех физических значениях параметров. Среди

ные элементы вносят в детерминант вклады O(ϵ⁴) и

всех корней уравнения он имеет максимальную дей-

выше, сокращение которых можно предвидеть зара-

ствительную часть и определяет показатель роста

нее. Поскольку ϵ² = W²/4δ² (см. разд. 3), комбина-

для вторых (x₂) или четвертых (x₄) моментов. По-

ции ϵ², ϵ⁴, . . . , ϵ¹⁰ и δ²ϵ⁴, δ²ϵ⁶ имеют сингулярности

ведение x₂ и x₄ как функций E/W4/3 показано на

при δ → 0, отсутствие которых очевидно из уравне-

рис. 6.

ний эволюции для координатной трансфер-матрицы

Нетрудно получить асимптотики для x₂ и x₄. В

(см. Приложение A). Допустимы лишь комбинации

глубине запрещенной зоны (δ ≫ ϵ²) из (44), (48) име-

δ²ϵ² и δ⁴ϵ², которые и входят в уравнения³⁾ (44) и

ем

(48). В глубине разрешенной и запрещенной зон воз-

x₂ = 2δ + ϵ² , x₄ = 4δ + 6ϵ² .

(50a)

можность ограничения диагональными элементами

позволяет установить показатели роста для высших

При переходе в разрешенную зону в (44), (48) проис-

моментов и убедиться в их соответствии логнор-

ходит замена δ → iδ, ϵ → -iϵ, после чего в глубине

мальному распределению.

зоны (δ ≫ ϵ²) получим

Для модели Андерсона (14) имеем δ2 = -E,

x₂ = 2ϵ² , x₄ = 6ϵ² .

(50b)

4ϵ²δ² = W², где E — энергия, отсчитанная от ниж-

него края зоны. Поэтому уравнения (44), (48) могут

В критической же области (δ ≪ ϵ²) справедливы ре-

быть переписаны в виде

зультаты

(

)

(

)1/3

(

)

x₂ = 2

ϵ²δ²

1/3 , x4 =2

21ϵ²δ²

(50c)

x² + 4E

= 2W²,

(

)(

)

(49)

x² + 4E

x² + 16E

= 42W²x² + 96W²E .

В терминах E и W имеем

x₂

= 2|E|1/2 + W²/4|E| , x₄ = 4|E|1/2 + 3W2/2|E| ,

-E ≫ W4/3,

(

)1/3

(

)1/3

x₂

2W²

x₄ =

42W²

|E| ≪ W4/3,

(51)

x₂

= W²/2E - W⁶/32E4 , x₄ = 3W²/2E + 27W⁶/64E4 , E ≫ W4/3 ,

где последний результат приведен с более высокой точностью.

³⁾ Выше мы перечислили все возможные комбинации. Действительно, изменение знака δ в выражениях (43), (47) приводит

к аналогичным матрицам, которые приводятся к прежнему виду, если перенумеровать компоненты столбцов в обратном по-

рядке. Поэтому нечетных степеней δ не возникает. Поскольку мы рассматриваем предел δ ∼ ϵ² → 0 (см. (45)), возможны лишь

комбинации δ2nϵ2m с 4n + 2m ≤ 6 в случае (43) и с 4n + 2m ≤ 10 в случае (47). Из них лишь комбинации с n ≥ m не имеют

сингулярностей при δ → 0.

959

И. М. Суслов

ЖЭТФ, том 156, вып. 5 (11), 2019

x/W^2/3

Подстановка асимптотик (50) дает

a = 2δ - ϵ2 , b = 4ϵ² (запрещенная зона),

a = ϵ2 , b = 2ϵ² (разрешенная зона),

x₄

(

)1/3

(

)1/3

(56)

a = 1.24

ϵ²δ²

b = 1.52

ϵ²δ²

(критическая область).

x₂

Использование асимптотик (51) дает для параметра

γ в распределении (5)

⎧

⎨

2|E|3/2/W²,

-E ≫ W4/3,

γ =

0.316,

|E| ≪ W4/3,

(57)

⎩

-4

-2

−33W⁴/32E³, E ≫ W4/3,

/W^4/3

тогда как параметр

α связан с b соотношением

Рис. 6. Положительные корни первого (x2) и второго (x4)

α = b/2a₀.

уравнений (49) как функции энергии E в приведенных ко-

Как показано в разд. 2, введение чужеродных

ординатах

контактов приводит к линейному преобразованию

элементов трансфер-матрицы, которое не влияет на

5. ПАРАМЕТРЫ ЛОГНОРМАЛЬНОГО

показатели роста x₂ и x₄ для вторых и четвертых

РАСПРЕДЕЛЕНИЯ

моментов. По этой причине последние не зависят от

свойств идеальных контактов, так же как и связан-

При больших L = na₀ для P (ρ) справедливо ло-

ные с ними параметры a, b, γ. От идеальных кон-

гнормальное распределение

тактов зависят лишь коэффициенты C₁ и C₂ в (53),

{

}

что изменяет абсолютный масштаб кондактанса и

(ln ρ - an)²

P (ρ) =

√

exp

(52)

начало отсчета n.

2πbn

2bn

которое для частных случаев получено во многих

6. ЗАВИСИМОСТЬ P (ρ) ОТ ИДЕАЛЬНЫХ

работах ( [1, 13-18, 21-24]) и наиболее общим обра-

КОНТАКТОВ

зом следует из модифицированного уравнения До-

рохова - Мелло - Перейра - Кумара [33]; при нали-

Согласно (12), для элементов трансфер-матрицы

чии чужеродных контактов оно выводится в разд. 7.

в волновом представлении справедливы соотноше-

Нетрудно найти моменты для распределения (52),

ния T₂₂ = T∗11, T₂₁ = T∗12, которые следуют из ин-

вариантности относительно обращения времени; по-

〈ρ^m〉 = exp(amn + bm²n/2).

этому достаточно рассматривать элементы

Поскольку ρ определяется выражением, квадратич-

T₁₁ = x + iy , T₁₂ = z + iω .

(58)

ным по элементам трансфер-матрицы, параметры a

и b могут быть установлены из сопоставления с рос-

Если известно распределение P (ρ, ϕ, θ) параметров

том вторых и четвертых моментов:

матрицы (12), то функция распределения x, y, z, ω

(

)

составляется по правилу

〈ρ〉 = exp an +

= C1 exp(x₂n),

∫

(53)

P₁(x, y, z, ω) = dρ dϕdθ P(ρ, ϕ, θ)×

ρ²

= exp(2an + 2bn) = C₂ exp(x₄n).

(

√

)

(

√

)

Легко видеть, что

×δ x-

1 + ρcosϕ δ y -

1 + ρsinϕ

× δ (z -

√ρ cos θ) δ (ω -√ρ sin θ) .

(59)

a = 2x₂ -

x₄ , b = x₄ - 2x₂ ,

(54)

Полагая ρ = r², 1 + ρ = R² и вводя под интеграл

тогда как для параметра γ в (5) имеем

разложение единицы

∫

3x₂ - x₄

(

)

γ =

(55)

1 = dR²δ

R² - r² - 1

(60)

x₄ - 2x₂

960

ЖЭТФ, том 156, вып. 5 (11), 2019

Распределение кондактансов в одномерных системах. . .

нетрудно получить связь P₁(x, y, z, ω) с P (ρ, ϕ, θ):

замена переменных (65) определяет распределение

P₁(x, y, z, ω), зависящее от идеальных контактов, а

(

ω⁾

P₁(x, y, z, ω) = P z² + ω², Arctg

, Arctg

формула (63) определяет P(ρ, ϕ, θ):

(

)

P (ρ, ϕ, θ) =

P (ρ^′, ϕ^′, θ^′) ,

× 4δ

x² + y² - z² - ω² - 1

(61)

(

√

ρ^′ = ρ cos² θ+ Δ₁

1+ρ sin ϕ+Δ₂

√ρ sin θ)2 ,

Обратно, если известно распределение P₁(x, y, z, ω),

то оно всегда содержит δ-функцию:

Δ₂

^√1 + ρ sin ϕ + Δ₁√ρ sin θ

(66)

tg ϕ^′ =

^√1 + ρ cos ϕ

P₁(x, y, z, ω) =

P (x, y, z, ω) ×

(

)

Δ₁

^√1 + ρ sin ϕ + Δ₂√ρ sinθ

× 4δ

x² + y² - z² - ω² - 1

(62)

tg θ^′ =

√ρ cos θ

Тогда распределение P (ρ, ϕ, θ) определяется соотно-

В запрещенной зоне при k = κ имеем

шением

(

π⁾

P (ρ, ϕ, θ) =

P (ρ)δ(ϕ)δ θ -

(67)

(√

P (ρ, ϕ, θ) =

1 + ρcosϕ,

где δ-функции нужно уширить на величину порядка

√

)

ϵ. В пренебрежении этим уширением нетрудно полу-

1 + ρsinϕ,

√ρ cos θ,√ρ sin θ

(63)

чить, что

Преобразование трансфер-матрицы T при изме-

(

)

нении свойств идеальных контактов определяется

P (ρ, ϕ, θ) =

Δ²²

Δ²

соотношениями (17), (18), которые могут быть за-

(

√

)

(

Δ₁

π⁾

писаны в более компактной форме. Как ясно из из-

× δ ϕ + arcsin

δ θ-

(68)

Δ₂

1+ρ

ложенного выше, для ситуации внутри запрещенной

зоны случай k = κ является выделенным — для него

и интегрирование по ϕ и θ дает результат (6), т. е.

граница раздела имеет максимальную прозрачность

форма распределения ρ не зависит от идеальных

(см. (4)), а фаза ψ = θ - ϕ при всех L локализована

контактов, и последние изменяют лишь абсолютный

вблизи π/2 (см. разд. 3). Отмечая чертой значения

масштаб кондактанса.

параметров при k = κ, нетрудно показать, что соот-

В разрешенной зоне при k =

k (рис. 2а) распре-

ношение (18) может быть записано в виде

деление

P (ρ, ϕ, θ) не зависит от фазовых перемен-

ных⁴⁾,

x= x, y=Δ₂y-Δ₁ω,

(64)

z = z, ω = -Δ₁y+ Δ₂ω ,

P (ρ, ϕ, θ) =

P (ρ) =

(2π)²

(

или, в обратную сторону,

ρ⁾

exp

t = αL,

(69)

(2π)² t

x=x,

y=Δ₂y+Δ₁ω,

(65)

P (ρ) определяется формулой (7) при γ = 0. Для

z=z,

ω=Δ₁y+Δ₂ω,

чужеродных контактов (рис. 2б) распределение ρ

где Δ₁ и Δ₂ определены в (9). Элементы

T₁₁ = x+iy

определяется интегралом

иT¯₁₂ = z+iω определяются лишь параметром κ, т.е.

∫

внутренними свойствами изучаемой системы, тогда

P (ρ) =

dϕ ×

как вся зависимость от фермиевского импульса k в

(2π)² t

-π

идеальных контактах содержится в Δ₁ и Δ₂.

∫π

{

}

Для ситуации внутри разрешенной зоны выде-

ρ + S(ρ,ϕ,θ)

× dθ exp

(70)

ленным является случай k =

k (см. рис. 2а). Отме-

чая чертой параметры, соответствующие этому слу-

−π

чаю, и полагая формально

k₌ κ, нетрудно убедить-

где

ся, что связь элементов T_ij и

T_ij по-прежнему вы-

S(ρ, ϕ, θ) = Δ²¹(1 + ρ) sin² ϕ +

ражается соотношениями (64), (65). Если известно

√

распределение

P (ρ, ϕ, θ) для двух указанных базо-

+ 2Δ₁Δ₂

(1 + ρ)ρ sin ϕ sin θ + Δ²¹ρ sin² θ .

(71)

вых ситуаций (полностью определяемое внутренни-

ми свойствами системы), то можно перейти к рас-

⁴⁾ Строго говоря, для этого надо усреднить (32) по измене-

пределению

P₁(x, y, z, ω) согласно (61), после чего

ниям n порядка 1/δ.

961

И. М. Суслов

ЖЭТФ, том 156, вып. 5 (11), 2019

Вычисление интеграла (см. Приложение B) приво-

При Δ²¹ ≪ 1 актуальны две области, t ≪ Δ²¹ и

дит к следующим результатам.

t ≫ Δ²¹. В первой из них имеем

⎧

√

(

⎪

ρ⁾

⎪

exp

ρ ≲ t,

⎪

πΔ²¹t

⎪

√

⎪

(

)1/2

⎪

⎨

t ≲ ρ, ρ_c-ρ ≳

tΔ²¹

π ρ(ρ_c-ρ)

P (ρ) =

(72)

⎪

√

⎪

(

)1/2

⎪

Γ(1/4) ,

|ρ_c - ρ| ≲

tΔ²¹

⎪

2π²

⎪

2ρ (tΔ²¹)1/2

⎪

(

)

⎪

S_c

(

)

⎩

√

exp

ρ-ρ_c ≳

tΔ²¹

1/2 ,

где

(

√

S_c = Δ₁

1+ρ-Δ₂

√ρ)2 Θ(ρ-ρ_c), ρ_c = Δ21,

√

(

)

A = 2Δ₁

1+ρ Δ₂

√ρ - Δ₁√1+ρ

(73)

(

)

B = 2Δ₁

√ρ Δ₂√1+ρ-Δ1

√ρ ,

а основная часть вероятности соответствует второму результату (72). Для области t ≫ Δ²¹ получим

⎧

]

(

⎪

ρ^)[

Δ²¹

Δ²¹ρ

Δ²¹Δ²²ρ(1 + ρ)

⎨

exp

ρ(1 + ρ) ≲ t²/Δ²¹,

2t²

P (ρ) =

(

)

(74)

⎪

S_c

⎩

√

exp

ρ(1 + ρ) ≳ t²/Δ²¹,

и нормировочный интеграл определяется первой асимптотикой. Эволюция распределения при Δ²¹ ≪ 1 по-

казана выше на рис. 5а. При малых t она сводится к сглаживанию сингулярностей распределения (8), а

при больших t значение P (ρ) при ρ = 0 стремится к таковому для распределения

P (ρ) и форма P (ρ) слабо

отличается от последнего.

При Δ²¹ ≫ 1 актуальны три области, t ≪ 1, 1 ≪ t ≪ Δ²¹ и t ≫ Δ²¹. В первой из них получаются

результаты

⎧

√

⎪

(

ρ⁾

⎪

exp

ρ ≲ t,

⎪

πΔ²¹

⎪

√

⎪

(

)1/2

⎪

⎨

t≲ρ, ρ_c -ρ≳

tΔ²¹ρ

π ρ(ρ_c - ρ)

P (ρ) =

(75)

⎪

√

⎪

(

)1/2

⎪

Γ(1/4) ,

|ρ_c - ρ| ≲

tΔ²¹ρ

⎪

2π²

⎪

2ρ (tΔ²¹ρ)1/2

⎪

(

)

⎪

S_c

(

)

⎩

√

exp

ρ-ρ_c ≳

tΔ²¹ρ

1/2 ,

аналогичные (72) и соответствующие размытию сингулярностей распределения (8). При этом основная ве-

роятность соответствует второй асимптотике. В области 1 ≪ t ≪ Δ²¹ имеем

962

ЖЭТФ, том 156, вып. 5 (11), 2019

Распределение кондактансов в одномерных системах. . .

⎧

√

(

⎪

ρ⁾

⎪

exp

ρ ≲ 1,

⎪

πΔ²¹t

⎪

√

⎪

ln ρ ,

1 ≲ ρ ≲ t,

⎪

π²

ρΔ²¹t

⎪

⎨

√

P (ρ) =

ln t ,

t ≲ ρ ≲ Δ²¹/t,

(76)

⎪

π²

ρΔ²¹t

⎪

√

(

)

⎪

Δ²

S_c

⎪

exp

Δ²¹/t ≲ ρ ≲ Δ²¹t,

⎪

2π²

ρΔ²¹t

⎪

(

)

⎪

S_c

⎩

√

exp

ρ ≳ Δ²¹t,

тогда как в области t ≫ Δ²¹

⎧

]

(

⎪

ρ^)[

Δ²¹

Δ²¹ρ

Δ²¹Δ²²ρ(1 + ρ)

⎪

exp

ρ ≲ t/Δ²¹,

⎪

2t²

⎪

√

⎪

Δ²¹ρ

⎨

t/Δ²¹ ≲ ρ ≲ t,

π²

ρΔ²¹t

P (ρ) =

(77)

√

(

)

⎪

Δ²t

S_c

⎪

exp

t ≲ ρ ≲ Δ²¹t,

⎪

2π²

ρΔ²¹t

⎪

(

)

⎪

S_c

⎩

√

exp

ρ ≳ Δ²¹t.

В обоих случаях основная вероятность сосредоточе-

K(ϕ, θ) = cos² θ + (Δ₁ sin ϕ + Δ₂ sin θ)² .

(78)

на на последних двух асимптотиках. Характерной

Подстановка в (5), (66), (69) дает

особенностью выражений (76) и (77) является нали-

чие быстрой экспоненты (exp(-ρ/2t) или exp(-ρ/t))

при малых ρ и медленной экспоненты exp(-ρ/Δ²¹t)

P (ρ, ϕ, θ) =

√

(2π)² ρK

4πt

при больших ρ, тогда как в промежуточной области

{

}

(ln Kρ - t)²

имеется степенное поведение P (ρ) ∝ ρ-1/2 с точно-

× exp

≈

√

(2π)² ρ

4πt

стью до логарифмических поправок. Эволюция рас-

{

}[

]

пределения при Δ²¹ ≫ 1 выше показана на рис. 5б.

(ln ρ - t)²

2(ln ρ - t) ln K

× exp

(79)

Выше мы учли, что результаты зависят лишь от

4tK

|Δ₁| (что проверяется заменой ϕ → ϕ + π в (70),

где мы провели разложение по 1/t, учитывая, что

√

(71)) и без ограничения общности можно считать,

(ln ρ - t) ∼

t для основной части распределения.

что Δ₁ > 0. Кроме того, мы предполагали, что рас-

Интегрируя по ϕ и θ, положим

пределение (69) задано аксиоматически, и не обсуж-

∫

дали условия его применимости: это позволяет луч-

dϕ

dθ

ше понять, как преобразуется распределение ρ за

≡

2π

2π K(ϕ, θ)

K₀

счет идеальных контактов. Фактически распределе-

−π

-π

(80)

ние (69) является решением уравнения (2) лишь для

∫

dϕ

dθ ln K(ϕ, θ)

ln K₁

ρ ≲ 1, что ограничивает применимость соотношений

≡

2π

2π K(ϕ, θ)

K₀

(76) и (77) условием ρ ≲ Δ²¹.

−π

-π

В логнормальном режиме, возникающем при t ≫

Тогда сохранение нормировки требует соотношения

≫ 1, в качестве

P (ρ) в (69) нужно подставлять вы-

K₀ = 1, после чего P(ρ) записывается в виде

ражение (5) с γ = 0. При этом типичные значения

{

}

ρ велики, и в формуле (66) можно положить ρ^′ =

(ln K₁ρ - t)²

P (ρ) =

√

exp

(81)

= ρK(ϕ, θ), где

(2π)² ρ

4πt

963

И. М. Суслов

ЖЭТФ, том 156, вып. 5 (11), 2019

K₁

1.0

0.8

0.6

0.4

0.2

Рис. 8. Физический смысл перенормировки ϵs состоит в

переходе от ситуации а к ситуации б. В последнем случае

для каждого рассеивателя создается потенциальная яма,

Рис. 7. Зависимость параметра K1 от Δ1

ширина которой стремится к нулю

Равенство K₀ = 1 действительно имеет место, что

В разрешенной зоне отличие

Tϵs от Tϵs сводится к

проверяется прямым вычислением интеграла. Мы

перенормировке ϵ_s → ϵ_s = ϵ_sk/k, которая имеет про-

видим, что идеальные контакты не изменяют пара-

стой физический смысл. Представим изучаемую си-

метров логнормального распределения и перенор-

стему (рис. 8а) в виде последовательности однотип-

мируют лишь абсолютный масштаб кондактанса,

ных рассеивателей (рис. 8б), создавая для каждо-

который определяется параметром K₁ (рис. 7):

го точечного рассеивателя потенциальную яму, ши-

{

рина которой стремится к нулю. Тогда параметр

1 - Δ²¹/2, Δ₁ ≪ 1,

K₁ =

(82)

ϵs = Vs/2ka0, определенный для фермиевского им-

const/Δ²¹ , Δ²¹ ≫ 1,

пульса

k изучаемой системы, заменяется на пара-

где численное значение константы близко к 4.

метр ϵ_s = V_s/2ka₀, содержащий фермиевский им-

В критической области при достаточно малых n

пульс k в идеальных контактах. При этом

T_δ являет-

удобно исходить из выражения (38), определяющего

ся трансфер-матрицей для потенциального барьера,

распределение

P (ρ, ϕ, θ) в виде (39). Преобразование

разделяющего два рассеивателя на рис. 8б:

переменных (64) приводит к замене S → S(Δ₂ - Δ₁)

(

)

в (38), (39) и перенормировке (6) абсолютного мас-

cosδ - iΔ₂ sinδ

iΔ₁ sinδ

T_δ =

≈

штаба кондактанса с A = 1/(Δ₂ - Δ₁)² в распреде-

-iΔ₁ sinδ

cosδ + iΔ₂ sinδ

лении (40).

(

)

1 - iΔ₂δ iΔ₁δ

≈

(85)

-iΔ

1δ

1 + iΔ₂δ

7. УРАВНЕНИЕ ЭВОЛЮЦИИ P (ρ) ПРИ

НАЛИЧИИ ИДЕАЛЬНЫХ КОНТАКТОВ

где Δ₁ и Δ₂ определяются при

k₌ κ формулой (9).

Ситуация в запрещенной зоне (рис. 2в) отличается

Согласно разд. 3, трансфер-матрица T для систе-

лишь тем, что высота барьеров на рис. 8б превыша-

мы точечных рассеивателей и «естественных» иде-

ет уровень Ферми, а

T_δ отличается от (84) заменой

альных контактов (рис. 2а) имеет вид (22). Соответ-

k на iκ:

ствующие параметры ϵ_s будем отмечать как ϵ_s. При

введении чужеродных контактов (рис. 2б) система

(

)

ch δ - iΔ₁ sh δ

iΔ₂ shδ

описывается трансфер-матрицей

T = T_aTT_b. Вводя

T_δ =

≈

между каждыми двумя множителями в (22) произ-

-iΔ₂ shδ

ch δ + iΔ₁ sh δ

(

)

ведение T_bT_a = 1, имеем

1 - iΔ₁δ iΔ₂δ

≈

(86)

T(n) =

Tϵ0

Tδ1

Tϵ1

Tδ2

Tϵ2 . . .

Tδn

Tϵn ,

(83)

-iΔ₂δ

1 + iΔ₁δ

где

Будем описывать потенциальный барьер тран-

Tϵs = T_a Tϵs T_b ,

T_δ = T_a T_δ T_b .

(84)

сфер-матрицей общего вида

964

ЖЭТФ, том 156, вып. 5 (11), 2019

Распределение кондактансов в одномерных системах. . .

(

)

A B

Уравнение (3) с параметрами (93) позволяет про-

T_δ =

анализировать выделенные ситуации с ϵ = ϵ, акту-

B^∗ A^∗

)

альные для разд. 6. В разрешенной зоне при k =

( √

1+Δ²e^iα

Δe^-iβ

имеем Δ₁ = 0 и Δ = 0 (ср. (85) и (87)). В случае од-

√

(87)

Δe^iβ

1+Δ²e^-iα

нородного распределения для ψ формулы (93) дают

α = ϵ², γ₁ = 0, γ₂ = 0, что согласуется с резуль-

близкой к единичной (α, Δ ≪ 1). Она имеет собст-

татами разд. 4, 5 в глубине разрешенной зоны. Та-

венные значения e^±δ, где δ² = Δ² - α². Согласно

ким образом, однородное распределение для ψ, по-

(83),

T(n) получается умножением

T(n-1) на

T_δTϵn .

лученное в разд. 3 для n ≲ 1/ϵ², сохраняется и при

Принимая

T(n-1) в виде (12), имеем

n ≳ 1/ϵ². В глубине запрещенной зоны при k = κ

√

имеем Δ₁ = 0 и Δ = δ (ср. (86) и (87)). Результа-

T(n)12 =

1+ρ e^iϕ(B+iϵC)+√ρ eiθ(A∗-iϵC∗),

(88)

ты α = 2ϵ², γα = δ из разд. 4 и 5 согласуются с

(93) при условии локализации ψ вблизи π/2, уста-

где C = B - A. Возводя по модулю в квадрат, полу-

новленной в разд. 3 для n ≲ 1/ϵ², и указывают на ее

чим значение ρ, соответствующее матрице

T(n):

сохранение при n ≳ 1/ϵ². Для критической области

√

(

)1/3

ρ=ρ+D

ρ(1 + ρ) + ϵ²(1 + 2ρ) ,

(89)

Δ₁ ≈ Δ₂ и Δ ∼ δ, и результаты α ∼

ϵ²δ²

, γ =

= γ₁ + γ₂ ∼ 1, полученные в разд. 4, 5, согласуются

где

с (93) при локализации ψ в области малых значений

(

)1/3

порядка

δ/ϵ²

в соответствии с анализом разд. 3.

D = 2Δcos(ψ + β) - 2ϵsinψ - 2ϵ2 cosψ ,

(90)

ψ = θ - ϕ,

(91)

8. ЭВОЛЮЦИЯ СРЕДНЕГО ЗНАЧЕНИЯ ρ

Эволюция 〈ρ〉 допускает полное описание и поз-

и мы сохранили члены первого порядка по δ и

воляет проиллюстрировать влияние идеальных кон-

второго по ϵ. Выражение (89) аналогично формуле

(A.2) работы [12], и дальнейшие вычисления следу-

тактов при произвольных размерах системы. Соот-

ношение

T(n) =

T(n-1)TδTϵn в терминах матричных

ют Приложению A этой работы. В результате полу-

элементов имеет вид

чается уравнение (3) с параметрами (мы полагаем

a₀ = 1)

T(n)11 = (1+iα-iϵ_n

T(n-1)11+(-iΔ+iϵ_n

T(n-1)12,

(94)

α=

D² , γ₁ α = ϵ² -

D² , γ₂ α =

(92)

T(n)12 = (iΔ-iϵ_n)T˜(n-1)11+(1-iα+iϵ_n)T(n-1)12,

где мы провели линеаризацию по α и Δ и положили

что после подстановки (90) дает

β = -π/2. Вводя для вторых моментов обозначения

(

)

α = 2ϵ²sin2 ψ , γ₁α = ϵ²

1 - 2sin2 ψ

)



(93)



z(n)1 =

T(n)11

z(n)2 =

T(n)11T(n)∗

γ₂ α = Δcos(ψ + β) - ϵ²cosψ ,

(95)

)



где в актуальном случае β = -π/2. Другие значе-

z(n)3 =

T(n)∗11T(n)12

z(n)4 =

T(n)12

ния β возникают при наличии на границах раздела

δ-образного потенциала.

получим систему разностных уравнений

⎛

⎞

⎛

⎞

⎛

⎞

(n)

z₁

1+ϵ²

iΔ - ϵ²

-iΔ - ϵ²

ϵ²

z(n-1)1

⎜

⎟

⎜

⎟

⎜

⎟

⎜

z(n)2

⎟

⎜

−iΔ + ϵ²

1 + 2iα - ϵ²

-ϵ²

-iΔ + ϵ²

⎟

⎜

z(n-1)2

⎟

⎜

⎟

⎜

⎟

⎜

^⎟ ,

(96)

⎜

⎟

⎜

⎟

⎜

n-1)

⎟

⎝ z³

⎠

⎝ iΔ + ϵ²

-ϵ²

1 - 2iα - ϵ²

iΔ + ϵ²

⎠

⎝ z³

⎠

(n-1)

z(n)

ϵ²

iΔ - ϵ²

-iΔ - ϵ²

1+ϵ²

z₄

решение которой ищется в экспоненциальной форме, z(n)i ∼ λⁿ, и λ есть собственное значение матрицы.

Полагая λ = 1 + x, получим уравнение

965

И. М. Суслов

ЖЭТФ, том 156, вып. 5 (11), 2019

[

(

)

]

x² + 4α² - 4Δ²

- 8ϵ²(Δ - α)²

=0,

(97)

В локализованном режиме (δ ≫ ϵ²) нетривиаль-

ные корни уравнения (97) имеют вид

имеющее решение x = 0 и три нетривиальных кор-

ня. Последние совпадают с корнями уравнения (44)

x₁ = 2δ + ϵ², x₂ = -2ϵ², x₃ = -2δ + ϵ²,

(103)

и не зависят от идеальных контактов, поскольку

так что

δ² = Δ² - α² и

Δ²²

8ϵ²(Δ-α)² = 8ϵ²δ² (Δ₂-Δ₁)² = 8ϵ²δ² = 2W².

(98)

〈ρ〉 = -

[exp(x₁n) + exp(x₃n)] -

Находя собственные векторы матрицы (96), полу-

Δ²¹

exp(x₂n).

(104)

чим общее решение системы

⎛

⎞

⎛

⎞

При больших n доминирует член с exp(x₁n) и под-

z(n)1

-1

тверждает перенормировку абсолютного масштаба

⎜

⎟

⎜

⎟

⎜

z(n)2

⎟

⎜

⎟

ρ на множитель Δ²², указанную в разд. 1. Измене-

⎜

⎟

=C₀

⎜

⎟₊

⎜

⎟

⎜

⎟

ние начала отсчета n (см. конец разд. 5) проявляется

⎝ z³

⎠

⎝

⎠

лишь при n ≲ 1/δ.

z(n)

⎛

⎞

В металлическом режиме нужно сделать замену

δ → iδ, ϵ → -iϵ и рассмотреть предел δ ≫ ϵ². Тогда

⎜

⎟

∑

⎜

⎟

2(xi)

⎜ e

C_i

^⎟ exp(x_in),

(99)

⎜

⎟

x₁ = 2ϵ², x₂ = -ϵ² + 2iδ, x₃ = -ϵ² - 2iδ

(105)

i=1

⎝ e3(xi)

⎠

где x₁, x₂, x₃ — нетривиальные корни уравнения (97)

Δ²²

〈ρ〉 = -

exp(2ϵ²n) -

∗

Δ²¹

Ax + B

A^∗x + B

exp(-ϵ²n) cos 2nδ,

(106)

e₂(x) =

e₃(x) =

p(x)

(100)

A = 2ϵ² - 2iΔ, B = 4αΔ + 4iϵ²(α - Δ),

что в ситуации рис. 2а (когда Δ₁ = 0) дает извест-

ный результат [1, 2, 15-17]

p(x) = x² + 2ϵ²x + 4α² .

[

]

Выбирая в качестве начального условия единичную

〈ρ〉 =

exp(2ϵ²n) - 1

(107)

трансфер-матрицу, имеем z⁽⁰⁾¹ = 1, z⁽⁰⁾²

= z(0)3 =

При конечных Δ₁ возникают осцилляции, период

= z⁽⁰⁾⁴ = 0, что позволяет установить значения ко-

которых определяется де-бройлевской длиной вол-

эффициентов C_i. Поскольку z(n)4 непосредственно

ны (так как 2nδ = 2kL). Их происхождение опреде-

определяет 〈ρ〉, имеем

ляется тем, что при ϵ = 0 ландауэровское сопротив-

ление ρ определяется трансфер-матрицей (85) по-

(x₂ - x₃) p(x₁)

〈ρ〉 = -

exp(x₁n) -

тенциального барьера,

(x₁ - x₃) p(x₂)

ρ = Δ21 sin² kL,

(108)

exp(x₂n) +

(x₁ - x₂) p(x₃)

и коэффициент отражения обращается в нуль, ес-

exp(x₃n),

(101)

ли на длине системы укладывается полуцелое число

длин волн де Бройля (аналогично просветлению в

где

оптике). При конечных ϵ осцилляции становятся за-

тухающими, но являются вполне наблюдаемыми: в

Q = x²¹(x₂ - x₃) - x²²(x₁ - x₃) + x²³(x₁ - x₂).

(102)

металлическом режиме среднее значение ρ является

Результат (101) имеет общий характер: при его вы-

репрезентативным, так как его флуктуации относи-

воде не сделано никаких приближений. При боль-

тельно малы.

ших n доминирует одна из экспонент и ситуация

В критической области (δ ≪ ϵ²) имеем

оказывается мультипликативной. При малых n экс-

(

)1/3

поненты могут быть разложены в ряд, что приводит

x₁ = 2

ϵ²δ²

x₂ = x₁ exp(2πi/3),

(109)

к омическому режиму ρ ∝ n.

x₃ = x₁ exp(-2πi/3).

966

ЖЭТФ, том 156, вып. 5 (11), 2019

Распределение кондактансов в одномерных системах. . .

Тогда

G, e /h²

[

(

x₁n⁾

〈ρ〉 =

exp(x₁n) + 2 exp

(_√

)

]

[

× cos

x₁n

-3

exp(x₁n) -

3x₁

(_√

)]

(

x₁n⁾

- 2exp

cos

x₁n +

[

(

-1

2α

x₁n⁾

exp(x₁n) - 2 exp

3x²¹

(_√

)]

B, Тл

× cos

x₁n -

(110)

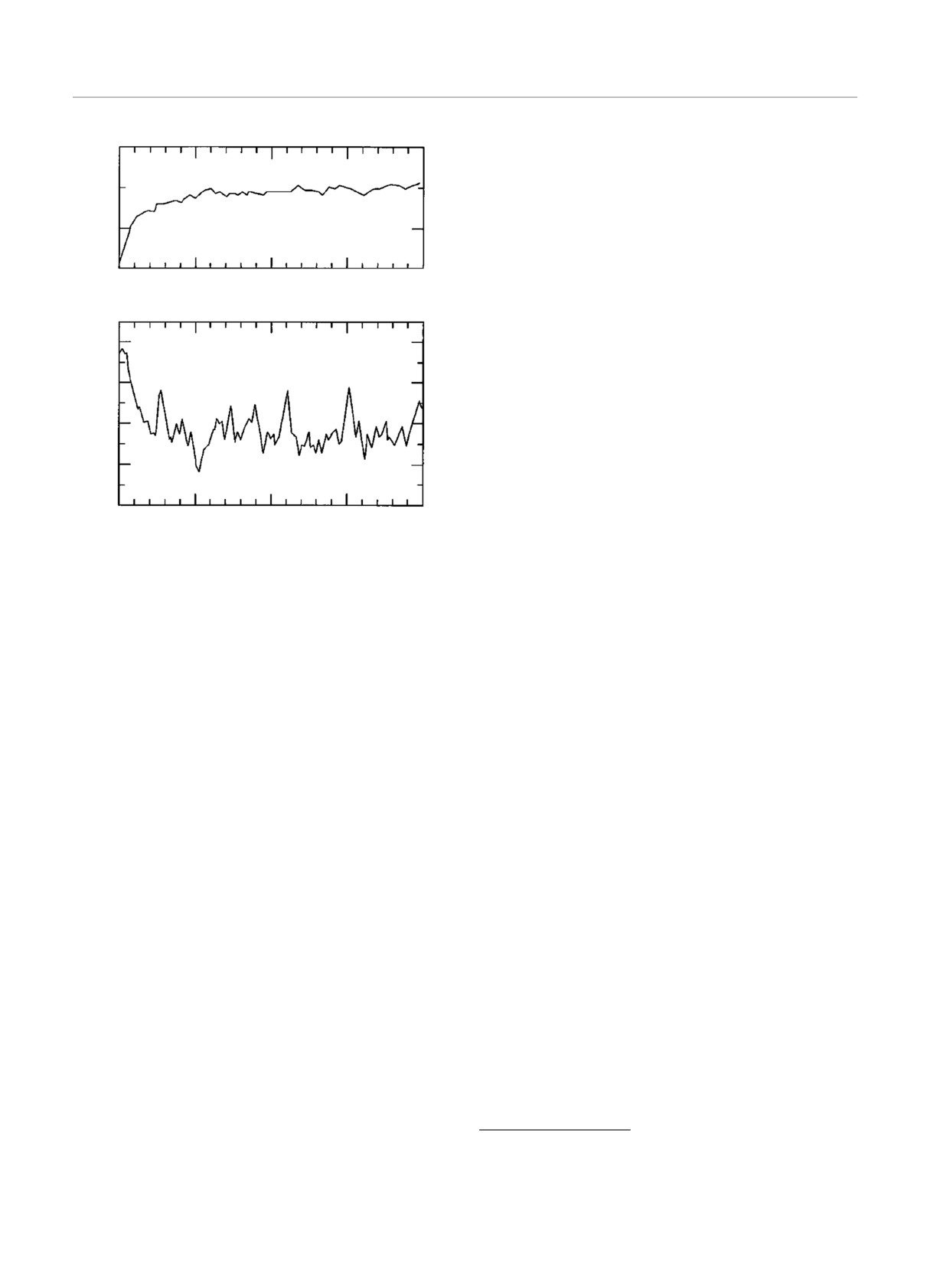
Рис. 9. Кондактанс G(B) тонкой проволочки из Au [34]

в магнитном поле B испытывает «универсальные» флук-

туации порядка e²/h при изменении конфигурации приме-

Если продвижение в критическую область происхо-

сей [25,26]. Флуктуации G(B) и G(B +ΔB) статистически

дит из разрешенной зоны, то возможно использова-

независимы, если ΔB превышает некоторый характерный

ние «естественных» идеальных контактов (рис. 2а),

масштаб [25,26]. Несмотря на случайный характер, карти-

для которых ϵ = ϵ; тогда в (109) доминирует второй

на флуктуаций полностью воспроизводима и характеризу-

член. Разложение по x₁n дает 〈ρ〉 = ϵ²n в согласии с

ет конкретную реализацию случайного потенциала («маг-

результатом из трансфер-матрицы (38), что опреде-

нитные отпечатки пальцев»)

ляет область применимости последней как n ≲ 1/x₁.

Результат (110) остается конечным при

k→ 0,

когда

Между тем высшие моменты ρ осциллируют с пе-

риодом того же порядка. Это связано с комплекс-

(

)2/3

ными корнями уравнения (48) и аналогичных урав-

ϵ²

2W²

2α²

2k²a

нений для высших моментов⁶⁾. Возникает сложная

3x₁

24k²a²⁰

3x²¹

3 (2W²)2/3

(111)

интерференция несоизмеримых осцилляций, приво-

(

)1/3

x₁ =

2W²

дящая к апериодическим осцилляциям для сопро-

тивления ρ в конкретном образце. Такие осцилляции

Аналогично (106), имеются затухающие осцилля-

наблюдаются в магнитосопротивлении тонких про-

ции, амплитуда которых существенно зависит от

волочек [34] (рис. 9) и имеют непосредственное от-

фермиевского импульса k в идеальных контактах:

ношение к изложенному выше: магнитное поле, пер-

она порядка единицы при ka₀ ∼ W2/3 (когда все

пендикулярное тонкой проволочке, создает вдоль

три члена в (110) одного порядка), но возрастает как

нее квадратичный потенциал, который эффектив-

при уменьшении k (когда доминирует второй член в

но ограничивает длину системы. Поэтому изменение

(110)), так и при его увеличении (когда доминирует

магнитного поля аналогично изменению L. В прин-

третий член). Период осцилляций определяется ам-

ципе, рис. 9 объясняется теоретическими результа-

плитудой случайного потенциала, а фазовый сдвиг

тами работ [25,26], но нам не известны попытки опи-

изменяется от π/3 до -π/3 при увеличении k от ма-

сания осцилляций как таковых.

лых до больших значений.

На рис. 10 приводятся экспериментальные ре-

Фактически наблюдаемая картина оказывается

зультаты работы [35], которые демонстрируют воз-

более сложной. В критической области флуктуации

ρ велики и форма функции распределения суще-

⁶⁾ Сопоставление (44) и (48) показывает, что периоды ос-

ственно зависит от нескольких первых моментов⁵⁾.

цилляций для 〈ρ〉 и 〈ρ²〉 различаются в 211/3 раз. Как ясно

из разд. 4 (см. примечание 3), в правой части уравнения для

⁵⁾ Напомним, что фурье-преобразование P (ρ) определя-

x допустимы лишь комбинации δ2nϵ2m с n ≥ m, из которых

ет характеристическую функцию F (t)

= e^iρt , кото-

конечными при δ → 0 остаются лишь δ2nϵ2n ∼ W2n. По-

рая является производящей функцией моментов, F (t)

скольку при x ∼ δ ∼ ϵ² все члены уравнения одного порядка,

∑_∞

(it)ⁿ 〈ρⁿ〉 /n!. Если известны все моменты распреде-

показатель роста x для 〈ρⁿ〉 при δ = 0 удовлетворяет уравне-

n=0

ления, то по ним можно построить F (t), после чего P (ρ) опре-

нию x2n+1 = c₁δ²ϵ²x2n-2 + c₂δ⁴ϵ⁴x2n-5 + . . . , нетривиальные

(

)1/3

деляется обратным фурье-преобразованием.

корни которого имеют порядок

δ²ϵ²

независимо от n.

967

И. М. Суслов

ЖЭТФ, том 156, вып. 5 (11), 2019

G/G₀

Используемое определение проводимости отно-

8.2

сится к составной системе «образец + идеальные

провода», тогда как вопрос о его отношении к изу-

чаемой системе остается открытым. В работе [11]

для его решения предлагается введение полупрони-

8.1

цаемых границ, отделяющих систему от идеальных

контактов. При переходе к пределу слабопрозрач-

0.05

0.10

0.15

0.20

ных границ возникают универсальные уравнения,

B, Тл

не зависящие от способа исключения контактного

10³

var(G/G )₀

сопротивления резервуара [10] (так как все форму-

лы ландауэровского типа [2,5,6,8,9] сводятся к вари-

0.8

анту Эконому - Соукоулиса [3,4]), которые затем мо-

гут быть экстраполированы к прозрачности поряд-

0.6

ка единицы. Такое определение заведомо относит-

ся к изучаемому образцу и обеспечивает бесконеч-

0.4

ное значение проводимости для идеальной системы.

При этом абсолютный масштаб кондактанса фик-

0.2

сируется лишь по порядку величины. Это не имеет

принципиального значения (физический смысл име-

0.05

0.10

0.15

0.20

ет лишь отношение кондактансов), но создает неко-

B, Тл

торые трудности при сопоставлении с другими ре-

зультатами. Как ясно из изложенного выше, абсо-

Рис. 10. Эволюция двух первых моментов кондактанса G

лютный масштаб кондактанса зависит от свойств

при изменении магнитного поля для тонкой проволочки из

идеальных контактов и в любом случае является

GaAs, легированного кремнием [35]

условной величиной. Для устранения его неопреде-

ленности нужно как-то оговаривать свойства кон-

тактов: например, можно принять «золотой стан-

можность наблюдения эволюции как полной функ-

дарт» и пересчитывать все результаты на контакты

ции распределения ρ или G, так и ее моментов. Неза-

из золота.

висимые примесные конфигурации в тонкой прово-

Согласно уравнению (2), распределение кондак-

лочке из GaAs, легированного кремнием, создава-

тансов одномерной системы определяется двумя

лись путем периодического отогрева ее до комнат-

параметрами,

αL и γ. Такое двухпараметриче-

ной температуры, после чего проводилось усредне-

ское описание естественным образом следует из

ние по 50 конфигурациям. Результаты для двух пер-

гипотезы однопараметрического скейлинга

[36],

вых моментов G указывают, что функция распреде-

согласно которой свойства d-мерной кубической

ления не является стационарной, а испытывает си-

системы размера L полностью определяются от-

стематические изменения, что согласуется с изло-

ношением L/ξ, где ξ — корреляционный радиус.

женным выше.

Составляя квазиодномерную систему размера

9. ЗАКЛЮЧЕНИЕ

Ld-1L_z из кубических блоков размера L, легко

Массивные идеальные контакты, которые прихо-

заключить, что ее кондактанс зависит от свойств

дится вводить для корректного определения прово-

одного блока (L/ξ) и числа кубиков (L_z/L). При

димости конечных систем, оказывают существенное

= a₀

квазиодномерная система становится

влияние на свойства изучаемого образца. В насто-

строго одномерной, но по-прежнему описывает-

ящей работе оно исследовано на примере одномер-

ся двумя параметрами. Однопараметрический

ных систем. В логнормальном режиме оно сводит-

скейлинг в одномерных системах реализуется в

ся к изменению абсолютного масштаба кондактанса,

глубине разрешенной зоны (когда справедливо

но в общем случае изменяет всю функцию распре-

уравнение (1)) и приближенно сохраняется в кри-

деления. При изменении длины системы могут воз-

тической области⁷⁾. Его нарушение в запрещен-

никать периодические или апериодические осцил-

ляции ρ. При сдвиге уровня Ферми происходят ка-

чественные изменения, напоминающие сглаженный

⁷⁾ В этом случае параметр γ порядка единицы и не имеет

переход Андерсона.

существенной эволюции.

968

ЖЭТФ, том 156, вып. 5 (11), 2019

Распределение кондактансов в одномерных системах. . .

ной зоне вполне естественно ввиду нарушения усло-

где z_n = τ(n-1)12, y_n = τ(n-1)11 с начальными услови-

вия ξ ≫ a₀. Необходимость двухпараметрического

ями z₁ = 0, y₁ = 1, либо z_n = τ(n-1)22, y_n = τ(n-1)21 с

описания одномерных систем обсуждалась в работе

начальными условиями z₁ = 1, y₁ = 0. Для вторых

[37] (см. также [21-24])) и в последнее время оно ак-

моментов нетрудно получить

тивно использовалось для описания распределения

⎛

⎞

кондактансов [12, 38] в рамках скейлинговой схемы

z2n+1

Шапиро [18].

⎜

⎟

⎜

⎟

⎝ z

n+1yn+1

⎠ =

Эволюция как полного распределения ρ, так и

его моментов может изучаться экспериментально в

y²

⎛

⎞

духе работы [35], в которой конфигурация примесей

n+1⎛

⎞

E² + W²

z2n

в изучаемом образце изменялась путем его отогрева

⎜

⎟

⎜

⎟

⎝

-E

-1

⎠

⎜

nyn

⎟

(A.2)

до достаточно высокой температуры.

⎝ z

⎠

Предполагая для моментов экспоненциальный рост

ПРИЛОЖЕНИЕ A

λn с λ = 1 + x, получим для x уравнение

Эволюция моментов для координатной

x³-x²(E²-4)-x(E²-4) = W²(2+3x+x²). (A.3)

трансфер-матрицы

Полагая E² - 4 = 4δ², W² = 4ϵ²δ², нетрудно убе-

Для координатной трансфер-матрицы справед-

диться, что в пределе δ → 0, ϵ → 0, δ/ϵ² = const

ливы уравнения эволюции

уравнение (A.3) совпадает с (44).

Аналогично для четвертых моментов имеем

zn+1 = (E - V_n)z_n + y_n , yn+1 = -z_n , (A.1) уравнение

⎛

⎞

⎛

⎞

⎛

⎞

z4n+1

z4n

E⁴ + 6E²W²

4E³ + 12EW²

6E² + 6W²

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

z3n+1yn+1

z3ny_n

⎜

⎟

⎜

−E³ - 3EW²

-3E² - 3W²

-3E

-1

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

z2n+1y2n+1

E² + W²

z2ny2n

(A.4)

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎝

-E

-1

⎠

⎜

⎟

⎝ z

n+1yn+1

⎠

⎝ z

nyⁿ

⎠

y4n+1

y⁴

Предполагая, что моменты растут как λⁿ с

ПРИЛОЖЕНИЕ B

λ = 1 + x, получим для x уравнение

Об асимптотиках интеграла (70)

Учитывая четность подынтегрального выраже-

- x⁵ + x⁴(E² + 1)(E² - 4) + x³(E² - 4)×

ния в (70) в переменных

ϕ = ϕ - π/2,

θ = θ - π/2 и

(

)

полагая x = sin ϕ, y = sin θ, имеем

-E⁴+5E²+1

-x²2E²(E²-4)²-xE²(E²-4)² +

[

∫

+W²

-6E²(E² - 4) - 15xE²(E² - 4) +

P (ρ) =

√

π² t

1-x²

1-y²

+ x²(-12E⁴+60E²-6)+x³(-3E⁴+30E²-9)+

-1

-1 {

}

S(x, y)

(A.6)

]

× exp

+ x⁴(6E² - 3)

= 0, (A.5)

(

√

S(x, y) = Δ₁

1+ρx+Δ₂

√ρy)2

+ρ(1-y²).

где опущены члены более высокого порядка по W².

Полагая E² - 4 = 4δ², W² = 4ϵ²δ² и сохраняя глав-

Конфигурация перевальных точек существенно раз-

ные члены при указанном предельном переходе, по-

лична для ρ < ρ_c и ρ > ρ_c, где ρ_c = Δ²¹. В пер-

лучим уравнение (48).

вом случае максимум экспоненты достигается при

969

ЖЭТФ, вып. 5 (11)

И. М. Суслов

ЖЭТФ, том 156, вып. 5 (11), 2019

x = x_c, y = -1 или x = -x_c, y = 1, где x_c =

определяющий предпоследнюю асимптотику в (76),

=Δ₂

√ρ/Δ₁√1 + ρ, а во втором — при x = 1, y = -1

(77). Условие A² ≪ Ct дает (ρ - ρ_c)² ≪ Δ²¹ρt, что

или x = -1, y = 1. Пусть δx и δy — отклонения x

при t ≫ 1 сводится к указанному в (A.12). Если ре-

и y от точки экстремума. При ρ < ρ_c сохраним в

зультат (A.11) справедлив в малой окрестности ρ_c,

S(x, y) квадратичный член по δx и линейный по δy,

то для применимости (A.12) возникает широкая об-

полагая в предэкспоненте x = x_c, 1-y² = 2δy. Тогда

ласть.

√

При малых ρ условия применимости перевально-

P (ρ) =

(A.7)

го приближения нарушаются и удобно пользоваться

π ρ(ρ_c - ρ)

исходной формой интеграла (70). Если t ≪ Δ²¹, то

перевальное интегрирование по ϕ все еще возможно

что есть предельная форма распределения при

и приводит к результату

t → 0.

При ρ > ρ_c имеем

√

∫

πt

P (ρ) =

dθ

S(x, y) = S_c + Aδx + Bδy +

π² t

Δ²¹ - ρ + Δ²²ρ sin² θ

-π/2

+ C (δx - x_cδy)² - ρ(δy)2 , (A.8)

{

}

× exp

sin² θ

(A.13)

где S_c, A, B определены в (73) и C = Δ²¹(1 + ρ). При

больших ρ достаточно сохранить в (A.8) линейные

по δx, δy члены и линеаризовать выражения под ра-

При Δ²¹ ≪ 1 имеем Δ₂ ≈ 1; если ρ ≪ t, то в знаме-

дикалами:

нателе дроби можно сохранить только Δ²¹, а интег-

√

(

)

рирование по θ проводится путем разложения экс-

S_c

поненты,

P (ρ) =

exp

(A.9)

π AB

√

(

ρ)

P (ρ) =

exp

ρ≪t,

(A.14)

что есть последняя асимптотика в (72), (74)-(77).

π Δ²¹t

Результаты (A.7), (A.9) неприменимы для ρ,

близких к ρ_c, поскольку коэффициент A обращается

что есть первый результат в (72), (75), (76). При

в нуль при ρ = ρ_c. Полагая δx = δx - x_cδy и опуская

ρ ≳ t справедливы перевальные результаты (A.7),

последний член в (A.8), имеем

(A.9), (A.10).

В случае Δ²¹ ≪ 1 и t ≫ Δ²¹ область малых ρ опре-

S(x, y) = S_c + Aδx + C (δx)² + 2ρδy .

(A.10)

, и вычисление

деляется условием ρ(1 + ρ) ≪ t²/Δ²¹

При A² ≪ Ct флуктуации δx определяются квад-

интеграла в ней осуществляется путем разложения

ратичным членом и Aδx можно опустить. Тогда в

по S(ϕ, θ)/t до второго порядка, что дает первый

малой окрестности ρ_c

результат в (74), (77). При обратном соотношении

√

имеем A ≈ B ≈ 2Δ₁Δ₂

ρ(1 + ρ) ≫ t и A² ≫ Ct,

Γ(1/4)

P (ρ) =

что обеспечивает справедливость (A.9).

2π

2πρ (Ct)1/4

(A.11)

В случае Δ²¹ ≫ 1 и t ≪ Δ²¹ по-прежнему справед-

|ρ - ρ_c| ≲ (Ct)1/2 ,

ливо выражение (A.13), но его исследование услож-

что устраняет расходимость при ρ → ρ_c и соот-

няется. При t ≪ 1 возникает знакомая ситуация: для

ветствует третьей асимптотике в (72) и (75). При

ρ ≲ t можно сохранить в знаменателе Δ²¹ и получить

указанном условии этот результат сохраняется и

(A.14), тогда как при ρ ≳ t справедливы переваль-

при ρ < ρ_c, когда коэффициент A отрицателен, но

ные результаты (A.7), (A.9), (A.10). Если же 1 ≪

мал по абсолютной величине. Фактически результат

≪ t ≪ Δ²¹, то результат (A.14) справедлив лишь при

(A.11) справедлив в случаях t ≪ Δ²¹ ≪ 1 и t ≪ 1 ≪

ρ ≲ 1. В интервале 1 ≲ ρ ≲ t в знаменателе (A.13)

≪ Δ²¹, когда флуктуация δy ∼ t/ρ мала по сравне-

доминирует Δ²²ρ sin² θ, а учет величины Δ²¹ - ρ тре-

√

нию с δx ∼

t/C, так что δx ≈ δx и в предэкспонен-

буется лишь для обрезания логарифмической расхо-

те можно положить 1-x² = 2δx, 1-y² = 2δy. Обрат-

димости; при этом

ная ситуация имеет место в случае Δ²¹ ≫ 1, t ≫ 1,

√

Δ²¹ρ

когда δy ≫ δx и в предэкспоненте 1 - x² ≈ 2δx =

P (ρ) =

1 ≲ ρ ≲ t. (A.15)

π²

ρΔ²¹t

ρ_c - ρ

= 2δx + 2x_cδy ≈ 2δy, что дает результат

√

(

)

Δ²¹t

S_c

В интервале t ≲ ρ ≲ ρ_c экспонента ограничивает ин-

P (ρ) =

exp

2π²

ρΔ²¹t

(A.12)

тегрирование значениями θ² ≲ t/ρ и Δ²¹ρ в (A.15)

ρ_c/t ≲ ρ ≲ ρ_ct ,

970

ЖЭТФ, том 156, вып. 5 (11), 2019

Распределение кондактансов в одномерных системах. . .

заменяется на Δ²¹t. Фактически оба результата ак-

16.

B. Shapiro, Phys. Rev. B 34, 4394 (1986).

туальны лишь при ρ ≪ ρ_c, так как при ρ ≳ ρ_c/t рас-

17.

P. Mello, Phys. Rev. B 35, 1082 (1987).

ходимость при ρ → ρ_c устраняется за счет нелиней-

ных членов в (A.8) и справедлив результат (A.12);

18.

B. Shapiro, Phil. Mag. 56, 1031 (1987).

поэтому возникает ln ρ для 1 ≲ ρ ≲ t и ln t для t ≲

19.

И. М. Лифшиц, С. А. Гредескул, Л. А. Пас-

≲ ρ ≲ ρ_c/t, как это и отражено в (76).

тур, Введение в теорию неупорядоченных систем,

В случае Δ21 ≫ 1 и t ≫ Δ21 разложение по

Наука, Москва (1982).

S(ϕ, θ)/t возможно при ρ ≲ t/Δ²¹, и оно приводит к

20.

X. Chang, X. Ma, M. Yepez, A. Z. Genack, and

первому результату (77). При ρ ≳ t/Δ²¹ справедливо

P. A. Mello, Phys. Rev. B 96, 180203 (2017).

выражение (A.13), где |Δ²¹ - ρ| ≪ t, Δ²²ρ ≫ t, и пото-

му в знаменателе сохраняется лишь последний член;

21.

L. I. Deych, D. Zaslavsky, and A. A. Lisyansky, Phys.

логарифмическая расходимость устраняется ввиду

Rev. Lett. 81, 5390 (1998).

ограничения (Δ²²ρ/t)sin² θ ≳ 1, которое необходимо

22.

L. I. Deych, A. A. Lisyansky, and B. L Altshuler,

для перевального интегрирования по ϕ и справед-

Phys. Rev. Lett. 84, 2678 (2000); Phys. Rev. B 64,

ливости (A.13). Если при этом ρ ≲ t, то экспонента

224202 (2001).

в (A.13) несущественна и получается второй резуль-

тат в (77). При ρ ≳ t ситуация перевальная и спра-

23.

L. I. Deych, M. V. Erementchouk, and A. A. Lisyan-

ведливы результаты (A.12) и (A.9).

sky, Phys. Rev. Lett. 90, 126601 (2001).

24.

Л. Д. Ландау, Е. М. Лифшиц, Квантовая механи-

ка, Наука, Москва (1974).

ЛИТЕРАТУРА

25.

Б. Л. Альтшулер, Письма в ЖЭТФ 41, 530 (1985);

P. W. Anderson, D. J. Thouless, E. Abrahams, and

Б. Л. Альтшулер, Д. Е. Хмельницкий, Письма в

D. S. Fisher, Phys. Rev. B 22, 3519 (1980).

ЖЭТФ 42, 291 (1985).

R. Landauer, IBM J. Res. Dev. 1, 223 (1957); Phil.

26.

P. A. Lee and A. D. Stone, Phys. Rev. Lett. 55, 1622

Mag. 21, 863 (1970); Z. Phys. 68, 217 (1987).

(1985); P. A. Lee, A. D. Stone, and Y. Fukuyama,

Phys. Rev. B 35, 1039 (1987).

E. N. Economou and C. M. Soukoulis, Phys. Rev.

Lett. 46, 618 (1981).

27.

D. Braun, E. Hofsteller, G. Montambaux, and

A. MacKinnon, Phys. Rev. B 64, 155107 (2001).

D. S. Fisher and P. A. Lee, Phys. Rev. B 23, 6851

(1981).

28.

I. Travenec, Phys. Rev. B 69, 033094 (2004).

D. C. Langreth and E. Abrahams, Phys. Rev. B 24,

29.

M. Ruhlender, P. Markos, and C. M. Soukoulis, Phys.

2978 (1981).

Rev. B 64, 172202 (2001).

P. W. Anderson, Phys. Rev. B 23, 4828 (1981);

30.

А. О. Гельфонд, Исчисление конечных разностей,

H. L. Engquist and P. W. Anderson, Phys. Rev. B 24,

Наука, Москва (1967).

1151 (1981).

31.

M. Kappus and F. Wegner, Z. Phys. B 45, 15 (1981).

D. J. Thouless, Phys. Rev. Lett. 47, 972 (1981).

32.

V. E. Kravtsov and V. I. Yudson, Ann. Phys. (NY)

M. Buttiker, Phys. Rev. Lett.

57,

1761

(1986);

326, 1672 (2011).

M. Buttiker, Y. Imry, R. Landauer, and S. Pinhas,

Phys. Rev. B 31, 6207 (1985).

33.

И. М. Суслов, ЖЭТФ 154, 152 (2018).

M. Ya. Azbel, J. Phys. C 14, L225 (1981).

34.

S. Washburn and R. A. Webb, Adv. Phys. 35, 375

(1986).

10.

A. D. Stone and A. Szafer, IBM J. Res. Dev. 32, 384

(1988).

35.

D. Mailly and M. Sanquer, J. de Phys. I 2, 357 (1992).

11.

И. М. Суслов, ЖЭТФ 142, 1020 (2012).

36.

E. Abrahams, P. W. Anderson, D. C. Licciardello,

and T. V. Ramakrishman, Phys. Rev. Lett. 42, 673

12.

И. М. Суслов, ЖЭТФ 151, 897 (2017).

(1979).

13.

В. И. Мельников, ФТТ 23, 782 (1981).

37.

A. Cohen, Y. Roth, and B. Shapiro, Phys. Rev. B 38,

14.

A. A. Abrikosov, Sol. St. Comm. 37, 997 (1981).

12125 (1988).

15.

N. Kumar, Phys. Rev. B 31, 5513 (1985).

38.

I. M. Suslov, Phil. Mag. 99, 247 (2019).

971