ЖЭТФ, 2019, том 156, вып. 5 (11), стр. 980-988

ФАЗОВЫЕ ПЕРЕХОДЫ И КРИТИЧЕСКИЕ СВОЙСТВА

АНТИФЕРРОМАГНИТНОЙ МОДЕЛИ ГЕЙЗЕНБЕРГА НА

ОБЪЕМНО-ЦЕНТРИРОВАННОЙ КУБИЧЕСКОЙ РЕШЕТКЕ С

ВЗАИМОДЕЙСТВИЯМИ ВТОРЫХ БЛИЖАЙШИХ СОСЕДЕЙ

А. К. Муртазаев, Д. Р. Курбанова^*, М. К. Рамазанов

Институт физики Дагестанского научного центра Российской академии наук

367015, Махачкала, Россия

Поступила в редакцию 26 апреля 2019 г.,

после переработки 28 мая 2019 г.

Принята к публикации 28 мая 2019 г.

На основе репличного алгоритма метода Монте-Карло выполнены исследования фазовых переходов и

критических свойств антиферромагнитной модели Гейзенберга на объемно-центрированной кубической

решетке с учетом взаимодействий первых и вторых ближайших соседей. Исследования проведены для

соотношений величины обменных взаимодействий первых и вторых ближайших соседей в интервале зна-

чений 0.0 ≤ r ≤ 1.0. Построена фазовая диаграмма зависимости критической температуры от величины

взаимодействия вторых ближайших соседей. На диаграмме обнаружена область, где переход из антифер-

ромагнитной фазы в парамагнитную является переходом первого рода. Рассчитан весь набор основных

статических критических индексов. Показано, что класс универсальности критического поведения со-

храняется в интервале значений 0.0 ≤ r ≤ 0.6. Установлено, что изменение величины взаимодействия

вторых ближайших соседей в диапазоне 0.8 ≤ r ≤ 1.0 приводит к неуниверсальному критическому

поведению.

DOI: 10.1134/S0044451019110142

использована для описания магнитных структур ре-

альных материалов. Например, при малых значени-

ях взаимодействий вторых ближайших соседей J₂

1. ВВЕДЕНИЕ

данная модель хорошо описывает свойства моносло-

ев оксида меди в высокотемпературных оксидных

Магнитные системы с конкурирующими анти-

сверхпроводниках на основе Cu [6, 7], а при боль-

ферромагнитными обменными взаимодействиями

ших значениях J₂ — антиферромагнитных матери-

первых и вторых ближайших соседей находятся

алов Li₂VOSi₂O₄ и Li₂VOGeO₄ [8, 9]. Наиболее хо-

в центре интенсивных исследований физики кон-

рошо двумерная модель Гейзенберга описывает мо-

денсированных сред уже более двух десятилетий

нослои Fe-As в сверхпроводниках LaOFeAs [10,11] и

[1-3]. Наличие конкурирующих обменных взаимо-

BaFe₂As₂ [12] на основе Fe.

действий в магнитных материалах может привести

к большому разнообразию магнитных упорядочен-

В отличие от двумерного случая, трехмерная ан-

ных состояний и фазовых переходов (ФП) между

тиферромагнитная модель Гейзенберга на объемно-

ними. Кроме того, особенности ФП при разных

центрированной кубической (ОЦК) решетке с кон-

значениях соотношения обменных взаимодействий

курирующими взаимодействиями [13-21] до сих пор

между первыми и вторыми ближайшими соседями

мало изучена. Имеются немногочисленные работы

известны лишь в общих чертах [4, 5].

по изучению фазовой диаграммы и термодинамиче-

В настоящее время двумерная модель Гейзенбер-

ских свойств квантовой антиферромагнитной моде-

га изучена достаточно хорошо и известны практиче-

ли Гейзенберга на ОЦК-решетке [13-16, 20, 21]. Для

ски все ее свойства [6-12]. Эта модель может быть

этой модели были получены интересные результа-

ты. Однако, насколько нам известно, исследование

^* E-mail: d_kurbanova1990@mail.ru

классической модели Гейзенберга на ОЦК-решетке с

980

ЖЭТФ, том 156, вып. 5 (11), 2019

Фазовые переходы и критические свойства...

конкурирующими взаимодействиями первых и вто-

рых ближайших соседей до сих пор никем не прово-

дилось.

AF2

Интерес к этой модели обусловлен еще и тем,

что учет взаимодействий вторых ближайших сосе-

дей может приводить к возникновению фрустраций,

J₂

что усложняет решение [17-21]. Известно, что мно-

гие физические свойства фрустрированных систем

J₁

AF1

сильно отличаются от соответствующих нефрустри-

рованных систем.

В связи с этим, в настоящей работе нами на осно-

ве метода Монте-Карло (MК) проводятся исследо-

вания ФП и критических свойств классической ан-

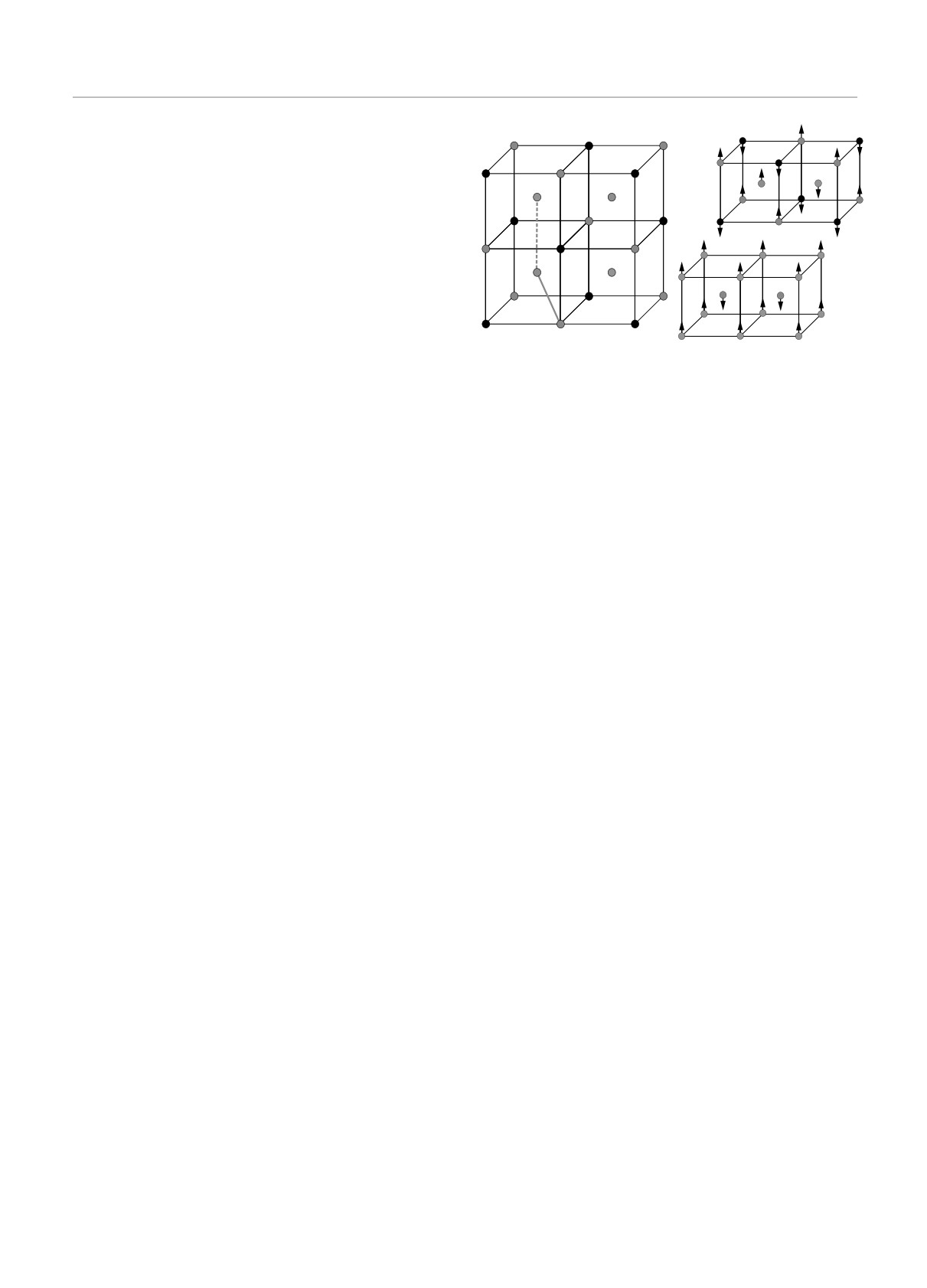
Рис. 1. a) ОЦК-решетка. Цифрами обозначены четыре

тиферромагнитной модели Гейзенберга на ОЦК-ре-

подрешетки; б) AF1 и AF2 — упорядоченные фазы

шетке для различных соотношений величины об-

менных взаимодействий первых и вторых ближай-

ших соседей.

личным упорядочением спинов [22]. Переход меж-

Из данных, полученных на сегодняшний день,

ду фазой Нееля (AF1) и коллинеарной фазой (AF2)

нельзя однозначно определить характер ФП и зако-

определяется соотношением взаимодействий J₂/J₁.

номерности изменения критического поведения дан-

Для ОЦК-решетки антиферромагнитную фазу AF1

ной модели, и эти вопросы до сих пор остаются от-

можно описать с помощью стандартной двухпод-

крытыми. Исследование антиферромагнитной моде-

решеточной системы, как в случае двумерных мо-

ли Гейзенберга на ОЦК-решетке с конкурирующи-

делей, характеризующейся волновыми векторами

ми взаимодействиями первых и вторых ближайших

(±π, 0, 0), (0, ±π, 0), (0, 0, ±π), в то время как для

соседей на основе современных методов и идей поз-

правильного описания антиферромагнитной фазы

волит получить ответ на ряд вопросов, связанных

AF2 с волновым вектором (±π/2, ±π/2, ±π/2) необ-

с ФП, термодинамическими и критическими свой-

ходимо ввести четыре подрешетки. Схематически

ствами фрустрированных спиновых систем.

эта модель представлена на рис. 1а.

Фаза AF1 соответствует состоянию, в котором

каждый спин имеет восемь ближайших соседей с

2. МОДЕЛЬ И МЕТОД ИССЛЕДОВАНИЯ

антипараллельным упорядочением, и его шесть вто-

рых ближайших соседей упорядочены параллельно

Антиферромагнитная модель Гейзенберга на

(рис. 1б). Фаза AF2 может быть описана как две

ОЦК-решетке с учетом взаимодействий первых и

взаимопроникающие простые кубические решетки,

вторых ближайших соседей описывается следую-

каждая из которых имеет антиферромагнитное упо-

щим гамильтонианом [13]:

рядочение (рис. 1б) [14-16, 23].

∑

В настоящее время ФП фрустрированных спино-

H = -J₁

(S_i · S_j ) - J₂

(S_i · S_l),

(1)

вых систем на основе микроскопических гамильто-

〈i,j〉

〈i,l〉

нианов довольно успешно изучаются методами МК

где |Si| — трехкомпонентный единичный вектор

[24-27]. Методы МК позволяют исследовать физиче-

S_i = (S^xi, S^yi, S^zi). Первый член в формуле (1) учиты-

ские свойства спиновых систем практически любой

вает обменное взаимодействие первых ближайших

сложности. На их основе на сегодняшний день изу-

соседей (J₁ < 0), а второй — вторых ближайших

чены целые классы спиновых систем и рассчитаны

соседей (J₂ < 0). Известно, что для данной моде-

критические индексы широкого спектра моделей. В

ли при J₂ = 0 основное состояние имеет обычное

данном исследовании мы использовали репличный

антиферромагнитное упорядочение. Ненулевое об-

обменный алгоритм метода МК [28], который явля-

менное взаимодействие J₂ может нарушить данный

ется наиболее мощным и эффективным для иссле-

порядок и привести к возникновению фрустраций.

дования фрустрированных спиновых систем. Более

Достаточно большое значение J₂ приводит к появ-

подробно этот алгоритм описан нами в работе [29].

лению страйп-структур.

Расчеты проводились для систем с периодичес-

Данные, полученные на основе теории среднего

кими граничными условиями и линейными размера-

поля, указывают на существование двух фаз с раз-

ми 2 × L × L × L = N, L = 24 ÷ 90, где L измеряется

981

А. К. Муртазаев, Д. Р. Курбанова, М. К. Рамазанов

ЖЭТФ, том 156, вып. 5 (11), 2019

C/k_B

250

3.0

L = 48

200

r = 0.1

2.5

r = 0.1

0.2

0.3

150

2.0

0.3

0.4

0.5

1.5

0.5

100

0.6

1.0

0.5

1.0

1.5

2.0

2.5

0.4

0.8

1.2

1.6

2.0

2.4

k_BT/|J |₁

Рис. 2. Зависимость теплоемкости C/kB от температуры

Рис. 3. Зависимость восприимчивости χ от температуры

kB T /|J1| для разных r при L = 48

температуры для всех значений r вблизи критичес-

в размерах элементарной ячейки. Соотношение ве-

кой температуры наблюдаются хорошо выраженные

личины обменных взаимодействий первых и вторых

максимумы, которые с ростом r смещаются в сто-

ближайших соседей r = |J₂/J₁| меняется в интерва-

рону более низких температур, причем увеличение

ле 0.0 ≤ r ≤ 1.0. Для вывода системы в состояние

значения r приводит к росту абсолютных значений

термодинамического равновесия отсекался неравно-

максимумов восприимчивости, что обусловлено уси-

весный участок длиной τ₀ = 4 · 10⁵ МК-шагов на

лением флуктуаций, вследствие увеличения конку-

спин, что в несколько раз больше длины неравновес-

ренции первых и вторых ближайших соседей.

ного участка. Усреднение термодинамических пара-

Для определения критической температуры T_N

метров проводилось вдоль марковской цепи длиной

был использован метод кумулянтов Биндера U_L чет-

до τ = 500τ₀ МК-шагов на спин.

вертого порядка [32]:

〈U⁴〉_L

3. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

VL = 1 -

(4)

3〈U²〉

Для наблюдения за температурным ходом теп-

лоемкости и восприимчивости использовались вы-

〈M⁴〉_L

U_L = 1 -

(5)

ражения [30, 31]

3〈M²〉²

(

)

где V_L — кумулянт по энергии, U_L — кумулянт по

C = (NK²)

〈U²〉 - 〈U〉²

(2)

намагниченности.

{

(

)

Выражения (4) и (5) позволяют определить кри-

(NK)

〈M²〉 - 〈|M|〉²

T <T_N,

χ=

(3)

тическую температуру T_N с большой точностью.

(NK)〈M²〉,

T ≥T_N,

Следует отметить, что применение кумулянтов Бин-

где K = |J₁|/k_BT , N — число частиц, T_N — критиче-

дера дает возможность также хорошо тестировать

ская температура (здесь и далее температура дана

тип ФП в системе. Известно, что в случае ФП вто-

в единицах |J₁|/k_B), U — внутренняя энергия, M —

рого рода кривые температурной зависимости куму-

подрешеточная намагниченность.

лянтов Биндера U_L имеют четко выраженную точку

На рис. 2 и 3 представлены температурные зави-

пересечения [32].

симости теплоемкости и восприимчивости, получен-

На рис. 4 представлена характерная зависимость

ные при L = 48 для различных значений r (здесь

U_L от температуры для r = 0.6 при разных значени-

и далее статистическая погрешность не превыша-

ях L. Этот рисунок демонстрирует точность опреде-

ет размеров символов, использованных для постро-

ления критической температуры. На рисунке видно,

ения зависимостей). На рисунках видно, что в за-

что в критической области наблюдается четко вы-

висимости теплоемкости C и восприимчивости χ от

раженная точка пересечения (T_N = 0.871(1)), что

982

ЖЭТФ, том 156, вып. 5 (11), 2019

Фазовые переходы и критические свойства...

U_L

1.4

0.66

T = 0.669

r = 0.6

0.670

L = 90

1.2

r = 2/3

L = 60

0.671

0.64

L = 48

1.0

L = 36

0.62

= 24

0.8

0.60

0.6

0.4

0.58

T_N = 0.871(1)

0.2

0.56

0.85

0.86

0.87

0.88

0.89

-1.083

-1.080

-1.077

-1.074

-1.071

-1.068

-1.065

k_BT/|J |₁

E/N

Рис. 4. Зависимость кумулянта Биндера UL от температу-

Рис. 5. Гистограмма распределения энергии для r = 2/3

ры kBT/|J1| для r = 0.6

при L = 90

свидетельствует о ФП второго рода. Аналогичным

образом были определены критические температу-

1.0

r = 0.7

L = 80

ры и для остальных значений r.

0.8

Для более подробного анализа характера ФП

T = 0.7638

0.7641

был также использован гистограммный анализ дан-

0.6

0.7643

ных метода МК [33, 34]. Этот метод позволяет на-

0.7650

дежно определить род ФП. Определение рода ФП

0.4

этим методом подробно описано нами в работах

[26, 27].

0.2

Для исследуемой модели при r = 1.0 в работе

[35] было показано, что для систем с малыми линей-

ными размерами (L < 48) наблюдается ФП перво-

го рода. Согласно данным работы [36], для модели

-1.05

-1.04

-1.03

-1.02

-1.01

-1.00

-0.99

-0.98

E/N

Изинга на ОЦК-решетке при значении r = 0.7 для

систем с малыми линейными размерами (L ≤ 60)

Рис. 6. Гистограмма распределения энергии для r = 0.7

наблюдается ФП первого рода. Однако для систем с

при L = 80

большими линейными размерами (L > 60) наблюда-

ется ФП второго рода. Таким образом, при анализе

ФП на основе гистограммного метода целесообраз-

На рис. 6 представлены гистограммы распреде-

но рассматривать системы с большими линейными

ления энергии для системы с линейными размерами

размерами (L > 60). В данной работе мы для по-

L = 80 для случая r = 0.7. Как видно на рисунке,

лучения достоверных результатов при построении

вблизи температуры ФП (T_N = 0.7643) в системе

гистограммы распределения энергии рассматрива-

наблюдается бимодальное распределение энергии.

ли системы с L ≥ 80.

Наличие двойного максимума в зависимости веро-

На рис. 5 представлены гистограммы распреде-

ятности W от энергии E/N является характерным

ления энергии для случая r = 2/3 с линейными раз-

признаком ФП первого рода.

мерами L = 90. Графики построены при критиче-

Это подтверждается данными, показанными на

ской температуре (T_N = 0.670(1)) и вблизи нее. На

рис. 7, где приведена временная динамика измене-

рисунке видно, что в зависимости вероятности W от

ния внутренней энергии в ходе компьютерного мо-

энергии E/N для всех значений температур наблю-

делирования для системы с линейными размерами

дается один хорошо выраженный максимум, кото-

L = 80 для случая r = 0.7. По горизонтальной оси

рый свидетельствует в пользу ФП второго рода.

отложено количество МК-шагов на спин (NMCS).

983

А. К. Муртазаев, Д. Р. Курбанова, М. К. Рамазанов

ЖЭТФ, том 156, вып. 5 (11), 2019

E/N

-0.96

T = 0.7700

r = 0.7

L = 80

-0.97

0.7643

0.7630

-0.98

-0.9861

-0.99

-0.9969

-1.00

-1.01

-1.0151

-1.02

-1.0271

-1.03

50000

100000

150000

200000

t, NMCS

Рис. 7. Временная динамика изменения внутренней энергии при различных температурах для r = 0.7 при L = 80

T_N

Результаты приведены для трех температур: в точ-

ке ФП (T_N = 0.7643), а также выше и ниже крити-

2.1

ческой температуры (T = 0.7700 и T = 0.7630). Как

1.8

видно на рисунке, в точке ФП имеются два мета-

стабильных энергетических уровня E₁ = -1.0151 и

1.5

E₂ = -0.9969. Система совершает случайные флук-

туации около этих двух энергетических состояний.

1.2

Энергия E₁ соответствует первому максимуму на

0.9

гистограмме распределения энергии, а E₂ — второ-

AF1

AF2

му максимуму (рис. 6). Такое поведение временной

0.6

динамики изменения внутренней энергии подтвер-

0.3

ждает наличие ФП первого рода. Аналогичное по-

ведение наблюдается в интервале 2/3 < r ≤ 0.75.

0.2

0.4

0.6

0.8

1.0

r = J /J₂₁

На рис. 8 приведена фазовая диаграмма зави-

симости критической температуры T_N от величины

Рис. 8. Фазовая диаграмма зависимости критической тем-

r взаимодействия вторых ближайших соседей. На

пературы от величины взаимодействия вторых ближайших

соседей

рисунке видно, что по мере приближения к точке

r = 2/3, где сосуществуют три фазы, температура

ФП уменьшается. Для рассмотренной модели при

r = 2/3 система имеет минимальную температуру

него поля [22], для модели Гейзенберга на ОЦК-

ФП k_B T/J₁ = 0.670(1). На диаграмме видно, что

решетке с взаимодействиями первых и вторых бли-

жайших соседей значение r = 2/3 является класси-

в точке r = 2/3 пересекаются три различные фа-

зы: антиферромагнитная — AF1, парамагнитная —

ческой точкой перехода, где происходит ФП из фазы

PM и антиферромагнитная — AF2 [15-18]. Переход

AF1 в фазу AF2.

из фазы AF1 к фазе AF2 в данной модели обуслов-

Наши результаты, полученные в рамках данного

лен изменением структуры основного состояния. Со-

исследования, показывают, что в интервалах 0.0 ≤

гласно данным, полученным на основе теории сред-

≤ r ≤ 0.6 и 0.8 ≤ r ≤ 1.0 наблюдается ФП второго

984

ЖЭТФ, том 156, вып. 5 (11), 2019

Фазовые переходы и критические свойства...

рода. Установлено, что в интервале 2/3 < r ≤ 0.75

V_n

(на рис. 8 выделено красным цветом) переход из ан-

тиферромагнитной фазы в парамагнитную реализу-

128

r = 0.2

n = 1

ется как ФП первого рода. Более подробное исследо-

n = 2

вание показало, что для случая r = 2/3 наблюдается

n = 3

ФП второго рода. Диаграмма, полученная для этой

модели, качественно совпадает с диаграммой трех-

мерной модели Изинга на ОЦК-решетке [37-39].

Для расчета статических критических индек-

сов теплоемкости α, восприимчивости γ, парамет-

ра порядка β, радиуса корреляции ν и индекса Фи-

шера η применялись соотношения теории конечно-

размерного скейлинга (КРС) [40].

Из теории КРС следует, что в системе с разме-

рами L × L × L при T = T_N и достаточно больших

Рис. 9. Зависимость параметра Vn от линейных размеров

L выполняются следующие выражения [40-42]:

системы L при T = TN для r = 0.2

M ∝L^-β/ν,

(6)

χ∝L^γ/ν,

(7)

V_n ∝ L1/νgVn,

(8)

r = 0.2

0.250

где gVn — некоторая постоянная, а в качестве V_n мо-

гут выступать

〈MⁿU〉

Vn =

- 〈U〉, n = 1, 2, 3.

(9)

〈Mⁿ〉

Эти выражения были нами использованы для опре-

деления β, γ и ν.

Для аппроксимации температурной зависимости

0.125

теплоемкости от L на практике, как правило, ис-

пользуется выражение

Рис. 10. Зависимость параметра порядка M от линейных

C_max(L) = A₁ - A₂L^α/ν,

(10)

размеров L системы при T = TN для r = 0.2

где A₁ и A₂ — некоторые коэффициенты.

На рис. 9 в двойном логарифмическом масштабе

4096

представлены характерные зависимости параметров

V_n при n = 1, 2, 3 от линейных размеров решетки L

r = 0.2

2048

для r = 0.2. Как видно на рисунке, все точки на гра-

фиках в пределах погрешности хорошо ложатся на

1024

прямые. Зависимости на рисунках, проведенные в

соответствии с методом наименьших квадратов, па-

512

раллельны друг другу. Углы наклона прямых опре-

деляют значения 1/ν. Вычисленные таким образом

значения ν использовались для определения крити-

256

ческих индексов теплоемкости α, восприимчивости

128

γ и параметра порядка β.

На рис. 10 и 11 в двойном логарифмическом мас-

штабе представлены характерные зависимости маг-

нитного параметра порядка M и восприимчивости

Рис. 11. Зависимость восприимчивости χ от линейных

χ от линейных размеров решетки L для r = 0.2. Все

размеров L системы при T = TN для r = 0.2

точки в пределах погрешности ложатся на прямые.

985

ЖЭТФ, вып. 5 (11)

А. К. Муртазаев, Д. Р. Курбанова, М. К. Рамазанов

ЖЭТФ, том 156, вып. 5 (11), 2019

Таблица. Значения критических индексов для трехмерной антиферромагнитной модели Гейзенберга на объем-

но-центрированной кубической решетке

T_N

α + 2β + γ = 2

0.0

2.056(1)

0.70(1)

-0.13(1)

0.37(1)

1.39(1)

0.02(1)

2.0

0.1

1.873(1)

0.70(1)

-0.12(1)

0.36(1)

1.38(1)

0.03(1)

1.98

0.2

1.687(1)

0.70(1)

-0.13(1)

0.37(1)

1.39(1)

0.02(1)

2.0

0.3

1.494(1)

0.70(1)

-0.12(1)

0.36(1)

1.39(1)

0.02(1)

1.99

0.4

1.301(1)

0.70(1)

-0.12(1)

0.36(1)

1.38(1)

0.03(1)

1.98

0.5

1.094(1)

0.70(1)

-0.12(1)

0.37(1)

1.39(1)

0.02(1)

2.01

0.6

0.871(1)

0.71(1)

-0.13(1)

0.37(1)

1.38(1)

0.03(1)

1.99

0.8

0.975(1)

0.60(1)

0.21(4)

0.29(4)

1.24(4)

0.01(4)

2.03

0.9

1.152(1)

0.61(1)

0.18(2)

0.30(1)

1.22(2)

0.02(2)

2.0

1.0

1.316(1)

0.60(1)

0.17(2)

0.30(1)

1.21(2)

0.02(2)

1.98

Нефрустриро-

ванная модель

0.7112(5)

-0.1336(15)

0.3689(3)

1.3960(9)

0.0375(5)

Гейзенберга [44]

Углы наклона этих прямых определяют значения

С помощью выражения (13) было определено

β/ν и γ/ν. По этой схеме были определены значе-

значение индекса Фишера η. Эти данные также

ния и для теплоемкости α/ν. С помощью данных ν

представлены в таблице.

вычислялись статические критические индексы α, β

Как следует из таблицы, почти все значения кри-

и γ.

тических индексов, рассчитанные нами в интерва-

Эта процедура использовалась для расчета кри-

ле 0.0 ≤ r ≤ 0.6, в пределах погрешности совпа-

тических индексов для значений r = 1.0; 0.9; 0.8;

дают между собой. Это свидетельствует о том, что

0.6; 0.5; 0.4; 0.3; 0.2, 0.1, 0. Все значения статических

в этом интервале система проявляет универсальное

критических индексов, полученные в данной работе,

критическое поведение. Отметим, что полученные

представлены в таблице.

нами значения критических индексов в пределах по-

Особо следует отметить процедуру, использован-

грешности совпадают с соответствующими значени-

ную нами для определения индекса Фишера η. На

ями критических индексов для нефрустрированной

основе отношения между восприимчивостью χ и ра-

трехмерной модели Гейзенберга [44]. Это подтвер-

диусом корреляции ξ [43]

ждает, что в интервале 0.0 ≤ r ≤ 0.6 исследуемая

модель принадлежит к тому же классу универсаль-

χ∝ξ^γ/ν,

(11)

ности критического поведения, что и трехмерная

модель Гейзенберга на кубической решетке.

а также соотношения η = 2 - γ/ν, связывающего

В интервале 0.8 ≤ r ≤ 1.0 значения критических

индексы η и ν, мы получаем

индексов отличаются от соответствующих значений

из интервала 0.0 ≤ r ≤ 0.6. Можно предположить,

ln(χ/ξ²) = c - η ln ξ,

(12)

что при увеличении величины взаимодействия вто-

рых ближайших соседей в системе происходит сме-

где c — некоторая константа. Для систем с конеч-

на класса универсальности критического поведения.

ными размерами ξ = L при k_BT/|J₁| = k_B T_N /|J₁|

Кроме того, в интервале 0.8 ≤ r ≤ 1.0 индексы ме-

имеем

няются с изменением r. Это позволяет нам говорить

о том, что в этом интервале наблюдается неунивер-

ln(χ/L²) = c - η ln L.

(13)

сальное критическое поведение.

986

ЖЭТФ, том 156, вып. 5 (11), 2019

Фазовые переходы и критические свойства...

Полученные в работе данные могут быть исполь-

H. T. Diep, Frustrated Spin Systems, World Scientific

зованы для описания конкретных антиферромаг-

Publishing Co. Pte. Ltd., Singapore (2004).

нитных материалов, таких как FeCr, FeAl, FeCo и

D. P. Landau and K. Binder, Monte Carlo Simula-

ряда других, имеющих ОЦК-решетку.

tions in Statistical Physics, Cambridge University

Press, Cambridge (2000).

F. A. Kassan-Ogly, B. N. Filippov, A. K. Murtazaev,

4. ЗАКЛЮЧЕНИЕ

M. K. Ramazanov, and M. K. Badiev, J. Magn.

Magn. Mater. 324, 3418 (2012).

Исследование фазовых переходов и критиче-

E. Dagotto and A. Moreo, Phys. Rev. Lett. 63, 2148

ских свойств антиферромагнитной модели Гейзен-

(1989).

берга на объемно-центрированной кубической ре-

шетке с взаимодействиями первых и вторых бли-

E. Manousakis, Rev. Mod. Phys. 63, 1 (1991).

жайших соседей выполнено с использованием вы-

H. Rosner, R. R. P. Singh, W. H. Zheng, J. Oitmaa,

сокоэффективного репличного алгоритма метода

and W. E. Pickett, Phys. Rev. B 67, 014416 (2003).

Монте-Карло. На основе гистограммного метода и

метода кумулянтов Биндера проведен анализ харак-

J. Sirker, Zheng Weihong, O. P. Sushkov, and J. Oit-

тера фазовых переходов для различных значений

maa, Phys. Rev. B 73, 184420 (2006).

величины взаимодействия r вторых ближайших со-

10.

Y. Kamihara, T. Watanabe, M. Hirano, and H. Ho-

седей. Построена фазовая диаграмма зависимости

sono, J. Amer. Chem. Soc. 130, 3296 (2008).

критической температуры от величины взаимодей-

11.

H. H. Wen, G. Mu, L. Fang, H. Yang, and X. Zhu,

ствия вторых ближайших соседей. Установлено, что

Europhys. Lett. 82, 17009 (2008).

в интервале значений 2/3 < r ≤ 0.75 в исследуе-

мой модели переход из антиферромагнитной фазы

12.

M. Rotter, M. Tegel, and D. Johrendt, Phys. Rev.

в парамагнитную реализуется как фазовый переход

Lett. 101, 107006 (2008).

первого рода.

13.

R. Schmidt, J. Schulenburg, J. Richter, and

Рассчитаны значения всех основных статических

D. D. Betts, Phys. Rev. B 66, 224406 (2002).

критических индексов в интервалах 0.0 ≤ r ≤ 0.6

14.

J. Oitmaa and W. Zheng, Phys. Rev. B 69, 064416

и 0.8 ≤ r ≤ 1.0. Показано, что в интервале 0.0 ≤

(2004).

≤ r ≤ 0.6 исследуемая модель проявляет универ-

сальное критическое поведение и принадлежит к то-

15.

K. Majumdar and T. Datta, J. Phys.: Condens. Mat-

му же классу универсальности критического поведе-

ter 21, 406004 (2009).

ния, что и трехмерная модель Гейзенберга. Обнару-

16.

M. R. Pantic, D. V. Kapor, S. M. Radosevic, and

жено, что изменение величины взаимодействия вто-

P. M. Mali, Sol. St. Comm. 182, 55 (2014).

рых ближайших соседей в интервале 0.8 ≤ r ≤ 1.0

приводит к неуниверсальному критическому пове-

17.

J. Richter, P. Müller, A. Lohmann, and

H.-J. Schmidt, Phys. Proc. 75, 813 (2015).

дению.

18.

P. Müller, J. Richter, A. Hauser, and D. Ihle, Eur.

Финансирование. Исследование выполнено

Phys. J. B 88, 159 (2015).

при поддержке Российского фонда фундаменталь-

19.

D. J. J. Farnell, O. Götze, and J. Richter, Phys. Rev.

ных исследований (проекты №№ 18-32-00391 мол-а,

B 93, 235123 (2016).

19-02-00153 а, 18-32-20098 мол-а-вед).

20.

Bin-Zhou Mi, Sol. St. Comm. 239, 20 (2016).

21.

Bin-Zhou Mi, Sol. St. Comm. 251, 79 (2017).

ЛИТЕРАТУРА

22.

J. S. Smart, Effective Field Theories of Magnetism,

Saunders, Philadelphia (1966).

1. Introduction to Frustrated Magnetism: Materials,

Experiments, Theory, Series in Solid-State Sciences

23.

J. R. Banavar, D. Jasnow, and D. P. Landau, Phys.

164, ed. by C. Lacroix, P. Mendels, and F. Mila,

Rev. B 20(9), 3820 (1979).

Springer, Berlin (2011).

24.

H. Kawamura, J. Phys. Soc. Jap. 61, 1299 (1992).

2. S. Sachdev, Quantum Phase Transitions, 1st ed.,

25.

A. Mailhot, M. L. Plumer, and A. Caille, Phys. Rev.

Cambridge University Press, Cambridge (2001).

B 50, 6854 (1994).

987

10*

А. К. Муртазаев, Д. Р. Курбанова, М. К. Рамазанов

ЖЭТФ, том 156, вып. 5 (11), 2019

26. М. К. Рамазанов, А. К. Муртазаев, Письма в

36. А. К. Муртазаев, М. К. Рамазанов, Д. Р. Курба-

ЖЭТФ 103, 522 (2016).

нова, М. К. Бадиев, Я. К. Абуев, ФТТ 59, 1082

(2017).

27. М. К. Рамазанов, А. К. Муртазаев, Письма в

ЖЭТФ 106, 72 (2017).

37. А. К. Муртазаев, М. К. Рамазанов, Ф. А. Кас-

сан-Оглы, Д. Р. Курбанова, ЖЭТФ

147,

127

28. A. Mitsutake, Y. Sugita, and Y. Okamoto, Biopoly-

(2015).

mers (Peptide Science) 60, 96 (2001).

38. А. К. Муртазаев, М. А. Магомедов, М. К. Рамаза-

29. A. K. Murtazaev, M. K. Ramazanov, and M. K. Ba-

нов, Письма в ЖЭТФ 107, 265 (2018).

diev, Physica A 507, 210 (2018).

39. A. K. Murtazaev, M. K. Ramazanov, D. R. Kurbano-

30. K. Binder and J.-Sh. Wang, J. Stat. Phys. 55, 87

va, M. A. Magomedov, and K. Sh. Murtazaev, Mater.

(1989).

Lett. 236, 669 (2019).

31. P. Peczak, A. M. Ferrenberg, and D. P. Landau, Phys.

40. А. Mailhot, M. L. Plumer, and A. Caille, Phys. Rev.

Rev. B 43, 6087 (1991).

B 50, 6854 (1994).

32. K. Binder and D. W. Heermann, Monte Carlo Simu-

41. P. Peczak, A. M. Ferrenberg, and D. P. Landau, Phys.

lation in Statistical Physics, Springer-Verlag (1988).

Rev. B 43, 6087 (1991).

33. F. Wang and D. P. Landau, Phys. Rev. E 64, 056101

42. A. K. Murtazaev, M. K. Ramazanov, and M. K. Ba-

(2001).

diev, Physica B: Cond. Matt. 476, 1 (2015).

34. F. Wang and D. P. Landau, Phys. Rev. Lett. 86(10),

43. Ch. Holm and W. Janke, Phys. Rev. B 48, 936 (1993).

2050 (2001).

44. M. Campostrini, M. Hasenbusch, A. Pelissetto,

35. А. К. Муртазаев, М. К. Рамазанов, Д. Р. Курбано-

P. Rossi, and E. Vicari, Phys. Rev. B 65, 144520

ва, М. К. Бадиев, ФТТ 60, 1162 (2018).

(2002).

988