ЖЭТФ, 2019, том 156, вып. 6 (12), стр. 1185-1191

О ФАЗОВОЙ ДИАГРАММЕ ОДНОМЕРНОЙ

МОДЕЛИ ХАББАРДА

Р. О. Зайцев^*

Московский физико-технический институт

141700, Долгопрудный, Московская обл., Россия

Поступила в редакцию 9 июня 2019 г.,

после переработки 9 июня 2019 г.

Принята к публикации 25 июня 2019 г.

На основе изучения уравнения состояния исследуются условия появления неоднородных состояний. Пред-

полагается, что энергия Хаббарда U > t, т. е. соответствует условию сильных электрон-электронных

корреляций. Получена магнитная фазовая диаграмма в широкой области электронных концентраций,

относящихся к нижней хаббардовской подзоне.

DOI: 10.1134/S0044451019120150

2. УРАВНЕНИЕ СОСТОЯНИЯ

В настоящей работе предполагается, что энер-

1. ВВЕДЕНИЕ

гия Хаббарда [7] является наибольшим энергетиче-

ским параметром. Поэтому гамильтониан записыва-

Настоящая статья является продолжением рабо-

ется через X-операторы Хаббарда. Одноэлектрон-

ты автора [1], в которой получена двумерная маг-

ные операторы рождения и уничтожения представ-

нитная фазовая диаграмма, относящаяся к нижней

ляются в виде суммы X-операторов перехода меж-

подзоне Хаббарда, в которой имеется полный нэс-

ду пустым |0〉 и одночастичным |σ〉, а также между

тинг. В разд. 2 будет получено уравнение состояния,

одночастичным | - σ〉 и двухчастичными |II〉 состо-

в котором можно обнаружить структурную неустой-

яниями:

чивость, а в разд. 3 получена магнитная фазовая

Xσ||0+σ XII||-σ_,

X 0||σ+σ X-σ||II_.

диаграмма, которая содержит связь между элек-

â+σ =

â_σ =

(1)

тронной концентрацией и волновым вектором спи-

Здесь и ниже Xαr — Х-операторы ферми-типа, удов-

ральности q. При этом при q = 0 мы получаем кри-

летворяющие нефермижидкостным перестановоч-

тическую концентрацию, соответствующую ферро-

ным соотношениям

магнитному упорядочению, а при q = π имеем кри-

{

}

(

)

тическую антиферромагнитную концентрацию, со-

X nm

X^kp

= δr,r′ δ_mk

X^np + δ_pn X^km

(2)

r^′

ответствующую удвоению периода.

Уравнения для одномерной модели неидеального

Уравнения для нахождения средних чисел запол-

ферми-газа были впервые получены в работах Мак-

нения n_m находим из определения температурной

гайра [2]. Они были записаны в «первичном» кван-

функции Грина для каждой пары сопряженных

товании, а затем развиты в работах Годена [3], Либа

X-операторов:

и Ву [4], и др. Ограниченность такого подхода впер-

вые отметил Галицкий [5], который показал, что в

D^α,β(r, τ; r, τ^′) = -Θ(τ - τ^′)〈Xαr(τ)Xβr′ (τ^′)〉+

«первичном» квантовании не учитываются никакие

+ Θ(τ^′ - τ)〈Xβr′(τ^′)

(τ)〉.

(3)

обменные эффекты. В этом смысле следует пони-

мать конечную область применимости линейных ин-

Для вычисления одночастичной функции Грина

тегральных уравнений, полученных Годеном в его

используем простейшее однопетлевое приближение

диссертации [3, 6].

самосогласованного поля. В этом приближении

компоненты Фурье одночастичной функции Грина

^* E-mail: zaitsev_rogdai@mail.ru

D^α,βω(p) только множителями f_β отличаются от так

1185

Р. О. Зайцев

ЖЭТФ, том 156, вып. 6 (12), 2019

называемой виртуальной функции Грина G^α,βω (p),

где

которая, в свою очередь, удовлетворяет уравнению

t_p

1^√

типа Дайсона:

ξ±p =

U² + t2p - 2U(1 - n)t_p - μ

(11)

{

}_α

— две энергетические ветви спектра.

D^α,βω(p) = G^α,βω(p)f_β;

Ĝ-1

(p)

Проводя разложение в правой части (10) на про-

= {iω - ϵ_m + ϵ_s}δ(α + β) - Σ^α,βω(p).

(4)

стые энергетические множители, находим

∑

Здесь ϵ_m - ϵ_s — энергия перехода, отвечающая но-

n=2

A^λ(p)n_F (ξλp),

меру перехода α, ω = T (2n + 1)π.

p,λ

При заданных номерах одночастичного перехода

⎡

⎤

β(m, s) каждый концевой множитель f_β равен сумме

t_p - U(1 - n)

средних чисел заполнения начального и конечного

A^±(p) =

⎣1±

√

⎦.

(12)

состояния. В нашем приближении собственно-энер-

U² + t2p - 2U(1 - n)t_p

гетическая часть есть сумма произведений концево-

Поскольку в уравнении подынтегральное выраже-

го множителя на обобщенную матрицу перескоков,

а также однопетлевой поправки: fα(s,m) = n_s + n_m,

ние зависит от импульса через функцию переско-

ка t_p, можно ввести функцию плотности состояний

∑

Σ^α,β(p) = f_αt^αβ(p) + Σ^α,β,

ρ(ϵ) =_p δ(ϵ - t_p).

(5)

t^αβ(p) = g^k,σαt^ks(p)g^s,σβ.

В нуль-петлевом приближении и при нулевом внеш-

3. УСЛОВИЯ СТРУКТУРНОЙ

нем магнитном поле f₁ = 1 - n/2, f₂ = n/2,

НЕУСТОЙЧИВОСТИ

[

]-1

Ĝσ

Для одномерной системы, для двумерной квад-

(p)

ратной решетки и трехмерной системы типа ГЦК

(

)

iω - ϵ + μ - f₁t_p

-σf₁t_p

плотности состояний записываются следующим об-

(6)

разом:

−σf₂t_p

iω-ϵ-U+μ-f₂t_p

(√

)

где n — электронная плотность.

ρ₁(ϵ) =

√

ρ₂(ϵ) =

1-ϵ²

Для получения уравнения состояния вычисляем

1-ϵ²

π²

(

)

(13)

две независимых комбинации одночастичной функ-

ρ₃(ϵ) =

√

ции Грина:

2 ln(e/2)

1-ϵ²

(√

)

G^σ-(ω, p) = (G^σω(p))1,1 + σ (G^σω(p))2,1 ,

(7)

где K

1-ϵ²

— полный эллиптический интеграл

Gσ+(ω, p) = σ (G^σω(p))1,2 + (G^σω(p))2,2 .

(8)

первого рода, который имеет логарифмическую осо-

бенность при |ϵ| → 0, две другие плотности состо-

Тогда с помощью определения среднего числа час-

яний ρ1,2 имеют краевую плотность состояний на

тиц с заданной проекцией σ находим

краю зоны (при |ϵ| → 1).

В пределе T = 0 и при заполнении нижней хаб-

n_σ = 〈â+σâ_σ〉 = n_II + n^σI = f-σ2 =

∑(

)

бардовской подзоны получаем

G^σ-(ω, p)e^iωδfσ1 + Gσ+(ω, p)e^iωδfσ2

(9)

p,ω

n=n₊ +n_- =

⎡

⎤

Для того чтобы просуммировать по комплекс-

∑

(

)

t_p - U(1 - n)

ным частотам iω = i(2n + 1)πT , подставим в пра-

⎣1-√

⎦_θ

-ξ(-)

(14)

U²+t2p-2Ut_p(1-n)

вую сторону определения (9) явное выражение для

одночастичной функции Грина из (6).

С помощью введения плотности состояний уравне-

В результате после суммирования по проекциям

ние (14) переписывается следующим образом:

спина получаем уравнение состояния

∑

[

]

∫

n = 2T exp(iωδ)×

ϵ - U(1 - n)

p,ω

√

]

U² + ϵ² - 2Uϵ(1 - n)

^[ (iω - U + μ)f₁ + (iω + μ)f₂

minϵ

(10)

(iω - ξ^p)(iω - ξ^p)

× θ(-ξ(-)(ϵ))ρ(ϵ)dϵ,

(15a)

1186

ЖЭТФ, том 156, вып. 6 (12), 2019

О фазовой диаграмме одномерной модели Хаббарда

0.51

D = 3

0.508

0.50

0.506

D = 1

0.49

0.504

0.48

D = 2

0.502

0.47

0.500

0.90

0.92

0.94

0.96

0.98

1.00

0.498

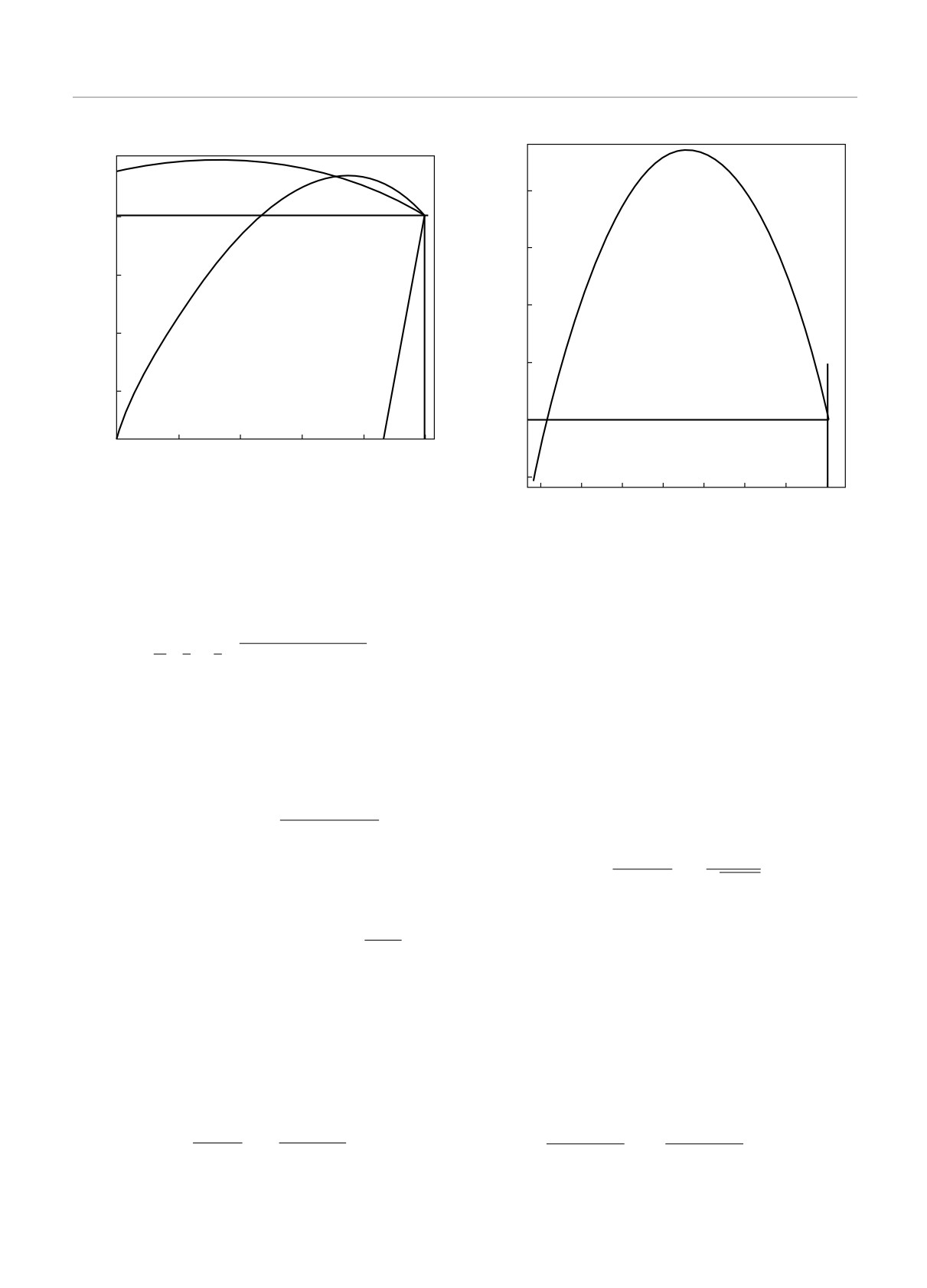
Рис. 1. Уравнение состояния μ(n) при значении энер-

0.86

0.88

0.90

0.92

0.94

0.96

0.98

1.00

гии Хаббарда U

= ∞, T

= 0, D = 1 и D = 2;

A(n = 0.946, μ = 0.5) — точка возникновения неоднород-

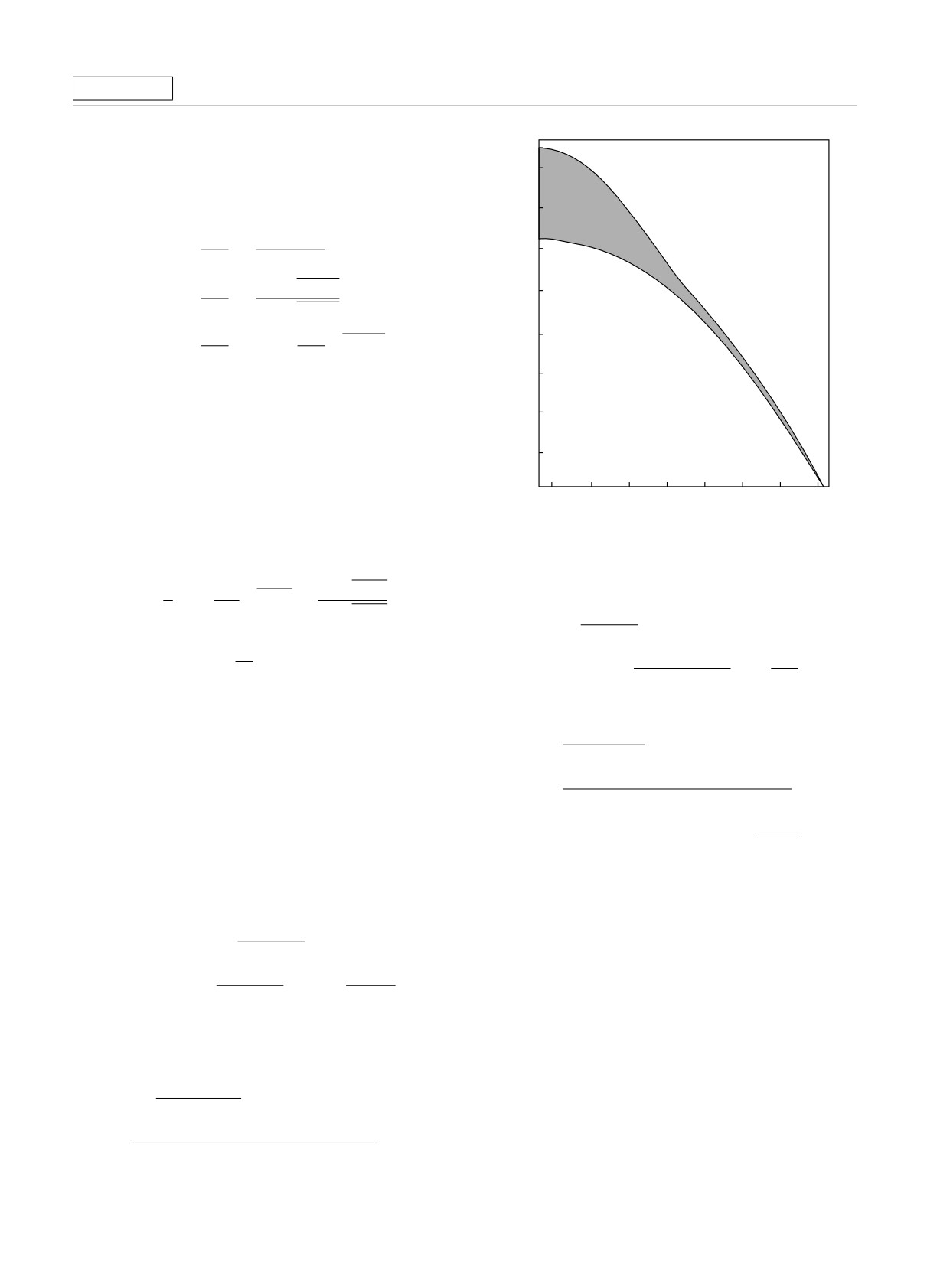
Рис. 2. Уравнение состояния μ(n) при значении энергии

ных состояний в одномерной системе

Хаббарда U = ∞, T = 0, D = 3; B(n = 0.863, μ = 0.5) —

точка возникновения неоднородных состояний в трехмер-

ной ГЦК-системе

где согласно (11)

√

ξ^±(ϵ) =

U²+ϵ²-2U(1-n)ϵ-μ.

(15b)

Соответствующие кривые изображены на рис. 1, из

которого следует, что расслоение невозможно для

Здесь интегрирование распространяется на области

двумерной системы.

заполнения в нижней подзоне Хаббарда. Нижний

Для случая трехмерной ГЦК-решетки расслое-

предел интегрирования в согласии с (13) равен -1,

ние также возникает при заполнении дырочной по-

а верхний предел интегрирования в (15a) определя-

верхности Ферми. При этом плотность состояний об-

ется из условия ξ(-)(ϵ) = 0, что соответствует

ращается в бесконечность по логарифмическому за-

кону: ρ ∼ ln(1 - ϵ) [1]. Для наглядности рассмотрена

2μ(U - μ)

f (n) ≡ f(n, U, μ) =

(16)

следующая плотность состояний:

(2 - n)U - 2μ

(

)

Рассмотрим уравнение состояния в пределе U =

ρ₃(ϵ) =

√

(19)

2 ln(e/2)

1-ϵ²

= ∞:

∫

которая при ϵ ≈ ±1 имеет логарифмическую осо-

2μ

бенность.

n = (2 - n)

ρ(x) dx, f(n, ∞) =

(17)

2-n

Проводя численные расчеты с помощью соот-

−1

ношения (17), получаем зависимость μ(n), которая

где верхний предел интегрирования в (17) опреде-

имеет максимум шириной Δϵ = 0.14, как показано

ляется из (16). Решение уравнения (17) находим по-

на рис. 2 — кривая D = 3.

сле подстановки плотности состояния и дальнейше-

Для нахождения точки расслоения в случае ко-

го интегрирования по параметру ϵ. В результате по-

нечных U запишем уравнение состояния (2a) в сле-

лучаем уравнение состояния μ = μ(n) для одномер-

дующем общем виде: ϕ(n, μ, U) = 0, а затем вычис-

ного случая (см. рис. 1):

лим производную μ^′n:

[

]

(2 - n)

π(3n - 2)

∂ϕ(n, μ, U)

μ=

sin

(18)

dn +

dμ = 0

(20)

2(2 - n)

∂n

∂μ

1187

Р. О. Зайцев

ЖЭТФ, том 156, вып. 6 (12), 2019

или

dμ

∂ϕ(n, μ, U)^∕∂ϕ(n, μ, U)

0.5

∂n

∂μ

12.0 t

Таким образом, появление точки максимума на кри-

вой возникновения точки расслоения совпадает с

0.4

условием обращения в нуль производной ϕ(n, μ, U)

по n:

⎧

⎫

0.3

1.0 t

∫

⎨

⎬

U² (U - x(1 - n))

0.8 t

1=-

] ρ(x) dx +₃

[√

⎩

⎪

0.6 t

-1

U²+x²-2Ux(1-n)

0.2

0.5 t

[

]

0.4 t

f (n) - U(1 - n)

+ f^′(n) 1-

√

0.3 t

U² + f(n)² - 2Uf(n)(1 - n)

0.1

0.2 t

× ρ(f(n)),

(21a)

U = 0.1 t

где

(1 -

n).

10³

∂f(n,U,μ)

2μU(U - μ)

f^′(n) ≡

(21b)

∂n

((2 - n)U - 2μ)²

Рис. 3. Положения максимумов уравнения состояния μ(n)

в зависимости от значения энергии Хаббарда (одномерная

Совместное решение уравнений (21a) и (21b) при за-

модель, T = 0), U = ∞(n = 0.9735, μ/t = 0.5065)

данном значении энергии Хаббарда U определяет

максимальное значение кривой химического потен-

циала μ в зависимости от плотности n. Для одно-

мерной плотности состояний имеем кривую¹⁾, изоб-

раженную на рис. 3.

Важно заметить, что возникновение максиму-

ма зависимости химического потенциала от плотно-

p + q/2

p - q/2

сти непосредственно связано с корневой сингулярно-

p + q/2

стью плотности состояний. Если же вместо одномер-

ной плотности состояний использовать затравочную

плотность состояний, соответствующую двумерной

квадратной или трехмерной простой кубической и

ОЦК-решеткам, то система уравнений (21a), (21b)

p - q/2

p + q/2

p - q/2

p + q/2

не будет иметь решения. Расслоения на фазы нет!

Используя эту аналогию, можно предположить,

Рис. 4. Аномальные магнитные собственно-энергетические

части, записанные в линейном приближении при U = ∞

что расслоение на фазы имеет место для ГЦК-ре-

шетки, поскольку ее плотность состояний на краю

зоны имеет логарифмическую плотность состояний.

Используя ее графическое представление, изобра-

женное на рис. 4, получим уравнения для опреде-

3.1. Магнитная фазовая диаграмма

ления коэффициентов C и D:

одномерной модели Хаббарда

∑

{

}

Рассмотрим условие магнитного упорядочения

C = -T G_ω(p^′-q/2)t_p′-q/2

C+Dt_p′+q/2

при заданном передаваемом импульсе q.

ω,p

Будем искать магнитную аномальную функцию

× G_ω(p^′ + q/2),

(22a)

Грина в следующем виде:

Σ(m)q(p) = C + Dtp+q/2.

∑

{

}

D = -T

G_ω(p^′ - q/2)

C + Dt_p′+q/2

¹⁾ Соответствующие интегралы сводятся к эллиптическим

ω,p

[8], однако получаемые таким образом выражения имеют

× G_ω(p^′ + q/2).

(22b)

весьма громоздкий вид [9].

1188

ЖЭТФ, том 156, вып. 6 (12), 2019

О фазовой диаграмме одномерной модели Хаббарда

Здесь G_ω(p^′) = 1/(iω - ft_p + μ) — одночастичная

W₂(q) =

функция Грина, t_p — интеграл перескока, f = 1 -

∫

- n/2-концевой множитель.

(cos(p) cos(q/2))²-(sin(p) sin(q/2))²

dp =

Требование разрешимости полученной системы

4πf sin(p)sin(q/2)

p=μ-q/2

уравнений дает условие возникновения магнитного

упорядочения:

∫

(cos(q/2))²

dp -

sin(q/2)4πf

sin(p)

sin(q/2)4πf

1 = W⁽⁺⁾¹(q) + W(-)1(q) - W₂(q)W₀(q)+

p=μ-q/2

+ W⁽⁺⁾¹(q)W(-)1(q),

(23)

∫

sin(p) dp.

(28)

где

p=μ-q/2

∑

W₀(q) = -T G_ω(p + q/2)G_ω(p - q/2),

(24a)

Здесь и ниже μ = arccos(μ/f),

ω,p

∫

{

}

sin(μ+q/2)

∑

ctg(p) dp = ln



^ sin(μ - q/2)

W±1(q) = -T tp±q/2 ×

p=μ-q/2

ω,p

× G_ω(p + q/2)G_ω(p - q/2),

(24b)

∫

∑

sin(p)

W₂(q) = -T tp+q/2tp-q/2 ×

p=μ-q/2

{

}

ω,p

[1-cos(μ+q/2)]

[1+ cos(μ-q/2)]



(29)

× G_ω(p + q/2)G_ω(p - q/2).

(24c)



^ [1- cos(μ-q/2)] [1+ cos(μ+q/2)]

В общем случае поляризационный оператор

3.2. Точка возникновения ферромагнетизма

W₀(q) имеет вид

в одномерной модели Хаббарда q = 0

∑

n_F (p + q/2) - n_F (p - q/2)

W₀(q) = -

(25)

Рассмотрим сначала область решений, когда

ft(p+q/2) -ft(p-q/2)

= 0, т.е. ферромагнитную область. При этом

W₂W₀ = W²¹.

При нулевой температуре

Таким образом, условие возникновения фазового

перехода:

W₀(q) =

∑

θ(μ - ft(p+q/2)) - θ(μ - ft(p-q/2))

∫

(26)

ctg(q/2)

ft(p+q/2) -ft(p-q/2)

ctg(p) dp =

2πf

p=μ-q/2

В одномерном случае t_p = t cos(p)

{

}

ctg(q/2)

sin(μ+ q/2)



2πf

^ sin(μ - q/2)

∫

{

}

ctg(q/2)

sin(μ)cos(q/2)+cos(μ)sin(q/2)

W₀(q) =

(27a)



≈

4πf sin(q/2)

sin(p)



2πf

^ sin(μ) cos(q/2)- cos(μ) sin(q/2)

p=μ-q/2

≈

ctg(μ) =

√

(30)

Аналогичным образом

πf

1 - (z)²

∫

где z = μ/f.

ctg(q/2)

W±1(q) =

ctg(p) dp ∓

(27b)

Решая это уравнение совместно с уравнением со-

4πf

2πf

стояния

p=μ-q/2

n = (2 - n)

(2arcsin(z) + π),

(31)

2π

∫

ctg(q/2)

находим критическое значение химического потен-

W⁺¹(q) + W-1(q) =

ctg(p) dp, (27c)

2πf

циала μ, а также критическую концентрацию: z =

p=μ-q/2

= 0.864, μ = 0.528, n = 0.908.

1189

Р. О. Зайцев

ЖЭТФ, том 156, вып. 6 (12), 2019

3.3. Точка возникновения

1.00

антиферромагнетизма в одномерной модели

0.98

Хаббарда q = π

При q = π имеем

0.94



1 + sin(μ)

W₀(π) =



0.90

⁼

4πf

^1 - sin(μ)



√



1+

1-z²

0.86



√

,

(32)

4πf

1-

1-z²

√

0.82

W₂(π) =

sin(μ) =

1-z²,

2πf

0.78

где z = μ/f — безразмерный параметр, который

связан с плотностью с помощью уравнения состоя-

0.74

ния (31).

При этом оказывается, что критическое значение

0.70

химического потенциала μ близко к нулю. По этой

2/3

причине можно положить, что W₁ = 0, а уравнение

0.2

0.6

1.0

1.4

1.8

2.2

2.6

для нахождения антиферромагнитной фазы имеет

вид 1 = W₀(π)W₂(π). Таким образом, имеем уравне-

Рис. 5. Область существования спиральной структуры, ко-

ние для нахождения критических значений z и n:

торая заключена между двумя кривыми



√

(

)₂

√



1+

1-z²

f² =

1-z² ln

√

 ,

(33)

8π²

1-

1-z²

ctg(q/2)

W±1(q) = -

4πf

{

}

(sin(μ+ q/2))

n = (2 - n)

(2arcsin(z) + π).



× ln

∓

(34b)

2π



^ (sin(μ - q/2))

2πf

Отсюда находим две критических точки, между ко-

торыми появляется антиферромагнитное упорядо-

чение: (n = 0.65925, z = -0.02607, μ = -0.01748)

(cos(q/2))²

W₂(q) =

и (n = 0.67400, z = 0.02607, μ = 0.01729).

sin(q/2)8πf

}



^{ (1- cos(μ+q/2))(1+cos(μ-q/2))



× ln



^ (1- cos(μ-q/2))(1+ cos(μ+q/2))

3.4. Условия возникновения спиральной

структуры q = 0

sin(μ)

(34c)

2πf

Удобно выразить переменную μ = arccos z через

плотность. Для этой цели находим z через n с помо-

где sin(μ) = sin(2π(1 - n)/(2 - n)), f = 1 - n/2.

щью уравнения состояния:

Далее находим соотношение между q и n из усло-

)

вия возникновения точки перехода:

⁽π(3n - 2)

z = sin

2(2 - n)

1 = W⁽⁺⁾¹(q) + W(-)1(q) - W₀(q)W₂(q)+

[

(34)

⁽π(3n - 2)^)]

(1 - n)

(+)

μ = arccos sin

= 2π

+W₁

(q)W(-)1(q).

(35)

2(2 - n)

(2 - n)

Как следует из рис. 5, спиральная антиферро-

В результате все три функции W_k(q) оказываются

магнитная структура может существовать в доста-

выраженными через плотность и q:

точно широкой области волновых векторов (от ну-

ля до q = π). При этом с уменьшением длины вол-

W₀(q) =

ны происходит понижение концентрационной обла-

8πf sin(q/2)

{

}

сти существования вплоть то величины q = 2.88,

(|1- cos(μ+q/2)|)(|1+ cos(μ-q/2)|)

начиная с которой эта область становится экспонен-

× ln

(34a)

(|1- cos(μ-q/2)|)(|1+ cos(μ+q/2)|)

циально малой, и, наконец, исчезает при q = π.

1190

ЖЭТФ, том 156, вып. 6 (12), 2019

О фазовой диаграмме одномерной модели Хаббарда

q^∑

- ctg

Π(c)p′+p(p^′′)cos(p^′)×

p^′,p^′′

]

^[θ(μ - ft_p′+q/2)) - θ(μ - ft_p′-q/2)

2 sin(p^′)

∫

cos(p^′)

= ctg

dp^′

16π²

sin(p^′)

μ-q/2

∫

dp^′′

p + q/2

p - q/2

|cos(p^′′)cos((p + p^′)/2) - μ/f|

Можно заметить, что результат интегрирования

приводит к логарифмически расходящемуся инте-

s=p+p

-p

+ s/2

гралу, но не дает дважды логарифмической рас-

ходимости по причине существенной анизотропии

двух пересекающихся поверхностей Ферми.

Таким образом, можно утверждать, что в реаль-

ной, анизотропной, модели Хаббарда влияние пар-

+ s/2

кетных диаграмм на магнитную фазовую диаграм-

p - q/2

p + q/2

му не является существенным, а фазовая диаграм-

ма определяется с помощью рис. 5 соответствующим

Рис. 6. Простейшая паркетная поправка к антиферромаг-

нитной вершинной части

однопетлевым приближениям.

Аналогичным образом, можно предположить,

что зависимость химического потенциала от концен-

Аналогичные результаты, относящиеся к одно-

трации (18), содержащая структурную неустойчи-

мерной модели, были получены в работe Дзялошин-

вость в одномерной модели, качественно определя-

ского - Ларкина [10]. Авторы получили достаточно

ется с помощью нуль-петлевого приближения.

общий результат, относящийся к модели Хаббарда:

при отрицательном знаке затравочной константы

ЛИТЕРАТУРА

взаимодействия система является сверхпроводящей,

1. Р. О. Зайцев, ЖЭТФ 152, 975 (2017).

а при положительном знаке, она оказывается анти-

ферромагнитной. Нетрудно проследить, что этот ре-

2. J. B. McGuire, J. Math. Phys. 6, 432 (1965); 7, 123

зультат справедлив при малой энергии Хаббарда U,

(1966).

в то время как наши результаты относятся к беско-

3. М. Годен, Волновая функция Бете, Мир, Москва

нечно большой, положительной энергии U.

(1987).

Полученная фазовая диаграмма обусловлена на-

4. E. Lieb and T. T. Wu, Phys. Rev. Lett. 20, 1445

личием амплитуды так называемого кинематическо-

(1968).

го взаимодействия [11], которое определяет также

5. В. М. Галицкий, ЖЭТФ 34, 151 (1958).

куперовскую петлю Πsc)(p), которая перенормиру-

ет вклад логарифмической антиферромагнитной по-

6. M. Gaudin, Thèse Univ. de Paris, Raport CEA.

правки (см. рис. 6). В одномерном случае и при

Saclay.: N 5, 3569 (1968).

T = 0 имеем

7. J. Hubbard, Proc. Roy. Soc. 281, 1386 (1964).

8. И. С. Градштейн, Н. М. Рыжик, Таблицы интегра-

Π(c)s(p) =

2|f cos(p^′′-s/2)+f cos(p+s/2)-μ|

лов, рядов, сумм и произведений, Изд. 5-е, Наука,

Москва (1977).

2|f cos p cos(s/2) - μ|

9. G. Iwata, Natural Science Rep., Ochanomozu Univ.

20, 13 (1969).

Дальнейшее вычисление суммы по импульсу p^′

10. И. Е. Дзялошинский, А. И. Ларкин, ЖЭТФ 61, 61

связано с условием s = p^′ + p. Запишем поэтому

(1971).

оставшуюся сумму по p^′ и p^′′ в следующем виде, со-

11. R. O. Zaitsev, Phys. Lett. A 134, 199 (1988).

держащем сингулярную сумму по p^′:

1191