ЖЭТФ, 2020, том 157, вып. 1, стр. 5-11

НАПРАВЛЯЕМЫЕ ОПТИЧЕСКИЕ МОДЫ С ПРОИЗВОЛЬНЫМИ

КОНСТАНТАМИ РАСПРОСТРАНЕНИЯ В ПЛОСКИХ МАССИВАХ

МЕТАЛЛИЧЕСКИХ ВОЛНОВОДОВ

А. А. Анастасиев^a, А. Л. Бурин^b, Ю. Каган^a, И. Я. Полищукc*, Ю. И. Полищук^a

^a Национальный исследовательский центр «Курчатовский институт»

123182, Москва, Россия

^b Кафедра химии, Тулейнский университет

70118, Новый Орлеан, Луизиана, США

^c Московский физико-технический институт (государственный университет)

141700, Долгопрудный, Московская обл., Россия

Поступила в редакцию 15 апреля 2019 г.,

после переработки 15 апреля 2019 г.

Принята к публикации 3 июня 2019 г.

Рассматриваются направляемые оптические моды в массивах одинаковых металлических волноводов

круглого сечения, оси которых параллельны друг другу, лежат в одной плоскости и эквидистантны. К

настоящему времени хорошо изучены свойства таких мод только в случае нулевой константы распро-

странения β = 0, когда оптический импульс распространяется строго перпендикулярно осям волноводов.

Показано, что в случае β = 0 возникает новая ветвь направляемых мод. Детально изучен случай, когда

волноводы изготовлены из серебра. Обнаружено, что при достаточно малых константах распространения

дисперсионная кривая новой моды целиком расположена ниже окна прозрачности материала волновода.

Получены условия, при которых дисперсионная кривая с β = 0 целиком попадает в окно прозрачности.

Для получения результатов использован формализм многократного рассеяния, основанный на разложе-

нии электромагнитных полей по векторным цилиндрическим гармоникам. Кратко обсуждается случай,

когда волноводы изготовлены из других материалов (медь и золото).

DOI: 10.31857/S0044451020010010

фотонных кристаллов, которые могут быть изго-

товлены на основе диэлектриков (полупроводников)

1. ВВЕДЕНИЕ

(см. [1]), металлов [2] и даже сверхпроводников [3].

Оптические волноводы являются неотъемле-

В работах [4, 5] было продемонстрировано, что

мыми компонентами разнообразных оптических и

оптоэлектронных устройств. В большинстве случа-

коллективные моды, возникающие вследствие взаи-

модействия диэлектрических микросфер, центры

ев они отвечают за передачу оптического сигнала

между различными частями того или иного устрой-

которых расположены на одной прямой или од-

ной окружности, обладают свойствами, которые не

ства. Тенденция к миниатюризации приводит к

тому, что взаимодействие различных волноводов

имеют места для изолированной микросферы. В

частности, добротность для мод шепчущей гале-

внутри устройства оказывается значительным.

На первый взгляд, это взаимодействие оказывает

реи (whispering gallery modes) существенно выше в

системе взаимодействующих микросфер. Направля-

только негативное влияние, в частности, разрушая

емым модам в плоских массивах цилиндрических

передаваемый сигнал. Однако в некоторых случаях

оно может быть использовано в практических

волноводов посвящено множество работ (см. [6] и

ссылки там же). В частности, в работе [6] показа-

целях. В частности, это касается плоских массивов

идентичных волноводов круглого сечения. Такие

но, что моды с большим показателем добротности

формируются исключительно благодаря взаимодей-

массивы относятся к семейству низкоразмерных

ствию волноводов, а соответствующий сигнал рас-

^* E-mail: iyppolishchuk@gmail.com

пространяется практически без потерь на излуче-

А. А. Анастасиев, А. Л. Бурин, Ю. Каган и др.

ЖЭТФ, том 157, вып. 1, 2020

ние, связанных с возможностью конверсии этого

Статья построена следующим образом. В разд. 2

сигнала в свободный фотон. Это условие опреде-

рассматривается плоская система металлических

ляется соответствующим законом дисперсии моды

волноводов. Следуя работе [6], мы приводим основ-

в массиве. Условие отсутствия потерь требует так-

ные соотношения формализма многократного рас-

же, чтобы частота направляемой моды находилась в

сеяния, который основан на точном решении задачи

пределах окна прозрачности материала волновода.

рассеяния плоской электромагнитной волны уеди-

Существенно, что оба этих критерия могут соблю-

ненным цилиндром бесконечной длины [18]. Здесь

даться в массивах волноводов, но вовсе не иметь ме-

же выводится дисперсионное уравнение для собст-

ста для уединенного волновода. В системах диэлек-

венных мод системы и описывается способ его реше-

трических волноводов, расположенных по окружно-

ния. В разд. 3 обсуждаются полученные результаты

сти, наблюдаются похожие коллективные эффекты

и проводится сравнение с имеющимися в литературе

[7]. Отметим, что существование коллективных мод

данными.

с аналогичными свойствами в периодических цепоч-

Всюду ниже мы полагаем магнитную проницае-

ках, образованных возбужденными ядрами, было

мость волноводов и окружающей среды равными 1.

предсказано более 50 лет назад [8]. В работе [9], по-

Показатель преломления окружающей среды n₀ =

священной нестабильности экситонного спектра мо-

= 1. Используется система единиц, в которой ско-

лекулярных кристаллов, также отмечались описан-

рость света в вакууме равна c = 1.

ные эффекты.

Распространение оптических импульсов в цепоч-

ке, образованной металлическими наночастицами,

2. ТЕОРИЯ

впервые было рассмотрено в работе [10]. В недавней

Рассмотрим плоский массив, состоящий из N

работе [11] были изучены плазмонные моды, про-

одинаковых цилиндрических волноводов. Расстоя-

странственно-локализованные вблизи плоского мас-

ние между ближайшими волноводами a, радиус

сива эквидистантно расположенных волноводов, из-

каждого волновода R, показатель преломления n

готовленных из серебра. Однако рассмотрение бы-

(рис. 1).

ло ограничено случаем нулевой константы распро-

Мы ищем решение уравнений Максвелла, кото-

странения β, которая является проекцией импуль-

рое является конечным внутри волноводов и убыва-

са плазмона на ось волновода. Интерес к исследо-

ет по мере удаления от системы, т. е. при y → ∞.

ванию плазмонов с β = 0 обусловлен тем, что они

Формализм многократного рассеяния, использован-

важны для ряда прикладных проблем. Кроме то-

ный ниже, основан на разложении электромагнит-

го, эти моды важны для моделирования оптичес-

ного поля в ряд по векторным цилиндрическим гар-

ких явлений, имеющих аналоги в физике твердо-

моникам.

го тела. В частности, к таким эффектам относят-

Далее при описании подхода мы главным обра-

ся андерсоновская локализация, оптические блохов-

ские осцилляции, туннелирование Блоха - Зинера и

зом следуем работе [6]. Однако, учитывая слож-

ности вычислительного характера, возникающие в

т. д. [12-17].

В настоящей работе мы изучаем направляемые

моды в плоских массивах металлических волно-

водов при ненулевых константах распространения.

Выбор именно серебра в качестве материала волно-

водов, в частности, обусловлен возможностью соот-

нести наши результаты с результатами работы [11].

Мы показываем, что в случае β = 0 возникает но-

вая ветвь направляемых мод. При достаточно ма-

лых значениях β эти моды расположены ниже окна

прозрачности материала волновода. По мере увели-

чения β они смещаются в сторону окна прозрачно-

сти. При определенном значении константы распро-

странения β_min щель между дисперсионной кривой

Рис. 1. Периодический массив волноводов. Показаны по-

и дном окна прозрачности исчезает. Начиная с β =

лярные координаты радиус-вектора r относительно раз-

= β_max, вся кривая располагается целиком внутри

личных волноводов

окна прозрачности.

ЖЭТФ, том 157, вып. 1, 2020

Направляемые оптические моды с произвольными константами...

процессе численного моделирования, целесообразно

определяющих парциальные амплитуды. В резуль-

представить электрическое поле в волноводе следу-

тате мы получаем систему однородных алгебраичес-

ющим образом (несколько отличном от работы [6]):

ких уравнений для амплитуд a_jm и b_jm:

(

)

∑

eimφj

a_jm

E_j

(t, r) = e-iωt+iβz

S_m

J_m (κR)

b_jm

m=-∞

[

]

∑

× c_jm

Ńω′βm (ρj) - djm^Mω′βm (ρj)

(1)

∑ H(1)m-n (κ₀a|l - j|)Jm (κ₀R)

Hn1) (κ₀R)

l=j n=-∞

Здесь r = (ρ, z); ρ_j = |ρ - aj| < R; φ_j — угол, кото-

(

)

[

]

a_ln

рый составляет вектор ρ - aj с осью x (см. рис. 1);

n-m

sign(l - j)

= 0,

(4)

ω и β — соответственно частота моды и констан-

b_ln

та распространения; ω^′ = nω; c_jm и d_jm — парци-

а парциальные амплитуды c_jm и d_jm выражаются

альные амплитуды при векторных цилиндрических

через решение уравнения (4) следующим образом:

гармониках

Ńω′βm и

Mω′βm (явное выражение гар-

моник приведено в [6]); J_m (x) — функция Бессе-

⎛

⎞

√

(

)

(

)

ля, κ =

n²ω² - β². Магнитное поле в волноводе

c_jm

⎜

⎟

a_jm

= -F

⎝

⎠

(5)

B_j (t, r) может быть получено из выражения (1) пу-

i A

d_jm

тем замены парциальных амплитуд c_jm и d_jm выра-

n E

жениями nd_jm и -nc_jm соответственно.

В формулах (4), (5) использованы следующие

Теперь рассмотрим электромагнитное поле вне

обозначения:

волноводов. Электрическое поле представляет собой

⎛

⎞

суперпозицию вкладов от каждого из N волноводов

BC - E²

в системе:

⎜

⎟

⎜

AB - E²

⎟

S_m = -

(6)

∑

⎝

⎠

AD - E²

E (t, r) =

E_j (t, r),

(2)

-F

AB - E²

j=1

где

1 J^′m (κ0R)

n² J^′m (κR)

κ₀ J_m (κ₀R)

κ Jm (κR)

∑

eimφj

E_j (t, r) = e-iωt+iβz

J^′m (κ0R)

1 J^′m (κR)

B =

m=-∞

Hm1) (κ₀R)

κ₀ J_m (κ₀R)

κ Jm (κR)

× [a_jmN_ωβm (ρ_j ) - b_jmM_ωβm (ρ_j )] .

(3)

1 Hm1)′ (κ₀R)

n² J^′m (κR)

C =

κ₀ Hm1) (κ₀R)

κ Jm (κR)

Здесь a_jm и b_jm — парциальные амплитуды при век-

торных цилиндрических гармониках N_ωβm и M_ωβm

Hm1)′ (κ₀R)

1 J^′m (κR)

другого типа (их явное выражение приводится в ра-

κ₀ Hm1) (κ₀R)

κ Jm (κR)

боте [6]). Далее, Hm1) (x) — функция Ганкеля первого

√

(

)

рода, κ₀ =

ω² - β². Магнитное поле вне волново-

βm

дов B_j (t, r) может быть получено из выражения (3)

ωR κ²⁰

κ²

путем замены парциальных амплитуд a_jm и b_jm вы-

ражениями b_jm и -a_jm соответственно.

F =

π κ²⁰R Jm (κ₀R)Hm1) (κ₀R) AB - E²

Отметим, что, в отличие от работы [6], в знаме-

нателях выражений (1) и (3) введены нормировоч-

причем штрих обозначает производную по аргумен-

ные множители J_m (κR) и Hm1) (κ₀R) с целью по-

ту соответствующей функции. Таким образом, для

вышения точности расчетов в процессе численного

определения электромагнитного поля, описывающе-

моделирования.

го направляемую моду, необходимо решить систе-

му однородных линейных уравнений (4). Поскольку

Электрическое и магнитное поля внутри и сна-

рассматриваемый нами массив волноводов являет-

ружи массива должны удовлетворять граничным

ся периодическим, решение уравнения (4) должно

условиям для уравнений Максвелла на поверхно-

иметь форму блоховской волны, характеризующей-

сти каждого из N волноводов, составляющих систе-

му. Это требование приводит к системе уравнений,

ся квазиволновым вектором k_x = k:

А. А. Анастасиев, А. Л. Бурин, Ю. Каган и др.

ЖЭТФ, том 157, вып. 1, 2020

(

)

(

)

a_jm

a_m

Решеточная сумма в выражении (9) сходится

e^ikaj,

-π < ka < π.

(7)

медленно. Для оптимизации временных затрат при

b_jm

b_m

численном моделировании целесообразно перепи-

Подстановка выражения (7) в уравнение (4) дает

сать U_n(x, y) в виде быстро сходящегося ряда. Для

(

)

этого используется подход, описанный в работе [19].

∑

a_m

J_m (κ₀R)

Таким образом, получаем

S_m

b_m

Hn1) (κ₀R)

n=-∞

)

)(

2i⁽

y⁾

⁽ka

κ₀a

a_n

U₀ (x, y) = -1 -

C + ln

√

×U_m-n

= 0,

(8)

πy

1-z²

b_n

⎛

⎞

∑

где

⎝

√

⎠,

(10)

πy

μ=1

1-z²

1-z

-μ

U_n (x, y) =

∑

(

)

где C = 0.577 . . . — постоянная Эйлера. Для поло-

H(1)n (πyL)

e^iπxL + (-1)ⁿe^-iπxL

(9)

жительных значений индексов ν имеем

L=1

-iπν

∑

e-iνarcsinzμ

eiνarcsinz-μ

(

)

U_ν (x, y) =

√

1+e^-iπν

π y

πy

πν

μ=0

1-z2μ

μ=1

1-z²

−μ

⎧

∑

⎪

(-1)^m22m(n + m - 1)!

⁽2)2m

⁽x⁾

⎪

B2m

ν = 2n,

⎨

(n - m)!(2m)!

m=1

(11)

⁺⎪⎪

∑

⎪

(-1)^m22m(n + m)!

⁽2)2m+1

⁽x⁾

⎩ -

B2m+1

ν = 2n + 1,

(n - m)!(2m + 1)! y

m=0

где z_μ = x/y+2μ/y, B_n(x) — полином Бернулли. Для

частот взята из работы [20]. Также был проведен

решеточных сумм с отрицательным индексом следу-

расчет в рамках модели Друде - Лоренца (см. [21]):

ет воспользоваться соотношением U_-ν = (-1)^νU_ν.

ω2p

ε₁ω²⁰

Уравнение (8) имеет нетривиальные решения

ε (ω) = 1 -

(13)

только при условии

ω (ω + iγ)

ω² + 2iωδ - ω²



Метод наименьших квадратов, использованный



J_m (κ₀R)

det

S_mδ_m,n -

для аппроксимации экспериментальных данных из



Hn1) (κ₀R)

[20] уравнением (13), дает ωp

= 9.146 эВ, γ

)

)(



= 1.899 · 10-2 эВ, ε₁ = 2.590, ω₀ = 6.527 эВ, δ =

⁽ka

κ₀a



× U_m-n



= 0.

(12)

= 2.189 эВ.



Это уравнение неявным образом определяет за-

Система уравнений

(12) решалась в среде

кон дисперсии направляемой моды ω = ω(β, k) как

MatLab с помощью разработанного нами программ-

функцию константы распространения β и квазивол-

ного кода. Результаты численного моделирования

нового вектора k.

приведены на рис. 2-4.

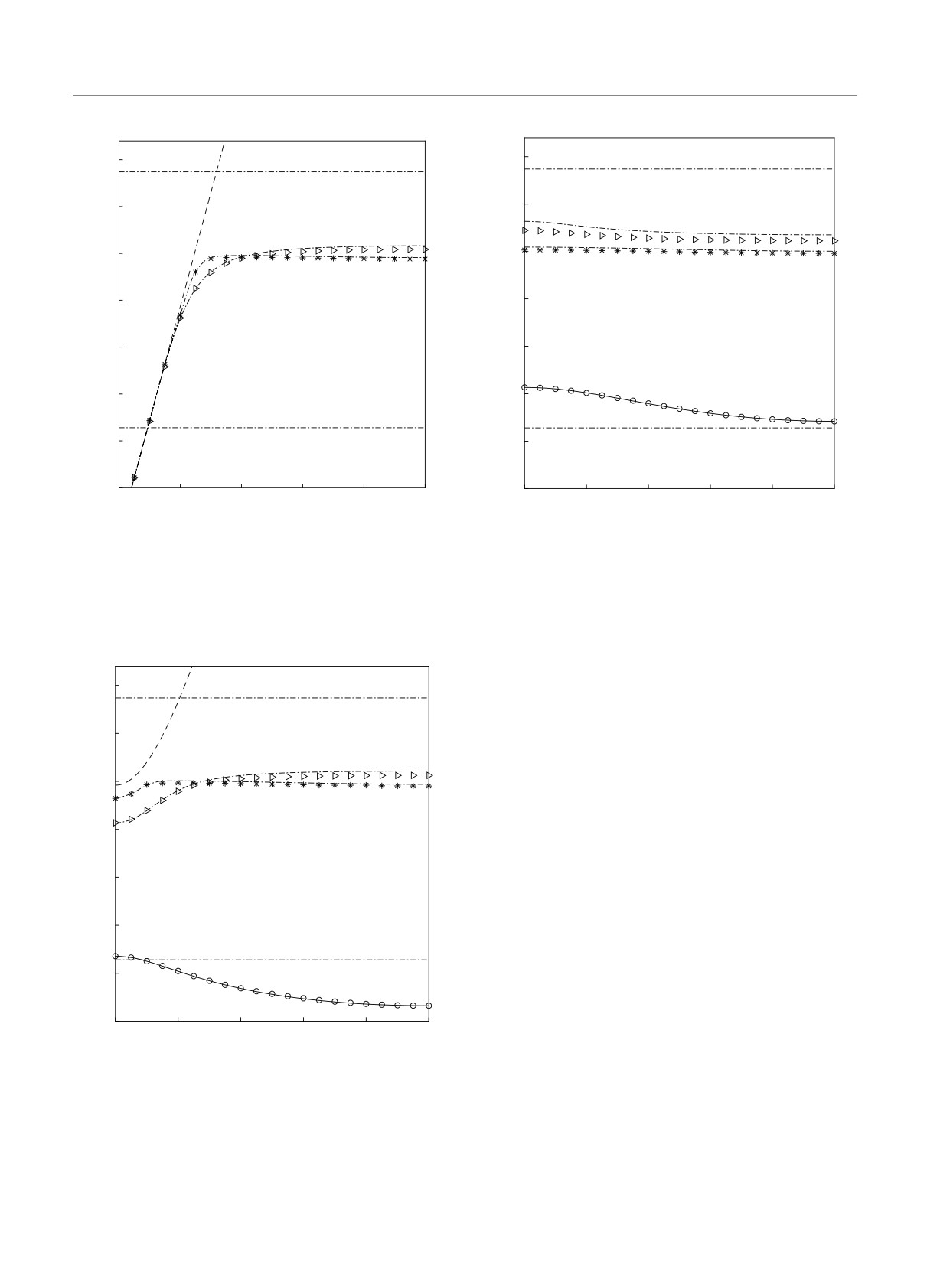
Дисперсионные кривые на рис. 2 отвечают на-

3. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

правляемым модам с нулевой константой распрост-

Применим полученные выше соотношения к ис-

ранения β = 0. Этот рисунок воспроизводит ре-

следованию направляемых мод в массиве, кото-

зультаты статьи [11]. Треугольниками изображена

рый был рассмотрен в работе [11]. Соответствен-

фундаментальная мода, звездочками — первая про-

но, радиус каждого волновода берется равным R =

дольная. Эти моды получены с использованием таб-

= 25 нм, расстояние между ближайшими волново-

личных данных для диэлектрической проницаемо-

дами a = 51 нм. Как и в работе [11], материалом

сти из [20]. Штрихпунктирные кривые отвечают тем

волноводов является серебро, диэлектрическая про-

же модам, полученным в рамках приближения Дру-

ницаемость которого в интересующем нас диапазоне

де - Лоренца.

ЖЭТФ, том 157, вып. 1, 2020

Направляемые оптические моды с произвольными константами...

, эВ

4.0

Световой конус

4.0

TWU

3.5

3.0

2.5

2.0

1.5

1.0

TWL

1.0

TWL

= 0

= 0.487

0.5

0.2

0.4

0.6

0.8

1.0

0.2

0.4

0.6

0.8

1.0

ka/

Рис. 2. Закон дисперсии ω (k) направляемой моды в слу-

Рис. 4. Дисперсионные кривые в случае β = 0.487π/a.

чае β = 0. Горизонтальные штрихпунктирные линии TWU

Обозначения такие же, как на рис. 2 и 3

и TWL отвечают соответственно верхней и нижней грани-

цам окна прозрачности

При ненулевых константах распространения β =

, эВ

= 0 возникает новая мода. Как показывает числен-

ное моделирование, при β < 0.244π/a она целиком

4.0

Световой конус

расположена ниже окна прозрачности серебра. Для

TWU

массива, рассмотренного в настоящей работе, это от-

3.5

вечает константе распространения β_min ≈ 15 мкм-1.

На рис. 3 новая мода изображается кружками в

случае диэлектрической проницаемости, взятой из

3.0

[20]. Сплошная кривая представляет закон диспер-

сии ω(k) новой моды, полученный в приближении

2.5

Друде - Лоренца.

При увеличении константы распространения от

2.0

0 до β_min моды, изображенные на рис. 2, эволю-

ционируют. На рис. 3 им соответствуют треуголь-

ники и звездочки, так же как и штрихпунктирные

1.5

линии рядом с ними. Обозначения такие же, как

на рис. 2. При дальнейшем увеличении константы

1.0

TWL

распространения длинноволновая часть дисперси-

онной кривой новой моды входит в окно прозрач-

= 0.244

ности. По достижении значения β_max = 0.487π/a

0.5

0.2

0.4

0.6

0.8

1.0

она целиком сдвигается в окно прозрачности, как

ka/

показано на рис. 4. Для рассматриваемого массива

β_max = 30 мкм-1.

Рис. 3. Закон дисперсии направляемых мод ω (k) в случае

Отметим, что результаты, полученные в рамках

βmin = 0.244π/a

модели Друде - Лоренца, отличаются от результа-

тов, полученных с использованием табличных дан-

ных о диэлектрической проницаемости, менее чем

А. А. Анастасиев, А. Л. Бурин, Ю. Каган и др.

ЖЭТФ, том 157, вып. 1, 2020

на 3 %. В процессе численного моделирования учи-

системах имеются моды, свойства которых схожи

тывается конечное количество членов в разложени-

со свойствами мод, описанных в работе [11]. Однако

ях (1) и (3), т. е. |m| < m_max. Как показывает ана-

они расположены вблизи верхней границы окна

лиз, m_max = 10 достаточно, чтобы воспроизводить

прозрачности и не обладают достаточно большой

новую моду с точностью не хуже 1 %. В то же время

добротностью. Как и в случае волноводов, изготов-

для воспроизведения результатов работы [11] с той

ленных из серебра, положение мод с β = 0 в этих

же точностью необходимо взять m_max = 20.

системах относительно окна прозрачности оказы-

вается сильно зависящим от величины константы

распространения. Таким образом, с помощью вы-

4. ЗАКЛЮЧЕНИЕ

бора подходящего значения β новую моду можно

переместить в область частот, где поглощение

Изучен закон дисперсии направляемых мод в

материала волновода минимально.

плоских массивах близко расположенных волново-

дов. Отметим, что, в отличие от работы [11], была

Благодарности. Авторы выражают благодар-

учтена мнимая часть диэлектрической проницаемо-

ность В. П. Крайнову за обсуждение полученных

сти. Показано, что в дополнение к результатам, по-

результатов.

лученным в [11], при ненулевых константах распро-

Финансирование. Работа выполнена при под-

странения β = 0 возникает новый тип направляе-

держке Российского фонда фундаментальных ис-

мых мод в системе серебряных цилиндров. В слу-

следований (гранты №№18-32-00204 (AAA, YuIP),

чае 0 < β < β_min новая мода сильно поглощается

19-02-00433 (IYP)) и Национального научного фон-

материалом волновода. Однако, начиная с некото-

да (грант NSF 1900568 (ALB)).

рых значений констант распространения β > β_max

она при всех значениях квазиволнового вектора k

попадает в окно прозрачности серебра, где потери

ЛИТЕРАТУРА

малы (тангенс угла потерь меньше 0.05). Также бы-

A. R. McCurn and A. A. Maradudin, Phys. Rev.

ла изучена эволюция фундаментальной поперечной

B 48, 17576 (1993).

и первой продольной мод при увеличении β от ну-

ля до β_max. В работе [11] было показано, что эти

V. Kuzmiak and A. A. Maradudin, Phys. Rev. B 55,

моды могут иметь одинаковую частоту при одном

7427 (1997).

и том же квазиволновом векторе. Описанное свой-

O. L. Berman, M. I. Gozman, S. L. Eiderman, and

ство может быть полезно для реализации переклю-

R. D. Coalson, Phys. Rev. B 74, 092505 (2006).

чения между этими модами. Однако, как следует из

рис. 4, при достаточно больших значениях β эта осо-

G. S. Blaustein, M. I. Gozman, O. Samoylova,

бенность спектра исчезает. Кроме того, при β = 0

I. Ya. Polishchuk, and A. L. Burin, Opt. Express 15,

моды, изображенные на рис. 2, обладают сильной

17380 (2007).

дисперсией, но по мере увеличения β они постепен-

I. Ya. Polishchuk, M. I. Gozman, G. S. Blaustein, and

но становятся бездисперсионными (рис. 3 и 4).

A. L. Burin, Phys. Rev. E 81, 026601 (2010).

Имеются два механизма затухания направляе-

мых мод. Первый из них — это поглощение мате-

I. Ya. Polishchuk, A. A. Anastasiev, E. A. Tsyv-

риалом волновода. Мы исключили такую возмож-

kunova, M. I. Gozman, S. V. Solov’ov, and Yu. I.

ность, поскольку рассматриваем моды, распростра-

Polishchuk, Phys. Rev. A 95, 053847 (2017).

няющиеся в окне прозрачности. Второй механизм

E. N. Bulgakov and A. F. Sadreev, Phys. Rev. A 97,

связан с возможностью перехода направляемой мо-

033834 (2018).

ды в свободный фотон. Этот канал затухания запре-

√

щен, если закон дисперсии удовлетворяет соотноше-

Yu. Kagan and A. M. Afanas’ev, JETPh 50, 271

нию ω <

k² + β² (см. работу [6]). Направляемые

(1966) [Sov. Phys. JETP 23, 178 (1966)].

моды на рис. 2-4 подчиняются этому условию и, сле-

V. M. Agranovich and O. A. Dubovskii, Pis’ma v Zh.

довательно, являются безызлучательными.

Eksp. Theor. Fiz. 3, 345 (1966) [Sov. Phys. JETP

В заключение коротко обсудим особенности

Lett. 3, 223 (1966)].

рассмотренных массивов, волноводы в которых

изготовлены из золота или меди. Аналогичное

10.

S. A. Maier, P. G. Kik, and H. A. Atwater, Phys. Rev.

моделирование показывает, что при β = 0 в таких

B 67, 205402 (2003).