ЖЭТФ, 2020, том 157, вып. 1, стр. 20-35

РАССЕЯНИЕ ВОЛНОВЫХ ПАКЕТОВ НА ПОВЕРХНОСТИ

ТОПОЛОГИЧЕСКИХ ИЗОЛЯТОРОВ В ПРИСУТСТВИИ

ПОТЕНЦИАЛЬНЫХ БАРЬЕРОВ С НАМАГНИЧЕННОСТЬЮ

Д. В. Хомицкий^*, Д. А. Кулаков

Национальный исследовательский Нижегородский государственный университет им. Н. И. Лобачевского

603950, Нижний Новгород, Россия

Поступила в редакцию 7 мая 2019 г.,

после переработки 2 сентября 2019 г.

Принята к публикации 3 сентября 2019 г.

На основе метода Кэли численно решается нестационарное уравнение Шредингера для волновых пакетов,

образованных из поверхностных состояний на поверхности топологических изоляторов и рассеивающихся

на потенциальном барьере, в том числе на барьере с намагниченностью. Рассчитываются коэффициент

прохождения и распределения спиновой плотности. Найдены выражения для статического коэффициента

прохождения через барьер с помощью приближения плоских волн и его обобщения для волновых паке-

тов. Показано, что двумерный характер волновых пакетов приводит к заметным различиям в поведении

коэффициента прохождения по сравнению с задачей о рассеянии плоских волн. Так, для двумерных паке-

тов наблюдается существенное подавление эффекта клейновского туннелирования в некоторых областях

энергии. Полученные результаты говорят о возможностях воздействия через потенциальные барьеры на

туннелирование и спиновую плотность локализованных электронных состояний типа волновых пакетов в

структурах на основе топологических изоляторов.

DOI: 10.31857/S0044451020010034

Это явление рассматривалось для различных струк-

тур с бессмассовым спектром. Можно упомянуть

некоторые работы для графена [7-10], а также для

других систем с дираковским спектром [11-13], в

1. ВВЕДЕНИЕ

том числе при наличии нестационарных барьеров

[14]. Прохождение состояний вида плоских волн че-

Управление электронными состояниями в топо-

рез поверхности топологических изоляторов и свя-

логических изоляторах [1-5] и подобных им струк-

занные с этим транспортные задачи изучались так-

турах представляет собой важную задачу этого ак-

же и при наличии магнитных барьеров [15-23]. Ос-

тивно развивающегося раздела физики конденси-

новной особенностью влияния магнитных барьеров

рованного состояния. Известно, что процессы рас-

в цитированных выше работах является существен-

пространения электронных состояний через такие

ная модификация эффекта клейновского туннели-

структуры даже в присутствии немагнитных потен-

рования, вплоть до его ослабления и исчезновения

циальных барьеров, например, в графене [6, 7] про-

при определенных энергиях. Также необходимо от-

текают с существенными особенностями, вызванны-

метить, что при наличии магнитных неоднородно-

ми линейным (или безмассовым) характером спек-

стей существенно изменяются транспортные и ста-

тра как функции квазиимпульса при малых энер-

тистические свойства поверхностных состояний в

гиях, для состояний, называемых фермионами Ди-

топологических изоляторах [1, 2, 24, 25]. Таким об-

рака. Так, при нормальном падении плоской волны

разом, уже намечены пути к управлению элект-

на немагнитный барьер наблюдается эффект полно-

ронными состояниями на поверхности топологичес-

го прохождения независимо от энергии волны, по-

ких изоляторов с помощью барьеров, которые мо-

лучивший название клейновского туннелирования.

гут создавать конфайнмент. Упомянутые выше ра-

боты также объединяет подход, при котором элект-

^* E-mail: khomitsky@phys.unn.ru

ронные состояния рассматриваются в виде плоских

ЖЭТФ, том 157, вып. 1, 2020

Рассеяние волновых пакетов на поверхности. . .

волн или их простых комбинаций, делокализован-

аналитического исследования, в той мере, в которой

ных в пространстве.

это допускают уравнения задачи.

Следует отметить, что помимо исследования ди-

В данной работе будет выполнено численное ис-

намики и транспорта для состояний вида плоских

следование динамики волновых пакетов на поверх-

волн представляют интерес и подобные задачи для

ности топологических изоляторов семейства Bi₂Te₃

локализованных электронных состояний на поверх-

в присутствии различных потенциальных барьеров,

ности (или на краю) топологических изоляторов,

как неполяризованных, так и поляризованных (маг-

имеющих при этом определенное направление дви-

нитных). Мы применяем вычислительную схему Кэ-

жения и определенные проекции спина. Наиболее

ли [42, 43] для решения нестационарного уравнения

простым образом такие состояния описываются в

Шредингера, которая позволяет аппроксимировать

терминах волновых пакетов. За последние годы про-

оператор унитарной эволюции с высокой точностью.

блемам динамики волновых пакетов в системах ти-

Будет рассмотрена динамика и коэффициенты про-

па топологический изолятор или полупроводник,

хождения для различных поляризаций барьера и

где важна роль спин-орбитального взаимодействия,

различных углов среднего волнового вектора па-

уделялось значительное внимание. Свободная ди-

кета с нормалью к барьеру. Также будет обсуж-

намика таких пакетов исследовалась уже около 10

даться эволюция распределений спиновой плотно-

лет назад [26-28]. Кроме того, изучалась динамика

сти на плоскости в области вблизи барьера. В рам-

релятивистских волновых пакетов, подчиняющих-

ках аналитического подхода будет рассмотрена со-

ся уравнению Дирака [29], коллапс, возрождение

ответствующая статическая задача о рассеянии со-

волновых пакетов и осцилляции типа zitterbewegung

стояний на немагнитных и магнитных барьерах, ре-

[27, 30-32], эффекты фазы Берри в магнитном по-

зультаты которой обобщаются на случай волновых

ле [33], а также динамика пакетов в графене в при-

пакетов, построенных из плоских волн. Вначале ста-

сутствии потенциала беспорядка [34]. Динамика од-

тическая задача решается нами для плоских волн,

номерных краевых состояний под действием им-

а затем полученный коэффициент прохождения ис-

пульсов электрического поля в двумерном тополо-

пользуется для расчета прохождения их интеграль-

гическом изоляторе изучалась в недавних работах

ной комбинации, дающей волновой пакет. Будет по-

[35-37]. Также рассматривались компактные объек-

казано, что именно двумерный характер волновых

ты типа квантовых точек, сформированных на базе

пакетов приводит к существенным различиям в по-

топологических изоляторов, в том числе две свя-

ведении коэффициента прохождения по сравнению

занные квантовые точки [38]. Задача о динамике

с задачей о рассеянии плоских волн. Именно, на-

пакетов в локализованной на краю топологическо-

личие в двумерном волновом пакете плоских волн

го изолятора квантовой точке исследовалась в на-

с различными проекциями волновых векторов от-

шей недавней работе [39]. Известно, что особенно-

носительно нормали к барьеру приводит к суще-

сти линейного спектра в топологических изолято-

ственному подавлению эффекта клейновского тун-

рах вместе с влиянием слагаемых высшего порядка

нелирования для налетающего на барьер пакета в

с различной симметрией, таких как кубические чле-

определенном интервале энергий. Подобные особен-

ны в гамильтониане, приводят к появлению новых

ности могут иметь существенное значение для со-

эффектов [40]. В частности, нами было обнаруже-

здания схем управления электронными состояниями

но появление новых пиков в частотной зависимо-

в структурах на основе топологических изоляторов,

сти коэффициента поглощения электромагнитного

если в них возбуждаются состояния вида локализо-

излучения и новых особенностей пространственной

ванных волновых пакетов.

траектории циклотронного движения волновых па-

Работа состоит из пяти разделов. В разд. 2 мы

кетов [41]. Следует ожидать появления новых эф-

описываем модель поверхностных состояний в то-

фектов и в динамических задачах, таких как про-

пологических изоляторах с барьерами и схему Кэ-

хождение волновых пакетов через структуру с по-

ли для моделирования динамики волновых пакетов.

тенциальными барьерами, в том числе при наличии

В разд. 3 обсуждаются основные результаты, полу-

у барьеров постоянной намагниченности. Такая по-

ченные в рамках этой модели. В разд. 4 приводятся

становка вопроса приводит к необходимости постро-

расчеты коэффициента прохождения для статичес-

ения как эффективной схемы численного решения

кой задачи, обсуждаются ее связи с динамической

нестацонарного уравнения Шредингера для дина-

задачей. В заключительном разд. 5 сформулирова-

мики волновых пакетов на поверхности топологиче-

ны выводы.

ских изоляторов с барьерами, так и сопутствующего

Д. В. Хомицкий, Д. А. Кулаков

ЖЭТФ, том 157, вып. 1, 2020

2. ГАМИЛЬТОНИАН ЗАДАЧИ И СХЕМА

Полный гамильтониан задачи, таким образом, име-

РЕШЕНИЯ

ет вид H = H₀ + f(x, y)(M · σ). Подобно прибли-

жению, принятому в работах [1, 15, 17, 18, 21, 23],

Низкоэнергетическая часть спектра поверхност-

этот гамильтониан записан с обменным слагаемым

ных состояний в трехмерных топологических изо-

f (x, y)(M · σ), обусловленным магнитным полем ба-

ляторах семейства Bi₂Te₃ может быть описана без-

рьера, и не содержит векторного потенциала маг-

массовым гамильтонианом для фермионов Дирака

нитного поля, генерируемого намагниченностью ба-

вида [1-5]

рьера, который использовался в ряде других ра-

бот со сходной постановкой задачи [16, 19, 22]. Та-

H₀ = C + A(k_xσ_y - k_yσ_x).

(1)

кое приближение можно обосновать тем, что взаи-

модействие со спином налетающих на барьер состо-

Здесь C — начало отсчета энергии (точки Дира-

яний имеет локальный характер и сосредоточено це-

ка) относительно спектра объемных состояний, зна-

ликом внутри области барьера с постоянной намаг-

чение которого зависит от выбора начала отсче-

ниченностью. Параметры барьера в гамильтониане,

та энергии в данной конкретной модели. Параметр

связанные со вторым слагаемым, являются управ-

A = ℏv_F, где v_F

— характерная скорость вбли-

зи поверхности Ферми. Для топологического изо-

ляющими параметрами задачи, наряду с энергией

состояний, для которых рассматривается прохожде-

лятора на базе Bi₂Te₃ значения параметров vF =

= 6.2 · 10⁷ см/с (что отвечает A = 406.8 мэВ · нм) и

ние через барьер. Мы будем рассматривать барьеры

с какой-либо одной компонентой намагниченности

C = -0.18 эВ [4,5]. Спектр (1) определяет две ветви

закона дисперсии:

M = (M_x,M_y,M_z). Немагнитный барьер описыва-

ется единичной матрицей σ₀ =

^Ê. Величина намаг-

√

ниченности будет учитываться нами в амплитуде U₀

ε1,2 = C ± A k2x + k2y.

(2)

пространственного профиля барьера U(x, y), имею-

В дальнейшем мы будем отсчитывать энергию от

щей смысл энергии обменного взаимодействия, ли-

точки Дирака поверхностных состояний с законом

бо высоты немагнитного барьера при σ_k = σ₀. Это

дисперсии (2). При моделировании состояний основ-

позволит записывать гамильтониан для барьера с

ной вклад вносит верхняя ветвь ε₁ закона дисперсии

намагниченностью вдоль x_k, где k = x, y, z, 0, в про-

(2), поскольку в известных к настоящему времени

стой форме

экспериментах с топологическим изолятором на ба-

H = H₀ + U(x,y)σ_k.

(3)

зе Bi₂Te₃ уровень Ферми был расположен в состоя-

ниях верхней ветви, где были обнаружены наиболее

Мы не рассматриваем дополнительные члены

интересные эффекты [3, 4, 9, 23, 40]. Как следствие,

для гамильтониана (3), связанные с рассеянием по-

нижняя ветвь спектра вносит пренебрежимо малый

верхностных состояний на дефектах, неоднородно-

вклад в волновой пакет, построенный из состояний

стях, а также на фононах. В качестве обоснования

вблизи уровня Ферми.

можно упомянуть, во-первых, изначальную устой-

Нашей целью является исследование динамики

чивость поверхностных состояний в топологических

системы, в которой к гамильтониану (1) добавле-

изоляторах к рассеянию на немагнитных примесях

но слагаемое, отвечающее потенциальному барье-

[1-4]. Во-вторых, мы рассматриваем задачу в отно-

ру с пространственным профилем f(x, y) и намаг-

сительно небольшой области вблизи потенциально-

ниченностью M, локализованной в области барье-

го барьера и с небольшим по сравнению с разме-

ра. Для постоянной в области барьера намагничен-

ром барьера волновым пакетом, что ограничивает

ности функция f(x, y) имеет вид локализованной

весь пространственный масштаб задачи величина-

ступеньки, отличной от нуля только внутри барье-

ми порядка 0.2 . . . 0.4 микрона. С учетом высокого

ра. Влияние намагниченности в этом случае можно

качества материалов, используемых при производ-

приближенно представить [1, 15, 17, 18, 21, 23] в виде

стве топологических изоляторов [1,2], такие разме-

обменного по форме оператора (M · σ) = M_xσ_x +

ры не превышают типичной длины свободного про-

+ M_yσ_y + M_zσ_z, описываемого в базисе состояний

бега электронов, что обосновывает пренебрежение

псевдоспина σ = (σ_x, σ_y , σ_z) для гамильтониана (1).

в нашей задаче эффектами релаксации импульса и

Следует отметить, что несмотря на представление

спина.

гамильтониана (1) в базисе псевдоспина, а не истин-

В этом разделе нашей целью является решение

ного спина, имеет место пропорциональность мат-

нестационарного уравнения Шредингера iℏ ∂Ψ/∂t =

риц σ = (σ_x, σ_y, σ_z ) оператору истинного спина [5].

= HΨ с гамильтонианом (3) при различных пара-

ЖЭТФ, том 157, вып. 1, 2020

Рассеяние волновых пакетов на поверхности. . .

метрах барьера и налетающего на него волнового

пакета. Для численного решения этого уравнения с

аппроксимацией оператора эволюции во втором по-

рядке точности по шагу временной дискретизации

| |

отн. ед.

Δt удобной является схема Кэли [42, 43], в которой

0.010

значение волновой функции — двухкомпонентного

спинора

0.005

(

)

-50

Ψn+1(x, y) =

Ψn+11, Ψn+12

x, нм

100

на n + 1-м шаге дискретизации по времени выража-

y, нм

200

ется через ее значение Ψⁿ(x, y) на n-м шаге с помо-

щью следующего оператора:

300

Рис. 1. Схема, показывающая исходное положение волно-

1 - iHΔt/2ℏ

Ψn+1 =

Ψⁿ.

(4)

вого пакета (7) с плотностью вероятности |ψ|² вблизи по-

1 + iHΔt/2ℏ

тенциального барьера-ступеньки, параллельного оси y и

занимающего область вдоль оси x c L = 100 нм. Направ-

Для практического применения схему (4) удоб-

ление распространения пакета k ориентировано вдоль оси

но переписать с помощью вспомогательной функции

x, начальная спиновая поляризация σ направлена вдоль y

Φ(x, y):

Ψn+1 = Φ - Ψⁿ,

(5)

3. РЕЗУЛЬТАТЫ РАСЧЕТА ДИНАМИКИ

где двухкомпонентная функция Φ(x, y) = (Φ₁(x, y),

ВОЛНОВОГО ПАКЕТА

Φ₂(x, y)) в каждой точке пространственной сетки

(x, y) определяется как решение уравнения

Мы находим численное решение системы урав-

(

)

нений (5), (6) для начального состояния, представ-

iHΔt

Φ = 2Ψⁿ.

(6)

ляющего собой с точки зрения пространственного

2ℏ

профиля волновой пакет, локализованный по обеим

координатам в плоскости (xy):

При использовании стандартных конечно-раз-

ностных аппроксимаций на пространственной сет-

(

)

{

}

ке (x = nxΔx, y = nyΔy) для операторов ki

C₁

(x - x₀)²

Ψ(x, y) =

exp

+ikxx

= -i∂/∂x_i, входящих в гамильтониан (3), уравне-

C₂

2Δx²

ние (6) переходит в систему линейных алгебраиче-

{

}

(y - y₀)²

ских уравнений для конечно-разностной аппрокси-

× exp

+ikyy

(7)

мации функции Φ(n_x, n_y), через которую с помо-

2Δy²

щью (5) определяются компоненты волновой функ-

ции Ψn1,2(n_x, n_y). Таким образом, для каждого мо-

Компоненты C1,2 спинорной части (7) определя-

мента времени t = nΔt необходимо решить систему

ют начальную спиновую поляризацию волнового па-

из N_x × N_y линейных уравнений, где N_x,y опреде-

кета, координаты (x₀, y₀) задают его начальное по-

ляют пределы покрытия области эволюции в про-

ложение, а значения (kx,ky) определяют средний

странственных координатах (x, y).

волновой вектор пакета, который налетает на ба-

Шаг по времени Δt в аппроксимации (4) выби-

рьер под углом θ = arctg(ky/kx). Значение моду-

рается нами, исходя из условия (EΔt)/(2ℏ) ≪ 1,

ля среднего волнового вектора связано со средней

обеспечивающего устойчивость схемы Кэли. Приме-

энергией пакета E через закон дисперсии (2). Для

нительно к типичным значениям средней энергии

собственных состояний гамильтониана (1) направ-

E, достигающей в наших расчетах нескольких со-

ление распространения в плоскости (k_x, k_y) задает и

тен мэВ, это дает типичную величину Δt ≤ 10-15 с.

спиновую поляризацию (S_x, S_y), перпендикулярную

Шаг по координатам (Δx, Δy) выбирается, исходя

волновому вектору [1-5].

из условия достаточного пространственного разре-

Наиболее простым случаем, важным с практи-

шения для структуры волнового пакета с типичной

ческой точки зрения, является прохождение через

полушириной около 10 нм, что дает типичную вели-

потенциальный барьер-ступеньку, занимающий ко-

чину Δx(y) ≤ 1 . . . 2 нм.

нечную область [-L/2, L/2] вдоль оси x и прости-

Д. В. Хомицкий, Д. А. Кулаков

ЖЭТФ, том 157, вып. 1, 2020

рающийся вдоль оси y, т. е. моделирование барьера

Для системы с безмассовым гамильтонианом, как

функцией

в нашей задаче, второй способ представляется оп-

тимальным. В самом деле, с учетом того, что для

U (x, y) = U₀,

-L/2 < x < L/2,

(8)

спектра (2) модуль групповой скорости всех состо-

и равной нулю в остальных точках плоскости. Схе-

яний с различным по модулю волновым вектором

матически исходное положение пакета вида (7) от-

одинаков и равен фермиевской скорости v_F , можно

носительно барьера, рассматриваемое в наших рас-

дать простую оценку для интервала взаимодействия

четах, показано на рис. 1. Мы используем типич-

Δt = t₁ - t₀ пакета с барьером:

ное значение полуширины пакета Δx

= Δy =

L+L_wp

= 10 нм, а ширины барьера варьируются в диапа-

Δt =

(10)

v_F

зоне L = 50 . . .200 нм. На рис. 1 для удобства вос-

приятия показан барьер c L = 100 нм. Направле-

В (10) L — ширина барьера, а L_wp — харак-

ние распространения пакета k здесь ориентировано

терный размер волнового пакета, связанный с па-

вдоль x перпендикулярно барьеру, начальная спино-

раметром полуширины Δx(y) в (7) соотношением

вая поляризация σ состояний, составляющих волно-

L_wp = pΔx, где p — множитель, определяющий то

вой пакет, направлена вдоль y, т.е. σ_y(t = 0) = 1.

расстояние от центра пакета, на котором уже есть

При этом коэффициенты двухкомпонентного спи-

заметный с вычислительной точки зрения вклад в

нора в (7) могут быть выбраны, например, в виде

плотность вероятности. В нашей модели мы выби-

√

(C₁, C₂) = (1, i)/

рали p = 5 . . . 6, что обеспечивает учет всей обла-

Вначале мы рассмотрим случай нормального па-

сти с существенно ненулевой плотностью вероятно-

дения на барьер, т. е. при θ = 0, при этом начальная

сти. Учитывая, что нами рассматривались узкие по

спиновая поляризация пакета будет направлена по

сравнению с шириной барьера (L = 200 нм) паке-

оси y. Параметры барьера будут такими: амплиту-

ты с Δx(y) = 10 нм, мы получим, что простран-

да U₀ = 300 мэВ, ширина L = 200 нм. В качестве

ственный параметр в (10) L + L_wp = 300 . . .320 нм.

первой функции, характеризующей рассеяние паке-

Принимая во внимание значение фермиевской ско-

та, мы рассмотрим коэффициент прохождения как

рости v_F = 6.2 · 10⁷ см/с, мы получим для времени

функцию средней энергии пакета E, определяемой

(10) значение порядка (4.8 . . . 5.1)·10-13 с. Мы брали

средними значениями компонент волнового векто-

всегда наибольшее из времен. Момент времени t₀ на-

ра (kx,ky) в начальном состоянии (7). Коэффици-

чала взаимодействия пакета с барьером определял-

ент прохождения T (E) мы определяем вначале че-

ся нами по достижению центром пакета расстояния

рез амплитуду волновой функции Ψ = (Ψ₁, Ψ₂) па-

L_wp = pΔx до начала барьера. Момент времени t₁

кета, прошедшего через барьер:

может быть определен после вычисления (10) как

∫

t₁ = t₀ + Δt.

|Ψ(x > L/2, t = t₁)|²dx dy

T (E) =

∫

(9)

Скажем еще несколько слов о наблюдении эф-

|Ψ(x < -L/2, t = t₀)|²dx dy

фектов, связанных с туннелированием дираковских

Интегрирование в (9) ведется в области справа

электронов. Для практического применения выра-

от барьера для прошедшей части пакета при t = t₁ и

жения (9), например, в экспериментах по электрон-

слева от барьера для налетающего пакета при t = t₀,

ному транспорту, можно представить расположен-

где t₀ и t₁ — моменты времени соответственно нача-

ные слева и справа от барьера детекторы локальной

ла и окончания взаимодействия пакета с барьером.

электронной плотности, фиксирующие налетающий

В процессе численного решения задачи эти моменты

и прошедший через барьер заряд (число электро-

времени определяются при непосредственном моде-

нов), сформированные волновым пакетом. Более де-

лировании эволюции по схеме Кэли.

тальное описание возможных здесь экспериментов,

Остановимся на определении моментов времени

однако, выходит за рамки данной работы.

t₀ и t₁ более подробно. Начиная с работы Бюттике-

Мы рассматривали несколько магнитных поля-

ра и Ландауэра [44] известны способы определения

ризаций барьера в гамильтониане (3), а также непо-

времени взаимодействия с барьером, применяемые

ляризованный барьер, когда матрица Паули в (3)

для задачи о туннелировании массивной частицы.

равна σ₀, т. е. единичной матрице. На рис. 2а по-

Также можно вводить время туннелирования, зная

казана зависимость коэффициента прохождения (9)

линейный размер проходимой пакетом области вза-

от средней энергии пакета для трех типов поляри-

имодействия с барьером и характерную скорость па-

зации барьера: σ₀ (немагнитный барьер), σ_x и σ_z.

кета, как это обсуждалось, например, в работе [45].

Видно, что для всех поляризаций барьера энерге-

ЖЭТФ, том 157, вып. 1, 2020

Рассеяние волновых пакетов на поверхности. . .

развитому для задачи о безмассовых фермионах в

графене в работе [8]. Именно, можно сопоставлять

плотность потока в прошедшем и падающем на ба-

рьер состоянии, т.е. анализировать среднее значе-

ние оператора скорости v_x = ∂H/ℏ∂k_x. Для гамиль-

тониана (1)-(3) это приводит к выражению

v_x =

σy,

(11)

ℏ

а вместо формулы (9) для коэффициента прохожде-

ния мы получим схожее по структуре выражение

T1(E) =

∫

Ψ⁺(x > L/2, t = t1)vxΨ(x > L/2, t = t1) dxdy

∫

Ψ⁺(x < -L/2, t = t0)vxΨ(x < -L/2, t = t0)dxdy

(12)

Энергетическая зависимость для коэффициен-

та прохождения в форме (12) показана на рис. 2б.

Можно видеть, что она во многом схожа с графи-

ком для коэффициента в форме (9) на рис. 2а. Это

можно объяснить доминирующей y-проекцией спи-

на в падающем на барьер волновом пакете, бла-

годаря чему распределения плотности вероятности

Рис. 2. a) Зависимость коэффициента прохождения (9) от

и y-компоненты спиновой плотности близки друг

средней энергии волнового пакета (7) для рассеяния на

барьере (8) с шириной L = 200 нм и амплитудой U0 =

к другу. Поскольку, как это будет показано ниже,

= 300 мэВ, для разных типов направления намагниченно-

при туннелировании через магнитный барьер может

сти барьера (σ0 — немагнитный барьер, σx, σz — магнит-

происходить поворот спина, значение y-компоненты

ные барьеры), при нормальном падении на барьер; б) то

спина в прошедшем состоянии может дать меньшее

же для коэффициента прохождения в форме (12)

значение коэффициента (12) по сравнению с коэф-

фициентом (9). Можно заметить подобное снижение

амплитуды коэффициента прохождения на рис. 2б

тическая зависимость коэффициента прохождения

по сравнению с рис. 2а, особенно существенное для

в целом схожая. Тем не менее различия в коэффи-

низких энергий E < U₀, отвечающих подбарьерному

циенте прохождения составляют от 10 % до 50 % в

прохождению.

области энергий E > U₀, отвечающей надбарьерно-

Анализируя результаты на рис. 2 для обоих под-

му прохождению. Такие различия являются значи-

ходов (9) и (12) к определению коэффициента про-

мым фактором для потенциальных приложений в

хождения, следует отметить существенное отличие

схемах со спиновым фильтром, когда прохождение

рассеяния двумерных волновых пакетов на электро-

зависит от поляризаций налетающего состояния и

статическом барьере-ступеньке (при σ_k

= σ₀) от

барьера. Интервал для средней энергии волнового

рассеяния на аналогичном барьере состояний вида

пакета на рис. 2а и для последующих расчетов мы

плоских волн [7,9,16]. В последнем случае при нор-

взяли в достаточно широких пределах, до 0.85 эВ.

мальном падении плоской волны наблюдается эф-

Для такой максимальной энергии следует ожидать

фект клейновского туннелирования, при котором

перекрытия зон краевых и объемных состояний в

коэффициент прохождения равен единице незави-

топологических изоляторах семейства Bi₂Te₃ [1-4].

симо от энергии падающей волны и высоты барье-

Мы сохранили подобный энергетический интервал

ра. Этот же эффект можно ожидать и для одно-

в расчетах с целью расширить наше моделирование

мерных волновых пакетов, волновые вектора для

на возможно большую область параметров, вклю-

которых располагаются вдоль прямой с ориентаци-

чая среднюю энергию пакета.

ей (k_x, 0). Для двумерного волнового пакета вида

Коэффициент прохождения через барьер мож-

(7) данный эффект в чистом виде, т. е. со значе-

но определить и иначе, следуя, например, подходу,

нием коэффициента прохождения T = 1, не имеет

Д. В. Хомицкий, Д. А. Кулаков

ЖЭТФ, том 157, вып. 1, 2020

места. Действительно, такой волновой пакет собран

из многих плоских волн с различной ориентацией

волнового вектора относительно нормали к барье-

ру. Клейновское туннелирование с T = 1 наблюда-

ется для нормального падения лишь для бесконечно

узкого в плоскости (k_x, k_y) вклада от участка волно-

вых векторов вида (k_x, 0), что не может дать суще-

ственного вклада в коэффициент прохождения для

всего волнового пакета. Этим объясняется характер

зависимости T(E) на рис. 2, которая не достигает

единицы даже для немагнитного, т. е. электростати-

ческого барьера. Подобная особенность свойствен-

на именно прохождению двумерных волновых паке-

тов, и может иметь важное значение при дальней-

ших исследованиях и приложениях их транспорт-

ных свойств.

Кроме энергетической зависимости коэффици-

ента прохождения представляет интерес также его

угловая зависимость, построенная при какой-либо

фиксированной средней энергии пакета. На рис. 3а

приведен пример такой зависимости для барьера

ширины L = 200 нм и амплитудой U₀ = 300 мэВ,

при падении на него волнового пакета со средней

энергией E = 600 мэВ, рассчитанной по формуле

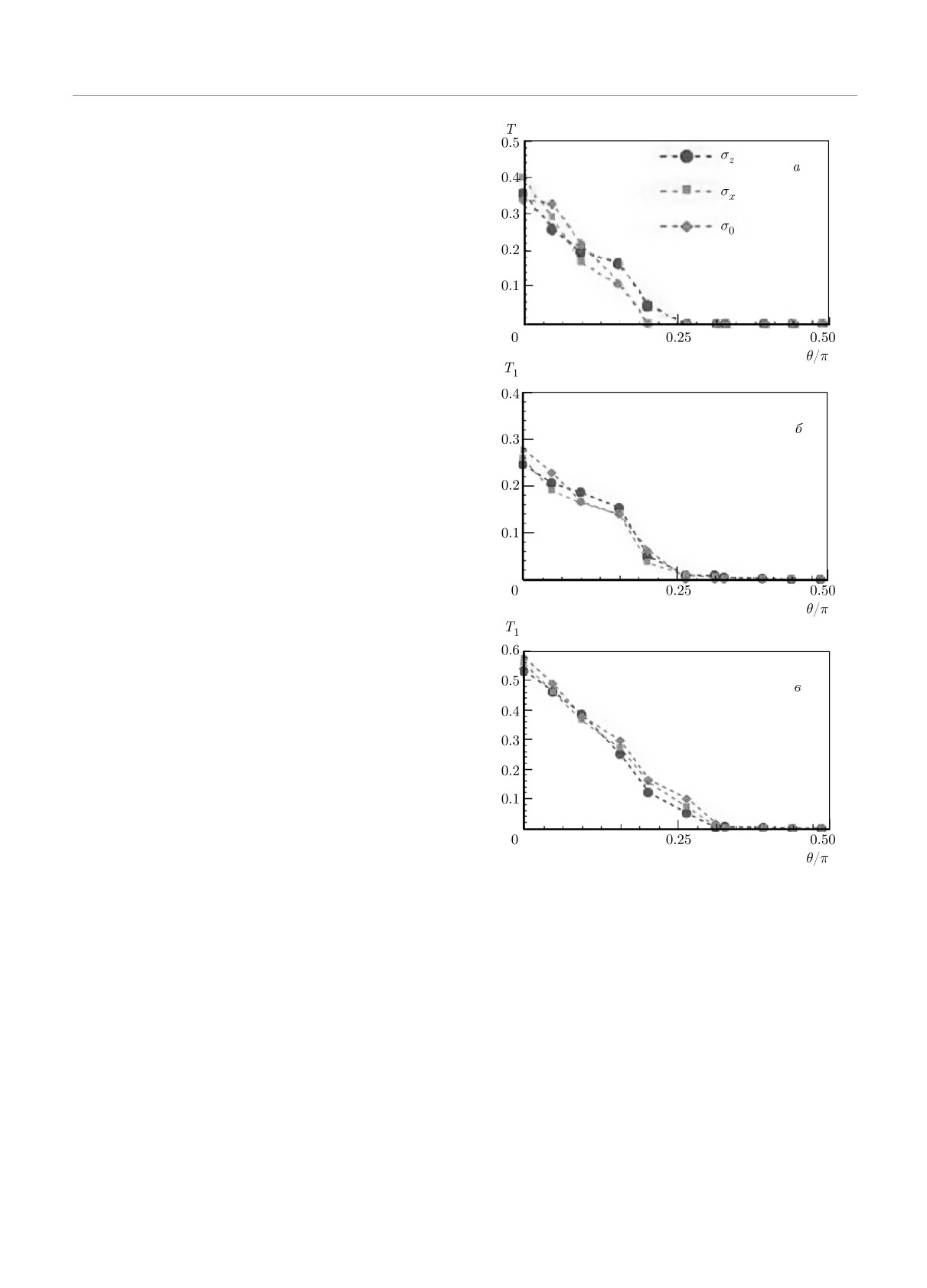
(9). На рис. 3б,в приведены примеры угловых зави-

симостей, полученных с использованием выражения

(12), причем на рис. 3в средняя энергия пакета рав-

на значению 1 эВ, большему по сравнению с графи-

ками на рис. 3а,б. Для всех случаев видно, что по

мере роста угла падения, отсчитываемого в радиа-

нах от нормали к барьеру, коэффициент прохожде-

ния убывает. Для энергии E = 600 мэВ он стано-

вится весьма малым уже при углах около θ = π/4

(рис. 3а,б), а для энергии E = 1 эВ область малых

значений сдвигается вправо (рис. 3в). Обращает на

себя внимание тот факт, что полученная угловая за-

висимость качественно схожа для барьеров с любой

поляризацией, в том числе для немагнитного, т. е.

Рис. 3. а) Угловая зависимость T (θ) коэффициента про-

электростатического барьера (кривая с индексом σ₀

хождения (9) для барьера с шириной L = 200 нм и ам-

на рис. 3). Такое быстрое убывание коэффициента

плитудой U0 = 300 мэВ при падении на него волнового

прохождения в отличие от рассеяния на барьере со-

пакета со средней энергией E = 600 мэВ, показанная для

стояний вида плоских волн [7,9,16] также обсуловле-

различных поляризаций барьера; б) то же для угловой за-

но двумерным характером волнового пакета в нашей

висимости коэффициента T1(θ) из (12); в) то же для коэф-

задаче, для которого отдельные составляющие его

фициента прохождения в форме (12) при средней энергии

плоские волны входят с разными проекциями вол-

пакета E = 1 эВ

нового вектора. При данном значении угла θ для

среднего волнового вектора пакета эти составляю-

щие могут быть ориентированы к нормали для ба-

дения также позволяют говорить о более эффектив-

рьера под значительно большими углами, чем θ. Это

ном механизме конфайнмента двумерных волновых

объясняет более быстрое убывание коэффициента

пакетов на поверхности топологических изоляторов

прохождения для двумерного пакета. Такие особен-

по сравнению с одномерными пакетами или состоя-

ности угловой зависимости коэффициента прохож-

ниями вида плоских волн.

ЖЭТФ, том 157, вып. 1, 2020

Рассеяние волновых пакетов на поверхности. . .

Помимо коэффициента прохождения представ-

ляет интерес воздействие барьера на спиновую плот-

ность налетающего волнового пакета. Можно ожи-

дать, что магнитный барьер будет поворачивать

спин в процессе прохождения пакета, что позволит

говорить о воздействии на спиновую степень сво-

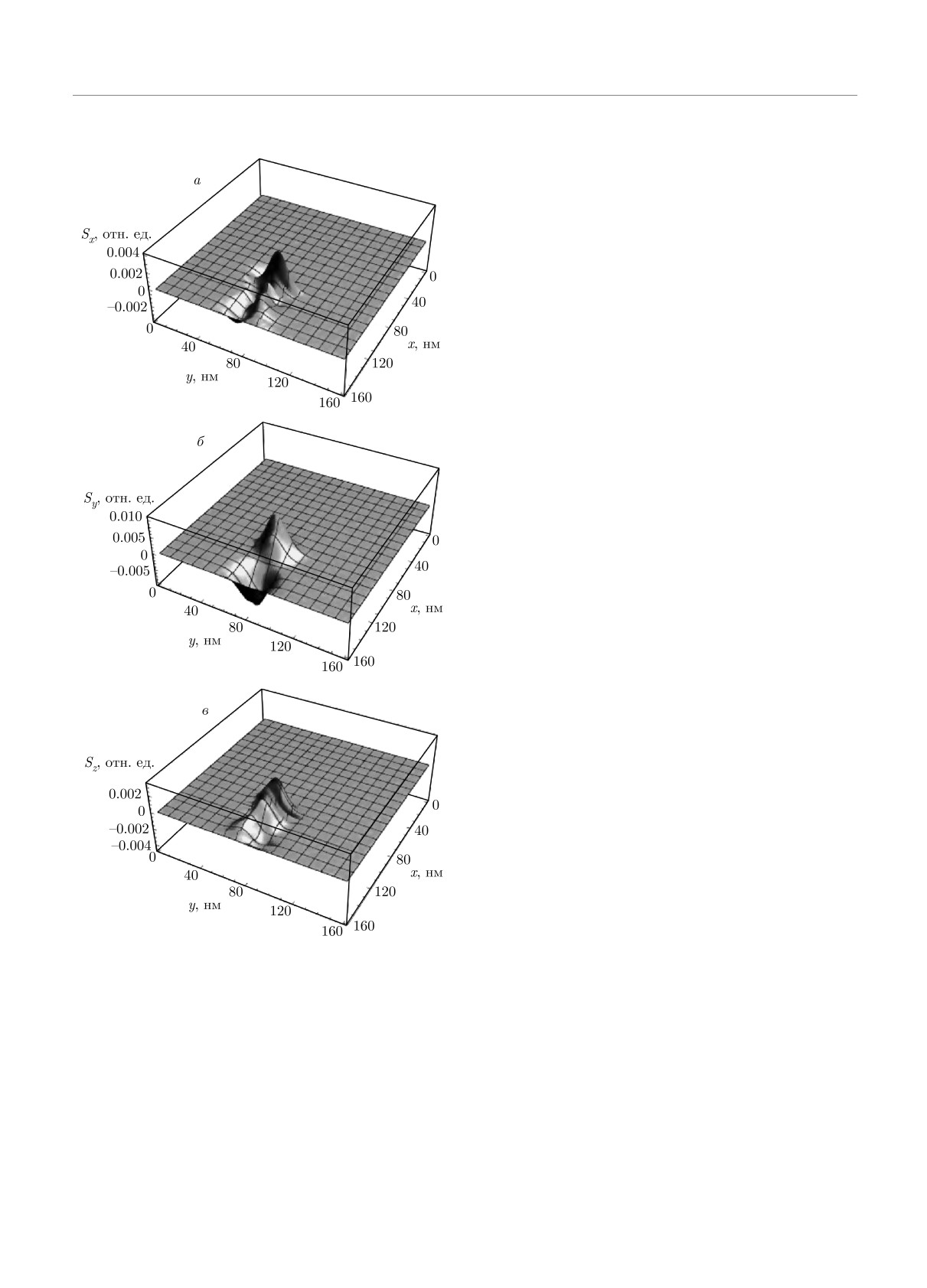
боды при туннелировании через барьер. На рис. 4

показано распределение компонент спиновой плот-

ности S_x(x, y), S_y(x, y) и S_z(x, y), сформировавших-

ся после взаимодействия волнового пакета со сред-

ней энергией 250 мэВ с барьером высотой 130 мэВ

и шириной L = 60 нм. Барьер поляризован вдоль

оси z, что обеспечивает эффективный поворот спина

из его первоначального положения в плоскости, об-

разованной средним волновым вектором пакета (по

оси x) и исходным вектором среднего спина (по оси

y). Начальное распределение спиновой плотности в

волновом пакете, напоминаем, отвечает поляриза-

ции вдоль оси y, т. е. из трех функций компонент

спиновой плотности до взаимодействия с барьером

была отлична от нуля лишь S_y(x, y). Из рис. 4 мож-

но сделать вывод, что наличие намагниченности у

барьера приводит к появлению двух остальных ком-

понент спиновой плотности S_x(x, y) и S_z (x, y), отсут-

ствовавших у исходного пакета.

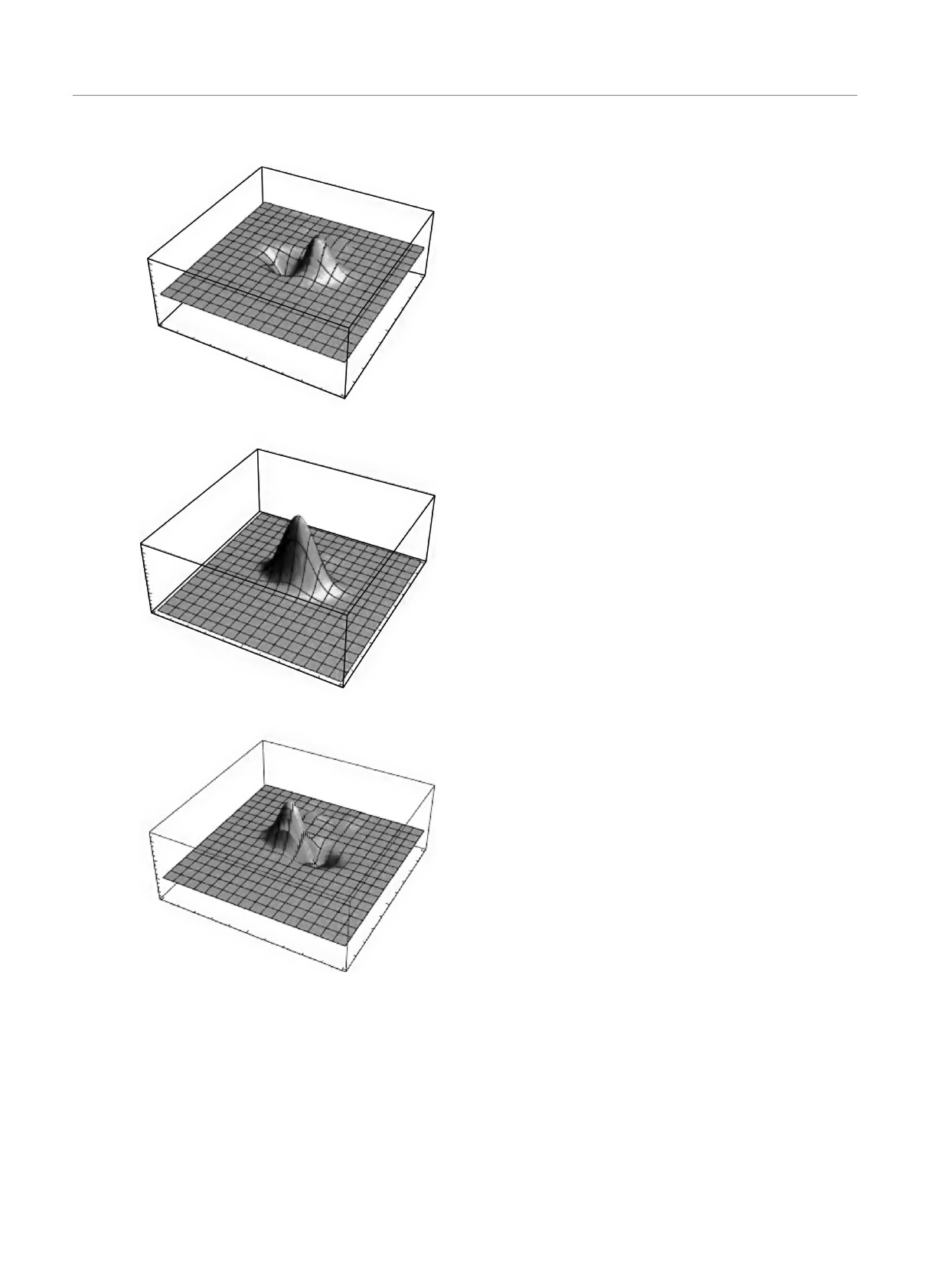
Если волновой пакет рассеивается на немагнит-

ном барьере, картина распределения спиновой плот-

ности после взаимодействия с барьером меняется.

На рис. 5 показано распределение спиновой плот-

ности, аналогичное показанному на рис. 4, но для

взаимодействия пакета со средней энергией 400 мэВ

с немагнитным барьером шириной L = 70 нм и с

амплитудой U₀ = 100 мэВ. Как и следовало ожи-

дать, доминирующей по амплитуде остается та ком-

понента спиновой плотности (в нашем примере S_y),

которую волновой пакет имел до взаимодействия с

барьером. Остальные компоненты спиновой плотно-

сти хотя и приобрели ненулевую амплитуду, но по

сравнению с S_y остаются на порядок меньшими, к

тому же их среднее значение по плоскости xy, как

это следует из рис. 5, близко к нулю. Таким образом,

Рис.

Распределение компонент спиновой плотности

эффективный поворот спина может быть достигнут

Sx(x, y),

Sy (x, y) и Sz (x, y), сформировавшихся после

лишь при наличии намагниченности у барьера.

взаимодействия волнового пакета со средней энергией

Можно сделать вывод, что выявлен механизм

250 мэВ с барьером высотой 130 мэВ и шириной L =

изменения спиновой плотности волнового пакета

= 60 нм. Барьер поляризован вдоль оси z. Начальное

на поверхности топологического изолятора, т. е. ло-

распределение спиновой плотности отвечало поляризации

кальное управление спиновой степенью свободы, с

вдоль оси y. Наличие намагниченности у барьера приводит

помощью потенциальных барьеров с намагниченно-

к появлению двух компонент спиновой плотности Sx(x, y)

стью. Подобный механизм для топологических изо-

и Sz(x, y), отсутствовавших у исходного пакета

ляторов с их жестким характером связи спина с на-

правлением движения является, по нашему мнению,

полезным инструментом для будущих приложений

Д. В. Хомицкий, Д. А. Кулаков

ЖЭТФ, том 157, вып. 1, 2020

топологических изоляторов в устройствах передачи

и обработки информации.

4. РАССЕЯНИЕ ПАКЕТОВ В СТАТИЧЕСКОЙ

ЗАДАЧЕ

S_x, отн. ед.

В данном разделе будет рассмотрен другой под-

0.0005

ход к задаче рассеяния волнового пакета на потен-

циальном барьере. Вначале мы получим выраже-

ние для коэффициента прохождения для состояния

-0.0005

100

вида плоской волны с двухкомпонентным спинор-

x, нм

ным множителем, а затем построим из таких состо-

100

яний волновой пакет и проинтегрируем коэффици-

y, нм

ент прохождения с соответствующим распределени-

200

ем для волнового пакета в k-пространстве. Схожая

задача рассматривалась для рассеяния состояний

типа плоских волн на квантовой яме в графене [6,7],

при этом потенциал ямы был немагнитный. Мы по-

лагаем, что решение подобной задачи для волно-

вого пакета, взаимодействующего с магнитным ба-

S_y, отн. ед.

рьером, будучи интересным само по себе, служит

0.003

также полезным дополнением к моделированию ди-

0.002

намической задачи о рассеянии пакета, описанной

0.001

выше. Возможность получения аналитического вы-

ражения для коэффициента прохождения позволит

100

x, нм

дать более обоснованную оценку значимости чис-

100

ленных результатов из предыдущего раздела нашей

y, нм

работы.

200

Отметим, что мы не ожидаем полного коли-

чественного согласия во всей области параметров

между двумя весьма разными подходами, первый

из которых был рассмотрен выше и описывал эво-

люцию во времени волнового пакета при рассеянии

на барьере. Второй подход, обсуждаемый в данном

S_z, отн. ед.

разделе, будет представлять волновой пакет через

0.0004

комбинацию плоских волн, и задача рассеяния вна-

чале будет решаться для одиночной плоской волны.

0.0002

Следует заметить, что даже для одного класса задач

-0.0002

(динамические либо статические задачи рассеяния)

100

применение различных методов решения может да-

x, нм

вать результаты, существенно отличающиеся друг

100

от друга в некоторых областях параметров. Так, в

y, нм

200

работе [46] моделировалось динамическое туннели-

рование волновых пакетов через различные потен-

Рис. 5. То же, что на рис. 4, но для взаимодействия паке-

циальные барьеры, и вероятность прохождения, по-

та со средней энергией 400 мэВ с немагнитным барьером

лученная в рамках различных приближений, в неко-

шириной L = 70 нм и с амплитудой U0 = 100 мэВ. Доми-

торых случаях отличалась на десятки процентов. В

нирующей по амплитуде остается та компонента спиновой

работе [47] исследовалась динамика волновых па-

плотности (Sy на рис. б), которую волновой пакет имел до

взаимодействия с барьером

кетов в модели Haldane и наблюдались существен-

ные различия между квазиклассическим и точным

решениями. В работе [12] изучалась динамика дву-

мерных гауссовских волновых пакетов для уравне-

ЖЭТФ, том 157, вып. 1, 2020

Рассеяние волновых пакетов на поверхности. . .

ния Дирака с немагнитными барьерами и неодно-

В области барьера -L/2 < x < L/2 система уравне-

родностями. Вновь можно заметить количественные

ний для функций φ1,2(x) имеет следующий вид:

различия между результатами различных методов,

причем даже для нормального падения на барьер

(C + U₀)φ₁ + A(φ₂k_y + φ′2) = εφ₁,

(14)

полного прохождения пакета для всех рассматрива-

(C + U₀)φ₂ + A(φ₁k_y - φ′1) = εφ₂,

емых параметров задачи не наблюдалось. В этой же

работе отмечалась ограниченность области приме-

где φ′1,2 = dφ1,2/dx. В случае магнитного барьера с

нимости приближения плоских волн для аналитиче-

поляризацией σ_k = σ_x система (14) примет вид

ского рассмотрения туннелирования пакета. Имен-

Cφ₁ + U₀φ₂ + A(φ₂k_y + φ′2) = εφ₁,

но, эта область в работе [12] оценивается как хорошо

(15)

работающая прежде всего для широких пакетов с

Cφ₂ + U₀φ₁ + A(φ₁k_y - φ′1) = εφ₂,

Δx(y) > L, что не имеет места в нашей задаче. Так-

и аналогично для других возможных поляризаций

же в этой работе можно заметить, что пакет тун-

барьера.

нелирует с высоким коэффициентом прохождения

Метод решения систем (14) или (15) одинаков. В

в случае, когда он широкий, т. е. Δx(y) ≥ L, что не

системе (14) можно выразить φ₂ как

имеет место в нашей задаче, где рассматриваются,

наоборот, очень узкие пакеты (или широкие барье-

A (φ₁(x)k_y - φ′1(x))

φ₂(x) =

(16)

ры) с Δx(y) << L. В этой связи можно отметить,

ε-C-U₀

что в работе [12] заметно уменьшение коэффициен-

что позволит получить уравнение второго порядка

та прохождения пакета при нормальном падении по

для φ₁ в виде φ′′1 + a²φ₁ = 0, где параметр

мере уменьшения отношения Δx(y)/L. Наконец, в

статье [48] изучалась статическая задача о рассе-

a² = (ε - C - U₀)²/A² - k2y.

(17)

янии состояний вида плоских волн на потенциале

круглой формы, и вновь наблюдались значитель-

Решением последнего уравнения будет комбина-

ные различия в характеристиках рассеяния, полу-

ция плоских волн вида φ₁ = β₁e^iax +β₂e^-iax с подле-

ченных в рамках разных приближений. Приведен-

жащими определению коэффициентами β₁, β₂. Ана-

ные примеры говорят о том, что в нашем сопостав-

логичную процедуру можно проделать для падаю-

лении двух задач из существенно различных клас-

щей на барьер волны с амплитудой, равной единице

сов (динамические и статические) можно рассчиты-

при x < -L/2, для которой решение имеет вид φ₁ =

вать в основном на качественное согласие резуль-

= 1e^ibx + αe^-ibx с

татов. Ценность статического подхода состоит глав-

b² = (ε - C)²/A² - k2y,

(18)

ным образом в возможности аналитического расче-

та характеристик рассеяния, что позволяет объяс-

и для прошедшей через барьер волны. Все это поз-

нить некоторые особенности коэффициента прохож-

воляет записать решение для компоненты φ₁ в сле-

дения.

дующей форме:

Мы решаем стационарное уравнение Шредин-

гера HΨ

= εΨ с гамильтонианом (3) и барье-

φ₁(x) =

ром (8) для двухкомпонентной спинорной функции

⎧

(Ψ₁(x, y), Ψ₂(x, y)). Для барьера (8) компонента k_y

⎨

1e^ibx + αe^-ibx,

x < -L/2,

квазиимпульса является хорошим квантовым чис-

β₁e^iax+β₂e^-iax,

-L/2 < x < L/2,

(19)

⁼⎪⎩

лом, поэтому компоненты волновой функции можно

δe^ibx,

x > L/2.

искать в виде

Вместе с (16) выражение (19) полностью опре-

Ψ1,2 = eikyyφ1,2(x).

(13)

деляет волновую функцию (13). Четыре коэффици-

ента α, β₁, β₂, δ в (19) при заданной энергии ε под-

После подстановки функции (13) в уравнение

лежат определению из четырех граничных условий,

Шредингера с гамильтонианом (3) мы получим си-

выражающих непрерывность функции φ₁ и ее про-

стему обыкновенных дифференциальных уравнений

изводной на границах барьера x = ±L/2.

для функций φ1,2(x), зависящую от поляризации ба-

Знание волновой функции (13) в виде двухком-

рьера. Мы опишем подробно решение для немагнит-

понентного спинора Ψ = (Ψ₁, Ψ₂) определяет коэф-

ного барьера, когда в формуле (3) σk = σ0. Для

фициент прохождения, который мы вначале запи-

магнитного барьера решение строится аналогично.

шем для отношения амплитуд падающей на барьер

Д. В. Хомицкий, Д. А. Кулаков

ЖЭТФ, том 157, вып. 1, 2020

и прошедшей волн, подобно тому как это было сде-

Из равенств (19) и (16) видно, что выражения

лано в предыдущем разделе для выражения (9):

для обеих компонент волновой функции для рас-

пространяющейся направо волны, рассматриваемые

|Ψ(x > L/2)|

T₀(ε, k_y) =

(20)

справа и слева от барьера, отличаются лишь на не

|Ψ_left(x < -L/2)|²

зависящий от координат множитель δ, определяю-

щий коэффициент прохождения (21). Поэтому для

где Ψ_left(x < -L/2) обозначает налетающую слева

определенного через оператор скорости выражения

на барьер волну. Согласно (13), (16) и (19) коорди-

(26) получается результат, совпадающий с (21):

натная часть двухкомпонентного спинора как для

прошедшего, так и для падающего состояния пред-

T₂(ε, k_y) = |δ|².

(27)

ставляет собой плоскую волну, поэтому зависимость

от координат в (20) и ниже в (26) пропадает. Для

Это дает нам основание применять одно выраже-

коэффициента (20) из равенств (19) и (16) следует,

ние (21) для последующих расчетов. Следует отме-

что

тить, что подобное совпадение коэффициентов (27)

T₀(ε, k_y) = |δ|²,

(21)

и (21) имеет место лишь для статической задачи с

барьером ограниченных размеров, что отличается

откуда после определения коэффициентов α, β₁, β₂,

как от случая полупространства, рассмотренного в

δ из граничных условий для (19) и (16) мы получим,

числе прочих в работе [8], так и от случая динамиче-

что в случае немагнитного барьера

ской задачи из предыдущего раздела нашей работы.



В динамической задаче прошедшая часть волново-

T₀(ε, k_y) =

 cos(aL) -

го пакета не связана простым соотношением с нале-

(√

)



тающим на барьер пакетом, как это имеет место в

- i (a²+k2y)(b²+k2y)-k²

sin(aL)/(ab)-2 .

(22)

равенствах (19), поэтому коэффициенты T и T₁ на

рис. 2 и рис. 3 несколько отличаются друг от друга,

Для магнитных барьеров можно получить ана-

хотя и имеют много общего в своем поведении.

логичное выражение, наиболее простая форма ко-

В формуле (22) квантовыми числами являются

торого имеет вид

k_y и ε, от которых зависят параметры a и b. Для



4a_nb

²

нормально падающего на немагнитный барьер со-



T₀(ε, k_y) =

(23)

^ (a_n + b)² - (a_n - b)²e2ian^L



стояния вида плоской волны с k_y = 0 из (22) сле-

= 1,

дует, что независимо от энергии значение T₀

где для барьеров с поляризацией n = x, z выраже-

т. е. имеет место клейновское туннелирование через

ние для b совпадает с (18), а параметр a_n равен

немагнитный барьер [7, 13]. Для магнитного барье-

ра с различной поляризацией эффект клейновско-

(ε - C)² - (U₀ + Ak_y)

a2x =

(24)

го туннелирования может не иметь места, как это

A²

следует из ранее выполненных работ по рассеянию

для барьера с x-поляризацией и

состояний вида плоских волн [15-23].

Нас интересует приложение формул (22) или (23)

(ε - C)² - U²⁰ - A²k2y

a2z =

(25)

не для одиночной плоской волны и ее комбина-

A²

ций вида (19), а для волнового пакета в форме (7).

для барьера с z-поляризацией.

Для него можно получить разложение по плоским

По аналогии с выводом выражения (12) для ди-

волнам (фурье-преобразование), которое мы обозна-

намической задачи можно записать и выражение

чим как ΨE,kx,ky , где E обозначает среднюю энер-

для коэффициента прохождения в статической за-

гию волнового пакета, фактически определяющую-

даче, основываясь на его определении через отноше-

ся значениями (kx,ky) в (7). Различные значения

ние потоков, т. е. через среднее значение оператора

(k_x, k_y) отвечают различным энергиям для спек-

скорости v_x = Aσ_y/ℏ [8] в прошедшей и налетающей

тра (2) и коэффициентам (22) или (23). Интегрируя

волне:

по (k_x, k_y), мы запишем коэффициент прохождения

T_s(E) для статической задачи как

T₂(ε, k_y) =

∫



T_s(E) =

ΨE,k

² T₀(ε, k_y)dk_x(ε)dk_y.

(28)

Ψ⁺(x > L/2)v_xΨ(x > L/2)dxdy

x,ky

=∫

(26)

Отметим, что аналогичное (28) выражение бы-

Ψ+left(x < -L/2)v_xΨ_left(x < -L/2)dxdy

ло использовано в работе [12] при анализе динами-

ЖЭТФ, том 157, вып. 1, 2020

Рассеяние волновых пакетов на поверхности. . .

ки гауссовских пакетов, подчинающихся уравнению

Дирака.

В формулу (28) следует подставить выражение

для фурье-образа волнового пакета (7), получаемое

элементарным интегрированием, и формулу (22) ли-

бо (23) соответственно для немагнитного или маг-

нитного барьера, определяющую коэффициент про-

хождения плоской волны. Получаемый для T_s(E)

интеграл уже не вычисляется в элементарных функ-

циях, и для получения приводимых ниже графи-

ков используются численные методы интегрирова-

ния. Отметим, что в выражении (28) интегрирова-

ние по k_x проводится с учетом того, что k_x опре-

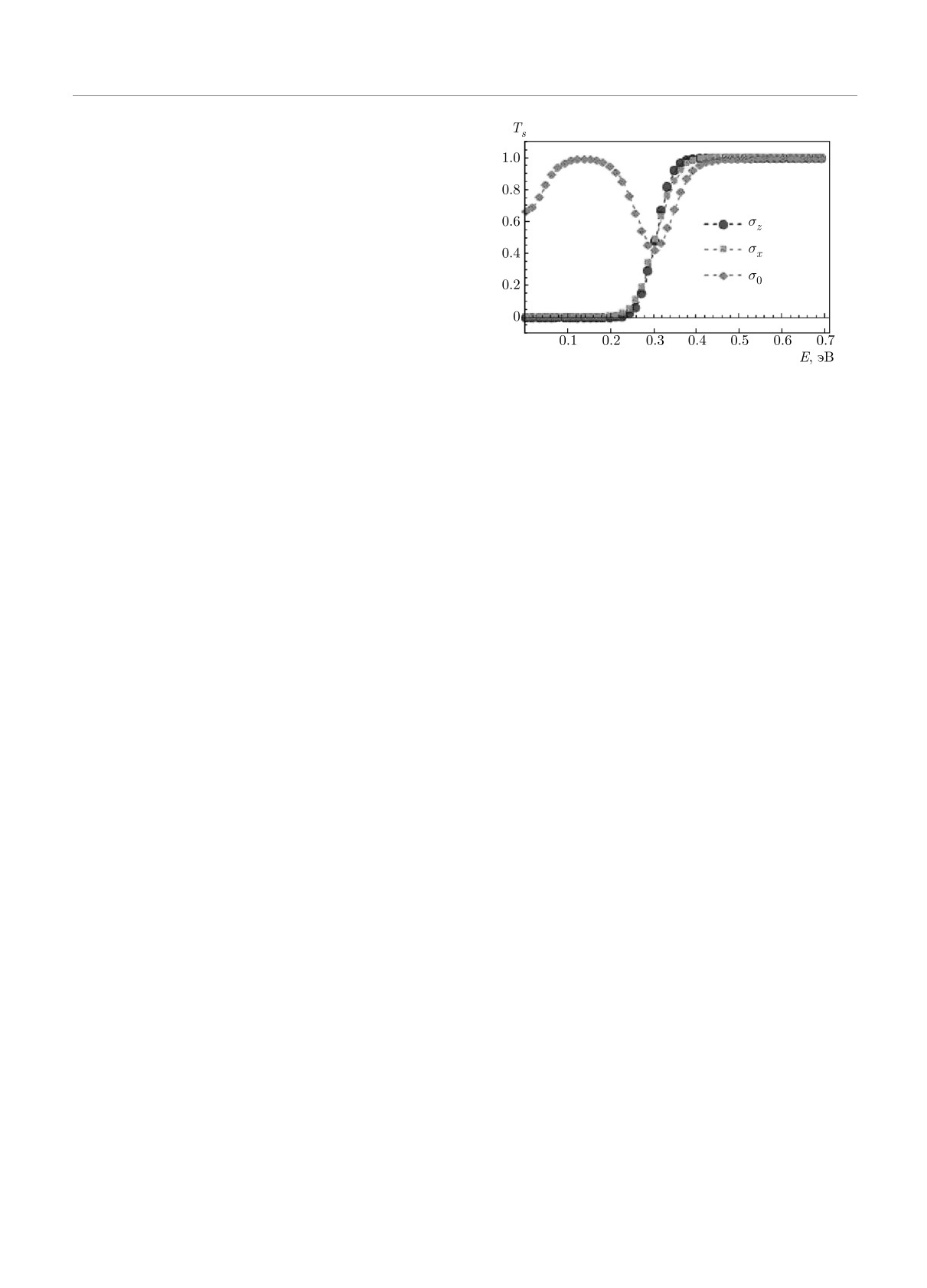
Рис. 6. Зависимости от средней энергии волнового пакета

деляется через k_y и ε согласно выражению (2) для

для коэффициента прохождения Ts(E) в статической за-

спектра энергии. Для нее мы учитываем обе ветви

даче о рассеянии пакета на барьере-ступеньке c L = 200 нм

спектра (2), причем для верхней ветви берутся со-

и U0 = 300 мэВ, для нормального падения на барьер. Ви-

стояния с k_x > 0, а для нижней ветви — состояния с

ден локальный максимум для случая немагнитного барье-

k_x < 0. Это обусловлено противоположным знаком

ра при энергии E ≈ U0/2, происхождение которого объяс-

групповой скорости на двух половинах дираковско-

няется резонансным прохождением плоских волн при вы-

го конуса (2), в то время как нас интересуют лишь

полнении условия (29)

состояния, налетающие на барьер слева, т. е. имею-

щие проекцию v_x > 0. Известно, что энергия Ферми

E_F для материалов семейства Bi₂Te₃ находится в

от энергии лишь для строго нормального падения

типичных образцах в интервале 0.2 . . . 0.5 эВ, где от-

одной плоской волны, входящей в разложение для

счет ведется от вершины конуса (2) [1-4]. Если сред-

волнового пакета. На рис. 6 показана зависимость

няя энергии пакета E расположена в области вблизи

T_s(E) в той же области средней энергии пакета и

или выше E_F , то состояния нижней ветви спектра с

для рассеяния на барьере с теми же параметрами,

отрицательными энергиями практически не вносят

что и на рис. 2: L = 200 нм и U₀ = 300 мэВ. Можно

вклад в коэффициент (28). Тем не менее, посколь-

видеть, что по амплитуде в динамической задаче ко-

ку мы рассматривали пакеты со средней энергией,

эффициент прохождения примерно в полтора раза

изменяющейся в широких пределах, в том числе и

ниже.

принимающей значения много меньше E_F , мы учи-

На рис. 6 также видны особенности коэффици-

тывали здесь обе ветви спектра (2).

ента для немагнитного барьера с σ_k = σ₀ при низ-

Выражение (28) может быть исследовано при

ких энергиях E < 0.3 эВ, т.е. при E < U0, от-

различных параметрах системы, в первую очередь,

сутствующие в динамической задаче. Здесь для ма-

как функция от средней энергии пакета при различ-

лых энергий коэффициент прохождения существен-

ной поляризации барьера, а также при различных

но выше, чем для магнитных барьеров с σ_k = σ_x,z,

углах встречи θ волнового пакета с барьером. Как и

для которых T_s(E) ≪ 1. Это можно объяснить час-

для динамической задачи, мы начнем с простейше-

тичным проявлением клейновского туннелирования

го случая нормального падения пакета на барьер с

для электростатического барьера, хотя и не в преде-

теми же параметрами: амплитудой U₀ = 300 мэВ и

ле T_s(E) = 1, который имеет место лишь для рассе-

шириной L = 200 нм. Следует отметить, что, как и

яния состояний типа плоской волны в стационарной

для динамической задачи, нормальное падение дву-

задаче.

мерного волнового пакета на барьер отличается от

Для магнитных барьеров, как известно, клей-

такового для плоской волны. Именно, для волнового

новского туннелирования с T_s(E) = 1 может не

пакета коэффициент прохождения (28) представля-

быть при любых энергиях состояния рассеяния

ет собой интеграл по вкладам от состояний с раз-

[15, 16, 19, 22], что подтверждается результатами на

личной ориентацией волнового вектора относитель-

рис. 6 для σk = σx,z. В области промежуточных

но нормали к барьеру, поэтому для него клейновское

энергий, 0.30 < E < 0.45 эВ, для немагнитного ба-

туннелирование с любой средней энергией может не

рьера и в области 0.25 < E < 0.45 эВ для магнитных

иметь места. Действительно, в (22) для немагнитно-

барьеров поведение коэффициента прохождения на

го барьера получается результат T₀ = 1 независимо

рис. 2 и рис. 6 в динамической и статической зада-

Д. В. Хомицкий, Д. А. Кулаков

ЖЭТФ, том 157, вып. 1, 2020

чах качественно схожее в смысле возрастания при

Для параметров нашей задачи с L = 200 нм, A =

увеличении энергии и слабой зависимости T_s(E) от

= 406.8 мэВ · нм и типичных энергиях плоских волн

поляризации барьера.

в интервале 100 . . . 500 мэВ мы видим, что значе-

Обсудим подробнее особенности коэффициента

ние параметра γ² = (πNA/LE)² в (33) много мень-

прохождения на рис. 6 при E < U₀, наблюдаемые

ше единицы для всех первых резонансов с N

≈

для немагнитного барьера. Из графика следует, что

≈ 0, . . ., 5, и для первоначальной оценки им можно

коэффициент имеет локальный максимум при сред-

пренебречь. В этом случае формула (33) дает нам

ней энергии пакета, равной приблизительно поло-

значение ξ ≈ 0.585. Это означает, что при средней

вине высоты барьера. Покажем, как это можно по-

энергии набора плоских волн, составляющих пакет,

яснить, исходя из выражения (22). Как известно из

в области половины высоты барьера U₀, коэффи-

работы [7], полное прохождение плоской волны в си-

циент прохождения должен иметь локальный мак-

стеме с дираковским спектром возможно не только

симум, который и наблюдается на рис. 6 вблизи

при нормальном падении на барьер, но и при неко-

E/U₀ ≈ 0.6. Отметим, что значение самого коэф-

торых других углах и/или энергиях волны, удовле-

фициента T_s(E) на рис. 6 для немагнитного барьера

творяющих условию резонанса, при котором выра-

при отношении энергий E/U₀ ≈ 0.6, равное пример-

жение (22) дает значение T₀ = 1:

но 0.95, находится в удовлетворительном согласии с

результатом, представленном на рис. 1 работы [12],

aL = πN,

(29)

где для наиболее узкого барьера оно равно пример-

но 0.75.

где N = 0, 1, . . . Подставляя в (29) выражение для√

a = (ε - C - U₀)²/A² - k2y и учитывая, что k_y =

Подчеркнем, что рассмотренное выше условие

локального максимума коэффициента прохождения

= k sinθ, где θ — угол падения волны на барьер,

неразрывно связано со скалярным (немагнитным)

а амплитуда волнового вектора k определяется при

характером потенциального барьера и рассеянием

заданной энергии из спектра (2), мы получим усло-

на нем состояний типа плоских волн в статической

вие (29) в виде

задаче. Для эволюции волнового пакета в динами-

√

ческой задаче, рассмотренной в предыдущем раз-

(E - U₀)² - E² sin² θ = πN.

(30)

деле, затруднительно сформулировать условие ре-

Вначале преобразуем уравнение (30), перейдя к

зонансного прохождения, подобное (29). Действи-

безразмерным переменным γ = πNA/LE, ξ = E/U₀:

тельно, для начального состояния вида (7) задает-

ся дисперсия в координатном пространстве, приво-

√(

)₂

дящая к наличию дисперсии в k-пространстве со-

- sin² θ = γ.

(31)

гласно соотношению неопределенностей. Дисперсия

в k-пространстве приводит к наличию дисперсии

Для волнового пакета, составленного из многих

энергии пакета, которая для типичной ширины па-

плоских волн, равенство (31) может выполняться

кета Δx ≈ 10 нм в нашей системе дает величину по-

для различных углов θ и различных энергий (т. е.

рядка 50 . . . 100 мэВ. При таком масштабе дисперсии

различных ξ и γ) для отдельной плоской волны, вхо-

энергии затруднительно сформулировать резонанс-

дящей в пакет. Чтобы учесть интегральный харак-

ное условие, подобное (29). Кроме того, в динами-

тер получаемого при этом эффекта, проведем усред-

ческой задаче пакет взаимодействует с барьером в

нение по углам θ падения плоских волн на барьер,

течение ограниченного интервала времени, оценива-

учитывая, что среднее значение sin² θ на интервале

емого согласно (10) в величинах порядка 10-13 с, в

[0, π/2] равно 1/2. После усреднения и возведения

то время как в статической задаче переменная «вре-

(31) в квадрат мы получим

мя» отсутствует, и каждая плоская волна из пакета

(

)₂

задается сразу во всей области пространства по ту

=γ².

(32)

или иную сторону от барьера. Это позволяет в ста-

тике описать процесс взаимодействия плоской вол-

Из (32) непосредственно следует выражение для

ны с барьером как бесконечный во времени и проис-

параметра ξ, определяющего отношение энергии

ходящий, вообще говоря, во всей области простран-

плоской волны к амплитуде барьера при условии

ства, что приводит к резонансному условию (29). В

подбарьерного прохождения, когда ξ < 1:

этих факторах мы видим причину отсутствия ре-

зонансного увеличения коэффициента прохождения

ξ=

√

(33)

1/2 + γ²

при энергиях E < U₀ на рис. 2 для динамической

ЖЭТФ, том 157, вып. 1, 2020

Рассеяние волновых пакетов на поверхности. . .

рис. 2 и рис. 3а,б для динамической задачи. Мож-

но видеть, что для средней энергии пакета, превы-

шающей высоту барьера, наблюдается эффективное

прохождение при малых углах падения, независимо

от поляризации барьера. При увеличении угла па-

дения для всех поляризаций коэффициент прохож-

дения убывает. Схожая зависимость с уменьшени-

ем коэффициента прохождения при увеличении уг-

ла падения пакета наблюдалась в работе [12]. Для

σ_z-поляризации барьера уменьшение T_s(θ) начина-

ется при больших углах падения. Такое поведение

зависимости T_s(θ) (по крайней мере в области про-

межуточных углов 0.05π < θ < 0.2π для поляри-

заций барьера σ₀ и σ_x) качественно согласуется с

Рис. 7. Угловая зависимость Ts(θ) для волнового пакета

представленными на рис. 3 результатами для дина-

со средней энергией 600 мэВ, налетающего на барьер c

мической задачи, при этом на рис. 3 максимальная

L = 200 нм и U0 = 300 мэВ

амплитуда T_s(θ) меньше. Как и для энергетических

зависимостей на рис. 2 и рис. 6, мы полагаем, что

это различие связано с более интенсивным отраже-

задачи в случае немагнитного барьера, что отража-

нием в динамической задаче гармоник с большим

ет указанные качественные различия динамической

волновым вектором, составляющих волновой пакет,

и статической задач.

из-за чего в динамической задаче максимальные ве-

(θ), умень-

личины T (E) и T (θ), а также T₁(E) и T₁

Что касается магнитных барьеров, то для них

шаются. Отметим, что для σ_z -поляризации барьера

выполнить условие T₀ = 1 для волнового пакета в

коэффициент T_s(θ) сохраняет большую амплитуду

случае подбарьерного прохождения с энергией E <

при больших углах падения на барьер, чем для дру-

< U₀ не представляется возможным. Действитель-

гих случаев. Это можно объяснить эффективным

но, запишем условие (29) для коэффициента про-

поворотом локальной спиновой плотности при по-

хождения плоской волны (23) с a = a_n. При его вы-

ляризации барьера вдоль направления z, перпенди-

полнении, как легко видеть, из (23) получаем T₀ =

кулярного плоскости, образованной средним волно-

= 1. Подставим в условие (29) выражения для па-

вым вектором пакета (по оси x) и исходным векто-

раметра a_x,z из (24) или (25), и для пакета выпол-

ром среднего спина (по оси y). При повороте спина

ним процедуру усреднения по углу θ с подстановкой

вклад гармоник в прошедшую часть пакета, имею-

〈sin θ〉 = 0, 〈sin2 θ〉 = 1/2, аналогичную проведен-

щих ту же поляризацию, что и сам барьер, увеличи-

ной выше для немагнитного барьера. После неслож-

вается, что увеличивает и коэффициент прохожде-

ных вычислений мы получим, что для обоих случаев

ния. Для двух других случаев с неполяризованным

a_n = a_x и a_n = a_z условие (29) может удовлетво-

барьером (σ_k = σ₀) и аналогично с барьером, поля-

ряться лишь для средней энергии пакета E > U₀,

ризованным вдоль оси x (σ_k = σ_x), эффективный

т. е. для надбарьерного прохождения. Это означа-

поворот спиновой плотности не происходит, как это

ет, что при подбарьерном прохождении с E < U₀

видно из сравнения результатов на рис. 4 и рис. 5.

для магнитных барьеров не следует ожидать появ-

Общим наблюдением по итогам исследования ди-

ления локального максимума в подбарьерной обла-

намической и статической задач является то, что да-

сти для коэффициента прохождения, что мы и ви-

же для нормальной ориентации среднего волнового

дим на рис. 6.

вектора двумерного волнового пакета при его взаи-

Наряду с энергетической зависимостью пред-

модействии с барьером эффект клейновского тун-

ставляет интерес и угловая зависимость коэффици-

нелирования, т. е. полное прохождение для любой

ента прохождения для статической задачи, анало-

энергии падающего состояния, в чистом виде не име-

гичная представленной на рис. 3. На рис. 7 пока-

ет места. Это, как уже было отмечено выше, обу-

зана угловая зависимость T_s(θ) для волнового па-

словлено именно двумерным характером рассматри-

кета со средней энергией 600 мэВ, налетающего на

ваемых волновых пакетов, в которые входят плос-

такой же барьер, для которого представлены ре-

кие волны с различной ориентацией волнового век-

зультаты на рис. 6 для статической задачи и на

тора относительно барьера, а не только с нормаль-

ЖЭТФ, вып. 1

Д. В. Хомицкий, Д. А. Кулаков

ЖЭТФ, том 157, вып. 1, 2020

ной, как для одномерных волновых пакетов. Ука-

Благодарности. Авторы посвящают эту ра-

занный эффект достигается как с помощью магнит-

боту светлой памяти своего учителя, профессора

ных, так и немагнитных, т. е. электростатических

В. Я. Демиховского, сформировавшего их интерес

барьеров. В немагнитном случае подобного умень-

к задачам о динамике волновых пакетов в тополо-

шения туннелирования при нормальном падении од-

гических изоляторах.

номерных пакетов или плоских волн добиться нель-

Финансирование. Работа выполнена при под-

зя как раз из-за клейновского туннелирования. Об-

держке гранта в рамках проектной части Государ-

наруженное появление конфайнмента (понимаемого

ственного задания Министерства науки и высшего

как сильное уменьшение коэффициента прохожде-

образования РФ 3.3026.2017/ПЧ.

ния) для двумерных пакетов дает основы для со-

здания механизмов воздействия на их прохождение

с помощью магнитных и немагнитных барьеров, что

ЛИТЕРАТУРА

может быть полезно при создании новых устройств

B. A. Bernevig, Topological Insulators and Topolo-

на основе трехмерных топологических изоляторов с

gical Superconductors, Princeton University Press,

хорошими транспортными свойствами краевых со-

Princeton, USA (2013).

стояний.

Topological Insulators. Fundamentals and Perspecti-

ves, ed. by F. Ortmann, S. Roche, and S. O. Va-

lenzuela, Wiley-VCH Verlag, Weinheim, Germany

5. ВЫВОДЫ

(2015).

M. Z. Hasan and C. L. Kane, Rev. Mod. Phys 82,

Получены решения нестационарного уравнения

3045 (2010).

Шредингера для волновых пакетов, образованных

X.-L. Qi and S.-C. Zhang, Rev. Mod. Phys. 83, 1057

из состояний безмассового спектра на поверхности

(2011).

топологических изоляторов, в присутствии потен-

циальных барьеров. Исследуется динамика паке-

C.-X. Liu, X.-L. Qi, H. Zhang, X. Dai, Z. Fang, and

тов в присутствии барьеров с различной магнит-

S.-C. Zhang, Phys. Rev. B 82, 045122 (2010).

ной поляризацией. Рассчитаны коэффициент про-

J. Milton Pereira Jr., V. Milnar, F. M. Peeters et al.,

хождения волнового пакета через прямоугольный

Phys. Rev. B 74, 045424 (2006).

барьер-ступеньку и распределения спиновой плот-

ности. Рассмотрены зависимости от средней энергии

M. I. Katsnelson, K. S. Novoselov, and A. K. Geim,

волнового пакета, угла падения, поляризации барье-

Nature Phys. 2, 620 (2006).

ра. Также получены результаты для статической за-

P. E. Allain and J.-N. Fuchs, Eur. Phys. J. B 83, 301

дачи с коэффициентом прохождения через барьер с

(2011).

намагниченностью и без с помощью приближения

плоских волн, с последующим обобщением резуль-

M.-H. Liu, C. Gorini, and K. Richter, Phys. Rev. Lett.

татов для волновых пакетов. Показано, что двумер-

118, 066801 (2017).

ный характер волновых пакетов приводит к замет-

10.

S.-H. Zhang and W. Yang, Phys. Rev. B 97, 035420

ным различиям в поведении коэффициента прохож-

(2018).

дения по сравнению с задачей о рассеянии плоских

волн. Именно, наличие в двумерном волновом паке-

11.

J.-H. Gao, J. Yuan, W.-Q. Chen, Y. Zhou, and

те плоских волн с различными проекциями волно-

F.-C. Zhang, Phys. Rev. Lett. 106, 057205 (2011).

вых векторов приводит к существенному подавле-

12.

S. Palpacelli, N. Mendoza, H. J. Herrmann, and

нию эффекта клейновского туннелирования для на-

S. Succi, Int. J. Mod. Phys. C 23, 1250080 (2012).

летающего на барьер пакета в некоторых областях

энергии. Полученные результаты свидетельствуют

13.

Y. Xie, Y. Tan, and A. W. Ghosh, Phys. Rev. B 96,

о возможностях воздействия через потенциальные

205151 (2017).

барьеры на туннелирование и спиновую плотность

14.

Y. Li, M. B. A. Jalil, S. G. Tan, W. Zhao, R. Bari,

состояний типа волновых пакетов в топологических

and G. H. Zhou, Sci. Rep. 4, 4624 (2014).

изоляторах, что может быть полезно при создании

спиновых фильтров, кубитов и других устройств об-

15.

J. Gao, W.-Q. Chen, X.-Y. Feng, X. C. Xie, and

работки информации на основе подобных структур.

F.-C. Zhang, arXiv:0909.0378 (2009).

ЖЭТФ, том 157, вып. 1, 2020

Рассеяние волновых пакетов на поверхности. . .

16.

Z. Wu, F. M. Peeters, and K. Chang, Phys. Rev. B 82,

32.

В. Я. Демиховский, А. В. Тележников, Письма в

115211 (2010).

ЖЭТФ 99, 110 (2014).

17.

B. D. Kong, Y. G. Semenov, C. M. Krowne, and

33.

В. Я. Демиховский, Р. В. Туркевич, Письма в

K. W. Kim, Appl. Phys. Lett. 98, 243112 (2011).

ЖЭТФ 101, 501 (2015).

18.

J. P. Zhang and J. H. Yuan, Eur. Phys. J. B 85, 100

34.

S. Choi, C.-H. Park, and S. G. Louie, Phys. Rev. Lett.

(2012).

113, 026802 (2014).

19.

Z. Wu and J. Li, Nanoscale Res. Lett. 7, 90 (2012).

35.

F. Dolcini, R. C. Iotti, A. Montorsi et al., Phys. Rev.

B 94, 165412 (2016).

20.

C. Ertler, M. Raith, and J. Fabian, Phys. Rev. B 89,

075432 (2014).

36.

F. Dolcini, Phys. Rev. B 95, 085434 (2017).

21.

Z.-Q. Liu, R.-Q. Wang, M.-X. Deng, and L.-B. Hu,

37.

M. V. Durnev and S. A. Tarasenko, Ann. Phys.

Commun. Theor Phys. 63, 777 (2015).

1800418 (2019).

22.

C. Yesilyurt, S. G. Tan, G. Liang, and M. B. A. Jalil,

38.

V. A. Sablikov and A. A. Sukhanov, Phys. Rev. B 98,

Sci. Rep. 6, 38862 (2016).

115423 (2018).

23.

B. Scharf, A. Matos-Abiague, J. E. Han, E. M. Han-

39.

D. V. Khomitsky, A. A. Chubanov, and A. A. Kona-

kiewicz, and I.

Žutic, Phys. Rev. Lett. 117, 166806

kov, ЖЭТФ 150, 1200 (2016).

(2016).

40.

L. Fu, Phys. Rev. Lett. 103, 266801 (2009).

24.

V. D. Kurilovich, P. D. Kurilovich, I. S. Burmistrov,

41.

Р. В. Туркевич, Д. В. Хомицкий, ЖЭТФ 153, 283

and M. Goldstein, Phys. Rev. B 99, 085407 (2019).

(2018).

25.

K. E. Nagaev, S. V. Remizov, and D. S. Shapiro,

42.

С. Кунин, Вычислительная физика, Мир, Москва

Письма в ЖЭТФ 108, 700 (2018).

(1992).

26.

V. Ya. Demikhovskii, G. M. Maksimova, and

43.

А. М. Сатанин, Динамика электронов в нано-

E. V. Frolova, Phys. Rev. B 75, 115401 (2008).

структурах, Изд-во ННГУ, Нижний Новгород

27.

E. Romera and F. de los Santos, Phys. Rev. B 80,

(2006).

165416 (2009).

44.

M. Büttiker and R. Landauer, Phys. Rev. Lett. 49,

28.

A. Chaves, L. Covaci, Kh. Yu. Rakhimov, G. A. Fa-

1739 (1982).

rias, and F. M. Peeters, Phys. Rev. B 82, 205430

45.

Yue Ban, E. Ya. Sherman, J. G. Muga, and M. Büt-

(2010).

tiker, Phys. Rev. A 82, 062121 (2010).

29.

V. Ya. Demikhovskii, G. M. Maksimova, A. A. Perov,

and E. V. Frolova, Phys. Rev. A 82, 052115 (2010).

46.

J. Ankerhold and M. Saltzer, Phys. Lett. A 305, 251

(2002).

30.

V. Ya. Demikhovskii, G. M. Maksimova, A. A. Perov,

and A. V. Telezhnikov, Phys. Rev. A 85, 022105

47.

S. Roy, A. G. Grushin, R. Moessner, and M. Haque,

(2012).

Phys. Rev. A 92, 063626 (2015).

31.

В. Я. Демиховский, А. В. Тележников, Е. В. Фро-

48.

J.-S. Wu and M. M. Fogler, Phys. Rev. B 90, 235402

лова, Н. А. Кравец, ФНТ 39, 26 (2013).

(2014).