ЖЭТФ, 2020, том 157, вып. 1, стр. 101-108

ИССЛЕДОВАНИЕ ДВУМЕРНОЙ АНИЗОТРОПНОЙ МОДЕЛИ

ИЗИНГА С КОНКУРИРУЮЩИМИ ВЗАИМОДЕЙСТВИЯМИ В

ОБЛАСТИ ПЕРЕХОДА ИЗ ФЕРРОМАГНИТНОГО СОСТОЯНИЯ

В ПАРАМАГНИТНОЕ

А. К. Муртазаев, Ж. Г. Ибаев^*

Институт физики им. Х. И. Амирханова Дагенстанского научного центра Российской академии наук

367003, Махачкала, Россия

Дагестанский государственный университет

367025, Махачкала, Россия

Поступила в редакцию 22 марта 2019 г.,

после переработки 3 июня 2019 г.

Принята к публикации 12 июня 2019 г.

Методами Монте-Карло на основе алгоритма Ванга - Ландау проведены исследования двумерной ани-

зотропной модели Изинга с конкурирующими взаимодействиями в области фазового перехода из фер-

ромагнитного состояния в парамагнитную фазу. Получены графики плотности распределения состояний

и вычислены значения параметра порядка, соответствующие различным значениям энергии. Рассчита-

ны температурные зависимости термодинамических параметров: внутренней энергии, намагниченности,

свободной энергии, энтропии, теплоемкости намагниченности и кумулянтов Биндера. Используя метод

кумулянтов Биндера и гистограммный анализ, мы показали, что при |J1/J| = 0.1, |J1/J| = 0.2 в двумер-

ной ANNNI-модели происходит один фазовый переход второго рода из ферромагнитного состояния в па-

рамагнитную фазу. Вычислены температуры фазовых переходов. С помощью теории конечно-размерного

скейлинга получены значения основных критических индексов.

DOI: 10.31857/S0044451020010125

и спиновой структуре основного состояния, которые

имеют большое значение для тестирования резуль-

1. ВВЕДЕНИЕ

татов численного моделирования [4-6]. Но, как пока-

Магнитные свойства кристаллических твердых

зывает практика, основные заключения о магнитной

тел, имеющих одномерные или двумерные магнит-

структуре, полученные в рамках этих упрощенных

ные подрешетки (KCuF₃, La₂Cu₂O₅, NH₄CuCl₃ и

моделей, как правило, не сохраняются при перехо-

др.), в значительной мере определяются электрон-

де к более сложным моделям, например, учитыва-

ной корреляцией [1-3]. Во многих случаях подобные

ющим отталкивание электронов, расположенных на

объекты не удается рассматривать как частный слу-

несоседних узлах кристаллической решетки [1, 4].

чай обычных трехмерных систем. Это существен-

Такое отталкивание порождает конкуренцию об-

но затрудняет теоретическое описание свойств низ-

менных взаимодействий, которая приводит к появ-

коразмерных магнетиков традиционными методами

лению различных типов магнитного упорядочения

статистической физики твердого тела [1-3].

(ферромагнитное, модулированное, парамагнитное

При изучении квазиодномерных и квазидвумер-

и т. д.). И соответственно в системах возможно

ных магнетиков в основном применяются упрощен-

несколько фазовых переходов различных типов. К

ные многоэлектронные подходы с использованием

примеру, в системах с модулированным упорядоче-

моделей Гейзенберга и Изинга [1,2]. Полученные для

нием (т. е. c периодическим изменением намагничен-

этих моделей результаты позволили доказать ряд

ности вдоль одного из кристаллографических на-

теорем о характере точного энергетического спектра

правлений) возможны переходы из ферромагнит-

ного состояния в модулированную фазу, переходы

^* E-mail: ibaev77@mail.ru

между структурами с различными значениями вол-

101

А. К. Муртазаев, Ж. Г. Ибаев

ЖЭТФ, том 157, вып. 1, 2020

1/111/101/9

2/17

2/15

1/17

1/72/13

3/17

2/11

3/16

1/16

1/13

1/12

1/5

1/15

1/14

1/8

1/6

3/14

J₁

1/4

0.2

0.3

0.4

0.5

0.6

0.7

-J / J₁

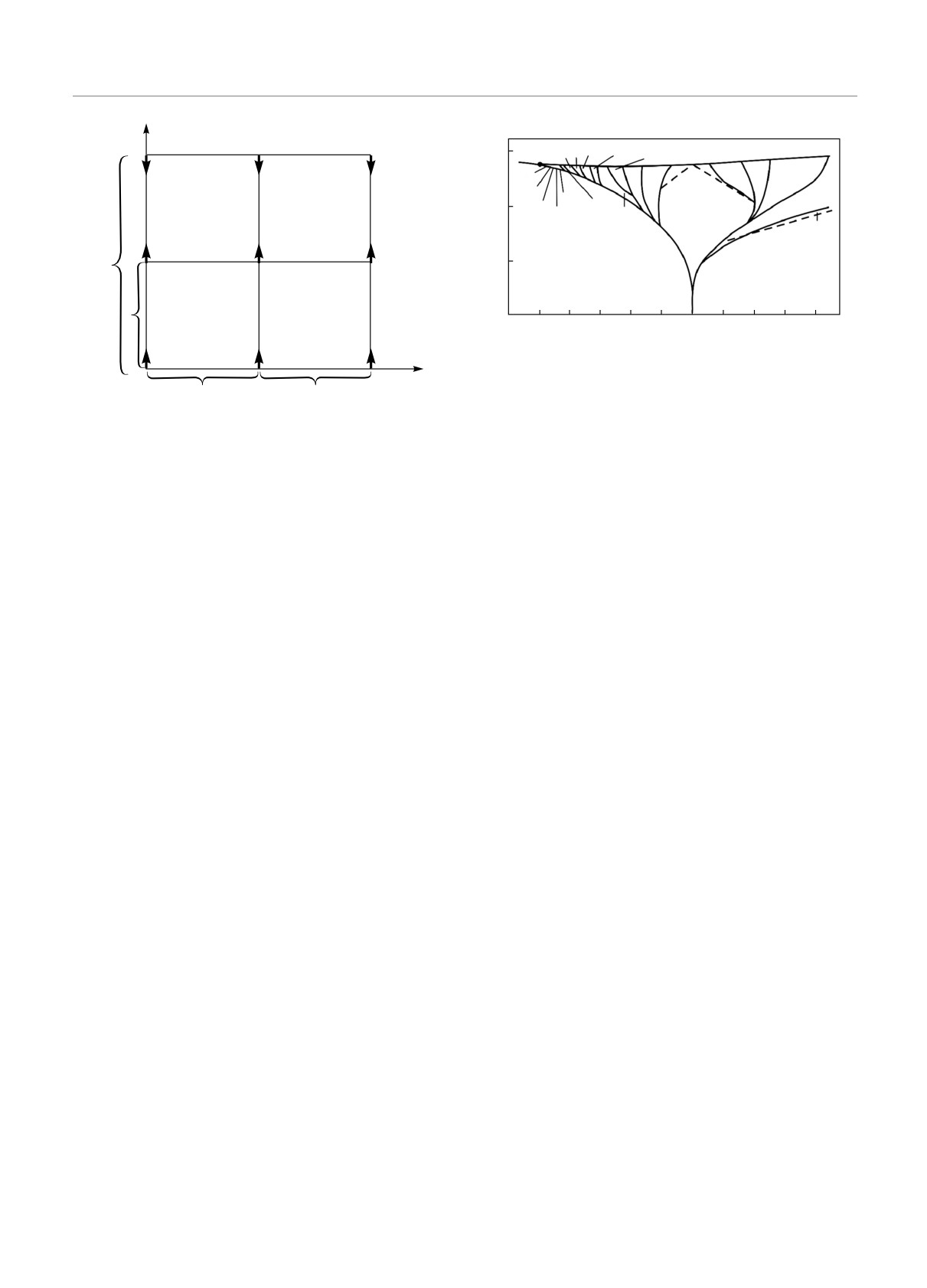
Рис. 2. Фазовая диаграмма анизотропной модели Изинга

с конкурирующими взаимодействиями [6] (FM — ферро-

магнитная фаза, PM — парамагнитная фаза, P — точка

Рис. 1. Двумерная анизотропная модель Изинга с конку-

Лифшица, дробные числа — значения волнового числа мо-

рирующими взаимодействиями

дулированной структуры)

нового числа в модулированной фазе и переход из

модулированной фазы в парамагнитную. Число ре-

ми (рис. 1) успешно используется для описания тер-

альных материалов с подобными свойствами давно

модинамики пленок масляных микроэмульсий на

уже перевалило за сотню [7].

поверхности твердых тел и носит название модели

На практике для описания систем с модулиро-

Видома [9]. Предполагается, что подобные модели

ванным упорядочением используются различные

могут быть использованы для оптимизации процес-

модели. Наиболее простой и эффективной среди них

сов экстракции, например, при нефтедобыче. Для

является анизотропная модель Изинга с конкури-

описания магнитных систем используется двумер-

рующими взаимодействиями вторых ближайших со-

ный аналог такой модели, которая впервые была

седей (рис. 1). Указанная модель, хотя и не позво-

введена для описания упорядоченных магнитных

ляет точно описать какую либо реальную систему,

фаз в кристаллах CeSb [6].

тем не менее, дает хорошее качественное объяснение

Гамильтониан модели имеет вид

свойств систем с модулированным упорядочением.

∑

H_ANNNI = -J s_is_j - J₁ s_isi+2,

(1)

Экспериментальное и теоретическое изучение

i,j

свойств реальных магнетиков является довольно

где s_i = ±1, J > 0 — параметр обменного взаимо-

сложной задачей даже для таких простых случа-

действия соседних пар спинов, J₁ < 0 — параметр

ев упорядочения, как ферромагнетики, антиферро-

конкурирующего взаимодействия спинов, следую-

магнетики и т. д. Поэтому в настоящее время наи-

более приемлемое и точное описание свойств си-

щих за ближайшими по оси y.

Для описания фазового поведения и свойств рас-

стем со сложным магнитным упорядочением можно

получить моделированием на основе методов Мон-

сматриваемой модели были использованы прибли-

женные теоретические методы, включая высоко- и

те-Карло и молекулярной динамики [8].

низкотемпературные разложения, теорию среднего

В данной работе приведены результаты, полу-

поля, методы Монте-Карло и другие теоретические

ченные при исследовании двумерной анизотропной

аппроксимации (см. ссылки в работе [10]).

модели Изинга с конкурирующими взаимодействи-

Согласно имеющимся в литературе данным,

ями, методами Монте-Карло на основе алгоритма

ANNNI-модель точно решена только в одномерном

Ванга - Ландау, для значений отношения констант

случае [7]. Получена фазовая диаграмма в коор-

обменных взаимодействий |J₁/J| = 0.1 и |J₁/J| =

динатах T -|J₁/J| [6]. На этой диаграмме (рис. 2)

= 0.2.

выделены три области, пересекающиеся в муль-

тикритической точке Лифшица P . При высоких

2. МОДЕЛЬ

температурах T система парамагнитна, с пониже-

нием T для |J₁/J| < 0.3 — ферромагнитна, а в

Модель Изинга с конкурирующими ферромаг-

остальном интервале изменения |J₁/J| образуются

нитными и антиферромагнитными взаимодействия-

модулированные фазы.

102

ЖЭТФ, том 157, вып. 1, 2020

Исследование двумерной анизотропной модели Изинга.. .

ln G

1200

24000

|J /J| = 0.1₁

L=16

1000

20000

800

16000

600

12000

400

8000

200

4000

-2.0 -1.6 -1.2 -0.8 -0.4

0.4

0.8

1.2

1.6

2.0

-2.0

-1.5

-1.0

-0.5

0.5

1.0

1.5

2.0

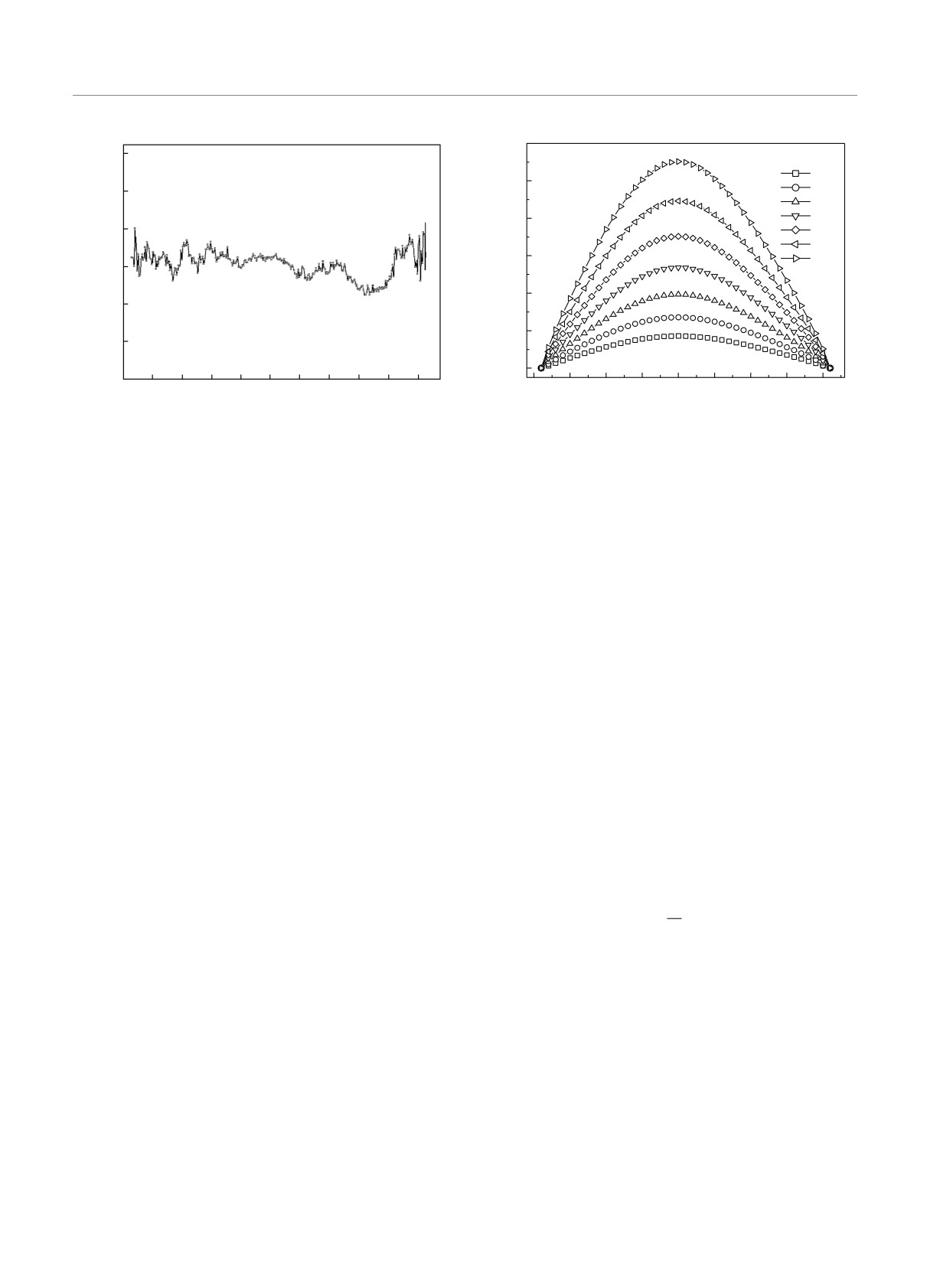
Рис. 3. Гистограмма посещения состояний для системы с

Рис. 4. Натуральный логарифм зависимости плотности

L = 40 (|J1/J| = 0.1)

распределения от энергии

Таким образом, в ANNNI-модели до точки Лиф-

пор, пока элементы вспомогательной матрицы H(U)

шица P происходит один фазовый переход из па-

отличались не более чем на 10 % (рис. 3). Процесс

рамагнитного состояния в ферромагнитную фазу.

моделирования завершался при значениях парамет-

После точки Лифшица возможны несколько пере-

ра алгоритма f близких к единице, т. е. ln f = 10-9.

ходов: 1) из парамагнитного состояния в модулиро-

Полученные при этом типичные графики зави-

ванную фазу; 2) переходы в модулированной фазе

симости натурального логарифма плотности состо-

между структурами с разными значениями волно-

яний от энергии системы при |J₁/J| = 0.1 представ-

вого числа и 3) переход из модулированной фазы в

лены на рис. 4.

ферромагнитную при |J₁/J| < 0.5 или антиферро-

Помимо этого можно определить спиновые кон-

магнитную фазу с волновым числом q = 1/4 при

фигурации, реализуемые в исследуемой системе для

|J₁/J| > 0.5. Точка с |J₁/J| = 0.5 является муль-

любых значений энергии, в частности, по нашим ис-

тифазной точкой с большой степенью вырождения

следованиям удалось установить, что основным со-

основного состояния.

стоянием двумерной ANNNI-модели при рассматри-

ваемых значениях |J₁/J| является двукратно вы-

3. МЕТОД ИССЛЕДОВАНИЯ И

рожденное ферромагнитное состояние.

ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ

Для изучения термодинамических свойств, зави-

сящих от параметра порядка, рассчитывалась вели-

Как известно, основной проблемой при реше-

чина

нии задач статистической физики является неиз-

вестность аналитической функции плотности рас-

∑

пределения состояний системы. Для решения ука-

M (U_i) =

s_i,j,

(2)

занной проблемы Вангом и Ландау [11] был пред-

i,j

ложен алгоритм, позволяющий достаточно просто

вычислить числовую функцию плотности распреде-

представляющая собой усредненную намагничен-

ность системы для различных значений энергий U_i.

ления.

При исследовании двумерной ANNNI-модели с

График зависимости M(U_i) (рис. 5) представля-

помощью указанного алгоритма на ЭВМ моделиро-

ет собой кривую, монотонно убывающую с увеличе-

вались квадратные решетки с периодическими гра-

нием энергии системы. Причиной такого поведения

ничными условиями и размерами L × L; L = 16,

является разрушение коллениарно упорядоченного

20, 24, 28, 32, 36, 40. Число спинов в моделируе-

состояния с ростом энергии.

мой системе Neff = L × L = 256-1600. Основной

Отметим, что подобные зависимости наблюдают-

цикл алгоритма состоял из 10⁴ · N_eff шагов Монте-

ся и при |J₁/J| = 0.2. Единственное отличие этих за-

Карло. Нормировка результатов проводилась до тех

висимостей в том, что максимальное значение плот-

103

А. К. Муртазаев, Ж. Г. Ибаев

ЖЭТФ, том 157, вып. 1, 2020

|J /J| = 0.1₁

-1.9

1.0

L=16

-2.0

0.8

-2.1

0.6

|J /J| = 0.1₁

-2.2

L=16

0.4

-2.3

0.2

-2.4

-2.0

-1.5

-1.0

-0.5

0.5

1.0

1.5

2.0

0.4

0.8

1.2

1.6

2.0

2.4

2.8

k T/|J_B|

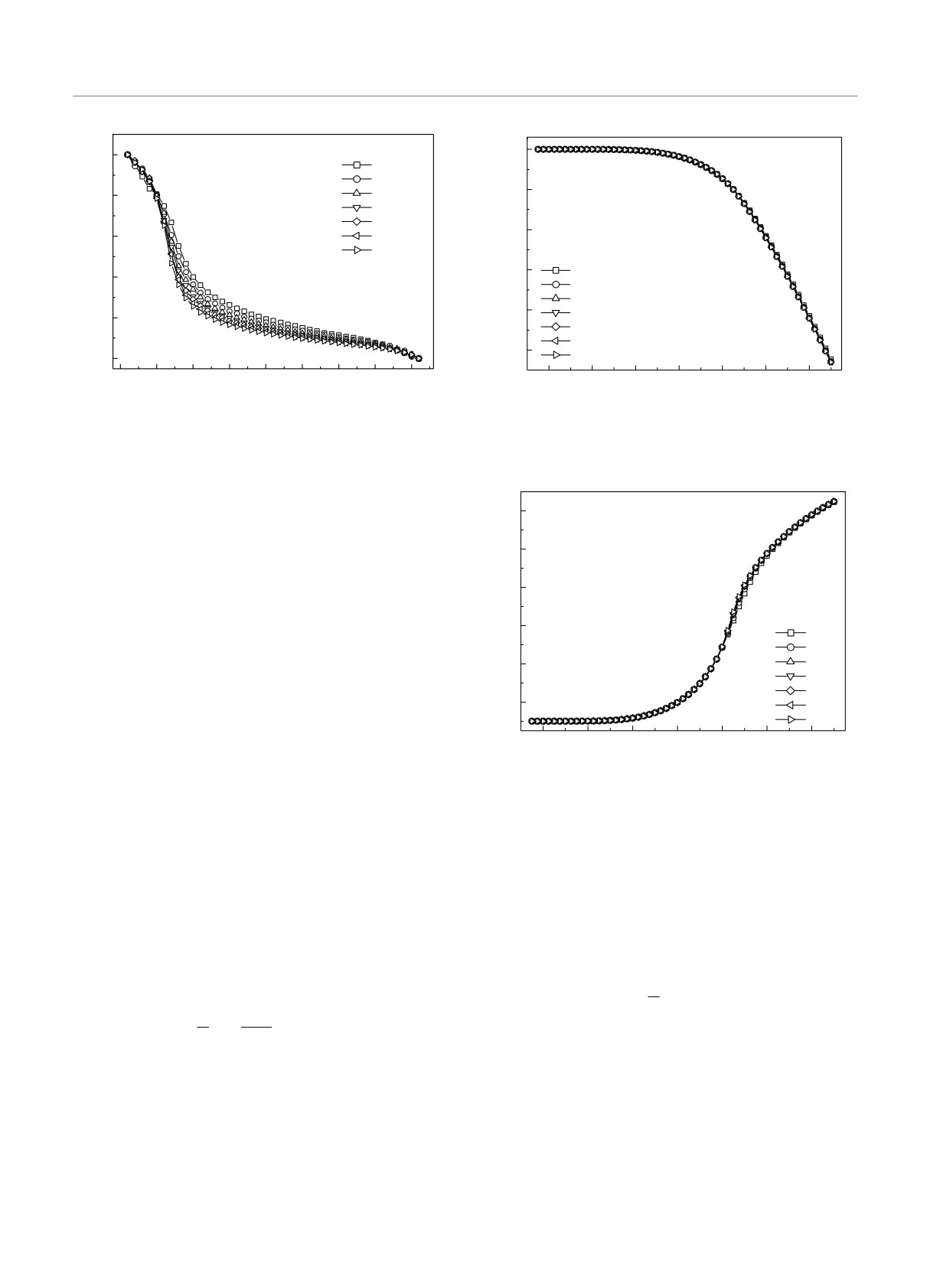
Рис. 5. График зависимости параметра порядка от энергии

Рис. 6. Зависимость свободной энергии от температуры

системы при |J1/J| = 0.1

ности распределения смещается от нуля в сторону

-0.8

отрицательных значений энергии.

По значениям плотности распределения состо-

-1.0

яний можно рассчитать один из важнейших пара-

метров термодинамической системы — статическую

-1.2

сумму Z:

|J /J| = 0.1₁

-1.4

L=16

∑

Z = G(U_i)e-Ui/kBT,

(3)

-1.6

i=1

Q — общее число состояний с различной энергией

-1.8

(Q = 2469-15909), G(U_i) — плотность распределе-

ния энергии U_i, T — температура, k_B — постоянная

0.4

0.8

1.2

1.6

2.0

2.4

2.8

Больцмана.

k T/|J_B|

По значениям Z можно легко рассчитать свобод-

Рис. 7. Зависимость внутренней энергии от температуры

ную энергию системы:

(|J1/J| = 0.1)

F = -T ln(Z).

(4)

Рисунок 6 демонстрирует, что зависимость сво-

образом зависимости представлены на рис. 7. Эти

бодной энергии от температуры имеет вид непре-

зависимости имеют вид непрерывно возрастающих

рывно убывающей кривой.

до нуля кривых без скачков и разрывов.

Остальные термодинамические параметры вы-

По значениям E и F получаем энтропию S

числяются путем усреднения по всем состояниям с

(рис. 8):

помощью формулы

(E - F ).

(6)

∑

A_i

A(T ) =

G(U_i)e-Ui/kB T ,

(5)

k_BT

Как видно на рис. 8, с повышением температуры

i=1

энтропия растет, стремясь к значению ln 2 характер-

где A_i — термодинамический параметр (внутренняя

ному для модели Изинга.

энергия — E или параметр порядка — M).

Заметим, что точки на графиках температурных

Для получения температурной зависимости

зависимостей внутренней энергии, свободной энер-

внутренней энергии в качестве параметра A_i в

гии и энтропии, полученные для систем с различны-

(5) используем значения U_i. Полученные таким

ми линейными размерами, не зависят от величины L

104

ЖЭТФ, том 157, вып. 1, 2020

Исследование двумерной анизотропной модели Изинга.. .

U_E

0.6

0.665

0.5

0.660

0.4

0.655

0.3

|J /J| = 0.1₁

L=16

0.650

0.2

0.1

0.645

0.640

0.4

0.8

1.2

1.6

2.0

2.4

2.8

0.4

0.8

1.2

1.6

2.0

2.4

2.8

k T/|J_B|

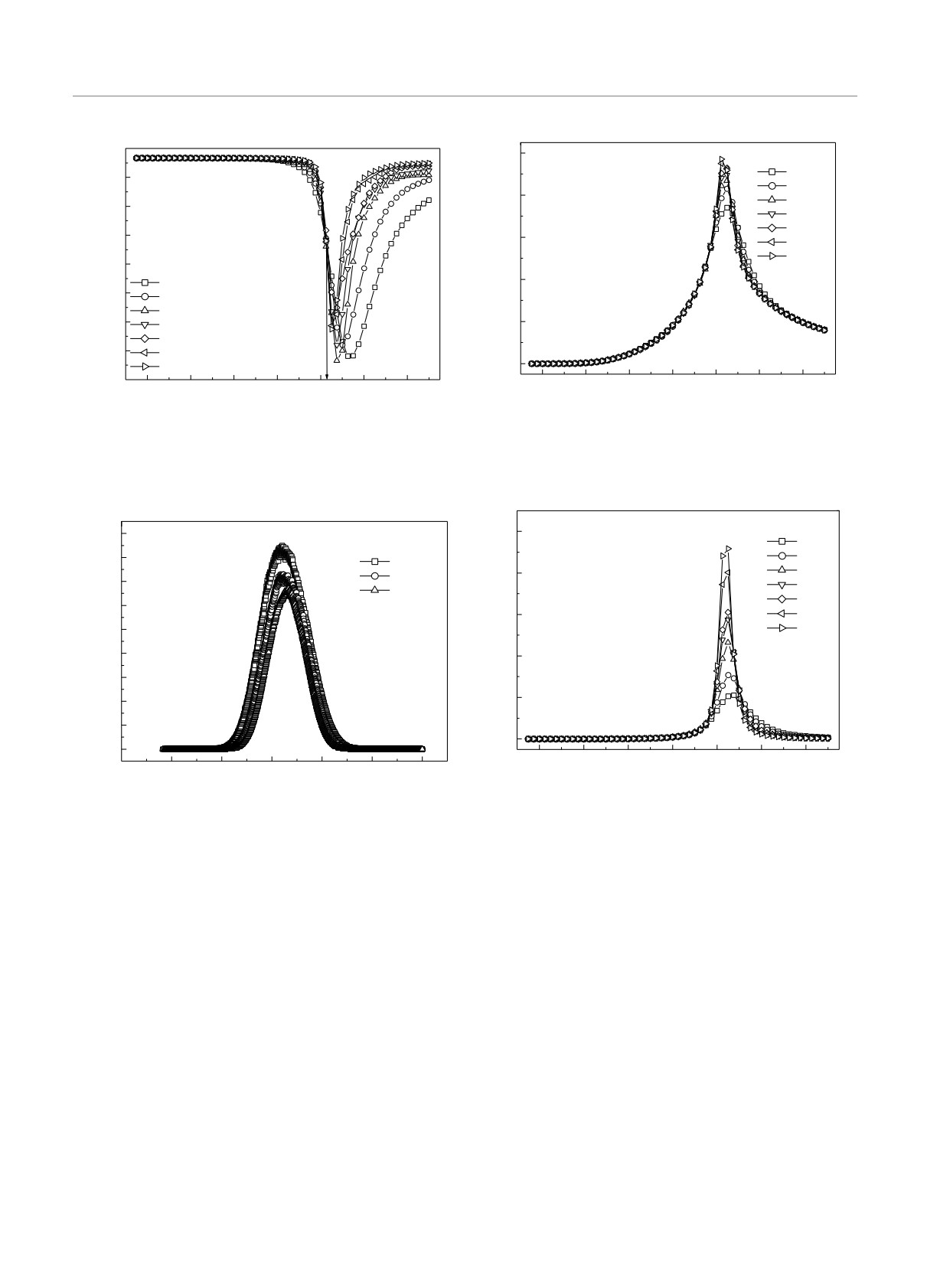
Рис. 10. Температурная зависимость кумулянтов Бинде-

Рис. 8. Зависимость энтропии от температуры

ра UE

Для определения типа фазового перехода и точ-

|J /J| = 0.1₁

1.0

ного определения критической температуры приме-

L=16

нялся метод кумулянтов Биндера четвертого поряд-

ка [8]. Известно, что величины, определяемые по

0.8

формулам

0.6

U_m = 1 - 〈E⁴〉/3〈E²〉²,

(7)

U_E = 1 - 〈m⁴〉/3〈m²〉²,

(8)

0.4

для переходов первого рода стремятся к некоторо-

му нетривиальному значению, а для переходов вто-

0.2

рого рода имеют общую точку пересечения и темпе-

ратура, при которой эти зависимости пересекаются,

0.4

0.8

1.2

1.6

2.0

2.4

2.8

является температурой фазового перехода второго

k T/|J_B|

рода [8].

Рис. 9. Температурные зависимости намагниченности

Представленные на рис. 10 и 11 температурные

зависимости кумулянтов Биндера демонстрируют

характерное для фазового перехода второго рода по-

ведение в точке k_BT_c/|J| = 2.07.

и практически ложатся на одну кривую. Это обстоя-

Для подтверждения рода фазового перехода так-

тельство может служить хорошим доказательством

же можно использовать метод гистограммного ана-

того, что полученные нами результаты рассчитаны

лиза.

с достаточно большой точностью. Средняя ошибка

В этом методе рассчитываются вероятности сос-

наших результатов не превышает 1 %.

тояний системы при температуре фазового перехода

Заменяя A_i в (5) на значения M(U_i), рассчитан-

с помощью формулы [11]

ные по формуле (2), получаем кривые температур-

ной зависимости намагниченности m (рис. 9).

∑

p(E, m) =

G(U_i) exp(U_i/k_BT ).

(9)

Эта зависимость имеет характерный для фазо-

i=1

вого перехода второго рода монотонный спад вбли-

зи критической температуры. Также можно отме-

На рис. 12 показаны гистограммы, рассчитанные

тить «высокотемпературные хвосты», характерные

при T = 2.07 и |J₁/J| = 0.1 для систем с линейными

для вычислений Монте-Карло и связанные с огра-

размерами L = 32, 36, 40. Как видно на этом ри-

ниченностью системы. Указанные хвосты исчезают

сунке, гистограммы распределения вероятности со-

с увеличением линейных размеров системы.

стояний имеют один максимум. Такая зависимость

105

А. К. Муртазаев, Ж. Г. Ибаев

ЖЭТФ, том 157, вып. 1, 2020

U_m

0.67

2.0

/J| = 0.1

L=16

0.66

1.6

0.65

0.64

1.2

0.63

|J /J| = 0.1₁

L=16

0.8

0.62

0.61

0.4

0.60

k T /|J_Bc| = 2.07

0.59

0.4

0.8

1.2

1.6

2.0

2.4

2.8

0.4

0.8

1.2

1.6

2.0

2.4

2.8

k T/|J_B|

Рис.

13. Зависимость теплоемкости от температуры

Рис. 11. Температурная зависимость кумулянтов Бинде-

ра Um

|J /J| = 0.1₁

0.0018

|J /J| = 0.1₁

L=16

0.0016

L=32

0.0014

0.0012

0.0010

0.0008

0.0006

0.0004

0.0002

0.4

0.8

1.2

1.6

2.0

2.4

2.8

–1.0

-0.9

-0.8

-0.7

-0.6

-0.5

-0.4

k T/|J_B|

Рис. 14. Температурная зависимость восприимчивости

Рис. 12. Гистограмма распределения энергии

p(E, m) свидетельствует о том, что переход, наблю-

максимумы, которые в пределах погрешности при-

даемый в системе при рассматриваемых значениях

ходятся на одно и то же значение температуры. Это

|J₁/J|, является фазовым переходом второго рода.

также подтверждает то, что в анизотропной модели

Значения внутренней энергии и намагниченнос-

Изинга с конкурирующими взаимодействиями при

ти позволяют рассчитать теплоемкость

|J₁/J| = 0.1 происходит фазовый переход второго

(

)

C = (NK²)

〈E²〉 - 〈E〉²

(10)

рода из ферромагнитного состояния в парамагнит-

ное. Заметим, что в качественном плане аналогич-

и восприимчивость

ная картина имеет место и при |J₁/J| = 0.2.

(

)

χ = (NK)

〈m²〉 - 〈m〉²

(11)

Имея значение критической температуры, мож-

но вычислить критические индексы намагниченнос-

где K = |J|/k_BT .

ти, восприимчивости, радиуса корреляции и теп-

Графики, представленные на рис. 13 и 14, пока-

лоемкости. Для этого воспользуемся теорией ко-

зывают, что температурные зависимости теплоемко-

нечно-размерного скейлинга. Согласно этой теории

сти и восприимчивости имеют хорошо выраженные

[12-15], при T = T_c и достаточно больших L

106

ЖЭТФ, том 157, вып. 1, 2020

Исследование двумерной анизотропной модели Изинга.. .

ln V_i

ln m

6.5

V₄

-0.40

6.0

V₃

-0.45

5.5

V₂

5.0

-0.50

4.5

V₁

-0.55

4.0

-0.60

3.5

-0.65

3.0

= 1.297

-0.70

2.5

3.9

4.1

4.3

4.5

4.7

4.9

5.1

5.3

= 0.191

–0.75

ln L

3.9

4.1

4.3

4.5

4.7

4.9

5.1

5.3

ln L

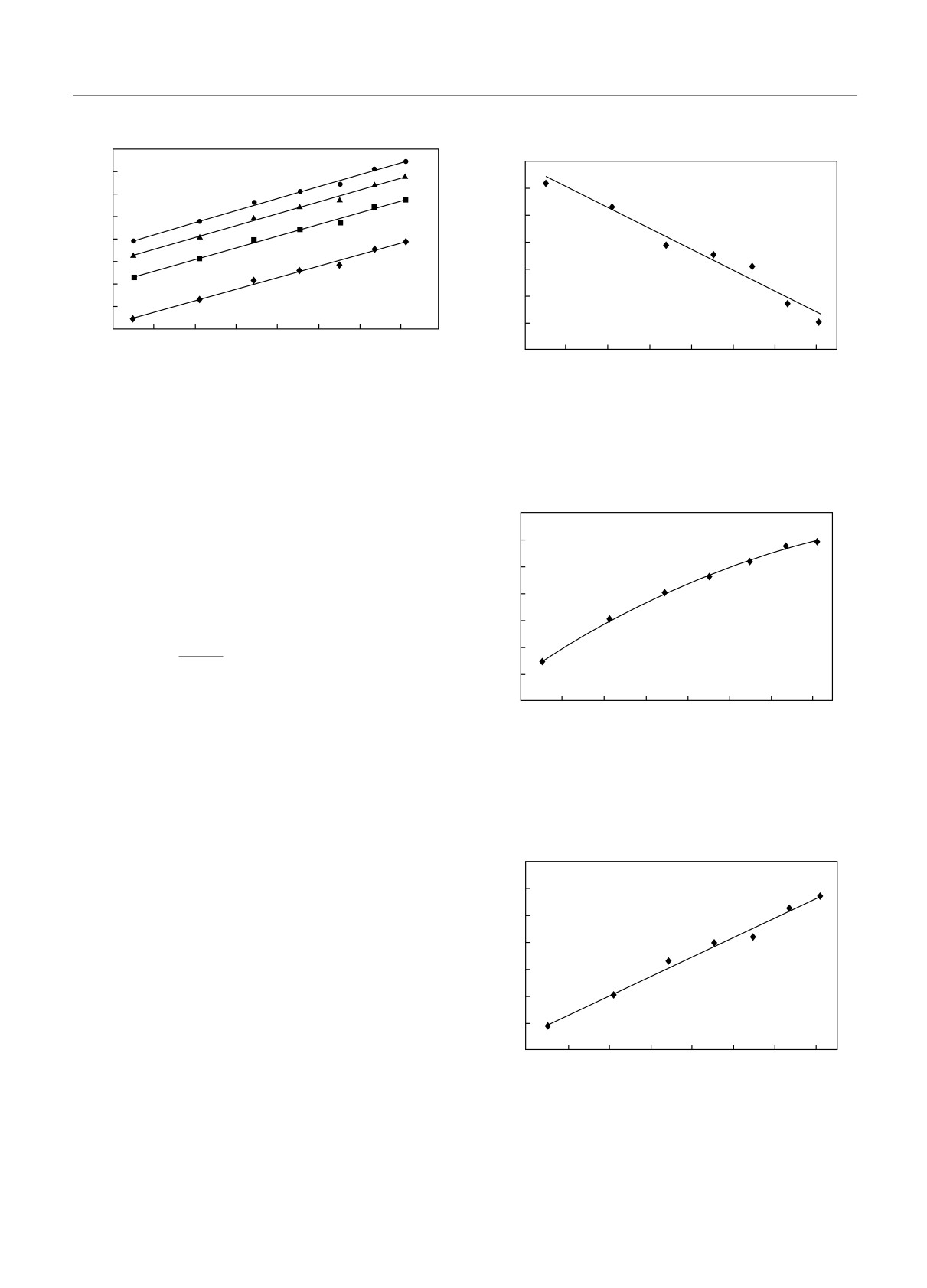
Рис. 15. Логарифмические зависимости параметров Vi от

линейных размеров системы при |J1/J| = 0.1

Рис. 16. Логарифмическая зависимость параметра поряд-

ка от линейных размеров при |J1/J| = 0.1

m∝L^-β/ν,

(12)

χ∝L^γ/ν,

(13)

ln C

1.1

V_n = L1/νgVn,

(14)

C_max(L) = C_max(L = ∞) - aL^α/ν,

(15)

1.0

0.9

где gVn — некоторая постоянная, a — коэффициент

пропорциональности, а в качестве V_n может высту-

0.8

пать

0.7

〈mⁱE〉

0.6

Vi =

- 〈E〉, i = 1, 2, 3, . . .

(16)

〈mⁱ〉

0.5

= 0.342

Значения критических индексов получаем мето-

0.4

3.9

4.1

4.3

4.5

4.7

4.9

5.1

5.3

дом наименьших квадратов, аппроксимируя форму-

ln L

лами (12)-(15) значения термодинамических пара-

метров при T = T_c. Для этого строились графики

Рис. 17. Логарифмическая зависимость теплоемкости от

зависимости натуральных логарифмов соответству-

линейных размеров системы (|J1/J| = 0.1)

ющих величин от ln L и проводился линейный рег-

рессионный анализ.

Представленные на рис. 15- 18 графики показы-

вают, что все точки в пределах погрешности хорошо

4.0

ложатся на прямые линии. Величина достоверности

3.5

аппроксимации R² > 0.97. Тангенсы углов накло-

на прямых на рис. 14-17 определяют значения β/ν,

3.0

γ/ν, α/ν и 1/ν.

2.5

Полученные значения критических параметров

2.0

представлены в таблице. По данным этой таблицы

видно, что температура фазового перехода и кри-

1.5

тический индекс намагниченности уменьшаются с

1.0

увеличением интенсивности конкурирующего взаи-

= 1.802

0.5

модействия. А индексы теплоемкости восприимчи-

3.9

4.1

4.3

4.5

4.7

4.9

5.1

5.3

вости и радиуса корреляции, наоборот, увеличива-

ln L

ются. Такое поведение можно объяснить тем, что

Рис. 18. Логарифмическая зависимость восприимчивости

добавление небольшой конкуренции к стандартной

от линейных размеров (|J1/J| = 0.1)

модели Изинга приводит к потере устойчивости си-

стемы и усилению таких ее свойств, как восприим-

107

А. К. Муртазаев, Ж. Г. Ибаев

ЖЭТФ, том 157, вып. 1, 2020

Таблица

|J₁/J|

T_c

1/ν

β/ν

α/ν

γ/ν

α + 2β + γ

0.1

2.07

1.297

0.191

0.342

1.802

0.771(3)

0.147(2)

0.264(3)

1.389 (7)

1.947

0.2

1.833

1.286

0.185

0.357

1.827

0.778(3)

0.144(2)

0.278(3)

1.421(7)

1.987

Изинг

0.125

1.75

d=2

чивость к внешним воздействиям и появление новых

ЛИТЕРАТУРА

состояний, которые не могли реализоваться в исход-

ной модели Изинга.

А. А. Овчинников, И. И. Украинский, Г. Ф. Квен-

Сравнивая полученные значения критических

цель, УФН 108, 81 (1972).

индексов со значениями для классической модели

S. R. White, Phys. Rep. 301, 187 (1998).

Изинга, можно заметить, что критическое поведе-

ние двумерной ANNNI-модели не может быть опи-

I. Moreira and R. Dovesi, Int. J. Quant. Chem. 99,

сано в рамках изинговского класса универсальности

805 (2004).

критического поведения.

E. H. Lieb, The Hubbard Model: Its Physics and

Mathematical Physics, ed. by D. Baeriswyl. Plenum

Press, New York (1995), NATO ASI Series B: Physics

Vol. 343, p. 1.

4. ЗАКЛЮЧЕНИЕ

D. J. Klein, Chem. Phys. 77, 3098 (1982).

В данной статье приведены результаты иссле-

дования двумерной анизотропной модели Изинга

R. J. Elliott, Phys. Rev. 124, 346 (1961).

с конкурирующими взаимодействиями на квадрат-

Ю. А. Изюмов, В. Н. Сыромятников, Фазовые пе-

ной решетке методами Монте-Карло на основе ал-

реходы и симметрия кристаллов, Наука, Москва

горитма Ванга - Ландау для значений |J₁/J| = 0.1

(1984).

и |J₁/J| = 0.2 при линейных размерах системы L =

= 16-40. Получены графики распределения плот-

И. К. Камилов, А. К. Муртазаев, Х. К. Алиев,

ности состояний и вычислены значения параметров

УФН 169, 773 (1999).

порядка, соответствующие различным значениям

энергий. Установлено, что для указанных значений

B. Widom, J. Chem. Phys. 84, 6943 (1986).

|J₁/J| основным состоянием двумерной ANNNI-мо-

10.

A. K. Murtazaev and J. G. Ibaev, Sol. St. Comm.

дели является двукратно вырожденное ферромаг-

152, 177 (2012).

нитное состояние. С помощью метода кумулянтов

Биндера и гистограммного анализа данных показа-

11.

F. Wang and D. P. Landau, Phys. Rev. Lett. 86, 2050

но, что при значениях |J₁/J| = 0.1 и |J₁/J| = 0.2

(2001).

в рассматриваемой модели происходит фазовый пе-

реход второго рода из ферромагнитного состояния

12.

A. Mailhot, M. L. Plumer, and A. Caille, Phys. Rev.

в парамагнитную фазу. Вычислены значения крити-

B 50, 6854 (1994).

ческих температур. Получены графики температур-

ных зависимостей термодинамических параметров.

13.

P. Peczak, A. M. Ferrenberg, and D. P. Landay, Phys.

Rev. B 43, 6087 (1991).

С использованием теории конечно-размерного скей-

линга вычислены значения основных критических

14.

D. Loison, Phys. Lett. A 257, 83 (1999).

индексов. Показано, что критическое поведение дву-

мерной анизотропной модели Изинга с конкурирую-

15.

A. K. Murtazaev, I. K. Kamilov, and K. K. Aliev, J.

щими взаимодействиями отличается от двумерного

Magn. Magn. Mater. 204, 151 (1999).

изинговского класса универсальности.

108