ЖЭТФ, 2020, том 157, вып. 1, стр. 144-155
© 2020
НЕЛИНЕЙНАЯ ДИНАМИКА ПАРАМЕТРИЧЕСКИХ
ОСЦИЛЛЯЦИЙ ЭКСИТОН-ПОЛЯРИТОНОВ В
ПОЛУПРОВОДНИКОВОМ МИКРОРЕЗОНАТОРЕ
О. Ф. Васильева*, А. П. Зинган, В. В. Васильев
Приднестровский государственный университет им. Т. Г. Шевченко
3300, Тирасполь, Молдова
Поступила в редакцию 11 июня 2019 г.,
после переработки 11 июня 2019 г.
Принята к публикации 20 июня 2019 г.
Изучена динамика поляритонов в микрорезонаторе в режиме параметрического осциллятора, когда два
поляритона накачки превращаются в поляритоны сигнальной и холостой мод и обратно. При этом на-
качка осуществляется двумя лазерными импульсами с близкими частотами. Найдены аналитические
решения системы нелинейных дифференциальных уравнений. Получены периодический и апериодиче-
ский режимы превращения пары поляритонов накачки в поляритоны сигнальной и холостой мод, а также
режим покоя системы.
DOI: 10.31857/S0044451020010174
тырехволновым смешением или параметрическим
рассеянием фотовозбужденных поляритонов накач-
1. ВВЕДЕНИЕ
ки в сигнальную и холостую моды. Эксперименталь-
но идентифицированы два механизма нелинейности:
Смешанные экситон-фотонные состояния в плос-
поляритонное параметрическое рассеяние [6,19,20] и
ких полупроводниковых микрорезонаторах с кван-
голубой сдвиг поляритонной дисперсии [2, 5]. С по-
товыми ямами в активном слое представляют собой
мощью pump-probe-метода в работах [8, 9] впервые
новый класс квазидвумерных квазичастиц с уни-
наблюдалось параметрическое усиление в микроре-
кальными свойствами [1-13]. Такие состояния назы-
зонаторе при возбуждении нижней поляритонной
вают микрорезонаторными экситон-поляритонами.
ветви пикосекундным импульсом накачки под углом
Они возникают благодаря сильной связи экситонов
падения 16.5◦. После возбуждения (с небольшой за-
с собственными модами электромагнитного излуче-
держкой) нижней поляритонной ветви дополнитель-
ния микрорезонатора. В условиях сильной связи эк-
но слабым пробным импульсом, падавшим нормаль-
ситонная и фотонная моды расталкиваются и воз-
но, обнаружилось, что этот импульс в отражении
никают верхняя и нижняя микрорезонаторные по-
усиливался более чем в 70 раз. При этом появлялась
ляритонные моды. Непараболичность нижней поля-
также холостая мода под углом 35◦. Именно для
ритонной ветви допускает возникновение парамет-
этих углов выполнялись резонансные условия. Ре-
рического процесса, в результате которого два по-
зультаты экспериментов [8, 9] были воспроизведены
ляритона накачки рассеиваются в сигнальную и хо-
также в [21] и моделировались в [7] с использовани-
лостую моды с сохранением энергии и импульса. По-
ем механизма поляритон-поляритонного рассеяния.
этому огромный интерес вызывает поляритон-поля-
Аналогичные процессы наблюдались в [22] при ис-
ритонное рассеяние, благодаря которому экситон-
пользовании двух пучков накачки под углами ±45◦
поляритонная система демонстрирует сильно нели-
и пробного пучка под углом 0◦. Режим параметри-
нейные свойства [6-13]. Такие нелинейности были
ческого осциллятора наблюдался в [9,14] при непре-
обнаружены в спектрах люминесценции микрорезо-
рывном возбуждении нижней поляритонной ветви
наторов [14-18] при резонансном возбуждении ниж-
излучением накачки под «магическим» углом 16◦
ней поляритонной ветви, которые объяснялись че-
без пробного импульса. Выше пороговой интенсив-
ности наблюдались сильные пучки сигнальной и хо-
* E-mail: florina_of@mail.ru
144
ЖЭТФ, том 157, вып. 1, 2020
Нелинейная динамика параметрических осцилляций. ..
лостой мод под углами 0◦ и 35◦ соответственно. В
создания спиновых запоминающих устройств [35],
работе [20] обнаружена сильная и необычная за-
логических вентилей
[36, 37] или переключате-
висимость поляризации света, излучаемого микро-
лей [38].
резонатором, от поляризации накачки. Эта зависи-
В работах [39-41] при исследовании свойств оп-
мость интерпретируется с использованием псевдо-
тического параметрического осциллятора использо-
спиновой модели в рамках квазиклассического фор-
вались два одинаковых фотона накачки на нижней
мализма, где параметрическое рассеяние описыва-
ветви поляритонного закона дисперсии. Однако в
ется как резонансное четырехволновое смешение. В
[42,43] было показано, что два различных пучка на-
работах [23-25] наблюдалось бистабильное пропус-
качки можно конвертировать в два вырожденных на
кание излучения в зависимости от интенсивности
частоте фотонов сигнальной и холостой мод. Нали-
накачки при возбуждении экситон-поляритонов в
чие двух различных пучков накачки дает большие
микрорезонаторе. Отметим, что процесс параметри-
возможности для генерации сигнального и холосто-
ческого рассеяния наблюдался как при импульсном
го пучков с заданными свойствами.
[20,26], так и при непрерывном [14,16,27] возбужде-
нии.
2. ПОСТАНОВКА ЗАДАЧИ. ОСНОВНЫЕ
Описание поляритонных параметрических ос-
УРАВНЕНИЯ
цилляторов и усилителей представлено в ряде работ
[2, 5, 7, 8, 12, 13, 28]. Экситон-экситонные взаимодей-
Цель данной работы — изучить изменение во
ствия играют ключевую роль в сильных нелиней-
времени плотности поляритонов при накачке ниж-
ностях, присутствующих в поляритонных системах
ней ветви в двух близких по энергии точках за-
микрорезонатора. Первой попыткой контроля этих
кона дисперсии. Мы будем считать, что оба пуч-
взаимодействий было использование концепции ди-
ка накачки различаются по амплитуде (интенсив-
поляритонов [29] путем включения двойных асим-
ности), однако энергии фотонов различаются сла-
метричных квантовых ям в электрически смещен-
бо. Рассматриваем ситуацию на временах поряд-
ный микрорезонатор. Как прямые, так и непрямые
ка либо меньших времени релаксации возбуждений
экситоны соединяются с одной и той же модой резо-
среды (экситон-поляритонов). В этом случае про-
натора, образуя новый тип поляритона с аналогич-
цессы релаксации не успевают срабатывать, а эво-
ными свойствами по отношению к экситон-поляри-
люция системы представляет собой предел опти-
тонной системе. В работе [30] теоретически иссле-
ческой нутации экситон-поляритонов под действи-
довалась динамика диполяритонов при учете трех
ем ультракоротких импульсов лазерного излучения,
каналов рассеяния. Получены апериодические и пе-
ответственных за создание начального условия си-
риодические режимы эволюции диполяритонов на-
стемы. Мы рассматриваем поведение системы по-
качки в диполяритоны сигнальной и холостой мод.
ляритонов в нестационарном режиме, когда накач-
В работе [31] путем объединения широких кванто-
ка осуществляется фемто- и пикосекундными им-
вых ям в простом волноводе наблюдалось образова-
пульсами лазерного излучения. В этом случае мож-
ние диполярных поляритонов. Основным ограниче-
но считать, что ультракороткие импульсы возбуж-
нием исследуемых поляритонных систем по сравне-
дения служат лишь для создания начальных плот-
нию с их атомными аналогами для изучения сильно
ностей поляритонов, т. е. начальных условий систе-
коррелированных явлений и физики многих тел яв-
мы. Затем система предоставляется самой себе и
ляется их относительно слабое двухчастичное взаи-
она эволюционирует во времени. Такая постанов-
модействие по сравнению с хаосом. В [32] показаны
ка задачи используется и при исследовании явления
новые возможности усиления таких локальных вза-
оптической нутации в пространственно-однородной
имодействий и нелинейностей путем настройки эк-
системе двухуровневых атомов [44] либо эксито-
ситон-поляритонного дипольного момента в элект-
нов [45]. Мы считаем, что с помощью ультракорот-
рически смещенных полупроводниковых микрорезо-
ких импульсов резонансного лазерного излучения
наторах, включающих широкие квантовые ямы.
в микрорезонаторе создается система когерентных
Микрорезонаторные экситон-поляритоны об-
экситон-поляритонов. Микрорезонатор обеспечива-
ладают бистабильностью при низких оптических
ет пространственное ограничение области существо-
мощностях благодаря их сильным нелинейностям
вания поляритонов, которые взаимно превращают-
[24]. Поляризационная зависимость нелинейностей
ся друг в друга. Квантовая яма, в которой возника-
вызывает поляризационную мультистабильность
ют поляритоны, вставляется в брэгговскую структу-
[33, 34], которая может быть использована для
ру, которая характеризуется определенным пропус-
145
10
ЖЭТФ, вып. 1
О. Ф. Васильева, А. П. Зинган, В. В. Васильев
ЖЭТФ, том 157, вып. 1, 2020
iap1 = ωp1ap1 + μa∗p
asai,
2
iap2 = ωp2ap2 + μa∗p
asai,
(2)
1
ias = ωsas+μap1ap2a∗i , iai = ωiai+μap1ap2a∗s.
–
cav
Систему уравнений (2) дополним начальными усло-
виями, которые запишем в виде
ap
1|t=0 =
ap10 exp(iϕp10),
ap
2|t=0 =
ap20 exp(iϕp20),
(3)
еx
as|t=0 = as0 exp(iϕs0), ai|t=0 = ai0 exp(iϕi0),
где ap10, ap20, as0, ai0 и ϕp10, ϕp20, ϕs0, ϕi0 — дейст-
+
вительные амплитуды и фазы поляритонов в на-
чальный момент времени.
Введем далее в рассмотрение плотности поляри-
k
тонов
np1 = a∗p
ap1 , np2 = a∗p
ap2 ,
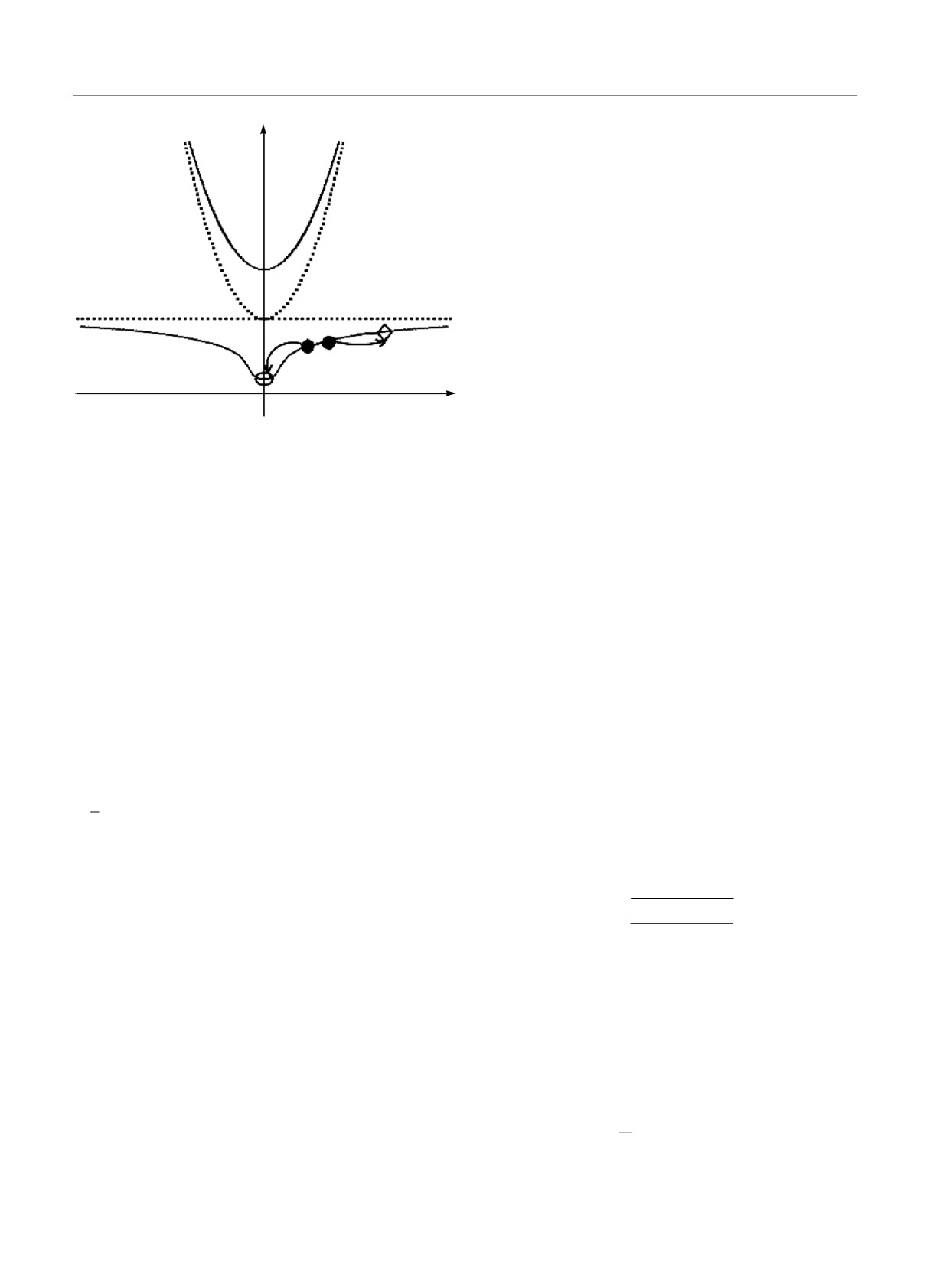
Рис.
1. Энергии поляритонов верхней и нижней вет-
1
2
вей (ω±). Дисперсия собственных частот микрорезонатора
ns = a∗sas, ni = a∗iai
ωcav и экситона ωex. Два поляритона накачки рассеивают-
и две компоненты «поляризации»
ся в сигнальную и холостую моды
(
)
∗
Q=i
ap1 ap2 a
a∗i - asaia∗p
a∗
,
s
1
p2
R=ap1ap2a∗sa∗i +asaia∗p
a∗ .p
1
2
канием, отражением и потерями [8,9,12,15,27]. Осо-
Используя (2), для введенных функций получа-
бенности эволюции системы будут проявляться в ге-
ем следующую систему нелинейных дифференци-
нерации вторичных субимпульсов либо периодиче-
альных уравнений:
ского излучения на частотах экситон-поляритонов.
Ниже мы рассматриваем ситуацию, когда поля-
np1 = μQ,
np2 = μQ,
ритоны возбуждаются на нижней ветви закона дис-
ns = -μQ,
ni = -μQ,
персии под «магическим» углом (рис. 1). В работах
(4)
Q=ΔR+2μ(nsni(np2 + np1) -
[4, 5] показано, что процесс параметрического рас-
R=-ΔQ,
сеяния двух поляритонов накачки в сигнальную и
- np1np2(ni + ns)),
холостую моды описывается гамильтонианом вида
где Δ = ωp1 + ωp2 - ωs - ωi — расстройка резонанса.
Используя (3), начальные условия для этих функ-
1
ций можно записать в виде
H =ωp1â†p
âp1 + ωp2 â†p
âp2 + ωsâ†sâs + ωiâ†iâi +
1
2
ℏ
(
)
np1|t=0 ≡ np10 = |ap10|2,
+μ â†sâ†iâp1âp2 +â†p
â†
âsâi
,
(1)
1
p2
np2|t=0 ≡ np20 = |ap20|2,
ns|t=0 ≡ ns0 = |as0|2, ni|t=0 ≡ ni0 = |ai0|2,
(5)
где ωp1 , ωp2 , ωs и ωi — собственные частоты поля-
Q|t=0 ≡ Q0 = 2
√np10np20ns0ni0 sin θ0,
ритонов накачки первого и второго импульса, сиг-
R|t=0 ≡ R0 = 2
нальной и холостой мод соответственно; âp1 , âp2 ,
√np10np20ns0ni0 cos θ0,
âs, âi — операторы уничтожения поляритонов; μ —
где θ0 = ϕs0 +ϕi0 -ϕp10 -ϕp20 — начальная разность
константа параметрической поляритон-поляритон-
фаз.
ной конверсии. Используя (1), легко получить си-
Из (4) нетрудно получить следующие интегралы
стему гайзенберговских уравнений для операторов
движения:
âp1 , âp2 , âs, âi. Усредняя эту систему уравнений и
np1 - np2 = np10 - np20, ns - ni = ns0 - ni0,
используя приближение среднего поля (mean field
approximation), применимость которого обоснова-
np1 + ns = np10 + ns0, np2 + ni = np20 + ni0,
на в [46], для комплексных амплитуд поляритонов
Q2 + R2 = 4np1np2nins,
(6)
ap1 = 〈âp1 〉, ap2 = 〈âp2 〉, as = 〈âs〉 и ai = 〈âi〉 можно
Δ
получить следующую систему нелинейных эволюци-
R=R0 +
(np10 - np1 ).
μ
онных уравнений:
146
ЖЭТФ, том 157, вып. 1, 2020
Нелинейная динамика параметрических осцилляций. ..
Дальнейшее рассмотрение удобнее провести для
энергии W от y при различных значениях парамет-
нормированных величин
ров. Вид решения y(τ) уравнения (7) определяется
np1
np20
ns0
ni0
корнями алгебраического уравнения W (y) = 0, ко-
y=
,
np20 =
,
ns0 =
,
ni0 =
,
np10
np10
np10
np10
торые зависят от параметров np20, ns0, ni0, α и θ0.
Δ
α=
,
τ = tμnp10.
2μnp10
Тогда систему уравнений (4) можно привести к од-
2.1. Эволюция при начальной разности фаз
ному нелинейному дифференциальному уравнению
θ0 = π/2
для нормированной плотности поляритонов накач-
ки первого импульса y:
Рассмотрим сначала случай, когда начальная
1
( dy)2
разность фаз равна π/2. Уравнение W (y) = 0 имеет
+ W(y) = 0,
(7)
2
dτ
четыре действительных корня, которые мы распола-
где
гаем в порядке убывания их значений и обозначим
[
соответственно y1 > yM > ym > y4. Здесь корни yM
W (y) = - 2y (y - 1 + np20) (1 + ns0 - y) ×
и ym имеют смысл максимальной и минимальной
]
(√
)2
плотности поляритонов накачки первого импульса,
× (1+ni0-y) -
(8)
np20ns0ni0 cos θ0+α(1-y)
которые они принимают в процессе эволюции. Да-
Уравнение (7) описывает колебания нелинейно-
лее для определенности будем считать ns0 > ni0. На
го осциллятора, где W (y) играет роль потенциаль-
рис. 2a показана эволюция корней в зависимости от
ной энергии осциллятора, а (1/2)(dy/dτ)2 — кинети-
параметра α. Видно, что с ростом этого параметра
ческой. Качественно поведение функции y(τ) мож-
корни y1 и ym растут, а yM и y4 убывают. Тогда ре-
но установить, изучая зависимость потенциальной
шение уравнения (8) можно представить в виде
)
y1(yM - ym)
(√
yM -
sn2
(y1 - ym)(yM - y4) τ ± f(ϕ0, k)
y1 - ym
y=
)
,
(9)
yM - ym
(√
1-
sn2
(y1 - ym)(yM - y4) τ ± f(ϕ0, k)
y1 - ym
где sn(x)
— эллиптическая функция Якоби,
нальной и холостой мод, т. е. процесс колебаний про-
f (ϕ0, k) = F(ϕ0,k) - K(k), F(ϕ0,k) — неполный
исходит без истощения плотности поляритонов на-
эллиптический интеграл первого рода с модулем k
качки. С ростом α при фиксированных np20, ns0 и
и параметром ϕ0, K(k) — полный эллиптический
ni0 амплитуда и период колебаний монотонно убы-
интеграл [47,48]. Величины k и ϕ0 выражаются как
вают (рис. 3б,в), а при фиксированных α, ns0 и ni0
они изменяются при изменении np20 (рис. 3б,в). Из
(y1 - y4)(yM - ym)
k2 =
,
рис. 3б видно, что чем больше плотность поляри-
(y1 - ym)(yM - y4)
√
тонов накачки второго импульса np20, тем больше
(10)
(yM - y4)(1 - ym)
амплитуда колебаний поляритонов накачки первого
ϕ0 = arcsin
импульса.
(yM - ym)(1 - y4)
Если нормированная расстройка резонанса α
Из (9) легко получить амплитуду A и период T коле-
равна нулю [49], то в зависимости от соотношения
баний плотности поляритонов накачки первого им-
между начальными плотностями поляритонов на-
пульса:
качки, сигнальной и холостой мод могут возникнуть
как периодический, так и апериодический режимы
2K(k)
A=yM -ym, T =
√
(11)
эволюции (рис. 3в).
(y1 - ym)(yM - y4)
Периодическая эволюция плотности полярито-
2.2. Эволюция при начальной разности фаз
нов накачки представлена на рис. 3а. Плотность по-
θ0 = 0
ляритонов периодически изменяется в пределах от
ym до yM. Следовательно, отсутствует полное пре-
Рассмотрим теперь эволюцию системы при на-
вращение поляритонов накачки в поляритоны сиг- чальной разности фаз θ0 = 0. Уравнение W (y) = 0
147
10*
О. Ф. Васильева, А. П. Зинган, В. В. Васильев
ЖЭТФ, том 157, вып. 1, 2020
по-прежнему имеет четыре действительных корня,
Однако, если в начальный момент времени плот-
y1 > yM > ym > y4. Если в начальный момент вре-
ности поляритонов сигнальной и холостой мод рав-
ны (ns0 = ni0) и плотности поляритонов накачки
мени ns0 = ni0 и np10 = np20, то эволюция системы
представляет собой периодическое превращение па-
первого и второго импульса равны (np10 = np20), то
ры поляритонов накачки в поляритоны сигнальной
будет наблюдаться как периодический, так и апе-
и холостой мод и обратно. Качественное поведение
риодический режим эволюции (рис. 4). Уравнение
корней совпадает с представленным рис. 2а. Реше-
W (y) = 0 имеет четыре действительных корня y1,
ние уравнения (7) в этом случае соответствует фор-
y2, y3 и y4, которые принимают следующие значе-
муле (9).
ния:
√
√(√
)2
√
2 (1 + ns0) - α +
2 (1 + ns0) - α
+4
2 (ns0 + α)
y1 =
√
,
2
2
√
√(√
)2
√
2 (1 + ns0) + α +
2 (1 + ns0) - α
-4
2 (ns0 + α)
y2 =
√
,
2
2
√
√(√
)2
√
2 (1 + ns0) + α -
2 (1 + ns0) - α
-4
2 (ns0 + α)
y3 =
√
,
2
2
√
√(√
)2
√
2 (1 + ns0) - α -
2 (1 + ns0) - α
+4
2 (ns0 + α)
y4 =
√
2
2
Исследование величин корней показывает, что при α = 1 корни y1 и y2 оказываются одинаковыми
(рис. 2б). Вырождение именно этих корней приводит к возникновению апериодической эволюции системы.
Апериодическая эволюция системы сводится к превращению поляритонов накачки в поляритоны сигналь-
ной и холостой мод и на этом заканчивается. Решение уравнения (7) можно записать в виде
(
√
)
√
(1 - y3)(y2 - y4)
y3(y2 - y4) - y4(y2 - y3)th2
(y2 - y3)(y2 - y4) τ ± arth
(1 - y4)(y2 - y3)
y=
(
√
)
(12)
√
(1 - y3)(y2 - y4)
y2 - y4 - (y2 - y3)th2
(y2 - y3)(y2 - y4) τ ± arth
(1 - y4)(y2 - y3)
При 0 < α < 1 все четыре корня различны и располагаются в следующем порядке: y1 > y2 > y3 > y4.
Эволюция системы описывается выражением
)
(√
y3(y2 - y4) - y4(y2 - y3)sn2
(y2 - y3)(y2 - y4) τ ± f(ϕ0, k)
y=
)
,
(13)
(√
y2 - y4 - (y2 - y3)sn2
(y2 - y3)(y2 - y4) τ ± f(ϕ0, k)
следовательно, плотность поляритонов накачки первого импульса изменяется периодически в пределах от
y3 до y2.
Величины k и ϕ0 определяются следующими соотношениями:
(y1 - y4)(y2 - y3)
k2 =
,
(y1 - y3)(y2 - y4)
√
(14)
(y2 - y4)(1 - y3)
ϕ0 = arcsin
(y2 - y3)(1 - y4)
Из (13) легко получить амплитуду A и период T колебаний плотности поляритонов накачки первого им-
пульса:
2K(k)
A=y2 -y3, T =
√
(15)
(y1 - y3)(y2 - y4)
148
ЖЭТФ, том 157, вып. 1, 2020
Нелинейная динамика параметрических осцилляций. ..
При α > 1 и y2 > y1 > y3 > y4 эволюция системы описывается выражением
(√
)
y3(y1 - y4) - y4(y1 - y3)sn2
(y1 - y3)(y1 - y4) τ ± f(ϕ0, k)
y=
)
(16)
(√
y1 - y4 - (y1 - y3)sn2
(y1 - y3)(y1 - y4) τ ± f(ϕ0, k)
и плотность поляритонов накачки первого импульса изменяется периодически в пределах от y3 до y1.
В выражении (16)
1 ≤ y ≤ yM. Следовательно, в зависимости от па-
раметров возможны колебания плотности поляри-
(y2 - y4)(y1 - y3)
тонов накачки в первом случае под фоном с амп-
k2 =
,
(y2 - y3)(y1 - y4)
литудой A = 1 - ym, а во втором — над фоном с
√
амплитудой A = yM - 1, где плотность фона равна
(y1 - y4)(1 - y3)
начальной плотности поляритонов накачки y0 = 1.
ϕ0 = arcsin
(y1 - y3)(1 - y4)
Решение уравнения (7) в случае, когда y1 > 1 >
>ym >y4, имеет вид
Амплитуда и период колебаний в этом случае бу-
y1(1 - ym)
√
дут соответственно равны
1-
sn2
(y1 - ym)(1 - y4) τ
y1 - ym
y=
,
(18)
2K(k)
1-ym
√
A=y1 -y3, T =
√
(17)
1-
sn2
(y1 - ym)(1 - y4) τ
y1 - ym
(y2 - y3)(y1 - y4)
где
Из рис. 4в видно, что период T колебаний плот-
(y1 - y4)(1 - ym)
k2 =
(19)
ности поляритонов накачки первого импульса сна-
(y1 - ym)(1 - y4)
чала растет с ростом α, расходится при значении
Во втором случае, когда y1 > yM > 1 > y4, соответ-
α = 1 (что соответствует апериодическому режи-
ственно получаем
му), при котором оба наибольших корня оказыва-
y4(yM - 1)
√
ются одинаковыми, а затем монотонно убывает. При
1-
sn2
(y1 - 1)(yM - y4) τ
yM - y4
фиксированных значениях α, np20 и увеличении на-
y=
,
(20)
yM - 1
√
чальной плотности поляритонов сигнальной моды
1-
sn2
(y1 - 1)(yM - y4) τ
yM - y4
ns0 амплитуда и период колебаний увеличиваются.
где
В условиях точного резонанса (α = 0), когда
начальная плотность одного из поляритонов накач-
(y1 - y4)(yM - 1)
k2 =
(21)
ки, например второго импульса, меньше либо равна
(y1 - 1)(yM - y4)
начальной плотности поляритонов холостой моды
Из
(18) и
(20) следует, что плотность по-
np20 ≤ ni0, при определенном соотношении между
ляритонов накачки эволюционирует периодически
начальными параметрами системы решение уравне-
(рис. 5б). При этом, как уже отмечалось, колеба-
ния (7) имеет вид y(τ) = 1, т. е. совпадает с началь-
ния плотности происходят как под фоном, так и
ным условием, что обусловлено пересечением двух
над фоном. Амплитуда колебаний, которая опреде-
средних корней уравнения W (y) = 0 (рис. 5). Это
ляется как разность двух средних корней уравнения
означает, что при отличных от нуля плотностях всех
W (y) = 0, при фиксированных ni0 и np20 сначала
поляритонов в системе невозможна нетривиальная
убывает с ростом начальной плотности полярито-
эволюция, так как начальные плотности полярито-
нов сигнальной моды ns0, затем обращается в нуль,
нов не изменяются во времени. То есть в системе
а потом монотонно растет (рис. 5в).
наблюдается режим покоя. В отсутствие вырожде-
ния двух средних корней уравнения W (y) = 0 воз-
2.3. Эволюция при начальной разности фаз
никают два случая эволюции. В зависимости от со-
θ0 = π
отношения между параметрами np20, ni0, ns0 в пер-
вом случае корни упорядочиваются так, что y1 >
Если начальная разность фаз θ0 = π, то корни
> 1 > ym > y4, а во втором — y1 > yM > 1 > y4
уравнения W (y) = 0 по-прежнему располагаются в
(рис. 5а). В первом случае плотность поляритонов
порядке y1 > yM > ym > y4, а yM и ym по-прежнему
накачки первого импульса изменяется в пределах
играют роль максимальной и минимальной плотно-
ym ≤ y ≤ 1, тогда как во втором — в пределах
сти поляритонов накачки. Если в начальный момент
149
О. Ф. Васильева, А. П. Зинган, В. В. Васильев
ЖЭТФ, том 157, вып. 1, 2020
ческий режимы эволюции. Вырождение корней воз-
времени ns0 = ni0 и np10 = np20, то эволюция систе-
мы представляет собой периодическое превращение
никает в точке α = ns0. В случае, когда все четыре
пары поляритонов накачки в поляритоны сигналь-
корня различны и располагаются в порядке y1 >
ной и холостой мод. Качественное поведение корней
> y2 > y3 > y4 и 0 < α < ns0, эволюция системы
совпадает с представленным на рис. 2а. Периодиче-
также описывается формулой (13) и, следователь-
ская эволюция системы будет описываться форму-
но, плотность поляритонов накачки изменяется пе-
лой (9).
риодически в пределах от y3 до y2 (рис. 6a). Если
α > ns0, то y1 > y2 > y4 > y3 и эволюция системы
Однако при ns0 = ni0 и np10 = np20 с ростом па-
раметра α возникает пересечение двух наименьших
описывается соотношением (16), плотность поляри-
корней уравнения W (y) = 0 (рис. 2в). Вырождение
тонов накачки изменяется периодически в пределах
этих корней приводит к возникновению апериоди-
от y4 до y2. Корни уравнения W(y) = 0 в этом слу-
ческой эволюции системы. Следовательно, при θ0 =
чае будут определяться выражениями
= π возможны как периодический, так и апериоди-
√
√(√
)2
√
2 (1 + ns0) + α +
2 (1 + ns0) + α
+4
2 (ns0 - α)
y1 =
√
,
2
2
√
√(√
)2
√
2 (1 + ns0) - α +
2 (1 + ns0) - α
+4
2 (α - ns0)
y2 =
√
,
2
2
(22)
√
√(√
)2
√
2 (1 + ns0) - α -
2 (1 + ns0) - α
+4
2 (α - ns0)
y3 =
√
,
2
2
√
√(√
)2
√
2 (1 + ns0) + α -
2 (1 + ns0) + α
+4
2 (ns0 - α)
y4 =
√
2
2
При совпадении двух наименьших корней решение уравнения (7) имеет вид
y2 - y3
y=y3 +
(
√
).
(23)
y1 - y2
√
(y2 - 1)(y1 - y3)
1+
sh2
(y3 - y2)(y1 - y3) τ ± arsh
y1 - y3
(1 - y3)(y1 - y2)
Из рис. 6а видно, что с ростом α периодический
фаз θ0 и выясним возможность фазового управле-
режим эволюции переходит в апериодический, за-
ния процессом без изменения начальных плотностей
тем снова в периодический.
поляритонов. Корни уравнения W (y) = 0 и в этом
Что касается амплитуды A и периода T коле-
случае расположим в порядке их убывания y1 >
баний плотности поляритонов накачки, то из
> yM > ym > y4. Они существенно зависят от па-
рис. 6б,в видно, что с ростом параметра α амплиту-
раметров np20, ns0, ni0, α, θ0. В общем случае, при
да колебаний сначала растет, достигая своего мак-
произвольных np20, ns0, ni0, α, θ0 решение уравне-
симального значения, а затем монотонно убывает,
ния (7) выражается по-прежнему формулой (9), а
тогда как период колебаний сначала также растет с
амплитуда и период колебаний — формулами (11).
ростом α, затем расходится при значении α, при ко-
тором оба наименьших корня, y4 и y3, оказываются
Рассмотрим случай ns0 = ni0 и np10 = np20. На
одинаковыми, а затем монотонно убывает.
рис. 8 показана временная эволюция плотности по-
ляритонов накачки в зависимости от начальной раз-
ности фаз θ0 для трех значений параметра α. Видно,
2.4. Эволюция при произвольном значении
что существуют как периодические, так и апериоди-
начальной разности фаз θ0
ческие режимы эволюции системы экситон-поляри-
тонов в микрорезонаторе. При α = 0.1 имеют место
Таким образом, видно, что в случаях θ0 = 0, π/2,
два пересечения двух наименьших корней (рис. 7а),
π динамика системы различна. Поэтому ниже рас-
в соответствии с чем возникают два перехода от пе-
смотрим случай произвольной начальной разности
риодического режима к апериодическому при раз-
150
ЖЭТФ, том 157, вып. 1, 2020
Нелинейная динамика параметрических осцилляций. ..
yi
yi
yi
а
б
в
0
1
2
0
1
2
0
1
2
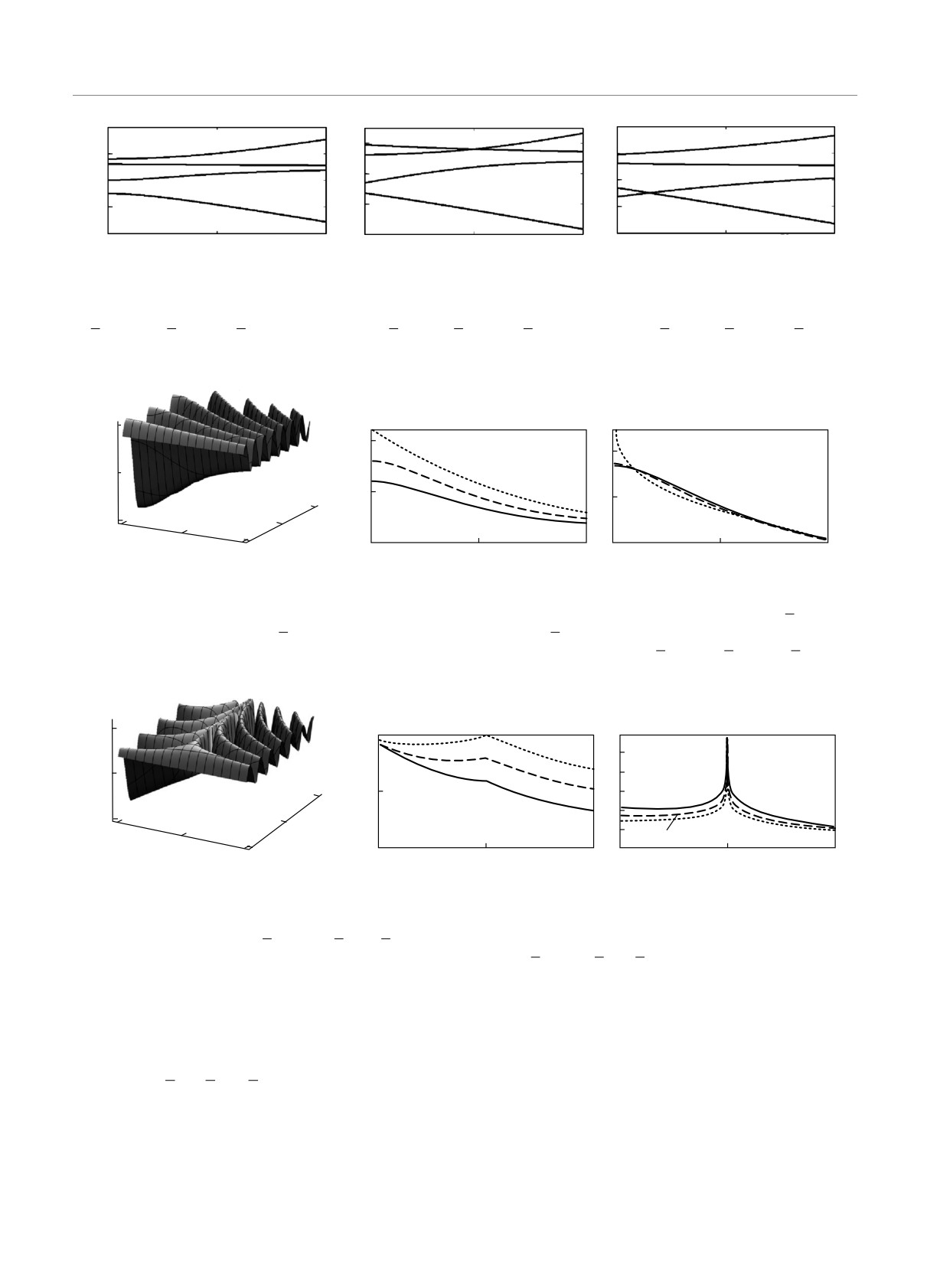
Рис. 2. Зависимости корней уравнения W (y) = 0 от нормированной расстройки резонанса α при фиксированных на-
чальных плотностях поляритонов накачки второго импульса и поляритонов холостой моды и начальной разности фаз:
а) np20 = 0.5, ns0 = 0.3, ni0 = 0.1, θ0 = π/2; б) np20 = 1, ns0 = 0.3, ni0 = 0.3, θ0 = 0; в) np20 = 1, ns0 = 0.3, ni0 = 0.3,
θ0 = π
y
1.1
A
T
1.0
б
6
в
3
2
0.8
2
1
0.5
3
1
4
а
15
0.5
0
1
2
0
2
0
1
2
0
1
2
Рис. 3. а) Временная эволюция плотности поляритонов накачки первого импульса y в зависимости от нормированной
расстройки резонанса α при фиксированных начальных плотностях поляритонов накачки второго импульса np20 = 0.5,
поляритонов сигнальной моды ns0 = 0.3 и поляритонов холостой моды ni0 = 0.1 и θ0 = π/2. Амплитуда (б) и период
колебаний (в) плотности поляритонов накачки первого импульса в зависимости от α при ns0 = 0.3, ni0 = 0.1, np20 = 0.5
(1), 0.7 (2), 1 (3)
y
A
1.4
T
1.0
10
в
3
0.7
8
0.5
6
15
2
1
4
а
1
б
3
0
2
2
0
2
0
1
2
0
1
2
Рис. 4. а) Временная эволюция плотности поляритонов накачки первого импульса y в зависимости от нормированной
расстройки резонанса при фиксированных начальных плотностях поляритонов накачки второго импульса, поляритонов
сигнальной и холостой мод np20 = 1, ns0 = ni0 = 0.3 и θ0 = 0. Амплитуда (б) и период колебаний (в) плотности
поляритонов накачки первого импульса в зависимости от α при np20 = 1, ns0 = ni0 = 0.3 (1), 0.5 (2), 0.7 (3)
личных θ0 (рис. 9б). При α = 1 существует только
(рис. 7в). На рис. 9 представлены зависимости ам-
один такой переход при θ0 = 0 (рис. 7б). При фик-
плитуды A и периода T колебаний плотности поля-
сированных np20, ni0 и ns0 дальнейшее увеличение
ритонов накачки от начальной разности фаз θ0 для
параметра α не приводит к возникновению апери-
ряда значений параметра α. Видно, что обе функ-
одических режимов, так как отсутствуют пересече-
ции изменяются в широких интервалах, причем эти
ния двух наименьших корней уравнения W (y) = 0
изменения могут быть и немонотонными.
151
О. Ф. Васильева, А. П. Зинган, В. В. Васильев
ЖЭТФ, том 157, вып. 1, 2020
y
yi
A
1.2
а
б
0.4
2
в
1
2
1
0.2
3
0
15
10
0
0.5
1.0
0.8
5
0
0
0.5
1.0
ns0
0.5
0
1.0
ns0
ns0
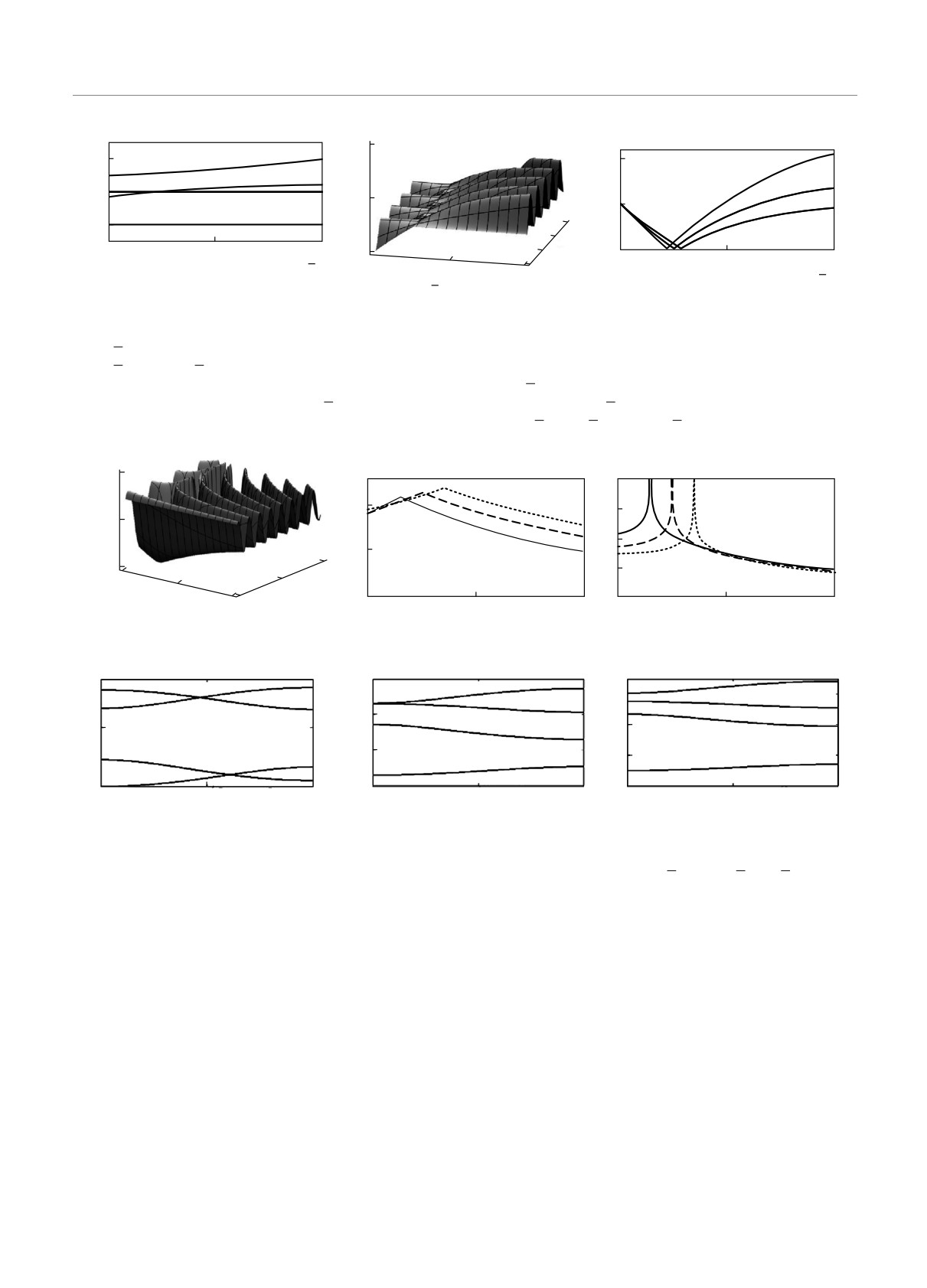
Рис. 5. а) Зависимости корней уравнения W (y) = 0 от нормированной начальной плотности поляритонов сигнальной
моды ns0 при фиксированных начальных плотностях поляритонов накачки второго импульса и поляритонов холостой
моды np20 = 0.2, ni0 = 0.5 и θ0 = 0. б) Временная эволюция плотности поляритонов накачки первого импульса y в
зависимости от начальной плотности поляритонов сигнальной моды ns0 при фиксированных начальных плотностях по-
ляритонов накачки второго импульса np20 = 0.2 и поляритонов холостой моды ni0 = 0.5. в) Амплитуда A колебаний
плотности поляритонов накачки первого импульса y в зависимости от ns0 при np20 = 0.2 и ni0 = 0.7 (1), 0.5 (2), 0.4 (3)
y
а
T
1.4
A
8
1.0
в
3
6
0.7
1
2
2
4
3
0.5
1
0
2
15
б
0
1
0
2
0
1
2
0
1
2
Рис. 6. То же, что и на рис. 4, но для θ0 = π
yi
yi
yi
а
в
б
0
/2
0
/2
0
/2
0
0
0
Рис. 7. Зависимости корней уравнения W (y) = 0 от начальной разности фаз θ0 при фиксированных начальных плот-
ностях поляритонов накачки второго импульса, поляритонов сигнальной и холостой мод np20 = 1, ns0 = ni0 = 0.3 и
различных значениях нормированной расстройки резонанса α: 0.1 (а), 1 (б), 1.5 (в)
3. ЗАКЛЮЧЕНИЕ
ритонов холостой моды. Периоды и амплитуды ко-
лебаний плотностей поляритонов существенно зави-
сят от начальных плотностей поляритонов накачки,
Таким образом, при накачке нижней поляритон-
сигнальной и холостой мод, начальной разности фаз
ной ветви в двух близких точках закона дисперсии
и расстройки резонанса. Существенная зависимость
возможен периодический и апериодический процес-
периода и амплитуды колебаний поляритонов от на-
сы превращения пары поляритонов накачки в по-
чальной разности фаз свидетельствует о возможнос-
ляритоны сигнальной и холостой мод, а также по-
ти фазового управления динамикой системы.
кой системы. Режим покоя будет наблюдаться толь-
ко в условиях точного резонанса при θ0 = 0, когда
Необходимо отметить, что при накачке поляри-
одна из начальных плотностей поляритонов накач-
тонной ветви в одной точке закона дисперсии в нере-
ки меньше либо равна начальной плотности поля-
зонансном случае при начальной разности фаз рав-
152
ЖЭТФ, том 157, вып. 1, 2020
Нелинейная динамика параметрических осцилляций. ..
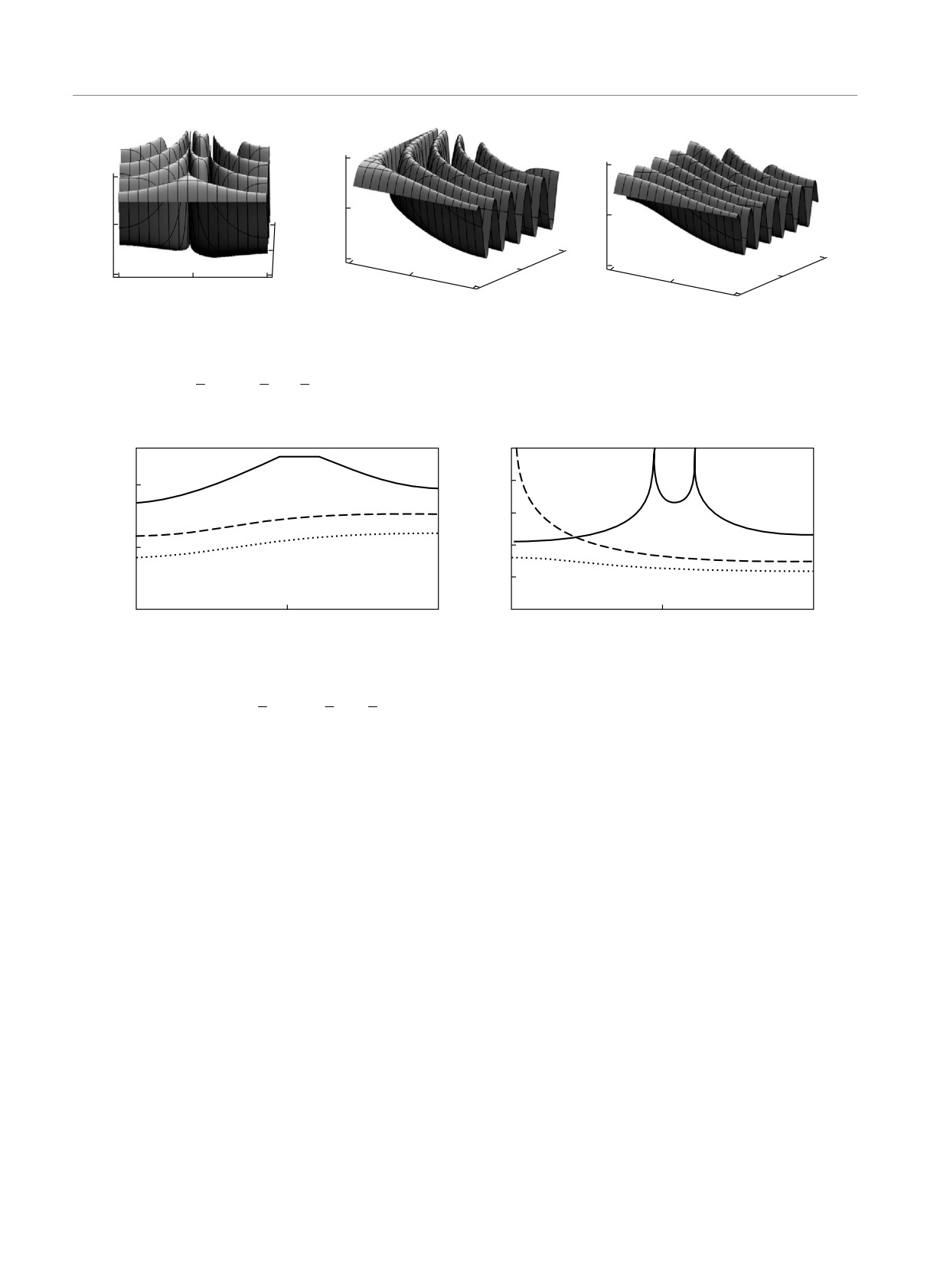
y
y
y
1.4
1.4
1.4
0.7
0.7
0.7
15
б
0
15
в
а
0
15
0
0
0
0
0
/2
/2
0
/2
0
0
0
0
Рис. 8. Временная эволюция плотности поляритонов накачки первого импульса y в зависимости от начальной разности
фаз θ0 при фиксированных начальных плотностях поляритонов накачки второго импульса, поляритонов сигнальной и
холостой мод np20 = 1, ns0 = ni0 = 0.3 и нормированной расстройке резонанса α, равной 0.1 (а), 1 (б), 1.5 (в)
A
Т
10
а
б
1
8
1.0
2
6
1
3
0.5
4
2
2
3
0
/2
0
/2
0
0
Рис. 9. Амплитуда (а) и период колебаний (б) плотности поляритонов накачки первого импульса в зависимости от на-
чальной разности фаз θ0 при фиксированных начальных плотностях поляритонов накачки второго импульса, поляритонов
сигнальной и холостой мод np20 = 1, ns0 = ni0 = 0.3 и нормированной расстройке резонанса α, равной 0.1 (1), 1 (2),
1.5 (3)
ной θ0 = 0 также наблюдался периодический режим
2. H. Deng, H. Haug, and Y. Yamamoto, Rev. Mod.
эволюции превращения пары поляритонов накачки
Phys. 82, 1489 (2010).
в поляритоны сигнальной и холостой мод, а также
3. A. Kavokin, Appl. Phys. A 89, 241 (2007).
покой системы при отличных от нуля начальных па-
раметрах системы, чего не наблюдается при накачке
4. M. M. Glazov and K. V. Kavokin, Phys. Rev. B 73,
245317 (2006).
в двух близких по энергии точках закона дисперсии.
В условиях точного резонанса при θ0 = π/2 наблю-
5. I. A. Shelykh, R. Johne, D. D. Solnyshkov, A. V. Ka-
дался только апериодический режим эволюции пре-
vokin, N. A. Gippius, and G. Malpuech, Phys. Rev.
вращения пары поляритонов накачки в поляритоны
B 76, 155308 (2007).
сигнальной и холостой мод [39-41]. Таким образом,
6. D. M. Whittaker, Phys. Rev. B 63, 193305 (2001).
введение двух независимых накачек приводит к уве-
личению степеней свободы системы. Возникают но-
7. C. Ciuti, P. Schwendimann, B. Deveaud, and
вые бифуркационные переходы от периодического
A. Quattropani, Phys. Rev. B 62, R 4825 (2000).
режима эволюции к апериодическому.
8. P. G. Savvidis, J. J. Baumberg, R. M. Stevenson,
M. S. Skolnick, D. M. Whittaker, and J. S. Roberts,
ЛИТЕРАТУРА
Phys. Rev. Lett. 84, 1547 (2000).
1. A. V. Kavokin and G. Malpuech, Thin Films and
9. J. J. Baumberg, P. G. Savvidis, R. M. Stevenson,
Nanostructures. Cavity Polaritons, ed. by V. M. Ag-
A. I. Tartakovskii, M. S. Skolniсk, D. M. Whittaker,
ranovich and D. Taylor, Amsterdam (2003).
and J. S. Roberts, Phys. Rev. B 62, R 16247 (2000).
153
О. Ф. Васильева, А. П. Зинган, В. В. Васильев
ЖЭТФ, том 157, вып. 1, 2020
10.
C. Ciuti, Phys. Rev. B 69, 245304 (2004).
27.
A. I. Tartakovskii, D. N. Krizhanovskii, D. A. Kurysh,
V. D. Kulakovskii, M. S. Skolnick, and J. S. Roberts,
11.
P. Schwendimann, C. Ciuti, and A. Quattropani,
Phys. Rev. B 65, 081308 (R) (2002).
Phys. Rev. B 68, 165324 (2003).
28.
L. Dominici, M. Petrov, M. Matuszewski, D. Bal-
12.
P. G. Savvidis, J. J. Baumberg, D. Porras,
larini, M. De Giorgi, E. Colas, E. Cancellieri,
D. M. Whittaker, M. S. Skolnick, and J. S. Roberts,
B. S. Fernandez, A. Bramati, G. Gigli, A. Kavokin,
Phys. Rev. B 65, 073309 (2002).
F. Laussy, and D. Sanvitto, Nat. Commun. 6, 8993
(2015).
13.
I. A. Shelykh, A. V. Kavokin, and G. Malpuech, Phys.
Stat. Sol. B 242, 2271 (2005).
29.
P. Cristofolini, G. Christmann, S. I. Tsintzos,
G. Deligeorgis, G. Konstantinidis, Z. Hatzopoulos,
14.
R. M. Stevenson, V. N. Astratov, M. S. Skolnick,
P. G. Savvidis, and J. J. Baumberg, Science 336, 704
D. M. Whittaker, M. Emam-Ismail, A. I. Tarta-
(2012).
kovskii, P. G. Savvidis, J. J. Baumberg, and J. S. Ro-
berts, Phys. Rev. Lett. 85, 3680 (2000).
30.
П. И. Хаджи, О. Ф. Васильева, И. В. Белоусов,
ЖЭТФ 153, 179 (2018).
15.
A. I. Tartakovskii, D. N. Krizhanovskii, G. Malpuech,
M. Emam-Ismail, A. V. Chernenko, A. V. Kavokin,
31.
I. Rosenberg, Y. Mazuz-Harpaz, R. Rapaport,
V. D. Kulakovskii, M. S. Skolnick, and J. S. Roberts,
K. West, and L. Pfeiffer, Phys. Rev. B 93, 195151
Phys. Rev. B 67, 165302 (2003).
(2016).
16.
A. I. Tartakovskii, D. N. Krizhanovskii, and
32.
S. I. Tsintzos, A. Tzimis, G. Stavrinidis, A. Trifonov,
V. D. Kulakovskii, Phys. Rev. B 62, R 13298 (2000).
Z. Hatzopoulos, J. J. Baumberg, H. Ohadi, and
P. G. Savvidis, Phys. Rev. Lett. 121, 037401 (2018).
17.
C. Ciuti, P. Schwendimann, B. Deveaud, and
A. Quattropani, Phys. Rev. B 63, 041303 (R) (2001);
33.
N. A. Gippius, I. A. Shelykh, D. D. Solnyshkov,
Semicond. Sci. Technol. 18, S 279 (2003).
S. S. Gavrilov, Y. G. Rubo, A. V. Kavokin, S. G. Ti-
khodeev, and G. Malpuech, Phys. Rev. Lett. 98,
18.
P. G. Savvidis, C. Ciuti, J. J. Baumberg, D. M. Whit-
236401 (2007).
taker, M. S. Skolnik, and J. S. Roberts, Phys. Rev.
B 64, 075311 (2001).
34.
T. K. Paraiso, M. Wouters, Y. Leger, F. Morier-Ge-
noud, and B. Deveaud-Plédran, Nat. Mater. 9, 655
19.
V. Savona, P. Schwendimann, and A. Quattropani,
(2010).
Phys. Rev. B 71, 125315 (2005).
35.
R. Cerna, Y. Leger, T. K. Paraiso, M. Wouters,
20.
A. Kavokin, P. G. Lagoudakis, G. Malpuech, and
F. Morier-Genoud, M. T. Portalla-Oberli, and B. De-
J. J. Baumberg, Phys. Rev. B 67, 195321 (2003).
veaud, Nat. Commun. 4, 2008 (2013).
21.
M. Saba, C. Ciuti, J. Bloch, V. Tierry-Mieg, R. Adre,
36.
T. C. H. Liew, A. V. Kavokin, and I. A. Shelykh,
L. S. Dang, S. Kundermann, A. Mura, C. Bongio-
Phys. Rev. Lett. 101, 016402 (2008).
vanni, J. E. Staehli, and B. Deveaud, Nature 414,
731 (2001).
37.
T. Espinosa-Ortega and T. C. H. Liew, Phys. Rev.
B 87, 195305 (2013).
22.
R. Huang, F. Tassone, and Y. Yamamoto, Phys. Rev.
B 61, R 7854 (2000).
38.
A. Amo, T. C. H. Liew, C. Adrados, R. Houdre,
E. Giacobino, A. V. Kavokin, and A. Bramati, Nat.
23.
A. Baas, J.-Ph. Karr, M. Romanelli, A. Bramati, and
Photon. 4, 361 (2010).
E. Giacobino, Phys. Rev. B 70, 161307 (R) (2004).
39.
О. Ф. Васильева, П. И. Хаджи, Опт. и спектр. 115,
24.
A. Baas, J.-Ph. Karr, H. Eleuch, and E. Giacobino,
922 (2013).
Phys. Rev. A 69, 023819 (2004).
40.
П. И. Хаджи, О. Ф. Васильева, Опт. и спектр. 111,
25.
D. N. Krizhanovski, S. S. Gavrilov, A. P. D. Love,
831 (2011); ФТТ 53, 1216 (2011).
D. Sanvitto, N. A. Gippius, S. G. Tikhodeev,
V. D. Kulakovskii, D. M. Whittaker, M. S. Skolnick,
41.
P. I. Khadzhi and O. F. Vasilieva, J. Nanophot.
and J. S. Roberts, Phys. Rev. B 77, 115336 (2008).
6, 061805 (2012); J. Nanoelectr. Optoelectr. 9, 295
(2014).
26.
P. G. Lagoudakis, P. G. Savvidis, J. J. Baumberg,
D. M. Whittaker, P. R. Eastham, M. S. Skolnick, and
42.
C. J. Mc Konstrie, S. Radic, and M. G. Raymer, Opt.
J. S. Roberts, Phys. Rev. B 65, 161310 (R) (2002).
Express 12, 5037 (2004).
154
ЖЭТФ, том 157, вып. 1, 2020
Нелинейная динамика параметрических осцилляций. ..
43. Y. Okawachi, M. Yu. K. Luke, D. O. Carvalho, S. Ra-
47. И. С. Градштейн, И. М. Рыжик, Таблицы интег-
melow, A. Farsi, M. Lipson, and A. L. Gaeta, Opt.
ралов, сумм, рядов и произведений, Физматлит,
Lett. 40, 5267 (2015).
Москва (1963).
44. А. И. Бурштейн, А. Ю. Пусеп, ЖЭТФ 69, 1927
(1975).
48. Г. Корн, Т. Корн, Справочник по математике для
научных работников и инженеров, Наука, Москва
45. П. И. Хаджи, Нелинейные оптические процессы в
(1971).
системе экситонов и биэкситонов в полупровод-
никах, Штиинца, Кишинев (1985).
49. О. Ф. Васильева, А. П. Зинган, П. И. Хаджи, Опт.
46. Л. П. Питаевский, УФН 168, 641 (1998).
и спектр. 125, 425 (2018).
155