ЖЭТФ, 2020, том 157, вып. 1, стр. 174-179

ПЕРЕРАСПРЕДЕЛЕНИЕ СТОХАСТИЧЕСКОЙ ЭНЕРГИИ ДЛЯ

АНСАМБЛЯ ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНОМ ПОЛЕ

О. С. Ваулина^*

Объединенный институт высоких температур Российской академии наук

125412, Москва, Россия

Московский физико-технический институт

141700, Долгопрудный, Московская обл., Россия

Поступила в редакцию 13 июня 2019 г.,

после переработки 10 июля 2019 г.

Принята к публикации 12 июля 2019 г.

Представлены результаты численного и аналитического исследований влияния постоянного магнитного

поля на перераспределение стохастической энергии для ансамбля заряженных частиц в электростатичес-

кой ловушке. Моделирование выполнялось для кластерных систем частиц с кулоновским взаимодействи-

ем в широком диапазоне их параметров. Предложены условия энергетического баланса для заряженных

частиц в системах с пространственно-неоднородными тепловыми источниками.

DOI: 10.31857/S0044451020010204

ку в постоянных электрических и магнитных полях

недавно исследовалось численно [11, 12].

1. ВВЕДЕНИЕ

Отдельный круг задач связан с условиями энер-

гетического баланса в системах частиц с прост-

Исследования физических свойств и процессов

ранственно-неоднородными тепловыми источника-

энергетического обмена в неоднородных системах

ми, которые обычно приводят к неравномерному

взаимодействующих частиц вызывает значитель-

распределению стохастической кинетической энер-

ный интерес в различных областях науки и техни-

гии в системе частиц. Основной источник неравно-

ки (физике плазмы, биологии, физике полимеров и

мерного распределения стохастической кинетичес-

т. д.) [1-7]. Особый интерес вызывает влияние внеш-

кой энергии для ионов/электронов плазмы связан с

них электрических и магнитных полей на стохасти-

ее неоднородными параметрами во внешних элект-

ческое (тепловое) движение ансамбля заряженных

рических полях [24, 25]. Что касается пылевых час-

частиц [8-12]. Данное обстоятельство отчасти свя-

тиц в комплексной плазме, то помимо неоднород-

зано с проблемами эффективности энергетических

ных условий на распределение их температур значи-

установок для управляемого термоядерного синте-

тельное влияние оказывают изменения их зарядов,

за, а также с развитием плазменных методов пере-

вызванные случайной природой ионных и электрон-

работки отработанного ядерного топлива (ОЯТ) и

ных токов, заряжающих пылевые частицы [26-31].

радиоактивных отходов [5-7].

Источниками неравномерного нагрева системы пы-

Исследования теплового движения взаимодей-

левых частиц также могут являться неоднородное

ствующих пылевых частиц в протяженных и огра-

распределение температуры окружающего газа, ла-

ниченных ансамблях, формирующихся в газораз-

зерное излучение, используемое для диагностики,

рядной плазме без магнитного поля, представлены в

протекание химических реакций и т. д. Перераспре-

различных теоретических и экспериментальных ра-

деление стохастической энергии в системах с таки-

ботах [13-19]. Эксперименты по изучению динамики

ми тепловыми источниками в отсутствие магнитно-

пылевых частиц в магнитном поле описаны в ра-

го поля исследовалось теоретически для кластеров

ботах [20-23]. Влияние теплового движения ограни-

заряженных частиц [26,27], а также численно и экс-

ченного облака заряженных частиц на их динами-

периментально для протяженных квазидвумерных

^* E-mail: olga.vaulina@bk.ru

слоев пылевых частиц в плазме [31, 32].

174

ЖЭТФ, том 157, вып. 1, 2020

Перераспределение стохастической энергии...

В перечисленных выше работах исследуемые ме-

В этом случае корреляторы смещений и скоро-

ханизмы перераспределения тепловой энергии в сис-

стей в рассматриваемой системе (2), (3) могут быть

темах базировались на передаче стохастических ко-

представлены в виде [26, 27] (см. Приложение)

лебаний отдельных частиц вблизи их равновесно-

δT_x + δT_z = 0,

(4)

го положения за счет межчастичного взаимодей-

ствия. В настоящей работе представлены результа-

- ν(δT_x - δT_z) + 2ω_B〈V_xV_z〉M = 0,

(5)

ты исследований влияния постоянного магнитного

− 2ν〈V_xV_z〉M - (ω2tx - ω2tz)〈xV_z〉M -

поля на перераспределение стохастической энергии

- ω_B(T_x - T_z) = 0,

(6)

по степеням свободы в ансамбле заряженных час-

ν〈xV_z 〉(ω2tx + ω2tz)M - (ω2tx - ω2tz)〈V_xV_z 〉M = 0,

(7)

тиц.

где T_x = M〈V2x〉, T_z = M〈V2z〉 — удвоенная кине-

тическая энергия стохастического движения частиц

2. ОСНОВНЫЕ СООТНОШЕНИЯ

по соответствующим степеням свободы в плоско-

сти, ортогональной направлению магнитного поля

Уравнения движения для одной частицы с мас-

B; δT_x = T0x - T_x, δT_z = T0z - T_z.

сой M и зарядом Q в постоянном электрическом по-

Решение системы уравнений (4)-(7) дает уравне-

ле ловушки E = [E_x, E_y, E_z] и в магнитном поле с

ние энергетического баланса в системе (2), (3), ко-

индукцией B = B_y (направленном по оси y) под воз-

торый возникает, когда T0x = T0z, и приводит к пере-

действием случайной силы F_b = [F_bx, F_by , F_bz ], кото-

распределению стохастической кинетической энер-

рая является источником стохастической (тепловой)

гии по степеням свободы:

энергии частиц, могут быть представлены в виде

dV_y

F_by

δT_x ≡ -δT_z = 0.5ω2B(T0x - T0z)×

= -νV_y - ω2tyy +

(1)

{

}-1

(ω2tx - ω2tz)

dV_x

F_bx

× ν² +ω2B +

(8)

= -νV_x - ω2txx + ω_BV_z +

(2)

ω2tx + ω²

dV_z

F_bz

Легко увидеть, что наибольшая интенсивность

= -νV_z - ω2tzz - ω_BV_x +

(3)

перераспределения энергии наблюдается при ω2tx -

- ω2tz = 0. Величина δT_x ≡ -δT_z = 0 в случае,

Здесь y, x, z — смещения частицы от ее равновесно-

когда ω_B = 0 (B = 0), а также δT_x ≡ -δT_z → 0

го положения, V_y = dy/dt, V_x = dx/dt, V_z = dz/dt,

для ν² ≫ ω2B. В противоположном случае, ν² ≪ ω2B,

ν — коэффициент трения заряженных частиц из-за

дополнительная стохастическая энергия будет рав-

их столкновений с нейтралами окружающего газа,

номерно перераспределяться по степеням свободы,

ω_ty(x, z) = (Qαy(x,z)/M)1/2 — характерная частота

T_x = T_z.

ловушки, ωB = QB/M — циклотронная частота,

Для случая α_y = α_x = α_z ≡ 0 уравнение (8) име-

αy(x,z) — величина градиента внешнего электриче-

ет вид

ского поля E по соответствующей степени свободы

(y, x, z).

T0x - T0z

δT_x ≡ -δT_z = 0.5ω²

(9)

Исследование корней характеристического урав-

^Bν² +ω²

нения для системы уравнений (1)-(3) показывает,

что данная система является устойчивой при всех

Отметим, что соотношение ω_B/ν

> 1, или

ν > 0 и ωty(x,z) > 0 [12].

ω_B/ν ≫ 1, легко реализуется в установках по раз-

Рассмотрим условия энергетического баланса в

делению компонентов ОЯТ для ионов отработан-

системе, описанной уравнениями (2), (3). Примем

ного ядерного топлива [12]. Что касается пыле-

во внимание, что в случае стохастического (тепло-

вой плазмы, то в большинстве существующих экс-

вого) движения частиц в ловушке 〈F_bx〉 = 〈F_bz〉 ≡ 0,

периментов по изучению динамики пылевых час-

〈xF_bx〉 = 〈zF_bz 〉 ≡ 0, 〈xV_x〉 = 0.5dx²/dt ≡ 0, 〈zV_z〉 =

тиц в магнитном поле B выполняется соотноше-

= 0.5dz²/dt ≡ 0, d〈xz〉/dt = 〈xVz 〉 + 〈zVy〉 ≡ 0,

ние ω_B/ν ≪ 1, поскольку используются достаточно

〈V_xF_bx〉 = νT0x и 〈V_z F_bz 〉 = νT0z, где T0x, T0z — темпе-

крупные (тяжелые) частицы при небольшом значе-

ратура тепловых источников для соответствующих

нии приложенного поля, B ≤ 2500 Гс [20-22]. Ис-

степеней свободы (x, z) [26,27]. Здесь и ниже угло-

ключение составляют эксперименты, описанные в

вые скобки обозначают усреднение по времени при

работе [23], где исследовалось влияние магнитных

t → ∞.

полей 4000-40000 Гс на плазменно-пылевые облака

175

О. С. Ваулина

ЖЭТФ, том 157, вып. 1, 2020

в радиочастотном разряде для частиц диаметром от

подробно описана в работе [4]. Влияние магнитного

0.1 мкм до 10 мкм; в качестве буферного газа ис-

поля на динамику движения частиц исследовалось

пользовался аргон с давлением P ∼ 0.01 Торр. В

численно в работах [11,12]. Отметим, что при нали-

рассматриваемых экспериментах при B = 40000 Гс

чии магнитного поля имеет место дополнительное

значение ω_B будет сравнимо с величиной ν (ω_B ∼ ν)

условие для шага интегрирования, связанное с на-

для частиц диаметром d < 0.4 мкм. А в предполо-

личием циклотронной частоты ω_B, см. ниже.

жении водорода H₂ в качестве буферного газа, со-

Шаг

интегрирования

составлял

от

отношение ω_B ∼ ν будет наблюдаться для частиц

Δt

(40 max[ω_t; ω_B; ν])-1 до Δt

диаметром d < 2 мкм. Здесь для оценок отношения

(100 max[ω_t; ω_B; ν])-1 в зависимости от на-

ω_B/ν использовались соотношения для зарядового

чальных условий задачи. Время расчетов t_c после

числа пылевых частиц Z ≈ (1.1±0.25)T_e [эВ]d [мкм],

установления равновесия в моделируемых си-

где T_e — температура электронов, принятая равной

стемах варьировалось от ∼

10³/min[ω_t; ω_B; ν] до

3 эВ [4], и для коэффициента трения частиц ν ≈

∼

10⁴/min[ω_t; ω_B; ν]. Температура тепловых ис-

≈ CP [Торр]/(ρ[г · см-3]d[мкм]), где ρ — плотность

точников (T0x, T0y, T0z) задавалась при помощи

материала частиц, C — коэффициент, зависящий от

случайной силы F_b = [F_bx, F_by, F_bz ] [4].

типа буферного газа (C ≈ 2000 для Ar и C ≈ 450

Расчеты проводились для систем частиц с куло-

для H₂) [33].

новским взаимодействием в широком диапазоне их

Отметим также, что для анализа физических

параметров неидеальности: от Γ ∼ 0.1 до Γ ∼ 100.

свойств однородных структур заряженных частиц

Значение параметра ξ = ω_t/ν варьировалось при-

(α_y = α_x = α_z ≡ α), которые можно характеризо-

мерно от 1 до 70, отношение ω_B/ν — примерно от

вать постоянной концентрацией n, обычно использу-

0.25 до 25. Во всех рассмотренных случаях моде-

ется параметр неидеальности Γ = Q²n1/3/T, отра-

лируемые системы являлись устойчивыми. Функции

жающий отношение энергии взаимодействия меж-

распределения частиц по скоростям соответствова-

ду частицами системы к их температуре. При этом

ли распределению Максвелла. При t → ∞ значения

в линейном электрическом поле концентрация час-

среднеквадратичного смещения центра масс систе-

тиц n может быть получена из уравнения Пуассо-

мы от его начального положения составляли

на: n

= 3α/(4πQ), и соответственно для среднего

2T_x

2T_y

2T_z

межчастичного расстояния имеет место соотноше-

〈x²〉⁼

〈y²〉⁼

〈z²〉⁼

NMω2t

NMω²

ние l_p = (4πQ/3α)1/3 [34]. Для оценки радиуса огра-

ниченной структуры в первом приближении мож-

где T_x = M〈V2x〉, T_y = M〈V2z〉, T_z = M〈V2z〉. Пар-

но использовать соотношение R= (3N/4πn)1/3, где

ные корреляционные функции g(l) для ансамблей из

N — число частиц.

N = 500 частиц с различными параметрами Γ для

В заключение раздела подчеркнем, что уравне-

случая T_x = T_y = T_z показаны на рис. 1. В качест-

ния типа (1)-(3) могут использоваться для анализа

ве нормировки величины g(l), представленной на

движения центра масс любого ограниченного ансам-

этом рисунке, использовалось предположение одно-

бля частиц с попарным взаимодействием, а также

родной концентрации частиц, равной n= 3α/(4πQ).

для отдельной частицы в системе, состоящей из N

Численные исследования показали, что вне зави-

частиц, когда влиянием межчастичного взаимодей-

симости от параметра неидеальности Γ и числа час-

ствия можно пренебречь (Γ ≪ 1) [34].

тиц N в моделируемых ансамблях результаты пе-

рераспределения энергии частиц по степеням сво-

боды в плоскости, ортогональной магнитному полю

3. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО

МОДЕЛИРОВАНИЯ

(B), хорошо соответствуют предлагаемому аналити-

ческому соотношению (9). Вдоль магнитного поля (в

Численное исследование энергетического балан-

направлении y) стохастическая кинетическая энер-

са в системах заряженных частиц с неоднородными

гия частиц не менялась и соответствовала темпера-

тепловыми источниками выполнялось методом мо-

туре заданных тепловых источников, T0y.

лекулярной динамики Ланжевена. Моделирование

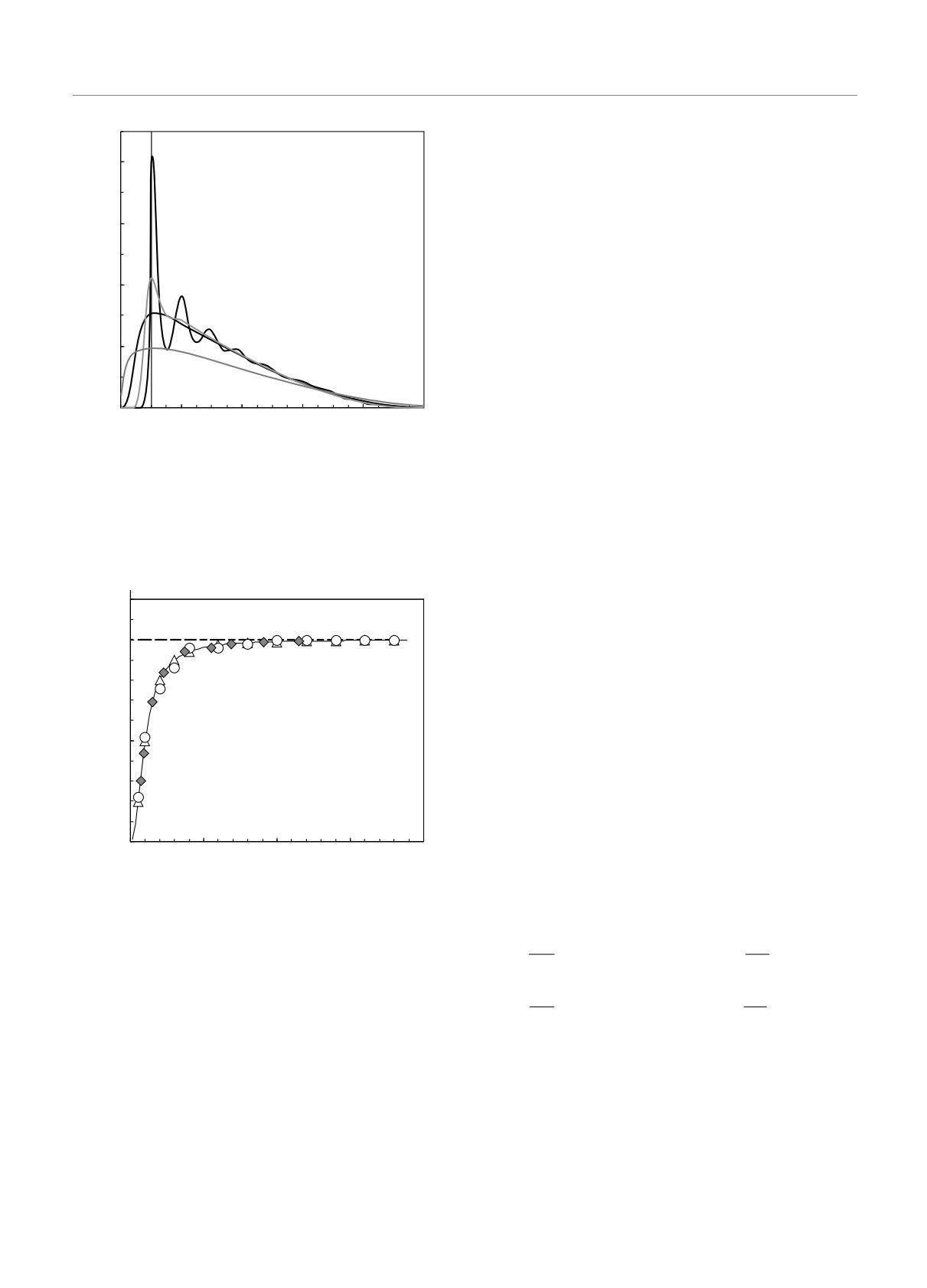
Отношение δT/ΔT (где δT = |δT_x| ≡ |δT_z|, ΔT =

выполнялось для ансамблей, состоящих из N = 50,

= |T0x - T0z|), полученное путем численного модели-

500, 1000 частиц, находящихся в электростатической

рования для различных значений ω_B/ν для одной

ловушке с параметрами α_y = α_x = α_z ≡ α. Техника

частицы (N = 1) и для центра масс ансамблей, со-

интегрирования уравнений движения для взаимо-

стоящих из N = 500 и N = 1000 частиц, представле-

действующих частиц в отсутствие магнитного поля

но на рис. 2 для различных значений Γ. Таким об-

176

ЖЭТФ, том 157, вып. 1, 2020

Перераспределение стохастической энергии...

4. ЗАКЛЮЧЕНИЕ

2.0

Выполнено аналитическое и численное исследо-

вание влияния постоянного магнитного поля на пе-

рераспределение стохастической энергии для ансам-

1.5

бля заряженных частиц в электростатической ло-

вушке. Моделирование выполнялось для кластер-

ных систем частиц с кулоновским взаимодействи-

1.0

ем в широком диапазоне их параметров. Предло-

жены соотношения для условий энергетического ба-

ланса для заряженных частиц в системах с прост-

0.5

ранственно-неоднородными тепловыми источника-

ми. Данные соотношения проверены путем числен-

ного моделирования для кластеров с различным ко-

личеством частиц в широком диапазоне параметров

анализируемых систем.

l/l_p

Численные исследования показали, что вне за-

висимости от параметра неидеальности Γ и числа

Рис. 1. Парная корреляционная функция g(l/lp) для ан-

частиц N в моделируемых системах перераспреде-

самблей из N = 500 частиц с различными параметрами

ление энергии по степеням свободы для центра масс

Γ = 90 (1), 9 (2), 0.9 (3), 0.09 (4). Здесь lp = (4πQ/3α)1/3

ансамблей хорошо соответствует предлагаемым ана-

литическим соотношениям и зависит только от от-

носительных значений параметров: ω_tx/ν, ω_tz/ν и

T/ T

ω_B/ν.

Таким образом, полученные результаты спра-

ведливы для частиц любой массы и зарядов,

0.5

например, для случая пылевой плазмы, для ионов

сепарируемого вещества ОЯТ и т. д., а также для

ограниченных систем при любом типе попарных

взаимодействий между заряженными частицами.

0.3

Финансирование. Работа частично поддержа-

на Российским фондом фундаментальных исследо-

ваний (проект №18-38-20175), а также Программой

Президиума РАН.

ПРИЛОЖЕНИЕ

Найдем корреляторы смещений и скоростей час-

Рис. 2. Зависимости отношения δT /ΔT от ωB/ν, где δT =

тицы для системы уравнений движения (2), (3)

= |δTx| ≡ |δTz|, а ΔT = |Tx - Tz |. Сплошная линия —

уравнение (9); символы — результаты численного модели-

dV_x

F_bx

= -νV_x - ω2txx + ω_BV_z +

(A.1)

рования: ◦ — N = 1; Δ — N = 1000, Γ ≈ 10; ♦ — N = 500,

Γ ≈ 70

dV_z

F_bz

= -νV_z - ω2tzz - ω_BV_x +

(A.2)

принимая во внимание соотношения для коррелято-

разом, при определенных условиях (с ростом B до

ров случайной силы F_b: 〈F_bx〉 = 〈F_bz 〉 ≡ 0, 〈xF_bx〉 =

значений ω_B ≫ ν, см. разд. 2 и рис. 2) применение

= 〈zF_bz〉 ≡ 0, 〈V_xF_bx〉 = νT0x и 〈V_z F_bz 〉 = νT0z , где T0x,

постоянного магнитного поля может быть исполь-

T0z — температуры тепловых источников для соот-

зовано в качестве метода выравнивания стохасти-

ветствующих степеней свободы (x, z) [26, 27]. Угло-

ческой кинетической энергии заряженных частиц в

вые скобки обозначают усреднение по времени при

плоскости, ортогональной вектору B.

t → ∞.

177

ЖЭТФ, вып. 1

О. С. Ваулина

ЖЭТФ, том 157, вып. 1, 2020

Учтем, что в состоянии равновесия все производ-

А. В. Тимофеев, Физика плазмы 33, 971 (2007).

ные корреляторов смещений и скоростей частицы

Н. А. Ворона, А. В. Гавриков, А. А. Самохин,

(при t → ∞) равны нулю, а также что при движе-

В. П. Смирнов, Ю. С. Хомяков, Ядерная физика

нии частицы в ловушке по замкнутым траекториям

и инжиниринг 5, 944 (2014).

dz²

J. I. Jiménez-Aquino, R. M. Velasco, and F. J. Uribe,

〈xV_x〉 = 0.5

≡ 0,

〈zV_z〉 = 0.5

≡ 0,

Phys. Rev. E 77, 051105 (2008).

d〈xz〉

L. J. Hou, Z. L. Mišković, A. Piel, and P. K. Shukla,

= 〈xV_z 〉 + 〈zV_y〉 ≡ 0.

Phys. Plasmas 16, 053705 (2009).

Далее, умножим уравнение (A.1) на V_x, а урав-

10.

B. Farokhi, M. Shahmansouri, and P. K. Shukla,

нение (A.2) на V_z , и усредним результат по времени.

Phys. Plasmas 16, 063703 (2009).

Тогда сумма полученных уравнений даст

11.

О. С. Ваулина, Е. А. Лисин, Э. А. Саметов, ЖЭТФ

δT_x + δT_z = 0,

(A.3)

152, 1144 (2017).

а их разность —

12.

E. A. Sametov, R. A. Timirkhanov, and О. S. Vauli-

na, Phys. Plasmas 24, 123504 (2017).

-ν(δT_x - δT_z) + 2ω_B〈V_xV_z〉M = 0.

(A.4)

13.

О. С. Ваулина, К. Г. Адамович, ЖЭТФ 133, 1091

Здесь δT_x = T0x - T_x, δT_z = T0z - T_z.

(2008).

Затем умножим уравнение (A.1) на V_z, а урав-

14.

О. С. Ваулина, К. Г. Адамович, О. Ф. Петров,

нение (A.2) на V_x, усредним по времени и получим

В. Е. Фортов, ЖЭТФ 134, 367 (2008).

сумму:

15.

О. С. Ваулина, Е. А. Лисин, А. В. Гавриков,

− 2ν〈V_xV_z〉M - (ω2tx - ω2tz)〈xV_z〉M -

О. Ф. Петров, В. Е. Фортов, ЖЭТФ 137, 751

(2010).

- ω_B(T_x - T_z) = 0, (A.5)

16.

O. S. Vaulina and E. A. Lisin, Phys. Plasmas 16,

где T_x = M〈V2x〉, T_z = M〈V2z〉 — удвоенная кине-

113702 (2009).

тическая энергия стохастического движения частиц

по соответствующим степеням свободы.

17.

В. Е. Фортов, О. Ф. Петров, О. С. Ваулина,

Далее, умножим уравнение (A.1) на z, а уравне-

К. Г. Косс, Письма в ЖЭТФ 97, 366 (2013).

ние (A.2) на x, усредним по времени и найдем сумму:

18.

G. A. Hebner, M. E. Riley, and K. E. Greenberg,

Phys. Rev. E 66, 046407 (2002).

ν〈xV_z 〉(ω2tx + ω2tz)M - (ω2tx - ω2tz) ×

19.

O. S. Vaulina and I. E. Drangevski, Phys. Scripta 73,

× 〈V_xV_z〉M = 0. (A.6)

577 (2006).

20.

M. М. Васильев, Л. Г. Дьячков, С. Н. Антипов,

ЛИТЕРАТУРА

О. Ф. Петров, В. Е. Фортов, Письма в ЖЭТФ 86,

414 (2007).

1. Photon Correlation and Light Beating Spectroscopy,

ed. by H. Z. Cummins and E. R. Pike, Plenum, New

21.

L. G. D’yachkov, O. F. Petrov, and V. E. For-

York (1974).

tov, Contrib. Plasma Phys. 49, 134 (2009).

2. R. Balescu, Equilibrium and Nonequilibrium Statis-

22.

V. Yu. Karasev, E. S. Dzlieva, A. Yu. Ivanov, and

tical Mechanics, Wiley Intersci., Chichester (1975).

A. I. Eikhval’d, Phys. Rev. E 74, 066403 (2006).

3. А. А. Овчинников, С. Ф. Тимашев, А. А. Белый,

23.

N. Sato, G. Uchida, and T. Kaneko, Phys. Plasmas

Кинетика диффузионно-контролируемых хими-

8, 1786 (2001).

ческих процессов, Химия, Москва (1986).

24.

А. В. Тимофеев, Б. Н. Швилкин, УФН 118, 273

4. О. С. Ваулина, О. Ф. Петров, В. Е. Фортов,

(1976) [A. V. Timofeev and B. N. Shvilkin, Sov. Phys.

А. Г. Храпак, С. А. Храпак, Пылевая плазма (экс-

Usp. 19, 149 (1976)].

перимент и теория), Физматлит, Москва (2009).

25.

Yu. P. Raizer, M. N. Shneider, and N. A. Yatsenko,

5. R. Aymar, P. Barabaschi, and Y. Shimomura, Plasma

Radio-Frequency Capacitive Discharges, CRC Press

Phys. Control. Fusion 44, 519 (2002).

(1995).

178