ЖЭТФ, 2020, том 157, вып. 2, стр. 295-307

САМОСОГЛАСОВАННЫЙ УЧЕТ ФЛУКТУАЦИЙ

В СИНГЛЕТНЫХ СВЕРХПРОВОДЯЩИХ ФАЗАХ

С s- И d-СИММЕТРИЕЙ

А. Г. Грошев^*, А. К. Аржников^**

Удмуртский федеральный исследовательский центр Уральского отделения Российской академии наук

426067, Ижевск, Россия

Поступила в редакцию 13 июля 2019 г.,

после переработки 19 июля 2019 г.

Принята к публикации 20 июля 2019 г.

Исследуется поведение термических флуктуаций сверхпроводящего параметра порядка с расширенной

s- и d_x2_-y2 -симметрией. Для этого в рамках теории функционального интегрирования разработан метод

самосогласованного учета флуктуаций параметра порядка и рассеяния носителей заряда на флуктуациях

связанных электронных пар. Исследование проводится на основе квазидвумерной однозонной модели с

притяжением между электронами, находящимися на соседних узлах. Получены функции распределения

вероятностей фазовых флуктуаций в зависимости от температуры, концентрации носителей заряда и

параметров модели. Показано, что в сверхпроводящей области фаза параметра порядка когерентна, а в

плотности состояний на уровне Ферми наблюдается провал. При приближении к некогерентной области

фазовой диаграммы провал в плотности состояний исчезает одновременно с потерей фазовой когерент-

ности. В то же время усредненная по флуктуациям амплитуда параметра порядка остается конечной

при любых температурах и концентрациях носителей заряда. Полученные результаты показывают, что

объяснение псевдощелевого состояния в рамках данного сценария невозможно.

DOI: 10.31857/S0044451020020091

ратуры T_c сверхпроводящего перехода [2]. Фазовая

когерентность возникает только в сверхпроводящей

области T < T_c. Во втором сценарии псевдощелевое

1. ВВЕДЕНИЕ

состояние определяется зарядовыми или спиновыми

флуктуациями (антиферромагнитными флуктуаци-

Несмотря на усилия, предпринятые как экспери-

ями или флуктуациями типа волн зарядовой плот-

ментаторами, так и теоретиками, природа высоко-

ности), которые по существу не связаны с явлением

температурной сверхпроводимости (ВТСП) до сих

сверхпроводимости [3].

пор остается до конца не выясненной. Возможно,

что ключом для понимания ее механизма является

Отметим, что рассматриваемые соединения

представляют собой сильно анизотропные системы

еще открытый вопрос о природе и свойствах псев-

дощелевого состояния, которое, как известно, отсут-

с эффективно пониженной (квазидвумерной) раз-

мерностью. Хорошо известно, что в таких системах

ствует в традиционных сверхпроводниках [1]. Реше-

ние этого вопроса остается одной из проблем при

возрастает роль флуктуаций параметра порядка

(ПП)

[4]. Учет этих флуктуаций существенно

описании ВТСП-соединений.

снижает температуру сверхпроводящего перехода

В настоящее время рассматриваются два основ-

и в некоторых случаях может приводить даже к

ных сценария при теоретическом объяснении псев-

изменению типа фазового перехода [5, 6]. Однако

дощелевого состояния в ВТСП-соединениях. В пер-

при рассмотрении флуктуаций сверхпроводящего

вом сценарии наблюдаемые псевдощелевые анома-

ПП Δ = |Δ| exp(iφ) обычно либо амплитудными,

лии возникают в результате образования некоге-

либо фазовыми флуктуациями пренебрегают (не

рентных связанных электронных пар выше темпе-

говоря уже о подходах, в которых эти флуктуа-

^* E-mail: groshev_- a.g@mail.ru

ции вообще не учитываются). В ряде случаев это

^** E-mail: arzhnikof@bk.ru

оказывается вполне приемлемым приближением.

295

А. Г. Грошев, А. К. Аржников

ЖЭТФ, том 157, вып. 2, 2020

Например, в работе [2] было показано, что вблизи

ем между электронами, находящимися на соседних

сверхпроводящего перехода амплитуда не имеет

узлах. Предполагается, что это притяжение не зави-

критического поведения и ее флуктуации не влияют

сит от температуры. Выбор такого взаимодействия

на фазовый переход. Тем не менее, в системах с

обусловлен следующими обстоятельствами. Во-пер-

пониженной размерностью при некоторых условиях

вых, принято считать, что основным механизмом

амплитудные флуктуации все же могут оказывать

спаривания электронов в ВТСП-соединениях яв-

существенное влияние на сверхпроводящие свойства

ляется спин-флуктуационный механизм

[12-15],

[6] и поэтому должны учитываться. Это обуслов-

который в простейшем приближении обеспечивает

лено тем, что наиболее вероятные амплитудные

эффективное притяжение между электронами,

и фазовые флуктуации оказываются эффективно

находящимися на соседних узлах. Во-вторых,

связанными. Такая взаимосвязь рассматривалась в

поскольку природа ВТСП до конца не ясна, пред-

работах [5,7] в рамках вариационного приближения.

полагается, что вклад в эффективное притяжение

Важным результатом исследований [5, 7] является

между электронами могут давать и другие механиз-

наличие двух областей псевдощелевого состояния

мы (например, поляронный). В-третьих, поскольку

выше температуры сверхпроводящего перехода с

характерные значения энергии взаимодействия,

частично коррелированной фазой, где основную

обеспечивающего эффективное притяжение между

роль играют фазовые флуктуации, и с полностью

электронами, много больше температуры перехода

разупорядоченной фазой, где основную роль иг-

в сверхпроводящее состояние (например, величина

рают амплитудные флуктуации. Используемые в

обменного взаимодействия в спиновых флуктуа-

этих работах приближения не лишены недостат-

циях, см. [12]), предполагается, что эффективное

ков. В частности, в этих работах не учитывалось

притяжение между электронами не меняется в

затухание одночастичных состояний, возникающее

рассматриваемой области температур. Наконец, по-

в результате учета рассеяния носителей заряда

скольку ВТСП являются слоистыми соединениями,

на флуктуациях связанных электронных пар.

рассматривается двумерный закон дисперсии с па-

Перенормировка спектра одночастичных состоя-

раметрами, соответствующими реальным системам

ний в результате такого рассеяния описывается

на основе купратов [16]. При этом не учитываются

собственно-энергетической частью одночастичной

флуктуации, разрушающие сверхпроводимость в

функции Грина, которая определяет спектральную

системах с размерностью D ≤ 2, обеспечивая тем

плотность, и ее самосогласованное вычисление

самым квазидвумерность рассматриваемой модели.

представляется необходимым при объяснении

Согласно теореме Мермина - Вагнера - Хоэнберга

псевдощелевого состояния. Одновременный учет

[17-19] в строго двумерной вырожденной системе

затухания одночастичных состояний и эффектив-

дальний порядок отсутствует при любой отличной

ной взаимосвязи между амплитудными и фазовыми

от нуля температуре и сверхпроводящие состояния

флуктуациями в рамках какого-либо самосогласо-

могут проявляться лишь в фазовых переходах

ванного подхода, по нашим сведениям, до сих пор

типа Березинского - Костерлица - Таулесса

[20].

не проводился.

Предлагаемый метод решения задачи основан на

В настоящей работе рассматриваются син-

самосогласованных уравнениях теории континуаль-

глетные сверхпроводящие состояния с расширен-

ного интегрирования в приближении когерентного

ной s-симметрией, в которых сверхпроводящая

потенциала, который в данном случае имеет недиа-

щель зависит от волнового вектора по закону

гональный беспорядок и требует особого подхода. В

Δ(k) ∝ cos k_x + cos k_y [8, 9], и d_x2_-y2 -симметрией с

предположении, что квантовые флуктуации сверх-

зависимостью Δ(k) ∝ cosk_x - cosk_y [10,11]. Иссле-

проводящего ПП важны только при достаточно

дуются особенности сверхпроводящих переходов,

низких температурах, внимание сосредоточено на

возникающие за счет термических флуктуаций

учете термических (классических) флуктуаций,

ПП с одновременным и самосогласованным учетом

играющих, по нашему мнению, главную роль в

как затухания одночастичных состояний, так и

подавляющей области фазовой диаграммы, и в

эффективной взаимосвязи между амплитудными

том числе в области псевдощели. Оценка вклада

и фазовыми флуктуациями. Исследуется возмож-

квантовых флуктуаций в подавление температуры

ность возникновения псевдощелевого состояния в

сверхпроводящего перехода, выполненная в работе

результате флуктуаций сверхпроводящего ПП. Ис-

[21], дает значение порядка 6 %. Сравнение фазовых

следование проводится на основе однозонной модели

диаграмм, вычисленных с учетом термических и

на квадратной решетке с эффективным притяжени-

квантовых фазовых флуктуаций, также говорит о

296

ЖЭТФ, том 157, вып. 2, 2020

Самосогласованный учет флуктуаций...

∫

∏

[

]

важности последних только при достаточно низких

Z =

dV+j,δdV^-j,δ exp

-βΩ(V⁺, V^-)

температурах [22].

j,δ

Ω(V⁺, V^-) = Ω⁰(V⁺, V^-) +

2. МОДЕЛЬНЫЙ ГАМИЛЬТОНИАН И

+ Ω^∗(V ⁺, V ^-) + . . . ,

МЕТОД ФУНКЦИОНАЛЬНОГО

∑[

]

ИНТЕГРИРОВАНИЯ

Ω⁰(V⁺, V^-) = V

(V+j,δ )² + (V^-j,δ

)2 ,

j,δ

Рассматривается однозонный гамильтониан

t-t^′-V модели с притяжением между электронами,

Ω^∗(V⁺, V^-) = -

ln Z^∗(V⁺, V^-),

находящимися на ближайших узлах квадратной

решетки:

Z^∗(V⁺, V^-) =

∑

Ĥ₌ t_ij ĉ^†isĉ_js -

μn_j - V

n_j↑nj+δ↓,

(1)

⎡

⎤

(3)

∫

i,j,s

j,δ

= Sp T_τ exp^⎣- dτ

^Ĥ(V⁺, V^-, τ)⎦,

где tij = -t — матричные элементы электронных

перескоков на ближайшие узлы, t_ij = t^′ — следую-

∑

^Ĥ(V⁺, V^-, τ) =

t_ij ĉ^†is(τ)ĉ_js(τ)-

щие за ближайшими; ĉ^†js(ĉ_js) — операторы рожде-

i,j,s

ния (уничтожения) электрона на узле j с проекци-

ей спина s; n_js = ĉ^†jsĉ_js, n_j — оператор электрон-

∑

V^∑

ной плотности; V — параметр межузельного при-

μn_j(τ) -

[n_j↑(τ) + nj+δ↓(τ) - 1] -

тяжения между электронами, μ — химический по-

j,δ

тенциал. С помощью коммутационных преобразова-

∑[

ний этот гамильтониан может быть приведен к га-

-V

(V+j,δ + iV^-j,δ)Ô†j,δ(τ) +

мильтониану взаимодействующих электронных пар

j,δ

в следующем виде:

]

+ (V_j

- iV ^-j,δ) Ôj,δ(τ) ,

,δ

∑

Ĥ₌ t_ij ĉ^†isĉ_js -

μn_j -

i,j,s

∑

где Sp — полный квантовомеханический след; T_τ —

[n_j↑ + nj+δ↓ - 1] -

оператор упорядочения по мнимому времени τ ∈

j,δ

∈ [0, β], β = 1/kBT; . . . — члены, не зависящие

∑[

]

от вспомогательных полей. Все зависящие от вре-

(Ô†j,δ +

j,δ

)² - (Ô†j,δ -

j,δ

)²

(2)

мени операторы являются операторами в представ-

j,δ

лении взаимодействия. Поскольку при T → 0 ме-

тод функционального интегрирования в статиче-

Здесь введены операторы рождения

Ô^†

= ĉ^†j↑ĉ†j+δ↓

j,δ

ском приближении воспроизводит результаты при-

и уничтожения

= ĉj+δ↓ĉ_j↑ электронной пары на

j,δ

ближения Хартри - Фока (ХФ), в качестве невозму-

узле j и его ближайшем соседе j + δ.

щенного гамильтониана удобно выбрать гамильто-

Задача решается в рамках метода функцио-

ниан рассматриваемой модели (1) в приближении

нального интегрирования с использованием преоб-

ХФ. В этом случае возмущение будет определять-

разования Хаббарда - Стратоновича в двухполевом

ся только термическими флуктуациями сверхпрово-

представлении (см., например, [23]). В этом методе

дящего ПП. Как отмечалось выше, мы пренебрег-

проблема вычисления статистической суммы взаи-

ли квантовыми флуктуациями, для учета которых

модействующих электронных пар сводится к про-

необходим выход за рамки статического приближе-

блеме вычисления статистической суммы независи-

ния. При вычислении статистической суммы в рас-

мых электронных пар, находящихся в расширенном

сматриваемом случае удобно перейти от перемен-

пространстве не зависящих от времени (в статичес-

ных V+j,δ и V^-j,δ к полярным переменным: модуль Δ_j,δ

ком приближении) вспомогательных флуктуирую-

и фаза φ_j,δ, вводя таким образом флуктуирующий

щих полей, V+j,δ и V^-j,δ,

комплексный ПП Δ_j,δ exp(iφ_j,δ):

297

А. Г. Грошев, А. К. Аржников

ЖЭТФ, том 157, вып. 2, 2020

∫∞

∫π

∏

В этом случае Δ_j,δ является амплитудой ПП, вычис-

Z =

Δ_j,δdΔ_j,δ dφ_j,δ exp[-βΩ(Δ, φ)],

ленной в приближении ХФ. Вычисление интеграла

j,δ

-π

по амплитудному полю Δ_j,δ в (4) проводится в при-

Ω(Δ, φ) = Ω⁰(Δ, φ) + Ω^∗(Δ, φ) + . . . ,

ближении «седловой точки», в котором переменное

∑

поле Δ_j,δ заменяется его значением в «седловой точ-

Ω⁰(Δ, φ) = V

Δ2j,δ,

ке» Δ_j,δ(φ). При этом учитываются наиболее веро-

j,δ

ятные амплитудные флуктуации. Это приближение

Ω^∗(Δ, φ) = -

ln Z^∗(Δ, φ),

предполагает, что амплитудные флуктуации гораз-

⎡

⎤

до быстрее, чем флуктуации фазы, и амплитудное

∫

поле успевает подстроиться под распределение фа-

Z^∗(Δ, φ) = SpT_τ exp⎣- dτ

^Ĥ(Δ, φ, τ)⎦,

зы равновесным образом. Аналогичное приближе-

ние использовалось в упомянутом выше вариацион-

^Ĥ(Δ, φ, τ) =

Ĥ_HF (Δ, α) +

U (Δ, φ, τ),

ном подходе [5, 7]. При вычислении «седловой точ-

∑

(4)

ки» важно учесть, что подынтегральная функция в

Ĥ_HF (Δ, α) = t_ijĉ+isĉ_js -

μn_j -

этой точке не должна обращаться в нуль. Для удо-

i,j,s

∑

влетворения этого требования необходимо включить

[n_j↑ + nj+δ↓ - 1] -

в термодинамический потенциал множитель Δ_j,δ из

j,δ

якобиана (4), как это было сделано в работах [5, 7].

∑

- V Δ_j,δ[exp(iα_j,δ) Ô†j,δ + exp(-iα_j,δ) Ôj,δ],

В результате уравнение для нахождения «седловой

j,δ

точки», получаемое из условия минимума термоди-

∑

намического потенциала ∂Ω/∂Δ_j,δ = 0, не имеет ре-

U (Δ, φ, τ) = -V

[Δ_j,δ exp(iφ_j,δ) -

шения Δ_j,δ = 0 ни при какой температуре, кроме

j,δ

]

T = 0. Заметим, что не все авторы учитывают эту

Ô^†

- Δ_j,δ exp(iα_j,δ)

(τ) -

j,δ

особенность [24-27], получая в результате нулевое

∑

-V

[Δ_j,δ exp (-iφ_j,δ) -

значение амплитуды сверхпроводящего ПП при ко-

j,δ

нечных температурах. После некоторых преобразо-

]

ваний уравнения для минимума термодинамическо-

- Δ_j,δ exp(-iα_j,δ)

(τ),

j,δ

го потенциала нетрудно получить самосогласован-

где

Ĥ_HF — гамильтониан рассматриваемой модели

ное уравнение для определения амплитуды сверх-

(1) в приближении ХФ;

U — потенциал флуктуи-

проводящего ПП Δ(φ):

рующих полей; Δ_j,δ — значение амплитуды усред-

Δ(φ)K(φ)

ненного по флуктуациям сверхпроводящего ПП;

Δ²(φ) -

= 0,

2βV

αj,δ — фаза ПП, определяющая его симметрию. В

1^∑

данной работе мы ограничимся изучением сверхпро-

K(φ) =

exp(iφ_δ)G↓↑j+δ,j(iω_n)+

(6)

водящих фаз с s- и d-симметрией. Для этого необ-

ходимо выбрать амплитуду в виде функции, не за-

1^∑

exp(-iφ_δ)G↑↓j,j+δ(iω_n),

висящей от узлов j и их ближайших соседей δ, при

этом фаза должна зависеть только от ближайших

соседей Δ_j,δ exp(iα_j,δ) = Δexp(iα_δ):

где G↓↑j+δ,j (iω_n) и G↑↓j,j+δ(iω_n) представляют собой

{

фурье-образы аномальных температурных гриновс-

α, δ = ±δ_x,

ких функций, определяемых стандартными соотно-

α_δ =

(5)

-α, δ = ±δ_y,

шениями:

где δ_x и δ_y — проекции δ на координатные оси. Тог-

G^↓↑j,j′ (τ - τ^′) = - Tτ ĉ^†j↓(τ)ĉ^†j′_↑(τ^′) ,

да значениям фазы α = 0 и α = π соответствует

(7)

G^↑↓j,j′ (τ - τ^′) = -

T_τ ĉ_j↑(τ)ĉ_j′_↓(τ^′)

s-симметрия, а α = ±π/2 — d-симметрия.

В основном состоянии термические флуктуации

ω_n

(2n + 1)π/β

— мацубаровские частоты

сверхпроводящего ПП отсутствуют и, следователь-

для ферми-частиц. Из явных выражений для

но, потенциал флуктуирующих полей

U исчезает,

G↓↑j+δ,j(iω_n) и G↑↓j,j+δ(iω_n) (см. Приложение) следу-

а функция распределения амплитудных и фазовых

ет свойство G^↓↑j±δ

(iω_n)

= G^{↑↓j,j±δ}

(iω_n), которое

флуктуаций сводится к дельта-функциям Дирака

x,j

приводит к независимости K(φ) от узлов и их

P (Δ_j,δ, φ_j,δ) = δ(Δ_j,δ - Δ_j,δ)δ(φ_j,δ - α_j,δ).

ближайших соседей. Выбирая решение уравнения

298

ЖЭТФ, том 157, вып. 2, 2020

Самосогласованный учет флуктуаций...

(6) с Δ(φ) > 0, можно представить его в следующем

где Tr — сумма диагональных элементов. Свойство

виде:

G^↓↑j±δ

(iω_n)

= G^{↑↓j,j±δ}

(iω_n), следующее из их яв-

√

x,j

ных выражений (см. Приложение), приводит к неза-

K(φ)

K²(φ)

Δ(φ) =

(8)

висимости от ближайших соседей выражения под

2V β

знаком суммы в (12). Для простоты индексы уз-

лов j и их ближайших соседей δ в дальнейшем

Известно, что термодинамический потенциал (4)

не указываются. С помощью уравнения Дайсона в

может быть выражен через температурные гриновс-

двухузельном приближении когерентного потенциа-

кие функции [28, 29]. Это преобразование удобнее

ла (two-site coherent-potential approximation, TCPA)

проводить в представлении матриц Намбу

(A.2) термодинамический потенциал Ω^∗ в расчете на

[

]

одну электронную пару выражается через темпера-

ĉj↑(τ)

ĉjδ(τ) =

турные гриновские функции после интегрирования

ĉ†j+δ↓(τ)

(9)

[

]

уравнения (12) по константе связи λ от λ = 0 до

ĉ†jδ(τ) =

λ = 1 с учетом того, что Ω^∗(λ = 0) = Ω_HF:

ĉ†j↑(τ)

ĉj+δ↓(τ)

∑

через которые выражается температурная функция

Ω^∗ = Ω_HF +

ln (det [1 + F (iω_n)Σ(iω_n)]) -

Грина и флуктуирующий потенциал (4):

∑

ln (det [1 - F (iω_n) (ΔU(φ) - Σ(iω_n))]).

(13)

G_jδ(τ - τ^′) = - T_τ ĉ_jδ(τ)ĉ^†jδ(τ^′)

[

]

↑↑

(τ - τ^′)

G↑↓j,j+δ(τ - τ^′)

Здесь Ω_HF = -1/β ln(Sp exp[-β

Ĥ_HF ]) — термодина-

j,j

мический потенциал в приближении ХФ, F (iω_n) —

G↓↑j+δ,j(τ - τ^′) G↓↓j+δ,j+δ(τ - τ^′)

∑

фурье-образ эффективной температурной гринов-

U (Δ, φ, τ) =

ĉ†jδ(τ)ΔU_jδ ĉ_jδ(τ),

ской функции в представлении матриц Намбу (A.9),

j,δ

ΔU(φ) — флуктуирующий потенциал (10), Σ(iω_n) —

[

]

(10)

↑↓

U_j

собственно-энергетическая часть в представлении

,j+δ

ΔU_jδ =

матриц Намбу (A.1). Суммирование по мацубаров-

U↓↑j+δ,j

[

]

ским частотам проводится стандартным образом, с

U↑↓j,j+δ = V

Δexp(iα_δ)-Δ(φ)exp (iφ_δ)

использованием выражения

U↓↑j+δ,j =

1^∑

[

]

f (iω_n) =

Δexp(-iα_δ) - Δ(φ)exp (-iφ_δ)

∞

∫

⁽βE⁾

[

(

)]

Здесь G^↑↑j,j(τ - τ^′) и G↓↓j+δ,j+δ(τ - τ^′) — нормальные

=±

dE th

E^±

(14)

температурные гриновские функции, определяемые

2π

−∞

стандартными соотношениями:

где E^± = E ± i0. После несложных преобразований

статистическая сумма в расчете на одну электрон-

G^↑↑j,j′ (τ - τ^′) = - Tτ ĉj↑(τ)ĉ^†j′_↑(τ^′) ,

(11)

ную пару представляется в виде интеграла только

G^↓↓j,j′ (τ - τ^′) = - Tτ ĉ+j↓(τ)ĉj′↓(τ^′)

по фазовому полю φ:

Отметим, что в представлении матриц Намбу для

Z = exp[-β(Ω_HF + Ω[Σ] + ΔΩ)],

∫

∞

температурной функции Грина (10) может исполь-

⁽βE⁾

зоваться обычная диаграммная техника без введе-

Ω[Σ] = -

dE th

2π

ния новых диаграмм для ее аномальных слагаемых.

−∞

Умножая флуктуирующий потенциал

U в (4) на

× arg(det[1 + F(E^-)Σ(E^-)]),⎛

⎞

константу связи λ и дифференцируя термодинами-

∫π

(15)

ческий потенциал Ω^∗(λ) по этой константе, можно

ΔΩ = -

ln^⎝ dφ Δ(φ) exp [-βΔΩ(φ)]⎠,

получить выражение для этой производной через

-π

∞

∫

температурную функцию Грина (10):

ΔΩ(φ) = V Δ²(φ) +

dE th (βE/2) ×

2π

∂Ω^∗(λ)

1^∑

-∞

Tr [ΔU_jδG_j,δ(iω_n, λ)] ,

(12)

(

[

]])

∂λ

n,j,δ

× arg

det

1 - F(E^-)

ΔU(φ) - Σ(E^-)

299

А. Г. Грошев, А. К. Аржников

ЖЭТФ, том 157, вып. 2, 2020

где Ω[Σ] — термодинамический потенциал эффек-

P V = t, t = 0.2t,

= -0.8t (n

0.83)

тивной среды, определяемый собственно-энергети-

T = 0.002t

ческой частью Σ(E) (A.1); ΔΩ — флуктуацион-

0.04t

0.1t

ная часть термодинамического потенциала. К этим

уравнениям необходимо добавить уравнение для

определения химического потенциала:

∫

∞

⁽βE⁾

n(μ) = 1 +

dE th

2π

−∞

[

]

× Im

F^↓(E^-) - F^↑(E^-)

(16)

где F^↑(E^-) и F^↓(E^-) представляют собой диа-

-1.0

-0.5

0.5

1.0

гональные элементы эффективной температурной

гриновской функции (A.2) (см. Приложение). Сред-

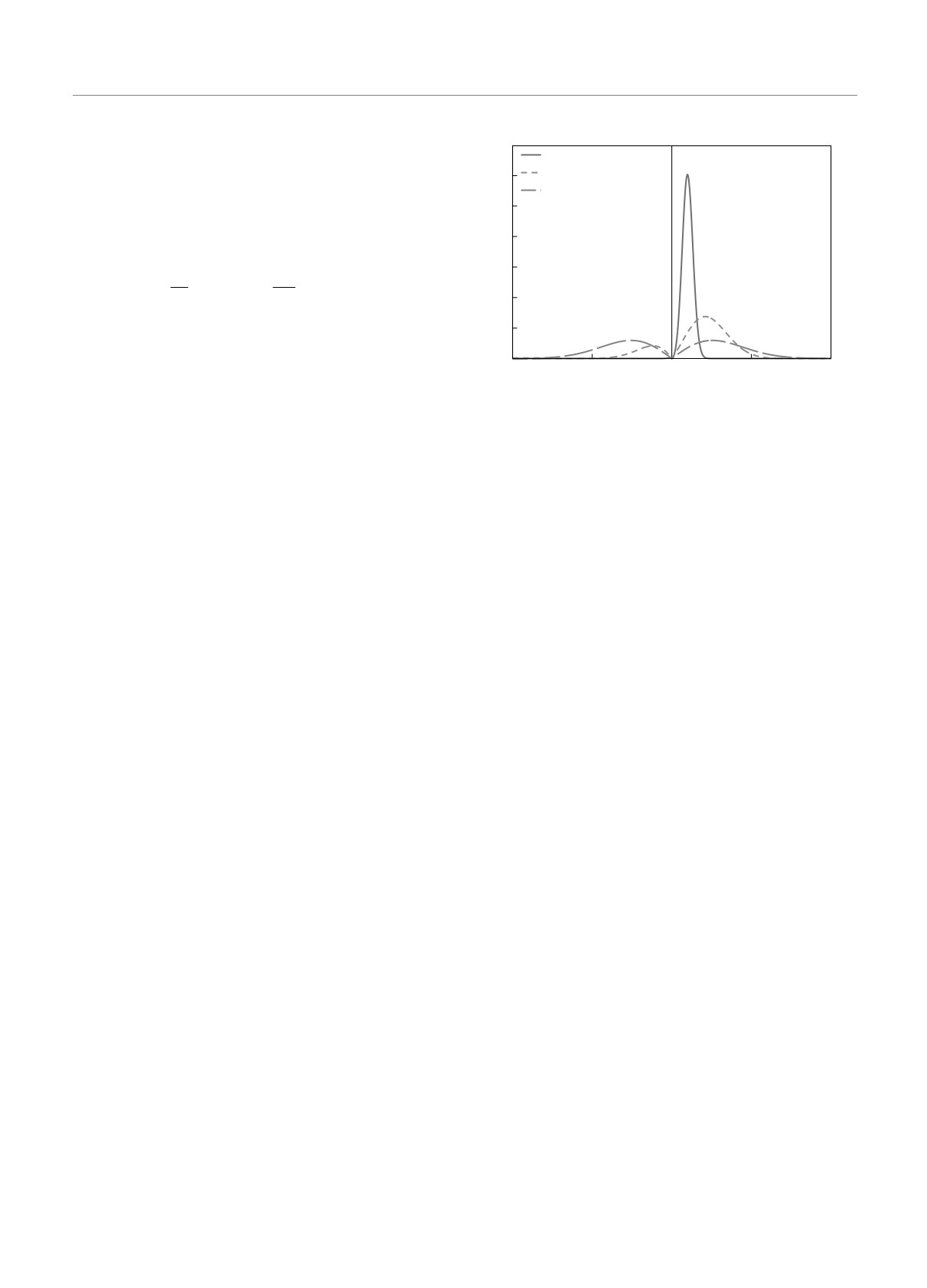
Рис. 1. Вероятности распределения амплитудных флукту-

ние значения термодинамических величин и сред-

аций сверхпроводящего ПП, рассчитанные при значении

няя матрица рассеяния в самосогласованных урав-

химического потенциала μ = -0.8t, соответствующем кон-

нениях TCPA для собственно-энергетической части

центрации электронов n ≈ 0.83

Σ(E) вычисляются следующим образом:

∫π

параметрах в большей части фазовой диаграммы

〈A〉 = dφ A(φ)P (φ),

(17)

реализуются сверхпроводящие состояния с расши-

-π

ренной s- и d_x2_-y2 -симметрией.

P (φ) = exp [-βΔΩ(φ) + βΔΩ].

Здесь A — усредняемая величина. Численное реше-

3.1. Учет ограниченных флуктуаций фазы

ние этих самосогласованных уравнений позволяет

(φ = ±0.5π)

определить сверхпроводящие свойства рассматрива-

емой системы при условии, что термодинамический

Для анализа приближения «седловой точки»,

потенциал для данного α является минимальным.

наиболее часто используемого в методе контину-

Из (17) следует, что вероятность флуктуации фа-

ального интегрирования, были проведены расчеты

зового поля Δφ = φ - α при температуре T опре-

сверхпроводящего состояния с d-симметрией и огра-

деляется разностью термодинамических потенциа-

ниченными (φ = ±0.5π) флуктуациями фазы. Такое

лов ΔF (φ) = ΔΩ(φ) - ΔΩ(α), где α — значение

ограничение позволяет при наименьших численных

фазы, при которой достигается глобальный мини-

затратах сравнить решения, полученные двумя спо-

мум термодинамического потенциала. Таким обра-

собами. В первом способе, без использования допол-

зом, ΔF(φ) представляет собой энергию, необходи-

нительных приближений, область изменения ампли-

мую для фазовой флуктуации Δφ, или фазовую

тудного поля расширяется на отрицательные значе-

жесткость. Именно фазовые флуктуации определя-

ния. В таком подходе положительные значения ам-

ют параметры эффективной среды (A.1) при конеч-

плитудного поля связаны с фазой φ = 0.5π, а отри-

ной температуре. При T ≥ T_c глобальный минимум

цательные — с фазой φ = -0.5π. Интегрирование

термодинамического потенциала исчезает и для ре-

проводится по всей области изменения амплитудно-

ализации любой фазовой флуктуации не требуется

го поля, включая его отрицательные значения. Во

энергии, ΔF (φ) = 0 (т. е. фазовая жесткость в сис-

втором способе используется приближение «седло-

теме отсутствует).

вой точки» для амплитудного поля, в котором инте-

грирование по этому полю заменяется суммировани-

ем по седловым точкам Δ(φ) с φ = ±0.5π. На рис. 1

3. РЕЗУЛЬТАТЫ

и 2 приведены примеры самосогласованного расчета

При расчетах использовались характерные для

вероятностей распределения амплитудных и фазо-

купратов параметры V = t и t^′ = 0.2t [16], которые

вых флуктуаций φ = ±0.5π ПП соответственно для

выбирались ранее при вычислении фазовых диа-

первого и второго способов. Из рисунков видно, что

грамм сверхпроводящих состояний без учета флук-

существует температура T_c, выше которой вероятно-

туаций ПП [30]. Как показано в работе [30], при этих

сти фазовых флуктуаций φ = ±0.5π сравниваются и

300

ЖЭТФ, том 157, вып. 2, 2020

Самосогласованный учет флуктуаций...

V = t, t = 0.2t,

= -0.8t (n

0.83)

V = t, t = 0.2t,

= -0.8t (n

0.83)

1.0

0.18

T = 0.002t

0.9

0.04t

0.16

0.8

0.08t

0.14

0.7

0.12

0.6

0.10

0.5

0.08

0.4

0.3

0.06

0.2

0.04

0.1

0.02

-1.0

-0.5

0.5

1.0

0.02

0.04

0.06

0.08

0.10

0.12

0.14

0.16

Рис. 2. Вероятности фазовых флуктуаций φ

= ±0.5π

Рис. 3. Температурные зависимости амплитуды усреднен-

сверхпроводящего ПП

ного ПП с d-симметрией в различных приближениях

система переходит в нормальное состояние. Темпе-

V = t, t = 0.2t, T = 0.002t

ратурные зависимости амплитуд усредненного ПП

0.07

и значения T_c, вычисленные в приближении «сед-

ловой точки» 〈Δ_sp〉 и без использования дополни-

0.06

тельных приближений 〈Δ_a〉 представлены на рис. 3.

0.05

Неплохое согласие между результатами двух спосо-

бов во всем рассматриваемом диапазоне температур

0.04

позволяет обосновать использование приближения

0.03

«седловой точки» в дальнейших расчетах. Допол-

нительно на рис. 3 приведена температурная зави-

0.02

симость амплитуды ПП Δ_HF , полученная в методе

0.01

ХФ [30] без учета флуктуаций. Из сравнения видно,

что флуктуации существенно изменяют ее поведе-

ние и температуру фазового перехода.

0.2

0.4

0.6

0.8

1.0

1.2

1.4

1.6

Рис. 4. Зависимость амплитуды усредненного ПП от кон-

3.2. Полный учет флуктуаций фазы

центрации носителя заряда при температуре T = 0.002t

φ ∈ [-π,π]

В этом разделе рассматриваются решения за-

дачи с учетом всех возможных фазовых флуктуа-

висимости амплитуд усредненного ПП в сверхпро-

ций из интервала [-π, π]. Результаты расчетов ам-

водящих областях с d- (n ≈ 0.83) и s-симметрией

плитуды 〈Δ〉 усредненного ПП представлены на

(n ≈ 0.108) соответственно. Отметим, что при уче-

рис. 3. Зависимость амплитуды усредненного ПП

те фазовых флуктуаций из интервала [-π, π] про-

от концентрации носителей заряда при температу-

исходит существенное изменение их температурного

ре T = 0.002t приведена на рис. 4. Видно, что при

поведения по сравнению с результатами, в которых

увеличении числа электронов происходит переход

учитывались только ограниченные значения фазы

из сверхпроводящего состояния с s-симметрией в

φ = ±0.5π, при этом существенно, приблизитель-

сверхпроводящее состояние с d-симметрией. Такая

но в 4 раза для состояния с d-симметрией и при-

же последовательность фазовых переходов получе-

близительно в 7 раз для состояния с s-симметрией,

на в приближении ХФ [30], однако даже при та-

снижается температура перехода в сверхпроводя-

кой относительно низкой температуре T = 0.002t

щее состояние. Согласно БКШ-теории отношение

сверхпроводящие области существенно сужаются.

энергетической щели Δ₀ к температуре сверхпрово-

На рис. 3 и рис. 5 представлены температурные за-

дящего перехода T_c имеет универсальное значение

301

А. Г. Грошев, А. К. Аржников

ЖЭТФ, том 157, вып. 2, 2020

V = t, t = 0.2t,

’

= -2.8t (n

0.108)

V = t, t = 0.2t,

= -0.8t (n

0.83)

0.030

0.8

T = 0.002t

0.7

0.02t

0.025

0.04t

0.6

0.020

0.5

0.015

0.4

0.3

0.010

0.2

0.005

0.1

–1.0

–0.5

0.5

1.0

0.002

0.004

0.006

0.008

0.010

0.012

T = 0.002t

Рис. 5. Температурная зависимость амплитуды усреднен-

0.20

0.02t

ного ПП с расширенной s-симметрией

0.04t

0.15

Δ₀/T_c = 1.76. Результаты, полученные в прибли-

жении ХФ [30] для рассматриваемой модели, дают

0.10

значения 1 ≲ Δ₀/T_c ≲ 1.4, которые незначитель-

но отличаются от результата БКШ. Такие преде-

0.05

лы изменения Δ₀/T_c получены в [30] для t^′/t = 0.2

и t^′/t = 0.7 при достаточно широком изменении

значений параметра межузельного притяжения V/t:

–1.0

–0.5

0.5

1.0

0.25, 0.5, 1. Предполагая, что и при учете флукту-

аций сохранится такая относительно слабая зави-

симость пределов изменения Δ₀/T_c от V/t, можно

Рис. 6. Вероятности распределения фазовых флуктуаций

говорить о том, что Δ₀/T_c в основном определя-

φ сверхпроводящего ПП с d-симметрией (а) и зависимости

ется параметрами t^′ и n. Заметим, что, поскольку

амплитуд ПП с d-симметрией от φ (б)

в Δ₀/T_c входит значение энергетической щели Δ₀

при T = 0, изменение Δ₀/T_c при учете флуктуа-

ций происходит в основном за счет понижения T_c.

ние Δ₀/T_c ≈ 5. В экспериментах на ВТСП-соеди-

Исходя из полученных в настоящей работе значе-

нениях Bi₂Sr₂CaCu₂O8+δ было получено значение

ний T_c для d- и s-симметрии, можно оценить пре-

Δ₀/T_c ≈ 3.95 [31].

делы изменения Δ₀/T_c с учетом фазовых флуктуа-

Результаты самосогласованного расчета вероят-

ций 4 ≲ Δ₀/T_c ≲ 9.8. Кроме того, приведенное на

ностей распределения фазовых флуктуаций и наи-

рис. 4 в [30] распределение энергетической щели Δ₀

более вероятных флуктуаций амплитуды, вычислен-

по фазовой диаграмме в переменных t^′-n позволя-

ные в приближении «седловой точки» для трех раз-

ет качественно понять зависимость Δ₀/T_c от t^′ и n.

личных температур, приведены на рис. 6. Видно,

В частности, максимальные значения Δ₀/T_c можно

что наиболее вероятное значение фазы соответству-

ожидать при значениях t^′ и n, соответствующих осо-

ет d-симметрии, а форма кривых далека от гаус-

бенностям Ван Хова, а уменьшение t^′ должно вести

совой даже при относительно низких температу-

к понижению нижнего предела изменения Δ₀/T_c.

рах T = 0.002t. Следует отметить не менее важ-

Проведенные в настоящей работе расчеты показы-

ный результат, связанный с существенной зависимо-

вают, что при учете фазовых флуктуаций это от-

стью наиболее вероятных значений амплитуды ПП

ношение действительно значительно увеличивает-

от фазы флуктуаций. Это означает, что приближе-

ся: Δ₀/Tc ≈ 5.3 для d-симметрии и Δ0/Tc ≈ 6.2

ния, в которых амплитудные флуктуации не учиты-

для расширенной s-симметрии (в принятых выше

ваются, а именно: амплитуда является константой и

обозначениях Δ₀ = 2V 〈Δ〉). Предварительные рас-

не зависит от фазовых флуктуаций, не оправданы.

четы при t^′/t = 0.7 дают для d-симметрии значе-

Важной величиной, на которую влияют флуктуации

302

ЖЭТФ, том 157, вып. 2, 2020

Самосогласованный учет флуктуаций...

V = t, t = 0.2t,

= -0.8t (n

0.83)

0.6

0.025

T = 0.002t

= 0.002t

0.5

0.02t

0.04t

0.020

0.04t

0.4

0.015

0.3

0.010

0.2

0.005

0.1

-4

-2

-8

-6

–4

–2

E/t

0.025

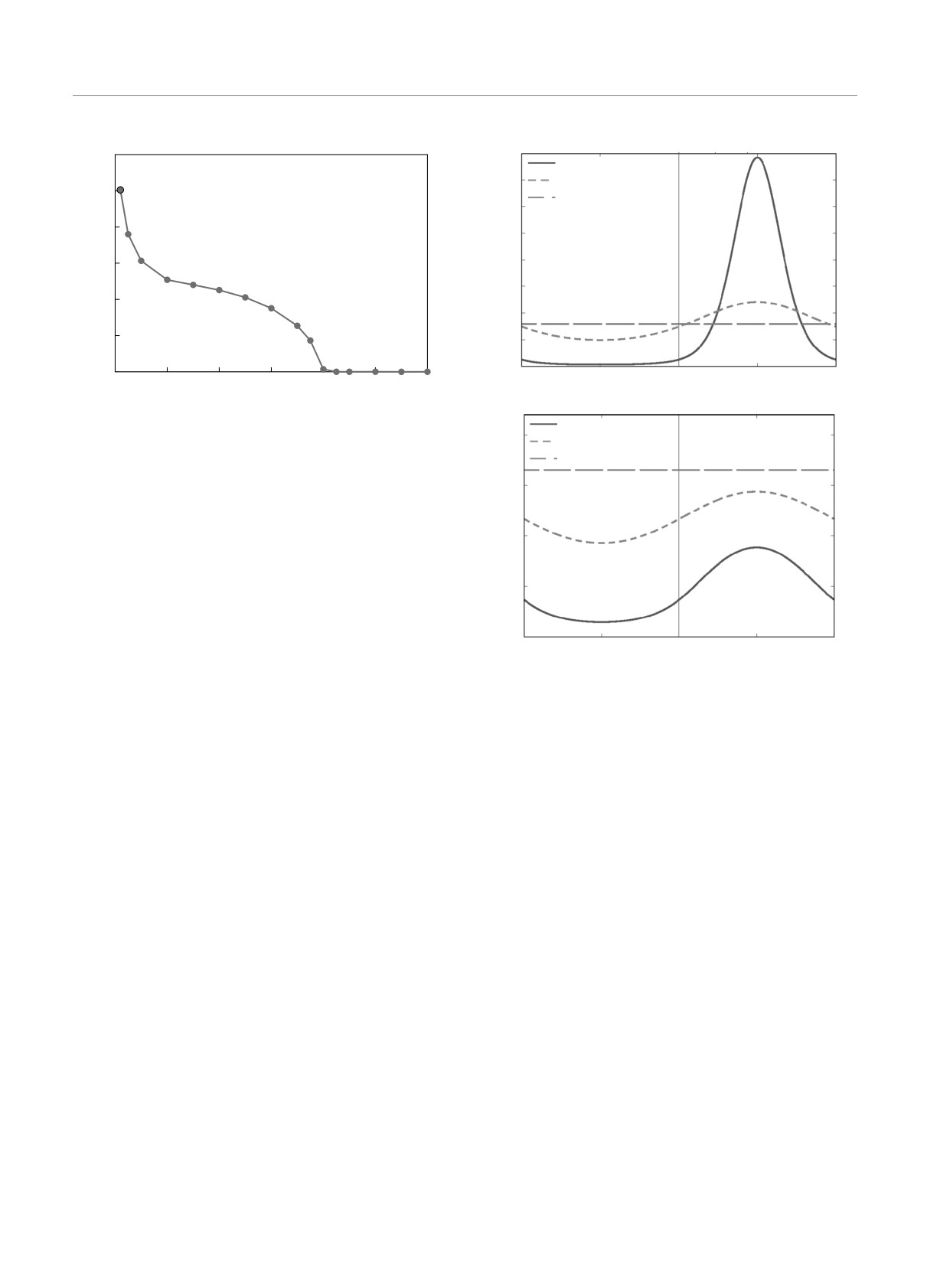
Рис. 7. Плотность электронных состояний, вычисленная

= 0.002t

для сверхпроводящего состояния с d-симметрией

0.020

0.02t

0.04t

0.015

сверхпроводящего ПП при самосогласованном под-

0.010

ходе является собственно-энергетическая часть од-

0.005

ночастичной функции Грина, определяющая плот-

ность состояний. Плотность состояний, мнимая и

действительная части собственной энергии для трех

-0.005

различных температур, представлены на рис. 7, 8.

-0.010

Из приведенных графиков видно, что провал в плот-

-0.015

ности электронных состояний с повышением темпе-

-8

-6

-4

-2

E/t

ратуры уменьшается и полностью исчезает в точке

фазового перехода одновременно с потерей фазовой

-0.0696

= 0.002t

когерентности ПП. Мнимая и действительная части

собственной энергии, напротив, с ростом темпера-

-0.0697

туры увеличиваются в результате усиления рассе-

яния на флуктуациях связанных электронных пар

-0.0698

и становятся значимыми вблизи фазового перехода

(рис. 8а,б).

-0.0699

Следует также отметить определенную структу-

-0.0700

ру в энергетической зависимости аномальной час-

ти собственной энергии (рис. 8в). Относительный

-0.0701

вклад этой структуры составляет порядка 10 % и,

вполне возможно, может влиять на возбуждение

–0.0702

-8

-6

–4

–2

электронов. С ростом температуры величина ано-

E/t

мальной части собственной энергии уменьшается и

обращается в нуль в точке фазового перехода.

Рис. 8. Мнимая (а), действительная (б) и недиагональная

(в) части собственной энергии одноэлектронной функции

Грина, вычисленные для сверхпроводящего состояния с d-

симметрией

4. ЗАКЛЮЧЕНИЕ

В работе проведено исследование влияния

(фазовых) флуктуаций сверхпроводящего ПП на

что при выбранных параметрах учет этих флукту-

поведение сверхпроводящей щели, одноэлектронной

аций не приводит к изменению рассматриваемых

плотности состояний и температуры фазового

типов симметрии, но существенно, примерно в 4

перехода в синглетных сверхпроводящих фазах с

раза в случае d-симметрии и примерно в 7 раз в

расширенной s- и d_x2_-y2-симметрией. Показано,

случае s-симметрии, снижает температуры пере-

303

А. Г. Грошев, А. К. Аржников

ЖЭТФ, том 157, вып. 2, 2020

∑

хода в сверхпроводящее состояние. В результате

Σ(iω_n) =

ĉ†jδΣ_jδ(iω_n)ĉ_jδ ,

этого отношение энергетической щели к темпе-

j,δ

ратуре сверхпроводящего перехода значительно

Σ_jδ(iω_n) =

превышает универсальное БКШ-значение, что

⎡

⎤

Σ^↑j,j(iω_n)

Σ↑↓j,j+δ(iω_n)

действительно наблюдается в экспериментах на

=^⎣

⎦,

ВТСП-соединениях. Усредненная амплитуда ПП

Σ↓↑j+δ,j(iω_n) Σ↓j+δ,j+δ(iω_n)

(A.1)

остается конечной при любых температурах и

Σ^↑j,j(iω_n) = Σ^↑(iω_n)/4,

концентрациях носителей заряда. Поэтому переход

в нормальное состояние происходит в результате

Σ↓j+δ,j+δ(iω_n) = Σ^↓(iω_n)/4,

потери фазовой когерентности ПП. Показано, что в

рассматриваемом самосогласованном подходе про-

Σ↑↓j,j+δ(iω_n) = Σ^↑↓(iω_n)exp(iα_δ),

вал в электронной плотности состояний на уровне

Σ↓↑j+δ,j(iω_n) = Σ^↑↓(iω_n)exp(-iα_δ),

Ферми отсутствует выше температуры фазового

перехода, несмотря на отличное от нуля среднее

которая имеет такую же функциональную форму,

значение амплитуды ПП. Таким образом, объяс-

как и

Ĥ_HF (4), и сохраняет полную симметрию рас-

нение псевдощелевого состояния в некогерентной

сматриваемой системы. Таким образом, температур-

области фазовой диаграммы в рамках рассмат-

ная функция Грина G_jδ (iω_n, λ) (10) в этом прибли-

риваемого подхода невозможно. Предложенный

жении описывается уравнением Дайсона с флукту-

метод может быть использован для исследования

ирующим потенциалом ΔU (4):

влияния фазовых флуктуаций на сверхпроводящие

фазы с различными (не только с s- и d-) типами

G_jδ(iω_n, λ) = F_jδ(iω_n)+

симметрии, в том числе в триплетном состоянии и

+ F_jδ(iω_n)[λΔU_jδ - Σ_jδ(iω_n)]G_jδ(iω_n,λ) =

при наличии примесей.

= F_jδ(iω_n) + F_jδ(iω_n)T_jδ(iω_n)F_jδ(iω_n), (A.2)

Финансирование. Работа частично поддержа-

где F_jδ(iω_n)

— фурье-образ эффективной тем-

на грантом Уральского отделения Российской ака-

пературной гриновской функции, T_jδ(iω_n)

—

демии наук № 18-2-2-12 и программой финансирова-

фурье-образ матрицы рассеяния электронной пары

ния AAAA-A16-116021010082-8.

с флуктуирующим потенциалом (4). Тогда собст-

венно-энергетическая часть Σ_jδ(iω_n) определяется

самосогласованным образом из требования отсут-

ствия рассеяния этой электронной парой в среднем,

ПРИЛОЖЕНИЕ

〈T_jδ(iω_n, λ)〉 = 0 или 〈G_jδ (iω_n, λ)〉 = F_jδ (iω_n).

Явные выражения для матричных элементов

Гриновские функции в TCPA

гриновских функций в представлении матриц Нам-

бу могут быть получены с помощью преобразования

Как было замечено выше, гамильтониан рас-

Фурье операторов рождения (уничтожения) ĉ^†js(ĉ_js)

сматриваемой модели в приближении ХФ H_HF (4)

1^∑

описывает свойства системы без учета флуктуаций

ĉ†js(ĉ_js) =

exp[∓ikR_j]ĉ^†ks(ĉ_ks),

(A.3)

сверхпроводящего ПП. Учет флуктуаций требует

введения флуктуирующего потенциала ΔU

(4) и

где N — число узлов в системе, R_j — векторы квад-

приводит к проблеме недиагонального беспорядка в

ратной решетки, ĉ^†ks(ĉ_ks) — операторы рождения

неупорядоченных системах. Эта проблема в данном

(уничтожения) электрона с импульсом k и спино-

случае может быть решена в рамках двухузельно-

вой проекцией s. В результате этого преобразования

го приближения когерентного потенциала (TCPA)

гамильтониан рассматриваемой системы в прибли-

[32-34]. Суть этого приближения в рассматриваемом

жении ХФ

Ĥ_HF (4) записывается в представлении

случае заключается в том, что рассеивающая па-

матриц Намбу

ра электронов с флуктуирующим потенциалом ΔU

[

]

[

]

(4) встраивается в эффективную среду, состоящую

ĉk↑

ĉk =

ĉ†k =

ĉ†

ĉ-k↓

(A.4)

из электронных пар с эффективными параметрами,

k↑

ĉ†

−k↓

определяемыми собственно-энергетической частью

Σ(iω_n):

следующим образом:

304

ЖЭТФ, том 157, вып. 2, 2020

Самосогласованный учет флуктуаций...

1^∑

F_k(E) = [E - H_eff (k)]-1 =

Ĥ_HF (Δ, α) =

ĉ†kH_HF (k)ĉ_k,

[

]

⎡

⎤

↑↑

F^↑k(E) F^↑↓k(E)

H_H

(k) H^↑↓HF (k)

H_HF (k) =^⎣

⎦,

F^↓↑k(E) F^↓k(E)

H^↓↑HF (k) H^↓↓HF (k)

E ± ε_k ∓ μ - Σ↓(↑)(E)

F↑(↓)k(E) =

(

) ,

H^↑↑HF (k) = ε_k - μ, H^↓↓HF (k) = -ε_k + μ,

−

E - E+k )(E - E

(A.5)

H^↑↓HF (k) = -2V ΔV_k(α),

Σ↑↓(↓↑)k(E) + H↑↓(↓↑)HF(k)

(

)_∗

F↑↓(↓↑)k(E) =

(

)

(A.8)

E - E+k )(E - E^-

H^↓↑HF (k) = H^↑↓HF (k)

Σ^↑(E) + Σ^↓(E)

ε_k = -2t (cosk_x + cosk_y) + 4t^′ cosk_x cosk_y,

E^±k =

[(

)₂

Vk(α) = cos α (cos kx + cos ky) +

Σ^↑(E) + Σ^↓(E)

± ε_k -μ+

+isinα(cosk_x - cosk_y),

]

1/2



↓



где ε_k — закон дисперсии энергии электронов на

+ Σ^↑(E)Σ^↓(E) +

Σ^↑

(E) + H^↑↓HF (k)

квадратной решетке с перескоками на ближайшие

и следующие за ними узлы, V_k(α) — закон диспер-

сии сверхпроводящего ПП с симметрией, задавае-

Явные выражения для матричных элементов эф-

мой значением фазы α. Флуктуирующий потенциал

фективной функции Грина в представлении матриц

(4) в этом представлении записывается в следующем

Намбу получаются в результате преобразования Фу-

виде:

рье (A.3):

∑

1^∑

U (Δ, φ, τ) =

ĉ†k(τ)ΔU(k)ĉ_k (τ),

F^↑↑j,j(E) =

F^↑k(E),

[

]

∑

ΔU^↑↓(k)

(A.6)

ΔU(k) =

(

)

∗

F↓↓j+δ,j+δ(E) =

F^↓k(E),

ΔU^↑↓(k)

[

]

1^∑

ΔU^↑↓(k) = 2V

ΔV_k(α) - Δ(φ)V_k(φ)

F↑↓j,j+δ(E) =

exp[ikR_δ]F^↑↓k(E) =

(A.9)

1^∑

Эффективная среда описывается гамильтонианом

cos(kR_δ)F^↑↓k(E),

1^∑

Ĥ_eff (E) =

Ĥ_HF +

Σ(E),

F↓↑j+δ,j(E) =

exp[-ikR_δ]F^↓↑k(E) =

1^∑

Σ(E) =

ĉ†kΣ_k(E)ĉ_k,

∑

cos(kR_δ)F^↓↑k(E).

[

]

↑↓

Σ^↑(E) Σ

(E)

(A.7)

Σ_k(E) =

Σ^↓↑k(E) Σ^↓(E)

При получении этих выражений использовалось

Σ^↑↓k(E) = 2Σ^↑↓(E)V_k(α),

свойство F_-k(E) = F_k(E), которое следует из ин-

Σ^↓↑k(E) = 2Σ^↑↓(E)V^∗k(α),

версионной симметрии законов дисперсии электрон-

ной энергии и сверхпроводящего ПП (A.5). Недиаго-

где Σ_k(E) — собственно-энергетическая часть (A.1)

нальные матричные элементы эффективной гринов-

в представлении матриц Намбу (A.4). Для учета ПП

ской функции (A.8) в представлении матриц Намбу

с рассматриваемыми типами симметрии необходи-

(A.4) обладают свойством F↑↓(↓↑)k(E) = F↓↑(↑↓)(E),k

y,kx

x,ky

мо, чтобы коэффициент Σ^↑↓(E) в недиагональных

которое связано с симметрией сверхпроводящего

матричных элементах собственно-энергетической

ПП (A.5). Это приводит к тому, что для недиаго-

части (A.7) был действительной функцией энер-

нальных матричных элементов эффективной гри-

гии, в то время как диагональные элементы Σ^↑(E)

новской функции в представлении матриц Нам-

и Σ^↓(E) в общем случае являются комплексны-

бу справедливо свойство F^{↑↓j,j±δ}

(E) = F^↓↑j±δ

(E).

x,j

ми функциями. Эффективная гриновская функ-

Явные выражения для матричных элементов гри-

ция (A.2) в представлении матриц Намбу (A.4) вы-

новской функции с флуктуирующим потенциалом

ражается через гамильтониан эффективной среды

G_j,δ(E) могут быть получены из уравнения Дайсо-

Ĥ_eff (E) (A.7):

на (A.2) следующим образом:

305

ЖЭТФ, вып. 2

А. Г. Грошев, А. К. Аржников

ЖЭТФ, том 157, вып. 2, 2020

G^↑↑j,j(E) =

V. J. Emery and S. A. Kivelson, Nature 374, 434

↑↑

(1995).

F_j

(E) + Σ^↓(E) det [F_jδ (E)]

[

P. Curty and H. Beck, Phys. Rev. Lett. 85, 796

det

1-F_jδ(E)(

U_jδ - Σ_jδ(E))

(2000).

G↓↓j+δ,j+δ(E) =

↓↓

D. Bormannt and H. Beck, J. Stat. Phys. 76, 361

F_j

(E) + Σ^↑(E) det [F_jδ(E)]

+δ,j+δ

[

(1994).

det

1-F_jδ(E)(

U_jδ - Σ_jδ(E))

(A.10)

P. Curty and H. Beck, Phys. Rev. Lett. 91, 257002

G↑↓j,j+δ(E) =

(2003).

↑↓

F_j

(E) + ΔΣ↑↓j,j+δ(E) det [F_jδ(E)]

,j+δ

I. I. Mazin, D. J. Singh, M. D. Johannes, and

det [1 - F_jδ (E)(ΔU_jδ - Σ_jδ(E))]

M. H. Du, Phys. Rev. Lett. 101, 057003 (2008).

G↓↑j+δ,j(E) =

↓↑

F. Wang, H. Zhai, Y. Ran, A. Vishwanath, and

F_j

(E) + ΔΣ↓↑j+δ,j (E) det [F_jδ(E)]

+δ,j

D. H. Lee, Phys. Rev. Lett. 102, 047005 (2009).

det [1 - F_jδ (E)(ΔU_jδ - Σ_jδ(E))]

10.

D. A. Wollman, D. J. Van Harlingen, W. C. Lee,

где

D. M. Ginsberg, and A. J. Leggett, Phys. Rev. Lett.

71, 2134 (1993).

ΔΣ↑↓j,j+δ(E) = ΔU↑↓j,j+δ - Σ↑↓j,j+δ(E),

ΔΣ↓↑j+δ,j (E) = ΔU↓↑j+δ,j - Σ↓↑j+δ,j (E),

11.

C. C. Tsuei and J. R. Irtley, Rev. Mod. Phys. 72, 969

(A.11)

(2000).

det [F_jδ (E)] = F^↑↑j,j(E)F↓↓j+δ,j+δ (E) -

-F↑↓j,j+δ(E)F↓↑j+δ,j(E);

12.

D. J. Scalapino, E. Loh, and J. E. Hirsch, Phys. Rev.

B 34, 8190(R) (1986).

det [1 - F_jδ(E)(ΔU_jδ - Σ_jδ(E))] =

13.

J. R. Schrieffer, Х. G. Wen, and S. С. Zhang, Phys.

= 1 + F^↑j,j(E)Σ^↑j,j(E)+

Rev. B 39, 11663 (1989).

+ F↓j+δ,j+δ(E)Σ↓j+δ,j+δ(E)-

14.

Ю. A. Изюмов, УФН 169, 225 (1999).

-F↑↓j,j+δ(E)ΔΣ↓↑j+δ,j(E)-

15.

D. J. Scalapino, Rev. Mod. Phys. 84, 1383 (2012).

-F↓↑j+δ,j(E)ΔΣ↑↓j,j+δ(E)+

(A.12)

+ det [F_jδ (E)] det [ΔU_jδ - Σ_jδ(E)],

16.

A. M. Hybertsen, E. Stechel, W. Foulkes, and

M. Schlüter, Phys. Rev. B 45, 10032 (1992).

det [ΔU_jδ - Σ_jδ(E)] =

= Σ^↑j,j(E)Σ↓j+δ,j+δ(E)-

17.

N. D. Mermin and H. Wagner, Phys. Rev. Lett. 17,

1136 (1966); P. C. Hohenberg, Phys. Rev. 158, 383

- ΔΣ↑↓j,j+δ(E)ΔΣ↓↑j+δ,j (E).

(1967); S. Coleman, Commun. Math. Phys. 31, 264

↓↑

(1973).

Легко убедиться, что ΔU^{↑↓j,j±δ}

= ΔU

j±δx,j

Σ^{↑↓j,j±δ}

(E)

= Σ^↓↑j±δ

(E). Как отмечалось выше,

18.

G. Su, A. Schadschneider, and J. Zittartz, Phys. Lett.

x,j

недиагональные матричные элементы эффективной

A 230, 99 (1997).

гриновской функции обладают таким же свойством.

19.

G. Su and M. Suzuki, Phys. Rev. B 58, 117 (1998).

Поэтому из (A.10) видно, что и недиагональные мат-

ричные элементы гриновской функции с флуктуи-

20.

V. L. Berezinskii, Zh. Eksp. Teor. Fiz. 59, 907 (1970);

рующим потенциалом обладают этим же свойством,

J. Kosterlitz and D. Thouless, J. Phys. C 6, 1181

(1973).

а детерминанты матриц (A.12) не зависят ни от ин-

дексов j, ни от их ближайших соседей δ.

21.

V. J. Emery and S. A. Kivelson, Phys. Rev. Lett. 74,

3253 (1995).

22.

D. Ariosa, H. Beck, and M. Capezzali, J. Phys. Chem.

ЛИТЕРАТУРА

Sol. 59, 1783 (1998).

1. T. Timusk and B. Statt, Rep. Progr. Phys. 62, 61

23.

Yu. A. Izyumov and Yu. N. Skryabin, Statistical

(1999).

Mechanics of Magnetically Ordered Systems, Sprin-

2. V. M. Loktev, R. M. Quick, and S. G. Sharapov,

ger-Verlag, New York (1988).

Phys. Rep. 349, 1 (2001).

24.

B. L. Gyorffy, J. B. Staunton, and G. M. Stocks, Phys.

3. М. В. Садовский, УФН 171, 539 (2001).

Rev. B 44, 5190 (1990).

306