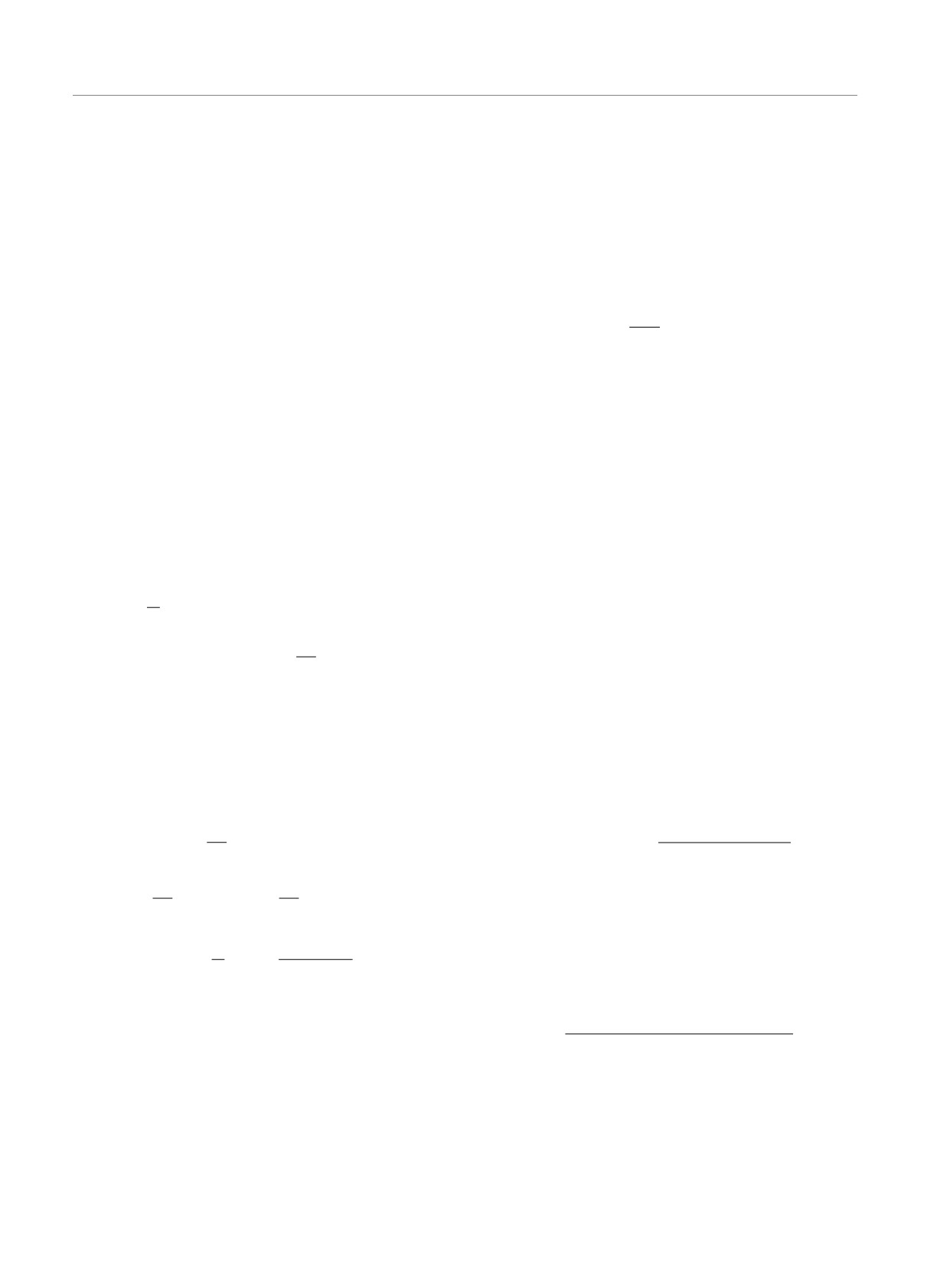ЖЭТФ, 2020, том 157, вып. 2, стр. 308-326

ИССЛЕДОВАНИЕ МАРГИНАЛЬНОГО ВЛИЯНИЯ ДЕФЕКТОВ

СТРУКТУРЫ НА НЕРАВНОВЕСНОЕ КРИТИЧЕСКОЕ

ПОВЕДЕНИЕ ДВУМЕРНОЙ МОДЕЛИ ИЗИНГА

В. В. Прудниковa*, П. В. Прудников^a, П. Н. Маляренко^a,b, Л. Н. Щур^b

^a Омский государственный университет им. Ф. М. Достоевского

644077, Омск, Россия

^b Институт теоретической физики им. Л. Д. Ландау Российской академии наук

142432, Черноголовка, Московская обл., Россия

Поступила в редакцию 1 августа 2019 г.,

после переработки 1 августа 2019 г.

Принята к публикации 12 августа 2019 г.

Осуществлено численное исследование методами Монте-Карло влияния различных начальных значений

намагниченности m0 и дефектов структуры на неравновесное критическое поведение двумерной моде-

ли Изинга. На основе анализа временной зависимости намагниченности, двухвременной зависимости

автокорреляционной функции и динамической восприимчивости выявлено проявление логарифмиче-

ских поправок и кроссоверных явлений перколяционного поведения на неравновесные характеристики

и критические индексы. Проведено исследование нарушений флуктуационно-диссипативной теоремы и

вычислены значения предельного флуктуационно-диссипативного отношения для случая высокотемпе-

ратурного начального состояния. Проведено исследование влияния различных начальных состояний на

значения предельного флуктуационно-диссипативного отношения. Показано, что неравновесная критиче-

ская динамика слабонеупорядоченных систем со спиновыми концентрациями p ≥ 0.9 относится к классу

универсальности неравновесного критического поведения чистой модели и характеризуется одинаковы-

ми критическими показателями и значениями предельного флуктуационно-диссипативного отношения,

а неравновесное критическое поведение систем с p ≤ 0.85 демонстрирует зависимость универсальных

характеристик неравновесного критического поведения от концентрации дефектов и нарушение динами-

ческого скейлинга, связанных с влиянием кроссоверных эффектов перколяционного поведения.

DOI: 10.31857/S0044451020020108

для которых выполняется следующий критерий:

2 - dν = α > 0, где d — пространственная размер-

1. ВВЕДЕНИЕ

ность системы, ν — критический индекс корреляци-

Разбиение систем, демонстрирующих фазовые

онной длины и α — критический индекс теплоемко-

переходы второго рода, на классы универсальности

сти для чистой системы. Критерий влияния точеч-

ных замороженных дефектов структуры на крити-

равновесного [1] и динамического [2] критического

поведения позволило придать теории фазовых пе-

ческое поведение выполняется только для систем,

описываемых трехмерной моделью Изинга, что на-

реходов и критических явлений необычную строй-

ность. Изучение критического поведения структур-

шло подтверждение в результатах как эксперимен-

тальных, так и теоретических ренормгрупповых и

но неупорядоченных магнитных систем со случай-

но распределенными немагнитными атомами приме-

численных исследований Монте-Карло [5-10]. Слу-

чай систем, критическое поведение которых описы-

си позволило расширить представление о факторах,

влияющих на систематизацию по классам универ-

вается двумерной моделью Изинга, является мар-

сальности [3]. Исследования показали [4], что при-

гинальным, так как критические индексы чистой

сутствие точечных замороженных дефектов струк-

модели ν = 1, α = 0. Теория критических явле-

туры изменяет критическое поведение тех систем,

ний предсказывает для маргинальных случаев появ-

ление логарифмических поправок в асимптотичес-

^* E-mail: prudnikv@univer.omsk.su

ком поведении термодинамических и корреляцион-

308

ЖЭТФ, том 157, вып. 2, 2020

Исследование маргинального влияния дефектов структуры.. .

ных функций при сохранении значений критических

со спиновой концентрацией p ≤ 0.85) динамический

индексов чистой модели. В работе [11] для слабо-

критический индекс z, определяющий температур-

неупорядоченной двумерной модели Изинга со слу-

ную зависимость времени релаксации, демонстриру-

чайными связями было аналитически показано, что

ет зависимость от концентрации дефектов с наруше-

теплоемкость и корреляционная длина вблизи кри-

нием стандартной формы динамического скейлинга

тической точки характеризуются следующими зави-

в виде z = A| ln(p - p_c)| + B. В связи с этим, ожи-

симостями:

дается весьма нетривиальным влияние дефектов на

характеристики неравновесного поведения двумер-

ξ ∝ |τ|-1 [1+g ln(1/|τ|)]1/2 , C_V ∝ ln|ln|τ||

(1)

ной модели Изинга.

В настоящее время поведение систем, характе-

с g = 4.8(1 - p)/p, где τ = (T - T_c)/T_c — приведен-

ризующихся аномально медленной динамикой, вы-

ная температура, а параметр p определяет спиновую

зывает большой интерес исследователей. Это обу-

концентрацию системы. В работах [12,13] для той же

словлено предсказываемыми и наблюдаемыми при

модели предсказывалось появление степенных лога-

медленной эволюции систем из неравновесного на-

рифмических поправок в температурном поведении

чального состояния свойствами старения и наруше-

магнитной восприимчивости

ниями флуктуационно-диссипативной теоремы [25].

Хорошо известными примерами подобных систем с

χ ∝ |τ|-7/4 ln7/8 |τ|.

(2)

медленной динамикой и эффектами старения явля-

Данные предсказания получили подтверждение в

ются такие сложные системы, как спиновые стек-

работах [14-17] при численных исследованиях ме-

ла [26]. Однако данные особенности неравновесного

тодами Монте-Карло.

поведения наблюдаются и в системах, испытываю-

Данная статья посвящена изучению критическо-

щих фазовые переходы второго рода [27,28], так как

го поведения двумерной модели Изинга с заморо-

критическая динамика таких систем характеризует-

женными дефектами структуры, для которой фа-

ся аномально большими временами релаксации.

зовая диаграмма содержит два устойчивых фокуса

Для описания неравновесных критических явле-

притяжения фазовых потоков: фиксированную точ-

ний наряду с аналитическими подходами широко

ку чистой модели Изинга и фиксированную точку

применяются численные методы, в частности, ме-

спиновой перколяции при спиновой концентрации

тоды статистического моделирования Монте-Карло

pcs) = 0.5927. Эта модель исследовалась численно

[28]. В данной работе планируется методами Мон-

в ряде работ [18-22]. Некоторые из авторов работ

те-Карло исследовать эффекты старения и нару-

[18, 19] утверждают, что статические критические

шения флуктуационно-диссипативной теоремы для

индексы β, γ, ν изменяются с изменением концен-

чистой и структурно неупорядоченной двумерной

трации дефектов, но при этом отношения β/ν, γ/ν

модели Изинга с эволюцией из различных началь-

остаются неизменными. Другие авторы [20-22] де-

ных состояний. Ставится цель выявить особенности

лают заключение, что влияние дефектов для сла-

влияния дефектов в широкой области изменения их

бонеупорядоченных систем приводит только к лога-

концентраций на неравновесную критическую дина-

рифмическим поправкам у характеристик критиче-

мику данной модели с выделением ее маргиналь-

ского поведения термодинамических и корреляци-

ных критических свойств. Отметим, что исследо-

онных функций чистой модели, в то время как в об-

вания неравновесной критической динамики мето-

ласти сильной неупорядоченности происходит уси-

дами Монте-Карло имеют целый ряд преимуществ

ление влияния логарифмической поправки в корре-

по сравнению со случаем их применения к описа-

ляционной длине

нию равновесного критического поведения, так как

временные характеристики дают гораздо более ши-

ξ ∝ |τ|-1 ln1/2 |τ|,

(3)

рокую базу данных для анализа асимптотических

свойств критического поведения, чем зависимость

и в других функциях, определяемых в критиче-

характеристик от температуры или линейного раз-

ской области их связью с корреляционной длиной, а

мера систем.

именно:

χ∝ξ7/4, M ∝ξ-1/8.

(4)

2. МОДЕЛЬ И МЕТОДЫ

В то же время, в работах [23,24] при исследова-

нии критической динамики модели было выявлено,

Гамильтониан ферромагнитной модели Изинга,

что вблизи порога спиновой перколяции (для систем

разбавленной немагнитными атомами примеси, с

309

В. В. Прудников, П. В. Прудников, П. Н. Маляренко, Л. Н. Щур

ЖЭТФ, том 157, вып. 2, 2020

учетом влияния внешнего магнитного поля h зада-

была использована методика, позволяющая рассчи-

ется выражением

тать функцию отклика без применения внешнего

∑

магнитного поля. Расчет обобщенной восприимчи-

H = -J p_ip_jS_iS_j - h p_iS_i,

(5)

вости осуществлялся в виде интегральной функции

〈i,j〉

отклика (термостатической восприимчивости):

где J > 0 характеризует короткодействующее об-

∫

менное взаимодействие между спинами S_i = ±1,

χ(t, t_w) = dt^′R(t, t^′) =

зафиксированными в узлах плоской квадратной ре-

шетки. Числа заполнения p_i вводятся как случай-

∑

ные числа, принимающие значения нуль или еди-

[〈p_iS_i(t)ΔS_i(t_w)〉] ,

(9)

T_cN

ница: p_i принимается равным единице, если в узле i

находится спин, и нуль в случае его отсутствия (маг-

где функция отклика R(t, t_w) задается соотноше-

нитный атом замещен немагнитным атомом приме-

нием (8), а функция ΔS_i(t_w) в (9) рассчитывается

си). Дефекты структуры распределялись в систе-

при моделировании состояний системы от начально-

ме каноническим образом в соответствии с функ-

го момента времени t = 0 до времени ожидания t_w

цией распределения P (p_i) = (1 - p)δ(p_i) + pδ(p_i), где

и определяется соотношением

p = 〈p_i〉 задает величину спиновой концентрации в

системе. Положение дефектов структуры фиксиро-

∑

валось для отдельной примесной конфигурации.

ΔS_i(t_w) =

[S_i(s) - S^Wi (s)],

(10)

В качестве характеристик неравновесного про-

s=0

цесса выступают такие величины, как намагничен-

где

⎛

⎞

ность

∑

∫

S^Wi (s) = th ⎝J p_jS_j/T⎠.

M (t) =

d^dx[〈S(x, t)〉] =

j=i

Для расчета характеристик неравновесного кри-

p_iS_i(t)

(6)

тического поведения было осуществлено компью-

s i=1

терное моделирование динамического процесса од-

носпиновых переворотов в рамках статистическо-

(N_s = pL² характеризует число спинов в решетке),

го метода Монте-Карло. Был реализован динамиче-

двухвременная корреляционная функция C(t, t_w) и

ский процесс односпиновых переворотов с примене-

линейная функция отклика R(t, t_w) на малое внеш-

нием алгоритма тепловой бани [33], задающего веро-

нее поле, примененное в момент времени t_w, которые

ятность перехода спина системы в новое состояние

могут быть определены соотношениями

S_i → S^′i посредством формулы

exp[-H(S^′i)/T ]

C_con(t, t_w) =

p_iS_i(t)S_i(t_w)

W_sp(S_i → S^′i) =

∑

(11)

s i=1

exp[-H(S_i)/T ]

∑

p_iS_i(t)

p_iS_i(t_w)

(7)

N_s

где суммирование по S_j в знаменателе проводится

i=1

s i=1

по всем возможным состояниям спина S_i до пере-

∫



δ[〈S(x, t)〉]

ворота. Для модели Изинга с двумя возможными



R (t, t_w) =

d^dx

(8)



δh(x, t_w)

состояниями S_j = ±1 указанную вероятность пере-

h=0

ворота можно записать в виде

где угловые скобки обозначают статистическое

усреднение по реализациям начального состояния,

exp(-H(S^′i)/T )

W_sp =

(12)

квадратные — усреднение по различным конфигу-

exp(H(S_i)/T) + exp(-H(S_i)/T)

рациям распределения дефектов в решетке.

Однако линейная функция отклика R(t, t_w), со-

с реализацией так называемой глауберовской дина-

ответствующая определению (8), не может быть

мики. В качестве единицы времени динамическо-

непосредственно измерена экспериментально или

го процесса выбирается шаг Монте-Карло на спин

получена методами компьютерного моделирования.

(MCS/s), который определяет N_s последовательных

В данной работе, по аналогии с работами [29-32],

переворотов спинов в узлах решетки.

310

ЖЭТФ, том 157, вып. 2, 2020

Исследование маргинального влияния дефектов структуры.. .

p = 0.9

p = 0.8

p = 0.7

^m0^{= 1.0}

0.9

0.8

0.6

0.5

0.4

0.3

0.2

0.1

0.05

0.02

0.01

0.1

100

1000

0.1

100

1000

0.1

100

1000

t, MCS/s

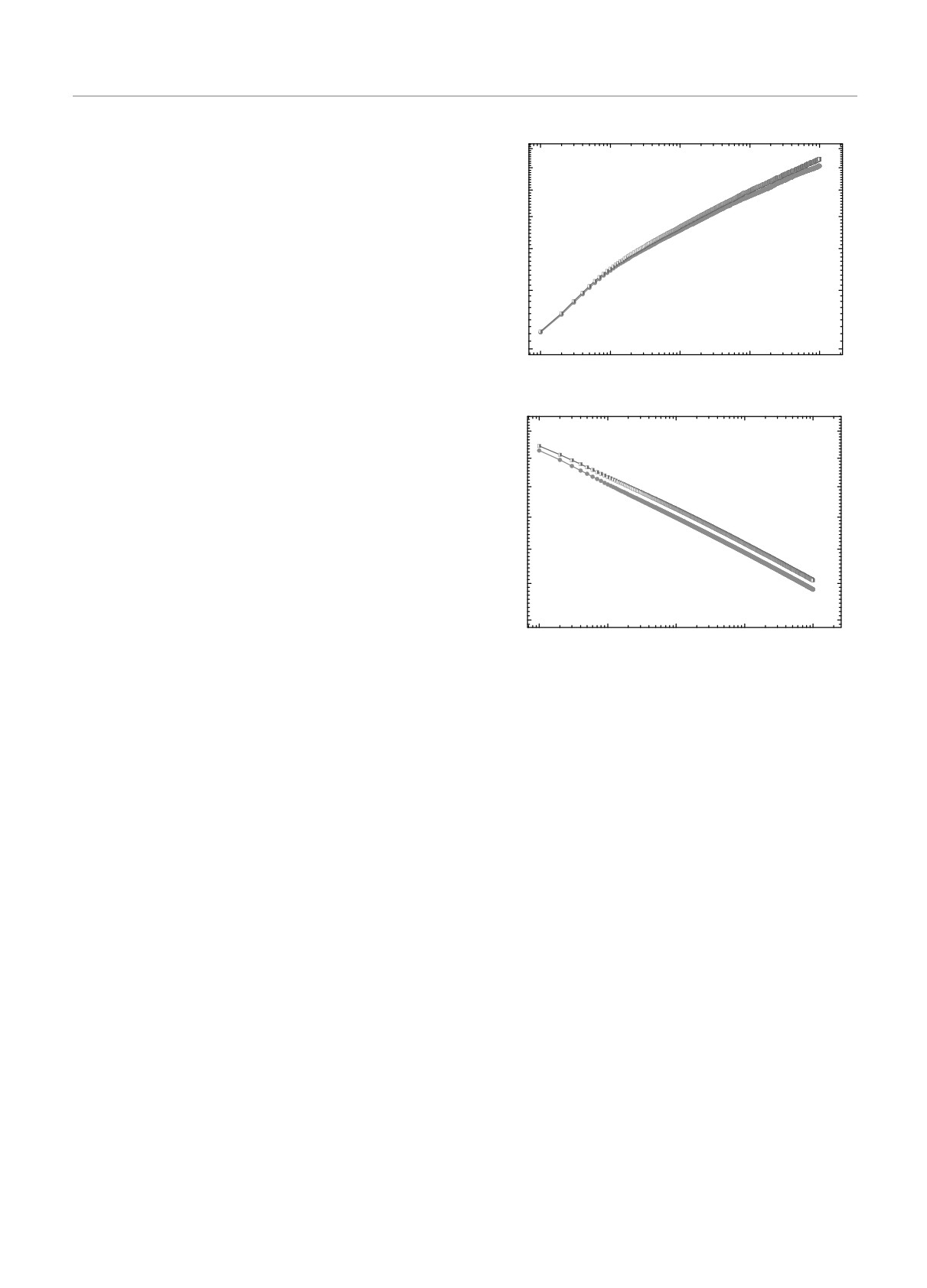
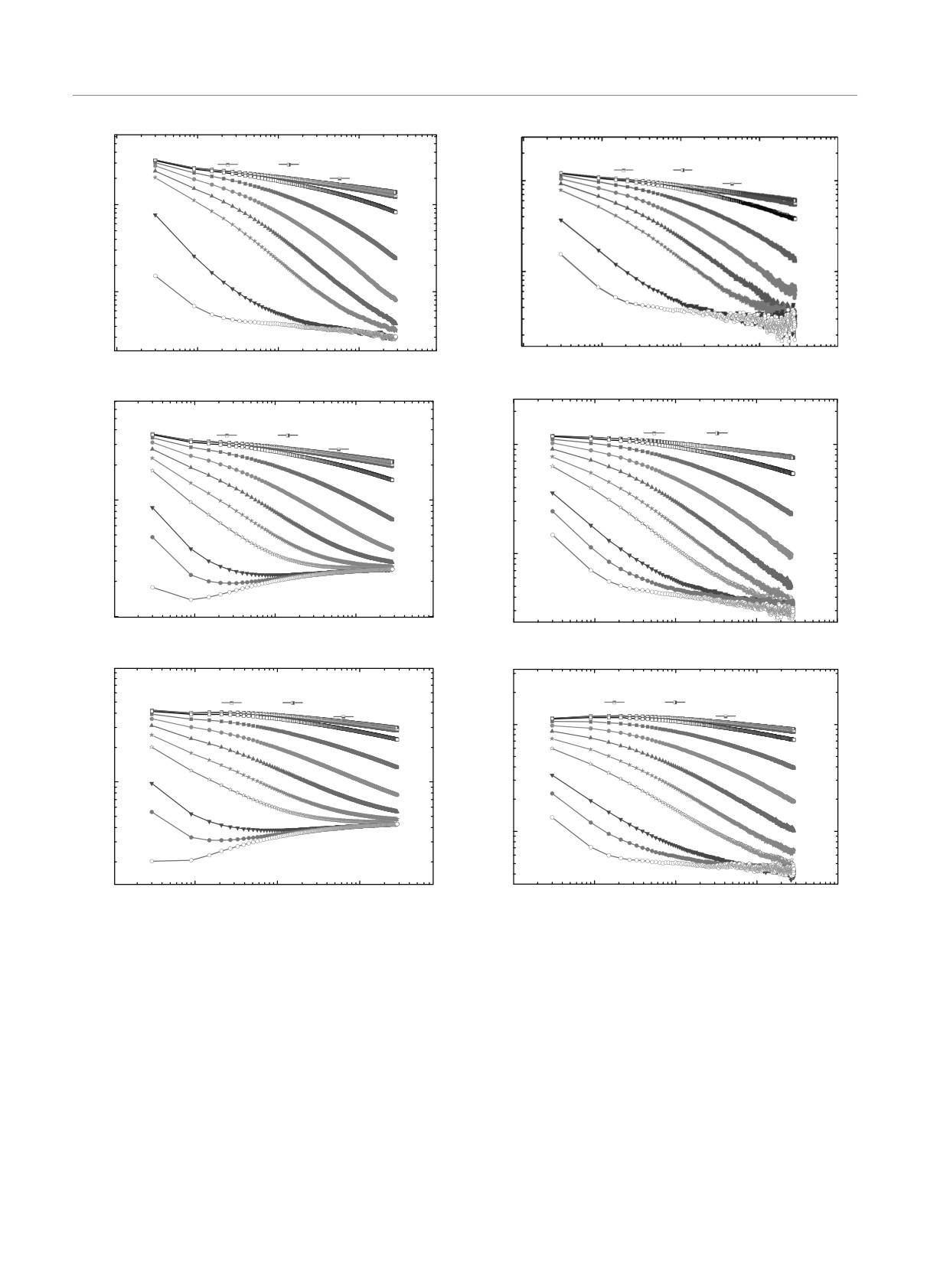
Рис. 1. Графики критической релаксации намагниченности M(t) для структурно неупорядоченной двумерной модели

Изинга с разными спиновыми концентрациями p с различными значениями начальной намагниченности m0

Моделирование проводилось на квадратной ре-

ченностью m₀, характеризуется в критической точ-

шетке с линейным размером L = 1024 в широ-

ке следующей скейлинговой зависимостью [28,35] —

ком интервале изменения спиновых концентраций

M (t, t_m) = A_mt^-β/zνF_m(t/t_m),

(13)

с p

= 1.0, 0.95, 0.9, 0.85, 0.8, 0.75,

0.7

при со-

ответствующих критических температурах T_c(p):

— с временным масштабом t_m = B_mm-k0, где по-

T_c(1.0) = 2.26918, T_c(0.95) = 2.08989(8), T_c(0.9) =

казатель k

= 1/(θ^′ + β/(zν)) > 0 и скейлинго-

= 1.9032(5), T_c(0.85) = 1.7098(4), T_c(0.8) = 1.5103(4),

вая функция F_m(t/t_m) = F_m(tmk0). Временная зави-

T_c(0.75) = 1.2980(10), T_c(0.7) = 1.0729(10) [22,34].

симость намагниченности M(t, t_m) на этапе нерав-

Системе задавался старт из различных началь-

новесной эволюции систем с m₀ ≪ 1 (высокотем-

ных состояний со значениями намагниченности в

пературное начальное состояние) определяется ха-

интервале от m₀ = 0.01 до m₀ = 1. Поведение систем

рактерным ростом, описываемым степенным зако-

исследовалось на временах до 10000 шагов Мон-

ном M(t) ≈ m₀tθ′, где θ^′ — показатель начальной

те-Карло на спин. При моделировании чистой систе-

эволюции системы, в то время как для начально-

мы с p = 1.0 проводилось статистическое усреднение

го низкотемпературного полностью упорядоченно-

по 15000 прогонок. При моделировании структур-

го состояния с m₀ = 1 убывающей степенной за-

но неупорядоченной модели Изинга усреднение вы-

висимостью M(t) ∝ t^-β/zν . Результаты моделиро-

числяемых величин проводилось по 2000 примесным

вания неравновесного критического поведения на-

конфигурациям и 15 прогонкам для каждой примес-

магниченности для различных начальных состоя-

ной конфигурации.

ний представлены на рис. 1 для спиновых концен-

траций p = 0.9, p = 0.8 и p = 0.7. Графики M(t)

наглядно демонстрируют существенные качествен-

ные и количественные различия в релаксации на-

3. МОДЕЛИРОВАНИЕ НЕРАВНОВЕСНОГО

магниченности из высокотемпературного начально-

КРИТИЧЕСКОГО ПОВЕДЕНИЯ

го состояния с m₀ ≪ 1, низкотемпературного пол-

НАМАГНИЧЕННОСТИ

ностью упорядоченного состояния с m₀ = 1 и про-

межуточных состояний с начальной намагниченно-

Неравновесное поведение намагниченности, ре-

стью 0.1 ≤ m₀ ≤ 0.9. Видно, что кривые релаксации

лаксирующей из начального состояния с намагни- для систем, стартовавших из начальных состояний

311

В. В. Прудников, П. В. Прудников, П. Н. Маляренко, Л. Н. Щур

ЖЭТФ, том 157, вып. 2, 2020

F_m

p = 0.9

p = 0.8

p = 0.7

0.1

0.01

10^-6

10^-3

10⁰

10³

10^-9

10^-6

10^-3

10⁰

10³

10^-10

10^-7

10^-4

10^-1

10²

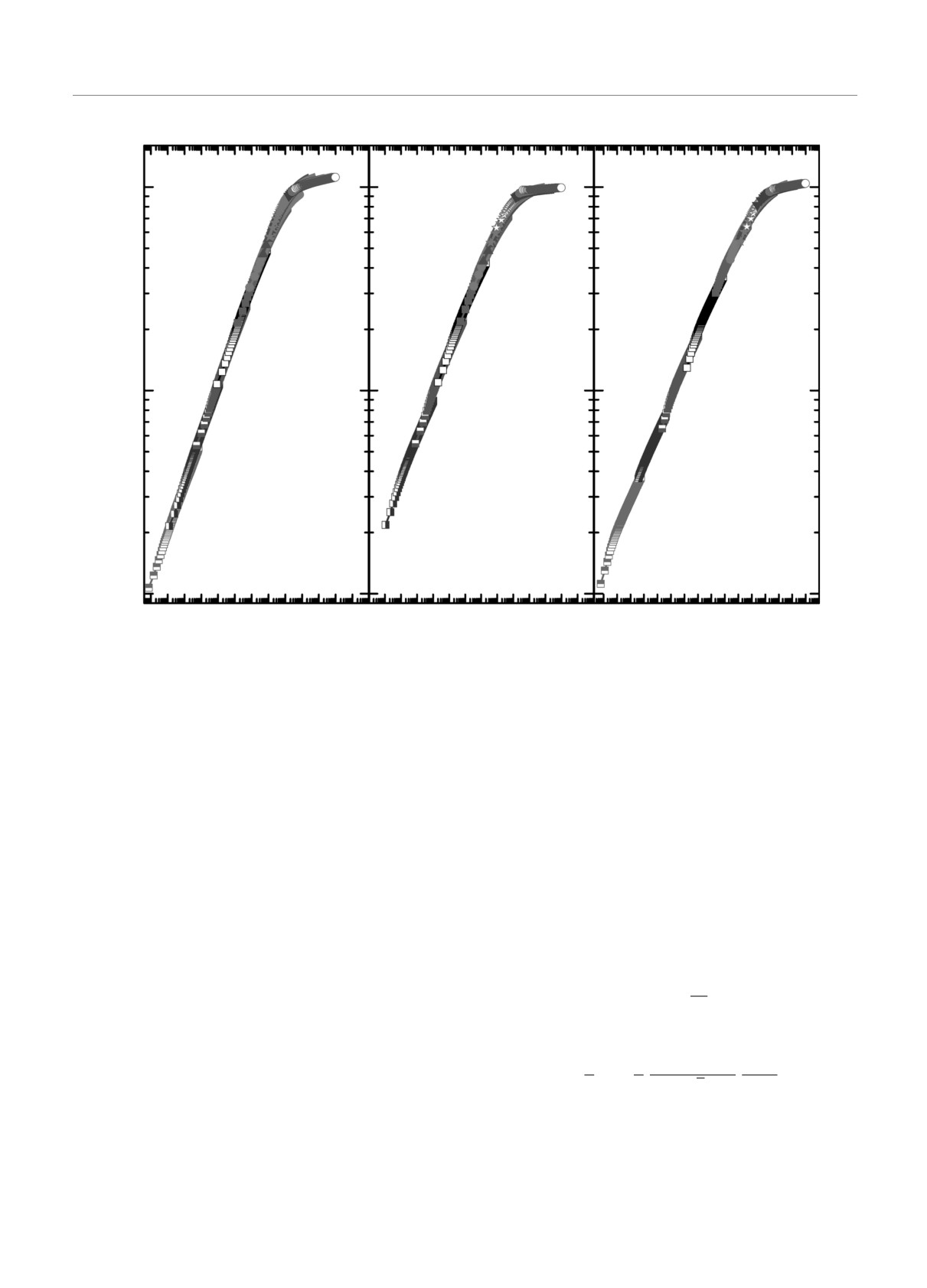
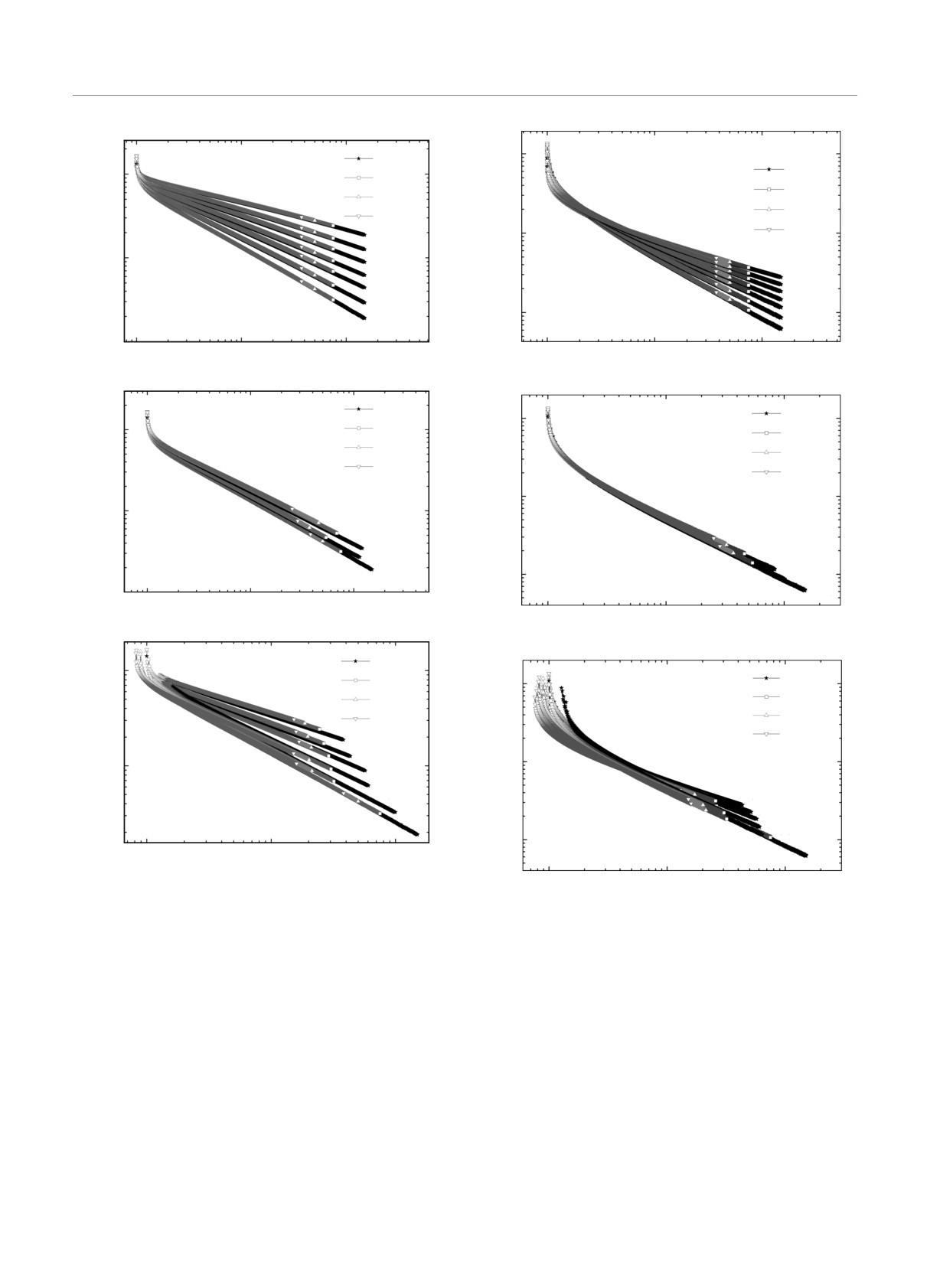
Рис. 2. Зависимость скейлинговой функции Fm(tm⁰) = t^β/zν M(t) от переменной x = tm⁰ для систем с разными спино-

выми концентрациями p

m₀ = 1, асимптотически стремятся к кривой релак-

m₀, на единой универсальной кривой с линейным

сации из низкотемпературного начального состоя-

начальным участком (в двойном логарифмическом

ния с m₀ = 1. В этом случае для систем с m₀ ≪

масштабе) с F_m(x) ∝ x1/k. Были получены следую-

≪ 1 характеристическое увеличение намагниченно-

щие значения показателя 1/k для двумерной модели

сти, описываемое степенной зависимостью с M(t) ≈

Изинга: 1/k = 0.248(3) для p = 0.9, 1/k = 0.216(2)

≈ m₀tθ′ с θ^′ = 0.190(3) для p = 0.9, θ^′ = 0.166(2)

для p = 0.8 и 1/k = 0.167(2) для p = 0.7.

для p = 0.8 и θ^′ = 0.128(3) для p = 0.7, на временах

Учтем во временной зависимости намагниченно-

t > t_cr = t_m ∼ m-k0 сменяется убывающей степенной

сти структурно неупорядоченной двумерной моде-

зависимостью M(t) ∝ t^-β/zν. При эволюции систе-

ли Изинга, релаксирующей из низкотемпературного

мы из начального низкотемпературного состояния

начального состояния с m₀ = 1, влияние логариф-

с m₀ = 1 временная зависимость намагниченности

мических поправок в следующей форме:

в критической точке сразу определяется степенной

(

)-β/2ν

зависимостью M(t) ∝ t^-β/zν со значениями показа-

M (t) ∝ t^-β/zν

ln t

(14)

zν

телей, зависящими от спиновой концентрации p.

На рис. 2 представлены результаты численной

где [11, 22]

проверки предсказания временной скейлинговой за-

1-p

висимости (13) для намагниченности M(t, t_m) как

g₀ =

√

π (1 +

2/π)²

функции на начальных значений намагниченности

m₀ для систем с p = 0.9, p = 0.8 и p = 0.7. Для

В долговременном режиме на временах t ≫ t_w ≫

скейлинговой функции F_m(x) от x = tmk0 наблюда-

≫ 1, а также для систем с более высокими концент-

ется «коллапс» данных, полученных для различных

рациями дефектов влияние дефектов может харак-

312

ЖЭТФ, том 157, вып. 2, 2020

Исследование маргинального влияния дефектов структуры.. .

теризоваться логарифмической поправкой следую-

щего вида:

M (t) ∝ t^-β/zν (ln t)-β/2ν .

(15)

0.95

m₀ = 1

0.90

В данных выражениях для намагниченности отно-

0.85

шение статических индексов β/ν можно считать не

p = 1.00

зависящим от концентрации дефектов и положить

0.80

0.95

равным значению β/ν = 1/8 для чистой модели.

0.90

0.75

0.85

Представленные на рис. 3a временные зависимо-

0.80

сти намагниченности M(t) при релаксации из на-

0.70

0.75

чального состояния с m₀ = 1 для систем с различ-

0.70

ными спиновыми концентрациями p демонстриру-

0.65

ют сильную зависимость от концентрации дефектов.

Если пренебречь влиянием логарифмических попра-

100

1000

вок и рассматривать временное изменение намагни-

t, MCS/s

ченности как M(t) ∝ t-β/z′ν , то получаемые эффек-

тивные значения динамического критического ин-

0.95

m₀ = 1

декса z^′(p) таковы: z^′(1.0) = 2.161(11), z^′(0.95) =

0.90

= 2.240(12), z^′(0.9) = 2.646(13), z^′(0.85) = 2.741(15),

z^′(0.8) = 3.085(19), z′(0.75) = 3.495(26), z′(0.7) =

0.85

p = 1.00

= 4.004(35). Отметим, что значение индекса z^′ для

0.80

0.95

чистой модели хорошо согласуется со значением

0.90

0.75

0.85

z(1.0) = 2.1665(12), определенным в работе [36].

0.80

Проведенный на рис. 3б учет влияния логариф-

0.70

0.75

мических поправок вида (14) на временное поведе-

0.70

ние намагниченности, представленное в виде

0.65

M (t)(1 + (g/zν) ln t)β/2ν ∝ t^-β/zν ,

100

1000

t, MCS/s

приводит к заметно другим значениям z(p):

z(0.95) = 2.161(12), z(0.9) = 2.424(15), z(0.85) =

1.05

= 2.491(16), z(0.8) = 2.724(18), z(0.75) = 2.992(23),

1.00

m₀ = 1

z(0.7) = 3.462(26). Учет влияния логарифмических

0.95

поправок вида (15), представленный как

0.90

0.85

M (t)(ln t)β/2ν ∝ t^-β/zν

0.80

p = 0.90

0.75

на рис. 3в, приводит к следующим значениям z(p):

0.85

0.70

0.80

z(0.95) = 1.912(11), z(0.9) = 2.158(13), z(0.85) =

0.75

= 2.293(15), z(0.8) = 2.508(17), z(0.75) = 2.774(21),

0.65

0.70

z(0.7) = 3.217(25).

0.60

Анализ полученных значений динамического

критического индекса z(p) с учетом логариф-

100

1000

10000

мических поправок к степенной зависимости

t, MCS/s

намагниченности приводит к пониманию, что лога-

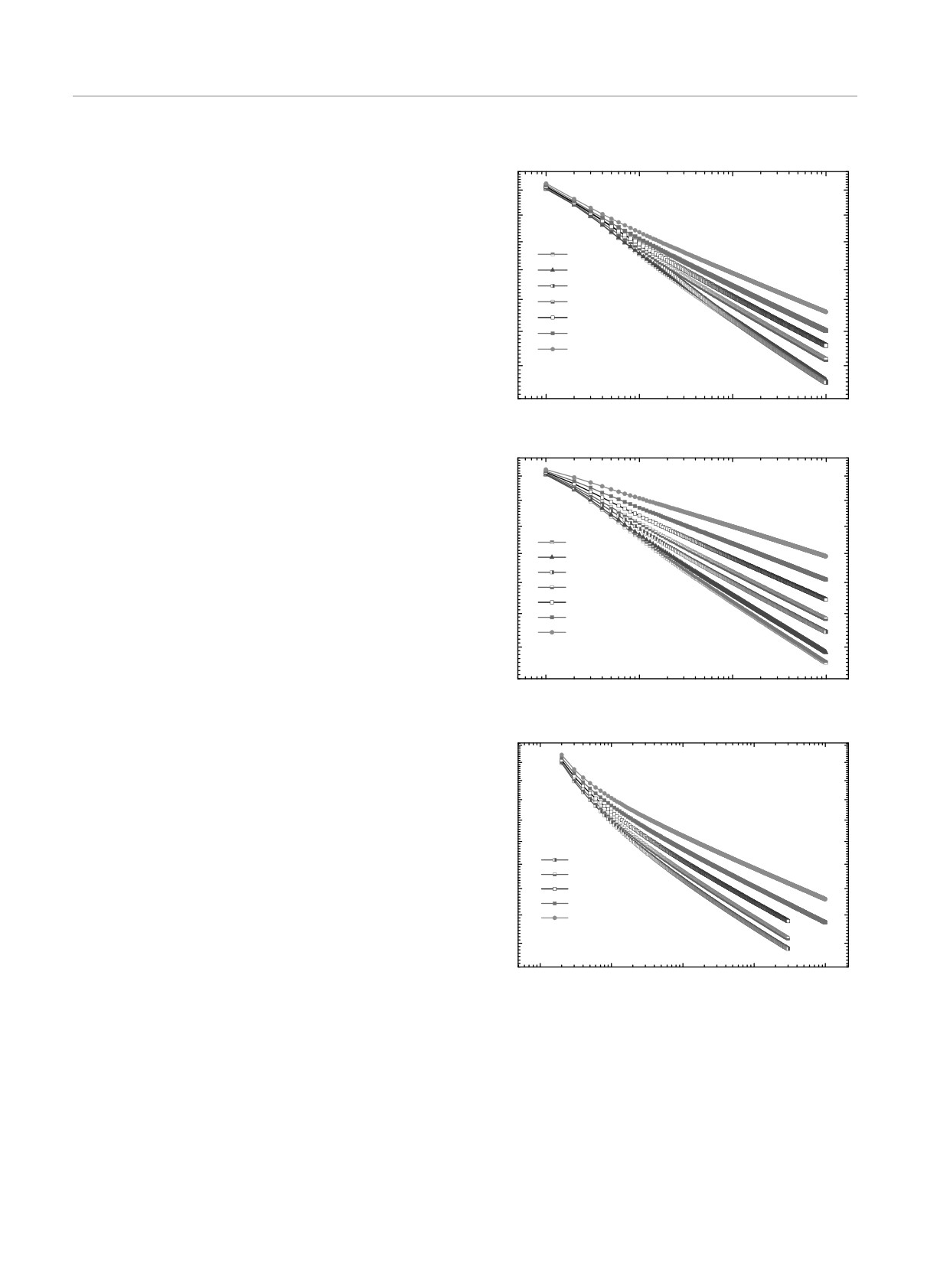
Рис.

Временная зависимость намагниченности M(t)

рифмические поправки вида (14) надо учитывать

при релаксации из начального состояния с m0 = 1 для

для слабонеупорядоченных систем со спиновыми

систем с различными спиновыми концентрациями p (а)

концентрациями p > 0.9, в то время как для си-

и с учетом влияния логарифмических поправок в виде

стем с p ≤ 0.9 надо учитывать логарифмические

M(t)(1 + (g/zν)lnt)β/2ν (б) и M(t)(ln t)β/2ν (в)

поправки вида (15). В результате мы выделяем

следующие значения динамического критического

индекса z(p): z(0.95) = 2.161(12), z(0.9) = 2.158(13),

313

В. В. Прудников, П. В. Прудников, П. Н. Маляренко, Л. Н. Щур

ЖЭТФ, том 157, вып. 2, 2020

0.19

0.18

3.0

0.17

0.16

2.5

0.15

0.14

0.13

2.0

0.8

1.0

1.2

1.4

1.6

1.8

2.0

2.2

0.12

0.8

1.0

1.2

1.4

1.6

1.8

2.0

2.2

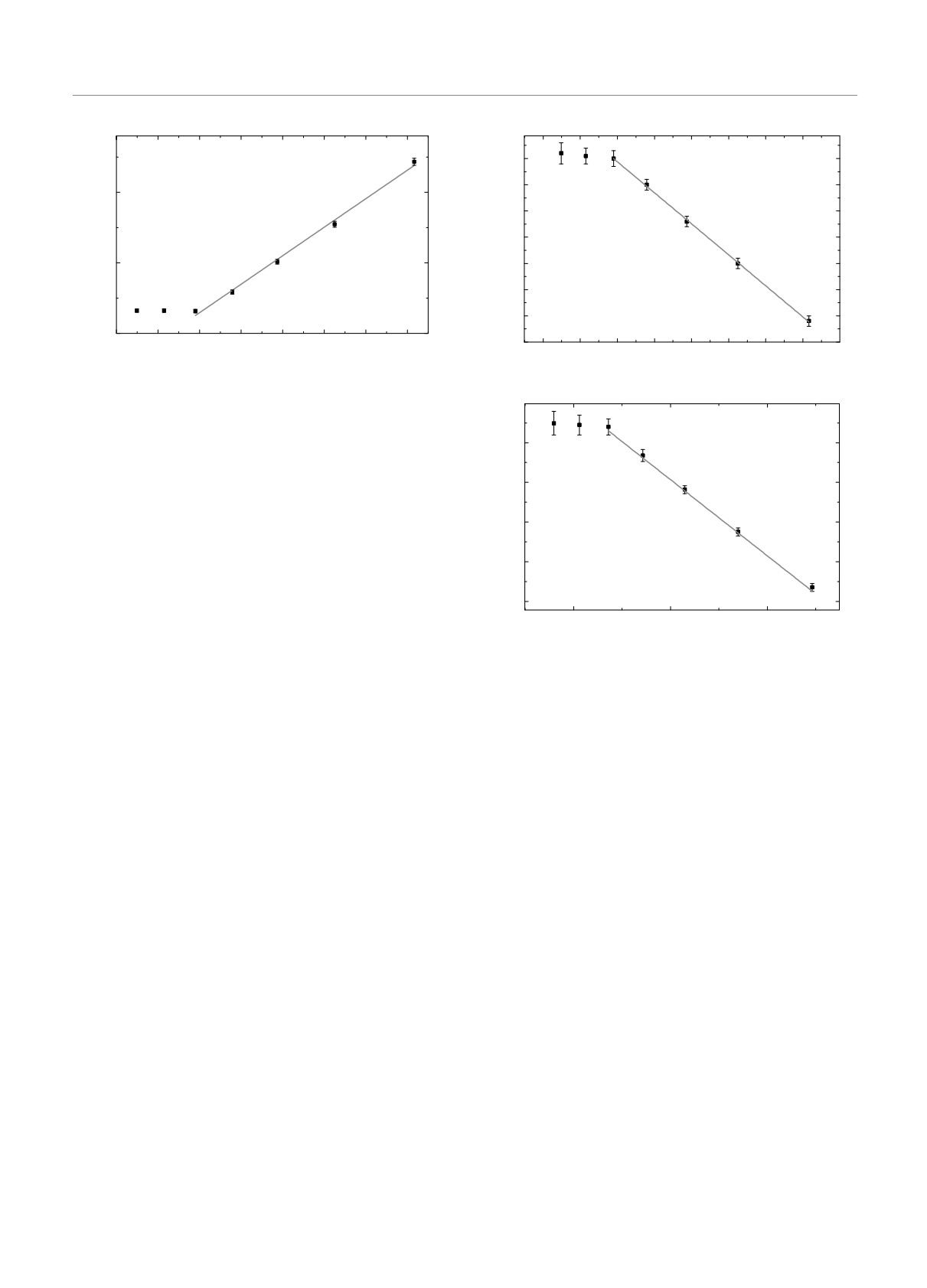
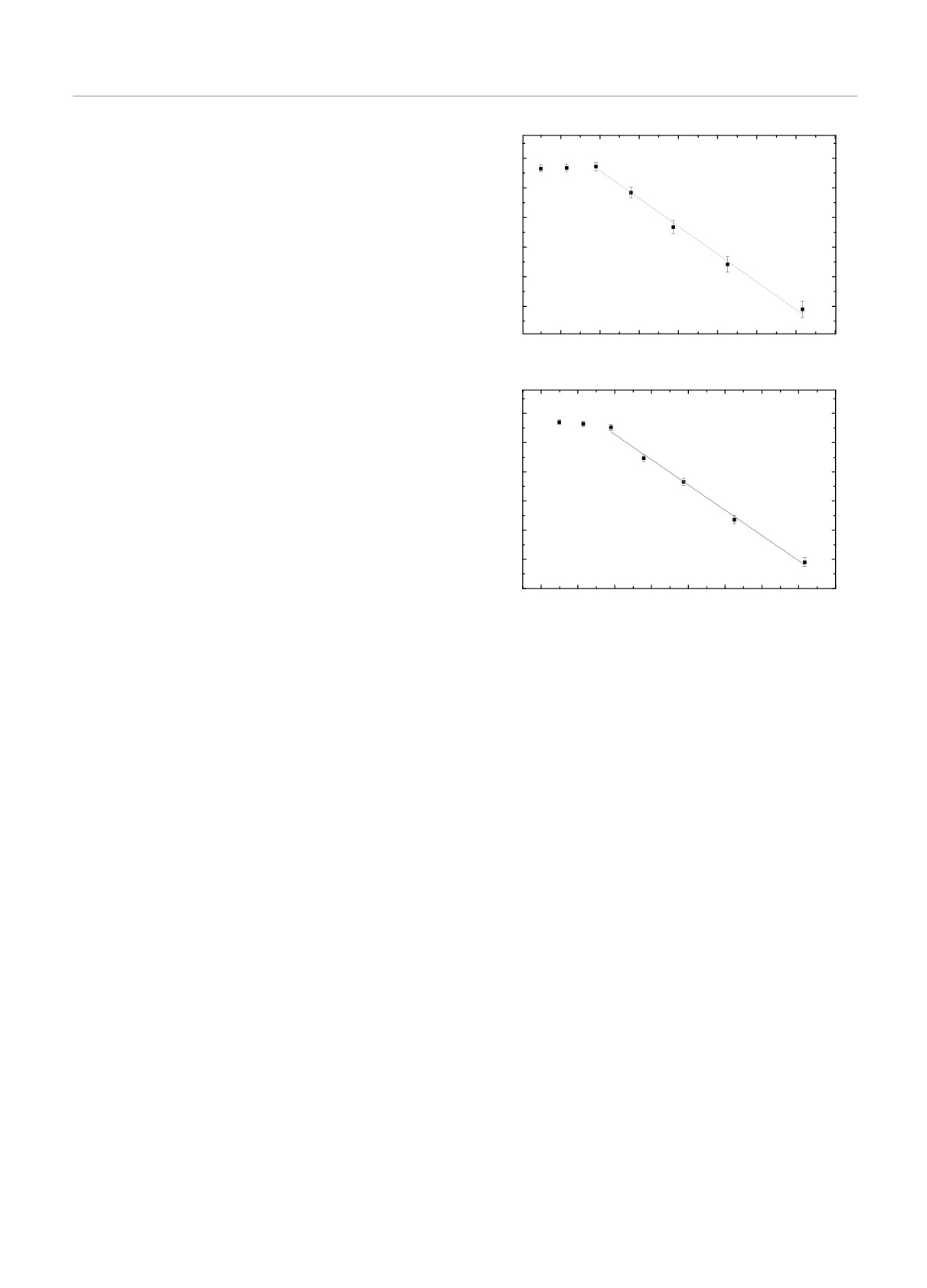
Рис. 4. Зависимость динамического критического индекса

1/k

z(p) от спиновой концентрации в логарифмическом мас-

штабе | ln(p - pc)|

0.24

0.22

z(0.85) = 2.293(15), z(0.8) = 2.508(17), z(0.75) =

= 2.774(21), z(0.7) = 3.217(25). Видно, что значения

0.20

показателей z(p) для систем со спиновыми концен-

трациями p = 0.95 и p = 0.9 в пределах погрешности

0.18

совпадают со значением z = 2.161(11) для чистой

системы. Данный результат подтверждает, что

0.16

значения динамического критического индекса

1.0

1.5

2.0

z(p) для слабонеупорядоченных систем с p ≥ 0.9

остаются постоянными и их критическая динамика

Рис. 5. Зависимость динамического критического показа-

принадлежит к классу универсальности чистой

теля начальной эволюции θ^′(p) (а) и показателя 1/k(p)

двумерной модели Изинга [23, 24]. В то же время

для скейлинговой функции Fm(tm⁰) (б) от спиновой кон-

для спиновых концентраций p < 0.85 зависимость

центрации p в логарифмическом масштабе | ln(p - pc)|

z(p), как видно из рис. 4, хорошо описывается

логарифмической зависимостью

чения z(p) приводит к модификации скейлинговой

z(p) = A| ln(p - p_c)| + B,

функции

F_m(t/t_m) = F_m(tmk0

характеризуемой нарушением стандартной формы

а следовательно, к изменению значений показате-

динамического скейлинга из-за влияния кроссовер-

ля k. Проведенный анализ показал, что зависимость

ных эффектов перколяционного поведения [23, 24].

показателя 1/k от спиновой концентрации также

Учет влияния логарифмических поправок вида

описывается логарифмической зависимостью

(14) и (15) на временное поведение намагниченности

при эволюции из высокотемпературного начального

1/k(p) = A^′′| ln(p - p_c)| + B^′′

состояния с m₀ ≪ 1 приводит также к логарифми-

ческой зависимости от спиновой концентрации по-

с A^′′ < 0, представленной на рис. 5б.

казателя начальной эволюции намагниченности

θ^′(p) = A^′| ln(p - p_c)| + B^′

4. ОСОБЕННОСТИ МОДЕЛИРОВАНИЯ

СИЛЬНОНЕУПОРЯДОЧЕННЫХ СИСТЕМ

с величиной A^′ < 0, представленной на рис. 5a.

Применение логарифмических поправок вида

Известно, что в термодинамическом пределе при

(14) и (15) к временному поведению намагниченно-

концентрации спинов в системе p > p_c существу-

сти при эволюции системы из различных начальных

ет только один перколяционный кластер, состоящий

состояний, характеризуемой выражением (13), при

из бесконечного числа узлов. Все остальные класте-

учете влияния логарифмических поправок на зна-

ры являются конечными и не вносят вклад в сред-

314

ЖЭТФ, том 157, вып. 2, 2020

Исследование маргинального влияния дефектов структуры.. .

ние значения термодинамических величин. В слу-

0.040

чае p < p_c в системе нет перколяционного класте-

0.035

m₀ = 0.01

ра и, следовательно, отсутствуют вклады в термо-

0.030

p = 0.7

динамические величины. Однако в системах конеч-

ных размеров малые кластеры могут вносить слу-

0.025

чайный шум в значения вычисляемых величин, уве-

0.020

личивая погрешность их вычислений. Для сильно-

неупорядоченных систем со спиновыми концентра-

0.015

циями, близкими к порогу спиновой перколяции, это

влияние усиливается. Таким образом, при модели-

ровании сильнонеупорядоченных систем можно уве-

личить точность вычислений, если рассматривать

0.010

100

1000

10000

для каждой примесной конфигурации только спи-

t, MCS/s

ны, принадлежащие перколяционному кластеру.

Мы провели исследование влияния неперколяци-

1.00

онных кластеров спинов на временное поведение на-

m₀ = 1

магниченности системы со спиновой концентрацией

0.95

p = 0.7

p = 0.7. Для идентификации кластеров был при-

0.90

менен алгоритм Хошена - Копельмана [37, 38]. По-

сле выращивания примесной конфигурации каждо-

0.85

му узлу решетки, занятому спином, ставится в со-

0.80

ответствие номер кластера, которому этот узел при-

надлежит. Среди всех кластеров системы выбирает-

0.75

ся перколяционный кластер, спины которого учиты-

ваются в процессе моделирования системы. Число

0.70

таких спинов для разных примесных конфигураций

100

1000

10000

может быть различным. С учетом этого, в выраже-

t, MCS/s

ниях (6), (7) усреднение проводится по числу спинов

Рис. 6. Сравнение неравновесных зависимостей намагни-

N_s в перколяционном кластере. Единицей измере-

ченности M(t) для m0 = 0.01 (а) и m0 = 1 (б) при учете

ния времени является шаг Монте-Карло на спин, ко-

всех спинов системы (1) и при учете только спинов перко-

торый соответствует возможности переворота всех

ляционного кластера (2)

спинов перколяционного кластера.

На рис. 6 приведены графики временных зави-

симостей намагниченности для m₀ = 0.01 и m₀ = 1,

показателя равны соответственно z = 3.461(19) и

вычисленных с учетом вкладов только спинов пер-

z = 4.001(29). Данные значения в пределах погреш-

коляционного кластера и при учете всех спинов сис-

ности совпадают со значениями, вычисленными при

темы. Из сравнения графиков видно, что для низ-

учете всех спинов системы.

котемпературного начального состояния с m₀ = 1

Таким образом, для сильнонеупорядоченных си-

влияние малых кластеров спинов более выражено

стем малые кластеры спинов действительно вносят

по сравнению со случаем высокотемпературного на-

случайный шум в характеристики системы, что уве-

чального состояния. Мы связываем данную особен-

личивает погрешность вычислений. В то же время,

ность начального состояния с m₀ = 1 с неравновес-

этот шум не оказывает существенного влияния на

ным изменением доменной структуры системы при

вычисленные значения критических показателей.

переходе от однодоменного состояния при T₀ = 0 к

многодоменной флуктуационной структуре, возни-

кающей при критической температуре T_c.

5. МОДЕЛИРОВАНИЕ НЕРАВНОВЕСНОГО

Критический индекс θ^′ для системы с p = 0.7,

КРИТИЧЕСКОГО ПОВЕДЕНИЯ

вычисленный при рассмотрении вклада перколяци-

АВТОКОРРЕЛЯЦИОННОЙ ФУНКЦИИ И

онного кластера спинов, принимает значение θ^′ =

ДИНАМИЧЕСКОЙ ВОСПРИИМЧИВОСТИ

= 0.131(2). Показатель z c учетом логарифмической

поправки в виде (15) равен z = 3.215(18). С учетом

На следующем этапе исследований был осу-

поправки в виде (14) и без учета поправок значения

ществлен расчет двухвременной зависимости

315

В. В. Прудников, П. В. Прудников, П. Н. Маляренко, Л. Н. Щур

ЖЭТФ, том 157, вып. 2, 2020

F_C

t_w = 20

m₀ = 0.01

t_w = 20

p = 0.70

0.1

0.75

0.1

0.80

0.85

p = 0.70

0.75

0.90

0.80

0.95

0.85

0.01

0.90

1.00

0.95

1.00

0.01

100

t/t

t/t_w

F_C

t_w

= 20

t_w = 20

m₀ = 0.01

0.1

p = 0.90

0.95

p = 0.90

1.00

0.95

0.01

1.00

0.01

100

t/t

100

F_C

t/t_w

m₀ = 0.01

t_w = 20

m₀ = 0.01

p = 0.70

0.75

0.1

0.80

0.85

0.90

p = 0.70

1.00

0.75

0.80

0.01

0.85

100

0.90

t/t_w

1.00

100

t/t_w

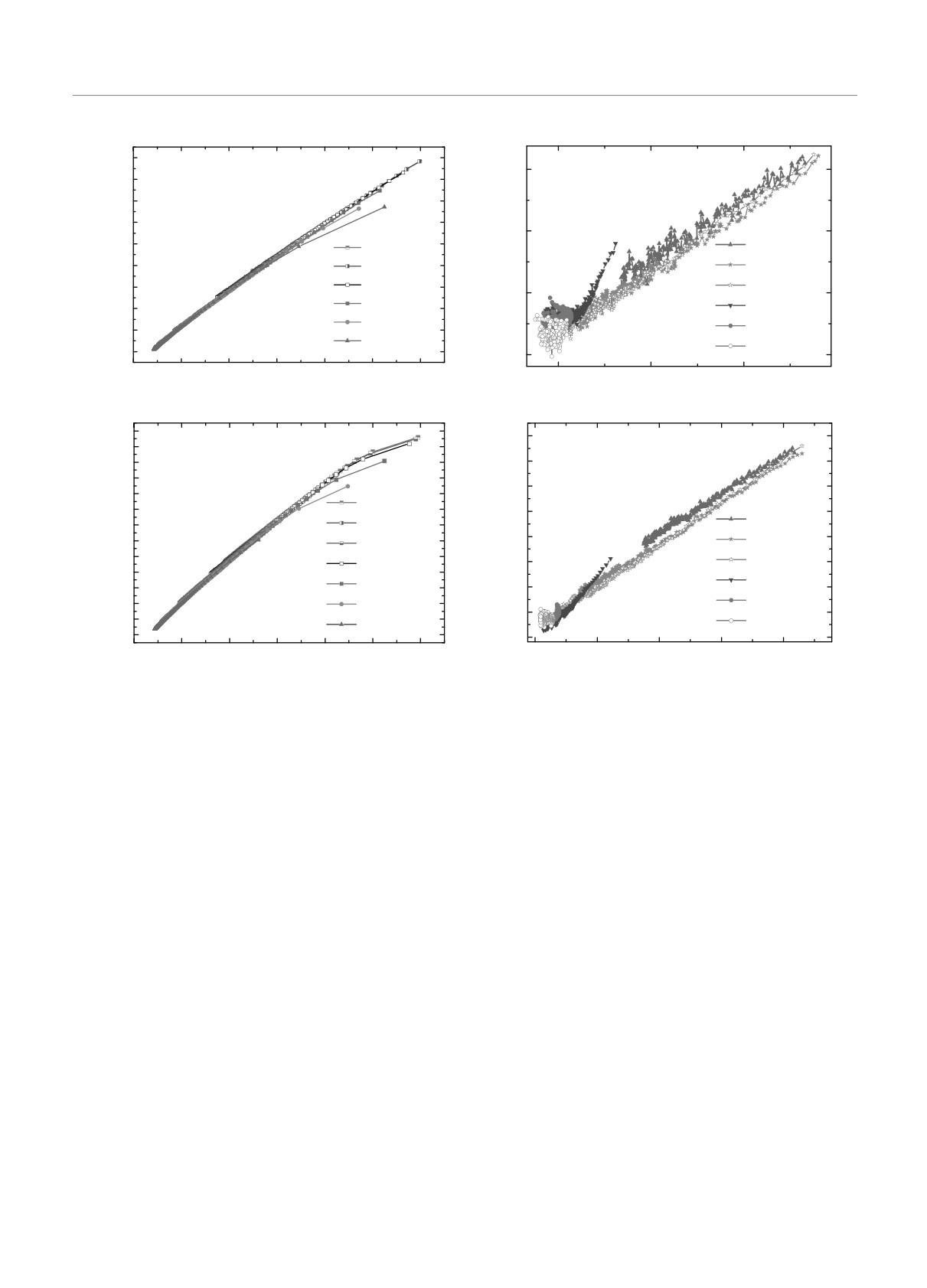
Рис. 7. Зависимости скейлинговых функций FC (t/tw) =

= twβ/(zν)C(t, tw) от t/tw (а) и с учетом логариф-

Рис. 8.

Зависимости скейлинговых функций Fχ(t/tw) =

мических поправок в виде FC(t(1 + (g/z)ln t)-zν/2/

= twβ/(zν)χ(t, tw) от t/tw (а) и с учетом логариф-

/(tw(1 + (g/z)ln tw)-zν/2)) для системы p = 0.95 (б) и в

мических поправок в виде Fχ(t(1 + (g/z)ln t)-zν/2/

виде FC(t(lnt)-zν/2/(tw(ln tw)-zν/2)) для систем с p ≤ 0.9

/(tw(1 + (g/z)ln tw)-zν/2)) для системы p = 0.95 (б) и в

(в) при эволюции из высокотемпературного начального со-

виде Fχ(t(lnt)-zν/2/(tw(ln tw)-zν/2)) для систем с p ≤ 0.9

стояния с намагниченностью m0 = 0.01

(в) при эволюции из высокотемпературного начального со-

стояния с намагниченностью m0 = 0.01

автокорреляционной функции C(t, t_w) (рис. 7) и

динамической восприимчивости χ(t, t_w) (рис. 8) как

m₀ = 0.01 ≪ 1 и низкотемпературного начального

интегральной характеристики функции отклика

состояния с m₀ = 1. Эффекты старения проявля-

при эволюции системы из высокотемпературно-

ются на временах t - t_w ∼ t_w и характеризуются

го начального состояния с намагниченностью

замедлением корреляции и релаксации системы

316

ЖЭТФ, том 157, вып. 2, 2020

Исследование маргинального влияния дефектов структуры.. .

с_а

с увеличением ее возраста — времени ожидания

t_w в соответствии с обобщенными скейлинговыми

0.75

формами [28]:

0.70

C(t, t_w) ∼ t-2β/zνw F_C (ξ(t)/ξ(t_w )),

0.65

(16)

χ(t, t_w) ∼ t-2β/zνw F_χ(ξ(t)/ξ(t_w )),

0.60

где F_C,χ — скейлинговые функции, зависящие от

0.55

корреляционных длин с учетом логарифмических

0.50

поправок (1) и (3) для структурно неупорядоченных

систем.

1.0

1.2

1.4

1.6

1.8

2.0

2.2

2.4

Для проверки реализации соотношений

(16)

были построены зависимости twβ/(zν)C(t, t_w),

twβ/(zν)χ(t, t_w) от t/t_w (при пренебрежении лога-

0.75

рифмическими поправками к корреляционным

длинам в системах с дефектами), показанные

0.70

на рис. 7a и рис.

8a при эволюции систем из

0.65

высокотемпературного начального состояния с

намагниченностью m₀

0.01. Представленные

0.60

графики демонстрируют коллапс полученных дан-

0.55

ных для различных t_w на универсальных кривых,

определяемых скейлинговыми функциями F_C,χ,

0.50

для каждой спиновой концентрации.

0.45

На долговременном этапе эволюции с t-t_w ≫ t_w

0.8

1.0

1.2

1.4

1.6

1.8

2.0

2.2

2.4

двухвременные зависимости скейлинговых функций

F_C,χ, согласно [28], характеризуются выражениями

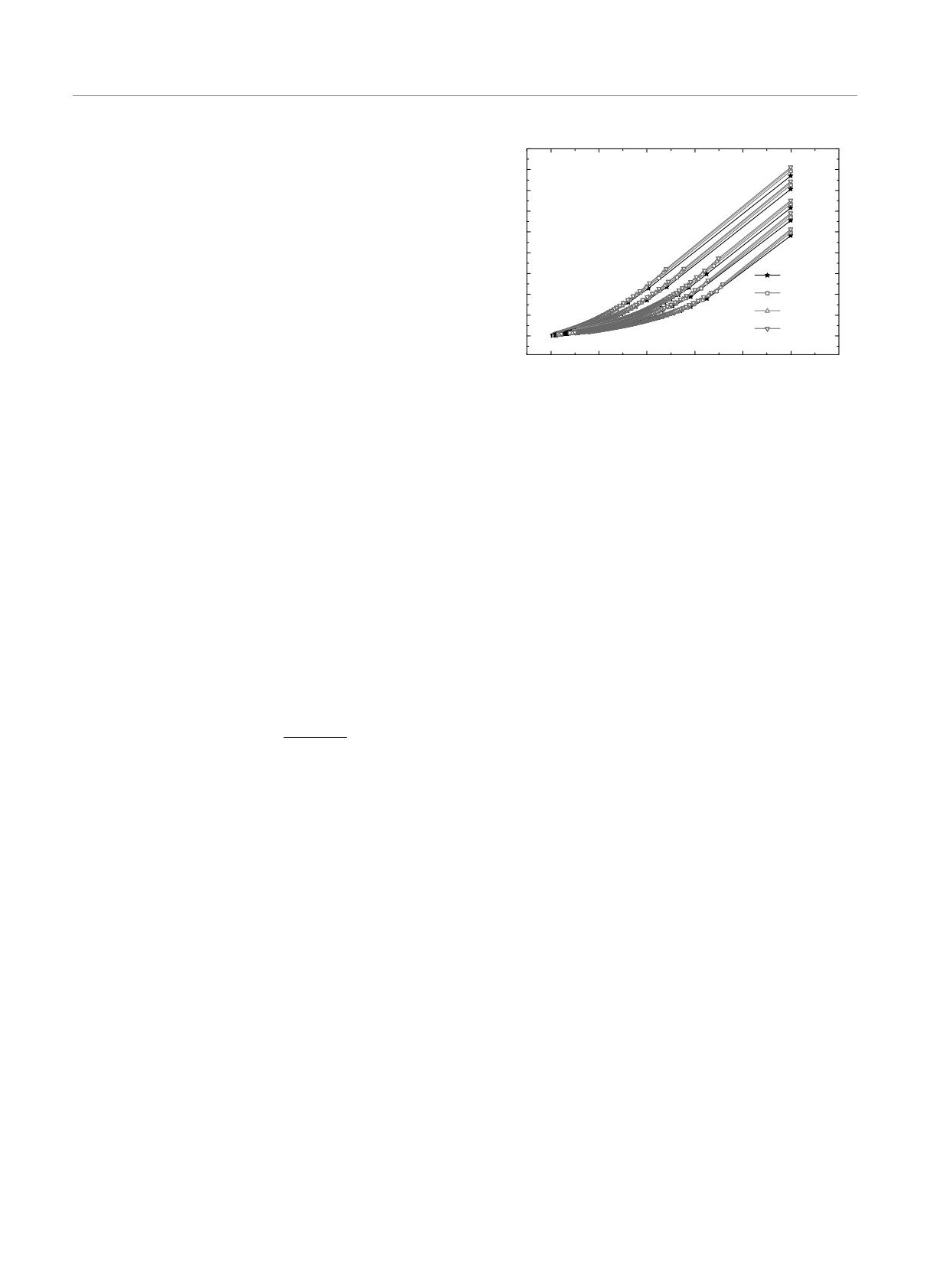
Рис. 9. Зависимости критических показателей ca,χ(p) для

автокорреляционной функции (а) и динамической воспри-

F_C(t/t_w) ∝ (t/t_w)-ca ,

имчивости (б), вычисленные с учетом логарифмических

(17)

F_χ(t/t_w) ∝ (t/t_w)-cχ

поправок от спиновой концентрации p, представленные в

логарифмическом масштабе | ln(p - pc)|

с показателями c_a,χ, связанными с критическими

индексами z, θ^′ соотношениями c_a,χ = d/z - θ^′, где

d = 2 — пространственная размерность системы. Из

временном интервале с t/tw ≫ 1 от переменных

асимптотического наклона изображающих кривых

t(1 + (g/z) ln t)-zν/2/(t_w(1 + (g/z) ln t_w)-zν/2) для

для скейлинговых функций F_C,χ на временном ин-

системы с p = 0.95 и от t ln-zν/2 t/(t_w ln-zν/2 t_w)

тервале с t/t_w ≫ 1 были определены значения по-

для систем с p ≤ 0.9. В результате были опре-

казателей c_a = 0.729(6) и c_χ = 0.735(4) для чистой

делены следующие значения показателей c_a,χ, а

модели Изинга, которые совпадают в пределах по-

именно, c_a(p): c_a(0.95) = 0.726(6), c_a(0.9) = 0.730(7),

грешностей расчета друг с другом, а также со зна-

c_a(0.85) = 0.681(9), c_a(0.8) = 0.627(11), c_a(0.75) =

чением c_a,χ = 0.733(4), вычисленным на основе зна-

0.557(13), c_a(0.7)

0.487(14); и c_χ(p):

чений критических индексов z = 2.161(11) и θ^′ =

c_χ(0.95) = 0.732(5), c_χ(0.9) = 0.726(5), c_χ(0.85) =

= 0.192(4).

= 0.673(6), c_χ(0.8) = 0.633(6), c_χ(0.75) = 0.568(7),

Для структурно неупорядоченной модели

c_χ(0.7)

= 0.495(8). Сопоставление данных зна-

Изинга в соотношениях

(16) для скейлинговых

чений показывает их хорошее согласие друг с

функций F_C,χ уже необходимо учитывать влия-

другом в пределах погрешности расчетов и со

ние логарифмических поправок к критическому

значениями c_a,χ(p), вычисленными с использо-

поведению корреляционной длины, которые в

ванием критических показателей z(p) и θ^′(p), а

той или иной мере должны привести к изме-

именно, c_a(0.95)

= 0.734(4), c_a(0.9)

= 0.736(4),

нению показателей c_a,χ в

(17). С учетом вида

c_a(0.85) = 0.692(4), ca(0.8) = 0.631(3), ca(0.75) =

логарифмических поправок показатели c_a,χ будем

= 0.571(3), c_a(0.7) = 0.493(3). Анализ показывает,

искать из асимптотического наклона изображаю-

что значения критических показателей c_a,χ(p),

щих кривых для скейлинговых функций F_C,χ на

вычисленные с учетом логарифмических поправок

317

В. В. Прудников, П. В. Прудников, П. Н. Маляренко, Л. Н. Щур

ЖЭТФ, том 157, вып. 2, 2020

T_c

для слабонеупорядоченных систем с p

≥ 0.9, в

0.9

пределах погрешности совпадают между собой

p=1.00

и с найденными для чистой модели значениями

0.8

0.90

m₀ = 0.01

c_a,χ(1.0) = 0.732(5) и в итоге критическая динамика

0.7

0.80

таких систем принадлежит к классу универсаль-

0.6

0.75

ности чистой двумерной модели Изинга [23, 24]. В

0.5

0.70

то же время для спиновых концентраций p < 0.85

0.4

зависимость c_a,χ(p), как видно на рис. 9, хорошо

0.3

t_w = 20

описывается логарифмической зависимостью

0.2

0.1

c_a,χ(p) = A_a,χ| ln(p - p_c)| + B_a,χ,

отражающей влияние кроссоверных эффектов пер-

0.2

0.4

0.6

0.8

1.0

коляционного поведения [23, 24]. Показатели c_a,χ,

вычисленные для системы с p = 0.7 c учетом вклада

Рис. 10. Параметрическая зависимость динамической вос-

перколяционного кластера спинов, принимают зна-

приимчивости Tcχ(t, tw) от автокорреляционной функции

чения c_a(0.7) = 0.485(12) и c_χ(0.7) = 0.494(7), кото-

C(t, tw) при эволюции систем с различными спиновыми

концентрациями p из высокотемпературного начального

рые хорошо согласуются с указанными выше значе-

состояния с m0 = 0.01

ниями и имеют меньшую погрешность.

значение предельного ФДО в пределах погрешности

6. ОПРЕДЕЛЕНИЕ

совпадает со значением для чистой модели, следо-

ФЛУКТУАЦИОННО-ДИССИПАТИВНОГО

вательно, эти системы относятся к одному классу

ОТНОШЕНИЯ ДЛЯ

ВЫСОКОТЕМПЕРАТУРНОГО

универсальности.

НАЧАЛЬНОГО СОСТОЯНИЯ

Для сильнонеупорядоченных систем предельное

значение ФДО начинает зависеть от концентрации

В данном разделе нами был проведен расчет

дефектов, что связано с влиянием кроссоверных

флуктуационно-диссипативного отношения (ФДО)

эффектов перколяционного поведения [23]. Расчет

в соответствии с соотношением [28]

предельных значений ФДО для структурно неупо-

рядоченной двумерной модели Изинга при эволю-

∂χ(t, t_w)

X (t_w) = lim

(18)

ции из низкотемпературного начального состояния

C→0

T_c ∂C(t, t_w)^,

с m₀ = 1 был представлен нами в работе [39], в ко-

с помощью которого можно определить предельное

торой были выявлены эффекты сверхстарения, при-

флуктуационно-диссипативное отношение X^∞

водящие к обращению значений предельного ФДО

= limtw →∞ X(tw).

X^∞LT в нуль, в то время как для чистой модели Изин-

На рис. 10 представлены графики параметри-

га X^∞LT = 0.751(24).

ческих зависимостей T_cχ(t, t_w) от C(t, t_w) для слу-

чая эволюции систем с различными спиновыми кон-

7. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ

центрациями p из высокотемпературного началь-

АВТОКОРРЕЛЯЦИОННОЙ ФУНКЦИИ И

ного состояния с m₀ = 0.01. Для получения пре-

ДИНАМИЧЕСКОЙ ВОСПРИИМЧИВОСТИ

дельного значения ФДО была проведена процедура

ПРИ ЭВОЛЮЦИИ ИЗ СОСТОЯНИЙ С

определения значений X(t_w) на основе соотношения

РАЗЛИЧНЫМИ ЗНАЧЕНИЯМИ

(18) для каждого значения времени ожидания t_w.

НАЧАЛЬНОЙ НАМАГНИЧЕННОСТИ

К полученным значениям X(t_w) была затем при-

менена линейная аппроксимация и экстраполяция

В данном разделе представлено исследование

X (t_w → ∞), которая и позволила определить ис-

двумерной структурно неупорядоченной модели

комые предельные значения ФДО (табл. 1). Найден-

Изинга, эволюционирующей из состояний с раз-

ное для чистой модели Изинга значение предельного

личными значениями начальной намагниченности

ФДО X^∞HT = 0.339(19) находится в очень хорошем

m₀ = 0.01, 0.02, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6,

согласии с результатом компьютерного моделирова-

0.8, 0.9, 1.0. Поведение систем исследовалось на

ния X^∞HT = 0.33(1), полученным в работе [32]. Для

временах до 10 000 шагов Монте-Карло на спин.

слабонеупорядоченных (p = 0.95 и p = 0.9) систем

При моделировании чистой системы с p

= 1.0

318

ЖЭТФ, том 157, вып. 2, 2020

Исследование маргинального влияния дефектов структуры.. .

Таблица 1. Значения флуктуационно-диссипативного отношения для различных спиновых концентраций p при

эволюции систем из высокотемпературного начального состояния с m0 = 0.01

p = 1.0

p = 0.95

p = 0.9

p = 0.85

p = 0.8

p = 0.75

p = 0.7

t_w

X(t-tw≫tw)_HT X(t-tw≫tw)_HT X(t-tw≫tw)_HT X(t-tw≫tw)_HT X(t-tw≫tw)_HT X(t-tw≫tw)_HT X(t-tw≫tw)_HT

0.347(19)

0.313(18)

0.264(17)

0.247(20)

0.216(21)

0.186(18)

0.166(17)

0.345(23)

0.322(20)

0.289(19)

0.265(22)

0.234(23)

0.190(19)

0.170(17)

0.343(26)

0.326(22)

0.297(23)

0.271(23)

0.241(25)

0.191(19)

0.172(18)

0.341(21)

0.327(21)

0.303(25)

0.275(26)

0.247(28)

0.192(21)

0.173(19)

∞

0.339(19)

0.332(19)

0.317(21)

0.283(21)

0.256(23)

0.194(19)

0.175(18)

X^∞HT

0.339(19)

0.332(19)

0.317(21)

0.283(21)

0.256(23)

0.194(19)

0.175(18)

проводилось статистическое усреднение по

15000

которое теперь демонстрирует временное убыва-

прогонок. При моделировании структурно неупоря-

ние в течение всего процесса эволюции системы.

доченной модели Изинга усреднение вычисляемых

Эффекты старения в поведении автокорреляци-

величин проводилось по 2000 примесным конфи-

онной функции и динамической восприимчивости

гурациям и 15 прогонкам для каждой примесной

наглядно проявляются (рис. 13, 14) через откло-

конфигурации.

нение зависимостей (1 + (g/z) ln t)-(zνca)/2 C(t, t/3),

Для выявления зависимости автокорреляцион-

(1 + (g/z)lnt)-(zνca)/2 χ(t, t/3) для системы с p =

ной функции и динамической восприимчивости от

= 0.95 и (lnt)-(zνca)/2 C(t, t/3), (lnt)-(zνca)/2 χ(t, t/3)

начальных значений намагниченности m₀ удобно

для p ≤ 0.9 от степенной (при постоянном значе-

в качестве времени ожидания выбрать величину,

нии t_w), имеющей вид прямой в двойном логариф-

пропорциональную времени наблюдения, например

мическом масштабе, и характеризуются замедлени-

t_w = t/3, тогда скейлинговые формы для данных

ем корреляции и релаксации системы с увеличением

функций примут вид [28]

ее «возраста» t_w. На представленных на рис. 13 и 14

C(t, t_w = t/3, t_m) = t-2β/zν G_C (tmk0),

графиках видно, что в поведении автокорреляцион-

(19)

ной функции эффекты старения проявляются силь-

χ(t, t_w = t/3, t_m) = t-2β/zν G_χ(tmk0),

нее, чем в поведении восприимчивости. Кроме того,

где G_C,χ(t/t_m) = G_C,χ(tmk0) — скейлинговые функ-

из анализа данных графиков можно сделать вывод,

ции.

что с ростом начального значения намагниченности

На рис. 11 и 12 представлены временные зави-

m₀ эффекты старения усиливаются.

симости автокорреляционной функции C(t, t_w, t_m) и

Для проверки осуществления скейлинговых

восприимчивости χ(t, t_w, t_m) для времен ожидания

соотношений

(19) были построены зависимости

t_w = t/3 и различных значений начальной намагни-

t2β/(zν)C(t, t/3) от x = tmk0. На рис. 15a видно, что

ченности для систем со спиновыми концентрациями

в случае чистой системы c p = 1.0 наблюдается

p = 1.0, p = 0.9, p = 0.8, p = 0.7. Наблюдаемый

коллапс данных для различных значений началь-

для структурно неупорядоченных систем c p = 0.9,

ной намагниченности m₀ на единой универсальной

p = 0.8, p = 0.7 нефизический рост автокорреляци-

кривой.

онных функций при эволюции из низкотемператур-

Однако временное поведение автокорреляци-

ного начального состояния с m₀ = 1 объясняется

онной функции для структурно неупорядоченных

необходимостью учета логарифмических поправок.

систем, представленное на рис. 15б,в, демонстри-

Введение временных логарифмических поправок

рует нарушение скейлингового соотношения (19),

в виде зависимости (1 + (g/z)lnt)-(zνca)/2 C(t, t/3)

что связано с существенным влиянием дефектов

от времени наблюдения t для системы с p = 0.95 и

структуры на корреляционные свойства систе-

(ln t)-(zνca)/2 C(t, t/3) от t для p ≤ 0.9 (c_a = 2/z-θ^′ —

мы на неравновесном этапе ее эволюции при

показатель убывания автокорреляционной функ-

старте из низкотемпературных начальных состоя-

ции) позволяет устранить такое нефизическое по-

ний с m₀

= 0 [39]. Представление зависимости

ведение автокорреляционной функции (рис.

13),

C(t, tw = t1/μ, tm)t2β/(μzν) от x = tμmk0 позволяет

319

В. В. Прудников, П. В. Прудников, П. Н. Маляренко, Л. Н. Щур

ЖЭТФ, том 157, вып. 2, 2020

p = 1.0

0.01

m₀ = 0.02

0.01

m₀

= 0.02

0.5

0.05

0.1

0.4

0.05

0.5

0.1

0.8

0.1

1.0

0.2

0.01

1.0

0.01

0.3

0.4

100

1000

100

1000

t, MCS/s

p = 0.9

0.01

m₀ = 0.02

0.01

m₀ = 0.02

0.1

0.05

0.5

0.1

0.6

0.1

0.8

0.1

0.8

0.9

0.2

0.9

1.0

0.3

0.01

0.3

0.4

1.0

0.4

0.01

100

1000

100

1000

10000

t, MCS/s

p = 0.8

0.01

m₀ = 0.02

0.01

m₀ = 0.02

0.05

0.1

0.5

0.1

0.5

0.1

0.6

0.2

0.8

0.1

0.8

0.3

0.9

0.3

0.9

0.4

1.0

0.01

0.4

1.0

100

1000

100

1000

10000

t, MCS/s

Рис. 11. Неравновесные зависимости автокорреляционной

Рис. 12. Неравновесные зависимости динамической вос-

функции C(t, t/3) от времени наблюдения t для систем с

приимчивости Tχ(t,t/3) от времени наблюдения t для си-

разными спиновыми концентрациями p при эволюции из

стем с разными спиновыми концентрациями p при эволю-

различных начальных состояний с 0.01 ≤ m0 ≤ 1.0

ции из различных начальных состояний с 0.01 ≤ m0 ≤ 1.0

при значениях показателя сверхстарения μ, рав-

кривых при значениях начальной намагничен-

ных μ(p = 0.95) = 6.10(5), μ(p = 0.9) = 6.25(5),

ности 0.5 ≤ m0 ≤ 1 и распределение данных в

μ(p

= 0.85)

= 6.50(5), μ(p

= 0.8)

= 6.75(5),

виде параллельно расположенных графиков для

μ(p = 0.75) = 7.05(5), μ(p = 0.7) = 7.50(5), получить

0.01 ≤ m₀ ≤ 0.4 (рис. 16). Это указывает на то,

совпадение данных для скейлинговой функции

что в структурно неупорядоченных системах для

GC (t^μm⁰) на соответствующих универсальных

автокорреляционной функции реализуется более

320

ЖЭТФ, том 157, вып. 2, 2020

Исследование маргинального влияния дефектов структуры.. .

p = 0.95

0.01

m₀

= 0.02

0.1

0.4

0.1

0.5

m₀ = 0.01

0.1

0.8

0.1

0.2

1.0

0.01

0.2

0.01

0.3

1.0

0.4

100

1000

10000

100

1000

10000

t, MCS/s

p = 0.9

0.1

p = 0.9

0.5

0.6

m₀ = 0.01

0.5

m₀ = 0.01

0.8

0.6

0.02

0.9

0.1

0.05

0.8

1.0

0.01

0.1

0.9

0.2

0.1

1.0

0.2

0.3

0.01

0.001

0.3

0.4

100

1000

10000

100

1000

10000

t, MCS/s

0.1

p = 0.8

m₀ = 0.01

0.6

0.5

0.02

m₀ = 0.01

0.8

0.05

0.6

0.02

0.9

0.05

1.0

0.1

0.8

0.01

0.2

0.9

0.1

0.3

0.2

0.4

1.0

0.5

0.3

0.001

0.4

0.01

100

1000

10000

100

1000

10000

t, MCS/s

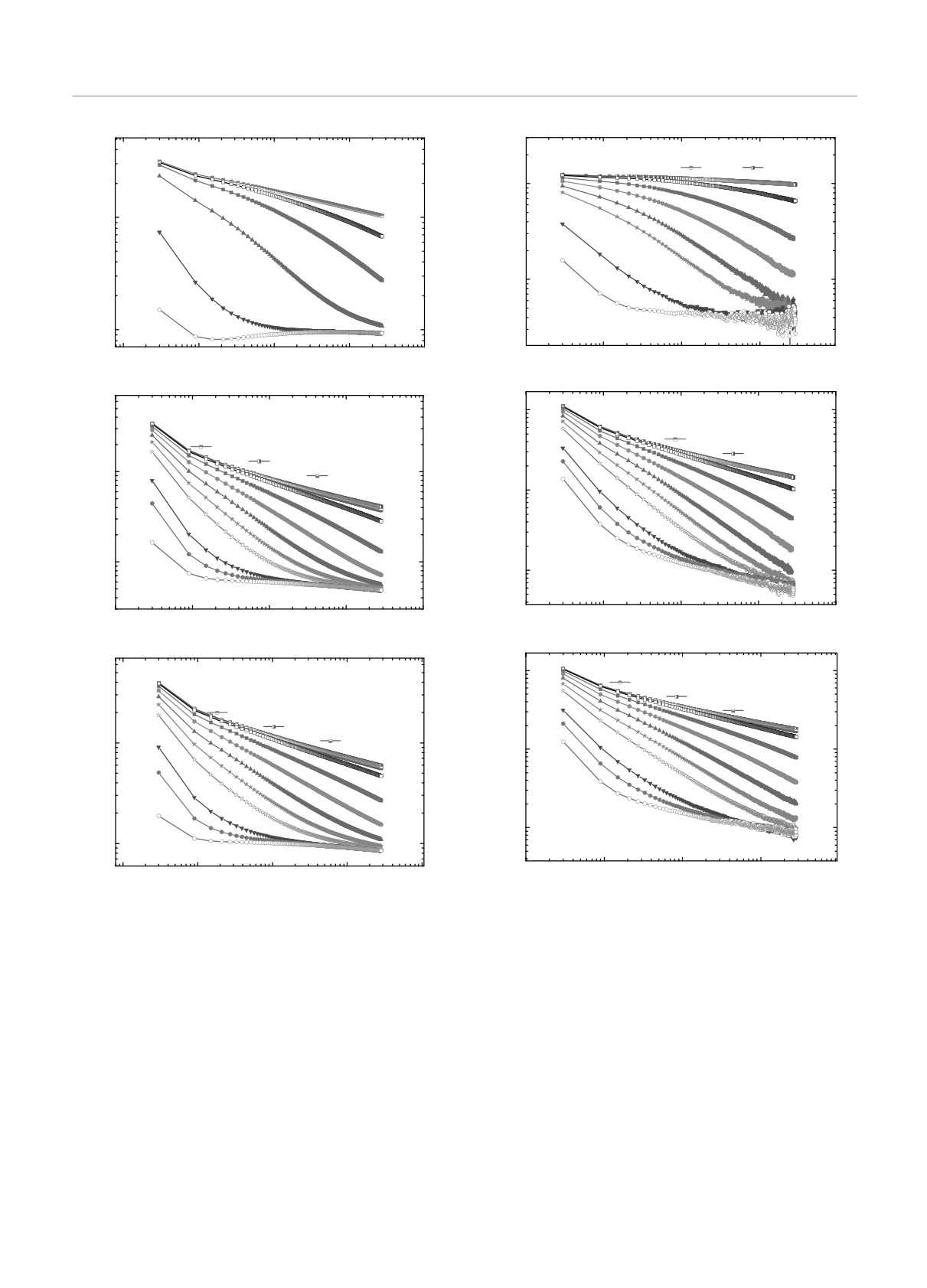
Рис.

14.

Неравновесные

зависимости

Рис.

13.

Неравновесные

зависимости

(1 + (g/z)ln t)-(zνca)/2 Tχ(t,t/3) для системы со спино-

(1 + (g/z) lnt)-(zνca)/2 C(t, t/3) для

системы со спи-

вой концентрацией p = 0.95 (а) и (ln t)-(zνca)/2 T χ(t, t/3)

новой концентрацией p = 0.95 (а) и (ln t)-(zνca)/2 C(t, t/3)

для систем с p = 0.9 (б) и p = 0.8 (в), демонстрирующие

влияние логарифмических поправок в поведении дина-

влияние логарифмических поправок в поведении авто-

мической восприимчивости при эволюции из различных

корреляционной функции при эволюции из различных

начальных состояний с 0.01 ≤ m0 ≤ 1.0

Таким образом, поведение автокорреляционной

сложная скейлинговая зависимость вида

функции для систем, релаксирующих из начальных

состояний с различными значениями начальной

C(t, t_w = t1/μ, t_m) = t-2β/μzν G_C (t^μmk0).

(20)

намагниченности m₀, характеризуется принад-

321

ЖЭТФ, вып. 2

В. В. Прудников, П. В. Прудников, П. Н. Маляренко, Л. Н. Щур

ЖЭТФ, том 157, вып. 2, 2020

p = 1.0

m₀ = 0.01

p = 0.9

m₀

= 0.01

0.02

0.05

0.1

0.2

0.3

0.4

0.5

0.8

0.6

0.9

= 6.25

0.8

0.01

1.0

0.01

0.9

1.0

10^-6

10^-3

10⁰

10³

10^-11

10^-5

10¹

10⁷

10¹³

10¹⁹

10²⁵

p = 0.9

m₀

= 0.01

m₀ = 0.01

0.02

p = 0.8

0.05

0.02

0.1

0.05

0.2

0.1

0.3

0.1

0.2

0.4

0.3

0.5

0.4

0.6

0.5

= 6.75

0.01

0.8

0.6

0.9

0.8

1.0

0.9

1.0

10^-7

10^-4

10^-1

10²

0.01

10^-12

10^-6

10⁰

10⁶

10¹²

10¹⁸

10²⁴

p = 0.8

m₀

= 0.01

0.02

m₀ = 0.01

p = 0.7

0.05

0.1

0.02

0.2

0.05

0.3

0.1

0.4

0.2

0.1

= 7.50

0.5

0.3

0.6

0.4

0.8

0.5

0.9

0.6

1.0

0.8

0.9

10^-8

10^-5

10^-2

10¹

1.0

0.01

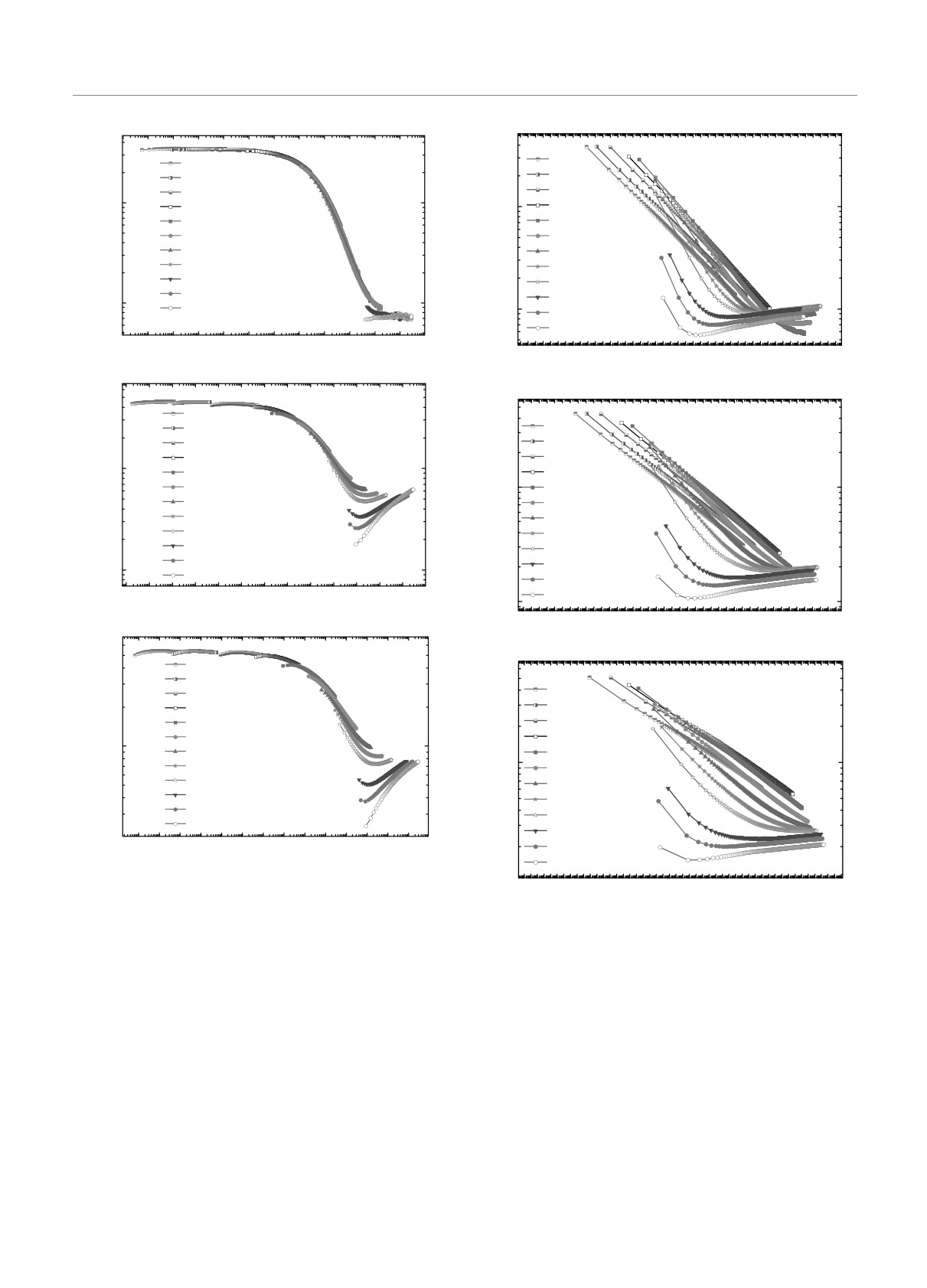
Рис. 15.

Скейлинговые зависимости t2β/(zν)C(t, t/3) от

10^-12

10^-6

10⁰

10⁶

10¹²

10²⁴

10³⁰

x = tmk0 для систем с разной концентрацией спинов p

Рис.

16. Эффекты сверхстарения, наблюдаемые в

зависимости скейлинговой функции GC (t^μm⁰)

лежностью к двум подклассам универсального

= C(t,tw = t1/μ,tm)t2β/(zν) от переменной x = t^μm⁰, с

μ = 6.25 для системы с концентрацией спинов p = 0.9 (а),

неравновесного критического поведения. Один

μ = 6.75 для p = 0.8 (б) и μ = 7.50 для p = 0.7

из них соответствует типу низкотемпературно-

го начального состояния, включающего в себя

состояния с 0.5 ≤ m₀ ≤ 1. В этом случае скейлин-

говая временная зависимость автокорреляционной

c μ > 1. Другой подкласс универсального нерав-

функции для чистой модели Изинга описывается

новесного критического поведения соответствует

соотношениями теории канонического старения c

типу высокотемпературного начального состояния,

μ = 1, а для структурно неупорядоченной модели

включающего в себя состояния с m₀ < 0.4. В этом

Изинга

— соотношениями теории сверхстарения

случае автокорреляционная функция описывается

322

ЖЭТФ, том 157, вып. 2, 2020

Исследование маргинального влияния дефектов структуры.. .

Таблица 2. Значения флуктуационно-диссипатив-

скейлинговыми формами, соответствующими кано-

ного отношения для систем с различными спино-

ническому старению как для чистой системы, так и

выми концентрациями p при различных значениях

для структурно неупорядоченных систем c μ = 1.

начальной намагниченности m0

Наблюдаемое для начальных состояний с намаг-

ниченностями 0.5 ≤ m₀ ≤ 1 изменение режима по-

X^∞(p, m₀)

ведения автокорреляционной функции на долговре-

m₀

менном этапе с t ≫ t_w связано с сильным замед-

p = 1.0

p = 0.9

p = 0.8

p = 0.7

лением эффектов корреляции вследствие пиннин-

0.01

0.335(17)

0.316(20)

0.255(21)

0.181(16)

га доменных стенок на дефектах структуры в про-

0.02

0.336(19)

0.317(19)

0.252(20)

0.181(15)

цессе неравновесного изменения доменной структу-

ры системы. Данная особенность в поведении авто-

0.05

0.338(18)

0.314(19)

0.251(19)

0.182(16)

корреляционной функции была выявлена нами ра-

0.1

0.334(19)

0.313(18)

0.255(19)

0.181(15)

нее в структурно неупорядоченной двумерной мо-

0.2

0.334(19)

0.316(19)

0.254(18)

0.182(16)

дели Изинга, эволюционирующей из низкотемпера-

0.3

0.331(18)

0.313(19)

0.256(19)

0.184(17)

турного полностью упорядоченного начального со-

0.4

0.339(19)

0.314(21)

0.258(20)

0.185(17)

стояния с m₀ = 1 с реализацией для C(t, t_w) эффек-

тов сверхстарения [39]. Для начальных состояний

0.5

0.742(32)

с 0.01 ≤ m₀ < 0.4 поведение автокорреляционной

0.6

0.749(31)

функции не меняется ни на этапе старения с t ≈ t_w,

0.8

0.752(33)

ни на долговременном этапе c t ≫ t_w и характери-

0.9

0.750(32)

зуется одним режимом поведения.

1.0

0.751(33)

8. ОПРЕДЕЛЕНИЕ

[

]

ФЛУКТУАЦИОННО-ДИССИПАТИВНОГО

∂ (ln t)-(zνca)/2 χ(t, t_w)

ОТНОШЕНИЯ ПРИ ЭВОЛЮЦИИ ИЗ

X (t_w) = lim

T_c

[

]

(22)

C→0

СОСТОЯНИЙ С РАЗЛИЧНЫМИ

∂ (ln t)-(zνca)/2 C(t, t_w)

ЗНАЧЕНИЯМИ НАЧАЛЬНОЙ

НАМАГНИЧЕННОСТИ

для систем со спиновыми концентрациями p ≤ 0.9.

Представленная на рис. 17 для систем со спино-

На следующем этапе мы исследовали влияние

выми концентрациями p = 0.9 и p = 0.8 парамет-

различных начальных состояний на значения пре-

рическая зависимость T_c(lnt)-(zνca)/2χ(t, t/9, t_m) от

дельного флуктуационно-диссипативного отноше-

(ln t)-(zνca)/2C(t, t/9, t_m) позволяет получить значе-

ния (ФДО). Рассчитывалась временная зависимость

ния предельного ФДО X^∞ в соответствии с соотно-

динамической восприимчивости χ(t, t_w, t_m) и авто-

шением (22). На рис. 17 видно, что в случае началь-

корреляционной функции C(t, t_w, t_m) для различ-

ных состояний с намагниченностью 0.01 ≤ m₀ < 0.4

ных значений начальных намагниченностей m₀ при

системы со всеми спиновыми концентрациями ха-

времени ожидания равном t_w = t/9, которое лучше

рактеризуются линейной зависимостью T_cχ от C и

соответствует условию t - t_w ≫ t_w для долговре-

предельными значениями ФДО, представленными в

менного этапа эволюции системы — области универ-

табл. 2. Эти значения в пределах погрешности сов-

сальности неравновесной динамики. С учетом ло-

падают со значениями для высокотемпературного

гарифмических поправок соотношение (18) перепи-

начального состояния X^∞HT = 0.339(19) (p = 1.0),

шется для структурно неупорядоченной двумерной

X^∞HT

= 0.317(21) (p

= 0.9), X^∞HT

= 0.256(23)

модели Изинга в виде

(p = 0.8) и X^∞HT = 0.175(18).

В случае начальных состояний с намагничен-

X (t_w) =

ностью 0.5 ≤ m₀ ≤ 1 предельное значение ФДО

[

]

для чистой системы (p = 1.0) хорошо согласует-

∂ (1 + (g/z) ln t)-(zνca)/2 χ(t, tw)

= lim

T_c

[

]

(21)

ся с найденным в [39] значением X^∞LT = 0.751(24)

C→0

∂

(1 + (g/z)lnt)-(zνca)/2 C(t, t_w)

для низкотемпературного полностью упорядоченно-

го состояния с m₀ = 1. Для структурно неупоря-

для систем со спиновыми концентрациями 0.9 < p <

доченных систем с начальными намагниченностями

< 1.0 и в виде

0.5 ≤ m₀ ≤ 1 предельное ФДО X^∞ = 0, что связано

323

В. В. Прудников, П. В. Прудников, П. Н. Маляренко, Л. Н. Щур

ЖЭТФ, том 157, вып. 2, 2020

T_c

0.018

0.0006

0.016

p = 0.9

0.014

0.012

0.0004

0.010

m₀ = 0.01

m₀ = 0.4

0.008

0.02

0.5

0.006

0.1

0.6

0.0002

0.2

0.8

0.004

0.3

0.9

0.002

0.4

1.0

0.01

0.02

0.03

0.04

0.05

0.06

0.0040

0.0045

0.0050

T_c

0.026

0.016

0.024

p = 0.8

0.014

0.022

0.020

0.012

0.018

m₀ = 0.01

0.016

0.010

0.02

m₀ = 0.4

0.014

0.008

0.5

0.012

0.05

0.010

0.1

0.006

0.6

0.008

0.8

0.2

0.006

0.004

0.9

0.004

0.3

0.002

1.0

0.002

0.4

0.02

0.04

0.06

0.08

0.10

0.12

0.007

0.008

0.009

0.010

0.011

Рис. 17. Параметрическая зависимость Tc(ln t)-(zνca)/2χ(t, t/9, tm) от (ln t)-(zνca)/2C(t, t/9, tm) для систем с разными

p при различных значениях начальной намагниченности m0

с сильным замедлением корреляционных эффектов

Показано, что неравновесное критическое пове-

на временах t ≫ t_w вследствие пиннинга доменных

дение систем, релаксирующих из начальных состоя-

стенок на дефектах структуры.

ний с различными значениями начальной намаг-

ниченности m₀, характеризуется принадлежностью

к двум подклассам универсального неравновесного

9. ЗАКЛЮЧЕНИЕ

критического поведения с характерными значения-

ми предельного флуктуационно-диссипативного от-

В заключение отметим, что в результате числен-

ношения. Один из них соответствует типу низко-

ных исследований выявлены существенные особен-

температурного начального состояния, включающе-

ности влияния дефектов структуры на неравновес-

го в себя состояния с 0.5 ≤ m₀ ≤ 1. В этом случае

ное критическое поведение двумерной модели Изин-

скейлинговая временная зависимость автокорреля-

га при ее эволюции из различных начальных со-

ционной функции для чистой модели Изинга опи-

стояний. На основе анализа временной зависимо-

сывается соотношениями теории канонического ста-

сти намагниченности, двухвременной зависимости

рения, а для структурно неупорядоченной модели

автокорреляционной функции и динамической вос-

Изинга — теории сверхстарения [28]. Другой под-

приимчивости было выявлено проявление логариф-

класс универсального неравновесного критического

мических поправок и кроссоверных явлений перко-

поведения соответствует типу высокотемпературно-

ляционного поведения на неравновесные характери-

го начального состояния, включающего в себя состо-

стики и критические индексы структурно неупоря-

яния с m₀ < 0.4. В этом случае автокорреляционная

доченной модели.

324

ЖЭТФ, том 157, вып. 2, 2020

Исследование маргинального влияния дефектов структуры.. .

функция описывается скейлинговыми формами, со-

Р. Фольк, Ю. Головач, Т. Яворский, УФН 173, 175

ответствующими каноническому старению, для си-

(2003).

стем со всеми значениями спиновых концентраций.

А. К. Муртазаев, И. К. Камилов, А. Б. Бабаев,

Случай начальной намагниченности m₀ = 0.4 явля-

ЖЭТФ 126, 1377 (2004).

ется переходным, когда поведение автокорреляцион-

ной функции на временах t ≥ t_w соответствует ти-

В. В. Прудников, П. В. Прудников, А. Н. Вакилов,

А. С. Криницын, ЖЭТФ 132, 417 (2007).

пу неравновесного критического поведения с высо-

котемпературным начальным состоянием, а на дол-

В. В. Прудников, П. В. Прудников, А. Н. Ваки-

говременном этапе c t ≫ t_w — низкотемпературно-

лов, Теоретические методы описания неравновес-

му типу начальных состояний. С увеличением кон-

ного критического поведения структурно неупо-

центрации дефектов поведение автокорреляционной

рядоченных систем, Наука, Москва (2013).

функции для системы с m₀ = 0.4 все более соответ-

P. E. Berche, C. Chatelain, B. Berche, and W. Janke,

ствует подклассу высокотемпературного начального

Eur. Phys. J. B 38, 463 (2004).

состояния.

Показано, что неравновесная критическая ди-

10.

M. Hasenbusch, F. P. Toldin, A. Pelissetto, and E. Vi-

намика слабонеупорядоченных систем со спиновы-

cari, J. Stat. Mech. 2007, P02016 (2007).

ми концентрациями p ≥ 0.9 относится к классу

11.

Вик. С. Доценко, Вл. С. Доценко, Письма в

универсальности неравновесного критического по-

ЖЭТФ 33, 40 (1981).

ведения «чистой» модели и характеризуется одина-

12.

Б. Н. Шалаев, ФТТ 26, 1811 (1984).

ковыми критическими показателями и значениями

предельного флуктуационно-диссипативного отно-

13.

B. N. Shalaev, Phys. Rep. 237, 129 (1994).

шения, а неравновесное критическое поведение си-

14.

J. S. Wang, W. Selke, Vl. S. Dotsenko, and V. B. And-

стем с p ≤ 0.85 демонстрирует зависимость универ-

reichenko, Physica A 164, 221 (1990).

сальных характеристик неравновесного критическо-

го поведения от концентрации дефектов и наруше-

15.

A. L. Talapov and L. N. Shchur, Europhys. Lett. 27,

ние динамического скейлинга, что связано с влия-

193 (1994).

нием кроссоверных эффектов перколяционного по-

16.

A. L. Talapov and L. N. Shchur, J. Phys.: Cond. Mat.

ведения [23,24,39].

6, 8295 (1994).

Для проведения расчетов были использованы

ресурсы суперкомпьютерного комплекса МГУ

17.

W. Selke, L. N. Shchur, and A. L. Talapov, Ann. Rev.

им. М. В. Ломоносова и межведомственного супер-

Comput. Physics I, ed. by D. Staufer, World Scientific

(1995), p. 17.

компьютерного центра РАН.

18.

J. K. Kim and A. Patrascioiu, Phys. Rev. Lett. 72,

Финансирование. Работа выполнена при под-

2785 (1994).

держке Российского фонда фундаментальных ис-

19.

S. L. A. de Queiroz and R. B. Stinchcombe, Phys.

следований (проекты №№ 17-12-00279, 18-42-550003,

Rev. B 50, 9976 (1994).

19-32-50006, 20-32-70189) и гранта МД-6868.2018.2

Президента РФ.

20.

H. G. Ballesteros, L. A. Fernandez, V. Martin-Mayor

et al., J. Phys. A 30, 8379 (1997).

21.

W. Selke, L. N. Shchur, and O. A. Vasilyev, Physica

ЛИТЕРАТУРА

A 259, 388 (1998).

1. M. E. Fisher, Rev. Mod. Phys. 46, 597 (1974).

22.

L. N. Shchur and O. A. Vasilyev, Phys. Rev. E 65,

016107 (2001).

2. P. C. Hohenberg and B. I. Halperin, Rev. Mod. Phys.

23.

О. Н. Марков, В. В. Прудников, Письма в ЖЭТФ

49, 435 (1977).

60, 24 (1994)

3. R. B. Stinchcombe, Dilute Magnetism, in Phase Tran-

24.

V. V. Prudnikov and O. N. Markov, Europhys. Lett.

sitions and Critical Phenomena, ed. by C. Domb and

29, 245 (1995).

J. L. Lebowitz, Vol. 7, Acad. Press, New York (1983),

p. 151.

25.

E. Vincent, J. Hammann, M. Ocio, J. P. Bouchaud,

and L. F. Cugliandolo, Lect. Notes Phys. 492, 184

4. A. B. Harris, J. Phys. C 7, 1671 (1974).

(1997).

325