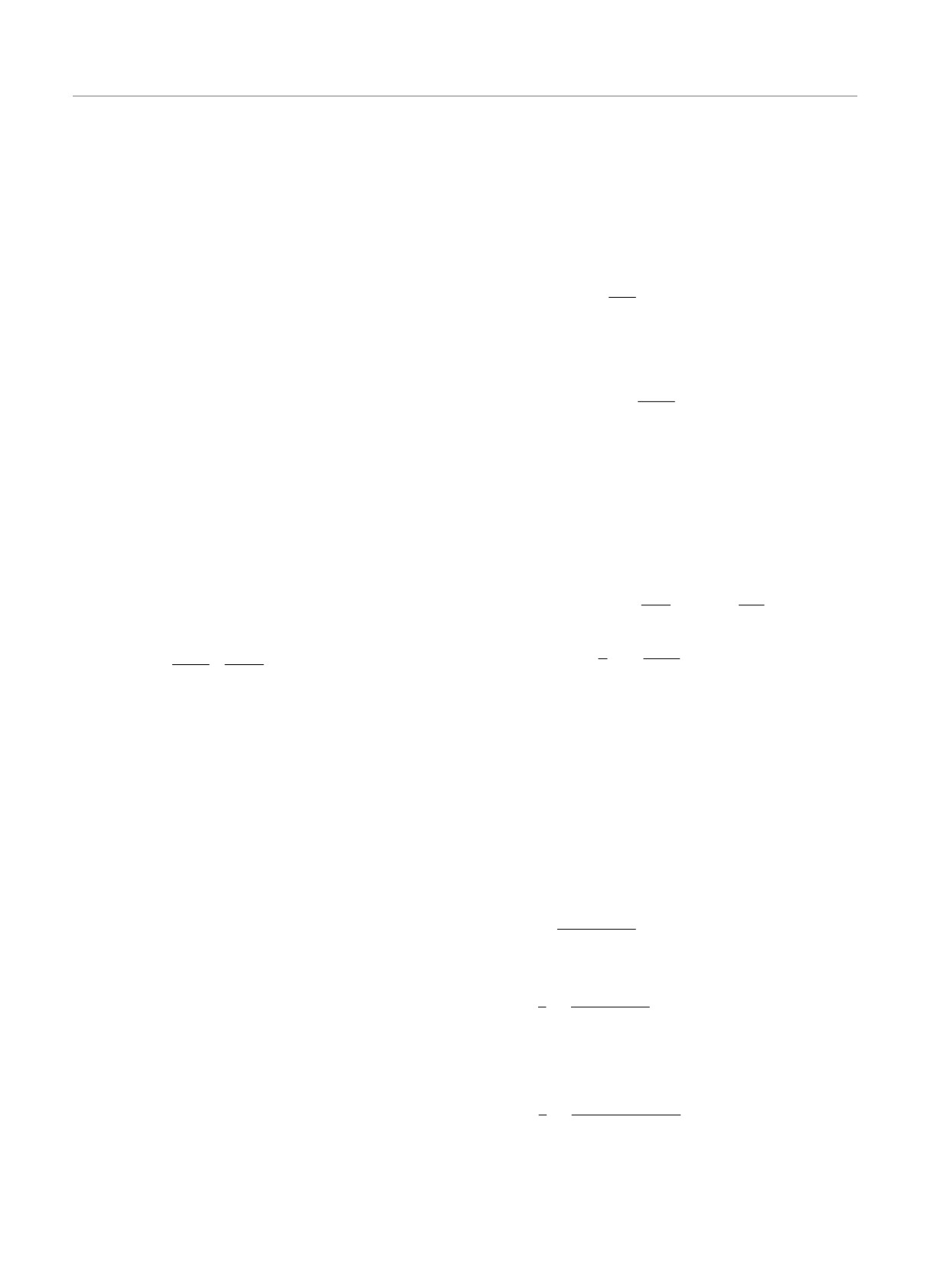ЖЭТФ, 2020, том 157, вып. 2, стр. 327-341

ГАМИЛЬТОНОВ ФОРМАЛИЗМ ДЛЯ БОЗЕ-ВОЗБУЖДЕНИЙ

В ПЛАЗМЕ С НЕАБЕЛЕВЫМ ТИПОМ ВЗАИМОДЕЙСТВИЯ

Ю. А. Марковa,d*, М. А. Марковаa**, Н. Ю. Марков^b, Д. М. Гитманc,d,e***

^a Институт динамики систем и теории управления им. В. М. Матросова

Сибирского отделения Российской академии наук

664033, Иркутск, Россия

^b Иркутский государственный университет

664003, Иркутск, Россия

^c Физический институт им. П. Н. Лебедева Российской академии наук

119991, Москва, Россия

^d Томский государственный университет

634050, Томск, Россия

^e Институт физики университета Сан-Паулу

05508-090, Сан-Паулу, Бразилия

Поступила в редакцию 17 июня 2019 г.,

после переработки 19 августа 2019 г.

Принята к публикации 28 августа 2019 г.

Построена гамильтонова теория для коллективных продольно-поляризованных бесцветных возбужде-

ний (плазмонов) в высокотемпературной глюонной плазме. Применяется общий формализм построения

теории волн в нелинейных средах с дисперсией, развитый В. Е. Захаровым. В рамках данного подхода

получено в явном виде специальное каноническое преобразование, позволяющее упростить гамильтониан

взаимодействия мягких глюонных возбуждений и тем самым определить новый эффективный гамиль-

тониан. Развитый подход использован для построения кинетического уравнения больцмановского типа,

которое описывает процесс упругого рассеяния коллективных продольно-поляризованных возбуждений

в глюонной плазме и эффект так называемого нелинейного затухания Ландау. Проведено детальное

сравнение эффективной амплитуды плазмон-плазмонного взаимодействия, найденной в рамках класси-

ческой гамильтоновой теории, и соответствующего матричного элемента, вычисленного в рамках высо-

котемпературной квантовой хромодинамики, что позволило определить границы справедливости чисто

классического подхода, представленного в работе.

DOI: 10.31857/S004445102002011X

происходящими без обмена энергией между части-

цами и волнами. В ряде работ [2-7] были постро-

ены и детально исследованы кинетические уравне-

1. ВВЕДЕНИЕ

ния для наиболее простых коллективных возбуж-

дений (ленгмюровских плазмонов) электрон-ионной

В теории обычной электрон-ионной плазмы было

плазмы, описывающие процессы упругого рассея-

показано, что слабая турбулентность плазмы может

ния плазмонов друг на друге.

быть двух типов (см., например, [1]). Слабая тур-

булентность первого типа обусловлена процессами

В настоящее время проявляется определенный

рассеяния волн на частицах плазмы. Слабая тур-

интерес к построению кинетического описания

булентность второго типа обусловлена процессами

нового фундаментального состояния материи:

распада, слияния и рассеяния волн друг на друге,

кварк-глюонной плазмы — плазмы, состоящей из

асимптотически свободных кварков, антикварков

^* E-mail: markov@icc.ru

^** E-mail: markova@icc.ru

и глюонов (см., например, обзор

[8]), которая,

^*** E-mail: dmitrygitman@hotmail.com

возможно, образуется при столкновении ультра-

327

Ю. А. Марков, М. А. Маркова, Н. Ю. Марков, Д. М. Гитман

ЖЭТФ, том 157, вып. 2, 2020

релятивистских тяжелых ядер. Показано, что

Статья имеет следующую структуру. В разд. 2

в пределе больших температур кварк-глюонная

приведен вывод оператора эффективного гамильто-

плазма хорошо описывается эффективной пер-

ниана четвертого порядка

H₄, описывающего про-

турбативной теорией

[9], переформулированной

цесс упругого рассеяния двух бесцветных плазмо-

на языке кинетических уравнений [10]. Глюонная

нов друг на друге. В разд. 3 введена в рассмотре-

плазма (для простоты в данной работе будем пре-

ние функция распределения плазмонов Nlk и дан

небрегать существованием кварков и антикварков)

анализ корреляционных функций четвертого и шес-

может быть представлена в виде двух подсис-

того порядков по операторам рождения и уничто-

тем: подсистемы жестких термальных глюонов

жения плазмонов ĉ†bk и ĉak. Раздел 4 посвящен вы-

и подсистемы мягких плазменных возбуждений,

воду кинетического уравнения для мягких глюон-

которые обмениваются энергией между собой. В

ных возбуждений больцмановского типа с учетом

высокотемпературной глюонной плазме, так же

эффекта нелинейного затухания Ландау плазмонов.

как и в обычной электрон-ионной, существует

Разделы 5 и 6 связаны с определением явного ви-

два типа коллективных плазменных возбуждений:

да трехплазмонных и четырехплазмонной вершин-

поперечно-поляризованные и продольно-поля-

ных функций в рамках приближения жестких тем-

ризованные (плазмоны). В отсутствие внешних

пературных петель и аппроксимации эффективно-

хромомагнитного или хромоэлектрического полей

го глюонного пропагатора в плазмонном полюсе. В

цветовая матрица плотности числа коллективных

заключительном разд. 7 намечены возможные пути

глюонных возбуждений является диагональной, и

обобщения гамильтонова описания на случай силь-

поэтому данные возбуждения следует трактовать

новозбужденной глюонной плазмы.

как бесцветные.

В Приложении приведены все основные выраже-

ния для эффективных глюонных вершинных функ-

В работе [11] развито кинетическое описание

ций и глюонного пропагатора в высокотемператур-

процессов нелинейного взаимодействия бесцветных

ном приближении жестких температурных петель.

и цветных плазмонов в рамках приближения жест-

ких температурных петель [9, 10]. Основой этого

подхода является вычисление некоторых эффектив-

2. ГАМИЛЬТОНИАН ВЗАИМОДЕЙСТВИЯ

ных токов, порождающих эти процессы. С помо-

БЕСЦВЕТНЫХ ПЛАЗМОНОВ

щью данных токов далее определяются матричные

Рассмотрим далее приложение общей теории

элементы процессов нелинейного взаимодействия

В. Е. Захарова к конкретной системе — высокотем-

произвольного (четного) числа бесцветных плазмо-

пературной глюонной плазме в квазиклассическом

нов. В данной работе представлен альтернативный

приближении. Потенциалы калибровочного поля,

путь кинетического описания нелинейной динами-

которые описывают глюонное поле в системе, яв-

ки плазмонов, основанный на классическом гамиль-

ляются N_c × N_c-матрицами в цветовом простран-

тоновом формализме для систем с распределенны-

стве и определены посредством A_μ(x) = A^aμ(x)t^a с

ми параметрами, систематически развитый в рабо-

N2c - 1 эрмитовыми генераторами t^a цветовой груп-

тах Захарова [5-7], Гитмана и Тютина [12]. Осно-

пы SU(N_c) в фундаментальном представлении¹⁾.

вой этого подхода в нашем случае является то, что

Тензор напряженности F_μν (x) = F^aμν (x) t^a, где

уравнения, описывающие бесстолкновительную вы-

сокотемпературную плазму в приближении жест-

F^aμν(x) = ∂_μA^aν - ∂_ν A^aμ + gf^abcA^bμA^cν,

ких температурных петель, обладают гамильтоно-

вой структурой, которая была найдена в работах

подчиняется уравнению Янга - Миллса в A₀-калиб-

[13-15]. Последнее обстоятельство позволяет нам

ровке:

развить (по крайней мере, для слабо-возбужденных

состояний, см. Заключение) независимый подход

∂_μF^μν(x) - ig[A_μ(x), F^μν(x)] - ξ-10n_μn^νA_ν(x) =

к выводу кинетического уравнения для мягких

продольно-поляризованных глюонных плазменных

= -j^ν(x),

возбуждений. В рамках гамильтонова подхода мат-

ричные элементы плазмон-плазмонного взаимодей-

¹⁾ Цветовой индекс a пробегает значения 1, 2, . . . , N2c - 1, в

то время как векторный индекс μ пробегает значения 0, 1, 2, 3.

ствия получаются в результате специальных кано-

Всюду в тексте статьи по дважды повторяющимся индексам

нических преобразований, упрощающих гамильто-

подразумевается суммирование и используется система еди-

ниан взаимодействия плазмонов.

ниц, в которой ℏ = c = 1.

328

ЖЭТФ, том 157, вып. 2, 2020

Гамильтонов формализм для бозе-возбуждений в плазме. . .

где ξ₀ — калибровочный параметр в данной калиб-

не имеющее элементарных коллективных возбужде-

ровке. 4-вектор n_μ будем далее отождествлять с гло-

ний. У операторов âak и â†ak отличны от нуля лишь

бальной 4-скоростью u_μ плазмы. Цветной ток j^ν

матричные элементы, соответствующие изменению

определяется обычным образом:

на единицу числа плазмонов.

∫

Запишем квантовомеханический аналог уравне-

j^ν(x) = gt^a d⁴p p^νTr(T^af_g(x, p)).

ния Гамильтона, а именно, уравнение Гейзенберга

для оператора âak:

Здесь x = (t, x) — пространственно-временная пере-

[

]

∂âak

менная исходной динамической системы, (T^a)^bc ≡

H,â^a

(2.3)

∂t

≡ -if^abc — цветовая матрица в присоединенном

представлении. Функция распределения глюонов

Здесь

H — гамильтониан системы плазмонов, рав-

f_g = f_g(x, p) является (N2c -1)×(N2c -1)-эрмитовой

ный сумме

H₌ H₀ +

H_int, где

матрицей в цветовом пространстве.

∫

Как известно, в равновесной горячей кварк-

H₀ =

ωlk â†ak âak

(2.4)

глюонной плазме существуют два типа физических

(2π)³

бозонных мягких полей: поперечно-поляризованное

— гамильтониан невзаимодействующих плазмонов,

и продольно-поляризованное

[8]. Для простоты

H_int — гамильтониан взаимодействия. Дисперсион-

ограничим свое рассмотрение только процессами с

ное соотношение для плазмонов ωlk удовлетворяет

участием продольно-поляризованных плазменных

следующему дисперсионному уравнению [16]:

возбуждений, которые носят название плазмонов.

Эти возбуждения являются истинно коллективным

Re ε^l(ω, k) = 0,

(2.5)

эффектом среды, не имеющим аналогов в обычной

квантовой теории поля. Рассмотрим продольную

где

[

(

)]

часть потенциала калибровочного поля в виде

3ω2pl

ε^l(ω, k) = 1 +

1-F

разложения

k²

|k|²

[



]

∫

)1/2

1+x

⁽Z^l(k)



F (x) =

iπθ(1 - |x|)

A^aμ(x) =

^-

^1-x

(2π)³

2ω^l

{

}

— продольная диэлектрическая проницаемость и

× ϵ^lμ âak e-ik·x +ϵ^∗lμ â†ak

eik·x

k₀ = ωlk,

(2.1)

ω2pl = g2NcT2/9, T — температура системы, g —

постоянная сильного взаимодействия. В приближе-

где ϵ^lμ = ϵ^lμ(k) — вектор поляризации продольного

нии малых амплитуд гамильтониан взаимодействия

плазмона, явный вид которого зависит от выбора

можно представить в виде формального интегросте-

калибровки (в частности, при A₀-калибровке дан-

пенного ряда по âak и â†ak:

ный вектор определяется выражением (5.6)). Мно-

житель Z^l(k) есть вычет эффективного глюонного

H_int =

H₃ +

H₄ + . . . ,

пропагатора в плазмонном полюсе. Коэффициенты

â a_k и â†ak будем рассматривать как квазичастич-

где гамильтонианы взаимодействия третьего и чет-

ные операторы уничтожения и рождения плазмо-

вертого порядков имеют следующую структуру:

нов, подчиняющиеся коммутационным соотношени-

∫

{

dk dk₁ dk₂

ям бозе-операторов

a1 a2

H₃ =

V a

k, k1, k2

â†ak âa1k1

[

]

[

]

(2π)⁹

}

âa_k, â^b

= â†ak, â^†b

= 0,

k^′

â a

(2π)³δ(k-k₁-k₂) +

[

]

(2.2)

, k1, k2

â†a1k1âk

∫

{

â a_k, â^†b

= δ ^ab (2π)³δ(k - k^′).

dk dk₁ dk₂

k^′

a a1 a

k, k

1, k2

âak âa1k1âk2 +

(2π)⁹

Многоплазмонные состояния получаются много-

}

кратным действием оператора â†ak на вакуумное

(2π)³δ(k+k₁+k₂),

(2.6)

k1, k2

â†ak â†a1k1^â

состояние

|0〉, которое подчиняется следующему

условию:

∫

dk dk₁ dk₂ dk₃

âak|0〉 = 0.

a1 a2 a3

H₄ =

T a

â†ak â

† a¹ ×

k, k1, k2, k3

(2π)¹²

Таким образом, под вакуумом понимается основное,

(2π)³δ(k + k₁ - k₂ - k₃)

(2.7)

невозбужденное состояние системы, т.е. состояние,

×âa2k2

329

Ю. А. Марков, М. А. Маркова, Н. Ю. Марков, Д. М. Гитман

ЖЭТФ, том 157, вып. 2, 2020

и т. д. Под символом «∗» понимается комплексное

Условия каноничности данного преобразования²⁾

сопряжение. В выражении (2.7) мы оставили лишь

{

}

∫

«существенный» по терминологии В. Е. Захарова

δâak

δâbk′′

δâak

δâbk′′

dk^′

= 0,

вклад, в силу того что резонансные условия

δĉ^c

δĉ†ck′

δĉ^†c

δĉ^c

k^′

{

}

∫

⎧

δâak

δâ†′k′

δâak

δâ†′k′

dk^′

= δ^abδ(k - k^′′)

⎨ k + k₁ + k₂ + k₃ = 0,

δĉ^c

δĉ†ck′

δĉ^†c

δĉ

k^′

⎩ ωlk +ωlk

+ωlk

=0,

налагают определенные ограничения на коэффици-

⎧

ентные функции ряда (2.10). Функции V(1)aa1 a² ,k,k

⎨ k=k₁ +k₂ +k₃,

1, k2

и V(3)aa1 a² должны удовлетворятьk,k

V(2

, k1, k2

1, k2

⎩ ωlk =ωlk

+ωlk

условиям

(2) a a1 a2

= -2V ∗(1) a1 a

a² ,

не имеют решений для спектра плазмонов, опреде-

k, k1, k2

k1, k, k2

ляемого дисперсионным уравнением (2.5).

V(3)aa1 ak,k

=V(3)a1 a² a_k

1, k2

=V⁽³

, k2, k1

1, k2, k

Отметим, что подобного рода представление га-

мильтониана взаимодействия в виде формальных

а функции W(i)

, i = 1,...,4 — условиям

k, k1, k2, k

бесконечных рядов по степеням операторов рожде-

∫ {

ния и уничтожения рассматривались в книге Швар-

a^′

V∗(1)a2 a

ца [17] в рамках квантовой теории поля для скаляр-

k1, k2, k3

k2, k, k^′

V∗(3)a1 a³ a^′k

, k3, k^′

}

ных полей.

dk = - W∗(3

) a1 a a2 a3 ,

−V⁽¹

, k2, k^′

V(1

^′, k1, k3

k1, k, k2, k3

a1 a2

U a

Коэффициенты

, k1, k2

k, k1, k2

a1 a2 a3

T a

обладают определенной симметри-

k, k1, k2, k3

∫ {

ей

k1, k2, k3

V(1

, k1, k^′

V∗(1)a3 a¹ a^′k

, k2, k^′

a1 a2

a^′

V a

=Vaa2 a¹ ,k,k

+V∗(1)a′ a

-V∗(1)a1 a

V (1) a′ a³ a² -_k′_,k

k, k1, k2

2, k1

k^′, k, k1

V(1

^′, k3, k2

k1, k, k^′

3, k2

(2.8)

a1 a2

}

U a

=Ua1 a² a_k

k, k1, k2

k2, k1

1, k2

, k

V∗(3)a3 a² a^′

dk^′ = -W∗(2)a3 a¹ a² a_k

−V⁽³

, k1, k^′

k3, k2, k^′

3, k1, k2, k

∫ {

k1, k2, k3

, k1, k^′

V(3

, k2, k^′

a1 a2 a3

a2 a3

T a

=Ta1 a

=Taa1 a³ a²

k, k1, k2, k3

k1, k, k2, k3

k, k1, k3, k2

a^′

+ V∗(1)a1 a

k1, k, k^′

k3, k2

=T∗a2 a³ a

a¹ .

(2.9)

k2, k3, k, k1

) a^′ a a

V∗⁽¹

−

− V∗(1)a1 a³ a^′k

, k3, k^′

k^′, k, k2

}

′

Эти коэффициентные функции определяют кон-

− V(1)aa1 ak,k

V(3)a3 a² a^′

dk^′ =

1, k^′

k3, k2, k^′

кретные свойства среды, в данном случае высоко-

=W(3)a3 a¹ a² a_k

температурной глюонной плазмы.

3, k1, k2, k

Рассмотрим преобразование от операторов âak к

∫ {

новым операторам ĉak:

V∗(1)a′ a

k1, k2, k3

k^′, k, k2

, k1, k^′

}

′

∫

[

V(3)aa2 a

dk^′ = 3W(4)a3 a¹ a² a_k

^′, k3, k1

k, k2, k^′

3, k1, k2, k

dk₁dk₂

âak = ĉak +

V(1

, k1, k2

ĉa¹k1ĉk2 +

(2π)⁶

]

²⁾ Вариационные производные по операторам ĉak и ĉ†ak сле-

дует понимать как пределы соответствующих функциональ-

+ V⁽²

, k1, k2

ĉ†a2k2

+V⁽³

, k1, k2

ĉ†a1k1^ĉk2

∫

ных производных по аддитивным классическим добавкам ϕak

[

dk₁dk₂dk₃

и ϕ∗ak к квантовым ĉak и ĉ†ak [18]:

k1, k2, k3

ĉa¹k1ĉk2 ĉk3 +^...

(2π)⁹

]

ĉak → ĉak + ϕak,

ĉ†

→ĉ†ak +ϕ∗ak.

ĉ†a3 +...

(2.10)

k1, k2, k3

ĉ†a1k1ĉk

330

ЖЭТФ, том 157, вып. 2, 2020

Гамильтонов формализм для бозе-возбуждений в плазме. . .

В силу специфики дисперсионного уравнения

связаны с взаимодействием трех плазмонов, порож-

(2.5) в горячей глюонной плазме резонансные усло-

и V a a1 a¹ с проме-k, k

, k2, k3

2, k3

вия

жуточными «виртуальными» колебаниями. Условие

⎧

малости амплитуд в нашем случае означает

⎨ k=k₁ +k₂,

⎨ k + k₁ + k₂ = 0,

(2.11)

∂ωlk

T⁽⁴⁾||c|² ≪ k ·

(2.14)

⎩ ωlk =ωlk

+ωlk

⎩ ωlk+ωlk

+ω^l

∂k

Таким образом, существуют два эквивалентных

не имеют решений, т. е. спектр продольных плаз-

описания гамильтоновой системы бесцветных плаз-

монов является нераспадным. Тогда каноническое

монов для одних и тех же физических процессов. В

преобразование (2.10) позволяет исключить «несу-

первом мы можем использовать исходный оператор

щественный» гамильтониан

H₃ (2.6), просто пола-

Гамильтона

гая

a a1 a2

H₌ H₀ +

H₃ +

H₄ + . . .,

(2.15)

Vk,

k1, k2

(2π)³δ(k - k₁ - k₂),

V(1

, k1, k2

ωlk - ωlk

-ω^l

где

H₀,

H₃ и

H₄ задаются выражениями (2.4), (2.6)

и (2.7) соответственно, а во втором — оператор Га-

∗ a a1 a2

U_k

, k1, k2

(2π)³δ(k + k₁ + k₂).

мильтона

H, полученный в результате нелинейно-

V(3

, k1, k2

ωlk + ωlk

+ω^l

го преобразования бозонных операторов рождения

Данная процедура исключения приводит нас к сле-

и уничтожения, â†ak и âak:

дующей структуре эффективного гамильтониана

H =

H₀ +

H₄ + . . .,

(2.16)

четвертого порядка

H₄:

∫

где, в свою очередь,

dk dk₁ dk₂ dk₃

∫

a1 a2 a3

H₄ =

T a

ĉ†

k, k1, k2, k3

(2π)¹²

H₀ =

ωlkĉ†akĉak

(2π)³

(2.12)

×ĉ†a1k1

ĉ a³k3 (2π)3δ(k + k1 ^-k2 ^-k3⁾,

определен выражением (2.12). Урав-

а оператор

H₄

где

нения Гейзенберга для операторов âak и ĉak имеют

полностью идентичную форму (2.3) с соответствую-

a1 a2 a3

T a

=Taa1 a² a³

k, k1, k2, k3

щими операторами Гамильтона (2.15) и (2.16).

b a2 a3

U_-

В связи с данным построением необходимо упо-

(k2+k3), k2, k3

(k+k1), k, k1

-2

мянуть близкую к теме нашего исследования рабо-

ωl-(k+k

+ωlk +ω^l

ту Манько и др. [19], в которой было введено новое

b a2 a3

b a a1

Vk2

V∗

+k3, k2, k3

k+k1, k, k1

важное понятие нелинейных f-осцилляторов. Авто-

-2

ωlk+k

-ωlk -ω^l

ры рассматривали задачу о квантовании гармониче-

a1 a2 b

a3 a b

ского осциллятора, где бозонные операторы рожде-

Vk1

V∗

, k2, k1-k2

k3, k, k3-k

-2

ния и уничтожения преобразовывались нелинейным

ωlk

+ωlk -ω^l

3-k

образом в новые операторы рождения и уничтоже-

a a2 b

a3 a1 b

Vk,

V∗

ния, определяющие квантовые f-осцилляторы. Тем

k2, k-k2

k3, k1, k3-k1

-2

ωlk

+ωlk

-ω^l

самым был получен новый оператор Гамильтона с

3-k1

весьма нетривиальной структурой, описывающий ту

a a3 b

a2 a1 b

V∗

Vk,

k3, k-k3

k2, k1, k2-k1

же самую динамику, что и исходный, как это имеет

-2

ωlk

+ωlk

-ω^l

2-k1

место и в нашем случае.

a1 a3 b

a2 a b

Однако несмотря на близкое сходство подходов,

Vk1

V∗

, k3, k1-k3

k2, k, k2-k

-2

(2.13)

представленных в нашей работе и в статье [19],

ωlk

+ωlk -ω^l

2-k

следует отметить их принципиальное различие. В

Найденная эффективная амплитуда имеет простую

представленном в данном разделе подходе операто-

диаграммную интерпретацию, которая представле-

ры рождения и уничтожения (â†ak, âak) и (ĉ†ak, ĉak)

на на рис. 1. Черный квадрат обозначает эффектив-

и соответствующие гамильтонианы (2.15) и (2.16)

a1 a2 a3

ную амплитуду

T a

. Первый член справа

связаны между собой каноническим преобразовани-

k, k1, k2, k3

на рис. 1 определяет прямое взаимодействие четы-

ем с сохранением стандартного вида коммутацион-

рех плазмонов, порождаемое обычной четырехплаз-

ных соотношений (2.2). В подходе работы [19] нели-

монной амплитудой Taa1 a² a³ . Остальные члены

нейные преобразования являются неканоническими,

k, k1, k2, k3

331

Ю. А. Марков, М. А. Маркова, Н. Ю. Марков, Д. М. Гитман

ЖЭТФ, том 157, вып. 2, 2020

k₂

k+k₁

k-k₁

k₁

k₃

Рис. 1. Матричный элемент для четырехплазмонного распада. Волновые линии обозначают плазмоны

и поэтому для сохранения идентичности описыва-

Если совокупность волн при малом уровне нели-

емой динамики авторы соответствующим образом

нейности (2.14) имеет случайные фазы, то эту со-

модифицировали коммутационные соотношения ти-

вокупность можно описывать статистически, вводя

па (2.2). По этой причине в нашем случае нелиней-

корреляционную функцию:

ные колебания, связанные с бозонными оператора-

ми, невозможно просто интерпретировать как коле-

〈 ĉ†ak ĉ bk′〉 = δ^ab(2π)³δ(k - k^′)Nlk.

(3.3)

бания со специфической зависимостью частоты ко-

лебаний от энергии, как это имеет место для нели-

нейных f-осцилляторов, хотя отчасти данный факт

Подчеркнем, что введение функции распределения

может иметь место.

Nlk ≡ N^l(k, x, t) квазичастиц (плазмонов), завися-

щей как от импульса ℏk плазмона, так и от коор-

динат x и времени t, имеет смысл только в том

3. КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ

случае, когда число плазмонов медленно меняется

ЧЕТВЕРТОГО ПОРЯДКА

в пространстве и времени. Это значит, что измене-

ние функции на расстояниях порядка длины волны

Гамильтониан (2.12) описывает процесс упруго-

λ = 2π/k и в течение промежутков времени порядка

го рассеяния цветных плазмонов друг на друге, т. е.

длины волны T = 2π/ωlk должно быть значительно

процесс 2 → 2. Уравнения движения для ĉak и ĉ†bk

меньше самой функции Nlk.

здесь определяются соответствующими уравнения-

ми Гейзенберга:

Исходя из уравнений Гейзенберга (3.1) и (3.2),

определим кинетическое уравнение для плотности

]

∂ĉak

[̃̂

числа плазмонов Nlk. Для этой цели умножим урав-

H₀ +

H₄, ĉ^a

= -iωlkĉak -

∂t

нения (3.1) и (3.2) соответственно на ĉ†bk′ и ĉak:

∫

dk₁ dk₂ dk₃

a1 a2 a3

− i

T a

ĉ†

k, k1, k2, k3

ĉ a²k2^ĉk3

(2π)⁹

∫

∂ĉak

dk₁ dk₂ dk₃

× (2π)³δ(k + k₁ - k₂ - k₃),

(3.1)

ĉ†bk′ = -iωlkĉakĉ†bk′ - i

∂t

(2π)⁹

a1 a2 a3

T a

k, k1, k2, k3

ĉ†bk ĉ†a1k1

ĉ a³k3(2π)3 δ(k+k1-k2-k3),

]

∂ĉ†ak

[̃̂

H₀ +

H₄, ĉ^†

=iωlk ĉ†ak +

∂t

∫

dk₁ dk₂ dk₃

+ i

ĉ†

∫

(2π)⁹

, k1, k2, k3

ĉa¹k1^ĉ

∂ĉ†bk′

dk₁ dk₂ dk₃

=iωlkĉakĉ†bk′ +i

ĉk

× (2π)³δ(k + k₁ - k₂ - k₃).

(3.2)

∂t

(2π)⁹

∗ b a1 a2 a3

T_k

^′, k1, k2, k3

ĉakĉa1k1ĉk

ĉ†a3k3(2π)3 δ(k′+^k1-k2-k3).

Данные точные уравнения, в отсутствие внешнего

цветного поля в системе, позволят определить ки-

нетическое уравнение для плотности числа бесцвет-

Складывая последние два уравнения и усредняя их,

ных плазмонов Nablk ≡ δ^abNlk.

получаем

332

ЖЭТФ, том 157, вып. 2, 2020

Гамильтонов формализм для бозе-возбуждений в плазме. . .

∫

{

∂Nlk

dk₁ dk₂ dk₃

′

ĉ a³〉 = 3(2π)⁹ δ^a3a3 δ^a2a2 δ^a1a1 ×_k

δ^ab(2π)³ δ(k - k^′)

=-i

ĉ†a1k1

∂t

(2π)⁹

{

× δ(k′3 - k₃)δ(k′2 - k₂)δ(k′1 - k₁)Nlk

Nlk

N^l

a1 a2 a3

T a

I b

(2π)³δ(k+k₁-k₂-k₃) -

k, k1, k2, k3

k^′, k1, k2, k3

+ δ^a3a3 δa1a² δa2a¹ ×

−

I a² a³ a

× δ(k′3 - k₃)δ(k₁ - k₂)δ(k′2 - k′1)Nlk

Nlk

Nlk′ +

^′, k1, k2, k3

k2, k3, k, k1

}

+ δa3a¹δa1a³δa2a2 ×

× (2π)³δ(k^′ + k₁ - k₂ - k₃) ,

(3.4)

× δ(k′3 - k′1)δ(k₁ - k₃)δ(k′2 - k₂)Nlk′

Nlk

+ δa3a¹δa1a²δa2a3 ×

где

× δ(k′3 - k′1)δ(k₁ - k₂)δ(k′2 - k₃)Nlk′

Nlk

+ δa3a2δa1a³δa2a¹ ×

a1 a2 a3

× δ(k′3 - k₂)δ(k₁ - k₃)δ(k′2 - k′1)Nlk

Nlk

Nlk′ +

I a

ĉa3 〉_k

k, k1, k2, k3

= 〈ĉ†akĉ†a1k1

+ δa3a2δa1a1δa2a3 ×

}

× δ(k′3-k₂)δ(k′1-k₁)δ(k′2-k₃)Nlk

Nlk

(3.6)

— четырехточечная корреляционная функция.

Дифференцируя далее корреляционную функцию

В данном выражении только первый и последний

I a

a1 a2 a3 по t, с учетом (3.1) и (3.2) мы получаем

k, k1, k2, k3

члены дают необходимый вклад в искомое кинети-

уравнение, правая часть которого будет содержать

ческое уравнение. Подставляем эти члены в первый

корреляционные функции шестого порядка по

интеграл в правой части (3.5) и выполняем сумми-

операторам ĉ†ak и ĉak:

рование по цветным индексам a′1, a′2, a′3 и интегри-

рование по импульсам k′1, k′2, k′3. В итоге получаем

{

[

]

, k1, k2, k3

a1 a2 a3

Nlk

N^l

ωlk+ωlk

-ωlk

I a

, k1, k2, k3

k, k1, k2, k3

∂t

∫

}

dk′1 dk′2 dk′3

′

a′2 a′3

+ i

T^∗aa

Nlk

(2π)³δ(k+k₁-k₂-k₃) =

k, k′1, k′2, k^′

, k1, k2, k3

(2π)⁹

′

ĉ†

〉(2π)³δ(k+k′1-k′2-k′3) +

Nlk

N^l

ĉa²k2

, k1, k2, k3

∫

dk′1 dk′2 dk′3

′

× (2π)³δ(k + k₁ - k₂ - k₃).

(3.7)

a′2 a′3

+ i

T∗a1 a

k1, k¹, k², k^′

(2π)⁹

′

Для примера приведем явный вид вклада, который

× 〈ĉ†ak ĉ^a

′

〉(2π)³ δ(k₁+k′1-k′2-k′3) -

k′1

ĉa²k2

генерирует второй член в разбиении корреляцион-

∫

dk′1 dk′2 dk′3

′

a′2 a′3

ной функции (3.6):

- i

Ta2 a

(2π)⁹

k2, k¹, k², k^′

∫

′

NlkNlk

δ(k₂-k₁)δ(k₃-k)δa1 a² i

Nlk′ dk^′.

× 〈ĉ†akĉ†a1k1ĉk

ĉ a³k3 〉(2π)3δ(k2+k1 -k2 -k3 )^-

, k^′, k^′, k

∫

dk′1 dk′2 dk′3

− i

(2π)⁹

k′1, k′2, k^′

Сравнивая два последних выражения, видим, что

′

они имеют совершенно разную структуру.

ĉ†a

′

〉×

× 〈ĉ†akĉ†a1k1ĉk

k′1

Смотрим далее вторую шеститочечную корре-

× (2π)³δ(k₃ + k′1 - k′2 - k′3).

(3.5)

ляционную функцию в (3.5). В данном коррелято-

ре выписываем в явном виде только «правильные»

члены:

Замкнем цепочку уравнений для корреляционных

функций тем, что выражения для корреляционных

′

ĉa²k2

функций шестого порядка выразим в терминах пар-

{

= 3(2π)⁹

δa

a′1 δ^a2a2 δ^a3a3 δ(k′1 - k )δ(k′2 - k₂)×

ных корреляционных функций. Так, например, пер-

}

вая корреляционная функция в правой части (3.5)

× δ(k′3 - k₃)NlkNlk

N^l

+ (2 ⇄ 3) +

имеет следующую структуру:

333

Ю. А. Марков, М. А. Маркова, Н. Ю. Марков, Д. М. Гитман

ЖЭТФ, том 157, вып. 2, 2020

Подставляя данное выражение во второй интеграл

где

в (3.5), получаем выражение, аналогичное выраже-

Δω ≡ ωlk + ωlk

-ωlk

-ω^l ._k

нию (3.7):

Здесь первый член в правой части, соответствую-

a2 a3

щий полностью некоррелированным волнам (чисто

T∗a1 a

NlkNlk

Nlk

(2π)³ δ(k+k₁-k₂-k₃).

k1, k, k2, k3

гауссовым флуктуациям), является решением одно-

родного уравнения для корреляционной функции

Аналогичные рассуждения для третьего и четвер-

четвертого порядка Iaa1 a² a³ . Второй член опре-k,k

того корреляторов в (3.5) дают нам два оставшихся

1, k2, k3

деляет отклонение четырехточечного коррелятора

вклада соответственно

от гауссова приближения для малого уровня нели-

-6i

Ta2 a³ a

NlkNlk

Nlk

(2π)³δ(k+k₁-k₂-k₃)

нейности взаимодействующих волн.

k2, k3, k, k1

Подставим первый член в правую часть уравне-

ния для Nlk (3.4):

∫

{

-6i

Ta3 a² a

NlkNlk

Nlk

(2π)³ δ(k+k₁-k₂-k₃).

dk₁

k3, k2, k, k1

- i(2π)³N^l

Nlk

a a1 b a1 δ(k-k^′) +

k, k1, k^′, k1

(2π)³

Учитывая соотношения симметрии для амплитуды

a1 a1 b

T a

δ(k - k^′) -

k, k1, k1 k^′

рассеяния

}

∗ b a1 a a1

−

T_k

δ(k^′-k)

T∗ba1 a¹ a_k′,k

δ(k^′-k)

^′, k1, k, k1

1, k1

, k

Ta2 a³ a

T∗aa1 a² a³ ,k,k

∫

k2, k3, k, k1

1, k2, k3

= -i2(2π)³δ(k - k^′)N^l

N^l

(2π)³

Ta3 a² a

T∗aa1 a² a³ ,k,k

k3, k2, k, k1

1, k2, k3

{

}

a1 b a1

T a

T∗ba1 a

(4.1)

находим уравнение для корреляционной функции

k, k1, k, k1

четвертого порядка, вместо (3.5):

Подставим далее второй член в правую часть урав-

нения (3.4):

[

]

, k1, k2, k3

a1 a2 a3

∫

{

(

)

ωlk+ωlk

-ωlk

I a

k, k1, k2, k3

dk₁ dk₂ dk₃

∂t

(

-6i

Taa1 a² a³

(2π)⁹

k, k1, k2, k3 Δω + i0

+ 6

NlkNlk

Nlk

+Nlk

Nlk

N^l

, k1, k2, k3

)

(2π)³ δ(k^′

+k₁ -k₂ -k₃)×

^′, k1, k2, k3

-NlkNlk

Nlk

-NlkNlk

N^l

[

]

× (2π)³ δ(k + k₁ - k₂ - k₃) Nlk Nlk

Nl +...

× (2π)³δ(k + k₁ - k₂ - k₃).

(3.8)

(

)

−

Ta2 a³ b

T∗a2 a³ a

k2, k3, k, k1

2, k3, k^′, k1 Δω - i0

4. КИНЕТИЧЕСКОЕ УРАВНЕНИЕ ДЛЯ

× (2π)³ δ(k+k₁-k₂-k₃)(2π)³ δ(k^′+k₁-k₂-k₃) ×

ГЛЮОННЫХ ВОЗБУЖДЕНИЙ

[

]

× NlkNlk

N^l

Перейдем теперь к непосредственному выводу

кинетического уравнения для плазмонов. В принци-

Принимая во внимание, что

пе, самосогласованная система двух уравнений (3.4)

δ(k^′ + k₁ - k₂ - k₃)δ(k + k₁ - k₂ - k₃) =

и (3.8) определяет эволюцию плотности числа плаз-

= δ(k - k^′)δ(k + k₁ - k₂ - k₃),

монов Nlk. Однако мы сделаем еще одно упроще-

ние: в уравнении (3.8) пренебрежем членом с про-

последнее выражение можно записать в более ком-

изводной по времени в сравнении с членом, содер-

пактной форме:

жащим разность собственных частот волновых па-

∫

dk₁ dk₂ dk₃

кетов. Вместо (3.8) тогда будем иметь

- 6i(2π)³δ(k - k^′)

(2π)⁹

[

]

a1 a2 a3

I a

≃NlkNlk

(2π)6 δaa2 δa1 a3 δ(k - k2)×

× (2π)³ δ(k + k₁ - k₂ - k₃) Nlk Nlk

Nl +...

k, k1, k2, k3

]

× δ(k₁ - k₃) + δa a3δa1 a²δ(k - k₃)δ(k₁ - k₂) -

, k1, k2, k3

^′, k1, k2, k3

(

Δω + i0

NlkNlk

Nlk

+Nlk

Nlk

N^l

}

, k1, k2, k3

Δω + i0

Ta2 a³ b

T∗a2 a³ a

)

k2, k3, k^′, k1

k2, k3, k, k1

(4.2)

-NlkNlk

Nlk

-NlkNlk

Nlk

(2π)³δ(k+k₁ -k₂ -k₃),

Δω - i0

334

ЖЭТФ, том 157, вып. 2, 2020

Гамильтонов формализм для бозе-возбуждений в плазме. . .

Свертывая далее полученные выражения (3.4), (4.1)

Здесь

и (4.2) с δ^ab, учитывая, что

w₄(k, k₁; k₂, k₃)=

= -2iπδ(Δω),

∗ a a1 a2 a3

Δω + i0

Δω - i0

(4.5)

, k1, k2, k3

k, k1, k2, k3

d_A

и сокращая на множитель (2π)³ δ(k - k^′), находим

— вероятность рассеяния для процесса упругого

искомое кинетическое уравнение для бесцветных

столкновения двух бесцветных плазмонов, а мера

продольных глюонных возбуждений:

интегрирования определена как

∫

[

]

dNlk

dk₁

dT⁽³⁾ ≡ (2π)⁴ δ(ωlk + ωlk

-ωlk

-ω^l )×_k

a1 a a1

N^l

Nlk

T a

k, k1, k, k1

d_A

(2π)³

dk₁ dk₂ dk₃

∫

× δ(k + k₁ - k₂ - k₃)

dk₁ dk₂ dk₃

(2π)

(2π)⁴ δ(ωlk+ωlk

-ωlk

-ω^l )×_k

d_A

(2π)⁹

В пределе больших чисел заполнения плазмонных

× δ(k + k₁ - k₂ - k₃

T∗aa1 a² a³

, k1, k2, k3

k, k1, k2, k3

состояний, Nlk ≫ 1, правая часть уравнения Больц-

(

мана (4.4) переходит в (4.3).

× NlkNlk

Nlk

+Nlk

Nlk

-NlkNlk

N^l

)

−NlkNlk

N^l

(4.3)

a a₁ a₂ a₃

k, k₁, k₂, k₃

5. ЯВНЫЙ ВИД ФУНКЦИИ T

Здесь d_A = N2c - 1. Первое слагаемое в правой час-

Нам осталось определить явный вид вершинных

ти (4.3) описывает процесс нелинейного затухания

и V a a1 a² , которыеk, k

k1, k2, k3

, k1, k2

1, k2

Ландау [20], декремент которого представляет со-

входят в эффективную амплитуду (2.13). В данном

бой линейный функционал плотности числа плаз-

k1, k2, k3

монов Nlk:

в приближении так называемых жестких темпера-

∫

[

]

турных петель (HTL) [8]. В работе [11], в рам-

{

}

dk₁

a1 a a1

Nlk

≡ γ^l(k) =

Nlk

T a

ках HTL-приближения была вычислена вероятность

k, k1, k, k1

d_A

(2π)³

упругого рассеяния двух плазмонов

Второе слагаемое в (4.3) связано с процессом упру-

w₄(k, k₁; k₂, k₃) = 3Maa1a²a³ (k, k₁, -k₂, -k₃)×

гого плазмон-плазмонного рассеяния. Уравнение

(4.3) можно представить также в более наглядном

× M∗aa1a²a³(k, k₁, -k₂, -k₃).

(5.1)

виде:

Здесь матричный элемент четырехплазмонного рас-

пада имеет следующую структуру:

dNlk

∂Nlk

≡

+vlk ·

∂t

∂x

)

1/2

⁽Z_l(k)

= -γ {Nlk} Nlk-NlkΓ_d[Nlk]+(1+Nlk)Γ_i[Nlk],

(4.4)

Maa1a²a³ (k, k₁, -k₂, -k₃) = g²

2ω

(

)

(

)1/2(

)

где

∏

ũ^μ(k)

Z_l(k_i)

ũμi (k_i)

√

[(

)-1^]

u²(k)i=1

2ωlk

u²(k_i)

∂ωlk

∂Re ε^l(k)

⁾⁽∂Re ε^l(k)



vlk =



∂k

∂ω



(k, k₁, -k₂, -k₃)

(5.2)

ω=ωlk

μ2μ3

on-shell

— групповая скорость продольных колебаний, а

и, в свою очередь, эффективная амплитуда

обобщенная скорость распада Γ_d и обратная ско-

∗Γa a1 a2 a3

(k, k₁, -k₂, -k₃) определяется выра-

μ μ1 μ2 μ3

рость регенерации Γ_i представляют собой нелиней-

жением

ные функционалы плотности числа плазмонов:

∗Γaa1a2a3

∫

(k, k₁, -k₂, -k₃) = -faa1bfba2a³ ×

μμ1μ2μ3

Γ_d[Nlk] = dT⁽³⁾w₄(k, k₁; k₂, k₃)Nlk

(1+Nlk

)(1+N^l )_k

× ∗Γμμ1μ2μ3(k, k1, -k2, -k3)-

- faa2bfba1a³ ∗Γμμ2μ1μ3(k, -k2, k1, -k3),

(5.3)

и соответственно

∫

где f^abc — антисимметричные структурные констан-

Γ_i[Nlk] = dT⁽³⁾w₄(k, k₁; k₂, k₃)(1+Nlk

)Nlk

Nlk

ты цветовой алгебры Ли su(N_c). Цветные факторы

335

Ю. А. Марков, М. А. Маркова, Н. Ю. Марков, Д. М. Гитман

ЖЭТФ, том 157, вып. 2, 2020

в последнем выражении умножаются на чисто кине-

вычисленным в рамках высокотемпературной

матические коэффициенты — эффективные субамп-

квантовой теории поля, т. е.

литуды, определяемые следующим образом:

∗Γ_μμ

1μ2μ3 (k, k1, -k2, -k3) ≡

a a1 a2 a3

k, k1, k2, k3

≡ ∗Γμμ1μ2μ3(k,k1,-k2,-k3)-

1/2

⁽d_A)

- ∗Γμμ1ν(k, k1, -k - k1)^∗Dνν′(k2 + k3)×

Maa1 a² a³ (k, k₁, -k₂, -k₃).

(5.7)

× ∗Γ_ν′μ2μ3(k2 + k3, -k2, -k3)-

- ∗Γμμ3ν(k, -k3, -k + k3)^∗Dνν′(k2 - k1)×

(5.4)

Из выражений для эффективных амплитуд (2.13)

× ∗Γ_ν′μ2μ1(k2 - k1, -k2, k1).

и (5.2), (5.3) мы можем сразу получить явный вид

В Приложении приведен вид вершинных функ-

амплитуды Taa1 a² a³

, которая входит в качестве

k, k1, k2, k3

ций

коэффициентной функции в определение оператора

^∗Γμμ1μ2μ3(k, k1, k2, k3) и

^∗Γμμ1μ2(k, k1, k2),

(A.1)-(A.7), а также глюонного пропагатора

Гамильтона четвертого порядка

H₄ (2.7):

∗D^νμ(k) в приближении жестких температурных

петель, (A.8)-(A.10). Два 4-векторa

(

)

)1/2

(

)

⁽d_A

ϵ^lμ(k)

g²

√

ũ_μ(k) =

k_μ - u_μ(k · u) и

, k1, k2, k3

(k · u)

(5.5)

2ω^l

u_μ(k) = k²u_μ - k_μ(k · u)

(

∏

)[

ϵ^lμ

(k_i)

√

faa1bfba2a³ ×

представляют собой проекторы на продольное на-

i=1

2ω^l

правление волнового вектора k, записанные в ло-

ренц-инвариантной форме в гамильтоновой и ло-

× ∗Γμμ1μ²μ³(k, k₁,-k₂,-k₃)+faa2bfba1a³ ×

ренцевой калибровках соответственно. Здесь u^μ —

]

4-скорость среды, которая в системе покоя равна



× ∗Γμμ2μ¹μ³(k,-k₂, k₁,-k₃)



(5.8)

u^μ = (1, 0, 0, 0). Наконец, 4-векторы вида

on-shell



)1/2



⁽Z_l(k)

ũ_μ(k)



√



≡

√

ϵ^lμ(k)

(5.6)

Здесь мы приняли во внимание связь продольно-

2ωlk

u²(k)

on-shell

2ω^l

го проектора с вектором поляризации, (5.6). Яв-

ный вид эффективной четырехглюонной вершины

в правой части (5.2) представляют собой обычные

^∗Γ^μνλσ(k,k₁,k₂,k₃) в правой части последнего вы-

волновые функции продольного физического глю-

ражения определяется формулами (A.5)-(A.7).

√

она в A₀-калибровке, где фактор

Z_l(k) обеспе-

чивает ренормировку глюонной волновой функции

за счет температурных эффектов. Множитель 3 в

правой части (5.1) учитывает три возможных ка-

нала четырехплазмонного распада, которые меняют

плотность числа плазмонов:

a a₁ a

6. ЯВНЫЙ ВИД ФУНКЦИЙ U

k, k1, k2

a a₁ a₂

Vk,

k₁, k₂

g^∗ + g∗1 ⇋ g∗2 + g∗3, g^∗ + g∗2 ⇋ g∗1 + g∗3,

g^∗ + g∗3 ⇋ g∗1 + g∗2.

Перейдем теперь к определению явного вида

Сравнивая два выражения для вероятности

и Vaa1 a² вk,k

, k1, k2

1, k2

плазмон-плазмонного рассеяния (4.5) и (5.1), ви-

подынтегральных выражениях оператора Гамильто-

дим, что эффективную амплитуду

Taa1 a² a³

на третьего порядка

H₃ (2.6). Однако в отличие от

k, k1, k2, k3

определяемую выражением

(2.13), с точностью

предыдущего случая, здесь мы имеем более слож-

до числового множителя следует отождествить с

ную ситуацию. С учетом (2.13) и (5.2)-(5.4) из (5.7)

матричным элементом Maa1a²a³(k, k₁, -k₂, -k₃),

следует исходное для анализа выражение

336

ЖЭТФ, том 157, вып. 2, 2020

Гамильтонов формализм для бозе-возбуждений в плазме. . .

a2 a3

U b

левую часть (6.1) можно привести к следующему ви-

-(k2+k3), k2, k3

(k+k1), k, k1

ду:

ωl-(k+k

+ωlk +ω^l

b a2 a3

b a a1

[

V_k

V∗

2+k3, k2, k3

k+k1, k, k1

U-(k

U∗-(k+k

2+k3), k2, k3

1), k, k1

ωlk+k

-ωlk -ω^l

faa1bfba2a³

ωl-(k+k

+ωlk +ω^l

a1 a2 b

a3 a b

V_k

V∗

1, k2, k1-k2

k3, k, k3-k

V_k

V∗_k+k

2+k3, k2, k3

1, k, k1

ωlk

+ωlk -ω^l

3-k

ω^l

-ωlk -ω^l

k+kl1

a a2 b

a3 a1 b

Vk,

V∗

k2, k-k2

k3, k1, k3-k1

V_k

V∗_k

1, k2, k1-k2

3, k, k3-k +

ωlk

+ωlk

-ω^l

3-k1

ωk3-k + ωk - ωk3

]

a a3 b

a2 a1 b

Vk,

V∗

Vk,k

V∗_k

k3, k-k3

k2, k1, k2-k1

3, k-k3

2, k1, k2-k1

ωlk

+ωlk

-ω^l

2-k1

ωk2-k1 + ωk1 - ωk2

[

a1 a3 b

a2 a b

V_k

V∗

1, k3, k1-k3

k2, k, k2-k

V_k

V∗_k

1, k2, k1-k2

-faa2bfba1a³

3, k, k3-k +

ωlk

+ωlk -ω^l

2-k

ωk3-k + ωk - ωk3

(

)

(

)

1/2

∏

∗

⁽d_A)

ϵ^lμ(k)

ϵ^lμ

(k_i)

Vk,k2, k-k2^V

k3, k1, k3-k1

g²

√

2ω^l

ωk3-k1 + ωk1 - ωk3

k i⁼¹

[

(

Vk,k3, k-k3

k2, k1, k2-k1 +

× faa1bfba2a³

^∗Γμμ1ν(k, k₁, -k-k₁)^∗D_νν′(k₂+k₃)×

ωk2-k1 + ωk1 - ω

]

×^∗Γν′μ²μ³ (k₂+k₃, -k₂, -k₃)+^∗Γμμ3ν(k, -k₃, -k+k₃)×

Vk1, k3, k1-k3

k2, k, k2-k

)

ωk2-k + ωk - ωk2

× ∗Dνν′(k₂ - k₁)^∗Γν′μ²μ¹(k₂ - k₁, -k₂, k₁) +

(

+ faa2bfba1a³

^∗Γμμ1ν(k, -k₂, -k + k₂)×

Сравнивая коэффициенты после произведе-

ний антисимметричных структурных констант

× ∗Dνν′(-k₁ + k₃)^∗Γν′μ²μ³(-k₁ + k₃, k₁, -k₃)+

f a

a1 bfba2 a³ и faa2 bfba1 a³ полученного выше

+ ∗Γμμ3ν(k, -k₃, -k + k₃)^∗D_νν′(-k₁ + k₂)×

выражения и правой части (6.1), находим

)]



× ∗Γν′μ²μ¹(-k₁ + k₂,k₁,-k₂)



(6.1)

on-shell

U-(k2+k3), k2, k3U−(k+k1), k, k1₊

ω-(k+k1) + ωk + ωk1

Первым шагом нам необходимо «распутать» цвето-

Vk2+k3, k2, k3

вую структуру данного выражения. Для этой цели

k+k1, k, k1 +

ωk+k1 - ω_k - ωk1

полагаем для трехточечных амплитуд U и V :

∗

k3, k, k3-k

Vk1, k2, k1-k2^V

ω-(k2-k1)+ωk2^-ωk1

, k1, k2

= faa1a² Uk, k1, k2,

Vk, k3, k-k3

k2, k1, k2-k1

k2-k1 + ωk1 - ωk2

a1 a2

(

)

(

)

k, k1, k2

= faa1a² Vk, k1, k2.

⁽d_A)1/2

ϵ^lμ(k)

∏

ϵ^lμ

(k_i)

g²

√

Такое представление является однозначным. В си-

2ω^l

k i⁼¹

лу полной антисимметричности структурных кон-

[

стант faa1 a² по перестановке цветных индексов,

^∗Γμμ1ν(k, k₁, -k - k₁)^∗D_νν′(k + k₁)×

из свойств (2.8) немедленно следует

(k₂ + k₃, -k₂, -k₃) +

× ∗Γν′μ²μ³

+ ∗Γμμ3ν(k, -k₃, -k + k₃)^∗D_νν′(k₂ - k₁)×

Vk, k1, k2 = -Vk, k2, k1 ,

(6.2)

]



Uk,k1, k2 = -Uk, k2, k1 = Uk1, k2, k .

× ∗Γν′μ²μ¹(k₂ - k₁, -k₂, k₁)



on-shell

Далее, используя тождество для антисимметрич-

плюс аналогичное соотношение для второй коэффи-

ных структурных констант

циентной функции. Наконец, из структуры данного

выражения ясно, что здесь мы фактически имеем

fa1a²bfba3a = -faa2bfba1a³ + faa1bfba2a³ ,

два независимых соотношения: первое

337

ЖЭТФ, вып. 2

Ю. А. Марков, М. А. Маркова, Н. Ю. Марков, Д. М. Гитман

ЖЭТФ, том 157, вып. 2, 2020

U-(k

U∗-(k+k

2+k3), k2, k3

1), k, k1

Используя данное приближение, получаем, в част-

ωlk+k

+ωlk +ω^l

ности, для первого пропагатора

V_k

V∗_k+k

2+k3, k2, k3

1, k, k1

Z_l(k + k₁)

^∗Δ^l(k + k₁) ≃ -

ωlk+k

-ωlk -ω^l

2ω^l

(

)

(

)

k+k

1/2

[

]

⁽d_A)

ϵ^lμ(k)

∏

ϵ^lμ

(k_i)

g²

√

(6.6)

ωlk+k

-ωlk -ωlk

ωlk+k

+ωlk +ω^l

2ω^l

k i⁼¹

[

и для второго

^∗Γμμ1ν(k, k₁, -k - k₁)^∗D_νν′(k + k₁)×

]

Z_l(k₂ - k₁)



^∗Δ^l(k₂ - k₁) ≃ -

× ∗Γν′μ²μ³(k₂ + k₃, -k₂, -k₃)



(6.3)

2ω^l

on-shell

k2-k1

[

]

и второе

(6.7)

ωlk

+ωlk

-ωlk

ωlk

+ωlk

-ω

2-k1

V_k

V∗_k

Принимая во внимание приведенные выше выраже-

1, k2, k1-k2

3, k, k3-k

ния (6.3)-(6.7), мы можем выписать искомый вид

ωlk

+ωlk

-ω^l

2-k1

трехплазмонных вершинных функций:

Vk,k3, k-k3

k2, k1, k2-k1

)1/4

ωlk

+ωlk

-ω^l

ϵ^lμ(k)

ϵ^lμ

(k₁)

ϵ^lμ

(k₂)

2-k1

⁽d_A

(

)

(

)

√

1/2

Vk, k1, k2 = g

∏

⁽d_A)

ϵ^lμ(k)

ϵ^lμ

(k_i)

2ω^l

2ωlk

2ω

g²

√



2ω^l



k i⁼¹

× ∗Γμμ1μ²(k, -k₁, -k₂)



(6.8)

[

on-shell

^∗Γμμ3ν(k, -k₃, -k + k₃)^∗D_νν′(k₂ - k₁)×

]



)1/4

× ∗Γν′μ²μ¹(k₂ - k₁, -k₂, k₁)



(6.4)

⁽d_A

ϵ^lμ(k)

ϵ^lμ

(k₁)

ϵ^lμ

(k₂)

on-shell

√

Uk,k1,k2 = g

2ω^l

2ωlk

2ω^l

В левых частях (6.3) и (6.4) мы учли четность дис-



персионного соотношения, т. е. ωl-k = ωlk.

× ∗Γμμ1μ²(-k, -k₁, -k₂)



(6.9)

on-shell

Далее, вторым шагом в эффективных глюонных

Отметим, что вершинные функции (6.8) и (6.9) опи-

пропагаторах^∗ D_νν′ в правых частях (6.3) и (6.4) мы

сывают существенно различные процессы. Возьмем

оставляем только члены с продольным проектором

для примера процесс, который описывается вторым

Qνν′ . Так, для первого пропагатора^∗ D_νν′ (k+k₁) де-

графиком на рис. 1 (s-канал). Фактически он вклю-

лаем замену

чает в себя два подпроцесса рассеяния. Первый из

них в рамках рассматриваемого приближения мож-

∗Dνν′(k + k₁) ⇒ -

Qνν′ (k + k₁)^∗Δ^l(k + k₁),

но описать следующим образом (рис. 2): два плаз-

мона с частотами ωlk и ω^l и волновыми векторами_k

где правая часть, с учетом (A.10) и (A.9), в явном

k и k₁ сливаются в вершине 1 в один плазмон с час-

виде задается выражением

тотой ωlk+k

и волновым вектором k + k₁, который

затем в вершине 2 распадается в два плазмона с ча-

ũ_ν(k+k₁) ũ_ν′ (k+k₁)

(6.5)

стотами ωlk

и ωlk

и волновыми векторами k₂ и k₃

u²(k+k₁)

(k+k₁)²-Π^l(k+k₁)

(рис. 2а). Функция 1/(ωlk+k

-ωlk -ωlk

) играет в

классическом гамильтоновом описании роль пропа-

и аналогично для второго пропагатора

∗Dνν′(k₂ - k₁). Вблизи полюса ω ∼ ωlk продоль-

гатора промежуточного «виртуального» состояния

коллективных продольных возбуждений, а взаимо-

ный скалярный пропагатор

^∗Δ^l(k)

^∗Δ^l(ω, k)

ведет себя как (см., например, [21])

действие в вершинах 1 и 2 здесь задается функцией

Vk,k1, k2 (6.8).

Второй подпроцесс определяется таким образом

Z_l(k)

^∗Δ^l(ω, k) =

≃

(рис. 2б): в вершине 2 происходит трехплазмонный

ω² - k² - Π^l(ω, k)

ω² - (ωlk)²

[

]

распад — два плазмона с частотами ωlk

иω^l

, и вол-

Z_l(k)

новыми векторами k₂ и k₃ уходят в систему, а тре-

2ω^l

ω-ωlk

ω+ω^l

тий плазмон с частотой ω^l

и волновым вектором

k2+k3

338

ЖЭТФ, том 157, вып. 2, 2020

Гамильтонов формализм для бозе-возбуждений в плазме. . .

k₂

В этом случае можно говорить, что теория плаз-

k+k₁

-k – k₂₃

мон-плазмонного взаимодействия для малых амп-

литуд мягких возбуждений является линейной, а

нелинейные эффекты, связанные с неравновесными

k₁

k₃

k₁

k₃

флуктуациями плотности числа плазмонов δNlk, мо-

гут трактоваться как возмущения.

Рис. 2. Подпроцессы четырехплазмонного упругого рас-

Ситуация качественно меняется, когда система

сеяния, определяемые процессами трехплазмонных распа-

сильно возбуждена, что может иметь место в столк-

дов и слияний в s-канале

новениях ультрарелятивистских тяжелых ионов в

экспериментах на Большом адронном коллайдере.

При увеличении интенсивности возбуждений в глю-

k₂ + k₃ в вершине 1 сливается с двумя плазмонами

онной плазме необходимо учитывать дальнейшие

с частотами ωlk и ω^l и волновыми векторами k и_k

члены в разложении

H_int. Так как процессы нели-

k₁, которые приходят из системы. Роль пропагатора

нейного взаимодействия с участием нечетного чис-

здесь играет функция 1/(ωlk+k

+ωlk +ω^l ). Взаимо-_k

ла плазмонов запрещены, то мы можем, в прин-

действие в вершинах 1 и 2 определяется функцией

ципе, определяя подходящим образом канонические

Uk,k1, k2 (6.9).

преобразования, избавиться от всех «нечетных» га-

мильтонианов взаимодействия

H2n+1, n = 1, 2, . . . В

7. ЗАКЛЮЧЕНИЕ

предельном случае сильных возбуждений, когда

В данной работе сделан первый шаг к построе-

|A_μ(x)| ∼ T и, соответственно, Nlk ∼

нию классического гамильтонова формализма для

g²

описания процессов нелинейного взаимодействия

данные канонические преобразования будут содер-

мягких глюонных возбуждений в высокотемпера-

жать бесконечное число членов произвольной сте-

турной теории поля Янга - Миллса. Построено в яв-

пени по операторам рождения ĉ†ak и уничтожения

ной форме каноническое преобразование (2.10), поз-

. Это, в свою очередь, приведет к необходимости

воляющее исключить гамильтониан взаимодействия

учета в правой части кинетического уравнения (4.4)

H₃

третьего порядка

(2.6) и тем самым опреде-

всех высших процессов упругого рассеяния плаз-

лить новый эффективный гамильтониан взаимодей-

монов: 3 → 3, 4 → 4, . . . , так как все они одного

ствия

H₄ (2.12), с калибровочно-ковариантной ам-

порядка по константе взаимодействия g. Ясно, что

a1 a2 a3

плитудой рассеяния

T a

. Данный гамильто-

k, k1, k2, k3

процедура линеаризации кинетического уравнения

ниан взаимодействия определяет конкретный физи-

для плотности числа плазмонов Nlk в данном слу-

ческий процесс — упругое рассеяние двух бесцвет-

чае становится неприменимой и здесь мы приходим

ных плазмонов друг на друге. Данный процесс рас-

к истинно нелинейной теории взаимодействия мяг-

сеяния будет доминирующим, когда значение ам-

ких глюонных возбуждений в плазме с неабелевым

плитуды калибровочного поля имеет порядок [11]

типом взаимодействия.

Таким образом, возникает нетривиальная проб-

|A_μ(x)| ∼

√gT и, соответственно, Nlk ∼

лема построения явного вида канонических преоб-

разований. Данные нелинейные канонические пре-

фактически отвечающий уровню тепловых флукту-

образования должны приводить исходный гамиль-

аций в горячей глюонной плазме. Для данного зна-

тониан взаимодействия к новому эффективному ви-

чения амплитуды калибровочного поля при g ≪ 1

ду:

плотность числа плазмонов Nlk является большой, и

использование чисто классического описания оправ-

H_int -→

H_int =

H₄ +

H₆ + . . . +

H2n+2 + . . .

дано. Более того, здесь справедливо использова-

ние линеаризованного уравнения Больцмана, вме-

Однако прямой подход в определении явного ви-

сто точного (2.12), для бесцветных плазмонов, так

да необходимых канонических преобразований, ко-

как распределение Планка, относительно которого

торый был использован в данной работе, стано-

измеряется отклонение плотности числа плазмонов

вится малоэффективным при попытке исключения

δNlk, имеет порядок

уже следующего нечетного гамильтониана

H₅ ввиду

чрезвычайной громоздкости вычислений. Для силь-

N^leq(k) ∼

∼

ωlk

новозбужденных состояний, когда мы имеем дело с

339

10*

Ю. А. Марков, М. А. Маркова, Н. Ю. Марков, Д. М. Гитман

ЖЭТФ, том 157, вып. 2, 2020

бесконечным числом членов, необходим качествен-

ПРИЛОЖЕНИЕ

но иной, более адекватный в данной ситуации ап-

Эффективные вершины и глюонный

парат, например, введение множества нелокальных

пропагатор

канонических переменных, зависящих от дополни-

тельного трехмерного единичного вектора, как это

В данном приложении мы приводим явный вид

было предложено в работе [22]. Другой подход за-

эффективных вершинных функций и глюонного

ключается в использовании связи

пропагатора в высокотемпературном приближении

жестких температурных петель (HTL) [8, 9].

A^aμ(k) = A(0)aμ(k) +^∗ D_μν(k)

J(2)aν(A⁽⁰⁾, A⁽⁰⁾)+

Эффективная трехглюонная вершина

}

+J˜(3)aν(A⁽⁰⁾,A⁽⁰⁾,A⁽⁰⁾) + ...

(7.1)

^∗Γ^μνρ(k, k₁, k₂) ≡ Γ^μνρ(k, k₁, k₂)+

где A^aμ(k) и Aμ0)a(k) представляют собой взаимодей-

+ δΓ^μνρ(k, k₁, k₂) (A.1)

ствующее и свободное калибровочные поля систе-

мы, а

μ (A⁽⁰⁾, A⁽⁰⁾, . . .) — некоторые эффектив-

представляет собой сумму голой трехглюонной вер-

ные токи, являющиеся нелинейными функционала-

шины

ми от свободного поля и определяемые рекуррент-

Γ^μνρ(k, k₁, k₂) = g^μν(k - k₁)^ρ + g^νρ(k₁ - k₂)^μ +

ным образом в рамках приближения жестких темпе-

ратурных петель [11]. Коэффициентные функции в

+ g^μρ(k₂ - k)^ν (A.2)

μ есть эффективные амплитуды типа (5.3). В ка-

и соответствующей HTL-поправки

честве взаимодействующего поля необходимо взять

∫

выражение (2.1), а в качестве свободного поля — вы-

dΩ v^μv^νv^ρ

δΓ^μνρ(k, k₁, k₂) = 3ω²

ражение вида

4π v · k + iϵ

(

)

∫

)1/2

ω₂

ω₁

⁽Z^l(k)

(A.3)

A(0)aμ(x) =

v · k₂ - iϵ

v · k₁ - iϵ

(2π)³

2ω^l

{

}

где v^μ = (1, v), k + k₁ + k₂ = 0, dΩ — элемент телес-

× ϵ^lμĉake-ik·x + ϵ^∗μĉ†ak

eik·x

ного угла. Ниже приведены полезные свойства трех-

с операторами

ĉa_k и

ĉ†ak, которые входят в пра-

глюонной HTL-ресуммированной вершинной функ-

вую часть канонических преобразований

(2.10).

ции при комплексном сопряжении и перестановке

Соотношение (7.1) фактически содержит в себе

импульсов:

искомое каноническое преобразование с любой

(^∗Γμμ1μ2 (-k1 - k2, k1, k2))^∗ =

степенью точности, если использовать соответ-

ствующие аппроксимации для пропагаторов типа

= -^∗Γμμ1μ2(k1 + k2, -k1, -k2) =

(6.6),

(6.7) и вершинных функций

(6.8),

(6.9),

= ∗Γμμ1μ2(k1 + k2, -k2, -k1). (A.4)

(5.7) и т. п. Соотношение (7.1) позволяет дать нам

Далее, эффективная четырехглюонная вершина

совершенно новую интерпретацию канонических

преобразований: преобразования (2.10) определяют

^∗Γ^μνλσ(k,k₁,k₂,k₃) ≡ Γ^μνλσ(k,k₁,k₂,k₃)+

переход от невзаимодействующего поля Aμ0)a(k) к

+ δΓ^μνλσ(k, k₁, k₂, k₃) (A.5)

взаимодействующему A^aμ(k), которое учитывает все

эффекты взаимодействия в среде. Анализ данной

есть сумма голой четырехглюонной вершины

связи требует отдельного рассмотрения.

Γ^μνλσ = 2g^μνg^λσ - g^μσg^νλ - g^μλg^σν

(A.6)

Финансирование. Работа Д. М. Гитмана и

и соответствующей HTL-поправки

Ю. А. Маркова поддержана программой повышения

∫

конкурентоспособности Национального исследова-

dΩ v^μv^νv^λv^σ

δΓ^μνλσ(k, k₁, k₂, k₃) = 3ω²

тельского Томского государственного университе-

4π v · k + iϵ

[

(

)

та среди ведущих мировых научно-образовательных

ω₂

ω₃

центров. Также работа Д. М. Гитмана частично под-

v · (k + k₁) + iϵ v · k₂ - iϵ

v · k₃ - iϵ

держана Российским фондом фундаментальных ис-

(

)]

следований (проект № 18-02-00149), Фондом иссле-

ω₁

ω₂

−

(A.7)

дований Сан-Паулу (FAPESP, грант 2016/03319-6)

v · (k+k₃)+iϵ v · k₁-iϵ

v · k₂-iϵ

и Национальным Советом по науке (CNPq).

340

ЖЭТФ, том 157, вып. 2, 2020

Гамильтонов формализм для бозе-возбуждений в плазме. . .

Наконец, выражение

V. E. Zakharov, Phys. Rep. 129, 285 (1985).

В. Е. Захаров, Изв. вузов. Радиофизика XVII, 431

∗ D_μν(k) = -P_μν(k)^∗Δ^t(k) -

Q_μν(k)^∗Δ^l(k)-

(1974).

k²

-ξ₀

D_μν(k) (A.8)

А. М. Балк, В. Е. Захаров, в сб. науч. тр. Инте-

(k · u)²

грируемость и кинетические уравнения для соли-

представляет собой модифицированный эффекта-

тонов, под ред. В. Г. Барьяхтара, В. Е. Захаро-

ми среды глюонный (запаздывающий) пропагатор

ва, В. М. Черноусенко, Наук. думка, Киев (1990),

в A₀-калибровке. Здесь «скалярные» поперечный и

с. 417-472.

продольный пропагаторы имеют вид

J.-P. Blaizot and E. Iancu, Phys. Rep. 359, 335

(2002).

^∗Δ^t(k) =

^∗Δ^l(k) =

, (A.9)

k² - Π^t(k)

k² - Π^l(k)

E. Braaten and R. D. Pisarski, Nucl. Phys. B 337,

где

569 (1990).

10.

J.-P. Blaizot and E. Iancu, Nucl. Phys. B 417, 608

Π^t(k) =

Π^μν(k)P_μν(k), Π^l(k) = Π^μν(k)Qμν(k).

(1994).

Поляризационный тензор Π_μν(k) в приближении

11.

Yu. A. Markov and M. A. Markova, Ann. Phys. 302,

жестких температурных петель имеет вид

172 (2002).

(

∫

)

12.

Д. М. Гитман, И. В. Тютин, Каноническое кван-

dΩ v^μv^ν

Π^μν(k) = 3ω2pl u^μu^ν - ω

тование полей со связями, Наука, Москва (1986).

4π v · k + iϵ

13.

V. P. Nair, Phys. Rev. D 48, 3432 (1993).

а продольный и поперечный проекторы определя-

ются, соответственно, следующими выражениями:

14.

V. P. Nair, Phys. Rev. D 50, 4201 (1994).

ũ_μ(k)ũ_ν(k)

15.

J.-P. Blaizot and E. Iancu, Nucl. Phys. B 434, 662

Q_μν(k) =

u²(k)

(1995).

(A.10)

(k · u)

P_μν(k) = g_μν - u_μu_ν -

Q_μν(k)

16.

О. К. Калашников, В. В. Климов, ЯФ 31, 1357

k²

(1980).

где, в свою очередь, лоренц-ковариантный 4-вектор

17.

А. С. Шварц, Математические основы квантовой

ũ_μ(k) задается формулой (5.5).

теории поля, Атомиздат, Москва (1975).

18.

Н. Н. Боголюбов, Д. В. Ширков, Введение в тео-

ЛИТЕРАТУРА

рию квантованных полей, Наука, Москва (1976).

1. Б. Б. Кадомцев, в сб. Вопросы теории плазмы,

19.

V. I. Man’ko, G. Marmo, E. C. G. Sudarshan, and

вып. 4, под ред. М. А. Леонтовича, Атомиздат,

F. Zaccaria, Phys. Scripta 55, 528 (1997).

Москва (1964), с. 188-339.

20.

А. И. Ахиезер, И. А. Ахиезер, Р. В. Половин и др.,

2. Л. Коврижных, ЖЭТФ 49, 237 (1965).

Элекродинамика плазмы, Наука, Москва (1974).

3. В. Е. Захаров, ЖЭТФ 51, 688 (1966).

21.

H. A. Weldon, Phys. Rev. D 58, 105002 (1998).

4. В. А. Липеровский, В. Н. Цытович, Изв. вузов. Ра-

22.

D. Metaxas and V. P. Nair, Int. J. Mod. Phys. A 16,

диофизика XII, 823 (1969).

1249 (2001).

341