ЖЭТФ, 2020, том 157, вып. 3, стр. 442-453

О ФУНДАМЕНТАЛЬНОМ ПРЕДЕЛЕ СКОРОСТИ ГЕНЕРАЦИИ

СЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ В КВАНТОВЫХ

ГЕНЕРАТОРАХ С НЕПРЕРЫВНОЙ ПЕРЕМЕННОЙ

С. Н. Молотков^*

Институт физики твердого тела Российской академии наук

142432, Черноголовка, Московская обл., Россия

Академия криптографии Российской Федерации

121552, Москва, Россия

Факультет вычислительной математики и кибернетики,

Московский государственный университет им. М. В. Ломоносова

119899, Москва, Россия

Центр квантовых технологий,

Московский государственный университет им. М. В. Ломоносова

119899, Москва, Россия

Поступила в редакцию 16 июля 2019 г.,

после переработки 16 июля 2019 г.

Принята к публикации 1 сентября 2019 г.

Минимальными математическими средствами получено фундаментальное ограничение на скорость ге-

нерации случайных чисел в квантовых генераторах случайных чисел с непрерывной переменной. Данное

ограничение справедливо при любой интенсивности сигнала — любого числа фотонов в квантовом состо-

янии. При больших числах заполнения скорость генерации случайных чисел логарифмически растет с

увеличением числа фотонов, но всегда остается конечной. При малом числе фотонов скорость генерации

пропорциональна числу фотонов. При любом числе фотонов предельная скорость генерации случайных

чисел пропорциональна частотной полосе сигнала — квантового состояния.

DOI: 10.31857/S0044451020030050

горитмов и систем квантового распределения клю-

чей. Практически для всех упомянутых применений

1. ВВЕДЕНИЕ

требуются случайные числа, полученные исключи-

Случайные числа и генераторы случайных чисел

тельно с физических генераторов.

широко используются в различных областях науки

В квантовой криптографии, которая по сути

и техники, например, в физике при моделировании

является процедурой согласования двух независи-

методом Монте-Карло. Наиболее широкое примене-

мых случайных последовательностей на передаю-

ние случайные числа находят в криптографии. В

щей и принимающей сторонах посредством посылки

криптографии, в том числе и квантовой, генератор

и измерения квантовых состояний, требуется очень

случайных чисел является одним из основных эле-

большой объем случайных чисел. Статистические

ментов, характеристики которого определяют крип-

свойства случайной последовательности и скорость

тостойкость системы.

генерации являются главными критериями качества

В криптографии случайные последовательности

таких генераторов.

используются для генерации секретных ключей в

системах симметричного шифрования, генерации

В математических генераторах случайных, точ-

паролей, PIN-кодов для различных типов пластико-

нее псевдослучайных, чисел случайная последова-

вых карт, кодов аутентификации, вероятностных ал-

тельность получается как результат математическо-

го преобразования, обычно рекуррентного, некото-

^* E-mail: sergei.molotkov@gmail.com

рого затравочного числа. Любой математический

442

ЖЭТФ, том 157, вып. 3, 2020

О фундаментальном пределе скорости генерации...

генератор выдает псевдослучайную последователь-

статистика фотоотсчетов, то возможна доказуемая

ность, которая полностью предсказуема, если из-

экстракция абсолютно случайной последовательно-

вестны начальные условия — затравочное число.

сти 0 и 1 [2].

Физические генераторы основаны на измерении

Вторая группа в качестве исходной случайности

состояния физической системы с дальнейшей экс-

использует непрерывную случайную величину. На-

тракцией последовательности 0 и 1 из результатов

пример, такой величиной может быть квадратур-

измерений. При измерении классической системы

ная компонента поля при гомодинном детектирова-

случайность результата измерения связана только с

нии [3]. В последнем случае, по-видимому, прихо-

неизвестностью начальных условий. В этом смысле

дится делать предположения о статистических свой-

последовательность результатов измерений являет-

ствах распределения флуктуаций фазы. Исходной

ся псевдослучайной — полностью определяется, при

случайной величиной для дальнейшего преобразо-

известном законе эволюции, начальными условия-

вания в последовательность 0 и 1 является разность

ми.

сигналов с двух классических детекторов, работаю-

В квантовых генераторах случайных чисел слу-

щих не в режиме счета фотонов, а в линейном ре-

чайность возникает как результат измерения состоя-

жиме. Случайная измеряемая величина возникает

ния квантовой системы. Эволюция квантовой сис-

как разность токов двух классических фотодетек-

темы самой по себе также полностью детерминиро-

торов. Поэтому в этом случае сложно контролиру-

вана, поскольку описывается дифференциальными

емым образом выделить квантовую составляющую

уравнениями с начальными условиями, но резуль-

сигнала. Например, шум Джонсона - Найквиста до-

тат измерений принципиально непредсказуем — яв-

вольно трудно, а практически, по-видимому, невоз-

ляется случайным, т. е. истинная случайность имеет

можно контролируемым образом отделить от кван-

место только в квантовой области.

тового шума. По этой причине практически невоз-

Результат измерения над квантовой системой,

можно доказать, что источник первичной физиче-

приготовленной каждый раз в одном и том же на-

ской случайности действительно является кванто-

чальном условии и испытывающей одну и ту же эво-

вым. Однако это не самая главная проблема с гене-

люцию, будет принципиально приводить к непред-

раторами случайных чисел с непрерывной перемен-

сказуемому результату. В этом смысле случайность

ной как с классическими, так и квантовыми. Суще-

встроена в микромире и возникает как результат из-

ствуют фундаментальные ограничения на скорость

мерения.

генерации случайных чисел в таких генераторах.

Принципиально важно уметь экспериментально

1. Любой случайный физический процесс

—

проверять источник первичной случайности, из ко-

квантовый или классический — имеет спектр на по-

торого посредством постобработки возникает слу-

ложительной полуоси частот. В этом случае степень

чайная последовательность 0 и 1. При разработке

убывания корреляций непрерывной случайной вели-

генераторов случайных чисел недостаточно того об-

чины в разнесенные моменты времени, строго го-

стоятельства, что тесты на случайность по неко-

воря, не может быть даже экспоненциальной, что

торому статистическому критерию проходят. Это

диктуется фундаментальной теоремой Винера - Пэ-

лишь необходимое условие. Принципиально важен

ли [4]. Это означает, что извлекаемые из случай-

источник первичной случайности, который исполь-

ного процесса в разные моменты времени резуль-

зуется для получения равнораспределенной после-

таты измерений могут оказываться коррелирован-

довательности 0 и 1 и который является действи-

ными (зависимыми). Формально независимыми из-

тельно источником случайности по соображениям,

мерения становятся только при разнесении момен-

не зависящим от тестов. Многие генераторы псевдо-

тов измерения во времени на бесконечный интервал.

случайных чисел проходят тесты, но, очевидно, не

В этом случае возникает вопрос: можно ли вообще

производят истинно случайных последовательно-

при таких редких измерениях добиться приемлемой

стей. Обзор различных реализаций квантовых гене-

скорости генерации и нужного статистического ка-

раторов случайных чисел можно найти в работе [1].

чества случайных последовательностей?

Квантовые генераторы случайных чисел можно раз-

2. Второй вопрос связан с «мелкостью» дискре-

делить на две группы.

тизации непрерывной случайной величины. Фор-

Первая группа квантовых генераторов случай-

мально значения непрерывной случайной величи-

ных чисел в качестве первичной физической случай-

ны можно дискретизировать со сколь угодно ма-

ности использует дискретные фотоотсчеты [2]. Ес-

лым масштабом. В этом случае, например, припи-

ли на физическом уровне достигнута пуассоновская

сывая каждому интервалу случайное число (случай-

443

С. Н. Молотков

ЖЭТФ, том 157, вып. 3, 2020

ный блок 0 и 1), можно получить за один акт из-

тод используется, например, для случайных генера-

мерения сколь угодно длинный блок случайных 0

торов в [6].

и 1 (конечно, с оговорками из предыдущего пунк-

Результаты последовательных актов измерений

та). Физически очевидно, что масштаб дискретиза-

(x₁, x₂, . . . , x_n) над квантовой системой в общем

ции измеряемой физической величины, из-за огра-

случае не являются статистически независимыми.

ничений квантовой механики, не может быть сколь

Функция распределения не распадается на произ-

угодно мелким.

ведение P_X(x₁, x₂, . . ., x_n) = P(x1)P(x2)...P(xn).

Ответам на эти принципиальные вопросы посвя-

Число истинно случайных битов дается минималь-

щена настоящая работа.

ной энтропией Реньи [7]

H_min = - log(

max P_X (x₁, x₂, . . . , x_n)),

(2)

2. МЕТОДЫ ЭКСТРАКЦИИ СЛУЧАЙНЫХ

PX(x1,x2,...,xn)

ПОСЛЕДОВАТЕЛЬНОСТЕЙ

ниже везде log

≡ log₂. Экстракторы позво-

Интуитивно понятно, что всякий случайный про-

ляют извлечь случайность из распределения

P_X(x₁, x₂, . . . , x_n) = PX(x1)PX(x2)...PX(xn) (см.,

цесс содержит некоторое максимальное количество

истинно случайных 0 и 1. При экстракции случай-

например, [5-7]).

ных битов 0 и 1 из значений случайной величины,

Однако проблема состоит в том, что в реальной

получаемой при измерении в физическом процессе,

ситуации значения случайной величины в разные

важно знать верхнюю границу этой истинной слу-

моменты измерений коррелированы и, соответствен-

чайности, для того чтобы гарантировать, что извле-

но, функция распределения P (x₁, x₂, . . . , x_n) не есть

каются истинно случайные, а не коррелированные

произведение отдельных независимых функций рас-

биты 0 и 1.

пределения и неизвестна, поэтому приходится стро-

Наша задача будет состоять в получении фунда-

ить предположения, которые трудно эксперимен-

ментальной верхней границы скорости экстракции

тально проверить. И, как следствие, трудно дока-

истинной случайности для непрерывной случайной

зать случайность извлекаемых битов 0 и 1.

величины в квантовом случае.

Вторая группа методов основана на том, что-

Методы извлечения случайности можно разде-

бы на физическом уровне реализовать такой про-

лить на два класса. Первый часто называют универ-

цесс, который обеспечил бы доказуемую на физи-

сальным. Универсальные методы экстракции слу-

ческом уровне независимость значений случайной

чайности (см., например, [5]) позволяют получить

величины в разные моменты времени. Такой под-

последовательность 0 и 1 сколь угодно близкую к

ход был реализован в работе [2]. При таком под-

истинно случайной. Мерой близости является сле-

ходе, когда последовательные исходы независимы,

довое расстояние — расстояние Колмогорова между

P_X(x₁, x₂, . . . , x_n) = P_X(x₁)P_X(x₂). . .P_X(x_n), мини-

двумя распределениями вероятностей

мальная энтропия при n → ∞ переходит в энтропию

∑

Шеннона, оценить которую для независимых испы-

||P_X - P_U ||₁ =

|P_X (x₁, x₂, . . . , x_n) -

таний можно гораздо проще и надежнее. И главное,

xi=0,1

для независимых испытаний доказывается, что по-

- P_U(x₁,x₂,...,x_n)| < ε,

(1)

лучаемые биты 0 и 1 действительно являются ис-

тинно случайными. При этом алгоритмически с по-

P_U (x₁, x₂, . . . , x_n) = P_U (x₁)P_U (x₂). . . P_U (x_n),

линомиальной сложностью можно извлечь всю слу-

чайность [8], содержащуюся в физическом процессе.

P_U (0) = P_U (1) =

Еще одно принципиально важное обстоятельство —

где P_X — функция распределения полученной по-

при таком подходе не требуется знать сами вероят-

следовательности 0 и 1. Вероятность P_X (x) назы-

ности P_X (x₁, x₂, . . . , x_n) = P_X (x₁)P_X (x₂) . . . P_X (x_n)

вается ε-близкой к истинно случайной. Параметр

при экстракции случайных 0 и 1 [2]. Методы и

близости ε определяется требованиями по использо-

устройства, использующие данную идеологию, ко-

ванию случайных последовательностей. Требуемая

гда алфавит исходной дискретной случайной вели-

близость к идеальной случайной последовательно-

чины является бинарным (есть фотоотсчет, нет фо-

сти достигается сжатием (хешированием) при по-

тоотсчета), были реализованы в работе [2]. Причем

мощи универсальных хеш-функций второго поряд-

методы, использованные в [2], переносятся на дис-

ка, которые сами являются случайными функция-

кретную случайную величину с произвольным ко-

ми, что требует затравочной случайности. Такой ме-

нечным алфавитом.

444

ЖЭТФ, том 157, вып. 3, 2020

О фундаментальном пределе скорости генерации...

3. ДИСКРЕТНЫЙ ИСТОЧНИК БЕЗ

следовательности символов x_i, генерируемых физи-

ПАМЯТИ ПЕРВИЧНОЙ СЛУЧАЙНОСТИ

ческим источником первичной случайности. Коли-

чество истинно случайных битов при условии неза-

Сначала рассмотрим процесс, когда при изме-

висимости отдельных исходов в первичной последо-

рениях над физической системой возникает слу-

вательности определяется как

чайная величина с дискретным алфавитом. Коли-

чество истинно случайных битов 0 и 1, которые

∑

можно извлечь при n-кратном использовании дис-

H_n(X) = -

P_X(xi1 )ni1 ×

кретного случайного источника с алфавитом X =

nⁱ1+ni2+...+niM=n

= {x_i}Mi=1 и распределением вероятностей над ал-

× P_X(xi2)ni2 . . . P_X(xiM

фавитом P_X(x_i) при больших n, определяется эн-

)niM ni1 !ni2 ! . . .niM !^×

(

)

тропией Шеннона

× log

(4)

∑

ni1 !ni2 ! . . . niM !

H(X) = - P_X (x_i) log(P_X (x_i)).

(3)

i=1

Согласно теореме об асимптотической равнораспре-

Число истинно случайных битов 0 и 1 стремится

деленности [9], типичные последовательности име-

к nH(X) и не превосходит эту величину. Данный

ют вероятность, стремящуюся к единице при боль-

факт следует из свойства асимптотической равно-

ших n. С учетом этого факта, а также используя

распределенности [9]. Неформально говоря, при n →

формулу Стирлинга

→ ∞ имеется 2nH(X) типичных последовательнос-

тей xi1 xi2 , . . ., xin , которые асимптотически равно-

√

⁽n

n! ≈

2πn

)ⁿ ,

(5)

вероятны.

В реальной ситуации извлечение случайных би-

тов происходит из конечных блоков первичной по- в главном приближении имеем

nⁿ

→

(6)

ni1 !ni2 ! . . . niM !

(P_X (x₁)n)^PX(x1)n(P_X (x₂)n)^PX(x2)n . . . (P_X (x_M )n)^PX(xM)n

Поскольку

∑

P_X(x_k) = 1,

(7)

k=1

с учетом (4)-(6) находим

(

)

H_n(X) → log

(P_X (x₁)n)^PX(x1)n(P_X (x₂)n)^PX(x2)n . . . (P_X (x_M )n)^PX(xM)n

∑

= -n P_X(x_i)log(P_X(x_i)) = nH(X),

(8)

i=1

где ik — номер позиции k-го элемента алфавита.

линга (5) и того факта, что число появлений каж-

Формула (8) имеет простую интерпретацию. Число

дого символа в асимптотическом пределе nik

→

последовательностей, которые содержат ni1 симво-

→ nP_X(x_i

), и соответственно вероятность появле-

лов xi1 , ni2 символов xi2 и т. д., равно биномиально-

ния стремится к P_X (x_i

)nPX (xik⁾. Как следствие, по-

му коэффициенту (второй сомножитель под знаком

лучаем формулу (8).

суммы), величина которого есть число способов раз-

мещения элементов в строке длиной n.

Дальнейшая задача состоит в экстракции слу-

Первый сомножитель — это вероятность появ-

чайных битов из блоков последовательностей дли-

ления каждой последовательности с данным чис-

ной n, генерируемых источником с дискретным ал-

лом каждого символа. При больших n величина

фавитом и представляющих собой первичную слу-

H_n(X) → nH(X), это следует из формулы Стир-

чайность.

445

С. Н. Молотков

ЖЭТФ, том 157, вып. 3, 2020

Все последовательности с одинаковым коли-

кие-то содержательные утверждения часто невоз-

чеством каждого символа, различающиеся лишь

можно. Поскольку любой реализуемый физический

порядком символов, являются равновероятными.

сигнал, при наблюдении которого возникает слу-

Все множество последовательностей разбивается на

чайная переменная x, имеет конечную мощность,

классы равновероятных последовательностей, каж-

то естественным ограничением является ограничен-

дый класс отвечает определенному разбиению n =

ность величины «мощности», имеем

= ni1 + ni2 + ... + niM (n_i

= 0, 1, . . ., n, k = 1,

∞

∫

2, . . ., M). После нумерации всех последовательнос-

x²p(x)dx ≤ σ².

(10)

тей в каждом классе, точнее, бинарное представле-

ние номера последовательности в классе дает блок

−∞

истинно случайных битов 0 и 1 (см. детали в [8] и в

При этом максимум дифференциальной энтропии

[2]). Возможен эффективный способ извлечения ис-

(9) достигается на гауссовском распределении [9,10]

тинно случайных битов при условии независимости

(

)

исходных символов [8], который был реализован в

x²

p(x) =

√

exp

устройствах [2].

2πσ

2σ²

В заключение данного раздела можно резюми-

ровать: мерой и верхней границей истинной случай-

В этом случае для дифференциальной энтропии (9)

ности в случае источника с дискретным алфавитом

получаем

является энтропия Шеннона, причем данная верх-

H(p) =

log(2πeσ²).

(11)

няя граница конструктивно достижима с полино-

миальными вычислительными ресурсами по длине

Если в случае дискретного источника, как было по-

первичной последовательности.

казано выше, энтропия Шеннона является мерой ис-

тинной случайности, содержащейся в источнике, то

в случае непрерывной случайной величины ситуа-

4. ДИФФЕРЕНЦИАЛЬНАЯ ЭНТРОПИЯ

ция сложнее.

НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

Дифференциальная энтропия не является пря-

мой мерой истинной случайности, которую можно

Принципиально иная ситуация возникает при из-

извлечь из источника случайного непрерывного сиг-

влечении истинно случайных битов 0 и 1 из непре-

нала. Более того, дифференциальная энтропия мо-

рывной случайной переменной. Как правило, в ре-

жет быть даже отрицательной.

альности непрерывная случайная величина возни-

В дальнейшем нас будут интересовать фунда-

кает при наблюдении физического процесса, завися-

ментальные ограничения на скорость извлечения

щего от времени. В каждый момент времени t изме-

истинно случайных битов 0 и 1 из непрерывного слу-

рение дает значение случайной физической величи-

чайного сигнала.

ны x(t). Для того чтобы обозначить суть проблемы

В классической области любая величина может

при работе с непрерывной переменной, рассмотрим

быть измерена со сколь угодно большой точностью.

для начала случайную величину x в некоторый фик-

Классическая физика не накладывает никаких фун-

сированный момент времени t, индекс t пока опу-

даментальных ограничений на точность измерения.

стим.

Это означает, что интервал изменений непрерывной

Аналогом энтропии Шеннона для дискретного

случайной классической величины может быть дис-

источника без памяти, которая служит мерой коли-

кретизирован на сколь угодные малые интервалы

чества информации (случайности), содержащейся в

Δ. Дискретизация превращает непрерывную слу-

дискретной случайной величине, в случае непрерыв-

чайную величину в дискретную случайную величи-

ной случайной величины x ∈ (-∞, ∞) с функцией

ну X_Δ.

плотности распределения вероятности p(x), являет-

Дискретизация состоит в следующем. При изме-

ся дифференциальная энтропия [9]. По определению

рении непрерывной случайной величины весь диа-

имеем

∫∞

пазон значений разбивается на интервалы Δ, при

этом функция распределения становится равной

H(p) = - p(x) d log(p(x)).

(9)

-∞

∫

Если не вводить никаких дополнительных ограни-

Δp(x_i) =

p(x) dx,

(12)

чений на случайную переменную x, то сделать ка-

iΔ

446

ЖЭТФ, том 157, вып. 3, 2020

О фундаментальном пределе скорости генерации...

где x_i — «средняя» точка в интервале (iΔ, (i + 1)Δ).

сигнал до масштабов, меньших отдельного фотона.

В результате дискретизации энтропия принимает

Любой интенсивный сигнал, хоть и содержит мак-

вид

роскопически большое число фотонов, но все же ко-

∑

нечное.

H(X_Δ) = - Δp(x_i) log(p(x_i)) - log Δ,

(13)

Кратко резюмируем сказанное — квантовая при-

рода микромира должна ограничивать степень дис-

ⁱ∑

при Δ → 0 имеем_i Δp(x_i) log(p(x_i)) → H(p), тогда

кретизации, что неизбежно должно приводить к ко-

энтропия

нечности энтропии сигнала, соответственно, накла-

H(X_Δ) = H(p) - log Δ.

(14)

дывать фундаментальные ограничения на скорость

экстракции истинно случайных битов 0 и 1.

Для гауссовского сигнала после дискретизации энт-

Для того чтобы выяснить фундаментальные

ропия становится равной

ограничения на скорость экстракции случайных би-

2πeσ

H (X_Δ) =

log

(15)

тов, необходимо сразу рассматривать сигнал как

квантовый — квантовое состояние, которое может

После дискретизации могут быть использованы ме-

содержать любое число фотонов.

тоды экстракции истинно случайных 0 и 1, описан-

Следующая проблема, которая возникает при

ные выше. Но при этом, при Δ → 0, энтропия дис-

экстракции случайных битов из непрерывного слу-

кретного источника (14), (15) стремится к бесконеч-

чайного классического или квантового сигнала, со-

ности.

стоит в следующем. Измерения над сигналом x(t)

Это означает, что за один акт измерения можно

проводится, как правило, через определенные про-

получить сколь угодно много случайных битов 0 и 1.

межутки времени τ. Обычно выбирается стационар-

Действительно, разобьем диапазон изменений

ный случайный процесс. Для того чтобы блоки слу-

непрерывной случайной величины на интервалы та-

чайных битов 0 и 1, извлекаемых из непрерывной

ким образом, чтобы вероятности попадания в каж-

случайной величины в момент t_i и момент ti±1, бы-

дый интервал были одинаковыми. Припишем каж-

ли независимыми, значения непрерывной случайной

дому интервалу его номер в лексикографическом

величины x(t_i) и x(ti±1) тоже должны быть стати-

порядке, начиная с 0. Бинарное представление но-

стически независимыми. В противном случае слу-

мера и будет случайным блоком 0 и 1. Очевидно,

чайные биты, полученные в разные моменты време-

что при стремлении масштаба дискретизации к ну-

ни, будут зависимыми (коррелированными), т. е. не

лю, Δ → 0, за один акт измерения можно получить

будут случайными.

сколь угодно большой блок истинно случайных 0 и

Для стационарного процесса степень корреля-

1, что является явным абсурдом.

ции случайной величины в разные моменты времени

Для того чтобы устранить данное противоречие

x(t_i) и x(ti±1) определяется корреляционной функ-

здравому смыслу, обычно говорятся слова, что про-

цией, зависящей только от разности моментов вре-

цесс измерений сам вносит шум, поэтому интервал

мени [10]:

дискретизации нельзя выбирать меньше амплитуды

K(τ) = E[x(t)x(t + τ)].

(16)

шума.

Такое заметание проблемы «под ковер» не яв-

Интуитивно ясно, что чем больше частотная поло-

ляется решением. Да и с логической точки зрения

са сигнала x(t), тем быстрее убывают корреляции

такой подход абсурден, поскольку измеряется об-

между значениями сигнала во времени. Чем быст-

щее значение переменной, которое содержит вклад

рее убывают корреляции в моменты t и t + τ, тем

от всех процессов, а процесс дискретизации являет-

большей скорости генерации случайных чисел мож-

ся внешним. Грубо говоря, количество извлекаемой

но достичь при измерении x(t) через меньшие интер-

случайности зависит от «волевого решения по дис-

валы времени τ. Однако и здесь возникают фунда-

кретизации», поэтому невозможно всерьез говорить

ментальные ограничения, которые имеют место как

о случайности извлекаемых битов 0 и 1.

в классическом, так и квантовом случаях (см. ни-

Ясно, что любой физический сигнал нельзя дис-

же).

кретизировать до бесконечности в сторону уменьше-

Любой физический сигнал имеет спектр на по-

ния интервала Δ. На каком-то этапе неизбежно воз-

ложительной полуоси частот ω, т. е. ω ∈ [0, ∞), что

никнут ограничения, диктуемые квантовой приро-

приводит к фундаментальным ограничениям на ско-

дой сигнала, причем независимо от его интенсивно-

рость уменьшения корреляционной функции K(τ)

сти. Фигурально говоря, нельзя дискретизировать

во времени. Согласно теореме Винера - Пэли [4], для

447

С. Н. Молотков

ЖЭТФ, том 157, вып. 3, 2020

любой квадратично интегрируемой функции по вре-

ограничено интервалом [0, T] и пусть вне этого ин-

мени (имеющей конечный интеграл, в нашем слу-

тервала сигнал исчезающе мал (точное условие ма-

чае K(τ)), имеющей спектр на полуоси (K(ω), ω ∈

лости см. ниже). Пусть источник непрерывного сиг-

∈ [0, ∞)), следующий интеграл должен сходиться

нала выдает только такие сигналы, которые имеют

(быть меньше бесконечности):

ограниченную частотную полосу и локализованы,

∞

насколько это допустимо природой, во временном

∫

| log(K(τ))|

окне [0, T ].

dτ < ∞.

(17)

1+τ²

Если источник может генерировать N ортого-

−∞

нальных состояний с такими свойствами и число

Из формулы (17) следует, что коррелятор K(τ) не

таких состояний ограничено (конечно), то при рав-

может уменьшаться даже экспоненциально. Экспо-

новероятной генерации состояний будет достигать-

ненциальное убывание (∝ e^-τ ) приводило бы к лога-

ся максимальная энтропия, величина которой и бу-

рифмической расходимости интеграла в (17). Хотя

дет определять скорость генерации случайных чи-

убывание, сколь угодно близкое к экспоненциально-

сел. Ортогональность состояний нужна для их раз-

му, не запрещается (см. ниже).

личимости.

Данное ограничение действительно является

фундаментальным и возникает во многих физичес-

ких ситуациях. Например, степень локализуемости

5. БАЗИСНЫЕ ФУНКЦИИ — ВОЛНОВЫЕ

безмассового квантового поля фотонов также регу-

ФУНКЦИИ ВЫТЯНУТОГО СФЕРОИДА

лируется теоремой Винера - Пэли [4] (см. детали в

Перейдем к более точным формулировкам. Воз-

работе [11]).

можны два способа представления сигналов с огра-

Идеальной ситуация для скорости экстракции

ниченным частотным спектром как функции вре-

случайных чисел была бы, если бы коррелятор был

мени. Первый способ основан на фундаментальной

δ-функционным:

теореме В. А. Котельникова об отсчетах [12]. Сиг-

K(τ) ∝ δ(τ).

(18)

нал с конечным частотным спектром и почти лока-

лизованный во временном окне [0, T ] представляется

В этом случае можно было бы измерять значение

в виде разложения в ряд по отсчетным функциям,

случайной величины через сколь угодно малые вре-

которые играют роль базисных функций. Для слу-

менные интервалы. Однако для такого поведения

чайного процесса x(t) имеем

коррелятора спектр должен быть равномерным на

[

(

)]

всей оси частот, включая отрицательные частоты,

2πn

ω ∈ (-∞,∞), что для физической системы невоз-

∑

⁽2πn)sinΩt-

x(t) =

(

)

(20)

можно. Спектр может быть только на положитель-

2πn

-∞

Ω t-

ной полуоси. Даже для равномерного спектра на по-

луоси, K(ω) ∝ θ(ω), временное поведение коррелято-

где значения сигнала c_n = x (2πn/Ω) в отсчетные

ра имеет вид

моменты t_n = 2πn/Ω являются случайными непре-

рывными величинами. Для случайного сигнала с

K(τ) ∝ δ(τ) +

(19)

ограниченным спектром, и приближенно ограничен-

т. е. коррелятор становится обобщенной функцией,

ного по времени, в разложении остаются только N =

которая имеет степенные хвосты.

= Ω T слагаемых.

Поскольку любое измерительное устройство име-

Второй способ описания состоит в выборе функ-

ет эффективно ограниченную частотную полосу,

ций с ограниченным спектром, максимально лока-

математически удобнее формулировать задачу сле-

лизованных в окне ]0, T ], в качестве базисных функ-

дующим образом (и, по-видимому, это единствен-

ций. Коэффициенты разложения сигнала по этим

ная формулировка, при которой можно получить

функциям будут играть роль непрерывных случай-

надежные результаты). Для того чтобы явно не

ных величин. Число таких ортогональных функций,

вводить в рассмотрение измерительное устройство,

локализованных почти целиком в окне ]0, T ], также

удобно считать, что сам физический сигнал имеет

равно N = ΩT .

конечную частотную полосу ω ∈ [0, Ω] (положение

Оба подхода приводят к одинаковым результа-

на оси частот, как увидим ниже, не важно, мож-

там, так как число независимых степеней свободы в

но всегда сдвинуть интервал частот в нужное по-

сигнале одинаково и определяется параметром N =

ложение). Далее, пусть время наблюдения сигнала

= ΩT . Мы выберем второй способ, поскольку он

448

ЖЭТФ, том 157, вып. 3, 2020

О фундаментальном пределе скорости генерации...

более удобен при описании ситуации в квантовом

(c)

случае. В классическом случае сигнал измеряется в

отсчетные моменты. В квантовом случае измерение

в том или ином виде является проектированием на

определенное квантовое состояние, поэтому (см. ни-

же) второй способ более удобен в этом случае.

Условие максимальной локализации сигнала во

временном окне [0, T ]

∫

max

x²(t)dt

(21)

ω∈[0,Ω]

приводит к известному интегральному уравнению

для (см. детали в [13-15])

ln(2

∫

sin[Ω(t - t^′)]

λ_n(c)ϕ_n(t, c) =

ϕ_n(t^′, c)dt^′,

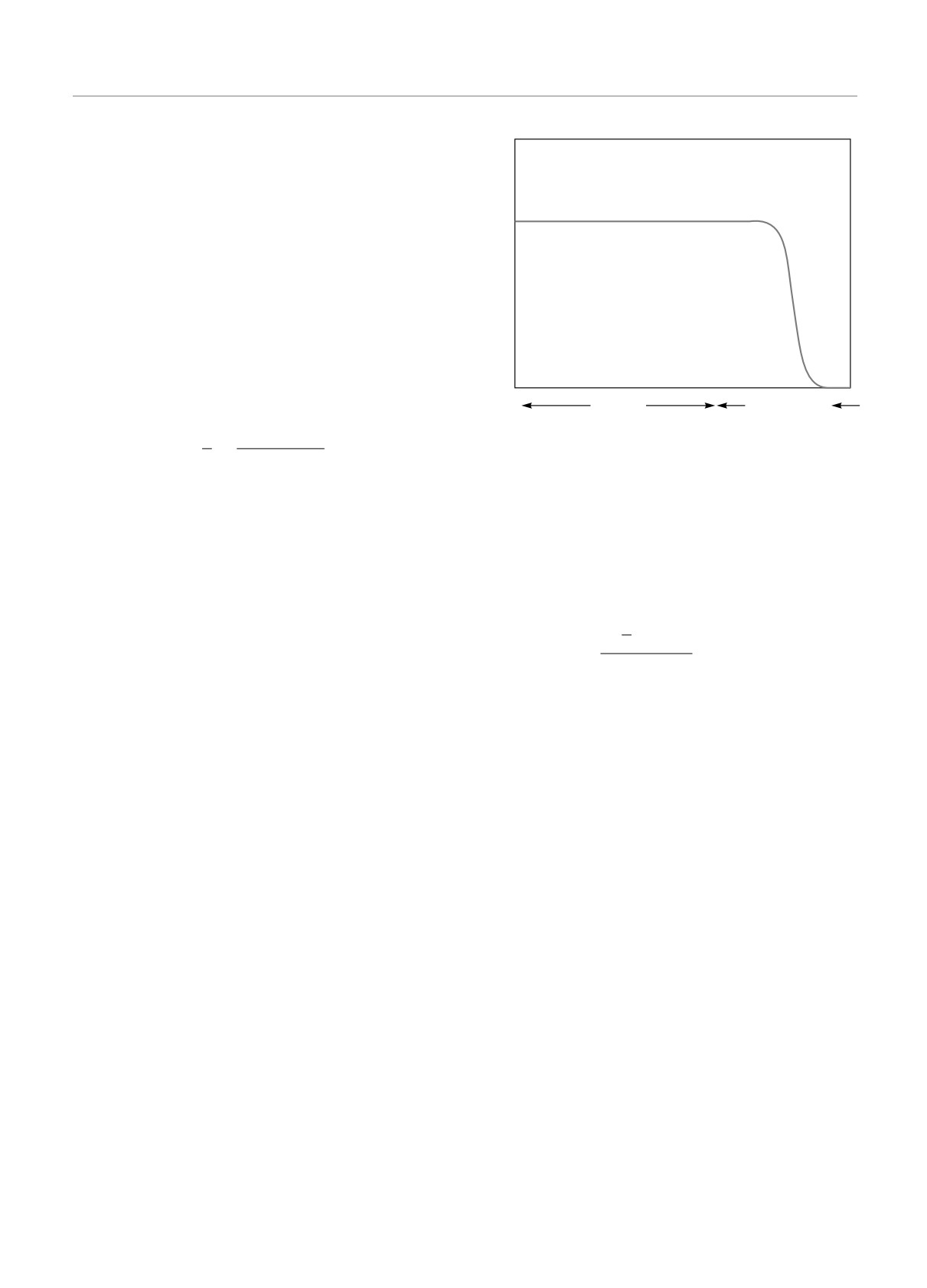
Рис. 1. Качественная иллюстрация поведения собственных

t-t^′

(22)

чисел в зависимости от номера собственного числа

2c = ΩT.

Решением являются замечательные функции, назы-

ваемые волновыми функциями вытянутого сферои-

временном окне с субэкспоненциальной точностью

да [13-15]. Данные функции возникают в ряде задач

(качественная иллюстрация этого свойства приведе-

математической физики.

на на рис. 1, см. детали в [13, 14]),

При разных n и n^′ функции ортогональны как

на конечном [0, T ], так и на бесконечном (-∞, ∞)

√π8ⁿcn+1/2

интервалах,

λ_n(c) ∼ 1 -

e^-c, c = ΩT.

(25)

∫

ϕ_n(t, c)ϕ_n′ (t, c)dt = λ_n(c)δ_n,n′ ,

Как видно из (25), степень локализации собствен-

(23)

ных значений при заданном номере n является суб-

∞

∫

экспоненциальной от временного окна T из-за мно-

ϕ_n(t, c)ϕ_n′ (t, c)dt = δ_n,n′ .

жителя cn+1/2 перед экспонентой. Имеется при-

-∞

мерно log(ΩT ) функций в переходной области (см.

Забегая вперед, скажем, что ортогональность как

рис. 1), остальные почти равны нулю в окне [0, T ].

на конечном, так и на бесконечном интервалах поз-

Принципиальным фактом при использовании в

воляет совершить аккуратный предельный переход

качестве базисных функций вытянутого сфероида

к бесконечности, когда временное окно наблюдения

является следующий результат [13, 14]. Для любого

→ ∞. Свойство ортогональности при предель-

ε > 0 имеют место равенства

ном переходе сохраняет свойство различимости ба-

зисных состояний.

Степень локализации во временном окне [0, T ]

lim

λΩT(1-ε) = 1,

lim

λΩT(1+ε) = 0.

(26)

ΩT →∞

собственной функции с номером n уравнения (22)

дается ее собственным числом:

Неформально это означает, что имеется ΩT номеров

∫

функций, которые почти целиком локализованы во

ϕ2n(t, c)dt = λ_n(c).

(24)

временном окне T . Для остальных номеров функции

равны нулю (при этом они остаются нормирован-

Замечательным свойством волновых функций вытя-

ными, нормировка набирается на всем бесконечном

нутого сфероида является их поведение в зависимо-

интервале). Переходная область по номерам имеет

сти от величины параметра ΩT . При ΩT ≫ 1 име-

масштаб ∼ ln(2πΩT ), т. е. является крайне узкой —

ется N = ΩT функций, которые локализованы во

логарифмически узкой по сравнению с ΩT .

449

ЖЭТФ, вып. 3

С. Н. Молотков

ЖЭТФ, том 157, вып. 3, 2020

6. ДИФФЕРЕНЦИАЛЬНАЯ ЭНТРОПИЯ

7. КВАНТОВЫЙ СЛУЧАЙ

НЕПРЕРЫВНОГО СИГНАЛА С КОНЕЧНЫМ

ЧАСТОТНЫМ СПЕКТРОМ

Будем рассматривать квантовые состояния с

ограниченным частотным спектром Ω. Пусть кван-

Сигналы, для наблюдения которых требуется

товое состояние поля содержит M фотонов — бо-

время T , могут быть представлены как

зе-частиц. Состояние имеет носитель в конечной ча-

стотной полосе Ω. В качестве одночастичных базис-

∑

ных состояний выберем волновые функции вытяну-

x(t) =

c_nϕ_n(t), ϕ_n(t) =

√

ϕ_n(t),

(27)

λ_n(c)

того сфероида ϕ_n(ω). Таких функций N = ΩT. Чис-

n≤N

ло многочастичных ортогональных векторов состоя-

где c_n является случайной величиной. Дифферен-

ний с M фотонами, локализованных во временном

циальная энтропия сигнала при наблюдении во вре-

окне T , равно числу способов размещения M фото-

менном окне [0, T ]

нов по N одночастичным состояниям. Число разме-

щений бозе-частиц по N состояниям равно [16]

∑

H(x)_T = - H(c_n),

(28)

(N - 1 + M)!

CMN-1+M =

(33)

n=1

(N - 1)!M!

Вектор состояния, отвечающий размещению — раз-

где H(c_n) — энтропия n-й моды. При ограничении

биению числа n₁ + n₂ + . . . + n_N = M, имеет вид

на мощность сигнала

∫

∑

|Φn1,n2,...,nN 〉= . . .

dω₁dω₂ . . . dωn1 . . . dωn1+1 ×

c2n ≤ σ²N

(29)

Ω Ω

n=1

× dωn1+2 . . . dωn2 , dωnN -1+1dωnN -1+2 . . . dωnN ×

максимум дифференциальной энтропии достигается

× ϕ₁(ω₁)ϕ₁(ω₂). . . ϕ₁(ωn1)ϕ₂(ωn1+1)×

для гауссовского раcпределения c_n, имеем

× ϕ₂(ωn1+2). . . ϕ2(ωn2). . . ϕN(ωnN-1+1)×

∑

× ϕ_N(ωnN-1+2). . . ϕN(ωnN)×

H(X) =

N log(2πeσ²).

(30)

× |ω₁, ω₂, . . . , ωn1 , . . . , ωn1+1, ωn1+2, . . . , ωn2 ,

n=1

(34)

ωnN-1+1, ωnN-1+2, . . . , ωnN 〉.

Опять при неограниченно мелкой дискретизации

Дальнейшая логика рассуждений следующая.

интервала изменений значений непрерывной слу-

При заданном числе фотонов в состоянии M име-

чайной величины энтропия становится равной

ется CMN-1+M (33) ортогональных, а значит, досто-

верно различимых квантовых состояний на интер-

∑

2πeσ²

вале [0, T], которые локализованы почти целиком в

H(X_Δ) =

N log

(31)

n=1

этом окне. Измерения во временном окне позволя-

ют различить все ортогональные состояния. Мак-

Соответственно скорость генерации дифференци-

симальная энтропия источника достигается в том

альной энтропии в единицу времени равна

случае, когда источник генерирует все CMN-1+M ор-

тогональных различимых состояний равновероятно.

H (X_Δ)

Такой источник описывается матрицей плотности —

lim

H (X_Δ)_T = lim

ΩT →∞

ΩT →∞ T

квантовым ансамблем

∑

2πeσ²

Ω log

(32)

ρ(N, M) =

n=1

C^M

N-1+M

∑

|Φn1,n2,...,nN 〉〈Φn1,n2,...,nN |.

(35)

Отсюда видно, что энтропия неограниченно возрас-

n1+n2+...+nN =M

тает с уменьшением Δ. Из формулы (32) видно,

что устранение проблемы с локализацией сигнала не

Измерение над квантовыми состояниями, генериру-

решает проблему с дискретизацией. Проблему дис-

емыми источником, которое позволяет различить

кретизации невозможно логически последовательно

все ортогональные состояния, локализованные во

решить в классической области, для этого нужно

временном окне [0, T ], дается следующим разложе-

квантовое рассмотрение сигнала с самого начала.

нием единицы:

450

ЖЭТФ, том 157, вып. 3, 2020

О фундаментальном пределе скорости генерации...

∑

IN,M =

P_T (n₁, n₂, . . . , n_N )+

Вклад в энтропию за счет исходов измерений вне ок-

n1+n2+...+nN =M

на [0, T ] не превосходит величину последнего слага-

+I^⊥N,M,

(36)

емого в (38) и стремится к нулю в пределе ΩT → ∞.

∑

Отметим, что энтропия в (38) — это просто эн-

I^⊥N,M =

P_⊥(n₁, n₂, . . . , n_N),

тропия Шеннона, а не дифференциальная энтропия.

n1+n2+...+nN =M

Напомним (см. разделы выше), что именно энтро-

где

пия Шеннона определяет число истинно случайных

битов 0 и 1, которые можно извлечь при измерени-

P_T (n₁, n₂, . . . , n_N) = |Φn1,n2,...,nN 〉〈Φn1,n2,...,nN |

ях.

Поскольку N ≫ 1, воспользовавшись формулой

— проектор на квантовое состояние, локализован-

Стирлинга (5) для значения факториала в главном

ное во временном окне [0, T ]; I^⊥N,M — дополнение до

приближении, получаем

полного пространства состояний на всей временной

оси;

(N + M)^N (N + M)^M

CMN-1+M ≈

N^NM^M

P_⊥(n₁, n₂, . . . , n_N ) = |⊥n1,n2,...,nN 〉〈⊥n1,n2,...,nN |

(

)_N (

)_M

(39)

— проектор на состояния, описывающие хвосты

волновых функций вытянутого сфероида вне ок-

на [0, T ].

где M — число фотонов во временном окне [0, T ].

Для вероятности исходов с учетом (36) получаем

Удобно для дальнейшего ввести обозначение M =

= mT, где m имеет смысл числа фотонов в единицу

P_T (n₁, n₂, . . . , n_N ) =

времени и имеет такую же размерность, как часто-

= Tr{P_T (n₁, n₂, . . . , n_N )ρ(N, M)} =

та Ω [1/с], поэтому отношение m/Ω является безраз-

мерным.

λ_N (n₁, n₂, . . ., n_N )

С учетом (38), (39) находим, что энтропия, гене-

C^M

N-1+M

(37)

рируемая источником в единицу времени, равна

P_⊥(n₁, n₂, . . . , n_N) =

= Tr{P_⊥(n₁, n₂, . . . , n_N )ρ(N, M)} =

H(mT, ΩT )

H(m, Ω) = lim

1 - λ_N(n₁,n₂,...,n_N)

ΩT →∞

[

(

)]

(

C^M

m⁾

N-1+M

= Ω log

log

(40)

В каждом акте измерения во временном окне [0, T ]

возникает случайно один из CMN-1+M исходов (37).

где отношение m/Ω имеет смысл числа фотонов в

Соответственно для энтропии фон Неймана источ-

единичной частотной полосе.

ника, которая для ортогональных состояний совпа-

Рассмотрим асимптотики (40) при различных

дает с энтропией Шеннона, получаем

числах фотонов в состоянии. При малом числе фо-

тонов — предельно квантовый сигнал, m/Ω ≪ 1,

H (mT, ΩT ) = H(N, M) =

выражение для скорости генерации энтропии при-

∑

нимает вид

λ_N (n₁, n₂, . . . , n_N )

C^M

⁽m⁾

N-1+M

n1+n2+...+nN =M

H(m, Ω) ≈ Ω

= m,

(41)

(

)

λ_N (n₁, n₂, . . . , n_N )

× log

и она пропорциональна числу фотонов в единич-

C^M

N-1+M

ную частотную полосу. Скорость генерации энтро-

∑

1 - λ_N(n₁,n₂,...,n_N)

пии фактически определяется частотной полосой

C^M

N-1+M

сигнала (или измеряющего устройства, см. замеча-

n1+n2+...+nN =M

(

)

ние выше). Формально ширина частотной полосы в

1 - λ_N(n₁,n₂,...,n_N)

× log

(38)

формуле (41) сокращается, скорость генерации энт-

C^M

N-1+M

ропии пропорциональна числу фотонов, но отсюда

где

не следует, что отсчеты можно делать с любой ско-

ростью — малым временным интервалом между от-

λN (n1, n2, . . . , nN ) = λ11 (N)λ22 (N) . . . λNM (N).

счетами.

451

С. Н. Молотков

ЖЭТФ, том 157, вып. 3, 2020

H(m,

лишь среднее число фотонов как, например, в ко-

герентном состоянии, то формула (40) для скорости

генерации переходит в следующую:

∑

(μ_Ω)^k

H(μ_Ω, Ω) = Ω

e-μΩ

H(k, Ω).

(44)

k=0

Здесь μ_Ω — среднее число фотонов в единичной час-

тотной полосе, H(k, Ω) — парциальная энтропия со-

стояния с k фотонами, см. (40), где нужно заменить

m/Ω → k.

8. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Полезно обсудить связь полученных результатов

2.10¹⁹

4. 10¹⁹

6. 10¹⁹

8. 10¹⁹

10²⁰

для квантового случая с известными результатами

в классической области. Обратимся к формуле (43),

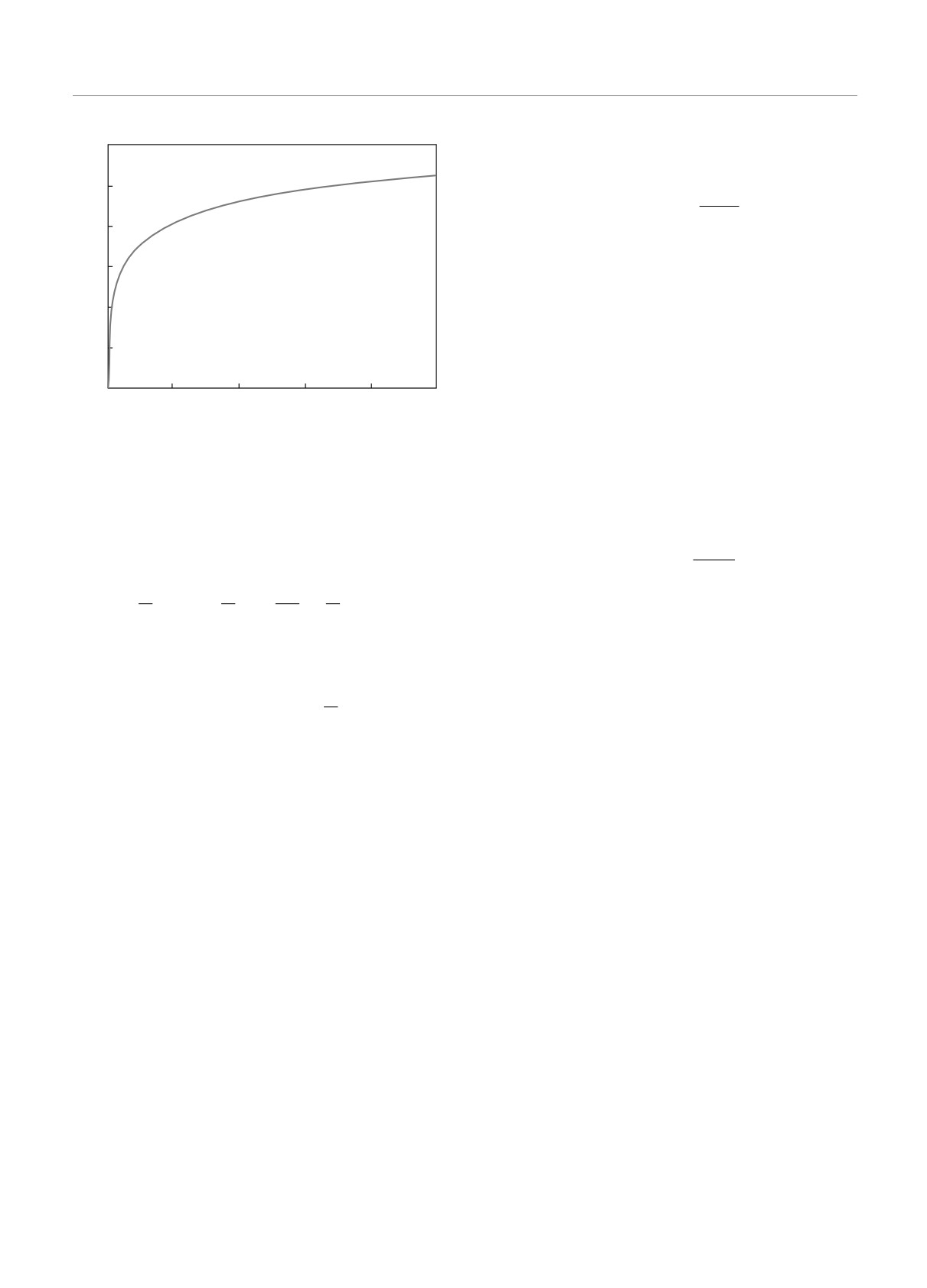
Рис. 2. Предельная скорость генерации случайных битов

которая структурно похожа на классическую фор-

как функция числа фотонов в единичной полосе частот

мулу Шеннона [17] для пропускной способности (C)

классического канала с информационным сигналом

с конечным спектром (Ω) и гауссовским шумом в

При большом числе фотонов, m/Ω ≫ 1 — клас-

канале,

(

)

сический предел, второе слагаемое в правой части

P_Ω

C = Ωlog

(45)

(40) остается конечным и стремится к

P_noise

(

)

Здесь P_Ω/P_noise

— известное отношение сиг-

log

→

→ ∞.

(42)

ln 2

нал-шум, PΩ — мощность сигнала в единичной

полосе частот, P_noise — мощность шума в канале в

Первое слагаемое в (40) логарифмически растет с

единичной полосе частот. При стремлении мощно-

увеличением числа фотонов (интенсивности сигна-

сти шума к нулю пропускная способность переходит

ла):

(

m⁾

в энтропию источника (передатчика) и стремит-

H (m, Ω) ≈ Ω log

(43)

ся к бесконечности. То есть без шума канал с

Единица в формуле (43) под логарифмом оставле-

непрерывной переменной позволяет в классическом

на специально для дальнейших обсуждений ниже.

случае передать сколь угодно большое количество

В итоге энтропия источника в единицу времени —

информации в единицу времени. Этот факт есть

скорость генерации истинно случайных битов, рас-

отражение проблемы дискретизации непрерывной

тет логарифмически с увеличением числа фотонов

случайной величины, которая обсуждалась выше.

(мощности сигнала), но при этом остается конечной.

По этой причине часть исследователей из-за

Подчеркнем, во избежание недоразумений, что дан-

неверной интерпретации классической формулы

ная величина энтропии достигается, если над кван-

(45) ошибочно считают, что шум играет фундамен-

товым состоянием, содержащим большое число фо-

тальную роль при описании каналов с непрерывной

тонов, проводится действительно квантовое измере-

переменной. Кстати, ничего подобного в рабо-

ние, которое позволяет различать разные компонен-

тах основателей теории информации никогда не

ты в квантовом ансамбле (35).

утверждалось. Введение шума, скорее, является

Скорость генерации энтропии как в квантовом

техническим приемом. Правильный ответ состоит

пределе малого числа фотонов, так и в пределе боль-

в том, что проблема дискретизации не имеет по-

шого числа фотонов остается пропорциональной ча-

следовательного решения в классической области.

стотной полосе сигнала Ω.

Естественное разрешение проблемы возникает

Для иллюстрации зависимость скорости генера-

при квантовом рассмотрении источника, при этом

ции энтропии — скорости генерации случайных би-

энтропия (см. формулу (40)), соответственно, про-

тов — как функции числа фотонов (интенсивности)

пускная способность остаются всегда конечными

представлена на рис. 2.

даже в отсутствие шума. Не следует «тянуть» клас-

Формулы (40)-(43) относятся к случаю, когда

сическое описание в ту область, где оно перестает

число фотонов задано. Если в состоянии задано

работать.

452

ЖЭТФ, том 157, вып. 3, 2020

О фундаментальном пределе скорости генерации...

Вернемся к обсуждению генерации случайных

L. Trevisan, J. ACM 48, 860 (2001).

чисел в квантовых генераторах с непрерывной пе-

W. Mauerer, C. Portmann, and V. B. Scholz, arXiv:

ременной. Во многих работах (см. ссылки в обзо-

1212.0520 (2012).

ре [1]) декларируются высокие скорости генерации

случайных чисел в квантовых генераторах с непре-

R. König, R. Renner, and C. Schaffner, IEEE Trans.

рывной переменной. В большинстве случаев такие

Inf. Theory 55, 4337 (2009).

генераторы основаны на гомодинном детектирова-

В. Ф. Бабкин, Проблемы передачи информации 7,

нии флуктуаций вакуума. Например, в работе [18]

13 (1971).

скорость генерации первичной случайности дости-

гала почти 480 Мбит/с при эффективной частот-

T. M. Cover and J. A. Thomas, Elements of Infor-

ной полосе квантовых флуктуаций Ω ≈ 150 МГц,

mation Theory, Wiley (1991).

что явно превышает теоретический предел. По этой

10.

Р. Галлагер, Теория информации и надежная

причине случайные последовательности на выходе

связь, Советское радио, Москва (1974).

такого генератора вряд ли можно признать истинно

случайными.

11.

Iwo Bialynicki-Birula, Phys. Rev. Lett. 80,

5247

(1998).

Благодарности. Автор выражает благодар-

12.

В. А. Котельников, О пропускной способности

ность И. М. Арбекову и С. П. Кулику за интересные

«эфира» и проволоки в электросвязи, Всесоюзный

и многочисленные обсуждения, а также коллегам по

энергетический комитет, Материалы к I Всесо-

Академии криптографии Российской Федерации за

юзному съезду по вопросам технической рекон-

обсуждения и поддержку.

струкции дела связи и развития слаботочной

Финансирование. Работа поддержана Россий-

промышленности, Изд. Управления связи Рабо-

ским научным фондом (грант № 16-12-00015 (П)).

че-крестьянской Красной армии (1933).

13.

H. J. Landau and H. O. Pollak, Bell Syst. Techn. J.

40, 65 (1961).

ЛИТЕРАТУРА

14.

D. Slepian and H. O. Pollak, Bell Syst. Techn. J. 40,

1. M. Herrero-Collantes and J. Carlos Garcia-Escartin,

43 (1961).

Rev. Mod. Phys. 89, 015004 (2017).

15.

W. H. J. Fuchs, J. Math. Anal. Appl. 9, 317 (1964).

2. К. А. Балыгин, В. И. Зайцев, А. Н. Климов,

С. П. Кулик, С. Н. Молотков, ЖЭТФ 153, 879

16.

Л. Д. Ландау, Е. М. Лифшиц, Статистическая

(2018).

физика, т. V, часть I, Наука, Москва (1995).

3. Q. Zhou, R. Valivarthi, C. John, and W. Tittel, arXiv:

17.

C. E. Shannon, Bell Syst. Techn. J. XXVII, 379

1703.00559 (2017).

(1948).

4. Н. Винер, Р. Пэли, Преобразование Фурье в комп-

18.

Yicheng Shi, Brenda Chng, and Ch. Kurtsiefer, Appl.

лексной области, Наука, Москва (1964).

Phys. Lett. 109, 041101 (2016).

453