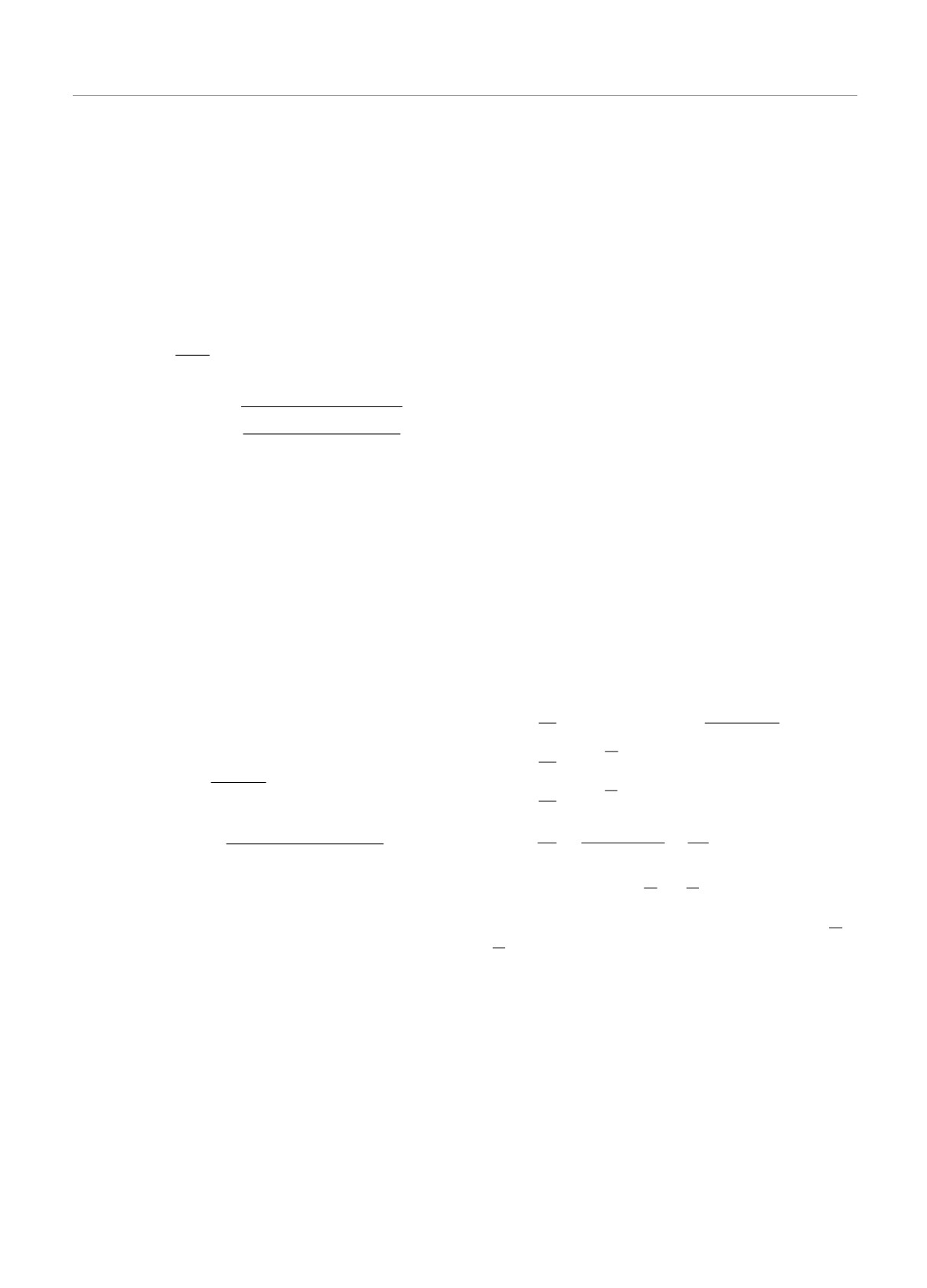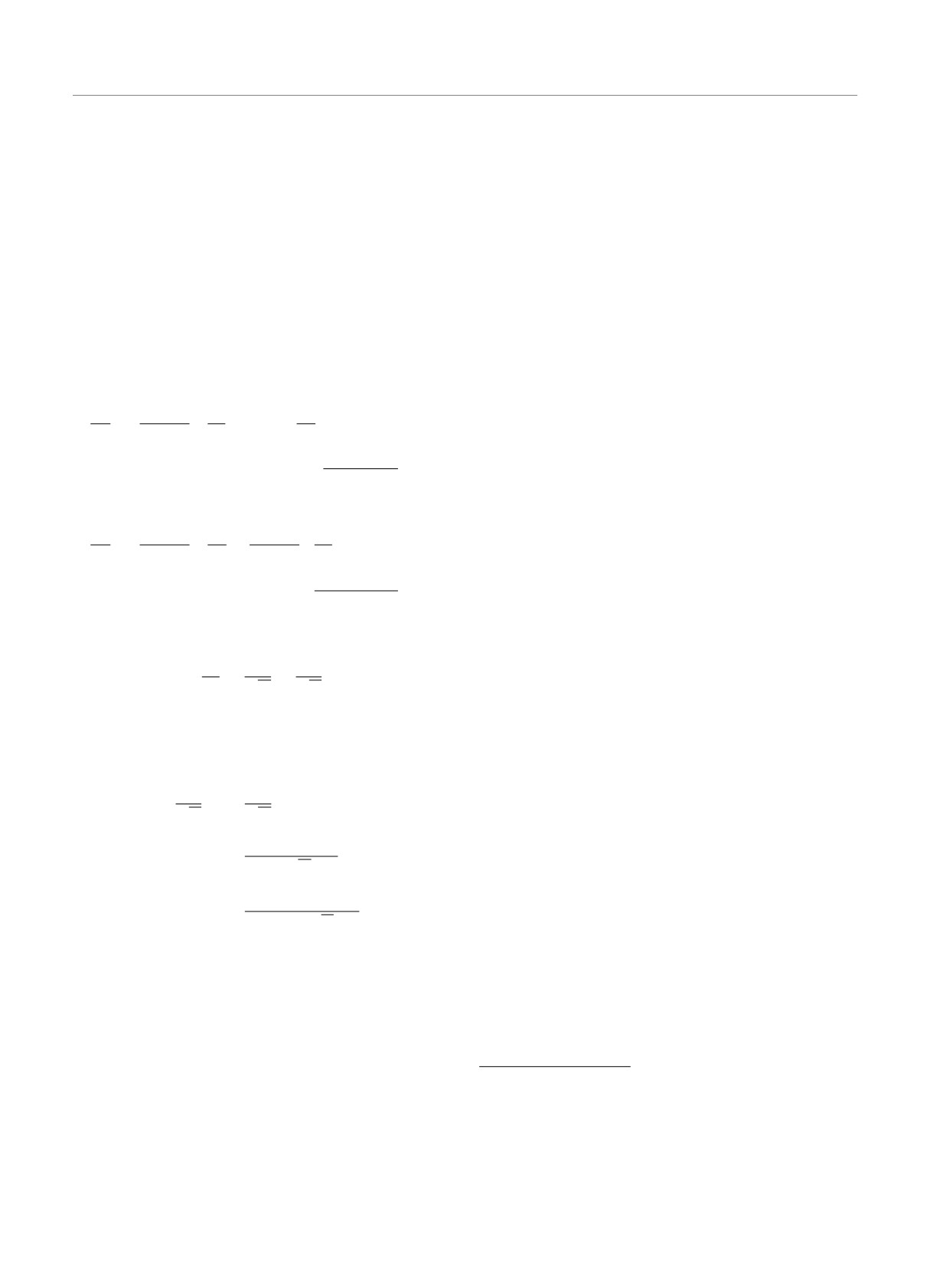ЖЭТФ, 2020, том 157, вып. 3, стр. 487-497

ИССЛЕДОВАНИЕ ТОПОЛОГИИ МЕТРИКИ КЕРРА

А. А. Шацкий^*

Московский государственный университет им. М. В. Ломоносова

119991, Москва, Россия

Поступила в редакцию 30 июля 2019 г.,

после переработки 17 сентября 2019 г.

Принята к публикации 17 сентября 2019 г.

Уравнения движения пробной частицы проинтегрированы для поля вращающейся черной дыры Керра

(в соответствии с работой [1]). Ввиду отсутствия аналитических преобразований для диаграмм Кар-

тера - Пенроуза для метрики Керра, исследование топологии черной дыры Керра было выполнено пу-

тем аналитического исследования уравнений движения. Выполнен анализ преобразований для диаграмм

Картера - Пенроуза для метрики Рейснера - Нордстрема. Исследована проблема граничных условий для

топологии Рейснера - Нордстрема. Предложено решение этой проблемы граничных условий. Доказано,

что в топологии Рейснера - Нордстрема возможен только единственный вариант перехода в другую все-

ленную. Для топологии Керра найдена возможность существования альтернативного перехода в другую

вселенную, не совпадающую со вселенной для обычного перехода. Этот альтернативный переход осу-

ществляется через поверхность с нулевой радиальной координатой (нулевой радиус). Найдены началь-

ные условия для падающей частицы, соответствующие альтернативному переходу в другую вселенную.

Оценены приливные силы, действующие на падающие тело в метрике Керра, и доказана возможность

прохождения тела в другие вселенные без разрушения приливными силами.

DOI: 10.31857/S0044451020030098

Кроме того, заряженные ЧД могут быть анали-

тически исследованы до конца, т.е. можно, напри-

мер, построить траектории пробных частиц в гра-

1. ВВЕДЕНИЕ

витационном поле этих ЧД. Более того, эти траек-

тории могут быть продолжены под горизонт ЧД,

Давно известно, что реальные черные дыры,

потом далее под горизонт Коши этой ЧД вплоть

существующие вечно (с самого рождения Вселен-

до точки поворота траектории. При этом слабая

ной¹⁾), находятся в пространстве со сложной топо-

сингулярность на горизонте Коши не является пре-

логией (см., например, [2]). Под реальными черны-

пятствием для продолжения этих траекторий через

ми дырами (ЧД) здесь и далее будем подразуме-

него (см. ниже). После точки поворота решение для

вать ЧД, обладающие либо угловым моментом (ре-

траектории пробной частицы переходит на новый

шение Керра), либо электрическим зарядом (реше-

лист (в другой вселенной) и гладко сшивается в точ-

ние Рейснера - Нордстрема), либо и тем и другим

ке поворота.

(решение Керра - Ньюмана).

При этом аналитическим признаком точки пово-

Для заряженных (но не вращающихся) ЧД суще-

рота траектории является обращение в нуль знаме-

ствует аналитическая (и графическая) диаграмма

нателя в подынтегральном выражении квадратуры

Картера - Пенроуза (см. ниже рис. 1), которая по-

траектории (см. ниже). Разумеется, эта же точка

казывает, что такие ЧД существуют в пространстве

совпадает с точкой поворота на диаграмме Карте-

со сложной топологией, объединяющей разные все-

ра - Пенроуза (ДКП) при построении на ней данной

ленные (разные части одной большой Вселенной).

траектории.

К сожалению, аналитических преобразований

^* E-mail: shatskiyalex@gmail.com

для двумерных ДКП вращающихся ЧД не суще-

¹⁾ С маленькой буквы будем писать слово «вселенная», под-

ствует, что сильно затрудняет аналитическое иссле-

разумевая под этим разные части одной большой Вселенной,

объединяющие разные участки в сложной топологии Вселен-

дование сложной топологии таких ЧД. Тем не менее

ной.

есть все основания считать, что топология вращаю-

487

А. А. Шацкий

ЖЭТФ, том 157, вып. 3, 2020

щихся ЧД также будет сложной, в отличие, напри-

f (r) := (1 - r^-h/r)(1 - r+h/r) ,

(2)

мер, от топологии незаряженных и невращающихся

(шварцшильдовских) ЧД.

ρ² := r² + a² cos² θ .

(3)

Основаниями для таких предположений являют-

ся несколько фактов, об исследовании которых и

Здесь Δ := r²f, a — угловой момент L вращения ЧД,

пойдет речь в данной работе.

выраженный в единицах ее массы M (a := L/M); ис-

пользуются безразмерные единицы G = 1 (гравита-

ционная постоянная) и c = 1 (скорость света).

2. ПРИЗНАКИ СЛОЖНОЙ ТОПОЛОГИИ

По асимптотике метрики (1) на бесконечности

получаем

Первым признаком того, что топология ЧД бу-

дет сложной является наличие R-области внутри

r^-h + r+h = 2M ,

(4)

ЧД, т.е. существование горизонта Коши в реше-

r^-hr+h = a² ,

(5)

нии. Ранее неоднократно было показано (см., напри-

√

мер, работу [3]), что сингулярность, возникающая

r+h : = M +

M² - a²,

(6)

√

на горизонте Коши, является слабой по классифи-

r^-h : = M -

M² - a².

(7)

кации Типлера [4], т. е. интегрируемой²⁾. В отличие

от сильной (по Типлеру) сингулярности (которая

Отсюда получаем

также обязательно существует внутри любой черной

дыры), материальные тела не успевают разрушить-

Δ := r²f = r² - 2Mr + a².

(8)

ся приливными силами при прохождении через сла-

Максимально возможное значение параметра a мо-

бую сингулярность, так как время воздействия сла-

жет быть равно массе M ЧД, и тогда внутренний

бой сингулярности на пролетающее тело стремится

горизонт Коши касается внешнего горизонта в та-

к нулю.

кой вырожденной ЧД. Быстрее чем при a = M чер-

Вторым признаком того, что топология ЧД бу-

ная дыра вращаться просто не может, иначе центро-

дет сложной, является «отталкивание» сильной син-

бежные силы не дали бы возможности гравитации

гулярностью пробных частиц от себя. Что касается

сформировать такую ЧД. Реально даже этот предел

не пробных частиц, а тех, которые настолько мас-

(когда a = M) не достижим — максимальной может

сивны, что сами оказывают обратное влияние на

быть величина a, примерно равная 0.998M [6].

гравитацию ЧД, то скорее всего они также будут от-

Как известно, сильная сингулярность в решении

талкиваться сильной сингулярностью ЧД, но мате-

Шварцшильда и в решении Рейснера - Нордстрема

матического (или численного) подтверждения этому

сосредоточена в одной точке, которая является цен-

пока нет. При этом под «отталкиванием» подразу-

тром симметрии решения. Что же касается решения

мевается отсутствие реальных траекторий частиц,

Керра (вращающейся ЧД), то здесь сильная сингу-

которые заканчивались бы на сильной сингулярнос-

лярность сосредоточена на кольце. Геометрическое

ти.

место точек этого сингулярного кольца соответству-

Для заряженных ЧД это было доказано анали-

ет радиальной координате r решения, которая ока-

тически (см., например, работу [5]).

зывается равна нулю на сингулярности. Под силь-

ной сингулярностью подразумевается обращение в

бесконечность скаляра Кречмана K.

3. ОСОБЕННОСТИ МЕТРИКИ КЕРРА

При вычислении K оказывается, что сингуляр-

ность в метрике Керра возникает не просто при r =

Решение для вращающейся ЧД (метрика Керра)

= 0 (как было для невращающейся ЧД), но также

в координатах (t, r, θ, ϕ) имеет вид

еще необходимо условие θ = π/2, т. е. сингулярность

лежит на экваториальной плоскости геометрии при

[

]₂

sin² θ

ρ = 0 [7]:

ds² =

dt - a sin² θ dϕ

ρ²

[

]₂

K := R_ijklR^ijkl =

(r² + a²)dϕ - a dt

dr² - ρ² dθ² ,

(1)

48M²(r⁶-15a²r⁴ cos² θ+15a⁴r² cos⁴ θ-a⁶ cos⁶ θ)

(9)

(r²+a² cos² θ)⁶

∫ √

²⁾ Речь идет о сходимости интеграла

K ds, где K — ска-

ляр Кречмана, а s — собственное время свободно падающей

Здесь R_ijkl — тензор Римана, который вычисляется

частицы [3].

на основе компонент метрики g_ik, см. (1).

488

ЖЭТФ, том 157, вып. 3, 2020

Исследование топологии метрики Керра

Вблизи кольцевой сингулярности (при θ = π/2

4. ДОКАЗАТЕЛЬСТВО

и r → 0), согласно (9), имеем асимптотику K

→

НЕДОСТИЖИМОСТИ ПРОБНОЙ

→ 48M²/ρ⁶. Следовательно, максимум приливных

ЧАСТИЦЕЙ КОЛЬЦЕВОЙ

СИНГУЛЯРНОСТИ

сил приходится на минимум величины ρ на траек-

тории, т. е. на кольцевой сингулярности.

Движение пробной частицы в поле вращающей-

При этом, согласно правилам римановой геомет-

рии, длина окружности такого сингулярного кольца

ся ЧД описывается с помощью четырех интегралов

оказывается равной 2πa, поскольку длина окружно-

движения (см. [8], § 33.5): массы μ частицы, ее энер-

сти вычисляется из (1) по формуле

гии ε, проекции l_z ее углового момента на ось вра-

щения ЧД и четвертого (картеровского) интеграла

движения Ω. Полученные в этом разделе уравнения

∫2π

√

будут использованы в разд. 6 для построения тра-

O = dϕ

|g_ϕϕ| =

ектории свободно падающей частицы.

Для упрощения вычислений удобнее записать

√

уравнения через удельные интегралы движения (де-

(r² + a²)² - Δa² sin² θ

= 2π sinθ

(10)

ленные на μ): ϵ := ε/μ (удельная энергия частицы),

r² + a² cos² θ

h := l_z/μ (прицельный параметр на ось вращения

ЧД), ω := Ω/μ² (удельный картеровский интеграл

Поэтому при r = 0 получаем

движения).

Введем необходимые для записи уравнений обо-

O(r=0) = 2πa sinθ,

(11)

значения:

[

]

Θ : = ω - cos2 θ

a²(1 - ϵ²) + h²/ sin² θ)

(14)

т. е. окружность при r = 0 оказывается обычной

окружностью на сфере радиуса a. Но это связано

P : = ϵ(r² + a²) - ha,

(15)

[

]

исключительно с особенностью выбранных коорди-

R:=P² -Δ

r² + (h - aϵ)² + ω

(16)

нат в метрике (1).

Запишем уравнения движения пробных частиц в

Кроме определения длины окружности можно

метрике Керра:

также определить еще поверхность при r = const.

Площадь этой поверхности вычисляется из (1) как

(r² + a²)P

ρ²

= a(h - aϵ sin² θ) +

(17)

интеграл:

dλ

√

=±

(18)

∫π

∫

dλ

√

dθ

√

S = dθ dϕ

|g_θθg_ϕϕ| =

ρ²

=±

Θ,

(19)

dλ

dϕ

h - aϵsin2 θ

∫π

√

ρ²

(20)

dλ

sin² θ

= 2π sinθ (r² + a²)² - Δa² sin² θ dθ.

(12)

Здесь λ — аффинный параметр траектории части-

√

цы, знаки «±» перед

Rи

Θ выбираются в конце с

учетом направления движения частицы. Далее для

Поэтому при r = 0 получаем

√

упрощения выражений убираем знаки перед

R и

√

Θ, подразумевая существование этих знаков.

S(r=0) = 2πa².

(13)

При определении азимутальной координаты ϕ

согласно метрике (1), на горизонте ЧД появляется

Величина S₀ := 2πa² соответствует площади круг-

сингулярность при ее вычислении. Из-за этой коор-

лой двусторонней мембраны радиуса a, т. е. в опре-

динатной сингулярности иногда возникает заблуж-

делении поверхности величина a ведет себя как ра-

дение, будто любая пробная частица в метрике Кер-

диус плоской мембраны. Различие в определении

ра совершает бесконечное число оборотов вокруг

радиуса при r = 0 для окружности O и для площа-

ЧД, прежде чем пересечет горизонт. На самом деле

ди поверхности S связано с сильным искривлением

бесконечное число оборотов совершит не свободно

пространства-времени вблизи кольцевой сингуляр-

падающая во вращающуюся ЧД частица, а фото-

ности.

ны, которые частица испускает на бесконечность с

489

А. А. Шацкий

ЖЭТФ, том 157, вып. 3, 2020

горизонта. Сама частица до пересечения горизонта

Выполним доказательство недостижимости проб-

ЧД успевает совершить поворот только на конечный

ной частицей кольцевой сингулярности методом от

угол. Это противоречие связано с тем, что фотону,

противного. Рассмотрим сначала случай R > 0 в

для того чтобы «вырваться» от самого горизонта

окрестности сингулярности. В этом случае величи-

ЧД на бесконечность, нужно бесконечное время. За

на ω согласно (26) должна быть отрицательной, но

это бесконечное время гравимагнитные силы (увле-

тогда из (14) на кольцевой сингулярности получаем,

кающие локально-инерциальную систему отсчета во

что Θ(θ=π/2) = ω < 0, что противоречит уравнениям

вращение) успевают повернуть фотон вокруг ЧД на

(23) и (25).

бесконечный угол. Для устранения этих временной

Отдельно рассмотрим случай R(r=0) = 0: в этом

и азимутальной координатных сингулярностей вве-

случае ω = 0 и, согласно (14), получаем Θ(θ=π/2) =

дем перенормированные временную T и азимуталь-

= 0. Этот вырожденный случай соответствует тра-

ную Φ координаты (Бойера - Линдквиста), согласно

екториям только в экваториальной плоскости, так

определениям

как в пределе θ → π/2 интегралы по θ от θ = π/2

логарифмически расходятся. Это означает, что при

)

r² + a²

⁽ dt

dϕ

R(r=0) = 0 для всей траектории должно выполнять-

- asin2 θ

dλ

ρ²

dλ

ся условие θ = π/2, или Θ = 0.

(r² + a²)P

Мера возможных начальных условий для таких

(21)

ρ²Δ

траекторий (только в экваториальной плоскости и

только при ω = 0) есть нуль на множестве всех воз-

можных начальных условий. Эта ситуация анало-

)

dΦ

r² + a²

⁽ dϕ

гична той, которая существует в случае траекторий

dλ

ρ²

dλ

r² + a²

dλ

для пробных частиц в поле заряженной ЧД Рейс-

h - aϵsin2 θ

нера - Нордстрема. Там центральной сингулярности

(22)

могут достигать только радиальные фотоны, а мера

ρ² sin² θ

начальных условий для радиальных фотонов также

Тогда с учетом

есть нуль на множестве всех возможных начальных1

условий (в том числе и нерадиальных фотонов).

dλ

dθ

√

Таким образом, было доказано, что пробные час-

ρ²

тицы в метрике Керра не достигают сильной кольце-

интегралы для вычисления траектории частицы

вой сингулярности, т.е. сильная сингулярность как

можно записать в виде

бы «отталкивает» частицы.

∫

dθ

√

(23)

5. ДИАГРАММА КАРТЕРА - ПЕНРОУЗА

ДЛЯ ЧД РЕЙСНЕРА - НОРДСТРЕМА

∫

(r² + a²)P dr

T =

√

(24)

Как уже было сказано, ввиду отсутствия цен-

тральной симметрии в решении для вращающейся

∫

(h - aϵ sin² θ) dθ

ЧД, невозможно построить двумерную аналитиче-

Φ=

√

(25)

скую ДКП для решения Керра³⁾. Однако из графи-

sin² θ

ческой ДКП рис. 1a очевидно, что для ЧД Рейс-

Уравнение (23) эквивалентно уравнению (33.37а) из

нера - Нордстрема могут существовать траектории,

книги [8], а уравнения (24) и (25) являются комби-

проходящие из одной и той же вселенной в разные

нацией уравнений (33.37в) и (33.37г) в соответствии

вселенные. При этом неясно, все ли такие траекто-

с определениями (21) и (22).

рии физичны, и если да, то каким начальным усло-

Из уравнений (23)-(25) видно, что условием до-

виям для траекторий соответствует граница пере-

стижения частицей кольцевой сингулярности с ко-

ординатами r = 0, θ = π/2 является неотрицатель-

³⁾ Однако для любого метрического тензора (в том числе и

ность величин R и Θ в окрестности сингулярности.

метрики Керра) возможно построить графическое представ-

ление ДКП (см., например, рис. 3). При этом такое графиче-

Согласно выражениям (8), (15), (16), получаем

ское представление ДКП не всегда будет подкреплено анали-

тическими преобразованиями этого раздела, которые найде-

R(r=0) = -a²ω.

(26)

ны только для центрально-симметричных решений.

490

ЖЭТФ, том 157, вып. 3, 2020

Исследование топологии метрики Керра

l⁺

g⁺

g^-

l^-

T⁺

T^-

l⁺

g⁺

Рис. 1. (В цвете онлайн) a) Диаграмма Картера - Пенроуза для заряженной ЧД Рейснера - Нордстрема. Сингулярность

при r = 0 отмечена жирными вертикальными линиями. Жирные кривые линии — возможные мировые линии частиц.

Они входят в ЧД из области R1, затем проходят области T^-, R4, T⁺ и выходят в области R2 или R3 через разные белые

дыры в разные вселенные. б) Линии r = const на соответствующих R- и T -областях диаграммы. в) Линии t = const на

соответствующих R- и T -областях диаграммы

хода в разные вселенные. Эти вопросы и будут рас-

Теперь запишем уравнение для траектории в ЧД

смотрены в данном разделе.

Рейснера - Нордстрема [5]:

Запишем метрику ЧД Рейснера - Нордстрема:

√

U^r :=

= ∓ϵ

1 - f(ϵ-2 + h²/r²),

(31)

(

)

ds² = f(r) dt² -

-r²

dθ² + sin² θ dϕ²

(27)

f (r)

√

= ∓|f|

1 - f(ϵ-2 + h²/r²).

(32)

√

r^±h := M ±

M² - Q².

(28)

Знак в (32) выбирается в соответствии с sign dr у

знака радиальной компоненты 4-скорости U^r — «ми-

Здесь функция f(r) также определяется формулой

нус» в R1- и T^--областях, а «плюс» в T⁺-, R2- и

(2), M и Q — соответственно масса и заряд ЧД, а

R3-областях. В области R4 величина U^r обращает-

r^±h — радиусы горизонтов.

ся в нуль, а затем меняет знак, и в этот момент

Запишем теперь преобразование от координат

также необходимо сменить знак в выражении (32).

(t, r) к «черепашьим» координатам (τ, ℓ), соответ-

Этой точке (точке поворота) соответствует выраже-

ствующим ЧД Рейснера - Нордстрема:

ние для радиуса поворота r_turn:

(

)

√

f dt² -

=fg²

dτ² - dℓ²

1 - f(rturn)(ϵ-2 + h²/rturn) = 0.

(33)

(29)

g(r) := ±

dℓ :=

dτ

|f| · |g|

Из (29) и (32) получаем

Здесь учтено, что dt > 0 и dτ > 0 всегда, а sign dℓ =

= signdr по определению. В соответствии с рабо-

dℓ =

(34)

|f|

той [9] получаем

∓dr

dτ = dt =

√

(35)

g := sign f = ±1.

(30)

|f|

1 - f(ϵ-2 + h²/r²)

491

А. А. Шацкий

ЖЭТФ, том 157, вып. 3, 2020

Преобразования для ДКП из «черепашьих» коорди-

только через противоположные стороны этих квад-

нат (τ, ℓ) в координаты ДКП (ψ, ξ) в соответствии с

ратов и не может проходить через их смежные сто-

работой [9] имеют вид

роны. Поэтому для ЧД Рейснера - Нордстрема путь

(траектория на ДКП) в другую вселенную может

ψ+ξ

ψ-ξ

τ + ℓ = ctg

τ - ℓ = tg

(36)

быть только один. Этот единственный путь соот-

ветствует линии, ведущей во вселенную R3 на ДКП

рис. 1a, а путь во вселенную R2 из вселенной R1

(

)

(

)

dτ² - dℓ²

= F(ψ,ξ)

dψ² - dξ²

(37)

невозможен.

Далее будет доказано, что в решении Керра для

Обозначим u^± := 0.5(ψ ± ξ). Согласно ДКП на

вращающейся ЧД возможен еще один (альтернатив-

рис. 1a видно, что координата u+ соответствует

ный) путь в другую вселенную на графической ДКП

направлению в квадратах диаграммы вправо-вверх,

для ЧД Керра.

а координата u^-

— направлению влево-вверх.

При движении по траектории частицы на ДКП в

T^--области координата u^- пробегает значения⁴⁾ от

6. ПРИЛИВНЫЕ СИЛЫ НА ТРАЕКТОРИИ

-π/2 до +π/2, а координата u⁺ пробегает значения

от константы c₁ до константы c₂.

Для графического отображения траектории па-

При движении до точки поворота в T^--области

дающего тела (рис. 2) удобно ввести понятие эффек-

диапазону изменения координат τ и ℓ соответствует

тивного радиуса r_eff :

диапазон изменения для разности координат τ -ℓ от

√

минус до плюс бесконечности, а для суммы τ + ℓ в

reff =

r² + a²,

(38)

пределах конечного диапазона. Так получилось по-

причем величина 4πr2eff совпадает на обоих горизон-

тому, что при движении в этой области интеграл от

комбинации dτ -dℓ стремится к бесконечности, если

тах с величинами площадей их поверхностей, вычис-

ленных по формуле (12).

пределы интегрирования (по координате r) прибли-

жаются к горизонтам. В то же время интеграл от

Несмотря на то что сама кольцевая сингуляр-

комбинации dτ + dℓ оказывается конечен, даже если

ность недостижима для падающих во вращающу-

пределы интегрирования лежат на горизонтах.

юся ЧД частиц, поверхность r = 0 достижима для

При движении после точки поворота в T⁺-облас-

частиц, имеющих определенные начальные условия.

ти все оказывается наоборот: интеграл от комбина-

Эта поверхность является множеством точек пово-

ции dτ +dℓ стремится к бесконечности, если пределы

рота (r_turn = 0) для достигающих ее траекторий.

интегрирования (по координате r) приближаются к

Аналогично формуле (33) для ЧД Рейснера - Норд-

горизонтам, а интеграл от комбинации dτ -dℓ оказы-

стрема, можно записать формулу для определения

вается конечен, даже если пределы интегрирования

точки поворота для ЧД Керра:

лежат на горизонтах.

R(r_turn) = 0.

(39)

В соответствии с этим величина u⁺ меняется

в диапазонах⁵⁾ [c₁, c₂] для T^--области, [c₂, π] для

Здесь функция R(r) определяется выражением (16).

R4-области и [π, 2π] для T⁺-области.

После точки поворота траектория переходит на но-

Величина u^- меняется в диапазонах [-π/2, π/2]

вый лист решения (в другую вселенную).

для T^--области, [π/2, c₃] для R4-области и [c₃, c₄]

При ω = 0, согласно (26), r_turn = 0, поэтому в ли-

для T⁺-области.

нейном приближении по малым величинам |ω| ≪

Этими диапазонами определяются граничные

≪ M2 и |r_turn| ≪ |M| можно записать

условия для преобразования (36). На рис. 1 вид-

но, что в ДКП ЧД Рейснера - Нордстрема траек-



dR

a²ω

тория свободно падающего тела проходит через T-

r_turn ≈ -R(r=0) :



(40)



2M(h - aϵ)²

r=0

и R-области, которые на графическом изображении

ДКП являются квадратами. Из граничных условий

Известно, что в ЧД приливные силы пропорци-

√

для преобразований (36) становится понятно, что в

ональны

K — см. (9), [10]. Поскольку траектория

квадратах T -областей траектория может проходить

не достигает сингулярности, приливные силы, дей-

ствующие на падающее тело, всегда остаются ко-

⁴⁾ Величины u⁺ и u^- определены с точностью до πn, где

n — целое число, так как период функций tg и ctg равен π.

нечными. Таким образом, при достаточной удален-

⁵⁾ Здесь {0 < c₁ < c₂ < π} и {π/2 < c₃ < c₄ < 3π/2}.

ности траектории от кольцевой сингулярности тело

492

ЖЭТФ, том 157, вып. 3, 2020

Исследование топологии метрики Керра

Рис. 2. (В цвете онлайн) Схематичное изображение траектории падающей частицы в ЧД Керра в декартовых коорди-

натах. Координаты (x, y, z) определяются стандартным образом — через сферические координаты (r_eff , θ, Φ), см. (23),

(25), (38). Красная (внутренняя) сфера с площадью 4πr2eff = 4πa² соответствует координате r = 0 — на этой сфере

лежит кольцевая сингулярность (красная окружность); голубая (промежуточная) сфера с площадью 4π[a² + (r^-h)²] со-

ответствует внутреннему горизонту Коши; желтая (внешняя) сфера с площадью 4π[a² + (r+h)²] соответствует внешнему

горизонту ЧД, см. (12), (38). Синяя кривая — траектория частицы, а серая кривая — проекция траектории на экватори-

альную плоскость. Начальные условия для траекторий: a = 0.95M, ϵ = 2, h = -0.5M, θ0 = π/4; ω = 2M², rturn > 0 для

варианта а) и ω = -M², rturn < 0 для варианта б); траектория построена до r = 0

способно попасть в другую вселенную через черно-

на уменьшиться после вылетания из нее частицы. В

белую дыру без разрушения. Это будет зависеть от

соответствии с этим изменяются и радиусы горизон-

массы ЧД и от начальных условий для траектории.

тов для черной и белой дыр.

Пролет частицы через вращающуюся черно-

При попадании в ЧД частицы с положительной

белую дыру возможен как с достижением нулевой

массой радиус r^-h ее горизонта Коши всегда умень-

мембраны с радиальной координатой r = 0 (точка

шается; соответственно, при вылетании этой части-

поворота r_turn < 0, рис. 2б), так и без достижения

цы из белой дыры радиус r^-h ее внутреннего гори-

(точка поворота r_turn > 0, рис. 2а). Реальная точка

зонта тоже должен уменьшиться, см. (6):

поворота не может быть отрицательной, так как в

dr^-h

a²

другой вселенной для частицы применимы уже но-

=1-

√

<0,

(41)

вые начальные условия.

M² - a²

dr_h

7. ПРОБЛЕМА ГРАНИЧНЫХ УСЛОВИЙ

√

(42)

ДЛЯ ДИАГРАММ КАРТЕРА - ПЕНРОУЗА

M² - a²

Как видно из ДКП для ЧД Рейснера - Нордстре-

В формуле (42) учтено возможное изменение r^-h,

ма, радиус r^-h внутреннего горизонта Коши для ЧД,

связанное с изменением углового момента L = aM

в которую падает частица, должен быть таким же,

ЧД. Из этих формул видно, что практически всегда

как и радиус горизонта Коши белой дыры, из кото-

изменение r^-h, связанное с пролетом частицы, отлич-

рой эта частица потом вылетает в другую вселен-

но от нуля. При вылете частицы в другую вселенную

ную, см. (6). При этом радиусы r+h внешних гори-

изменение r^-h для белой дыры должно быть таким

зонтов для черной и белой дыр не обязаны быть

же по модулю и знаку, чего очень сложно добиться

одинаковыми, а равенство радиусов внутренних го-

подбором начальных условий для частицы.

ризонтов должно сохраняться и до, и после пролета

Поэтому для положительных масс условия ра-

частицы. Поскольку частица обладает массой (энер-

венства радиусов внутренних горизонтов до и после

гией) μ > 0, масса ЧД после попадания в нее части-

пролета частицы оказываются практически несов-

цы должна увеличиться, а масса белой дыры долж-

местимыми. Это обстоятельство послужило глав-

493

А. А. Шацкий

ЖЭТФ, том 157, вып. 3, 2020

ным препятствием в развитии теории черно-белых

дование в работе [11] — там было показано, что дви-

дыр.

жение частицы с отрицательной массой в нашей все-

В §34.6 [8] Мизнер, Торн и Уилер рассмотрели

ленной не приводит ни к каким аномалиям. А вооб-

три разные возможности для частицы, попадающей

ще знак и величина массы во вселенной определяет-

в реальную ЧД. Вылет этой частицы из черно-белой

ся степенью инерции, т. е. принципом Маха. Хокинг

дыры был там третьей возможностью. Однако по

в подтверждение принципа Маха написал: «Наблю-

указанной выше причине эта третья возможность

даемая изотропия микроволнового фона указывает

была отвергнута авторами так же, как и остальные

на то, что вращение Вселенной очень мало, если оно

возможности (отвергнутые ими по другим причи-

вообще есть. .. Это можно считать эксперименталь-

нам). Комбинации этих трех возможностей также

ным подтверждением принципа Маха» [12].

не дали искомого ответа на вопрос о судьбе части-

Кроме решения проблемы согласования гранич-

цы, участвующей в гравитационном коллапсе.

ных условий для черно-белых дыр возможность ис-

Однако если предположить, что частица в дру-

пользования отрицательных масс дает и дополни-

гой вселенной вылетает из черно-белой дыры с отри-

тельные преимущества: без проблем можно будет

цательной массой, то это сразу решило бы проблему

объяснить гравитационное отталкивание белой ды-

для третьей возможности (проблему равенства ра-

рой (с отрицательной массой) частицы с положи-

диусов внутренних горизонтов до и после пролета

тельной массой, которая вылетает из нее, так как

частицы).

тела с разными по знаку массами гравитационно от-

Действительно, после вылета частицы с массой

талкиваются друг от друга.

μ > 0 из белой дыры с отрицательной массой M_wh <

Частица с положительной массой уже не смо-

< 0, масса белой дыры уменьшается на величину

жет попасть в ЧД в отрицательной вселенной, по-

μ, т. е. δM_wh < 0, но M_wh увеличивается при этом

скольку она будет гравитационно отталкиваться ото

по модулю. Это увеличение (по модулю) будет со-

всех массивных (отрицательных) тел в отрицатель-

ответствовать увеличению радиуса горизонта Коши

ной вселенной. Но если эту положительную частицу

на δr^-h > 0 для белой дыры. И это увеличение уже

как-то «привязать» к телу с отрицательной массой

можно будет без проблем согласовать с увеличением

в отрицательной вселенной, то эта связанная пара

на δr^-h > 0 для ЧД, в которую частица влетела.

сможет упасть в черно-белую дыру в отрицательной

Далее для краткости будем называть нашу все-

вселенной и вылететь уже в положительной вселен-

ленную положительной, а вселенную с отрицатель-

ной⁶⁾ аналогично падению положительной частицы

ными массами (в которую вылетает частица с по-

в ЧД нашей вселенной. В этом случае такая связан-

ложительной массой из нашей вселенной) — отри-

ная пара вылетит из белой дыры не обязательно в

цательной. Поскольку величина радиусов горизон-

ту же вселенную, в которой живем мы.

тов ЧД определяется в общей теории относительно-

В этом разделе было сделано предположение о

сти по асимптотике метрики на бесконечности, для

возможности пренебрежения гравитационными воз-

устранения противоречия в отрицательной вселен-

мущениями, вызванными пролетом частицы через

ной у формул (4), (6), (8) и (28) достаточно будет

ЧД и связанным с этим пролетом излучением гра-

поставить знак «минус» везде перед M. По этой же

витационных волн. Такое предположение обосновы-

причине знак «меньше» в формуле (41) сохранится

вается тем, что относительное изменение радиусов

и для отрицательных M.

всех горизонтов при пролете пробной частицы ока-

Мы все еще со школы привыкли к тому, что мас-

зывается порядка μ/M, а относительное изменение

са любого тела должна быть всегда неотрицатель-

этих радиусов, связанное с излучением гравитаци-

ной. Однако достаточно очевидно, что знак перед

онных волн пробной частицей, оказывается порядка

массой в любых уравнениях может быть выбран

10-2μ²/M² [13].

произвольно — это не приведет к нарушению фи-

Как известно, массивные тела двигаются в про-

зических законов и уравнений при условии, что и

странстве по траекториям, притягиваясь к миниму-

во всех остальных уравнениях знаки перед массами

мам гравитационного потенциала. В главном при-

также будут изменены на противоположные. Эта си-

ближении задачи двух тел эти траектории имеют

туация полностью аналогична ситуации со знаками

форму кеплеровских орбит (эллипсов, гипербол и

зарядов в электромагнетизме: заменой всех знаков у

электрических зарядов на противоположные мы ни-

⁶⁾ Однако вероятно, что любая такая связь будет разруше-

чего не нарушим, это будет просто переобозначение.

на бесконечными гравитационными силами внутри черно-бе-

Более подробно на эту тему было проведено иссле-

лой дыры.

494

ЖЭТФ, том 157, вып. 3, 2020

Исследование топологии метрики Керра

парабол). Для тел с отрицательной массой в таком

же гравитационном поле принципиально ничего не

R₅

R₂

R₃

меняется — тела также будут двигаться по кеплеров-

ским орбитам, но уже не вокруг минимумов, а во-

T⁺

круг максимумов гравитационного потенциала. Эти

максимумы гравитационного потенциала в далеком

Космосе соответствуют центрам межгалактических

R4-

R₄

R R

пустот (войдов), а расстояния между войдами обыч-

но составляют сотни мегапарсек. В этих войдах час-

T^-

тицы с отрицательной массой могут накапливаться.

Аналогичная ситуация должна быть для частиц с

R₀

R₁

положительными массами в отрицательной вселен-

ной. Накопление частиц с отрицательными массами

в войдах может приводить к космологическим эф-

фектам, аналогичным влиянию на космологию тем-

Рис. 3. (В цвете онлайн) Диаграмма типа Картера - Пен-

роуза для ЧД Керра с альтернативным вариантом пере-

ной энергии.

хода в другую вселенную. Вертикальными жирными ли-

ниями отмечены поверхности r = 0. Стандартный пере-

Возможно, что отрицательные частицы будут

ход в другую вселенную осуществляется через области

накапливаться вблизи точек Лагранжа в звездных

R1-T^--R4-T⁺-R3 (в соответствии с ДКП рис. 1 для

системах типа Солнечной, но скорее всего их ско-

ЧД Рейснера - Нордстрема) — штриховая линия справа,

рости будут порядка или более средних галактиче-

а альтернативный переход осуществляется через области

ских — порядка 300 км/с. Поэтому, вероятно, отри-

R1-T^--R4-R4--T⁺-R5 — штриховая линия слева

цательные частицы будут вылетать без задержек из

родительских галактик и только «гравитационные

холмы» войдов смогут их захватить. Более подроб-

Можно доказать⁷⁾, что ds² = dλ². Тогда, соглас-

ное и количественное исследование этих вопросов

но (18), (19), имеем

требует отдельного рассмотрения.

√

dθ

^r =

=∓

U^θ =

=±

(43)

dλ

ρ²

dλ

ρ²

Кроме того, согласно выражению (40), отрицатель-

ность величины r_turn возможна только при ω < 0.

Отметим, что реально траекторию имеет смысл

8. АЛЬТЕРНАТИВНЫЙ ВАРИАНТ

строить не далее чем до нулевого радиуса r, а отри-

цательность величины r_turn свидетельствует толь-

ко о возможности альтернативного перехода в дру-

гую вселенную при данных начальных условиях для

Решение Керра для вращающейся ЧД, в отличие

падающей частицы. Чтобы построить продолжение

от решения Рейснера - Нордстрема для заряженной

этой траектории в другой вселенной, нужно в дру-

ЧД, предоставляет еще одну уникальную возмож-

гой вселенной построить новую траекторию обрат-

ность для перехода в другую вселенную. Эта воз-

но во времени и гладко сшить обе части траектории

можность связана с тем, что в решении Керра (1)

при r = 0.

площадь поверхности, соответствующей нулевой ра-

Отсюда становится более понятен физический

диальной координате, больше нуля: S₀ = 2πa² — см.

смысл удельного картеровского интеграла ω. Со-

(12), а также с тем, что тело может находиться на

гласно выражениям (14), (23), при ω < 0 траек-

этой поверхности (мембране) без разрушения при-

тория не может пересекать экваториальную плос-

√

ливными силами, если это тело будет не у сингуляр-

кость. Поскольку U_θ = ±

Θ, при ω > 0 и θ = π/2 из

ности. Поэтому возможен переход через нуль по ра-

(43) имеем Uθ(θ=π/2) = ±√ω, т. е. при положитель-

диальной координате в решении (1) и дальнейшее

ных ω корень из удельного картеровского интегра-

движение в том же направлении при условии от-

ла имеет смысл проекции, ортогональной оси z, для

рицательности радиальной компоненты 4-скорости

U^r := dr/ds для падающего в ЧД тела при r = 0,

⁷⁾ Это следует после подстановки в (1) значений для dt, dr,

рис. 3.

dθ и dϕ, выраженных из формул (17)-(20) через dλ.

495

А. А. Шацкий

ЖЭТФ, том 157, вып. 3, 2020

удельного углового момента частицы в момент пе-

кое должно быть полное решение (соответствующее

ресечения ею экваториальной плоскости. Как видно

какой-то диаграмме Картера - Пенроуза) для ЧД,

из соотношения (14), эта проекция не является ин-

образующейся в результате коллапса звезды (т. е.

тегралом движения. В поле вращающейся ЧД эта

уже после Большого Взрыва). Понятно пока, что

величина не сохраняется, а сохраняется только про-

— у любой реальной ЧД будет не только внешний

екция полного углового момента частицы на ось z —

горизонт, но и внутренний горизонт Коши;

величина μh.

— физические тела способны без разрушения

Если траектория переходит через r = 0 (в дру-

преодолевать слабую сингулярность на горизонте

гую вселенную), то для устранения путаницы со зна-

Коши;

ками r можно переобозначить знак радиальной ко-

— сильная сингулярность внутри реальной ЧД

ординаты, r → -r, и проводить дальнейшие вычис-

будет отталкивать любую материю под внутренним

ления в другой вселенной так же, как и в нашей.

горизонтом;

Этот альтернативный вариант интересен еще и тем,

— приливные силы будут конечными, посколь-

что не требует гладкой сшивки граничных условий

ку траектория падающего тела не касается сильной

на горизонте, которая требовалась в разд. 7. Свя-

сингулярности;

зано это с тем, что в другой вселенной аналогич-

— обратно из этой же ЧД эта материя вылететь

но будет вращающаяся ЧД с нулевой мембраной

уже не сможет.

(при r = 0), площадь которой не обязательно долж-

Но вот что будет с этой материей, пока не понят-

на быть равна площади мембраны в нашей вселен-

но — полного решения для ЧД, родившихся уже пос-

ной. Поэтому провести сшивку на этой мембране не

ле Большого Взрыва, пока не найдено, так же как

составит труда.

и не найдено пока самосогласованных полных ре-

Обратим внимание, что решение (1) зависит от

шений, учитывающих обратное влияние падающей

r линейно только в одном месте (член с 2Mr в Δ),

материи на гравитацию всей системы.

в остальных местах зависимость от r квадратичная.

В работе получены следующие результаты.

Поэтому другая вселенная может быть как положи-

- Доказана недостижимость пробной падающей

тельной, так и отрицательной. При отрицательном

частицей сильной кольцевой сингулярности внутри

варианте даже не нужно будет переобозначать знак

черной дыры Керра.

радиальной координаты, r → -r, поскольку реше-

- Найдено решение проблемы граничных усло-

ние (1) и так сохранит свой вид.

вий для топологии Рейснера - Нордстрема.

Однако, возможно, что никакого альтернативно-

- Доказано, что в топологии Рейснера - Норд-

го варианта для перехода во вселенную R₅ просто не

стрема возможен только единственный вариант пе-

существует, так как если рассматривать нулевую по-

рехода в другую вселенную.

верхность r = 0 именно как плоскую мембрану (13),

- Для топологии Керра найдена возможность

а не как сферу (11), то пролет частицы через мем-

существования альтернативного перехода в другую

брану может просто означать выход в ту же R₄-об-

вселенную, не совпадающую со вселенной для обыч-

ласть на ДКП рис. 3 только с другой стороны мем-

ного перехода.

браны. В этом случае частица как бы отразится от

- Найдены начальные условия для падающей

мембраны на ДКП рис. 3 и вылетит во вселенную R₃

частицы, соответствующие альтернативному пере-

по обычному варианту, рассмотренному в предыду-

ходу в другую вселенную.

щих разделах.

- Оценены приливные силы, действующие на па-

дающее тело в метрике Керра, и доказана возмож-

ность прохождения тела в другие вселенные без раз-

9. ОБСУЖДЕНИЕ

рушения приливными силами.

Также была предложена гипотеза существова-

Пока еще теория гравитации не может дать одно-

ния «отрицательных вселенных» и отрицательных

значного ответа на вопрос о возможности существо-

масс, позволяющая состыковать граничные условия

вания в нашей Вселенной черно-белых дыр. Мате-

в черной и белой дырах.

матически известно только «вечное» полное реше-

Несмотря на привлекательность аргументов в

ние для черно-белых дыр (оно изображено на ДКП

пользу выдвинутой гипотезы о существовании аль-

рис. 1a), т. е. это такое решение, которое существует

тернативного перехода в другую вселенную, окон-

вечно — с самого рождения Вселенной (с момента

чательного математического доказательства такого

Большого Взрыва). И практически не понятно, ка-

перехода пока не получено.

496