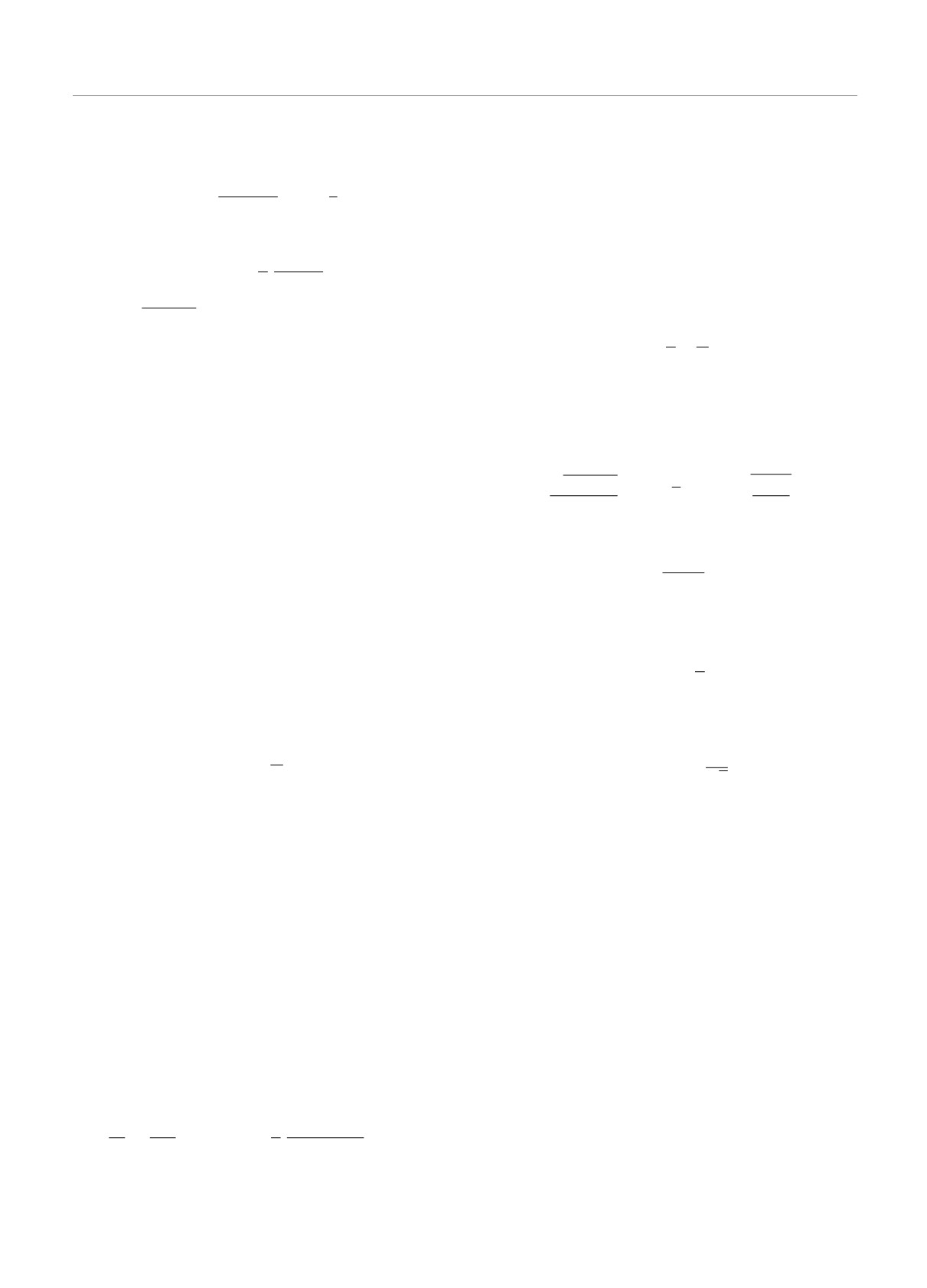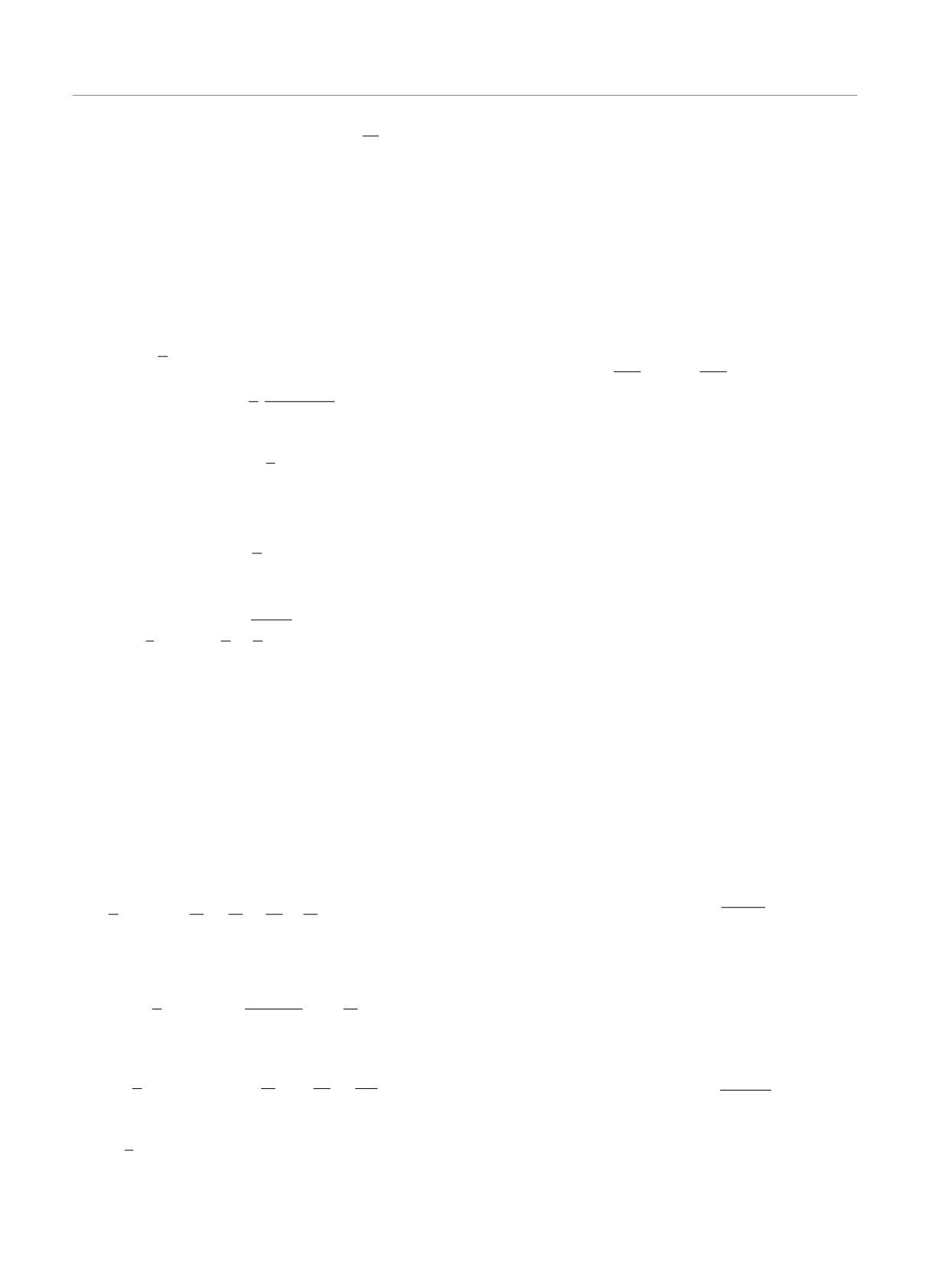ЖЭТФ, 2020, том 157, вып. 4, стр. 669-678

ПРОВОДИМОСТЬ ДВУМЕРНОЙ МОДЕЛИ РЭЛЕЯ

В ОКРЕСТНОСТИ ПОРОГА ПРОТЕКАНИЯ.

ПРЕДПОРОГОВАЯ ОБЛАСТЬ КОНЦЕНТРАЦИЙ

Б. Я. Балагуров^*

Институт биохимической физики им. Н. М. Эмануэля Российской академии наук

119334, Москва, Россия

Поступила в редакцию 12 октября 2019 г.,

после переработки 12 октября 2019 г.

Принята к публикации 24 октября 2019 г.

Исследуется проводимость двумерной модели Рэлея вблизи критической точки — порога протекания.

В бинарном (парном) приближении вычислена эффективная проводимость модели с фазовым перехо-

дом типа металл - идеальный проводник. Для альтернативной модели с фазовым переходом типа ме-

талл - диэлектрик соответствующая эффективная проводимость определена из соотношения взаимности

Келлера - Дыхне.

DOI: 10.31857/S0044451020040100

исследование проводимости модели в критической

области численными методами.

В настоящей работе проводимость двумерной

1. ВВЕДЕНИЕ

модели Рэлея вблизи точки фазового перехода рас-

смотрена аналитическим методом. Для этого ис-

Двумерная модель композита с двоякопериоди-

пользуется бинарное приближение, в котором исход-

ческим расположением включений круговой формы

ная задача сводится к изучению протекания тока че-

впервые рассматривалась в работе Рэлея [1]. Для

рез пару соседних включений с точечными источни-

проводимости этой модели в случае малой концен-

ком и стоком. В результате потенциал задачи выра-

трации (доли занимаемой площади) включений бы-

жается через электростатическую функцию Грина

ло найдено [1] несколько первых членов соответству-

для пары круговых включений.

ющего вириального ряда. В дальнейшем в работах

[2, 3] разными методами было дано полное решение

Согласно

[5, 6], электростатическая функция

этой задачи, позволяющее вычислить любой член

Грина для макроскопического тела заданной фор-

упомянутого ряда. Подход, использованный в рабо-

мы выражается через систему его собственных

те [3], был затем обобщен на двоякопериодические

функций. В работе найдены все собственные функ-

модели с включениями произвольной формы [4].

ции для «тела» в виде пары даваемых гипотезой

Согласно работам [2, 3], определение эффектив-

подобия включений, что позволило вычислить

ной проводимости σ_e рассматриваемой модели сво-

потенциал и определить эффективную проводи-

дится к решению некоторой бесконечной системы

мость исследуемой модели. Для модели с фазовым

алгебраических уравнений. Проведенный числен-

переходом типа металл-диэлектрик выражение для

ный анализ [3,4] показал, что для нахождения вели-

соответствующей эффективной проводимости σ_e

чины σ_e в широком диапазоне изменения входящих

следует из соотношения взаимности Келлера - Дых-

в задачу параметров достаточно ограничиться ре-

не [7, 8] (см. также [4]). В последнем случае для

величины σ_e в работе получено разложение по сте-

шением конечной подсистемы уравнений небольшо-

го размера. Однако при приближении к точке фазо-

пеням h, сходное с аналогичным рядом, даваемым

гипотезой подобия [9, 10].

вого перехода размер соответствующей подсистемы

неограниченно растет, что существенно затрудняет

Знание системы собственных функций для неко-

торого макроскопического тела позволяет дать ре-

^* E-mail: balagurov@deom.chph.ras.ru, byabalagurov@mail.ru

шение ряда связанных с ним электростатических за-

669

Б. Я. Балагуров

ЖЭТФ, том 157, вып. 4, 2020

=-₀

=₀

-c

–a

r₂

r₁

Рис. 2

а низкопроводящую прослойку он преодолевает по

кратчайшему пути между ними в виде тоненькой

струйки. В данном случае ток сосредоточен в ос-

новном внутри рассматриваемой цепочки и отсутст-

вует во внешней по отношению к ней области. Это

обстоятельство позволяет упростить задачу, сведя

ее к изучению уединенной цепочки, помещенной в

неограниченного размера матрицу.

Таким образом, величина эффективной прово-

димости определяется прежде всего наличием низ-

копроводящих прослоек между включениями. Для

Рис. 1

оценки вклада такой прослойки в величину σ_e выде-

лим пару соседних включений. С остальными частя-

ми цепочки эту пару связывают входящий и исхо-

дач. Кроме определения функции Грина это, напри-

дящий ток I. Соответствующие плотности тока бу-

мер, краевые задачи (внутренние и внешние) Дири-

дем аппроксимировать дельта-функциями. В полу-

хле и Неймана для уравнений Лапласа и Пуассона

ченном таким образом бинарном приближении ис-

[5,6], а также вычисление поляризуемости этого те-

ходная задача сводится к нахождению потенциала

ла. В качестве примера в Приложении найден тен-

в погруженной в матрицу уединенной пары включе-

зор дипольной поляризуемости для пары круговых

ний с точечными истоком и стоком (рис. 2). На рис. 2

включений (двух параллельных цилиндров круго-

показаны выделенная штрихпунктиром на рис. 1 об-

вой формы в трехмерной постановке задачи).

ласть, где

√

a² - R²

a² - R² , ξ₀ = ln

(1)

2. БИНАРНОЕ ПРИБЛИЖЕНИЕ

U — разность потенциалов и через ρ обозначен ради-

Двумерная модель Рэлея (рис. 1) представляет

ус-вектор точки, принадлежащей поверхности тела

собой изотропную матрицу проводимости σ₁ c вклю-

(границе раздела).

чениями круговой формы радиуса R и проводимо-

В данном случае уравнение сохранения тока при-

сти σ₂. Центры включений расположены в узлах

нимает вид

квадратной решетки с периодом 2a. На рисунке раз-

ность потенциалов приложена в направлении оси x,

{

}

div j = I

δ(r - ρ₂) - δ(r - ρ₁)

(2)

так что штриховые линии являются эквипотенциа-

лями, а сплошные — линиями тока. В силу перио-

Здесь j — плотность тока,

дичности модели при изучении картины протекания

тока достаточно ограничиться рассмотрением одной

j = -σ(r)∇ϕ(r),

(3)

горизонтальной цепочки включений.

В ситуации, близкой к фазовому переходу ме-

σ(r) — проводимость среды, ϕ(r) — электрический

талл - идеальный проводник, имеем h = σ₂/σ₁ ≫ 1

потенциал. Положим

и (a - R)/R ≪ 1. В этом случае ток сосредоточен

σ(r) = σ₁[1 - (1 - h)v(r)] , h = σ₂/σ₁ ,

(4)

в основном внутри высокопроводящих включений,

670

ЖЭТФ, том 157, вып. 4, 2020

Проводимость двумерной модели Рэлея...

где v(r) = 1 внутри включения и v(r) = 0 вне его.

где интегрирование распространяется на все про-

В этом случае уравнение для потенциала принимает

странство, или

вид

∫

(

)

∇ψ_μ(r) · ∇ψ_ν (r)

[1 - v(r)] dr =

δ_μν .

(12)

{

]

}

1+ε_ν

∇

[1 - (1 - h)v(r)

∇ϕ(r)

I {

}

Здесь интеграл берется по области вне тела.

δ(r - ρ₁) - δ(r - ρ₂)

(5)

Функции зарядовых состояний

ψ_k(r) вне тела

σ₁

также подчиняются уравнению Лапласа и облада-

Введем, следуя [5, 6], функцию Грина G(r, r^′),

ют монопольной асимптотикой. Им отвечает одно и

подчиняющуюся уравнению

то же собственное значение ε_k = ∞. Для монолит-

{

}

ного (неразъемного) тела зарядовая функция

ψ(r)

∇_r

[1 - (1 - h)v(r)] ∇_r G(r, r^′)

= δ(r - r^′).

(6)

одна. На поверхности тела она принимает постоян-

ное значение:

С учетом формулы (6) для потенциала ϕ(r) из урав-



нения (5) получаем следующее выражение:



ψ(e)(r)

= Ψ = const.

(13)

I {

}

ϕ(r) =

G(r, ρ₁) - G(r, ρ₂)

(7)

В то же время

ψ(i)(r) =

Ψ в любой точке внутри

σ₁

тела.

Разъемному «телу», состоящему из n частей, от-

Величина G(r, r^′), подчиняющаяся уравнению

вечают n зарядовых функций

ψ_k(r) (где k = 1,

(6), определена в [5, 6] с помощью метода собствен-

2, . . . , n). Каждая из них принимает постоянные (во-

ных функций. Для функции Грина G(r, ρ), где ρ

обще говоря, разные) значения на поверхностях ча-

принадлежит поверхности тела, имеет место следу-

стей этого тела.

ющее выражение [5, 6]:

¯k(r) ортонормированы согласно соот-

Функции

∑

ношению

1+ε_ν

G(r, ρ) = -

Ψ_ν(ρ)ψ_ν(r)-

∫

h+ε_ν

(

)

ψ_k(r) ·

ψ_k′ (r)

[1 - v(r)] dr = δ_kk′ .

(14)

∑

Ψ_k(ρ)ψk(r).

(8)

Подсистемы поляризационных {ψ_ν (r)} и зарядовых

ψ_k(r)} функций взаимно ортогональны:

Здесь вектор r произволен и может принадлежать

∫

как телу, так и пространству вне его.

(

)

∇ψ_ν (r) ·

ψ_k(r)

[1 - v(r)] dr = 0 .

(15)

В выражении (8) ψ_ν(r) и

ψ_k(r) — регулярные

и обращающиеся в нуль при r → ∞ собственные

Таким образом, совокупность {ψ_ν (r),ψk(r)} пред-

функции; Ψ_ν(ρ) и

Ψ_k(ρ) — их значения на поверх-

ставляют собой ортонормированную систему функ-

ности тела при r = ρ. Поляризационные функ-

ций. Заметим, однако, что эта совокупность полной

ции ψ_ν (r), обладающие мультипольной асимптоти-

системой не является [5, 6]. Отметим также, что в

кой, удовлетворяют уравнению Лапласа внутри (i)

рассматриваемой в работе двумерной задаче функ-

и вне (e) тела:

ции с монопольной асимптотикой логарифмически

∇² ψ(i)ν(r) = 0 ,

∇² ψ(e)ν(r) = 0 .

(9)

расходятся при r → ∞. В этом случае на зарядо-

вые функции накладывается условие

ψ_k(r) = 0 на

На поверхности S тела (при r = ρ) для функции

окружности достаточно большого радиуса.

ψ_ν(r) имеем следующие граничные условия:



∂ψνe)

∂ψνi)

3. БИПОЛЯРНАЯ СИСТЕМА КООРДИНАТ

ψ(e)ν

=ψ(i)ν

= -ε_ν

(10)

∂n

В рассматриваемой геометрии (см. рис. 2) зада-

Здесь ∂/∂n — нормальная производная, ε_ν > 0 —

чу вычисления собственных функций естественно

собственное значение для поляризационного состо-

решать в системе биполярных координат [11]. Де-

яния. Система {ψ_ν (r)} ортонормирована по соотно-

картовы координаты (x, y) связаны с биполярными

шению

(ξ, θ) с помощью соотношения [11]

∫

(

)

ξ + iθ

∇ψ_μ(r) · ∇ψ_ν (r)

dr = δ_μν ,

(11)

x + iy = c th

(16)

671

Б. Я. Балагуров

ЖЭТФ, том 157, вып. 4, 2020

откуда следует

Здесь e_ξ и e_θ — орты нормалей к координатным ли-

ниям соответственно ξ = const и θ = const,

shξ

sinθ

x=c

y=c

(17)

ch ξ + cos θ

H_ξ = H_θ = H(ξ, θ) =

(23)

ch ξ + cos θ

имеем

— коэффициенты Ламе. Для ортов e_ξ и e_θ

(c + x)² + y

2cy

следующие выражения:

ξ=

tg θ =

(18)

(c - x)² + y²

c² - x² - y²

1 + chξ cosθ

shξ sinθ

e_ξ = i_x

-i_y

(24)

Координата ξ меняется в пределах (-∞, +∞), а

ch ξ + cos θ

угол θ — в интервале от 0 до 2π. Положительным

ξ соответствует полуплоскость x > 0, а отрицатель-

shξ sinθ

1 + chξ cosθ

ным ξ — полуплоскость x < 0. В точках (± c , 0) ве-

e_θ = i_x

+i_y

(25)

ch ξ + cos θ

личина ξ обращается в бесконечность: ξ = ±∞. При

√

r =

x² + y² → ∞ имеем ξ → 0 и θ → π. Поло-

где i_x и i_y — орты декартовых осей соответственно x

жив θ = π - α, из (17) и (18) при r → ∞ найдем

и y. Отметим, что e_ξ является единичным вектором

асимптотику

внутренней нормали к правой (ξ = +ξ₀) и внешней

нормали к левой (ξ = -ξ₀) окружностям.

(19)

Уравнение Лапласа в биполярных координатах

ξ² + α²

имеет вид

∂²ϕ

2cx

2cy

=0.

(26)

(20)

∂ξ²

∂θ²

x² + y²

Периодическими по углу θ решениями этого урав-

Отрезку оси x от -c до c (на рис. 2 выделен жир-

нения являются

ной линией) соответствуют -∞ ≤ ξ ≤ ∞ и θ = 0

при y → +0 или θ = 2π при y → -0. Координата

ξ , e^±nξ cosnθ, e±nξ sinnθ, shnξ cosnθ,

θ на интервале (-c, c) оси x оказывается разрывной

со скачком в 2π. Бесконечным отрезкам (-∞, -c) и

ch nξ sin nθ , . . .

(27)

(c, ∞) этой оси отвечают θ = π и значения ξ в диапа-

При этом, например, e^-nξ cos nθ и e^-nξ sin nθ регу-

зонах соответственно (-0, -∞) и (∞, +0). Наконец,

лярны в точке c оси x, а

оси y отвечает ξ = 0, причем положительная полу-

ось y > 0 проходится при изменении угла θ от 0 (где

ξ , shnξ cosnθ, shnξ sinnθ, chnξ sinnθ,

y = +0) до π (y = +∞), а отрицательная полуось —

(28)

ch nξ cos nθ - (-1)ⁿ

при изменении θ от π (y = -∞) до 2π (y = -0).

Координатными линиями биполярной систе-

исчезают на бесконечности.

мы являются два набора взаимно ортогональных

окружностей с центрами на осях x и y. Так,

исключая из равенств (17) угол θ, приходим к

4. СИСТЕМА СОБСТВЕННЫХ ФУНКЦИЙ

уравнению

С рассматриваемой парой круговых включений

(

)₂

c²

связаны четыре типа поляризационных функций

x - ccthξ

+y² =

(21)

sh² ξ

ψ_λn(r) = ψ_λn(ξ, θ) (λ = 1, 2, 3, 4; n = 1, 2, . . .), кото-

рым отвечают дважды вырожденные собственные

так что постоянным значениям ξ = ±ξ₀ отвечают

значения ε1n = ε3n и ε2n = ε4n.

окружности радиуса R = c/| sh ξ₀| с центрами в сим-

Нормированные функции первого типа, ψ1n(r), с

метричных точках ±c cth ξ₀ на оси x. Поэтому для

собственными значениями

констант c и ξ₀ получаем выражения (1).

В биполярных координатах для градиента потен-

ε1n = thnξ₀

(29)

циала ϕ имеем

имеют вид

eξ ∂ϕ

eθ ∂ϕ

∇ϕ =

(22)

H_ξ ∂ξ

H_θ

∂θ

ψ(e)1n(r) = A_n chnξ sinnθ ,

|ξ| ≤ ξ₀,

(30)

672

ЖЭТФ, том 157, вып. 4, 2020

Проводимость двумерной модели Рэлея...

вне включений и

Наконец, антисимметричные и по x, и по y функ-

ции четвертого типа, ψ4n(r), с собственными значе-

ψ(1)1n(r) = A_n chnξ₀ e-n(ξ-ξ0⁾ sinnθ, ξ ≥ ξ₀,

(31)

ниями ε4n = ε2n = cth nξ₀ имеют вид

ψ(e)4n(r) = B_n shnξ sinnθ ,

|ξ| ≤ ξ₀,

(43)

ψ(2)1n(r) = A_n chnξ₀ en(ξ+ξ0) sinnθ , ξ ≤ -ξ₀

(32)

(1)

ψ₄

(r) = B_n sh nξ₀ e-n(ξ-ξ0⁾ sin nθ , ξ ≥ ξ₀,

(44)

внутри соответственно первого (правого) и второго

(левого) кругов. Здесь

ψ(2)4n(r) = -B_n shnξ₀ en(ξ+ξ0⁾ sinnθ , ξ ≤ -ξ₀

(45)

√

1-ε1n

e^-nξ0

с B_n из формулы (39).

A_n =

(33)

2πn

2πn chnξ₀

Так как в данном случае включение состоит из

двух частей, ему отвечают две зарядовые функции.

Функции первого типа обладают следующими

Первая из них, антисимметричная по x (т. е. по ко-

свойствами симметрии:

ординате ξ), имеет простой вид:

ψ1n(-x, y) = ψ1n(x, y),

ψ(e)1(r) =

A₁ ξ ,

A₁ =

√

(46)

(34)

4πξ₀

ψ1n(x, -y) = -ψ1n(x, y).

√

Антисимметричные по x и симметричные по y

ξ₀

ψ⁽¹⁾¹ =

ψ⁽²⁾¹ =

(47)

собственные функции второго типа ψ2n(r) с соб-

4π

ственными значениями

Эта функция, согласно (20), имеет не монопольную,

а дипольную асимптотику. Дело в том, что в физи-

ε2n = cth nξ₀

(35)

ческой постановке задачи данному потенциалу от-

вечают одинаковые по модулю, но разные по знаку

имеют вид

заряды на отдельных частях тела. Поэтому в этом

ψ(e)2n(r) = B_n shnξ cosnθ ,

|ξ| ≤ ξ₀ ,

(36)

случае включение, состоящее из пары кругов, пред-

ставляет собой диполь.

Вторая, симметричная по x, зарядовая функ-

ψ(1)2n(r) = B_n shnξ₀ e-n(ξ-ξ0) cosnθ , ξ ≥ ξ₀,

(37)

ция

ψ₂(r) имеет монопольную (логарифмическую)

асимптотику, и поэтому на нее необходимо нало-

жить условие

ψ₂(r) = 0 при r = L (где L ≫ a).

ψ(2)2n(r) = -B_n shnξ₀ en(ξ+ξ0⁾ cosnθ, ξ ≤ -ξ₀,

(38)

Кроме того, функция

ψ₂(r) должна принимать по-

стоянное и одинаковое значение при ξ = ±ξ₀. Удов-

где

летворяющая этим требованиям зарядовая функция

√

ψ₂(r) при ξ > 0 имеет вид

ε2n - 1

e^-nξ0

B_n =

(39)

{

2πn

2πn shnξ₀

∑

(-1)ⁿ

ψ(e)(r) =

A₂

2 ln

+ξ-2

e^-nξ cosnθ +

Для обращающихся в нуль при r → ∞ симмет-

n=1

}

∑

]

ричных и по x, и по y собственных функций третье-

(-1)ⁿ e^-nξ0 [

ch nξ cos nθ - (-1)ⁿ

(48)

го типа, ψ3n(r), с собственными значениями ε3n =

n ch nξ₀

n=1

= ε1n = thnξ₀ имеем следующие выражения:

С учетом разложения

[

]

ψ(e)3n(r) = A_n

ch nξ cos nθ - (-1)ⁿ

|ξ| ≤ ξ₀,

(40)

[

]

∑

(-1)ⁿ

2(ch ξ + cos θ)

= ξ-2

e^-nξ cosnθ

(49)

[

]

n=1

ψ(1)3n(r) = A_n chnξ₀

e-n(ξ-ξ0) cosnθ - (-1)n ,

(41)

отсюда следует

ξ≥ξ₀,

{

[

]

[

]

ψ(e)2

(r) =

A₂

2 ln

+ ln

2(ch ξ + cos θ)

ψ(2)3n(r) = A_n chnξ₀

en(ξ+ξ0⁾ cosnθ - (-1)ⁿ

(42)

}

∑

]

ξ ≤ -ξ₀

(-1)ⁿ e^-nξ0 [

ch nξ cos nθ - (-1)ⁿ

(50)

n ch nξ₀

с A_n из формулы (33).

n=1

673

ЖЭТФ, вып. 4

Б. Я. Балагуров

ЖЭТФ, том 157, вып. 4, 2020

Здесь

Используя приведенные в предыдущем разделе

(e)

выражения для функций ψ_λ

(r) и

ψ(e)k(r), найдем

[

]-1/2

∑

1 e^-nξ0

A₂ =

√

2 ln

+ξ₀ -2

(51)

4π

n ch nξ₀

Ψ(1)1n(θ) = Ψ(2)1n(θ) = A_n chnξ₀ sinnθ ,

(58)

n=1

При ξ = ±ξ₀ из выражения (48) следует

Ψ(1)2n(θ) = -Ψ(2)2n(θ) = B_n shnξ₀ cosnθ ,

(59)

ψ₂(±ξ₀, θ) =

(52)

4πA2

[

]

(1)

(θ) = Ψ(2)3n(θ) = A_n

ch nξ₀ cos nθ - (-1)ⁿ

(60)

В пределе r ≫ a имеем следующую асимптотику:

ψ(e)2(r)

A₂ ln

(53)

(1)

(θ) = -Ψ(2)4n(θ) = B_n sh nξ₀ sin nθ,

(61)

откуда

(1)

(θ) = Φ(2)1n(θ) = -

nA_n shnξ₀ sinnθ ,

(62)

A₂ .

(54)

H₀

Здесь q — заряд, приходящийся на одно круговое

включение.

Φ(1)2n(θ) = -Φ(2)2n(θ) = -

nB_n chnξ₀ cosnθ ,

(63)

5. ПОВЕРХНОСТНЫЕ СОБСТВЕННЫЕ

Φ(1)3n(θ) = Φ(2)3n(θ) = -

nA_n shnξ0 cosnθ,

(64)

ФУНКЦИИ

H₀

Согласно [5, 6], собственные функции ψ_ν (r) и

ψ_k(r) образуют полную систему на поверхности S

Φ(1)4n(θ) = -Φ(2)4n(θ) = -

nB_n chnξ0 sinnθ,

(65)

соответствующего тела (при r = ρ). При этом соот-

H₀

ношение полноты формулируется для пары сопря-

женных поверхностных функций — это Ψ_ν (ρ) (зна-

Ψ⁽¹⁾(θ) = -Ψ(2)1(θ) =

A₁ ξ₀ ,

(66)

чение ψ_ν (r) при r = ρ) и Φ_ν (ρ) , вводимая следую-

щим образом:

(

)

(1)

(θ) =

Ψ⁽²⁾(θ) =

Φ_ν(ρ) =

n · ∇ψ(e)ν(r)

|r=ρ ,

(55)

[

]

∑

1 e-nξ0

где n — орт внешней к поверхности тела нормали.

=A¯₂ ln

+ξ₀ -2

(67)

n ch nξ₀

Аналогичным образом вводятся зарядовые поверх-

n=1

ностные функции

Ψ_k(ρ) и

Φ_k(ρ).

Для рассматриваемой в работе задачи имеем

Φ⁽¹⁾(θ) = -Φ(2)1(θ) = -

¯1 ,

(68)

Ψ(1)λn(θ) = ψ_λn(+ξ₀, θ), Ψ(2)λn(θ) = ψ_λn(-ξ₀, θ),

(56)



(e)



∂ψ_λ



Φ⁽¹⁾

Φ⁽²⁾

(θ) =

Φ(1)λn(θ) = -



H₀

∂ξ



[

]

ξ=+ξ0

∑

(-1)ⁿ



(57)

A₂

1+2

cosnθ

(69)

(e)



∂ψ_λ



H₀

ch nξ₀

n=1

Φ(2)λn(θ) =



H₀

∂ξ



ξ=-ξ0

Система функций (58)-(69) ортонормирована со-

где H₀ = H(ξ₀, θ) — коэффициент Ламе. Выбор зна-

гласно соотношениям

ков в выражениях (57) обусловлен тем, что согласно

∫

формуле (24) единичный вектор e_ξ является ортом

внутренней нормали для правой (ξ = +ξ₀) окруж-

Ψ(σ)λn(θ)Φ(σ)λ′n′ (θ)H(ξ0, θ)dθ =

ности и внешней нормали для левой (ξ = -ξ₀). Та-

σ=1 0

ε_λn

ким же образом вводятся зарядовые поверхностные

δ_λλ′ δnn′ ,

(70)

Ψ⁽¹⁾

Ψ⁽²⁾

Φ⁽¹⁾

1+ε_λn

функции

и Φ(2)k.

674

ЖЭТФ, том 157, вып. 4, 2020

Проводимость двумерной модели Рэлея...

∫

Здесь r — любой, а вектор ρ₁ равен (a + R, 0) в де-

Ψ(σ)λn(θ)Φ(σ)k(θ)H(ξ₀, θ)dθ = 0 ,

картовых координатах и (ξ₀, π) в биполярных. Для

(71)

σ=1 0

потенциалов вне включений (|ξ| ≤ ξ₀) и внутри пра-

k = 1,2,

вого круга (ξ ≥ ξ₀) имеем соответственно

{

∫

∑

(-1)ⁿ

Ψ(σ)(θ) Φ(σ)λn(θ) H(ξ0, θ) dθ = 0 ,

ϕ(e)(r) = -

ξ+2

2πσ₁

n h + cthnξ

(72)

n=1

σ=1 0

}

shnξ cosnθ

k = 1,2,

(77)

shnξ

∫

Ψ(σ)(θ)

Φ(σ)(θ) H(ξ0, θ) dθ = -δkk′ ,

k^′

(73)

σ=1 0

ϕ⁽¹⁾(r) = -

2πσ₁

k, k^′ = 1, 2.

{

}

∑

(-1)ⁿ

e-n(ξ-ξ0)

С помощью этих соотношений найдены нормировоч-

× ξ₀ +2

cosnθ

(78)

n h + cthnξ₀

ные коэффициенты A_n, B_n,

A₁ и

A₂, приведенные

n=1

выше.

На границе раздела (при ξ = ξ₀) потенциалы ϕ(e)(r)

Для соотношения полноты системы поверхност-

и ϕ⁽¹⁾(r), как и должно быть, совпадают.

ных собственных функций имеем следующее выра-

Используя выражения (77), (78), найдем

жение:



∂ϕ(e)

∂ϕ⁽¹⁾



-h

∑

1+ε_λn



∂ξ

Ψ(σ)λn (θ) Φ(σ′)_λn

(θ^′) +

ξ=ξ0

{

}

λn

λ=1 n=1

∑

1+2

(-1)ⁿ cos nθ

∑

2πσ

Ψ(σ)(θ)

Φ(σ′)

(θ^′) =

n=1

k=1

∑

ein(θ-π) .

(79)

2πσ₁

δ(θ - θ^′) δ_σσ′ .

(74)

n=-∞

H(ξ₀, θ)

Отсюда получаем равенство

Нетрудно убедиться, что подстановка выражений



∂ϕ(e)

∂ϕ⁽¹⁾

(58)-(69) в равенство (74) обращает его в тождество.



-h

δ(θ - π) ,

(80)



∂ξ

σ₁

ξ=ξ

ξ=ξ0

которое совпадает с граничным условием для пра-

6. ПОТЕНЦИАЛ

вого круга, следующее из уравнения (5). Такое же

Искомый потенциал задачи ϕ(r) находим под-

граничное условие справедливо и для левого круга.

Для модели с идеально проводящими (σ₂ = ∞)

становкой общего выражения для функции Грина

G(ρ, r), имеющей в данном случае вид

включениями потенциал вне кругов принимает вид

h = ∞ : ϕ(e)(r) = -

ξ.

(81)

∑

1+ε_λn

2πσ₁

G(ρ, r) = -

Ψ_λn(ρ)ψ_λn(r)-

h+ε

λn

λ=1 n=1

Используя формулу (81), для плотности тока

∑

∂ϕ(e)(r)

Ψ_k(ρ)ψk(r),

(75)

j(r) = -σ₁

(82)

k=1

H(ξ, θ)

∂ξ

на оси y (при ξ = 0) получаем

в формулу (7). В результате получаем

{

j(0, y) =

(83)

2π H(0, θ)

ϕ(r) = -2

Ψ₁(ρ₁)ψ1(r) +

σ₁

Согласно формуле (23),

}

∑

1+ε2n

Ψ2n(ρ₁)ψ2n(r)

(76)

(1 + cos θ) =

(84)

h+ε2n

n=1

H(0, θ)

c 1 + tg²(θ/2)

675

Б. Я. Балагуров

ЖЭТФ, том 157, вып. 4, 2020

С другой стороны, из формулы (17) при ξ = 0 сле-

Выражением (90) для σ_e, справедливым при h =

дует

= σ₂/σ₁ ≫ 1 и (a - R)/R ≪ 1, дается эффективная

проводимость исследуемой модели с фазовым пере-

sinθ

y=c

= ctg

(85)

ходом металл - идеальный проводник.

1 + cosθ

Величину σ_e как функцию ее аргументов запи-

так что

шем в виде

j(0, y) =

(86)

σe = σe(p; σ1, σ2) ,

(91)

π y² +c²

√

где

где c =

a² - R² .

Согласно соотношению

(86),

в случае

⁽R)2

p=1-

(92)

(a - R)/R ≪ 1 (c ≪ a) в распределении плот-

ности тока при y = 0 имеется острый пик шириной

— безразмерная концентрация (доля занимаемой

порядка c. Следовательно, низкопроводящую про-

площади) первой компоненты — матрицы, σ₁ и σ₂ —

слойку между включениями ток преодолевает по

проводимости соответственно матрицы и включе-

кратчайшему пути в виде узкого канала. Тем самым

ний. При (a - R)/R ≪ 1 для ξ₀ из (1) имеем

подтверждается обсуждавшаяся в разд. 2 картина

√

протекания тока в модели с фазовым переходом

a² - R²

4-π

металл - идеальный проводник. Заметим, что в

ξ₀ ≃

≃ βρ√τ, β =

(93)

пределе a → R (c → 0) распределение тока (86)

принимает вид дельта-функции: j(0, y)

= Iδ(y).

Здесь

Поэтому точность использованного в работе бинар-

p-p_c

τ =

(94)

ного приближения тем выше,чем ближе модель к

p_c

точке фазового перехода.

— параметр близости к порогу протекания (точке

фазового перехода)

7. ЭФФЕКТИВНАЯ ПРОВОДИМОСТЬ

p_c = 1 -

(95)

Эффективная проводимость σ_e модели в целом

совпадает с проводимостью отдельной ячейки, так

по концентрации. При σ₂ = ∞ (h = ∞) и a → R из

что

(90) следует

σ₁

σ_e =

(87)

σ_e(p; σ₁, ∞) ∼

(96)

√τ

Здесь I — полный ток, текущий через ячейку, U —

Формулой (96) дается закон возрастания эффек-

приложенная к ней разность потенциалов. В соот-

тивной проводимости при приближении к точке

ветствии с рис. 2 величина U выражается через по-

фазового перехода металл- идеальный проводник

тенциал ϕ(r) следующим образом:

и определяется соответствующий критический ин-

декс.

U = ϕ⁽²⁾(r₂) - ϕ⁽¹⁾(r₁) = -2ϕ⁽¹⁾(r₁)

(88)

Эффективная проводимость альтернативной мо-

дели с фазовым переходом металл - диэлектрик мо-

с ϕ⁽¹⁾(r) из формулы (78) при r = r₁ = (a, 0). Точке

жет быть найдена из полученных выше результатов

x = a, y = 0 соответствуют биполярные координаты

с помощью так называемого соотношения взаимнос-

(ξ₁, π), где

ти Келлера - Дыхне [7, 8]. Как отмечено в работах

[7, 8] (см. также [4]), в двумерном случае имеет ме-

ξ₁ = ξ(a, 0) = 2ξ₀

(89)

сто соотношение, связывающее эффективные про-

с ξ₀ из формулы (1). Вычислив с помощью выраже-

водимости взаимных, отличающихся друг от друга

ния (78) для ϕ⁽¹⁾(r) разность потенциалов U, найдем

заменой σ₁ ⇄ σ₂, систем:

величину σ_e, которую представим в виде

σ_e(p; σ₁, σ₂)σ_e(p; σ₂, σ₁) = σ₁σ₂ .

(97)

{

}

∑

e-nξ0

ξ₀ + 2

(90)

Введя безразмерную эффективную проводимость f

σ_e

πσ₁

n h + cthnξ₀

n=1

согласно соотношению

676

ЖЭТФ, том 157, вып. 4, 2020

Проводимость двумерной модели Рэлея...

σ₂

σ_e(p; σ₁, σ₂) = σ₁ f(p, h), h =

(98)

дают искомые выражения для безразмерной эффек-

σ₁

тивной проводимости двумерной модели Рэлея с фа-

зовым переходом металл - диэлектрик в предпорого-

приведем равенство (97) к следующему виду:

вой области концентраций — в ее «металлической»

f (p, h) f(p, 1/h) = 1 .

(99)

фазе.

Разложение (104) по форме совпадает (за ис-

Из этого соотношения, используя выражение (90),

ключением логарифмического множителя) с соот-

после замены h → 1/h находим безразмерную эф-

ветствующим разложением f(p, h) в рамках гипоте-

фективную проводимость модели с фазовым пере-

зы подобия [4,9]:

ходом металл - диэлектрик:

f (p, h) =

{

}

(

)₂

f (p, h) =

{

}

=τ^t

A₀ + A₁

+A₂

(107)

∑

τ^t/s

th nξ

× ξ₀ + 2h

e-nξ0

(100)

n h + thnξ₀

Здесь малым параметром является отношение

n=1

h/τ^t/s, где s — второй критический индекс, ха-

Выражение (100) справедливо в критической облас-

рактеризующий пороговое значение эффективной

ти h = σ₂/σ₁ ≪ 1 и ξ₀ ∼

√τ ≪ 1 .

проводимости: f(p_c, h) ∼ hs. Поскольку в разло-

В случае диэлектрических (σ₂ = 0) включений

жении (104) t

= 1/2, можно ожидать, что для

имеем [2, 3]

двумерной модели Рэлея индекс s = 1. Отметим,

что численное исследование этой модели [3] дает

f (p, 0) =

ξ₀ ≃ A₀ τ^t

(101)

s ≃ 0.95.

с τ из (94) и

Благодарности. В заключение выражаю бла-

√

годарность Д. А. Головневой и Н. А. Хлопотуновой

за помощь в подготовке рукописи статьи к печати.

A₀ =

- 1 = 0.166...

(102)

Отметим, что численное исследование проводимос-

ПРИЛОЖЕНИЕ

ти двумерной модели Рэлея дает следующие значе-

ния [3]:

Знание полной системы собственных функций

позволяет решать и некоторые другие задачи, свя-

t ≃ 0.51, A₀ ≃ 0.18,

(103)

занные с данным включением — макроскопическим

телом, например, о его дипольной поляризуемости.

согласующиеся с (102). При h = 0 (но по-прежнему

В случае тела, помещенного в однородное элек-

h ≪ 1 и ξ₀ ≪ 1) из общего выражения (100) получа-

трическое поле напряженности E₀, соответствую-

ем следующее разложение по степеням h:

щий потенциал имеет следующую асимптотику (в

двумерном случае):

f (p, h) =

{

}

(

)

(

)

p·r

⁽h)2

r → ∞ : ϕ(r)

E₀ · r

+ ... (A.1)

ξ₀

1+2

(104)

r²

ξ₀

Здесь

Здесь учтено, что

ˆ E0

(A.2)

∑

e-nξ0 = ln

≃ ln

(105)

— дипольный момент тела,

Λ — тензор дипольной

1 - e^-ξ0

ξ0

n=1

поляризуемости. Для составляющих этого тензора

согласно [5,6] имеем

∑

π²

d_να d_νβ

cth nξ₀ e-nξ0 ≃

(106)

Λ_αβ = -4π(1 - h)

(A.3)

ξ₀

n²

6ξ

h+ε_ν

n=1

Параметром разложения в (104) является h/ξ₀ ∼

где d_ν — аналог дипольного момента в асимптотике

∼ h/√τ ≪ 1. Формула (100) и разложение (104)

поляризационной собственной функции:

677

Б. Я. Балагуров

ЖЭТФ, том 157, вып. 4, 2020

(

)

r·d

ЛИТЕРАТУРА

r→∞: ψ_ν(r)

+...

(A.4)

r²

1. Lord Rayleigh, Phil. Mag. 34(211), 481 (1892).

В формуле (A.3) h = ε₂/ε₁ — отношение диэлектри-

ческих проницаемостей тела и окружающей среды.

2. W. T. Perrins, D. B. McKenzie, and B. C. McPhed-

Для рассматриваемой пары кругов дипольным по-

ran, Proc. Roy. Soc. London A 369, 207 (1979).

ведением при r → ∞ обладают функции ψ(e)2n(r) и

3. Б. Я. Балагуров, В. А. Кашин, ЖЭТФ 117, 978

ψ(e)1n(r). Для соответствующих дипольных моментов

(2000).

имеем

4. Б. Я. Балагуров, Электрофизические свойства

d2n = n(-1)ⁿcB_n i_x, d1n = n(-1)ⁿcA_n i_y. (A.5)

композитов. Макроскопическая теория, URSS,

Москва (2015).

Для составляющих тензора поляризуемости

Λполу-

чаем

5. Б. Я. Балагуров, ЖЭТФ 94, 95 (1988).

∑

1-h e-nξ0

6. Б. Я. Балагуров, Метод собственных функ-

Λ_xx = -2c²

(A.6)

h + cthnξ₀ shnξ₀

ций в макроскопической электростатике, URSS,

n=1

Москва (2016).

∑

7. J. B. Keller, J. Math. Phys. 5, 548 (1964).

1-h e-nξ0

Λ_yy = -2c²

(A.7)

h + thnξ₀ chnξ₀

n=1

8. А. М. Дыхне, ЖЭТФ 59, 110 (1970).

Отметим, что выражения (A.6), (A.7) удовлетворя-

9. A. L. Efros and B. I. Shrlovskii, Phys. Stat. Sol. (b)

ют равенствам

76, 475 (1976).

Λ_xx(h) = -Λ_yy(1/h), Λ_yy(h) = -Λ_xx(1/h), (A.8)

10. J. P. Straley, J. Phys. C 9, 783 (1976).

являющимся следствием соотношения взаимности

11. Ф. М. Морс, Г. Фешбах, Методы теоретической

(см. [4]).

физики, т. II, Изд-во иностр. лит., Москва (1960).

678