ЖЭТФ, 2020, том 157, вып. 5, стр. 796-801

УЧЕТ ВРАЩЕНИЯ ЧЕРНОЙ ДЫРЫ ПРИ МОДЕЛИРОВАНИИ

ФОРМЫ ЕЕ ТЕНИ В РАСШИРЕННЫХ МОДЕЛЯХ ГРАВИТАЦИИ

С. О. Алексеев^a,b, В. А. Прокоповa,c*

^a Государственный астрономический институт им. П. К. Штернберга,

Московский государственный университет им. М. В. Ломоносова

119234, Москва, Россия

^b Кафедра квантовой теории и физики высоких энергий, Физический факультет,

Московский государственный университет им. М. В. Ломоносова

119234, Москва, Россия

^c Кафедра астрофизики и звездной астрономии, Физический факультет,

Московский государственный университет им. М. В. Ломоносова

119234, Москва, Россия

Поступила в редакцию 26 ноября 2019 г.,

после переработки 26 ноября 2019 г.

Принята к публикации 23 декабря 2019 г.

С получением изображения тени сверхмассивной черной дыры в центре галактики М87 открылась но-

вая эра в наблюдениях компактных объектов, а улучшение разрешения подобных наблюдений позволит

использовать их для проверки расширенных теорий гравитации на масштабах горизонта событий. Мы

усовершенствовали метод учета вращения для вычисления параметров тени черной дыры с учетом по-

правок от расширенных теорий гравитации. Показано, что тень черной дыры с диаметром, меньшим

4RSw шварцшильдовского радиуса (RSw = 2M), невозможно описать только в рамках метрики Кер-

ра- Ньюмана, поэтому обнаружение тени такого размера покажет необходимость учета следующих чле-

нов разложения, что даст новые указания о теории гравитации, реализующейся на рассматриваемом

пространственно-временном масштабе.

DOI: 10.31857/S0044451020050041

дели f(R) гравитации, скалярно-тензорные теории,

включая модели Хорндески [8-10].

Модель модифицированной гравитации стоит

1. ВВЕДЕНИЕ

рассматривать как альтернативу ОТО в случае луч-

шего описания ею гравитационных явлений, хотя бы

В настоящее время общая теория относительнос-

ти (ОТО), являясь общепризнанной теорией гра-

на каком-то одном пространственно-временном мас-

штабе. Вследствие этого, особый интерес представ-

витации, предоставляет корректное описание ши-

ляют модели, удовлетворяющие, прежде всего, гра-

рочайшего спектра гравитационных явлений [1, 2].

витационным тестам в Солнечной системе, а именно,

В то же время, существование таких феноменов,

модели, чьи постньютоновские (а также посткепле-

как темная материя и темная энергия, дает осно-

ровские) параметры согласуются с эмпирическими

вание полагать, что ОТО корректно описывает гра-

данными [1, 7, 11]. С получением изображения тени

витационные явления лишь в ограниченном диапа-

зоне пространственно-временных масштабов [3-5].

сверхмассивной черной дыры (ЧД) в центре галак-

тики M87 [12] открывается новая возможность для

Поэтому в настоящее время в литературе широко

обсуждаются базовые физические принципы, кото-

проверки расширенных теорий гравитации на мас-

штабах горизонтов событий. Существует надежда

рые можно положить в основу модификации ОТО

обнаружить на таких масштабах эффекты поправок

[6, 7]. Таким образом, спектр таких модифициро-

к ОТО, быстро ослабевающие с расстоянием [13,14].

ванных теорий включает в себя разнообразные мо-

Метрику Шварцшильда (как самую простую мо-

^* E-mail: slaprok777@gmail.com

дель) можно расширить, учтя приливный заряд,

796

ЖЭТФ, том 157, вып. 5, 2020

Учет вращения черной дыры при моделировании формы. . .

(

)

являющийся эффективным проявлением дополни-

2m(r)r

4m(r)ar sin² θ

ds² = -

dt² -

dφ dt +

тельных измерений [15]. Таким образом, метрика

ρ²

Рейснера - Нордстрома приобретет дополнительный

ρ²

dr² + ρ²dθ² +

смысл, так как знак приливного заряда может быть

(

)

противоположен знаку электромагнитного [16]. Са-

2m(r)a²r sin² θ

+ r² +a² +

sin² θ dφ²,

(2)

мо расширение выглядит как добавление в метри-

ρ²

ческую функцию следующего члена разложения по

где

1/r. Поэтому в самом общем случае для любой мо-

ρ² = r² + a² cos² θ,

дифицированной теории гравитации компоненту g₀₀

(3)

Δ(r) = r² - 2m(r)r + a²,

можно представить в виде бесконечного ряда (фак-

a = J/M — угловое ускорение ЧД, M — ее масса, а

тически, это ряд Тейлора), численные коэффициен-

ты которого будут заданы теорией. Например, в слу-

J — угловой момент. Положив

чае модели эффективного действия струнной грави-

Q²

m(r) = M -

(4)

тации с поправками второго порядка по кривизне —

модель Гаусса - Боне [17, 18] — численное решение

где Q — электрический заряд, получим, что этот ал-

аппроксимировано именно таким полиномом. Ранее

горитм превращает метрику Рейснера - Нордстрома

[19] мы исследовали влияние такого расширения на

в метрику Керра - Ньюмана [22, 23]. Для ЧД с при-

форму тени для невращающейся ЧД и радиус ее по-

ливным зарядом

следней устойчивой орбиты. В настоящей работе мы

m(r) = M -

(5)

обобщим эти результаты на случай вращения ЧД.

Здесь необходимо отметить, что вращение искажа-

где q — это приливный заряд. Еще раз напомним,

ет форму тени, превращая фотонную сферу в на-

что, в отличие от электрического заряда, параметр

бор различных орбит, благодаря чему каждая точка

q может быть как положительным, так и отрица-

края тени становится уникальной пробой потенциа-

тельным.

ла ЧД, т. е. по форме тени можно определить или

Далее необходимо отметить, что метрики

существенно ограничить параметры разложения в

Шварцшильда, Рейснера - Нордстрома, Кер-

ряд метрики ЧД.

ра - Ньюмана не всегда являются точными ре-

В разд. 2 мы обсудим метод генерации враща-

шениями в расширенной теории гравитации, часто

ющегося решения из невращающегося, разд. 3 по-

играя роль лишь первого приближения. Итак, если

священ построению тени для вращающейся ЧД, в

в невращающемся случае метрическая функция

разд. 4 мы обсудим полученные формы теней, а

представима как бесконечный ряд Тейлора по 1/r,

разд. 5 посвящен сделанным нами выводам.

то (Δ = g₀₀)

Все расчеты представлены в планковской систе-

С₁

С₂

С₃

ме единиц (G = c = ℏ = 1).

Δ=1-

+...

(6)

r²

r³

Под C₁ можно понимать удвоенную Массу ЧД, под

C₂ — какой-либо из ее зарядов. Если помимо этих

членов в разложении следующие коэффициенты не

2. МЕТРИКА ВРАЩАЮЩЕЙСЯ ЧЕРНОЙ

равны нулю, то их вклад сильнее ослабевает с рас-

ДЫРЫ

стоянием. Примером наблюдений, в которых воз-

можно их обнаружить, является сильное гравитаци-

Для получения метрики вращающейся ЧД вос-

онное линзирование и его предельный случай — тень

пользуемся методом, предложенным в [20] и разви-

ЧД [12], для которой уже получены первые изобра-

тым нами в [21]. Итак, с помощью алгоритма Нью-

жения. Однако разрешения пока недостаточно для

мана - Яниса [22] из метрики вида

анализа формы тени, поэтому мы оценим потреб-

ную точность наблюдений для определения после-

(

)

(

)-1

2m(r)

дующих членов разложения.

ds² = -

dt² +

dr² +

Применяя алгоритм Ньюмана - Яниса к метри-

+ r²(dθ² + sin2 θ dφ²)

(1)

ческой функции (6), получаем метрику (2)

C₃

C_n

m(r) = M -

-...-

-...,

(7)

можно получить описание пространства-времени

2r²

2rn-1

следующей структуры:

где мы ограничимся анализом C₃.

797

С. О. Алексеев, В. А. Прокопов

ЖЭТФ, том 157, вып. 5, 2020

Итак, для метрики (2) с учетом (7) функции ξ

и η_- выглядят следующим образом:

4r²⁰ξ_A - (r²⁰ + a²)ξ_B

ξ_- =

aξ

(12)

r³⁰[η_Aa² - r₀η²

]

η_- =

a²η2C

2.0

2.5

3.0

3.5

4.0

r₀

где

-10

C₃

C_n

ξ_A = M -

...-

-...,

-20

^- 2r²⁰ -

2rn-1

–30

C₃

(n - 2)C_n

ξ_B = r₀ + M +

+...+

+...,

2r²⁰

2rn-1

Рис. 1. Диапазон значений r0, в котором β² > 0

(n - 2)C_n

ξ_C = r₀ - M -

-...-

-...,

n-1

2r²⁰

3. МОДЕЛИРОВАНИЕ ФОРМЫ ТЕНИ В

6C₃

2nC_n

η_A = 4M -

-...-

-...,

СЛУЧАЕ ВРАЩАЮЩЕЙСЯ ЧЕРНОЙ

r₀

r²⁰

rn-1

ДЫРЫ

5C₃

(n + 2)C_n

η_B = r₀-3M+

+...+

+...,

r₀

2r²⁰

2rn-10

Согласно методу [20] для построения тени вра-

C₃

(n - 2)C_n

щающейся ЧД необходимо получить функции

η_C = r₀ - M -

-...-

-...

n-1

2r²⁰

4m₀r²⁰ - (r₀ + f₀m₀)(r²⁰ + a²⁰)

ξ_- =

Для удобства можно нормализовать полученную

a(r₀ - f₀m₀)

(8)

модель на массу ЧД M, тогда величины r и a будут

r³⁰[4(2-f₀)a²m₀-r₀(r₀-(4-f₀)m₀)²]

η_- =

измеряться в единицах M, а коэффициенты разло-

a²(r₀ - f₀m₀)²

жения C_n в единицах Mⁿ.

где

4. АНАЛИЗ ТЕНЕЙ

m^′(r₀)r₀

f₀ = 1 +

(9)

m(r₀)

Под размером тени будем понимать ее диаметр

а r₀ — радиус фотонной орбиты, соответствующий

вдоль оси вращения. Таким образом, если угол на-

краю тени. Каждой точке края тени вращающей-

клона θ_i равен ±π/2, размеры теней вращающейся и

ся ЧД соответствует свой r₀. Аналогично [20] эти

покоящейся ЧД совпадут (рис. 2). Далее, как видно

функции можно перевести в координаты [α, β] кар-

на рис. 3, при уменьшении угла наклона тень также

тинной плоскости следующим образом:

уменьшается. В предельном случае θ_i = 0 тень ста-

нет симметрично круглой (как и у невращающейся

ξ_-

ЧД), но сжатой из-за вращения. Ранее [19] мы пока-

α=

sinθ_i

зали, что один и тот же размер тени может соответ-

√

(

)₂

(10)

ствовать разным невращающимся ЧД. Например, у

ξ_-

β = ± η_- + (a - ξ_-)² - asinθ_i -

ЧД с параметрами q = 0.17, C₃ = -0.5 тень совпадет

sinθ_i

со шварцшильдовским случаем. Поэтому необходи-

мы несколько разных наблюдений ЧД для точно-

где θ_i — угол наклона оси вращения ЧД к лучу зре-

го определения ее параметров. Далее, каждая точка

ния. Знак «+» соответствует верхней части тени, а

края тени вращающейся ЧД может быть использо-

«-» — нижней. Чтобы получить диапазон r₀, со-

вана как уникальная проба потенциала ЧД (7), так

ответствующий всем точкам края тени, необходимо

как ей соответствует свой радиус фотонной орбиты

решить следующее уравнение:

r₀. Чем шире диапазон r₀, тем легче найти различия

β² = 0,

(11)

в потенциале ЧД. Именно поэтому наилучшей точ-

кой обзора является угол наклонения θ_i = ±π/2. В

выбрав те корни, между которыми β² > 0 (рис. 1).

случае θ_i = 0 уже невозможно отличить уменьшение

В настоящей работе это сделано с использованием

размера тени за счет заряда, спина или параметров

численных методов.

разложения, не используя другие наблюдения ЧД.

798

ЖЭТФ, том 157, вып. 5, 2020

Учет вращения черной дыры при моделировании формы. . .

-5

–5

-5

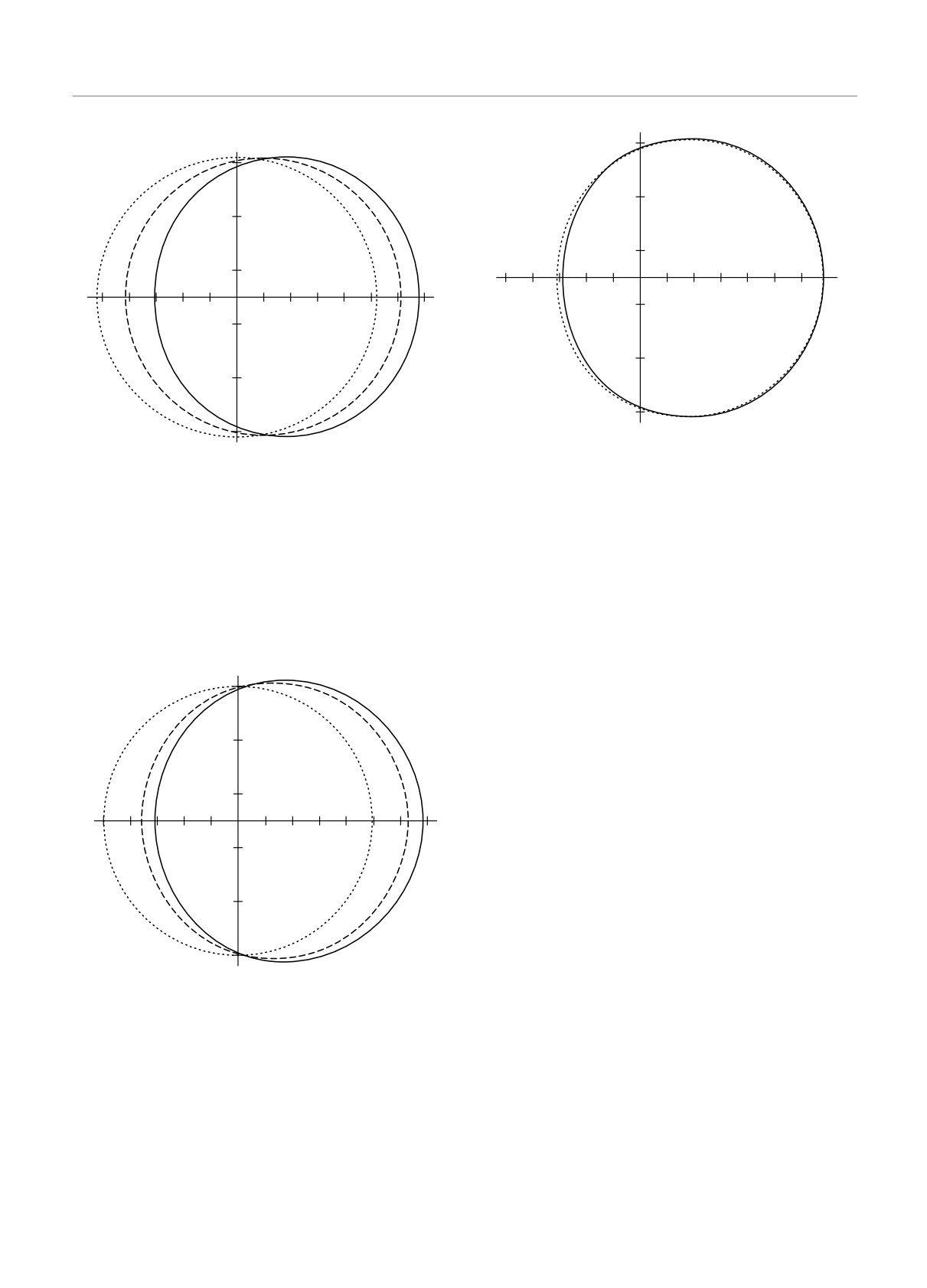
Рис. 4. Сравнение теней черных дыр с одинаковым значе-

Рис. 2. Зависимость формы теней черной дыры от момен-

нием отношения момента вращения к массе, равным a =

та вращения. Черная дыра видна под углом θi = -π/2 при

= 0.9, но с различающимися значениями приливного заря-

значениях приливного заряда и третьей поправки, равных,

да и третьей поправки. Пунктиром обозначена тень от чер-

соответственно, q = 0.17, C3 = -0.5. Пунктир соответству-

ной дыры с приливным зарядом и третьей поправкой, рав-

ет невращающемуся случаю (a = 0), штриховая линия —

ными соответственно q = 0.17, C3 = -0.5. Сплошной ли-

среднему значению отношения момента вращения к мас-

нией обозначена тень от черной дыры с приливным заря-

се, равному a = 0.5, сплошная — быстрому вращению с

дом и третьей поправкой, равными соответственно q = 0,

a = 0.9. Ось вращения направлена вдоль оси β

C3 = 0. Ось вращения черной дыры направлена вдоль оси

β, угол наклона равен θi = -π/2

Для оценки необходимой точности наблюдений

сравним тени ЧД с разными параметрами, но име-

ющие одинаковый размер при наблюдении с θ_i =

= -π/2. Например, керровскую (q = 0, C₃ = 0) и с

(q = 0.17, C₃ = -0.5). При отсутствии вращения их

тени совпадут, но с увеличением скорости вращения

расстояние между двумя соответствующими точка-

ми тени будет увеличиваться. Для наблюдения из

-5

экваториальной плоскости место c наибольшим рас-

хождением находится со стороны, где тень наиболее

сжата из-за вращения. При среднем значении отно-

шения момента к массе, равном 0.5, это расстояние

порядка 0.05M, что составляет всего 0.5 % от раз-

мера тени. Для быстро вращающейся ЧД с отноше-

нием момента к массе, равным 0.9, это расстояние

-5

станет 0.2M (рис. 4), что составляет 2 % от разме-

Рис. 3. Зависимость формы теней черной дыры от угла,

ра тени (порядка 1 μas для Sag A* и M87*). Поэто-

под которым ее наблюдают. Черная дыра имеет значения

му ЧД с более быстрым вращением лучше подходят

приливного заряда, третьей поправки и отношения момен-

для оценки или ограничения ее параметров по фор-

та вращения к массе, равные соответственно q = 0.17,

ме ее тени.

C3 = -0.5, a = 0.9. Пунктиром обозначена тень, видимая

Наименее удачная позиция для наблюдения тени

под углом θi = 0, штриховая линия — θi = -π/4, сплош-

вращающейся ЧД — это θ_i = 0. Однако существуют

ная линия — θi = -π/2. Ось вращения ЧД направлена

пределы, до которых тень можно «уменьшить» по-

вдоль оси β

средством «изменения» вращения и заряда, не пре-

вращая объект в голую сингулярность. В случае

799

С. О. Алексеев, В. А. Прокопов

ЖЭТФ, том 157, вып. 5, 2020

достигнутое в наблюдении М87, составило около

половины размера тени (20 μas) [12], что является

недостаточным даже для определения момента

вращения. При значительном улучшении разреше-

ния такие наблюдения можно будет использовать

и для измерения и/или селекции расширенных

теорий гравитации, создав на основе этих данных

аналог ППН формализма [1]. Однако возможен

-5

уникальный случай, когда, как и в невращающемся

случае, размер тени окажется менее 4RSw, при

этом для моделирования тени недостаточно лишь

метрики Керра - Ньюмана или учета других про-

цессов (например, [24, 25]). Обнаружение подобного

размера тени сразу покажет необходимость учета

-5

расширенных теорий гравитации.

Рис. 5. Минимальные размеры теней черных дыр с враще-

Финансирование. Работа выполнена при под-

нием и разными значениями приливного заряда, видимых

держке Программы развития МГУ «Ведущая науч-

под углом наклона, равным θi = 0. Сплошная линия со-

ная школа Физика звезд, релятивистских объектов

ответствует минимальному размеру тени керровской чер-

и галактик».

ной дыры (значения приливного заряда, третьей поправки

и отношения момента вращения к массе, равны соответ-

ственно q = 0, C3 = 0, a = 1). Штриховая линия со-

ответствует минимальному размеру черной дыры Керра -

ЛИТЕРАТУРА

Ньюмана (значения приливного заряда, третьей поправки

C. V. Will, Living Rev. Rel. 17, 4 (2014).

и отношения момента вращения к массе, равны соответ-

ственно q = 1, C3 = 0, a = 0). Пунктир соответствует

D. H. Abbott и др. (Virgo, LIGO Scientific), Phys.

черной дыре, метрика которой включает третью поправку

Rev. Lett. 116, 221101 (2016).

(значения приливного заряда, третьей поправки и отно-

шения момента вращения к массе равны соответственно

S. Weinberg, Rev. Mod. Phys. 61, 123 (1989).

q = 1.4, C3 = -0.5, a = 0.5)

D. Clowe, M. Bradac, A. Gonzalez, M. Markevitch,

S. W. Randall, C. Jones, and D. Zaritsky, Astrophys.

J. 648, L109 (2006).

ЧД Керра - Ньюмана минимальный размер дости-

гается при критическом заряде q = 1 и равен 4R_Sw

P. A. R. Ade и др. (Planck Collaboration), Astron.

шварцшильдовским радиусам (R_Sw = 2M) (рис. 5).

Astrophys. 594, A13 (2006).

При учете следующих поправок можно построить

S. Capozziello and M. De Laurentis, Phys. Rep. 509,

сколь угодно малую тень ЧД [19]. Считаем чрезвы-

167 (2011).

чайно важным подчеркнуть, что тень ЧД с разме-

ром, меньшим 4R_Sw, невозможно описать метрикой

E. Berti и др., Class. Quant. Grav. 32, 243001 (2015).

Керра - Ньюмана, поэтому обнаружение тени тако-

T. P. Sotiriou and V. Faraoni, Rev. Mod. Phys. 82,

го размера покажет необходимость учета следую-

451 (2010).

щих членов разложения, что даст новые указания

о теории гравитации, реализующейся на рассматри-

A. De Felice and S. Tsujikawa, Living Rev. Rel. 13,

ваемом пространственно-временном масштабе.

3 (2010).

10.

C. Charmousis, E. J. Copeland, A. Padilla, and

P. M. Saffin, Phys. Rev. Lett. 108, 051101 (2012).

5. ВЫВОДЫ

11.

P. I. Dyadina, N. A. Avdeev, and S. O. Alexeyev,

С ростом разрешения инструментов, использу-

Mon. Not. Roy. Astron. Soc. 483, 947 (2019).

емых для наблюдений теней черных дыр, станет

12.

K. Akiyama и др. (Event Horizon Telescope), Astro-

возможным прямое использование этих наблю-

phys. J. 875, L1 (2019).

дательных данных для проверки и селекции

расширенных теорий гравитации. Разрешение,

13.

A. F. Zakharov, Phys. Rev. D 90, 062007 (2014).

800