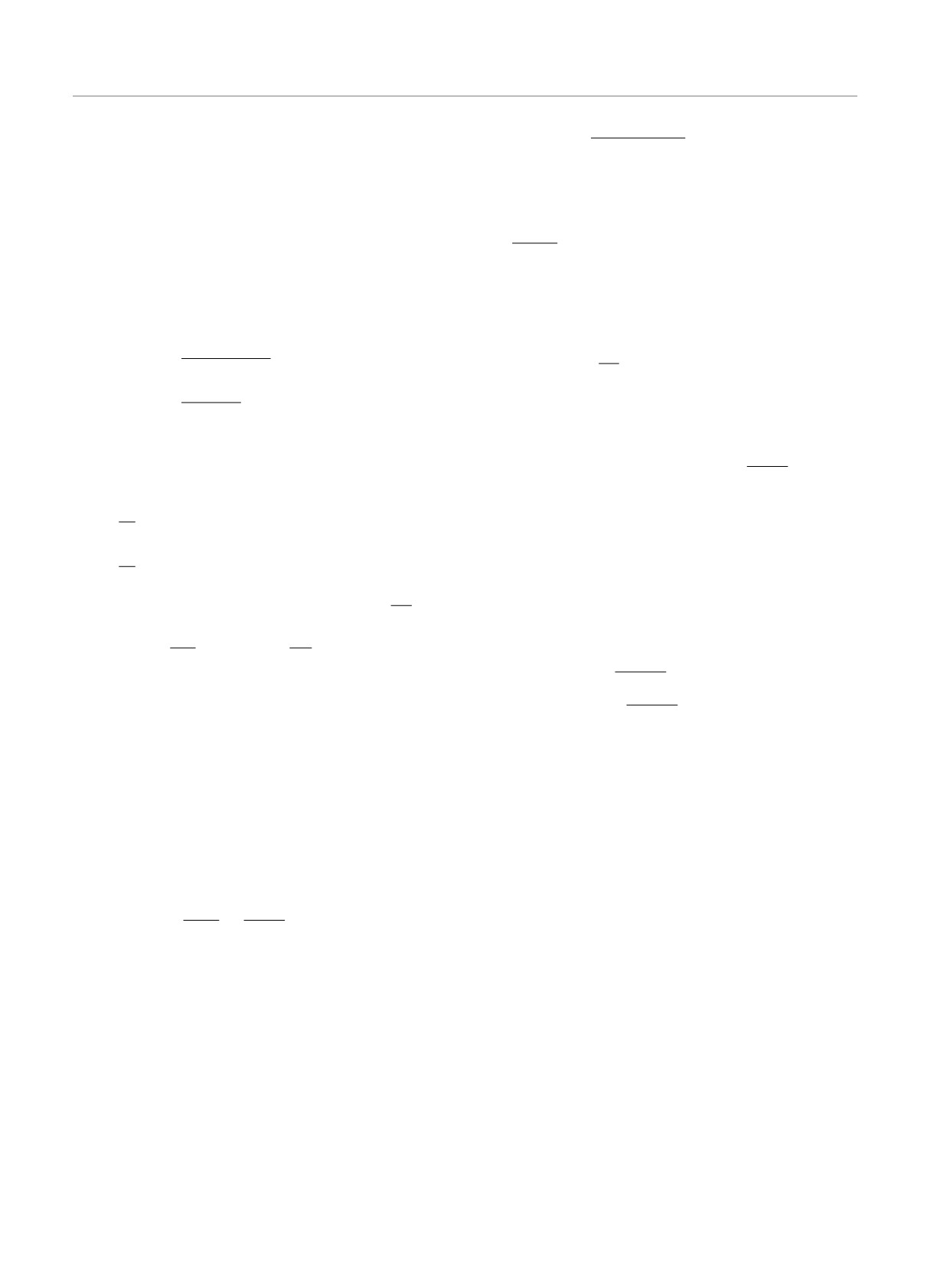ЖЭТФ, 2020, том 157, вып. 5, стр. 847-876
© 2020
СПЕКТРЫ ЭЛЕКТРОННЫХ ВОЗБУЖДЕНИЙ В ГРАФЕНЕ
В ОКРЕСТНОСТИ КУЛОНОВСКИХ ПРИМЕСЕЙ
А. И. Бреевa*, Р. Феррейраb**, Д. М. Гитманa,b,c***, Б. Л. Вороновc****
a Томский государственный университет
634050, Томск, Россия
b Институт физики университета Сан-Паулу
70297-400, Сан-Паулу, Бразилия
c Физический институт им. П. Н. Лебедева Российской академии наук
119991, Москва, Россия
Поступила в редакцию 9 октября 2019 г.,
после переработки 20 ноября 2019 г.
Принята к публикации 21 ноября 2019 г.
Исследуется спектр электронных возбуждений при наличии точечных и регуляризованных кулоновских
примесей в допированном графене. Для кулоновского поля точечного заряда используются модель Ди-
рака и теория самосопряженных расширений симметрических операторов. Построено семейство самосо-
пряженных гамильтонианов, описывающих возбуждения для любого заряда примеси. Найдены спектры
и (обобщенные) собственные функции для всех таких гамильтонианов. Также рассматривается спек-
тральная задача для регуляризованного кулоновского потенциала примеси для случая специальной регу-
ляризации. Исследуются точные уравнения для зарядов примесей, которые могут генерировать связан-
ные состояния с энергией, совпадающей с верхней границей отрицательной ветви непрерывного спектра
(сверхкритические заряды), и вычисляются эти заряды.
DOI: 10.31857/S0044451020050107
существенен и в лабораторных условиях почти лю-
бое электрическое внешнее поле является сверхкри-
тическим1), и эффект рождения частиц оказывает-
1. ВВЕДЕНИЕ
ся доминирующим (при определенных условиях) в
различных квантовых процессах во внешнем элект-
Хорошо известно, что низкоэнергетические элек-
рическом поле в графене. Применение КЭД с силь-
тронные возбуждения в монослое графена в присут-
ным полем и неустойчивым вакуумом для описания
ствии внешнего электромагнитного поля могут быть
квантовых процессов в графене требует непертур-
описаны моделью Дирака на соответствующем фоне
бативных методов. В частности, при помощи дан-
[1], а именно 2 + 1 квантованным полем Дирака. На
ных методов в работе [4] была изучена проводимость
самом деле, в рамках последней модели правиль-
графена, особенно в так называемом нелинейном ре-
нее говорить о квазичастицах, которые являются
жиме. Рождение электронно-дырочных пар недавно
киральными дираковскими фермионами в 2 + 1 из-
наблюдалось в графене при исследовании поведения
мерениях. Учитывая, что дисперсионными поверх-
его вольт-амперных характеристик [5].
ностями являются так называемые конусы Дирака,
щель между верхней и нижней ветвями в соответ-
Известно, что одним из свойств графена являет-
ствующих спектрах дираковских частиц очень мала,
ся его большая чувствительность к примесям и де-
а носители заряда безмассовые, можно ожидать, что
механизм вакуумной неустойчивости Швингера уже
1)
Заметим также, что стандартный вакуум КЭД в (3 + 1)
становится нестабильным из-за кулоновского притяжения
* E-mail: breev@mail.tsu.ru
между электроном и позитроном выше критического значе-
** E-mail: rafaelufpi@gmail.com
ния постоянной тонкой структуры [2, 3], αcr = π/8, или при
*** E-mail: dmitrygitman@hotmail.com
ее истинном значении α = 1/137, если наложено внешнее маг-
**** E-mail: voronov@lpi.ru
нитное поле выше 1042 Гс [3].
847
А. И. Бреев, Р. Феррейра, Д. М. Гитман, Б. Л. Воронов
ЖЭТФ, том 157, вып. 5, 2020
фектам, что связано с убыванием плотности состо-
Статья организована следующим образом. Оп-
яний носителей тока. Транспорт электронов в при-
ределения базовых понятий и соотношений, объяс-
сутствии заряженных примесей, таких как кулонов-
няющих постановку задачи, приведены в разд. 2.
ские центры, становится одной из наиболее важных
В разд. 3 описывается математически строгая про-
задач, касающихся достижения максимальной по-
цедура сведения проблемы построения с. с. враща-
движности носителей в графене [6]. Поскольку за-
тельно-инвариантного дираковского гамильтониана
кон Кулона остается неизменным в недопированном
в полном гильбертовом пространстве к задаче по-
графене и приблизительно сохраняется при малом
строения с. с. одномерных парциальных радиаль-
и умеренном допировании, процессы рассеяния в
ных гамильтонианов с определенным угловым мо-
основном контролируются неэкранированным куло-
ментом. Дальнейшее исследование делится на две
новским потенциалом, в отличие от обычных метал-
части. В первой части (разд. 4-6) рассматривает-
лов, где экранирование является полным [7].
ся кулоновское поле точечных примесей в допиро-
Потенциал, индуцированный подложкой, может
ванном графене. В разд. 4 строится общее реше-
нарушить симметрию решетки и создать щель в
ние радиальных уравнений, а также некоторые кон-
спектре электронов графена. Наличие щели говорит
кретные решения этих уравнений, используемые в
о том, что движение электронов необходимо описы-
дальнейшем. Раздел 5 посвящен построению с. с.
вать массивным уравнением Дирака 2 + 1. Задача
парциальных радиальных гамильтонианов с произ-
расчета электронных спектров в допированном гра-
вольным допустимым значением углового момента
фене в присутствии кулоновских примесей рассмат-
j. При решении соответствующих спектральных за-
ривалась в работах [8-11].
дач в четырех различных областях верхней полу-
В релятивистской теории рассеяния для 2 + 1
плоскости изменения параметров j, Z области раз-
электронов Дирака в графене на кулоновских при-
личаются по характеру с. с. граничных условий в
месях используются решения спектральной задачи
начале координат, которые задают парциальные ра-
для дираковского гамильтониана в 2+1 измерениях
диальные гамильтонианы. Раздел 6 посвящен опи-
с соответствующим точечным или регуляризован-
санию особенностей полного гамильтониана в зави-
ным трехмерным кулоновским потенциалом. Соот-
симости от заряда примеси Z. Вторая часть иссле-
ветствующая спектральная задача в 3 + 1 подробно
дования (разд. 7-10) посвящена регуляризованному
обсуждалась в работах [12-15] для точечного куло-
кулоновскому полю примесей в допированном гра-
новского потенциала и в [15,16] для регуляризован-
фене. В случае специальной регуляризации куло-
ного кулоновского потенциала. Для точечного ку-
новского поля получены точные уравнения, которые
лоновского потенциала непротиворечивая трактов-
позволяют найти точечный спектр (расположенный
ка этой задачи существенно зависит от правильного
в полуинтервале [-m, m)) и соответствующие свя-
определения дираковского гамильтониана как само-
занные состояния, см. разд. 7. В разд. 9 приведены
сопряженного (в дальнейшем с. с.) оператора в соот-
точные уравнения для зарядов, которые дают свя-
ветствующем гильбертовом пространстве. Тогда как
занные состояния с энергией E = -m, совпадающей
в 3 + 1 измерениях особенности такого определения
с верхней границей отрицательной ветви непрерыв-
проявляются только для ядер с большими Z, Z >
ного спектра. В разд. 10 обсуждается понятие сверх-
> 119, которых нет в лабораторных условиях, для
критического заряда примеси. Раздел 11 посвящен
кулоновских примесей в графене этот порог значи-
обсуждению результатов, полученных в первой и
тельно меньше из-за свойств дираковских квазича-
второй частях статьи.
стиц в графене.
В этой статье мы рассматриваем задачу коррект-
ного определения дираковского гамильтониана для
2. УРАВНЕНИЕ ДИРАКА В 2 + 1
квазичастиц в допированном графене в присутствии
ИЗМЕРЕНИЯХ В КУЛОНОВСКОМ ПОЛЕ
кулоновской примеси с зарядом Z как с. с. опера-
ТОЧЕЧНОГО ЗАРЯДА
тора и его спектральный анализ. Мы представля-
ем строгое рассмотрение всех аспектов этой задачи,
Рассмотрим спектр возбуждений квазичастиц в
основанное на теории с. с. расширений симметри-
присутствии одной кулоновской примеси с зарядом
ческих операторов [13]. Также мы исследуем спек-
Ze, помещенной в середину шестиугольника решет-
тральную задачу для случая регуляризованного ку-
ки графена. При этом мы ограничиваемся окрестно-
лоновского поля примеси, который позволяет полу-
стями двух так называемых точек Дирака, которые
чить ее точное аналитическое описание.
являются областями спектра квазичастиц, наиболее
848
ЖЭТФ, том 157, вып. 5, 2020
Спектры электронных возбуждений в графене...
чувствительных к воздействию примеси. Кроме то-
Как уже говорилось выше, мы ограничиваем-
го, мы предполагаем, что примесь является ионом,
ся рассмотрением окрестностей двух точек Дира-
полностью лишенным электронов, поэтому Z явля-
ка, что означает, что рассматриваем низкоэнерге-
ется его атомным номером.
тические квазичастичные возбуждения и электрон-
Введем декартову систему координат с осями x и
ные переходы между ближайшими атомами углеро-
y, лежащими в плоскости графена, и осью z, перпен-
да. В этом приближении полное гильбертово прост-
дикулярной плоскости. Примесь находится в начале
ранство Htot квантовых состояний квазичастицы в
координат. Кулоновское поле ослабляется поляриза-
графене является прямой ортогональной суммой
цией кристалла на расстояниях, больших межатом-
двух гильбертовых пространств Hs, s = ±1, каж-
ных. Чтобы учесть этот эффект, в кулоновский по-
дое из которых связано с соответствующей точкой
тенциал необходимо ввести макроскопическую ди-
Дирака Ks. Пространства Hs являются гильберто-
электрическую проницаемость ϵ (которая также на-
выми пространствами двумерных дублетов, так что
зывается эффективной диэлектрической проницае-
Htot = H1 ⊕ H-1, H1 = H-1 = H = L2(R2) ⊕ L2(R2).
мостью):
Обычно в графене междолинные процессы не
учитываются ввиду дальнодействующей природы
2
√
Ze
1
кулоновского поля. Формально это означает, что пе-
V (ρ) = -
,
ρ = |r| =
x2 + y2,
ϵ ρ
реходы между гильбертовыми пространствами H
s
не рассматриваются, так что полный эффективный
где r = (x, y) — двумерный вектор (лежащий в плос-
гамильтониан
Ĥtot является прямой ортогональной
кости графена z = 0).
суммой двух гамильтонианов
Hs, s = ±1, каждый
Квазичастицы в графене находятся в двумерном
из которых действует в соответствующем гильбер-
пространстве, тогда как кулоновское поле, создан-
товом пространстве Hs и может быть рассмотрен
ное примесью, — в трехмерном пространстве, и по-
отдельно.
этому кулоновский потенциал в плоскости графена
В рамках приближения сильной связи и для ма-
z = 0 ведет себя как ρ-1. Если бы мы рассматрива-
лой энергии квазичастиц стационарное уравнение
ли электрическое поле, создаваемое примесью заря-
Шредингера для электрона сводится к следующим
да q, который находится в двумерном пространстве,
двум независимым уравнениям для огибающих бло-
то электрический потенциал Φ был бы равен Φ =
ховских функций в окрестности каждой точки Ди-
= q/(2πϵ)ln(1/ρ), как следует из уравнения Пуассо-
рака Ks [19]:
на ΔΦ = -(q/ϵ)δ(r) в двумерном пространстве.
HsΨs = EΨs, s = ±1.
(1)
В случае, когда экранирование заряда происхо-
дит из-за электронов в графене, метод RPA дает
Здесь волновые функции Ψs являются дублетами,
значение ϵ ≈ 5 (см. [17]). Если мы полностью прене-
зависящими от r, Ψs = Ψs(r) = {ψsα(r), α = 1, 2},
брегаем эффектами поляризации в графене, но гра-
компоненты ψsα(r) представляют собой огибающие
фен находится на подложке SiO2, то ϵ ≈ 2.5 (см.
блоховских функций в двух подрешетках A и B со-
также [18]).
ответственно,
Hs — дифференциальные выражения,
отвечающие уравнению Дирака в 2 + 1:
Отметим, что потенциалы, индуцированные под-
(
)
ложкой, могут нарушать симметрию решетки и соз-
g
Δdop
Hs = ℏvF
-i [sσx∂x + σy∂y] -
+
σz,
давать щель в электронном спектре между зоной
ρ
2
(2)
проводимости и валентной зоной. Выбирая подлож-
1
Ze2
Z
Z
ку, можно регулировать эффективную массу носи-
g=
=αF
=αFZeff, Zeff =
,
ℏvF
ϵ
ϵ
ϵ
телей заряда и исследовать явления, отсутствующие
где vF
≈ 106 см/с — скорость Ферми, Δdop
=
в безмассовом случае. В этой статье мы предполага-
= 2m∗v2F — ширина щели, αF = e2/(ℏvF ) — «посто-
ем, что носители заряда в графене имеют некоторую
янная тонкой структуры» в графене, {σx, σy, σz } —
эффективную массу m∗ > 0.
матрицы Паули.
Чтобы различить две разные точки Дирака в
В дальнейшем мы будем использовать следую-
графене, введем параметр (или индекс) s = ±1, ко-
щие обозначения:
Hs = (ℏνF )-1 Hs, E = (ℏνF )-1E
торый будем называть изоспином из-за определен-
и m = (2ℏvF)-1Δdop. Заметим, что переменная E
ной аналогии с последним. Обозначим через Ks точ-
и параметр m имеют размерность обратной длины.
ки Дирака, координаты которых в зоне Бриллюэна
Уравнение (1) принимает вид
выбраны в виде Ks = (4πs/(3a), 0), где a = 2.46Å —
постоянная решетки.
HsΨs(r) = EΨs(r), s = ±1,
(3)
849
6
ЖЭТФ, вып. 5
А. И. Бреев, Р. Феррейра, Д. М. Гитман, Б. Л. Воронов
ЖЭТФ, том 157, вып. 5, 2020
где
Hs — дифференциальные выражения в декарто-
Мы строим с. с. гамильтонианы
Ĥs как с. с. рас-
вой и полярной системах координат ρ, φ (x = ρ cosφ,
ширения соответствующих исходных симметричес-
y = ρsinφ) соответственно:
ких операторов
Ĥ in
. Для того чтобы подчеркнуть
s
g
это обстоятельство, введем дополнительный индекс
Hs = -i (sσx∂x + σy∂y) -
+ mσz =
Ĥe
ρ
e для
Ĥs,
Ĥs →
s
. Существуют разные с. с. расши-
рения данного оператора
Ĥ in
, так что в дальнейшем
∂
s
= -i(s cosφσx + sinφσy)
+
∂ρ
индекс e будет заменен другим, более информатив-
ным.
i
∂
g
+
(s sin φσx - cos φσy )
-
+ mσz.
(4)
Ĥe
Потребуем, чтобы операторы
s
были враща-
ρ
∂φ
ρ
тельно-инвариантными, так же как исходные сим-
Для того чтобы придать смысл квантовомехани-
Ĥ in
метрические операторы
. Смысл этого требова-
s
ческой задаче на собственные значения (3) для га-
ния мы поясним ниже.
мильтонианов
Ĥs, мы должны решить две пробле-
Существуют два разных унитарных представле-
мы. Первая — определить или построить гамильто-
ния Us группы вращений Spin(2) в H, которые свя-
нианы
Ĥs как с. с. операторы с областями опреде-
Ĥ in
заны с соответствующими операторами
. Генера-
s
ления в гильбертовом пространстве H = L2(R2) ⊕
тор
Js представления группы Us, называемый опе-
⊕ L2(R2) функций, действующих на свои обла-
ратором углового момента (их два), является с. с.
сти определения соответствующими дифференци-
оператором в H, определенным на абсолютно непре-
альными выражениями
Hs (4) (для краткости будем
рывных и периодических по φ ∈ [0, 2π] дублетах и
говорить, что операторы
Ĥs связаны с дифференци-
ассоциированным с дифференциальным выражени-
альными выражениями
Hs). Вторая проблема — вы-
ем
Js = -i∂/∂φ+sσz/2. Для каждого s гильбертово
полнить спектральный анализ полученных гамиль-
пространство H представляется в виде прямой орто-
тонианов, т. е. вычислить их спектры и соответству-
гональной суммы
ющие (в общем случае обобщенные) собственные
∑
функции. Решая обе проблемы, мы следуем пути,
H=
⊕Hsj, j = ±1/2, ±3/2, . . .,
(5)
принятому в работе [12] в случае (3 + 1)-мерного
j
уравнения Дирака в регуляризованных и нерегуля-
подпространств Hsj , которые являются собственны-
ризованных кулоновских полях.
ˆs,
ми пространствами оператора углового момента
3. РЕДУКЦИЯ К РАДИАЛЬНОМУ
соответствующими всем его собственным значениям
УРАВНЕНИЮ
j = ±1/2,±3/2,... Подпространство Hsj с данными
Начнем с определения начальных симметричес-
s и j состоит из дублетов Ψsj вида
Ĥ in
ких операторов
s
в гильбертовом пространстве
(
)
H = L2(R2) ⊕ L2(R2), ассоциированных с соот-
1
e-isφ/2f(ρ)
Ψsj(r) =
eijφ
∈Hsj.
(6)
ветствующими дифференциальными выражениями
√2πρ
-iseisφ/2g(ρ)
Hs (4). Поскольку коэффициентные функции диф-
ференциальных выражений
Hs являются гладкими
Данные дублеты являются собственными функ-
вне начала координат, мы выбираем пространство
циями оператора
Js с собственным значением j,
гладких дублетов с компактным носителем для об-
JsΨsj(r) =
JsΨsj(r) = jΨsj(r). Отметим, что спект-
Ĥ in
Ĥ in
ластей определения D(
s
) операторов
s
ры двух операторов
J-1 и
J1 совпадают. Функции
Чтобы обойти проблемы с сингулярностью ти-
f (ρ) и g(ρ) называются радиальными функциями.
па 1/ρ кулоновского потенциала, дополнительно по-
На физическом языке разложения (5) и (6) соот-
требуем обращения в нуль дублетов D(
Ĥ in
) в неко-
ветствуют разложению дублетов Ψ(r) ∈ H по соб-
s
торой окрестности начала координат, разной для
ственным функциям двух разных операторов угло-
каждого дублета. Заметим, что области определе-
вого момента
J-1 и
J1.
Ĥ in
ния D(
s
) (которые совпадают для обоих значений
В дальнейшем для нас является существенным
s) плотны в пространстве H. Таким образом, опера-
следующий факт. Пусть L2(R+) есть гильбертово
Ĥ in
торы
s
определяются как
пространство радиальных дублетов,
{
{
}
(
)
Ĥ in
D(
s
)=
Ψ(r) : ψα(r) ∈ C∞0(R2 \ {0})
,
f (ρ)
Ĥ in
s
=
F (ρ) =
∈ L2(R+),
Ĥ in
s
Ψ(r) =
HsΨ(r).
g(ρ)
Очевидно, что оператор
Ĥ in
симметрический.
со скалярным произведением
s
850
ЖЭТФ, том 157, вып. 5, 2020
Спектры электронных возбуждений в графене...
∫∞
симметрии в физической литературе на приведен-
(F1, F2) = F+1(ρ)F2 (ρ) dρ =
ном выше примере вращательной симметрии. В фи-
0
зической литературе утверждение о том, что опера-
∫∞
Ĥ in
[
]
торы
s
вращательно-инвариантны и, как следст-
=
f1(ρ) f2(ρ) + g1(ρ) g2(ρ) dρ,
вие, их исследование сводится к изучению их частей
0
Ĥ in
, действующих в Hsj , обычно отождествляется с
sj
утверждением, что операторы
Ĥ in
коммутируют с
s
так что L2(R+) = L2(R+) ⊕ L2(R+). Тогда из (6) и
соответствующими генераторами
Js группы враще-
соотношения
ний, а это, в свою очередь, часто отождествляется с
∫∞
коммутативностью дифференциальных выражений
[
]
∥Ψsj∥2 =
|f(ρ)|2 + |g(ρ)|2
dρ
Hs и
Js,
[Ĥins,Js] = [
Hs,Js] = 0. Строго говоря,
0
такое утверждение некорректно: формальная ком-
мутативность дифференциальных выражений нико-
следует, что пространство Hsj ⊂ H унитарно экви-
им образом не подразумевает коммутативность со-
валентно гильбертову пространству L2(R+),
ответствующих операторов, тем более что коммута-
тор двух неограниченных операторов в гильберто-
Ψsj(r) = VsjF(ρ), F(ρ) = V-1sjΨsj(r).
(7)
вом пространстве, вообще говоря, не определен.
Ĥ in
При необходимости легко записать явную форму
Каждый оператор
является симметричес-
sj
операторов Vsj и V-1sj.
ким оператором, действующим в подпространстве
Ĥ in
Hsj. Очевидно, он индуцирует симметрический
Начальные симметрические операторы
s
являются вращательно-инвариантными. А именно,
оператор
ĥin(Z, j, s) в гильбертовом пространстве
каждый оператор
Ĥ in
инвариантен относительно
L2(R+),
который унитарно эквивалентен опе-
s
представления Us группы вращений. По определе-
ратору
Ĥ in
,
= V-1sj ĤinsjVsj, так что
sj
нию это означает, что каждое подпространство Hsj
ĥin(Z, j, s)F
= V-1sj ĤinsjΨsj, Ψsj = VsjF. Оператор
(собственное пространство генератора
Js с собствен-
ĥin(Z, j, s) определяется следующим образом:
ным значением j) приводит оператор
Ĥ in
. Другими
s
Ĥ in
словами, оператор
s
коммутирует с проекторами
ĥin(Z, j, s) =
Psj на подпространства Hsj, см. [20]. Это означает
∑
{
следующее. Пусть Ψs(r)
).
= jΨsj(r)∈D(
s
Dhin(Z,j,s) = C0(R+),
=
(8)
Тогда
ĥin(Z, j, s)F(ρ) =
h(Z, j, s)F (ρ),
∑
Ĥ in
Ĥ in
Ĥ in
Ψsj = PsjΨs ∈ D(
s
),
s
Ψs =
sj
Ψsj,
где C∞0(R+) = C∞0(R+)⊕C∞0(R+). Дифференциаль-
j
ное выражение
ˇ(Z, j, s),
где операторы
Ĥ in
=Psj
Ĥ in
Psj =
Ĥ in
Psj представ-
sj
s
s
Ĥ in
d
κ
g
ляют собой так называемые части оператора
s
,
h(Z, j, s) = -iσy
+
σx -
+ mσz,
dρ
ρ
ρ
(9)
действующие в Hsj . Их правило действия дается
дифференциальным выражением первого порядка
κ = -sj, g = αFϵ-1Z,
по переменной ρ, которое легко вычисляется и будет
будем называть парциальным радиальным диффе-
приведено ниже. Таким образом, каждый началь-
ный симметрический оператор
Ĥ in
является прямой
ренциальным выражением.
s
ортогональной суммой своих частей,
Построение с. с. вращательно-инвариантных га-
∑
мильтонианов
Ĥs как с. с. расширений начальных
Ĥ in
⊕ Ĥin
s
=
sj
,
симметрических операторов
Ĥ in
,
Ĥs =
Ĥe
сводит-
s
s
j
ся к построению с. с. парциальных радиальных га-
и исследование вращательно-инвариантного опера-
мильтонианов
ĥ(Z, j, s) в L2(R+) как с. с. расшире-
Ĥ in
Ĥ in
ний начальных симметрических парциальных ради-
тора
s
сводится к изучению операторов
sj
Заметим, что эти факты основаны на формаль-
альных операторовĥin(Z, j, s),
ĥ(Z, j, s) =
ĥe(Z, j, s).
ной коммутативности дифференциальных выраже-
Это происходит следующим образом. Пусть опе-
ний
Hs и
Js, [
Hs,Js] = 0.
раторы
ĥe(Z, j, s) являются такими расширениями.
Ĥe
Сделаем общее замечание относительно доволь-
Они, очевидно, индуцируют с. с. расширения
sj
=
но популярного понимания квантовомеханической
= Vsjĥe(Z,j,s)V -1sj начальных симметрических опе-
851
6*
А. И. Бреев, Р. Феррейра, Д. М. Гитман, Б. Л. Воронов
ЖЭТФ, том 157, вып. 5, 2020
раторов
Ĥ in
в подпространствах Hsj . Тогда прямая
h(Z, j, s)F (ρ) = W F (ρ),
sj
(
)
Ĥe
ортогональная сумма парциальных операторов
,
(12)
sj
f (ρ)
F (ρ) =
,
W ∈ C,
∑
g(ρ)
Ĥe
=
⊕ Ĥe
,
(10)
s
sj
которое необходимо при вычислении спектров и соб-
j
ственных функций парциальных радиальных га-
представляет собой вращательно-инвариантное рас-
мильтонианов; систему (12) иногда называют (ста-
ширение начального симметрического оператора
ционарным) парциальным радиальным уравнением
Ĥ in
s
, причем с. с. вращательно-инвариантный га-
Шредингера. Действительные значения W в даль-
мильтониан
Ĥs =
Ĥe
в H. И обратно, любое с. с.
нейшем будут обозначаться буквой E. Для наших
s
вращательно-инвариантное расширение начального
целей достаточно рассмотреть значения W , принад-
симметрического оператора
Ĥ in
имеет структуру
лежащие верхней комплексной полуплоскости, W =
s
Ĥe
(10). Спектр гамильтониана
s
дается объединени-
= E + iy, y ≥ 0. Также нас интересует предел W →
ем спектров парциальных радиальных гамильтониа-
→ E + i0.
Ĥe
нов, spec
= ∪j specĥe(Z,j,s), и соответствующие
Система (12) для функции f(ρ) и g(ρ) представ-
s
собственные функции, связанные с Hsj , получают-
ляется в виде
ся из собственных функций операторов
ĥe(Z, j, s) в
(
)
df
κ
g
L2(R+) при помощи преобразования Vsj, см. (7).
+
f (ρ) - W + m +
g(ρ) = 0,
dρ
ρ
ρ
Как было сказано выше, мы действуем по анало-
(
)
(13)
dg
κ
g
гии с построением с. с. вращательно-инвариантного
-
g(ρ) + W - m +
f (ρ) = 0.
dρ
ρ
ρ
(относительно группы Spin(3)) дираковского га-
мильтониана для электрона в кулоновском поле
Будем называть уравнения (13) радиальными урав-
в трех пространственных измерениях [12-14, 16].
нениями. Радиальные уравнения для трехмерной за-
Напомним, что в работах [12-14, 16] была реше-
дачи те же.
на проблема построения и спектрального анали-
Для полноты приведем общее решение ради-
за с. с. парциальных радиальных гамильтонианов
альных уравнений, следуя стандартной процедуре
ĥe(Z, j, ζ) в L2(R+) как с. с. расширений началь-
[13, 21]. Начнем с замены переменных:
ных симметричных парциальных радиальных опе-
f (ρ) = zΥe-z/2 [Q(z) + P (z)] ,
раторов
ĥin(Z, j, ζ), определенных в пространстве
C∞0(R+) и связанных с дифференциальными выра-
g(ρ) = iΛzΥe-z/2 [Q(z) - P (z)] , z = -2iKρ,
жениями вида
где
d
κ
q
h(Z, j, ζ) = -iσy
+
σx -
+ mσz,
(11)
Υ2 = κ2 - g2, W ± m = r±eiφ±,
dr
r
r
0 ≤ φ± ≤ π, r± ≥ 0,
√
√
где r =
x2 + y2 + z2, κ = ζj, j = 1/2, 3/2, . . . —
W -m
квантовое число, отвечающее трехмерному углово-
Λ=
=
√r- e-i(φ+-φ-)/2,
W +m
r+
му моменту, ζ = ±1 — спиновый индекс, q = αZ, α —
√
постоянная тонкой структуры, m — масса электро-
K =
W2 - m2 =
√r+r- ei(φ++φ-)/2.
на. Дифференциальное выражение (11) отличается
В новых переменных система радиальных уравне-
от дифференциального выражения
h(Z, j, s) в (9)
ний (13) имеет вид
только значениями коэффициентов и физическим
смыслом параметров. Для сравнения наших резуль-
d2Q(z)
dQ(z)
z
+ (β - z)
- αQ(z) = 0,
татов с данной трехмерной задачей удобно ввести
dz2
dz
(
)
параметр ζ = ζ(j, s) = -s sgn(j) = ±1, κ = ζ(j, s) |j| .
1
d
P (z) = -
z
+ α Q(z),
b+
dz
(14)
β = 1 + 2Υ, α = α+,
4. ОБЩЕЕ РЕШЕНИЕ РАДИАЛЬНЫХ
gW
gm
УРАВНЕНИЙ
α+ = Υ +
,
b+ = κ +
iK
iK
Перейдем к общему решению системы двух ли-
Уравнение для функции Q(z) представляет собой
нейных обыкновенных дифференциальных уравне-
известное конфлюэнтное гипергеометрическое урав-
ний
нение.
852
ЖЭТФ, том 157, вып. 5, 2020
Спектры электронных возбуждений в графене...
-Υ
(-2iK/m)
Пусть Υ = -n/2, n ∈ N. Общее решение конфлю-
X (ρ, Υ, W ) =
zΥe-z/2 ×
1-a
энтного гипергеометрического уравнения является
[
линейной комбинацией стандартных гипергеометри-
× Φ(α, β; z)ϱ+ + aΦ(α + 1, β; z)ϱ-] =
ческих функций Φ(α, β; z) и Ψ(α, β; z):
(mρ)Υ
Q(z) = AΦ(α, β; z) + BΨ(α, β; z),
(15)
=
[Φ+(ρ, Υ, W ) + Φ-(ρ, Υ, W ) Ξ] d+,
2
Φ+(ρ, Υ, W) = eiKρΦ(α, 1 + 2Υ, -2iKρ)+
где A, B = const,
(17)
+ e-iKρΦ(α-, 1 + 2Υ, 2iKρ),
[
Γ(1 - β)
1
Ψ(α, β; z) =
Φ(α, β; z) +
Φ-(ρ, Υ, W) =
eiKρΦ(α, 1 + 2Υ, -2iKρ)-
Γ(α - β + 1)
iK
Γ(β - 1)
]
+
z1-βΦ(α - β + 1, 2 - β; z).
Γ(α)
- e-iKρΦ(α-, 1 + 2Υ, 2iKρ) ,
(
)
(
)
T
0
m+W
κ±Υ
Затем, используя выражения
Ξ=
, d± =
1,
m-W
0
g
(
)
d
В дальнейшем будем использовать некоторые част-
z
+ α Φ(α,β;z) = αΦ(α + 1,β;z),
dz
ные решения радиальных уравнений (13), соответст-
(
)
d
вующие определенному выбору констант A и B и
z
+α Ψ(α, β; z) = α(α-β+1)Ψ(α+1, β; z),
dz
параметра Υ. Сначала введем новую величину Υ
+
следующим образом:
α - β + 1 = -α-, α+α- = b+b-, a =
α+ ,
b+
gW
gm
α- = Υ -
,
b- = κ -
,
Υ+ = Υ+(g, j) =
iK
iK
⎧
√
⎨γ =
κ2 - g2 ≥ 0,
g ≤ |κ|,
(18)
найдем общее решение системы (14) в виде
= ⎩iσ = i√g2 - κ2, σ > 0, g > |κ|.
Величина Υ+ как функция параметра g имеет нули
Q(z) = AΦ(α, β; z) + BΨ(α, β; z),
в точках g = gc(j) = |κ| = |j|.
P (z) = -AaΦ(α+1, β; z)+Bb-Ψ(α+1, β; z).
В случае Υ+ = 0 (g = gc(j)) имеем два линейно
независимых решения F1 и F2, образующих фунда-
Окончательно, используя выражения
ментальную систему решений системы (13):
F1(ρ; W) = X(ρ, Υ+, W) =
Φ(α + 1, β; z) = ezΦ(β - α - 1, β; -z),
1+a
κ+Υ
= (mρ)Υ+d+ + O(ρΥ++1), ρ → 0,
iΛ
=
,
1-a
g
(19)
F2(ρ; W) = X(ρ, -Υ+, W) =
представим общее решение радиальных уравнений
= (mρ)-Υ+d- + O(ρ-Υ++1), ρ → 0.
(13) в следующей форме:
Заметим, что оба дублета F1 и F2 являются веще-
ственными целыми функциями от W . Их вронски-
F = AX(ρ,Υ,W)+
ан равен Wr(F1, F2) = -2Υ+g-1. Если ImW > 0 и
+ BzΥe-z/2 [Ψ(α, β; z)ϱ+-b-Ψ(α+1, β; z)ϱ-] ,
(16)
ρ → ∞, то оба дублета F1(ρ;W) и F2(ρ;W) экспо-
ненциально растут.
ϱ± = (±1, iΛ)T ,
Другое полезное решение F3 дается выражени-
ем (16) при A = 0, Υ = Υ+ и специальном выборе
где дублет X(ρ, Υ, W ) есть
параметра B = B(W ),
853
А. И. Бреев, Р. Феррейра, Д. М. Гитман, Б. Л. Воронов
ЖЭТФ, том 157, вып. 5, 2020
[
]
F3(ρ; W) = B(W)zΥe-z/2
Ψ(α, β; z)ϱ+ - b-Ψ(α + 1, β; z)ϱ-
=
ω(W )F2(ρ; W )
= Γ(-2Υ+)F1(ρ; W) -
,
Wr(F1, F2)
(20)
(
)-2Υ
+
Γ(1+2Υ+)Γ(-α-) [igK+(κ+Υ+)(W + m)]
K
ω(W ) =
2e-iπ/2
= -Wr(F1, F3),
gΓ(α)[igK+(κ-Υ+)(W + m)]
m
[
](
)-Υ
+
1
(m + W )(κ + Υ+)
K
B(W ) =
Γ(-α-) 1 +
2e-iπ/2
2
igK
m
При Im W > 0 и ρ → ∞ дублет F3(ρ; W ) убывает
в (11), возникающим при решении трехмерной ку-
экспоненциально (с точностью до полинома).
лоновской задачи в [13], вплоть до замены и дру-
В специальном случае Υ+ = γ = 0 (g = gc(j)),
гой интерпретации параметров κ
→ κ, g → q,
когда дублеты F1 и F2 совпадают, будем рассматри-
мы можем использовать некоторые результаты ра-
вать два линейно независимых решения F(0)1, F(0)2 и
бот [12-14, 16] относительно с. с. парциальных ра-
их линейную комбинацию F(0)3,
диальных гамильтонианов
ĥe(Z, j, ζ) в пространстве
) для определения и спектрального анали-
L2(R+
F(0)1(ρ; W) = F1(ρ; W)|γ=0 = d+|γ=0 + O(ρ),
за с. с. парциальных радиальных гамильтонианов
(21)
ρ → 0, d+|γ=0 = (1,ζ(j,s))T ,
ĥe(Z, j, s) в пространстве L2(R+) при замене и со-
ответствующей интерпретации параметров κ → κ,
F(0)2(ρ; W) = ∂γF1(ρ; W)|γ=0-ζ(j,s)F(0)1(ρ; W) =
q→g.
gc(j)
Так как все возможные с. с. парциальные ра-
= d0(ρ) + O(ρ ln ρ), ρ → 0,
(22)
диальные гамильтонианы
ĥe(Z, j, s) ассоциируются
с общим дифференциальным выражением
h(Z, j, s)
(
d0(ρ) =
ln(mρ) - ζ(j, s)g-1c(j),
в (9), см. ниже, их определение сводится к ука-
занию их области определения Dh(Z,j,s) ⊂ L2(R+).
ζ(j, s) ln(mρ))T ,
(23)
ˆe(Z, j, s) представляет собой с.с.
Каждый оператор
расширение начального симметрического оператора
F(0)3(ρ; W) = - lim
F3(ρ; W) = F(0)2(ρ; W)+
γ→0
ĥin(Z, j, s) в (8), ассоциированного с дифференци-
альным выражением
h(Z, j, s) в (9), с. с. по Лагран-
+ f(W)F(0)1(ρ;W), F(0)3 ∈ L2(R+),
(24)
жу, и определенного в пространстве C∞0(R+) глад-
ких дублетов с компактным носителем на полуоси
f (W ) = gc(j)ω(0)(W ) =
R+. В то же время каждый оператор
ĥe(Z, j, s) есть
с. с. сужение, может быть тривиальное, сопряжен-
= ln(2e-iπ/2K/m) + ψ(-igc(j)W K-1) +
ĥ+
ного оператора
(Z, j, s), который ассоциирован
in
+ (ζ(j, s)(W - m) + iK)(2gc(j)W )-1 - 2ψ(1),
(25)
с тем же самым дифференциальным выражением
h(Z, j, s) (так как каждый оператор
ĥe(Z, j, s) ассо-
ψ(x) = Γ′(x)/Γ(x).
циируется с одним и тем же дифференциальным вы-
Соответствующие вронскианы имеют вид
ражением
h(Z, j, s)) и определен на так называемой
Wr(F(0)1, F(0)2) = g-1c(j), Wr(F(0)2, F(0)3) = -ω(0),
естественной области определения D∗ˇ
(R+) для
h(Z,j,s)
h(Z, j, s), состоящей из дублетов F (ρ) ∈ L2(R+), аб-
где ω(0) = ω(0)(W ).
солютно непрерывных в пространстве R+ и таких,
что
5. САМОСОПРЯЖЕННЫЕ РАДИАЛЬНЫЕ
h(Z, j, s)F (ρ) ∈ L2(R+),
ГАМИЛЬТОНИАНЫ
Здесь полезно вспомнить, что было сказано в
Dhin(Z,j,s) ⊂ Dhe(Z,j,s)⊆Dh(Z,j,s)(R+).
конце разд. 3. Поскольку радиальное дифференци-
Определение с. с. радиальных гамильтонианов
альное выражение
h(Z, j, s) в (9) совпадает с ради-
ĥe(Z, j, s) существенно зависит от значений парамет-
альным дифференциальным выражением
h(Z, j, ζ)
ров Z и j и в особенности от параметра Υ+ (18).
854
ЖЭТФ, том 157, вып. 5, 2020
Спектры электронных возбуждений в графене...
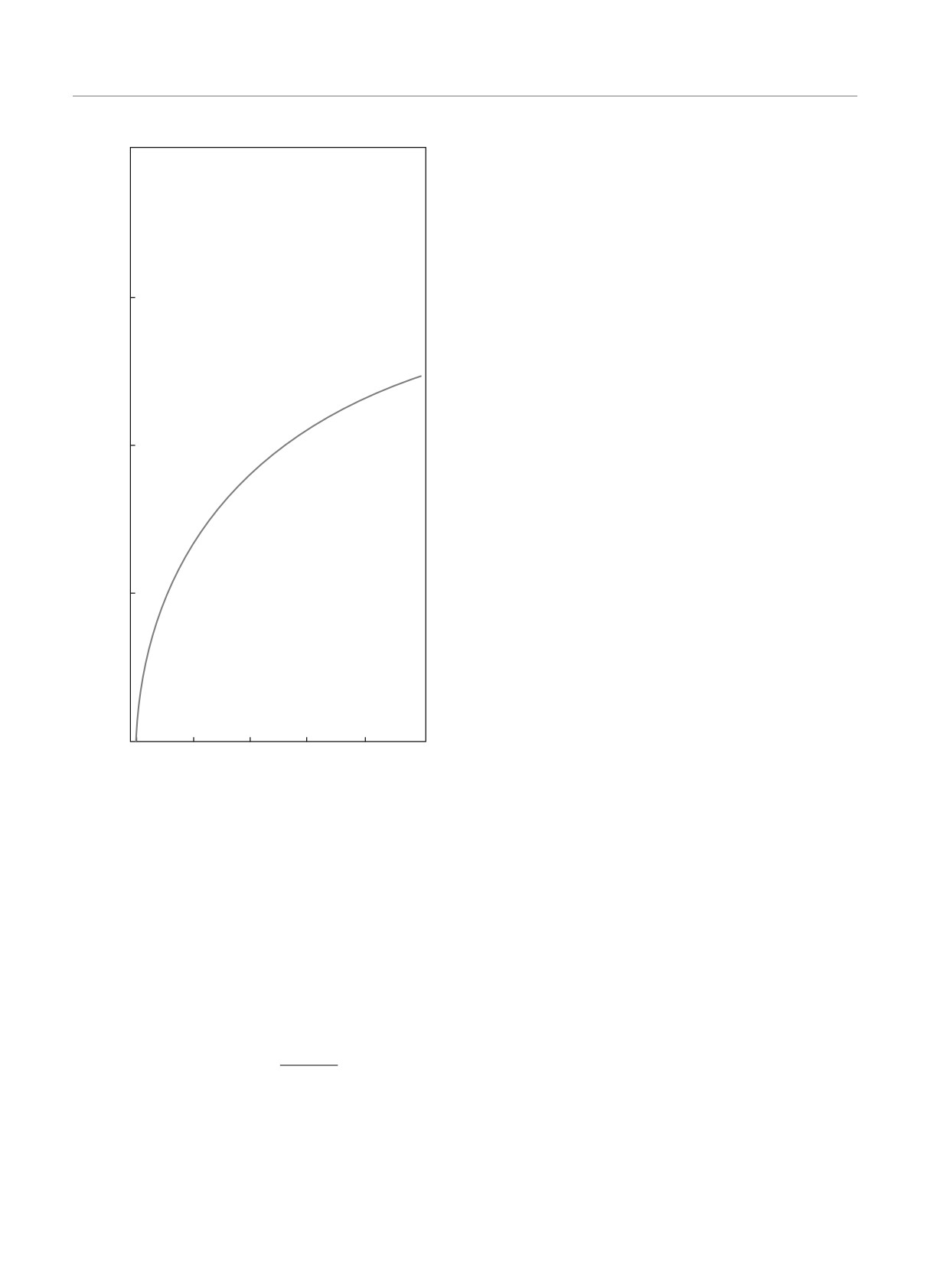
Z
(находится внизу) определяется неравенством Z ≤
2.5
Overcritical region
Z (jc)
≤ Zs(j), что эквивалентно Υ+ = γ ≥ 1/2. Сингуляр-
Critical region
{
ная область (находится вверху) определяется нера-
2.0
Subcritical region
венством Z > Zs(j), что равносильно 0 ≤ Υ+ = γ <
1.5
< 1/2 или Υ+ = iσ, σ > 0, см. (18).
Singular region
Заметим, что сингулярная кривая является
1.0
верхней границей несингулярной области. Значение
0.5
Nonsingular
Zs(j) будем называть максимальным несингуляр-
region
Z j (
)
ным значением Z для данного j. Для примера
0
(j) для малых полуце-
приведем первые значения gs
-5/2
-3/2
-1/2
1/2
3/2
5/2
лых j:
j
√
gs (±1/2) = 0, gs (±3/2) =
2,
Рис. 1. Области в плоскости (j, Z): несингулярная (non-
√
√
singular region) и сингулярная (singular region). Последняя
gs (±5/2) =
6, gs(±7/2) = 2
3.
состоит из субкритической (subcritical region), критической
(critical region) и сверхкритической (overcritical region) под-
Далее будем рассматривать с. с. радиальные га-
областей
мильтонианы
ĥ(Z, j, s) в несингулярной и сингуляр-
ной областях отдельно.
По определению переменная j принимает полу-
5.1. Несингулярная область
целые значения, положительные и отрицательные,
j = ±(n+1/2), n ∈ Z+, тогда как переменная Z при-
В несингулярной области, Z ≤ Zs(j), каждый
нимает неотрицательные целые значения, Z ∈ Z+.
парциальный радиальный гамильтониан обозначим
Таким образом, мы имеем дело с дискретными зна-
через
ĥ1(Z, j, s), где нижний индекс «1» использует-
чениями данных переменных в верхней полуплос-
ся вместо индекса e как символ несингулярной обла-
кости (j, Z). Однако удобнее рассматривать пере-
сти (нижние индексы «2», «3», «4» вместе с другими
менную Z, как величину, принимающую непрерыв-
соответствующими индексами будут использоваться
ные значения и лежащую на неотрицательной вер-
вместо индекса e в качестве индексов, относящихся
тикальной полуоси, Z ∈ R+, и возвращаться к ее
к определенным подобластям сингулярной области),
естественным целочисленным значениям в случае
он определяется единственным образом:ĥ1(Z, j, s) =
необходимости.
= ĥ+in(Z, j, s). Другими словами, начальный симмет-
Верхняя полуплоскость (j, Z) (см. рис. 1 для
рический оператор
ĥin(Z, j, s) является существенно
α-1Fϵ = 1) разбивается на так называемую несин-
с. с. оператором, так как его индексы дефекта рав-
гулярную и сингулярную области, в которых про-
ны (0, 0), а область определения оператораĥ1(Z, j, s)
блема нахождения с. с. расширений
ĥin(Z, j, s) име-
является естественной областью определения для
ет принципиально разные решения: в несингулярной
h(Z, j, s), Dh
1(Z,j,s) =Dh(Z,j,s)(R+).Функции,лежа-
области с. с. радиальные гамильтонианы
ĥe(Z, j, s)
щие в D∗ˇ
(R+) имеют следующее асимптотиче-
h(Z,j,s)
определяются единственным образом, тогда как в
ское поведение в нуле и на бесконечности:
сингулярной области они определяются неоднознач-
но.
F (ρ) = O(ρ1/2) → 0, ρ → 0; F (ρ) → 0, ρ → ∞.
Эти области разделяются симметричной сингу-
Заметим, что точки (j, Z = 0) для любого значе-
лярной кривой Z = Zs(j), где
ния j принадлежат несингулярной области, а имен-
√
но ее нижней границе, из чего следует, что оба пол-
1
Zs (j) = α-1Fϵ j2 -
,
Ĥ1
ных свободных дираковских гамильтониана
,s=
4
s
= ±1, однозначно определяются как с. с. операторы
√
на которой g = gs(j) =
j2 - 1/4, или Υ+ = γ =
в H = L2(R2) ⊕ L2(R2). Их спектры и (обобщенные)
= 1/2, см. (18); данная кривая состоит из двух вет-
собственные функции хорошо известны.
вей: правая ветвь начинается в точке (j = 1/2, Z =
Возвращаясь к парциальным радиальным га-
= 0) и идет вверх направо, приближаясь к асимп-
мильтонианам
ĥ1(Z, j, s) с Z = 0, отметим, что
тоте Z = α-1Fϵj, а левая ветвь начинается в точке
несингулярная область (где γ2 = j2 - g2 ≥ 1/4) не
(j = -1/2, Z = 0) и идет вверх влево, приближаясь
содержит точек j = ±1/2 (напомним, что ветви осо-
к асимптоте Z = -α-1Fϵ j. Несингулярная область
бой кривой начинаются в точках (j = 1/2, Z = 0)
855
А. И. Бреев, Р. Феррейра, Д. М. Гитман, Б. Л. Воронов
ЖЭТФ, том 157, вып. 5, 2020
и (j = -1/2, Z = 0)). Следовательно, парциальные
(n + γ)m
En = E1n(Z, j, s) =
√
,
n∈Nζ,
радиальные гамильтонианы
ĥe(Z, ±1/2, s) с Z = 0
g2 + (n + γ)2
не определены однозначно.
Nζ =
Прежде чем перейти к спектрам и (обобщенным)
{
N = {1,2,...},
ζ = 1, или sj < 0,
собственным функциям данных парциальных ради-
=
(26)
альных гамильтонианов
ĥ1(Z, j, s) с Z = 0 (т.е. |j| >
Z+ = {0, 1, 2, . . . }, ζ = -1, или sj > 0,
√
> 1/2: j = ±3/2, ±5/2, . . .), напомним некоторые по-
γ =
j2 - g2 ≥ 1/2, j = ±3/2, ±5/2, . . .
нятия, связанные с классификацией точек спектра
с. с. оператора, следуя математической терминоло-
Спектры операторов
ĥ1(Z, j, s) можно получить из
гии, которая, вообще говоря, не совпадает с физи-
спектров соответствующих радиальных гамильто-
ческой.
нианов
ĥ1(Z, j, ζ) в трехмерном случае (они постро-
Мы называем собственными значениями с. с.
ены в работах [12-14, 16]) при помощи замен
оператора только те точки его спектра, которые
j = 1/2,3/2,... → j = ±3/2,±5/2,...,
соответствуют его связанным состояниям, т.е. соб-
ственные состояния, волновые функции (дублеты)
ζ = ±1 → ζ = -ssgn(j),
√
√
которых квадратично интегрируемы. Заметим, что
γ=
(j + 1/2)2 - q2 → γ =
j2 - g2.
в физической литературе любая точка спектра с. с.
оператора часто называется его собственным зна-
Отметим, что дискретные энергетические уров-
чением. Напомним, что в физической литературе
ни с данными Z и j не зависят от s и формально
собственные значения гамильтониана условно назы-
совпадают при s = ±1, но множества Nζ , последо-
вают уровнями энергии.
вательности целых чисел n, обозначающие энергети-
Множество всех собственных значений данного
ческие уровни, различаются (т. е. для разных значе-
с. с. оператора называется его точечным спектром.
ний переменной ζ = -s sgn(j) = ±1) первым членом.
Множество всех изолированных собственных значе-
В дальнейшем будем говорить, что множество N1
ний данного с. с. оператора называется его дискрет-
принадлежит сектору ζ = +1, а множество N-1 —
ным спектром. Он, очевидно, является подмножест-
сектору ζ = -1.
вом точечного спектра, если они не совпадают. В
Ортонормированные (обобщенные) собственные
физической литературе понятия точечного и диск-
функции U1E(ρ), |E| ≥ m, непрерывного спектра и
ортонормированные собственные функции U1n(ρ)
ретного спектров часто отождествляются.
связанных состояний с энергией En, отвечаю-
Замыкание дополнения точечного спектра во
щие парциальным радиальным гамильтонианам
всем спектре с. с. оператора называется его непре-
ĥ1(Z, j, s), образуют полную ортонормированную
рывным спектром. В физической литературе, вклю-
систему в пространстве L2(R+) в смысле формул
чая учебники, строгое определение непрерывного
обращения (см. [13]) и имеют вид
спектра обычно отсутствует, оно заменяется эврис-
тическими аргументами и примерами.
U1E(ρ) = QEF1(ρ; E), QE > 0,
|E| ≥ m,
Может случиться так, что точка спектра с. с.
(27)
U1n(ρ) = QnF1(ρ; En), n ∈ Nζ,
0 < E < m,
оператора принадлежит его точечному и непрерыв-
ному спектрам одновременно. Такая точка спектра
где дублет F1(ρ; E) определяется в (17) и (19),
не является точкой дискретного спектра.
Q2E =
Спектр каждого парциального радиального га-
мильтониана
ĥ1(Z, j, s) в несингулярной области яв-
2πg2k (|E| - sgn(E)m) (2k/m)2γ eπgE/k
=
(
)
×
ляется простым (невырожденным). Он состоит из
2
Γ2(2γ + 1)Γ
-γ + igk |E|
непрерывного спектра, занимающего как отрица-
(
)-1
тельную, так и положительную полуоси (-∞, -m]
×
(κ + γ)2k2 + g2(E - m)2
×
(
(
)
)-1
и [m, ∞), и дискретного спектра, расположенного в
g
× ch 2π
E - cos(2πγ)
,
(28)
интервале (0, m) и состоящего из растущего беско-
k
нечного числа энергетических уровней En, которые
Γ (2γ + 1 + n) τ3n (2τn/m)2γ
Q2n =
×
накапливаются в точке m,
m2n!Γ2(2γ + 1)
g (m - En) - (κ - γ)τn
×
,
specĥ1(Z, j, s) =
g (m - En) - (κ + γ)τn
√
= {E ∈ (-∞, -m] ∪ [m, ∞)} ∪ {En ∈ (0, m)} ,
k=
E2 - m2, τn = gm[g2 + (n + γ)2]-1/2.
856
ЖЭТФ, том 157, вып. 5, 2020
Спектры электронных возбуждений в графене...
В заключение отметим, что справедливо равенство
ся простым (невырожденным в физической тер-
ĥ1(Z, j, s) =
ĥ1(Z, -j, -s).
минологии). В таком случае основным инструмен-
том спектрального анализа является спектральная
функция σkν(E) и ее (обобщенная) производная
5.2. Сингулярная область
σ′kν (E), где E ∈ R — вещественная переменная. По
В сингулярной области, находящейся в верхней
определению, функция σ′kν (E) определяется выра-
плоскости изменения параметров (j, Z), Z > Zs(j)
жением
(что эквивалентно Υ2+ = j2 - g2 < 1/4), с. с. пар-
1
1
σ′kν (E) =
Im
,
циальные радиальные гамильтонианы
ĥe(Z, j, s) как
π
ωkν(E + i0)
с. с. расширения начальных симметрических опе-
где функция ωkν (W ), W = E + iy ∈ C, y = 0, опре-
раторов
ĥin(Z, j, s) не определены однозначно для
деляется функцией Грина оператора
ĥkν, а именно,
каждой тройки параметров Z, j и s. Причина со-
из множителя в представлении функции Грина в ви-
стоит в том, что индексы дефекта m+, m- каж-
де произведения дублетов Ukν (ρ; W ) и F3(ρ; W ) (20).
дого симметрического оператора
ĥin(Z, j, s) равны
Дублет Ukν(ρ; W) является линейной комбинацией
(1, 1) и, следовательно, существует однопарамет-
дублетов F1(ρ; W ) и F2(ρ; W ) (19), удовлетворяющей
рическое семейство расширений, так что с. с. пар-
асимптотическим с. с. граничным условиям. Отме-
циальные радиальные гамильтонианы параметризу-
тим, что функция Грина является ядром интеграль-
ются параметром ν ∈ [-π/2, π/2], -π/2 ∼ π/2. Пар-
ного представления резольвенты (ĥkν -W )-1 опера-
циальные радиальные гамильтонианы с одинаковы-
тора
ĥkν.
ми значениями параметров Z, j и s, но с разны-
Спектр оператора
ĥkν является носителем
ми значениями ν ассоциированы с одним и тем же
функции σ′kν(E) и ограничение Ukν(ρ; E) дубле-
дифференциальным выражением
h(Z, j, s), но раз-
ĥkν
та Ukν (ρ; W ) на точку спектра E оператора
личаются областями определения, которые являют-
является соответствующей собственной функцией
ся подмножествами естественной области определе-
оператора
ĥkν.
ния D∗ˇ
(R+) дляh(Z, j, s) и задаются некоторы-
h(Z,j,s)
ми асимптотическими граничными условиями в на-
В частности, функция σ′kν в точке En, яв-
чале координат, которые явно содержат параметр ν.
ляющейся простым нулем вещественной функции
Как и в трехмерной кулоновской задаче, мы
ωkν(E), ωkν(En) = 0, Imωkν(E) = 0, |E - En| < δ,
делим сингулярную область на три подмножества:
имеет особенность типа дельта-функции. А точка
субкритическую, критическую и сверхкритическую
En является собственным значением соответствую-
подобласти, которые различаются характером
щего парциального гамильтониана.
асимптотических с. с. граничных условий в начале
Точки E, в которых функция ωkν (E) отлич-
координат.
на от нуля, непрерывна и принимает комплексные
Обозначим через
ĥkν, k = 2, 3, 4, с. с. парци-
значения, являются точками непрерывного спектра
альные радиальные гамильтонианы в субкритичес-
оператора
ĥkν. В данных точках спектра функ-
кой k = 2, критической k = 3 и сверхкритической
ция σ′kν (E) положительна, σ′kν (E) = Q2kν (E) > 0,
√
k = 4 подобластях соответственно (для краткости
где Qkν (E) =
σ′kν(E) — нормировочный множи-
опускаем здесь аргументы Z, j, s). С. с. граничные
тель для соответствующей (обобщенной) собствен-
условия, задающие гамильтонианы
ĥkν, не сильно
ной функции Ukν (ρ; E) непрерывного спектра. Зара-
отличаются друг от друга для разных подобластей
нее скажем, что во всех трех подобластях сингуляр-
сингулярной области. И решение спектральной за-
ной области непрерывный спектр каждого операто-
дачи для оператора
ĥkν при разных k проводится
ра
ĥkν представляет собой объединение двух полу-
аналогичным образом.
осей (-∞, -m] ∪ [m, ∞).
Для полноты изложения кратко напомним ос-
В интервале (-m, m) любая функция ωkν (E)
новные моменты спектрального анализа с. с. ради-
принимает вещественные значения, но она имеет
альных гамильтонианов
ĥkν, основанные на мето-
изолированные простые нули в некоторых точках
де направляющих функционалов Крейна, подробнее
Ekn(ν), ωkν(Ekn(ν)) = 0, n = 1, 2, . . . (нумерация мо-
см. [13].
жет быть разной, см. ниже). Эти точки являются
Заранее скажем, что во всех трех подобластях
изолированными собственными значениями опера-
сингулярной области для каждого оператора
ĥkν су-
тора
ĥkν, формирующими его дискретный спектр, а
ществует простой направляющий функционал. От-
дублеты Ukν (ρ; Ekn(ν)) представляют собой соответ-
сюда следует, что спектр оператора
ĥkν являет-
ствующие (нормированные) собственные функции.
857
А. И. Бреев, Р. Феррейра, Д. М. Гитман, Б. Л. Воронов
ЖЭТФ, том 157, вып. 5, 2020
Действительно, в окрестности точек Ekn(ν) функ-
5.2.1. Субкритическая область
ция 1/ωkν (E + i0) имеет вид
Субкритическая область в верхней полуплоскос-
ти (j, Z) определяется неравенствами Zs(j) < Z <
1
Q2kν,n
=-
+ O(1),
< Zc(j), что эквивалентно 0 < Υ+ = γ < 1/2, где
ωkν(E + i0)
E - Ekn(ν) + i0
Zc(j) = α-1Fϵ |j|, т. е. g = gc(j) = |j| и γ = 0, см.
1
рис. 1.
Q2kν,n = -
> 0,
ω′kν (Ekn(ν))
Значение Zc(j) будем называть критическим зна-
чением Z для данного j. Для примера выпишем
так что σ′kν (E) = Q2kν,nδ(E - Ekn(ν)), Qkν,n > 0 —
несколько первых значений gc(j) для малых полу-
нормировочный множитель для собственной функ-
целых j:
ции Ukν (ρ; Ekn(ν)). Во всех трех подобластях сингу-
gc (±1/2) = 0.5, gc (±3/2) = 1.5, gc (±5/2) = 2.5.
лярной области дискретный спектр {Ekn(ν)} пред-
ставляет собой бесконечный набор возрастающих
В субкритической области с. с. радиальные га-
собственных значений (уровней энергии), стремя-
мильтонианы
ĥ2ν(Z, j, s) характеризуются с. с. гра-
щихся к точке E = m.
ничными условиями в начале координат следующим
Примечательно, что для каждого семейства
образом:
{ĥkν(Z, j, s)} парциальных радиальных гамильто-
нианов с данным k существует некоторое значе-
F (ρ) = c[(mρ)γ d+ cos ν + (mρ)-γ ×
ние ν
= ν-m параметра расширения, такое что
× d- sinν] + O(ρ1/2),
(29)
ωkν-m(-m) = 0, а точка E = -m — собственное
ĥkν
d± = (1, (κ ± γ)/g)T , ρ → 0,
значение оператора
-m
с соответствующей нор-
мированной собственной функцией Ukν-m (ρ; -m),
где c — произвольное комплексное число. Область
т. е. данная точка принадлежит точечному спектру
определения Dh2ν(Z,j,s) гамильтониана
ĥ2ν(Z, j, s)
оператора
ĥkν
. При этом данная точка E = -m
-m
есть
также принадлежит непрерывному спектру опе-
{
ĥkν
F (ρ) :F (ρ) ∈ Dˇ
(R+) и
ратора
-m
и является верхней границей его
Dh2ν(Z,j,s) =
h(Z,j,s)
}
нижней ветви. Таким образом, мы сталкиваемся с
F удовлетворяет (29)
упомянутым выше случаем, когда гамильтониан
ĥkν
имеет нетривиальный точечный спектр,
Базисная функция ω2ν (W ) и дублет U2ν (ρ; W ) опре-
-m
который не сводится к чисто дискретному спектру.
деляются соотношениями
Нормированные (обобщенные) собственные
2γ ω(W)cosν + g-1Γ(1 - 2γ)sinν
функции Ukν,E(ρ) = Qkν(E)Ukν(ρ; E) непрерывного
ω2ν(W) =
,
g ω(W)sinν - g-1Γ(1 - 2γ)cosν
спектра (в физической терминологии они «нормиру-
ются на дельта-функцию») и нормированные собст-
где функция ω(W ) дана в (20), и
венные функции Ukν,n(ρ)
= Qkν,nUkν(ρ; Ekn(ν))
U2ν(ρ; W) = F1(ρ; W)cosν + F2(ρ; W)sinν.
дискретного спектра образуют полную ортонорми-
рованную систему в пространстве L2(R+) в смысле
Дублеты F1(ρ; W) и F2(ρ; W) определены в (19).
формул обращения. Будем называть функцию
Производная σ′2ν (E) спектральной функции имеет
ωνk(E) базисной функцией, а дублет Ukν(ρ; W) —
вид
базисным.
1
1
σ′2ν(E) =
Im
Отметим, что спектральный анализ в несингу-
π
ω2ν(E + i0)
лярной области (мы приведем только его результа-
Не составляет трудности найти носитель функции
ты) проводится аналогичным образом. В качестве
σ′2ν(E) и простой спектр гамильтониана
ĥ2ν(Z, j, s),
базовой функции берется функция ω(W)/Γ(-2γ),
где ω(W ) задается выражением (20) вместо ωkν (W ),
specĥ2ν (Z, j, s) =
а базовый дублет F1(ρ; W) — выражением (19) вмес-
= {E ∈ (-∞, -m] ∪ [m, ∞)}∪{E2n(ν) ∈ [-m, m)},
то Ukν(ρ; W).
Далее мы рассмотрим парциальные радиальные
который состоит из непрерывного (-∞, -m]∪[m, ∞)
гамильтонианы
ĥkν, исследуем их точечный спектр
и точечного спектров. Точечный спектр представ-
и кратко опишем результаты спектрального анализа
ляет собой возрастающую бесконечную последова-
для каждой сингулярной подобласти.
тельность {E2n(ν) = E2n(Z, j, s; ν)} энергетических
858
ЖЭТФ, том 157, вып. 5, 2020
Спектры электронных возбуждений в графене...
уровней E2n(Z, j, s; ν), расположенных на полуин-
замены γ → -γ. В частности, дискретный спектр
тервале [-m, m) и стремящихся к E = m. Энергети-
задается выражением
ческие уровни определяются как корни уравнения
(n - γ)m
E2n = E2n(±π/2) =
√
,
n ∈ Nζ, (32)
2γ ω(E)cosν + g-1Γ(1 - 2γ)sinν
ω2ν(E) =
=
g2 + (n - γ)2
g ω(E)sinν - g-1Γ(1 - 2γ)cosν
(30)
= 0, E ∈ [-m, m).
где Nζ определено в (26). Отметим, что неявная за-
висимость дискретных энергетических уровней E2n
Отметим, что множество {n} целых чисел n, нуме-
от s проявляется на множестве Nζ целых чисел
рующих энергетические уровни, зависит от пара-
n, нумерующих уровни энергии, согласно форму-
метра s (так же как в несингулярной области).
ле (26).
Нормированные (обобщенные) собственные
2. Пусть ν = 0. В этом случае имеем
функции U2ν,E(ρ), соответствующие непрерывному
спектру, и нормированные собственные функции
2γ
ω(W )
ω2ν(W)|ν=0 = -
ω(W ) =
,
U2ν,n(ρ), относящиеся к точечному спектру, даются
Γ(1 - 2γ)
Γ(-2γ)
выражениями
U2ν(ρ, W)|ν=0 = F1(ρ; W).
U2ν,E(ρ) = Q2ν(E)U2ν(ρ; E) =
Отсюда следует, что в случае ν = 0 все результаты,
= Q2ν(E)(F1(ρ;E)cosν + F2(ρ;E)sinν),
касающиеся спектра и собственных функций, явля-
E ∈ (-∞,-m] ∪ [m,∞);
ются прямым обобщением соответствующих резуль-
(31)
татов, включая (26), (27), (28) для несингулярной
U2ν,n(ρ) = Q2ν,nU2ν (ρ; E2n(ν)) =
(
области, где γ ≥ 1/2, на субкритическую область,
=Q2ν,n
F1 (ρ; E2n(ν)) cosν +
)
где 0 < γ < 1/2.
+ F2 (ρ;E2n(ν))sinν
,
Исследование общего случая |ν| < π/2 полнос-
где
тью аналогично тому, которое выполнено для син-
√
гулярной области в трехмерной кулоновской зада-
√
1
че (см. [13]). Мы приведем только самые важные
Q2ν(E) = σ′2ν(E), Q2ν,n =
-
,
ω′2ν (E2n(ν))
свойства точечного спектра. Во-первых, для каж-
дого Z, j, s и ν = ν-m, см. (33), точечный спектр
и формируют полную ортонормированную систему
является чисто дискретным. При ν = ν-m диск-
в пространстве L2(R+) в смысле формул обращения.
ретный спектр дополняется энергетическим уров-
Явные выражения для спектра и собственных
нем E = -m, который одновременно является точ-
функций, включая точное решение уравнения (30),
кой непрерывного спектра (верхней границей его
можно получить в двух случаях: когда ν = ±π/2 и
нижней ветви). Значение ν-m можно определить из
ν = 0.
уравнения (30), полагая E = -m и учитывая, что
1. Пусть ν = ±π/2. Тогда
ω(-m) = g-1Γ(1 + 2γ)(2g)-2γ:
2γ Γ(1 - 2γ)
ω2ν(W)|ν=±π/2 =
,
Γ(1 + 2γ)
g2
ω(W )
tg ν-m = -
(2g)-2γ
(33)
Γ(1 - 2γ)
U2ν(ρ, W)|ν=±π/2 = F2(ρ; W).
Отметим, что ν-m = ν-m(Z, j) зависит только от |j|
Как говорилось выше, спектральный анализ в
и не зависит от параметра s.
несингулярной области строится по базисной функ-
Для иллюстрации на рис. 2 приведен график из-
ции ω(W )/Γ(-2γ) и базисному дублету F1(ρ; W ).
менения параметра ν-m как функции от g для фик-
Заметим, что
сированного j = ±1/2.
2γ Γ(1 - 2γ)
ω(W )
Во-вторых, как следует из (9) и подтверждает-
=
,
g2
ω(W )
Γ(-2γ)
ся (26) и (32), следует различать секторы ζ = 1 и
γ→-γ
ζ = -1 уровней энергии, в частности, из-за раз-
F2(ρ; W) = F1(ρ; W)|
γ→-γ
личных последовательностей целых чисел Nζ , см.
Отсюда следует, что все результаты, касающиеся
комментарий к формуле (26). Более того, становит-
спектра и собственных функций, могут быть полу-
ся очевидной зависимость энергетических уровней
чены из результатов для случая несингулярной об-
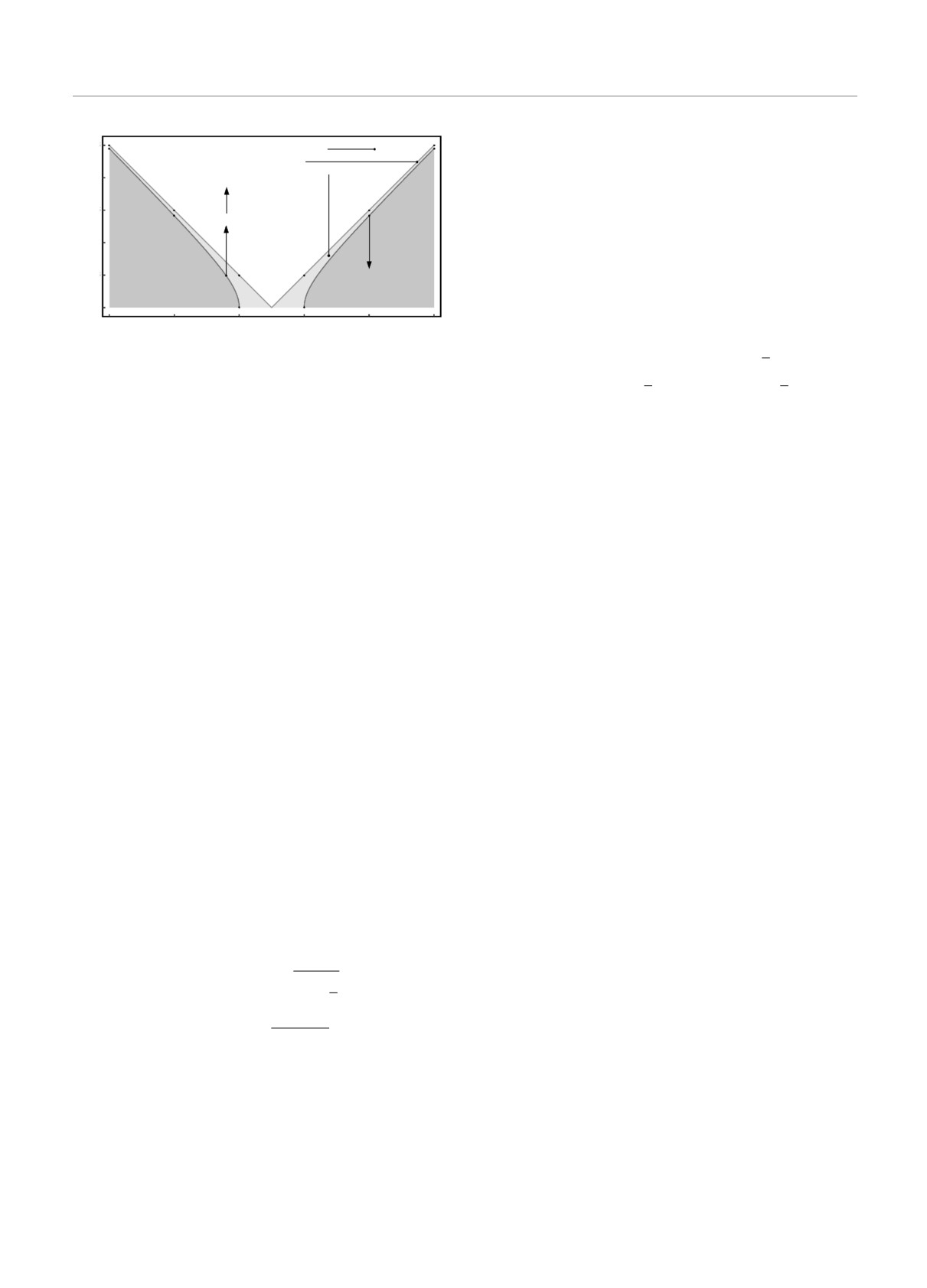
E2n(Z, j, s; ν) от параметра s в общем случае 0 <
ласти, включая (26), (27), с помощью формальной
< |ν| < π/2.
859
А. И. Бреев, Р. Феррейра, Д. М. Гитман, Б. Л. Воронов
ЖЭТФ, том 157, вып. 5, 2020
На рис. 3 приведены графики нижних энергети-
-m0
ческих уровней для j = 1/2 и g = 0.4 как функций
параметра ν для s = ±1.
В заключение отметим, что имеет место замеча-
тельное равенство
ĥ2ν(Z, j, s) =
ĥ2ν(Z, -j, -s),
– /12
так как с. с. граничные условия (29) инвариантны
относительно замены j → -j, s → -s.
5.2.2. Критическая область
Критическая область представляет собой крити-
ческую кривую Z = Zc(j), что равносильно g =
- /6
= gc(j) или Υ+ = γ = 0. Отметим, что в данной
области физические значения пар j (полуцелое чис-
ло) и Z (целое число) лежат на критической кривой
для очень специальных значений «постоянной тон-
кой структуры» в графене αF /ϵ, αF /ϵ = |j|/Z. В
частности, если αF /ϵ — иррациональное число, ни-
какая физическая пара (j, Z) не лежит на крити-
- /4
ческой кривой. В этой области с. с. радиальные га-
мильтонианы
ĥ3ν(Z, j, s) задаются асимптотически-
ми с. с. граничными условиями в начале координат
в виде
F (ρ) = c[d0(ρ) cos ν + d+ sin ν] + O(ρ1/2 ln ρ),
(34)
ρ → 0, ν ∈ [ - π/2,π/2],
-π/2 ∼ π/2,
- /3
0
0.1
0.2
0.3
0.4
0.5
где постоянный дублет d+
= d+|γ=0
и дублет
g
d0(ρ), зависящий от ρ, определяются соотношения-
Рис. 2. Зависимость ν-m от g для j = 1/2
ми (21) и (23) соответственно. Область определения
Dh3ν (Z,j,s) гамильтониана
ĥ3ν(Z, j, s) есть
{
Обозначим через nζ первый член в последова-
Dh3ν(Z,j,s) =
F (ρ) :F (ρ) ∈ Dˇ
(R+) и
h(Z,j,s)
}
тельности Nζ: n1 = 1, n-1 = 0. Следует подчерк-
F удовлетворяет (34)
нуть, что в каждом секторе самый низкий энерге-
тический уровень E = -m соответствует одному и
Базисная функция ω3ν (W ) имеет вид
тому же значению ν-m (33), в частности E2n
> -m.
ζ
f (W ) cos ν - sin ν
Обозначим этот уровень как E2(nζ-1)(ν-m).
ω3ν(W) =
,
gc(j)[f(W)sinν + cosν]
В полуинтервале энергий [-m, E2nζ ) для каждого
значения ν ∈ (-π/2, ν-m] существует один уровень
где функция f(W ) определена в (25). Базисный дуб-
энергии E2(nζ -1)(ν), который монотонно увеличива-
лет U3ν (W ) определяется выражением
ется от -m до E2nζ -0, когда значение ν меняется от
ν-m до -π/2 + 0. Для значений ν ∈ (ν-m, π/2) дан-
U3ν(W) = F(0)1(ρ, W)sinν + F(0)2(ρ, W)cosν,
ный уровень энергии отсутствует. В каждом энер-
где дублеты F(0)1(ρ, W ) и F(0)2(ρ, W ) даны в (21) и
гетическом интервале E2n, E2(n+1), n ≥ nζ, для лю-
(22), (23) соответственно. Причем в качестве дуб-
бого значения ν ∈ (-π/2, π/2) существует один уро-
лета F3(ρ, W ) берем дублет F(0)3(ρ, W ), определен-
вень E2n(ν), монотонно возрастающий от E2n + 0 до
ный в (24) и (25). Производная σ′3ν (E) спектральной
E2(n+1) - 0 при изменении ν от π/2 - 0 до -π/2 + 0.
функции имеет вид
Стоит отметить, что
1
1
lim
E2(n-1)(ν) = lim
E2n(ν) = E2n, n ∈ Nζ.
σ′3ν(E) =
Im
ν→-π/2
ν→π/2
π
ω3ν(E + i0)
860
ЖЭТФ, том 157, вып. 5, 2020
Спектры электронных возбуждений в графене...
E /m2n
E /m2n
1.0
n = 2
1.0
n = 2
n = 1
n = 1
б
а
0.5
0.5
0
0
-0.5
-0.5
n = 0
n = -1
–1.0
n = 0
-1.0
- /2
0
/2
– /2
0
/2
Рис. 3. Зависимости энергетических уровней E2n от параметра ν для s = 1 (а), -1 (б)
Для вычисления функции σ′3ν (E) требуется вы-
Определение носителя функции σ′3ν (E) и вычисле-
ражение для сужения f(E) = f(E + i0) функции
ние соответствующих величин (что довольно утоми-
f (W ) (24) на действительную ось. Для |E| ≥ m име-
тельно) приводит к заключению, что простой спектр
ем
гамильтониана
ĥ3ν(Z, j, s) дается выражением
(
) (
)
k
|E|
specˆ3ν (Z, j, s) =
f (E) = ln
2e-iϵπ/2
+ψ
-igc(j)
+
m
k
= {E ∈ (-∞, -m] ∪ [m, ∞)}∪{E3n(ν) ∈ [-m, m)}
ζ(E-m)+iϵk
+
-2ψ(1),
|E| ≥ m,
2gc(j)E
и состоит из непрерывного (-∞, -m] ∪ [m, ∞) и
точечного спектров. Точечный спектр представля-
а для |E| < m получаем
ет собой возрастающую бесконечную последова-
(Z, j, s; ν)} энергетических
тельность {E3n(ν) = E3n
(
)
(
τ )
E
уровней E3n(Z, j, s; ν), которые определяются как
f (E) = ln
2
+ψ
-gc(j)
+
m
τ
корни уравнения ω3ν (E) = 0, E ∈ [-m, m), которое
ζ(E - m) - τ
эквивалентно уравнению
+
- 2ψ(1),
|E| < m,
(35)
2gc(j)E
f (E) cos ν - sin ν
= 0,
|E| < m.
(36)
где
f (E) sin ν + cos ν
√
√
Данные энергетические уровни локализованы на по-
k=
E2 - m2, τ =
m2 - E2,
луинтервале [-m, m) и накапливаются в точке E =
ϵ = sgn(E), ζ = ζ(j,s), ψ(z) = Γ′(z)/Γ(z).
= m. Зависимость бесконечной последовательнос-
861
А. И. Бреев, Р. Феррейра, Д. М. Гитман, Б. Л. Воронов
ЖЭТФ, том 157, вып. 5, 2020
ти {n} целых чисел n, нумерующих энергетические
функции ψ(-z) в точках zn = n, n ∈ Z+, и полюсом
уровни, от параметра s будет исследована ниже.
в третьем члене в правой части выражения (35)
Из (36) и (35) следует, что энергетические уров-
при ζ = 1 в точке E = 0, получим
ни с заданными значениями Z, j явно зависят от
∑
σ′3ν(E)|ν=±π/2 =
Q23ν,n
δ(E - E3n);
ζ, т.е. от s. Нормированные (обобщенные) собствен-
ν=±π/2
n∈Nζ
ные функции U3ν,E (ρ), отвечающие непрерывному
спектру, и нормированные собственные функции
здесь нормировочные множители Q3ν,n|ν=±π/2
U3ν,n(ρ), относящиеся к точечному спектру, имеют
для собственных функций U3ν (ρ; E3n))|ν=±π/2
=
вид
= F(0)1(ρ, E3n) связанных состояний определяются
U3ν,E(ρ) = Q3ν(E)U3ν(ρ; E) =
выражениями
(
)
= Q3ν(E) F(0)1(ρ;E)cosν + F(0)2(ρ;E)sinν
,
3/2
τ
n
gc(j)m
Q3ν,n|ν=±π/2 =
,
τn =
√
,
n∈Nζ.
E ∈ (-∞,-m] ∪ [m,∞);
m
g2c(j)+n2
(37)
U3ν,n(ρ) = Q3ν,nU3ν (ρ; E3n(ν)) =
(
Соответствующие дискретные энергетические уров-
= Q3ν,n F(0)1(ρ;E2n(ν))cosν +
ни E3n = E3n(ν = ±π/2) есть
)
nm
+ F(0)2(ρ;E2n(ν))sinν ,
E3n =
√
,
n∈Nζ.
g2c(j) + n2
где
√
Отметим, что все результаты для спектра и соб-
√
1
ственных функций в критической области γ = 0
Q3ν(E) = σ′3ν(E), Q3ν,n =
-
,
ω′3ν (E3n(ν))
для случая ν = ±π/2 получаются из соответствую-
щих результатов для несингулярной области, вклю-
и образуют полную ортонормированную систему в
чая (26)-(28), путем предельного перехода к точке
пространстве L2(R+) в смысле формул обращения.
γ = 0.
Для случая ν = ±π/2 имеем явные выражения
Что касается общего случая |ν| < π/2, мы приве-
для спектра и собственных функций:
дем только наиболее важные свойства дискретного
спектра, которые аналогичны результатам, получен-
1
ω3ν(W)|ν=±π/2 = -
,
ным для субкритической области.
gc(j)f(W)
Во-первых, для любых значений j, s в критичес-
U3ν(W)|ν=±π/2 = F(0)1(ρ, W) = F1(ρ, W)|γ=0,
кой области (где Z однозначно определяется j) и
gc(j)
ν =ν-m
(см. (38) ниже) точечный спектр является
σ′3ν(E)|ν=±π/2 = -
Im f(E + i0).
π
чисто дискретным. При ν = ν-m дискретный спектр
дополняется энергетическим уровнем E = -m, ко-
В диапазоне |E| ≥ m, когда спектр непрерывен, ис-
торый одновременно является точкой непрерывно-
пользуя выражение (35) для функции f(E) и соот-
го спектра, а именно, верхней границей его нижней
ношение ψ(z) - ψ(-z) = -π ctg(πz) - z-1, получим
ветви. Данное значение ν-m = ν-m(|j|, ζ) определя-
ется из уравнения (36), в котором положим E = -m
σ′3ν(E)|ν=±π/2 = Q23ν(E)
=
ν=±π/2
и учтем, что f(-m) = ln(2gc(j)) - 2ψ(1) + ζ/gc(j):
(
)
gc(j)
|E|
=
cth(πgc(j)
)+ϵ
,
|E| ≥ m.
ζ
2
k
tg ν-m(|j|, ζ) = ln(2gc(j)) - 2ψ(1) +
(38)
gc(j)
Заметим, что σ′3ν(E)|ν=±π/2 ≥ 0 для |E| ≥ m, как
Примечательно, что параметр ν-m как функция от
и должно быть. А квадрат нормировочного мно-
j и ζ зависит только от |j|. Также стоит отметить,
жителя Q23ν (E)
для собственных функций
ν=±π/2
что для ν-m(|j|, ζ) справедливы неравенства
U3ν(ρ; E)|ν=±π/2
= F(0)1(ρ, E), отвечающих непре-
рывному спектру, неотрицателен.
ν-m(|j|, 1) > ν-m(|j|, -1), ν-m(|j|, 1) > 0 ∀j;
Для
|E|
< m, используя выражение
(35)
ν-m(1/2, -1) < 0; ν-m(|j|, -1) > 0,
|j| > 3/2.
для f(E) и учитывая, что полюсы функции
σ′3ν(E)|ν=±π/2,
определяющие энергетические
Во-вторых, для заданных значений j, ζ в полу-
уровни гамильтонианов, представлены полюсами
интервале энергий [-m, E2nζ ) (напомним, что nζ = 1
862
ЖЭТФ, том 157, вып. 5, 2020
Спектры электронных возбуждений в графене...
E3n/m
E3n/m
1.0
n = 2
1.0
n = 2
n = 1
n = 1
б
а
0.5
0.5
n = 0
0
0
-0.5
-0.5
–1.0
n = -1
n = 0
–1.0
- /2
0
/2
– /2
0
/2
Рис. 4. Зависимости энергетических уровней E3n от параметра ν для s = 1 (а), -1 (б)
для ζ = 1 и nζ = 0 для ζ = -1) для всех ν ∈
5.2.3. Сверхкритическая область
∈ (-π/2, ν-m(|j|, ζ)], где ν-m(|j|, ζ) дано в (38), су-
Сверхкритическая область изменения парамет-
ществует один энергетический уровень E3(nζ-1)(ν),
ров (j, Z) в верхней полуплоскости определяется
который монотонно возрастает от -m до E3nζ -0 при
неравенством Z > Zc(j) = α-1ϵ |j|, которое эквива-
изменении ν от ν-m(|j|, ζ) до -π/2 + 0, тогда как
√
лентно тому, что Υ+ = iσ, где σ =
g2 - j2 > 0.
при ν ∈ (ν-m(|j|, ζ), π/2) энергетических уровней
В этой области с. с. радиальные гамильтонианы
нет. Для каждого интервала (E3n, E3(n+1)), n ≥ nζ ,
ĥ4ν(Z, j, s) определяются следующими асимптотиче-
при ν ∈ (-π/2, π/2) существует энергетический уро-
скими с. с. граничными условиями в начале коорди-
вень E3n(ν), монотонно возрастающий от E3n + 0 до
нат:
E3(n+1) -0, когда параметр ν меняется от π/2-0 до
(
-π/2 + 0. Заметим, что справедливы соотношения
F (ρ) = c
ieiν(mρ)iσd+ -
)
- ie-iν(mρ)-iσd-
+ O(ρ1/2),
lim
E3(n-1)(ν) = lim E3n(ν) = E3n, n ∈ Nζ.
(39)
ν→-π/2
ν→π/2
d± = (1, (κ ± iσ)/g)T , ρ → 0,
ν ∈ [-π/2,π/2],
-π/2 ∼ π/2.
На рис. 4 приведены графики нижних энергети-
ческих уровней для j = 1/2 и g = 0.5 как функций
Область определения Dh4ν(Z,j,s) гамильтониана
параметра ν для s = ±1.
ĥ4ν(Z, j, s) определяется выражением
В заключение отметим, что так как с. с. гра-
{
ничные условия (34) инвариантны относительно за-
Dh4ν(Z,j,s) =
F (ρ) :F (ρ) ∈ D∗ˇ
(R+) и
h(Z,j,s)
мены j → -j, s → -s, то справедливо равенство
}
F удовлетворяет (39)
ĥ3ν(Z, j, s) =
ĥ3ν(Z, -j, -s).
863
А. И. Бреев, Р. Феррейра, Д. М. Гитман, Б. Л. Воронов
ЖЭТФ, том 157, вып. 5, 2020
Базисная функция ω4ν (W ) есть
Преобразуем спектральное уравнение (40) в дру-
гую форму, более удобную для дальнейшего анали-
g
за. Достаточно отметить, что
1-
ω(W )e2iν
4iσ
Γ(1 - 2iσ)
ω4ν(W) = -
,
g
gω(E)
g
1+
ω(W )e2iν
-
=
Γ(1 - 2iσ)
Γ(1 - 2iσ)
E
Γ(2iσ)Γ(-iσ - g
)[τ(κ + iσ) - g(m - E)]
τ
=
×
где функция ω(W ) определена в (20). Базисный дуб-
Γ(-2iσ)Γ(iσ - gEτ )[τ(κ - iσ) - g(m - E)]
лет U4ν (W ) имеет вид U4ν (W ) = ieiνF1(ρ; W) -
(2τ)-2iσ
-ie-iνF2(ρ; W), где дублеты F1(ρ; W) и F2(ρ; W) да-
×
=e-2iΘ(E),
m
ны в (19). Производная σ′4ν (E) спектральной функ-
ции есть
{
2τ
1
1
1
Θ(E) = σ ln
+
ln Γ(-2iσ) - ln Γ(2iσ) +
σ′4ν(E) =
Im
m
2i
π
ω4ν(E + i0)
(
)
(
)
E
E
+ ln Γ
iσ - g
- ln Γ
-iσ - g
+
τ
τ
Определяя носитель функции σ′4ν (E) и вычис-
+ ln[τ(gc - iζσ) - ζg(m - E)] -
ляя соответствующие величины, получим простой
}
спектр гамильтониана
ĥ4ν(Z, j, s):
- ln[τ(gc + iζσ) - ζg(m - E)]
,
specĥ4ν (Z, j, s) =
и уравнение (40) примет вид cos[Θ(E) - ν] = 0. За-
= {E : |E| ≥ m} ∪ {E4n(ν) ∈ [-m, m)}.
метим, что Θ(E) — гладкая функция на интервале
(-m, m).
Нормированные (обобщенные) собственные
Простой спектр состоит из непрерывного
функции U4ν,E(ρ), отвечающие непрерывному
(-∞, -m] ∪ [m, ∞) и точечного спектров. Точечный
спектру, и нормированные собственные функции
спектр представляет собой возрастающую бесконеч-
U4ν,n(ρ), соответствующие дискретному спектру,
ную последовательность {E4n(ν) = E4n(Z, j, s; ν)}
формируют полную ортонормированную систему в
энергетических уровней E4n(Z, j, s; ν), которые
пространстве L2(R+) в смысле формул обращения
определяются корнями уравнения
и имеют вид
g
1-
ω(E)e2iν
U4ν,E(ρ) = Q4ν(E)U4ν(ρ; E) =
4iσ
Γ(1 - 2iσ)
(
)
ω4ν(E) = -
= 0,
= Q4ν(E)
ieiνF1(ρ; E) - ie-iνF2(ρ; E)
,
g
g
1+
ω(E)e2iν
Γ(1 - 2iσ)
E ∈ (-∞,-m] ∪ [m,∞);
E ∈ [-m,m).
U4ν,n(ρ) = Q4ν,nU4ν (ρ; E4n(ν)) =
(41)
(
(ν)) -
= Q4ν,n ieiνF1 (ρ;E4n
Последнее эквивалентно уравнению
)
− ie-iνF2 (ρ; E4n(ν))
,
2iν
gω(E)e
1-
= 0, E ∈ [-m, m),
(40)
Γ(1 - 2iσ)
где
√
√
которое будем называть спектральным уравнением.
1
Q4ν(E) = σ′4ν(E), Q4ν,n =
-
Данные энергетические уровни содержатся в по-
ω′4ν (E4n(ν))
луинтервале [-m, m) и накапливаются в точке E =
= m. Бесконечные последовательности {n} целых
Теперь подробнее опишем свойства дискретного
чисел n, обозначающих дискретные уровни энергии,
спектра.
мы определим ниже. Очевидно, что энергетические
Во-первых, для каждых значений параметров Z,
уровни с заданными Z, j явно зависят от s (т. е. от
j, s в сверхкритической области и для ν = ν-m, см.
ζ), ввиду явной зависимости функции ω(E) от s.
(42), точечный спектр является чисто дискретным.
864
ЖЭТФ, том 157, вып. 5, 2020
Спектры электронных возбуждений в графене...
-m
На рис. 5 приведен график изменения параметра
/3
ν-m как функции параметра g для j = 1/2.
Во-вторых, в отличие от остальных областей, ну-
мерация энергетических уровней в сверхкритиче-
ской области не зависит от ζ.
В-третьих, для описания точечного спектра
в этой области представляется удобным ввести
двойную маркировку дискретных уровней энергии
/4
при ν = ±π/2. Мы формально различаем значения
ν = -π/2 и ν = π/2, помечая энергетические уров-
ни ν = -π/2 целыми неотрицательными числами,
E4n(-π/2), n ∈ Z+ = {0, 1, 2, 3, . . .}, в то время как
уровни энергии с ν = π/2 нумеруются натураль-
ными числами, E4n(π/2), n ∈ N+ = {1, 2, 3, . . . }.
Данное различие можно устранить, полагая
E4n(-π/2) = E4(n+1)(π/2), n ∈ Z+.
/6
Относительно данной нумерации уровней, точеч-
ный спектр гамильтонианов
ĥ4ν(Z, j, s) выглядит
следующим образом. В интервале [-m, E40(-π/2) =
= E41(π/2)) нет энергетических уровней для зна-
чений ν ∈ (ν-m, π/2). При этом для любого ν ∈
∈ (-π/2, ν-m] существует один энергетический уро-
вень E40(ν), который монотонно возрастает от -m
/12
до E40(-π/2) - 0, когда ν меняется от ν-m до
-π/2 + 0. В каждом интервале энергий [E4n(π/2),
E4(n+1)(π/2) = E4n(-π/2)), n ∈ N+, существует
один уровень E4n(ν), который монотонно возрастает
от E4n(π/2) до E4n(-π/2)- 0, когда параметр ν ме-
няется от π/2 до -π/2 + 0. В частности, мы имеем
-m ≤ E40(-π/2) < E4n(-π/2) < E4(n+1)(-π/2) <
<m ∀n∈Z+.
0
0.5
0.6
0.7
0.8
0.9
1.0
На рис. 6 приведены графики нижних энергети-
g
ческих уровней как функций ν для s = ±1 при j =
= 1/2 и g = 0.7.
Рис. 5. Зависимость параметра ν-m от g для j = 1/2
В заключение отметим, что выполняется равен-
ство
ĥ4ν(Z, j, s) =
ĥ4ν(Z, -j, -s),
При ν = ν-m дискретный спектр дополняется энер-
гетическим уровнем E = -m, который одновремен-
так как с. с. граничные условия (39) не меняются
но является верхней границей нижней ветви непре-
при замене j → -j, s → -s.
рывного спектра. Значения ν-m (Z, j) определяются
из уравнения (40) при E = -m. Так как
6. САМОСОПРЯЖЕННЫЕ ПОЛНЫЕ
gω(-m) = Γ(1 + 2iσ)(2g)-2iσ,
ГАМИЛЬТОНИАНЫ И ИХ СПЕКТР В
КУЛОНОВСКОМ ПОЛЕ ТОЧЕЧНОГО
то
ЗАРЯДА
Γ(-2iσ)
В разд. 5.1 и 5.2 мы построили все с. с. парциаль-
e2iν-m = e-iπ(2g)2iσ
,
Γ(2iσ)
(42)
ные радиальные гамильтонианы
ĥe(Z, j, s) для всех
ν-m ∈ [-π/2, π/2],
-π/2 ∼ π/2.
значений заряда Z как с. с. расширения исходных
симметрических операторов
ĥin(Z, j, s) для любых
Отметим, что величина ν-m (Z, j) не зависит от па-
значений j и s, а также исследовали спектральную
раметра s.
задачу для всех таких гамильтонианов. В результа-
865
7
ЖЭТФ, вып. 5
А. И. Бреев, Р. Феррейра, Д. М. Гитман, Б. Л. Воронов
ЖЭТФ, том 157, вып. 5, 2020
E4n/m
E4n/m
а
б
1.0
1.0
n = 2
n = 2
n = 1
0.5
0.5
n = 1
0
0
–0.5
-0.5
–1.0
n = 0
–1.0
n = 0
– /2
0
/2
- /2
0
/2
Рис. 6. Зависимости энергетических уровней E4n от параметра ν для s = 1 (а), -1 (б)
(
)
те, формула (10) позволяет нам восстановить все с.
1
Δ(0) =
0;
,
с. операторы
Ĥe
, ассоциированные с дифференци-
2
s
альным выражением (4) для любого значения пара-
Δ(k) = (gc(k), gc(k + 1)] = (k, k + 1],
)
метра g, а также описать решение соответствующих
{
(
)}
(⋃
Ĥe
1
спектральных задач для всех гамильтонианов
s
(0, ∞) = Δ(0) ∪ gc
±
∪ Δ(k)
2
Для удобства введем множества значений заря-
k
да, для которых спектральная задача описывает-
Ввиду (43), каждый интервал Δ(k) можно предста-
ся похожим образом. Эти множества определяются
вить как Δ(k) = ∪i=1,2,3Δi(k), где
при помощи функций gc(k) и gs(k), принимающих
значения в характеристических точках k = l + 1/2,
Δ1(k) = (gc(k), gs(k + 1)],
l∈Z+,
Δ2(k) = (gs(k + 1), gc(k + 1)),
√
Δ3(k) = {gc(k + 1)}.
1
gc(k) = k, gs(k + 1) = (k + 1)2 -
,
4
В соответствии с этим разложением определим три
⋃
множества Gi =k Δi(k), i = 1, 2, 3, изменения па-
и удовлетворяющих следующим неравенствам:
раметров связи g, таких что любому значению g >
(±1/2) = 1/2 можно сопоставить пару двух це-
>gc
gc(k) < gs(k + 1) < gc(k + 1) < gs(k + 2).
(43)
лых чисел, k и i = 1, 2, 3: g =⇒ (k, i), такую, что
g ∈ Gi. Тогда, следуя разд. 5.1, 5.2, получим следу-
Введем интервалы Δ(k) следующим образом:
ющую классификацию.
866
ЖЭТФ, том 157, вып. 5, 2020
Спектры электронных возбуждений в графене...
A. Пусть g =⇒ (k, 1), так что g ∈ Δ1(k) для неко-
C. Пусть g =⇒ (k, 3), т.е. g ∈ Δ3(k) для тех k,
торых k, откуда следует, что
которые удовлетворяют уравнению g = gc(k + 1) =
√
= k + 1.
1
Рассмотрим квантовые числа |j| ≤ k. Тогда g =
k = gc(k) < g ≤ gs(k + 1) = (k + 1)2 -
4
= gc(k+1) > gc(k) ≥ gc(j), откуда g > gc(j). Данные
квантовые числа j отвечают сверхкритической об-
Рассмотрим квантовые числа |j| ≤ k. В этом слу-
ласти, см. разд. 5.2.3.
чае g > gc(k) ≥ gc(j), следовательно, g > gc(j). Та-
Рассмотрим квантовые числа |j| = k + 1. Тогда
кие квантовые числа j характеризуют сверхкрити-
g = gc(j). Данные квантовые числа j отвечают кри-
ческую область, см. разд. 5.2.3.
тической области, см. разд. 5.2.2.
Для квантовых чисел |j| ≥ k + 1 будем иметь
Рассмотрим случай |j|
> k + 1. Тогда g
=
g ≤ gs(k +1) ≤ gs(j). Тогда квантовые числа j отве-
= gc(k + 1) < gs(k + 2) ≤ gs(j), откуда g < gs(j).
чают несингулярной области, см. разд. 5.1.
Данные квантовые числа j отвечают несингулярной
Таким образом, для данных значений g имеем
области, см. разд. 5.1.
{
Таким образом, имеем
U4ν,E(ρ),
|j| ≤ k,
UE(ρ) =
|E| ≥ m,
⎧
U1E(ρ),
|j| ≥ k + 1,
⎨U4ν,E(ρ),
|j| ≤ k,
{
U4ν,n(ρ),
|j| ≤ k,
UE(ρ) =
U3ν,E(ρ),
|j| = k + 1,
|E| ≥ m,
Un(ρ) =
(44)
⎩
U1n(ρ),
|j| ≥ k + 1,
U1E(ρ),
|j| > k + 1,
{
⎧
E4n(ν),
|j| ≤ k,
⎨U4ν,n(ρ),
|j| ≤ k,
En =
E1n(Z, j, s),
|j| ≥ k + 1.
Un(ρ) =
U3ν,n(ρ),
|j| = k + 1, ,
(46)
⎩
U1n(ρ),
|j| > k + 1,
B. Пусть g =⇒ (k, 2), так что g ∈ Δ2(k) для тех
⎧
⎨E4n(ν),
|j| ≤ k,
k, которые удовлетворяют неравенствам
√
En =
E3n(ν),
|j| = k + 1,
⎩
1
(k + 1)2-
= gs(k+1) < g < gc(k+1) = k+1.
E1n(Z, j, s),
|j| > k + 1.
4
D. Пусть g ∈ Δ(0), т. е. g < gc(±1/2). Рассмотрим
Рассмотрим квантовые числа |j| ≤ k. Тогда g >
квантовые числа |j| > 1/2. Тогда
> gs(k + 1) > gc(k) ≥ gc(j), откуда g > gc(j). Дан-
(
)
√
ные квантовые числа j отвечают сверхкритической
1
1
1
g<gc
±
=
< j2 -
= gs(j).
области, см. разд. 5.2.3.
2
2
4
Рассмотрим случай, когда |j| = k + 1. Тогда
Данные квантовые числа j отвечают несингулярной
gs(j) < g < gc(j). Такие квантовые числа j отве-
области, см. разд. 5.1.
чают субкритической области, см. разд. 5.2.1.
Рассмотрим также случай |j| = 1/2. Тогда 0 =
Рассмотрим случай |j|
> k + 1. Тогда g
<
= gs(j) < g < gc(j) = 1/2. Данные квантовые числа
< gc(k+1) < gs(k+2) ≤ gs(j), т.е. g < gs(j). Данные
j отвечают субкритической области, см. разд. 5.2.1.
квантовые числа j отвечают несингулярной области,
Таким образом, имеем
см. разд. 5.1.
{
Таким образом, имеем
U2ν,E(ρ),
|j| = 1/2,
UE(ρ) =
|E| ≥ m,
⎧
U1E(ρ),
|j| > 1/2,
⎨U4ν,E(ρ),
|j| ≤ k,
{
UE(ρ) =
U2ν,E(ρ),
|j| = k + 1,
|E| ≥ m,
U2ν,n(ρ),
|j| = 1/2,
⎩
Un(ρ) =
,
(47)
U1E(ρ),
|j| > k + 1,
U1ν,n(ρ),
|j| > 1/2,
{
⎧
⎨U4ν,n(ρ),
|j| ≤ k,
E2n(ν),
|j| = 1/2,
En =
Un(ρ) =
U2ν,n(ρ),
|j| = k + 1,
(45)
E1n(ν),
|j| > 1/2.
⎩
U1n(ρ),
|j| > k + 1,
E. Осталось рассмотреть случай g = gc(±1/2).
⎧
Рассмотрим квантовые числа |j| > 1/2. Тогда
⎨E4n(ν),
|j| ≤ k,
(
)
√
En =
E2n(ν),
|j| = k + 1,
1
1
1
⎩
g=gc
±
=
< j2 -
= gs(j).
E1n(Z, j, s),
|j| > k + 1.
2
2
4
867
7*
А. И. Бреев, Р. Феррейра, Д. М. Гитман, Б. Л. Воронов
ЖЭТФ, том 157, вып. 5, 2020
Данные квантовые числа j отвечают несингулярной
стояниям энергии En, обозначаются как UEn(ρ) =
области, см. разд. 5.1.
= Un(ρ). Все дублеты UE(ρ) и Un(ρ), а также спект-
Рассмотрим случай |j| = 1/2. Тогда g = gc(j).
ры En зависят от параметров расширения, от кван-
Данные квантовые числа j отвечают критической
товых чисел j, параметра s и константы связи g со-
области, см. разд. 5.2.2.
гласно (44)-(48). Отметим, что параметры расши-
Следовательно, имеем
рения зависят как от квантовых чисел j, так и от
{
параметра s.
U3ν,E(ρ),
|j| = 1/2,
UE(ρ) =
|E| ≥ m,
U1E(ρ),
|j| > 1/2,
{
7. СПЕКТРАЛЬНАЯ ЗАДАЧА ДЛЯ
U3ν,n(ρ),
|j| = 1/2,
Un(ρ) =
(48)
РЕГУЛЯРИЗОВАННОГО КУЛОНОВСКОГО
U1ν,n(ρ),
|j| > 1/2,
ПОЛЯ ПРИМЕСИ
{
E3n(ν),
|j| = 1/2,
En =
В этом разделе мы рассмотрим связанные состо-
E1n(ν),
|j| > 1/2.
яния и точечный спектр (для краткости в дальней-
шем будем говорить о задаче точечного спектра)
Теперь мы можем описать спектральную пробле-
для квазичастиц в графене с примесью, генериру-
му для всех с. с. дираковских гамильтонианов для
ющей электрическое поле с регуляризованным ку-
любых значений g. Отметим, что из неравенства g >
лоновским потенциалом V (ρ) вида
> gs(±1/2) = 0 и формулы (10) следует важный
Ĥs
{
факт: полный с. с. дираковский гамильтониан
1/ρ0, ρ ≤ ρ0,
не определен однозначно для любого заряда Z =
V (ρ) = -g
(49)
1/ρ, ρ ≥ ρ0.
= ϵg/αF .
Рассмотрим собственные векторы Ψsj (r) для лю-
Ĥe
Данный потенциал соответствует полю положитель-
бого с. с. дираковского гамильтониана
s
, которые
ной заряженной примеси, равномерно распределен-
удовлетворяют следующей системе уравнений (см.
ной по сферической поверхности радиуса обрезания
разд. 3):
ρ0 (рис. 7). Параметр g определен в (2).
HsΨsj(r) = E Ψsj(r),
JsΨsj(r) = j Ψsj(r),
Предположим, что примесь находится в сере-
дине шестиугольника решетки графена. Регуляри-
где собственные векторы имеют вид Ψsj (r)
=
зация (49) представляет собой ситуацию, в которой
= VsjUE(ρ), см. (7).
параметр решетки a — самое близкое расстояние,
Для любых констант связи g энергетический
на которое возможны переходы электронов между
спектр любого с. с. дираковского гамильтониана
ячейками углерода в окрестности примеси [8]. Тогда
Ĥe
содержит непрерывный спектр, занимающий
s
предположим, что радиус обрезания имеет порядок
как отрицательную, так и положительную полу-
постоянной решетки a. Для численных расчетов ис-
оси (-∞, -m] и [m, ∞), а также имеет дискретный
пользуем значение ρ0 = 0.6a.
спектр в интервале (0, m) и включает в себя беско-
Ĥreg
Дираковский гамильтониан
s
представляет
нечное число возрастающих уровней энергии, кото-
собой дифференциальный оператор в гильбертовом
рые накапливаются в точке E = m. Как и в случае
3 + 1 измерений (см. [13]), асимптотическая форма
V( )
спектра при n → ∞ задается известной нереляти-
вистской формулой:
0
0
2
mg
Enonreln = m - En =
2n2
Собственные функции ΨsjE (r), |E| ≥ m, которые со-
ответствуют непрерывной части спектра, являются
обобщенными собственными функциями оператора
V(
)
0
Ĥe
Ĥe
s
. А собственные функции ΨsjEn(r) оператора
s
соответствуют связанным состояниям энергии En и
принадлежат гильбертовому пространству H. Дуб-
Рис. 7. Регуляризованный кулоновский потенциал
леты UE (ρ), которые соответствуют связанным со-
868
ЖЭТФ, том 157, вып. 5, 2020
Спектры электронных возбуждений в графене...
пространстве H =L2(R2) (см. разд. 2), ассоциирован-
Соответствующие собственные функции Ψsj(r) опе-
ный с дифференциальным выражением
ратора
Ĥs(Z) в пространстве L2(R2) получаются
(см. (7))
при помощи унитарного преобразования Vsj
Hreg
s
= -i (sσx∂x + σy∂y) + mσz + V (ρ)
собственных функций F (ρ) оператора
ĥreg(Z, j, s) в
пространстве L2(R+).
и имеющий естественную область определения.
Точечный спектр и соответствующие собствен-
Каждый гамильтониан
Ĥs(Z) однозначно опреде-
ные функции парциального радиального гамильто-
лен как с. с. оператор для всех значений Z, так
ниана
ĥreg(Z, j, s) определяются как решения ста-
как он представляет собой сумму однозначно опре-
ционарного парциального радиального уравнения
деленного свободного дираковского гамильтониана
Шредингера:
(см. разд.
5.1) и ограниченного с. с. операто-
ра умножения на ограниченную вещественную
ĥreg(Z, j, s)F(ρ) = EF(ρ),
функцию V (ρ).
E ∈ [-m,m], F(ρ) ∈ Dh(Z,j,s).
Гамильтониан
Ĥreg
является вращательно-ин-
s
вариантным с точки зрения представления груп-
Из данного уравнения, для фиксированных Z, j и
пы вращений Us, и так же, как для кулоновс-
s следует система дифференциальных радиальных
кого поля точечного заряда (см. разд. 3), спект-
уравнений для радиальных функций f(ρ) и g(ρ):
ральная задача для точечного спектра операто-
Ĥreg
ра
s
сводится к спектральной задаче точечно-
κ
f′(ρ) +
f (ρ) - k+(ρ)g(ρ) = 0,
го спектра для парциальных радиальных гамиль-
ρ
тонианов
ĥreg(Z, j, s) с фиксированным значением
κ
g′(ρ) -
g(ρ) + k-(ρ)f(ρ) = 0,
(50)
момента j = ±1/2, 3/2, . . . Каждый парциальный
ρ
радиальный гамильтониан
ĥreg(Z, j, s) для фикси-
k±(ρ) = E - V (ρ) ± m.
рованных значений параметров Z, j и s являет-
ся с. с. оператором в гильбертовом пространст-
Система радиальных уравнений (50) должна быть
ве L2(R+) = L2(R+) ⊕ L2(R+) дублетов F(ρ) =
дополнена условием -m ≤ E ≤ m и функции f(ρ) и
= (f(ρ), g(ρ))T (функции f(ρ) и g(ρ) будем назы-
g(ρ) должны быть абсолютно непрерывны по пере-
вать радиальными функциями) и ассоциируется с
менной ρ на (0, ∞), удовлетворять нулевым гранич-
парциальным радиальным дифференциальным вы-
ным условиям в начале координат, f(0) = g(0) = 0, и
ражением
быть квадратично интегрируемыми на (0, ∞) (фак-
тически на бесконечности).
d
κ
hreg(Z, j, s) = -iσy
+
σx + V (ρ) + mσz.
При нахождении точечных спектров {En(Z, j, s)}
dρ
ρ
на отрезке -m ≤ E ≤ m необходимо рассматривать
открытый интервал -m < E < m и его конечные
Данный оператор определяется на естественной об-
точки E = m и E = -m отдельно по техническим
ласти определения для
h: область определения Dh
причинам, которые станут ясны ниже. Начнем с об-
для каждого оператора
ĥ состоит из множества аб-
ласти энергий -m < E < m.
солютно непрерывных дублетов F (ρ) на (0, ∞), об-
ращающихся в нуль в начале координат, f(0) =
= g(0) = 0, и квадратично интегрируемых вместе
с hF(ρ) на (0, ∞).
8. ДИСКРЕТНЫЙ СПЕКТР НА ИНТЕРВАЛЕ
(-m, m)
Поскольку потенциал V (ρ) убывает на бесконеч-
ности, спектр каждого парциального радиального
8.1. Решение радиальных уравнений в
гамильтониана
ĥreg(Z, j, s) состоит из непрерывной
области 0 ≤ ρ ≤ ρ0
части спектра (-∞, -m]∪ [m, ∞) и точечного спект-
ра {En(Z, j, s), n ∈ Z+}, расположенного на отрез-
Во внутренней области 0 ≤ ρ ≤ ρ0, где мы пола-
ке [-m, m]. Полный точечный спектр p.spec
Ĥreg
(Z)
s
гаем f(ρ) = fin(ρ) и g(ρ) = gin(ρ), функции k±(ρ) в
дираковского гамильтониана
Ĥreg
(Z), являющийся
s
(50) и (49) постоянны,
предметом нашего основного интереса, представля-
g
ет собой объединение точечных спектров парциаль-
k+(ρ) = k+ = E +
+ m,
ных радиальных гамильтонианов
ĥreg(Z, j, s),
ρ0
g
k-(ρ) = k- = E +
- m, E ∈ (-m, m).
p.spec
Ĥreg
(Z) = ∪j p.specĥreg(Z, j, s).
ρ0
s
869
А. И. Бреев, Р. Феррейра, Д. М. Гитман, Б. Л. Воронов
ЖЭТФ, том 157, вып. 5, 2020
В этой области первое уравнение в (50) можно пе-
где α — постоянная тонкой структуры, а параметр
реписать в виде
κ = -sj, s = ±1, j = ±1/2,±3/2,..., заменяется
[
]
на κ = ζ(j + 1/2), ζ = ±1, j = 1/2, 3, 2, . . . Общее
1
κ
gin(ρ) =
f′in(ρ) +
fin(ρ)
решение последней системы хорошо известно. В на-
k+
ρ
шем случае система уравнений (50) и (49) дополня-
ется условием, что функции fout(ρ) и gout(ρ) долж-
Тогда второе уравнение в (50) дает дифференциаль-
ны быть квадратично интегрируемыми на бесконеч-
ное уравнение второго порядка для функции fin(ρ),
ности. Тогда решение системы определяется следу-
(
)
d2fin(ρ)
ν2-1/4
ющим образом:
+ η2-
fin(ρ) = 0, ν ∈ Z+,
dρ2
ρ2
√
(
)2
2m
√
g
fout(ρ) = B
(2βρ)μe-βρ ×
η=
k+k-, k+k- = E +
-m2,
m-E
(51)
ρ0
[
]
{
× b-Ψ(a + 1, c; 2βρ) + Ψ(a, c; 2βρ) ,
1
ζ
|j|+1/2, ζ = 1,
ν =
+
|j|+
=
κ
=
√
(54)
2
2
|j|-1/2, ζ = -1.
2m
gout(ρ) = B
(2βρ)μe-βρ ×
m+E
Уравнение
(51) дополняется двумя граничными
[
]
условиями в начале координат:
× b-Ψ(a + 1, c; 2βρ) - Ψ(a, c; 2βρ) ,
[
]
κ
где
fin(0) = 0,
f′in(ρ) +
fin(ρ)
= 0,
ρ
ρ=0
√
√
β =
m2 - E2, μ =
κ2 - g2,
где последнее условие является следствием требова-
(55)
gE
gm
ния gin(0) = 0 и нетривиально только в случае ν = 0.
a=μ-
,
c = 1 + 2μ, b- = κ +
,
β
β
Для ν = 0 второе условие является следствием пер-
вого.
Ψ — стандартная конфлюэнтная гипергеометричес-
Общее решение уравнения (51), удовлетворяю-
кая функция, убывающая на бесконечности,
щее данным граничным условиям, имеет вид
см. (15).
(см. [22]):
В дальнейшем будем использовать функции
Уиттекера, см. [23],
fin(ρ) = c√ρJν (ηρ) =
{
c
c-1
J|j|+1/2(ηρ), ζ = 1,
Wλ,μ(x) = e-x/2xc/2Ψ(a, c; x), λ =
-a, μ =
,
=c√ρ
c ∈ C.
(52)
2
2
J|j|-1/2(ηρ), ζ = -1,
где новая переменная ε определяется как E
=
Используя соотношение J′ν(z)∓(ν/z)Jν(z) = ∓Jν±1(z),
= mcosε, ε = arccos(E/m) ∈ (0,π). Окончательная
см. [23], получим
форма решений системы уравнений (50) и (49) во
внешней области ρ0 ≤ ρ < ∞ имеет вид
√
gin(ρ) = c√ρ
k- ζJν-ζ(ηρ) =
(ε)
k+
fout(ρ) = B cosec
(2βρ)-1/2 ×
2
√
{
[
]
k-
J|j|-1/2(ηρ), ζ = 1,
× (g cosec ε + κ)Wλ′,μ(2βρ) + Wλ,μ(2βρ) ,
=c√ρ
(53)
k+
-J|j|+1/2(ηρ), ζ = -1.
(ε)
gout(ρ) = B sec
(2βρ)-1/2 ×
2
[
]
8.2. Решение радиальных уравнений в
× (g cosec ε + κ)Wλ′,μ(2βρ) - Wλ,μ(2βρ) ,
области ρ0 ≤ ρ < ∞
Во внешней области ρ ∈ [ρ0, ∞), где мы полага-
где
ем f(ρ) = fout(ρ), g(ρ) = gout(ρ), система уравне-
ний (50), (49) по форме идентична системе уравне-
gE
1
1
β = msinε, λ =
+
= gctgε +
,
ний в трехмерной кулоновской задаче с точечным
β
2
2
зарядом, см. [13, 16]. Единственное отличие состоит
1
λ′ = λ - 1 = g ctg ε -
в том, что параметр g = αF Z/ϵ заменяется на αZ,
2
870
ЖЭТФ, том 157, вып. 5, 2020
Спектры электронных возбуждений в графене...
E/m
8.3. Численные решения для дискретного
спектра в области (-m, m)
1.0
После того как мы нашли общее решение урав-
0.5
нений (50) в соответствующих областях 0 ≤ ρ ≤ ρ0 и
ρ0 ≤ ρ < ∞, осталось учесть условие непрерывности
0
решения в целом (т. е. сшить полученные решения),
что сводится к требованию непрерывности решения
в точке ρ = ρ0:
-0.5
fin(ρ0) = fout(ρ0), gin(ρ0) = gout(ρ0).
(56)
-1.0
Если константы c и B не равны нулю, условие сов-
0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
g
местности этих условий приводит к трансцендент-
ному уравнению, которое определяет дискретный
Рис. 8. Зависимости нижних энергетических уровней от
энергетический спектр в области (-m, m) в терми-
параметра g для j = 1/2 и s = 1
нах переменной ε,
)
(ε
Jν(ηρ0)sec
[(κ + g cosec ε)Wλ′,μ(2βρ0) -
для ζ = 1 и
2
√
√
k-
(ε)
k- J|j|+1/2(ηρ0)
(ε)
- Wλ,μ(2βρ0)] -
ζJν-ζ(ηρ0)cosec
×
+ tg
×
k+
2
k+ J|j|-1/2(ηρ0)
2
× [(κ+g cosec ε) Wλ′,μ(2βρ0)+Wλ,μ(2βρ0)] = 0,
(57)
[(- |j| + g cosec ε) Wλ′,μ(2βρ0) - Wλ,μ(2βρ0)]
×
=0
[(- |j| + g cosec ε) Wλ′,μ(2βρ0) + Wλ,μ(2βρ0)]
где k± = m(cos ε ± 1) + g/ρ0. Это базовое уравнение
будем называть спектральным уравнением для ин-
для ζ = -1.
тервала (-m, m). Строго говоря, мы имеем дело с
Результаты численных расчетов для частного
серией точных спектральных уравнений для задан-
случая j = 1/2, s = 1, который соответствует са-
ных значений Z, j и s.
мым нижним энергетическим уровням, показаны на
После решения спектрального уравнения, т.е.
рис. 8.
нахождения собственных значений En(Z, j, s) пар-
циальных радиальных гамильтонианов
ĥreg(Z, j, s),
9. СОБСТВЕННЫЕ СОСТОЯНИЯ ДЛЯ
соответствующие собственные функции Fn(Z, j, s) ∈
E = ±m
∈ L2(R+) связанных состояний гамильтонианов
ĥreg(Z, j, s) получаются путем подстановки вы-
Полученные выше результаты требуют уточне-
численных собственных значений энергии E
=
ния в точках E = m и E = -m, потому что соглас-
= En(Z, j, s)) в формулы (52)-(54) с учетом условия
но уравнениям (54) и (55) в этих точках переменная
√
сшивки (56). Так что остается неопределенность
β =
m2 - E2 обращается в нуль, тогда как коэф-
√
√
только в нормировке волновых функций (дублетов).
фициенты 1/
m - E, 1/
m + E, b- = κ + gm/β и
Аналитическое решение спектрального уравнения
параметр a = μ - gE/β расходятся. Поэтому эти
(57) для всех значений параметров Z, j и s выхо-
точки необходимо рассмотреть отдельно.
дит за рамки наших возможностей. В настоящее
время мы представляем только численное решение
9.1. Точка E = m
спектрального уравнения.
Эквивалентная форма спектрального уравнения
Достаточно исследовать соотношения (50) и (49)
(57) с некоторой фиксированной величиной ζ, кото-
при E = m во внешней области ρ0 ≤ ρ < ∞, где они
рая, возможно, более подходит для численных рас-
имеют вид
(
)
четов, имеет вид
κ
g
f′(ρ) +
f (ρ) -
2m +
g(ρ) = 0,
√
ρ
ρ
(58)
k- J|j|-1/2(ηρ0)
(ε)
κ
g
- tg
×
g′(ρ) -
g(ρ) +
f (ρ) = 0.
k+ J|j|+1/2(ηρ0)
2
ρ
ρ
[(|j| + g cosec ε) Wλ′,μ(2βρ0) - Wλ,μ(2βρ0)]
Данную систему уравнений необходимо рассматри-
×
=0
[(|j| + g cosec ε) Wλ′,μ(2βρ0) + Wλ,μ(2βρ0)]
вать в классе абсолютно непрерывных функций f(ρ)
871
А. И. Бреев, Р. Феррейра, Д. М. Гитман, Б. Л. Воронов
ЖЭТФ, том 157, вып. 5, 2020
и g(ρ), которые являются квадратично интегрируе-
9.2.1. Решения в области 0 ≤ ρ ≤ ρ0
мыми вместе с их производными на (ρ0, ∞).
Общее решение системы (60) и (49) во внутрен-
Из второго уравнения (58) находим, что функция
ней области 0 ≤ ρ ≤ ρ0, где мы полагаем f(ρ) =
g(ρ) удовлетворяет дифференциальному уравнению
= fin(ρ) и g(ρ) = gin(ρ), при указанных выше усло-
второго порядка
виях имеет вид
)
2
1
(2gm
κ2 - g
{
g′′(ρ) +
g′(ρ) +
-
g(ρ) = 0.
(59)
J|j|+1/2(η0ρ), ζ = 1,
ρ
ρ
ρ2
fin(ρ) = c√ρJν (η0ρ) = c√ρ
J|j|-1/2(η0ρ), ζ = -1,
При помощи замены g(ρ) = w(z), z = 2√2gmρ урав-
√
нение (59) приводится к уравнению Бесселя,
2mρ0
gin(r) = c√ρ 1-
ζJν-ζ(η0ρ) =
(
)
g
1
ν2
{
√
w′′(z) +
w′(z) +
1-
w(z) = 0,
2mρ
J|j|-1/2(η0ρ), ζ = 1,
z
z2
0
=c√ρ 1-
√
g
-J|j|+1/2(η0ρ), ζ = -1,
с ν = 2μ = 2
j2 - g2, 2√2gmρ0 ≤ z < ∞. Общее
√
решение данного уравнения есть w(z) = c1H(1)˜ν(z) +
где η0 = (g/ρ0)
1 - 2mρ0/g. Достаточно положить
+c2H(2)˜ν(z), где
ν (z) и
ν (z) — функции Ханке-
E = -m в (51)-(53).
ля первого и второго рода соответственно, см. [23].
Асимптотическое поведение общего решения на бес-
9.2.2. Решения в области ρ0 ≤ ρ < ∞
конечности (z → ∞) определяется соотношением
Во внешней области ρ0 ≤ ρ < ∞ мы полагаем
√
[
][
2
i
(1)]
f (ρ) = fout(ρ), g(ρ) = gout(ρ), и уравнения (60) и
w(z) = c1
exp
(4z-2πν-π)
1+O
+
πz
4
z
(49) принимают вид
√
[
][
κ
g
2
i
(1)]
f′out(ρ) +
fout(ρ) -
gout(ρ) = 0,
+c2
exp -
(4z-2πν-π)
1+O
ρ
ρ
πz
4
z
(
)
(61)
κ
g
Из второго уравнения (58) следует, что асимптоти-
g′out(ρ) -
gout(ρ)-
2m -
fout(ρ) = 0.
ρ
ρ
ческое поведение обеих функций f(ρ) и g(ρ) на бес-
конечности оценивается как f(ρ) = O(ρ-1/4), g(ρ) =
Мы накладываем на функции fout(ρ) и gout(ρ) усло-
вие абсолютной непрерывности и квадратичной ин-
= O(ρ-1/4), ρ → ∞, так что обе функции не яв-
тегрируемости вместе с их производными на интер-
ляются квадратично интегрируемыми на бесконеч-
вале (ρ0, ∞).
ности. Это означает, что система уравнений (58) не
С учетом уравнения (61) получим
имеет квадратично интегрируемых решений и, сле-
довательно, не существует связанных состояний с
1
энергией E = m, т. е. с нулевой энергией связи. То
f ′′out(ρ) +
f ′out(ρ)-
ρ
же справедливо и для фермиона как в регуляризо-
2gm
κ2 - g2
ванном кулоновском поле произвольного заряда Z с
-
fout(ρ) -
fout(ρ) = 0.
(62)
ρ
ρ2
обрезанием (49), так и в кулоновском поле точечно-
го заряда.
Подстановка fout(ρ) = w(z), z = 2√2gmρ приво-
дит (62) к модифицированному уравнению Бесселя,
см. [23],
9.2. Точка E = -m
(
)
2
1
ν
Система радиальных уравнений (50) для связан-
w′′(z) +
w′(z) -
1+
w(z) = 0,
z
z2
ных состояний с E = -m, т. е. с энергией связи 2m,
√
√
имеет вид
ν = 2μ = 2
j2 - g2,
2
2gmρ0 ≤ z < ∞.
κ
f′(ρ) +
f (ρ) + V (ρ)g(ρ) = 0,
Из требования квадратичной интегрируемости
ρ
(60)
функции fout(ρ) на бесконечности получаем
κ
g′(ρ) -
g(ρ) - [V (ρ) + 2m] f(ρ) = 0.
fout(ρ) = AKν(z), где Kν(z) — функция Макдо-
ρ
нальда,
При этом требуется абсолютная непрерывность
π
Kν(z) =
[I-ν(z) - Iν(z)] ,
ν=n∈Z+,
функций f(ρ) и g(ρ) вместе с их первыми произ-
2 sinπν
водными, квадратичная интегрируемость на (0, ∞)
∑
(z/2)2m+ν
и обращение данных функций в нуль в начале
Iν(z) =
,
Kν(z) = K-ν(z).
m!Γ(m + ν + 1)
координат, f(0) = 0, g(0) = 0.
m=0
872
ЖЭТФ, том 157, вып. 5, 2020
Спектры электронных возбуждений в графене...
Для ν = n ∈ Z+ функции Kn(z) содержат члены с
Существует бесконечная возрастающая последова-
логарифмическим множителем, см. [23].
тельность {gn-m)(j, s), n ∈ N}, gn-m)(j, s) → ∞ при
Таким образом, мы получили общее решение
n → ∞, корней данного уравнения для любых фик-
уравнений (61):
сированных значений параметров j и s, см. [16]. Дан-
√
ной бесконечной последовательности соответству-
fout(ρ) = AKν(z), z = 2
2gmρ,
ет бесконечная возрастающая последовательность
[
]
-1
A
z d
{Zn-m)(j, s) = α
ϵ gn-m)(j, s), n ∈ N} зарядов Z.
F
gout(ρ) =
Kν(z) + κKν(z)
=
g
2 dz
Мы определяем сверхкритический заряд
{
}
A
z
Zscr(j, s) для каждой пары параметров j и s
=
-
[Kν-1(z) + Kν+1(z)] + κKν(z)
,
как целое число, ближайшее к Z1(j, s) (первое сла-
g
4
гаемое в последовательности {Zn-m)(j, s), n ∈ N})
где воспользовались известным соотношением
сверху:
Kν-1(z) + Kν+1(z) = -2K′˜ν(z) (см. [23]).
{
[Z1(j, s)] + 1, Z1(j, s) ∈ N,
Zscr(j, s) =
10. СВЕРХКРИТИЧЕСКИЕ ЗАРЯДЫ
Z1(j, s), Z1(j, s) ∈ N,
После того как общее решение системы (60) най-
Z1(j, s) = (α-1Fϵ)g(-m)1(j, s),
дено в соответствующих областях 0 ≤ ρ ≤ ρ0 и
где скобки [. . .] обозначают целую часть веществен-
ρ0 ≤ ρ < ∞, остается выполнить основное условие
ного числа.
непрерывности решения в целом (другими словами,
Мы считаем, что сверхкритический заряд опре-
гладко сшить парциальные решения), которое сво-
деляется минимумом всех зарядов Zn-m)(j, s), кото-
дится к требованию непрерывности решения в точке
рый достигается, когда j = 1/2 и s = 1:
ρ=ρ0,
{
fin(ρ0) = fout(ρ0), gin(ρ0) = gout(ρ0).
(63)
[Z1(1/2, 1)] + 1, Z1(1/2, 1) ∈ N,
Zscr =
(1/2, 1) ∈ N.
Z1(1/2, 1), Z1
Вместе с условиями c = 0, A = 0 равенство (63) дает
уравнение
Соответствующую константу связи gscr = g(-m)1 ×
{
z0
× (1/2, 1) будем называть сверхкритической кон-
Jν(η0ρ0)
-
[Kν-1(z0) + Kν+1(z0)] +
4
стантой связи.
}
+ κKν(z0)
-(η0ρ0)ζJν-ζ (η0ρ0)Kν(z0) = 0,
Стоит отметить, что сверхкритические заряды
(64)
√
зависят от регуляризации кулоновского поля, т. е.
2mρ0
√
η0ρ0 = g
1-
,
z0 = 2
2gmρ0,
сверхкритические заряды зависят от рассматрива-
g
емой модели. И кроме того, они зависят от парамет-
которое можно рассматривать как уравнение для
ров αF и ϵ.
констант связи g, определяющее связанные состоя-
Для определения gn-m)(1/2, 1) удобно предста-
ния с энергией E = -m. Константы связи, удовле-
вить уравнение (65) в виде φ(g) = 0,
творяющие данному уравнению, будем обозначать
J1(η0ρ0)
как g(-m)(j, s).
φ(g) = (η0ρ0)
-
J0(η0ρ0)
Найти аналитическое решение g(-m)(j, s) урав-
]
нения (64) для произвольных значений j и s в на-
[z0 [K˜ν-1(z0) + K˜ν+1(z0)]
1
-
+
,
стоящее время вряд ли возможно. Мы можем только
4
Kν(z0)
2
провести его качественный анализ и решать числен-
√
но.
где ν =
1 - 4g2.
Эквивалентная форма уравнения (64), более под-
Результаты численных расчетов представлены
ходящая для качественного анализа и численного
на рис. 9. Приведем также первые несколько зна-
решения, имеет вид
чений gn-m)(1/2, 1):
{
ζJν-ζ(η0ρ0)
(η0ρ0)
+
{g(-m)n(1/2, 1)} =
0.54731, 0.767737, 1.05737,
Jν(η0ρ0)
]
}
[z0 K˜ν-1(z0) + K˜ν+1(z0)
+
- κ = 0.
(65)
1.35964, 1.65711, . . .
,
(66)
4
Kν(z0)
873
А. И. Бреев, Р. Феррейра, Д. М. Гитман, Б. Л. Воронов
ЖЭТФ, том 157, вып. 5, 2020
экспериментально с помощью метода сканирующей
туннельной микроскопии [24]. Важность расчетов в
20
графене с кулоновскими примесями подтверждает-
ся результатами работы [9], где было показано, что в
10
отличие от недопированного графена имеются суще-
ственные различия в поведении локальной плотнос-
0
ти состояний вблизи границы положительного кон-
-10
тинуума.
Интересно отметить, что в нашей задаче крити-
-20
ческая константа связи gc(±1/2) = 1/2 и нижняя
(±1/2) = 0, тогда
критическая константа связи gs
0
0.5
1.0
1.5
2.0
как в трехмерном случае они равны gc(1/2) = 1,
g
√
gs(1/2) =
3/2. Кроме того, из-за большого значе-
Рис. 9. Графическое решение уравнения (65)
ния постоянной тонкой структуры в графене, αF ≈
≈ 2.2, критическое значение заряда примеси мало:
Zc = Zc(±1/2) ≈ 1, что открывает возможность про-
для m = 0.26 эВ. Последовательность (66) соответ-
верки сверхкритической нестабильности в графене
ствует последовательности {Zn-m)(1/2, 1)}. Таким
[7]. Действительно, атомный коллапс в графене на-
образом, мы получаем, что
блюдался экспериментально и описан в работе [25].
В отличие от трехмерного случая, в рассматри-
gscr = g(-m)1(1/2, 1) = 0.54731.
ваемой задаче для всех значений заряда примеси со-
ответствующие с. с. гамильтонианы не определены
однозначно. Напомним, что дираковский гамильто-
11. ЗАКЛЮЧЕНИЕ
ниан для электрона в кулоновском поле в трех изме-
рениях определяется однозначно для Z ≤ 118. Отме-
В результате решения спектральных задач для
тим, что переход через критическое значение заряда
электронных возбуждений в графене в присутствии
не приводит к каким-либо качественным изменени-
точечных кулоновских примесей показано, что с ма-
ям в математическом описании системы.
тематической точки зрения нет проблем в вычисле-
Следует отметить, что в работе [26] спектр свя-
нии с. с. гамильтонианов, которые определяют энер-
занных состояний низкоэнергетических возбужде-
гетические спектры и соответствующие полные на-
ний в допированном графене с заряженной приме-
боры собственных функций для любого заряда при-
сью изучался без убедительного анализа асимптоти-
меси. Построены семейства всех возможных с. с. га-
ческого поведения волновых функций, основанного
мильтонианов, которые параметризуются парамет-
на правильном построении соответствующего с. с.
рами расширения. Общая теория описывает все воз-
дираковского гамильтониана. Кроме того, в работе
можности, которые математика предоставляет фи-
[27] рассмотрены с. с. дираковские гамильтонианы
зику на выбор. При этом физическая интерпретация
с кулоновским полем в сочетании с полем Аароно-
выбора с. с. расширений является чисто физической
ва - Бома в 2+1 и их спектральный анализ. Однако
проблемой.
в этой работе не были приняты во внимание особен-
Вычислены уровни энергии и соответствующие
ности данной задачи в графене. Из-за этого ради-
(обобщенные)собственные функции для любого за-
альные гамильтонианы, которые рассматривались в
ряда примеси (см. (44)-(48)). Для несингулярной об-
данной работе, параметризованы особым образом,
ласти (g ≤ gs(j)) энергетические уровни и норми-
что не позволяет отождествлять их с соответствую-
рованные (обобщенные) собственные функции бы-
щими гамильтонианами реальной задачи в графене.
ли получены в (26) и (27), (28) соответственно. Для
Более того, случай, когда дополнительное внешнее
субкритической области (gs(j) < g < gc(j)) они по-
поле (поле Ааронова - Бома) равно нулю, который
лучены в (30), (31), для критической области (g =
необходим для возможного сравнения, не был изу-
= gc(j)) — в (36), (37), для сверхкритической облас-
чен и представляется нетривиальной задачей.
ти (g > gc(j)) — в (40), (41).
Исследуя спектральную задачу в графене в при-
Подчеркнем, что полученные собственные функ-
сутствии примеси с регуляризованным кулоновским
ции можно использовать для расчета локальной
потенциалом (см. разд. 7), мы нашли так называе-
плотности состояний, которая может быть измерена
мые сверхкритические заряды, для которых самые
874
ЖЭТФ, том 157, вып. 5, 2020
Спектры электронных возбуждений в графене...
низкие уровни энергетических спектров достигают
ЛИТЕРАТУРА
значения -m. Формально (см. обсуждение в [16], где
1.
G. W. Semenoff, Phys. Rev. Lett. 53, 2449 (1984).
изучался соответствующий трехмерный случай, и в
[28, 29]) это может указывать на то, что для таких
2.
J. S. Goldstein, Phys. Rev. 91, 1516 (1953); P. I. Fo-
зарядов вакуум становится нестабильным относи-
min, V. P. Gusynin, V. A. Miransky et al., Rivista
тельно возможного создания пар. Также это может
Nuovo Cim. 6, 5 (1983); N. Setŏ, Progr. Theor. Phys.
указывать на то, что задача становится многочас-
Suppl. 95, 25 (1988).
тичной, и поэтому одночастичная релятивистская
3.
A. E. Shabad and V. V. Usov, Phys. Rev. Lett. 96,
квантовая механика, основанная на гамильтониане
180401 (2006); Phys. Rev. D 73, 125021 (2006).
Дирака, терпит неудачу. Тогда вычислений в рам-
ках последней модели может быть недостаточно для
4.
S. P. Gavrilov, D. M. Gitman, and N. Yokomizo,
утверждений о существовании реальных физичес-
Phys. Rev. D 86, 125022 (2012).
ких эффектов, таких как рождение частиц. Поэтому
5.
N. Vandecasteele, A. Barreiro, M. Lazzeri et al., Phys.
мы считаем, что проблема рождения электрон-по-
Rev. B 82, 045416 (2010).
зитронных пар из вакуума сверхкритическим ку-
лоновским полем еще далека от своего решения.
6.
K. Nomura and A. H. MacDonald, Phys. Rev. Lett.
Вот почему мы не можем принять заключение ра-
98, 076602 (2007).
боты [15] о том, что реальное рождение электрон-
7.
V. N. Kotov, B. Uchoa, V. M. Pereira et al., Rev.
позитронных пар регуляризованным сверхкритиче-
Mod. Phys. 84, 1067 (2012).
ским кулоновским полем невозможно.
8.
V. M. Pereira, V. N. Kotov, and A. C. Neto, Phys.
Заметим, что уравнение (65), которое определя-
Rev. B 78, 085101 (2008).
ет сверхкритическую константу связи gscr, имеет
9.
W. Zhu, Z. Wang, Q. Shi et al., Phys. Rev. B 79,
решения только для gscr > gc(±1/2) = 0.5. Для
155430 (2009).
ρ0
= 0.6a и m = 0.26 эВ мы получили gscr
=
= 0.54731, что соответствует небольшим значениям
10.
E. V. Gorbar, V. P. Gusynin, and O. O. Sobol, Low
заряда Zscr ≃ Zc ≃ 1 для диэлектрической про-
Temp. Phys. 44, 371 (2018).
ницаемости в диапазоне ϵ ≈ 2.4-5. Таким образом,
даже после регуляризации сверхкритический заряд
11.
O. V. Gamayun, E. V. Gorbar, and V. P. Gusynin,
Phys. Rev. B 80, 165429 (2009).
совпадает с критическим зарядом для случая ку-
лоновского поля точечного заряда. Отметим, что в
12.
B. L. Voronov, D. M. Gitman, and I. V. Tyutin,
трехмерном случае для регуляризованного кулонов-
Theor. Math. Phys. 150, 34 (2007).
ского потенциала сверхкритический заряд Zscr =
13.
D. M. Gitman, I. V. Tyutin, and B. L. Voronov,
= 174 больше соответствующего критического за-
Self-adjoint Extensions in Quantum Mechanics:
ряда Zc = 138 [16].
General Theory and Applications to Schrödinger and
Заметим, что в работах
[10, 11] использова-
Dirac Equations with Singular Potentials, Birkäuser,
New York (2012).
лась та же регуляризация для кулоновского поля
примесей, и уравнение для спектра (с точностью
14.
D. M. Gitman, A. D. Levin, I. V. Tyutin et al., Phys.
до обозначений) в случае s = 1 имеет вид (57).
Scripta 87, 038104 (2013).
Однако результаты численных расчетов относятся
15.
V. M. Kuleshov, V. D. Mur, N. B. Narozhny et al.,
к другим физическим параметрам, чем в нашей
Phys. Usp. 58, 785 (2015).
работе. Кроме того, расчеты критического заряда
проводились только в нулевом пределе параметра
16.
B. L. Voronov, D. M. Gitman, A. D. Levin et al.,
обрезания. Отметим, что изучение критических
Theor. Math. Phys. 187, 633 (2016).
зарядов, аналогичное настоящей работе, было пред-
17.
J. González, F. Guinea, and M. A. H. Vozmediano,
принято в работах [8, 9], где, однако, дискретный
Nucl. Phys. B 424, 595 (1994).
спектр не исследовался.
18.
T. Ando, J. Phys. Soc. Japan 75, 074716 (2006).
Финансирование. Исследование выполнено за
19.
H . Raza (Ed.)Ģraphene Nanoelectronics. Metrology,
счет гранта Российского научного фонда (проект
Synthesis Properties, and Applications, Springer,
№19-12-00042).
New York (2012).
875
А. И. Бреев, Р. Феррейра, Д. М. Гитман, Б. Л. Воронов
ЖЭТФ, том 157, вып. 5, 2020
20. N. I. Akhiezer and I. M. Glazman, Theory of Linear
25. Y. Wang, V. W. Brar, A. V. Shytov et al., Nat. Phys.
Operators in Hilbert Space, Pitman, Boston (1981).
8, 653 (2012).
21. A. I. Akhiezer and V. B. Berestetskii, Elements of
26. K. S. Gupta and S. Sen, Phys. Rev. B 78, 205429
Quantum Electrodynamics, Israel Program for Sci.
(2008).
Tr., London (1962).
22. I. S. Gradshteyn and I. M. Ryzhik, Tables of Integrals,
27. V. R. Khalilov and K. E. Lee, Theor. Math. Phys.
Series, and Products, Acad. Press, San Diego (2014).
169, 1683 (2011).
23. A.
Érdelyi, W. Magnus, F. Oberhettinger et al., Hig-
28. V. S. Popov, Sov. J. Nuc. Phys. USSR 12, 235 (1971);
her Transcendental Functions, Vol. 2, McGraw-Hill,
Sov. Phys. JETP 60, 1228 (1971).
New York (1953).
24. M. I. Katsnelson, Graphene: Carbon in Two Dimen-
29. Ya. B. Zel’dovich and V. S. Popov, Sov. Phys. Usp.
sions, Cambridge Univ. Press, New York (2012).
14, 673 (1972).
876